Radiation protraction schedules for low-grade gliomas: a comparison between different mathematical models

Abstract

We optimize radiotherapy (RT) administration strategies for treating low-grade gliomas. Specifically, we consider different tumour growth laws, both with and without spatial effects. In each scenario, we find the optimal treatment in the sense of maximizing the overall survival time of a virtual low-grade glioma patient, whose tumour progresses according to the examined growth laws. We discover that an extreme protraction therapeutic strategy, which amounts to substantially extending the time interval between RT sessions, may lead to better tumour control. The clinical implications of our results are also presented.

1. Introduction

Diffuse WHO grade II gliomas, commonly referred to as low-grade gliomas (LGGs), are a histologically and genetically heterogeneous subgroup of primary central nervous system tumours. They encompass approximately 5–10% of all primary brain tumours in adults and have a moderate incidence rate (about 1/100 000 person-year). Compared with high-grade gliomas (WHO grades III and IV), they occur mostly in patients between ages 35 to 44 years and have a median survival time of approximately 13 years after diagnosis using aggressive treatments [1]. LGGs also account for the majority of pediatric central nervous system tumours [2]. The 2016 WHO classification [3] redefines grade II gliomas with respect to morphological and molecular tumour alterations, the latter ones displaying a higher correlation with prognosis and therapy response [4]. Although primary brain tumours very rarely metastasize, approximately 70% of LGGs eventually progress towards a more malignant type such as anaplastic astrocytoma (WHO grade III) and secondary glioblastoma (WHO grade IV glioma), thus becoming fatal. This is specifically observed in those of astrocytic origin (oligodendrocytic being the other origin). Therefore, different therapeutic modalities are required at a certain point, which usually involve neurosurgery, radiotherapy (RT), chemotherapy or a combination of these [1].

Management of LGGs is controversial because they very often remain indolent during a significant fraction of their natural history. This is due to a relatively slow proliferation coupled with a mild diffusively infiltrative pattern, and so, owing to the brain’s plasticity, functionalities affected by the presence of the tumour may partially be relocated to healthy regions, thus causing subtle neurological symptoms, whose severity does not manifest until tumour cell density exceeds some threshold. When this last process occurs a malignant transformation is triggered, whose median time after diagnosis ranges from 2.7 to 5.4 years [5]. Recent evidence supports that the early use of surgery results in a better outcome than the traditionally followed ‘watch and wait’ approach [6]. Equally, although treatment administration is usually aimed at the total elimination of tumour cells, most LGGs are rarely completely curable. Thus, current treatment focuses on increasing the patient’s survival time, diminishing symptoms and reducing harmful side effects that affect a patient’s quality of life.

It is now well known that immediate RT after surgery increases the duration of response (progression-free survival), but does not seem to improve overall survival [1]. The standard RT treatment involves administration of a total dose of 54 Gy distributed over the course of six weeks (typically 1.8 Gy daily doses, five days per week). Toxicity associated with RT constitutes an important constraint. The most frequent side effects include fatigue, weakness, skin disorders, inflammation of the irradiated area, immunodeficiency, nausea, drowsiness and dizziness [7,8]. In addition, in the medium and long term, cognitive impairment eventually occurs due to damage of the normal brain parenchyma tissue. Although, in clinical practice, radiation beams are intensity modulated and distributed in such a way as to be primarily focused onto the tumour area, healthy tissue cells are also affected to some extent. The toxicity of, and tolerance to, RT on healthy tissue has been reviewed in detail [9], and those of the central nervous system entail severe risks for health when reaching certain dose levels. Specifically, for the brain, a maximum dose below 60 Gy implies a probability of 3% necrosis [10]. This is the reason why in clinical practice this maximum total dose is not normally exceeded.

Mathematical modelling has the potential to help in identifying LGG patients who may benefit from RT and in developing specific optimal fractionation schemes for selected patient subgroups. Most of the mathematical research on gliomas has been focused on the study of high-grade gliomas, with special emphasis on glioblastoma [11–24]. Models specifically devoted to LGG growth have also been proposed [25–31]. The theoretical approaches have resorted to either ordinary or partial (reaction–diffusion-type) differential equations. The effect of RT alone or with chemotherapy on gliomas has also been studied, both in LGGs and high-grade gliomas [15,32–41]. In LGGs, response to different therapeutic modalities is often described in terms of a number of undetermined parameters that can be fitted to individual patient data, with good qualitative agreement [35]. More recently, in [39], a simple spatial model was developed to describe the known phenomenology of the response of LGGs to RT including the clinical observations from [42]. An alternative explanation to the phenomenon has been put forward in [37] using a model that included tumour and oedema compartments.

As mentioned above, the total maximum dose with which the brain can be irradiated is not administered in a single session, but is fractionated into several (typically 30) smaller doses. One particular dose strategy, known as extended (or protracted) therapy, consists of increasing the time between doses. Extended therapy is especially suitable for LGGs. This is due to the fact that it allows the healthy tissue to recover in the time that elapses between doses, since this time is considerably longer than the time between doses of a standard scheme. In addition, some studies have shown that in LGGs, at any time, most tumour cells are not proliferating [43], and therefore they would be considerably less sensitive to RT. This fact suggests that a greater spacing between doses would achieve greater efficacy of the treatment. We seek to address the veracity of this hypothesis through in silico modelling. Specifically, in [40], the authors proposed that an ‘extreme protraction’ therapeutic strategy (i.e. substantially enlarging the time interval between RT fractions) could lead to better tumour control. They based their dose scheduling assuming a logistic tumour growth law (without including any spatial dependence). One of the objectives of the present article is to generalize this strategy to other growth laws and to also incorporate the role of space.

Our plan in this paper is as follows. First, in §2, we establish the methods. Thus, we formulate the mathematical model and we establish the optimization problem for different tumour growth laws (exponential, Gompertz, logistic, Skellam and Fisher–Kolmogorov equation). In §3, we solve the previous problems, finding the optimal therapeutical protocols and discuss the expected gain as a function of the parameters for each equation. Explicit formulae are found providing the spacing between doses as a function of the biological parameters of the tumour. Moreover, we suggest a suboptimal protocol that could be easily applied in clinical practice as it does not depend on the values of the parameters or the growth law. Finally, in §5, we discuss the biological implications of our results and summarize our conclusions.

2. Methods

2.1. Formulation of the mathematical model

Tumour growth modelling can be tackled at various levels. One first, very simple, approach is to focus on the temporal evolution of the tumour volume (or its total mass) and, thus, one could employ well-known ordinary differential equations (ODEs) that essentially incorporate the role of proliferation and competition for resources, as reviewed in [44,45]. For LGGs, this is a possible path to follow to partially circumvent the complexities associated with their spatial heterogeneity (which is, nonetheless, much lower than in high-grade gliomas). In the present work, we are interested in maintaining the approach sufficiently simple but, at the same time, to capture one key physiopathological aspect of LGGs, their cellular density, as this plays a prominent role in their malignant progression. To this end, we begin by considering a non-negative function u = u(t) that represents a cell density at time t ≥ 0 that has been spatially averaged over a sufficiently large domain that includes the tumour region. The dynamics of u(t) is governed by the following ODE:

$$\frac{\text{d}u}{\text{d}t}=\frac{\rho }{\alpha }u[1-\hspace{0.17em}{\left(\frac{u}{K}\right)}^{\alpha }],u(0)=u_1,$$ 2.1

where ρ and K denote the proliferation rate and the tissue carrying capacity, respectively, and α ⩾ 0 is a parameter that accounts for the crowding effect strength, with respect to K (the maximum cell density). The explicit solution of equation (2.1) can be found in appendix A.

Critically, the solution of (2.1) takes specific forms under certain limits. Specifically, these are:

• (i)
  exponential growth

  $$K\to \mathrm{\infty }\hspace{0.17em}\Rightarrow \hspace{0.17em}u(t)=u_1{\text{e}}^{\rho t},$$ 2.2
• (ii)
  Gompertz growth

  $$\alpha \to 0\hspace{0.17em}\Rightarrow \hspace{0.17em}u(t)={\text{e}}^{\log (u_1)\hspace{0.17em}{\mathrm{e}}^{-\rho t}},$$ 2.3
• (iii)
  logistic growth

  $$\alpha \to 1\hspace{0.17em}\Rightarrow \hspace{0.17em}u(t)=\frac{u_1}{u_1+\hspace{0.17em}{\text{e}}^{-\rho t}(1-u_1)}.$$ 2.4

See figure 1 for a comparison of the growth curve forms.

Figure 1.

Comparing the considered growth curves; see legend for details. The values of the parameters are ρ = 0.007 and u₁ = 0.1. (Online version in colour.)

To further include spatial effects during LGG progression we define a n-dimensional spatial domain, B, with boundary ∂B and we will use diffusive–proliferative models, such as the Skellam model and the Fisher–Kolmogorov equations (see [11,13,27,39,46–49]), which are given, respectively, by

$$\begin{array}{rl}& u_t=D\mathrm{\Delta }u+\rho u,u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in B\\ & \mathbf{n}\cdot \mathrm{\nabla }u=0,\mathbf{x}\in \mathrm{\partial }B\end{array}\}$$ 2.5

and

$$\begin{array}{rl}& u_t=D\mathrm{\Delta }u+\rho u(1-u),u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in B\\ & \mathbf{n}\cdot \mathrm{\nabla }u=0,\mathbf{x}\in \mathrm{\partial }B,\end{array}\}$$ 2.6

where D and ρ are the diffusion and proliferation coefficients, respectively, and n is the unit normal vector to the boundary, ∂B. Namely, in each case, the domain has zero-flux boundary conditions, meaning that no tumour cells are able to leave the domain in accordance with the fact that gliomas very rarely metastatize. Note that u still represents a tumour cell density, albeit with no spatial averaging.

The explicit solution of equation (2.5) is shown in appendix A, whereas, for the Fisher–Kolmogorov model (2.6), we resort to numerical methods to calculate the solution, although, for a one-dimensional spatial scenario, it would alternatively be possible to apply the effective particle method to this equation, as described in [27]. The biological and clinical parameters used throughout this paper are summarized in table 1.

Table 1.

Values of the biological and clinical parameters used in this study. The cell densities are expressed in units of the carrying capacity K.

variable	description	values	references
ρ	proliferation rate	0.003–0.01 d−1	[26]
D	diffusion coefficient	0.0025–0.02 mm2 d−1	[50]
d	dose per fraction	1.8 Gy	[51]
N	total number of doses	30	[43]
S	survival fraction	0.8–0.9	[39]
u1	initial cell density	0.01–0.3	etimated
u*	critical cell density	0.3–0.6	estimated

Finally, these different kinetics between equations (2.2), (2.3), (2.4), (2.5) and (2.6) could indicate different LGG conditions in different patients.

2.2. Optimization problem

Damage to both cancer and normal tissues caused by ionizing radiation can be estimated using the standard linear–quadratic model [52],

$$S(d_{\hspace{0.17em}j})={\text{e}}^{-{\alpha }_i{d}_{\hspace{0.17em}j}-{\beta }_i{d}_{\hspace{0.17em}j}^2},$$ 2.7

where d_j is the radiation dose given at time t_j and the parameters α_i and β_i (i = t, n) are, respectively, the linear and quadratic coefficients for tumour (i = t) and normal (i = n) cell damage. Thus, S(d_j) corresponds to the survival fraction of cells that are not damaged by RT.

In our specific investigation into LGG, our goal is to optimize the treatment strategy in order to delay the malignant transformation of tumour into a high-grade glioma, while controlling the disease symptoms. Thus, we design the therapy to maintain the tumour density, given by equations (2.2)–(2.6), below a critical level u_* for the longest time possible, i.e. to find the time, T_mt, as large as possible, such that

$$u(t)\le u_{\ast },\mathrm{\forall }t\in (0,T_{\mathrm{mt}}],$$ 2.8

for equations (2.2)–(2.4) and

$$\underset{\mathbf{x}\in B}{max}u(\mathbf{x},t)\le u_{\ast },\mathrm{\forall }t\in (0,T_{\mathrm{mt}}],$$ 2.9

for equations (2.5) and (2.6). We call T_mt the ‘time to malignant transformation’. This general approach was previously considered in [40].

We solve this optimization problem for the number of doses N, irradiation times ${\{t_{\hspace{0.17em}j}\}}_{\hspace{0.17em}j=1}^N$ and doses ${\{d_{\hspace{0.17em}j}\}}_{\hspace{0.17em}j=1}^N$. Specifically, we fix the number of radiation doses to N = 30 and doses per fraction to d_j = 1.8 Gy, which are typical values for most extended RT protocols for these tumours. Thus, our only optimization parameter will be the time spacing between doses. Henceforth, we will consider only the case when doses are equispaced:

$$\mathrm{\Delta }=t_{\hspace{0.17em}j+1}-t_{\hspace{0.17em}j}.$$

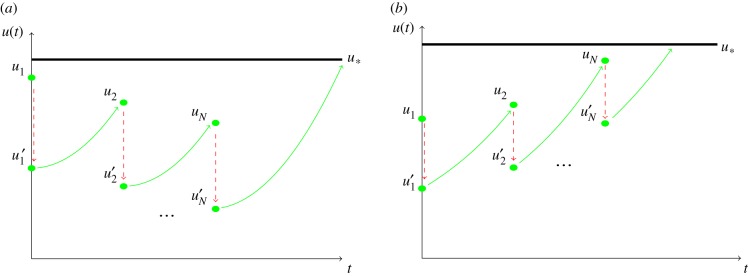
In figure 2, we present the situation where there is a uniform schedule of fractionated irradiation, i.e. the first fraction is given on day zero, the second fraction on day Δ, the third on day 2Δ and so on, with the Nth fraction being given on day (N − 1)Δ. Define u₁, u₂, …, u_N to denote the tumour cell density immediately before the administration of RT and u₁′, u₂′, …, u_N′ the tumour cell density immediately after RT, i.e.

$$u_i^{\prime }(t^{+})=S{u}_i(t^{-}),i=1,2,\dots ,$$ 2.10

where S is the survival fraction for each of the given doses, and t⁻ (and t⁺) denotes the time just before (just after) the irradiation that takes place at time t. Figure 2 illustrates these facts. Finally, we define the improvement in time to malignant transformation as the time to malignant transformation for the optimal spacing between doses Δ_Opt, T_mt(Δ_Opt), minus the time to malignant transformation for the ‘standard’ choice Δ = 1, T(1):

$$\mathrm{\Delta }{T}_{\mathrm{mt}}=T_{\mathrm{mt}}({\mathrm{\Delta }}_{\mathrm{Opt}})-T(1).$$ 2.11

See figures 3–7 for a better understanding of these concepts.

Figure 2.

Different scenarios for the response of the tumour to radiotherapy. (a) The therapy provides a net decrease of the tumour amplitude between doses and the maximum is reached after the treatment is completed. (b) The tumour continues growing during the therapy. (Online version in colour.)

Figure 3.

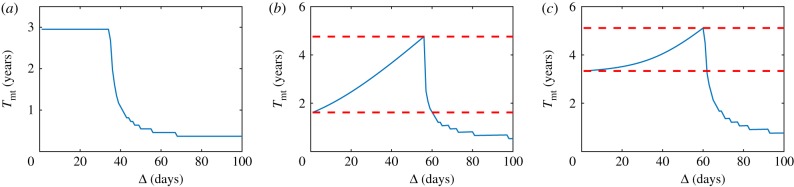
T_mt given for (a) exponential growth with ρ = 0.005, (b) Gompertz growth with ρ = 0.003756 and (c) logistic growth with ρ = 0.004. Global parameters for all scenarios are u₁ = 0.3, u_* = 0.5 and S = 0.85. These behaviours correspond to equations (2.2)–(2.4), respectively. Red dashed lines indicate T_mt gain for optimal spacing versus unit spacing. In particular, upper and lower red dashed lines correspond to T_mt(Δ_Opt) and T(1), respectively (see equation (2.11)). (Online version in colour.)

Figure 7.

(a) Prediction of the time to the malignant transformation given by the Fisher–Kolmogorov equation in one dimension for different spacing between doses for D = 0.0025 mm² d⁻¹. (b) Prediction of the time to malignant transformation given by the Fisher–Kolmogorov equation in one dimension for different spacing between doses and different values of the diffusion coefficient. For all the simulations, the values of the parameters used were S = 0.85, u₁ = 0.3, u_* = 0.5, ρ = 0.005 d⁻¹ and σ = 10 mm². Upper and lower red dashed lines correspond to T_mt(Δ_Opt) and T(1), respectively (see equation (2.11)). (Online version in colour.)

3. Results

Here, we simply state the final formulae, which we use and illustrate. Full derivation details can be found in appendix B.

3.1. Results for proliferative models

3.1.1. Exponential model

We start our results with the simplest case: the exponential growth model. Solving explicitly equation (2.2) and using the recursion formula (2.10), we get a recursive equation providing the tumour density after every dose (figure 3a). Thus, the time to malignant transformation is given by

$$T_{\mathrm{mt}}(\mathrm{\Delta })=(N-1)\mathrm{\Delta }+\frac{1}{\rho }\log \hspace{0.17em}\left(\frac{u_{\ast }}{u_N^{\prime }}\right),$$ 3.1

with u′_N given by equation (B 6) with j = N.

It is straightforward to check that, except for an interval of measure zero,

$$\frac{\text{d}{T}_{\mathrm{mt}}(\mathrm{\Delta })}{\text{d}\mathrm{\Delta }}=0,\mathrm{\forall }\mathrm{\Delta }>0.$$

Thus, for the exponential model, the change in temporal spacing between doses does not represent any gain in time to malignant transformation with respect to standard therapy (figure 3a).

3.1.2. Gompertz model

Solving equation (2.3) and using the recursion formula, as in the previous case, we get a recursive equation providing the tumour density after every dose d_j (figure 3b). The time to malignant transformation is, thus,

$$T_{\mathrm{mt}}(\mathrm{\Delta })=(N-1)\mathrm{\Delta }+\frac{1}{\rho }\log \hspace{0.17em}\left(\frac{\log (u_N^{\prime })}{\log (u_{\ast })}\right),$$ 3.2

with u′_N given by equation (B 11) when j = N.

As in the previous case, it is straightforward, but tedious, to derive dT_mt(Δ)/dΔ (see equation (B 14)). However, we note that dT_mt(Δ)/dΔ is positive for the values of the parameters considered in the present work, which means that the optimum value for Δ within this interval is reached exactly on its border (figure 3b), where the border is defined as the largest value of Δ for which the therapy is completed before the tumour reaches the critical value u_*. Hence, we derive

$${\mathrm{\Delta }}_{\mathrm{opt}}\approx -\frac{1}{\rho }\log \hspace{0.17em}\left(\frac{\log u_{\ast }}{\log S{u}_{\ast }}\right).$$ 3.3

Equation (3.3) provides a simple solution to the Gompertz model optimization problem, which is quite accurate in the range of parameters of interest.

3.1.3. Logistic model

As previously mentioned, the optimization for the logistic model was studied in [40]. Here, we briefly discuss this result to make our study self-contained (figure 3c). In the range of parameters of interest $(0<u_1<u_{\ast }<S<1)$ and for N ≫ 1, it is possible to find an approximation of Δ_opt:

$${\mathrm{\Delta }}_{\mathrm{opt}}\approx \frac{1}{\rho }\log \hspace{0.17em}\left(\frac{1/S-u_{\ast }}{1-u_{\ast }}\right).$$ 3.4

Details can be found in appendix B.3.

3.2. Results for Skellam model

We now consider two different initial conditions for equation (2.5): (i) Dirac delta and (ii) Gaussian initial conditions. Full derivations can be found in appendix B.4.

3.2.1. Dirac delta initial condition

Intuitively, and as shown in appendix B, it can be seen that the maximum density for each instant of time is obtained at the origin, x = 0 and, therefore, we get the following expression:

$$u(t)=\frac{u_1}{{(4\pi Dt)}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho t}$$

from the complete solution, equation (B 20).

Using this formula iteratively as in appendix B, we can construct a uniform schedule of fractionated irradiation. Equally, we wish to find the best choice of Δ providing the maximum T_mt given by equation (2.8). Furthermore, we are interested in the range of values of Δ for which the therapy can be completed before the tumour density reaches u_*. Choosing Δ above (and perhaps below) this range leads to a suboptimal use of therapy and to smaller values of the objective function, T_mt.

The time to malignant transformation T_mt is given by

$$T_{\mathrm{mt}}=(N-1)\mathrm{\Delta }-\frac{n}{2\rho }W\hspace{0.17em}(-\frac{\rho u_N^{\prime 2/n}}{2\pi dD{u}_{\ast }^{2/n}}),$$ 3.5

where W is the Lambert function [53]. Critically, we are not able to analytically solve for the optimum value for Δ as derived from dT_mt(Δ)/dΔ = 0; instead we have to resort to numerical methods to calculate the value of Δ_opt.

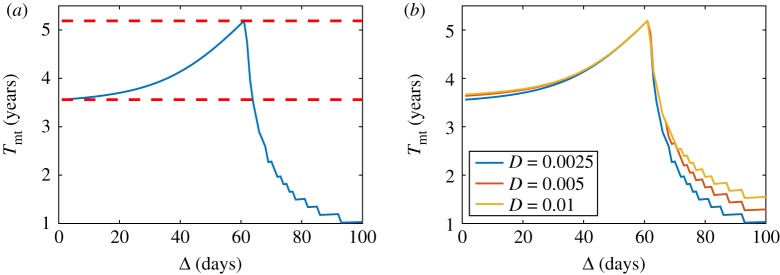
Figure 4 shows an example computed directly from equation (2.5) in one dimension with doses given at equispaced times (according to equation (B 21)) showing the existence of a single global maximum T_mt given by equation (2.8). An interesting aspect that allows us to analyse the Skellam model is the influence of the diffusion coefficient on the T_mt curve versus the Δ spacing; that is, this model gives us information on how the optimal therapy is influenced by the tumour’s infiltrative characteristics. Figure 4 illustrates this variability by presenting different T_mt curves, which can be simulated from the Skellam model in one dimension and considering the initial Dirac delta condition. In these curves, all the parameters have been fixed except for the diffusion coefficient, D, which takes values between 0.0025 and 0.1 mm² d⁻¹. The differences between these graphs are notable for two reasons and can be explained from the analytical expression of time to the malignant transformation, equation (B 30).

Figure 4.

Prediction of the time to malignant transformation given by the Skellam model in one dimension with a Dirac delta initial condition, for different spacing between doses. The values of the parameters used are ρ = 0.007 d⁻¹, S = 0.85, u₁ = 0.1 and u_* = 0.3. The values of the diffusion coefficient employed in the simulations are: (a) D = 0.0025 mm² d⁻¹, (b) D = 0.0035 mm² d⁻¹, (c) D = 0.005 mm² d⁻¹ and (d) D = 0.01 mm² d⁻¹. Upper and lower red dashed lines correspond to T_mt(Δ_Opt) and T(1), respectively (see equation (2.11)). (Online version in colour.)

First, for n = 1, the higher the diffusion coefficient, the greater the value of the time until the malignant transformation associated with the spacing of the standard therapy. Explicitly, the standard therapy has unit time spacing (Δ = 1 day). According to equation (B 31) and given that we are only varying the value of the diffusion coefficient, this difference is due exclusively to the different values that the argument of the Lambert function, W, takes (figure 4).

Second, there is a significant difference in the gain in T_mt of the optimal spacing compared to the standard, this gain being greater for smaller values of D (table 2). From a biological point of view, the model predicts that, for a fixed proliferation rate, low-grade tumours with small diffusion rates (low cell infiltration into the healthy brain parenchyma) benefit most (in terms of survival) from the optimized therapy.

Table 2.

Summary of T_mt gain for the Skellam model in one dimension with an initial Dirac delta condition. Proliferation rate is fixed (ρ = 0.007 d⁻¹). Only the diffusion coefficient is allowed to vary.

D (mm2 d−1)	Δopt (days)	gain in terms of Tmt (days)
0.0025	53	≃1055
0.0035	55	≃675
0.005	44	≃372
0.01	38	≃201

In order to analyse the influence of the proliferation rate on the T_mt curve and on the optimum spacing, Δ_opt, all the parameters have now been fixed, except the proliferation rate, taking this values between 0.0045 d⁻¹ and 0.01 d⁻¹. A remarkable behaviour, observed in figure 5, is that the optimal spacing is lower in tumours with higher proliferation rate. This seems a logical result since the faster the tumour grows, the more likely it is for the tumour to undergo malignant transformation before the end of therapy (figure 2b).

Figure 5.

Prediction of time to malignant transformation given by the Skellam model in one dimension with an initial Dirac delta condition, for different spacing between doses. The values of the parameters used are D = 0.007 mm² d⁻¹, S = 0.85, u₁ = 0.1 and u_* = 0.3. The values of the proliferation rate are: (a) ρ = 0.0045 d⁻¹, (b) ρ = 0.007 d⁻¹, (c) ρ = 0.009 d⁻¹ and (d) ρ = 0.01 d⁻¹. Upper and lower red dashed lines correspond to T_mt(Δ_Opt) and T(1), respectively (see equation (2.11)). (Online version in colour.)

It is observed that T_mt(Δ = 1) is very sensitive to the rate of proliferation. Namely, the greater ρ is, the smaller T_mt(Δ = 1) is. An explanation for this fact is that the time of regrowth in equation (B 30) is shorter for higher proliferation rates (table 3).

Table 3.

Summary of results for the Skellam model in a dimension with the initial Dirac delta condition, considering different proliferation rates and with the fixed diffusion coefficient (D = 0.007 mm² d⁻¹).

ρ (d−1)	Δopt (days)	gain in terms of Tmt (days)
0.0045	59	≃299
0.007	40	≃262
0.009	33	≃256
0.01	31	≃261

3.2.2. Gaussian initial condition

Here, we will consider an initial Gaussian condition,

$$u(\mathbf{x},0)=u_0(\mathbf{x})=u_1{\text{e}}^{-{\mathbf{x}}^2/\sigma },$$ 3.6

instead of a Dirac delta initial condition. This condition implies that the tumour initially follows a Gaussian profile, whose width is controlled by the parameter σ. This scenario is more realistic than the Dirac delta-type condition since the detection of a macroscopic tumour with these characteristics is possible. The solution of equation (2.5) with the initial condition given by (3.6) is presented in appendix B.2. In the same way as was done for the initial Dirac delta condition, we consider only the density at x = 0. Critically, T_mt once again cannot be calculated analytically and we have to resort to numerical methods to obtain it (figure 6).

Figure 6.

T_mt for the Skellam model in (a) one dimension, (b) two dimensions and (c) three dimensions, with initial Gaussian condition. The values of the parameters are D = 0.0025 mm² d⁻¹, ρ = 0.007 d⁻¹, σ = 4 mm², S = 0.85, u₁ = 0.1 and u_* = 0.3. Upper and lower red dashed lines correspond to T_mt(Δ_Opt) and T(1), respectively (see equation (2.11)). (Online version in colour.)

In this case, we are most interested in how space dimensions influence the information provided by the model. Fundamentally, the gain in T_mt is greater in three dimensions when compared with two dimensions and, analogously, T_mt is greater in two dimensions when compared with one dimension (table 4 and figure 6). In addition, an important variation in the optimal spacing is observed depending on the spatial dimension considered.

Table 4.

Summary of results for the Skellam model with the initial Gaussian condition for one, two and three dimensions.

spatial dimension	Δopt (days)	gain in terms of Tmt (days)
One dimension	33	≃86
Two dimensions	41	≃248
Three dimensions	55	≃556

3.3. Results for Fisher–Kolmogorov equation

Finally, we consider the Fisher–Kolmogorov equation, which constitutes a generalization of the logistic equation. When diffusive effects are small, both models provide similar results. Thus, we seek to illuminate the influence of diffusion on optimal therapy times.

Figure 7a shows the results of the time to malignant transformation T_mt for the Fisher–Kolmogorov equation in one dimension for different spacing between doses. This result is similar to that obtained with the logistic equation (equation (2.4)). Figure 7b illustrates how T_mt depends on the diffusion coefficients. It is observed that, despite there being a variation of up to an order of magnitude in the diffusion coefficient, the curves remain similar. This is particularly true in the monotonically increasing region, which is the pertinent region for determining an optimal therapy. In view of this, it can be stated that the Fisher–Kolmogorov equation suggests that the infiltrative character of the tumour can be neglected, at least for the range of values of the diffusion coefficient characteristic of LGGs.

4. Applications to clinical practice

As shown in the previous sections, it seems that allowing a spacing between doses of greater than 1 day is beneficial for patients, as a gain is obtained in terms of time to the malignant transformation.

However, fundamentally, which tumour growth law is correct remains controversial. Furthermore, as illustrated in the analysis and shown in figures 3–7, optimizing the exact dose spacing is delicate because slightly increasing the dose separation beyond optimal results in a worse prognosis compared to the standard treatment. For these reasons, the application of the optimal protocol for each patient could be difficult to implement in clinical practice. Thus, we suggest that although the dose spacing should be increased beyond one day, which is the standard routine, the chosen protocol should not be pushed towards complete optimality, for conservative reasons.

One difficulty, which can be overcome, is that, in clinical practice, the values of some parameters are not easy to be calculated. Critically, choosing optimal conditions is heavily dependent on these values, specifically, the critical tumour density, u_*. However, this can be conservatively estimated since tumour volume is (roughly) related to average cell density and, so, the critical tumour density will be linked to a critical tumour volume, V_*. Thus, the initial tumour volume, V₁, can be estimated using magnetic resonance imaging techniques. Crucially, even if the exact value of V_* is not known, it is clear that $V_{\ast }>V_1$. We can make a conservative choice by establishing $V_{\ast }=V_1$; even if sometimes this value could be far from the real one, errors produced by overestimating V_* are avoided.

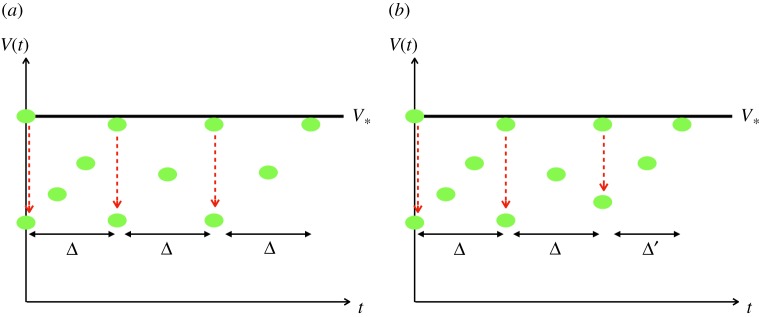
Furthermore, with periodic control, it is possible to monitor the tumour growth evolution. For example, after the first RT dose and accompanying tumour volume reduction another RT dose would be administered when the tumour volume is close to V₁, thereby defining Δ. A basic scheme can be seen in figure 8a. This protocol is easily modifiable, since it can occur that after some doses of RT tumour cells develop RT resistance and, thus, the tumour does not respond uniformly to the treatment over time. In this case, the critical value, V_*, would be reached before the time Δ. With a periodic control, a new time between doses Δ′ < Δ can be recalculated and the treatment can be adapted, as in figure 8b.

Figure 8.

(a) Basic treatment schedule. (b) Treatment adaptation if radiotherapy resistance, or faster growth, occurs. (Online version in colour.)

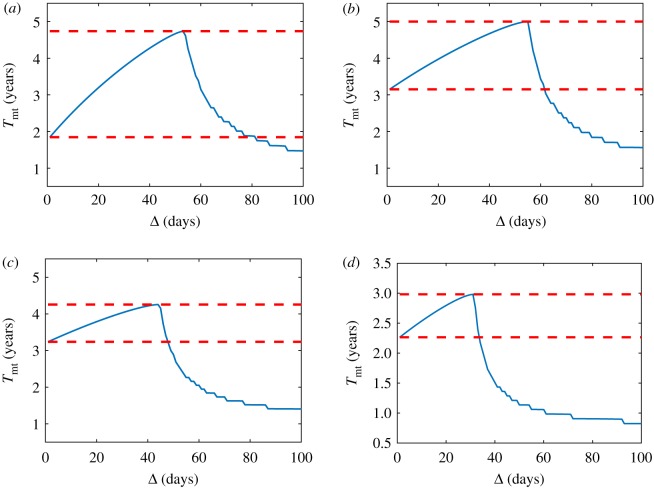
To demonstrate this idea, simulations were performed and illustrated in figure 9. Specifically, we compared four protocols assuming a fixed law growth and fixed values for the parameters. The four simulations we compare are

• —Standard protocol, Δ = 1.
• —Optimal protocol for a wrong u_*, i.e. u_*,wrong where u_*,wrong = 1.05u_*; Δ = Δ′_opt.
• —Suboptimal protocol, Δ = Δ_subopt < Δ_opt.
• —Optimal protocol Δ = Δ_opt.

Figure 9.

(a) Gompertz growth, with ρ = 0.003756 d⁻¹, S = 0.85, u₁ = 0.3 and u_* = 0.5. (b) Logistic growth, with ρ = 0.004 d⁻¹, S = 0.85, u₁ = 0.3 and u_* = 0.5. Units for T_mt and Δ are years and days, respectively. Blue curve corresponds to the standard protocol, purple curve corresponds to the optimal protocol for a wrong u_*, yellow curve corresponds to suboptimal protocol and red curve corresponds to optimal protocol. Black horizontal line represents u_*. (Online version in colour.)

In figure 9, it is possible to see two examples of these different protocols. In figure 9a, Gompertz growth is assumed. In this case, the worst scenario in terms of survival is the standard protocol, as the time to malignant transformation is 1.6 years. Of course, the best protocol is the optimal one, with a time to malignant transformation equal to 4.6 years. However, with an overestimation of only 5% of the critical tumour density, the resulting time to malignant transformation would have been 1.8 years, which is better than the standard protocol but worse than the suboptimal protocol, which provides a time to malignant transformation of 3.2 years.

Similar results are seen in figure 9b, with the additional note that, in this case, the 5% critical tumour overestimation simulation is worse than the standard protocol, as the time to malignant transformation is 3.9 versus 4.2 years, respectively. The suboptimal protocol also gives a benefit compared to the standard one (5.2 years) and, even if it is not the optimal dose spacing (6.2 years), it provides a close approximation.

5. Discussion and conclusion

5.1. Medical applications

The primary aim of this work was to improve the efficacy of RT for the management of LGG using different mathematical models. Thus, the results of §3 provide a theoretical support for extremely protracted therapies for LGG. Notably, the results have a clear biological meaning. Since tumour regrowth is known to be faster for small tumour densities, which is called the accelerated repopulation phenomenon, it is preferable to leave the tumour density to grow, while keeping its damage to the surrounding healthy brain parenchyma under control (particularly if eloquent areas are affected). Our mathematical models (except the exponential model) capture this phenomenon.

Our results can further be extended to include the knowledge that radiation treatment is most effective on proliferating cell populations. Thus, if we were able to time the dosage with reference to the cell cycle our treatments would be more effective. Although not presently accounted for in our model, such effects may be incorporated by including a quiescent population along with any of the models of proliferative cells studied in this article.

Critically, taking the time spacing Δ above the optimal value in any of our models, leads to a sharp drop of the gain in time to the malignant transformation and even a worse outcome than the choice of Δ = 1 day. This is why we suggest a suboptimal protocol that could be applied in clinical practice. The result of mis-estimating the parameter values, or the growth law, when calculating the optimal time spacing between doses can be avoided using the suboptimal protocol that is proposed in this paper, which is not dependent on parameter values or growth laws. The time spacing between doses depends on just the tumour volume that is a measure that can be quantified with the current imaging techniques.

Protracted therapies are, of course, quite a radical suggestion, thus, there is little research done to support our predictions. Ongoing phase II clinical trials will try to determine whether protracted RT doses may exhibit a significant benefit on both progression free survival and overall survival in newly diagnosed LGG adult patients. Moreover, we expect that, inspired by the present study, more sophisticated mathematical models will be needed to account for the observed results in LGG patients.

5.2. Conclusion and future works

In this article, we compared a number of model equations (exponential, Gompertz, logistic, Skellam and Fisher–Kolmogorov equations), which are widely used when quantifying the kinetics of LGGs. Specifically, we have investigated optimal dose interspacing in RT protocols for LGGs, under the assumptions of equal doses per fraction and fixed spacing between doses. As each model uses a different functional form and captures specific characteristics of the growth of LGGs, the results based on each of the models share certain behaviours, but at the same time they present several differences.

Some of these particularities even point to some disagreement. Specifically, a given model can suggest guidelines for action in clinical practice, while another model suggests a totally different set of guidelines. For example, in the case of the exponential model, there is no benefit in increasing the temporal spacing between doses greater than 1 day. However, this result differs radically from those provided by the other models considered in this study. Indeed, the logistic model indicates a certain gain in T_mt is made by taking a time spacing, Δ > 1. Namely, an optimal therapy requires approximately 60 days to pass between consecutive doses. The Gompertz model yields qualitatively similar results to those of the logistic model. However, quantitatively there are significant differences, the main one being a greater gain in time until the malignant transformation of the optimal spacing compared to the unit spacing. Still, it should be pointed out that the use of extremely protracted schemes would be of special interest for pediatric LGG patients, since one of the complications associated with RT toxicity is the manifestation of cognitive disability later in life. Employing longer time spacings between doses is expected to significantly reduce the occurrence of such secondary effects.

One limitation of our work is that we are, currently, restricted to equispaced doses. However, one could take a much more granular view of, at one extreme, varying the specific days of the week at which dosage occurs. The question then becomes a much larger optimization problem. Although we expect the problem to be analytically intractable, accompanying simulations should be quite forthcoming and will be considered as part of our future work. However, it should be noted that we do not foresee that subweekly variations would have a large impact on our results, which often suggest multiple weeks are missed between doses.

The diffusive–proliferative models are a way of introducing another relevant characteristic of LGGs: their infiltrative character. After using an initial condition given by a highly localized tumour applied to the Skellam model, we conclude that the variation in the diffusion coefficient, D, decisively influences both the gain of the optimized therapy versus the standard one, as well as the time to malignant transformation associated with unit spacing. On the other hand, the observed dependence of the optimal spacing with the diffusion coefficient, although if it exists, is not relevant. Thus, therapy optimization does not depend strongly on the diffusion coefficient, even though therapy gain does. In addition to the influence of the diffusion coefficient on T_mt, the role of the proliferation rate has also been analysed. From this last analysis, it can be concluded that the value of the proliferation rate does have a decisive influence on the value of the optimal spacing and that, in contrast to variations of the diffusion coefficient, there are no significant differences in the gain in T_mt when the proliferation rate is varied.

Another interesting result obtained in this work is provided by the Skellam model with Gaussian initial condition. Namely, with fixed values for diffusion and proliferation rate, the model shows a marked effect of dimensionality. Specifically, gain in T_mt is highest in the three-dimensional case. Similarly, the Fisher–Kolmogorov equation yields a revealing result. Specifically, the time to malignant transformation depends weakly on the diffusion coefficient. Our conclusion is that, to a good approximation, the problem can be studied without taking into account the effects of diffusion, at least for the diffusion coefficient values pertinent to LGGs. Of course, it could be argued that if the diffusion coefficient changes (increases) as the LGG progresses into a high-grade glioma, such an approximation may be questionable.

Finally, as a future extension of this work, by adding a healthy tissue population one could increase the number of doses and run the treatment for longer times. This is motivated by our previous work [54], where estimates of the retreatment radiation tolerances of the spinal cord at different times after initial treatment where proposed. In the present work, healthy tissue has only been considered through the limitation of the total dose administered. A possible avenue to explore consists of taking into account the healthy brain tissue through the evolution of the fraction of survival of healthy cells and their recovery when the doses are sufficiently spaced over time. It should be noted that since the recovery of healthy tissue is considerably smaller compared to that of tumour tissue, it is only necessary to regard the healthy tissue recovery in protracted therapies such as those analysed here. Another extension would encompass both the concomitant action of RT and chemotherapy. As shown in [55], the outcome of LGG patients is highly variable when single-modality treatment strategies of standard RT versus primary temozolomide chemotherapy are administered. An open problem is whether it would be possible to generalize the framework presented here to such a therapeutic scenario. Finally, including radio-resistant cells in the model would be another possible extension, that could be done along the lines presented in [56]. We hope that the results obtained in this article will stimulate further research for identifying optimal treatments for LGG patients.

Appendix A. Explicit solutions

Explicit solutions will be used throughout this paper to reduce the number of approximations. Such solutions are commonly derived using standard techniques [57].

The general solution of (2.1) is

$$u(t)=u_1{[{\left(\frac{u_1}{K}\right)}^{\alpha }+\hspace{0.17em}{\text{e}}^{-\rho t}(1-{\left[\frac{u_1}{K}\right]}^{\alpha })]}^{-1/\alpha }.$$ A 1

The formal solution of the Skellam model (2.5) in infinite space is given by

$$u(\mathbf{x},t)=\hspace{0.17em}\frac{{\text{e}}^{\rho t}}{{(4\pi Dt)}^{n/2}}{\int }_{{\mathbb{R}}^n}\hspace{0.17em}{\text{e}}^{-{(\mathbf{x}-\alpha )}^2/4Dt}{u}_0(\alpha )\hspace{0.17em}\text{d}\alpha ,$$ A 2

where n is the dimension considered.

Appendix B. Calculating time to malignant transformation

The time to malignant transformation, T_mt, will be found in the case of each tumour growth model as the total treatment time, T_t, plus the time that elapses until the critical tumour density, u_*, is reached from the tumour density obtained when the therapy is finished, u′_N, which is denoted by T_r:

$$T_{\mathrm{mt}}=T_t+T_r=N\mathrm{\Delta }+T_r.$$ B 1

Keep in mind that equation (B 1) is only valid when the tumour density, u(t), remains below, or equal to, the critical value, u_*. It may happen, for spacings between sufficiently large doses, that the critical density is reached before the end of the treatment. In this case, we will find the last session, j, for which $u\le u_{\ast }$. In this case, the time to malignant transformation will be given by

$$T_{\mathrm{mt}}=j\mathrm{\Delta }+T_r^{\hspace{0.17em}j},$$

where $T_r^{\hspace{0.17em}j}$ is the time that elapses until the density u_* is reached starting from u′_j.

B.1. Exponential model

Using the recursion formula (2.10) and equation (2.2), we get a recursive equation providing the tumour density after every dose t_j, d_j:

$$u_1^{\prime }(t)=S{u}_1(t)$$ B 2

$$u_2^{\prime }(t)=S{u}_2(t)=S{u}_1^{\prime }\hspace{0.17em}{\text{e}}^{\rho (t_2-t_1)}=S^2{u}_1\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}$$ B 3

$$u_3^{\prime }(t)=S{u}_3(t)=S{u}_2^{\prime }\hspace{0.17em}{\text{e}}^{\rho (t_3-t_2)}=S^3{u}_1\hspace{0.17em}{\text{e}}^{2\rho \mathrm{\Delta }}$$ B 4

$$⋮$$ B 5

$$u_{\hspace{0.17em}j}^{\prime }(t)=S{u}_{\hspace{0.17em}j}(t)=S{u}_{\hspace{0.17em}j-1}^{\prime }\hspace{0.17em}{\text{e}}^{t_{\hspace{0.17em}j}-t_{\hspace{0.17em}j-1}}=S^{\hspace{0.17em}j}{u}_1\hspace{0.17em}{\text{e}}^{(j-1)\rho \mathrm{\Delta }}.$$ B 6

Thus, the time to malignant transformation is given by equation (3.1).

We noted, in §3.1.1, that dT_mt(Δ)/dΔ = 0, $\mathrm{\forall }\mathrm{\Delta }>0$. However, this does not mean that T_mt is stationary with respect to Δ. Critically, because of its piecewise nature it can have both a zero-derivative and be monotonically decreasing (figure 3a).

B.2. Gompertz model

This time we combine equations (2.3) and (2.10) to get a recursive equation providing the tumour density after every dose t_j, d_j:

$$u_1^{\prime }(t)=S{u}_1(t)$$ B 7

$$u_2^{\prime }(t)=S{u}_2(t)=S{u_1^{\prime }}^{{\mathrm{e}}^{-\rho \mathrm{\Delta }}}=S^{{\mathrm{e}}^{-\rho \mathrm{\Delta }}+1}{u}_1^{{\mathrm{e}}^{-\rho \mathrm{\Delta }}}$$ B 8

$$u_3^{\prime }(t)=S{u}_3(t)=S{u_2^{\prime }}^{{\mathrm{e}}^{-\rho \mathrm{\Delta }}}=S^{1+\hspace{0.17em}{\mathrm{e}}^{-\rho \mathrm{\Delta }}+\hspace{0.17em}{\mathrm{e}}^{-2\rho \mathrm{\Delta }}}{u}_1^{{\mathrm{e}}^{-2\rho \mathrm{\Delta }}}$$ B 9

$$⋮$$ B 10

$$\begin{array}{rl}{u}_{\hspace{0.17em}j}^{\prime }(t)& =S{u}_{\hspace{0.17em}j}(t)=S{u_{\hspace{0.17em}j-1}^{\prime }}^{{\mathrm{e}}^{-\rho \mathrm{\Delta }}}=S^{\sum _{k=0}^{\hspace{0.17em}j-1}\hspace{0.17em}{\mathrm{e}}^{-k\rho \mathrm{\Delta }}}{u}_1^{{\mathrm{e}}^{-(j-1)\rho \mathrm{\Delta }}}\\ & =S^{{\gamma }_{\hspace{0.17em}j}}{u}_1^{{\mathrm{e}}^{-(j-1)\rho \mathrm{\Delta }}},\end{array}$$ B 11

where the geometric progression is expressed as follows:

$${\gamma }_{\hspace{0.17em}j}=\sum _{k=0}^{\hspace{0.17em}j-1}\hspace{0.17em}{\text{e}}^{-k\rho \mathrm{\Delta }}=\frac{{\text{e}}^{-j\rho \mathrm{\Delta }}-1}{{\text{e}}^{-\rho \mathrm{\Delta }}-1}.$$ B 12

Thus, the time to malignant transformation is given by

$$T_{\mathrm{mt}}(\mathrm{\Delta })=(N-1)\mathrm{\Delta }+\frac{1}{\rho }\log \hspace{0.17em}\left(\frac{\log (u_N^{\prime })}{\log (u_{\ast })}\right),$$ B 13

with u′_N given by equation (B 11) with j = N.

It is straightforward to show that

$$\frac{\text{d}{T}_{\mathrm{mt}}(\mathrm{\Delta })}{\text{d}\mathrm{\Delta }}=N-1+\frac{1}{u_N^{\prime }\log u_N^{\prime }}\frac{\text{d}{u}_N^{\prime }}{\text{d}\mathrm{\Delta }},$$ B 14

where

$$\begin{array}{rl}\frac{\text{d}{u}_N^{\prime }}{\text{d}\mathrm{\Delta }}& =S^{{\gamma }_{\hspace{0.17em}j}}{u}_1^{{\mathrm{e}}^{-N\rho \mathrm{\Delta }}}[\log S\hspace{0.17em}(\frac{{\text{e}}^{-\rho \mathrm{\Delta }}({\text{e}}^{-N\rho \mathrm{\Delta }}-1)}{{({\text{e}}^{-\rho \mathrm{\Delta }}-1)}^2}-\frac{N\hspace{0.17em}{\text{e}}^{-N\rho \mathrm{\Delta }}}{{\text{e}}^{-\rho \mathrm{\Delta }}-1})\\ & \phantom{\left(\frac{N\hspace{0.17em}{\text{e}}^{-N\rho \mathrm{\Delta }}}{{\text{e}}^{-\rho \mathrm{\Delta }}-1}\right)}-(N-1)\log u_1\hspace{0.17em}{\text{e}}^{-(N-1)\rho \mathrm{\Delta }}].\end{array}$$

The expression (B 14) is positive for the values of the parameters considered in the article, which means that the optimum value for Δ within this interval is reached exactly on its border, where the border is defined as the largest value of Δ for which the therapy is completed before the tumour reaches the critical value u_*.

Since equation (3.2) is valid while u(t) ≤ u_* and u′_j gives the tumour density after the radiation doses, this means that the condition for this scenario to hold is (figure 2)

$$u_N^{\prime }/S\le u_{\ast }.$$ B 15

Figure 3b shows a simulation computed from equation (2.3), with doses given equally spaced in time and according to equation (2.10). This picture shows the existence of a single global maximum in the time to malignant transformation, given by equation (2.8). It is possible to calculate this maximum quantitatively by inserting equation (B 11), for j = N, into equation (B 15) and solving for Δ:

$$S^{{\gamma }_N-1}{u}_1^{{\mathrm{e}}^{-(N-1)\rho \mathrm{\Delta }}}=u_{\ast }.$$ B 16

Using formula (B 12) and defining α = e^−ρΔ, after some algebra, we obtain

$$P(\alpha )\equiv {\alpha }^N\log S{u}_1-{\alpha }^{N-1}\log u_1-\alpha \log S{u}_{\ast }+\log u_{\ast }=0.$$ B 17

In the range of parameters of interest, i.e. $0<u_1<u_{\ast }<S<1$, it is straightforward to prove that the previous equation has at least one root. Thus, we can get an estimation for the value of the root by taking into account that α < 1 and N ≫ 1 and thus equation (B 17) becomes

$$-\alpha \log S{u}_{\ast }+\log u_{\ast }\approx 0$$

and from here

$$\alpha \approx \frac{\log u_{\ast }}{\log S{u}_{\ast }},$$

which, finally, leads to the result in equation (3.3).

B.3. Logistic model

For this case, as in the exponential model, the general formula for the tumour density corresponding to the jth irradiation can be calculated:

$$u_{\hspace{0.17em}j}^{\prime }(t)=\frac{u_1{S}^{\hspace{0.17em}j}\hspace{0.17em}{\text{e}}^{(j-1)\rho \mathrm{\Delta }}}{1+S{u}_1({\text{e}}^{\rho \mathrm{\Delta }}-1)[(S^{\hspace{0.17em}j-1}\hspace{0.17em}{\text{e}}^{(j-1)\rho \mathrm{\Delta }}-1)/(S\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}-1)]}.$$ B 18

Thus, for this model, the time to malignant transformation is given by

$$T_{\mathrm{mt}}(\mathrm{\Delta })=(N-1)\mathrm{\Delta }+\frac{1}{\rho }\log \left[\frac{u_{\ast }(1-u_N^{\prime })}{u_N^{\prime }(1-u_{\ast })}\right]$$ B 19

and, for the parameters of the model,

$$\frac{\text{d}{T}_{\mathrm{mt}}(\mathrm{\Delta })}{\text{d}\mathrm{\Delta }}>0,\mathrm{\forall }\mathrm{\Delta }>0,$$

which means that the optimum value for Δ within this interval is reached again exactly on its border. As in the Gompertz model, the condition $u_N^{\prime }/S\le u_{\ast }$ must be satisfied, and thus we obtain the following algebraic equation:

$$u_1{\beta }^N(\frac{1}{u_{\ast }}-1)+u_1{\beta }^{N-1}(S-\frac{1}{u_{\ast }})+\beta (u_1-1)+1-S{u}_1=0,$$

where β = e^ρΔS. In the range of parameters of interest $(0<u_1<u_{\ast }<S<1)$ and for N ≫ 1 it is possible to find an approximation of Δ_opt:

$${\mathrm{\Delta }}_{\mathrm{opt}}\approx \frac{1}{\rho }\log \hspace{0.17em}\left(\frac{1/S-u_{\ast }}{1-u_{\ast }}\right).$$

B.4. Results for Skellam model

B.4.1. Dirac delta initial condition

Combining the Dirac delta initial conditions, u(x, 0) = u₁δ(x), with (A 2) generates the solution of equation (2.5)

$$u(\mathbf{x},t)=\frac{u_1\hspace{0.17em}{\text{e}}^{\rho t}}{{(4\pi Dt)}^{n/2}}\hspace{0.17em}{\text{e}}^{-{\mathbf{x}}^2/(4Dt)},$$ B 20

where n refers to the spatial dimension. Such a solution represents the tumour density at each point x and at each time t. From this solution, it can be seen that the maximum density for each instant of time is obtained at the origin, x = 0, i.e. u(t) = max_x∈B{u(x, t)} = u(0, t). Since we are interested in the maximum value of the density, in what follows we will take the value of x = 0 and, therefore, we get the following expression:

$$u(t)=\frac{u_1}{{(4\pi Dt)}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho t}.$$

Consider again figure 2 in the situation where there is a uniform schedule of fractionated irradiation, i.e. the first fraction is given on day zero, the second fraction on day Δ, the third on day 2Δ and so on, with the Nth fraction being given on day (N − 1)Δ. Define u₁, u₂, …, u_N to denote the tumour cell density immediately before the administration the RT and u′₁, u′₂, …, u′_N the tumour cell density immediately after RT, i.e.

$$u_i^{\prime }(x,t_{\hspace{0.17em}j}^{+})=S{u}_i(x,t_{\hspace{0.17em}j}^{-}),i=1,2,\dots ,$$ B 21

where i is the number of fractions and thus, from figure 2 and using formula (B 20), it is straightforward to get the following recursive iteration:

$$u_1^{\prime }=S{u}_1,$$ B 22

$$u_2^{\prime }=S{u}_2=S\frac{u_1^{\prime }}{{(4\pi D\mathrm{\Delta })}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}=S^2\frac{u_1}{{(4\pi D\mathrm{\Delta })}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }},$$ B 23

$$u_3^{\prime }=S{u}_3=S\frac{u_2^{\prime }}{{(4\pi D\mathrm{\Delta })}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho (2\mathrm{\Delta }-\mathrm{\Delta })}=S^3\frac{u_1}{{(4\pi D\mathrm{\Delta })}^n}\hspace{0.17em}{\text{e}}^{2\rho \mathrm{\Delta }},$$ B 24

$$⋮$$ B 25

$$\begin{array}{rl}{u}_k^{\prime }& =S{u}_k=S\frac{u_{k-1}^{\prime }}{{(4\pi D\mathrm{\Delta })}^{n/2}}\hspace{0.17em}{\text{e}}^{\rho ((k-1)\mathrm{\Delta }-(k-2)\mathrm{\Delta })}\\ & =S{u}_1{\left[\frac{S\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}}{{(4\pi D\mathrm{\Delta })}^{n/2}}\right]}^{k-1}.\end{array}$$ B 26

Thus, given D, ρ, S and u_*, we wish to find the best choice of Δ providing the maximum T_mt given by equation (2.8). Furthermore, we are interested in the range of values of Δ for which the therapy can be completed before the tumour density reaches u_*. Choosing Δ above (and perhaps below) this range leads to a suboptimal use of therapy and to smaller values of the objective function, T_mt.

We can compute explicitly the time T_r in equation (B 1) from the equation

$$\frac{u_{\ast }}{u_N^{\prime }}=\hspace{0.17em}\frac{{\text{e}}^{\rho T_r}}{{(4\pi D{T}_r)}^{n/2}}.$$ B 27

This is done using the Lambert function [53], W, defined by z = W(z e^z), which is useful to solve certain transcendental equations. Thus, the solution of (B 27) is given by

$$T_r=-\frac{n}{2\rho }W\hspace{0.17em}(-\frac{\rho u_N^{\prime 2/n}}{2\pi nD{u}_{\ast }^{2/n}}),$$ B 28

with u′_N given by equation (B 26) with k = N,

$$u_N^{\prime }=\hspace{0.17em}{\left(\frac{S\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}}{{(4\pi D\mathrm{\Delta })}^{n/2}}\right)}^{N-1}S{u}_1.$$ B 29

Therefore, the time to malignant transformation T_mt is given by

$$T_{\mathrm{mt}}=(N-1)\mathrm{\Delta }-\frac{n}{2\rho }W\hspace{0.17em}(-\frac{\rho u_N^{\prime 2/n}}{2\pi \hspace{0.17em}\text{d}D{u}_{\ast }^{2/n}}).$$ B 30

The optimum value for Δ is derived from

$$1-\frac{n}{2\rho }\left[\frac{W(z)}{1+W(z)}\right]\hspace{0.17em}(2\rho -\frac{1}{\mathrm{\Delta }})=0,$$ B 31

where $z=-\rho u_N^{\prime 2/n}/u_{\ast }^{2/n}2\pi nD$. Since it is not possible to solve equation (B 31) explicitly in terms of Δ we have to resort to numerical methods to calculate the value of Δ_opt. From equation (B 28), we can obtain the regrowth time for different spatial dimensions. Thus, for one, two and three spatial dimensions, the regrowth time is reflected in table 5.

Table 5.

Re-growth time in one, two and three dimensions for the Skellam equation with a Dirac delta initial condition.

spatial dimensions	Tr
One dimension	$(-1/2\rho )W(-\rho u_N^{\prime 2}/u_{\ast }^{2}2\pi D)$
Two dimensions	$(-1/\rho )W(-\rho u_N^{\prime }/u_{\ast }4\pi D)$
Three dimensions	$(-3/2\rho )W((-\rho /6\pi D){(u_N^{\prime }/u_{\ast })}^{2/3})$

B.4.2. Gaussian initial condition

Solving equation (2.5) with the initial condition given by (3.6) we obtain the following analytic solution:

$$u(\mathbf{x},t)=u_1\hspace{0.17em}{\text{e}}^{\rho t}\hspace{0.17em}{\left(\frac{\sigma }{4Dt+\sigma }\right)}^{n/2}\hspace{0.17em}{\text{e}}^{-{\mathbf{x}}^2/(4Dt+\sigma )}.$$ B 32

In the same way as was done for the initial Dirac delta condition, we consider only the density at x = 0,

$$u(t)=u_1\hspace{0.17em}{\text{e}}^{\rho t}\hspace{0.17em}{\left(\frac{\sigma }{4Dt+\sigma }\right)}^{n/2},$$ B 33

which will be the point of highest tumour density. Again, it is possible to calculate the iterative formula,

$$u_k^{\prime }={[S\hspace{0.17em}{\text{e}}^{\rho \mathrm{\Delta }}\hspace{0.17em}{\left(\frac{\sigma }{4D\mathrm{\Delta }+\sigma }\right)}^{n/2}]}^k{u}_1.$$ B 34

The elapsed time T_r can also be calculated from the following relation:

$$\frac{u_{\ast }}{u_N^{\prime }}=\hspace{0.17em}{\text{e}}^{\rho T_r}\hspace{0.17em}{\left(\frac{\sigma }{4D{T}_r+\sigma }\right)}^{n/2}.$$ B 35

Unfortunately, this time cannot be calculated analytically and we have to resort to numerical methods to obtain it.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Spanish Ministerio de Economía y Competitividad/FEDER (grant no. MTM2015-71200-R), the Consejería de Educación Cultura y Deporte from Junta de Comunidades de Castilla-La Mancha (Spain) (grant no. PEII-2014-031-P) and the James S. McDonnell Foundation (USA) 21st Century Science Initiative in Mathematical and Complex Systems Approaches for Brain Cancer (collaborative awards 220020450 and 220020560). A.A.-A. was supported by a fellowship from UCLM (2015/4062).