A minimal computational model for three-dimensional cell migration

Abstract

During migration, eukaryotic cells can continuously change their three-dimensional morphology, resulting in a highly dynamic and complex process. Further complicating this process is the observation that the same cell type can rapidly switch between different modes of migration. Modelling this complexity necessitates models that are able to track deforming membranes and that can capture the intracellular dynamics responsible for changes in migration modes. Here we develop an efficient three-dimensional computational model for cell migration, which couples cell mechanics to a simple intracellular activator–inhibitor signalling system. We compare the computational results to quantitative experiments using the social amoeba Dictyostelium discoideum. The model can reproduce the observed migration modes generated by varying either mechanical or biochemical model parameters and suggests a coupling between the substrate and the biomechanics of the cell.

1. Introduction

Many eukaryotic cells can move and the resulting motion is a critical component of a number of physiological and pathological processes, including wound healing, embryology and cancer metastasis [1–4]. Single-cell migration can be either spontaneous or can be guided by external cues such as gradients in chemicals [5,6]. In either case, the intracellular signalling components, many of them conserved across different cell types, take on an asymmetric distribution, leading to a polarized cell [7–9]. Most studies use experimental assays where cells move on flat surfaces and are visualized as two-dimensional (2D) objects, using either confocal microscopy, which can capture a slice of a cell, or other microscopic techniques, which represent the cell as a projection onto the 2D surface. While these experiments have resulted in significant progress and a better understanding of cell migration, they fail to capture three-dimensional (3D) aspects of single cell motion and intracellular signalling [10]. These aspects might be important to fully understand cell motility and are increasingly captured with novel imaging techniques [11].

Capturing 3D information is especially important if cells can transition between different morphologies and can alter their way of migration. Recent work has shown that cells do not always adopt a single, conserved migration mode but can change between different modes [12,13]. These transitions can be induced either by a change of the extracellular environment or by exposing cells to extracellular stimuli and may be crucial for many important biological processes, including embryological development, tissue homeostasis, immune defence and cancer metastasis [3,14,15]. Importantly, the transitions occur on short timescales, which implies that the different migration modes involve the same signalling components.

A striking example of these transitions was recently demonstrated using engineered cells of the social amoeba Dictyostelium discoideum. These cells normally migrate using an amoeboid-like mode during which actin-rich pseudopods are repeatedly protruded and retracted. As a result, the motion of a cell is very irregular while the morphology is constantly changing [16]. However, by synthetically decreasing phosphatidylinositol-4,5-bisphosphate levels or increasing Ras/Rap-related activities the migration mode can be switched to either keratocyte-like, characterized by a stable fan-shaped morphology and unidirectional motion, or oscillatory during which the cell displays a repeated cycle of spreading and contracting [13]. The keratocyte-like migration mode has also been observed in certain mutants [17] while all three modes can also be found in wild-type cells that are developed under low cell density conditions [18].

Many studies have attempted to model cell migration, most of which treat cells as 2D objects [19,20], although some recent studies have started to address 3D migration [21–25]. Obviously, distinctly 3D features of cell migration can only be captured by 3D models. For the oscillatory motion describe before, for example, the basal surface is shown to exhibit periodic changes in area. This implies that the 3D morphology must change considerably during the spreading–contraction cycle. Furthermore, for amoeboid motion, pseudopods can be formed not only along the substrate but also away from the basal surface. Thus, capturing these morphological changes, along with the dynamics of signalling molecules throughout the cell and along the entire membrane, requires a 3D model that can couple intracellular signalling and morphology changes. Developing such 3D models, however, is challenging, not only due to a lack of quantitative experimental 3D data but also due to the complexity of modelling deforming cells in 3D. Since the cell’s morphology is continuously changing, traditional methods that discretize the surface are cumbersome and inefficient. Furthermore, solving equations within the intracellular space with the appropriate boundary conditions also poses significant computational challenges.

The vast majority of the computational models for cell motility focus on a single migration mode and do not address mode transitions [26–35]. Recently, a number of studies have presented models that were able to switch between different migration modes by varying system parameters [13,36–38]. In some of these studies, feedback between cell shape deformations and signalling components together with changing system parameters can result in transitions between amoeboid-like and keratocyte-like cells [36,37]. In another study, Miao et al. presented a computational model which was able to exhibit transitions by changing the qualitative dynamics of the underlying biochemical module from excitable to oscillatory [13,39]. Although these models are able to capture some or all of the migration modes, they are implemented in 2D. Thus, it is still unclear how to generate distinct migration modes in a 3D computational model that involves a minimum number of biochemical components.

In this study, we develop a computational model that is able to simulate deforming 3D single cells moving on a flat surface. Our model couples a simple intracellular reaction–diffusion model to a mechanics module which describes cell motion. The mechanics module is based on the phase field method, which has been used extensively in cell migration and which takes into account the physical properties of the membrane [33–35,40–43]. In our model, membrane protrusions are generated by the output of a two component reaction–diffusion model that only contains an inhibitor and an activator.

Although our modelling approach can be applied to different cell types, we used it to simulate migrating engineered Dictyostelium cells. To facilitate a direct comparison between simulations and experimental morphology of engineered cells, we performed experiments to determine the 3D cell shapes for the three migration modes exhibited by these cells. We furthermore analysed the actin dynamics on the cortex of oscillatory cells using lattice light sheet microscopy (LLSM). We show that our model is able to faithfully reproduce the observed cell shapes in a computationally efficient way. Furthermore, we show that the model is able to generate different migration modes by varying a single parameter in the model, the protrusive strength of the activator. Finally, our results point to a specific role of the substrate. Our simulation platform should be able to be extended to model cell migration in more complex and physiologically relevant geometries.

2. Model

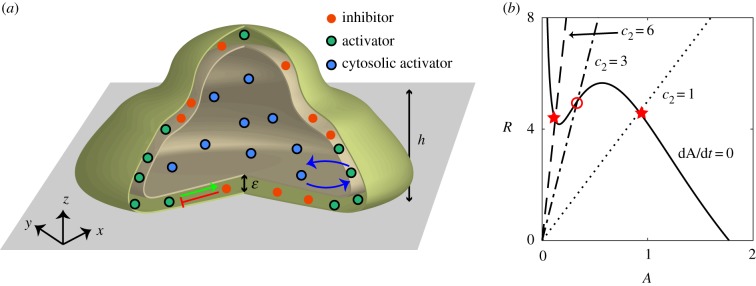
As schematically shown in figure 1, we model a 3D cell that moves on a flat substrate representing the x–y plane and with z = 0. Our model consists of a biochemical activator–inhibitor system that is coupled to equations that describe the deformation of the cell membrane and cell motion. The inhibitor is localized on the cell membrane (red symbols in figure 1a) and its concentration is denoted by R(r, t). The activator can switch between an active form, A(r, t), localized at the membrane, and an inactive form, A_cyt(r, t), which is present in the cytosol (blue and green symbols in figure 1a, respectively). Both A and R diffuse within the membrane while the inactive form A_cyt is assumed to be uniformly distributed in the cytosol due to fast diffusion. We assume that the total number of molecules of active and inactive activator is conserved, resulting in the conservation relation $A_{\mathrm{cyt}}V+{\int }_S\alpha A\text{d}S=N_{\mathrm{tot}}$, where N_tot is the total number of molecules, V is the volume of the cell, and S is the boundary surface. In this expression, α parametrizes the coupling strength between cytosolic activator and membrane-bound activator, and depends on the stoichiometry and kinetic rates of the transition between active and inactive form [44]. Although we do not specify the exact biochemical nature of A, it can be thought of as an F-actin promoting factor such as Ras or PIP3 and is therefore responsible for protrusive forces at the membrane. The inhibitor, on the other hand, deactivates the activator and can thus be thought of as PTEN or as a component with a similar function [13,32,45]. Consistent with our model, the active form of PTEN is membrane bound [46].

Figure 1.

(a) Schematic drawing of a computational cell moving on a flat surface. The model contains a membrane bound inhibitor (red symbols), together with an activator that can be both cytosolic (blue symbols) and membrane-bound (green symbols). The cell is modelled using the phase field with a membrane width of ε. The protrusive strength is a sigmoidal function of the height above the surface and reaches its median value at z = h. (b) Nullclines of the activator (solid line) and of the inhibitor for different values of the inhibitor activation rate c₂ (dashed lines) for the reaction–diffusion model with constant cytosolic activator concentration. The fixed point, represented by the intersection of the two nullclines, is either excitable (c₂ = 6), oscillatory (c₂ = 3), or non-excitable (c₂ = 1). The stable fixed points are indicated by a star while the unstable one is indicated by an open circle. (Online version in colour.)

The activator and inhibitor fields obey, as in our recent study [18], nonlinear reaction–diffusion equations:

$$\frac{\mathrm{\partial }A}{\mathrm{\partial }t}=D_A\mathrm{\nabla }\cdot (\mathrm{\nabla }A)+F(A)A_{\mathrm{cyt}}-G(R)A+{\zeta }_1(t)$$ 2.1

and

$$\frac{\mathrm{\partial }R}{\mathrm{\partial }t}=D_R\mathrm{\nabla }\cdot (\mathrm{\nabla }R)+\frac{c_{2}A-c_{1}R}{\tau }+{\zeta }_2(t),$$ 2.2

where D_A and D_R are the membrane diffusion coefficients for A and R, respectively, and are taken to be identical. In these expressions, F(A) is the self-activation of the activator with a functional form that is similar to previous studies: $F(A)=[k_a{A}^2/(K_a^2+A^2)+b]$ [13]. The activator is inhibited by R through the negative feedback G(R) = d₁ + d₂R while R is linearly activated by A, controlled by the parameter c₂. We will show below that varying this single parameter changes the dynamics of the model and can result in different migration modes (figure 1b). The timescale of the inhibitor τ is taken to be much larger than the timescale of the activator. Finally, to ensure robustness to stochasticity and to allow fluctuations, we add uniformly distributed spatial white noise terms 〈ζ_i(r, t)ζ_j(r′, t′)〉 = σδ_ijδ(r − r′)δ(t − t′).

To generate cell motion, we follow earlier studies and couple the output of the biochemical model to a mechanical module that incorporates membrane tension and cell–substrate adhesion [33,35]. To accurately capture cell deformations in simulations, we use the phase field method [33–35,47–50]. Here, an auxiliary field ϕ is introduced to distinguish between the cell interior (ϕ = 1) and exterior (ϕ = 0), separated by a diffuse layer of width ε (figure 1a). In this scheme, the membrane can be efficiently tracked by a contour of ϕ. We will take the protrusive forces, generated at the cell membrane, to be proportional to the levels of activator A and normal to the membrane. The phase field formalism has been shown to accurately reproduce shapes that minimize surface energy [50].

The evolution of the phase field is then determined by the force balance equation [33,51]:

$$\xi \frac{\mathrm{\partial }\varphi }{\mathrm{\partial }t}=\frac{\eta (z)A}{K_0+A}|\mathrm{\nabla }\varphi |-\frac{\delta H(\varphi )}{\delta \varphi },$$ 2.3

where the first term on the right-hand side is the active force that only acts at the membrane due to the $|\mathrm{\nabla }\varphi |$ term. Similar to earlier work [21], we assume that this protrusive force depends on the distance from the substrate, varying smoothly between approximately η₀ (close to the surface) to roughly η₀/2 (far away from the surface), with a midpoint located at z = h (see electronic supplementary material for details and for possible extensions to more complex environments). Furthermore, H(ϕ) is a potential describing the cell membrane tension, the adhesive interaction between cell membrane and the substrate, and the volume and surface conservation (see the electronic supplementary material for details). Finally, ξ is a viscous damping coefficient. Model parameters are estimated from known data or experiments and given in electronic supplementary material, table S1. We have verified that all biochemical parameters and tension and adhesion parameters can be varied by 10% without changing the qualitative results.

3. Results

3.1. Experimental determination of cell morphologies and signalling component distributions

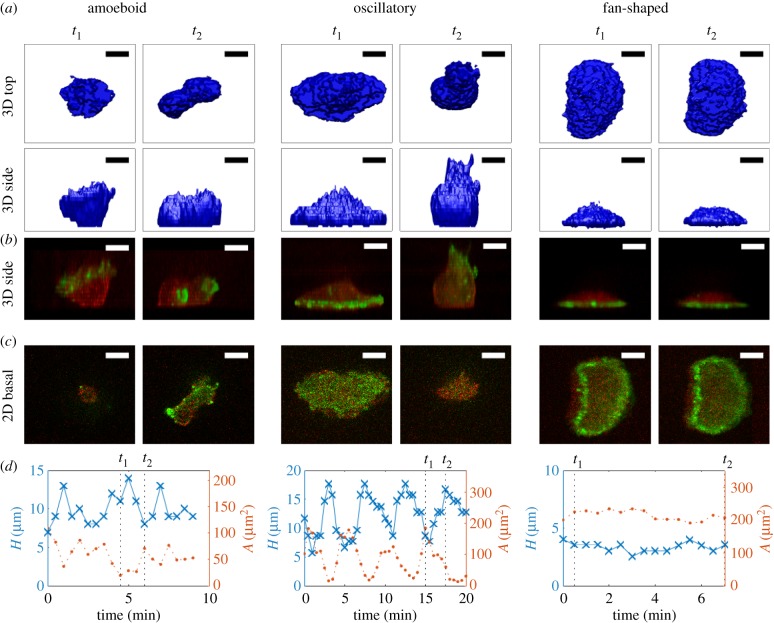
We first used the engineered Dictyostelium cells with fluorescent markers described in Miao et al. [13] combined with confocal microscopy to visualize the cell membrane (mCherry-FRB-Inp54p) and freshly polymerized actin filament (limE-YFP) during the three migration modes (see Methods). In figure 2a, we show snapshots of a top and side view of the morphology of an amoeboid-like cell at two different timepoints t₁ and t₂. The corresponding side view of the distribution of limE-YFP in green and mCherry-FRB-Inp54 in red is shown in figure 2b while these distributions for the basal plane are shown in figure 2c. As is well known, the morphology for this migration mode is constantly changing with pseudopods, which show elevated levels of freshly polymerized actin, protruding and retracting at different locations. This is also evident from the limE distribution in the basal plane that displays irregular patches of finite spatial size. As a consequence, the time dependences of the maximum height of the cell and the basal surface area are changing in a non-regular fashion (figure 2d) and the cell exhibits random movement. Importantly, the total surface area as well as the volume of the migrating cell remain roughly constant (electronic supplementary material, figure S1).

Figure 2.

Experimental 3D shapes and distributions for different migration modes. (a) Top and side view of the reconstructed 3D morphology of Dictyostelium cells migrating using the amoeboid mode (left two panels), the oscillatory mode (middle two panels) and fan-shaped mode (right two panels). (b) Corresponding side view, showing the distribution of mCherry-FRB-Inp54 in red and limE in green. (c) Distribution of mCherry-FRB-Inp54 and limE in the basal plane. (d) The height (blue line) and the basal surface area (orange line) as a function of time for the three different migration modes. The panels in (a–c) correspond to the timepoints t₁ and t₂, indicated by the dashed lines. (Online version in colour.)

The middle panels of figure 2a present two snapshots of an oscillatory cell. As is clearly seen from the plots of the maximum height and basal surface area (figure 2d), this cell shows a periodic spreading–retraction cycle with a period that is roughly 5 min. To distinguish these cells from amoeboid ones, we can employ several different metrics, including the variance in area [13], the centre of mass speed [18] or the autocorrelation of the time trace of the basal surface area. The latter is shown in electronic supplementary material, figure S2, where we plot this autocorrelation for both an amoeboid cell and an oscillatory cell. Fitting this autocorrelation with an exponentially decaying sinusoidal function reveals that the height oscillations of the amoeboid cell have a much smaller decay constant (24 s) than the oscillatory cell (570 s), allowing us to easily identify oscillating cells.

For the oscillating cells, limE-GFP appears in waves that rapidly travel to the periphery of the cell area during the spreading phase of the cycle while limE-GFP intensity is low during the retracting phase (figure 2b,c). Thus, the sizes of the elevated limE domains are much larger than the limE patches in the amoeboid-like cells. Since retraction is associated with the extension of the cell away from the surface, the cell height is negatively correlated with basal surface area (figure 2d). As in the previous migration mode, the total surface area and the cell volume remain constant (electronic supplementary material, figure S1). Oscillatory cells, however, do not migrate over significant distances [13].

In contrast to the previous two morphologies, a keratocyte-like cell takes on a near constant fan-shaped morphology (right panels of figure 2a). Indeed, both the maximum height and basal surface area are nearly constant (figure 2d) and we have verified that this is also the case for the total surface area and cell volume (electronic supplementary material, figure S1). As also shown by Miao et al., these cells display a near constant distribution of fluorescence intensity in the basal plane, corresponding to a ring of elevated level of limE near the periphery of the cell (figure 2c). This ring can also be seen in the side views presented in figure 2b, which demonstrate that it is localized close to the surface. The curved part of the membrane corresponds to the front of the cell, which moves at a constant speed in a persistent fashion [13,17,18] (electronic supplementary material, movie S1).

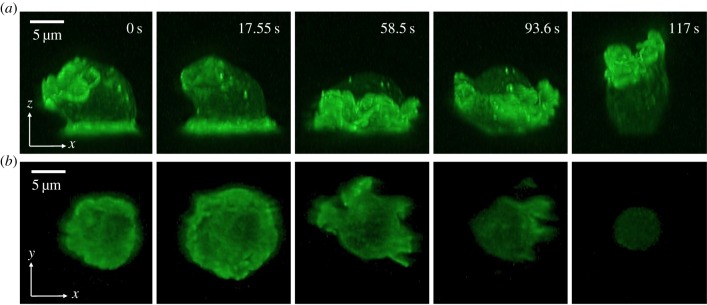
In the oscillatory cells, the limE-GFP wave in the basal plane travels to periphery, after which it disappears. We asked whether this wave continues and moves in the z-direction away from the surface, similar to waves of PtdInsP3 recently observed in immobilized cell [10]. Since it is challenging to track rapidly moving waves that propagate in the z-direction with confocal microscopy, we employed LLSM, which can acquire images with superior spatio-temporal resolution and minimal phototoxicity [52]. In figure 3a, we present five snapshots of a side view of an oscillating cell containing limE-GFP obtained using LLSM (see also electronic supplementary material, movies S2 and S3). The corresponding limE distribution in the basal plane is shown in figure 3b. The snapshots reveal a limE wave on the basal surface that is associated with an expanding area (wave speed 6 ± 2 μm min⁻¹, N = 7 waves). Once reaching the periphery of the basal plane, this wave continues to propagate along the membrane, away from the substrate and towards the ‘top’ of the cell. During this continuation, membrane in contact with the substrate moves upward and away from the surface, presumably due to contractile forces. The wave, however, continues to propagate along the membrane and reaches the substrate, after which the basal area expands again (electronic supplementary material, movies S2 and S3). As a result, the area of the basal surface shows a distinct oscillation.

Figure 3.

Light sheet microscopy of an oscillating cell. (a) Five different snapshots of the side view of an oscillating cell with limE-GFP. (b) The limE distribution in the basal surface plane for the time points corresponding to (a). (Online version in colour.)

3.2. Parameter tuning in model results in switching between migration modes

We next turned to simulations in an attempt to reproduce the experimentally observed morphologies and migration modes. Our activator–inhibitor system can exhibit different types of dynamics depending on parameter values. This can be most easily seen by examining equations (2.1) and (2.2) for constant values of A_cyt and plotting the nullclines of the resulting reaction–diffusion system (figure 1b). These nullclines intersect at the fixed point and its stability determines the ensuing dynamics. In our case, the location of the fixed point depends critically on the slope c₂ of the inhibitor nullcline [13,53]. For steep slopes, the intersection occurs for smaller values of A than its minimum, resulting in excitable dynamics: the system is stable but can be excited in finite time by sufficiently strong noise. For intermediate values of the slope, there is one unstable fixed point and the dynamics is oscillatory. Finally, for small values of c₂, the fixed point is stable [53].

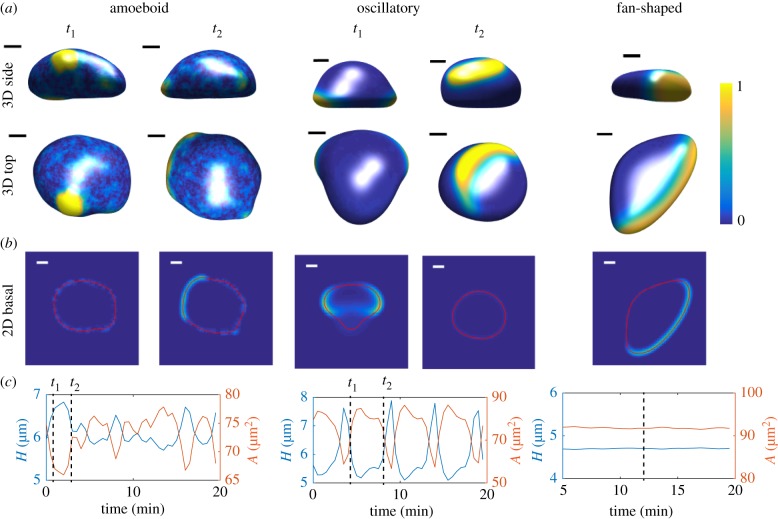
In our simulations, we systematically varied the activation rate c₂ to access the different dynamical regimes. For large values of c₂, corresponding to excitable dynamics, the cell will stay quiescent until noise generates fluctuations in A that pushes the system past the threshold and creates an excitation. During this excitation, the activator increases rapidly, followed by a slower increase of the inhibitor. Importantly, due to the conservation of activator, the spatial extent will be limited and the system will return to its steady state, resulting in local excitations with a finite lifetime. In our 3D simulations, this is manifested by randomly placed patches of activator. This can be seen in the left panels of figure 4a where we show the distribution of the activated membrane-bound A for two different times (see also electronic supplementary material, movie S4). These patches, also visible on the membrane of the corresponding basal planes (figure 4b), result in local protrusive forces and protrusions that have a finite size and lifetime, key criteria for pseudopods. Since the excitation of these patches is stochastic, the cell will show random movement while the surface area and cell height as a function of time are irregular (figure 4c).

Figure 4.

Three-dimensional simulations of migrating, deformable cells (η₀ = 6 pN). (a) Snapshots at two different time points t₁ and t₂ of the top and side view of a computational cell for c₂ = 6, resulting in amoeboid-like motion, c₂ = 4, resulting in an oscillatory cell, and c₂ = 1, resulting in a keratocyte-like cell with a fan-shaped morphology. The membrane-bound activator distribution is displayed using the colour scheme shown. (b) Corresponding distribution of activator in the basal plane (space bar here and elsewhere 5 μm). (c) Corresponding height (blue line) and basal surface area (orange line) as a function of time. The time points corresponding to the snapshots in (a) and (b) are indicated by the dashed lines. (Online version in colour.)

When the inhibitor’s activation rate is decreased to intermediate values the dynamics of the signalling system becomes oscillatory with both the activator and inhibitor exhibiting a stable limit cycle. As a result, in the spatially extended system, waves of activator and inhibitor continuously sweep over the surface of the cell (middle panels figure 4a; electronic supplementary material, movie S5). When an activator wave on the basal surface propagates to the periphery (i.e. the location where the membrane curves away from the surface) it exerts a protrusive force, which leads to an increase in the basal surface area (figure 4b). A continuous sequence of these events results in an oscillatory cell characterized by a basal surface area that shows clear periodic fluctuations (middle panels figure 4c). Due to the conservation of membrane area and cell volume, the height of the computational cell also shows oscillations that are out of phase with area of the basal surface.

As the inhibitor’s activation rate is further decreased, the spatially homogeneous system will only have a single steady state in which the activator’s concentration is high. In the full 3D system, however, the total amount of activator is conserved. The ensuing balance between the active and inactive activator is controlled by the parameter α and for large enough values the activator will only be activated in a limited region with the rest part of the cell remaining at a low level of the activator. The result is an activator wave and, as we have shown earlier, the coupling of this wave and cell mechanics can result in a cell with a fan-shaped morphology, moving with the speed of the propagating wave [18] (electronic supplementary material, movie S6). The top and side view of this cell is shown in the right panels of figure 4a. The distribution of the activator shows a large crescent at the front of the cell (figure 4b) and elevated levels close to the substrate (figure 4a). Furthermore, as the height and basal surface area plots show (figure 4c), this cell has a stable morphology and the cell moves persistently and with constant velocity.

3.3. Interplay of cell mechanics and signalling determines cell migration modes

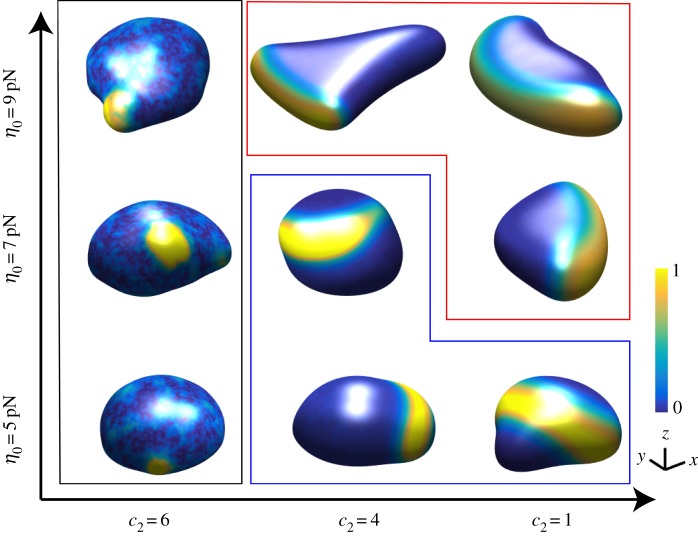
The results presented above show that changing a single parameter in the signalling model (the activation rate of the inhibitor) can determine the cell morphology and migration mode of the cell. We next checked whether changing the cell mechanics, specifically the protrusive strength η, can also change the migration mode. This was motivated by our recent 2D computational study, where we showed that changing the protrusive strength can have profound effects on the cell migration mode and morphology [18]. In figure 5, we show snapshots of simulations in the (c₂, η₀) parameter space. There results show that for intermediate and small values of c₂ we can change the migration mode from oscillatory to fan-shaped by increasing the protrusive strength. For small values of the protrusive strength, the wave speed is larger than the membrane speed, resulting in a wave that, when reaching the basal boundary, continues its propagation away from the basal surface. For larger values of η₀, the membrane speed matches the speed of the wave, resulting in a steady propagating front [18].

Figure 5.

Snapshots of cell morphologies (front view) in the in c₂, η₀ phase space. The activated membrane-bound activator is plotted using the colour scheme indicated by the bar. Cells within the black frame are amoeboid, within the blue frame are oscillatory and within the red frame are fan-shaped. (Online version in colour.)

4. Discussion

In this study, we have presented the results of a fully 3D simulation of cell migration. Most computational studies to date have focused on 2D shapes and morphologies. Restricting the numerical simulation to 2D obviously simplifies the computational complexity of the problem and greatly reduces simulation times. Although many interesting questions can be addressed by these 2D simulations, cell migration is ultimately a 3D process. In particular, events that explicitly involve the third dimension cannot be captured by 2D simulations and require a fully 3D model.

Our model uses the phase-field method to describe the cell mechanics. The advantage of this method is that it avoids the use of computationally expensive regridding of surfaces. Through the use of parallel computing on GPUs, we were able to make our simulations quite efficient. For example, a simulation that reproduces the results of figure 4c (i.e. 20 min of model time) only took 10 min of wall clock. This means that future extensions that address more complicated processes and geometries, further discussed below, should become feasible.

Our model is able to capture all three migration modes (amoeboid-like, oscillatory and fan-shaped) and produces morphologies that are qualitatively similar to the experimentally observed cell shapes (cf. figures 2 and 4). Furthermore, our activator dynamics and distributions are similar to the actin distribution found in our experiments (figure 2). The simulated amoeboid cell shows patches of elevated A at random sites with limited spatial extent, similar to the patches of actin that are present in the Dictyostelium cells [54,55]. The size of these patches, approximately 10 μm across, as well as their lifetime, roughly 60 s, are similar to experimental values (figure 4).

The computational fan-shaped cell shows a wide front characterized by a stably propagating wave of activator and a persistent mode of migration. This is qualitatively similar to the experimentally observed fan-shaped cells (figure 2) [13,18]. It is straightforward to measure the speed of the computational cell, and its value, approximately 7 μm min⁻¹, is similar to experimental values [18].

Finally, the oscillatory cells in our simulations show activator waves that continuously propagate along the membrane. Similar types of waves are also present in our engineered cells. Specifically, when we visualized actin using LLSM, we observed waves that propagate along the basal surface and continued their propagation along the membrane extending away from the surface (figure 3). Capturing this wave dynamics using confocal microscopy would be challenging. In fact, imaging the basal surface would result in waves that appear to stop at the boundary and would miss the continuous propagation. Our observations are consistent with recent work that shows 3D PtdInsP3 waves in Dictyostelium cells [10]. The resulting periodic modulation of surface area in our simulations has a period (approx. 5 min, figure 4) that is similar to the experimentally observed one (figure 2). The experimental period can also be obtained examining the autocorrelation, as we show in electronic supplementary material, figure S2 for the cells in figure 2. In addition, we can compare the wave speed on the basal plane using the LLSM results and the wave speed on the computational cell boundary that is in contact with the substrate. The experimental value and the numerical value were again found to be in close agreement: 6 ± 2 μm min⁻¹ versus 6.5 μm min⁻¹.

While the period and speed found in the model are close to the experimental values, the numerically obtained values for the area and height for the different modes presented in figure 4c are smaller than the experimental data (figure 2d). Our numerical results, however, were obtained using the same initial conditions and, thus, identical cell volume. Since the cell volume in our simulations is conserved, small initial cell volumes will result in small surface areas and heights. For example, the initial volume of our computational oscillatory cell was roughly three times smaller than the corresponding experimental one (see electronic supplementary material, figure S1), leading to a smaller amplitude in the height oscillations. Importantly, we can rescale length in our simulations, which will result in larger cells, provided that we rescale the diffusion length accordingly. We have verified that we are able to obtain the three different migration modes for a wide range of diffusion constants such that our model can produce a large range of cell sizes. One morphodynamic feature in the experiments cannot be captured by a simple rescaling of our model. The surface area of the oscillating cell varies by a factor of roughly nine during the oscillations (figure 2d), much larger than in the simulations (figure 4c). The small value of the minimum surface area is most likely due to contractile forces generated by myosin, a feature that is currently not present in our model.

Crucial in our computational approach is the coupling between intracellular signalling and cell mechanics. The membrane-bound activator A is responsible for generating protrusive forces and these forces result in membrane deformations and cell motion. Membrane deformations, however, also couple back to the signalling pathways [40,49]. As we have described recently, and also shown here, the motion of fan-shaped cells is determined by an activator wave that pushes the front of the cell forward. This wave is only stable if the membrane can ‘keep up’ with the speed of the wave [18,56]. This coupling between cell deformation and signalling is also evident in oscillatory cells where a wave of activator propagating along the basal surface results in spreading of the cell (figure 4). Once this wave leaves the basal surface, it continues to propagate along the membrane where it exerts protrusive forces. Consequently, the basal surface area decreases and a repetitive cycle of this event results in an oscillatory cell.

Our study uses a very simple biochemical reaction–diffusion model with only two components. Key in generating different migration modes is the ability to switch between different dynamics of the underlying model (figure 1). Note that this switching has also been part of earlier models for cell migration [13,18]. Interestingly, our results point to a possible role for the substrate. In our model, the protrusion strength was made larger close to the surface than further away. This assumption was motivated by earlier experimental results, which show that actin polymerization is localized close to the substrate [50,57]. We have explicitly verified this asymmetry in our fan-shaped cells (electronic supplementary material, figure S3). Without this asymmetry, the activator concentration in the fan-shaped cell is not constrained to the substrate and is thus at odds with the actin distribution observed in the experiments (figure 2). Furthermore, without the asymmetry, the front of a computational fan-shaped cell will not be as thin as the front observed in experiments (figure 2).

We have verified that making other model parameters, and in particular biochemical ones, dependent on z can also generate the observed migration modes. Specifically, when the activation rate of the inhibitor c₂ depends on z, we can obtain comparable cell morphologies and a similar phase diagram as in figure 5 (see electronic supplementary material and figure S4). In these simulations, we have taken the value of c₂ to be large away from the substrate. As a result, waves along the basal surface will not extend in the third dimension, effectively constraining wave propagation to the cell bottom. Thus, this version of the model is close to a 2D model, as studied in our earlier work [18].

Even though our simulations can reproduce the experimental morphologies, there are differences between the experiments and our simulations. Specifically, the morphology of the simulated fan-shaped cell shows minor differences compared to experimental morphology. Particularly, the back of the experimental fan-shaped cell is more straight and less ‘triangular’ than in the simulations. This slightly triangular back is most likely due the absence of any contractile forces in our computational model. Experimentally, these forces are generated by myosin which, in actual keratocytes, shows elevated levels close to the back [58].

Although we have applied our computational model to engineered Dictyostelium cells, our methodology should be applicable to other cell types as well. Specifically, our model predicts that wave propagation should underlie cell migration in different cells, including neutrophils and neutrophil-like HL-60 cells. In that case, one should be able to produce and switch between the different migration modes described here by manipulating the protrusive strength. Furthermore, it can be extended to address more migration under different conditions and in more complicated geometries. For example, it is possible to couple the reaction–diffusion model to an external chemoattractant gradient, as carried out before [13,32,39]. This would allow to simulate 3D cells chemotaxing to gradients. Also, migration within confined geometries such as narrow channels or capillaries can be addressed with proper extensions [25,57,59]. Finally, extensions that can simulate migration within physiologically relevant extracellular matrix fibres [23] could potentially result in a deeper understanding of cell migration.

5. Methods

5.1. Cell culture and preparation

For the confocal experiments, wild-type AX2 cells were transformed with the plasmids pB18 expressing mCherry-FRB-Inp54p and pDM358 expressing both N150-FKBP-FKBP and LimE-YFP. For the lattice light sheet microscope experiments, AX2 were transformed with the plasmids pDM358 expressing N150-Inp54p and pDM115 expressing limE-delta-coil-YFP. Cells were grown at 22^°C in HL5 media supplemented with G418 (20 μg ml⁻¹) and hygromycin (50 μg ml⁻¹) in 10 cm Petri dishes and used when 50–80% confluent. On the day of the experiment, cells were washed with DB (5 mM Na₂HPO₄, 5 mM KH₂PO₄, 200 μM CaCl₂, 2 mM MgCl₂, pH6.5) and collected from the Petri dish. 3 × 10⁵ cells were then plated in 6 ml of DB in a 50 mm round chamber with glass bottom (WillCo). After 15 min, cells attached to the substrate and rapamycin was added if required (cells expressing mCherry-FRB-Inp54p and N150-FKBP-FKBP). To add the drug, a 1 μl aliquot of rapamycin at 10 mM was diluted in 200 μl DB, vortexed and transferred to the sample. Final concentration was 1.7 μM. About 20 min later, experiments were performed.

5.2. Imaging and analysis

For the confocal microscopy experiments, fluorescent images (488 nm and 561 nm excitation) were captured every 15 s with a 100 × oil objective on a spinning-disc confocal Zeiss Axio Observer inverted microscope equipped with Roper Quantum 512SC cameras. For each timepoint, a z-stack was recorded first for the RFP channel collecting light with a 575–650 nm filter and then for the GFP channel (500–550 nm filter). About 25–30 planes every 500 nm or 1 μm were captured for each channel in a total time of less than 2 s for each timepoint.

To visualize and analyse the cell surface area, we used the RFP channel that quantified the localization of mCherry-FRB-Inp54p at the membrane after the addition of rapamycin. Pixels within this boundary were detected using a custom MATLAB algorithm (2018a; The Mathworks) and basal surface area and height were then computed as a function of time. 3D fluorescent views were obtained from Slidebook 6 (Intelligent Imaging Innovations).

LLSM imaging was performed on a home built lattice light-sheet microscope following the design described by Chen et al. [52]. Detailed design information was graciously provided by the Betzig group at the Howard Hughes Medical Institute Janelia Research Campus. We modified the optical layout, while maintaining the same relative optical component locations to match the original design and achieve the same optical performance. A 488 nm laser beam (Coherent Genesis MX), with a total output of 0.2 mW, was shaped with two cylindrical lens pairs to illuminate a square lattice pattern, corresponding to 73 Bessel beams, displayed on a spatial light modulator (Forth Dimension Displays, SXGA3DM) positioned conjugate to the sample focal plane. The Fourier transform of the resulting beams was projected by a 500 mm lens onto an annular mask, conjugate to the back focal plane (BFP) of the excitation objective lens. The annular mask placed at the BFP, numerical aperture 0.40 (outer diameter) and 0.35 (inner diameter) of the excitation objective lens, spatially filtered the pattern to remove unwanted diffraction orders. This annular mask provided for a beam waist with a 30 μm full width half maximum and sheet thickness at the centre of 0.96 μm, measured by scanning and imaging 0.2 μm beads (Thermo Fisher Scientific F8811). The BFP was projected onto galvo mirrors and used to dither the lattice pattern in the x-direction continuously over a 30 μm range in 0.15 μm steps for even sheet illumination. The fluorescence signal was imaged with a sCMOS camera (Hamamatsu Photonics Orca Flass4.0 v3) through a bandpass filter ET525/50m (Chroma Technology) with a 20 ms exposure time. All imaging was performed at room temperature in DB (5 mM Na₂HPO₄, 5 mM KH₂PO₄, 200 μM CaCl₂, 2 mM MgCl₂, pH6.5). To acquire 3D images, the sample was moved in 0.9 μm steps over a 35 μm range by the piezo stage it was mounted on. This corresponds to 0.47 μm steps and 18 μm range in the detection optical axis because of a 31.5^° angle between the stage axis and the light-sheet plane. The image volumes were de-skewed accordingly and deconvoluted based on a measured point spread function with the publicly available software algorithm cudaDecon (https://github.com/dmilkie/cudaDecon). Post-processing of the lattice light was carried out using the open-source Python library llspy (https://github.com/tlambert03/LLSpy).

Data accessibility

Data are provided in the electronic supplementary material.

Authors' contributions

Y.S. developed algorithms and carried out the simulations, participated in data analysis, participated in the design of the study and helped draft the manuscript; E.G. carried out all experiments, carried out statistical and data analyses and critically revised the manuscript; Y.M. advised on experimental protocols and critically revised the manuscript; C.M. aided with the LLSM experiment analysis and critically revised the manuscript; H.H. participated in the LLSM experiments and analysis and critically revised the manuscript; S.L.R.P. advised on LLSM and its analysis and critically revised the manuscript; P.N.D. participated in study design and critically revised the manuscript; W.J.R. designed the study, coordinated the study and drafted the manuscript. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Science Foundation under grant no. PHY-1707637, the National Institutes of Health under grant no. R35GM118177, and by Human Frontier Science Program grant no. LT000371/2017-C.