Behavioural analysis of single-cell aneural ciliate, Stentor roeseli, using machine learning approaches

Abstract

There is still a significant gap between our understanding of neural circuits and the behaviours they compute—i.e. the computations performed by these neural networks (Carandini 2012 Nat. Neurosci. 15, 507–509. (doi:10.1038/nn.3043)). Cellular decision-making processes, learning, behaviour and memory formation—all that have been only associated with animals with neural systems—have also been observed in many unicellular aneural organisms, namely Physarum, Paramecium and Stentor (Tang & Marshall2018 Curr. Biol. 28, R1180–R1184. (doi:10.1016/j.cub.2018.09.015)). As these are fully functioning organisms, yet being unicellular, there is a much better chance to elucidate the detailed mechanisms underlying these learning processes in these organisms without the complications of highly interconnected neural circuits. An intriguing learning behaviour observed in Stentor roeseli (Jennings 1902 Am. J. Physiol. Legacy Content 8, 23–60. (doi:10.1152/ajplegacy.1902.8.1.23)) when stimulated with carmine has left scientists puzzled for more than a century. So far, none of the existing learning paradigm can fully encapsulate this particular series of five characteristic avoidance reactions. Although we were able to observe all responses described in the literature and in a previous study (Dexter et al. 2019), they do not conform to any particular learning model. We then investigated whether models inferred from machine learning approaches, including decision tree, random forest and feed-forward artificial neural networks could infer and predict the behaviour of S. roeseli. Our results showed that an artificial neural network with multiple ‘computational’ neurons is inefficient at modelling the single-celled ciliate's avoidance reactions. This has highlighted the complexity of behaviours in aneural organisms. Additionally, this report will also discuss the significance of elucidating molecular details underlying learning and decision-making processes in these unicellular organisms, which could offer valuable insights that are applicable to higher animals.

1. Introduction

Since the 1700s, many behaviours observed in lower unicellular organisms, such as Physarum, Paramecium or Stentor, have been successfully demonstrated to satisfy many of the existing learning paradigms, from simple non-associative [1–5] to more complex associative models [6,7]. These observations have left scientists puzzled. To what extent do these organisms possess an awareness of their surroundings? Is it at all comparable to that experienced by higher animals? Herbert Jennings—one of the most influential biologists in the field of behaviours in aneural organisms—published some very detailed written accounts of the unique response seen in the single-cell ciliate Stentor roeseli upon mechanical or chemical stimulation [8]. In particular, when stimulated with carmine particles (figure 1), the organisms were described to perform a series of five characteristic observable avoidance reactions in order to remove themselves (or ‘to leave’) from the noxious stimulus, provided that the particles were persistently present in the surrounding environment. This complicated sequence of reaction or avoidance behaviours was acknowledged as one of ‘the most intricate behaviours so far recorded in unicellular animals' by Dennis Bray [10]. The five reactions are generally seen to occur in a particular order (figure 2), albeit with several variations. These hierarchical avoidance behaviours indicate that the internal state of the organism has changed to respond differently to the same stimulus. In this study, we have considered this hierarchical avoidance reaction of Stentor as a consequence of cell decision-making process at each stage and investigated it. Jennings was able to follow the same organism through multiple rounds of stimulations and show that sometimes, the typical response order is not strictly followed, or that time taken to switch between different avoidance reactions varies widely from one organism to another. He was also able to demonstrate that these differences in response are not due to fatigue, and thus concluded that the organism had performed some form of complex learning—an altered response due to prior experience [8]. We will not be discussing this aspect of Jennings' work.

Figure 1.

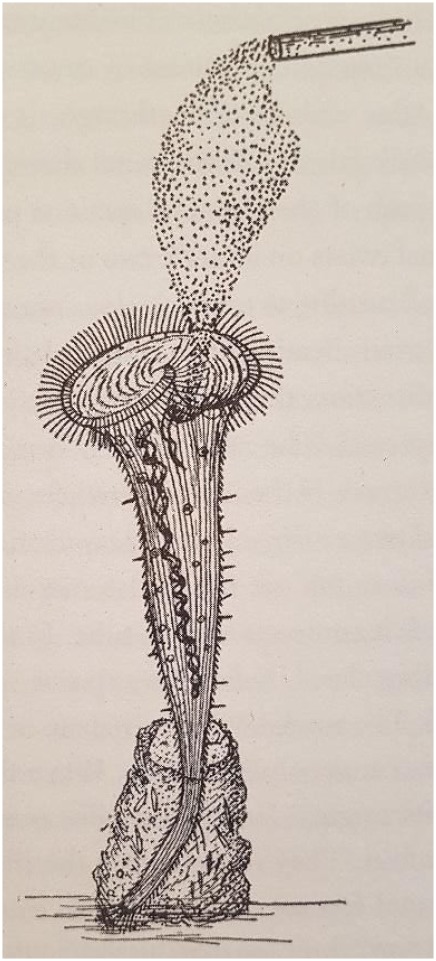
A sketch of carmine particles introduced to the buccal cavity of a S. roeseli. Illustration of the experiment from Jennings' paper [9]. Carmine particles are released over the mouth of a S. roeseli that are attached to a surface via its tube and holdfast. (Online version in colour.)

Figure 2.

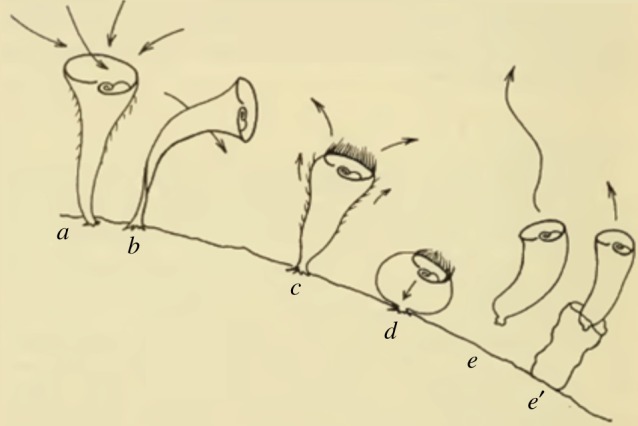
Series of five avoidance reactions observed in S. roeseli. This is Vance Tartar's illustration of the five reactions of S. roeseli stimulated by carmine in the order described by Jennings [11]. As long as the stimulus is still present in the surrounding environment, these five reactions are: (a) no response—at rest. (b) Bending away from the source. (c) Transient stop of cilia beating, reversal of spiralling direction. (d) Strong full contraction. (e) Detachment and swim away. (Online version in colour.)

Multiple attempts to characterize this intriguing behaviour were later carried out, some of which challenged Jennings' proposition [12,13]. However, some of these subsequent experiments used a related but more motile species—S. coeruleus. Thus, the exact Jennings' observations were not seen and hence the avoidance behaviours were considered irreproducible. In an earlier work [14], S.P. and colleagues developed a video-microscopy experimental paradigm and used S. roeseli to duplicate Jennings' experiments. This study verified Jennings' findings of a complex hierarchy of avoidance behaviours, which indicated a complex decision-making process underlying the behaviours. These earlier studies were able to demonstrate that the observations in S. roeseli did not conform to any existing learning model for single-cell organisms—they did not indicate habituation nor adaptive sensitization (which may require more than a lifetime to acquire!). Staddon had earlier suggested that it could be operant behaviour—behaviour ‘guided by its consequences’, and proposed some possible mechanisms, yet, no concrete conclusion was made [15].

Since there is no current learning model that can fully explain the series of avoidance reactions or cell decision-making process in S. roeseli, we examined if the decision ‘to leave’ could be predicted from time spent performing each of the avoidance reactions using models based on decision tree, random forest and artificial neural network (ANN) machine learning algorithms. ANNs have proven their power with notable successes in applications across numerous fields, including modelling complex cognitive activities in higher animals [16,17]. We set out to explore how effective ANNs are at predicting S. roeseli's behaviour, and are particularly interested to find out the number of computational neurons required for an ANN to be proficient at predicting the behaviour observed in a single-celled organism.

2. Replication of Jennings' original experiment and heterogeneity in Stentor roeseli's behaviour

We replicated Jennings' experiment and validated the complexity of the observed behaviours by Dexter et al. [14]. Upon stimulation with red-fluorescent latex beads, we were able to observe all of the five avoidance reactions described by Jennings (electronic supplementary material, video-1). Electronic supplementary material, figure S1 shows our simple experimental set-up. When unstimulated, Stentor do not show any behavioural changes (electronic supplementary material, video-2). This is important to note because we want to assert that the hierarchical behavioural response that we see is only after stimulation with the beads.

We used a light microscope to observe and record the behaviour of S. roeseli and a gravity-based water reservoir was used for pulsed bead stimulations. Since observations provided by Jennings were only a qualitative description via words and sketches, with experimental methods not being documented in detail, all observations were subjected to our own interpretation as illustrated in figure 3. The high level of heterogeneity in S. roeseli's behaviour upon stimulation noted by Jennings [8] was also detected. The order of the series of reaction is not always the same as that illustrated in figure 2. In many instances, halting and reversing in direction of cilia beating took place before obvious bending was seen, but contraction always preceded leaving. The extent to which bending movements were performed varied massively. Generally, each of the five responses was repeated for a while before the organism decided to move on to the next, with large differences in the number of repeats for each response between organisms. Moreover, many individual S. roeseli did not demonstrate all five reactions, with some omitting bending, and others immediately detaching. Occasionally, some S. roeseli immediately contracted upon stimulation. However, this could have been a reaction to the strong water pressure from releasing the beads into the environment.

Figure 3.

Example observations of S. roeseli's different behavioural responses upon stimulation with polystyrene beads. (a) At rest: S. roeseli is fully extended with cilia beating to generate a vortex current. (b). Bending. (c) Transient halting of cilia beating (arrow). (d,e) Full contraction after encountering the fluorescent beads. (f) The organism slowly extended after contraction until full length is reached. (g,i) Tube abandonment and leaving. (Online version in colour.)

Performing the experiment repeatedly with absolute consistency of control variables was challenging. This may or may not have affected the behaviour of S. roeseli across experiments. For instance, experiments typically involved recording over five sessile S. roeseli simultaneously due to time limitations. Thus, it can be hard to distinguish if contraction of these organisms was a response to stimulation or due to collision with others swimming in close vicinity. Additionally, the amount of beads released into the environment for each experiment was, although roughly the same, not exact. In five out of 188 organisms that we recorded, we could not attribute the contractions to stimulation by beads, hence we removed those observations from the machine learning models.

Analysis of the video recordings was not always straightforward. Cilia movement was only clearly observable when the organisms were positioned correctly in the plane of focus. Quite often, the organism bent in multiple directions throughout the course of the experiment, and therefore, their cilia were not always observable. Moreover, the reversal of cilia beating is usually accompanied by a twist or slight bending, which could lead to potential mis-classification of response if cilia were not observable. Another factor that could impact the quality of input variables is that the videos collected are of different length (see Material and methods). In an attempt to mitigate these factors, experiments where these issues were more pronounced were discarded from analysis. Being aware of all the complications and the wide variation in the behaviours of S. roeseli, we were extremely cautious and very careful to make the most consistent and quantitative analysis possible.

3. Stentor avoidance behaviour does not fit into any existing learning paradigms, including operant behaviour

Operant behaviour is described as a form of goal-directed behaviour. This learning model suggests that S. roeseli's decision of switching from one response to the next is underpinned by a mechanism that ‘compute[s] the relative importance of time [spent repeating a particular response] and concentration [of the noxious substance in its vicinity]’ [15]. Staddon suggested a mechanism whereby the five reactions were graded according to their cost (energy expenditure ± forgoing the opportunity to obtain further food), with each successive reaction only occurring above a certain threshold concentration of noxious beads. Additionally, each threshold elevates as the reaction continues to occur—i.e. a form of habituation—and eventually, will overtake that of the next reaction in the series, resulting in a switch in behaviour. However, this seems to imply that the organism needs to go through the whole sequence of five reactions in the exact order every time it is stimulated. Yet, this was not always the case in our experiments. There were multiple instances where the first two or three stages were skipped, or the order of reactions was not followed. Staddon also mentioned that the above mechanism was just one of the many possibilities one could come up with. Ultimately, he conceded that the exact operant behaviour mechanism could not be verified without further physiological and behavioural analysis.

4. Modelling Stentor roeseli's avoidance behaviour using machine learning approaches

We decided to use the time (in seconds) spent performing each of the avoidance reactions described by Jennings as features to train our machine learning models. This includes the duration of (1) being at rest, (2) bending, (3) cilia reversal and (4) contraction (electronic supplementary material, video 1). Detachment was used as an outcome in our model, and so the fifth feature included was (5) number of contractions observed. There are many more features that can be extracted from the raw data collected from analysing the videos, such as dynamics of contraction and retraction, time taken for each contraction or order of events taking place, etc. Nonetheless, as the dataset is relatively small, it is not appropriate to use too many features to train the models. A summary of compiled raw data that were used in the machine learning analysis can be found in table 1 and links to the videos of all organisms are given in electronic supplementary material, table S1.

Table 1.

Stentor roeseli behaviours. Behaviours are summarized in a symbol sequence, as described in figure 3. A comma (,) separates behaviours of different organisms in the same experiment. Days on which the data is collected are listed. Videos for each experiment are available on Mendeley; see electronic supplementary material, table S1 for access information.

date	exp no.	duration (s)	pre-stimulation	behavioural sequence
6 Feb 2019	1.1	225	n.a.	BR, BL, BL, RBC
	1.2	712	r(0 : 5)	BRCL, BRCL, BRCBCL, BRCBRCL, BRCBRCL, BRCL, BRCBRCL, BRCL, BRCL, BRCBRC
	1.3	168	rB(1 : 17)	BRCL, RCL
8 Feb 2019	2.1	840	n.a.	BCRL, BRL, RBRB, BRCBRC
	2.2	677	rB(0 : 36)	BRCL, BRL, BRCL, BRCL, BRL
	2.3	526	r(0 : 7)	BRCL, BRCL, BL, RBL, BRCL, BRCL, RBCBRL, BRCBRCL, BRL, BRL, BL, BCL, BL
11 Feb 2019	3.1	174	r(0 : 11)	RBCL
	3.2	760	rB(0 : 9)	RCBRCL, BRCL, RBRB
	3.3	822	rB(0 : 11)	BRCL, BRL, BRL, BRL
12 Feb 2019	4.1	1248	rB(0 : 10)	L, BL, BRCL, BRL, BRBRL
	4.2	1141	r(0 : 13)	BRL, RBRB, BRL, RBRBC, BRBRCBR, BRBR, BRBRL, BRL, BRBR
22 Feb 2019	5.1	191	r(0 : 5)	BRL
	5.2	169	rB(0 : 12)	RBCL, RBRBL
	5.3	308	r(0 : 11)	RBL
26 Feb 2019	6.1	388	r(0 : 6)	BRCBRC, RCRBRC, CRCL
	6.2	543	rB(0 : 7)	BRL, BRCBR, BCRBCRBL, BRCBRL, BRL, BRL, BCRCRCL, BRCBRCRC,
	6.3	607	rB(0 : 8)	BRCBRC, BRCRCR, BRBRCR
27 Feb 2019	7.1	579	r(0 : 7)	BCRL, BCRBCRC, RBCRBCL, BCRBCRCL, BCRBRCL, BRCRCL, BCL, BRCL, BCRCR, BRCL, BCRCL, BCRBCRBCL, BCRBCRC
	7.2	708	n.a.	BCRCRC, CBRC, BCRCL, CRCRC, BCRCBRCL, BRCRC, CBRCL, BCRCL, CRBCRBCRCL, CBRCRC, RCBRCRCL, RCRC, BRL, BRC, CRCL
	7.3	944	n.a.	BRCL, CBCRCR, BCRCL, CBCRCL, BRBCL, CBCRCL, CBRCL, CBCRCR, BCRCRCL, BCRC, CRC, BCRCL, RCBCRL, RCBCL, BRCL, BCRCL, CRCL, BRCBRCL
28 Feb 2019	8.1	238	r(0 : 12)	RBCL
	8.2	933	r(0 : 9)	BCRCL, BCRCR, BRCRCL
	8.3	719	r(0 : 7)	BRCL, BCRCL, BCRCL, BRCL, BCBCRCL, BCRCL, BCRCL, RL
	8.4	702	rB(0 : 7)	RBCL, RCBCL, BCRCL, CRCL, CL, CRBCL, BCRCL, BCRL, BCL, BCL
	8.5	949	rB(0 : 11)	BCRCL, RCRCL, BCRCL, CRC, CBCR, CBCL, BCL, CRCL, BCRCL, CRCL, CRCL, BCRCL
4 Mar 2019	9.1	852	rB(0 : 7)	BRL, RBCL, CRCL, CRC, CRCL, CRCL
	9.2	765	n.a.	BCL, RBC, BRL, CRCRC, RL
	9.3	865	n.a.	BCL, BCRCR, BRCR, CBRC, BRC, RCL, BCRL, BRCL, BRCL, BRCL
	9.4	704	r(0 : 11)	RC
5 Mar 2019	10.1	964	n.a.	RBCL, RCRC, BRCL, BRCR, BCR, RCR, BR

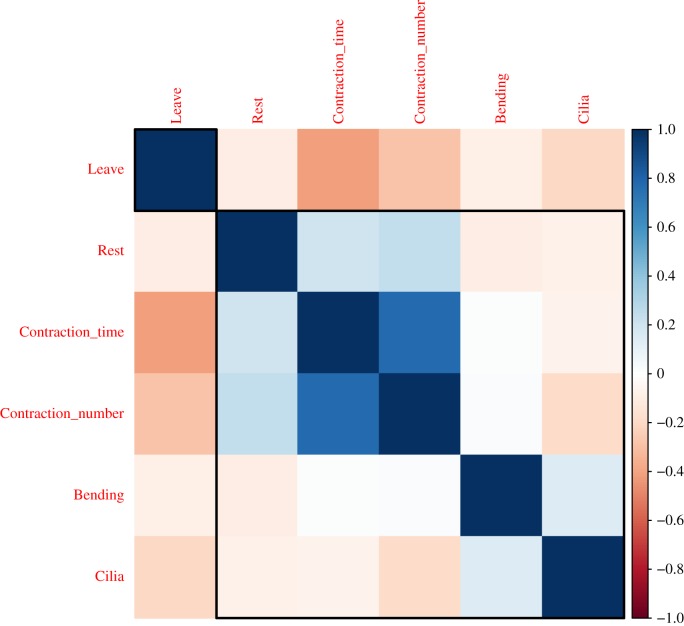
The correlations between these features were investigated (figure 4). The results showed that contraction time and number of contractions are highly positively correlated, which is to be expected as the longer the organism spent in the contraction stage, the more opportunities they would have to perform contractions. With respect to the outcome ‘Leave’, the duration of contraction and cilia reversal stages are the most negatively correlated features, with the number of contractions having a slightly less negative correlation.

Figure 4.

Correlation between five input features and output. The five input features that were used in the analysis are time spent at rest (Rest), bending (Bending), halting and reversing cilia (Cilia), contraction (Contraction_time) and number of contractions (Contraction_number) and output is determined as whether or not the organism detached and swam away (Leave). The correlation plot shows Contraction_time, Contraction_number and Cilia being negatively correlated (orange/light pink) to the outcome (in order of decreasing correlation strength—indicated by the decrease in the colour darkness). (Online version in colour.)

The first classification model was based on the decision tree algorithm. The tree-like flowchart (figure 5) was generated, with each internal node representing a ‘test’ on an attribute, and the outcome of the test—the decision—is displayed on the branch. The decision is made at each branch until it comes to the termination point. At each node, data points are initially segregated based on all input variables individually, and the split that generates the most homogeneous classes will be chosen and displayed. Thus, the decision tree model identifies the significance hierarchy of input features used by the model after being trained. Figure 5 shows the result from decision tree analysis, the condition to split the observations at each node is written. For each observation at each node, if the answer to the condition stated is ‘yes’, it is branched to the left, otherwise (i.e. ‘no’) branched to the right. Those observations with Contraction_time greater than or equal to 0.29 (after normalization), they are classified as 0 (i.e. not Leave), with a probability of 0.88. Those with Contraction_time shorter than this threshold, if their time spent in Cilia Reversal is greater than or equal to 0.5 (after normalization) are also classified as 0. Only those with Contraction_time shorter than 0.29, and Cilia time shorter than 0.5 are classified as 1 (Leave) with a probability of 1.00. Thus, the result implies that organisms spent a long time performing contractions and reversing cilia tend to be classified as ‘not Leave’.

Figure 5.

Tree representation of the classification process performed by the decision tree model on the training dataset. At each branch, a decision was made based on the feature printed to classify the dataset into class 0 (did not leave) or class 1 (did leave). The model used Contraction_time and then Cilia to classify the whole training dataset in two steps. Each box represents a group being classified, showing the class predicted, the probability of a correct prediction and the size of the group as a percentage of the whole training dataset (e.g. in box 2, the probability of an organism in this group belonging to class 0 is 0.88, and the group contains 24% of the whole training dataset). (Online version in colour.)

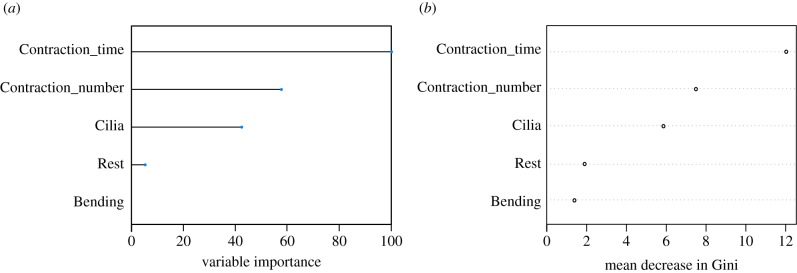
The second model we used was random forest. It is a different tree-based model, in which multiple trees are generated at the same time instead of the single tree approach that decision tree uses. Each tree will categorize a subset of the training dataset based on a random selection of input features, but only the variable with the highest association with the target will be chosen. The predictions generated from this collection of decision trees will be analysed further and the class of highest ‘votes’ will be chosen as an overall result. Random forest model also allows variable importance to be assessed and extracted in the format of a ranking (figure 6). The mean decrease Gini measures the average reduction in purity of splitting events. Features that are highly correlated with the outcome seem to contribute more to the variation, hence, usually found most useful for prediction as they tend to help splitting mixed nodes into those with higher purity (indicated by Gini index). Here, the top three variables chosen by the model are, again, time spent in contraction, cilia reversal and number of contractions, in order of decreasing importance.

Figure 6.

Variable importance extracted from random forest model. (a) The degree of importance of each input feature in classifying the training dataset, represented as percentage: Contraction_time being the most important variable with 100% importance; followed by Contraction_number, Cilia, Rest and Bending. (b) Contribution of each feature to the mean decrease in Gini index (indication of node impurity). The higher the decrease in Gini index, the higher the contribution of the feature to the nodes homogeneity. (Online version in colour.)

The algorithms performed by decision tree are relatively clear, as we can examine the computations generated by the model, while random forest is more complicated with a big forest of deep trees. To gain a full understanding of the decision process by examining each tree is almost impossible. Although these approaches are easy to interpret and provide straightforward visualizations, their level of depth in inferring relationships and patterns from the dataset is relatively poor. Since they mainly pick out variables that have the most significant impact on making predictions, they fail to capture other finer and more subtle details from the training dataset involving the rest of the input variables. Although the first two reactions in the series of five were not useful predictors in the decision tree model, this does not imply that these behaviours do not serve some function to Stentor.

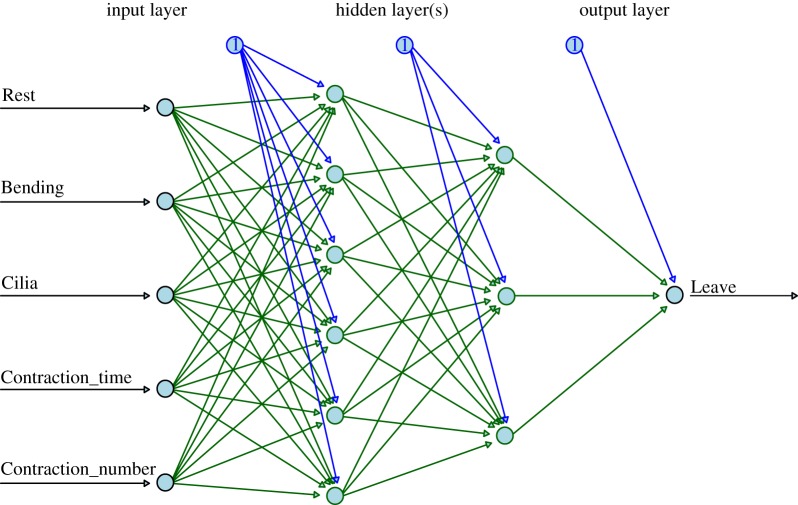
Hence, feed-forward neural networks were used to further investigate the series of response in S. roeseli. These networks are made up of structured layers of computational neurons called ‘perceptrons’ (figure 7), mimicking actual biological input and activation architecture of real neurons. An input layer takes in information from all training features, which are then passed on to hidden layer(s). There can be more than one hidden layer, and the perceptrons architecture can be customized. The more hidden layers there are, with highly intricate connecting algorithms, the more complex the network is, and hence the ‘deep’ learning. These layers then perform computations that cannot, yet, be understood. The output of one layer is used as an input for the next layer. Eventually, it will reach the final output layer, where the predictions are made.

Figure 7.

Schematic of an ANN architecture. This particular ANN has an input layer with five perceptrons (circles) for five input features; two hidden layers: the first one with six perceptrons, and the second one with three perceptrons; and one output layer with one perceptron for binary classification outcome. Circles with number 1 are bias nodes that are added in order to increase the freedom/flexibility allowing the model to perform best at learning the dataset. Without bias nodes, output of each layer is just the multiplication of input values to corresponding weights. (Online version in colour.)

Three feed-forward models were compiled with different hidden layer architecture and complexity (table 2). Briefly, the collected dataset (188 observations) was scaled and randomly split into training (70%) and test dataset (30%). A down-sampling method was applied to the training dataset to ensure a 1 : 1 ratio between two classes (‘Leave’ and ‘Did not leave’), avoiding potential problems (such as over-fitting) caused by imbalanced data. The new training dataset is then shuffled before being used to train the models. A 10-fold cross-validation with 10 repetitions was used to train the models.

Table 2.

Metrics used to evaluate performance of three multilayer neural network models.

	model 1	model 2	model 3
hidden layer architecture	1 hidden layer 6 nodes	3 hidden layers 20, 10, 6 nodes respectively	2 hidden layers 9, 18 nodes respectively
accuracy (%)	58.93	64.29	58.93
F1 score	0.4091	0.2857	0.4889
specificity	0.5952	0.7619	0.5238
sensitivity	0.5714	0.2857	0.7857
AUC (%)	63.2	66.2	73.0

After being trained, the performance of these models on a novel dataset can be evaluated using several different metrics. Some of these are summarized in table 2, as well as being demonstrated through the receiver operator curves (ROC) curves (figure 8). Accuracy implies the ratio of the number of correct predictions out of all predictions made, and therefore, it seems like the higher the accuracy, the better the performance intuitively. Yet, this is not always the case, especially if statistical tests show that it is not significant, or if the dataset is imbalanced. F₁ scores are one of the most popular metrics used for the evaluation of machine learning algorithms. It is a measure of the model's precision and robustness. Generally, the higher the F₁ score, the better the performance, as it shows that not only could the model make predictions with adequate accuracy, but it also did not miss out too many difficult instances. Other evaluation metrics include the model's sensitivity (i.e. true positive rate or TPR) and specificity (can be interpreted by false positive rate or FPR), which can be summarized into ROC curves (figure 8). TPR indicates the proportion of class 1 samples that were correctly classified, whereas FPR indicates the proportion of samples classified as class 0 that are false positives. When the ROC curve is above the diagonal line, it means that the proportion of correctly classified samples in class 1 is greater than the proportion of samples that were incorrectly classified as class 0. The area under this curve (AUC) is particularly widely used as an evaluation metric for binary classification problems, which is very applicable in our experiment. The AUC helps to compare different ROC curves for multiple machine learning models, and therefore, provides a measurement of model performance. Typically, the higher the AUC value, the better the performance.

Figure 8.

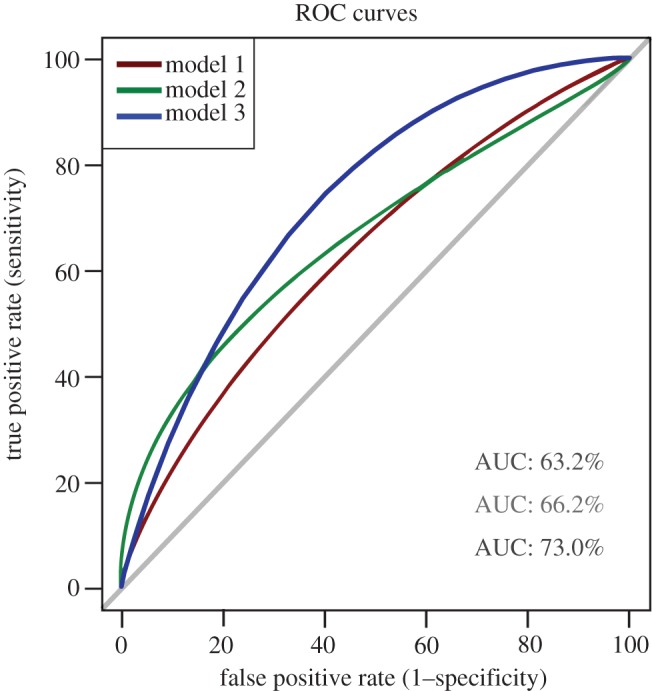
Receiver operating characteristic (ROC) curves (smoothened) for the three multilayer neural network models. These curves were generated and the corresponding AUCs were calculated using R Studio, showing that model 3 gives the best performance overall at classifying the dataset. (Online version in colour.)

Taking all these metrics into account, we have concluded that model 3, with the average level of network architecture complexity (of the 3), was the best model used for inferring meaningful patterns from the S. roeseli behavioural dataset to make predictions. It is important to emphasize that a simple ANN like model 1 is of no benefit. Even the best model (with the highest F1 score) can only produce roughly 59% accuracy. Yet, these ANNs contain many more ‘neurons’ than the organism—S. roeseli is a single-cell aneural ciliate. What does this really mean? How we can unravel the mechanistic details and computations that a highly complex brain does when we are not yet able to fully understand what a simple organism like Stentor is doing?

These results suggest a high level of complexity in the behaviours of S. roeseli in response to external stimulation. It cannot be fully explained by habituation, sensitization or operant behaviour. Our machine-learning based models, though impressive in modelling activities of neural systems like the brain [16,17], have been largely unsuccessful when applied here. Some machine learning approaches, such as ANN and random forest, are considered to be greedy algorithms and are often criticized for over fitting, yet in our case we do not observe an accuracy of above 59% in our test dataset even with a complex ANN architecture.

We realize that the prediction of ‘Leave’ is not an implication of complete understanding of the decision-making process and we did not intend to infer the implication in this work. It is probably reasonable to select any of the behaviours as the outcome to predict cell decision-making process but ‘Leave’ is the most appropriate choice because it is downstream of the other responses and therefore the maximum number of potential predictor variables are available. Its strong implication is that if an organism decides to ‘Leave’ after the sequence of behaviours, an internal decision-making process has occurred.

Stentor is not the only example of a unicellular organism displaying learning behaviours; many more aneural organisms [5,7,18–20] have been extensively studied, leading to surprising results. For example, the slime mould, Physarum, has also taught us immensely on the ability of single-cell organism to exhibit learning [21,22]. Even the pathways regulating Escherichia coli's chemotaxis behaviour—possibly the most well-characterized pathway in biology to date—has taught us many critical lessons that can be applied to higher organisms, including humans, which also helped to develop general biological principles.

But the most critical aspect of all the above studies, including ours, is ‘can invertebrates learn?’. This cannot and will not be answered unless we all agree on the taxonomy of learning. Unfortunately, nothing has changed since McConnell's extensive review of invertebrate learning [23], where he laments that there is no ‘systematics’ in behaviour and that comparative psychology is still awaiting its Linnaeus. He asserts that unless we define ‘learned responses’ and ‘unlearned responses’ we cannot explore the question of what learning is.

A true definition of ‘learning’ in single-cell organisms has to be able to explain both Innate response and Enactivism [24] arguments. The innate response argument suggests that an organism always comes with a highly complex pattern of ready-made responses and ‘learning’ is what the environment imposes on this ready-made system. On the other hand, the enactivism argument posits that an organism creates its own reality through dynamic interaction with their environment, assimilating information about the outside world into their own ongoing dynamics, not in a reflexive way, but through active inference, such that the main patterns of activity remain driven by the system itself.

For the lack of proper definition of learning yet, if we agree that these aneural organisms exhibit complex internal decisions leading to fascinating behaviours, our question is, how do they do it without possessing the complex neural networks of higher animals? The ability of Stentor to perform complex internal decisions based on environmental factors and respond appropriately is what we attempted to probe and capture in this study. Hence we have chosen a simple unambiguous observable decision ‘Leave’ as the outcome of the complex decision-making process in Stentor and attempted to capture the (nonlinear) relationships between the parameters of different avoidance reactions as a machine learning model. Our attempt was not to unravel the molecular details from these inferred patterns of relationships between the parameters through machine learning.

Exploring the mechanistic details underpinning these behaviours can indeed reveal profound insights into how neural circuits function in higher animals. Bray has argued extensively in his book ‘Wetware: a computer in every living cell’ [10] how a system of protein molecules can perform all the tasks needed for a cell to sense and respond to its environment. The switching in behaviour of S. roeseli indicates an adaptational change in its internal state—i.e. the state of existing internal molecular networks (since the timescale is too short to allow for modifications in gene expression). The organism is changed by its previous experience, implying some form of memory. Molecular networks in single-cell organism and neural circuits in higher animals may have been independent evolutionary events but may also be fundamentally related. Subsequent work by Gilles Laurent and others have reinforced this idea for neurons and other cells, that is, identifying the molecular players and understanding their dynamics will deepen our knowledge of what living systems are doing.

Here comes the immense power of studying underlying mechanisms in lower single-cell organisms. These ANNs, however, can be further developed, both by improving the experimental design and establishing more fine-tuned, advanced models. Our training dataset was relatively small and highly imbalanced. We addressed this issue by applying down-sampling method, however, it resulted in an even smaller set. It would be much more beneficial to have a bigger dataset of higher control and filming quality, as these directly impact the performance of the ANNs. Equally, these ANNs can be further developed to a higher level of complexity, with better suited and tuned parameters to increase their performance. This would allow more features to be extracted from the raw data. The best source to search for guidance to improve computer-based models is from our understanding and knowledge of the underlying biology [25]. We also do recognize that perhaps the accuracy measures can be improved with more training data but it is not within the scope of the study because the study dwells on a central question of how difficult it is to interpret the decision-making process of a single aneural cell.

We recognize and realize that it is not a trivial task. The extended ANN models that we are proposing would be based on Boltzmann machines [26–28]. We chose the Boltzmann machine approach to more traditional ANN models because Boltzmann machines can indicate what exact features are important and can help in the interpretation of models. Wang et al. [28] present an example case where it is actually being used to identify interpretable deep learning models to understand cellular and molecular disruptions in the human brain in schizophrenia. It can do this because it can encapsulate gene, protein and any other molecular components and their inferred and real network of interactions. These encapsulated networks can be perturbed and the outcome of the perturbation can be scored and weighted. This will eventually enable us to unravel ‘molecular wiring’ that may be responsible for the cell decision process. We hope this explanation clarifies our approach.

How do we accurately predict and come up with mechanistic insights for the decision-making process of Stentor to understand basal cognitive process is something we hope to investigate in future studies. We hope that this study illustrates the limitations of our understanding of cellular decision-making processes, which will stimulate further discussion and work not only in our laboratory but also in the wider community. It is probable that the internal decision­-making process can indeed be simple but nevertheless we are not able to capture it with our simple model with ‘Leave’ as the main attribute.

We now know that learning and memories are required even at the single-cell level. All living cells must have an awareness of their immediate environment to a certain extent. Components of the immune system, like macrophages or neutrophils, are constantly required to learn and form memories [29]. We are now in a much better position to study these intriguing behaviours in aneural organisms, or single-cell behaviours generally, which were undreamt of by scientists like Jennings a hundred years ago. With the abundance of advanced biochemical and genetic tools, we are able to unravel the molecular circuits inside these single cells in much more detail. These results are then combined with computational simulation and computer-based artificial intelligence, creating a powerful synergistic effect which will one day decode the mystery behind these observations. One might question the validity of using ANNs in modelling biological molecular networks. Despite many differences in details, general principles and properties are still shared [10]. This research contributes significantly to our ultimate goal of elucidating general principles of computations taking place in the brain [30]. Nonetheless, the biggest drawback of this approach is, indeed, its black-box nature. There have been multiple efforts recently to open this black box and reveal the computations performed by ANNs [31,32].

As Richard Feyman's famously said—whether it be ANN computations or living cellular behaviours—‘What I cannot create, I do not understand’. Our work is just an initial quest in that direction. We are excited to share these results with the wider community and hope that this study illustrates the limitations of our understanding of cellular decision-making processes, which will stimulate further discussion.

5. Material and methods

5.1. Stentor roeseli source and maintenance

Cultures of S. roeseli were purchased from Sciento (Manchester, UK) approximately every week over a period of one month. Sciento harvested the organisms from a pond on the property of Whitefield Golf Club (83 Higher Lane, Whitefield, Manchester, UK). In the laboratory, S. roeseli was maintained in well-aerated glass flasks in pond water, which were kept mainly in the dark, with partial sunlight. All behaviour experiments were performed on organisms purchased no more than 7 days beforehand.

5.2. Micro-stimulation apparatus and set-up

Custom-built apparatus to deliver controlled pulses of polystyrene beads directly near the mouth of the organism was used. A small clamp was placed next to the microscope. The microinjection glass needle was loaded with the suspension of fluorescent-red latex beads (fluorescent-red, carboxylate-modified polystyrene beads in aqueous suspension with 0.1% NaN3 (Sigma-Aldrich; mean diameter 2 µm)) and connected to an elevated reservoir of distill water. The needle was then held next to the microscope by the clamp.

One drop of S. roeseli culture was placed on a glass slide for each observation. The droplet culture was allowed to settle down for few minutes. The microinjection needle was positioned next to the mouth of the organism by hand, and its position was adjusted as needed throughout the experiment using the clamp. Short pulses of beads were generated as a gravity flow with the opening and closing of a two-way stopcock connected to the bottom of the reservoir, or adjusting the height of the reservoir.

5.3. Microscopy

All images were acquired using a Leica MZ16F Stereoscope equipped with a 11.25× objective lens and a QImaging Retiga 2000R monochrome camera. Images were collected at a rate of 15 frames per second for time lapse experiments, using an exposure time of 16.184 ms using Micro-Manager [33]. All microscopy experiments were performed at the Imaging Facility, Zoology Department, University of Cambridge.

5.4. Video analysis

Twenty-nine collected videos were analysed and investigation was performed on 188 individual organisms. Detailed description of the behaviours of S. roeseli was recorded along with the corresponding time in the video. A video would be terminated if: (1) all sessile S. roeseli ‘decided’ to leave and swam away, or (2) the specimen dried out even though there were still organisms being attached to the piece of algae.

5.5. Modelling

Raw data collected from video analysis were converted into time spent (1) at rest, (2) bending, (3) reversing cilia, (4) contraction, (5) number of contractions and (6) leave (or did not leave). These data were then scaled and randomly split into a training dataset (70%) and a testing dataset (30%). A down-sampling method was applied to the training dataset to ensure a 1 : 1 ratio between two classes (‘Leave’ and ‘Did not leave’). New training dataset is then shuffled before being used to train the models.

All modelling was done using R Studio.

Decision tree and random forest models were compiled using rpart, randomforest (respectively), and caret packages in R. A 10-fold cross-validation with 10 repetitions were used to train the models.

Feed-forward neural networks were compiled, trained and evaluated using the Keras package.

Data accessibility

All videos are available to download from Mendeley and the links to download are given in electronic supplementary material, table S1. Processed information from all the videos that were used in the machine learning models are given in table 1.

Authors' contributions

M.K.T. performed all the experiments, analysed the data and extensively contributed to the draft. M.T.W. helped with the microscopy experiments and ordering the organisms. He also critically evaluated the analysis, results and manuscript. S.P. designed and supervised the project, analysed the data and wrote the manuscript.

Competing interests

S.P. is a co-founder of NonExomics, LLC. M.T.W. and S.P. are co-founders at CAM-ML.

Funding

M.K.T. is funded by Cambridge Trust Scholarship and Trinity Overseas Bursaries; S.P. is funded by the Cambridge-DBT lectureship.