Electrostatic steering enables flow-activated von Willebrand Factor to bind platelet glycoprotein, revealed by single-molecule stretching and imaging

Abstract

Von Willebrand factor (VWF), a large multimeric blood protein, senses changes in shear stress during bleeding and responds by binding platelets to plug ruptures in the vessel wall. Molecular mechanisms underlying this dynamic process are difficult to uncover using standard approaches due to the challenge of applying mechanical forces while monitoring structure and activity. By combining single-molecule fluorescence imaging with high-pressure, rapidly-switching microfluidics, we reveal the key role of electrostatic steering in accelerating the binding between flow-activated VWF and GPIbα, and in rapidly immobilizing platelets under flow. We measure the elongation and tension-dependent activation of individual VWF multimers under a range of ionic strengths and pH levels, and find that the association rate is enhanced by four orders of magnitude by electrostatic steering. Under supraphysiologic salt concentrations, strong electrostatic screening dramatically decreases platelet binding to VWF in flow, revealing the critical role of electrostatic attraction in VWF-platelet binding during bleeding.

Introduction

Von Willebrand factor (VWF), a large multimeric blood glycoprotein, plays a critical role in stopping bleeding by binding platelets at sites of injury to plug ruptures in vessel walls—a process known as primary hemostasis [1,2]. To maintain the delicate balance between thrombosis and hemostasis, adhesiveness of VWF must be activated when and where it is needed, a task enabled by its unique long linear structure, which enables it to act as a force sensor. Each 250kD monomer of VWF consists of a linear lineup of multiple domains with different roles: the D’D3 assembly, A1, A2, A3 domains, D4 assembly, C modules 1-6 and CTCK domain. During biosynthesis, monomers of VWF dimerize between CK domains and then multimerize between D3 domains via disulfide bonds to form long molecules microns in length (Figure 1a). Proper functioning of VWF is critical for maintaining hemostasis, with loss or inadequacy of function resulting in von Willebrand disease (VWD), the most common hereditary bleeding disorder, which affects 1% of the US population[3]. VWD, and the excessive bleeding that can result, is not only inherited but can also be acquired through pathological changes in flow patterns within the circulatory system[4,5]. In the other direction, VWF must avoid forming platelet plugs at the wrong time or location, as this can lead to dangerous thrombotic events that cut off the circulation, such as in the case of stroke and heart attack[6–9].

Figure 1.

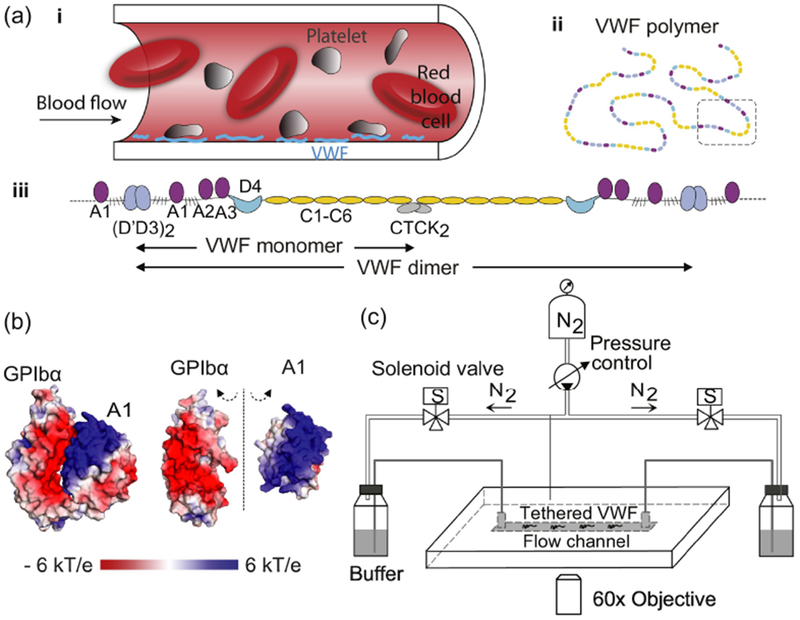
VWF multimer can be elongated and activated by flow. (Adapted from Fu et al10]) (A) (i) Schematic of platelet binding to VWF that is tethered to the blood vessel wall, (ii) a VWF multimer, and (iii) the domain lineup of a dimer segment. (B) Views of the GPIbα–A1 complex crystal structure [11] with electrostatic surface potentials colored according to the key. In the open-book view on the right-hand-side, GPIbα and A1 are rotated 90° towards the viewer around the dashed axis to show their highly electrostatic interfaces. (C) Schematic of the TIRF microscope with pressure-actuated flow.

So how does VWF undertake the challenging task of binding platelets in fast flowing blood near sites of injuries while avoiding binding elsewhere? Understanding this unique capability of VWF would not only be important for managing bleeding and clotting disorders, but could also inspire the design of mechanochemically-active multimers to target abnormal stresses in the body or in engineered structures[12]. Nature has engineered VWF multimers to sense flow and activate their platelet binding sites in response to high tensile forces induced by high shear stresses that can occur near blood vessel rupture sites [13–17]. Yet the molecular mechanisms underlying this medically significant process can be difficult to untangle for two reasons. First, measuring molecular interactions under force generally requires the use of specialized and technically-challenging biophysical assays such as single-molecule force spectroscopy. Secondly, even though VWF multimers are the natural functional units, most of the previous biophysical force measurements have studied the mechanical regulation of isolated VWF domains or segments [18–22], due to the lack of methods to precisely apply and characterize force in the heterogeneously-sized VWF multimers. Force could induce conformational changes in VWF multimers across a hierarchy of levels, from extending the overall shape of the multimer from a compact conformation to an elongated form, to breaking weak non-covalent bonds between or within monomers, to unfolding individual domains[18,23,24]. These structural changes could potentially activate VWF by allowing conformational access, opening cryptic binding sites, allosterically modulating the affinity of binding sites, and other mechanisms[18,25,26]. Characterization of the force-dependent structural and functional changes of VWF multimers is needed to reveal the molecular mechanisms underlying VWF activation, yet is not possible with standard ensemble-averaged or single-domain experiments.

To address these challenges, we recently developed a rapidly actuated flow and synchronized single-molecule imaging system to measure the affinity between platelet membrane receptor GPIbα and individual flow-activated VWF multimers[10]. We experimentally demonstrated the long-standing hypothesis that as a long linear multimer, VWF can change its conformation from a compact to an elongated state under increases in shear stress[27,28]. Furthermore, we showed that this change in shape can reroute tension along VWF’s central spine. Above a critical threshold, this force switches the platelet-binding A1 domain from a low affinity to a high-affinity GPIbα binding state. We further proposed that this force breaks hydrogen bonds between residues that are external and internal to A1’s long-range disulfide bond and shifts A1 to the high-affinity state. Not only did our work directly establish the role played by flow and force in activating VWF function, but it also provided a new platform for exploring the molecular mechanisms underlying VWF adhesion, which we use in the present study.

Once activated by flow, VWF A1 domains have to rapidly bind platelets at picomolar concentrations (0.5-0.83 pM or 3-5×10¹¹ L⁻¹) in flowing blood in order to initiate hemostasis in time. This requires rapid association between the force-activated, high-affinity state of A1 and platelet GPIbα. Our previous experiments[10] measured the association rate to be 5×10⁷ M⁻¹s⁻¹ at 150 mM NaCl—almost two orders of magnitude higher than the majority of diffusion limited antibody-protein association rates[29], which range from 10⁵ to 10⁶ M⁻¹s⁻¹—and measured the association rate to be even higher at 10 mM NaCl. Considering the fact that A1 and GPIbα are positively and negatively charged, respectively, at their binding interface (Figure 1b), these results suggested that electrostatic steering may be playing a role in accelerating the association rate. Such electrostatically-enhanced protein association would not be without precedent, as this phenomenon has been observed in a variety of biological processes, including regulation of blood coagulation in normal physiology and by modulators introduced by predators and parasites[28–31]. Using single-molecule manipulation and imaging, here we investigate the role of electrostatic interactions in the force-driven activation of full-length VWF and its subsequent binding to platelet GPIbα. By varying the ionic strength and the pH of the buffer over a wide range of values, we can modulate the electrostatic interactions between activated VWF and GPIbα and observe the effects on extension, tension-mediated activation, and binding. We show that electrostatic acceleration of intermolecular binding is an essential mechanism for enabling platelet immobilization in blood flow, revealing nature’s molecular design strategy for enabling rapid and stable binding under acute conditions of significant stress.

Results

1. VWF extension under flow depends only weakly on NaCl concentration

To quantify the role of electrostatic interactions on VWF function, we varied the concentration of NaCl to change the screening length while measuring the effects of this perturbation on VWF elongation, activation and binding. Since the extension of VWF from a compact to an elongated conformation is the first step in activating the A1 domain to bind platelet GPIbα, we first probed intramolecular interactions by measuring how the extension of VWF as a function of flow depends on NaCl concentration. Using a custom flow system, fluorescently-labeled VWF was tethered to a coverslip and then subjected to shear flow that could be rapidly modulated using electronically-controlled pressure valves (Figure 1c)[10]. VWF conformation was monitored in real-time at the single-molecule level using total internal reflection fluorescence (TIRF) microscopy. The extension of each VWF molecule was measured under shear stress at different salt conditions by varying the buffer from 150 mM NaCl, to 10 or 500 mM NaCl, then back to 150 mM NaCl. For each buffer condition, the shear stress was varied from 10 to 1280 dyn cm⁻², and measured in both flow directions to confirm that the measured molecules behaved symmetrically and were not sticking to the surface (Figure 2a). In the absence of flow and under low levels of shear stress, i.e. < 15 dyn cm⁻², VWF multimers were compact and globular; at higher flow rates VWF was elongated with an extension length that increased with increasing shear stress (Figure 2b and c). VWF multimers, with maximum end-to-end distances ranging from 1.0 to 6.5 μm, showed similar flow-extension curves, once extension was normalized to the length initially observed at 1280 dyn cm⁻² (L/L₀, Figure 2b and c) in 150 mM NaCl.

Figure 2.

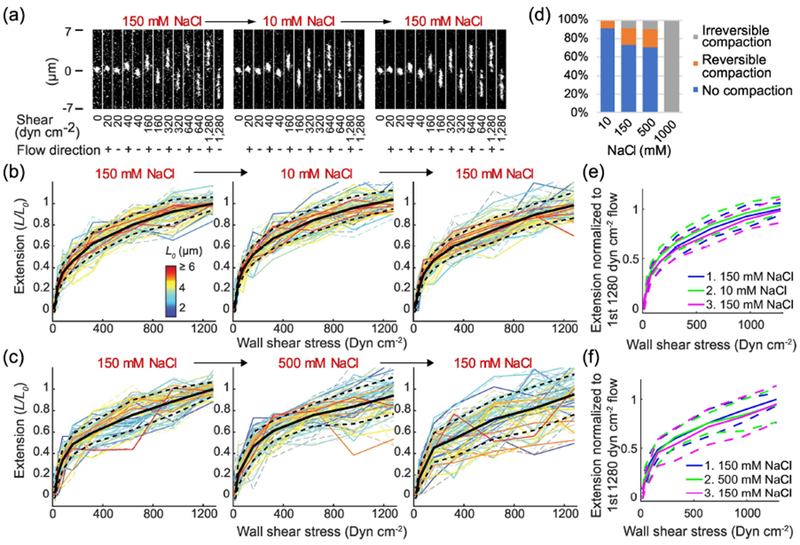
VWF extension does not significantly depend on [NaCl] from 10 to 500 mM. (A) Representative images of a single VWF molecule extending under shear stress following the indicated buffer exchange. For each buffer condition, a typical flow profile consists of cycles of start- and stop-flow in forward (+) and backward (−) directions at multiple different shear stresses, which are indicated below each image (10 ms exposure every second). (B, C) Normalized extension of VWF multimers vs. wall shear stress is presented, with the length of each molecule normalized by its fully-stretched length, as measured during the first instance of 1280 dyn cm⁻² flow (L₀, color key). Extension is presented under forward (solid lines) and backward (dash lines) flow following 150 -> 10 -> 150 mM NaCl (b, N=46 multimers) or 150 -> 500 -> 150 mM NaCl (c, N=44 multimers) buffer exchanges. Black solid and dashed lines in (B) and (C) are the average and the standard deviation of the extension of individual molecules, respectively. They are also overlaid as blue, green and magenta lines in (E) and (F), to aid in comparing the results from the indicated buffer exchange sequences. (D) Percentage of VWF compaction in 10 mM to 1 M NaCl buffer.

By subjecting each observed molecule to different buffer conditions, we were able to detect both the effects of perturbations and any resulting hysteresis. When stretched repeatedly by flow, most VWF molecules extended to similar lengths every time. However, some VWF molecules occasionally appeared shorter during some flow events but normal during the other flow events, a phenomenon we are calling reversible compaction (Supplemental Figure 1a). Some other VWF molecules transformed to and stayed in more compact conformations (<80% extension) after one of the flow events, which we are calling irreversible compaction (Supplemental Figure 1b). As a baseline, for VWF molecules exposed to only 150 mM NaCl, a small fraction exhibited reversible compaction (18%) while even fewer molecules exhibited irreversible compaction (8.8%) (Figure 2d, Supplemental Figure 2). When the buffer was changed from 150 to 10 mM NaCl, the average extension of VWF under the same shear stresses increased slightly, by approximately 3.8% (Figure 2b and e, Supplemental Figure 3a). Hysteresis was not observed, with extension returning to about the same levels once the molecules were brought back into 150 mM NaCl. Regarding compaction, the percentage of reversible compaction was 8.7%, similar to the baseline level, while irreversible compaction completely disappeared in our measurement (Figure 2d). When the buffer was switched from 150 to 500 mM NaCl, the average extension of VWF under the same shear stresses slightly decreased, by approximately 4.9% (Figure 2c and f, Supplemental Figure 3b). The percentage of VWF molecules that reversibly or irreversibly compacted in 500 mM NaCl is very similar to 150 mM (Figure 2d) but the decrease in extension length was greater in 500 mM NaCl.

While increasing NaCl concentration caused slightly higher rates of compaction and slightly shorter extensions, overall, the extension of VWF depended very little on NaCl concentration as it was varied from 10 mM to 500 mM. On average, the extension of VWF varied by less than 10% in this range (Supplemental Figure 4a and b). This result suggests that the long-range intramolecular interactions in VWF multimers are not dominated by charge-charge interactions. However, we note that under extreme conditions, i.e. when the buffer was switched from 150 mM to 1 M NaCl, most molecules irreversibly compacted and few molecules could be stretched open after only a few flow events (Figure 2d). We therefore limited our investigation to 500 mM NaCl and below.

2. Dramatic enhancement of the VWF-GPIbα association rate by electrostatic interactions

Next, we examined electrostatic enhancement of VWF-GPIbα binding by measuring the binding kinetics under different NaCl concentrations under flow (Figure 3a). To get a sufficient binding signal at high NaCl concentrations, in which the affinity is lower, a GPIbα construct containing platelet-type von Willebrand disease (PT-VWD) mutations G233V and M239V was used[34]. These mutations increase the affinity between GPIbα and VWF, but do not alter the charges on GPIbα. Furthermore, the tension-dependence of VWF-GPIbα binding does not appear to be significantly altered, with model fitting parameters agreeing within experimental error between wild type and high-affinity GPIbα (Supplemental Figure 5), which is not too surprising as the activation force in this assay is applied along the central spine of the VWF multimer, rather than between VWF and GPIbα. Tension within VWF multimers is induced by the viscous drag of the flow, and its magnitude, in this tethered flow assay, is proportional to the number of monomers downstream [10]. The tension is thus maximal at the upstream, tethered end and zero at the downstream, free end. The drag force per monomer was estimated to be 0.5 pN at 1280 dyn cm⁻² (for example, at this shear stress the maximum tension at the tether point of a VWF with n monomers would be 0.5n pN). Consistent with our previous results, lower ionic strength increased the association rate and did not significantly affect the dissociation rate (Figure 3b and c). For each NaCl concentration we tested, the association rate between VWF and GPIbα as a function of tension followed a sigmoidal curve. Each curve was fit to a two-state model in which tension along the central spine of VWF switches the A1 domain from a low-affinity state (1) to a high-affinity state (2). Force f alters the free energy difference ΔG between the two states by −f · Δx[10]. The force needed to activate 50% of the A1 domains was the same within error between 80 mM and 500 mM NaCl (Figure 3d), suggesting that the interactions that holds A1 in the low-affinity state are not strongly affected by ionic strength. On the other hand, the association rate in the activated high-affinity state increased dramatically, going up by almost 2 orders of magnitude as the salt concentration was varied from 500 to 80 mM NaCl (Figure 3e). This enhancement is among the largest that has been measured, as compared to other electrostatically-enhanced protein-protein association rates in the literature[35–37].

Figure 3.

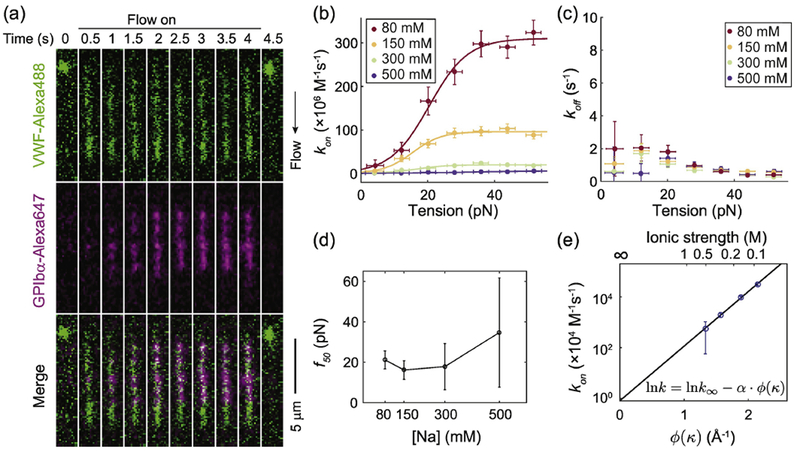
VWF-GPIbα association kinetics are salt dependent. (A) Representative time-lapse dual color fluorescence images of VWF extension and binding to GPIbα at 80 mM NaCl after 1280 dyn cm⁻² wall shear flow was turned on and off at 0 and 4 second, respectively. Association rates (B) and dissociation rates (C) between VWF and GPIbα under different [NaCl]. Lines in (b) are two-state model fit. (D) The 50% activation force vs [NaCl] (E) Association rate of the high affinity state vs the square root of ionic strength matches the electrostatic steering model. See equation (3) for details about the x axis. Error bars indicate 95% confidence intervals.

To understand the dependence of the association rate on the ionic strength, consider a pair of proteins whose association rate is enhanced by an electrostatic attraction between opposite net charges on the two surfaces. Changes in the ionic strength of the surrounding buffer will lead to a change in the distribution of counter-ions near these charged surfaces, altering the effective electrostatic attraction between the two proteins and therefore the encounter rate. According to Debye–Hückel theory[38,39], the electrostatic potential between ions i and j separated by a distance r_ij is given by (see Materials and Methods Section 9 for details):

$$\psi (r)=\frac{q_i{q}_j}{8\pi {ϵ}_0{ϵ}_r}\left(\frac{e^{\kappa R_i}}{1+\kappa R_i}+\frac{e^{\kappa R_j}}{1+\kappa R_j}\right)\frac{e^{-\kappa r_{ij}}}{r_{ij}}$$ (1)

Here, 1/κ is the Debye length in angstroms (Å) with $k=\sqrt{2N_A{e}^{2}I/k_{B}T{ϵ}_0{ϵ}_r}=0.325{\AA }^{-1}{M}^{-1/2}\times \sqrt{I}$; I is the ionic strength; q_i and q_j are the charges of ions i and j; ϵ₀ϵ_r is the permittivity of water; and R_i, and R_j are the hydrated radii of the ions in Å. Let us simplify things by assuming that R_i = R_j = R. Then, summing Equation (1) over all charge pairs (i, j) between the A1 and GPIbα binding interfaces yields:

$$\psi (r)=\sum _{i,j}\frac{q_i{q}_j}{8\pi {ϵ}_0{ϵ}_r}\left(\frac{e^{\kappa R}}{1+\kappa R}+\frac{e^{\kappa R}}{1+\kappa R}\right)\frac{e^{-\kappa r_{ij}}}{r_{ij}}=\frac{1}{4\pi {ϵ}_0{ϵ}_r}\sum _{i,j}{q}_i{q}_j.\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+\kappa R)}$$ (2)

As explained in Materials and Methods Section 9, the association rate should scale as $k\propto \langle \exp (-\frac{\psi }{k_{B}T})\rangle$, so we can use equation (2) to relate k to the physical parameters governing the electrostatic attraction. As detailed in Materials and Methods Section 9, this gives us:

$$\ln {k=\ln k}_{\infty }+\alpha \sum _{i,j}-\frac{q{}_{i}q{}_j}{{\mathrm{e}}^2}.\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+\kappa R)}=\ln k_{\infty }+\alpha \varphi (\kappa )$$ (3)

where α = e²/(4πk_BTϵ₀ϵ_r) and $\varphi (\kappa )={\sum }_{i,j}-\frac{q_i{q}_j}{{\mathrm{e}}^2}.\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+kR)}$. k_∞ is the association rate at I = ∞, i.e. when electrostatic interactions are completely screened.

To calculate ϕ(κ), we assume the encounter state of A1 and GPIbα to be the same as their bonded state crystal structure[11] (protein data bank file 1SQ0). As an approximation, for each κ, we integrate over all charge pairs (i, j) between the A1 and GPIbα binding interfaces with r_ij 10.4 Å, the Debye length at 80 mM NaCl.

Because the Debye length is the longest at the lowest ionic strength and the effective electrostatic potential from the charged residue decays rapidly for distances longer than the Debye length, contribution from further separated charge pairs can largely be neglected. The first hydration layer for a protein near oxygen and nitrogen atoms is about R = 3.5 Å thick[40]. Our data is in good agreement with Equation (3), consistent with electrostatic steering between force-activated A1 and GPIbα. As shown in Figure 3e, the relationship between the measured k_on,2 and ϕ(κ) is linear as predicted. Linear fitting yields the intercept k_∞ = 8.05 × 10^3±0.44 M⁻¹s⁻¹ and slope $\alpha =4.95\pm 0.57\AA =(0.71\pm 0.08)\times \frac{{\mathrm{e}}^2}{4\pi k_{B}T{ϵ}_0{ϵ}_r}$. While the experimentally determined slope is 30% lower than the predicted theoretical value $\frac{{\mathrm{e}}^2}{4\pi k_{B}T{ϵ}_0{ϵ}_r}$, the agreement is quite good given the simplifications used in the derivation. This discrepancy may be caused by minor inaccuracies in the asssumptions made above, such as the geometry of protein hydration, the encounter complex, etc. In fact, increasing the distance between encounter state A1 and GPIbα in our model by 2.8 Å, the diameter of a water molecule, can reconcile this difference, as discussed in Materials and Methods Section 9.

According to this result, the charges on the interface between A1 and GPIbα enhance the association rate by 4 orders of magnitude at 150 mM NaCl. The enhancement of the association rate can be crucial for the binding of platelets because the concentration and the diffusion coefficient of platelets are much lower than most freely-suspended protein molecules.

3. Strong electrostatic screening prevents platelet binding to VWF under flow

To test the role of the strong electrostatic attraction between A1 and GPIbα in a more physiological setting, we measured the binding and translocation of platelets on a VWF-coated surface under flow at both physiological and extreme salt concentrations. Human platelets were washed and fixed to prevent osmotic damage. They were introduced to VWF coated flow channels in buffer at either 150 mM or 500 mM NaCl. In 150 mM NaCl buffer, platelets bound to and slowly translocated in the direction of flow on the VWF coated surface for shear stresses between 0.1 and 100 dyn cm⁻² (Figure 4a, Supplemental Videos). Platelet binding was more pronounced between 2 and 50 dyn cm⁻², with binding peaking at 20 dyn cm⁻² (Figure 4b). The translocation of bound platelets slowed down as the wall shear stress increased from 0.1 up to 1 dyn cm⁻² (Figure 4c). The translocation then stayed slow and sharply sped up above 10 dyn cm⁻². In stark contrast, in 500 mM NaCl buffer, when electrostatic interactions were largely screened, under most conditions very few platelets bound and the translocation was much faster (Figure 4). As a control, platelets were also flowed through channels coated with BSA and casein but not VWF. In the control channel, no binding was observed with either NaCl concentration.

Figure 4.

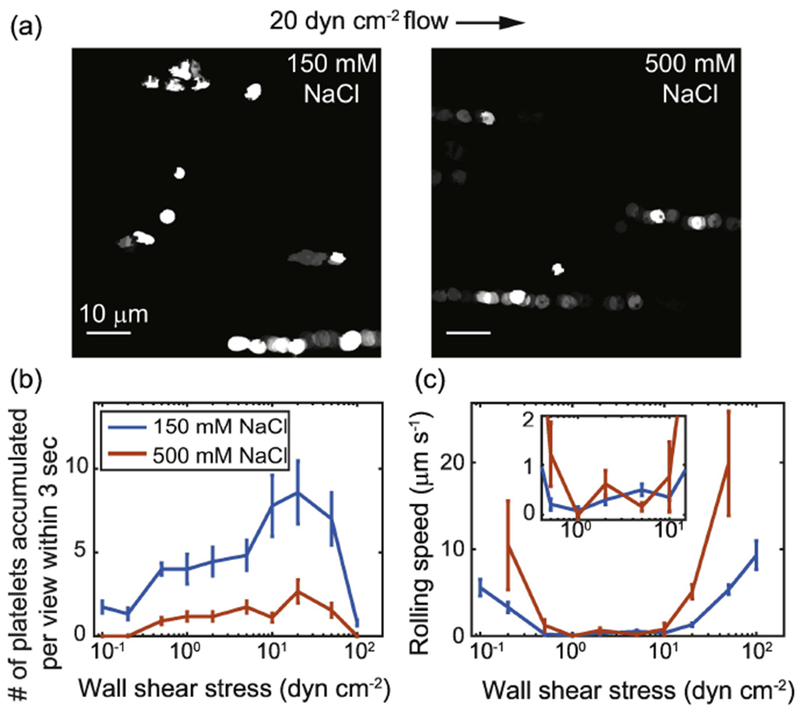
Fixed platelets bind to and roll on VWF-coated surface under flow. (A) Footprints of platelets rolling on VWF-coated surface under 20 dyn cm⁻² wall shear in 150 mM and 500 mM NaCl in the first 8 seconds of flow. Brighter patterns indicate overlapped footprints. The accumulated number of platelets bound to the surface (B) and the average speed of platelet rolling on the surface (C) are plotted as a function of wall shear stress. The inset shows a zoom-in of the rolling speed between 0.5 and 10 dyn cm⁻² for easier viewing. For shear stresses lower than 0.2 dyn cm⁻² and higher than 50 dyn cm⁻² in 500 mM NaCl buffer, fewer than 3 platelets bound to the surface and the rolling speed was not plotted. Error bars indicate standard errors of the mean.

4. Deviation from physiological pH reduces VWF binding to GPIbα

Another way to perturb the electrostatic interactions within VWF and between VWF and GPIbα is altering the net charge on amino acid side chains by changing the pH. We first probed intramolecular interactions by measuring how the extension of VWF as a function of flow depends on pH. When buffer was switched from pH7.4 to pH6.2, the average extension of VWF under the same shear stresses slightly decreased, by approximately 5.6% (Figure 5a, c Supplemental Figure 3c and 4). The percentage of reversible and irreversible compaction in VWF molecules was similar to the baseline at pH7.4 (Figure 5a and e). When buffer was switched from pH7.4 to 9.8, the average extension of VWF under the same shear stresses decreased by approximately 10% (Figure 5b, d, Supplemental Figure 3d and 4). More VWF molecules were irreversibly compacted and slightly more were reversibly compacted than at pH7.4 (Figure 5b and e). When the pH was returned to 7.4, even more VWF molecules appeared irreversibly compacted. These compaction events likely happened during the pH9.8 incubation at a low shear stress and were not noticed until the molecules were again subjected to higher shear stress during the subsequent pH7.4 incubation (Figure 5b). This brought the average extension of VWF down to 77% of the initial value at pH7.4

Figure 5.

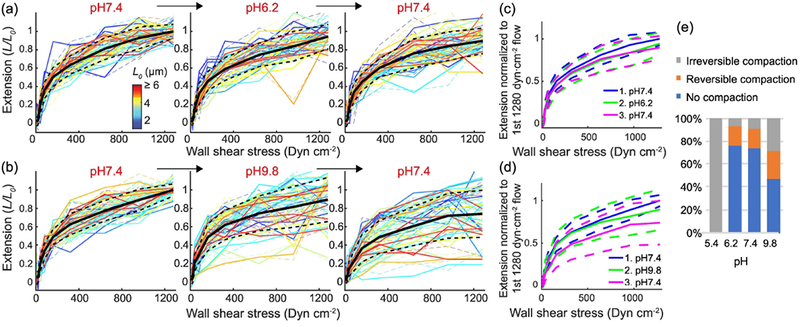
VWF extension slightly depends on pH from 6.2 to 9.8. VWF multimer extension normalized to length during the first 1280 dyn cm⁻² flow (L₀, color key) vs. wall shear stress under forward (solid lines) and backward (dash lines) flow following pH 7.4 -> 6.2 -> 7.4 (a, N=35 multimers) or pH 7.4 -> 9.8 -> 7.4 (b, N=38 multimers) buffer exchanges. Black solid lines and the black dashed lines in (A) and (B) are the average and the standard deviation of the extension of individual molecules. They are also overlaid as blue, green and magenta lines in (C) and (D), to aid in comparing the results from indicated buffer exchanges. (E) Percentage of VWF compaction in pH 5.4 to 9.8 buffer.

While deviation from physiological pH caused slightly more severe compaction, overall, the extension of VWF only weakly depended on pH between 6.2 and 9.8. On average, the extension of VWF varied by 23% in this range (Supplemental Figure 4c and d). This result confirms the result in Result Section 1 that the long-range intramolecular interactions in VWF multimers are not dominated by charge-charge interaction. However, extreme pH caused compaction in VWF. For example, when buffer was switched to pH 5.4, the compaction was so severe that few molecules could be stretched open after only a few flow events (Figure 5e). We therefore limited our investigation to between pH6.2 and pH9.8.

In contrast, pH significantly affects the binding between VWF and GPIbα, consistent with the result in Result Section 2 that electrostatic attractions are highly involved in binding. At each of the four pH conditions we tested, 6.2, 7.4, 8.6 and 9.8, the association rate between A1 and GPIbα as a function of tension follows a sigmoidal curve (Figure 6a). Each curve was fitted to the two-state model described in Result Section 2. to calculate the association rate of the high-affinity state of A1 and the force needed to activate 50% of the A1 domains. The dissociation rate and the f₅₀ did not change significantly within this pH range (Figure 6b and c). The association rate of the high-affinity state of A1 was the highest at pH8.6 and decreased as pH increased or decreased (Figure 6a and d). Even though it is very difficult to predict the exact protonation and deprotonation state of each amino acid side chain, this observed trend in binding rate can be qualitatively explained by the pH-dependent charge state of the amino acid side chains. Because His residues have pKa ~6.0, His¹² and His³⁷ in two of the negative charge clusters on GPIbα (Materials and Methods Section 9) likely become more positively charged when pH decreases from 7.4 to 6.2, decreasing the electrostatic attraction between A1 and GPIbα. When the pH is increased from 7.4 to 8.6, the two histidine residues become more negatively charged than at pH 7.4 and increased the attraction between the two proteins. When pH gets to 9.8, the positively charged lysine residues on A1, whose pKa is −10.53, may become less positively charged, reducing the electrostatic attraction. Overall, the pH-dependent binding rate confirms the major role played by electrostatic attraction in VWF-GPIbα binding.

Figure 6.

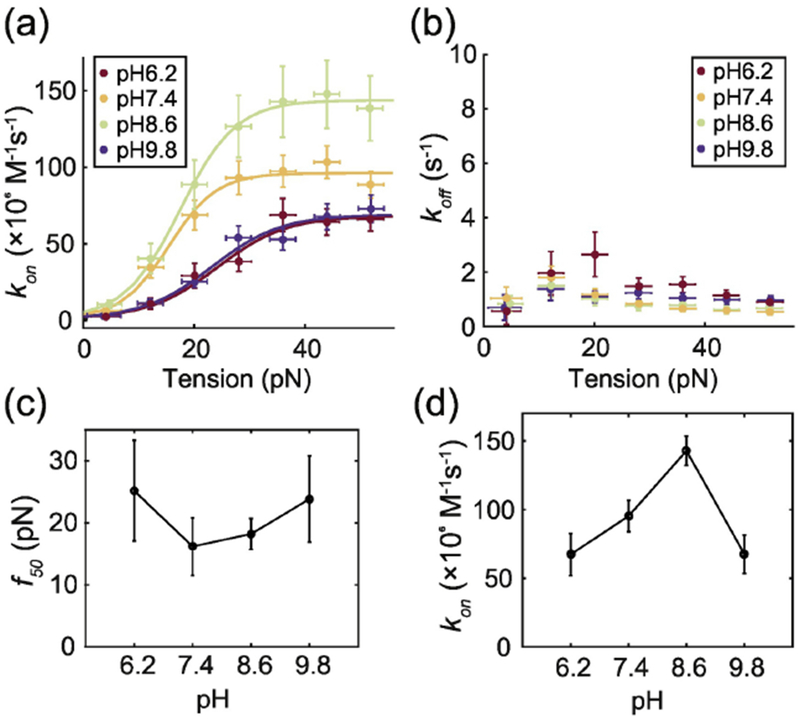
VWF-GPIbα association kinetics are pH dependent. Association rates (A) and dissociation rates (B) between VWF and GPIbα at different levels of pH. The lines in (a) are two-state model fits. The 50% activation force (C) and the association rate of the high affinity state (D) vs pH. Error bars indicate 95% confidence intervals.

Discussion

We have measured and analyzed the dramatic enhancement in the association rate between VWF and GPIbα that results from electrostatic interactions. We have also demonstrated a striking contrast in the platelet binding rate on VWF-coated surfaces between normal and high ionic strength buffer. This result, anticipated by the ionic-strength dependent GPIbα binding rate that we measured, suggests that rapid electrostatically-steered binding is critical for the binding of platelets in blood flow. We can estimate the binding rate between wall-tethered VWF and platelets in blood, k_P, from the encounter rate, k_e, between platelets and VWF, the concentration of platelet [P], the dwell time Δt of each platelet encounter, the association rate k_on between A1 and platelet-bound GPIbα, and the effective concentration of GPIbα near the platelet surface [G] (see Materials and Methods Section 10 for details). k_e is dominated by the advection of blood flow and therefore proportional to the linear flow rate of blood. Δt is inversely proportional to the linear flow rate. Using a platelet concentration in healthy adult blood of 3 × 10⁵ mm⁻³ or 0.5 pM, we estimate k_e · [P] · Δt to be 9.4 × 10⁻⁴, independent of flow rate (see Materials and Methods). According to the literature, [G] is about 47μM[41,42]. Previously, we measured k_on = 5 × 10⁷M⁻¹s⁻¹ between activated A1 and wild type GPIbα[10], which all together yields k_P = k_e · [P] · Δt · k_on [G] = 3s⁻¹. In contrast, if k_on were to fall in the range of typical protein-antibody association rates and be below 10⁶ M⁻¹s⁻¹, k_P would be below 0.06 s⁻¹, almost 2 orders of magnitude slower and likely not sufficient for forming a platelet plug. We note that while VWF- GPIbα binding rates previously measured with isolated A1 domains were generally much lower than our result, with published values of 5×10⁴ M⁻¹s⁻¹ or below[34,43–45], this discrepancy may have resulted from the more physiological context of our measurements. Our approach uses full-length VWF multimers, rather than isolated domains, and applies tension along the central spine of each multimer—a force modality capable of effectively shifting A1 into a high-affinity state, and of revealing its unusually high on-rate. Experimentally, a salt concentration of 500 mM NaCl reduces k_on by a factor of almost 100, bringing it into the range of a typical protein-antibody association rate, according to the results in the previous section, and dramatically inhibits platelet binding to a VWF-coated flow channel in vitro. These results support the vital role of electrostatically-enhanced rapid protein association in platelet binding.

When an injury happens to a blood vessel, elevated wall shear stresses activate VWF secreted by endothelial cells or attached to exposed collagen matrix. The activated A1 domains must quickly recruit platelets and keep them bound in order for platelets to be activated[46]. As estimated above, rapid binding is particularly important for binding platelets at physiological concentrations. The rapid association rate may also allow for fast formation of new binding points on platelets if a single attachment is broken by the drag force exerted by blood flow. Physiological wall shear stresses can be as high as 50 dyn cm⁻² in arterioles[47,48]. This would induce a drag force of 24 pN on a single platelet. Even if multiple bonds are formed, the most upstream bond might still bear a large fraction of the drag force. Thanks to catch bond or flex bond characteristics, the A1-GPIbα bond shifts to a more stable state when pulling force is applied[19,20]. Nevertheless, a single A1-GPIbα will break on the time scale of 34 ms under 24 pN force. When there is an injury, the wall shear stress in arterioles may increase up to 12-fold higher due to the drop in back pressure[49] and vessel constriction[50]. This would induce a drag force of 283 pN on a single platelet, in which case the lifetime of a single A1-GPIbα bond will be below a femtosecond and not relevant at all. Once the bond breaks, the platelet will rapidly detach and drift away if not tethered by a new bond. At 600 dyn cm⁻² wall shear stress or γ = 37500 s⁻¹ shear rate in plasma with 1.6 cP viscosity, which is possible in injured vessels, the time scale of free rolling is about 1/γ = 26.7μs. Given the A1-GPIbα association rate k_on = 5 × 10⁷ M⁻¹s⁻¹ and the effective concentration [G] = 4.7 × 10⁻⁵ M of GPIbα on the platelet surface (see Materials and Methods Section 10 for details), on average about γ/(k_on [G]) = 16 activated A1 domains need to contact the platelet in order to form a bond during the first round of rolling. In the absence of electrostatic attraction, in which case the A1-GPIbα association rate decreases by 4 orders of magnitude, 160,000 activated A1 domains would be needed. VWF monomers would need to be closely packed right next to each other and all the A1 domains would need to be activated in order to provide 160,000 activated A1 domains in the area covered by a platelet, a condition that is not physiological. If the A1-GPIbα association rate was on the order of 10⁶ M⁻¹s⁻¹, similar to typical protein-antibody pairs, 800 activated A1 would be needed. According to the results in our previous work[10], only high molecular weight VWF multimers can be activated at 600 dyn cm⁻²—for example, a 30-mer VWF would have about one A1 domain activated. Because the size distribution of VWF multimers is roughly exponential[51], we estimate that at most 0.2% of the A1 domains in the total VWF population would be activated. Therefore, more than 400,000 A1 domains would be needed to provide 800 activated A1 at 600 dyn cm⁻², which is again not physiological. Moreover, when additional VWF molecules and platelets bind to the first platelet, even more drag force is applied to this platelet and more activated A1 domains are required for stable platelet tethering, making it even less likely that this lower A1-GPIbα association rate would be viable for keeping platelets attached to surface. Therefore, rapid A1-GPIbα association rate facilitated by electrostatic interactions may be necessary for hemostasis.

A study by Interlandi et al also supports the critical role of electrostatic interactions in the binding between VWF and GPIbα, observing that when charged residues of A1 at the binding interface are mutated into neutral ones, the binding affinity of VWF with platelets and GPIbα decreases [52]. The electrostatic attractions between A1 and GPIbα also provides an opportunity for specific regulation of VWF by force. Also shown by Interlandi et al, the N-terminal linker between the A1 and D’D3 domains contains a negatively charged residue Asp¹²⁶¹ that can neutralize the positive charges on A1’s binding interface in the low force state. Tensile force along the VWF central spine may pull the N-terminal linker away from A1 and enable rapid binding to GPIbα. According to our observations, the electrostatic attraction between Asp¹²⁶¹ and the binding interface of A1 may not be solely responsible for the inhibition of VWF at low shear rate because the activation force we measured for GPIbα binding was not significantly dependent on the ionic strength of the buffer. Other intramolecular interactions such as the A1-A2 interaction[22,53], the flex-bond behavior[10,19], and the transition of A1 to an intermediate state between the native and unfolded states[54] may also play a role.

We also found that extreme pH-levels, by physiological standards, like 6.2 or 9.8 significantly decrease the affinity between activated A1 domains and GPIbα, potentially by altering the charges on amino acids and decreasing the electrostatic attractions between the two. The affinity between A1 and GPIbα peaks around pH 8.6 rather than the physiological value of 7.4 in blood. Given that the pH of blood can temporarily drop to 6.8 due to the accumulation of carbon dioxide but rarely go higher than 8[55,56], the optimization of A1-GPIbα affinity at pH8.6 might not be physiologically significant. Extreme pH also slightly increases the activation force for A1. Higher activation force and lower affinity together reduce the potential of VWF-GPIbα binding at low pH. On the other hand, changes in pH did not significantly affect the measured elongation of VWF. In contrast, Muller et al predicted that low pH will lower the critical shear rate to elongate and activate VWF by measuring the pH-dependent rupture forces of intradimer interactions in VWF dimers using AFM[21]. However, we observed that low pH had no effect on the elongation of VWF and increased the critical shear to activate VWF binding.

In summary, electrostatic attractions between flow-activated VWF and GPIbα greatly enhance their association rate. This mechanism may be vital to platelet plug formation in rapid blood flow—consistent with our demonstration that strong electrostatic screening dramatically hinders platelet binding to VWF in flow. Furthermore, as a physiologically-significant example of electrostatically-accelerated protein association, this study improves our understanding of how complementary charges on protein surfaces allow rapid and stable binding, which may aid in the design of proteins and drugs for acute conditions or for systems under strong mechanical forces.

Materials and Methods

1. VWF and high-affinity GPIbα

Recombinant human VWF(Baxter BioScience, Vienna, Austria) was expressed, conjugated with Alexa Fluor 488 (Thermo Fisher Scientific) and biotin (EZ-link Sulfo-NHS-LC-Biotin, Thermo Fisher Scientific, Waltham, MA, USA), and purified as previously described[10]. The cDNA for human platelet GPIbα (His¹–Arg²⁹⁰) was mutated using QuikChange (Stratagene) and cloned into the ET8 vector[57] with a C-terminal His₆ tag and transiently transfected into HEK293T cells (ATCC, Manassas, VA, USA) using polyethylenimine (Sigma-Aldrich, St. Louis, MO, USA). Cell line was verified free of mycoplasma contamination using mycoplasma detection kit (Lonza Biologics, Portsmouth, NH, USA). Culture supernatants in FreeStyle 293 medium (Thermo Fisher Scientific) were harvested 3 days after transfection and proteins were purified using Ni-NTA affinity chromatography (Qiagen, Valencia, CA, USA) followed by size-exclusion chromatography (Superdex 200 10/300 GL, GE Healthcare Life Sciences) in 150 mM NaCl and 20 mM HEPES (pH 7.4)[19]. Alexa Fluor 647 NHS Ester (Thermo Fisher Scientific) (103 μM) was conjugated to GPIbα (1.5 mg ml–1) in the above buffer with NaHCO3 added to a final concentration of 130mM for 1 h at 22 °C. Free dye was removed by dialysis in 150 mM NaCl, 20mM HEPES (pH 7.4) at 4 °C. Concentrations of GPIbα and Alexa Fluor 647 were calculated from A280 and A650 measurements (NanoDrop, Thermo Fisher Scientific). The molar ratio of fluorophore: GPIbα used in experiments was 2.34:1. VWF and GPIbα samples were stored in aliquots at −80 °C.

2. Buffers

Fluorescence imaging experiments were in 80-500 mM NaCl as noted, 20 mM HEPES (pH 7.4), 0.02% Tween 20, 0.1 mM D-biotin (Invitrogen, Carlsbad, CA, USA), 0.5 mg ml⁻¹ BSA together with 2.2mM protocatechuic acid (Santa Cruz Biotechnology, Santa Cruz, CA, USA) and 37nM protocatechuate-3,4-dioxygenase (Sigma-Aldrich) as oxygen scavengers[58]. 20 mM Bis-Tris (pH 6.2), 20 mM Tris (pH 8.6) or 20 mM CHES (pH 9.8) was used instead of 20 mM HEPES (pH 7.4) when noted. 20 mM HEPES (pH 7.4), 20 mM Bis-Tris (pH 6.2), 20 mM Tris (pH 8.6) or 20 mM CHES (pH 9.8) contributed 0.008, 0.014, 0.005 or 0.015 M to ionic strength[59]. For fine-tuning the driving pressure of the flow system in experiments that included measurements below 80 dyn cm⁻², 2.5 × 10–6 w/v 1 μm diameter polystyrene particles (PP-10-10, Spherotech, Lake Forest, IL, USA) were added as flow tracers. Some VWF multimers tethered to the surface appear to become more compact after being stretched repeatedly. The fraction of VWF molecules becoming compact increases at extremely high salt concentrations and extreme pH levels. This compaction is perhaps due to the formation of extra attachments between VWF and the surface near the tether point.

3. Human platelets

Platelet rich plasma (PRP, apheresis platelet, 5 days old) was obtained from the Boston Children’s Hospital blood bank. 2 mL PRP and 2 mL of 2 μM Prostaglandin E1 (PGE1, P5515, Sigma-Aldrich) in 1xPBS were gently mixed together and spun at 100 × g for 10 min at room temperature (with no brake applied) to pellet contaminating red and white blood cells. The supernatant was transferred into new plastic tubes using a wide orifice pipet tip. Platelets were pelleted by centrifugation at 800 × g for 10 min at room temperature (with no brake applied), washed with 1mL of platelet wash buffer (11 mM glucose, 128 mM sodium chloride, 4.3 mM sodium phosphate monobasic, 7.5 mM sodium phosphate dibasic, 4.8 mM sodium citrate, 2.4 mM citric acid, pH 6.5, 1uM PGE1) 3 times without disturbing the pellet, and resuspended in 4 mL Tyrode’s buffer (7 mM NaC1, 2.8 mM KC1, 1 mM MgC12, 12 mM NaHCO3, 0.4 mM Na2HPO4, 5.5 mM glucose, 10 mM HEPES, 0.35% BSA) with or without 1 μM PGE1 by rotating on a 30rpm rotator. The platelets resuspended with PGE1 were fixed by mixing 100 μL platelets and 900 μL of 1.1% paraformaldehyde in 1xPBS in each tube and incubating them on a rotator at room temperature for 30 min. Fixed platelets were then spun at 800 × g for 4 min. The pellets were washed with 1mL of platelet wash buffer 3 times without disturbing the pellet and resuspended in 100 μL Tyrode’s buffer by directing the jet of buffer from the pipet onto the pellet ~ 10 times. Both fixed and non-fixed platelets were counted on a microscope and diluted to ~ 10¹¹ L⁻¹ for experiments.

4. Shear-stress control and dual-color TIRF imaging system

Microfluidic control and calibration was previously described[10] except for the platelet binding experiments. For platelet experiments, microfluidic channels were constructed similarly except detergent cleaned #1.5 cover glass (Gold Seal, Thermo Scientific, Waltham, MA, USA) were used instead of biotin-PEG/PEG-coated cover glasses. The #1.5 cover glasses were immersed in 1% (v/v) Hellmanex III solution (Hellma, Müllheim, Germany), heated to about 80°C, sonicated for 1 minute and rinsed with Millipore water before being assembled for flow channels.

Fluorescence microscopy used a dual-color TIRF microscope built on a vibration damping optical table (RS4000, Newport, Irvine, CA, USA) with a 60× oil TIRF objective (NA 1.49, CFI Apo TIRF 60× H, Nikon, Japan), 485nm laser (CUBE 485-30C, Coherent, Santa Clara, CA, USA), 642nm laser (DL640-050, Crystalaser, Reno, NV, USA) with an oscillating diffuser (laser speckle reducer, Optotune, Switzerland), an EMCCD camera (DU-897, Andor, UK) for the 485nm channel, and an EMCCD camera (C9100, Hamamatsu, Japan) for the 642nm channel. Synchronized image recording and flow was controlled with custom software (LabView, National Instruments, Austin, TX, USA).

Bright-field microscopy used an inverted microscope (TE2000-E, Nikon, Japan) with a 60× oil objective (NA 1.40, CFI Plan Apo Lambda 60× Oil, Nikon, Japan) and an EMCCD camera (C9100, Hamamatsu, Japan). Image recording and flow was controlled with custom software (LabView, National Instruments, Austin, TX, USA)

5. Platelet rolling experiment

The 15 mm long, 0.5 mm wide and 100 μm high channel was incubated with 1.5 μL of 1.5 mg mL⁻¹ VWF for 4 hours at room temperature and then a mixture (1:1) of BSA (BSA-Block, Candor, Germany) and casein (The Blocking Solution, Candor, Germany) for 1 hour at room temperature. For control experiments, the channel was incubated with BSA and casein only. 3 μL of ~ 10¹¹ L⁻¹ platelets were pipetted to the flow channel and allowed to settle for 1 minute. Buffer containing 150 or 500 mM NaCl, 20 mM HEPES (pH 7.4), 0.02% Tween 20 and 0.5 mg ml⁻¹ BSA was infused into the flow channel with a 250 μL syringe (1725 TLL SYR, Hamilton Company, Reno, NV) driven by a syringe pump (Pump 11 Elite, Harvard Apparatus, Holliston, MA). The images were recorded at 20 frames per second.

6. Statistical analysis

Sample size was not predetermined. Sample sizes for each experiment were reported in corresponding figure legends. Experiments were repeated in different flow channels on at least 2-3 separate occasions with similar results.

7. Image analysis

Fluorescence image analysis was previously described[10]. Platelet movies were analyzed using the ImageJ particle tracker plugin as part of the Mosaic Suite (http://mosaic.mpi-cbg.de/). The number of particles right before the start of flow was recorded as N₀. After turning on the flow, most unbound particles moved so fast that their images are blurred and not detected by the particle tracking code. At low shear stresses, 0.1-0.2 dyn cm⁻², some particles were not bound but slowly transported by flow near the surface (Supplemental Figure 6a). Any such particles with speeds higher than 15 or 25 μm/s at 0.1 or 0.2 dyn cm⁻², respectively, were considered unbound. 15 and 25 μm/s were the lowest speeds of platelets flowing along the control surfaces at 0.1 and 0.2 dyn cm⁻², respectively. The rest of the particles translocated on VWF coated surface in varying speed with irregular stops (Supplemental Figure 6b). For 100 dyn cm⁻², the settled platelets upstream to the field of view are depleted by flow after 3 seconds. Therefore, we compare the number of bound platelets in the field of view 3 seconds after the start of flow for all shear stresses (Figure 4b). The step sizes of each translocating platelet were calculated as the displacement between each pair of consecutive frames over the entire time window in which the platelet was detected. The rolling speed was calculated by multiplying the step size with the frame rate. The mean and the standard error of the mean for the speed of all translocating platelets were plotted in Figure 4c. Platelets that were stuck to surface before flow started were excluded from analysis.

8. VWF tension estimation and the two-state model for force-activated GPIbα binding

VWF tension estimation and the application of a two-state model for force-activated GPIbα binding were carried out as previously described[10]. Briefly, assuming that the inactive state (1) and the high-affinity state (2) of A1 are separated by an energy barrier along the molecular reaction axis and the free energy of state 1 is higher than state 2 by ΔG, an external force f adds a mechanical potential −f · Δx, where f is the external force, and Δx is the displacement between the two states along the direction of the external force. If state 2 has a binding rate of k_on,2 and state 1 has a binding rate that is ~0 for GPIbα binding, the apparent binding rate for regions of VWF subject to tension f would be

$$k_{on}=k_{on,2}·\frac{1}{1+\exp ((\Delta G-f·\Delta x)/(k_{B}T))}$$ (4)

With a force of f₅₀ = ΔG/Δx, half of the binding sites would be activated, making the average binding rate k_on,2/2.

9. Charge-charge interactions between A1 and GPIbα

Calculation of the electrostatic potential between two charged protein surfaces based on Debye-Hückel theory was adapted from Vijayakumar et al.[38]. The following derivation uses SI units.

In ionic solution, a charged moiety, such as an arginine, lysine, aspartic acid or glutamic acid side chain, is surrounded by opposite charges in solution. Assuming the distribution of an ion with charge number z_i in solution due to a charged particle j follows the Boltzmann distribution:

$$n_i^{\prime }(r)=n_i\exp \left(\frac{-z_{i}e{\psi }_j(r)}{k_{B}T}\right)$$ (5)

where n_i, is the number density of an ion infinitely faraway, ψ_j(r) is the electrostatic potential a distance r away from the center of the particle j, e is the elementary charge, k_B is the Boltzmann constant, and T is the

$${\nabla }^2{\psi }_j(r)=-\frac{1}{{ϵ}_0{ϵ}_r}{\rho }_j(r)$$ (6)

temperature. ψ_j(r) follows Poisson’s equation:

where ${\rho }_j(r)={\Sigma }_i{n}_i^{\prime }(r)z_i\mathrm{e}$ is the charge density. This makes

$${\nabla }^2{\psi }_j(r)={\kappa }^2{\psi }_j(r)$$ (7)

where 1/κ is Debye length.

$$\begin{gathered} \kappa =\sqrt{\frac{{\mathrm{e}}^2}{{ϵ}_0{ϵ}_r{k}_{B}T}\sum _i{n}_i{z}_i^2}=\sqrt{\frac{2N_A{\mathrm{e}}^{2}I}{k_{B}T{ϵ}_0{ϵ}_r}} \\ ={\left(\frac{2\times 6.02\times {10}^{23}\times {(1.6\times {10}^{-19}C)}^2·I}{4.11pN·nm\times 80.1\times 8.85\times {10}^{-12}{C}^2·N^{-1}·m^{-2}}\right)}^{\frac{1}{2}} \\ ={(1.06\times {10}^{16}m·mo{l}^{-1}\times I)}^{1/2}=0.325n{m}^{-1}{M}^{-1/2}\times \sqrt{I} \end{gathered}$$ (8)

Debye and Hückel provide a solution to the above equations[39]:

$$\psi =A·\frac{e^{-\kappa r}}{r}$$ (9)

Consider two ions with hydration radii R_i, and R_j each carrying a point charge (q_i and q_j) at the center. If in the encounter state, the centers of the two ions are seperated by r_ij, the electropotential of the charges is

$$\psi (r)=\frac{q_i{q}_j}{8\pi {ϵ}_0{ϵ}_r}\left(\frac{e^{\kappa R_i}}{1+\kappa R_i}+\frac{e^{\kappa R_j}}{1+\kappa R_j}\right)\frac{e^{-\kappa r_{ij}}}{r_{ij}}$$ (10)

Based on the protein data bank file 1SQ0, we listed charged residue pairs between A1 and GPIbα that are separated by r_ij < 10.4Å, the Debye length at 80 mM NaCl, in Table 1. Assuming R_i=R_j=R, the total electrostatic potential of the system is

$$\psi (r)=\sum _{i,j}\frac{q_i{q}_j}{8\pi {ϵ}_0{ϵ}_r}\left(\frac{e^{\kappa R}}{1+\kappa R}+\frac{e^{\kappa R}}{1+\kappa R}\right)\frac{e^{-\kappa r_{ij}}}{r_{ij}}=\frac{1}{4\pi {ϵ}_0{ϵ}_r}\sum _{i,j}{q}_i{q}_j·\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+\kappa R)}$$ (11)

Table 1.

Distances between charges on A1 and GPIbα binding interfaces. Only distances shorter than 10.4 Å, the Debye length at 80 mM NaCl, are listed.

rij (Å)	Glu225	Asp222	Glu128	Glu151	His12	Asp175	Lys152	Asp18	Glu5	His37	Asp235	Asp63	Glu14	Asp83	Glu40
Arg1395	2.5	10.1
Glu1359	6.7
Arg1399	7.1
Arg1392	8.1
Lys1362	6.7					9.4
Lys1371			5.7	9.2	10.3		9.2
Lys1407			9	6.2		6.7	7.4
Asp1373			9.7		6.5					9.2			8.5
Lys1332			6.6				10.1			10.1				9.6
Arg1334								3.3		3.4		4.6		6.7	6.8
Lys1312								8.9	3.3	8			6.5
Lys1335											3.9				10.2
Arg1342											4.5
Glu1339											4.7
Arg1374										9.7			5.8
Arg1280													5.8
Asp1333											7.2			10
Arg1285													8.8
Arg1336								9.9	9.2

According to the collision theory, this negative electrostatic potential lowers the activation energy barrier and therefore accelerates the binding according to a relation k_on ∝ ⩽exp(−ψ/k_BT)⩾[60,61]

$$\begin{gathered} \mathit{ln}{k}_{\mathit{\text{on}}}=\mathit{ln}{k}_{\mathit{\text{on}}}(I=\infty )-\frac{1}{4\pi k_{B}T{ϵ}_0{ϵ}_r}\sum _{i,j}{q}_i{q}_j·\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+\kappa R)} \\ =\mathit{ln}{k}_{\mathit{\text{on}}}(I=\infty )+\alpha \varphi (\kappa ) \end{gathered}$$ (12)

$$\alpha =\frac{{\mathrm{e}}^2}{4\pi k_{B}T{ϵ}_0{ϵ}_r}=6.97\AA$$ (13)

$$\varphi (\kappa )=\sum _{i,j}-\frac{q_i{q}_j}{{\mathrm{e}}^2}·\frac{e^{-\kappa (r_{ij}-R)}}{r_{ij}(1+\kappa R)}$$ (14)

k_on(I = ∞) in Equation (12) is the on-rate at infinite ionic strength, i.e. when electrostatic interactions are completely screened. The first hydration layer of protein near oxygen and nitrogen atoms is about R = 3.5 Å thick[40]. In agreement with Equation (12), the logarithm of measured k_on,2 linearly depends on ϕ(κ) (Figure 3e), which was calculated using Table 1. q is taken to be +1, +1, +0.1, −1 and −1 for Arginine, Lysine, Histidine, Glutamic acid and Aspatic acid at pH7.4. The slope obtained from fit to our data

$$\alpha =4.95\pm 0.57\AA =(0.71\pm 0.08)\times \frac{{\mathrm{e}}^2}{4\pi k_{B}T{ϵ}_0{ϵ}_r}$$

is 30% lower than the theoretical value in Equation (13). This is in reasonably good agreement with the predicted value given the many simplifications used in the derivation. The discrepancy in the α value may be caused by minor inaccuracies in the asssumptions made above, such as the geometry of protein hydration, the encounter complex, etc. In fact, if we test the case in which A1 and GPIbα are further seperated in their encounter state by adding 2.8 Å, the diameter of a water molecule, to all the r_ij, we will get a good linear fit with the slope matching $\frac{{\mathrm{e}}^2}{4\pi k_{B}T{ϵ}_0{ϵ}_r}$. The other fitting parameter is

$$k_{on}(I=\infty )=8.05\times {10}^{3\pm 0.44}{M}^{-1}{s}^{-1}$$

10. Estimation of GPIbα binding rates in blood

Assuming VWF is immobilized, the binding rate between wall-tethered VWF and platelets in blood k_P can be estimated from the encounter rate k_e between platelets and VWF, the concentration of platelet [P], the dwell time Δt, the association rate k_on between A1 and the GPIbα on a platelet, and the effective concentration of GPIbα near platelet surfaces [G].

$$k_P=k_e·[P]·\Delta t·k_{on}·[G]$$

First, we calculate k_e · [P] · Δt contributed by diffusion. The diffusion-limited collision rate between platelet and A1 is

$$k_D=4\pi ·(r_A+r_P)·D_P$$

where we let the radius of the A1 domain r_A = 3 nm, and D_P is the diffusion coefficient of platelet. Assuming platelets are disks with thickness L = 0.5μm and radius r_P = 1μm, the thickness-to-diameter ratio is p = 0.25, and the average diffusion coefficient can be calculated as[62]:

$$D_P=\frac{k_{B}T}{f}=\frac{k_{B}T}{\frac{f}{f_0}·f_0}$$

$$\frac{f}{f_0}=1.009+1.395\times {10}^{-2}(\ln p)+7.880\times {10}^{-2}{(\ln p)}^2+6.040\times {10}^{-3}{(\ln p)}^3=1.13$$

$$f_0=6\pi \mu L{\left(\frac{3}{16p^2}\right)}^{1/3}=6\pi \times 1.6mPa·s\times 0.5\mu m\times {\left(\frac{3}{16\times {0.25}^2}\right)}^{\frac{1}{3}}=2.17\times {10}^{-8}N·m^{-1}·s$$

where the viscosity of plasma is μ = 1.6mPa · s. k_BT = 4.28pN · nm at 37 °C, which yields

$$D_P=\frac{4.28pN·nm}{1.13\times 2.17\times {10}^{-8}N·m^{-1}·s^{-1}}=0.175\mu m^2·s^{-1}$$

$$k_D=4\pi ·(r_A+r_P)·D_p=2.29\times {10}^{-18}{m}^3{s}^{-1}=1.36\times {10}^9{M}^{-1}{s}^{-1}$$

The dwell time of each platelet for diffusional collision is approximately:

$$\Delta t_A=\frac{{(r_A+r_G)}^2}{D_P}=\frac{{(6nm)}^2}{0.175\mu m^2·s^{-1}}=2.06\times {10}^{-4}s$$

where we set the radius of GPIbα to r_G = 3nm.

Next, we calculate the binding rate of GPIbα due to advection. The advection induced collision rate between platelet and A1 at a 5000 s⁻¹ shear rate is approximately

$$\begin{gathered} k_A=\pi {(r_A+r_P)}^{2}v=\pi ·{(r_A+r_P)}^2·\gamma h\approx \pi ·{(1\mu m)}^2·5000s^{-1}\times 1\mu m=1.57\times {10}^{-14}{m}^3{s}^{-1} \\ =9.45\times {10}^{12}{M}^{-1}{s}^{-1} \end{gathered}$$

where the average distance between the colliding platelet and the surface is estimated to be r_P. The dwell time of each platelet due to advectional collision is approximately:

$$\Delta t_A=\frac{r_P}{v}=\frac{1\mu m}{5000s^{-1}\times 1\mu m}=2\times {10}^{-4}\mathrm{s}$$

For both the diffusion and advection cases, the approximate total binding rate of GPIbα is proportional to the product of the platelet collision rate, the number of GPIbα collisions during each platelet collision, and the A1-GPIbα association rate that is assumed to be the same for both processes. Therefore, under these conditions, the contribution due to diffusion, k_DΔt_D, is 3 orders of magnitude lower than the contribution due to advection, k_AΔt_A. and can be neglected. We now take k_eΔt ≈ k_AΔt_A. The total binding rate of platelet per activated A1 domain is then k_P = k_A · [P] · Δt_A · k_on · [G].

Finally, we estimate [G] from the surface density of GPIbα on platelet membrane ρ_G = 1.3 × 10³μm⁻²[41] and the linker length of GPIbα l_t = 46 nm[42],

$$[G]=\frac{{\rho }_G}{l_t}=\frac{1.3\times {10}^3\mu m^{-2}}{46nm}=4.7\times {10}^{-5}M$$

and use a platelet concentration [P] = 3 × 10⁵mm⁻³ = 0.5 × 10⁻¹² M, to determine the approximate total binding rate of platelet per activated A1 domain:

$$k_P=4.7s^{-1}\times 2\times {10}^{-4}s\times k_{on}\times 4.7\times {10}^{-5}M=44nM\times k_{on}$$

If a typical protein association on-rate is used, k_on = 10⁶M⁻¹s⁻¹, we obtain a total binding rate of platelet for each activated A1 domain of k_P = 0.04s⁻¹. Using the rapid, electrostatically-accelerated on-rate of 5 × 10⁷M⁻¹s⁻¹ that we measured, we obtain a much higher total binding rate of platelet for each activated A1 domain of k_P = 2s⁻¹.

11. Estimation of drag force on platelets

We approximate platelets as 0.5 μm radius spheres and use Stoke’s law to calculate the drag force on a platelet next to the surface in 5000 s⁻² wall shear flow.

$$f_{drag}=6\pi \mu rv=6\pi \mu r·\gamma h\approx 6\pi \times {10}^{-3}N·s·m^{-2}\times 0.5\times {10}^{-6}m\times (0.5\times {10}^{-6}m\times 5000s^{-1})=23.6pN$$

Highlights.

• VWF mechanically senses bleeding and binds platelets to plug ruptures.

• We stretched and imaged single VWF molecules using a flow-based assay.

• Electrostatic steering accelerates the binding of receptors to force-activated VWF.

• Strong electrostatic screening markedly decreases platelet binding to VWF in flow.

• Electrostatic attraction is critical to VWF-platelet binding in fast flowing blood.

Abbreviations

VWF

Von Willebrand factor

VWD

von Willebrand disease

GPIbα

glycoprotein Ibα

TIRF

total internal reflection fluorescence