Extensive subclonal mutational diversity in human colorectal cancer and its significance

Significance

Cancers evolve many mutations. Clonal driver mutations are selected early. Subsequent evolution occurs in a branching fashion, possibly without selection (“neutral evolution”). Rarer mutations occur later on smaller branches of the evolutionary tree. Using a DNA-sequencing method, duplex sequencing, with unprecedented accuracy and sensitivity, we quantified rare unique subclonal mutations in diagnostic specimens from 5 human colorectal cancers. Rarer subclones probe later evolutionary time points than previously possible. We confirm neutral evolution at later times and find many more subclonal mutations than expected. A theoretical method allowed us to extrapolate further forward in time to diagnosis. At diagnosis, every DNA base is mutated in at least one cancer cell. In particular, any therapy resistance mutation would be present.

Abstract

Human colorectal cancers (CRCs) contain both clonal and subclonal mutations. Clonal driver mutations are positively selected, present in most cells, and drive malignant progression. Subclonal mutations are randomly dispersed throughout the genome, providing a vast reservoir of mutant cells that can expand, repopulate the tumor, and result in the rapid emergence of resistance, as well as being a major contributor to tumor heterogeneity. Here, we apply duplex sequencing (DS) methodology to quantify subclonal mutations in CRC tumor with unprecedented depth (10⁴) and accuracy (<10⁻⁷). We measured mutation frequencies in genes encoding replicative DNA polymerases and in genes frequently mutated in CRC, and found an unexpectedly high effective mutation rate, 7.1 × 10⁻⁷. The curve of subclonal mutation accumulation as a function of sequencing depth, using DNA obtained from 5 different tumors, is in accord with a neutral model of tumor evolution. We present a theoretical approach to model neutral evolution independent of the infinite-sites assumption (which states that a particular mutation arises only in one tumor cell at any given time). Our analysis indicates that the infinite-sites assumption is not applicable once the number of tumor cells exceeds the reciprocal of the mutation rate, a circumstance relevant to even the smallest clinically diagnosable tumor. Our methods allow accurate estimation of the total mutation burden in clinical cancers. Our results indicate that no DNA locus is wild type in every malignant cell within a tumor at the time of diagnosis (probability of all cells being wild type, 10⁻³⁰⁸).

Accumulation of somatic mutations is a characteristic of cancer. Solid tumors contain numerous selected clonal driver mutations, as well as unselected clonal passenger mutations (1). Subclonal mutations—which we define operationally in this study as those present in ≤10% of malignant cells—also contribute to phenotypic and morphologic heterogeneity within a tumor (2), and potentially to therapeutic resistance (3). We note by way of definition that a driver mutation that is initially subclonal may become clonal if it is able to increase its relative prevalence in the tumor. If such a selective sweep occurs, it cannot be distinguished from initial presence in the founder cell, and such cells may be viewed as additional founder cells. The extent of subclonal mutations in cancer has been difficult to quantify, as the high error rate of next-generation sequencing precludes reliable detection of mutations present in fewer than 5% of cells (4).

Here, we apply the highly accurate duplex sequencing (DS) methodology to quantify the extent of subclonal mutations, each present in less than 10% of the genomes, in colorectal cancers (CRCs) and adjacent “normal” mucosa. The accuracy of DS (<1 artifactual background mutation in 10⁷) bases (5) is >10,000-fold greater than routine next-generation sequencing, enabling quantification of subclonal mutations at very high depth. Both strands of single DNA molecules are sequenced, and mutations are defined as those that are present in both strands of the same molecule at the same position and are complementary (6). We conducted ultradeep sequencing of 11 microsatellite instability (MSI)-negative CRCs (T) and adjacent normal (N) tissues. We assembled 2 gene libraries, a 10-kb library encoding replicative DNA polymerase delta and epsilon active sites (5 T/N pairs), and a 13-kb library encoding genes frequently mutated in CRC (11 T/N pairs). No clonal mutations were detected in the evolutionarily conserved DNA polymerase genes, but clonal mutations were plentiful within the second library in tumors as expected based on The Cancer Genome Atlas (TCGA) data (TP53, 5/11; KRAS, 5/11; BRAF, 1/11; PIK3CA, 5/11; UMPS, 1/11) (7).

Results

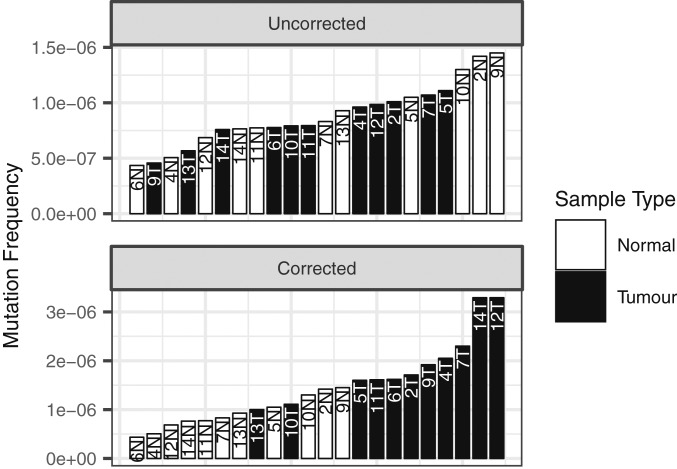
The mean subclonal mutation frequency was 8.4 × 10⁻⁷ ± 6 × 10⁻⁸ per nucleotide sequenced (n = 11) in the tumors and 9.2 × 10⁻⁷ ± 1 × 10⁻⁷ in the “normal” colon. The mutational burden in adjacent normal tissue is not statistically different from the uncorrected mutational burden in the tumor (Fig. 1, Top), but when the tumor mutational burden is corrected for the percentage of normal tissue present, estimated with digital imaging analysis (SI Appendix), tumors exhibit a 1.9-fold increase in the mutational burden compared to normal tissue, which is statistically significant (Fig. 1, Bottom). The presence of numerous subclonal mutations in normal colon expands on the results of Martincorena et al. (8, 9), who observed clonal mutations throughout normal esophageal tissue. There are several possible explanations for this phenomenon. First, it is difficult to compare the mutation frequencies in normal colonic tissue and relate them to relative mutation rates without knowing the corresponding proliferation histories. In normal colon, stem cells divide unequally, one daughter replacing the parental stem cell while the other differentiates into the intestinal lumen; in tumors, each cell undergoes symmetric divisions. Furthermore, it has been estimated that one-half of the mutational burden in a tumor was acquired in cells before birth of the founder due to the large number of cell divisions over many years before the founder cell is formed, which could also explain the observed results (10). Finally, with age, more and more “normal” cells may simply acquire a mutator mutation but still have an incomplete set of oncogenic driver mutations, whereas malignant cells may have a complete set (11).

Fig. 1.

Mutation frequencies in CRCs before and after correction for the presence of normal cells. (Top) Mutation frequencies in tumor (uncorrected) and paired normal tissues obtained at a distance 1 cm from the tumor margin. Tumor and normal tissue are not significantly different by Wilcoxon rank sum test, P = 0.84. Conservative, lower tumor mutation frequencies from this figure are reported in the manuscript. (Bottom) Mutation frequencies in tumor (corrected) and paired normal tissues. Tumor mutation frequency corrected for admixture with normal tissue. Percent normal tissue in tumor samples estimated with an automated image analysis system (SI Appendix). Tumor and normal significantly different by Wilcoxon rank sum test, P = 7.0 × 10⁻⁵.

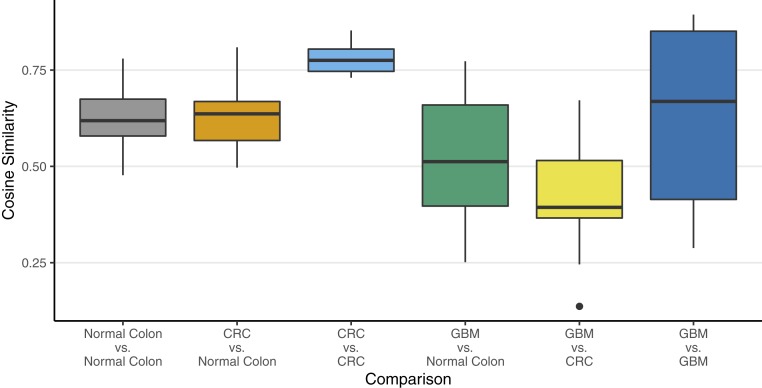
We measured the mutational spectrum of the 96 possible triplets (consisting of the mutation and 3′ and 5′ bases flanking each substitution) in CRCs, adjacent normal colon, and glioblastomas (CRC data in SI Appendix, Fig. S2). CRCs cluster closely in triplet space, and the distribution does not differ statistically from normal colon. Cosine analysis indicates that the landscape of triplets (12) is different in the highly conserved polymerase sequences in glioblastomas than in CRCs (Fig. 2 and SI Appendix) in accord with Hoang et al. (13), who found mutational spectra similar between T and N within a single tumor but different between different tumor types.

Fig. 2.

Plot of cosine similarities of mutation signatures, grouped by type of comparison. These results show that there is a significant difference between a CRC tumor sample and a glioblastoma multiforme (GBM) sample. Detailed results of an ANOVA of these data are discussed in SI Appendix, Table S6.

The contribution of selection in tumor evolution is still debated. It is generally agreed that oncogenic driver mutations conferring critical cancer phenotypes are often clonal and positively selected. Some models assume successive purifying selective sweeps associated with acquisition of additional drivers (14), while others (11, 15) assume neutral evolution after malignant transformation, where neutral evolution refers to the idea that shortly after cellular transformation the malignant cell has acquired an assortment of driver mutations, and mutations thereafter do not confer a further fitness advantage or disadvantage in the absence of therapy. Thus, these further mutations are randomly acquired, neither enriched nor purified away during subsequent tumor evolution prior to therapy. The latter neutral evolution models featured an early mutator mutation (11, 15, 16) increasing the mutation rate and accelerating the acquisition of driver mutations. In a subsequent “Big Bang model” (17), selective sweeps also need not be invoked. Several experimental studies at varying depths supported neutral evolution (13, 17, 18). Our work sequences more deeply and omits clonal mutations, both driver and passenger, in the analysis. In this work, we have operationally defined the subclonal space as ≤10% allele frequency; it is these mutations that are evaluated for neutral evolution.

Determination of Mutation Rate and Mutation Burden via Sequencing the Same Sample at Different Duplex Depths.

As it is not possible to sequence every genome present in a tumor, rare mutations (i.e., mutations present in one cell or a small number of cells) are infrequently sampled. Due to the branching nature of evolution, the earliest mutational events near the trunk of the evolutionary tree are scored in the majority of cells and can be detected at low DS depth. As we increase DS depth, additional recent mutations that are present in a smaller fraction of the cells are also detected. As the number of nucleotides sequenced at a given genomic position is nearly always less than the number of cells in the tumor, we are unlikely to detect evidence of recent mutational events late in the tumor’s evolution. Thus, the full mutation burden in the tumor cannot be directly determined, and the estimate of mutation rates is based on an incomplete dataset.

We developed a method to estimate the mutation rate and the full mutation burden in the tumor by comparing measurements at several different DS depths. Herein and in SI Appendix, we present the theoretical analysis for mutation rate estimation, and then evaluate 5 colorectal tumors by DS at a depth of up to 20,000× and an accuracy of <10⁻⁷.

We define the following terms and concepts (SI Appendix, Table S2): 1) Number of effective cell divisions: N_E the net number of times a single cell in the tumor produces a new living daughter cell to become 2 living cells, both of which survive. This is defined only for growing tissues like tumors. In nonmalignant tissues, the total number of cells remains constant due to a balance of cell birth and death rates (b and d, respectively). In a tumor, b > d, and therefore the tumor grows over time. However, as d ≠ 0, it takes more than one actual cell division to make an effective cell division. That is, following any actual cell division, the daughter or parent cell may die. In such a case, that cell division does not count as an effective cell division, which refers only to cell divisions that result in an increase in cell number by 1. This simple concept is convenient for analysis because, for any tumor of N cells that grew from a single founder cell, the number of effective cell divisions is, by definition, always N – 1, whereas the actual number of cell divisions is greater than or equal to the number of effective cell divisions, and cannot be determined due to the unknown history of the tumor. It is also important to distinguish cell divisions, which we have equated to the net number of all cells that have divided, from cell generations or doublings, each of which involves a very large number of individual cell divisions, the more so later in the tumor’s history. 2) Relationship between number of actual cell divisions (N_A) and effective cell divisions (N_E): The rate of increase in a population due to a single cell (not including further proliferation from its daughters) is simply b in the absence of cell death, whereas the net rate of increase in a population in the presence of cell death is b – d. The ratio of these 2 quantities determines the relationship between actual and effective cell divisions:

$$N_{\mathrm{A}}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \underset{0}{\overset{T}{\int }}\frac{b\left(t\right)N_{\mathrm{E}}}{b\left(t\right)-d\left(t\right)}dt}.$$ [1]

We have expressed this as a time integral since b and d may vary over time. This relationship does not apply for adult tissues without net growth, and would be mathematically undefined when b = d.

Average values of b and d have been estimated using histologic techniques as the ki-67 index and the caspase 3 index, respectively. These rates are subject to both spatial and temporal heterogeneity that characterize tumor evolution, and, therefore, precise inference of the actual number of cell divisions has been difficult to obtain.

Estimates of b for CRC have also been provided using labeled nucleotides, leading to an overall estimate of 0.25/d on average (19). Comparing this estimate to the actual rate of increase of resistant subclones in CRC by noninvasive monitoring, an estimate for d of 0.18/d on average is obtained (3). For example, using Eq. 1, if b and d have the above values, the number of actual cell divisions exceeds the number of effective cell divisions by a factor of 3.57. Note: The number of actual cell divisions is not utilized in the model described in this paper. 1) DS depth: defined as number of duplex molecules sequenced at each nucleotide position, symbolized by D. 2) Number of cells in the tumor at the time of sampling: N. 3) Number of cells in the tumor at an earlier timepoint t: n(t) < N. 4) Mutation rate per nucleotide per effective cell division: k_mut-eff. 5) Mutation rate per nucleotide per actual cell division: k_mut-actual. Note: This parameter is not utilized in the model because it is not directly measurable. 6) Fraction of apparently unmutated single-base loci at each position: F_{apparent-unmutated}. The fraction of single-base loci sequenced for which there is no unique subclonal mutation detected when sequencing a tumor of N cells at depth D. 7) Reference sequence for defining unique subclones: The consensus clonal sequence of the normal in that individual is the reference against which unique subclonal mutations are defined. Compared to the host germline, the founder cell(s) harbors: 1) clonal mutations that were selected during carcinogenesis, and 2) random drift from the germline, which occurred during the life span of the individual, during which the entire colonic epithelium was repopulated on a weekly basis, leading to a variation among normal colonic cells (10). By discarding clonal passenger and driver mutations occurring in the tumor at greater than 10% allele frequency in the analysis, the reference becomes in effect the founder cells, which may be new founder cells or “founder cells” after subsequent selective sweeps. Our analysis is independent of the history of the tumor prior to the birth of the founder cell(s).

The goal of the analysis is to infer the mutational diversity of a tumor from sequencing at a variety of depths, and to discuss the consequences for therapy. The analysis does not use the traditional input and output parameters of actual number of cell divisions N_A and mutation rate per base per actual cell division k_mut-actual, which can only be inferred based on assumptions that are highly dependent on the unknown tumor history. Rather, it uses the input parameter of the number of effective cell divisions N_E, which can be directly obtained from the tumor size and the corresponding output parameter of mutation rate per effective cell division k_mut-eff. Bozic and Nowak (20) have previously used tumor size as an approximation for the number of cell divisions, as we have in this work. The other input parameters, DS depth D, and fraction of apparent unmutated single-base loci (relative to a tumor consensus reference) are also experimentally obtained.

We can use this analysis to characterize the mutational diversity of a tumor, including the likelihood of the presence of a mutation at an arbitrarily selected site in one or more cells of a tumor, and discuss the clinical consequences. A mathematical model for optimizing targeted therapy while accounting for tumor evolution, as parameterized by the net birth rate (birth rate minus death rate) and the effective mutation rate has previously been published. Simulations using this model demonstrate the utility of this approach, which is similar to the approach described herein (21). However, the model cannot provide a definitive estimate of the tumor’s mutation rate per actual cell division k_mut-actual, nor can it compare such a value with a comparable parameter from normal tissue to evaluate the validity of the mutator hypothesis (which states that tumors have a greater mutation rate than normal tissue). Resolution of this question requires determination of actual mutation rates, which in turn requires knowledge of the mitotic history of both the tumor and normal tissue. An illustration of the dependence of the inferred actual mutation frequency on the growth pattern is provided in SI Appendix. Furthermore, Eq. 1 is not designed to be informative for homeostatic tissues, where b = d.

Mathematical Approach.

In order to model the fraction of apparently unmutated single-base loci, we integrate over the entire history of the tumor, determine the fraction of apparently unmutated single-base loci for daughter cells born at different times, and obtain the average fraction of apparently unmutated single-base loci, weighted by the number of daughter cells born at different times. For mutations detected at a given DS depth, the fraction of apparently unmutated single-base loci is constant [independent of n(t)], making the average simple to calculate. At early time points, when there are few cells, it is less likely that a mutation will arise because there are fewer cells dividing at that time. However, if a mutation arises at this early time, it will be present in a larger fraction of the cells in the final tumor, because it is closer to the trunk of the evolutionary tree, and therefore will be more likely to be detectable. These 2 factors (the lower likelihood of a mutation at earlier times but greater likelihood of detecting a mutation that does occur at an earlier time) exactly counterbalance each other to give a constant number of expected detectable mutations arising at any time. These considerations lead to the following equation, which was used in our primary data analysis:

$$\ln \left(F_{\mathrm{apparent}-\mathrm{unmutated}}\right)=-k_{\mathrm{mut}-\mathrm{eff}}D.$$ [2]

The derivation of this equation is given in SI Appendix. Plotting the natural logarithm of F_{apparent-unmutated} vs. D is thus expected to lead to a straight line, with slope of −k_mut-eff, which parallels our data very accurately (SI Appendix, Fig. S1 A–E). The expression differs from related methods (22) due to the absence of the infinite-sites assumption (23). In SI Appendix, we show that, at sequencing depths below 1/k_mut-eff, Eq. 2 predicts a linear relationship between number of unique subclonal mutations and sequencing depth, similar to other methods (22). Fig. 3 is plotted in this manner due to the intuitive clarity of presentation. However, at very high depth, this simple linear relationship breaks down and greatly underestimates the total mutational burden of a tumor (see Figs. 5–7). These points are shown mathematically in SI Appendix.

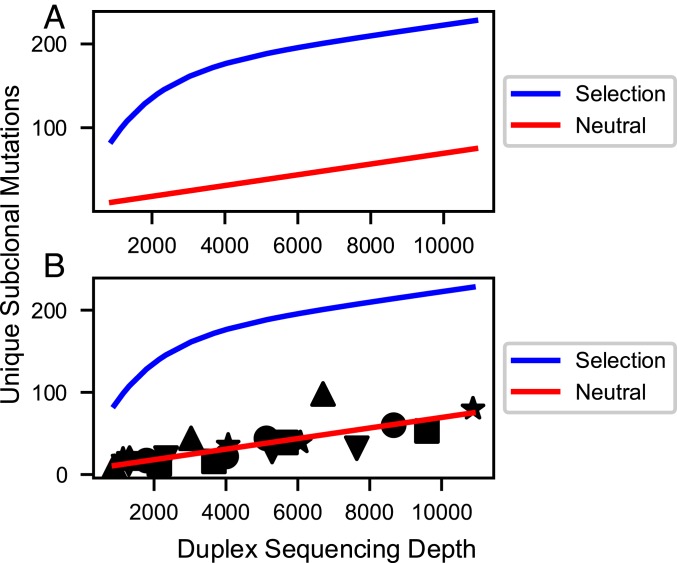
Fig. 3.

Simulated (A) and actual (B) curves for the number of nucleotide sites uniquely mutated in the DNA polymerase library (10 kb) vs. DS depth. (A) Simulations assume most subclonal mutations are neutral passenger mutations (red line) or assume significant purifying selection (blue line). Simulation methods and parameters are given in SI Appendix. Neutral model: The curve for neutral mutations alone is predicted to be approximately linear for sequencing depths up to 100,000 and after that to approach saturation in an exponential fashion. A mathematical transformation of the number of mutated sites, which is predicted to be exactly linear for all sequencing depths, is given in SI Appendix. Selection model (blue line): This curve is the sum of curves for 3 classes of sites (positively selected, neutral, and negatively selected) exponentially approaching saturation of their respective sites at different rates. Positively selected sites approach saturation rapidly, while negatively selected sites approach saturation slowly, if at all. The resulting simulation shows sharp curvature. The figure is only illustrative; the curvature shown may not be detectable for weak selection (s < 0.2) combined with low mutation rate, or for a small number of positively selected sites (<1%). (B) Observed data superimposed on the selected and neutral models from A. The observed data fit the latter neutral model with correlation coefficients ranging from 0.953 to 0.999 for 5 tumors (shape-coded) independently sequenced at multiple depths (SI Appendix, Table S3 and Fig. S1). The plotted line is the optimal regression line through all of the data points from the 5 tumors, less precise than individual regressions for each tumor.

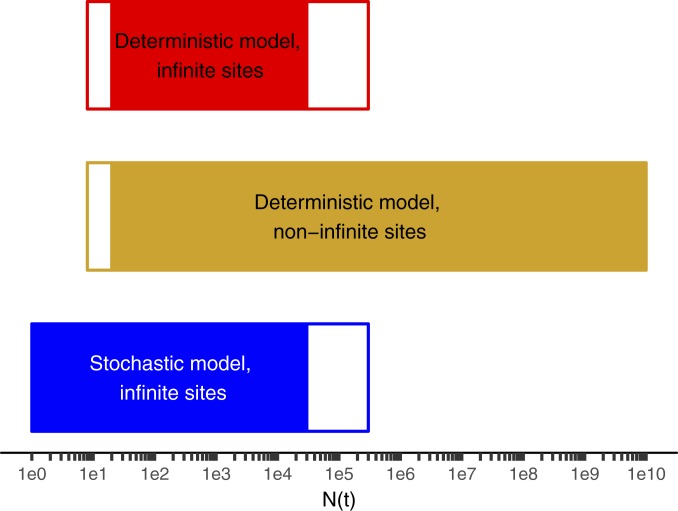
Fig. 5.

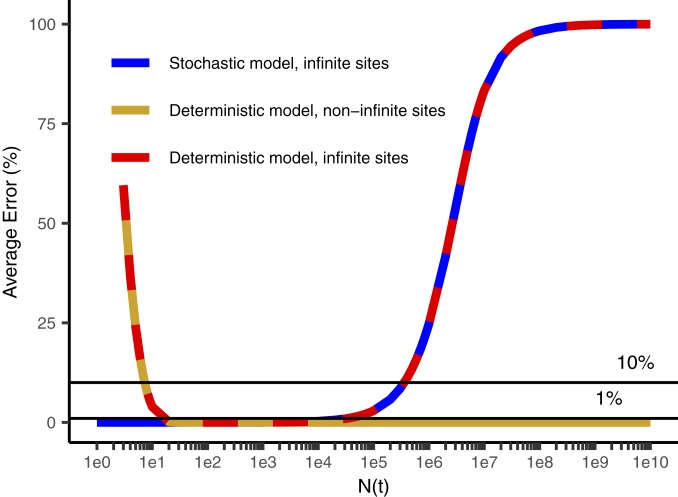
Range of applicability of various models of intratumoral diversity vs. the number of cells in the tumor N(t) when the mutation was acquired. Sequencing to a depth D queries, on average, mutational events occurring when N(t) = D. Stochastic models such as that of Bozic et al. (26, 32) are more accurate than deterministic models at early times when the tumor is small. Models without the infinite-sites assumption (this manuscript) are more accurate than those with it (22, 26, 32) for larger tumor masses in which the number of cell approaches or exceeds the reciprocal of the effective mutation rate. The white parts of the bar represent zones where a method is not the best method but is within 10% of the best method. The solid bars indicate the method is the best method or within 1% of it. In the range of N(t) ∼ D corresponding to typical current experimental depths, all 3 methods are within less than 1% of each other. Parameters are b = 0.25/d, d = 0.18/d, and k_mut-eff = 6.1 × 10⁻⁷.

Fig. 7.

Average percentage error in determining mutant allele frequency (MAF) for each intratumoral diversity model compared to the most accurate model as a reference for the stochastic model with the infinite-sites assumption (26, 32) (blue), and the deterministic model with (22) (red) and without (gold, this manuscript) the infinite-sites assumption (32). Because the x axis is on a log scale, the errors made by models with the infinite-sites assumption in estimating total tumor diversity in the high N(t) range on the Right of the graph is highly significant.

If we could sequence every single cell in the tumor, we could determine the total mutational burden of the tumor. In Eq. 2, we would substitute D = N. Raising e to the power of each side of Eq. 2, with D = N, we obtain the following:

$$\text{Fraction}\hspace{0.17em}\text{of}\hspace{0.17em}\text{single}\hspace{0.17em}\text{base}\hspace{0.17em}\text{loci}\hspace{0.17em}\text{unmutated}\hspace{0.17em}\text{in}\hspace{0.17em}\text{the}\hspace{0.17em}\text{entire}\hspace{0.17em}\text{tumor}\hspace{1em}=e^{-k_{\mathrm{mut}-\mathrm{eff}}N}.$$ [3]

If there are R single-base loci in the genome, mutation of which can lead to drug resistance to a single drug, and there are K non–cross-resistant drugs administered, we modify Eq. 3 to predict the probability of no cross-resistance to all K therapies, due only to mutation:

$$P_{\text{no}\hspace{0.17em}\hspace{0.17em}\text{simultaneous}\hspace{0.17em}\hspace{0.17em}\text{cross}\hspace{0.17em}\hspace{0.17em}\text{resistance}}=e^{-{\left(R\hspace{0.17em}{k}_{\text{mut}-\text{eff}}\right)}^{K}N}.$$ [4]

This equation was used to calculate the values in Table 1. A detailed derivation and more results of these calculations are given in SI Appendix.

Table 1.

Probability of emergence of multiply resistant cells

No. of cells (N)	No. resistant loci (R)	Therapies (K)	PNSCR
109	1	2	0.999
109	100	2	6.5 × 10−3
109	100	3	>0.999
1011	100	3	0.965
1012	1	2	0.604
1012	100	3	0.699

Probability P_NSCR that no cell in a cancer of N total cells will be mutationally resistant to all of K non–cross-resistant therapies, where in each case there are R neutral single bases in the genome, mutation of which confers resistance in selected scenarios. See SI Appendix, Table S5, for additional scenarios.

In SI Appendix, the following additional topics are considered: application of the method to the 5 individual CRC tumors sequenced at multiple depths, the relationship of this theoretical work to earlier work with particular emphasis on the mutant allele fraction as a function of sequencing depth, discussion of assumptions and approximations of the model, illustration of the dependence of actual mutation frequency on the growth pattern (e.g., Gompertzian growth), evaluation of the likely consequences for the estimate of tumor mutational burden and for the mutator hypothesis, and simulations defining the sensitivity of the method for detecting deviations from neutral evolution.

Because of the branching nature of tumor evolution, increasingly rare private mutations are found in later, more numerous branches. Thus, our ability to sequence more deeply with DS gives us a window into evolution further forward in time from the birth of the founder cell. In order to determine whether neutral evolution continues at a constant high mutation rate at later time points, we sequenced multiple independent samples from 5 tumors to progressively increasing depths up to 20,000, using capture probes consisting of oligonucleotides complementary to exons of replicative DNA polymerases. Our mathematical analysis is similar but not identical to the approach Williams et al. (22) devised to analyze the TCGA database. Both methods support the neutral model, in which most mutations do not affect fitness, and a linear relationship is predicted between the number of unique subclonal mutations and the sequencing depth up to depths approaching the reciprocal of the effective mutation rate (i.e., ∼1.5 million; see below); this is confirmed in Fig. 3 and in SI Appendix, Fig. S1 A–E.

Purifying selection, as well as changes in growth dynamics or mutation rates, could each result in deviations from linearity (SI Appendix, text and Table S4). For example, exact simulation of a selection model will in general not give a straight line, but a curve with 3 phases, each with progressively decreasing absolute value of the slope with increasing DS depth, resulting in curvature [upward slope with downward curvature for the Williams et al. (22) formulation; downward slope with upward curvature for our approach]. The initial phase at low depth (high variant fractions) is dominated by selected loci that accumulate mutations rapidly in the majority of cells. Then a second phase follows representing the neutral loci, which accumulate mutations more slowly and at lower variant fractions, and thus become visible at higher depth. Finally, a third phase representing small numbers of negatively selected genes at still lower variant fractions may be observed. We assume the approximation that mutations in different sites are independent with respect to their effect on fitness and additive. With this assumption, cells with or without a selected mutation may appear in different cells with different genetic contexts as the tumor evolves, but on average will be more fit than the comparable population without the selected gene. If we had modeled a continuous distribution of fitness, there would be a continuous downward curvature rather than 3 phases. However, the ability to observe all 3 phases, or indeed to observe curvature, depends on the parameters and the sequencing depths chosen.

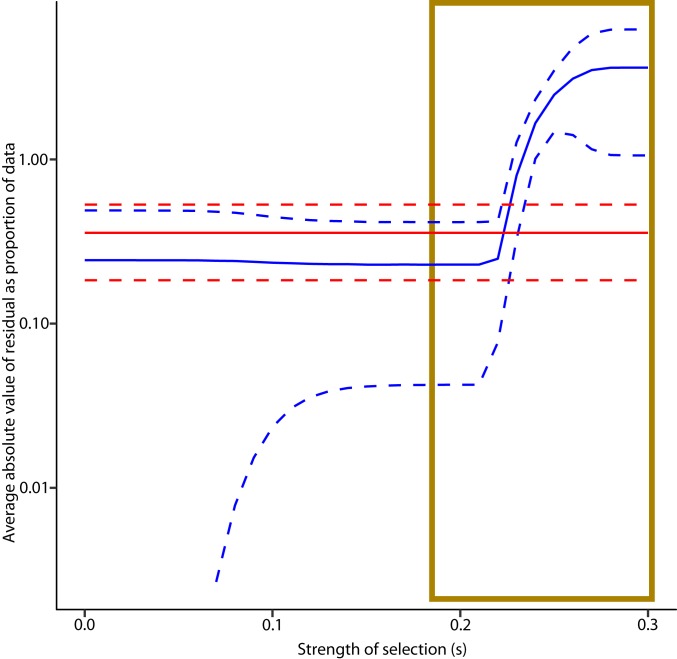
However, curvature was not observed (Fig. 3 and SI Appendix, Fig. S1 A–E), indicating that within the limits of our sensitivity these effects do not skew the average frequency and types of single-base substitutions in the subclonal mutational landscapes. We evaluated the sensitivity for ruling out selection by varying the selection coefficient s, and the percentage of bases in the genome subject to selection. A selection coefficient s means that cell with that selected mutation will be more fit by a factor of 1 + s, increasing in number by this factor relative to a cell with fitness 1 each effective cell division. For each set of sensitivity parameters, we compared the average absolute fractional residual error (i.e., absolute value of the experimental data minus that predicted by the model, all divided by the experimental data). If a model had an average absolute fractional residual error above the upper 95% confidence interval of the average absolute fractional residual error of a competing model, it was considered ruled out. Fig. 4 shows that while there was no statistically significant difference between weak selection and neutral models, selection models with s ≥ 0.23 are ruled out. Weak selection models that fit the data must be paired with lower mutation rates. Despite having more parameters for fitting, they generally required y intercepts further from the theoretical value of zero than their neutral counterparts. In addition to not being able to rule out weak selection, we cannot rule out selection occurring at ≤1% of base loci. Weak or infrequent selection approaches neutral evolution in that the term neutral evolution is not meant to be absolute. The results suggest that neutral evolution at a high mutation rate (or weak selection at lower mutation rates if present) continues as far forward in time as we can see, i.e., until the tumor reaches 20,000 cells.

Fig. 4.

Sensitivity threshold for ruling out selection models. Average absolute fractional residual curves for best fit neutral (red) and selection (blue) models are plotted (solid lines) along with their 95% confidence limits (dashed lines) as a function of the strength of selection s. Reference data were 1 of the 5 fresh frozen CRC tumors that we sequenced at multiple depths, plotted according to the approach in SI Appendix, Methods, with the natural logarithm of the unmutated fraction of the capture set plotted against depth. For the selection model, a₁ was set at 0.015, indicating 1.5% of loci were positively selected (97% were neutral and 1.5% negatively selected). For each model, k_mut-eff and the y intercept value (theoretically zero) were varied in a search for the optimal fit. k_mut-eff was constrained to be ≥10⁻¹⁰. For each point in the data, absolute values of the residual as a fraction of the data point itself were recorded. These values were averaged across the data points for each model. For s > 0.23, the average absolute fractional residual is greater than the upper 95% confidence limit of the same statistic for the neutral model, suggesting that this strength of selection is ruled out. Strong drivers typically have s on the order of 1–4 (37). See SI Appendix, Methods, for details of simulation.

The slope of the lines plotted for individual tumors determine a mutation rate per template nucleotide locus per effective cell division, or “effective mutation rate” (Methods and SI Appendix), in a manner similar but not identical to that of Williams et al. (22). An effective cell division is defined by the addition of one new cell to the tumor, and consists of multiple actual cell divisions depending upon the differences between cell birth and death rates. Thus the “actual mutation rate” will in general be lower than the effective mutation rate. The observed effective mutation rate may change without a change in the actual mutation rate if the balance between birth and death rates changes during tumor growth, but our conclusions below remain robust for different growth patterns (SI Appendix). The number of effective cell divisions is based on tumor size, in that an effective cell division adds one net new cell to the tumor. The actual mutation rate cannot be determined without knowledge of cellular birth and death rates throughout the tumor’s history. Effective mutation rates can be used to estimate total mutational burden of a tumor (below) and to govern evolutionarily optimized therapy (21).

Among the 5 tumors sequenced at different depths, the average effective mutation rate is 7.1 × 10⁻⁷. This is substantially higher than previously estimated for actual mutation rates in normal tissues based on human population genetics and/or tissue culture studies (∼10⁻¹⁰) (24). However, one cannot compare an effective mutation rate to an actual one without knowledge of the proliferation history, and thus cannot definitively state whether this is indicative of a mutator phenotype.

Given a genome length of 3.1 × 10⁹, multiplying by the effective mutation rate per nucleotide, we estimate 2,200 new mutations per new daughter cell added to the tumor, or for 32 doublings between the founder cell and a recently born cell when the tumor is large enough to be detected radiologically, a genetic difference of ∼65,000 subclonal mutations. In interpreting this very high number, we note that the vast majority of these mutations would be private mutations detectable only by single-cell or single-molecule sequencing, including mutations in noncoding DNA.

Discussion

Quantification of intratumoral genetic diversity and its relationship to therapy resistance began with the landmark 1965 use of combination therapy to prevent emergence of resistance in childhood leukemia (25). Numerous authors have concluded that each tumor cell is genetically distinct (18, 22, 26–28). Both Loeb et al. (29) and Sottoriva et al. (17) pointed out that a high mutation rate facilitates drug resistance, and Sottoriva et al. (17) made a similar point for neutral evolution. Preexisting mutations have been linked to resistance in preclinical experimental models (30), in single-cell analysis of subclones expanded in 3D culture (28), and in clinical cases (31). Thus, preexisting resistance to single agent therapy is likely in many cases.

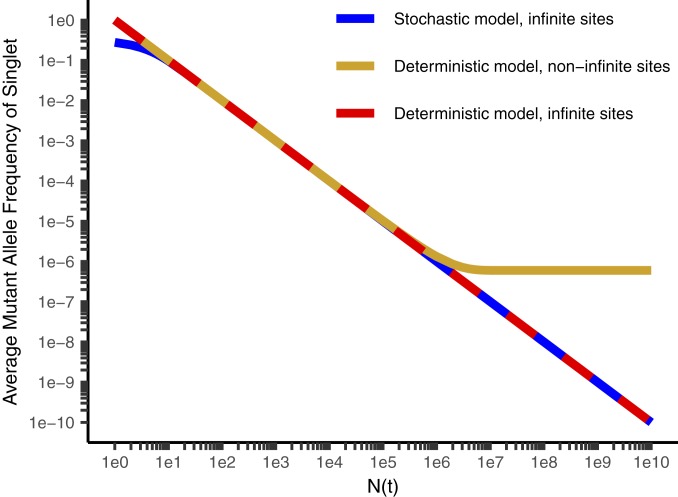
We estimate the total burden of unique subclones in a tumor from an analysis of the unique subclones detectable at different depths by extrapolation of our data to single-cell depth in tumors of different sizes (Methods and SI Appendix). At very high depth (greater than the reciprocal of the effective mutation rate, ∼1.5 million), the Williams et al. (22) model and related stochastic analyses (26, 32) substantially underestimate the tumor diversity (Figs. 5–7, Methods, and SI Appendix). These approaches utilize the “infinite-sites assumption” (23) that any mutation is unique when first formed. This assumption requires that the number of cells in the dividing population is less than the reciprocal of the effective mutation rate (i.e., 1 million cells dividing with an effective mutation rate of 10⁻¹⁰). In these cases, there will be no mutations at the majority of sites in the population, and more than one cell with a mutation in the same site is unlikely. We have, however, inferred a higher effective mutation rate than previous authors with the exception of Williams et al. (22). What will be the total tumor diversity if this high mutation rate continues until the tumor reaches its minimum radiologically diagnosable size of 10⁹ cells or even beyond to the terminal phase of the disease with many more cells present in the total cancer? The infinite-sites assumption is no longer applicable due to the large number of individual cell divisions per cell generation, and at each nucleotide locus we expect multiple cells will acquire the same mutation simultaneously (expected number of new cells with the given mutation = mutation rate per nucleotide locus per cell × number of cells dividing >> 1). Cheek and Antal (33) have recently objected to the infinite-sites assumption on identical grounds. A mathematical approach independent of the infinite-sites assumption, suitable for accurate estimation of tumor mutation burden, is given in SI Appendix, and the predictions are confirmed in each of the 5 tumors sequenced at multiple differing depths (Fig. 3 and SI Appendix, Fig. S1 A–E). We note that stochastic models (26, 32) and deterministic models with (22) and without (this manuscript) the infinite-sites assumption, despite their different mathematical forms, give similar results over a wide range of typical experimental conditions (Figs. 5 and 6; see mathematical proof in SI Appendix). Stochastic models are more accurate than others at low cell number, and models without the infinite-sites assumption are more accurate for cancers large enough to be clinically diagnosed (Figs. 5 and 6 and SI Appendix). The difference in predicted diversity is highly significant at diagnosis and increases dramatically as the total cancer burden increases (Figs. 6 and 7).

Fig. 6.

Average mutant allele frequency (MAF) for a given mutation vs. N(t), the number of cells at the time it is formed, for the stochastic model with the infinite-sites assumption (26, 32) (blue), the deterministic model with the infinite-sites assumption (22) (red), and without the infinite-sites assumption (gold; this manuscript). The deterministic model with the infinite-sites assumption leads to a reciprocal relationship between N(t) and the average MAF and a straight line with a slope of −1 on a log–log plot. The deterministic model without infinite sites has an asymptotic limit for the MAF of k_mut-eff for N(t) comparable to 1/k_mut-eff and larger. Parameters are b = 0.25/d, d = 0.18/d, and k_mut-eff = 6.1 × 10⁻⁷.

In essence, the cancer gradually approaches and then enters a new quantitative phase when it grows to a total number of cells beyond the reciprocal of the effective mutation rate, acquiring substantially greater diversity. The approach is governed by SI Appendix, Eq. S16 and illustrated in Fig. 6. This equation is derived in SI Appendix, and it is shown that at depths well below the sequencing of all tumor cells (i.e., all experimental studies to date), allele frequency will be inversely proportional to sequencing depth, as claimed by Williams et al. (22). However, unlike the Williams et al. (22) model, this will not continue indefinitely, resulting in the allele frequency approaching zero. Rather, according to SI Appendix, Eq. S16, the allele frequency will smoothly approach a minimum of k_mut-eff (Fig. 6). The underlying molecular biology may not have changed, but based on altered probabilities there are important clinical and biological considerations. Simulation studies of tumor evolution often focus on 10⁶ cells or less due to computational limitations. Based on our results, we do not believe these studies can be simply “scaled up” to larger tumors without taking into account the progressive violation of the infinite-sites assumption. Experimental small animal studies are limited in tumor size due to ethics considerations. Patients, at current levels of diagnostic sensitivity, are diagnosed in the unexplored region of larger tumors, and move further into this region as they move through their clinical course. Under neutral evolution, the result has limited or no dependence on whether the cells are in one or numerous lesions. Subject to the assumptions that neutral evolution and a high mutation rate continue, we conclude from this analysis that every nucleotide locus is mutated in one or more cells in a clinically detectable tumor. The chance that every cell is “wild type” at any given neutral locus is 10⁻³⁰⁸. This conclusion differs from the idea that all tumor cells are genetically distinct (which could result from variation at a limited number of sites) or that preexisting resistance is frequent or likely. Our work suggests that preexisting resistance to single-agent therapy is universal and inevitable.

[Note that, in this work, the reference sequence is the normal consensus sequence for the given individual, meaning that “wild type” refers to that sequence. Relative to a general human consensus sequence, this tumor consensus sequence may contain numerous passenger mutations as well as single-nucleotide polymorphisms (SNPs) unique to the host. We discard tumor mutations occurring at allele frequency greater than 10%, and thus the reference effectively includes clonal driver and passenger mutations occurring in >10% of the tumor cells. The “founder cells” may be original founder cells or may have arisen from selective sweeps. Given that these founder passenger mutations and SNPs will be passed on to most of the daughter cells derived from the founder(s), these mutations will almost certainly be retained in one or more tumor cells in the final tumor as well.]

Furthermore, we are able to calculate the likelihood of simultaneous resistance at diagnosis to multiple non–cross-resistant therapies preexisting in a single cell based on mutational resistance alone, and how this probability increases as the tumor grows (Table 1 and SI Appendix, text and Table S5). The trend toward greater likelihood of simultaneous resistance to combinations as the tumor grows is in accord with Bozic et al. (32). However, our estimates benefit from deeper sequencing at higher accuracy as well as independence from the infinite-sites assumption. Table 1 contains several rows, each representing a different clinical scenario or presentation. The tumor burden and the number of relevant non–cross-resistant therapies will certainly vary between patients. The number of bases, mutation of which may lead to resistance, is unknown and highly variable. Resistance can be due to mutations anywhere in the pathway where the drug acts, in parallel redundant pathways, or in feedback loops, and also can affect protein coding regions, transcription factor binding sites, microRNA, and so on. Often new resistance mechanisms still remain to be discovered. A recent description of clinical resistance mechanisms in BRAF directed melanoma therapy is illustrative (34). The scenarios illustrate that the greater the tumor burden and the greater the number of resistance mechanisms, the more non–cross-resistant therapies would be required to make it likely that no single cell will have simultaneous resistance. Optimal therapy must not only consider preexisting resistance but also the risk of new multiply resistant subclones emerging during tumor growth (21, 35).

Our work has limitations (see SI Appendix for additional discussion). It assumes that the mutation frequency in the purified gene fragments is representative of the whole genome. Mutational hot spots were not evident within our capture set, which was selected because it is tightly conserved in evolution.

The data do not rule out weak selection with a selection coefficient less than 0.23 (i.e., a 23% net growth advantage per cell generation), nor can it rule out the presence of a very small number of selected sites (<1%) (SI Appendix). This is in accord with sensitivity limits reported by Williams et al. (22).

Weak selection by many “minidriver” genes is an alternative theory of interest to many. Bozic et al. (36) have modeled the selection coefficient based on evaluation of putative passenger and driver mutations in astrocytic glioblastoma and pancreatic adenocarcinoma sequences, and validated their conclusions by predicting the kinetics of appearance and growth of polyps in familial adenomatous polyposis in 2 of 3 datasets. They reached the conclusion that, even for APC, s is very small: 0.004. However, the key equation in their analysis is Eq. 2, in which s appears in a ratio with the mutation rate. They then use a mutation rate 3 orders of magnitude lower than what we have determined. Using our mutation rate, their Eq. 2 would give a value of s of nearly 4, which is in accord with the value of 2.76 more recently measured by direct observation of colonic stem cell crypt evolution using fluorescently labeled cells in genetically engineered mice (37). Moreover, in our view, the modeling of polyp appearance kinetics does not account for host factors such as success or failure in establishing the tumor vasculature, or the possible elimination of most nascent polyps by immune surveillance. These and other factors may confound comparisons of tumor initiation kinetics with clinical observations (11). Williams et al. (38) have examined bulk sequencing data from multiple sources, looking for deviations from neutral evolution in the curve of variant allele frequency vs. total mutation burden (as a surrogate for time). They have not detected evidence of a value of s below 0.2, which they also state as their limit of sensitivity. While we believe neutral evolution is the most straightforward interpretation of our data, weak selection also remains a possibility, and the extent and biological significance of weak selection remain unknown.

Our calculations are based on the use of the zero term of the Poisson distribution given the mean expected number of mutations. However, the scenario we are modeling has similarities to the work of Luria and Delbrück (39) (L–D), who evaluated the incidence of acquired mutation in bacterial cultures grown from a single cell. A mutation that occurs early is considered a “jackpot” in that it will be present in a large number of daughter cells despite initially being only one mutational event. The probability distribution function giving the probabilities of detecting a particular number of mutations in an (L–D) experiment has been, and continues to be, a subject of advanced mathematical research (33, 40, 41). However, the probability of observing zero mutations is agreed to correspond to the zero term of the Poisson distribution in continuous models (39), or its related binomial equivalent in stochastic models (41) if the experimental protocol is free of certain biases that cause the mean to be underestimated in (L–D) experiments. Specifically, in the original (L–D) experiment, jackpot mutations that occur early on in the experiment are rare events due to the low mutation frequency. Unless a very large number of observations are made, the expectation value for these jackpot mutations is a very small real number between 0 and 1. Since the experiment can only read out whole numbers, the most common readout is zero, leading to an underestimate of the average mutation rate (on rare occasions, the readout will be 1 or a higher integer, leading to an overestimate). However, in our experiment, we are observing 10⁴ bases in parallel at a depth of up to 2 × 10⁴ for a total of 2 × 10⁸ observations. Luria and Delbrück (39) state that the complex (L–D) distribution applies to a small number of observations, and the number of observations must be greater than the reciprocal of the apparent mutation rate to avoid these complexities. Based on the apparent mutation rate we observed, our number of observations exceeds this criterion 70-fold. Luria and Delbrück (39) further point out that a hallmark of the (L–D) distribution is a variance substantially exceeding the mean, and in their paper the ratio of variance to mean ranged from 2 to 3 to over 600, whereas the Poisson has a variance equaling the mean. They report a 5-fold overestimate of the mutation rate under these conditions when estimating based on the zero term of the Poisson distribution. In Table 2, we report that the variance/mean ratio in our experimental data for observed mutations across the 10,000 bases we have sequenced is close to 1 for all our experimental data points. This is not surprising given our large number of observations. In addition, our mutation rate is estimated using multiple time points and the slope between them, rather than a single time point as in the L–D experiment. Since the linear regression slope is influenced by the difference between successive points, any jackpots at early time points may influence the y intercept more than the slope, further mitigating any artifacts. Finally, we discard any mutations with a 10% or greater allele fraction, minimizing jackpots.

Table 2.

Mean number of mutations detected per nucleotide locus and associated variance

No.	Mean depth	Mean mutations per nucleotide	Variance in mutations per nucleotide	Variance/mean
1	1,783.71	1.6449E-03	1.6422E-03	0.9984
	19,453.23	1.4611E-02	1.8267E-02	1.2503
2	1,134.24	1.9355E-03	1.9318E-03	0.9981
	21,986.85	1.8484E-02	3.4788E-02	1.8820
3	2,131.11	1.2575E-03	1.2559E-03	0.9987
	20,897.13	1.2091E-02	1.4073E-02	1.1639
4	890.51	1.0647E-03	1.2571E-03	1.1808
	11,902.35	1.7809E-02	2.8525E-02	1.6018
5	1,285.00	1.2581E-03	1.2565E-03	0.9987
	16,433.63	9.5810E-03	1.6070E-02	1.6773

For low and high depth data points, left to right: the mean depth of sequencing, the mean number of mutations detected per nucleotide averaged across the DNA polymerase delta and epsilon capture set, the variance associated with the mean number of nucleotides, and the variance/mean ratio are given. The variance/mean ratio near 1 is characteristic of the Poisson distribution. Data for intermediate depths are similar.

Our major analyses in this paper, including the mutation rate estimation, the estimation of the probability that no cell will be mutated at a given site with respect to the founder cell reference, and the estimation of the probability of resistance to multiple cross-resistant therapies, rely only on the average and the zero term of the Poisson distribution, which should be accurate given the data in Table 2 and other considerations listed above. If the mutation rate were slightly higher than we have estimated, it would only strengthen the major qualitative conclusions of this paper: that diversity of subclonal mutations is extensive and that every site in the genome differs from the founder cell in at least one tumor cell once the tumor is large enough to be clinically diagnosed.

Our model neglects reversions, in contrast to the models of Jukes and Cantor (42) and Kimura (43), both of which use the infinite-sites assumption, and the more recent study by Cheek and Antal (33), which, like ours, does not employ the infinite-sites assumption. The Jukes and Cantor (42) and Kimura (43) models also differ from our model in that they describe an approach to a steady state in a large fixed size population. When steady state is achieved, the reversion of preexisting mutations exactly counterbalances the formation of new mutations. The equilibrium state is approached over millions of generations, on the order of the reciprocal of the mutation rate. Under these conditions, a large number of mutations are preexisting in a large population.

In contrast, in our case, we are interested in the divergence from the reference sequence in a single founder cell. Since the founder cell is the reference, it has no mutations by definition.

Thus, we cannot have a reversion at a site in a given cell without first having a mutation. We have considered the Jukes and Cantor (42) and Kimura (43) models, and while the mutation rate observed in our work is high enough to violate the infinite-sites assumption that mutations will not arise at the same base in more than one cell in a large population [requires k_mut ≥ 1/N(t)], it is not high enough for a large number of mutated cells to revert [requires k²_mut ≥ 1/N(t) since it would have to be likely that the same base in the same cell mutates and back mutates]. Moreover, a second mutation at the same base has only 1 chance in 3 to revert back to the reference sequence.

Looked at another way, a cell that has just had a mutational event at a given site has ∼40 cell doublings before that single cell has 10¹² progeny, the largest total cancer cell burden we consider in the paper. This is much fewer than the millions of generations required to reach equilibrium in the Jukes and Cantor (42) and Kimura (43) models. As the effective mutation rate is calibrated to cell doublings, the expected fraction of the progeny of the mutated cell reverting is at most 40× the effective mutation rate or 3 × 10⁻⁵ (if the mutation arises very early in tumorigenesis). This means that only a very small proportion of mutated cells will revert. Our system is far from equilibrium, and the correction to our calculations due to reversions is expected to be very small.

We further assume that the effective mutation rate is a population-weighted average of different subclones and the population weighting is stable, an expected consequence of neutral evolution.

Our theoretical treatment does not consider spatial effects. However, our experimental data use pooled DNA from 5 widely separated locations. Sottoriva et al. (17) concluded from multiple measurements that carcinomas are well mixed. Mixing may not affect growth and diversity under neutral evolution.

Drug resistance calculations assume that neutral evolution and a high mutation rate continue throughout a cancer’s lifetime. A continued high mutation rate is supported by high effective mutation frequencies in cell lines derived from mature cancers, and by experiments showing mutators are stably selected in mixed bacterial populations (44). Genetic studies find that only a small minority of mutations are selected, consistent with neutral evolution throughout (SI Appendix).

Drug resistance calculations are also limited to point mutations and do not include other genetic mechanisms and nongenetic resistance mechanisms, nor do they consider that hyperploidy and copy number variation may provide additional sites for mutation. These additional mechanisms further strengthen our conclusion about the inevitability of preexisting resistance to single-agent therapy, while potentially increasing the number of non–cross-resistant agents necessary to reliably eliminate a cancer compared to our estimate.

In summary, we have utilized DS to explore rare subclonal mutations at very high depth and accuracy in fresh frozen MSI-negative CRC and neighboring normal tissue, allowing us to see further in time from tumor initiation than previously and revealing profound subclonal diversity. Our experimental data confirm a high mutation rate and neutral evolution (or weak selection with a lower mutation rate) as far forward in time as we can see. Using a theoretical method not confounded by the infinite-sites assumption, we calculate the total tumor mutational burden assuming the high mutation rate and neutral evolution continue throughout tumor progression. We conclude, subject to this assumption, that preexisting resistance in at least one cell to any single therapeutic agent is inevitable in any colorectal tumor large enough to be detected radiologically.

Methods

Specimens and DNA Isolation.

All participating patients gave informed consent, and all ethical guidelines for tissue acquisition from human participants were followed. Guidelines for study procedures were provided by the University of Utah and the Cleveland Clinic. Following surgery, tumor tissue was snap-frozen and stored at −80 °C. Complete clinical, surgical, and pathological data were available for all cases. Pathology was classified according to the World Health Organization classification (https://www.uicc.org/resources/tnm/) of colorectal tumors. All tumors were grade II. Genomic DNA was extracted using the Qiagen DNeasy Blood and Tissue Kit (69504). Histologic annotation to confirm diagnosis and cellularity of the extracted tumor was performed by frozen section microscopy of immediately adjacent tissue located within 5 μm. Tumor cellularity was estimated microscopically on the frozen section slides, yielding a mean adenocarcinoma cell percentage of greater than 50%. MSI status was determined with BAT26 size analysis and immunohistochemical staining of MLH1, MSH2, MSH6, and PMS2 (45).

All samples were deidentified prior to use in this study. Deidentified samples were collected under an institutional review board on file with the University of Utah, in compliance with US Code of Federal Regulations, 45 CFR Part 46. The content is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health.

DS.

Sequencing library preparation was carried out as previously described with minor modifications (6, 46, 47). See SI Appendix for further details, including capture sets, adaptor sequences, capture probes, data processing, and code availability.

Subsampling of Tumor Libraries.

A tumor library may be computationally subsampled in which all of the DNA molecules in the library are randomly divided into sublibraries of desired sizes, never reusing the same DNA molecule (sampling without replacement). A single library may be used to generate points along the linear curves here rather than performing separate experiments. Although we have performed separate experiments in this study, we have also shown for the future that subsampling gives valid results. See SI Appendix, Fig. S1 A–E for details.

Evaluation of Signatures.

We created signatures for 5 CRC tumors and associated normal samples sequenced using the polymerase delta and epsilon capture set, as well as for 5 glioblastoma multiforme samples sequenced using a capture set of glioblastoma multiforme, by comparing the number of mutations of different types (C>A, C>G, C>T, T>A, T>G, T>C) at each different trinucleotide context (NCN or NTN). Detailed analytic methods are presented in SI Appendix.

Data Availability.

Data from this paper have been deposited in the NCBI Sequence Read Archive under accession no. SRP135906 (48). GBM data have been deposited in the NCBI database (BioProject PRJNA590549) (49).