Significance
Epithelial–hybrid-mesenchymal transitions play critical roles in cancer metastasis, drug resistance, and tumor relapse. Recent studies have proposed that cells in a hybrid-epithelial/mesenchymal (E/M) phenotype may be more aggressive than those on either end of the spectrum. However, no biomarker to predict upcoming transitions has been identified. Here, we show that critical slowing down-based early warning signals can detect sudden transitions among epithelial, hybrid-E/M, and mesenchymal phenotypes. Importantly, our results highlight how stable a hybrid-E/M phenotype can be and how a transition to this state can be avoided. Thus, our study provides valuable insights into restricting cellular plasticity en route metastasis.
Keywords: critical transitions, indicators of critical slowing down, alternative stable states, epithelial–hybrid-mesenchymal transition, cancer biology
Abstract
In the vicinity of a tipping point, critical transitions occur when small changes in an input condition cause sudden, large, and often irreversible changes in the state of a system. Many natural systems ranging from ecosystems to molecular biosystems are known to exhibit critical transitions in their response to stochastic perturbations. In diseases, an early prediction of upcoming critical transitions from a healthy to a disease state by using early-warning signals is of prime interest due to potential application in forecasting disease onset. Here, we analyze cell-fate transitions between different phenotypes (epithelial, hybrid-epithelial/mesenchymal [E/M], and mesenchymal states) that are implicated in cancer metastasis and chemoresistance. These transitions are mediated by a mutually inhibitory feedback loop—microRNA-200/ZEB—driven by the levels of transcription factor SNAIL. We find that the proximity to tipping points enabling these transitions among different phenotypes can be captured by critical slowing down-based early-warning signals, calculated from the trajectory of ZEB messenger RNA level. Further, the basin stability analysis reveals the unexpectedly large basin of attraction for a hybrid-E/M phenotype. Finally, we identified mechanisms that can potentially elude the transition to a hybrid-E/M phenotype. Overall, our results unravel the early-warning signals that can be used to anticipate upcoming epithelial–hybrid-mesenchymal transitions. With the emerging evidence about the hybrid-E/M phenotype being a key driver of metastasis, drug resistance, and tumor relapse, our results suggest ways to potentially evade these transitions, reducing the fitness of cancer cells and restricting tumor aggressiveness.
Biological systems often display nonlinear dynamics and emergent complex behavior and consequent multistability (1, 2). This nonlinear behavior in many cases leads to “tipping points”—threshold values at which the system abruptly shifts from one state to another, in response to small stochastic perturbations (3). Such changes—referred to as “critical transitions”—have been observed in multiple instances of ecosystems, climate, financial markets (4–6), and more recently in many cases of health and disease (1, 7, 8). The consequences of critical transitions are often large and undesirable, for instance, the switch from a healthy state to a diseased state such as the onset of type 2 diabetes (9) or that of depression (10). Moreover, these transitions are often difficult to reverse, potentially due to self-reinforcing positive feedback (11), thus predicting the tipping points can be crucial for preventing such catastrophic changes.
A critical transition is usually identified after a tipping point and is difficult to predict beforehand, because the equilibrium state of the system stays relatively unchanged until the tipping point is reached (1). Thus, static observations may not be sufficient to predict these abrupt transitions. Many indicators of changing system dynamics have been suggested as early-warning signals (EWSs) for the impending critical transitions and have been experimentally shown to predict transitions in alternative states in yeast cultures (12) and plankton chemostats (13). The most important clues for EWSs arise from “critical slowing down” of the system as it approaches the tipping point. At the onset of a tipping point, the rate of return of the system to the current equilibrium state upon a random disturbance decreases as the dominant eigenvalue approaches zero, and, eventually, this equilibrium state is replaced by the alternative state. Thus, under conditions of critical slowing down, the state of the system at a given time becomes increasingly like that at a previous moment, leading to higher temporal autocorrelation. Similarly, due to moving into a shallower well closer to the bifurcation point, the variance in data is increased (6). Hence, 2 canonical statistical measures that are mostly used as EWSs to indicate the proximity of a system to a tipping point are increasing variance and temporal lag-1 autocorrelation, AR(1) (3). Few other measures used as EWSs are recovery rate/return time (13, 14), skewness (15), conditional heteroskedasticity (16), spectral reddening (17), likelihood ratio (18), and interaction network-based indicators (19).
While EWSs and critical transitions have been well studied in ecological and climate systems, their application in predicting disease onset is relatively recent and remains largely conceptual (1, 8, 11). Particularly, in cancer, critical transitions have been predicted in metabolic reprogramming (20)—a hallmark of cancer (21). Here, we investigate critical transitions and EWSs in another hallmark of cancer—invasion and metastasis. Metastasis—the spread of cancer cells from one organ to another—accounts for nearly all cancer-related deaths in solid tumors (22). Despite extensive genomic efforts, no specific mutational signatures have been yet identified for metastasis (23), thus limiting the druggable targets to restrict metastasis. Therefore, identifying tipping points for predicting and preventing metastasis can be beneficial in curbing tumor aggressiveness.
Most solid tumors originate in epithelial organs where cells do not typically migrate or invade, rather maintain tight cell–cell adhesion and a specific tissue organization. Thus, to metastasize, they typically undergo a phenotypic switch known as epithelial–mesenchymal transition (EMT) where they lose cell–cell adhesion and gain the traits of migration and invasion (24). Cells undergoing EMT get launched into the bloodstream, and also gain the ability to initiate new tumors at metastatic sites, gain resistance against multiple drugs (25), and evade attacks by the immune system (26). Thus, EMT provides multiple survival advantages to disseminated cells that typically undergo a mesenchymal–epithelial transition (MET) to colonize distant organs. Recent investigations, including ours, have identified that EMT and MET need not be binary processes, instead cells can undergo partial EMT/MET and stably maintain one or more hybrid-epithelial/mesenchymal (E/M) phenotype(s) (24). Importantly, cells in hybrid-E/M phenotype(s), i.e., those that undergo partial EMT, maybe even more aggressive than cells that have undergone “full EMT” (27, 28). However, no specific biomarker has been identified that can a priori predict the onset of transitions among epithelial (E), mesenchymal (M), and hybrid-E/M states. Thus, identifying EWSs for transitions among these cell states can be a valuable contribution toward restricting them.
Here, we identify critical slowing down-based EWSs in a core regulatory network of EMT/MET. Three well-known indicators—AR(1), variance, and conditional heteroskedasticity—work well to forewarn upcoming transitions among E, hybrid-E/M, and M states, thus opening the possibility of considering EWSs as biomarkers to forewarn cancer metastasis. We also calculate the basin-stability measure to evaluate the probability of occurrence of a particular state in various multistable regions. A higher basin-stability measure corresponding to a particular state determines the larger possibility of attaining the state in a multistable region. Complementing our basin-stability measures with potential landscapes and phase diagrams for EMT circuit, we identify how a monostable hybrid-E/M state can be maintained and thus suggest mechanisms to avoid it. Overall, our results highlight the ability to predict cellular transitions in metastasis before they occur and may provide a dynamic biomarker to gauge metastatic potential.
Model
We consider an analytical model of microRNA (miR)-based chimeric circuit developed by Lu et al. (29). The model incorporates the features of miR-mediated regulation in the translation-transcription processes and captures the formation of various miR–messenger RNA (mRNA) complexes by the binding/unbinding dynamics of miR and mRNA (Fig. 1A). The deterministic equations of the circuit that govern the combined dynamics of miR (), mRNA (), and TF protein () are given by:
| [1a] |
| [1b] |
| [1c] |
where and are the synthesis rates of and , respectively, and is the translation rate of protein for each in the absence of . , , and are the degradation rates of , , and , respectively. , , and are -dependent functions (29) denoting various effects of miR-mediated repression. Thus, Eq. 1 a–c represents that miR and mRNA can be both produced at some fixed production rate and degraded with first-order kinetics. Additionally, they can be degraded due to miR–mRNA complexes (, functions). The rate of production of protein from mRNA can be affected by the function that denotes sequestration of mRNA by miR.
Fig. 1.
(A) Schematic diagram of the miR-based chimeric circuit. (B) Bifurcation diagram depicting the changes in ZEB mRNA levels with variations in the levels of SNAIL. The lowest levels of ZEB mRNA correspond to an E state, intermediate levels to a hybrid-E/M state (E/M), and the highest ones to an M state, as shown by corresponding cartoons. Stable steady states are plotted by solid (blue) lines; unstable steady states, by dashed (red) lines. “K Molecules” indicates 103 molecules. (C–F) An overview of critical transition in the circuit, which has multistability. (C and D) Schematic potential landscapes representing 2 stable states (i.e., E and hybrid E/M) of deterministic system: high resilience of the E state when it is far from the tipping point (C) and low resilience of the E state close to a tipping point, when the system approaches a sudden shift from E to hybrid-E/M state (D). (E and F) Stochastic time series of the system Eq. 2: with SNAIL (S) = 197,000 (far from the tipping point) (E) and with S = 207,000 (close to the tipping point) (F), respectively. (G and H) In the vicinity of a tipping point, due to decreasing resilience, the system has a stronger memory for perturbation in comparison to that of far from a tipping point and that are characterized by larger SD and AR(1). All of the other parameters for the circuit are given in the SI Appendix, Tables S1–S3.
The corresponding chimeric tristable miR-200/ZEB circuit is modeled as:
| [2a] |
| [2b] |
| [2c] |
where is the Hill function (details are in SI Appendix, section 1: The Chimeric Circuit and section 2: The Deterministic Model).
As a stochastic description of Eq. 2 can accurately capture the dynamics of the system, we derive the corresponding chemical Master equation, which follows from the birth–death processes (30). The Master equation is given by:
| [3] |
where is the grand probability function. Eq. 3 is a birth–death process for the probabilities of the separate states specified by the values of . All of the terms appear in the equation as pairs: 1) birth of a state due to transition from other states and 2) death due transition from into other states. There are 10 such processes associated with birth and death of miR, mRNA, and ZEB in our model (SI Appendix, section 3: The Stochastic Model). We have simulated this Master equation with the Gillespie algorithm (31) to obtain the stochastic trajectory of the system (SI Appendix, section 3.B: Monte Carlo Simulation). The stochastic trajectory of the system identifies the occurrence of critical transitions between different phenotypes and using critical slowing down-based EWSs, we can forecast such transitions beforehand.
Results
Bifurcation-Induced Tipping Signs in Epithelial–Hybrid-Mesenchymal Transition.
A mutually inhibitory feedback loop between members of ZEB transcription factor and those of miR-200 has been postulated to govern EMT/MET; ZEB can drive EMT by inhibiting cell–cell adhesion and cell polarity, while miR-200 tends to maintain an E phenotype (24). Unlike mutually inhibiting feedback loops where both players are transcription factors, this loop is chimeric, i.e., it contains both transcriptional and translational regulation (29, 32). First, we perform the numerical bifurcation analysis (Materials and Methods) of this deterministic tristable chimeric circuit Eq. 2 with variations in the SNAIL concentration (S) (Fig. 1B). The values of all of the other model parameters of this circuit are presented in SI Appendix, Tables S1–S3. We denote 3 coexisting stable states: high miR-200/low ZEB, low miR-200/high ZEB, and medium miR-200/medium ZEB. These states correspond to E, M, and hybrid-E/M phenotypes, respectively (24, 33). For increasing levels of S, the circuit first exhibits monostable E state; an increase in S leads to bistability between E and M states; a further increase enables tristability between E, hybrid-E/M, and M states; then bistability between hybrid-E/M and M states, and finally a monostable M state. The existence of multistable regions includes the appearance of saddle-node bifurcations and hysteresis loops that triggers the possibility of occurrence of catastrophic critical transitions in the presence of intrinsic stochastic perturbations (34).
Since this feedback loop exhibits tristability, it may pass through 2 critical points (or tipping points) and, therefore, can reach 2 alternative states, one after another. A systematic analysis of such critical transition is commonly done by analyzing a stochastic trajectory. In Fig. 1, we present a brief overview of critical transition in the EMT circuit from pure E to hybrid-E/M phenotype transition with variations in the levels of protein SNAIL, when the system is far from or close to a tipping point (Fig. 1 C and D). More specifically, larger variance and increased AR(1) determine the proximity to a tipping point (Fig. 1 G and H). With increasing SNAIL value, the system may experience 2 subsequent transitions, one from E to hybrid-E/M state and another from hybrid-E/M to M state. However, decreasing SNAIL value results in a direct transition from M to E state which bypasses the hybrid E/M state.
EWSs for Transitions among E, Hybrid E/M, and M States.
We began our search for signals of critical slowing down by calculating EWSs of critical transitions in datasets obtained from stochastic simulations (Materials and Methods) of the chimeric circuit. The stochastic trajectory (time series) representing ZEB mRNA levels, with continuously increasing SNAIL value, exhibits sudden transitions from E state to hybrid-E/M state and further hybrid-E/M state to M state (Fig. 2A). The trajectory is generated with time-varying signal SNAIL. The SNAIL level starts at 150,000 molecules at day 0 and then increases up to 250,000 molecules at day 20. This increase in SNAIL levels can drive EMT in a cell, i.e., moving from a monostable E region to a monostable M region (Fig. 1B), and the timescale over which SNAIL levels are varied are commensurate with those over which EMT is observed (35, 36).
Fig. 2.
Critical transitions between different cell states of the regulatory circuit that are driven by forward change in the control parameter SNAIL, and indicators of critical slowing down. (A) Transitions from E state to hybrid-E/M state and hybrid-E/M state to M state. Solid (blue) lines indicate stable steady states, and dashed (red) lines indicate unstable steady states of the deterministic model. Stochastic time series is indicated by the fluctuating (black) line. (B) Stochastic time-series segment of the system before the transition to hybrid-E/M state (a segment as indicated by the boxed region in A). (C) Residual time series after applying a Gaussian filter (red curve in B is the trend used for filtering). (D and E) EWSs calculated from the filtered time series after using a rolling window of 60% of the data length: variance (D) and AR(1) (E). (F–I) Sensitivity analysis of the filtering bandwidth and the rolling-window size used to calculate the EWSs. (F and H) Contour plots reveal the effect of variable rolling-window size and filtering bandwidth on the observed trend in the EWSs, variance (F) and AR(1) (H), for the filtered data as measured by the Kendall value. The triangles indicate the rolling-window size and bandwidth used to calculate the EWSs. (G and I) Frequency distributions of Kendall values for variance (G) and AR(1) (I).
First, we evaluate the effectiveness of different EWSs to positively alarm an impending sudden catastrophic transition from E state to hybrid-E/M state, by tracking the values of ZEB mRNA. For EWS analysis, we consider a time-series segment before the transition to hybrid-E/M state (Fig. 2B). To filter the possible nonstationarities in the data, we subtracted a Gaussian-kernel smoothing function across the time-series segment and used the remaining residuals (Fig. 2C) for EWS analysis (37). We calculate the variance and AR(1) (SI Appendix, section 4: Early Warning Indicators) values with a rolling window having a length of 60%, the length of the residual time-series segment, and found both the variance and AR(1) values to be increasing (Fig. 2 D and E). A concurrent increase in the EWS is a well-known indicator of an upcoming critical transition (3, 5). The performance of EWSs is, in general, known to be sensitive to the choice of the filtering bandwidth used in the Gaussian-kernel smoothing and also on the rolling-window size (38, 39). The bandwidth of kernel smoothing determines the degree of data smoothing without filtering the low frequencies from the data, and the choice of rolling-window size depends on a trade-off between data resolution and reliability of the estimation of EWSs. Therefore, rather than choosing arbitrary values, here we perform sensitivity analysis of the filtering bandwidth and rolling-window size (Fig. 2 F–I). For sensitivity analysis, the rolling-window size was varied from 25 to 75% of the data length in increments of 15 points, together with variations in the filtering bandwidth ranging from 5 to 100 in increments of 10. For all of the possible combinations of these 2 parameters, the observed trends in variance and AR(1) were quantified using the nonparametric Kendall rank correlation coefficient. A positive Kendall determines an increasing trend in the EWS prior to a critical transition. To maximize the estimated trends for the EWSs, we have used the sensitivity plot to select a particular filtering bandwidth and window size. See Fig. 2F for variance and Fig. 2H for AR(1) (for details, see SI Appendix, section 4.B: Sensitivity Analysis). The frequency distributions of the Kendall trend statistic for the variance and the AR(1) are presented in Fig. 2 G and I, respectively.
The EWSs work well for capturing the transition from hybrid-E/M state to M state (SI Appendix, section 5: Transition from Hybrid-E/M State to M State and the Corresponding Early Warning Signals and Fig. S1), suggesting that transitions in the forward direction (i.e., increase in SNAIL) can be captured by stochastic time series of ZEB mRNA. We generate the stochastic time series of ZEB mRNA from the probabilistic model through the Monte Carlo simulations (31), which incorporates intrinsic cellular noise. We vary both the time and the parameter (the number of SNAIL molecules) together, which carries the signature of critical slowing down while shifting to an alternative stable state. We carried out our simulations for a period of 0 to 20 d along with the simultaneous variations in the number of SNAIL molecules, which varies from 150,000 to 250,000 molecules.
Next, we investigated whether these EWSs can also be observed in backward transitions, i.e., with decreasing value of SNAIL (Fig. 3). Due to the hysteresis and asymmetry in transitions in both directions (E to M vs. M to E), we observe a sudden direct transition from M to E state (Fig. 3A) bypassing the hybrid-E/M state. We consider a time-series segment prior the transition to E state (Fig. 3B) and further used the residual time series for EWS analysis (Fig. 3C). Importantly, both the EWS markers—variance and AR(1)—showed an increasing trend closer to the tipping point for this transition from M to E (Fig. 3 D and E). Reinforcing our previous analysis, these EWSs were evaluated with specific choices of detrending bandwidth and rolling-window size to maximize their trends. Put together, these results highlight that the transitions among E, hybrid-E/M, and M states can be predicted before they occur, using EWS variance and AR(1).
Fig. 3.
Critical transition between different cell states of the regulatory circuit that is driven by backward change in the control parameter SNAIL, and indicators of critical slowing down. (A) Transition from M state to E state that bypasses the hybrid-E/M state. (B) Stochastic time-series segment of the system before the transition to E state (a segment as indicated by the boxed region in A). (C) Residual time series after applying a Gaussian filter (red curve in B is the trend used for filtering). (D and E) EWSs calculated from the filtered time series after using a rolling window of 80% of the data length: variance (D) and AR(1) (E). (F and H) Contour plots reveal the effect of variable rolling-window size and filtering bandwidth on the observed trend in the EWSs, variance (F) and AR(1) (H), for the filtered data as measured by the Kendall value. The triangles indicate the rolling-window size and bandwidth used to calculate the EWSs. (G and I) Frequency distributions of Kendall values for variance (G) and AR(1) (I).
Further, for the aforementioned 3 transitions, E to hybrid E/M, hybrid E/M to M, and M to E state, we evaluate the robustness of EWS trends to all of the rolling-window sizes depicted as the distribution of the Kendall statistic around their median, for both the “original” and “surrogate” time series (SI Appendix, section 6: Box Plot and Fig. S2). In the case of original datasets, most of the trends for AR(1) and variance are robust to rolling-window sizes as the majority of the associated box plots stays above the -zero axes (40).
Conditional Heteroskedasticity Applied as EWSs.
To evaluate the robustness of the predictions made by the EWS variance and AR(1), we calculate conditional heteroskedasticity—one of the other measures known to forewarn critical transitions (16). Conditional heteroskedasticity is indicated by the persistence in the conditional variance of the error term in time-series models (41). The advantage of this indicator over others is that it minimizes the chance of the occurrence of false-positive signals in time series that does not have any critical transition. To calculate conditional heteroskedasticity, time series is modeled as an autoregressive process, and the residuals are obtained. The persistence of the conditional variance of the residuals then determines the conditional heteroskedasticity (see SI Appendix, section 4.C: Conditional Heteroskedasticity for details of the procedure). Before a critical transition, significant conditional heteroskedasticity is expected to be visible in the time series (16).
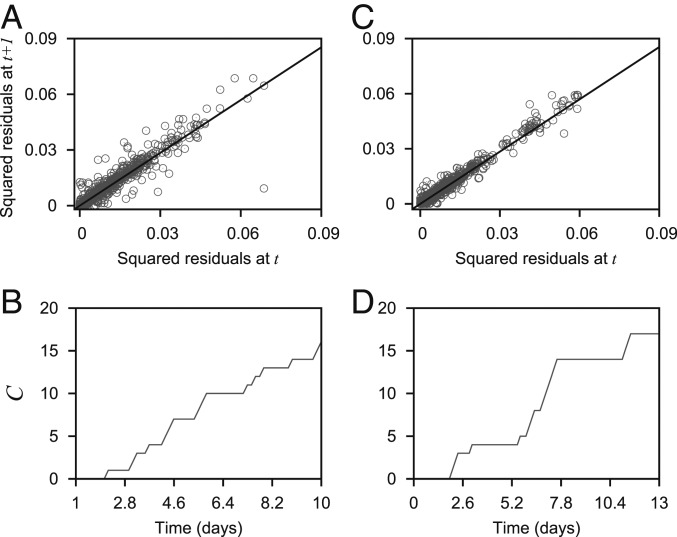
We consider the time-series segments before the critical transitions for both the cases; E to hybrid-E/M transition and MET (Figs. 2B and 3B). Fig. 4A presents the squared residuals from an autoregressive lag-1 model applied to the time-series segment of E to hybrid-E/M transition (Fig. 2B) plotted with the residuals at the next time step. The slanted line is the regression line. The positive correlation between the squared residuals at time step and time step indicates conditional heteroskedasticity. We also apply the cumulative number of significant Lagrange multiplier tests () to the time series (Fig. 4B). The cumulative increases before the critical transition indicate that a significant number of tests shows conditional heteroskedasticity in the time series. For the transition to M to E state, we get similar results (Fig. 4 C and D).
Fig. 4.
Squared residuals from an autoregressive lag-1 model plotted with the next squared residuals (A and C) and cumulative number of significant Lagrange multiplier test () (B and D), both applied to the data presented in Fig. 2B (for A and B) and Fig. 3B (for C and D), respectively. In A and B, the black slanted lines are fitted regression lines at lag-1.
Stochastic-Potential and Basin-Stability Analyses Reveal Relative Stability of the Three Cell States.
For a dynamical system, a potential well represents the existence of a steady state. Here, we projected the stochastic potential of the system in ZEB mRNA–miR-200 plane for different values of the parameter SNAIL (Fig. 5). The lowest value of the potential corresponds to the existence of a deep well and hence subsequently the existence of a steady state. Here, for different SNAIL values, the stochastic potentials clearly exhibit bistable/multistable states. Consistent with the deterministic dynamics of the system (Fig. 1B), we note the coexistence of E and M states (Fig. 5A), the coexistence of all of the 3 E, hybrid-E/M, and M states (Fig. 5B) and the coexistence of hybrid-E/M and M states (Fig. 5C). The details of the method used to calculate the stochastic potentials are given in SI Appendix, section 7: Stochastic Potential.
Fig. 5.
The potential landscapes of the genetic circuit in a 2-dimensional mRNA–miR plane for different values of SNAIL (S). The blue regions represent lower potential and the correspondingly higher probability of occurrence of a steady state. Identifying the existence of: E and M states at S = 188,000 (S = 188K) (A); E, hybrid-E/M, and M states at S = 200,000 (S = 200K) (B); and hybrid-E/M and M states at S = 213,000 (S = 213K) (C).
Given that the hybrid-E/M state has been proposed to be the “fittest” for metastasis (42) and that we observed a relatively larger region denoting the stability of hybrid E/M in the tristable region (Fig. 5), we investigated the probability of attaining the hybrid-E/M state in a tristable region in the presence of random perturbations. This probability can be calculated by performing basin-stability measure (43).
For a complex system, the basin stability is a measurement of the stability/resilience of a steady state in a probability sense that pivots on the volume of the basin of attraction. In other words, it measures the likelihood of a return to a steady state after random, nonsmall perturbations. Thus, for a high-dimensional multistable system, it is a powerful tool to measure the basin volume (SI Appendix, section 8: Basin Stability). For our system, we observe multistability for different parameter values of SNAIL (S). For S = 188,000 (Fig. 1B), the system has coexisting E and M states. Basin stability measures that for a sufficiently large set of random initial conditions, E and M states have probabilities 0.91 and 0.09 of return to their original state, i.e., among all random initial conditions and trajectories will reach E and M states (Fig. 6A), respectively. For S = 200,000, the system has probabilities 0.1, 0.76, and 0.23 of reaching to E, hybrid-E/M, and M states (Fig. 6B), respectively, from a set of random initial states. Similarly for S = 213,000, the corresponding probabilities of return to hybrid-E/M state and M state are 0.62 and 0.38 (Fig. 6C), respectively. Further, increase in the levels of SNAIL at S = 220,000 reduces the probability of attaining hybrid-E/M state, which becomes 0.52, and the remaining 0.48 is the probability of attaining the M state (Fig. 6D), indicating that as we proceed from a bistable M–E/M phase to a monostable M phase, the basin stability of E/M decreases, being conceptually consistent with the mean residence time analysis for this circuit (44).
Fig. 6.
Pie diagrams representing basin stability of the system for different values of SNAIL (S): S = 188,000 (S = 188K) (A), S = 200,000 (S = 200K) (B), S = 213,000 (S = 213K) (C), and S = 220,000 (S = 220K) (D). The percentages of simulations with random initial conditions reaching a particular steady state in a bistable/multistable region are shown. Blue, red, and yellow regions correspond to the percentage of simulations reaching to any one of the , hybrid-, and states, respectively.
Hence, the basin-stability results suggest that an E state is more stable in the bistable region containing both E and M states, but the hybrid-E/M state is more stable for the 2 latter cases. Thus, in the (miR-200/ZEB) loop, the chances of getting a hybrid-E/M state seems relatively very high compared to the other 2 states (SI Appendix, Fig. S3). This result is reminiscent of mean residence-time calculations for E, hybrid-E/M, and M states (44) and suggests that the hybrid-E/M state is not perhaps as “metastable” as was initially postulated experimentally (24).
Identifying Mechanisms to Evade the Transition into Aggressive Hybrid-E/M State.
Next, we sought after mechanisms to evade transition to a hybrid-E/M state, given its association with higher aggressiveness and worse patient survival. We first identified what mechanisms can lead to stabilized hybrid-E/M state. So far, our results have identified monostable E, monostable M, and other bistable and tristable regions, but not a monostable hybrid-E/M state. Including other factors such as GRHL2, NUMB in the network can enable the existence of a monostable hybrid-E/M region (28). Here, we analyzed the parameter space of the miR-200/ZEB feedback loop to identify regions enabling the existence of a hybrid-E/M state as a monostable phase, without adding more components in the network. We varied the levels of SNAIL, and the threshold (half-maximal concentration) value of ZEB in the shifted Hill function corresponding to ZEB inhibiting miR-200, and calculated the phase diagram shown in Fig. 7. The different phases in the diagram are separated by 4 saddle-node bifurcation curves. We could identify a large parameter region in which the monostable hybrid-E/M phase appears—high levels of both SNAIL and the threshold of ZEB (Fig. 7A). This result suggests that as the strength of inhibition of miR-200 by ZEB is weakened, the progression to a complete EMT may be halted and cells can stably occupy a hybrid-E/M state for higher values of SNAIL (Fig. 7A). Conversely, as this inhibition is made stronger, the stability of the hybrid-E/M state gradually decreases (Fig. 7C) and eventually the hybrid-E/M state disappears (Fig. 7B). Here, the hybrid-E/M state disappears when the systems response curve changes from “folded” to “smooth,” in response to the variations in the input condition. In fact, the folded response curve looks like a typical first-order (i.e., abrupt) or discontinuous transition (Fig. 7C), however contains 2 unstable states and one stable hybrid-E/M state which in general shows 2 stable and one unstable states in most of the studies on critical transitions (45, 46). The smooth response curve corresponds to second-order (i.e., continuous) phase transition that has only one unstable state here (Fig. 7B), in contrast to a bistable system, which has a stable state. Therefore, the dynamical mechanism behind the disappearance of the hybrid-E/M state is the changeover from first- to second-order phase transition in the system’s response curve.
Fig. 7.
The phase diagram and corresponding bifurcation diagrams of the genetic circuit. (A) The phase diagram of the genetic circuit with variations in SNAIL and (threshold of ZEB’s inhibition of miR-200) levels. Each phase corresponds to either any of the monostable state or coexisting bistable/multistable states. For example, in E, the E state is stable; in {E, hybrid-E/M}, both E and hybrid-E/M states coexist. (B–F) Bifurcation diagrams of mRNA with variations in the level of SNAIL for different values of : 100,000 (100K) (B), 140,000 (140K) (C) , 280,000 (280K) (D), 320,000 (320K) (E), and 380,000 (380K) (F). As we move from D to F, the monostable region for hybrid- state (marked by the shaded regions) increases. In B–F, stable steady states are plotted by solid (blue) lines; unstable steady states, by dashed (red) lines.
Similarly, we also varied the levels of SNAIL and the threshold of self-activation of ZEB (SI Appendix, section 9: Phase Diagram with Variations in the Signal SNAIL and the Threshold for ZEB Self Activation Levels). Reduced threshold, i.e., a stronger self-activation, enables a monostable hybrid-E/M phase at lower SNAIL values, while it disappears with increased threshold, i.e., weaker self-activation of ZEB (SI Appendix, Fig. S4). Increasing SNAIL values and weakening self-activation drive the system toward a bistable E, M phase, i.e., disappearance of E/M state. These results suggest that a balance between the strengths of mutual inhibition and self-activation can enable the existence of a hybrid-E/M phenotype (32).
Discussion
Anticipating critical transitions remains an extremely challenging task in multiple scenarios, including the eutrophication of lakes, the crash of financial markets, and, more importantly, the onset of diseases. The system typically displays almost no sign of the impending transition until it happens, thus using EWSs such as variance, autocorrelation, and conditional heteroskedasticity can be used to forecast the critical transitions, which are often catastrophic. Here, we show that these EWSs can capture the transitions among E, M, and hybrid-E/M phenotypes. This phenotypic plasticity drives cancer metastasis and drug resistance in cancer—the cause of almost all cancer-related deaths. Given that no unique mutational signature has been yet identified for metastasis, despite extensive genomic efforts (23), these EWSs that can predict the onset of these cellular transitions that govern metastasis can serve as potentially important dynamic biomarkers. Recent efforts have focused on identifying such dynamic biomarkers in the context of pulmonary metastasis of hepatocellular carcinoma (47). With more single-cell dynamic data emerging in the context of epithelial–hybrid-mesenchymal transitions (48, 49), using EWSs can help predict the tipping point of metastasis initiation. Dynamic network biomarkers is a set of molecules that show collective and strong fluctuations close to a tipping point (47); thus, such dynamic biomarkers can be potentially identified through collecting transcriptomic signatures for epithelial–hybrid-mesenchymal transitions using inducible systems/reporter constructs in vitro (50, 51). EMT can be induced via various extracellular mechanisms as well (52); thus, these dynamic biomarkers are likely to be reflective of cellular plasticity and adaptability—a crucial feature for the process of metastasis that has an extremely high attrition rate, yet claims more than 90% of all cancer-related deaths (22). Moreover, another interpretation of tipping point in EMT can be the point of irreversibility, i.e., inducing EMT for a shorter duration and then withdrawal of the EMT-inducing signal enables reversal; however, induction for a longer timescale typically leads to irreversible EMT, possibly due to epigenetic effects (35, 36, 53). Thus, our results indicate the possibility of identifying EMT before the tipping point of transition.
Cancer metastasis has been long thought to be driven solely by individual cell migration (i.e., a M state); however, recent studies have questioned this dogma, highlighting not only that clustered cell migration can be possible during metastasis but also can be the predominant driver of metastasis (54, 55). These clusters, typically 5 to 8 cells large, can pass through capillaries by arranging themselves transiently into a single-file chain (56) and can contain noncancerous cells that can facilitate metastasis (57). A hybrid-E/M phenotype has been associated with such collective/clustered cell migration (58, 59); thus, our analysis identifying the relatively high basin stability of the hybrid-E/M phenotype can help explain the ability of cancer cells to form clusters of circulating tumor cells.
Here, our analysis focused on temporal dynamics of a gene regulatory network for EMT; however, EWSs have also been identified in spatiotemporal dynamics, particularly in ecology (60, 61). Thus, EWSs can also be potentially identified in a spatially extended regulatory networks for EMT, for instance, investigating the varying extents of EMT induction in different parts of a tissue, as have been experimentally observed (62, 63), or identifying critical transitions in cancer–immune interplay (64). Further, besides EMT, there are other axes of phenotypic plasticity in cancer, such as metabolic plasticity, switching back and forth between a cancer stem cell (CSC) and a noncancer stem cell. With recent developments in identifying the multistable dynamics of the networks regulating these transitions (65), EWS analysis can be applied to these networks to identify promising novel dynamic biomarkers. However, an open question remains: can we identify the strongest and most robust signal of critical transition, among many that might show EWSs? For instance, during metastasis, players involved in EMT, CSCs, and metabolic plasticity may all show EWSs and vary dynamically, but which among these interconnected axes can be considered as the Achilles heel of metastatic potential needs to be identified rigorously?
The majority of the critical slowing down-based EWSs used to predict critical transitions in natural systems involves saddle-node bifurcation under the presence of white noise (temporally uncorrelated noise) that perturbs the abundance of the system (66). For a large class of systems that exhibit other types of bifurcations apart form the saddle node, the effectiveness of EWSs remains largely unknown. For different types of bifurcations (e.g., transcritical, pitchfork, supercritical Hopf bifurcation) with diverse noise (e.g., colored [temporally correlated] noise), EWSs do not always work reliably to forecast sudden critical transitions (67). They were found to be very sensitive to the length of pretransition time-series data and also to other decisions like filtering bandwidth and rolling-window size (39). There also exist systems in which bifurcations occur without critical slowing down, such as in a structured consumer-resource model where the upper-point equilibrium coexists with a lower-limit cycle (68), the occurrence of basin-boundary collisions (69) and as a result in these systems, EWSs do not work properly. In fact, in general, EWSs work well for the situations when critical slowing down and critical transition cooccur (67). Although robustness of EWSs has been successfully shown in some cases (3, 66), a detailed analysis of their effectiveness is still an open challenge (18, 67, 70).
In summary, our analysis strongly indicates the presence of EWSs during epithelial–hybrid-mesenchymal transitions—a central motor of cellular plasticity during cancer metastasis and the emergence of therapy resistance (71). We show that many robust measures of EWSs—increased variance, autocorrelation, and conditional heteroskedasticity—vary dynamically as cells transition among these 3 phenotypes. Our results also identify increased basin stability of a hybrid-E/M phenotype—considered to be the fittest for metastasis—and suggest ways to elude transitions into the hybrid-E/M state, potentially restricting cancer spread.
Materials and Methods
Numerical Simulations and Bifurcation Diagrams of the Deterministic System.
We have used Matlab (R2015b) for numerical simulations of the deterministic system (Eq. 2). The codimension–one bifurcation diagrams involving 2 or more saddle-node bifurcation points were obtained using the continuation package MATCONT (72). The 2-parameter bifurcation diagram (i.e., the phase diagram) with variations in the parameters SNAIL and miR-200/ZEB was obtained through the calculations of multiple codimension–one bifurcation points. Later, the bifurcation curves separating monostable, bistable, and tristable existence regions of the steady states were presented by connecting multiple codimension–one bifurcation points.
Stochastic System and Monte Carlo Simulations.
The time series of ZEB mRNA levels was generated from the probabilistic model through Monte Carlo simulation (31), which incorporates the intrinsic cellular noise. The algorithm considers each of the reaction events as individual realizations of the Markov process. The time and species numbers are updated stochastically by choosing a random reaction event. The miR ()-based chimeric tristable miR-200/ZEB circuit is simulated by realizing 10 reaction events as a function of the number of SNAIL molecules. The reaction events are listed in SI Appendix, Table S4. All biochemical parameters are based on ref. 33, and those are listed in SI Appendix, Tables S1–S3 for completeness. Both the time and the parameter (number of SNAIL molecules) are varied together to obtain the time series of ZEB mRNA levels that carry the signature of critical slowing down while shifting to an alternative stable state. In particular, we perform our simulations for a period of 20 d, along with the simultaneous variations in the number of SNAIL molecules, that ranges from 150,000 to 250,000 molecules. The chosen time period and the range of SNAIL molecules are consistent in the context of the EMT period (33). More details of the simulation are presented in SI Appendix, section 3: The Stochastic Model.
Statistical Analysis of CSD Indicators.
In the stochastic time series analyzed here, we first visually identified shifts between E-to-E/M state and M-to-E state. Then we took time-series segments (the regions marked with boxes in Figs. 2 and 3) before a critical transition and examined them for the presence of EWSs. For stationarity in residuals, we used the Gaussian detrending before performing any statistical analysis of the data. The residuals were then used to calculate the EWS variance, AR(1), and conditional heteroskedasticity. The time-series analysis has been performed using the “Early Warning Signals Toolbox” (http://www.early-warning-signals.org). A concurrent rise in the variance and/or AR(1) forewarn an upcoming critical transition. The indicator conditional heteroskedasticity also works similarly (for details, see SI Appendix, section 4: Early Warning Indicators).
Data Availability.
Code and data are available in the Zenodo repository (73).
Supplementary Material
Acknowledgments
S.S. acknowledges financial support from Department of Science and Technology (DST), India under the scheme DST-Inspire (IF160459). S.K.S. is supported by Science and Engineering Research Board (SERB), Department of Science and Technology, Government of India (ECR/2018/000514). M.K.J. is supported by the Ramanujan Fellowship awarded by SERB, Department of Science and Technology, Government of India (SB/S2/RJN-049/2018).
Footnotes
The authors declare no competing interest.
Data deposition: The code and data reported in this paper are available in the Zenodo repository, https://doi.org/10.5281/zenodo.3531202.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1913773116/-/DCSupplemental.
References
- 1.Trefois C., Antony P. M., Goncalves J., Skupin A., Balling R., Critical transitions in chronic disease: Transferring concepts from ecology to systems medicine. Curr. Opin. Biotechnol. 34, 48–55 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Angeli D., Ferrell J. E., Sontag E. D., Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. U.S.A. 101, 1822–1827 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Scheffer M., et al. , Early-warning signals for critical transitions. Nature 461, 53–59 (2009). [DOI] [PubMed] [Google Scholar]
- 4.May R. M., Levin S. A., Sugihara G., Complex systems: Ecology for bankers. Nature 451, 893–895 (2008). [DOI] [PubMed] [Google Scholar]
- 5.Scheffer M., et al. , Anticipating critical transitions. Science 338, 344–348 (2012). [DOI] [PubMed] [Google Scholar]
- 6.Lenton T. M., Early warning of climate tipping points. Nat. Clim. Chang. 1, 201–209 (2011). [Google Scholar]
- 7.Korolev K. S., Xavier J. B., Gore J., Turning ecology and evolution against cancer. Nat. Rev. Cancer 14, 371–380 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Scheffer M., et al. , Quantifying resilience of humans and other animals. Proc. Natl. Acad. Sci. U.S.A. 115, 11883–11890 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li H., Toward better understanding of artifacts in variant calling from high-coverage samples. Bioinformatics 30, 2843–2851 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Van de Leemput I. A., et al. , Critical slowing down as early warning for the onset and termination of depression. Proc. Natl. Acad. Sci. U.S.A. 111, 87–92 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sharma Y., Dutta P. S., Gupta A., Anticipating regime shifts in gene expression: The case of an autoactivating positive feedback loop. Phys. Rev. E 93, 032404 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Dai L., Vorselen D., Korolev K. S., Gore J., Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336, 1175–1177 (2012). [DOI] [PubMed] [Google Scholar]
- 13.Veraart A. J., et al. , Recovery rates reflect distance to a tipping point in a living system. Nature 481, 357–359 (2012). [DOI] [PubMed] [Google Scholar]
- 14.Carpenter S., Brock W., Cole J., Kitchell J., Pace M., Leading indicators of trophic cascades. Ecol. Lett. 11, 128–138 (2008). [DOI] [PubMed] [Google Scholar]
- 15.Guttal V., Jayaprakash C., Changing skewness: An early warning signal of regime shifts in ecosystems. Ecol. Lett. 11, 450–460 (2008). [DOI] [PubMed] [Google Scholar]
- 16.Seekell D. A., Carpenter S. R., Pace M. L., Conditional heteroscedasticity as a leading indicator of ecological regime shifts. Am. Nat. 178, 442–451 (2011). [DOI] [PubMed] [Google Scholar]
- 17.Carpenter S. R., et al. , Early warnings of regime shifts: A whole-ecosystem experiment. Science 332, 1079–1082 (2011). [DOI] [PubMed] [Google Scholar]
- 18.Boettiger C., Hastings A., Quantifying limits to detection of early warning for critical transitions. J. R. Soc. Interface 9, 2527–2539 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tirabassi G., et al. , Interaction network based early-warning indicators of vegetation transitions. Ecol. Complex. 19, 148–157 (2014). [Google Scholar]
- 20.Kianercy A., Veltri R., Pienta K. J., Critical transitions in a game theoretic model of tumour metabolism. Interface Focus 4, 20140014 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hanahan D., Weinberg R. A., Hallmarks of cancer: The next generation. Cell 144, 646–674 (2011). [DOI] [PubMed] [Google Scholar]
- 22.Gupta G. P., Massagué J., Cancer metastasis: Building a framework. Cell 127, 679–695 (2006). [DOI] [PubMed] [Google Scholar]
- 23.Celià-Terrassa T., Kang Y., Distinctive properties of metastasis-initiating cells. Genes Dev. 30, 892–908 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jolly M. K., et al. , Implications of the hybrid epithelial/mesenchymal phenotype in metastasis. Front. Oncol. 5, 155 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Singh A., Settleman J., Emt, cancer stem cells and drug resistance: An emerging axis of evil in the war on cancer. Oncogene 29, 4741–4751 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tripathi S. C., et al. , Immunoproteasome deficiency is a feature of non-small cell lung cancer with a mesenchymal phenotype and is associated with a poor outcome. Proc. Natl. Acad. Sci. U.S.A. 113, E1555–E1564 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pastushenko I., et al. , Identification of the tumour transition states occurring during emt. Nature 556, 463–468 (2018). [DOI] [PubMed] [Google Scholar]
- 28.Jolly M. K., et al. , Hybrid epithelial/mesenchymal phenotypes promote metastasis and therapy resistance across carcinomas. Pharmacol. Ther. 194, 161–184 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Lu M., et al. , Tristability in cancer-associated microrna-TF chimera toggle switch. J. Phys. Chem. B 117, 13164–13174 (2013). [DOI] [PubMed] [Google Scholar]
- 30.Van Kampen N. G., Stochastic Processes in Physics and Chemistry (Elsevier, 1992), Vol. 1. [Google Scholar]
- 31.Gillespie D. T., Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 (1977). [Google Scholar]
- 32.Jia D., et al. , Operating principles of tristable circuits regulating cellular differentiation. Phys. Biol. 14, 035007 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Lu M., Jolly M. K., Levine H., Onuchic J. N., Ben-Jacob E., Microrna-based regulation of epithelial–hybrid–mesenchymal fate determination. Proc. Natl. Acad. Sci. U.S.A. 110, 18144–18149 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scheffer M., Critical Transitions in Nature and Society (Princeton University Press, 2009), Vol. 16. [Google Scholar]
- 35.Katsuno Y., et al. , Chronic tgf- exposure drives stabilized emt, tumor stemness, and cancer drug resistance with vulnerability to bitopic mtor inhibition. Sci. Signal. 12, eaau8544 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jia W., Deshmukh A., Mani S. A., Jolly M. K., Levine H., A possible role for epigenetic feedback regulation in the dynamics of the epithelial-mesenchymal transition (emt). Phys. Biol. 16, 066004 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dakos V., et al. , Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS One 7, e41010 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lenton T., Livina V., Dakos V., Van Nes E., Scheffer M., Early warning of climate tipping points from critical slowing down: Comparing methods to improve robustness. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 370, 1185–1204 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dutta P. S., Sharma Y., Abbott K. C., Robustness of early warning signals for catastrophic and non-catastrophic transitions. Oikos 127, 1251–1263 (2018). [Google Scholar]
- 40.Gsell A. S., et al. , Evaluating early-warning indicators of critical transitions in natural aquatic ecosystems. Proc. Natl. Acad. Sci. U.S.A. 113, E8089–E8095 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Engle R. F., A general approach to Lagrange multiplier model diagnostics. J. Econom. 20, 83–104 (1982). [Google Scholar]
- 42.Jolly M. K., Mani S. A., Levine H., Hybrid epithelial/mesenchymal phenotype (s): The ‘fittest’ for metastasis?. Biochim. Biophys. Acta Rev. Canc. 1870, 151–157 (2018). [DOI] [PubMed] [Google Scholar]
- 43.Menck P. J., Heitzig J., Marwan N., Kurths J., How basin stability complements the linear-stability paradigm. Nat. Phys. 9, 89–92 (2013). [Google Scholar]
- 44.Biswas K., Jolly M. K., Ghosh A., Stability and mean residence times for hybrid epithelial/mesenchymal phenotype. Phys. Biol. 16, 025003 (2019). [DOI] [PubMed] [Google Scholar]
- 45.Scheffer M., Carpenter S., Foley J. A., Folke C., Walker B., Catastrophic shifts in ecosystems. Nature 413, 591–596 (2001). [DOI] [PubMed] [Google Scholar]
- 46.Martín P. V., Bonachela J. A., Levin S. A., Muñoz M. A., Eluding catastrophic shifts. Proc. Natl. Acad. Sci. U.S.A. 112, E1828–E1836 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yang B., et al. , Dynamic network biomarker indicates pulmonary metastasis at the tipping point of hepatocellular carcinoma. Nat. Commun. 9, 678 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Puram S. V., et al. , Single-cell transcriptomic analysis of primary and metastatic tumor ecosystems in head and neck cancer. Cell 171, 1611–1624 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karacosta L. G., et al. , Mapping lung cancer epithelial-mesenchymal transition states and trajectories with single-cell resolution. Nat. Commun. 10, 5587 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stylianou N., et al. , A molecular portrait of epithelial–mesenchymal plasticity in prostate cancer associated with clinical outcome. Oncogene 38, 913–934 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xu S., et al. , An integrative systems biology and experimental approach identifies convergence of epithelial plasticity, metabolism, and autophagy to promote chemoresistance. J. Clin. Med. 8, 205 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kumar S., Das A., Sen S., Extracellular matrix density promotes emt by weakening cell–cell adhesions. Mol. Biosyst. 10, 838–850 (2014). [DOI] [PubMed] [Google Scholar]
- 53.Gregory P. A., et al. , An autocrine tgf-/zeb/mir-200 signaling network regulates establishment and maintenance of epithelial-mesenchymal transition. Mol. Biol. Cell 22, 1686–1698 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jolly M. K., Ware K. E., Gilja S., Somarelli J. A., Levine H., Emt and met: Necessary or permissive for metastasis?. Mol. Oncol. 11, 755–769 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cheung K. J., Ewald A. J., A collective route to metastasis: Seeding by tumor cell clusters. Science 352, 167–169 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Au S. H., et al. , Clusters of circulating tumor cells traverse capillary-sized vessels. Proc. Natl. Acad. Sci. U.S.A. 113, 4947–4952 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Szczerba B. M., et al. , Neutrophils escort circulating tumour cells to enable cell cycle progression. Nature 566, 553–557 (2019). [DOI] [PubMed] [Google Scholar]
- 58.Sarioglu A. F., et al. , A microfluidic device for label-free, physical capture of circulating tumor cell clusters. Nat. Methods 12, 685–691 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jolly M. K., et al. , Inflammatory breast cancer: A model for investigating cluster-based dissemination. NPJ Breast Cancer 3, 21 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Dakos V., Kéfi S., Rietkerk M., Van Nes E. H., Scheffer M., Slowing down in spatially patterned ecosystems at the brink of collapse. Am. Nat. 177, E153–E166 (2011). [DOI] [PubMed] [Google Scholar]
- 61.Kefi S., et al. , Early warning signals of ecological transitions: Methods for spatial patterns. PLoS One 9, e92097 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bocci F., et al. , Toward understanding cancer stem cell heterogeneity in the tumor microenvironment. Proc. Natl. Acad. Sci. U.S.A. 116, 148–157 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Celià-Terrassa T., et al. , Hysteresis control of epithelial-mesenchymal transition dynamics conveys a distinct program with enhanced metastatic ability. Nat. Commun. 9, 5005 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Li X., Levine H., Bistability of the cytokine-immune cell network in a cancer microenvironment. Convergent Sci. Phys. Oncol. 3, 024002 (2017). [Google Scholar]
- 65.Jia D., et al. , Quantifying cancer epithelial-mesenchymal plasticity and its association with stemness and immune response. J. Clin. Med. 8, 725 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Scheffer M., Carpenter S. R., Dakos V., van Nes E. H., Generic indicators of ecological resilience: Inferring the chance of a critical transition. Annu. Rev. Ecol. Evol. Syst. 46, 145–167 (2015). [Google Scholar]
- 67.Dakos V., Carpenter S. R., van Nes E. H., Scheffer M., Resilience indicators: Prospects and limitations for early warnings of regime shifts. Philos. Trans. R. Soc. Biol. Sci. 370, 20130263 (2015). [Google Scholar]
- 68.Schreiber S., Rudolf V. H., Crossing habitat boundaries: Coupling dynamics of ecosystems through complex life cycles. Ecol. Lett. 11, 576–587 (2008). [DOI] [PubMed] [Google Scholar]
- 69.Hastings A., Wysham D. B., Regime shifts in ecological systems can occur with no warning. Ecol. Lett. 13, 464–472 (2010). [DOI] [PubMed] [Google Scholar]
- 70.Boettiger C., Ross N., Hastings A., Early warning signals: The charted and uncharted territories. Theor. Ecol. 6, 255–264 (2013). [Google Scholar]
- 71.Brabletz S., Brabletz T., The ZEB/miR-200 feedback loop–a motor of cellular plasticity in development and cancer? EMBO Rep. 11, 670–677 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Dhooge A., Govaerts W., Kuznetsov Y. A., MATCONT: A MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math Software 29, 141–164 (2003). [Google Scholar]
- 73.Sarkar A., et al. , SUKANTA EMT: Source code for EMT simulation. Zenodo. 10.5281/zenodo.3531202. Deposited 7 November 2019 (2019). [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code and data are available in the Zenodo repository (73).