Type I Error Probability Spending for Post-Market Drug and Vaccine Safety Surveillance With Poisson Data

Abstract

Statistical sequential hypothesis testing is meant to analyze cumulative data accruing in time. The methods can be divided in two types, group and continuous sequential approaches, and a question that arises is if one approach suppresses the other in some sense. For Poisson stochastic processes, we prove that continuous sequential analysis is uniformly better than group sequential under a comprehensive class of statistical performance measures. Hence, optimal solutions are in the class of continuous designs. This paper also offers a pioneer study that compares classical Type I error spending functions in terms of expected number of events to signal. This was done for a number of tuning parameters scenarios. The results indicate that a log-exp shape for the Type I error spending function is the best choice in most of the evaluated scenarios.

1. Introduction

In statistical inference, the classical non-sequential approach for hypothesis testing consists on defining the test criterion as a function of an unique batch of data, and hence only one test is performed. Differently, in sequential hypothesis testing multiple tests are performed sequentially, each based on information formed by a combination of new data with data observed in previous tests. Although the historic development of sequential analysis theory can be undoubtedly credited to challenges appearing in clinical trials (Jennison and Turnbull 2000), applications for post-market drug and vaccine safety surveillance of adverse events is now in the fringe of the sequential analysis practice (Davis et al. 2005; Lieu et al. 2007; Kulldorff et al. 2011; Yih et al. 2011; Leite et al. 2016).

In the context of post-market drug and vaccine safety surveillance, a very useful model is the Poisson distribution. Following the construction used by Leite et al. (2016), Silva and Kulldorff (2015), Kulldorff et al. (2011), and Yih et al. (2011), let X_t denote the number of adverse events observed within the (0,t] time interval after a vaccination, where Xt follows a Poisson distribution with average (R × μ_t ). In this construction, μ_t is a known function of the exposed population, and R is the relative risk reflecting the effect of the vaccine in the risk of occurring an adverse event. Basically, under the null hypothesis, the vaccine is safe, hence the relative risk is smaller than or equal to 1. Otherwise, the expected number of events is greater than μ_t, i.e. R > 1. This problem motivates the discussion in the present paper, which is directed to one tailed-tests with hypothesis of the form:

$$H_0:R\le 1\hspace{0.17em}\text{against}\hspace{0.17em}{H}_1:R>1.$$ (1)

Usually, sequential methods for testing the hypotheses in Eq. 1 are based on monitoring a real valued test statistic, say W (X_t ), t (0,T], in comparison to a signaling threshold CV_t. The null hypothesis is rejected for the first t such that W (X_t) CV_t, or the null is taken as true if W (X_t ) < CV_t for each t ∈ (0,T]. The tuning parameter T, called maximum length of surveillance, is an arbitrary constant defined by the investigator. The time dependent function CV_t is specified in a way that the overall Type I error probability is safely smaller than or equal to a desired significance level, α. This type of threshold-based testing design is in the essence of established methodologies, such as e.g. Wald’s SPRT test (Wald 1945), the method of Pocock (1977), the O’Brien & Fleming’s statistic (O’Brien and Fleming 1979), the maximized sequential probability ratio test (MaxSPRT) introduced by Kulldorff et al. (2011), and the modified MaxSPRT introduced by Gombay and Li (2015).

An important design issue is the choice between continuous or group sequential fashions. With the continuous design, each t ∈ (0,T] can lead to the null rejection. Unlike, under a group sequential design, only selected points t₁ < t₂ < … < t_G are taken as testing times. Naturally, the choice between continuous versus group designs depends on logistical/financial aspects of data collection since continuous analysis can only be applied if it is feasible to observe the arrival time of each single new observation. But, in situations where the choice between continuous and group approaches is feasible prior to start the surveillance, a question that emerges is if one should be adopted in detriment of the other. Based on simulation studies, the works of Zhao et al. (2012) and Nelson et al. (2012) seemed to suggest that group sequential designs should be preferred even when data is extracted continuously. But, the work of Silva and Kulldorff (2013) put a light in the subject. They used analytical arguments to show that, if expected number of events to signal and expected length of surveillance are the design criterion for fixed power and alpha level, then continuous designs should always be used in place of group designs if logistically/financially possible. It is worth noting that similar evaluations for other statistical performance measures, such as the risk function, are still pending in the literature. In order to cover this lack, the present paper shows that continuous sequential analysis is also uniformly better than group sequential in terms of expected loss (risk function), expected number of events to signal, and expected number of events.

Another important design issue is the shape of CV_t. While some classical methods establish flat thresholds in the scale of W (X_t ) (Wald 1945; Pocock 1977; Kulldorff et al. 2011), others are defined under increasing or decreasing CV_t functions (O’Brien and Fleming 1979; Gombay and Li 2015). But, all these methods can be rewritten in terms of a more comprehensive approach, the approach based on the Type I error probability spending function. Type I error spending functions, usually denoted by S (t), are meant to dictate the amount of Type I error probability to be applied for each t ∈ (0,T]. A traditional choice is the so-called power-type function:

$$S(t)=\alpha \times {\left(\frac{t}{T}\right)}^{\rho },\hspace{0.17em}\rho >0,\hspace{0.17em}t\in (0,\hspace{0.17em}T].$$ (2)

A number of Type I error spending functions are available in the literature. The comparison among many S (t) shapes has historically been made having expected sample size as the statistical performance measure of interest (Lan and DeMets 1983; Kim and Demets 1987). Unfortunately, the comparison of S (t) shapes in terms of expected number of events to signal (instead of expected sample size) has not been explored for the Poisson data yet. This paper brings a comparison study among four established Type I error spending functions. This is done having expected number of events to signal as the statistical performance measure of interest. Our results show that the log-exp function introduced by Lan and DeMets (1983) seems to be the best one.

This material is organized in the following way: the next section extends the results of Silva and Kulldorff (2013) about the optimality of continuous sequential analysis over group sequential analysis. Section 3 presents analytical expressions for statistical power calculation of continuous sequential designs. Section 4 compares four different Type I error probability spending functions in terms of expected number of events to signal for fixed statistical power. Section 5 closes the paper with the last considerations.

2. Continuous Designs are Uniformly Better than Group Designs

Continuous and group sequential designs are now formally defined.

Definition 1 (Group Sequential Design)

For a set of constants a₁ ≤ a₂ ≤ … ≤ a_G, and a sequence ${\left\{t_i\right\}}_{i=1}^G$ of times, where t_G = T, a group sequential analysis design for Poisson data is a procedure that takes H₁ as true if $W(X_{t_i})\ge a_i$ for some i ∈ {1, …, G}, and takes H₀ as true otherwise.

Definition 2 (Continuous Sequential Design)

Let CV_t denote a continuous function in the (0,T ] interval. A continuous sequential analysis design for Poisson data is any procedure that takes H₁ as true if W (X_t ) ≥ CV_t for some t ∈ (0,T ].

The notion of “uniformly better design” is another important topic for the goals of this paper. It was introduced by Silva and Kulldorff (2013) having T, significance level, power, expected time to signal, and expected length of surveillance as the target statistical performance measures, and now we extended this definition to arbitrary set of statistical performance measures.

Definition 3 (Uniformly Better Design)

Let D₁ and D₂ denote two sequential analysis designs for hypothesis testing for an unknown P -dimensional parameter θ. Let $\overrightarrow{M}(\theta )=(M_1(\theta ),\hspace{0.17em}\cdots \hspace{0.17em},M_K(\theta ))$ denote a K-dimensional row vector of statistical performance measures, and for i = 1, 2, let ${\overrightarrow{M}}_i(\theta )=(M_{1,i}(\theta ),\hspace{0.17em}\cdots \hspace{0.17em},M_{K,i}(\theta ))$ denote the vector of measures associated to D_i. Thus, D₁ is uniformly formly better than D₂ over $\overrightarrow{M}(\theta )$ if M_j,1(θ) ≤ M_j,2(θ) for each j = 1,… 4, and M_j,1 (θ) < M_j,2 (θ) for some j.

Evidently, the parameter of interest in the present work is the one-dimensional relative risk, i.e. here θ = R. For the target performance measures, define the 8-dimensional vector:

$$\overrightarrow{M}(R)=(T,\hspace{0.17em}\hspace{0.17em}\beta (1),\hspace{0.17em}\hspace{0.17em}\beta (R),\hspace{0.17em}\hspace{0.17em}E[\tau |H_0\hspace{0.17em}\text{rej}.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}E[X|H_0\hspace{0.17em}\text{rej}.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}E[\tau |R],\hspace{0.17em}\hspace{0.17em}E[X|R],\hspace{0.17em}\hspace{0.17em}\varphi (R)),$$ (3)

where β(1) is the overall Type I error probability (which equals to the desired α level), β(R) is the overall statistical power, E[τ|H₀ rej., R] is the expected time to signal, E[X|H₀ rej., R] is the expected number of events to signal, E[τ|R] is the expected time of surveillance, E[X|R] is the expected number of events. The term φ (R) represents the risk function, also called expected loss, defined by:

$$\varphi (R)=l_1(R)\times \beta (R)\times I(R\le 1)+l_2(R)\times [1-\beta (R)]\times I(R>1),$$ (4)

where l_j (R), j 1, 2, is an arbitrary real-valued function of R that measures the undesirable effects, losses, followed by the Type I and Type II errors. The loss function is arbitrated by the analyst in such a way that l₁ (R) represents the loss followed by the Type I error, and l₂ (R) represents the loss followed by the error of Type II. For example, one way to construct a loss function is to consider the financial costs involved in the development and implementation of a recently approved and commercialized vaccine.

As proved by Silva and Kulldorff (2013), continuous sequential analysis is uniformly better than group sequential over the measures T, β(1), β(R), E[τ|H₀ rej., R and E[τ|R]. Now we extend their results for the performance vector in Eq. 3.

Theorem 1 For a Poisson stochastic process X_t indexed by continuous or discrete time, let

$$\begin{gathered} {\overrightarrow{M}}_1(R)=(T_1,\hspace{0.17em}\hspace{0.17em}{\beta }_1(1),\hspace{0.17em}\hspace{0.17em}{\beta }_1(R),\hspace{0.17em}\hspace{0.17em}{E}_1[\tau |H_0\hspace{0.17em}rej.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}{E}_1[X|H_0\hspace{0.17em}rej.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}{E}_1[\tau |R], \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{E}_1[X|R],\hspace{0.17em}\hspace{0.17em}{\varphi }_1(R)) \end{gathered}$$ (5)

denote the performance measure of an arbitrary group sequential design D₁ that takes H₁ as true for large values of X_t. Thus, there always exists a continuous sequential design, with performance measure

$$\begin{gathered} {\overrightarrow{M}}_2(R)=(T_2,\hspace{0.17em}\hspace{0.17em}{\beta }_2(1),\hspace{0.17em}\hspace{0.17em}{\beta }_2(R),\hspace{0.17em}\hspace{0.17em}{E}_2[\tau |H_0\hspace{0.17em}rej.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}{E}_2[X|H_0\hspace{0.17em}rej.,\hspace{0.17em}R],\hspace{0.17em}\hspace{0.17em}{E}_2[\tau |R], \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{E}_2[X|R],\hspace{0.17em}\hspace{0.17em}{\varphi }_2(R)) \end{gathered}$$ (6)

such that:

1. T₂ = T₁,

2. β₂(1) = β₁(1),

3. β₂(R) = β₁(R),

4. E₂[τ |H₀ rej., R] < E₁[τ |H₀ rej., R],

5. E₂[X|H₀ rej., R] < E₁[X|H₀ rej., R],

6. E₂[τ |R] < E₁[τ |R],

7. E₂[X|R] < E₁[X|R], and

8. φ₂(R) = φ₁(R).

Therefore, for each group sequential design, there always exists a continuous sequential design which is uniformly better over the vector of performance measures in Eq. 3.

Proof For a given group sequential design constructed according to Definition 1, consider an associated continuous sequential design having T = t_G and, if t ∈ (t_i−1, t_i ], then CV_t = a_i.

With this associated continuous design, the proof of item (i) is trivial.

Items (ii) and (iii) follow from the fact that the associated continuous design rejects H₀ if, and only if, the group sequential also does, which holds for each R ∈ (0, ∞).

To prove items (iv) to (vii), let τ_c denote the time when the associated continuous design is stopped. If the null hypothesis is rejected, then τ_c = inf{t ∈ (0,T] : W (X_t ) ≥ CV_t }. It means that, if τ_G ∈ {t₁, ·… , t_G} is the stopping time of the group sequential design, then τ_c ≤ τ_G. In addition, define j = min{i : W (X_t ) ≥ a_i }, therefore t_j−1 < τ_c < t_j, with t₀ = 0. Because X_t is a Poisson stochastic process, there exists an t_i < m < t_i+1 such that $E[X_m|R]-E[X_{t_i}|R]>0$ and hence $PR(X_m-X_{t_i}>k|R)>0$ for any value of k, i.e. the probability that the continuous sequential analysis rejects the null hypothesis at time m is $Pr(X_{t_i}<a_i,X_m\ge a_{i+1}|R)>0$, which implies that E[τ_c|R < E[τ_g|R]. Then expected time to signal and expected number of events to signal with the associated continuous design are smaller than those from the group design.

Item (viii) follows from item (iii). □

It is important to stress that the proof of the Theorem does not require the presence of all the 8 measures of Eq. 3. Furthermore, follows also from this proof that the continuous design is uniformly better than the group over any subset of $\overrightarrow{M}(R)$.

Corollary 1 If X_t is a Poisson stochastic process, then for each group sequential design there always exists an uniformly better group sequential design over any subset of measures taken from the vector in Eq. 3.

Under a practical perspective, Theorem 1 can be used to support the practice of adopting a continuous sequential approach in post-market-safety surveillance, where data is collected in a near continuous matter (Silva and Kulldorff 2013). Under a theoretical perspective, its importance relates to the implication that optimal sequential analysis designs are in the class of continuous designs.

Corollary 2 An optimal sequential hypothesis testing design for hypotheses of the form in Eq. 1, and having one or more of the performance measures in Eq. 3, is a continuous sequential design.

Inspired by the corollary above, hereinafter the content of this paper is directed for continuous sequential analysis. To do so, next section uses recursive expressions to derive analytical calculation of power and expected number of events to signal followed by continuous sequential designs. Such expressions shall be useful in the subsequent sections.

3. Recursive Power Function

Assume that W (X_t ) is: (i) monotone increasing with μ_t for each fixed X_t = x > 0, and (ii) monotone increasing with x for each fixed X_t = x > 0 and μ_t > 0. With this, for a given threshold CV_t, let τ_x denote the arrival time of the x-th adverse event for x = 1, …, N, where:

$$N:=\max \{x\in \mathbb{N}:W(x)\le C{V}_t\}.$$

Hence, there always exist thresholds 0 < μ₍₁₎ ≤ μ₍₂₎ … ≤ μ_(N), with μ_(N) = T, such that the probability of rejecting H₀ can be written as:

$$\mathrm{Pr}[\text{rej}.\hspace{0.17em}{H}_0|R]=\mathrm{Pr}[W(X_t)\ge C{V}_t\hspace{0.17em}\text{for}\hspace{0.17em}\text{some}\hspace{0.17em}t\hspace{0.17em}\in \hspace{0.17em}(0,\hspace{0.17em}T)|R]$$ (7)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\mathrm{Pr}[X_t\ge W^{-1}(C{V}_t)|R]$$ (8)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\mathrm{Pr}[{\cup }_{x=1}^N\{{\tau }_x\le {\mu }_{(x)}\left\}\right|R].$$ (9)

where μ_(x) = sup{t : x ≥ W ⁻¹ (CV_t )}, and W ⁻¹ (CV_t ) is the value y such that W (y) = CV_t.

Since X_t ~ Poisson (μ_t ), write μ_t = λt, where λ is a known constant, and the time index t is a deterministic function of intrinsic characteristics of the analyzed phenomena, like for example the effects of covariates at each analysis combined with the proportion of exposed individuals of the population. Thus, the joint density of the vector (τ₁, … , τ_N ) is:

$$f_{\tilde{\tau }}(y_1,\hspace{0.17em}\cdots \hspace{0.17em},y_N|R)={(R\lambda )}^N{e}^{-y_{N}R\lambda }I(y_N>0).$$ (10)

Consider the transformation $\tilde{T}=\lambda \tilde{\tau }=(T_1,\hspace{0.17em}\cdots \hspace{0.17em},T_N)$, which has density:

$$f_{\tilde{T}}(t_1,\hspace{0.17em}\cdots \hspace{0.17em},t_N|R)=R^N{e}^{-t_{N}R}I(t_N>0).$$ (11)

Hence, the overall probability of rejecting H₀, denoted by β(R), is given by:

$$\begin{gathered} \beta (R)=\mathrm{Pr}[\text{rej}.\hspace{0.17em}{H}_0|R]=\mathrm{Pr}\left(\underset{x=1}{\overset{N}{\cup }}\left\{T_x\le {\mu }_{(x)}\right\}|R\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\sum _{x=1}^N\mathrm{Pr}(\text{N}=x|R), \end{gathered}$$ (12)

where N is the cumulative number of observed events at to the signaling time. For N = 1:

$$\mathrm{Pr}(\mathrm{N}=1|R)=\mathrm{Pr}(T_1\le {\mu }_{(1)})=1-e^{-{\mu }_{(1)}R}.$$

For N=2:

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Pr}(\mathrm{N}=2|R)=\mathrm{Pr}\left(T_1>{\mu }_{(1)}\cap T_2>{\mu }_{(2)}\right) \\ ={\int }_{{\mu }_{(1)}}^{{\mu }_{(2)}}{\int }_{{\mu }_{(1)}}^{t_2}{R}^2{e}^{-R{t}_2}d{t}_{1}d{t}_2 \\ =\mathrm{Pr}\left({\mu }_{(1)}\le T_2\le {\mu }_{(2)}|R\right)-R^{-1}{\mu }_{(1)}\mathrm{Pr}\left({\mu }_{(1)}\le T_1\le {\mu }_{(2)}|R\right). \end{gathered}$$

For N=3:

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Pr}(\mathrm{N}=3|R)=R^{-1}\mathrm{Pr}\left(T_1>{\mu }_{(1)}\cap T_2>{\mu }_{(2)}\cap T_3>{\mu }_{(3)}\right) \\ ={\int }_{{\mu }_{(2)}}^{{\mu }_{(3)}}{\int }_{{\mu }_{(2)}}^{t_3}{\int }_{{\mu }_{(1)}}^{t_2}{R}^3{e}^{-R{t}_3}d{t}_{1}d{t}_{2}d{t}_3 \\ =\mathrm{Pr}\left({\mu }_{(2)}\le T_3\le {\mu }_{(3)}|R\right)-R^{-1}{\mu }_{(1)}\mathrm{Pr}\left({\mu }_{(2)}\le T_2\le {\mu }_{(3)}|R\right) \\ \hspace{1em}+R^{-2}\left({\mu }_{(1)}{\mu }_{(2)}-{\mu }_{(2)}^2/2\right)\mathrm{Pr}\left({\mu }_{(2)}\le T_1\le {\mu }_{(3)}|R\right). \end{gathered}$$

For N=4:

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{Pr}(\mathrm{N}=4|R)=R^{-1}\mathrm{Pr}\left(T_1>{\mu }_{(1)}\cap \hspace{0.17em}\cdots \hspace{0.17em}\cap T_4>{\mu }_{(4)}\right) \\ ={\int }_{{\mu }_{(3)}}^{{\mu }_{(4)}}{\int }_{{\mu }_{(3)}}^{t_3}{\int }_{{\mu }_{(2)}}^{t_3}{\int }_{{\mu }_{(1)}}^{t_2}{R}^4{e}^{-R{t}_1}d{t}_{1}d{t}_{2}d{t}_{3}d{t}_4 \\ =\mathrm{Pr}\left({\mu }_{(3)}\le T_4\le {\mu }_{(4)}|R\right)-R^{-1}{\mu }_{(1)}\mathrm{Pr}\left({\mu }_{(3)}\le T_3\le {\mu }_{(4)}|R\right) \\ \hspace{1em}+R^{-2}\left({\mu }_{(1)}{\mu }_{(2)}-{\mu }_{(2)}^2/2\right)\mathrm{Pr}\left({\mu }_{(3)}\le T_3\le {\mu }_{(4)}|R\right) \\ \hspace{1em}-R^{-3}\left[\frac{{\mu }_{(3)}^3}{3!}-\frac{{\mu }_{(1)}{\mu }_{(3)}^2}{2}+{\mu }_{(3)}\left({\mu }_{(1)}{\mu }_{(2)}-\frac{{\mu }_{(2)}^2}{2}\right)\right] \\ \hspace{1em}\times \mathrm{Pr}\left({\mu }_{(3)}\le T_1\le {\mu }_{(4)}|R\right). \end{gathered}$$

Thus, a recursive expression, with respect to N, can be written to express β(R):

$$\begin{gathered} \beta (R)=\sum _{\text{N}=1}^N\sum _{i=1}^{\text{N}}{(-1)}^{i+1}{\psi }_i\mathrm{Pr}\left({\mu }_{(\text{N}-1)}\le T_{\text{N}+1-i}\le {\mu }_{(\text{N})}|R\right) \\ \hspace{1em}\hspace{1em}\hspace{0.17em}=\sum _{\text{N}=1}^N{\beta }_{\text{N}}(R). \end{gathered}$$ (13)

where μ₀ = 0, ψ₁ = 1, and for i = 2, …, N,

$${\psi }_i=\sum _{j=1}^{i-1}{(-1)}^{j+1}\frac{{\left(r{\mu }_{(i-1)}\right)}^j}{j!}{\psi }_{i-j}.$$

It merits remark that β_N(1) is the punctual Type I error probability spending associated to the N(th) event, which depends only on μ_(N), μ_(N−1), …, μ₍₁₎. This way, given a target Type I error probability spending S(t), one can ways elicit μ_(N) such that β_N(1) equals to S(μ_(N)) for each N = 1, …, N.

The expected number of events to signal can also be calculated in a recursive way using the following:

$$E[X|H_0\hspace{0.17em}\text{rejected}]=\frac{{\sum }_{\text{N}=1}^{\text{N}}\text{N}\left[{\sum }_{i=1}^N{(-1)}^{i+1}{\psi }_i\mathrm{Pr}\left({\mu }_{(\text{N}-1)}\le T_{\text{N}+1-i}\le {\mu }_{(\text{N})}|R\right)\right]}{\beta (R)}.$$ (14)

4. Comparing Type I Error Spending Functions

The expressions for power and expected number of events to signal in Eqs. 13 and 14, respectively, are used in the present section to perform a comparison study among four Type I spending functions. The first one is the power-type function already shown in the Introduction:

$$S_1(t)=\alpha \times {\left(\frac{t}{T}\right)}^{\rho },\rho >0.$$ (15)

According to Kim and Demets (1987), Jennison and Turnbull (1989), and Jennison and Turnbull (1990), under appropriate choices for ρ the function S₁(t) can mimic Pocock’s and O’Brien & Fleming’s methods with reasonable precision.

The second Type I error spending considered in this section was firstly suggested by Lan and DeMets (1983) as a good approximation for the O’Brien & Fleming’s test, and it is given by:

$$S_2(t)=2-2\times \Phi \left(x_{\alpha }\times \sqrt{T/t}\right),$$ (16)

where x_α is such that Φ⁻¹ (1 − α/2) = x_α.

Our third function, also introduced by Lan and DeMets (1983), is the log-exp function, which is meant to approximate the Pocock’s test, and it is given by:

$$S_3(t)=\alpha \times \log \left\{1+[\exp (1)-1]\times \frac{t}{T}\right\}.$$ (17)

Finally, the fourth function considered in this comparison study, suggested by Hwang et al. (1990), is also designed to mimic Pocock’s test, and its shape is as follows:

$$S_4(t)=\alpha \times \frac{1-\exp \left\{-\frac{t}{T}\gamma \right\}}{1-\exp \{-\gamma \}},\hspace{0.17em}\hspace{0.17em}\gamma \in (0,\hspace{0.17em}0.5].$$ (18)

All these functions were extensively studied by Lan and DeMets (1983), Kim and Demets (1987), Jennison and Turnbull (1989), Jennison and Turnbull (1990), and Jennison and Turnbull (2000) to explore the balance among statistical power, expected sample size, and maximum length of surveillance. In general, convex shapes lead to small expected sample sizes. Jennison and Turnbull (2000) shows that, for fixed statistical power, the function S₁(t) promotes small expected samples sizes using ρ around 1.5 or 2.

The maximum length of surveillance and the expected sample size are historically used as target measures in sequential analysis. This is due to challenges arising in clinical trials, where it is usually difficult to recruit many patients for the clinical experiment. Differently, in post-market drug and vaccine safety surveillance the maximum sample size can be arbitrarily large when a surveillance system is up and running. By another hand, since a lot of people is exposed to the drug, a delayed signalization of actual risks from the drug can potentially cause real damages to the health of many patients (Silva and Kulldorff 2015). In this scenario, the meaningful performance measure is no longer maximum length of surveillance or expected sample size, but expected number of events to signal for fixed power. As stressed earlier in this paper, there are no studies comparing Type I error spending functions in terms of the trade-off between expected number of events to signal and power.

4.1. Tuning Parameters Settings

A total of 600 scenarios were considered, each corresponding to a specific choice among α = 0.01, 0.05, R = 1, 1.1, …, 3, and T = 10, 20, …, 100. For each scenario, power and expected number of events to signal were calculated for each of the four Type I error functions. Note that S₁(t) and S₄(t) define families of functions since different shapes are obtained if different values of ρ and γ are fixed. Because of this, each of the 600 designs described above were evaluated in the following set of meaningful values: ρ = 0.1, 0.2 …, 2, and γ = 0.1, 0.2, …, 0.5.

All calculations were executed using the R language (Team 2015), and can be reproduced with the code available as a Supplementary Material.

4.2. Results

We first investigate the best choice among ρ and γ values for using S₁(t) and S₄(t), respectively. We start with S₁(t). After analyzing the overall numerical evolution of the expected number of events to signal as a function of power, we find out that, in general, the choice ρ = 0.5 is always either the best or near to the best choice, depending on the actual value of R. Unfortunately, due to space limitations, we are not able to show figures and tables containing all results from each of the tuning parameters explored in this work. But, some numerical results can be shown in order to illustrate the general conclusions. For example, Fig. 1 brings expected number of events to signal as a function of power for ρ = 0.1, 0.5, 0.7, 1, 1.5. The x-axis, given in the log-scale, represents the actual power for each of the different values of T. For R = 1.5, the best curve is associated to ρ = 0.7, but the curve for ρ = 0.5 is very close to it for each power. For scenario R = 2, the choice ρ = 0.5 is the best one. These results is uniformly observed for each of the tuning parameters considered.

Fig. 1.

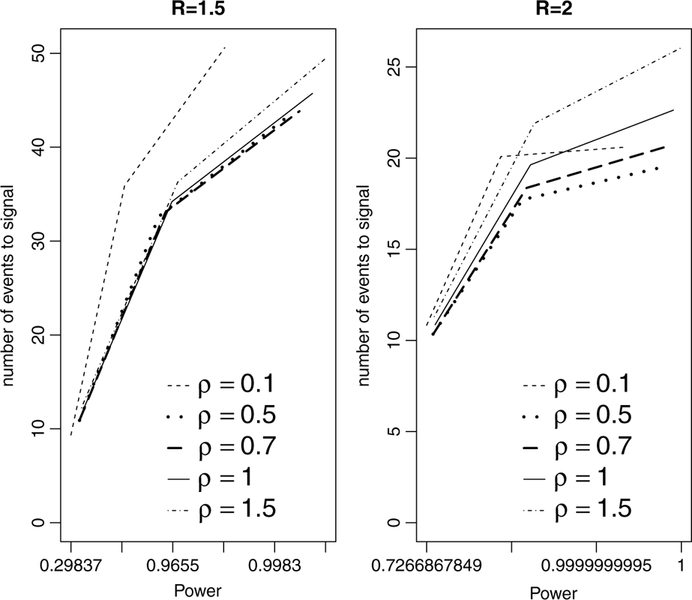
Expected number of events to signal versus power using the S₁(t) shape based on ρ = 0.1, 0.5, 0.7, 1, 1.5. The tuning parameters used were R = 1.5, 2, α = 0.05, and selected maximum length of surveillance T. Note the log-scale for power

Concerning the best choice for γ in S₄(t), the global behavior can be illustrated considering the sample of γ values of 0.1, 0.3, and 0.7. Figure 2 illustrates the general behavior that identifies γ = 0.5 as the best choice in terms of minimizing expected number of events to signal for fixed power.

Fig. 2.

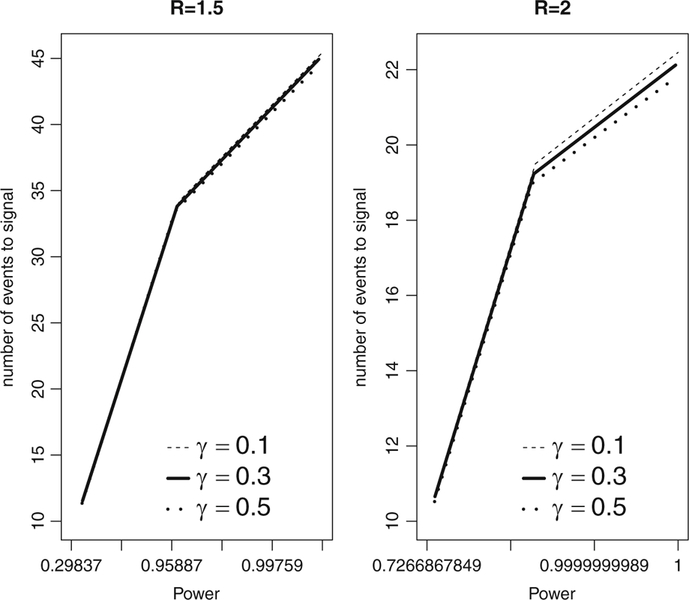
Expected number of events to signal versus power using the S₂(t) shape based on γ = 0.1, 0.3, 0.5. The tuning parameters used were R = 1.5, 2, α = 0.05, and selected maximum length of surveillance T. Note the log-scale for power

Now we compare S₁(t), S₂(t), S₃(t) and S₄(t). For this, we use ρ = 0.5 and γ = 0.5. Figure 3 shows the comparison using R = 1.5, 2. It is evident that the S₃(t) shape represented by the dotted line, called log-exp function, leads to the smallest expected number of events to signal among these four functions. Therefore, the final conclusion after all these massive numerical investigation is that the log-exp function should be adopted for sequential analysis with Poisson data when expected number of events to signal is the meaningful statistical performance measure.

Fig. 3.

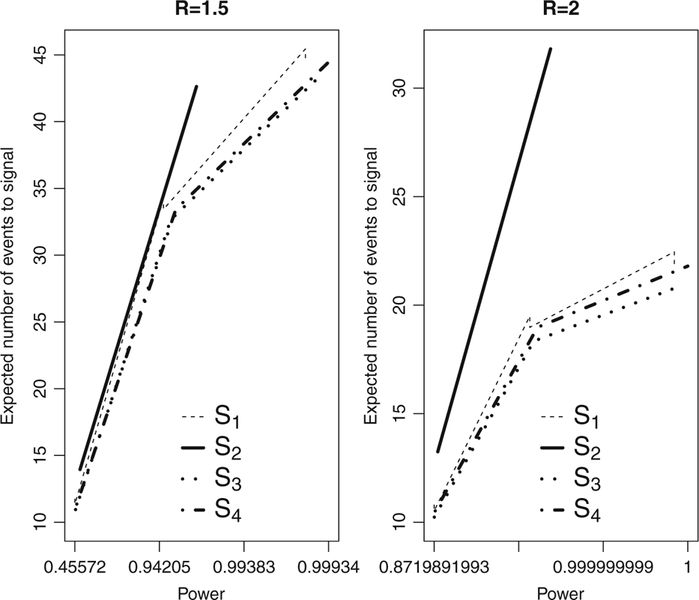
Expected number of events to signal versus power comparing the shapes S₁(t) with ρ = 0.5, S₂(t), S₃(t), and S₄(t)with γ = 0.5. Each design is based on the tuning parameters R = 1.5, 2, α = 0.05, and selected maximum length of surveillance T. Note the log-scale for power

5. Last Comments

The behavior of the expected number of events to signal in a continuous sequential surveillance is interesting. Because the continuous approach allows to look to the data as many times as wanted, the maximum length of surveillance is increased comparatively to a group sequential testing. This sample size enlargement also increases the expected length of surveillance. This explains why expected number of events to signal and expected sample size are not positively related, which, by its turn, explains the discordance between the findings of the present work and the findings of many authors. While former works indicate usage of a convex Type I error spending function, such as promoted by the O’Brien & Fleming’s method, the present work suggests usage of a concave function. The former is concentrated on minimizing expected length of surveillance, and the later is directed to minimize expected number of events to signal. Therefore, if expected sample size or maximum length of surveillance are used as design criterion, then O’Brien & Fleming’s test is known to be the good choice. Instead, if expected number of events to signal is the design criterion, then the concave shape promoted by the log-exp function S₃(t) should be used.