ACCELERATED CORONARY MRI USING 3D SPIRIT-RAKI WITH SPARSITY REGULARIZATION

Abstract

Coronary MRI is a non-invasive radiation-free imaging tool for the diagnosis of coronary artery disease. One of its limitations is the long scan time, due to the need for high resolution imaging in the presence of respiratory and cardiac motions. Machine learning (ML) methods have been recently utilized to accelerate MRI. In particular, a scan-specific ML technique, called Robust Artifical-neural-network for k-space Interpolation (RAKI) has shown promise in cardiac MRI. However, it requires uniform undersampling. In this study, we sought to extend this approach to arbitrary sampling patterns, using coil self-consistency. This technique, called SPIRiT-RAKI, utilizes scan-specific convolutional neural networks to nonlinearly enforce coil self-consistency. Additionally, regularization terms can also be incorporated. SPIRiT-RAKI was used to accelerate right coronary MRI. Reconstructions were compared to SPIRiT for different undersampling patterns and acceleration rates. Results show SPIRiT-RAKI reduces residual aliasing and blurring artifacts compared to SPIRiT.

1. INTRODUCTION

Coronary artery disease (CAD) is the number one cause of death in the United States [1]. While invasive methods are considered to be the gold standard for its diagnosis [2], several non-invasive imaging modalities have also been proposed [3, 4]. Coronary MRI is a radiation-free non-invasive method for the assessment of CAD [4]. Despite several advances over the past decade, coronary MRI is still challenging due to its lengthy acquisition time and low signal-to-noise ratio (SNR).

Multiple accelerated MRI approaches have been used to accelerate coronary MRI. These include non-Cartesian trajectories [5], parallel imaging [6, 7], compressed sensing [8] or their combinations [9, 10]. Coronary MRI can be performed using whole-heart or targeted acquisitions. The former is easy to prescribe, however acquisition of a large volume necessitates long acquisitions. On the other hand, the limited coverage of the latter leads to a shorter acquisition, but also limited SNR, which in turn limits the acceleration rates that can be achieved. Thus, more efforts have focused on whole-heart coronary MRI, where acceleration rates of up to six have been reported [9]. However, targeted coronary MRI is attractive, since its nominal acquisition time, assuming 100% navigator gating efficiency is approximately two minutes. Thus, an acceleration rate of five can bring this acquisition into a breath-hold duration, reducing the total scan time more than ten-fold by removing inefficient respiratory motion compensation.

Recently, machine learning (ML) methods have been proposed for improving image reconstruction in accelerated MRI [11–19]. One such technique that has shown promise in cardiac MRI is a method called Robust Artificial-neural-networks for k-space Interpolation (RAKI) [19]. This approach uses scan-specific convolutional neural networks (CNN) to nonlinearly interpolate the missing data in k-space, extending the linear convolutional kernels of GRAPPA [20]. These CNNs can be calibrated using scan-specific auto-calibration signal (ACS), which can, for instance be acquired as a a small fully-sampled central k-space region within the same scan. This alleviates the need for large training databases that is used in most ML methods.

RAKI was originally designed for uniform undersampling patterns that are typically used in parallel imaging [19]. However, previous work has shown the benefit of random undersampling in high-resolution three-dimensional (3D) applications, including coronary MRI, in conjunction with regularized reconstruction [9]. For such patterns, k-space interpolation exploiting redundancies in the multi-coil data can be performed via a self-consistency approach, as proposed in iterative self-consistent parallel imaging reconstruction (SPIRiT) [21]. SPIRiT calibrates linear convolutional kernels on ACS data to impose consistency among coils. Then an objective function is minimized iteratively to yield the desired reconstructed data by enforcing this self-consistency, as well as consistency with the acquired k-space measurements, and optionally performing image regularization.

In this study, we utilize the notion of self-consistency of SPIRiT to extend RAKI to arbitrary undersampling patterns for accelerating targeted coronary MRI. In accordance with SPIRiT, additional priors and regularization terms can be incorporated to this formulation as well. Our technique, called SPIRiT-RAKI is evaluated on targeted coronary MRI datasets, and compared to SPIRiT for various undersampling patterns and acceleration rates.

2. MATERIALS AND METHODS

2.1. SPIRiT-RAKI Calibration and Reconstruction

RAKI trains a CNN using ACS data to learn a nonlinear mapping function from acquired data points to missing data [19]. Since RAKI is designed for a uniform undersampling pattern only, it uses dilated convolutional kernels in training to match the uniform spacing in the undersampling phase. In contrast, for SPIRiT-RAKI, such dilation does not apply and is not needed for arbitrary undersampling patterns. Furthermore, the mapping in [19] is from acquired points in all coils to missing data in one coil, necessitating the training of many CNNs. In contrast, in SPIRiT-RAKI, since self-consistency is being imposed, the output of the mapping is the k-space across all coils instead of only missing lines in a single coil. This modification significantly reduces the number of unknowns for calibration and consequently the running time for both calibration and reconstruction

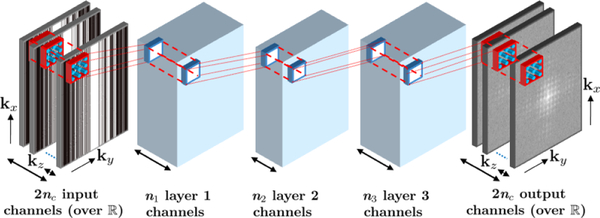
A 4-layer CNN architecture was employed for coil self-consistency (Fig. 1). The CNN has 2n_c input and output channels, where n_c is the number of coils. The factor of 2 is due to complex k-space being mapped to the real field. Since targeted coronary MRI is a 3D acquisition, which can be undersampled in both k_y and k_z phase encoding directions, a 3D CNN was used in this study. All layers except the output layer included rectifier linear units (ReLU), which forms the nonlinear component of the mapping learned by the CNN. The network was then trained on ACS data with a mean square error objective function, which was minimized using an ADAM optimizer. Further details on CNN and training parameters are provided in Section 2.2. After calibration of the CNN on ACS data, reconstruction was performed by minimizing:

$$\Vert \mathbf{y}-Dx{\Vert }_2^2+\beta \Vert x-G\left(x\right){\Vert }_2^2+\gamma \Vert WEx{\Vert }_1$$ (1)

where x is the desired k-space data across all coils, y is the noisy acquired data, D is the undersampling operator, G(·) represents the CNN nonlinear operations to enforce self-consistency, E is an operator that transforms k-space into image domain first and then combines coil images into a SENSE Rate-1 image, and W transforms this image into a sparsity domain, which a wavelet transform in this study. The objective function in (1) was minimized using variable splitting for the regularization term and a quadratic penalty [22]. The ℓ₂ terms were minimized using gradient descent, which was implemented using the formulation of the ADAM optimizer. Note G(·) is implicitly defined through the CNN, thus the derivative of this term was calculated using backpropagation. Furthermore, in this setting, we are only interested in the derivative with respect to the input, and not with respect to the CNN parameters. The remaining ℓ₁ term was implemented using a proximal operator.

Fig. 1:

The 4-layer CNN architecture to enforce self-consistency among all coils.

2.2. Implementation details

The parameters for the CNN and training were as follows: The kernel size of the first and fourth layers were 5 × 5 × 5, whereas it was 3 × 3 × 3 for the second and third layers. The first, second and third layers had 32, 16 and 32 output channels, respectively. All layers included a bias term. Tikhonov regularization was used for training to avoid over-fitting, and the regularization parameter was set to 0.001 for all layers. In addition, a default learning rate of 0.001 was used for the ADAM optimizer in the training phase.

For the minimization of (1), the learning rate in ADAM was set to 1 for the gradient descent. β and the quadratic penalty term was optimized empirically. The threshold for the proximal operator corresponded to 0.001 of the largest wavelet coefficient. Additionally, SPIRiT was implemented for comparison based on the online code [21], where the kernel size was set to 5 × 5 × 3. The thresholding parameter was set to 0.001 of the largest wavelet coefficient. The maximum number of iterations was set to 50 for both methods in all cases except for the non-regularized SPIRiT, where this number was finely tuned to 75.

2.3. In Vivo Coronary MRI

Targeted right coronary MRI was acquired on two healthy subjects at 3T with a 30-channel body-coil using a T₂-prepared GRE sequence. Relevant imaging parameters were FOV=300 × 300 × 60 mm³ and resolution=1 × 1 × 3mm³. The data were retrospectively under-sampled, both uniformly and randomly. For the uniform pattern, the data were under-sampled at an acceleration rate of 2 × 2 along k_y and k_z directions. ACS region was selected as the central 45 × 10 k_y − k_z lines. This led to an approximate net acceleration rate of 4, using an elliptical mask in the k_y − k_z plane. For these patterns, no sparsity regularization was utilized for consistency with traditional parallel imaging methods. Random undersampling was implemented using variable-density sampling with Gaussian weights. Two undersampling rates were used; the first one matching the net uniform undersampling rate, and the second one yielding a net undersampling rate of 5 to assess the performance in applications where scan duration is in the breath-held acquisition range.

3. RESULTS

Fig. 2 demonstrates a representative slice from the right coronary MRI of a healthy subject using SPIRiT and SPIRiT-RAKI with uniform k_y − k_z undersampling rate of 4. As described in Section 2.3, no regularization was used for uniform undersampling patterns to ensure similarity to traditional parallel imaging reconstructions. Both techniques are successful in removing fold-over artifacts, although fewer blurring artifacts (see the right coronary artery area) and noise amplification are observed for SPIRiT-RAKI. This observation also holds in Fig. 3, where results are shown on another subject for the same undersampling pattern and rate.

Fig. 2:

A representative slice from the right coronary MRI of a healthy subject using SPIRiT and SPIRiT-RAKI with uniform k_y − k_z undersampling rate of 4.

Fig. 3:

A slice from the right coronary MRI of another healthy subject using SPIRiT and SPIRiT-RAKI with uniform k_y − k_z undersampling rate of 4.

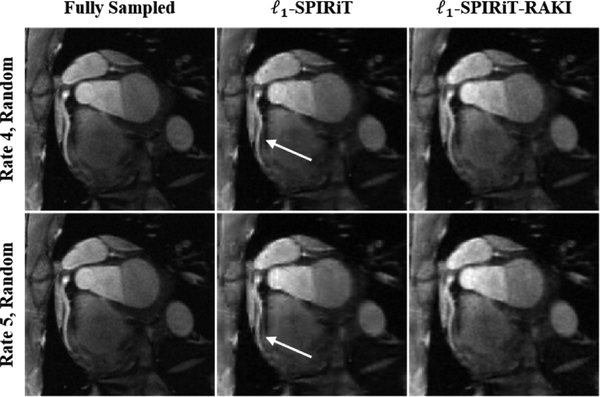
Results from random k_y − k_z undersampling are depicted in Fig. 4 for the same subject in Fig. 3. The reconstruction were performed with wavelet regularization for ℓ₁-SPIRiT and ℓ₁-SPIRiT-RAKI for undersampling rates of 4 (top row) and 5 (bottom row). Both results suffer from blurring artifacts, with more blurring visible for ℓ₁-SPIRiT.

Fig. 4:

The same slice from the dataset in Fig. 3 using ℓ₁-SPIRiT and ℓ₁-SPIRiT-RAKI when random k_y − k_z undersampling rates of 4 and 5 are utilized.

For the 3D kernels and ACS region sizes used in this study, SPIRiT-RAKI was approximately two times faster in calibration/training than SPIRiT. However, it was %50 slower in reconstruction compared to SPIRiT due to the need for solving a non-linear gradient descent at each iteration.

4. DISCUSSION

We have proposed an MRI reconstruction technique, SPIRiT-RAKI, which employs a CNN to nonlinearly enforce self-consistency among multi-coil MRI data using k-space interpolation. The CNN is trained on scan-specific ACS data, making this method independent of large training databases, unlike most ML methods. This technique successfully extends the RAKI method [19] to arbitrary sampling patterns. Its performance was shown in both uniform and random 3D undersampling, with results indicating improvement over SPIRiT, and at high acceleration rates for targeted coronary MRI. Specifically, the 5-fold undersampled acquisition may reduce the total duration of a targeted coronary MRI scan to a breath-hold, which can in turn remove inefficiencies associated with respiratory motion compensation procedures [4], reducing the true scan time more than 10-fold.

Several modifications were made to the CNNs used in [19]. First, the input-output relationship was changed. In the CNNs used in RAKI, the mapping was from acquired zero-filled k-space across all coils to the missing lines in one coil for 2D uniform undersampling patterns. This required 2n_c CNNs, leading to long training times. In order to extend the method to arbitrary undersampling patterns, the output was changed to all of the k-space across all coils. This required training of one large CNN, which also enabled inclusion of an additional layer. Second, in order to enable undersampling in both k_y and k_z, a 3D CNN was utilized. The kernel sizes were chosen empirically for these convolutions. Therefore, additional optimization may further improve the reconstruction performance, which will be explored in future work.

Wavelet regularization was used in this work for consistency with [21]. However, previous data on coronary MRI indicate that such regularization may result in blurring artifacts [23], which was also observed here. Hence, more advanced regularizers, which have proven effective in coronary MRI [9, 23], can help reduce these remaining artifacts more. This will be explored in future studies in order to improve the reconstruction of coronary MRI quality further.

5. CONCLUSION

SPIRiT-RAKI reconstruction, which uses a scan-specific CNN to enforce coil self-consistency in an iterative algorithm that allows sparsity regularization, was proposed to accelerate targeted coronary MRI.