Accelerated Simultaneous Multi-Slice MRI using Subject-Specific Convolutional Neural Networks

Abstract

Simultaneous multi-slice or multi-band (SMS/MB) imaging allows accelerated coverage in magnetic resonance imaging (MRI). Multiple slices are excited and acquired at the same time, and reconstructed using the redundancies in receiver coil arrays, similar to parallel imaging. SMS/MB reconstruction is currently performed with linear reconstruction techniques. Recently, a nonlinear reconstruction method for parallel imaging, Robust Artificial-neural-networks for k-space Interpolation (RAKI) was proposed and shown to improve upon linear methods. This method uses convolutional neural networks (CNN) trained solely on subject-specific calibration data. In this study, we sought to extend RAKI to SMS/MB imaging reconstruction. CNN training was performed on calibration data acquired prior to SMS/MB imaging, in a manner consistent with the existing linear methods. These CNNs were used to reconstruct a time series of functional MRI (fMRI) data. CNN network parameters were optimized using an extensive search of the parameter space. With these optimal parameters, RAKI substantially improves image quality compared to a commonly used linear reconstruction algorithm, especially for high acceleration rates.

I. Introduction

Acquisition times in Magnetic Resonance Imaging (MRI) remain long, especially compared to other imaging modalities. Therefore several methods for accelerating MRI have been proposed. Parallel imaging is the most clinically utilized strategy [1]–[3]. These methods use the differences in the receiver profiles of coil arrays [4], which lead to redundancies in acquisition. Redundancies in these profiles are estimated from calibration data that is acquired at the beginning of each MRI exam or scan [2], [3]. The reconstruction can be performed in image domain using a least squares formulation [2] or in k-space using linear shift-invariant interpolation [3].

A related acceleration technique, called simultaneous multislice or multi-band (SMS/MB) imaging provides fast coverage of the scans by encoding and acquiring multiple slices simultaneously [5]. The images are then recovered in a manner similar to parallel imaging, using the distinct sensitivities of the coils, which exhibit further variations for different slices. Several reconstruction methods have been proposed, including image domain techniques [6]–[8] and k-space interpolation strategies [9], [10]. For all these methods, scan-specific calibration data is acquired prior to SMS/MB imaging. The SMS/MB calibration data is often higher resolution compared to parallel imaging, as one calibration dataset is typically used to reconstruct series of images. SMS/MB imaging has been used in large-scale NIH projects, such as the Human Connectome Project [11], for fast acquisition of functional MRI (fMRI) and diffusion MRI.

The linear reconstruction approaches that are frequently used for accelerated MRI suffer from noise amplification that increases with higher undersampling rates [2], [3]. Thus, alternative strategies have been explored. Recently, multiple methods that use machine learning for improved regularization have been suggested [12]–[19]. These regularizers are learned on large training databases, which deviates from the scan-specific calibration of the linear strategies. In another line of work, a method called Robust Artificial-neural-networks for k-space Interpolation (RAKI) has been proposed for improving parallel imaging in a scan-specific manner [20]. RAKI uses multi-layer CNNs, trained on subject-specific calibration data, to interpolate missing points in k-space, extending on the linear convolutional kernels of conventional methods, such as Generalized Autocalibrating Partial Parallel Acquisition (GRAPPA) [3]. This method was shown to reduce the noise amplification in parallel imaging compared to GRAPPA [20].

In this study, we sought to extend the utility of RAKI to SMS/MB imaging. Subject-specific training of the CNNs was performed using the SMS/MB calibration data. Due to the higher resolution of the calibration data, bigger networks or convolutional kernels can be utilized, while over-fitting of the CNNs may also be a concern. Thus, extensive search of the parameter space was performed to yield CNNs that are robust to over-fitting, while improving noise performance. SMS/MB RAKI was applied to 8-fold and 16-fold accelerated fMRI, and compared to a conventional linear method called RO-SENSE-GRAPPA [21], showing improved robustness to noise.

II. Methods

A. Background on k-space Interpolation and RAKI

k-space interpolation approaches are widely used for parallel imaging reconstruction of undersampled MRI data, with GRAPPA [3] being one of the most clinically-used methods. In GRAPPA, the ACS can be obtained integrally or as a separate scan. A set of linear shift-invariant convolution kernel are estimated from this ACS data, which are subsequently utilized to interpolate the missing points in a uniformly undersampled k-space acquisition using the acquired ones in its vicinity [3]. As with other linear approaches, GRAPPA suffers from noise amplification at high acceleration rates [2].

RAKI extends on this linear convolution by performing nonlinear interpolation using CNNs [20]. Similar to GRAPPA, the CNNs are trained from the ACS data, which are subsequently used to interpolate the missing k-space points from the acquired ones. In [20], a three-layer CNN was used, although deeper architectures are also possible for larger ACS data. The first two layers of the network include convolutions and a point-wise non-linear operation via the rectified linear unit (ReLU), defined as ReLU(x) = max(x, 0). The last layer of the network only contains convolutions to generate the final estimates. This non-linear interpolation strategy was shown to improve upon the noise amplification associated with GRAPPA [20].

B. RAKI for SMS/MB Imaging

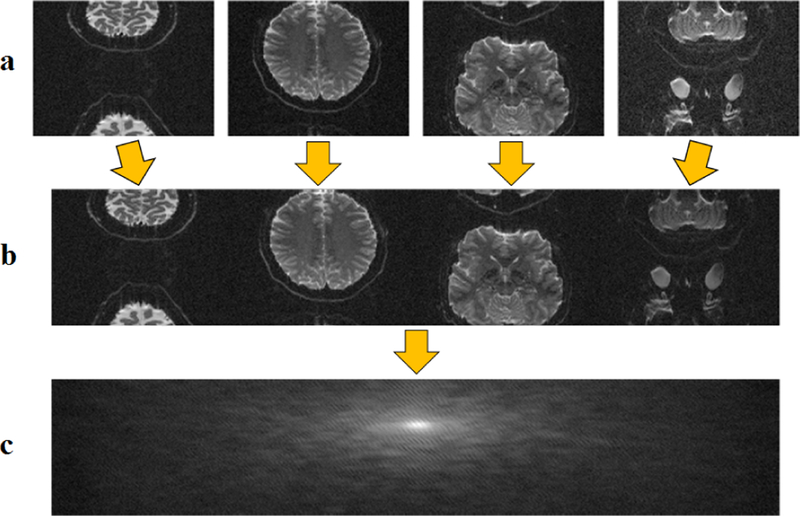
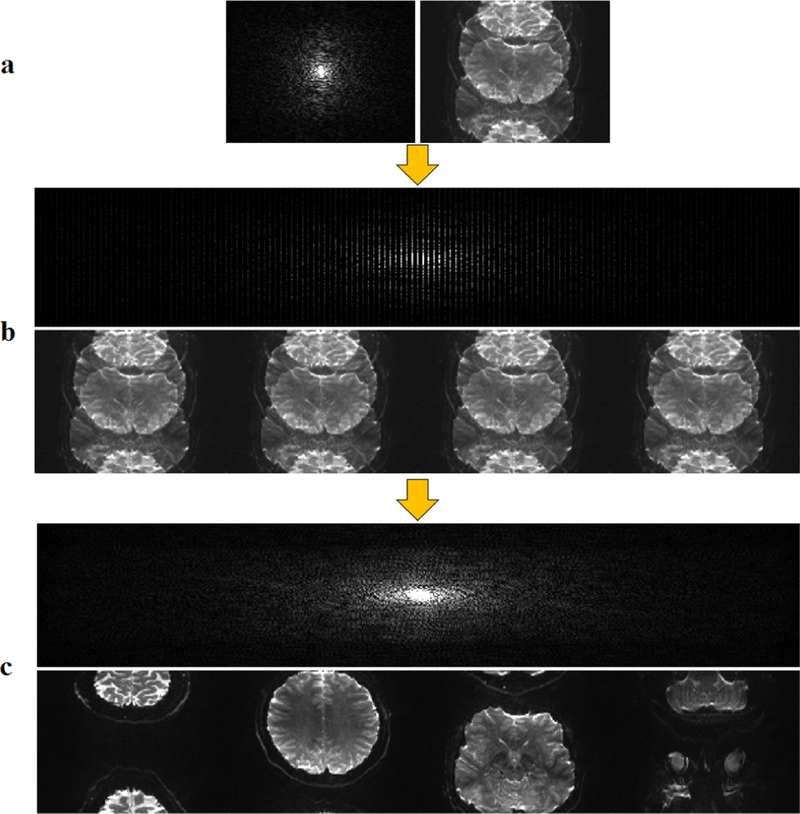
In extending RAKI to SMS/MB imaging, we used a readout concatenation strategy to transform the SMS/MB reconstruction into a one-dimensional interpolation problem [21]. To generate the ACS signal, fully sampled slices were obtained in individual scans prior to the fMRI acquisition. These were concatenated along the readout direction in image domain (Figure 1) to generate the calibration data that was used for CNN training. Subsequently, the SMS/MB-encoded images (Figure 2a) were zero-filled in k-space with the corresponding MB rates (Figure 2b). Image unfolding was then achieved by k-space interpolation using RAKI trained on the subject-specific calibration data (Figure 2c).

Fig. 1.

Generation of ACS signal for SMS/MB reconstruction. a) Fully sampled slices were obtained from calibration scans prior to fMRI acquisition. b) Image slices were concatenated in image domain along the readout direction. c) This readout-concatenated image was transformed to k-space, which served as the calibration data for CNN training.

Fig. 2.

Reconstruction procedure for SMS/MB imaging. a) Folded image in k-space (left) and image domain (right) at the acquisition matrix size. b) Zero-filled k-space data in k-space (top) and image domain (bottom). c) Reconstructed image after using k-space interpolation in k-space (top) and image domain (bottom).

For SMS/MB RAKI, we used a three-layer CNN similar to RAKI [20]. The input to the network is the acquired and zero-filled k-space data across all coils (mapped to the real field), and the output is the missing points in each coil. For an SMS/MB acceleration rate of R, the output contains R − 1 channels. For outputting coil c, the first two layers of the network implement non-linear functions $F_1^c\left(x\right)=\text{ReLU}\left({\text{w}}_1^C*x\right)$, and $F_2^c\left(x\right)=\text{ReLU}\left({\text{w}}_2^C*x\right)$, while the last layer is given by $F_3^c\left(x\right)={\text{w}}_3^C*x$. Here, ${\text{w}}_1^C$, ${\text{w}}_2^C$, ${\text{w}}_3^C$ are sets of convolutional operators used in reconstructing the data in the c^th channel, which were respectively in size $x_p^c\times y_p^c,\times i_p^c\times o_p^c$, where p ∈{1, 2, 3}. By design $o_3^c=R-1$. The overall interpolation function is given as $F^c\left(x\right)=F_3^c\left(F_2^c\left(F_1^c\left(x\right)\right)\right)$. For each channel in the receiver coil array, a corresponding CNN is trained from the ACS data based on the mean-square error loss function. A total of 2n_c such CNNs are trained, where n_c is the number of coils in the receiver array, and the factor of 2 is due to the mapping of the complex k-space values to $ℝ$.

C. In Vivo Imaging Experiments

Imaging was performed on a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) scanner with a 32-channel receiver head coil-array. fMRI acquisition was performed using the Human Connectome Project protocol [22] with resolution = 2 × 2 × 2mm³, using blipped-CAIPI encoding [23] with a field-of-view/3 shift between adjacent multiband slices. Images were acquired using a multiband rate of 8 (MB8) with echo time = 37ms, repetition time = 800ms, in accordance with the Human Connectome Project protocol, as well as at a higher multiband rate of 16 (MB16) with echo time = 37ms, repetition time = 1000ms. Calibration data containing the individual slices was acquired prior to the fMRI image series at the same resolution.

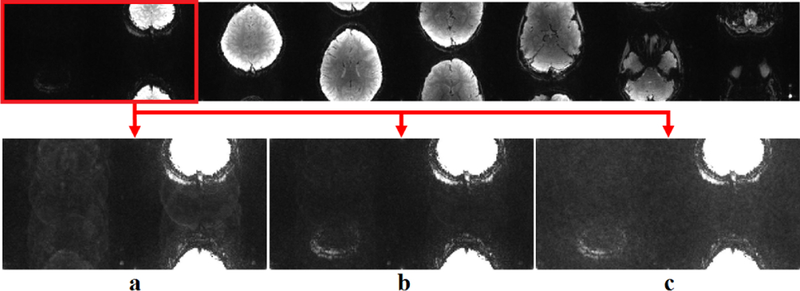
The subject-specific ACS data was used for training of the CNN as described in Section II-B. The mean-square error loss function was minimized using the Adam optimizer [24]. Network parameters were optimized using an extensive search of the parameter space, through the following values: $x_p^c\in \left\{1,3,5,7\right\}$, $y_p^c\in \left\{1,2,4,6\right\}$, $i_p^c$, $o_p^c\in \left\{18,16,32,64,128\right\}$, for p ∈ {1, 2, 3}. As noted earlier, $o_3^c=R-1$ was fixed. The trained network corresponding to each set of values was used to reconstruct both MB8 and MB16 data. These reconstructions were qualitatively evaluated by an observer for certain fidelity criteria (Figure 3), which included a) the reconstruction of low-intensity slices in the higher part of the skull, b) robustness to overfitting with respect to ghosting artifacts, c) resilience to noise amplification. The optimized network parameters were subsequently used for the reconstruction of MB8 and MB16 datasets. To further test noise sensitivity, Gaussian white noise was retrospectively added to MB8 datasets, which were subsequently reconstructed. For comparison in all cases, conventional RO-SENSE-GRAPPA reconstruction using a 5 × 4 kernel was also implemented on the same ACS data.

Fig. 3.

Reconstruction quality varies among different CNNs. a) A CNN that failed to recover the first slice properly. b) A CNN capable of reconstructing all slices while controlling the noise level. c) A CNN that recovers the first slice but suffers from noise amplification.

SMS/MB RAKI was implemented using python 3.6.2 and TensorFlow 1.3.0, supported by CUDA 8.0 and CuDNN 7.0.5. Python environment was created by Anaconda 3.8.3. GRAPPA was implemented using Matlab R2012b (MathWorks Inc., Natick, MA). All experiments were performed on a server with two Intel E5–2643 CPUs (6 cores each, 3.7 GHz), 256 GB memory, a NVIDIA Tesla K80 GPU (single precision 8.74 TFLOPS, 24 GB memory), running Linux 3.10.0 OS with GCC 4.8.5.

III. Results

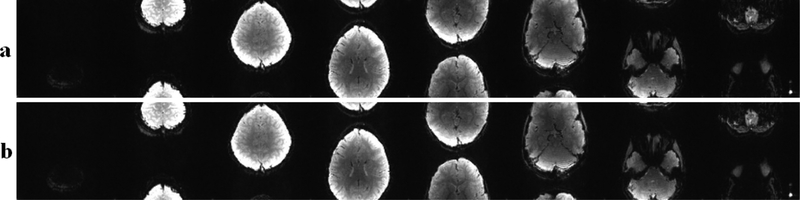
Based on the criteria outlined in Section II-C, the extensive search of the CNN parameter space yielded two sets of network parameters for both MB8 and MB16. The first set corresponded to convolutional kernels of size 3 × 2 × 2n_c × 32, 1 × 1 × 32 × 32, 5 × 4 × 32 × R −1 for ${\text{w}}_1^C$, ${\text{w}}_2^C$, ${\text{w}}_3^C$ respectively. The second set led to kernels of size 3 × 2 × 2n_c × 32, 1 × 1 × 32 × 128, 5 × 4 × 128 × R − 1 for ${\text{w}}_1^C$, ${\text{w}}_2^C$, ${\text{w}}_3^C$ respectively. Figure 4 shows the reconstruction results using these two networks. No apparent visual difference between these two results were observed. Thus, the first set of parameters were used for the remainder of the experiments in order to reduce running time.

Fig. 4.

Reconstruction results using the two networks with the optimal set of parameters as determined by extensive search of the parameter space, a) The reconstruction results for the first set of parameters. b) The reconstruction results for the second set of parameters.

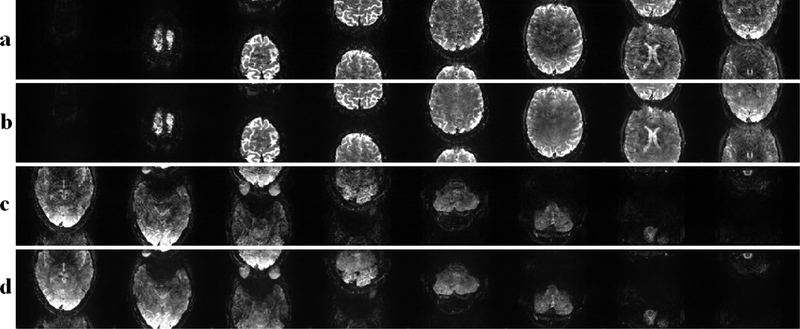
Figure 5 depicts the results of the MB16 fMRI reconstruction. Figure 5a and c show the results of the conventional RO-SENSE-GRAPPA reconstruction for the first and second set of eight slices respectively. These reconstructions exhibit noise amplification at this high acceleration rate. These noise artifacts are visibly reduced using the proposed SMS/MB RAKI approach, as shown in Figure 5b and d for the same sets of slices, respectively.

Fig. 5.

MB16 reconstruction results. a) Slice 1 to 8 using RO-SENSE-GRAPPA, b) Slice 1 to 8 using SMS/MB RAKI. c) Slice 9 to 16 using RO-SENSE-GRAPPA. d) Slice 9 to 16 using SMS/MB RAKI.

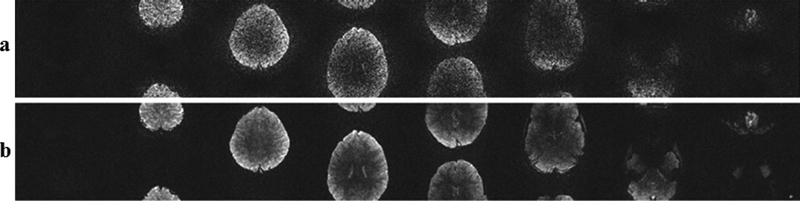
Figure 6 shows the results of noise sensitivity for an MB8 reconstruction, when noise is retrospectively added to the acquired data to simulate a low-SNR acquisition. The reconstruction noise in RO-SENSE-GRAPPA reconstruction scales with the increased input noise, rendering these images unusable. The SMS/MB RAKI approach exhibits higher robustness to input noise, enabling the reconstruction of these eight slices from low-SNR k-space data.

Fig. 6.

Noise sensitivity test using MB8 data using a) RO-SENSE-GRAPPA, b)SMS/MB RAKI reconstructions.

IV. Conclusion

In this paper we extended the subject-specific CNN interpolation of the RAKI reconstruction to SMS/MB imaging. Parameter selection for the CNN was highlighted in this application due to the availability of higher resolution calibration data. SMS/MB RAKI provided improved noise robustness and reconstruction quality at high SMS/MB rates compared to a conventional linear reconstruction approach.