Subject-Specific Convolutional Neural Networks for Accelerated Magnetic Resonance Imaging

Abstract

Magnetic Resonance Imaging (MRI) is one of the leading modalities for medical imaging, providing excellent soft-tissue contrast without exposure to ionizing radiation. Despite continuing advances in MRI, long scan times remain a major limitation in clinical applications. Parallel imaging is a technique for scan time acceleration in MRI, which utilizes the spatial variations in the reception profiles of receiver coil arrays to reconstruct images from undersampled Fourier space, i.e. k-space. One of the most commonly used parallel imaging techniques employs interpolation of missing k-space information by using linear shift-invariant convolutional kernels. These kernels are trained on a limited amount of autocalibration signal (ACS) for each scan. We propose a novel method for parallel imaging, Robust Artificial-neural-networks for k-space Interpolation (RAKI), which uses scan-specific convolutional neural networks (CNNs) to perform improved k-space interpolation. Three-layer CNNs are trained using only scan-specific ACS data, alleviating the need for large training databases. The proposed method was tested in ultra-high resolution brain MRI and quantitative cardiac MRI, acquired with various acceleration rates. Improved noise resilience as compared to existing parallel imaging methods was observed for high acceleration rates or in the presence of low signal-to-noise ratio (SNR). Furthermore, RAKI successfully reconstructed images for quantitative cardiac MRI, even when using the same CNN across images with varying contrasts. These results indicate that RAKI achieves improved noise performance without overfitting to specific image contents, and offers great promise for improved acceleration in a wide range of MRI applications.

I. INTRODUCTION

Even with significant advances over the past three decades, the acquisition time in magnetic resonance imaging (MRI) remains long compared to other medical imaging modalities. This often necessitates trade-offs between image resolution and SNR in clinical MRI. Several methods have been proposed to reduce the scan time in MRI, including partial Fourier imaging [1], parallel imaging [2]–[4] and compressed sensing [5], [6]. Parallel imaging techniques are the current clinical standard for accelerated MRI. They utilize the variations in the local reception profile of sensors (or receiver coils) to reduce scan time [2]. These reception profiles (or coil sensitivities) are mapped from calibration data, acquired at the beginning of each scan on a subject-specific basis [3], [4]. They are then used in a linear reconstruction framework to reconstruct undersampled MRI datasets, where the number of receiver coils is greater than the undersampling factor.

Following the overwhelming success of deep learning in multiple applications, e.g. [7]–[11], machine learning (ML) techniques have recently gathered interest in the MRI community. ML has been proposed as a possible means to improve reconstruction quality in MRI, by providing advanced regularizers for non-linear reconstruction [12]–[16]. So far, the MRI reconstruction community has focused on generating such regularizers by training on large amounts of datasets showing initial promise for improved reconstruction quality [12]–[16]. However, these methods require large databases of MR images for rigorous training, and do not exhibit any adaptation in a subject-specific manner. On the other hand, the recent push for precision medicine suggests that the medical community considers taking individual variability into account as generally favorable for diagnosis [17].

In this work, we introduce a reconstruction method, called Robust Artificial-neural-networks for k-space Interpolation (RAKI), where convolutional neural networks (CNNs) are trained on a small amount of subject-specific calibration data and utilized for reconstructing undersampled MRI acquisitions. The method is studied in brain and cardiac imaging applications in terms of improvement in reconstruction quality, noise resilience, and robustness to contrast variations.

II. METHODS

A. Multi-Coil MRI Acquisition and Reconstruction

MRI signal is generated from the hydrogen atoms in a tissue [18]. A strong magnetic field is used to create net magnetization, which is perturbed using a radio-frequency excitation to create a transverse magnetization component, which is measured at a receiver coil. Spatial information is encoded into this signal, using spatially-varying magnetic fields on top of the main magnetic field. With this spatial information, the measured MRI signal can be shown to correspond to a Fourier transform of the underlying image. The final sampled measurements are in the Fourier domain, referred to as the k-space, which is the Fourier transform of the desired MR image [18].

Modern MRI scanners come equipped with a number of sensors for signal reception, referred to as receiver coil-arrays [19]. Each of these coils see a limited part of the field-of-view, where the image in coil i, denoted by m_i is the desired image, m modulated pixel-wise with the diagonal entries of a coil sensitivity profile, C_i [3]. Thus, at each of the receiver coils, the received k-space signal is given as

$$s_i=F_{\Omega }{C}_{i}m+n,$$

where F_Ω is a partial Fourier sampling operator, sampling locations Ω, and n is measurement noise.

Parallel imaging techniques are linear algorithms for reconstructing such datasets. The two most commonly used parallel imaging approaches are sensitivity encoding (SENSE) [3] and generalized autocalibrating partially parallel acquisition (GRAPPA) [4]. The former is formulated as a least-squares problem for estimating, m from ${\left\{s_i\right\}}_{i=1}^{n_c}$, where n_c is the number of coils. This requires estimation of coil sensitivities, C_i, which is performed using low-resolution images of the anatomy of interest on a subject-specific basis [3]. GRAPPA reconstruction essentially formulates this image-domain multiplication approach with C_i in the Fourier domain, i.e. k-space, as a convolution. It uses linear interpolation in k-space with shift-invariant convolutional kernels to estimate missing k-space data from acquired ones. The interpolation is performed across all coils, in essence, capturing the geometry of the receiver coil array. Similar to SENSE, these convolutional kernels are determined from a small amount of calibration data, referred to as autocalibration signal (ACS) [4].

As evident from the formulation, in theory, parallel imaging allows for acceleration rates up to the number of receiver coils (e.g., 16 to 32). However, in practice, due to dependencies between coil coverage and noise amplification, the acceleration rates are limited to ≤4.

B. Proposed Reconstruction

Our proposed reconstruction aims to utilize CNNs for non-linear estimation of missing k-space data, in contrast to the linear convolutional estimation in existing methods. There are several reasons for using a non-linear estimation procedure. First, there is noise present in the ACS data used for calibration. In the GRAPPA reconstruction, the linear convolutional kernels are estimated from the ACS data using a mean square error (MSE) loss function, via linear least squares [4]. However, due to the noise in ACS data, both the dependent and independent variables are noisy, which was shown to lead to a bias in the convolutional kernels [20]. Furthermore, the bias was shown to induce non-linearity in the estimation of k-space, which can be mitigated by using non-linear kernels [20]. Second, the linear convolutional kernels in GRAPPA have very few degrees of freedom, due to small kernel sizes. Thus, their ability to approximate the underlying reconstruction operator for the multi-coil MRI acquisition is limited. Hence, use of a non-linear approximation with similarly few degrees of freedom may improve this approximation to the underlying reconstruction operator.

In the proposed RAKI method, the CNNs for estimating the missing k-space method are trained from the ACS data. We next describe the specifics of our method. The k-space data in MRI is complex-valued, thus prior to any processing these are mapped to the real-field, effectively increasing the total number of channels to 2n_c, where n_c is the number of physical receiver coils in the receiver coil-array for the MRI acquisition. The input to the CNN is the undersampled k-space, where the unacquired positions are filled with zeros. Note in parallel imaging, the undersampling is performed by acquiring every R^th line in the phase encoding (i.e., the so-called k_y) direction for an acceleration rate of R.

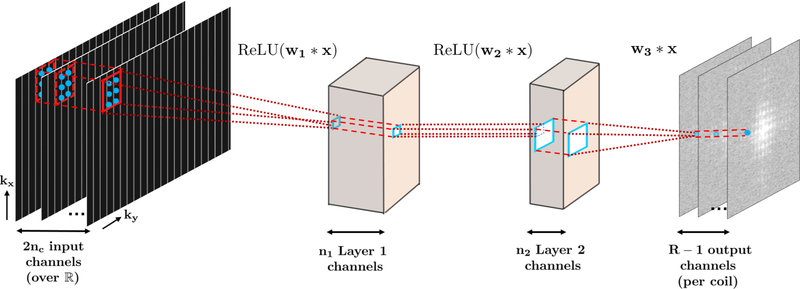
A three-layer CNN was implemented to reconstruct the missing lines in each receiver coil, as depicted in Figure 1. The first and second layers of the network perform convolutions, followed by a rectified linear unit, defined as ReLU(x) = max(x, 0), i.e., F_i(x) = ReLU(w_i * x), for i = 1, 2, thus processing the acquired k-space lines non-linearly. This processing performs a combination of coil compression [21] and virtual channel creation [20], which are techniques that have been explored for improved reconstruction in MRI. The last layer performs only a convolution, with no non-linear operation, i.e. F₃(x) = w₃ * x, generating the final estimate. In our implementation, w₁ were taken to be of size 5 × 2 × 2n_c × 32, w₂ had size 1 ×1 × 32 × 8, and w₃ were of size 3 × 2 × 8× R − 1, i.e. all the missing k-space lines inone output coil were estimated concurrently.

Fig. 1.

The three-layer CNN used in this study. The input to the CNN is the undersampled k-space across all the n_c receiver coils, embedded over the real field, leading to 2n_c input channels. The first two layers apply convolutions and ReLU, while the last layer only applies convolutions and generates the unacquired k-space lines for a given coil as output.

We note that the proposed CNN does not contain a bias term, which is typically used in other applications. The inclusion of a bias term, however, sensitizes the network to linear scalings of the input k-space. Such linear scalings may happen in MRI acquisitions due to changes in receiver gain, or due to inherent differences in signal among acquisitions that are acquired in the same position, but with underlying contrast changes, as utilized in quantitative MRI. Thus, the CNN was designed to capture dependencies among receiver coils due to their physical positioning and coverage for a specific scan, and not the underlying signal characteristics, which may be affected by changes in the acquisition contrast.

A CNN was trained for each of the receiver coils. In other words, all the missing lines in coil j were reconstructed with a 3-layer CNN, using all the acquired lines among all the coils, j = 1, …, n_c. Note this is the standard practice, in linear reconstruction approaches as GRAPPA [4], and was implemented in the proposed RAKI method for a fair comparison. To process the acquired zero-filled k-space, kernel dilation of R was was utilized in the undersampled k_y dimension [22]. The CNNs were trained on the scan-specific ACS calibration data, using an MSE loss function. Gradient descent with momentum was implemented with momentum rate, μ = 0.9. Due to the limited nature of scan-specific ACS data, batch gradient descent was used. Thus one epoch corresponded to one iteration. The number of iterations was limited to 1000. The input k-space was scaled to have a maximum value of 0.015, set arbitrarily, and the corresponding learning rates were η = 100 for the first layer, and η = 10 for the last two layers. Slower learning rates for later layers have been reported previously in image processing applications [10], [11]. The implementation for CNN training and the subsequent reconstruction was implemented in Matlab, with convolution and backpropagation operation implemented based on the MatConvNet toolbox [23].

C. In Vivo Imaging Experiments

Brain MRI was performed on a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) scanner with a 32-channel receiver head coil-array. Structural, T₁-weighted images were acquired with a 3D-MPRAGE [24] sequence in a healthy subject at a resolution of 0.7 × 0.7 × 0.7 mm³ and a 3D array size of 320 × 320 × 256. 40 k_y lines of ACS data were acquired and two separate acquisitions were performed with parallel imaging acceleration factors of R = 2 and 5. A two-dimensional slice was extracted from the three-dimensional data set and was processed for the rest of the study. Acceleration rates of 4 and 6 were generated by retrospectively undersampling the R = 2 data set. GRAPPA and RAKI reconstructions for acceleration rates of 2, 4, 5, 6 were examined to test the robustness of RAKI at very high resolutions, in terms of its noise resilience for a high-resolution low-SNR regime, and to identify potential blurring artifacts.

To further test the robustness of the proposed method to contrast changes in the acquired data, cardiac imaging was performed with a 30-channel receiver body coil-array on the same system. Quantitative myocardial (i.e. heart muscle) T₁ mapping was acquired using a SAPPHIRE sequence [25] in a mid-ventricular short-axis slice on four healthy volunteers. In quantitative myocardial T₁ mapping, multiple images of the same anatomy are acquired in a single breath-hold with electrocardiogram triggering to minimize effects of respiratory and cardiac motions [26]. These multiple images are designed to have different T₁ weightings, where T₁ is a tissue-dependent parameter which reflects the rate at which the system recovers to thermal equilibrium. Using these images with different T₁ weightings and the knowledge of how these weightings were varied, a parameter estimation is performed at every pixel to generate a pixel-wise map of the underlying quantitative T₁ values [26]. Such quantification has advantages for robustness across imaging sites and detection of diffuse diseases [27]. In the SAPPHIRE sequence, 11 images with different T₁ weightings were acquired with a balanced steady-state free precession image acquisition at a resolution of 1.1 × 1.1 mm², a matrix size of 272 × 272 and slice thickness of 6 mm. In-plane acceleration of R = 5 was used. A separate calibration scan with a single T₁ weighting was acquired, containing 64 ACS k_y lines for training purposes.

In order to assess the robustness of RAKI across different contrasts, underlying the CNNs were estimated using ACS data from only one T₁ weighted image. Correspondingly, the GRAPPA kernels were calibrated from one data set only as well, noting that the robustness of GRAPPA across different contrasts is well-established [28], [29]. All 11 images were reconstructed with these CNNs or linear convolutional kernels, despite the varying underlying T₁-weighted contrast. To measure the performance of the proposed reconstructions, myocardial T₁ times were quantified, since this is the relevant biomarker for evaluating numerous cardiac diseases [27]. Regions-of-interest (ROIs) were manually drawn in the myocardium. As the myocardial T₁ value is expected to be homogenous in a healthy subject, the mean value in the ROI was recorded as an estimate of the underlying T₁ value, capturing accuracy; while the standard deviation in the ROI was recorded as spatial variability, a surrogate for precision and noise performance [26]. This T₁ analysis enables a quantitative comparison between the proposed RAKI method and existing methods. If the proposed RAKI method is invariant to contrast changes, it is expected to produce a similar estimated T₁ value to GRAPPA reconstruction on the same dataset. Similarly, if RAKI has better noise performance, it should have lower spatial variability than GRAPPA.

III. RESULTS

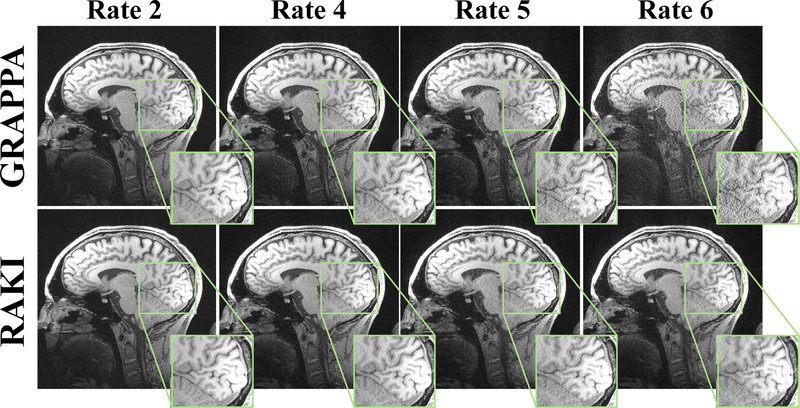
Figure 2 shows reconstructions of the high resolution brain image at acceleration rates 2, 4, 5 and 6, reconstructed with both conventional GRAPPA and the proposed RAKI technique. For lower accelerations up to rate 4, both methods provide artifact-free image reconstructions of visually high quality. However, at rate 5, RAKI performs noticeably better than GRAPPA in terms of noise resilience, without inducing detrimental reconstruction artifacts or blurring. The same trend can observed at rate 6, albeit at a generally higher artifact level, with slight residual artifacts for both techniques.

Fig. 2.

A 2D slice of a high-resolution brain scan, acquired at 0.7 × 0.7 × 0.7 mm³ resolution. The scans were acquired with R = 2 and R = 5, and undersampling rates R = 4 and R = 6 were retrospectively generated from the R = 2 acquisition. At lower rates, the clinically-utilized linear convolutional approach, GRAPPA [4], and the proposed CNN-based approach, RAKI perform similarly. At R = 5, RAKI performs visibly better than GRAPPA in terms of noise resilience, without reconstruction artifacts or blurring. The same trend is observed at R = 6, albeit at a generally higher artifact level for both reconstructions.

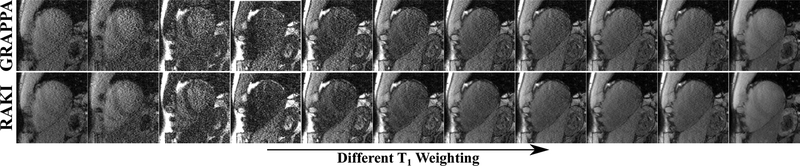
The series of T₁ weighted baseline images reconstructed with RAKI and GRAPPA using only a single ACS for calibration/training are shown in Figure 3. For this high-resolution acquisitions, RAKI yields visually improved image quality across all the baseline images, reducing noise artifacts, without compromising sharpness of tissue borders. Furthermore, the proposed RAKI method successfully maintains quantitative accuracy of the technique with negligible difference in the quantified T₁ time (< 1.5% difference). Additionally, the spatial variability of myocardial T₁ times, a surrogate for precision, is improved by 48% across all subjects, when using RAKI compared with GRAPPA.

Fig. 3.

All 11 T₁ weighted images acquired for quantitative myocardial T₁ mapping on a healthy volunteer, showing visual improvement in noise performance using the proposed RAKI method. The acquisition resolution was 1.1 × 1.1 × 6 mm³, with undersampling rate R = 5. The linear convolutional kernels for GRAPPA and the CNNs for RAKI were trained using ACS data from one T₁ weighting, in order to test the robustness to contrast variations. Quantitative analysis of T₁ maps showed no change of accuracy between two methods, showing the robustness of the proposed RAKI method to contrast changes. However, the precision of T₁ maps were improved by 48% across 4 subjects, using RAKI versus GRAPPA, which is in agreement with the visual improvement in noise performance.

IV. DISCUSSION

We developed and evaluated a subject-specific machine learning technique to perform noise-resilient reconstruction of undersampled MRI data, allowing for improved image quality at higher acceleration rates, enabling shorter scan times. Our approach is based on training a CNN from limited scan-specific ACS calibration data in order to capture information about the receiver coil-array, which is used for non-linear estimation of unacquired k-space lines from acquired ones. Thus, our focus on using scan-specific ACS data deviates from the trend in machine learning applications in MRI that employ massive training databases [12]–[16]. Instead it requires a limited amount of training data, providing adaptivity for each data set. Brain and cardiac imaging data show increased noise performance at higher acceleration rates, as well as robustness to variations in the image contrast between the ACS data and the final image.

Machine learning is increasingly being applied to the problem of MRI reconstruction [12]–[16], stemming from the overwhelming success of deep learning in other areas of image processing, e.g. [7]–[11]. However, these efforts have focused on training reconstruction algorithms on large amounts of datasets so far, which have been used to generate advanced regularization approaches for MR images [12]–[16]. In contrast, our RAKI approach considers the problem of estimation in k-space, instead of regularization in image domain, allowing the training to performed on subject-specific ACS data of a single image.

The use of non-linearity in estimation using CNNs was shown to improve the noise performance compared to the clinically-utilized linear convolutional approach, GRAPPA [4]. Several other studies had proposed the use of non-linearity to improve GRAPPA. These include using non-linear kernel methods with pre-defined feature spaces on which linear estimation is performed [20], as well as use of compressed sensing to regularize the GRAPPA coefficients [30]. However, our approach is inherently different, as it does not make any assumptions about either the properties of k-space or image compressibility, and uses CNNs to learn a non-linear estimation function without modeling assumptions.

In contrast to many existing deep learning applications, we have chosen not to use bias terms in our CNNs. The main rationale for this decision was that the additive nature of the bias terms results in scaling dependence on the ℓ_∞ norm of the k-space. For MRI applications, such as T₁ mapping, where the underlying contrast of the images, and thus the SNR among corresponding k-spaces changes significantly [26], but where the CNNs are trained on only one set of contrast weighting, the inclusion of bias terms becomes challenging. However, further work is required on the utility of biases in other MRI applications or with new pre-processing steps to re-scale the k-space data across contrast changes.

A further design choice was to train separate CNNs to reconstruct all receiver coil channels independently, even though the reconstructions used the available data across all coils as input. This was done to provide a fair comparison to the existing linear k-space interpolation approach, GRAPPA [4]. However, in principle, the CNN can be trained to simultaneously reconstruct all the missing k-space lines in all n_c coils, using the acquired data across all coils as input. While this may necessitate deeper networks and larger kernel sizes, it may improve reconstruction quality by enabling interactions across coils, which will be explored in future work. Furthermore, due to the limited ACS data, only a network with three layers was studied. Networks with deeper structure may suffer from insufficient training due to the size of the ACS data. However, more complex CNNs with higher amounts of scan-specific ACS data may facilitate advanced reconstructions, such as acquisitions with ultra-high channel counts, simultaneous multi-slice imaging or temporal image series.

In summary, the proposed RAKI method provides novel means to utilize the versatility of model-free function approximation with CNNs in parallel imaging MRI reconstruction. The proposed scheme is fully compatible with present clinically-used acquisition techniques. Our initial data indicates improved noise resilience, potentially enabling higher rates of scan time acceleration. These factors bear promise for clinical integration in numerous applications, ultimately alleviating the problem of long scan-times in MRI, for the benefit of patient comfort and health-care costs.