FULLY AUTOMATIC SEGMENTATION OF THE RIGHT VENTRICLE VIA MULTI-TASK DEEP NEURAL NETWORKS

Abstract

Segmentation of ventricles from cardiac magnetic resonance (MR) images is a key step to obtaining clinical parameters useful for prognosis of cardiac pathologies. To improve upon the performance of existing fully convolutional network (FCN) based automatic right ventricle (RV) segmentation approaches, a multi-task deep neural network (DNN) architecture is proposed. The multi-task model can employ any FCN as a building block, allows for leveraging shared features between different tasks, and can be efficiently trained end-to-end. Specifically, a multi-task U-net is developed and implemented using the Tensorflow framework. Numerical tests on real datasets showcase the merits of the proposed approach and in particular its ability to offer improved segmentation performance for small-size RVs.

1. INTRODUCTION

The clinical relevance of the RV in cardiovascular diseases such as cardiomyopathy is nowadays widely accepted [1]. To assess RV function, MR imaging constitutes a rather powerful tool [2]. Here we will focus on estimating the endocardial contours of the RV on short-axis cardiac cine MR images, a problem referred to as RV segmentation. Once these contours are estimated, several clinical parameters such as the end-diastolic volume, end-systolic volume, and as a result the RV ejection fraction, can be obtained [1]; note that the latter is considered to be a prognostic indicator in cardiopulmonary disorders [3].

Typically, RV segmentation is performed by medical professionals, requiring approximately 15 minutes for a single subject, while also being susceptible to inter and intraoperator variability [2, 4]. The development of automatic RV segmentation methods, such as the one examined in this work, is therefore well motivated.

A number of deep learning based approaches have been proposed in this context. In [5], a three step approach was developed. In particular, the center of the RV is first estimated using a convolutional neural network (CNN), followed by initial estimates of the contours using two stacked auto-encoders (one for large and one for small-sized contours); a deformable model, then, yields the final contour. In contrast to the complex pipeline in [5], an RV segmentation approach based on a FCN that is trained end-to-end has been proposed in [6]. Finally, several variants of FCN-based approaches have been recently used for right ventricle segmentation; see for example the 3D [7], multi-class [8], and times-series [9] FCN models that were recently devised for the MICCAI’17 automated cardiac diagnosis challenge.

All the aforementioned FCN-based methods employ a single model for all the training examples. It has been observed, however, that their empirical segmentation performance tends to be suboptimal for inputs with small-size RVs, see e.g. [6, Fig. 4]. To boost the segmentation accuracy, [5] divided the training data into two parts based on the area of the RVs, and trained two separate neural networks for small-and large-size RVs, respectively. While this can lead to improved performance, the separated training strategy suffers from three inherent inefficiencies. First, it is hard to decide whether RVs are large or small in an automated fashion in the test phase. Second, splitting the training data reduces the number of training examples available for each neural network while also rendering it impossible to leverage the common features shared between large and small RV images. Third, training two models is time consuming.

Fig. 4:

A sample image from the validation dataset with relatively small-size RV.

To overcome the aforementioned limitations, a multi-task DNN for automated RV segmentation is put forth in this work. The novel model merits a shared CNN module that extracts features for three different tasks, namely classifying whether the RV is small or large and generating segmentation masks for small and large RVs. Furthermore, the segmentation header for the small-size RV examples works with cropped CNN features. This cropping strategy increases the proportion of the image area covered by the RV, and as it will become evident, it yields markedly improved segmentation performance for small-size RVs. Intuitively, our multi-task approach can be viewed as a scheme for enhancing the segmentation accuracy for small objects by zooming in them for a closer look. Although our multi-task approach works with any FCN model, a multi-task U-net is used in this work.

The performance of the developed multi-task U-net was evaluated on the MICCAI’12 RV segmentation challenge (RVSC) dataset [2]. Numerical tests showcase the improvement in segmentation accuracy achieved by the multi-task U-net over its single-task U-net counterpart. With only minimal parameter tuning, the multi-task U-net achieves competitive segmentation accuracy on the MICCAI ‘12 RVSC test sets.

To the best of our knowledge, this is the first application of multi-task DNNs to the problem of RV segmentation. Nonetheless, multi-task learning has been employed in different tasks, see e.g., faster region-based CNN (R-CNN) for object detection [10], mask R-CNN for instance segmentation [11], and multi-task DNNs for natural language processing [12].

Notation.

Lower- (upper-) case boldface letters denote column vectors (matrices). The symbol ^⊤ is reserved for transposition. Finally, the operator ln(x) returns the natural logarithm of x, whereas exp(x) denotes Euler’s number to the power of x.

2. METHODOLOGY

Given N training pairs ${\left\{\left(X_n,Y_n\right)\right\}}_{n=1}^N$ of input matrices $X_n\in {ℝ}^{d_1\times d_2}$ and the corresponding matrix outputs $Y_n\in {\{0,1\}}^{d_1\times d_2}$, our goal is to estimate the function f(X) so that a certain loss $\frac{1}{N}{\sum }_{n=1}^N\mathcal{l}\left(f\left(X_n\right),Y_n\right)$ is minimized. In the context of RV segmentation the given inputs {X_n} are a series of cardiac MR images, whereas the outputs are manually labeled images whose pixel values are binary. Regarding the latter, without loss of generality, assume that pixels within the endocardium of the RV are labeled 1, while the rest are labeled 0.

2.1. U-net

Since the relationships between X_n and Y_n are complex, f(X) is typically assumed to be a nonlinear function. To render nonlinear estimators tractable, kernel [13] or DNN-based approaches are commonly relied upon. More specifically, FCN-based approaches [14] are proving highly successful in image segmentation tasks. Among the available variants of 2D FCNs, the so-termed “U-net” has achieved remarkable experimental results in medical image segmentation [15]. In this subsection, a U-net tailored for RV segmentation is devised. Compared to the original U-net in [15], the devised U-net features less layers and as a result, much fewer parameters. This modification is well motivated since the number of training examples for the RV segmentation task is limited.

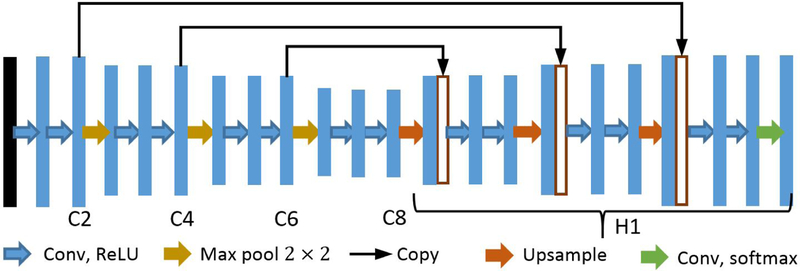
The architecture of our U-net is shown in Fig. 1, where C2, C4, C6, and C8 denote the feature maps obtained from the 2nd, 4th, 6th, and 8th convolution stages, respectively. In particular, the input image is first passed through 7 × 7 convolutions followed by rectified linear units (ReLUs). The subsequent downsampling path consists of repeated application of 3 × 3 convolutions, followed by ReLUs and max pooling operations. The number of filters employed in the first to eighth convolution stage is 32, 32, 64, 64, 128, 128, 256, and 256, respectively. For all max pooling operations, the kernel size is set to 2 × 2 and the stride is fixed to be 2. As a result, the dimension of the features is halved after each max pooling operation.

Fig. 1:

Schematic representation of the employed U-net architecture. Each blue box represents a feature map, whereas while boxes denote copied feature maps. The arrows stand for the different operations.

Since the segmentation task entails pixel-wise classification, upsampling is necessary for obtaining an output that has the same dimensions as the input. Specifically, the expansive path, denoted by H1, starts with upsampling the feature map C8 (cf. Fig. 1) by a factor of 2 by repeating each row and column of the feature map twice. The upsampled features are then concatenated with a copy of C6. This concatenation turns out being beneficial as the lower level features contain more accurate localization information, which is important for improving segmentation accuracy. Repeated application of convolutions, ReLUs, upsampling, and concatenation operations follows the upsampling. In the final layer, the soft-max activation function is used, after a 1 × 1 convolution, in order to obtain a distribution over the number of classes for each pixel.

Our U-net was implemented and trained using the Tensorflow framework. Unfortunately, U-net architecture alone may not be sufficient for the challenging task of RV segmentation, especially in the case of small RVs in the short-axis stack, as it becomes evident in Fig. 4c; see also [6, Fig. 4]. Therefore, we complement this architecture with a multi-task approach.

2.2. The proposed multi-task DNN model

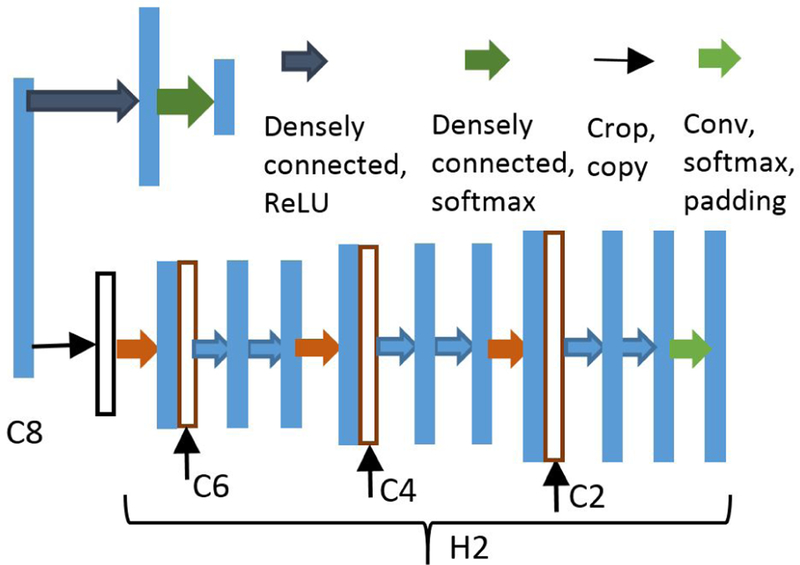
The success of transfer learning indicates that lower levels of CNNs can be viewed as feature extractors, where the obtained features can be used for different learning tasks [16]. Based on this observation, we will use the C8 features (cf. Fig. 1) for inferring whether the RV in the input is small-sized or not, in addition to using them for contour estimation. To that end, a classification header consisting of two densely connected layers is added on top of C8 as shown in Fig. 2.

Fig. 2:

Headers for classifying and segmenting small RVs.

Once we determine that the input has a small-size RV, we can crop the image to a smaller size in order to get rid of irrelevant information. Given that the RVs are always located around the center of the input, one can simply center crop the image rather than training an additional localization network as in [5]. To segment the small-size RVs, another expansive header denoted as H2 (cf. Fig. 2) is introduced, which has the same structure as the expansive header H1 in Fig. 1. The input to H2, however, is the cropped C8 (instead of the entire map) since we know that our region of interest will be of small size. In order to make the concatenation operation feasible, the features from C6, C4 and C2 must be cropped as well. Finally, the output of H2 is zero padded to ensure its spatial dimensions are the same as those of the inputs.

To summarize, our proposed multi-task DNN has three distinct headers that are responsible for classifying the size of RVs, segmenting the large-size RVs, and segmenting the small-size RVs, respectively. Our approach, therefore, features three outputs from a single model, which is trained end-to-end using the whole dataset. Although we use the U-net as a building block for the multi-task DNN, it is worth stressing that the multi-task DNN can also be built on other FCN models such as the one reported in [6].

2.3. Multi-task DNNs: training and testing

In this subsection, the loss functions for the employed headers will be detailed. Moreover, the joint training process, as well as the deployment phase, will be outlined.

To train the classification header, each training example needs to be labeled based on its RV contour size. To that end, the average area of all the segmentation masks is first computed as $\overline{\alpha }={\sum }_{n=1}^N{\alpha }_n$, where α_n denotes the area of the segmentation mask of the nth image. Letting c_n represent the classification label of the nth image, we define c_n := 1 for α_n ≥ 0.45ᾱ and 0 otherwise, where the constant 0.45 is selected empirically so that the number of small-size RVs is about half of the number of large-size RVs. With the labels ${\left\{c_n\right\}}_{n=1}^N$ obtained, the cross-entropy loss for the classification header is given by

$$E_0(w)=-\frac{1}{N}\sum _{n=1}^N\left[c_n\text{\hspace{0.17em}ln\hspace{0.17em}}{p}_n(1)+\left(1-c_n\right)\text{\hspace{0.17em}ln\hspace{0.17em}}{p}_n(0)\right]$$

where w collects all the weight variables in the DNN, and p_n = [p_n(0), p_n(1)]^⊤ is the vector output from the classification header for input X_n.

For the segmentation header H1, the cross-entropy loss is used for the output at each pixel (i, j), yielding the following per-example loss

$$\mathcal{l}\left(P_n^{(1)},Y_n\right):=-\frac{1}{d_1{d}_2}\sum _{i=1}^{d_1}\sum _{j=1}^{d_2}\left[Y_n(i,j)\text{\hspace{0.17em}ln\hspace{0.17em}}{P}_n^{(1)}(i,j,1)+\left(1-Y_n(i,j)\right)\text{\hspace{0.17em}ln\hspace{0.17em}}{P}_n^{(1)}(i,j,0)\right].$$

in which $P_n^{(1)}$ denotes the tensor output from header H1 for input X_n. Likewise, the per-example loss $\mathcal{l}\left(P_n^{(2)},Y_n\right)$ for header H2 is defined. Subsequently, the loss functions for headers H1 and H2 over all examples are given by

$$E_1(w):=\frac{1}{N}\sum _{n=1}^N\tau \left(c_n\right)\mathcal{l}\left(P_n^{(1)},Y_n\right),$$

$$E_2(w):=\frac{1}{N}\sum _{n=1}^N\left(1-\tau \left(c_n\right)\right)\mathcal{l}\left(P_n^{(2)},Y_n\right)$$

respectively, where τ(c_n) equals 1 when c_n = 1 and it is 0 otherwise.

In order to train the proposed model jointly (over w), we use a multi-task loss in the training process, which is given by

$$E(w)={\mathrm{\lambda }}_0{E}_0(w)+{\mathrm{\lambda }}_1{E}_1(w)+{\mathrm{\lambda }}_2{E}_2(w)$$

with λ₀, λ₁, and λ₂ denoting preselected non-negative weights for the objective functions. When setting λ₀ = λ₂ = 0 and ${\left\{c_n=1\right\}}_{n=1}^N$, training our multi-task model boils down to training its single-task U-net (cf. Fig. 1) counterpart. By minimizing E(w), the weight variables w can be learned.

Regarding the deployment phase, when a new datum arrives, the segmentation headers predict two masks. The output is taken as the mask corresponding to the class predicted by the classification header.

3. NUMERICAL TESTS

In this section the performance of the proposed multi-task DNN will be evaluated on the MICCAI’12 RVSC dataset [2]. The original dataset comprises images of two different sizes, that is, 256×216 and 216×256. For consistency, we rotate the latter ones so that all images have the same size (256 × 216). Subsequently, all images are center cropped to size 208×208. Feature map C8 is further cropped to half its size before being fed into H2. To avoid overfitting, dropout with rate 0.5 is used after C8. No additional preprocessing or data augmentation techniques have been used. In order to obtain a single contour, only the largest connected component is kept in the output. No further post processing is performed. The hyper-parameters λ₀, λ₁, and λ₂ are selected as 1, 208, and 208, respectively.

The first experiment assesses the performance of the U-net and that of our multi-task DNN using the training dataset only. To that end, the provided dataset is randomly shuffled and split into 70/30% training/validation subsets. Both the U-net and the multi-task DNN model are implemented leveraging the Tensorflow framework [17] and they are trained using the so-termed “Adam” optimizer for 100 epochs with a learning rate of 0.0001. The performance of the two models is tested on the validation set after running each epoch. Among the 100 runs, the highest mean Dice scores achieved for the U-net and the multi-task DNN are 0.859 and 0.872, respectively. The improvements in the Dice coefficient showcase the merits of our multi-task DNN. The original input image, the ground truth mask as well as the ones predicted by the U-net and the multi-task DNN, for two sample examples in the validation set, are shown in Figs. 3 and 4, where a white square signifies a pixel within the RV. Notice that both models work well for the input in Fig. 3, which has a large-size RV. However, when the size of the RV is small, as shown in Fig. 4a, the multi-task DNN still yields rather accurate segmentation while its single task counterpart makes totally wrong predictions (cf. Figs. 4c, 4d).

Fig. 3:

A sample image from the validation dataset with relatively large-size RV.

In the second experiment, the multi-task DNN is trained using the whole training dataset for 100 epochs. The RV endocardial contours for sets test1 (262 examples) and test2 (252 examples), predicted by the multi-task DNN, were submitted to the challenge organizers for independent evaluation¹. The obtained mean Dice scores for the end diastolic/systolic (ED/ES) phases of set test1 and the corresponding phases of set test2 are 0.839/0.714 and 0.874/0.767, respectively. All the mean Dice scores achieved outperform the ones obtained from the DNN outputs in [5]. The mean Dice scores for sets test1 and test2 are 0.783 and 0.827, respectively. Importantly, the mean Dice score for the whole test set (0.805) corresponds to an (albeit limited) improvement over that achieved (0.80) by a carefully tuned FCN model in [6]. We also noticed some unpublished results on Github [18], which use the Dice coefficient instead of the negative cross-entropy as the training loss and obtain a mean Dice score of 0.82.

4. CONCLUSIONS

This paper dealt with automated segmentation of the endocardium of the RV. To improve the segmentation accuracy for small-size RVs, a multi-task DNN model was developed, that merits cropped inputs for small-size RVs, leverages the shared features between different tasks, and enjoys end-to-end training. Numerical tests using our multi-task U-net demonstrated the effectiveness of the novel approach.

Several improvements can be made to our multi-task DNN model. Recently developed regularization approaches, including batch and layer normalization, can be leveraged to further enhance our model. Incorporating the Dice coefficient loss, augmenting the training data, performing more careful layer parameter tuning, employing deeper models, and devising tailored post-processing stages in order to obtain improved performance constitute current research directions.