Detecting, categorizing, and correcting coverage anomalies of RNA-seq quantification

Summary

Due to incomplete reference transcriptomes, incomplete sequencing bias models, or other modeling defects, algorithms to infer isoform expression from RNA-seq sometimes do not accurately model expression. We present a computational method to detect instances where a quantification algorithm could not completely explain the input reads. Our approach identifies regions where the read coverage significantly deviates from expectation. We call these regions “expression anomalies”. We further present a method to attribute their cause to either the incompleteness of the reference transcriptome or algorithmic mistakes. We detect anomalies for 30 GEUVADIS and 16 Human Body Map samples. By correcting anomalies when possible, we reduce the number of falsely predicted instances of differential expression. Anomalies that cannot be corrected are suspected to indicate the existence of isoforms unannotated by the reference. We detected 88 common anomalies of this type and find that they tend to have a lower-than-expected coverage towards their 3′ ends.

Graphical Abstract

eTOC

Ma et al. develop an anomaly detection method to identify RNA transcripts with inconsistent read coverage. These anomalies indicate potential misquantifications due to algorithmic mistakes, missing transcripts, or errors in the input transcriptome. A method is given to categorize anomalies into potential causes. A major advantage of the anomaly detection method is that it does not depend on ground truth to suggest misquantified transcripts.

Introduction

While modern RNA-seq quantification algorithms (e.g. Li et al., 2009a, Jiang and Wong, 2009, Li and Dewey, 2011, LeGault and Dewey, 2013, Hensman et al., 2015, Bray et al., 2016, Patro et al., 2017) often achieve high accuracy, there remain situations where they give erroneous quantifications. For example, most quantifiers rely on a predetermined set of possible transcripts; missing or incorrect transcripts may cause incorrect quantifications. Read mapping mistakes and unexpected sequencing artifacts also lead to misquantifications. Incomplete sequencing bias models can mislead the inferred probability that the reads are generated by each transcript. Quantification algorithms themselves could introduce errors since their objectives cannot typically be guaranteed to be solved optimally in a practical amount of time.

When interpreting an expression experiment, particularly when a few specific genes are of interest, the possibility of misquantification must be taken into account before inferences are made from quantification estimations or differential gene expression predictions derived from those quantifications. Expression quantification is the basis for various analyses, such as differential gene expression (Costa-Silva et al., 2017), co-expression inference (van Dam et al., 2018), disease diagnosis, and various computational prediction tasks (e.g., Hoadley et al., 2014, Weinstein et al., 2013, Morán et al., 2012). Statistical techniques such as bootstrapping (Al Seesi et al., 2014) and Gibbs sampling (Li et al., 2009a, Turro et al., 2011, Glaus et al., 2012) can associate confidence intervals to expression estimates, but these techniques provide little insight into the causes of low confidence or misquantification and detect only a subset of misquantifications.

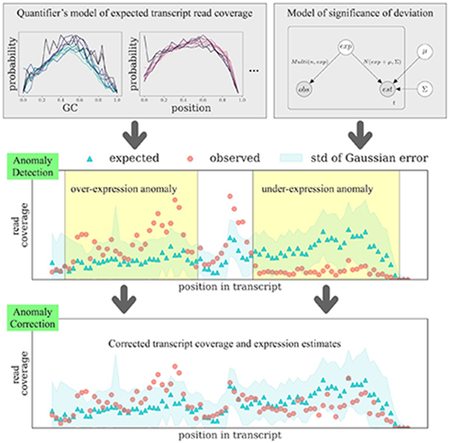
We introduce a method to identify potential misquantifications by designing an anomaly detection approach. This approach automatically identifies regions of known transcripts where the observed fragment coverage pattern significantly disagrees with what the coverage is expected to be. These regions indicate that something has gone “wrong” with the quantification for the transcripts containing the anomaly: perhaps a missing transcript, missing features in the probabilistic model, an algorithmic failure to optimize the likelihood, or some other unknown problem.

One advantage of this model-based anomaly detection approach is that it does not require any known ground truth to discover potential errors. The expected and observed coverages are intermediate values in the quantifier. The expected coverage is derived from a bias correction model that is used by modern RNA-seq quantification algorithms to model fragment generation biases with varied GC content, sequence, and position in the transcript (Love et al., 2016, Patro et al., 2017). In order to take into account other aspects of sequencing (such as read mapping quality, fragment length distribution), quantifiers sometimes cannot assign fragment in proportion to the expected coverage. By comparing the expected and observed coverages, anomaly detection identifies cases where it is not possible to satisfy the assumed model of fragment generation.

Another advantage of our proposed anomaly detection method is that it can provide more insight into what is causing the misquantification by identifying specific regions of specific transcripts for which the assumed theoretical model of read coverage does not match what is observed. These anomaly patterns can then be used to derive hypotheses about the underlying cause. For example, systematic lower-than-expected expression across an exon may indicate the existence of an unknown isoform that omits that exon. In this way, anomalies are more informative and suggestive of the cause of misquantifications than confidence intervals.

A third advantage of the approach is that the anomalies can be used to design better quantification algorithms. When there is a good reason to believe the transcriptome annotations and sequencing are of high quality, analyzing the cause of anomalies could reveal aspects of the sequencing experiment that may improve the quantification model, and may therefore be used to inspire improvements to, e.g., bias correction models or optimization approaches.

Anomaly detection has been applied to other areas in genomics where it has proved its usefulness. In genome assembly, anomaly detection has been used to detect low-confidence assembled sequences. Genome assembly algorithms seek a set of sequences that can concordantly generate the WGS reads and can be assumed to have near uniform coverage. The assembled sequences that do not fit this assumption can be hypothesized to contain errors and have low reliability (Phillippy et al., 2008). Similarly, anomaly detection in transcriptome assembly identifies unreliable transcript sequences (Smith-Unna et al., 2016). Low-confidence assembly detection has been used to analyze non-model organisms and incorporated into analysis workflows (Zimin et al., 2009, Cabau et al., 2017, Geniza and Jaiswal, 2017).

In RNA-seq expression quantification, some research has been conducted on identifying anomalous predictions. For example, Robert and Watson (2015) identify uncertainties in gene-level quantification that are due to gene sequence similarity. However, uncertainties do not necessarily indicate anomalous quantification. In addition, external information about sequence similarity provides limited insight on how to improve the quantification models. Soneson et al. (2019) use a compatibility score between observed and predicted junction coverage to indicate genes with inconsistent splicing junction supports. However, read coverage inconsistency does not only occur at splicing junctions. In addition, the cause of inconsistency is not categorized in their work.

In this work, we detect quantification anomalies using the disagreement between the modeled expected coverage and the observed fragment coverage distribution that is obtained after the quantifier has allocated fragments to transcripts. We do this by introducing an anomaly score to quantify regions of high disagreement. Specifically, we identify the contiguous regions that have the largest difference between these two distributions. This score has the natural biological meaning as the largest over- or under-expression (compared with what is expected) of any region within the transcript. We further begin to categorize the anomalies by their causes: adjustable anomalies are the ones possibly caused by quantification algorithm mistakes, and unadjustable anomalies are those possibly caused by transcripts missing from the reference transcriptome. This categorization is done by reassigning fragments using a linear programming (LP) procedure in an attempt to reduce the coverage inconsistency and correct the anomalies. Those anomalies that can be corrected this way are candidates for having been caused by algorithmic errors. The fragment reassignment procedure also generates an adjusted abundance estimation for the adjustable anomalies.

Because it includes a rich bias model, we focus on Salmon (Patro et al., 2017) as the base quantifier on which to build and test anomaly detection, and we term our implementation Salmon Anomaly Detection (SAD). However, the idea of anomaly detection can be applied to any method that generates an internal model of expected sequence coverage. To show this, we apply anomaly detection using another quantifier with a rich bias model, RSEM (Li and Dewey, 2011), and compare the detected anomalies with SAD.

Applied to 30 GEUVADIS (Lappalainen et al., 2013) samples and 16 Human Body Map (The Illumina Body Map 2.0 data, 2011) samples, SAD identifies both adjustable and unadjustable anomalies. For example, in one of the GEUVADIS sample, the gene BIRC3 has an adjustable anomaly in one of its transcripts, suggesting that a change in read assignment across isoforms should be made. An isoform of the gene UBE2Q1 is identified to be an unadjustable anomaly in the heart sample of Human Body Map dataset, and it is the only isoform in the gene to contain the ubiquitin-conjugating enzyme domain. Using the adjusted abundance estimates corresponding to the adjustable anomalies, the number of falsely detected differentially expressed transcripts is reduced by 2.29% – 3.84% in the GEUVADIS samples.

We observe a common pattern in the unadjustable anomalies that are shared among all GEUVADIS and Human Body Map samples: anomalous transcripts usually contain an under-expressed region at the 3′-most exon, suggesting an early transcription stop.

We further validate SAD’s predictions via simulation and show that both adjustable and unadjustable anomalies of SAD describe the corresponding types of misquantification with high precision. The read reassignment procedure of SAD generates an adjusted quantification that is closer to the simulated expression and reduces the mean absolute relative distance (ARD) by about 0.05 on the adjustable anomalies. Surprisingly, in simulation, unadjustable anomalies reflect the existence of unannotated isoforms using existing splice junctions with 3% – 35% higher precision compared with applying transcriptome assembly.

Results

Overview of anomaly detection and categorization

SAD defines transcripts with anomalous read coverage (Supplementary Figure S1) as those for which the observed coverage distribution contains a significantly over-expressed or under-expressed region compared to the expected coverage. Both the observed and the expected distribution are calculated by the Salmon (Patro et al., 2017) (or RSEM (Li and Dewey, 2011)) quantifier. The observed distribution is the weighted number of reads assigned to each position in the transcript as processed by the quantifier. The expected distribution estimated by the quantifier is the probability of generating a read at each position: Salmon’s bias model uses the surrounding GC content, the sequence k-mers, and the read position; RSEM models bias using the read position. The anomaly score can be confounded by either a low expression abundance or an estimation error of the expected distribution. To remove the confounding effect, we model the anomaly score probabilistically and use the empirical p-value to determine whether the observed difference is statistically significant and whether the transcript should be labeled as an anomaly.

To apply the anomaly detection and categorization approaches on other quantification software, the quantification software should output the assignment of each read and the sequencing bias model it learns. Different quantification software may output the read assignment and the biases in different format, and converting their output to vectorized observed and expected coverages that SAD can read is required. The Method section summarizes how to convert the output from Salmon and RSEM to the vector of observed coverage and expected coverage. For the other quantification software, a customized processing script may be needed for the format conversion.

SAD gives rise to two outputs: (1) a list of unadjustable anomalies and (2) the adjusted quantification for the adjustable anomalies. Assuming the expected coverage distributions are correct, the unadjustable anomalies are potentially caused by the incompleteness of reference transcriptome. Given a reference transcriptome or a reference splice junctions, we use “unannotated” to describe an item if it does not appear in the reference. The adjustable anomalies are likely caused by the error in the quantification probabilistic model or optimization algorithm.

Anomaly categorization is done by reassigning the reads across the isoforms using linear programming (LP) and checking whether the anomaly score becomes insignificant after the reassignment. Otherwise, it is labeled an adjustable anomaly. The LP also produces a new set of read assignments for the adjustable anomalies. An adjusted abundance estimation is constructed by combining the new read assignments of the transcripts with adjustable anomalies with the original read assignments of the other transcripts. This combined expression quantification is referred to as SAD-adjusted quantification. If the anomaly score remains significant after the reassignment, the anomaly is labeled an unadjustable anomaly.

Examples of detected anomalies

We provide some examples of the detected anomalies found by applying SAD to 30 GEUVADIS (Lappalainen et al., 2013) and 16 Human Body Map datasets (The Illumina Body Map 2.0 data, 2011). The 30 GEUVADIS samples are ones used in the work of Patro et al. (2017), in which 30 lymphoblastoid cell lines from the Toscani in Italia (TSI) population are sequenced at two different sequencing centers. The Human Body Map project data consists of 16 samples each from a different tissue, including adrenal, adipose, brain, breast, colon, heart, kidney, liver, lung, lymph, ovary, prostate, skeletal muscle, testes, thyroid, and white blood cells.

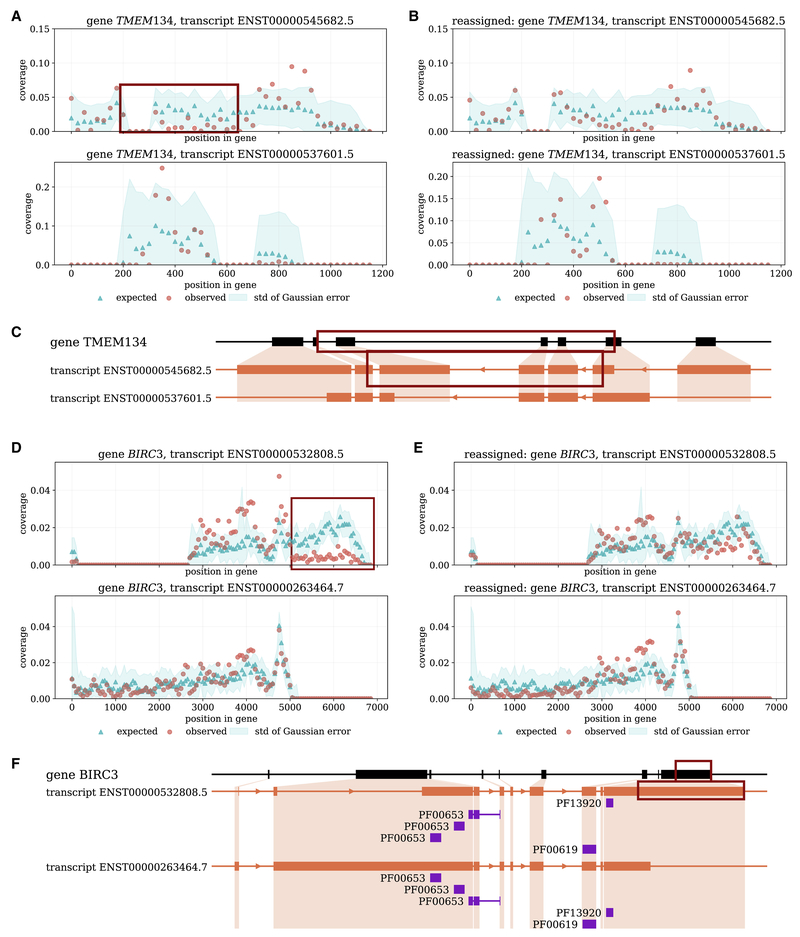
SAD identifies an adjustable anomaly in the gene TMEM134 in the kidney sample from the Human Body Map dataset. The TMEM134 gene encodes a trans-membrane protein that is associated with Parkinsons disease (Jansen et al., 2017). One isoform (ENST00000545682.5) of this gene has an under-expression anomaly after its first splicing junction (Figure 1A). See Supplementary Figure S2 for IGV visualization. This under-expression anomaly can be adjusted by reassigning reads to this isoform from another isoform, ENST00000537601.5 (Figure 1B). The expression estimates are changed according to the adjustment: before adjustment, the isoform with the under-expression anomaly has a 1.4 times larger expression than the other isoform, and after adjustment, the ratio of expression is enlarged to 9.0. The two isoforms are different from each other by two splicing junctions (Figure 1C). With the quantification more consistent with the read coverage of both isoforms, the analysis on the function and effect of the alternative splicing may benefit.

Figure 1: Examples of adjustable anomalies.

(A)–(C) The kidney sample of the Human Body Map dataset. (A) Red and blue points are the observed and expected coverage distribution before SAD adjustment. The expected distribution refers to the estimated expected distribution by the quantifier subtracted by the mean of Gaussian error. Each point is a 50 bp bin along the transcript. The anomaly transcript ENST00000545682.5 has an under-expression after its first splicing junction (top), marked by the red box. Another transcript is involved in the adjustment (bottom). (B) The distributions of the same pair of transcripts after SAD adjustment. (C) The protein domain annotation of the two transcripts. In the plot, for readability, exon regions are expanded and intron regions are reduced. The lengths are in proportion to the genomic lengths for exons and introns separately. The under-expression anomaly region is marked by the red boxes. (D)–(F) A sample from the GEUVADIS dataset (accession ERR188088). (D) The top transcript ENST00000532808.5 is identified to be an adjustable anomaly, and its under-expression anomaly region is marked by the red box. The bottom transcript is involved in the read reassignment. (E) The observed and expected distribution after SAD adjustment. (F) The protein domain annotation of the previous transcripts. The under-expression anomaly region is marked by the red boxed.

Another example of an adjustable anomaly is within the BIRC3 gene in one GEUVADIS sample. This gene is involved in apoptosis inhibition under certain conditions. The second half of the isoform ENST00000532808.5 is under-expressed under Salmon’s read assignment (Figure 1D). See Supplementary Figure S3 for IGV visualization. Reassigning the reads between this isoform and another isoform, ENST00000263464.7, removes the under-expression phenomenon (Figure 1E) and at the same time alters the expression level of both isoforms. The original expression abundances of the two isoforms were similar to each other, but after SAD adjustment the expression of ENST00000263464.7 is 3 times that of ENST00000532808.5. The two isoforms are different in their starting and ending positions but have the same set of internal exons. The protein domains between the two isoforms are the same according to Pfam (El-Gebali et al., 2018) annotations (Figure 1F) but the 5′ and 3′ UTR sequences are different.

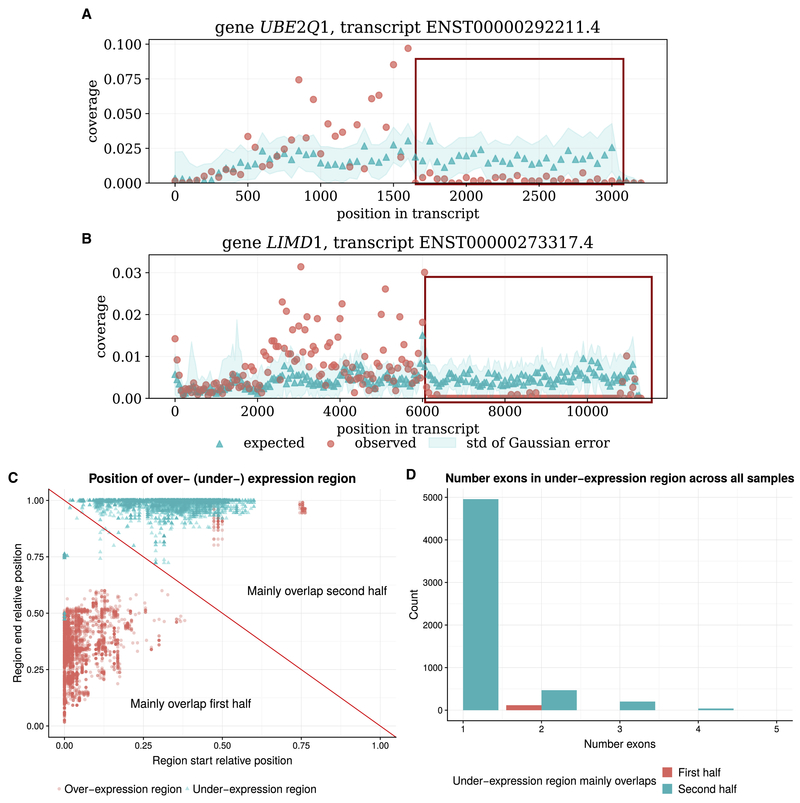
SAD also reveals unadjustable anomalies in isoforms that have a different set of protein domains from the other isoforms of the same gene. For example, gene UBE2Q1 and gene LIMD1 in the heart sample of the Human Body Map dataset contain unadjustable anomalies (Figure 2A–B, Supplementary Figure S4). In both genes, the protein domains in the anomalous isoform are different from those in the other annotated isoforms: ENST00000292211.4 of gene UBE2Q1 is the only annotated isoform that has ubiquitin-conjugating enzyme domain, and ENST00000273317.4 of gene LIMD1 contains three zinc-finger domains annotated by Pfam while the other isoforms only contain two or zero. The over-expressed regions of both genes contain the full set of protein domains, while parts of 3′ UTRs are barely expressed for both anomalies. The large unexpressed regions suggest the unadjustable anomalies are unlikely to be explained by the inaccuracy of the expected distribution, instead they imply the existence of unannotated isoforms. The Scallop transcript assembler (Shao and Kingsford, 2017) is able to assemble a unannotated sequence of LIMD1 without the under-expressed region, thus supporting this detected anomaly. Studies have shown that alternative cleavage can generate isoforms with various 3′ UTRs in some cells (Guvenek and Tian, 2018) and the length of the 3′ UTR is correlated with the transcript degradation rate (Zheng et al., 2018). The detected unadjustable anomalies may be an example of such alternative cleavage or lower degradation rate.

Figure 2: Examples and characteristics of unadjustable anomalies.

(A) An example of unadjustable anomaly of gene UBE2Q1 (B) An example of unadjustable anomaly of gene LIMD1. Both examples are found in the heart sample of the Human Body Map dataset. Red and blue points are the observed and expected coverage distribution of the anomaly transcripts, and the blue shade is the standard deviation of the expected distribution estimation. The red box indicates the under-expression anomaly region. For both genes, the transcript region near the 5′ end is over-expressed, and the region near the 3′ end is under-expressed. (C) The start and end proportion of the over-expressed and under-expressed region of common anomalous transcripts. The red diagonal line separates between anomalies of which the over- (under-) expression regions mainly overlaps with the first half (5′ half), and the second half (3′ half) of the transcripts. For most of the anomalies, the over-expressed region mainly overlaps with the first half of the anomalous transcript, and the under-expressed region mainly overlap with the second half of the anomalous transcript. (D) Histogram of the number of exons spanning the under-expressed region of the common anomalies. Y-axis is the count summed over all 46 samples. The under-expressed region usually only contain one or a partial exon.

Adjustable anomalies give an adjusted quantification that reduces false positive differential expression detections

The adjusted quantification of SAD reduces the number of false positive calls in detecting differentially expressed transcripts. Previously, Patro et al. (2017) showed that the 30 TSI samples from GEUVADIS dataset (Lappalainen et al., 2013) likely do not have differentially expressed transcripts, but quantification mistakes can lead to false positive differential expression (DE) predictions across sequencing center batches. They also showed that a more accurate quantification can reduce the number of false positive detections. We apply SAD to the same samples and compare the number of differentially expressed transcripts detected using Salmon’s original quantification and the SAD-adjusted quantification. There are 1938 – 3385 adjustable anomalies within each sample, each of which have SAD-adjusted expression estimates. The estimates for the rest of the transcripts remain the same as Salmon. Differential expression is inferred by DESeq2 (Love et al., 2014) on the transcript level. With Salmon expression estimates, 6088 – 13 555 transcripts out of 198 541 are detected to be differentially expressed across the two sequencing centers under various FDR thresholds. With SAD-adjusted quantification, the relative number of DE transcripts is reduced by 2.29% – 3.84% (Supplementary Table S1). This provides evidence that these anomalies are likely real misquantifications that are correctable using a different read reassignment procedure.

An isoform of gene HDAC2 and an isoform of gene NDUFA13 are two examples of transcripts that have decreased p-value of differential expression after SAD adjustment. Gene HDAC2 encodes proteins to form histone deacetylases complexes and is important in transcriptional regulation (O’Leary et al., 2015). One of its isoforms, ENST00000519065.5, is differentially expressed with an adjusted p-value of 0.0008 under Salmon quantification. SAD adjusts its expression by redistributing its reads to the other 16 transcripts of the gene, increasing the p-value of differential expression to 0.075 (Supplementary Figure S5C). With SAD-adjusted quantification, this isoform is not differentially expressed under a p-value threshold of 0.05 or 0.01. The gene NDUFA13 encodes a subunit of the mitochondrial electron transport chain (O’Leary et al., 2015). Over-expression or under-expression of the gene has been associated with multiple cancer types (Máximo et al., 2008). Transcript ENST00000428459.6 from this gene was significantly differentially expressed. After SAD reassigns reads from the other transcripts to it, the transcript is no longer differentially expressed (Supplementary Figure S5D).

Whether a transcript is detected to be differentially expressed under SAD-adjusted quantification may be influenced by that only some of the samples undergo the quantification adjustment of the transcript. In the case where the transcript abundances are similar within each condition and are adjusted only in a subset of samples, the within-condition variance may increase, the p-value of DE may increase, and the transcript is less likely to be detected as DE under a given FDR threshold. In this case, DE detection is more conservative by using SAD-adjusted quantification. When the conservation is preferred, especially when trying to avoid uncertain DE calls due to the inconsistencies between the observed and the expected coverage distribution, using SAD-adjusted quantification is helpful. Nevertheless, the influence of the partial adjustment is mild because the majority of the DE predictions under Salmon and SAD-adjusted quantification agree with each other. Many transcripts do not have an increased within-condition variance as what partial adjustment may induce (Supplementary Figure S5E). The switch from DE to not DE after SAD-adjustment is not purely caused by the increase of within-condition variance, but the decrease of across-condition expression differences is also a contributor as well (Supplementary Figure S5A–B). In the case where the abundances are adjusted for all samples in one condition but no samples in the other, it is not predetermined whether the DE detection is more conservative or more aggressive. Whether the transcript is detected as DE depends on whether the adjustment increases or decreases the expression difference between the conditions. Both increase and decrease of expression differences happen with similar frequency empirically (Supplementary Figure S5F).

Occasionally, there are are multiple optimal solutions to the likelihood function of quantification models and the quantifier will output only one of the optimal solutions. The multiple optima scenario is called the non-identifiability problem, and the transcripts with multiple optimal abundances are said to have non-identifiable abundances. However, the majority of anomalies detected by SAD do not suffer from the non-identifiability problem (Supplementary Figure S6B). Accordingly, the SAD-adjusted quantification is not another optimal solution to Salmon’s objective, but rather an assignment under a different model. The quantification improvement using SAD’s adjusted anomalies lies in the model of using the expected coverage to explain the observed coverage. See Method Section for how non-identifiable transcripts were detected.

Common unadjustable anomalies tend to have an under-expressed region in the 3′ exon

Applying SAD reveals 774–1288 unadjustable anomalies per sample on the 30 GEUVADIS samples, and 2029–8269 per sample for the 16 Human Body Map samples. Among the unadjustable anomalies, 88 of them are common in all samples in both datasets (see Supplementary Table S2 for the full list). The 88 common unadjustable anomalies span 22 chromosomes. The genes they belong to have various numbers of annotated isoforms ranging from 1 to 15. The common unadjustable anomalies generally follow the transcript length distribution of the commonly expressing transcripts (Supplementary Figure S6A).

For most of the common anomalies, the over-expressed regions tend to mainly overlap with the first half of the transcripts near the 5′ end (Figure 2C). Correspondingly, the under-expressed regions are usually located towards the second half of the transcripts near the 3′ end. The under-expressed anomaly regions usually only span one exon or a partial exon (Figure 2D). Assuming the bias model in Salmon estimates the expected distribution with reasonable accuracy, the unadjustable anomalies are likely to indicate the existence of unannotated transcripts. These unannotated transcripts will share the over-expressed region and exclude the under-expressed region compared to the anomalous transcripts. That is, they will have the same intron chain but different transcript ending locations.

About 40%–60% of the detected unadjustable anomalies have a corresponding unannotated isoform assembled by transcriptome assembly algorithms, specifically StringTie (Pertea et al., 2015) and Scallop (Shao and Kingsford, 2017) (Supplementary Figure S7A–B). (See Method Section for the details of running transcriptome assembly software.) An assembled isoform corresponds to a predicted unadjustable anomaly if the assembled isoform contains all the splicing junctions within the over-expressed region and excludes at least half of the under-expressed region. Meanwhile, the rest 40%–60% of the unadjustable anomalies do not have a corresponding isoform assembled by transcriptome assemblers. Assuming the expected coverage distribution is modeled correctly, these unadjustable anomalies are likely to indicate true unannotated isoforms that are not able to be detected by transcriptome assemblers. The sensitivity of assembling unannotated transcripts is usually low, which partially explains the difference between the existence of unannotated isoforms indicated by unadjustable anomalies and by transcriptome assembly methods.

While we hypothesize that the unadjustable anomalies are caused by the existence of unannotated transcripts, we cannot rule out the possibility that some of the unadjustable anomalies can be an artifact of inaccurate modeling of the expected coverages or an unsuitable assumption of the Gaussian error of the expected coverages. Neither is it clear whether the unannotated transcripts are natural, well-functioning isoforms, or non-functioning sequences due to errors in transcription, or alternative cleavage and polyadenylation that retain various lengths of UTR (Guvenek and Tian, 2018).

Unadjustable anomalies detected based on RSEM have 20% – 50% overlap with those detected based on Salmon

To show the applicability of the anomaly detection method on multiple quantification methods, we apply anomaly detection using the RSEM (Li and Dewey, 2011) quantifier and identify unadjustable and adjustable anomalies in the same 30 GEUVADIS samples and 16 Human Body Map samples. See the Method Section for the details of obtaining the expected and observed coverage distributions from RSEM. With these coverages, the anomaly detection and categorization methods we present are able to be directly applied.

About 20%–50% of the RSEM unadjustable anomalies are shared with the ones detected using Salmon (Patro et al., 2017) (Supplementary Figure S7C–D). The expected distribution estimated by RSEM only depends on the positional bias and is computed at a coarser resolution than is modeled in Salmon. RSEM does not model sequence-specific or GC content biases. Therefore, it is not surprising that there is a large difference between unadjustable anomalies based on Salmon and those based on RSEM. Indeed, the percentage is much higher than random (hypergeometric test p-value < 10⁻³⁰⁰). These results show that when applied with quantifiers that coarsely estimate the expected distribution, the anomaly detection method can still predict many unadjustable anomalies.

There are 219 – 527 transcripts per GEUVADIS sample and 509 – 1972 per Human Body Map sample that are detected to be unadjustable anomalies only under RSEM quantification. For the ones that are detected as unadjustable anomalies only under Salmon quantification, the number is 258 – 714 per GEUVADIS sample and 1168 – 5657 per Human Body Map sample. The causes of the difference include: (1) Salmon and RSEM estimate different expected coverages but assign similar observed read coverages to the transcript (Supplementary Figure S8A–B); (2) Salmon and RSEM assign obtain different observed coverages (Supplementary Figure S8C–F) and the difference remains after SAD read re-assignment; (3) both expected coverages and observed coverages are similar for Salmon and RSEM, but the variances of Gaussian error in the expected distribution estimation are different (Supplementary Figure S8G–H); (4) a mixture of the above causes. When the cause of different predictions is due to the difference in Gaussian error variances, Salmon tends to predict the transcripts as unadjustable anomalies while RSEM may not. The expected coverage in RSEM is estimated only based on positional bias, which is coarser and usually farther away from the observed read coverage than Salmon’s expected coverage. Thus the variance of the Gaussian estimation error is usually larger in RSEM than in Salmon. When the variance of error in expected distribution estimation is larger, the likelihood of observing a large deviation by chance increases and the p-value also increases. The mixture and interplay among the possible causes may be complicated, therefore we do not assign the uniquely detected anomalies to the causes or estimate the weights of the causes.

Simulation supports the accuracy of SAD for detecting and categorizing anomalies

On simulation data, the predictions of both unadjustable and adjustable anomalies precisely capture the mis-quantification due to those causes. We created 24 datasets by varying the number of simulated unannotated isoforms, the gene annotations, and the expression matrices. (See Method Section for the details of the simulation procedure.)

Unadjustable anomalies are able to predict the existence of simulated unannotated isoforms that do not contain unannotated splicing locations with 3%–35% higher precision than transcriptome assembly methods (Supplementary Figure S9A–B). Precision is computed as the fraction of “marked” genes that contain simulated transcripts that are unannotated in the reference. For SAD, a gene is marked if it contains a transcript that is detected as an unadjustable anomaly. For the transcript assembler, a gene is marked if it has an assembled transcripts with predicted RPKM ≥ a parameter θ, and that transcript either: (1) only uses existing splicing junctions and does not match the intron chains of any existing transcript or (2) matches the intron chain of an existing transcript, but has a starting position or stopping position more than 200 bp away from the matched existing transcript. The parameter θ is chosen so that the transcript assembler marks the same number of genes as SAD does.

Note in this comparison, we compute precision only considering isoforms that use existing splicing junctions in unannotated combinations or with alternative start or termination locations. These are generally the harder transcripts to detect, since for these isoforms, transcript assembly methods can only depend on coverage to assemble transcripts. SAD benefits from using the well modeled expected coverage distribution to identify unadjustable anomalies. On the other hand, the main advantage of SAD is precision, but not sensitivity, because not all unannotated isoforms will significantly alter the coverage of known ones (Supplementary Figure S9C).

In addition, the LP read reassignment is more accurate than the original Salmon quantification (Patro et al., 2017) on the adjustable anomalies in simulated data (Supplementary Figure S9D–E). The accuracy of quantification is measured by mean ARD (absolute relative difference) (Patro et al., 2017). ARD is calculated by taking the absolute difference between the estimation and the true expression and normalizing it by the sum of the estimation and the truth. A smaller value of mean ARD indicates an estimator that is closer to the ground truth. The decrease of ARD on adjustable anomalies is usually more than 0.05. The accuracy improvement of SAD decreases as more isoforms of one gene are involved in the read reassignment. The decrease of improvement is possibly because small estimation errors in the expected distribution are magnified when the LP coefficient matrix used by SAD is large in size and potentially ill-conditioned. When the coefficient matrix is ill-conditioned in the linear system, the output can greatly change even with a small error in the input.

Unadjustable anomalies are supported by long read sequencing data in 1000 Genome samples

To further verify that in real RNA-seq the unadjustable anomalies are likely caused by the incompleteness of the reference transcriptome, we use long-read sequencing evidence to show the existence of unannotated isoforms that are suggested by unadjustable anomalies. In the 1000 Genome (Consortium et al., 2015) samples, 3 trios (9 samples) were sequenced using both short-read RNA-seq and PacBio SMRT technology to obtain expressed full-length transcripts. We apply SAD to the short-read RNA-seq data and compare the detected unadjustable anomalies to sequenced PacBio reads of full-length transcripts. A isoform that is derived from the full transcripts sequences and not included in the reference annotation is considered to correspond to the unadjustable anomaly prediction if it covers 75% of the over-expressed region and excludes 75% of the under-expressed region of the anomaly. Unadjustable anomalies that have corresponding PacBio reads are considered true predictions of the existence of unannotated isoform and are used to calculate precision.

For all 9 samples, the precision of unadjustable anomalies of SAD is within the range of 23% – 32% (Supplementary Figure S10). See Supplementary Table S3 for a full list of unadjustable anomalies and their correspondence to the long reads. The precision is within the range observed in the simulated RNA-seq data. The rest of the unadjustable anomalies are not supported by the long reads. Instead, they may correspond to true unannotated isoforms that are not sequenced by long reads or arise from an inaccurate estimation of the expected distribution of the anomalous transcripts.

Discussion

We present Salmon Anomaly Detection (SAD), an anomaly detection approach to identify potential misquantification of expression. SAD detects anomalies by comparing the expected and the observed coverage distribution and calculating the significance of the over- or under-expression. SAD also categorizes the anomalies into adjustable anomaly and unadjustable anomaly categories to indicate two possible causes of misquantifications: algorithmic errors and reference transcriptome incompleteness. The categorization is done by reassigning reads across isoforms to minimize the number of significant anomaly scores. We show on simulation data that the detected anomalies and their categorizations are reasonable: the unadjustable anomalies predict the existence of unannotated isoforms (using existing splice junctions) with higher precision than transcriptome assembly methods, and the read reassignment of adjustable anomalies leads to adjusted quantification that is closer to the simulated ground truth compared to the original quantification.

The explanation for LP read assignment leading to a better quantification than Salmon for some transcripts is that the LP focuses only on the base-to-base coverage distribution consistency while Salmon combines multiple aspects into its probabilistic model and also groups reads into equivalent classes. For example, transcript lengths and fragment lengths are considered in its probabilistic model. One equivalence class may include reads starting at various positions, which have various expected coverages. Because Salmon balances these multiple aspects and treats each equivalent class as a unit, it may generate a coverage distribution deviated from the expectation. When this deviation is very large, the quantification results tend to be inaccurate. In the case of a very large deviation, reassigning reads purely based on coverage consistency using the LP leads to a more accurate quantification.

Applying SAD on GEUVADIS and Human Body Map datasets, we are able to identify adjustable and unadjustable anomalies that affect isoforms with different protein domains from other isoforms and isoforms from cell type marker genes. Using the adjusted quantification associated with the adjustable anomalies, the number of false positive predictions of differentially expressed transcripts can be reduced. There are common unadjustable anomalies across all samples. Most of the common unadjustable anomalies have an under-expressed region towards the 3′ end of the transcript.

SAD is only able to detect the subset of misquantifications that have distorted the observed coverage from the expected one. However, some misquantifications may not alter the shape of the observed coverage distribution. For example, high sequence similarity between a pair of transcripts can also lead to severe misquantification, however, the read coverage can be close to the expectation for both. Alternatively, the coverage distribution of a lowly expressed existing isoform can be affected by a lowly expressed unannotated isoform. In this case, the p-value of the anomaly score may not be significant due to the large fluctuation of the observed coverage due to the low expression. Developing other scores, for example, using transcript similarity or discordant read mapping, could potentially increase the sensitivity and the types of possible misquantification of detection.

Some of the causes of anomalies are not covered by the current anomaly categorization method. For example, when an anomaly is caused by a mixture of incomplete reference transcriptome and mistakes of the quantification methods, SAD cannot label the cause as the mixture but is only able to attribute to one of the two causes based on the read reassignment outcome. In addition, unadjustable anomalies can be further subcategorized by whether the corresponding unannotated isoforms are splicing variants or gene-fusions. One contribution of this work is to inspire more systematic investigation of the causes of expression anomalies. Refining the methods to determine the causes of anomalies is a potential direction for future work.

For unannotated isoform detection, only transcript existence is predicted by SAD, not the sequence or exon-intron structure of the unannotated isoforms. Retrieving the exon-intron structure remains a problem. Simply combining the prediction of SAD with the assembled sequences from transcriptome assembly does not solve the problem of reconstructing unannotated isoform sequences. About 40%–60% of SAD’s predictions are not assembled by transcriptome assembly methods in the GEUVADIS and the Human Body Map datasets. Incorporating the expected coverage distribution during transcriptome assembly may be a direction to predict the exact exon-intron structure of the unannotated isoforms.

SAD suggests an analysis workflow that contains three steps: quantification, anomaly detection, followed by specialized quantification focusing on the anomalies. The middle step, anomaly detection, and the last step, specialized quantification, can be treated separately and enhancements in either step are needed to improve the accuracy of the adjusted expression estimates. For example, SAD’s read reassignment only shuffles the reads across isoforms within the same gene. A better read reassignment across genes can be developed.

An improvement in the accuracy of the approximation of the expected distribution may further increase the accuracy of unannotated isoform prediction and re-quantification by SAD. Currently, the expected distribution is approximated by a bias correction model that uses GC, sequence, and position biases. The sequence bias may also be affected by the secondary structure of cDNA, which is not considered in current modeling of biases.

SAD takes about 8 hours to run on each RNA-seq sample using eight threads on the GEUVADIS samples and about 23 hours on the Human Body Map samples. Empirically the running time scales linearly with the number of sequencing reads as the sequencing depths of Human Body Map samples are about three times those of GEUVADIS samples. The long running time is mainly due to the sampling procedure in the empirical p-value calculation for all transcripts. A derivation of a p-value approximation to avoid sampling could potentially decrease the computational requirements. Implementation engineering can also be applied to reduce the running time, however, this is out of the scope of this work.

Our formulation of anomaly detection is an example of algorithmic introspection: algorithms that can automatically identify where their predictions do not fit the assumptions of the algorithm. This type of algorithmic reasoning is likely to become even more useful as the sophistication of bioinformatics analysis tools increases.

STAR Method

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Carl Kingsford (carlk@cs.cmu.edu). This study did not generate new unique reagents.

METHOD DETAILS

An anomaly detection score

Definition 1 (Expected coverage distribution).

Given transcript t with length l, and a fragment f that is sequenced from t, the starting position of f is a random variable with the possible positions {1, 2, 3, ⋯, l} as its domain. The expected coverage distribution of t is the probability distribution of the starting position of any fragment f. The expected coverage distribution for each transcript t sums to 1.

With a non-zero fragment length, the viable starting position excludes the last several positions in the transcript. Given a minimum fragment length, it is not possible for a fragment to start at a position within a distance of the minimum fragment length to the end of the transcript. The probability of such positions is set to 0. After aligning and assigning the sequencing reads to transcripts, the number of fragments starting at each position can be counted; this is referred to as the observed coverage. The observed coverage can be converted to distribution by normalizing the coverage to sum to 1. The normalized observed coverage is called the observed coverage distribution, which is comparable to the expected coverage distribution.

We use a slightly different definition of coverage from its classic meaning. We define the coverage of each transcript position to be the number of fragments starting at this position, while the classic definition considers the number of fragments spanning the position. We use the fragment start definition for calculating both the observed and the expected coverage distribution. The observed and the expected coverage are comparable if they are calculated using the same definition. Since the fragment length distribution is often assumed to be a Gaussian distribution with a smaller variance compared to the mean, the coverage distribution under the fragment start definition is approximately the same as the one under the classic definition plus a shift.

Definition 2 (Regional over-(under-)expression score).

Given transcript t with length l, denote the expected coverage distribution as exp, and the observed coverage distribution as obs, the over-expression score of region [a, b] (1 ≤ a < b ≤ l) is

$$O_t\left(a,b\right)=\max \left\{\sum _{a\le i\le b}\left(obs\left[i\right]-exp\left[i\right]\right),0\right\}.$$ (1)

where index i denotes the positions in the transcript. The under-expression score of region [a, b] is

$$U_t\left(a,b\right)=\max \left\{\sum _{a\le i\le b}\left(exp\left[i\right]-obs\left[i\right]\right),0\right\}.$$ (2)

The over-expression and under-expression scores are defined as the probability difference between the observed coverage and the expected coverage distribution within region [a, b]. The probability difference represents the degree of inconsistency between the two distributions at the given region. The scores indicate the fraction of reads to take away (or add to) from the region in order for the two distributions to match each other.

Definition 3 (Transcript-level anomaly score).

For a transcript t with length l, the over-expression anomaly of the transcript is defined as

$$O{A}_t=\underset{1\le a<b\le l}{\max }{O}_t\left(a,b\right).$$ (3)

The under-expression anomaly of the transcript is defined as

$$U{A}_t=\underset{1\le a<b\le l}{\max }{U}_t\left(a,b\right).$$ (4)

These transcript-level anomaly scores are defined by the largest over- or under-expression score across all continuous regions.

Probabilistic model for coverage distribution

The value of the anomaly score cannot be directly used to indicate an anomaly because its value can be confounded by transcript abundances and the estimation error of the expected distribution. When there are only a few reads sequenced from the transcript, randomness in read sampling can dominate the observed distribution. Because of this, the observed distribution will have large fluctuations along the transcript positions, and thus appear to have a large deviation from the expected distribution. In addition, when the estimation of the expected distribution is inaccurate, the difference between the two distributions can also be large. To address these two confounding factors, we model the relationship between the coverage distributions using a probabilistic framework and calculate the p-value of the anomaly score. With the statistical significance of an anomaly score, we are able to distinguish between true quantification anomalies and randomness from known confounding factors.

We model the value of the anomaly score probabilistically given the two confounding factors (Supplementary Figure S11). We use the model to indicate the distribution of the anomaly score under the null hypothesis that it is not a true anomaly. For the transcript abundance confounding factor, we assume the observed distribution is generated from the hidden expected distribution through a multinomial distribution parameterized by the given number of reads, n:

$$obs\sim multinomial\left(N,exp\right).$$ (5)

For the estimation error of the expected distribution, we assume the error in the expected distribution is Gaussian with mean μ and covariance Σ. Let est to be estimation of the expected distribution and let exp be the true hidden expected distribution, the estimation error follows:

$$est-exp\sim N\left(\mu ,\Sigma \right).$$ (6)

We further assume that the Gaussian estimation error is generally the same across all transcripts. In practice, transcripts have different lengths and the Gaussian error vectors differ relative to the lengths. We therefore separate positions in each transcript into several bins and transcripts with similar lengths have the same number of bins. A shared mean shift parameter μ and covariance Σ is estimated for the transcripts with the same number of bins.

The variables and parameters of the model (Supplementary Figure S11) can be retrieved or estimated as follows. obs refers to the observed distribution and can be retrieved from the quantification algorithm (Section). est refers to the estimation of the expected distribution, which is processed from the bias correction result of the quantification (Section). exp stands for the expected coverage distribution that is latent. μ and Σ in the probability could be estimated with a Bayesian estimator or maximum a priori (MAP) estimator with a likelihood function. Using subscript t to represent transcripts, the likelihood function is

$$L\left(\mu ,\Sigma \right)=\mathbf{\prod }_t{\int }_{{exp}_t:{exp}_t\ge 0,\Sigma {exp}_t=1}\mathbb{P}\left(ob{s}_t|{exp}_t\right)\mathbb{P}\left(es{t}_t|{exp}_t,\mu ,\Sigma \right)\mathbb{P}\left({exp}_t\right)d\left({exp}_t\right).$$ (7)

However, the above likelihood function does not have a closed form solution and may require using expectation maximization (EM) for optimization. Instead, we estimate μ and Σ using the following approximation: the multinomial distribution for the observed coverage can be approximated by a Gaussian distribution when the number of reads n is large enough:

$$obs\sim Multi\left(n,exp\right)\stackrel{n\to \infty }{\to }N\left(exp,\frac{f\left(exp\right)}{n}\right)$$ (8)

where $f:{\mathbb{R}}^m\to {\mathbb{R}}^{m\times m}$ maps the m-dimension probability vector of the multinomial distribution into the covariance matrix of the approximating multi-variate Gaussian distribution. Therefore, the difference between obs and est can be approximated by the following Gaussian distribution

$$est-obs\sim N\left(\mu ,\Sigma +\frac{f\left(exp\right)}{n}\right)\stackrel{n\to \infty }{\to }N\left(\mu ,\Sigma \right).$$ (9)

We therefore approximate μ and Σ by selecting transcripts with enough reads for each length group, and fit a Gaussian distribution to est – obs of the selected transcripts.

This probabilistic model serves as the null model that assumes the transcript is not an anomaly. That is, the model describes the distribution of the anomaly score under the case where the deviation between the observed and the expected distribution is only due to the two confounding factors: read sampling randomness of sequencing and the estimation inaccuracies of the expected distribution. When the deviation is so large that this null model cannot explain it, we attribute the deviation to an anomaly. To determine whether the deviation is so large that it is unlikely to be observed under the null model, a p-value is calculated. The details of this calculation are explained below.

Statistical significance of the anomaly score

The statistical significance of a value of the anomaly score is the probability of observing an even larger anomaly value given the probabilistic model. Let O_t(a, b) and U_t(a, b) be the random variables of the regional over- and under-expression score of region [a, b], and let o_t(a, b) and u_t(a, b) be the corresponding observed values. Similarly, let OA_t and UA_t be the random variable of transcript-level anomaly score, and oa_t and ua_t be the corresponding observed values. The p-values for a regional over- and under-expression score are

$$\begin{gathered} \mathit{p-value}\text{of}{O}_t\left(a,b\right)=\mathbb{P}\left(O_t\left(a,b\right)>o_t\left(a,b\right)|exp,n,\mu ,\Sigma \right) \\ \mathit{p-value}\text{of}{U}_t\left(a,b\right)=\mathbb{P}\left(U_t\left(a,b\right)>u_t\left(a,b\right)|exp,n,\mu ,\Sigma \right) \end{gathered}$$ (10)

where exp, n, μ and Σ are defined as in Supplementary Figure S11. The p-values for transcript-level over- and under-expression anomaly score are

$$\begin{gathered} \mathit{p-value}\text{of}O{A}_t=\mathbb{P}\left(O{A}_t>o{a}_t|exp,n,\mu ,\Sigma \right) \\ \mathit{p-value}\text{of}U{A}_t=\mathbb{P}\left(U{A}_t>u{a}_t|exp,n,\mu ,\Sigma \right). \end{gathered}$$ (11)

The statistical testing of the transcript-level anomaly score is more strict to the null hypothesis than that of the regional one, and tends to have a larger p-value. Given transcript t and the largest over-expressed region [i, j], the following inequality between the two p-values holds:

$$\begin{gathered} \mathit{p-value}\text{of}O{A}_t=\mathbb{P}\left(\underset{1\le a<b\le l}{\max }{O}_t\left(a,b\right)>o{a}_t|exp,n,\mu ,\Sigma \right) \\ =\mathbb{P}\left(\underset{1\le a<b\le l}{\max }{O}_t\left(a,b\right)>o_t\left(i,j\right)|exp,n,\mu ,\Sigma \right) \\ \ge \mathbb{P}\left(O_t\left(i,j\right)>o_t\left(i,j\right)|exp,n,\mu ,\Sigma \right) \\ =\mathit{p-value}\text{of}{O}_{\text{t}}\left(i,j\right). \end{gathered}$$ (12)

Conceptually, because the whole transcript contains multiple regions that may have a large over- (under-) expression score, it is easier to observe a large over- (under-) expression score when we look at all possible regions compared to when we focus on only one specific region. From the perspective of statistical testing, the p-value of OA_t and UA_t tend to be larger and less significant than those of O_t(a, b) and U_t(a, b) for any region [a, b]. Taking advantage of the different level of strictness about the null model, we use the significance of O_t and U_t for the initial selection of anomalies to adjust read assignment, and use the significance of OA_t and UA_t for the final selection of anomalies within the unadjustable anomaly category.

The p-value of both anomaly scores can be calculated empirically. Specifically, the hidden expected coverage can be sampled from the estimation using multi-variate Gaussian distribution, and the observed coverage can be sampled from the new hidden coverage using multinomial distribution. The null distribution for O_t(a, b), U_t(a, b), OA_t and UA_t can be generated using the sampled observed and hidden expected coverage. The empirical p-value is the portion of times that the anomaly scores exceed the observed valued in the null distribution.

We also derive a numerical approximation for the p-value of regional anomaly score. Empirical p-value calculation requires sampling distributions from a multinomial or multi-variate Gaussian distribution multiple times, which takes a long time computationally. A numerical approximation without sampling can greatly reduce the calculation time. Denote the region as [a, b] and the current under-expression anomaly score as v. The significance of the over- (under-) expression score under regional null distribution is given by

$$\begin{gathered} \mathit{p-value}\text{of}{U}_{\text{t}}\left(a,b\right)=\mathbb{P}\left(\sum _{i=a}^b\left(exp\left[i\right]-obs\left[i\right]\right)>\upsilon |\sum _{i=a}^{b}est\left[i\right]\right) \\ =\mathbb{P}\left(\sum _{i=a}^{b}obs\left[i\right]<\sum _{i=a}^{b}exp\left[i\right]-\upsilon |\sum _{i=a}^{b}est\left[i\right]\right) \\ ={\int }_{x}GaussianPDF\left(x|\sum _{i=a}^{b}est\left[i\right],\mu ,\Sigma \right)\mathbb{P}\left(\sum _{i=a}^{b}obs\left[i\right]<x-\upsilon \right)dx \\ ={\int }_{x}GaussianPDF\left(x|\nu ,\sigma \right)BinomCDF\left(n\ast \left(x-\upsilon \right)|n,x\right)dx \end{gathered}$$ (13)

where $x={\sum }_{i=a}^{b}exp\left[i\right],\nu ={\sum }_{i=a}^b\left(est\left[i\right]-\mu \left[i\right]\right),\sigma ={\sum }_{i=a}^b{\sum }_{j=a}^b\Sigma \left[i,j\right]$ and n is the number of reads assigned to the transcript. In the numerical approximation, the function inside the integral is approximated by a step function with small step sizes of x and the integral is approximated by summing up the area under the step function. Since the regional anomaly score focuses on a fixed region, the multinomial distribution can be collapsed into binomial distribution to represent the probability of generating a read from that region. The multi-variate Gaussian distribution can also be collapsed to a single-variate Gaussian distribution to present the expected estimation bias and variance of the region. With all multi-variate distributions collapsed into single-variate distributions, it is feasible to numerically calculate the integral in equation (13). In SAD, the p-value of the regional over- (under-) expression score is always calculated using the numerical approximation, while the p-value of the transcript-level anomaly is calculated empirically by sampling.

In practice, we do not calculate the p-value for transcripts with very low abundance. When the randomness of read sampling is very large, we simply assume that the p-value will be dominated by the randomness instead of anomalies. We only calculate a p-value for transcripts with average base pair coverage > 0.01. Using a threshold of 0.01 is equivalent to requiring that on average at least one read is sequenced for every 100 base pairs.

Benjamini-Hochberg correction is used to control the rate of falsely discovered transcripts with regional or transcript-level expression anomaly. A threshold of 0.05 is used in the regional anomaly score. For transcript-level anomalies, 0.01 is used as the threshold. The varied thresholds are set according to their separate purposes: regional anomalies are the initial candidates and do not need to be as precise; after read reassignment, the transcript-level anomalies are the final predictions of unadjustable anomalies and require higher precision.

Categorizing anomalies by read reassignment

We categorize the causes of anomalies into whether or not they are caused by read assignment mistakes of the quantifier’s probabilistic model. This is done by seeking an alternative read assignment for the transcripts with significant regional anomaly score to reduce the inconsistency with the expected coverage.

We use linear programming (LP) to reassign the reads in anomalies. The LP formulation tries to use a linear combination of the expected distributions to explain the aligned reads. By explicitly using the expected coverage to re-distribute the observed number of reads, the deviation between the observed and the expected distribution after the re-distribution is naturally reduced. Accordingly, the anomaly score will decrease and the p-value will increase. We apply LP redistribution separately for each gene since most misassignments of reads by the quantifier occur among isoforms of the same gene rather than across genes and gene-level expression estimation is more accurate than isoform-level quantification (Soneson et al., 2015, Dapas et al., 2016).

The formulation of the LP is

$$\begin{gathered} \underset{\left\{{\alpha }_t:t\in T\right\}}{\min }\parallel \sum _t{\alpha }_t{exp}_t-\sum _{t}ob{s}_t{\parallel }_1+\sum _{j\in J}\parallel \left(\sum _t{\alpha }_t{\delta }_t^j{exp}_t-\sum _{t}ob{s}_t^j\right)\cdot P^j{\parallel }_1 \\ s.t.{\alpha }_{\text{t}}\ge 0(\forall \text{t}\in T) \end{gathered}$$ (14)

where t is the index for transcript set T and j is the index of splicing junction set J. Let n be the length of the unique exon positions of the gene. $ex{p}_t\in {\mathbb{R}}^n$ is the expected coverage distribution (normalized) for transcript t under gene level coordinate. $ob{s}_t\in {\mathbb{R}}^n$ is the observed coverage (unnormalized) for transcript t under gene level coordinate. $ob{s}_t^j\in {\mathbb{R}}^n$ is the observed coverage of reads that are assigned to transcript t and spanning junction j. ${\delta }_t^j$ is an indicator that takes value 1 if transcript t has splicing junction j and 0 otherwise. P^j ∈ {0, 1}ⁿ indicates which positions are considered close to junction j. Specifically, entries of P^j that represent positions 50 bp to the 5′ side of the splicing junction position are 1 and the rest are 0. “·” is the dot product.

In the LP objective function multiple isoforms of various lengths are included in the same matrix expression. A coordinate conversion is needed to adjust the coverages of multiple isoforms to have the same length. Because each reassignment is performed on isoforms within the same gene, the coverage in transcript coordinates is converted to gene coordinates. In the gene coordinates, each nucleotide is indexed in the sequence of the concatenation of unique exons (or subexons) of the gene. For a given transcript, the coverage is set to 0 for the exons it does not contain.

Let I₁ = ∥∑_tα_texp_t − ∑_tobs_t∥₁ be the first term in the objective function. This is the main minimization goal to reassign reads to isoforms according to their expected coverage distribution. ∑_tobs_t is the aggregated read coverage along the gene. Under the assumption of correct gene-level read assignment but deviated transcript-level read assignment, obst may not represent the correct read coverage of transcript t, but ∑_tobs_t represents the correct coverage of the gene. This term seeks to use a linear combination of expected coverage distributions to explain the observed gene coverage.

Let $I_2={\sum }_{j\in J}\parallel \left({\sum }_t{\alpha }_t{\delta }_t^j{exp}_t-{\sum }_{t}ob{s}_t^j\right)\cdot P^j{\parallel }_1$ be the second term in the objective function. This term serves as a penalty on the coverage inconsistency around each splicing junction. Because the coverages store only the fragment start positions but not the junction spanning information, a fragment aligning onto a retained intron may have the same starting position of another fragment spanning a splicing junction. Thus an additional penalty is added to control the assignment of junction-spanning reads. The penalty imposed by I₂ encourages that the coverage of the junction-spanning reads should be explained by a linear combination of the expectation from transcripts with the junction. When transcript t does not contain splicing junction j, we set ${\delta }_t^j=0$ to make sure that transcript t has no contribution to the junction coverage. The start positions of the junction-spanning reads are usually near the 5′ side of the junction. Start positions separated from the junction can contain reads both spanning and not spanning the junction. We specify a 50 bp window to the 5′ side of the junction to enforce that penalty to be restricted to the most relevant positions to each splicing junction.

Variables α_t stand for the expected number of expressed reads from transcript t. To obtain the actual number of reads reassigned to transcript t at position k, we re-distribution the junction reads and non-junction reads in proportion to α_t. Specifically, the reads starting at position k and spanning junction j are assigned to transcript t with weight $\left({\Sigma }_{t^{\prime }}ob{s}_{t^{\prime }}^j[k]\right)\frac{{\alpha }_t{\delta }_t^{j}ex{p}_t[k]}{{\Sigma }_{t^{\prime }}{\alpha }_{t^{\prime }}{\delta }_{t^{\prime }}^{j}ex{p}_{t^{\prime }}[k]}$. Let n_t[k] be the sum of weights assigned to t at position k. The actual total number of reads reassigned to transcript t is ∑_kn_t[k].

After adjusting read assignments using the LP, some transcripts have an insignificant transcript-level anomaly score. These transcripts are labeled “adjustable anomalies” and are considered to have misquantifications due to quantification algorithm mistakes. On the other hand, if the transcript-level anomaly scores are still significant, the corresponding transcripts are labeled “unadjustable anomalies”. Assuming the expected distributions are estimated with reasonable accuracy, we suspect the unadjustable anomalies are affected by the expression of unannotated transcripts’ expression and indicate incompleteness of the reference transcriptome. Benjamini-Hochberg correction is used to adjust the p-value of transcript-level anomaly score to control for the false positive labeling of anomalies for all transcripts.

Reducing number of transcripts involved in reassignment

In practice, we try to keep the number of transcripts involved in the LP as small as possible. When the quantification of a transcript is good enough, reassigning the reads may lead to a decrease of quantification accuracy. The correctness of the LP reassignment largely depends on the accurate estimation of the expected distribution. However, the accuracy assumption of the expected distribution may not hold for all transcripts. An inaccurate estimation at some positions for one transcript can perturb the reassignment result across all involved isoforms. The perturbation can be large when the coefficient matrix in the LP has a large condition number (called ill-conditioned), which tends to occur more often as the number of isoforms involved in the LP increases. The ill-condition will make the output very sensitive to a small change or error of the input distributions. To reduce this problem in the LP reassignment, we only apply the LP reassignment on a small number of isoforms and reset the other isoforms to the quantifier’s read assignments. The choice of isoforms is determined by the following principle: the largest number of transcripts should have insignificant regional anomaly scores across all regions while at the same time minimizing the number of isoforms involved in the LP.

To obtain the largest number of transcripts with insignificant regional anomaly scores, we initially run the LP using all transcripts. Then we exclude each transcript one-by-one from the LP. If excluding a transcript from the LP does not change the set of transcripts with insignificant regional anomaly scores, the transcript is excluded forever from the LP, otherwise, it is kept in the LP. When excluding any transcript from the LP increases the number of transcripts with significant regional anomaly scores, the iterative process is terminate and the final set of transcripts involved in LP is determined.

Retrieving the expected distribution from Salmon

We processed the auxiliary output from Salmon to obtain the estimated expected distribution. The expected distribution is estimated for each transcript using the bias model from Patro et al. (2017). In the ideal case of sequencing, where the read is sampled randomly without any biases, the expected coverage is uniform along the positions of any transcript. However, in the real sequencing experiments, cDNA fragmentation and PCR amplification have preferences towards certain positional, sequence, and GC patterns, and the coverage is not expected to be uniform. The expected distribution is calculated to represent the probability of sampling a read at a given position of a given transcript. Salmon estimates the positional, sequence, and GC biases by adjusting the uniform distribution based on the read mapping. There could be other biases affecting the expected distribution. However, other biases are not considered in the model, and thus the bias correction model is only an approximation for the true expected distribution.

Retrieving observed coverage from Salmon

The observed coverage is the actual read coverage for each transcript. It is calculated by counting the weighted number of reads at each position at a given transcript after the weights are optimized by Salmon’s algorithm (Patro et al., 2017). Specifically, when a read is multi-mapped to several transcripts, the weight represents the probability that the read is generated from the transcript.

Retrieving expected and observed coverages from RSEM

The expected coverage can be estimated in RSEM by using the “--estimate-rspd” option. RSPD stands for read start position distribution and this models the 3′ positional bias, which is the only bias considered by RSEM. RSEM discretizes all transcripts into 20 bins (default parameter of RSEM) and estimates a single probability distribution for all transcripts to describe the probability of sequencing a read from each bin. To recover the estimated expected distributions of each transcript, we extend the single probability distribution to the length of each transcript by uniformly distributing the probability to all transcript positions in the corresponding bin. The expected distribution of each transcript will look like a step function with the step size equal to the transcript length divided by the number of bins.

The observed coverage is directly processed from the BAM file output by RSEM, where each alignment record has an additional tag to denote the weight assigned to the corresponding transcripts. Summing up the weight of each alignment starting positions generates the observed coverage of RSEM.

With the expected and observed coverage calculated from RSEM, the anomaly scores and p-values can be calculated in the same way as with Salmon. However, because RSEM has a single, binned expected distribution for all transcripts, the assumption that estimation error of expected distributions follows a Gaussian error may not be true. The estimated error of the expected distributions may not be small enough for the LP read reassignment to achieve an accurate adjusted quantification.

Simulation procedure

To mimic the real scenario where the target transcriptome contains unannotated transcripts outside reference transcriptome, we simulated target and reference transcriptomes as follows. Using the Gencode annotation (Frankish et al., 2018), we randomly selected 200, 500, 1000, 1500 genes, remove one transcript per gene, and use the rest of the transcript sequences as reference transcripts. For the target transcriptome, we simulated 200, 500, 1000, 1500 fusion genes, added them to Gencode transcript sequences, and use the combined full Gencode transcripts and fusion sequences as the target transcriptome that generates RNA-seq data. Each fusion transcript is simulated by randomly choosing a pair of transcripts that have not been involved in other fusion events, randomly choosing breakpoints within the transcript that are at least 20 bp away from the endpoints, and finally concatenating the pair of transcripts at their breakpoints. The 20 bp threshold ensures there is a distinction between indels when aligning or mapping the reads to the reference. In this case, the target transcriptome contains both unannotated isoforms and fusion sequences compared to the reference. We use both the protein-coding-only annotation and full annotation for removal and fusion simulation, to test both polyA RNA-seq and total RNA-seq techniques.

Reads are simulated using the target transcriptome by Polyester (Frazee et al., 2015). A count matrix is used as input in Polyester to denote the theoretical number of reads to be simulated for each transcript in the transcriptome. The count matrix is generated by quantifying RNA-seq datasets (GEUDAVIS, GM12878, K562) using Salmon (Patro et al., 2017) and the original Gencode annotation. With the simulation datasets, Salmon version 0.9.1 is used to quantify the reads against the reference transcriptome.

Detecting transcripts with non-identifiable abundances

The software eXpress (version v1.5.1) (Roberts and Pachter, 2013) is used to identify transcripts with non-identifiable abundances. eXpress is a quantification tool that depends on a probabilistic model involving fragment lengths, transcript lengths, and mapping positions variables. It outputs whether the abundance of a transcript can be uniquely maximized, which is the identifiability under its objective. We use the identifiability under eXpress as a proxy for the identifiability under the Salmon quantifier.

Though the quantification model of eXpress is different from that of Salmon, we expect that for many transcripts their identifiability statuses are the same under both models. Identifiability of a probabilistic model is largely determined by the parameter space, objective function and the probability assumptions. Both models maximize the probability of observing the given set of reads and use the same parameter space, which is the abundances vector of all transcripts. The basic model assumption, that the probability of observing a read from a transcript is proportional to the abundance of the transcript, is also shared. Under these input and assumptions, whether the optimal parameter settings are multiple largely depends on the similarity among input transcripts, specifically whether a subset of transcripts can be linearly represented by another subset of transcripts. We therefore expect the identifiability statuses are similar between the two quantification models, despite the difference in their objective functions and their optimal solutions.

STAR version 2.6.0 (Dobin et al., 2013) is used to align RNA-seq reads to Gencode version 26 transcriptome sequences. The alignment is the input to eXpress quantifier. The identifiability is indicated in the “solvable” column of eXpress output.

Running transcriptome assembly on simulated and real data

RNA-seq reads are aligned to GRCh38 genome (Schneider et al., 2017) using STAR version 2.6.0 (Dobin et al., 2013). We ran Scallop version v0.9.8 on the alignments of all simulated, GEUVADIS and Human Body Map samples, and set all parameters to their default. We also ran StringTie (Pertea et al., 2015) version 1.3.1c on all these samples, using the option “–G” for guiding the transcriptome assembly by the reference transcriptome. When guided by reference transcriptome, the precision of StringTie can be better than Scallop on some samples. We do not guide the Scallop assembly by reference transcriptome since it does not have the option. We use gffcompare (Pertea, 2018) to compare the assembled transcripts with the reference transcript.

QUANTIFICATION AND STATISTICAL ANALYSIS

The main statistical analysis used in this paper is the p-value calculation for determining whether an anomaly score is significant. This p-value calculation is described in detail in the Method Details section, specifically the “Statistical significance of the anomaly score” section. Here, we review the steps in the method where these p-values are used.

The first step that uses the p-value calculation determining the initial anomaly candidates using the Salmon-computed distributions. The p-value is calculated for regional anomaly scores. In the anomaly categorization step, read assignments are adjusted by LP iteratively. In each iteration, the p-value is calculated for the regional anomaly scores calculated based on the reassigned observed distribution. After the termination of LP read reassignment, the p-value calculation is performed for the transcript-level anomaly scores that are based on the final LP reassigned observed distribution. All p-values for regional anomaly scores are calculated using the numerical approximation in equation (13). All p-values for transcript-level anomaly scores are calculated empirically by sampling from the assumed probability distribution.

The p-values are adjusted by Benjamini-Hochberg method. For regional anomaly scores, a threshold of 0.05 for the adjusted p-value is used to determine the significance of coverage inconsistency of each region. Transcripts with at least one region with significant regional anomaly scores are considered as candidate anomalous transcripts and included in all iterations of LP reassignment. For transcript-level anomaly scores, a threshold of 0.01 for the adjusted p-value is used to label unadjustable anomalies.

DATA AND CODE AVAILABILITY

The code used during this study is available at https://github.com/Kingsford-Group/sad.

Supplementary Material

Supplemental Table and figures

SupplementaryFile.pdf: Supplementary Table S1 and Supplementary Figures S1–S11. Related to Figure 1, Figure 2 and STAR Method.

Table S2

CommonUnadjustableAnomalies.xlsx: Supplementary Table S2. List of unadjustable anomalies shared among all GEUVADIS and Human Body Map samples. Related to Figure 1 and Figure 2.

Table S3

LongreadValidation.xlsx: Supplementary Table S3. Validation result of unadjustable anomalies using full-length transcript sequencing in 1000 Genome trios. Related to Figure 2.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
GEUVADIS	Lappalainen et al. (2013)	SRA:ERR188297, ERR188088, ERR188329, ERR188288, ERR188021, ERR188356, ERR188145, ERR188347, ERR188382, ERR188436, ERR188052, ERR188402, ERR188343, ERR188295, ERR188479, ERR188204, ERR188317, ERR188453, ERR188258, ERR188114, ERR188334, ERR188353, ERR188276, ERR188153, ERR188345, ERR188192, ERR188155, ERR188132, ERR188408, ERR188265
Human Body Map	The Illumina Body Map 2.0 data	SRA:ERP000546
1000 Genome Trio short read	Clarke et al. (2016)	SRA:ERP012633
1000 Genome Trio long read	Chaisson et al. (2019)	SRA:ERP015321
Human Reference Genome GRCh38	Schneider et al. (2017)	ftp://ftp.ebi.ac.uk/pub/databases/gencode/Gencode_human/release_26/GRCh38.primary_assembly.genome.fa.gz
Gencode annotation v26	Frankish et al. (2018)	ftp://ftp.ebi.ac.uk/pub/databases/gencode/Gencode_human/release_26/gencode.v26.annotation.gtf.gz
Software and Algorithms
SAD	this work	https://github.com/Kingsford-Group/sad
Salmon	Patro et al. (2017)	https://salmon.readthedocs.io/en/latest/
RSEM	Li and Dewey (2011)	https://deweylab.github.io/RSEM/
STAR	Dobin et al. (2013)	https://github.com/alexdobin/STAR
Scallop	Shao and Kingsford (2017)	https://github.com/Kingsford-Group/scallop
StringTie	Pertea et al. (2015)	http://ccb.jhu.edu/software/stringtie/
gffcompare	Pertea (2018)	http://ccb.jhu.edu/software/stringtie/gffcompare.shtml
Polyester	Frazee et al. (2015)	https://github.com/alyssafrazee/polyester
samtools	Li et al. (2009b)	http://samtools.sourceforge.net/
eXpress	Roberts and Pachter (2013)	https://pachterlab.github.io/eXpress/index.html

Highlights.

• A method to identify regions of transcripts that have inconsistent read coverage.

• Read re-assignment to reduce coverage anomaly generates adjusted quantification.

• Labeling anomalies as unadjustable or adjustable based on the reduction of anomaly.

• Common unadjustable anomalies usually have under-expressed regions on their 3′ exon.