Kinetic Modeling of Hyperpolarized Carbon-13 Pyruvate Metabolism in the Human Brain

Abstract

Kinetic modeling of the in vivo pyruvate-to-lactate conversion is crucial to investigating aberrant cancer metabolism that demonstrates Warburg effect modifications. Non-invasive detection of alterations to metabolic flux might offer prognostic value and improve the monitoring of response to treatment. In this clinical research project, hyperpolarized [1-¹³C] pyruvate was intravenously injected in 10 brain tumor patients to measure its rate of conversion to lactate (k_PL) and bicarbonate (k_PB) via echo-planar imaging. Our aim was to investigate new methods to provide k_PL and k_PB maps with whole-brain coverage. The approach was data-driven and addressed two main issues: selecting the optimal model for fitting our data and determining an appropriate goodness-of-fit metric. The statistical analysis suggested that an input-less model had the best agreement with the data. It was also found that selecting voxels based on post-fitting error criteria provided improved precision and wider spatial coverage compared to using signal-to-noise cutoffs alone.

I. Introduction

Dissolution Dynamic Nuclear Polarization (dDNP)^1,2 is a powerful technique that enhances nuclear polarization by up to 5 orders of magnitude.

Its chemical^3–5, biological^6–9, physical^10–14, pre-clinical^15–21 and clinical^22–28 potentials have been investigated in the last two decades. The use of hyperpolarized (HP) substrates has provided important insights into cancer metabolism^6,22,29–31 and cardiac imaging^23,32–36. Thus far, HP pyruvate is the most common substrate for in-vivo applications of dDNP because of both its relatively long T₁(¹³C), high biological relevance, and rapid uptake and conversion.

The first phase I clinical trial of HP [1-¹³C]pyruvate was reported in 2013²² on patients with prostate cancer and it demonstrated feasibility and safety for this approach to monitoring cancer progression and treatment response by quantifying the Warburg effect³⁷ that is expressed through increased lactate dehydrogenase (LDH) activity. Several institutions around the globe are now performing clinical cancer research of HP pyruvate in prostate, breast³⁸, liver³⁹ and brain²⁸, in order to investigate the clinical value of dDNP HP MRI and its advantages over current molecular imaging methods including Fludeoxyglucose Positron Emission Tomography (FDG-PET)^40,41.

FDG-PET is an imaging technique used for the diagnosis of cancer based on the uptake and trapping of the radioactive substrate, but it does not track its kinetic conversion into downstream metabolites. Furthermore, it is of limited use in brain tumors since high glucose uptake is observed not only in cancerous tissues, but also in healthy cortical gray matter^42,43, confounding the discrimination of brain tumors. There is an unmet clinical need for a more precise diagnosis of brain tumors which might be overcome by the capability of dDNP to track the pyruvate-to-lactate conversion and the Warburg effect, provided that a robust and reproducible kinetic modeling of the conversion of pyruvate is achieved^44–51.

The goal of this work is to develop, implement and test methods for calculating precise k_PL and k_PB maps describing the enzymatic conversion of [1-¹³C]pyruvate to lactate and bicarbonate in the human brain. We acquired 22 datasets though a dynamic 2D multislice Echo Planar Imaging (EPI)⁵² sequence. Dynamic acquisition of MR images has the advantage to provide robust quantification of kinetic processes⁵³, regardless of differences in bolus delivery, which influences, for instance, area-under-curve (AUC) ratios. EPI acquisition of HP substrates offers improved temporal resolution and greater spatial coverage than Echo Planar Spectroscopic Imaging (EPSI) techniques. We present and compare several models and two approaches to cut off voxels with improper fitting, in order to provide precise and spatially-resolved kinetic maps.

II. METHODS

Sample preparation

The sample preparation was carried out in collaboration with UCSF Radiopharmacy. Each sample consisted of a mixture of Good Manufacturing Practices (GMP) [1-¹³C]pyruvic acid (14.2 M; MilliporeSigma Isotec) and 15 mM Electron Paramagnetic Agent (EPA), (AH111501, GE Healthcare).

Samples were prepared the same morning of each study and they were inserted, under aseptic conditions, into pharmacy kits from GE Healthcare.

Polarization

A SPINlab⁵⁴ polarizer (GE Healthcare) was used to polarize [1-¹³C]pyruvate at 5 T and about 0.8 K. The sample was irradiated with microwave at f_MW = 140.02 GHz for at least 2 hours, boosting the ¹³C polarization up to 40% in the liquid state back-calculated to the time of dissolution.

Pre-injection quality check

After the dissolution, the EPA was filtered mechanically and quality control was carried out prior to injection: pH, pyruvate and EPA concentrations, polarization, and temperature were measured and compared to ranges of acceptability. Contemporarily, the integrity of the 0.2 µm sterile filter was tested following manufacturer specifications on its resistance to a pressure-stress of 50 psi. Following the release by the pharmacist, ~250 mM pyruvate was injected at a dose of 0.43 mL/kg and a rate of 5 mL/s, followed by a 20 mL saline flush. A pause of 5 s preceded the acquisition.

Acquisition

All experiments were performed on a 3T clinical MR scanner (MR750, GE Healthcare) with multi-nuclear excitation and 32-channel reception capability. Carbon-13 RF excitation was achieved with a volume transmit coil and detected with custom ¹³C RF coils with either 8 or 32 channels⁵⁵.

Images of pyruvate, lactate and bicarbonate were acquired through a 2D EPI dynamic sequence⁵³, capable of exciting multiple ¹³C frequencies sequentially, and having the following characteristics: 8 slices, 1.5 or 2 cm thick axial slice, TR = 62.5 ms, TE = 21.9 ms, 20 time-points with a 3 s temporal resolution, in-plane resolutions of 1.2 × 1.2, 1.5 × 1.5 or 2 × 2 cm². In order to improve image quality, we applied noise pre-whitening⁵⁶ in k-space prior to sum-of-squares coil combination.

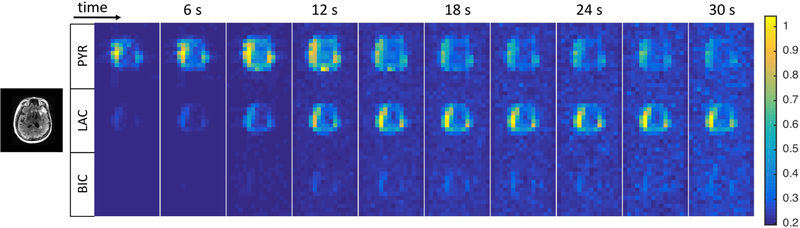
In Fig. 1 we show the temporal trends of the signals of pyruvate, lactate and bicarbonate in a single slice.

Figure 1.

Temporal dynamics of the signals of pyruvate, lactate and bicarbonate in a single slice (data set 3 in Table 1), acquired with the EPI dynamic sequence (see text for details). For anatomic reference, a ¹H FLAIR image on the left. Note that data have not been coil corrected and reflect the sensitivity profile of the 8-channel receive-array used in this study.

III. KINETIC MODELING

In the last decade, substantial efforts have been dedicated to developing kinetic models of MRI signals of HP metabolites in vivo. Despite several approaches available in literature ^14,25–30, no gold-standard is available because strategies may vary according to specific experimental conditions.

Since kinetic modelling might suffer from errors induced by several factors (e.g., variable bolus delivery, acquisition sequence, magnitude images with non-zero mean noise etc), discarding voxels with poor fitting is critical to provide precise kinetic maps.

In this section, we describe kinetic models and fitting criteria to address these issues and to quantify kinetic rate constants in a precise way.

First, suitable models for fitting our data are presented.

Then, we describe two criteria to decide how to discard voxels with suboptimal fitting.

Models

While studying the human brain, in order to obtain insights into complicated metabolic pathways, it is crucial to investigate the kinetics of several metabolites in different cellular environments. Although it is an oversimplification, we consider a three-site system (i.e., pyruvate, lactate and bicarbonate) in a single compartment. In such a system, the magnetization $\overline{M}(t)$ is exchanged and relaxes according to the following equations (single macrons refer to vectors, double macrons to matrixes):

$$\frac{d}{dt}\overline{M}(t)=\overline{\overline{K}}\cdot \overline{M}(t)+\overline{\mathrm{\Gamma }}(t)$$ [1]

$$\overline{\overline{K}}=\left[\begin{array}{ccc}-R_1-k_{PL}-k_{PB}& k_{LP}& k_{BP}\\ k_{PL}& -R_1-k_{LP}& 0\\ k_{PB}& 0& -R_1-k_{BP}\end{array}\right]$$ [2]

$$\overline{M}(t)=\left[\begin{array}{c}{M}^{pyr}(t)\\ M^{lac}(t)\\ M^{bic}(t)\end{array}\right]$$ [3]

$$\overline{\mathrm{\Gamma }}(t)=\left[\begin{array}{c}\mathrm{\Gamma }(t)\\ \mathrm{\Gamma }(t)\cdot c_{lac}\\ \mathrm{\Gamma }(t)\cdot c_{bic}\end{array}\right]\hspace{0.17em}where\hspace{0.17em}\mathrm{\Gamma }(t)=\alpha \cdot e^{\beta t}\cdot t^{\gamma }$$ [4]

We defined:

• $k_{PL}$ and $k_{PB}$ as the rates of labelling exchange from pyruvate to lactate and to bicarbonate (respectively). Note they are first order apparent rate constants and not absolute flux measurements.

• $R_1=\hspace{0.17em}1/T_1$ as spin longitudinal relaxation rate.

• $M_{EXP}^{pyr}$ as the experimental temporal trend of the magnetization of pyruvate.

• ${\overline{M}}_{EXP}(0)$ as the experimental magnetization vector $\overline{M}(t)$ at the first time point.

• ${\overline{M}}_{EXP}(\infty )$ as the experimental magnetization vector $\overline{M}(t)$ at the last time point.

Overall, 5 approaches were tested:

1. $\mathrm{\Gamma }(t)=0$, $k_{LP}=k_{BP}=0$, $M^{pyr}(t)=M_{EXP}^{pyr}(t)$, $\overline{M}(0)={\overline{M}}_{EXP}(0)$, $\overline{M}(\infty )={\overline{M}}_{EXP}(\infty )$.

   This is a model with no input-function⁵⁷: the fitted signal of pyruvate is bounded to the experimentally acquired signal. The first and last time points are fixed to the experimental values (for all metabolites). Just forward reactions are considered.

   Fitted parameters: $R_1$, $k_{PL}$, $k_{PB}$.

2. Same as A) except for having now $k_{LP}\ne \hspace{0.17em}0$ (back reaction now allowed with a different rate). Fitted parameters: $R_1$, $k_{PL}$, $k_{PB}$, $k_{LP}$

3. Same as A) except for having now ${\overline{M}}^T(\infty )=M_{\infty }^{fit}[1\hspace{1em}1\hspace{1em}1]$ (last time points are now estimated from the fitting). Fitted parameters: $R_1$, $k_{PL}$, $k_{PB}$, $M_{\infty }^{fit}$.

4. Same as A) except for having now ${\overline{M}}^T(\infty )=M_{\infty }^{fit}[1\hspace{1em}1\hspace{1em}1]$ and ${\overline{M}}^T(0)=M_0^{fit}[1\hspace{1em}1\hspace{1em}1]$ (both first and last time points are estimated from the fitting). Fitted parameters: $R_1$, $k_{PL}$, $k_{PB}$, $M_{\infty }^{fit}$, $M_0^{fit}$.

5. $k_{LP}=k_{BP}=0$, $\overline{M}(0)={\overline{M}}_{EXP}(0)$, $\overline{M}(\infty )={\overline{M}}_{EXP}(\infty )$. In this model $\mathrm{\Gamma }(t)\ne 0$, meaning that there is an input function $\mathrm{\Gamma }(t)$ (defined in Eq. 4) simulating the arrival of the bolus in the region of interest. The magnetization of pyruvate is also fitted. First and last points are set equal to experimental values. Just forward reactions are considered. Fitted parameters: $R_1$, $k_{PL}$, $k_{PB}$, $\alpha$, $\beta$, $\gamma$, $c_{lac}$, $c_{bic}$.

The differential equations 1–4 were solved through a discrete model. The transverse magnetization, ${\overline{M}}_{xy}$, and the residual longitudinal component along the z axis, ${\overline{M}}^{res}$, were computed in Eq 5 and 6 at each time step $\mathrm{\Delta }t\cdot N$ (where $\mathrm{\Delta }t$ = TR and N = 1, 2, …, 20), taking into account the excitation flip angles $\overline{\alpha }$ for each metabolite.

The magnetization at time step N+1 was calculated in Eq. 7 by considering the exchange matrix $\overline{\overline{K}}$, $\mathrm{\Delta }t$ and ${\overline{M}}^{res}(\mathrm{\Delta }t\cdot N)$.

$${\overline{M}}^{res}(\mathrm{\Delta }t\cdot N)=\overline{M}(\mathrm{\Delta }t\cdot N)\cdot \cos (\overline{\alpha })$$ [5]

$${\overline{M}}_{xy}(\mathrm{\Delta }t\cdot N)=\overline{M}(\mathrm{\Delta }t\cdot N)\cdot \sin (\overline{\alpha })$$ [6]

$$\overline{M}(\mathrm{\Delta }t\cdot [N+1])=e^{\overline{\overline{K}}\cdot \mathrm{\Delta }t}{\overline{M}}^{res}(\mathrm{\Delta }t\cdot N)$$ [7]

All models were solved via custom MATLAB routines involving minimization of non-linear least-square problems (i.e., difference between fitted and experimental magnetization). σ_kPL is half the 95% confidence interval, calculated with MATLAB functions lsqnonlin and nlparci. In all cases, boundary conditions were: 1/80 s⁻¹ < R₁ < 1 s⁻¹ and 0 < k_PL < 1 s⁻¹.

Experimental T₁s of lactate and pyruvate vary significantly in solution. However, a recent work⁵³ has shown that the input-less model is insensitive to errors in pyruvate T₁ and that T₁ values for pyruvate and lactate are similar in vivo (respectively 30 and 25 s, in patient studies at 3 T). We, therefore, chose to have equal T₁ values to improve the stability of the model.

After fitting to experimental data, models were classified according to 3 indicators, Akaike Information Criterion (AIC), $n_{vox}^{perc}$ and $\mathrm{\Delta }{\overline{k}}_{PL}^{perc}$, defined as:

$$AIC=2k-2\ln (L)$$ [8]

$$n_{vox}^{perc}=100\frac{n_{vox}^i}{n_{vox}^A}$$ [9]

$$\mathrm{\Delta }{\overline{k}}_{PL}^{perc}=100\left[1-\left(\raisebox{1ex}{${\overline{k}}_{PL}^i$}\!\left/ \!\raisebox{-1ex}{${\overline{k}}_{PL}^A$}\right.\right)\right]$$ [10]

where k is the numbers of parameters estimated in the model, L is the maximum value of the likelihood function for the model (i.e., chi squared in our case), $n_{vox}^i$ is the number of voxels, in all data sets, that are fitted according to the i^th model (with i = A-E), $n_{vox}^A$ is the $n_{vox}^i$ corresponding to model A, ${\overline{k}}_{PL}^i$ is the mean k_PL, averaged over all data sets, for the i^th model and ${\overline{k}}_{PL}^A$ is the ${\overline{k}}_{PL}^i$ corresponding to model A.

The AIC is a measure of the statistical significance of several models with a different number of parameters to be estimated (i.e., the lower the better statistical significance for the model). $n_{vox}^{perc}$ is informative of how many voxels are fitted if compared to model A (chosen arbitrarily as a standard) and $\mathrm{\Delta }{\overline{k}}_{PL}^{perc}$ is a measure of how much k_PL varies with models.

To assess the reproducibility of the pyruvate bolus delivery, we define a “mean pyruvate time” $t_{arr}^{mean}$ as the center of mass of the pyruvate signal over time on a voxel-wise basis⁵³:

$$t_{arr}^{mean}=\frac{{\sum }_n{S}_{pyr}(n)t(n)}{{\sum }_n{S}_{pyr}(n)}$$ [11]

Criteria to mask voxels on k_PL maps

In this paragraph, we introduce two approaches to mask voxels with improper fitting in order to provide “reasonable” k_PL maps with an acceptable compromise between precision of the fitting in a voxel and the numbers of voxel for which the fitting itself is retained (i.e. the coverage). Due to low SNR, k_PB maps describing the conversion of pyruvate into bicarbonate will not be considered in this analysis. In the “SNR criterion”, prior to fitting temporal trends to a model, we create a mask discarding voxels with peak SNR lower than a set of two SNR thresholds, one for pyruvate and one for lactate, labeled as [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$]. In the “error criterion”, prior to fitting temporal trends to a model, we mask voxels based on [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$], as in the SNR criterion, but, after fitting, we discard all the voxels where ${\text{σ}}_{\text{kPL}}$ is bigger than a fraction of k_PL itself.

In this way, the global masking procedure depends on both the set of SNRs and on the statistical outcome of the fitting.

To compare the outcomes of fitting with the two criteria, we will take into account $n_{vox}^{perc}$ (as in Eq. 9 but now the index refers to the criterion) and R², defined as:

$$R^2=1-\frac{{\sum }_k{(y_k-f_k)}^2}{{\sum }_k{(y_k-\overline{y})}^2}$$ [12]

where y_k and f_k refer to the experimental and fitted signals at the k^th time point and $\overline{y}$ is the average over time of y_k. R² is preferred over AIC or chi squared since these last two vary with different SNR (i.e., if data with lower SNR are filtered, the residuals ${(y_k-f_k)}^2$ are bigger).

IV. RESULTS AND DISCUSSION

The subject population comprised 10 patients with recurrent glioma who had received prior surgery and were undergoing standard-of-care treatment, including radiation therapy and temozolomide chemotherapy, along with a variety of adjuvant therapies. A subset of these patients was imaged serially, and all received a single injection per day. Table 1 includes the experimental conditions under which the 22 data sets were acquired (i.e., coil, voxel size, excitation flip angles) and estimation of ${\text{SNR}}^{max}$ (the peak SNR in all voxels and slices in the given data set), $t_{arr}^{mean}$(mean arrival time of pyruvate) and $k_{PL}^{mean}$ (mean k_PL rate).

Table 1.

Summary of the experimental conditions of the 22 human brain data sets. We report coil used, voxel size, flip angles of excitation for each metabolite, peak SNR (along all voxels and slices in the given data set), mean kinetic rate k_PL and its standard deviation (calculated with “model A” and the error criterion, described later on in the manuscript) and mean and standard deviation of the mean arrival time of pyruvate t_arr.

	Set	Coil	Voxel (cm3)	αpyr(°)	αlac(°)	αbic(°)	${\text{SNR}}_{pyr}^{max}$	${\text{SNR}}_{lac}^{max}$	${\text{SNR}}_{bic}^{max}$	$k_{PL}^{mean}(s^{-1})$	$t_{arr}^{mean}(s)$
Patient 1	1	8ch	2 × 2 × 2	33.4	33.4	33.4	393	53	15	0.021±0.008	6±2
	2	32ch	1.2 × 1.2 × 2	10	33.4	33.4	120	22	27	0.013±0.006	7±3
	3	8ch	2 × 2 × 2	33.4	33.4	33.4	437	79	13	0.05±0.02	7±4
	4	32ch	1.2 ×1.2 × 2	20	30	30	306	22	18	0.010±0.005	6± 3
Patient 2	5	8ch	1.2 ×1.2 × 2	33.4	33.4	33.4	306	20	n/a	0.024±0.009	11±4
	6	8ch	2 × 2 × 2	20	30	30	170	26	11	0.018±0.007	8±5
	7	32ch	2 × 2 × 2	20	30	30	504	30	15	0.016±0.007	7±2
	8	8ch	1.5 ×1.5 × 2	20	30	30	403	42	18	0.022±0.009	7±2
Patient 3	9	8ch	2 × 2 × 2	20	30	30	281	41	12	0.018±0.008	7±2
	10	32ch	1.2 ×1.2 × 2	20	30	30	576	21	29	0.009±0.004	9±3
Patient 4	11	8ch	2 × 2 × 2	20	30	30	225	43	13	0.03±0.01	10±2
	12	32ch	1 × 1 × 2	20	30	30	492	25	32	0.012±0.006	8±3
	13	32ch	1.5 × 1.5 × 1.5	20	30	30	181	16	12	0.022±0.008	7±3
	14	32ch	1.5 × 1.5 × 1.5	20	30	30	361	24	14	0.02±0.01	7±2
Patient 5	15	8ch	1.2 × 1.2 × 2	10	33.4	33.4	101	22	26	0.015±0.007	6±3
	16	32ch	1.5 × 1.5 × 2	20	30	30	392	35	15	0.015±0.008	7±2
	17	32ch	1.5 × 1.5 × 2	20	30	30	392	35	15	0.017±0.007	11±3
Patient 6	18	8ch	1.2 × 1.2 × 2	33.4	33.4	33.4	559	22	12	0.012±0.004	10±3
Patient 7	19	8ch	2 × 2 × 2	20	30		271	41	13	0.03±0.01	9±3
Patient 8	20	8ch	2 × 2 × 2	20	30		568	58	16	0.03±0.01	8±2
Patient 9	21	8ch	1.2 × 1.2 × 2	10	33.4		128	25	13	0.02±0.01	6±3
Patient 10	22	32ch	1.5 × 1.5 × 2	20	30	30	162	13	13	0.009±0.005	7±3

In Fig. 2, we can see typical temporal trends of the signal-to-noise ratio of pyruvate, lactate and bicarbonate in a single voxel, selected from a slice (also shown for all metabolites). The SNR did not go to zero at later time-points due to the sum-of-squares coil combination used in this work, which results in non-zero mean noise caused by noise rectification of magnitude data.

Figure 2.

[Top] ¹H FLAIR and ¹³C total signal AUC images (data set 3) from the raw data. [Bottom] Temporal dynamics of signals of pyruvate, lactate and bicarbonate in the selected voxel.

While there has been no comprehensive study on the impact of spatial resolution on the measured reaction rate, larger voxels would have a greater risk of partial-volume effects, reducing the measured reaction rate because of the strong vascular pyruvate signal⁵⁸. Confounding factors such as Rician bias in magnitude data and variations in bolus delivery between patients are global factors that impact quantification. On a voxelwise level, regional variations in perfusion, signal loss from susceptibility/B₀ inhomogeneities and reduced SNR in voxels at the center of the brain, farthest from the multichannel receive array, can also impact quantification. The choice of flip angles will also have an impact on the precision of rate constant estimates^57,59,60. Using a variable (across frequency) flip angle scheme, with a higher flip angle for downstream metabolites and a lower flip angle for pyruvate, is commonly used to compensate for the lower metabolite concentration and to reduce saturation of pyruvate. This leads to more precise fitting in the presence of noise by increasing the metabolite SNR⁶¹. While variable (through time) flip angle schemes can improve SNR, they are also more sensitive to transmit B₁ inhomogeneity^59,62.

The ${\text{SNR}}^{\max }$ was excellent for pyruvate and lactate (i.e., greater than 100 and 13, respectively, for all datasets) but greatly variable for bicarbonate.

The mean arrival time of the pyruvate bolus, $t_{arr}^{mean}$, was calculated for every data set via Eq. 11. While there is variability throughout the brain due to differences in arrival time between arterial and venous voxels, the mean pyruvate time ranged from 6 s to 11 s post injection, with an average value of 8 ± 2 s across patients. Compared to initial results from the prostate⁶³, the mean arrival time in the brain appears fairly reproducible in our initial cohort.

Mean k_PL and its standard deviation were also calculated on each data set, with the approach described in the next paragraphs.

Let us define σ_kPL as half the 95% confidence interval from non-linear least-square fitting to “model A” with the error criterion with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [20, 5] and σ_kPL < 0.6·k_PL. We have applied the error criterion with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [20, 5] and σ_kPL < 0.6·k_PL to compare models A to E. Values of AIC, $\mathrm{\Delta }{\overline{k}}_{PL}^{perc}$ and $n_{vox}^{perc}$ are reported in Table 2: model A was the best model at describing data (highest $n_{vox}^{perc}$ and lowest AIC) and model B the worst (high AIC and negligible $n_{vox}^{perc}$). Model E, which is the only one including an input function, performed worse than model A (the simplest assumption-less model), due to a poor agreement between the input function and our data which may be improved with an earlier start of acquisition.

Table 2.

Comparison of models A-E according to Akaike Information Criterion (AIC) and percentage deviation from model A of mean $kPL(\mathrm{\Delta }{\overline{k}}_{PL}^{perc})$ and of number total voxel fitted $(n_{vox}^{perc})$.

Model	AIC	$\mathrm{\Delta }{k}_{PL}^{perc}$	$n_{VOX}^{perc}$
A: inputless, $\overline{M}(0)$ and $\overline{M}(\infty )$ bounded, no back reaction	4	0	100
B: inputless, $\overline{M}(0)$ and $\overline{M}(\infty )$ bounded, no back reaction	11	−363	85
C: inputless, $\overline{M}(0)$ bounded, no back reaction	6	−5	85
D: inputless, no back reaction	10	−7	86
E: input $\mathrm{\Gamma }$ function, $\overline{M}(0)$ and $\overline{M}(\infty )$ bounded, no back reaction.	13	−40	55

Parameters used in both the SNR and the error criterion should be optimized in order to find a compromise between precision and number of voxels fulfilling the statistical requirements based on σ_kPL (i.e., spatial coverage).

The analysis has been carried out on datasets with peak SNR of lactate lower than 25, by using model A, since it is the one providing the best fit quality.

In the SNR criterion, we have to choose [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] namely the set of thresholds for masking voxels with low SNR (before fitting). We tested 22 sets obtained by all the possible combinations between ${\text{SNR}}_{pyr}^{max}$ = [5, 10, 50, 100] and ${\text{SNR}}_{lac}^{max}$ = [2, 3, 4, 5, 6, 7].

In the error criterion, the SNR mask was computed based on 6 threshold sets, obtained by combining ${\text{SNR}}_{pyr}^{max}$ = 5 and ${\text{SNR}}_{lac}^{max}$ = [2, 3, 4, 5, 6, 7]. After fitting, we discarded all the voxels with σ_kPL < c∙k_PL where c = [0.4, 0.6, 0.8, 1.0].

Values of $n_{vox}^{perc}$ and R² are reported in Tables 3a and 3b (respectively) for both the SNR criterion and the error criterion. To produce kinetic maps, it is necessary to find a compromise between statistical precision and available number of voxels (or alternatively the voxel count within the FOV) and the final decision may vary from one user to the other.

Table 3a.

Values of $n_{vox}^{perc}$ for the SNR criterion and the error criterion using model A as standard. Several combinations of ${\text{SNR}}_{pyr}^{max}$ and ${\text{SNR}}_{lac}^{max}$ were used for both criteria. In the SNR criterion no conditions are set on σ_kPL (error of k_PL), whereas, in the error criterion, fitting is accepted for σ_kPL < c·k_PL and rejected otherwise.

${\mathit{n}}_{\mathit{v}\mathit{o}\mathit{x}}^{\mathit{p}\mathit{e}\mathit{r}\mathit{c}}$	SNR criterion (no check on σkPL after fitting)				Error criterion:σkPL< c · kPL
					c =1.0	c = 0.8	c = 0.6	c = 0.4
${\text{SNR}}_{\mathrm{lac}}^{\max }$╲${\text{SNR}}_{\mathrm{pyr}}^{\max }$	5	10	50	100	5	5	5	5
2	100	86	26	6	51	45	34	18
3	50	47	19	5	33	31	27	17
4	30	29	13	3	21	20	19	14
5	17	17	9	3	12	12	12	10
6	11	11	6	3	8	8	8	7
7	6	6	4	2	4	4	4	4

Table 3b.

Values of R² for the SNR criterion and the error criterion using model A as standard. Several combinations of SNR^pyr and SNR^lac were used for both criteria. In the SNR criterion no conditions are set on σ_kPL (error of k_PL), whereas, in the error criterion, fitting is accepted for σ_kPL < c·k_PL and rejected otherwise.

R2	SNR criterion (no check on σkPL after fitting)				Error criterion:σkPL< c · kPL
					c =1.0	c = 0.8	c = 0.6	c = 0.4
${\text{SNR}}_{\mathrm{lac}}^{\max }$╲${\text{SNR}}_{\mathrm{pyr}}^{\max }$	5	10	50	100	5	5	5	5
2	0.27	0.30	0.38	0.43	0.37	0.40	0.47	0.60
3	0.39	0.41	0.44	0.49	0.43	0.50	0.53	0.60
4	0.41	0.42	0.51	0.57	0.42	0.49	0.60	0.65
5	0.53	0.53	0.66	0.58	0.53	0.54	0.64	0.67
6	0.66	0.66	0.67	0.57	0.66	0.66	0.67	0.69
7	0.70	0.70	0.71	0.59	0.70	0.70	0.70	0.72

Tables 3a and 3b provide insight on how to set limits in our case. In Tab. 3a, $n_{vox}^{perc}$ drops with higher ${\text{SNR}}_{pyr}^{max}$, higher ${\text{SNR}}_{pyr}^{max}$ and lower c, showing that any stricter requirement diminishes the numbers of accepted voxels. For the SNR criterion (Tab. 3b), R² increases with higher ${\text{SNR}}_{lac}^{max}$ but not necessarily with higher ${\text{SNR}}_{pyr}^{max}$. This suggests that the precision of methods based on the SNR alone depends more critically on lactate rather than on pyruvate. In Tab. 3b, as for the error criterion, R² increases with both higher ${\text{SNR}}_{lac}^{max}$ and lower c, meaning that both parameters affect the statistical precision.

In Tab. 3b, let us consider the R² values corresponding to ${\text{SNR}}_{pyr}^{max}=5$ in both criteria (i.e., first column in the SNR criterion and all columns in the error criterion). Values of R² in case of ${\text{SNR}}_{lac}^{max}=2,\hspace{0.17em}3,\hspace{0.17em}4$ in the SNR criterion are smaller than any R² in the error criterion (regardless of c). However, R² for ${\text{SNR}}_{lac}^{max}=5,\hspace{0.17em}6,\hspace{0.17em}7$ in the SNR criterion are comparable to those in the error criterion. This means that at low ${\text{SNR}}_{lac}$ the error criterion performs better than the SNR criterion, while they are comparable at higher ${\text{SNR}}_{lac}$.

By comparing Tab. 3a and 3b, we can see that, at similar precisions, the error criterion gives, on average, more voxels with proper fitting (i.e., higher $n_{vox}^{perc}$), yielding to a better spatial coverage in k_PL maps. The trend is particularly evident at low ${\text{SNR}}_{lac}^{max}$.

For example, let us consider two cases with R² = 0.43 in Tab. 3b: those with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [100, 2] for the SNR criterion and [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [5, 3] with σ_kPL < 1.0∙k_PL for the error criterion. These two cases exhibit the most dramatic difference since their corresponding values of $n_{vox}^{perc}$ in Tab. 3a would be 6 and 33, meaning that the error criterion provided 5 times more voxels despite having similar statistical precision.

Furthermore, if one wanted to base the selection on the SNR alone, removing the check on σ_kPL, in order to choose precise values, it would be necessary to perform many fittings at different SNR thresholds in every dataset and to fix a reasonable threshold.

The error criterion is an easier option since it is sufficient to set ${\text{SNR}}_{pyr}^{max}$ and ${\text{SNR}}_{lac}^{max}$ to reasonably low thresholds (high enough to avoid to retain voxels with noisy trends) and leave the main filtering task to the criterion based on σ_kPL.

We investigated the performances of the error criterion when applied to random noise.

To do so, we generated several sets of lactate signals consisting of Gaussian noise and associated them to the experimental signals of pyruvate from data set 3. Then, we applied the error criterion with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [5, 3] and σ_kPL < 0.6∙k_PL and calculated the number of fitted voxels, namely those where the fitting fulfils the requirements of the error criterion. We found that, if compared to experimental signals from data set 3, random noise provides, at best, 40 times less fitted voxels.

This suggests that the improvements introduced by the error criterion on $n_{vox}^{perc}$ and R² in Tables 3a and 3b are barely influenced by the noise.

All these findings speak in favor of the error criterion, which seems to be more reasonable than the SNR approach at masking voxel to be displayed in k_PL maps.

The choice of [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] and c is arbitrary and looking at the outcome alone might be misleading, as shown in Fig. 3. On the quest to opt for specific values, we started by considering the approach which has been often used in our group so far, namely [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [10, 5]. According to tables 3a and 3b, it has $n_{vox}^{perc}$ = 17 and R² = 0.53.

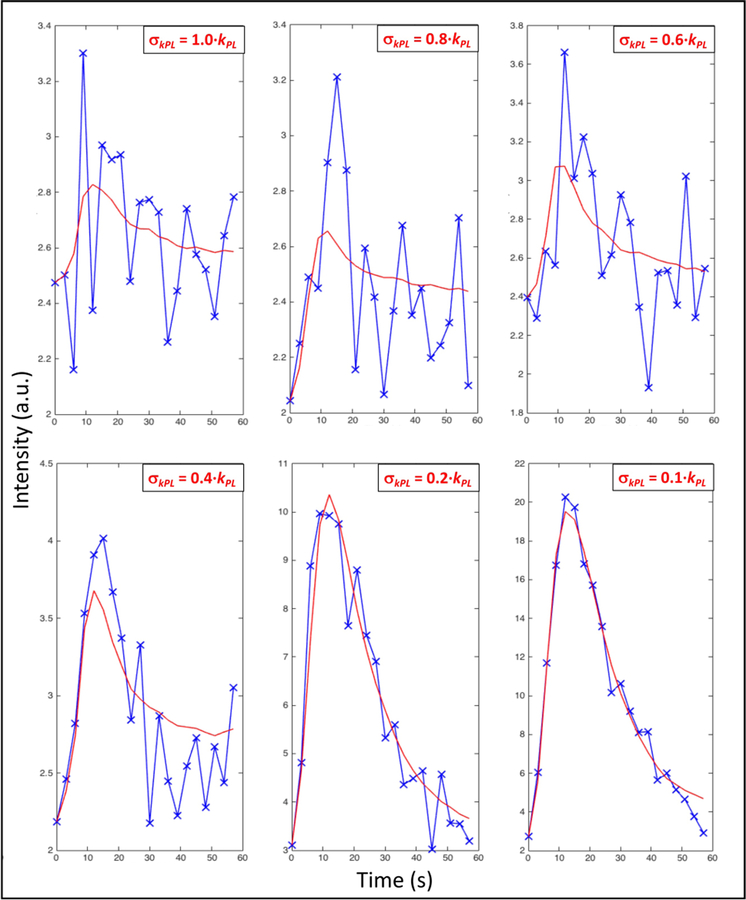
Figure 3.

Temporal dynamics of the signal of lactate in a voxel (blue crosses) and fitting (red line) using model A and the error criterion in 6 cases with different values of the parameter c in the condition σ_kPL < c k_PL (see text for details).

Bearing this in mind, we created k_PL and k ⁶⁴ maps for every data set, by using model A combined with the error criterion with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [5, 3] and c = 0.6.

These set of values has $n_{vox}^{perc}$ = 27 and R² = 0.53, meaning that, if compared to the former approach, it provides about 60% more voxels albeit keeping similar statistical precision.

As for data sets in Table 1, the mean value of the fractional error c = σ_kPL / k_PL in a single data set varies between 0.16 and 0.34, giving an idea of how they link to the graphic outcomes of fitting in Fig. 3.

In Fig. 4 we show examples of 5 k_PL maps superimposed to FLAIR images of a patient affected with gliosarcoma (data set 14) and of 5 k_PB maps superimposed to T1-weighted images of a patient affected with gliosarcoma (data set 16).

Figure 4.

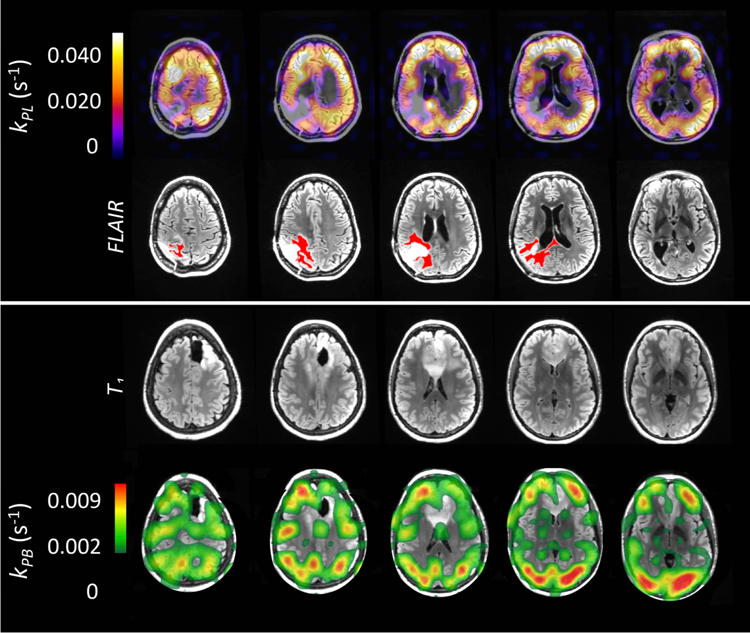
[Top] Examples of k_PL maps superimposed to FLAIR images of a patient (data set 14) affected with glioma (active tumor highlighted in red) [Bottom] Examples of k_PB maps superimposed to T₁-weighted images of a patient (data set 16). Sinc interpolation and the error criterion (σ_kPL < 0.6∙k_PL) were used to generate kinetic maps in both cases (see text for detail).

All the k_PL maps have been computed by using the error criterion with [${\text{SNR}}_{pyr}^{max}$, ${\text{SNR}}_{lac}^{max}$] = [5, 3] and σ_kPL < 0.6∙k_PL. The patient affected with gliosarcoma has previously received radiation and temozolomide chemotherapy, along with adjuvant agent pembrolizumab.

The interpretation of the correspondence between higher or lower k_PL values and presence of tumor is deferred to future studies since it is beyond the scope of this communication, that is mainly focused on methods to compute kinetic maps for our brain data sets.

V. CONCLUSIONS

We conducted preliminary studies of hyperpolarized [1-¹³C] pyruvate injected in 10 patients affected with glioma, demonstrating the feasibility for quantifying kinetic rates k_PL and k_PB, which describe the conversion of pyruvate into lactate and bicarbonate. We compared five kinetic models and two approaches for discarding voxels with improper fitting and we provided quantitative and spatially resolved maps of kinetic rates. Such hyperpolarized MRI experiments enable an unprecedented window into cerebral metabolism, which is not provided by other molecular imaging techniques.