Abstract
Outliers in times series data can be more problematic than in independent observations due to the correlated nature of such data. It is common practice to discard outliers as they are typically regarded as a nuisance or an aberration in the data. However, outliers can also convey meaningful information concerning potential model misspecification, and ways to modify and improve the model. Moreover, outliers that occur among the latent variables (innovative outliers) have distinct characteristics compared to those impacting the observed variables (measurement outliers), and are best evaluated with different test statistics and detection procedures. We demonstrate and evaluate the performance of an outlier detection approach proposed by De Jong, and Penzer (1998) for single-subject state-space models and extended by Chow, Hamaker, and Allaire (2009) to multi-subject models in a Monte Carlo simulation study. Based on our simulation results, we propose some slight adaptations to the procedures proposed by earlier authors to improve power and reduce false detection rates. Furthermore, we demonstrate the empirical utility of the proposed approach using data from an ecological momentary assessment study of emotion regulation together with an open-source software implementation of the procedures.
Real-world data often contain outliers that may impact parameter estimates, prediction, and inferential results. Earlier approaches to detecting outliers were based on the assumption of independence — an assumption that is typically violated in longitudinal data. Much of the work on outlier detection in longitudinal data originated from the time series literature, which typically involves data from a single unit (e.g., one subject) with many time points. In a seminal study on outlier detection within a time series framework, Fox (1972) suggested differentiating additive and innovative outliers to clarify whether the outlier affects subsequent observations beyond the time point at which it occurs. Thereafter most outlier detection methods have been developed based on Fox’s classification.
Since Fox (1972), many subsequent developments on outlier detection techniques in the time series literature were either linked to specific models, or specific types of outlier characteristics. For instance, Box and Tiao (1975) studied the effects of additive and innovative outliers using pulse and step function input, whereas Tsay (1988) investigated level shifts, namely, irreversible changes in the levels of time series data in the autoregressive moving average (ARMA) model. Later, an iterative outlier detection procedure was developed and applied to identify outliers in autoregressive moving average models by Chang, Tiao, and Chen (1988). The iterative outlier detection procedure uses test statistics to perform likelihood ratio comparisons between a null model and a model with innovative or additive outliers for each time point, and the outlying time point with the most extreme test statistic value that also exceeds a pre-set critical value (e.g., test statistic at the 95% level) is iteratively dropped from subsequent outlier detection until no further outliers that exceed the critical threshold are found.
Harvey and Koopman (1992) were among the first to use standardized smoothed residuals obtained as by-products of the Kalman filter and smoother (Kalman et al., 1960) — procedures that are routinely used to estimate latent variable scores in state-space models (SSMs)— for outlier detection purposes. This opened up opportunities for performing outlier detection and examining unusual changes in repeated measures data within the relatively broad and convenient framework of state-space modeling, which subsumes all linear time series and related change models as special cases (Chow, Ho, Hamaker, & Dolan, 2010; Harvey, 2001). A test for excess kurtosis was also proposed as a way to determine the statistical significance of the outliers.
Building on the work of Harvey and Koopman (1992) and others (Carter & Kohn, 1994; Cook & Weisberg, 1982; McCulloch & Tsay, 1993; Shephard, 1994), De Jong and Penzer (1998) formalized the procedures for diagnosing additive and innovative outliers in SSMs, and devised multiple test statistics for detecting these two kinds of outliers at an overall (model-based) level, as well as at the level of individual variables. The former is guided by a set of chi-square test statistics performed for each individual time point, whereas the latter is based on a series of Wald tests for each latent or observed variable at each time point. Included in their proposed approach are procedures for handling model (re-)estimation and inferences after the detection of outliers. This approach has been utilized to address problems such as the detection of level changes in intensive care online monitoring (Fried, Gather, & Imhoff, 2001), and irregular breaks in oil prices (Hazrana, 2017). A subset of the diagnostic statistics proposed by De Jong and Penzer (1998) have also been incorporated into software packages, such as in the SAS PROC UCM procedure for fitting unobserved components models (Selukar, 2011).
De Jong and Penzer’s (1998) method has some computational advantages compared to other approaches. One of the notable advantages is that diagnostic statistics for determining outliers as well as estimated magnitudes of the outliers can be obtained simultaneously from a single round of model estimation. This is in contrast, for instance, to approaches such as Chang et al.’s (1988) iterative procedure, which involves re-fitting the ARMA model repeatedly with each outlier removed in turn until no outliers are diagnosed. This process requires intensive computations, and often results in an overly specialized model. As another example, Harvey and Koopman’s (1992) approach also yields diagnostic statistics as by products of a single round of model estimation process. However, the excess kurtosis test proposed by Harvey and Koopman (1992) can only indicate the temporal locations of the outliers, but do not readily provide the estimated magnitudes of the outliers. Building on the strengths of De Jong and Penzer’s approach, Chow, Hamaker, and Allaire (2009) extended the procedures to enable outlier detection in fitting multiple-subject SSMs, and applied the proposed procedure to cognitive performance data from a group of older adults.
Previous studies are limited thus far in utilizing De Jong and Penzer’s (1998) method for outlier detection (e.g., Fried et al., 2001; Hazrana, 2017), and/or proposing extensions to accommodate data from broader settings (e.g., Chow et al., 2009). No studies to date have investigated the performance and utility of these diagnostic statistics’ performance in multiple-subject settings under finite sample sizes, or ways to strategically integrate information from multiple test statistics, for instance, to maximize power. The current study fills this gap through a formal Monte Carlo (MC) simulation. Results from the MC simulation are used to propose slight adaptations to the multi-subject procedures proposed by Chow et al. (2009) to improve power and lower false detection rates in finite sample sizes. The corresponding procedures have been implemented as part of a freely available R package, dynamic modeling in R (dynr; Ou, Hunter, & Chow, 2016, 2018, revised and resubmitted).
For the remainder of the present article, we first provide a brief introduction of the state–space modeling framework and outline Chow et al.’s (2009) multiple-subject adaptation of De Jong and Penzer’s (1998) approach to detect outliers in linear SSMs. We then highlight some unanswered issues with regard to how to best utilize the test statistics and other diagnostic output to aid outlier identification and subsequent inferential processes under finite sample sizes. Finally, an empirical data analysis follows to illustrate the use of the proposed approach.
State–Space Modeling Framework
SSMs have been utilized to describe the one-step-ahead relationships among dynamic latent variables (or ‘state variables’), and the associated observed repeated measures emanating from the latent processes. The basic linear SSM takes the following form:
| (1) |
| (2) |
| (3) |
where ηit contains the w latent variables of the system for person i at time t (i = 1, … N; t = 1, … , Ti; where Ti is the total time points for a participant i.), and yit is a p × 1 vector of manifest variables for person i at time t. The process or dynamic equation (Equation 1) describes the evolution of the latent variables using a w × w transition matrix B that links the immediately preceding latent states, ηi,t−1, to the current states, ηit. The w × 1 vector, α, is a vector of intercept terms. In the present context, the w-dimensional process errors in ζit are assumed to follow a multivariate normal distribution, The term ηi0 (Equation 2) is the initial condition from which the one-step-ahead process equation (Equation 1) proceeds, and is assumed in this article to follow a multivariate normal distribution with a mean a and covariance matrix P.
The measurement equation (Equation 3) describes the relations among the observed variables, yit, and the latent variables ηit both at time t, by using a p × w factor loadings matrix Λ. The observed variables yit are linear functions of a vector of intercepts, τ, and measurement errors, ϵit, again assumed to follow a multivariate normal distribution, . All the system parameters in α, τ, B, and Λ, are constrained to be invariant across subjects and time points for inferences at the group level.
Innovative and Additive Outliers in State–Space Models
Previous research has introduced two types of outliers in time series – additive and innovative outliers (Fox, 1972; Harvey & Koopman, 1992; Tsay, 1988). Additive outliers refer to data points that show unusual magnitude and only affect the particular time points at which they occur. Innovative outliers, in contrast, indicate that the effect of an unusual shock recursively influences subsequent observations in the dynamics of the model. In the SSM, outliers can be simply interpreted as additive outliers when they occur in the measurement equation, in that they would not extend their impact on successive observations. In contrast, when outliers arise in the process equation, they would be innovative outliers which continue to have their effect on future values of the latent, and hence observed variables beyond the current time point. That is, an innovative outlier can be regarded as an uncharacteristically large value in ζit in Equation 1, and an additive outlier can be thought of as an uncharacteristically large value in ∈it in Equation 3. Importantly, these instances of unusually large values of process or measurement errors would typically inflate the estimated values of the process and measurement noise variance-covariance parameters, and may at times lead to substantial biases in the estimates of other parameters.
Innovative and additive outliers can be distinguished more clearly in a specific example. Consider a situation in which an individual’s cognitive ability is measured by using the Wechsler Adult Intelligence Scale (WAIS; Wechsler, 2008). One might be interested in assessing cognitive domains related to Attention Deficit Hyperactivity Disorder (ADHD) using the WAIS to evaluate the impact of ADHD medication. If an individual performed very well on scales related to information processing speed after taking stimulants (Nielsen, Wiig, Bäck, & Gustafsson, 2017), for example, this occasion-specific performance can be categorized as an additive outlier as the individual would not show such strong performance when not having taken stimulants. In contrast, the WAIS can also be administered to assess the impact of a traumatic brain injury. If an individual shows any suddenly reduced performance in information processing speed after being injured in an automobile accident, this lowered performance is expected to maintain to a degree (Mathias & Wheaton, 2007). In this case, the shock due to the accident would be classified as an innovative outlier.
The Kalman Filter (KF) and the Fixed Interval Smoother (FIS)
The outlier detection approaches considered in this article generally use by-products from running the Kalman Filter (KF) and the Fixed Interval Smoother (FIS) for estimating latent variable scores in linear SSMs under unknown values of the modeling parameters. In this section, we outline the basics of the KF and FIS, and summarize how parameter and standard error (SE) estimates can be obtained by means of parallel optimization of a raw data log-likelihood function, often termed the prediction error decomposition function (De Jong, 1988; Schweppe, 1965), constructed using by-products of the KF to yield maximum likelihood point estimates; and SE estimates from numerical Hessians of this log-likelihood function.
Starting from initial state estimate, η0, and initial process covariance matrix, P0, the KF (Kalman et al., 1960) recursively estimates each subsequent state vector and state covariance matrix using the following prediction and update processes for t = 1, … , Ti and i = 1, … N.
| (4) |
The subscript notation of it|t − 1, represents the prediction step at time t given observations up to time t − 1 for a subject i, and it|t represents the update step at the same time t now including the observation at time t for subject i. The basic idea of the KF is to recursively compute states based on prediction from the model and updates from measurements taking into account the reliability of the observed measurements (more details to follow). The KF starts with the prediction of state, ηit|t−1, from the previous state ηi,t−1|t−1 using the process equation (Equation 1). The Pit|t−1 is the covariance matrix of the predicted state, ηit|t−1, which indicates the magnitude of error by the prediction.
| (5) |
Next, the KF updates the state at time t, ηit|t, by taking a weighted average of the prediction and the measurement, based on the weights in the Kalman gain matrix, Kit. Intuitively, the Kalman Gain provides a proxy for the reliability of the measurements at time t as the ratio of the covariance variance of the prediction errors at the latent level, Pit|t−1, and the total covariance matrix of the prediction errors at the manifest level, Fit. Thus, the larger the absolute magnitudes of values in the Kalman gain, the more the update is affected by the observed measurements. Fit can be obtained from the covariance matrix of the manifest-level predictor errors or the individual innovation vector, υit, that is, the difference between the actual measurements and the measurement predictions from measurement equation in (Equation 3). Finally, the covariance update, Pit|t, is the covariance matrix of ηit|t.
As the KF recursively go through the all observations Y (across Ti timepoints and N participants) estimating parameters, the log-likelihood function or also called prediction error decomposition function can be written as a function of the computational by-products from the KF, the individual innovation vector, υit, and its associated covariance matrix, Fit,
| (6) |
where pit is the number of complete observed variables for participant i at time t. The log-likelihood function can be used to yield ML estimates of all pertinent modeling parameters in the set of time- and person-invariant parameters, θ = {λ, τ, B, α, Ψ, Θ}.
The FIS (Anderson & Moore, 1979) is a variant of the Kalman smoother, a backward recursive process for refining estimates of the states (i.e., latent variable scores) from the KF using observations from up to and beyond the current time point. This is in contrast to the KF, which derives state estimates at time t based on observations from k = 1, … , t, namely, information from up to and including the current time point, t. Doing so improves the accuracy of the state estimates when all observations have already been collected, as is the case in most social and behavioral sciences applications. The goal of FIS is to obtain estimates of ηit using observations from a fixed observation interval beyond time t, namely, yik for which t < k ≤ T , to refine the state estimates. Typically, k is set to T to yield the following backward recursive process that utilizes all available observations to estimate the states for t = T, … 1 as:
| (7) |
where Lit = B − KitΛ. The recursion begins with setting riT = 0 and NiT = 0, and computes new ri,t−1 and Ni,t−1 backwards in time.
Two types of shocks or disturbances have been newly defined in Equation 7. The first type is uit, which De Jong and Penzer (1998) referred to as smoothations, and it encompasses the weighted discrepancies between the observed measurements at time t, and their expected values given all but the t-th occasion of observed measurements. Thus, uit has the same size (p) as yit and can, alternatively, be obtained as (see Equation 7; De Jong and Penzer (1998)), with Mit being the covariance matrix of uit, and includes all but the t-th observed measurements from individual i. In other words, uit includes prediction errors that cannot be explained by all observations across the T measurement occasions, except for the information at the t-th time point. This may be contrasted with υit, the prediction errors that cannot be explained by all observations prior to time t (i.e., from the first to occasion t−1). The second type of disturbances is rit, which is a w-dimensional vector (i.e., the same size as the number of latent variables) that can alternatively be obtained as (see Equation 8; De Jong and Penzer (1998)), or in other words, from uit that accumulates from time t + 1 through T. These terms are key elements for constructing the diagnostic statistics to be described next.
Diagnostic statistics and Estimates of Outliers
Under the null hypothesis of no shocks, the maximum shocks to a person i’s data at any particular time t can be quantified as:
| (8) |
where rit, Nit, υit, and Fit, are components of the FIS, and the two parts of the statistic, and , are used to assess the potential of any particular time point as innovative and additive outliers, respectively. Here, combines the additive and innovative information, following a χ2 distribution with w + p degrees of freedom (df). Thus, an atypically large value of indicates that the data for participant i at time t are potentially either an innovative or additive outlier.
In the original proposal of De Jong and Penzer (1998), chi-square test statistics obtained from (8) would be used as a yardstick for initial screening of (any) outliers. As a supplementary note, they pointed out that the components of approximate independent chi–squared variables with df equal to p and w, respectively, and the components can be used as the statistic for independently detecting additive and innovative outliers:
| (9) |
| (10) |
where is the chi–square statistic for detecting innovative outliers, and is the chi–square statistic to detect additive outliers. An unusually large value of represents that person i’s latent scores at time t are potential innovative outliers, and an unusually large value of for person i at time t suggests the possibility of an additive outlier. To distinguish these statistics for the purposes of this study, hereafter the chi–square statistic, ρ*2, in Equation 8 will be called the joint chi–square statistic, whereas (Equation 9) and (Equation 10) will be called independent chi–square statistics for detecting innovative outliers and additive outliers, respectively.
The chi-square test statistics may be seen as a way to perform likelihood ratio comparisons between the null SSM in Equations (1)–(3) and an alternative model that includes vectors of innovative and additive outliers (referred to herein as the shock model) as:
| (11) |
| (12) |
where is the w × 1 vector containing the innovative outliers, and is the p × 1 vector consisting of the additive outliers. Let δit the magnitudes of the outliers for person i at time t. We can obtain , estimated outlier values, through the generalized least squares (GLS) procedure:
| (13) |
where Wit and Xit can be called the “shock design” matrices for innovative and additive outliers, and all the other elements in these equations are defined earlier for FIS (Equation 7). Consideration should be given to the design of Wit and Xit to acquire outlier estimates that are meaningful for the researchers’ desired purpose. First, if the design matrices are set as Wit = I and Xit = 0, then the w × 1 vector contains only the estimated innovative outliers. Second, if the matrices are set as Wit = 0 and Xit = I, then the p × 1 vector consists of only the estimates of the additive outliers. Third, if both innovative and additive outliers are of interest, the shock design matrices can be set as , then the first p elements of the p + w vector are the additive outliers estimates, and the last w elements of are the estimates of the innovative outliers. We provide options for specifying these three special cases of design matrices in our R package.
In addition to the chi–square tests, which offer overall assessments of the presence of outliers that impact all of the latent and manifest variables, De Jong and Penzer (1998) also suggested an alternative diagnostic measure based on t statistics obtained by dividing the estimated outliers, , by their standard errors. The t statistics allow the implementation of Wald tests of the extremeness of each latent and manifest variable value, if so desired. The t statistic for each latent and observed variable can be constructed as
| (14) |
where sh,it is the h-th element of sit and Sh,it indicates the hth diagonal element of the Sit. Note that the dimensions of the sit and Sit are also determined by the definition of the shock design matrices. For innovative outliers, t–tests evaluate the significance of the estimates of outliers at different time points with Ti − w degrees of freedom for the innovative outliers, and with Ti − p degrees of freedom for the additive outliers.
Following the diagnoses and estimation of outlier values, the shock model in Equations(11)—(12) would be re-fitted with the values of δit fixed at their estimated values, to yield final parameters estimates for inferential purposes. The values now give individuals with outlying values on particular variables at particular time points a unique set of deviations in intercept values. Doing so reduces the impact of the outlying data points in influencing the parameter estimates of the group as a whole. The full procedures from fitting the null SSM to the final shock model are outlined in Table 1.
Table 1.
Steps for Detecting Innovative and Additive Outliers.
| Steps | Procedures |
|---|---|
| 1 | Fit the null Model using KF. Estimate the set of person- and time-invariant parameters, θ, using the log-likelihood function. |
| 2 | Run the FIS to smooth ηit|T and estimate the associated covariance matrix. |
| 3 | Use by-products from Step 1, 2 to derive chi-square statistics, and use GLS procedure to derive and t statistic. |
| 4 | Identify potential outliers, for each person using the chi-square statistics or t statistic. |
| 5 | Incorporate the potential outliers into the shock Model. |
| 6 | Reestimate parameters in θ based on the shock Model. |
In summary, the joint chi–square statistic can be used as a global test of the existence of any outliers (irregardless of type), the independent chi–square statistics offer alternative chi–square tests that can distinguish between innovative and additive outliers, and lastly, the t statistic indicate shock points for specific latent or manifest variables. Despite the known asymptotic properties of these test statistics, the practical utility of these test statistics and the proposed outlier treatment strategy when used to evaluate the presence of outliers under finite sample sizes — either in conjunction or in isolation — remains unclear and has not been systematically evaluated.
Shock Signature for SSM
The model–implied means structure, E(yit), of the null model differs from the shock model due to the inclusion of additive and innovative outliers. The differences in E(yit) between the null and the shock model can be deduced from inspection of the “shock signature” Dit(j), which illustrates the effects of a single occurrence of an outlier through time (Chow et al., 2009; De Jong & Penzer, 1998). That is, all Wit and Xit are set to 0 except at a point t = j, with
| (15) |
where Bj indicates j repeated matrix multiplication of B, and Dit(j) describes the impact of the outlier at time t = j on the observed variables. The shock signature Dit(j) is equivalent to iteration of Equations (11) and (12). The shock signature focuses on the impact of outliers through the iteration excluding the influence due to the noise and the intercept terms (see Footnote 4 for a derivation of Dit(j); Chow et al., 2009). The shock signature equations also highlight the difference between additive and innovative outliers. If an additive and an innovative outlier both occurred at the same time t = j, the additive outlier would only affect the observed variables at the time t = j; however, the effect of the innovative outlier would be propagated forward in time by the transition matrix, B, and would be scaled by the factor loading matrix, Λ, from t = j + 1 onward.
Simulation Study
Even though De Jong and Penzer (1998) have shown analytically the asymptotic properties of their proposed test statistics, the practical performance of these test statistics under finite sample sizes is not well understood. In particular, issues related to the power (sensitivity) of the different test statistics when used in isolation or in conjunction with each other are not well understood. In addition, the practical implications of the outlier treatment strategy proposed by De Jong and Penzer (1998) also have not been systematically investigated. These practical implications are non-trivial given that falsely detected outlying points, when treated as outliers (i.e., with δit added to the associated time points), may also bias the inferential results.
We conducted a Monte Carlo (MC) simulation study to assess the performance of the proposed test statistics, and the utility as well as limitations of the proposed outlier treatment strategy in influencing final influential results. We considered the use of these outlier detection and treatment procedures under a process factor analysis model Browne and Nesselroade (2005), and with several finite sample size and parameter value conditions selected to mirror common sample sizes and parameter estimates reported for this model in the literature (e.g., Chow, Nesselroade, Shifren, & McArdle, 2004; Zhang, Hamaker, & Nesselroade, 2008).
We have three specific goals. Our first specific goal was to examine the Type–I error rates of the chi–square and t–test statistics. In order to validate whether the hypothesis testing procedure attain the advertised level of significance, We investigated that the three sets of test statistics yield the correct nominal levels of Type–I error (false detection) rates in the null case of no true shocks. In the context of outlier detection, a Type–I error occurs when the test statistics detect a shock, but no shock is truly present. We defined Type-I error rate to be the proportion of time points within a particular replication identified by the proposed test statistics as potential outliers, even though no true shocks were incorporated in the data generation process.
The next goal was to investigate power of the diagnostic statistics. In our definition, a desirable test statistic would detect the true outliers with high sensitivity (power), and would show low false detection rates. we examined the diagnostic statistics’ power to detect 3 known outliers each individual’s latent process time series and 3 known outliers in each individual’s observed time series. In summary, a total of 6 true outliers (3 innovative; 3 additive) were added to each individual’s data at randomly selected locations and for randomly selected variables. The average percentage of true vs. false detection was obtained to compare the performance of the joint chi-square test (, Equation 8), the independent chi-square tests ( in Equation 9 and in Equation 10), and the individual t-tests (Equation 14).
Our third specific goal was to examine the consequences of using the proposed outlier treatment strategy to remove the influence of the outliers identified using the three test statistics outlined. We examined the performance measures for the parameter estimates from the power simulation results, including relative bias, root mean square error, coverage, and difference between the standard deviations of parameters and average of the standard errors. We obtained relative bias where E represents the true parameter value, Ê is a parameter estimate from each MC replication, and R is the designated number of replications. Here, the RB was reported based on the rule to use RB not just bias when the true parameters are nonzero (Muthén & Muthén, 2002). An additional accuracy indicator of root mean square error (RMSE; ) was calculated. We also reported coverage which can be obtained by calculating the proportion of replications for which the true parameter is within the (1 – α) confidence interval. To evaluate the precision of the standard error estimates, we examined whether the estimated standard errors correctly represent the true sampling variation. We compared the average of the standard error estimates across MC replications and the MC standard deviations (). The latter is defined as the standard deviation of parameter estimates among MC replications. The difference between the mean standard error and the MC standard deviation should be minimal to indicate that standard error estimates suitably approximate the true sampling variation. We were specifically interested in how the performance measures change before and after re-fitting the data by applying the estimated outliers. To recall our notations, the model would be referred as null model before including the outliers (Equations 1 and 3) and as shock model after applying the outliers (Equation 11 and 12). The sample size and the S-to-N ratio were varied across the three simulation goals.
Simulation Design
The data were generated based on an SSM (Equation 1–3) with 2 latent variables, and 3 observed variables for each latent variable. For simplicity, both the intercepts in measurement and process equations, α and τ, were set to zero. The process noise, ζit, and the measurement errors, ∈it, were specified to be normally distributed with zero means and the covariance matrices Ψ and Θ, respectively. The covariance matrix of the process noise, Ψ, and the factor loading matrix, Λ, were set to have the following elements:
The covariance matrix of the measurement errors Θ, were set to a diagonal matrix with nonzero elements (0.2, 0.2, 0.2, 0.2, 0.2, 0.2).
In conditions where the goal was to evaluate power in the presence of real outliers, 3 known shock points were randomly introduced to both the latent and observation processes. Three random shocks were applied to latent process (η in Equation 1) to create innovative outliers. The magnitude of the outliers was set to 2.5 standard deviations from the diagonal element of the model-implied steady state covariance matrix, σ, (du Toit & Browne, 2007; Kitagawa, 1977):
| (16) |
Three random shocks were also added to observation process (y in Equation 3) to generate additive outliers, and the magnitude of the outliers were selected to be 2.5 standard deviations from the diagonal elements of the measurement covariance matrix, (ΛPΛ′ + Θ).
We evaluated the performance of the test statistics and outlier treatment strategy under different sample sizes and magnitudes of process dynamics. In order to examine the effects of sample size, 4 sample size configurations were considered: (a) T = 60, n = 100; (b) T = 60, n = 300; (c) T = 100, n = 60; (d) T = 300, n = 60. The magnitudes of process dynamics were manipulated by the following index of signal-to-noise ratio (S-to-N),
| (17) |
This S-to-N ratio begins with the asymptotic covariance of the latent variables (Equation 16). The denominator is a measure of the total dynamic noise variance: that is, the sum of the diagonal elements of the dynamic noise covariance matrix Ψ. The numerator is a measure of the variation in a dynamic system that is due to its intrinsic autoregressive properties. This S-to-N ratio similar to variance reduction factors sometimes discussed in a radar tracking context (e.g., Brookner, 1998). Equation 17 has the following properties:(1) it increases with as absolute value of the diagonal elements of B increase (i.e., stronger autoregressions lead to higher values), (2) it decreases with increasing diagonal elements of dynamic noise, (3) it has a discontinuity when the dynamics matrix B has eigenvalues on the imaginary unit circle (e.g., a multivariate random walk setting B to an identity matrix), and (4) it is not defined for unstable dynamics.
The effect of the process S-to-N ratio was examined in two different conditions of transition matrix B:
where B1 is for the high S-to-N condition that included larger elements of autoregression than the low S-to-N condition, B2. Following Equation 17 the high S-to-N condition has S-to-N value 28.74, whereas the low S-to-N condition has S-to-N value roughly one fourth the size at 7.74. Each simulated condition contained 500 replications, and the α–level was set to 0.01 for all conditions.
Simulation 1: Type–I Error Rates under the Null Model
We examined whether the proposed diagnostic procedure identifies “spurious” outliers at the expected Type–I error rates when the correctly specified model was fitted (i.e., the null hypothesis is the true model). The observed average Type–I error rates from MC simulations should approximate the pre-determined α-level.
The first simulation study was conducted to validate the nominal performance of the three sets of test statistics under moderate to large sample sizes, specifically the four sample size conditions were considered. In order to assess the effect of the process S-to-N ratio, the two different transition matrices defined earlier, B1 and B2, were also considered for the factor of the simulation. Data were generated from the SSM (Equation 1 and 3) with 2 latent variables, and 3 observed variables for each latent variable, which does not include any outliers. Thus, the proposed test statistics were expected to identify artificial outliers close to the chosen α-level of 0.01 which is the probability of a Type–I error: the probability of rejecting the null hypothesis when it is true. Table 2 shows the percentage of detected outliers from 500 replications with chi–square and t statistics.
Table 2.
The Type–I Error Simulation Results of the Chi-square and t statistics from 500 Replications. The Values are Percentage of the Detected Outliers.
| Factors | Jointa | Independent | t statistic | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-to-N | T | n | Innb. | Addc. | η1 | η2 | y1 | y2 | y3 | y4 | y5 | y6 | |
| High | 60 | 100 | .014 | .010 | .014 | .008 | .008 | .008 | .007 | .008 | .007 | .007 | .007 |
| 60 | 300 | .014 | .010 | .015 | .008 | .008 | .008 | .008 | .007 | .008 | .007 | .007 | |
| 100 | 60 | .013 | .010 | .013 | .009 | .009 | .008 | .008 | .009 | .008 | .008 | .008 | |
| 300 | 60 | .011 | .010 | .011 | .010 | .009 | .009 | .010 | .009 | .010 | .010 | .009 | |
| Low | 60 | 100 | .010 | .010 | .010 | .008 | .008 | .007 | .007 | .008 | .007 | .007 | .007 |
| 60 | 300 | .010 | .010 | .010 | .008 | .008 | .007 | .007 | .007 | .008 | .007 | .007 | |
| 100 | 60 | .010 | .010 | .010 | .009 | .008 | .009 | .009 | .008 | .008 | .009 | .009 | |
| 300 | 60 | .010 | .010 | .010 | .010 | .009 | .010 | .010 | .009 | .010 | .009 | .010 | |
Joint chi–square statistic ()
Independent chi–square statistic for innovative outlier ()
Independent chi–square statistic for additive outlier ()
The columns labeled “Joint”, “Inno” and “Add” summarize the Type–I error (false detection rates) associated with using the chi–square test statistic in Equation 8, 9, and 10, respectively, for outlier detection. The column labeled “t statistic” summarize the Type–I error using the t statistic in Equation 14.
We observed the clear tendency to approach the pre-defined nominal level of .01 as the number of time points increased from T = 60 to T = 300. The independent chi–square statistic for innovative outlier and t statistic approached the α–level from the lower value (e.g., .008). On the contrary, the joint chi–square and independent chi–square statistics for additive outlier moved toward the α–level from the higher values (e.g., .014). Importantly, increasing in the number of subjects did not have an impact on approaching magnitude of Type–I error. These results indicated that the proposed diagnostic statistics accomplished the advertised level of significance, and thus the following power simulations could be interpreted with confidence.
Simulation 2: Performance of Test Statistics in the Presence of Outliers
The goal of this simulation was to investigate power of the diagnostic statistics. We examined the time series data containing 6 true outliers (3 innovative; 3 additive) using the three diagnostic statistics. The average percentage of true and false detection was obtained.
The Table 3 shows the simulation results with regard to the power of the chi–square tests, and the simulation results for t–test are shown in Table 4. In addition to the percentage of the true detection, the false detection rates are shown in parenthesis. As noted, the joint chi–square statistic does not distinguish innovative from additive outliers. However, given that the nature of the outliers was known in the simulation study, we computed power separately for the innovative and additive outliers when the joint chi–square statistic was used to compare the relative sensitivity of this statistic in detecting the two kinds of outliers, especially in comparison to other test statistics.
Table 3.
The Power Simulation Results of Chi-square Tests from 500 Replications. The Values are Percentage of Power to Detect Outliers, and the Values in the Parenthesis are the False Detection Rates.
| Factors | Joint () | Independent | |||||
|---|---|---|---|---|---|---|---|
| S-to-Nd | T | n | Totala | Innb | Addc | Inn () | Add () |
| High | 60 | 100 | .764 (.148) | .565 (.081) | .963 (.060) | .917 (.002) | .963 (.060) |
| 60 | 300 | .764 (.148) | .566 (.081) | .963 (.060) | .917 (.002) | .977 (.041) | |
| 100 | 60 | .886 (.111) | .787 (.057) | .984 (.051) | .969 (.003) | .990 (.030) | |
| 300 | 60 | .967 (.047) | .939 (.024) | .995 (.023) | .993 (.006) | .997 (.014) | |
| Low | 60 | 100 | .218 (.037) | .090 (.024) | .347 (.011) | .181 (.007) | .402 (.010) |
| 60 | 300 | .219 (.038) | .090 (.025) | .347 (.011) | .181 (.006) | .401 (.010) | |
| 100 | 60 | .240 (.032) | .096 (.020) | .385 (.011) | .207 (.008) | .442 (.010) | |
| 300 | 60 | .268 (.025) | .111 (.014) | .425 (.011) | .249 (.009) | .484 (.010) | |
The power and the false detection rates for the joint chi-square statistics, when the total of the given 6 outliers (3 for latent and 3 for measurement component) were considered.
The abbreviation for innovative outliers.
The abbreviation for additive outliers.
The abbreviation for S-to-N.
Table 4.
The Power Simulation Results of t Tests from 500 Replications. The Values are Percentage of Power to Detect Outliers, and the Values in the Parenthesis are the False Detection Rates.
| S-to-N | Variables | T=60, n=100 | T=60, n=300 | T=100, n=60 | T=300, n=60 |
|---|---|---|---|---|---|
| High | η1 | 0.981 (.001) | 0.982 (.002) | 0.996 (.003) | 1.000 (.006) |
| η2 | 0.933 (.002) | 0.936 (.002) | 0.976 (.003) | 0.995 (.006) | |
| y1 | 1.000 (.004) | 1.000 (.004) | 1.000 (.005) | 1.000 (.007) | |
| y2 | 1.000 (.004) | 1.000 (.004) | 1.000 (.005) | 1.000 (.008) | |
| y3 | 1.000 (.004) | 1.000 (.004) | 1.000 (.005) | 1.000 (.008) | |
| y4 | 0.999 (.004) | 0.999 (.004) | 1.000 (.005) | 1.000 (.008) | |
| y5 | 0.999 (.004) | 0.999 (.004) | 1.000 (.005) | 1.000 (.008) | |
| y6 | 0.998 (.004) | 0.997 (.004) | 0.999 (.005) | 1.000 (.008) | |
| Low | η1 | 0.253 (.005) | 0.256 (.005) | 0.304 (.007) | 0.363 (.009) |
| η2 | 0.203 (.006) | 0.200 (.006) | 0.237 (.007) | 0.291 (.009) | |
| y1 | 0.749 (.005) | 0.743 (.005) | 0.778 (.007) | 0.816 (.009) | |
| y2 | 0.730 (.005) | 0.723 (.005) | 0.769 (.007) | 0.799 (.009) | |
| y3 | 0.694 (.005) | 0.694 (.005) | 0.737 (.007) | 0.772 (.009) | |
| y4 | 0.700 (.005) | 0.698 (.005) | 0.738 (.007) | 0.777 (.009) | |
| y5 | 0.680 (.005) | 0.686 (.005) | 0.726 (.007) | 0.762 (.009) | |
| y6 | 0.658 (.005) | 0.659 (.005) | 0.693 (.007) | 0.732 (.009) |
Results indicate that in the high S-to-N condition, all diagnostic statistics (the joint and independent chi–square and t statistics) showed higher power than the low S-to-N setting across all sample size conditions. Because more stable latent processes (as generated using relatively large autoregression parameters in B in the high S-to-N condition) allow the influence of outliers to persist longer in the system, the diagnostic statistics were also characterized by higher power under high S-to-N settings.
As the number of time points increased (from T=60 to 300), all the test statistics showed higher power to detect true outliers. Descending each column of Table 3 or traversing each row of Table 4 shows the change in power as a function of number of time points. Both the joint and the independent chi–square statistics generally showed reduced false detection rates as the number of time points increased. Although the t tests showed increasing false detection rates with temporal sample size, the rates were still below the nominal α–level of .01. Importantly, increasing in the number of subjects did not have an impact on the power to detect outliers (e.g., see power in the conditions with T = 60 and n = 100 compared to that in the conditions with T = 60 and n = 300). The results suggest that the number of time points provides more information to improve power for detecting outliers than corresponding increase in the number of persons. Furthermore, the interesting result is additive outliers were always detected with higher power than innovative outliers. In addition to showing lower power, the joint chi–square approach was also characterized by inflated false detection rates relative to the nominal level of .01. In contrast, the independent chi–square approach and the t–test always yielded false detection rates that were below, or close to the nominal level.
In summary, the power to detect outliers increased as in systems with larger S-to-N ratio, and as the number of time points increased. Among the proposed methods, the t statistic showed the greatest power, followed by the independent chi-square statistic. The false detection rates were substantially lower in the t–test results than in either of the chi-square results. Therefore, we can conclude that the t statistic is the most powerful and trustworthy in detecting outliers among the three sets of test statistics. In contrast, the joint chi-square approach consistently yielded lower power and higher false positive rates than the other two test statistics and is thus not recommended.
Simulation 3: Performance Evaluation – Point Estimates
In this section, the indicators of parameter accuracy measures such as RB, RMSE, coverage, difference between the standard deviations of parameters and average of the standard errors were used to evaluate the quality of the inferential results prior to and following the treatment of the identified outliers. As the accuracy of the estimate increases, smaller values would be expected from these measures.
Because our simulation results suggested that t–tests have the highest power and the lowest false detection rates compared to other chi–square tests, we focus on summarize inferential results after t–tests were used to identify outliers. We expected that: (a) Refitting the model after including the estimated outliers would improve the accuracy and precision of parameter estimation. (b) However, falsely detected outliers and non-detected true outliers may lower the accuracy and precision of parameter estimation.
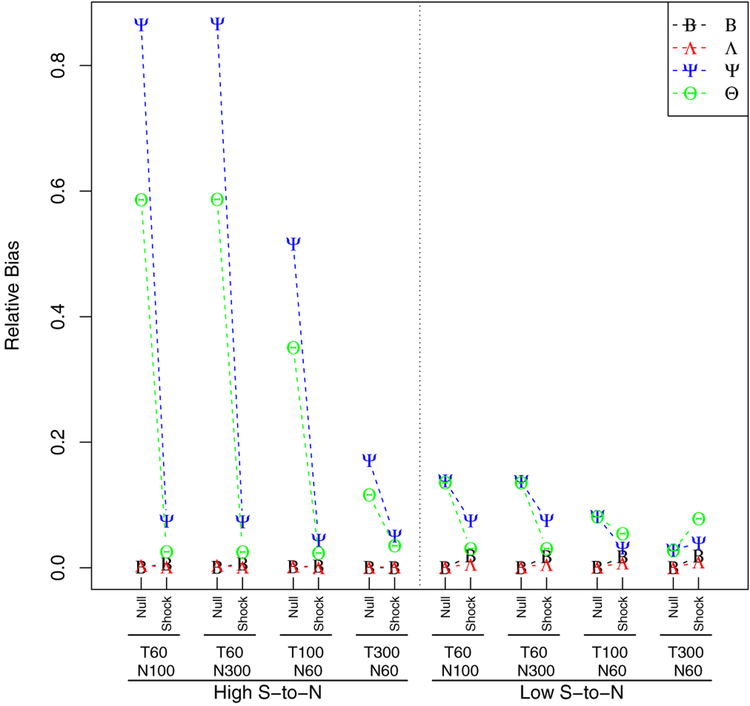
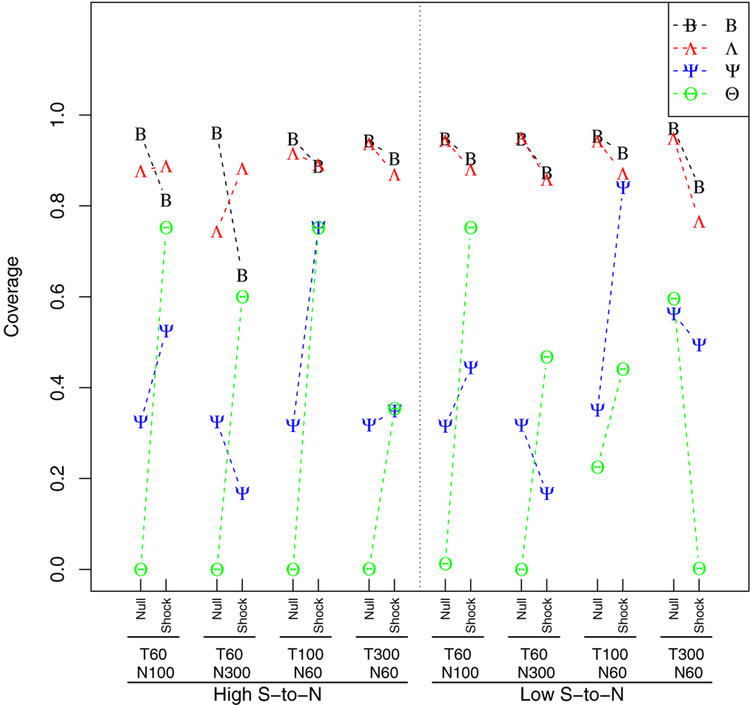
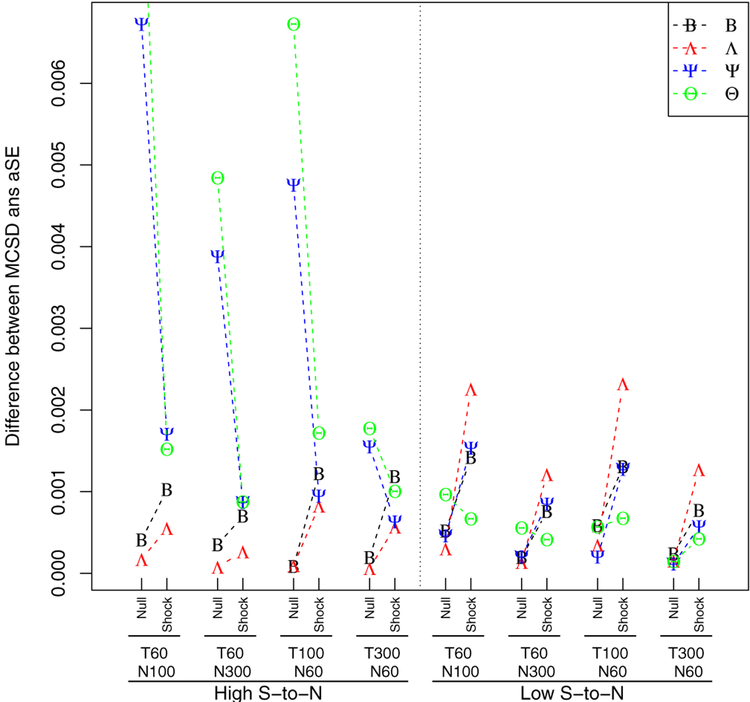
Results showed that the performance measures of individual parameters within B (transition matrix), Λ (factor loading matrix), Ψ (process noise matrix), and Θ (measurement noise or error matrix) produced largely comparable outcomes. Therefore, we grouped the parameters according to the matrix from which they come. Figures 1 - 3 present the average of the absolute values of the performance measures for the parameters related to each matrix (e.g., b11, b12, b21 and b22 in B). For each condition with a different sample size, the performance measures were calculated for the null model and the shock model.
Figure 1.
Relative Bias across the 500 MC Replications.
Figure 3.
Coverage across the 500 MC Replications.
The RB across 500 replications is shown in Figure 1. The results showed that the accuracy of parameter estimates as indicated by RB is influenced by the S-to-N. Specifically, the null model showed a large RB in the noise matrices (Ψ and Θ), indicating that the unusually large magnitude of outliers causes the variance estimates to deviate from their true values. Moreover, in the high S-to-N setting, the RB was larger in the process noise parameters than the measurement noise parameters. Given that the 3 known outliers were applied across 2 latent variables whereas the other 3 outliers were applied across 6 observed variables, the impact of introduced outliers was likely greater with regard to the latent variables (vs. observed variables). In other words, the outliers were spread more thinly over the observed variables than the latent variables. Thus the RB in the process noise parameters, Ψ was higher than in the measurement noise parameters, Θ.
The RB for the noise parameters was higher in the high S-to-N setting than in the low S-to-N setting. This result suggests that the influence of the outliers would persist more in the high S-to-N condition due to the larger autocorrelations, which leads to the large RB. For both the noise matrices, the large RB in the null model was substantially reduced after re-fitting the shock model. By contrast with the noise matrices, results showed a low RB for the parameters that are related to B and Λ. Although the RB tended to decrease slightly after applying the outliers (in the shock model), the magnitude of RB was still small.
Figure 2 shows the differences between the standard deviations of parameters across replications and the mean of the standard errors of the parameter estimates across the MC replications. The standard error is theoretically the standard deviation of the sampling distribution of a statistic, and thus the standard deviation of the collection of parameter estimates obtained by repeated sampling is an estimate of the standard error. For all conditions, the differences were fairly minimal, indicating that the standard errors from the simulation properly approximated the true sampling variation. Moreover, the standard deviations of parameters across the simulation were small, as all were smaller than .01. Note that mean square error consists of square of bias and square of standard error. Because of the ignorable standard errors, the results from RMSE were fairly close to the results from the RB, thus the Figure for the RMSE was omitted.
Figure 2.
The Difference between the Standard Deviations of Parameters and the Average of the Standard Errors across the 500 MC Replications.
These results indicate that the true outliers largely influence the estimation accuracy of the noise matrices but have little impact on the accuracy of the transition and the factor loading matrices. The true outliers had a stronger effect in the high S-to-N setting than in the low setting, indicating that the true outliers caused a more sustaining impact with a larger autoregression in the transition matrix B compared to the smaller autoregression in the low S-to-N condition. Additionally, the RB reduced as the number of time points increased, which indicates that the estimation became more accurate as the time points increased.
The coverage probability is shown in Figure 3. For the transition and factor loadings matrices (B and Λ), the coverage was reasonably high considering that the true outliers were included in the null model and that the falsely detected outliers and non-detected outliers were in the shock model. Contrary to the loadings and transition matrices, the noise matrices (Ψ and Θ) showed noticeably low coverage in both the low and high S-to-N settings. The noise matrices of the null model in the high S-to-N setting consistently showed low coverage for all sample sizes. In the low S-to-N condition, however, the coverage of the noise matrices of the null model increased as the number of time points increased. Here, the coverage for the shock model appears to change as a function of the number of the falsely detected outliers applied in the shock model, as opposed to just the rate of falsely detected outliers. Specifically, the number of the falsely detected outliers can be calculated based on the total number of time points and the false detection rates as shown in Table 4. We calculated the approximate number of the falsely detected outliers as follows: 20 (T=60, n=100), 50 (T=60, n=300), 25 (T=100, n=60), and 110 (T=300, n=60) for the low S-to-N setting, and 30 (T=60, n=100), 90 (T=60, n=300), 40 (T=100, n=60), and 160 (T=300, n=60) for the low S-to-N setting. Thus, as the number of falsely detected outliers increases, the parameter coverage tends to decrease.
Summary of Simulation Results
We conducted three simulation studies to evaluate the Type-I error rates (Simulation 1), the quality of the test statistics (Simulation 2), and the effects of the outlier handling procedures on point estimates (Simulation 3). The Type–I error rates simulation confirmed that all three types of the test statistics were valid, thus the subsequent power simulation results could be regarded with confidence. S-to-N variations were the most influential among the conditions studied. In the low S-to-N setting, the overall power was low across all sample size conditions, but increasing the number of time points measurably increased the power to detect outliers. However, an increase in the number of subjects had no such effect.
De Jong and Penzer (1998) initially proposed using the both joint and independent chi-square statistics as initial omnibus tests for the existence of outliers, and suggested the possible use of the t statistic as post hoc follow-up tests to further clarify the locations and nature of these outliers. In Simulation 2, we found that the performance of the both chi–square statistics in terms of power and false detection rate was less satisfactory compared to that associated with the t statistic. The joint chi-square statistic showed the lowest power and the highest false detection rate for all simulation conditions.
In addition to studying power, we also evaluated the performance of the estimates when ignoring the true outliers in a null model and when including the outliers detected by the proposed procedures in a shock model. In the null model, the estimates of the variances (Ψ and Θ) were biased. The biases were substantially reduced in the shock model by including the estimated outliers. The coverages also showed overall improvement when the estimated outliers were applied.
Empirical Data Analysis
In this section, we illustrate the usage of the diagnostic statistics for outlier detection procedures (see Table 1). The simulation study showed improved shock model performance by including estimated outliers as compared to the null model which ignored them. Therefore, using real data we compare the null and shock models with respect to parameter estimates, fit indices, and number of estimated outliers.
Data Descriptions
The data used in this application were part of a larger data set from the Affective Dynamics and Individual Differences (ADID; Emotions and Dynamic Systems Laboratory, 2010) study. Participants (ages ranging between 18 and 86 years) were asked to rate their momentary emotions 5 times a day, every day for one month. Items from the Positive Affect and Negative Affect Schedule (PANAS; Watson, Clark, & Tellegen, 1988) and the Circumplex Scale (Russell, 1980) were used to assess emotions at both low- and high-activation. The Circumplex Scale is known to capture more of the low-activation emotions whereas the PANAS tends to get at high-activation emotions.
The PANAS is an extensively used measure that assesses self-rated mood on two affective dimensions: Positive Affect (PA) and Negative Affect (NA). This is based on the two-factor model suggested by Watson and Tellegen (1985). The PA dimension reflects the extent to which an individual experiences high energy, alertness, and pleasurable feelings. The NA dimension reflects the extent to which an individual is in unpleasant, anhedonic, and aversive mood states (Watson et al., 1988). The Circumplex Scale postulates that the underlying structure of affective experience can be characterized as an ordering of affective states. The scale is constructed as a spatial model in which different sets of emotions fall along a continuum in a circle: pleasure, excitement, arousal, distress, displeasure, depression, sleepiness, and relaxation. According to this model, emotions should have decreasing positive correlations with one another as their separation approaches 90°. For example, at 90° separation, two affective states should be uncorrelated with one another, and should be negatively correlated as the separation approaches 180°.
Participants were asked to keep 1.5 to 4 hours between assessments, and at least one assessment was conducted in the evening. Due to this measurement schedule, the original data were irregularly spaced. Since the SSM, as a discrete time model, is designed to fit equally-spaced data, we aggregated the data to yield two composite scores per day. Participants with more than 65 % of missing data were excluded from our analysis, as well as participants with insufficient variability in their responses. As a result, our analyzed sample had 217 out of the original 273 participants. The number of measurements (i.e., time points) for each participant ranged from 26 to 74, and the mean missing data proportion was 18%. As Barton and Cattell (1974) suggested, three-item parcels were created as indicators for each of the two latent variables (PA and NA). We removed the linear trend in each indicator for each individual prior to the analysis.
Model Descriptions: Process Factor Analysis Model
The preliminary examination of the empirical data indicated that partial autocorrelations were significant at lag-1 but not at higher lags. Thus, we assume a simple SSM: the null model (Equation 1, 2, and 3) with the following parameter matrices
where all the elements of the transition matrix B were estimated. We assumed that the process noise ζit followed a multivariate normal distribution of . A simple two-factor model was set for the measurement equation: the first column of Λ represented the three positive item parcels were related to PA, and the second column represented the three negative item parcels related to NA. The latent state ηit comprised two latent variables: PAit and NAit. The mean vector a and the covariance matrix P for the multivariate normally distributed initial state, ηi0, were estimated. The measurement error ∈it followed a multivariate normal distribution of N(0, Θ), where Θ was a diagonal matrix with unique diagonal elements. Note that the intercepts of the process and measurement equations, α and τ , were set to 0.
Once we performed the outlier detection procedure using the null model (described in greater detail in the next section), we proceeded with the shock model. To demonstrate how to update the model via refitting and taking outliers into account (Equation 11 and 12), the shock design matrices and the estimated outliers are shown below:
where the shock design matrices Wi,t−1 and Xit were fixed to be identity matrices of the appropriate sizes, and contained the estimated outliers associated with the latent variables, PA and NA, and comprised the estimated outliers for the observed variables. We used the estimated outliers from the t-tests to diagnose outliers and then used GLS to estimate the magnitudes of the outliers determined to be statistically significant by means of the t-tests.
Outlier Detection with the Null and the Shock Model
We report the results from all the three diagnostic statistics for real world analysis in Table 5. The interpretation, however, is restricted mainly to the t–test results because the simulation suggested that the t statistic outperformed both of the chi–square statistics. Table 6 then shows the parameter estimates from the null and shock models. The outliers and the estimates were compared to examine whether the included outliers would improve model. For demonstration of the interpretation of the outliers, we used a pattern of outliers from a chosen participant. For all tests, α–level of .01 was applied. The shock model was constructed by incorporating the estimated outliers from the statistically significant t–tests.
Table 5.
The Number and the Percentage of Detected Outliers Using the Set of Diagnostic Outliers.
| Jointa | Innb | Addc | PA | NA | p1d | p2 | p3 | n1e | n2 | n3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Null | 700 (5.4%) | 365 (2.8%) | 635 (4.9%) | 212 (1.6%) | 237 (1.8%) | 202 (1.5%) | 201 (1.5%) | 179 (1.3%) | 250 (1.9%) | 247 (1.8%) | 253 (1.9%) |
| Shock | 387 (2.9%) | 144 (1.1%) | 444 (3.4%) | 89 (0.7%) | 127 (1.0%) | 106 (0.8%) | 120 (0.9%) | 113 (0.9%) | 209 (1.6%) | 172 (1.3%) | 180 (1.4%) |
Joint chi–square statistic.
Independent chi–square statistic for innovative outliers.
Independent chi–square statistic for additive outliers.
The first item parcel for PA
The first item parcel for NA
Table 6.
The Parameter Estimates from the Null Model and the Shock Model.
| Null Model | Shock Model | |||
|---|---|---|---|---|
| Parameter | Estimate | Std. Error | Estimate | Std. Error |
| bPP | 0.247*** | 0.012 | 0.250*** | 0.011 |
| bPN | −0.015 | 0.011 | −0.008 | 0.009 |
| bNP | −0.061*** | 0.013 | −0.069*** | 0.012 |
| bNN | 0.315*** | 0.012 | 0.296*** | 0.010 |
| λ21 | 1.004*** | 0.009 | 0.985*** | 0.008 |
| λ31 | 0.830*** | 0.009 | 0.827*** | 0.008 |
| λ53 | 1.021*** | 0.012 | 0.981*** | 0.009 |
| λ63 | 1.005*** | 0.012 | 0.975*** | 0.009 |
| ψ11 | 0.712*** | 0.013 | 0.645*** | 0.011 |
| ψ12 | −0.181*** | 0.008 | −0.146*** | 0.006 |
| ψ22 | 0.555*** | 0.012 | 0.422*** | 0.008 |
| θ1 | 0.202*** | 0.006 | 0.149*** | 0.004 |
| θ2 | 0.196*** | 0.006 | 0.162*** | 0.004 |
| θ3 | 0.443*** | 0.007 | 0.363*** | 0.006 |
| θ4 | 0.334*** | 0.007 | 0.216*** | 0.005 |
| θ5 | 0.306*** | 0.007 | 0.229*** | 0.005 |
| θ6 | 0.327*** | 0.007 | 0.229*** | 0.005 |
| aPA | 0.203* | 0.097 | 0.274** | 0.092 |
| aNA | 0.696*** | 0.106 | 0.611*** | 0.100 |
| p11 | 1.712*** | 0.186 | 1.604*** | 0.172 |
| p12 | 0.169 | 0.144 | 0.165 | 0.132 |
| p22 | 2.038*** | 0.224 | 1.891*** | 0.203 |
p <.05.
p <.001.
The number as well as the percentage of detected outliers are reported in Table 5. The percentages were calculated as the number of outliers detected divided by the total number of time points (12,972) across all the participants. The columns under the names of “Joint”, “Inn” and “Add” represent the detected outliers using the joint, independent innovative, and independent additive chi–square tests for outliers, respectively. The t–tests for each latent variable are in the columns PA and NA, and the t–tests for the item parcels are in the columns from p1 to n3. The three item parcels for PA are p1, p2, and p3, and for NA are n1, n2, and n3.
In the null model, the percentage of the detected outliers from the t–tests results for the latent and the measured variables all indicated a higher percentage of outliers than the nominal α–level of .01. In the shock model, however, the rate of outliers is reduced and, more notably, near the pre-specified α–level, especially for PA. It is also noteworthy that the sum of the number of outliers from the t–tests were smaller than the the number of outliers from the chi–square test, (i.e., 212 for PA plus 237 for NA was smaller than 365 from the independent chi–sqaure test for innovative outliers). Thus, the chi–square tests would contain a considerable proportion of falsely detected outliers, even accounting for the decreased number of outliers that could be caused by overlapping outlier time points among variables.
The number of detected outliers were all noticeably reduced in the shock model compared to the null model. The results in the shock model suggest the validity of the detected outliers using the t statistic, especially for PA (see the independent chi–square statistic for innovative and the t statistic related to PA, p1, p2, and p3), because the number of the newly detected outliers was close to the pre-defined α–level of .01. If all true outliers were removed, the expected rate of outliers would be the nominal .01 α–level (see the simulation results of Type–I error in Figure 2). Such was not the case for the outliers related to NA The percentages of outliers were reduced in the shock model but remained higher than .01. Note that if the null model explains the data well, then the shock model would effectively remove outliers and would achieve the α–level of outlier percentage. On the contrary, the rate of ouliers in the shock model exceeds the α–level. Thus, with this specific SSM for the empirical data, the shock model provided evidence of model misspecification related to NA.
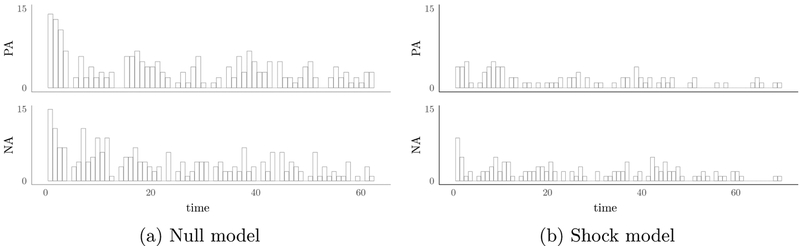
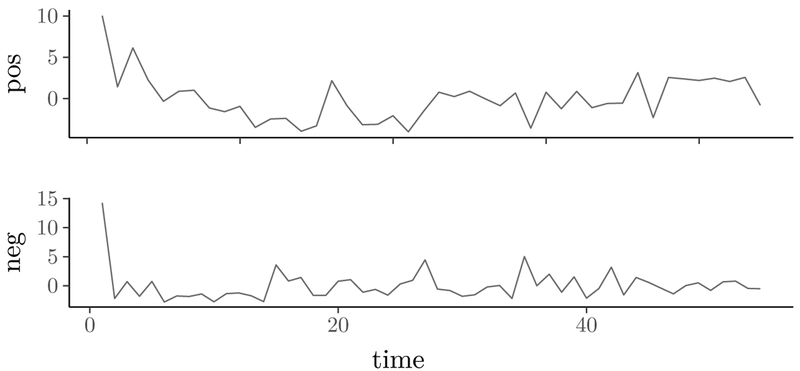
The outlier detection process could be used to recognize abnormalities in data. Empirically, we observed that there was a preponderance of outliers in the latent variables at the first few time points in the null model. The measured variables also showed a relatively large number of outliers in the first several time points. Figure 4a is the histogram of innovative outliers through time for all participants on PA and NA when the t–test was used for diagnosis. We noticed that the data from the participants who had outliers at the first time points had a tendency to show a peak of their observed variables at the first few time points. Figure 5 shows illustrative plots from two such participants. Prominent in both plots are the clear initial trends (declines) in “pos” (summed values of the 3 item pacels for PA) and “neg” (aggregated values of the 3 item pacels for NA) for these participants. Such trends were not captured by the null model and were identified by the diagnostic measures to be potential outliers. We proceeded with the shock model to examine changes in parameter estimates after outliers from the null model were incorporated. The relatively high frequency of the outliers at the first several time points disappeared (Figure 4b). Additionally, the shock model, which incorporates the estimated outliers, showed enhanced model fit in terms of parameter estimates. The parameter estimates for the null and the shock model are displayed in the Table 6. Although there were no drastic changes in the parameter estimates between the null and shock model, the shock model produced more efficient parameter estimates (i.e., smaller standard errors). Moreover, consistent with results from the simulation study, the variances (Ψ, Θ, and P) were reduced in the shock model compared to the null model.
Figure 4.
The Histogram of the Innovative Outliers for PA and NA through Time for all Participants when the t Test was Used for Diagnosis.
Figure 5.
The Observed Values Related to the PA and NA. The ‘pos’ Represents the Aggregated 3 Item Parcels for PA, and ‘neg’ Indicates the Aggregated 3 Item Parcels for NA. Representative participants 1141 for PA and 1089 for NA who showed a peak toward the first time points.
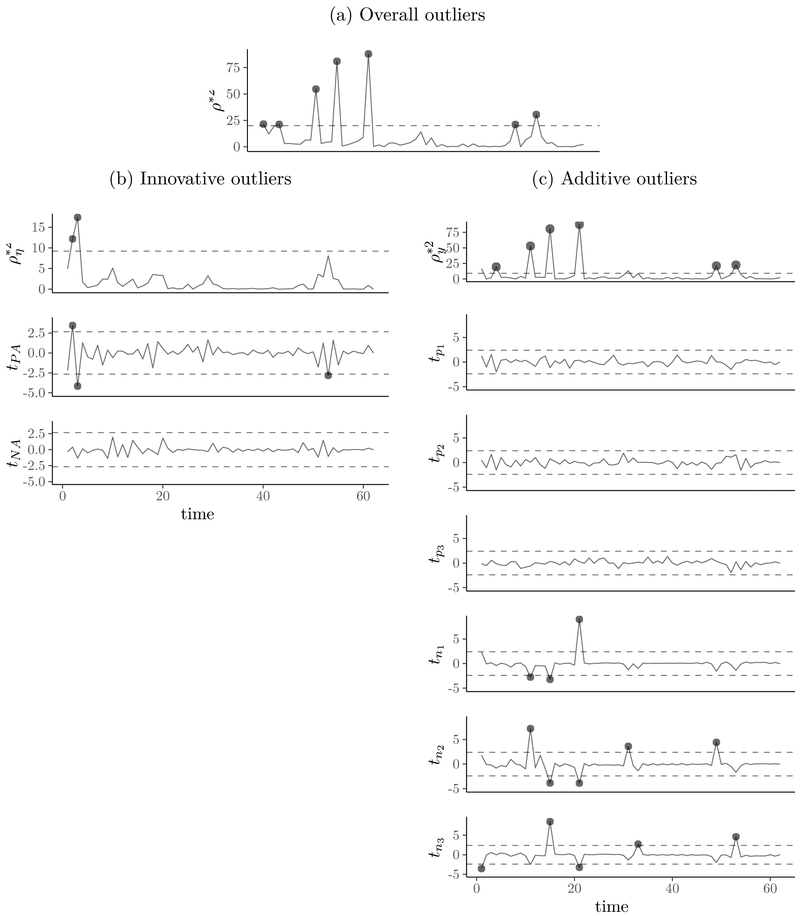
To illustrate how to interpret detected outliers, we show plots from a participant (ID number 1166) of the three diagnostic statistics with detected outliers according to the predefined α–level (Figure 6). Figure 6a shows the joint chi–square statistic with 8 degrees of freedom (df) for overall outlier detection. The outliers from the latent (Figure 6b) and measurement (Figure 6c) components follow below. The first graphs of the Figure 6b and 6c display the independent chi-square statistics with 2 df for innovative and 6 df for additive outliers. The other graphs are for the t statistics. To identify the innovative outliers, two t tests with 60 df (62 time points - 2) were conducted for PA and NA. Six individual t-tests with 56 df (62 - 6) were conducted to uncover the additive outliers related to the 6 observed variables. The black circles indicate the time points where the diagnostic statistics were significant, and the dashed lines represent the critical values of the chi–square and t statistics (.01 α–level in this analysis).
Figure 6.
Chi–square and t Statistics Associated with Outliers to the State and Measurement Components. The First Graph is for the Joint Chi–square Statistic, the Second Graph is for the Independent Chi–square Statistic, and the Other Graphs are for t Statistic. The Dashed Lines Indicate the Critical Values of Chi–square and t Statistics.
In Figure 6b, the independent chi–square statistic for innovative outliers () detected two outliers from the participant. The t statistic reported that the source of the outliers is NA. On the other hand, the t statistic describes the source of the additive outliers is PA (Figure 6c). According to the definition of outliers, We represent how to interpret the detected outliers in Figure 6 as follows. The abrupt up-shift at the item parcels related to PA, such as occasion t = 11 of the t–test tn2 in the Figure 6c, might indicate that the participant experienced sudden pleasant mood surge at the time, but its impact would disappear at the next time point. Specifically, in Equation 12, Xitδit only has impact at time t. In contrast, the innovative outliers incurred shocks to the state PA component continued to impact PA at subsequent time points. Hence, innovative outliers in state component could be regarded as “qualitative shocks”. As the participant experienced a positive outlier at time 2 for PA (Figure 6b), those pleasant or positive feelings permeate forward in time. More precisely, Wi,t−1δi,t−1 influences ηit, and then subsequently has impact on ηi,t+1 by multiplying B (Equation 11). In this manner, the innovative outlier has a continued effect on later η through time recursively, and also on measurement yit by means of Λ. In summary, the participant experienced a fundamental change in positive affect penetrating through time from the innovative outliers, and sudden volatile change related to negative affect by the additive outliers.
In this section, we investigated an empirical application of the outlier detection process. We showed the diagnostic approaches could be used as an indicator of model misspecification, and identified which part of the model should be scrutinized. Correspondingly, if the shock model achieves outlier reduction to the α–level for all variables especially from the t–tests, it might indicate the null model is sufficiently correct to represent the data with the detected outliers. In this case, fitting a shock model could offer an improved model by providing more refined parameter estimates by removing influential outliers. Additionally, a histogram of the estimated outliers could reveal an abnormal pattern in the data, such a large peak of outliers may indicate a training/habituation effect or may mark some external event impacting several participants.
Discussion
The objectives of this study were twofold: first, to evaluate the performance of a suite of outlier detection procedures using an MC simulation study, and second, to illustrate how these methods could be applied and enhanced to improve power and reduce false detection rates with real data.
We conducted three simulation studies to evaluate the Type-I error rates (Simulation 1), the quality of the test statistics (Simulation 2), and the effects of the outlier handling procedures on point estimates (Simulation 3). The Type-I error rates of the test statistics under conditions with no shock were found to be satisfactory and were close to the nominal rates. The power to detect outliers increased with increase in S-to-N ratio and the number of time points. Based on the simulation results, the t statistic showed the greatest power among the test statistics evaluated, followed by the independent chi-square statistic. The joint chi-square statistic showed notably poorer performance both in terms of false detection rates and power and is thus not recommended. Simulation 3 confirmed the utility of the proposed procedures in improving the quality of the point estimates when data with sufficiently high S-to-N ratio are available to allow for correct detection of outliers. This last simulation study also helped clarify the types of parameters that are more adversely affected by outliers if they are left undetected in the data set.
We recommend that researchers use the t–tests for their main outlier detection approach and use the independent chi–square statistics for checking the pattern of outliers and for overall outlier examination. For all conditions, the t–test outperformed the chi-square tests in both power and false detection rate. It should be noted, however, that although the false detection rate was lower with t–tests, the total number of false detections was often higher. Specifically, when detecting outliers for a model with T time points, w latent variables, and p observed variables, there will be T joint chi-square tests, 2T independent chi-square tests, and Twp t–tests. Thus, if w > 1 or p > 1 then Twp ≥ 2T > T with equality holding only when either w = 1 and p = 2 or w = 2 and p = 1. Thus, although the t statistic showed the highest power and low false detection rates, it is noteworthy that issues of multiple testing are aggravated by an increasing number of variables. Thus, researchers are advised to use theory or a priori knowledge to reduce the number of variables subjected to tests. In addition, when the shock model is examined, it is advisable to use the independent chi–square statistic as an additional gauge for successful outlier removal. For example, t–tests for PA (0.7%) and NA (1.0%) results were close to the α–level (1.0%), and the independent chi–square statistics upheld the removal of the innovative outliers (1.1%) (Table 5). As a counterexample, the outliers in the three item parcels for PA were successfully eliminated but the percentages of the ones for NA failed to reach the α–level, which was also reflected in the result of the independent chi–square test for additive outliers.
Simulation studies are always performed under highly controlled settings, thus generalization of results from the simulation study is limited. Results from designs other than those simulated may not be predicted directly from the results presented here. First, “in this study, the α–level was fixed to .01 for all statistics and conditions. Alternative scenarios that might give a fairer comparison between the chi–square and t-test approaches were not tested, such applying Bonferroni or Tukey multiple testing corrections to the t–test. Both power and false detection rate would decrease as the more strict α–level would raise the threshold for determining outliers (see the dashed bars in Figure 6b and 6c). Future studies should examine the effects of α–level corrections on the power and the false detection rate of the statistics.
Second, the finding of the positive relation between S-to-N and power for outlier detection might not be directly generalizable. In real data analysis, the parameter estimates from a null model would be used to calculate the S-to-N, but these estimates were biased when outliers existed. Moreover, the S-to-N is a relative metric, as the two components B and Ψ can vary, and small changes in the transition matrix alter the S-to-N dramatically due to the Kronecker product and the matrix inverse (Equation 17). Consequently, even when the true parameter were known, the value obtained could not be directly interpreted as low or high in an absolute sense without a baseline against which to compare. For example, in the simulation study, B1 was set to have relatively higher S-to-N compared to B2 when the noise matrix Ψ was fixed, but very different S-to-N values would result with different values of Ψ. One possibility to get a sense of range of the S-to-N ratio from an empirical analysis is to quantify the sampling variability or standard error for the S-to-N ratios using standard errors of the parameters via the delta method.
Third, the constant high power in detecting additive outliers for all conditions might be particular to our simulation settings. The results might indicate a larger ‘signal’ of the additive outliers compared to that of the innovative outliers. The true additive outliers were supposedly salient to be detected (i.e., 2.5 standard deviation of the model-implied covariance matrix), compared to the arbitrarily chosen S-to-N ratios of true innovative outliers. Future studies should investigate whether power or false detection rates response to different magnitude of additive outliers.
By definition an influential observation is one that has strong impact on the inferential results, such as values of the parameter estimates. In the present approach, we only performed rudimentary explorations of the influence of the outliers in affecting parameter estimates and other modeling results. The need to treat particular outliers was assessed only on the basis of whether their estimated magnitudeswere significantly different from zero. An alternative route would be to quantify the influence of the outliers, and only remove or attend to outliers that are influential (e.g., Banerjee & Frees, 1997; Cook, 1986; Kass, Tierney, & Kadane, 1989; Tang, Chow, Ibrahim, & Zhu, 2017; Zhu, Ibrahim, Lee, & Zhang, 2007). Future studies should evaluate the merits and limitations of different approaches for detecting and screening for outliers.
Even though we focused on evaluating the utility of the proposed diagnostic approaches for outlier detection and removal purposes, these methods can also be used as a tool for detecting change points. Specifically, the idea of change point studies is to detect locations that mark segments of piecewise homogeneous data. In a similar vein, the outlier detection approaches considered in this article can also be used to identify the time points (i.e., locations of the outliers) at which abrupt changes occurred, within the context of a given SSM, relative to other observations in the data. Because the proposed approach locates an unspecified number of outliers, the approach is akin to an unknown number of change points with unknown values (Chib, 1998; Harchaoui & Lévy-Leduc, 2010; Picard, Robin, Lavielle, Vaisse, & Daudin, 2005; Rabiner, 1989; Yao, 1988). In fact, outlier detection approaches provide an alternative way of evaluating whether it is necessary to incorporate potential “outliers” as change points.
Other extensions to the work presented in the current study may be considered. Thus far, the proposed approach is designed to work with linear, discrete time SSMs. Moreover, the simulation study only considered one model, the dynamic factor analysis model in the form of a SSM. Extensions of the approach to other models, such as continuous-time models (Chen, Chow, & Hunter, in press, 2017; Hamerle, Singer, & Nagl, 1993; Oud & Jansen, 2000; Singer, 1998; Voelkle & Oud, 2013), nonlinear dynamic models (Chow, Zu, Shifren, & Zhang, 2011; Fan & Yao, 2008; Molenaar & Raijmakers, 1998; Pagan, 1980), and regime-switching models (Bar-Shalom, Li, & Kirubarajan, 2004; Chow & Zhang, 2013; Kim & Nelson, 1999) would be helpful for generalization of the results.
Acknowledgments
Funding for this study was provided by the Intensive Longitudinal Health Behavior Cooperative Agreement Program funded by the National Institutes of Health under Award Number U24AA027684; and National Science Foundation grants IGE-180687 and SES-1357666, NIH grants R01HD07699, R01GM105004, Penn State Quantitative Social Sciences Initiative and UL TR000127 from the National Center for Advancing Translational Sciences.
Appendix
Sample dynr Code for Detecting Outliers.
The R package, dynr can be downloaded from CRAN. Here, we include some sample codes for fitting the model and re-fitting the model applying the detected outliers using simulated data. The data was generated from a SSM with 2 latent and 6 observed variables. The simulated data contains 3 innovative outliers, and 6 additive outliers.
library(dynr)
data(“Outliers”)
true_params <- c(.6, −.2, −.2, .5,# beta
.9, .8, .9, .8,# lambda
.3, −.1, .3,# psi
.2, .2, .2, .2, .2, .2)# theta
data_shk <- dynr.data(Outliers, id=‘id’, time=‘time’,
observed=c(‘V1’,’V2’,’V3’,’V4’,’V5’,’V6’))
meas_shk <- prep.measurement(
values.load=matrix(c(1.0, 0.0, 0.9, 0.0, 0.8, 0.0,
0.0, 1.0, 0.0, 0.9, 0.0, 0.8), ncol=2, byrow=TRUE),
params.load=matrix(c(‘fixed’,’fixed’,’l_21’,’fixed’,
‘l_31’,’fixed’,’fixed’,’fixed’,
‘fixed’,’l_52’,’fixed’,’l_62’), ncol=2, byrow=TRUE),
state.names=c(‘eta_1’,’eta_2’),
obs.names=c(‘V1’,’V2’,’V3’,’V4’,’V5’,’V6’) )
nois_shk <- prep.noise(
values.latent=matrix(c(0.3, −0.1,
−0.1, 0.3), ncol=2, byrow=TRUE),
params.latent=matrix(c(‘psi_11’,’psi_12’,
‘psi_12’,’psi_22’), ncol=2, byrow=TRUE),
values.observed=diag(c(0.2, 0.2, 0.2, 0.2, 0.2, 0.2), ncol=6, nrow=6),
params.observed=diag( paste0(‘e_’, 1:6), 6) )
init_shk <- prep.initial(
values.inistate=c(0,0), params.inistate=c(‘mu_1’,’mu_2’),
values.inicov=matrix(c(0.3,−0.1,−0.1,0.3), ncol=2, byrow=TRUE),
params.inicov=matrix(c(’c_11’,’c_12’,’c_12’,’c_22’), ncol=2, byrow=TRUE) )
dynm_shk <- prep.matrixDynamics(
values.dyn=matrix(c(0.8,−0.2,−0.2,0.7), ncol=2, byrow=TRUE),
params.dyn=matrix(c(‘b_11’,’b_12’,’b_21’,’b_22’), ncol=2, byrow=TRUE), isContinuousTime=FALSE)
model_shk <- dynr.model(dynamics=dynm_shk, measurement=meas_shk,
noise=nois_shk, initial=init_shk,
data=data_shk, outfile=paste0(“model_shk.c”))
cook_shk <- dynr.cook(model_shk, debug_flag=TRUE)
plotFormula(model_shk2, cook_shk2@transformed.parameters)
taste_shk <- dynr.taste(model_shk, cook_shk, conf.level=.99)
taste_plot <- autoplot(taste_shk)
taste2_shk <- dynr.taste2(model_shk, cook_shk, taste_shk,
newOutfile=“taste2_shk.c”)
# compare the true parameters and the estimated parameters data.frame(true=true_params, cook=coef(cook_shk)[1:17])
References
- Anderson BDO, & Moore JB (1979). Optimal filtering. Englewood Cliffs: Prentice Hall. [Google Scholar]
- Banerjee M, & Frees EW (1997). Influence diagnostics for linear longitudinal models. Journal of the American Statistical Association, 92, 999–1005. [Google Scholar]
- Bar-Shalom Y, Li XR, & Kirubarajan T (2004). Estimation with applications to tracking and navigation: theory algorithms and software. John Wiley & Sons. [Google Scholar]
- Barton K, & Cattell R (1974). Changes in psychological state measures and time of day. Psychological Reports, 35 (1), 219–222. [DOI] [PubMed] [Google Scholar]
- Box GE, & Tiao GC (1975). Intervention analysis with applications to economic and environmental problems. Journal of the American Statistical Association, 70 (349), 70–79. [Google Scholar]
- Brookner E (1998). Tracking and Kalman filtering made easy. New York: Wiley. [Google Scholar]
- Browne MW, & Nesselroade JR (2005). Representing psychological processes with dynamic factor models: Some promising uses and extensions of autoregressive moving average time series models In Maydeu-Olivares A & McArdle JJ (Eds.), Contemporary psychometrics: A Festschrift for Roderick P. McDonald (p. 415–452). Mahwah, NJ: Erlbaum. [Google Scholar]
- Carter CK, & Kohn R (1994). On gibbs sampling for state space models. Biometrika,81 (3), 541–553. [Google Scholar]
- Chang I, Tiao GC, & Chen C (1988). Estimation of time series parameters in the presence of outliers. Technometrics, 30 (2), 193–204. [Google Scholar]
- Chen M, Chow S-M, & Hunter M (in press, 2017). Stochastic differential equation models with time-varying parameters In Continuous-time modeling in the behavioral and related sciences. Berlin: Springer-Verlag. [Google Scholar]
- Chib S (1998). Estimation and comparison of multiple change-point models. Journal of Econometrics, 86 (2), 221–241. [Google Scholar]
- Chow S-M, Hamaker EL, & Allaire JC (2009). Using innovative outliers to detect discrete shifts in dynamics in group-based state-space models. Multivariate Behavioral Research, 44 (4), 465–496. [DOI] [PubMed] [Google Scholar]
- Chow S-M, Ho M-HR, Hamaker EJ, & Dolan CV (2010). Equivalences and differences between structural equation and state-space modeling frameworks. Structural Equation Modeling, 17 (303–332). [Google Scholar]
- Chow S-M, Nesselroade JR, Shifren K, & McArdle JJ (2004). Dynamic structure of emotions among individuals with Parkinson’s disease. Structural Equation Modeling, 11, 560–582. doi: 10.1207/s15328007sem1104_4 [DOI] [Google Scholar]
- Chow S-M, & Zhang G (2013). Nonlinear regime-switching state-space (RSSS) models. Psychometrika: Application Reviews and Case Studies, 78 (4), 740–768. [DOI] [PubMed] [Google Scholar]
- Chow S-M, Zu J, Shifren K, & Zhang G (2011). Dynamic factor analysis models with time-varying parameters. Multivariate Behavioral Research, 46 (2), 303–339. doi: 10.1080/00273171.2011.563697 [DOI] [PubMed] [Google Scholar]
- Cook RD (1986). Assessment of local influence (with Discussion). Journal of the Royal Statistical Society, Series B: Methodological, 48, 133–169. [Google Scholar]
- Cook RD, & Weisberg S (1982). Residuals and influence in regression. New York: Chapman and Hall. [Google Scholar]
- De Jong P (1988). The likelihood for a state space model. Biometrika, 75 (1), 165–169. doi: 10.2307/2336450 [DOI] [Google Scholar]
- De Jong P, & Penzer J (1998). Diagnosing shocks in time series. Journal of American Statistical Association, 93, 796–806. [Google Scholar]
- du Toit SH, & Browne MW (2007). Structural equation modeling of multivariate time series. Multivariate Behavioral Research, 42 (1), 67–101. [DOI] [PubMed] [Google Scholar]
- Emotions and Dynamic Systems Laboratory. (2010). The affective dynamics and individual differences (ADID) study: developing non-stationary and network-based methods for modeling the perception and physiology of emotions [Computer software manual]. [Google Scholar]
- Fan J, & Yao Q (2008). Nonlinear time series: nonparametric and parametric methods. Springer Science & Business Media. [Google Scholar]
- Fox AJ (1972). Outliers in time series. Journal of the Royal Statistical Society, Series B, 34, 350–363. [Google Scholar]
- Fried R, Gather U, & Imhoff M (2001). Online pattern recognition in intensive care medicine. In Proceedings of the amia symposium (p. 184). [PMC free article] [PubMed] [Google Scholar]
- Hamerle A, Singer H, & Nagl W (1993). Identification and estimation of continuous time dynamic systems with exogenous variables using panel data. Econometric Theory, 9 (2), 283–295. [Google Scholar]
- Harchaoui Z, & Lévy-Leduc C (2010). Multiple change-point estimation with a total variation penalty. Journal of the American Statistical Association, 105 (492), 1480–1493. [Google Scholar]
- Harvey AC (2001). Forecasting, structural time series models and the Kalman filter. Cambridge: Cambridge University Press. [Google Scholar]
- Harvey AC, & Koopman SJ (1992). Diagnostic checking of unobserved components time series models. Journal of Business and Economic Statistics, 10, 377–389. [Google Scholar]
- Hazrana J (2017). Modelling international oilseed prices: an application of the structural time series model. International Journal of Food and Agricultural Economics, 5 (2), 25. [Google Scholar]
- Kalman RE, et al. (1960). A new approach to linear filtering and prediction problems.Journal of basic Engineering, 82 (1), 35–45. [Google Scholar]
- Kass RE, Tierney L, & Kadane JB (1989). Approximate methods for assessing influence and sensitivity in Bayesian analysis. Biometrika, 76, 663–674. [Google Scholar]
- Kim C-J, & Nelson CR (1999). State-space models with regime switching: Classical and Gibbs-sampling approaches with applications. Cambridge, MA: MIT Press. [Google Scholar]
- Kitagawa G (1977). An algorithm for solving the matrix equation X = FXFT + S. International Journal of Control, 25 (5), 745–753. doi: 10.1080/00207177708922266 [DOI] [Google Scholar]
- Mathias JL, & Wheaton P (2007). Changes in attention and information-processing speed following severe traumatic brain injury: a meta-analytic review. American Psychological Association. [DOI] [PubMed] [Google Scholar]
- McCulloch RE, & Tsay RS (1993). Bayesian inference and prediction for mean and variance shifts in autoregressive time series. Journal of the American Statistical Association, 88 (423), 968–978. [Google Scholar]
- Molenaar PC, & Raijmakers M (1998). Fitting nonlinear dynamical models directly to observed time series. Applications of Nonlinear Dynamics to Developmental Process Modeling, 269–297. [Google Scholar]
- Muthén LK, & Muthén BO (2002). How to use a monte carlo study to decide on sample size and determine power. Structural Equation Modeling, 9 (4), 599–620. [Google Scholar]
- Nielsen NP, Wiig EH, Bäck S, & Gustafsson J (2017). Processing speed can monitor stimulant-medication effects in adults with attention deficit disorder with hyperactivity. Nordic Journal of Psychiatry, 71 (4), 296–303. [DOI] [PubMed] [Google Scholar]
- Ou L, Hunter MD, & Chow S-M (2016). dynr: Dynamic modeling in r [Computer software manual]. (R package version 0.1.7–22) [Google Scholar]
- Ou L, Hunter MD, & Chow S-M (2018, revised and resubmitted). What’s for dynr:A package for linear and nonlinear dynamic modeling in R. The R Journal. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oud JH, & Jansen RA (2000). Continuous time state space modeling of panel data by means of sem. Psychometrika, 65 (2), 199–215. [Google Scholar]
- Pagan A (1980). Some identification and estimation results for regression models with stochastically varying coefficients. Journal of Econometrics, 13 (3), 341–363. [Google Scholar]
- Picard F, Robin S, Lavielle M, Vaisse C, & Daudin J-J (2005). A statistical approach for array cgh data analysis. BMC Bioinformatics, 6 (1), 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner LR (1989). A tutorial on hidden markov models and selected applications in speech recognition. Proceedings of the IEEE, 77 (2), 257–286. [Google Scholar]
- Russell JA (1980). A circumplex model of affect. Journal of Personality and Social Psychology, 39 (1-sup-6), 1161–1178. [Google Scholar]
- Schweppe FC (1965). Evaluation of likelihood functions for Gaussian signals. IEEE Transactions on Information Theory, IT-11, 61–70. [Google Scholar]
- Selukar R (2011). State space modeling using SAS. Journal of Statistical Software, 41 (12),1–13. [Google Scholar]
- Shephard N (1994). Partial non-gaussian state space. Biometrika, 81 (1), 115–131. [Google Scholar]
- Singer H (1998). Continuous panel models with time dependent parameters. Journal of Mathematical Sociology, 23 (2), 77–98. [Google Scholar]
- Tang N, Chow S-M, Ibrahim JG, & Zhu H (2017, December 01). Bayesian sensitivity analysis of a nonlinear dynamic factor analysis model with nonparametric prior and possible nonignorable missingness. Psychometrika, 82 (4), 875–903. doi: 10.1007/s11336-017-9587-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsay RS (1988). Outliers, level shifts, and variance changes in time series. Journal of Forecasting, 7 (1), 1–20. [Google Scholar]
- Voelkle MC, & Oud JHL (2013). Continuous time modelling with individually varying time intervals for oscillating and non-oscillating processes. British Journal of Mathematical and Statistical Psychology, 103–126. doi: 10.1111/j.2044-8317.2012.02043.x [DOI] [PubMed] [Google Scholar]
- Watson D, Clark LA, & Tellegen A (1988). Development and validation of brief measures of positive and negative affect: the panas scales. Journal of Personality and Social Psychology, 54 (6), 1063. [DOI] [PubMed] [Google Scholar]
- Watson D, & Tellegen A (1985). Toward a consensual structure of mood. Psychological Bulletin, 98 (2), 219–235. [DOI] [PubMed] [Google Scholar]
- Wechsler D (2008). Wechsler adult intelligence scale–Fourth Edition (WAIS–IV). San Antonio, TX: NCS Pearson, 22, 498. [Google Scholar]
- Yao Y-C (1988). Estimating the number of change-points via schwarz’criterion. Statistics & Probability Letters, 6 (3), 181–189. [Google Scholar]
- Zhang Z, Hamaker EL, & Nesselroade JR (2008). Comparisons of four methods for estimating a dynamic factor model. Structural Equation Modeling, 15, 377–402. doi: 10.1080/10705510802154281 [DOI] [Google Scholar]
- Zhu H, Ibrahim JG, Lee SY, & Zhang HP (2007). Appropriate perturbation and influence measures in local influence. Annals of Statistics, 35 (6), 2565–2588. doi: 10.1214/009053607000000343 [DOI] [Google Scholar]