Tensors and compositionality in neural systems

Abstract

Neither neurobiological nor process models of meaning composition specify the operator through which constituent parts are bound together into compositional structures. In this paper, we argue that a neurophysiological computation system cannot achieve the compositionality exhibited in human thought and language if it were to rely on a multiplicative operator to perform binding, as the tensor product (TP)-based systems that have been widely adopted in cognitive science, neuroscience and artificial intelligence do. We show via simulation and two behavioural experiments that TPs violate variable-value independence, but human behaviour does not. Specifically, TPs fail to capture that in the statements fuzzy cactus and fuzzy penguin, both cactus and penguin are predicated by fuzzy(x) and belong to the set of fuzzy things, rendering these arguments similar to each other. Consistent with that thesis, people judged arguments that shared the same role to be similar, even when those arguments themselves (e.g., cacti and penguins) were judged to be dissimilar when in isolation. By contrast, the similarity of the TPs representing fuzzy(cactus) and fuzzy(penguin) was determined by the similarity of the arguments, which in this case approaches zero. Based on these results, we argue that neural systems that use TPs for binding cannot approximate how the human mind and brain represent compositional information during processing. We describe a contrasting binding mechanism that any physiological or artificial neural system could use to maintain independence between a role and its argument, a prerequisite for compositionality and, thus, for instantiating the expressive power of human thought and language in a neural system.

This article is part of the theme issue ‘Towards mechanistic models of meaning composition’.

1. Introduction

Our ability to use language indicates something foundational about how our minds and brains represent, transform and reason about the world around us. Namely, it indicates that we are able to think of combinations of words, concepts, objects, features, and events, and their organization [1–5]. The language we use to denote such meanings consists of sequences of words, whose meanings, like the conceptual representations underlying them, must be composed. Importantly, the composition process need not mirror regularities in our experience of the world: for example, while all bananas are naturally shades of green, yellow, brown or black, we can easily conceive of a hot pink banana, encode this thought in a phrase like ‘A hot pink banana’, and safely assume that anyone who hears it or reads it will share the same thought we started with.¹ In this sense, meaning composition might be the lynchpin of cognition, necessary for explaining the formal expressive power and creativity of human thought, reasoning, language and communication [6]. To this point, meaning composition has been called the ‘holy grail’ of cognitive science [7].

Compositionality is a property of a system. In a compositional system, complex entities are built as collections of simpler entities, and the meanings of these entities are a function of the meaning of the constituent simpler entities and their arrangement (see [8], for a category theoretic formalization, [9] for a hybrid distributional typed formalism; [10]). Compositionality has been a subject of interest in philosophy, logic and linguistics for nearly as long as these disciplines, both modern and ancient, across east and west, have existed (see [11] for a historical perspective; particularly the contribution of the Vedic scholar Śabara-svāmin in the fourth/fifth century CE;² also [13–16]). In the language domain, compositionality typically refers to the property that meanings of composed structures are a function of the meanings of constituent units and the rules used to combine those units into that structure [14,16–19]. For example, we combine individual words like ‘Jane’, ‘goes to’ and ‘the store’ to form the sentence ‘Jane goes to the store’. The meaning of the resulting phrase is a function not only of the individual words, but their order (e.g., ‘the store goes to Jane’ means something different). In the limit (as long as recursion is supported), compositionality represents the capacity to combine a finite set of objects into an infinite set of combinations [20,21].

Two key properties of a compositional system are that the meaning of a compositional structure is a function of the constituent elements and their arrangement, and, simultaneously, that the meaning of the individual elements do no systematically vary as a function of their position in the compositional structure. Following the above example, the meaning of ‘Jane goes to the store’ is a function of the words and their arrangement, but the arrangement does not change what Jane or store means.³ For a system to have the expressive power that compositionality imbues (viz., human language), and, at the same time, to arise in the mind and brain, implies that at some level individual meaning parts (e.g., concepts, words, predicates, inflectional and derivational morphemes) and larger meaning structures (e.g., conceptual combinations, phrases, propositions, sentences) must coexist or co-occur in the system. Yet crucially, as we will argue in this paper, they must do so independently from one another, at least at certain moments in processing, in the space–time of neural representations, such that words and concepts can be combined together without compromising the system's access (in the limit) to the representation and meaning of the original constituent parts. Instantiating a neural system such that it can support compositionality requires solving the problem of binding elements together in a manner that maintains their structure and their independence (e.g., [3,10]). Several mechanisms for instantiating binding in a neural system have been proposed. One of the most popular involves using tensor products (TPs) to bind elements ([23–26]; but see [3,27]).

In the following, we present simulations and data from two behavioural experiments that suggest that conjunctive and multiplicative operators, such as the TP, lead to system behaviour that is at odds with human behaviour. We show that TPs, and other conjunctive coding schemes, violate the independence of a variable and its value for binding representations together [3,28], an operation that is crucial for meaning composition and cognition more broadly [1,2,5,29–32]. We demonstrate how this violation occurs, and discuss why variable-value independence is important for theories and models of human cognition, including for natural language [3,27], and for any system to have compositionality. We describe an existing compositional solution implemented in a neural network [1,5,30,33] and its origins [34,35]. We conclude that tensor-based systems cannot support compositionality without additional modeller-derived interventions (e.g., modeller-determined labelling, specialized deconvolution functions or look-up tables) and suggest that the representational basis of the human mind and brain, and any system that desires to emulate it, should be built on a neurophysiological system that can support compositionality during processing.

For the present purposes, we are interested in binding as instantiating links between roles and their fillers (e.g., [2,29,32]). The role represents the filler's place in the larger structure, be it as the argument to a single-place predicate, or a phrase, sentence or proposition. The filler occupies the argument role and is operated on by the predicate during interpretation to produce meaning [18]. In this sense, binding can be seen as an elementary subroutine of meaning composition. However, we stress that in order for a system to be compositional, the mechanism that carries binding information must be completely independent of the representational elements that specify the identity of the active fillers, roles and predicates within that system [1,3,5,10,28,29], and so, in the case of neural systems, in neural space–time. For example, the representational elements fuzzy and penguin, and prickly and cactus might be bound to form the propositions fuzzy(penguin) and prickly(cactus). While the statement fuzzy(penguin) has meaning (a penguin that has the property of having fuzz or being fuzzy), the elements fuzzy and penguin remain independent when so bound. That is, the predicate fuzzy means the same thing whether it is bound to ‘penguin’, ‘cactus’ or ‘dendrite’.⁴ Second, the binding tag (the signal carrying the binding information) must be dynamic. That is, it must allow bindings to be created and destroyed on the fly. For instance, if the penguin in the above example gets a buzz-cut, the binding of fuzzy and penguin must be broken, and the very-same representation of penguin must be bound to the prickly predicate to form prickly(penguin) where the same representational element coding for prickly in prickly(cactus) is bound to the same representational element coding for the penguin in fuzzy(penguin).

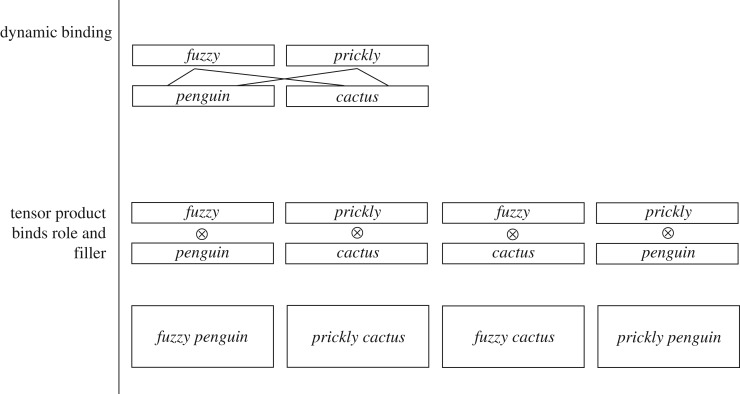
In tensor-based systems, TPs are used to bind information, including argument roles and their fillers [3,10,23,25,26,29,36]. Figure 1 illustrates how a tensor-based system would represent the examples (i) fuzzy cactus and (ii) fuzzy penguin. Hummel and colleagues [3,10] have shown mathematically that TPs violate role–filler independence. In short, because TPs rely on a multiplicative operation, the binding of two items is an interactive rather than independence-maintaining, or additive, operation. We provide details of simulations demonstrating this point in electronic supplementary material, appendix A, but in short, once the roles and fillers are bound into a TP, the similarity of a word or concept to itself (e.g., fuzzy(penguin) versus fuzzy(cactus)) changes as a function of the similarity of the other words or concepts it is bound to. So, a fuzzy penguin and a fuzzy cactus will not be similar unless penguins and cactus are also similar. In fact, in the limit, the similarity between fuzzy(x) and fuzzy(y) approaches zero as the similarities of x and y approach zero.

Figure 1.

An illustration of two representational coding schemes for the predicates fuzzy (penguin), fuzzy (cactus), prickly (penguin) and prickly (cactus). In a role–filler binding calculus, these propositions can be represented as one-place predicates. The top panel is a cartoon illustration of how a compositional system that uses dynamic binding would bind the predicates and arguments. The bottom panel is a cartoon illustration, inspired by Dolan & Smolensky [23], of how a tensor-based system would perform binding.

Essentially by composing fuzzy with penguin or cactus using TPs, information about being in the set of fuzzy things is being shared across fuzzy cactus and fuzzy penguin. But, in a system that uses TPs for binding, the information that both cactus and penguin belong to the set of fuzzy things is not available during composition without an additional mechanism for tracking the binding relation between fuzzy penguin and fuzzy and penguin (e.g., a function that indicates which arguments (cactus, penguin) went into which TP (fuzzy cactus, fuzzy penguin), a look-up table with that information or simply the knowledge of the modeller looking at the values in the network). Another consequence of a TP-based architecture without a tracking mechanism is that binding information (viz., the fact that fuzzy penguin goes with fuzzy and penguin) is not available to other neurons in the network during meaning composition; binding information must be available to downstream neurons in order for the system to maintain variable-value independence—for the system to be functionally symbolic, and for the behaviour of the system to align with that of humans.

By contrast, in a binding system that maintains role–filler independence, the similarity of x to itself is fixed, regardless of what it is bound to. This makes the prediction that in prickly penguin and fuzzy penguin, the representation of penguin will be the same, or have identity with itself. And fuzzy penguin and fuzzy cactus will share the property of being fuzzy in the system, and as such, should not be judged as completely dissimilar.

To address the question of whether people can judge the similarity of a composed phrase independently of similarity judgements of the words that compose it, we performed two behavioural experiments probing the similarity of words and phrases and then modelled how they relate to each other. In experiment 1, we asked participants to rate the perceived similarity of nouns and predicates (adjectives and verbs) as single words compared to each other. In experiment 2, we asked a different set of participants to rate the similarity between two phrases (always a noun combined with an adjective or a verb) against each other. In one condition, we presented the maximal identity case, where both words and phrases were identical. Otherwise, we varied whether the noun or the predicate was identical (but not the other word), or varied the similarity between nouns and predicates as estimated by the cosine similarity between word2vec representations [37] of the words. We then applied a hierarchical model testing scheme that pitted the predictions of a TP-based system against an asynchronous dynamic binding (ADB) system. We note that when both fillers and roles are similar to each other, both models predict the same thing—maximal similarity as identity is approached. The key prediction regards cases where the fillers and roles are not a priori similar to each other; TP predicts these have (cosine) similarity of zero, ADB predicts they will be judged as similar despite constituent relative dissimilarity. Below, we present the methods of both experiments 1 and 2 before discussing their results together.

2. Experiment 1: word similarity ratings

(a). Participants

Participants were recruited from the Max Planck Institute for Psycholinguistics participant pool. Twenty-one Dutch native speakers took part in the study; 17 were female and 4 were male. The average age of the participants was 22.93 years (s.d. = 2.54, range 19.04–29.93) and they gave informed consent before participating in the study. They received €6 for their participation.

(b). Stimuli

The stimuli were either nouns or predicates (adjectives or inflected verbs) derived from the noun phrases and sentences of the second experiment. There were 48 different nouns. Each noun appeared in three trials: once in the ‘same’ condition, where the same noun was shown as ‘word1’ and ‘word2’ and twice in the ‘different’ condition, where the word was paired with one other noun, and shown in both orders (word1/word2 position). See the electronic supplementary material, appendix for all conditions. This led to a total of 96 noun trials and there were 96 different predicates. As for the nouns, each predicate appeared in three trials. This led to a total of 192 predicate trials.

(c). Task and procedure

Participants read pairs of words on a computer screen and judged how similar the words were to each other. In each trial, the instruction was summarized again at the top of the screen (‘How similar are these words?’). Below, the two words were presented, one on the right and one on the left. Beneath the words, there was a slider bar. The left of the slider bar was marked as ‘totally not’ (helemaal niet) and the right of the slider bar was marked as ‘totally similar’ (helemaal wel). At the bottom of the screen, it said that participants could finish the trial and go to the next one by pressing Enter/return. The slider bar ranged in value from −300 to 300 and could be moved with an interval of 3. These values were not visible to the participant. The scores were later converted to a scale of −100 to 100 (the same slider bar was used in experiment 2). The task consisted of 288 trials. First, the participants rated the 96 noun trials. The order of the trials was randomized per participant. After a short break, they rated the 192 predicate trials.

3. Experiment 2: phrase similarity ratings

(a). Participants

Participants were recruited from the Max Planck Institute for Psycholinguistics participant pool. Thirty-eight Dutch native speakers took part in the study. Twenty-nine were female and 9 were male. The average age of the participants was 22.99 years (s.d. = 2.32, range 18.84–28.89). Participants gave informed consent before participating in the study. They received €10 for their participation.

(b). Stimuli, task and procedure

The stimuli were either noun phrases consisting of an article, adjective and noun, or full sentences consisting of an article, noun and inflected verb; see the electronic supplementary material, appendix for a full list. Three lists of 24 word pairs were used to construct the stimuli: one list of noun pairs, one list of adjective pairs and one list of verb pairs. The pairs were selected using the co-sine similarity of word2vec vectors between nouns. The list of 24 was then divided into four blocks of 6 pairs each: one ‘very similar’, one ‘similar’, one ‘dissimilar’ and one ‘very dissimilar’ block. The noun pairs were matched to the adjective and verb pairs in a counterbalanced way to form the phrases/sentences. Each noun pair was matched to a verb pair and an adjective pair from each of the four blocks. Hence, each noun was combined once with a very similar verb/adjective, once with a similar verb/adjective, once with a dissimilar verb/adjective and once with a very dissimilar verb/adjective. Each noun pair therefore occurred in eight different combinations: four with a verb and four with an adjective for a total of 192 pairs of phrases. Finally, to create conditions, the similarity of the phrase pairs was varied. All eight versions of the noun pair therefore occurred in four different conditions. In the first condition, both pairs were the same (identity condition). In the second condition, the subjects were the same, but the predicate was different (different predicate condition). In the third condition, the predicate was the same, but the subject was different (different subject condition). In the fourth and final condition, both the subject and the predicate were different (both different/opposite condition). There were a total of 768 trials. The task and slider bar from experiment 1 were used in experiment 2.

(c). Results of experiments 1 and 2

Our goal is to determine the binding mechanism that best fit the human predicate–filler rating data. Using the similarity ratings of single words from experiment 1 (see below), we determined predicted predicate–filler similarities for all word pairs in the experiment. As noted above, the similarity between two TP bindings is equal to the product of the similarity of the roles to the similarity of the filler, or

$$\text{cos}(rf,r^{\mathrm{\prime }}{\hspace{0.17em}f}^{\mathrm{\prime }})=\cos (r,r^{\mathrm{\prime }})\text{cos}(\hspace{0.17em}f,{\hspace{0.17em}f}^{\mathrm{\prime }}),$$

where rf is the TP of r and f. Similarly, for ADB, the similarity between two role filler bindings is equal to the weighted average of the similarity of the roles and the similarity of the fillers, or

$$\text{cos}\hspace{0.17em}(A(r,f),A(r^{\mathrm{\prime }}{\hspace{0.17em}f}^{\mathrm{\prime }}))=(\cos (r,r^{\mathrm{\prime }}))+(1-n)(\text{cos}\hspace{0.17em}(f,f^{\mathrm{\prime }})),$$

where A(r,f) is the binding of r to f via systematic asynchrony, and n is a weighting parameter, here set to 0.5 to get an unbiased average.

Dynamic binding can be implemented as synchronous or asynchronous binding (see [32–34]). However, modelling the result of synchrony-based binding is not so straightforward, as the results of the binding process vary greatly when r and f are coded on independent or non-independent dimensions. See the electronic supplementary material, appendix for more discussion of this issue and illustration by simulation.

After calculating the predicted similarities of predicate–filler bindings using both TP and ADB, we used both to model the human similarity ratings. We built two hierarchical models with TP and ADB predicting human ratings, with participants as a random variable (intercept only; modelling participants with independent slopes produced similar results). The results are presented in table 1.

Table 1.

Summary of results of quality of models using TP and ADB to predict human ratings of similarities of role–filler pairs. AIC, Akaike Information Criterion; BIC, Bayesian Information Criterion.

model	AIC	BIC	estR2
rating∼TP	261 721	261 754	0.58
rating∼ADB	258 088	258 121	0.63

In short, participants' similarity ratings followed the predictions of ADB rather than TP. Moreover, the relative closeness of the estimated R² was in large part a product of the similar predictions made by both ADB and TP for a subset of the similarities of predicate–filler pairs (e.g., both models predict maximal similarity when both roles and fillers are identical). In line with this observation, adding the TP predictions to a model with ADB increased estimated R² by 0.002.

4. Discussion

The similarity ratings of individual words did not determine the similarity ratings of the composed phrases. A tensor-decomposition of these same data showed that in a tensor-based system, the similarity of individual words drives the similarity of the phrases they appear in (see the electronic supplementary material, appendix for simulation details). If people can separate the similarity of roles, fillers and the predicates those constituents create, then they cannot be relying on tensors, or any other conjunctive operator, to perform binding during processing. We note, however, that in the limit, TPs of composed phrases could still be used during long-term storage if access to the constituent parts is not needed for behaviour or interpretation.

For a system to be compositional in the sense that human cognition is compositional, bindings between roles and fillers must be constructed on the fly, or dynamic, and these bindings must not affect the core representation of the constituent words or concepts beyond what is needed in the moment of processing to determine compositional meaning. The core representations of words and concepts, such as the examples fuzzy and prickly, should apply to whatever argument is predicated, just as the system should not instantiate multiple representations of the same entity when a single entity is referred to.

Dynamic binding requires: (i) states that carry information about the world via its representational elements (i.e., specifying what is present in a given situation or dataset), (ii) a mechanism that carries binding information (specifying how those elements are arranged) must be independent from the coding of representational elements, and (iii) processes by which new representational structures are inferred from the existing structures.⁵ These three sources of information must be independent (i.e., the binding operator must not affect the meaning of the bound items; [3]). Any system that can represent these three independent sources of information can, in principle, attain variable-value independence, a pre-requisite for compositionality.

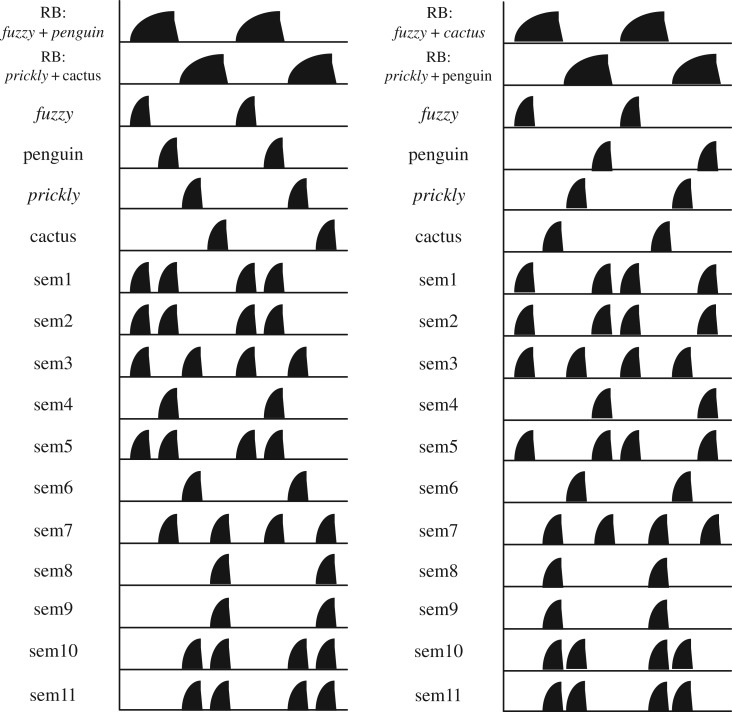
An instantiation of dynamic binding that exploits the asynchrony of unit firing in order to represent a predicate, role and argument can be seen in the model DORA (Discovery of Relations by Analogy; [1,5,29,30,33]), which is descended from the symbolic-connectionist system LISA (Learning and Inference with Schemas and Analogies; [34,35]). DORA implements two fundamental concepts from cognitive science and neuroscience: (i) that learning and generalization are based in a process of comparison [38,39], and (ii) that information in distributed neural computing systems is carried by the oscillations that emerge as its component units fire in excitatory and inhibitory cycles [32,40]. DORA uses oscillatory regularities in the network to dynamically bind predicates and arguments, without fundamentally changing the meaning of any elements so bound (though, in principle, statistics about the bindings could be tracked), resulting in a compositional system (see figure 2 for illustration).

Figure 2.

A snapshot of neural space–time of ADB of fuzzy penguin prickly cactus, fuzzy cactus and prickly penguin using the same constituent representations and composing them through dynamic binding with a features layer and a separate conjunctive coding layer.

In conclusion, the predictions of a tensor-based system were not borne out in human similarity ratings. The representational implications of using TPs for binding (namely, the violation of independence; see the electronic supplementary material, appendix) contradict both formal accounts of relational and analogical reasoning and formal theories of language. In our view, the empirical result we presented here, in combination with the aforementioned representational conflicts, highlights the importance of being faithful to certain computational system properties of the human mind and brain when deriving models of human cognition and behaviour. If a high-level desideratum like compositionality can be achieved while obeying the basic constraints of neurophysiological computation, the hope of accounting for the expressive power of the human mind in both formal and biological models is not yet lost.

Ethics

Ethics and consent for human participants from the Ethics Committee of the Faculty of Social Science of Radboud University.

Data accessibility

Data and analysis scripts are available at github.com/AlexDoumas/tensorsPhilB_1.

Authors' contributions

A.E.M. and L.A.A.D. designed research, conducted research and wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

A.E.M. was supported by the Max Planck Research Group ‘Language and Computation in Neural Systems’ and by the Netherlands Organization for Scientific Research (grant 016.Vidi.188.029).