Studying language in context using the temporal generalization method

Abstract

The temporal generalization method (TGM) is a data analysis technique that can be used to test if the brain’s representation for particular stimuli (e.g. sounds, images) is maintained, or if it changes as a function of time (King J-R, Dehaene S. 2014 Characterizing the dynamics of mental representations: the temporal generalization method. Trends Cogn. Sci. 18, 203–210. (doi:10.1016/j.tics.2014.01.002)). The TGM involves training models to predict the stimuli or condition using a time window from a recording of brain activity, and testing the resulting models at all possible time windows. This is repeated for all possible training windows to create a full matrix of accuracy for every combination of train/test window. The results of a TGM indicate when brain activity patterns are consistent (i.e. the trained model performs well even when tested on a different time window), and when they are inconsistent, allowing us to track neural representations over time. The TGM has been used to study the representation of images and sounds during a variety of tasks, but has been less readily applied to studies of language. Here, we give an overview of the method itself, discuss how the TGM has been used to analyse two studies of language in context and explore how the TGM could be applied to further our understanding of semantic composition.

This article is part of the theme issue ‘Towards mechanistic models of meaning composition’.

1. Introduction

Some of the first works incorporating brain imaging into psycholinguistics compared the brain’s responses to grammatically/semantically correct versus incorrect sentences, and the field has continued to focus on these types of paradigms [1–4]. Such comparisons across conditions identified brain areas that responded more to particular kinds of language violations, in turn, revealing the areas of the brain involved in comprehension and compositional processes. More recently, there has been interest in where information is represented in the brain. Several key works in this area compared not across condition, but rather by using brain activation to discriminate between the stimuli themselves (coined decoding) [5–7]. Initially, these studies used hand-derived semantic features, but eventually it was shown that similar performance could be achieved with a purely corpus-driven approach [8,9], marrying together fields of computational linguistics and the neuroscience of language.

Decoding methodology (which identifies the particular word/stimuli a person is reading/experiencing) has been largely focused on high accuracy predictions, without concern for variance in the brain’s representations over time. This obscures a dimension of the data that is pertinent to composition: how stable is the representation of a word over time? That is, is the neural representation of a word the same for the whole period of time that it can be detected using decoding methodology? Or does the neural pattern change over time, perhaps as a function of context? Is the neural representation of a word available at later time points during phrase or sentence processing? Is that later representation consistent with the representation while reading that word? The types of decoding analyses presented in the first decoding studies do not consider these questions.

The temporal generalization method (TGM) [10] allows us to tackle these questions of consistency in time. The TGM tests if the brain’s representation for a word is stable over time by training a decoding model using brain imaging data from one time period and then testing it using data from another time period. This is particularly useful when brain imaging data have good time resolution, as in magnetoencephalography and electroencephalography (MEG and EEG). We can use the TGM to study the signatures of composition that require the recall of specific words, and test if the representation of composed meaning has a signature that looks like the brain’s representations for any of the individual words.

The TGM has been used in a variety of neuroimaging experiments involving memory [11,12], vision [13], audition [14] and even taste [15]. There are a few examples using the TGM to study language; we will cover two of them as case studies in §4, and other examples exist [16,17]. In addition to the case studies, this paper gives a basic overview of decoding methodology, and then describes the TGM. We close with caveats and future work. The intent of this paper is to (1) illustrate how more detailed study of the mechanisms of composition can be executed using the TGM, and (2) provide interpretation for the kinds of results that the TGM can provide.

2. Predicting stimuli identity

A traditional decoding approach detects the brain’s representation for a stimulus during a particular window of time. Decoding involves training a machine learning model (e.g. regression model, classifier) to predict the stimulus (e.g. word, phrase) as a function of the brain imaging signal. There are two general approaches in this space: one that depends on predicting the word by first predicting the dimensions of an intermediate feature space (IFS) [18]; and one in which we train a classifier to distinguish words/conditions as if they are discrete and equally distinct classes. These methods both have their pros and cons, which we will describe in turn.

In order to test our ability to predict a stimuli, we perform some sort of cross validation, which involves reserving a subset (n) of our N brain imaging signal, and use the remaining N − n examples to train our machine learning model. Then, at test time, we use the n held out examples to test our model. In this way, we have an independent test of the ability of the model to identify the stimuli, and can measure our model’s ability to generalize to unseen stimuli. See Kriegeskorte et al. [19] for more information on properly testing such models.

(a). Prediction through classification

Prediction by classification is by far the simplest approach, with only a few design decisions to make. In a set of N stimuli, a classifier is trained to predict, using a brain image, which of the N stimuli (or N stimuli classes, or N conditions) is being experienced by the participant. There are a few constraints on this system, the largest being that every one of the N stimuli that appear in the test data must also appear in the training data. This requires that more trials per stimuli be collected (at least two) and even more if the trials are to be averaged before analysis. It also assumes no difference in similarity amongst the stimuli. That is, if the stimuli consist of animals and tools, the classifier is unaware of the fact that animals are more similar to other animals than to tools. There are many classification algorithms; support vector machine (SVM) is a reasonable first choice, and our case study uses a ridge regression classifier. Often, the accuracy of the classifier is reported: the total number of examples correctly classified divided by the total number of examples. In §3b, area under the receiver operating characteristics curve is reported (AUC ROC), which measures the predictor’s ability to produce true positives (correct predictions) without also producing more false positives (incorrect predictions). A value of 1 is ideal for AUC ROC, 0.5 is random guessing.

(b). Prediction using an intermediate feature space

Another approach is to train an algorithm not to predict the stimuli directly, but rather to predict a vector of properties associated with the stimuli, called an IFS [18]. At the word level, these properties can be actual behavioural norms collected about the stimuli as in Sudre et al. [6], or be based on word co-occurrence statistics calculated over a large text corpus, as in Mitchell et al. [5], or based on the hidden representations of a word embedding model (called word vectors) as in Fyshe et al. [20]. In each case, the word is defined by a point in high dimensional space (tens to hundreds and sometimes even thousands of dimensions). These high dimensional word embedding spaces have been shown to correlate with human judgements of word similarity [21,22] and also with behavioural norms [23]. There is some disagreement about whether the vectors correlate with semantics versus other properties (e.g. word length, word frequency), but the previously mentioned studies show that there is a strong relationship to semantic meaning, though the influence of other non-semantic properties may be difficult to completely eliminate.

Prediction using an IFS has an advantage over classification: during training, the model does not need to observe an example of every item in the test set. Instead, so long as the multidimensional space is fairly well represented, novel examples become predicted points in the multidimensional space and we can predict their identity based on that point [24]. This is called zero shot learning [25], and allows experimenters to collect responses to very diverse stimuli, sometimes even without repeated trials [7].

Once an IFS has been chosen to represent the stimuli, regression models are trained to predict each dimension of the IFS. Typically, one independent model is trained for each dimension, though some parameter sharing could improve performance. Then, we are tasked with evaluating the performance of the model by comparing the predicted vector (generated by the regression models) to the true vector associated with the stimuli. There are several possibilities: correlation, rank accuracy and 1 versus 2 or 2 versus 2 accuracy; the case study included here uses 2 versus 2 accuracy.

2 versus 2 accuracy involves leaving out two words during cross validation (words i and j), and thus two true word vectors (v_i and v_j). After training, the model produces two predicted vectors for the held out words (${\hat{v}}_i$ and ${\hat{v}}_j$). The 2 versus 2 test determines if the cosine similarity (cos) of properly matched true to predicted vectors (left hand of equation (2.1)) is greater than the correlation of mismatched vectors (right hand of equation (2.1)):

$$\cos (\widehat{v_i},v_i)+\cos (\widehat{v_j},v_j)\hspace{0.17em}\stackrel{?}{>}\cos (\widehat{v_i},v_j)+\cos (\widehat{v_j},v_i).$$ 2.1

If the correlation of properly matched vectors is greater, the 2 versus 2 test is said to have passed. There is one test per pair of held out words, and 2 versus 2 accuracy is the percentage of 2 versus 2 tests that pass. 2 versus 2 accuracy is often calculated using all possible pairs of stimuli. For even a modest stimuli set, this can result in thousands of tests. For example, for 60 stimuli, there are 1770 possible unique pairs for which we can run the 2 versus 2 test, each of which requires training a new prediction model. All tests are averaged to compute a final 2 versus 2 accuracy.

3. Temporal generalization method

Typically, we look at the accuracy of a trained model using all the data during stimuli presentation (e.g. 0–800 ms), or the accuracy if we use a sliding window over the full presentation time (e.g. 0–100 ms, 10–100 ms, etc.). This tells us at what time during the stimuli presentation there is information available in the brain images that we can differentiate between stimuli.

But we may be interested in asking a different question: does the brain’s representation for a stimulus change over time? To test the consistency of the ‘neural code’ in time, we use the TGM to produce TGM matrices [10]. TGM matrices use train and test data from different time windows, thus measuring the stability of the neural representation over time. Each of the case studies covered here used a variant of the prediction framework described in §2, and mixed training and testing data from different time windows. In a TGM (T), the entry at (i, j) (T_(i,j)) contains the accuracy when we train using brain imaging data from a time window centred at time i, and test using brain imaging data from a time window centred at time j. Thus, depending on the values of i and j we may use train and test data from different time periods, possibly comparing times when the participant is viewing a different word, or no stimuli at all. If the neural representation of a concept is stable across time, then models can be trained and tested with data from different time windows with little or no impact on accuracy.

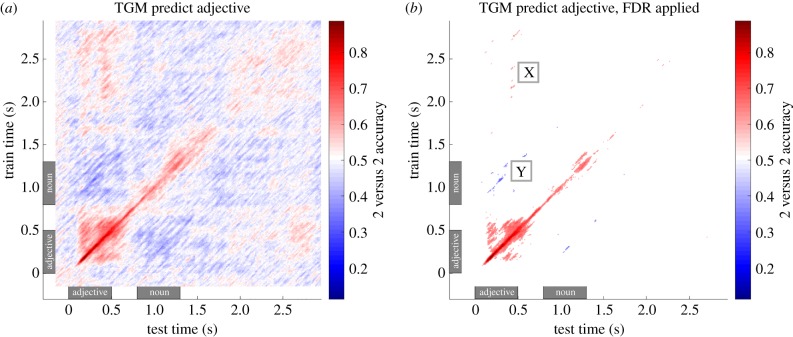
King & Dehaene [10] include several illustrative examples of hypothetical TGM matrices in their paper (see fig. 2 of their article). In their examples, and in figure 1, the y-axis represents the time used to train a model, and along the x-axis is the time used to test the model (generalization time), and the colour of each cell of the matrix corresponds to the accuracy level. The diagonal of the TGM matrix (i.e. T_i,i for all i) corresponds to the typical analysis regime, under which we train and test using data from the same time window (as plotted in figure 2b). As we will see in our case studies, the TGM matrices can identify patterns in data that might otherwise go undetected. For example, in figure 1b, we have annotated an area with the symbol ‘Y’. Near the ‘Y’, we are viewing the results when we train a model using data collected around 1.25 s, and test using data collected around 0.5 s. Thus, the results near the ‘Y’ annotation tell us if the representation during adjective comprehension matches the representation during noun comprehension. This mixing of training and testing time windows is what gives the TGM its power.

Figure 1.

2 versus 2 accuracy for predicting the adjective when presented as part of a phrase, presented as a TGM matrix. (a) All results, (b) false discovery rate (FDR) thresholded. A TGM matrix mixes training and testing data in all possible combinations to track the similarity of a neural representation in time. Within each TGM matrix, the colour at point i, j indicates the prediction accuracy when the model is trained using data from an interval centred at time point i, then tested with data centred at time point j. Time windows are 90 ms wide and overlap by 10 ms with adjacent windows. Time 0 is the onset of the adjective, 0.8 is onset of the noun, as annotated with grey rectangles. The adjective representation is still available after the presentation of the noun, and matches the representation observed during adjective presentation (patches near the ‘X’ annotation in (b)). In addition, there are significantly below chance regions when training during adjective presentation and testing during noun presentation (near the ‘Y’ annotation in (b)). From Fyshe et al. [26].

Figure 2.

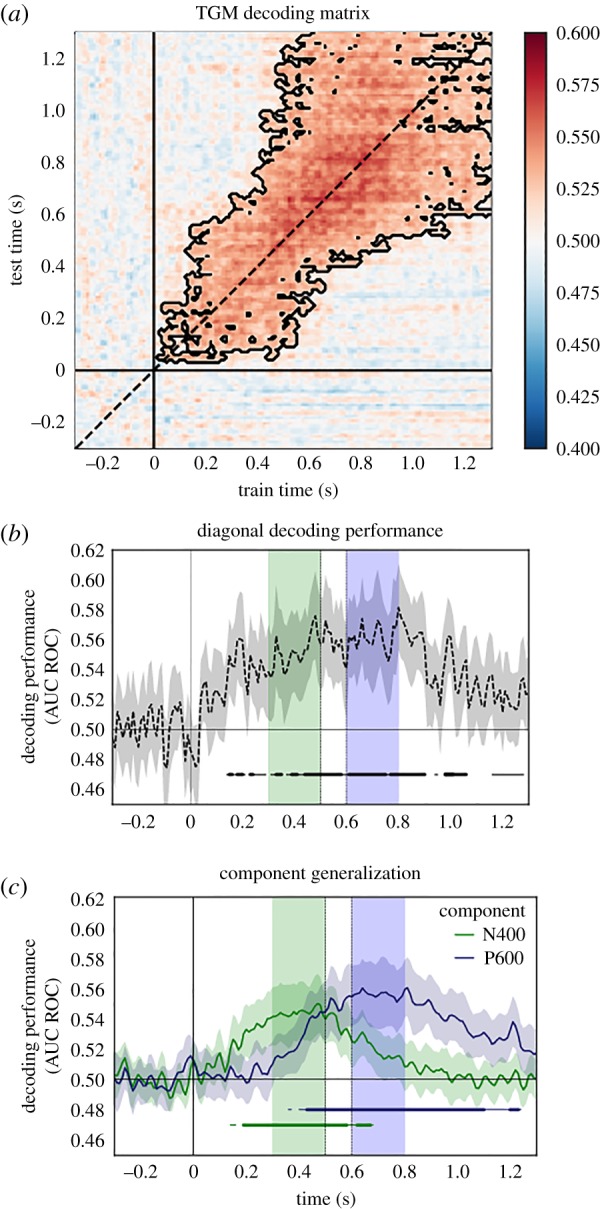
Generalization in time for distinguishing between congruent and incongruent trials, which elicit both N400 and P600. (a) A TGM matrix showing the ability to distinguish malformed versus correct sentences. Training times are along the x-axis, test on the y-axis. Black contours indicate above chance performance. (b) The diagonal decoding from figure (a). (c) Decoding performance for time periods corresponding to the N400 (300–500 ms; green) and P600 (600–800 ms; blue), averaged over rows of the TGM matrix in (a). Shaded regions represent 95% bootstrapped confidence intervals. Horizontal lines indicate time points significantly above chance (thick lines p < 0.01; thin lines p < 0.05). These results support the hypotheses that the N400 and P600 are cascading processes. The TGM matrix shows that the information processing regimes underlying the processes are not interchangeable. Adapted from Heikel et al. [27].

(a). What can the temporal generalization method show us?

Models trained on brain imaging data can leverage multiple kinds of information. For example, a classifier trained to distinguish between words might operate solely on visual features of the stimuli such as the number of white pixels on the screen, if that value happens to be correlated with some aspect of semantics. When the visual information is no longer salient in the brain activity (because the stimuli are no longer displayed), the classifier may still be able to distinguish words based on semantic features maintained in the brain. In a typical analysis, we would have no way to differentiate a period that used visual features from a period using semantic features. However, a TGM matrix can signal if these two windows of high accuracy are represented the same way in the brain (even if the features are highly correlated, e.g. if the short word stimuli are all animals). This differentiation is possible because the areas of the brain tasked with processing low level visual word form information are not known to be involved in the representation of semantics. Thus, models trained during a visual processing time window will leverage brain signals from the visual cortex, and models trained during a semantic window will leverage brain signals from other areas of the brain. Thus there will be no off-diagonal accuracy in the TGM matrix where models trained on visual time windows and tested semantic time windows meet (or vice versa). In §4b, we will see an example that compares information processing regimes, and shows that the brain representations during the two regimes are not identical, and thus high off-diagonal accuracy does not appear in the TGM matrix during all train/test time window combinations. TGM matrices can also show us when the brain’s representations are the same. We will see this in §4a.

Though both case studies covered here use a whole-brain analysis (i.e. use all sensors or all sources computed from the EEG/MEG data), TGM matrices can also be created by selecting only a subset of sensors or sources from specific regions of interest (ROIs). Thus the TGM matrix will tell us if the same representation is present in a specific area of the brain during two time windows. A TGM matrix generated using whole-brain recordings just indicates if the same representation is present anywhere in the brain during the two time windows.

4. Temporal generalization method case studies

The TGM framework described above is very general purpose and can be applied to a variety of stimuli and conditions to explore different aspects of semantic composition. We will discuss two case studies wherein the TGM was used to explore different aspects of language processing.

(a). Adjective noun phrases

Perhaps the simplest example of composition is phrase reading. Fyshe et al. [26] used an adjective-noun phrase reading paradigm to explore the semantic representation of adjectives and nouns when presented in phrases. The stimuli were 30 phrases created from four adjectives (plus the determiner ‘the’) and six nouns. Phrases were presented to nine participants while MEG data were recorded. Words were presented for 500 ms, with 300 ms between the words of a phrase and 3 s total between subsequent phrases. A regression model was trained to predict each dimension of an IFS, which was built from statistics based on sentence dependency structures in a large corpus. Because there was a correlation between the adjectives and nouns in the phrases, when decoding the adjective, the 2 versus 2 accuracy is reported for all pairs of phrases that share a noun. When decoding the noun, the 2 versus 2 accuracy is reported for only those pairs that share an adjective. This way, a model that leverages correlated noun semantics when being trained to predict the adjective would not be able to use that correlated information, since the noun is the same for both words in the 2 versus 2 pair (and similarly so for predicting the noun).

In their original paper, Fyshe et al. [26] present two TGM matrices, one for predicting the adjective of the phrase and one for predicting the noun. Here, we focus on the TGM matrix for the adjective (figure 1). The TGM matrix for adjective decoding shows both above and below chance decoding in off-diagonal regions. The significantly above chance decoding appears when training on the inter-stimulus interval (ISI), when a fixation cross is present (2–3 s after adjective onset), and testing on the time during which the adjective is displayed (0.4–0.5 s after adjective onset; figure 1b, near the ‘X’ annotation). This patch shows that the same brain areas are representing the same information at two points in time, and indicates that the meaning of the adjective is recalled during what can be assumed to be the compositional period (i.e. during the ISI). It should be noted, however, that the paradigm for this study did not include a non-compositional task, which would allow us to definitively confirm that the phenomenon is indeed owing to composition.

Especially after false discovery rate (FDR) correction, it is clear that the TGM matrices is not symmetric. What is the source of this asymmetry? There are differing noise properties for different time windows, and this affects the ability of the regression model to generalize across those time windows. This difference in noise is probably because one window is closer to the onset of the stimuli and thus is more likely to be tightly time-locked to stimulus onset, reducing noise. When we train on data that is noisier than our test data, the model can learn to discount features affected by noise [28]. Then, at test time, a model trained on the noisier time window will still have the capacity to predict on data taken from a less noisy time window. On the other hand, a model trained on data from the lower noise time window may rely on features that are corrupted by noise in the test time window, leading to less accurate predictions. It should be noted that the asymmetry in figure 1b may very well be a threshold effect, and a separate statistical analysis would be required to determine if there is a statistically different value in symmetric coordinates.

Another interesting feature of the adjective TGM matrix is the appearance of significantly below chance accuracy (figure 1b, near ‘Y’ annotation). Below chance accuracy indicates that the predictions are not random, but are systematically inverted. This means that in the 2 versus 2 test, equation (2.1), the left side is very often less than than the right, causing the 2 versus 2 test to fail a significant number of times. Because of the regression framework, this systematically incorrect prediction can be traced to MEG data having opposite sign during this time period (see Fyshe et al. [26] for a full explanation). That is, the MEG features on which the model depends have changed sign, causing the 2 versus 2 prediction to be systematically wrong. The underlying cause of this phenomenon has yet to be explained, but the implication is that, though the brain is clearly still representing the adjective, its form has changed in a way that is negatively correlated with the original representation. This is the sort of information that is not observable in a diagonal decoding experiment, and only measurable in the TGM matrix.

(b). N400 and P600 effects

N400 and P600 effects have been studied for decades, and the neural processes they represent have been widely studied and debated [3,29,30]. Decoding analyses can help us to decipher what each of these processes is related to, and a TGM matrix can help us to contrast the brain’s representations present during each of these processing steps. Heikel et al. [27] propose four possible hypotheses to explain the N400 and P600: a single process (not consistent with the N400 and P600 literature, as the two are dissociable), two strictly serial processes, two cascading processes that overlap in time, and a latency shift in which the same process produces both N400 and P600, but a delay in timing (stemming from sentence difficulty) that causes two distinct effects.

Heikel et al. [27] used a classic sentence listening paradigm in which 80 sentences with noun violations were analysed (40 congruent and 40 incongruent sentences). The sentences were presented to 40 participants while EEG was collected. The paradigm elicited a strong N400 and a weak P600. A ridge classifier, which uses ridge regression to perform binary classification, was used to distinguish congruent from incongruent stimuli. The authors defined the N400 time window to be 300–500 ms, and P600 to be 600–800 ms post-stimulus onset. They found that the congruent versus incongruent sentences could be distinguished from each other (using diagonal decoding) from as early as 270 ms and as late as 1270 ms after stimulus onset (see dots at the bottom of figure 2b). However, the TGM matrix (figure 2a) shows that not all time windows during the N400 and P600 timeframes are interchangeable. If the N400 and P600 time windows were completely interchangeable, we would observe above chance performance at off-diagonal locations in the TGM matrix that correspond to training on N400 and testing on P600 time windows (or vice versa). Because we do not observe this, we can infer that the processes create different brain representations. In other words, the N400 classifier performs significantly above chance during the time period 140 to 770 ms, and the P600 classifier during the time period 360 and 1270 ms (figure 2c). Though there is overlap between these two time periods, they do not completely overlap, indicating that the underlying processes differ in some respects.

These results could support two of the four proposed hypotheses. First, the results could indicate that a single computational process is acting during both time periods, but that a different kind of linguistic information is being processed in different brain areas during each time period (however, if the same process can act on different information facilitated by differing brain regions, the definition of process becomes unclear). The data are also consistent with two cascading processes that overlap in time, as indicated by the overlap in above chance performance for classifiers trained during N400 and P600 time windows. This result (and indeed all brain imaging results) hinges on the assumption that differing neural processes produce measurably different EEG signals.

5. Caveats

TGM matrices are an interesting analysis tool, but a few caveats must be considered. First, oscillations in data that are time-locked to the onset of stimuli will produce oscillatory results. For example, alpha oscillations will entrain to a visual stimuli [31], and this can show up as diagonal lines in the TGM matrix. This is observable in the TGM matrices in figure 1, made especially strong by lack of stimuli jitter between trials. To avoid these effects, one should jitter stimuli, and/or average the time course within windows to reduce the effect of oscillations. However, averaging the signal within windows before training a machine learning algorithm can result in lower accuracies owing to lost signal.

It is also important to recognize that interpreting a TGM matrix requires multiple comparisons, and these must be corrected for when determining statistical significance. One of the easier ways to do this is with the Benjamini–Hochberg–Yekutieli correction [32], which is less conservative than a simple Bonferroni correction.

6. Potential future uses

The TGM tells us more than the typical diagonal-only decoding analysis. Most importantly, it allows us to track and measure the stability of a representation as a function of time. As we consider next steps in the study of composition, how could the TGM best be used?

There are multiple studies emerging that use long short-term memory (LSTM) neural networks to study the effect of context on brain activity. LSTMs are neural network models that are trained to predict the next word in a sequence, and have the ability to keep contextual information in ‘memory’ for long periods of time. Though the human brain is certainly doing more than just predicting the next word in a sequence, several studies have found that the context vectors correlate well to the brain activity observed before the onset of a word [8,33]. Using a TGM-style analysis could provide information about how these context vectors are used over time, such as if they are predictably recalled at future points in the sentence or story.

The idea that a full sentence (or even a document) can be represented by a vector has garnered a lot of interest [34,35]. Some work has shown that the identity of words is available at later points during the processing of a sentence [17]. Compositional processes could also be identified by searching not just for some theoretical composed representation, but also by looking for the signatures of key words in the sentence. This is where the TGM becomes useful, as it provides a scan of the sentence showing where word signatures appear and reappear (see examples of such an analysis in Rafidi [17]). And, as computational models for composition improve, the TGM may prove to be an even more useful technique.

It is important to remember that a TGM matrix showing no off-diagonal accuracy is still an interesting result; it is evidence that the signature for the word is not consistent over time. During more complex reading paradigms (e.g. story reading), words and concepts must be remembered in order to successfully understand the material. If individual words cannot be detected at later time points this could mean that the word has been incorporated into a composed representation that no longer resembles the constituent words. If a TGM matrix shows no high off-diagonal accuracy, this is further evidence for pursuing a compositional model that modifies single word semantics.

7. Conclusion

The TGM is a powerful tool for searching for compositional processing in the brain. It allows us to probe for the representation of meaning at multiple time points, and also to compare the representation of meaning across time. It should be noted that computing TGM matrices is computationally expensive, as models trained at each time window need to be tested across multiple time windows. However, the process of parallelizing this computation is fairly straightforward, because the value of each cell in the TGM matrix can be computed independently, and furthermore, the same trained model can be tested across multiple time windows without retraining. Recall that, because each TGM matrix represents multiple comparisons, we must account for this by adjusting our statistical significance thresholds.

The TGM can help detect the resurgence of word meaning later in time, as seen in §4a. This suggests that the meaning of the word is recalled at a particular time, possibly in preparation for, or for use in, a compositional process. As our understanding of composed meaning improves, we can further explore the recollection of composed meaning as a function of time using the TGM.

The TGM can also distinguish between conditions, as seen in §4b. Here, a classifier was trained to differentiate between congruent and incongruent sentences that elicited both an N400 and a P600. The brain activation signatures during N400 and P600 windows were somewhat consistent in time, but not entirely interchangeable. This indicates that the neural activity underlying the N400 and P600 correspond to different processes, not simply a delay in the same process. The TGM provides a pivotal piece of evidence for this argument.

At a higher level, the TGM is useful when we wish to study the dynamics of brain activation, and how representations change over time. This is useful across myriad applications, but is particularly interesting when considered in the context of language. As we read and understand text, our brain is performing multiple ongoing processes to understand words, integrate them into context and anticipate future words. The TGM provides a framework for studying those processes when they require the retention or recall of previous brain activation states.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

A.F. is funded by a Natural Sciences and Engineering Research Council Discovery Grant, by the Canadian Institute for Advanced Research (CIFAR), and holds a Canada CIFAR AI Chair.