Abstract
Study Design
Prognostic study and validation using prospective clinical trial data Objective
To derive and validate a model predicting curve progression to 45+ degrees prior to skeletal maturity in untreated patients with adolescent idiopathic scoliosis (AIS).
Summary of Background Data
Studies have linked the natural history of AIS with characteristics such as sex, skeletal maturity, curve magnitude and pattern. The Simplified Skeletal Maturity Scoring System may be of particular prognostic utility for the study of curve progression. The reliability of the system has been addressed, however, its value as a prognostic marker for the outcomes of AIS has not. The BrAIST trial followed a sample of untreated AIS patients from enrollment to skeletal maturity, providing a rare source of prospective data for prognostic modeling.
Methods
The development sample included 115 untreated BrAIST subjects. Logistic regression was used to predict curve progression to 45+ degrees (or surgery) prior to Risser 4. Predictors included the Cobb angle, age, sex, curve type, triradiate cartilage and skeletal maturity stage (SMS). Internal and external validity was evaluated using jackknifed samples of the BrAIST dataset and an independent cohort (n=152). Indices of discrimination and calibration were estimated. A risk classification was created and the accuracy evaluated via the positive (PPV) and negative predictive values (NPV).
Results
The final model included the SMS, Cobb angle, and curve type. The model demonstrated strong discrimination (c-statistics 0.89 - 0.91) and calibration in all datasets. The classification system resulted in PPV’s of 0.71-0.72 and NPV’s of 0.85-0.93.
Conclusions
This study provides the first rigorously-validated model predicting a short-term outcome of untreated AIS. The resultant estimates can serve two important functions: 1) setting benchmarks for comparative effectiveness studies and 2) most importantly, providing clinicians and families with individual risk estimates to guide treatment decisions.
Level of Evidence:
Prognostic, Level 1
INTRODUCTION
Despite years of research, an extensive systematic review published in 2015 did not find any high-quality validated prognostic models to guide the treatment of adolescent idiopathic scoliosis (AIS). [1] Classic studies have linked the short and long-term natural history of AIS with characteristics such as sex, skeletal and sexual maturity, curve magnitude and curve type. [2-5] Recent work has expanded the number and complexity of factors under study, including genotypes, [6] bone mineral density, [7-9] paraspinal muscle function [10], body morphology, [11] hormones or proteins (e.g. melatonin and calmodulin) [12, 13] and combinations of multiple measurements from 2D images or 3D models of the spine. [14-18] Most studies have included only braced subjects, but others included both braced and unbraced subjects without accounting for the effect of treatment. True natural history has rarely been studied, [3, 5, 7, 14, 19] and never to an endpoint approximating surgical indications, arguably the primary concern of most families.
The Simplified Skeletal Maturity Scoring System (Sanders maturity system, SSMS) was proposed in 2007 in response to the known issues with other maturity staging systems, including complexity, and lack of precision and sensitivity. [20] A simplification of the Tanner-Whitehouse system, the SSMS may be of particular utility for the study of AIS, as the 8 stages map well onto the periods before, during and after the curve acceleration phase (most rapid curve progression). [21] The intra- and inter-rater reliability of the system has been satisfactorily addressed, [20, 22-26] however, its clinical value as a prognostic marker for the short- and long-term outcomes of AIS has not. The purpose of this study is to build on previous work with this system [20, 23] to develop and evaluate a prognostic model estimating the risk of curve progression to surgical indications in patients with untreated AIS using the Sanders maturity system. In addition, we propose and evaluate a prognostic risk classification system based on the model.
Human subjects’ research approval was obtained from the relevant institutions. This report follows the TRIPOD (Transparent Reporting of a Multivariate Prediction Rule for Individual Prognosis or Diagnosis) guidelines. [27] Additional details and data are presented in the Appendix.
MATERIALS AND METHODS
BrAIST sample for model development and internal validation
Data for model development was selected from the BrAIST (Bracing in Adolescent Idiopathic Scoliosis Trial; ClinicalTrials.gov ) [28] database specifically for this study. BrAIST prospectively enrolled 383 subjects from 25 centers. Subjects were randomized or chose between full-time bracing and observation and were followed to either a 50 degree Cobb angle, surgery or skeletal maturity. Two reviewers, blinded to treatment, prospectively evaluated all radiographs and jointly determined the Sanders maturity stage (SSMS) and Cobb angles. Participants were included in the current study if they were 1) not braced, 2) had a SMS recorded at initial visit and 3) had at least one Cobb angle progressing to ≥45 degrees, fusion surgery , or reached skeletal maturity (SMS ≥ 7 and/or Risser ≥ 4) during the trial.
Independent sample for external validation
The external validation sample was collected from three sources. The first (n=161) was used in the aforementioned validation study. [23] No independent verification of these data was attempted for this study. The second source was the electronic medical record of 122 patients followed for AIS at the authors’ institution. When required radiographic data were not recorded, we accessed the available radiographs and measurements were made by the second author. The third source was the BrAIST dataset. Of the 243 subjects who received a brace, 50 had a calculated average wear time of less than 6 hours per day (range 0.10 to 5.85, median = 2.34).
Given current knowledge about the relationship between wear time and outcomes, it is reasonable to consider these subjects as essentially untreated. [28-30] Therefore, a total of 333 subjects were consider for including in the external validation study and subjected to the aforementioned inclusion criteria.
Outcome – Prognosis
Two prognostic outcomes were defined based on radiographic criteria. Subjects with a “Poor” prognosis developed a Cobb angle ≥45 degrees or had spinal fusion prior to maturity and those with a “Good” prognosis reached maturity with a curve <45 degrees. The prognoses were assigned by the first author using data coding and without knowledge of the values of the predictor variables.
Statistical Analyses
Analyses were conducted using SAS® (Version 9.4), Cary, NC. Descriptive and inferential statistics were calculated to describe the samples. The model was developed using the BrAIST data only. Of numerous characteristics associated with the risk of curve progression, we only considered those that could be routinely and accurately assessed during a typical initial clinic visit: baseline age, sex, curve pattern, Cobb angle, status of the triradiate cartilage (open or closing) and SSMS. Using logistic regression, we selected the variables to be included in the final model based on the Akaike information criteria. [31] Then, the model coefficients were estimated using penalized logistic regression. [32]
Indices of Model Performance
Calibration (match between the predictions and the observed outcomes) was assessed via calibration plots. Discrimination (ability to distinguish between those with and without a poor prognosis) was evaluated by the c-statistic (area under the receiver-operator curve). Models are typically considered reasonable when the c-statistic is higher than 0.70 and strong when it exceeds 0.80. [33]
Risk Classification
To classify subjects at either low- or high-risk for a poor prognosis, we chose the cut-point (estimated probability) that maximized both the sensitivity and specificity of the model. The positive and negative predictive values associated with the classification were also calculated.
Model Validation
Internal validity (reproducibility of the model performance in a similar population) was assessed by applying the model to jackknifed samples of the BrAIST dataset. External validity (generalizability) was assessed by applying the model to the external validation dataset. Calibration and discrimination of the model and the accuracy of classification system were estimated in these samples and compared to model performance in the BrAIST sample.
RESULTS
Sample characteristics
BrAIST cohort.
Of the 383 participants enrolled in BrAIST, 5 were withdrawn from the clinical trial for ineligibility and 243 were braced. Of the 135 untreated subjects, 19 did not reach the endpoints defined for this study. The final sample thus included 115 subjects.
External Validation cohort.
Of the 333 available for study, 181 did not meet inclusion criteria, resulting in a sample size of 152 in the external validation cohort.
Baseline characteristics and the observed prognoses are summarized in Table 1. Compared with the external validation cohort, the BrAIST sample included a higher percentage of subjects at Risser 0 (67 vs. 55%, p=0.02), at SMS 1-2 (36 vs. 20%, p=0.02), and a higher percentage with a poor prognosis (52 vs. 37%, p=0.01).
Table 1.
Summary Baseline and Outcome Characteristics of the BrAIST, External Validation and Combined Samples
| Characteristics | BrAIST (n=115) |
External Validation (n=152) |
p- value* |
Combined (n=267) |
|---|---|---|---|---|
| Age (mean ± SD (range)) | 12.5±1.2 (10-15) | 12.6±1.3 (9-16) | 0.35 | 12.57±1.2 (9-16) |
| Sex – Female (n, %) | 100 (87) | 123 (81) | 0.24 | 223 (84) |
| Curve Classification (n, %) | ||||
| Thoracic | 25 (22) | 45 (30) | 0.10 | 70 (26) |
| Thoracolumbar or Lumbar | 18 (16) | 35 (23) | 53 (20) | |
| Thoracic with Thoracolumbar or Lumbar | 54 (47) | 55 (36) | 109 (41) | |
| Double Thoracic | 9 (8) | 12 (8) | 21 (8) | |
| Triple | 9 (8) | 5 (3) | 14 (5) | |
| Thoracic Apex (1 or more) | 97 (84) | 117 (77) | 0.16 | 214 (80) |
| Maximum Cobb Angle (mean±SD (range)) | 29.6±6.5 (18-47) | 26.6±8.3 (11-44) | <0.01 | 27.9±7.7 (11-47) |
| Risser Grade (n, %) | ||||
| 0 | 77 (67) | 84 (55) | 0.02 | 161 (60) |
| 1 | 22 (19) | 29 (19) | 51 (19) | |
| 2 | 13 (11) | 19 (13) | 32 (12) | |
| 3+ | 3 (3) | 20 (13) | 23 (9) | |
| Maturity Stage# (SMS) (n, %) | ||||
| 1 | 1 (1) | 0 | <0.02 | 1 (1) |
| 2 | 40 (35) | 31 (20) | 71 (27) | |
| 3 | 32 (28) | 46 (30) | 78 (29) | |
| 4 | 17 (15) | 44 (29) | 61 (23) | |
| 5 | 9 (8) | 5 (3) | 14 (5) | |
| 6 | 15 (13) | 24 (16) | 39 (15) | |
| 7 | 1 (1) | 2 (1) | 3 (1) | |
| Triradiate# – Open (n, %) | 30 (28) | 8 (22) | 0.52 | 38 (26) |
| Poor Prognosis^ (n, %) | 60 (52) | 56 (37) | 0.01 | 116 (43) |
SD, standard deviation; SMS, skeletal maturity stage
Poor Prognosis was defined as a Cobb angle ≥45° prior to reaching Risser 4
status of the triradiate was not available for 7 subjects in the BrAIST cohort and for 115 of the subjects in the External validation cohort
Fisher’s exact test or t-test for differences between BrAIST and Validation sample
Model Development
The relationship between the measured baseline risk factors (age, sex, curve pattern, Cobb angle, status of the triradiate cartilage, and SMS) were evaluated using univariable logistic regression (Appendix Table 2). All factors were included in the initial multivariate model. The model with the lowest AIC included three factors: SMS, Cobb angle and presence of at least one thoracic curve (Table 2). After adjustment for the other variables, an increase in the Cobb angle was associated with higher odds of a poor prognosis (OR=1.28, 95% CI=1.15-1.43), as was the presence of a thoracic curve (relative to a single lumbar or thoracolumbar curve, OR=4.09, 95% CI=0.88-18.96). Compared to less mature subjects with an SMS 1-2, those at SMS 3 (OR=0.10, 95% CI=0.03-0.39), or 4+ (OR=0.01, 95% CI=0.002-0.07) had lower odds of a poor prognosis. An online calculator based on this model can be found at https://uichildrens.org/ais-prognosis-calculator-simplified.
Table 2.
Multivariable Prediction of Poor Prognosis in the BrAIST Sample (n=115)
| B Coefficient |
Std Error |
Adjusted OR (95% CI*) |
p value |
||
|---|---|---|---|---|---|
| Intercept | −5.9775 | 1.5908 | <0.01 | ||
| Maximum Cobb Angle | 0.2446 | 0.0558 | 1.28 (1.15, 1.43) | <0.01 | |
| Thoracic Apex (1 or more) | No | Ref. | |||
| Yes | 1.4086 | 0.7825 | 4.09 (0.88, 18.96) | 0.07 | |
| SMS | 1-2 | Ref. | |||
| 3 | −2.3003 | 0.6977 | 0.10 (0.03, 0.39) | <0.01 | |
| ≥4 | −4.3398 | 0.8427 | 0.01 (0.002, 0.07) | <0.01 |
Wald confidence intervals
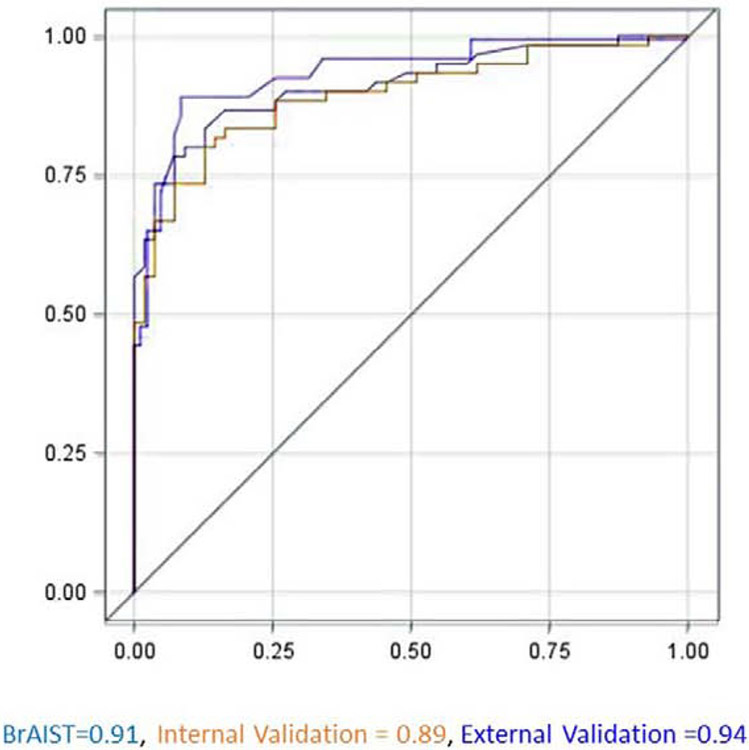
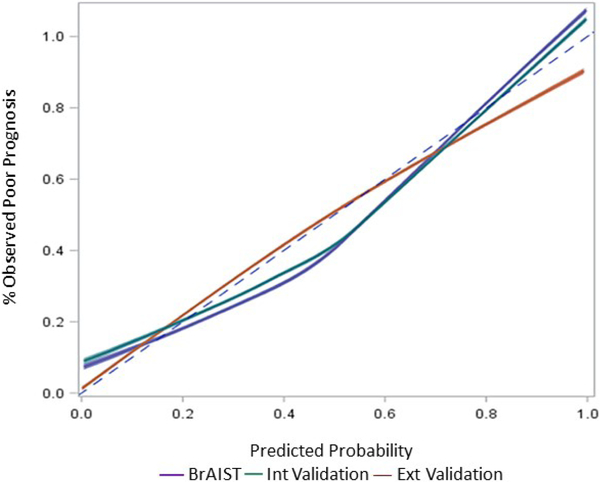
Figures 1 and 2 summarize model performance (receiver-operator curves, c-statistics and calibration plots) in the BrAIST, internal and external validation samples. The c-statistic in the BrAIST sample was 0.91 (95% CI=0.86-0.97), and was similarly high in the internal (0.89, 95% CI=0.83-0.95) and external validation data (0.90, 95% CI=0.84-0.95), indicating strong discrimination between subjects with a poor and a good prognosis. In terms of overall calibration, the model accurately predicted the prevalence of a poor prognosis in the external validation cohort (37% predicted vs. 37% observed). The calibration plot shows the predictions are well aligned with the observed outcomes in the three samples. Some degree of over-prediction (percent predicted > percent observed) is noted in the mid-range for the BrAIST and internal validation cohorts, and in the high end of the distribution in the external validation cohort.
Figure 1.
Receiver operating characteristic (ROC) curves for identifying patients with a poor prognosis using the model. The c-statistic (area under the curve) and 95% confidence intervals were 0.91 (0.86, 0.97) in the model development (BrAIST) dataset, 0.89 (0.83, 0.95) in the internal and 0.90 (0.84, 0.95) in the external validation datasets. The reference line indicates no discrimination.
Figure 2.
Calibration plot for the Sanders model when applied to the development (BrAIST, blue line), internal (green line) and external validation (red line) samples. The distribution of predicted probabilities from each sample was divided into deciles and the average predicted probability per decile (x-axis) was plotted against the percentage of patients in each decile observed to have a poor prognosis (y-axis). Loess smoothing was used to generate the calibration lines. Perfect calibration is represented by the dotted line.
Risk Classification
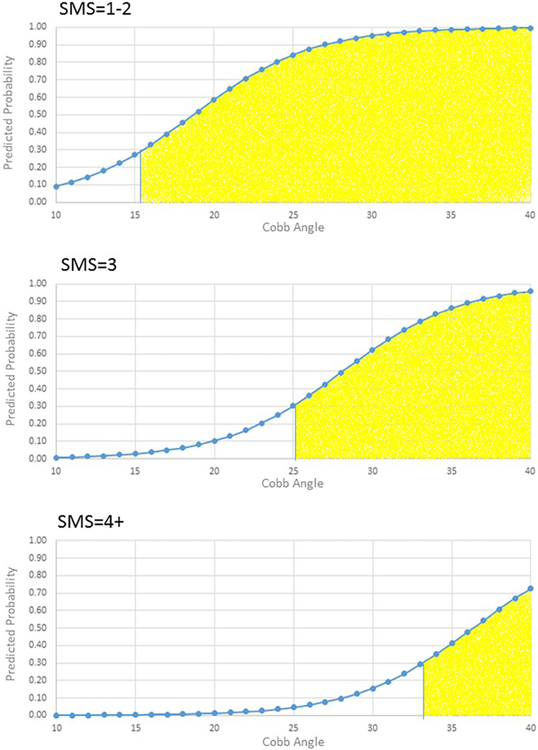
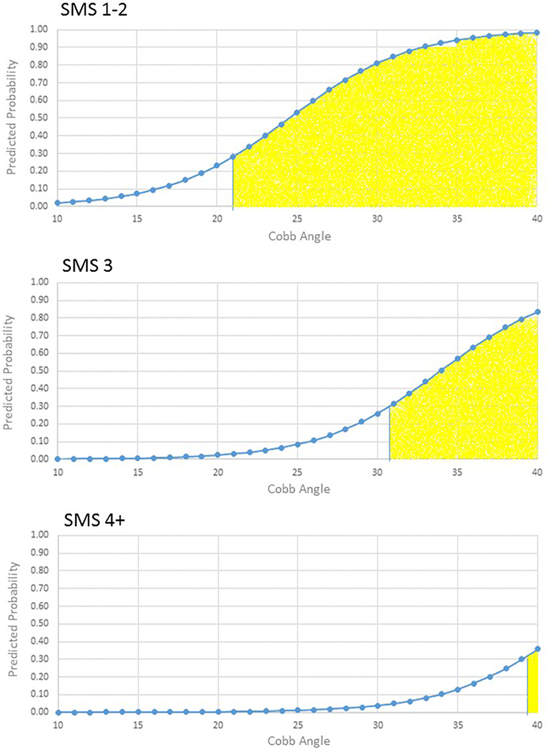
The probability cut-point associated with the highest degree of sensitivity (90%) and specificity (62%) in the BrAIST dataset was 0.31. Table 3 and Figures 3-4 summarize the characteristics of subjects classified into the low- and high-risk groups. For example, subjects with one or more thoracic curves and an SMS of 1-2 and Cobb angles of 16 degrees or greater would be classified as high risk. The accuracy of the classifications is summarized in Table 4. In the BrAIST dataset, the low risk group included 40 (35%) subjects, of whom 85% were correctly classified as having a good prognosis. Of the 75 subjects in the high risk group, 72% were correctly classified as having a poor prognosis.
Table 3.
Patient Characteristics and Risk Classification*
| Low Risk | High Risk | ||
|---|---|---|---|
| SMS | Cobb Angle | ||
| Single Thoracic, Double Major, Double or Triple Thoracic curves | 1-2 | ≤15 | 16+ |
| 3 | ≤25 | 26+ | |
| 4+ | ≤33 | 34+ | |
| Single Lumbar/Thoracolumbar curve | 1-2 | ≤21 | 22+ |
| 3 | ≤30 | 31+ | |
| 4+ | ≤39 | 40+ | |
SMS, skeletal maturity stage
Low Risk defined as predicted probability of a poor prognosis of <0.31; high risk as ≥0.31
Figure 3.
Model predictions for curve patterns involving thoracic vertebrae by SMS and Cobb angle. Yellow shaded area indicates the subjects would be classified as high risk for a poor prognosis (predicted probability ≥0.31).
Figure 4.
Model predictions for single lumbar or thoracolumbar curve patterns by SMS and Cobb angle. Yellow shaded area indicates the subjects would be classified as high risk for a poor prognosis (predicted probability ≥0.31).
Table 4.
Performance Validation of Risk Classification (Estimates and 95% Confidence Intervals)
| BrAIST (n=115) |
Internal Validation (n=115) |
External Validation (n=152) |
|
|---|---|---|---|
| Sensitivity | 0.90 (0.79, 0.96) | 0.90 (0.79, 0.96) | 0.89 (0.78, 0.96) |
| Specificity | 0.62 (0.48, 0.75) | 0.62 (0.48, 0.75) | 0.79 (0.70, 0.87) |
| PPV* | 0.72 (0.65, 0.78) | 0.72 (0.65, 0.78) | 0.71 (0.63, 0.79) |
| NPV# | 0.85 (0.78, 0.93) | 0.85 (0.72, 0.93) | 0.93 (0.86, 0.96) |
PPV (positive predictive value) = percentage of subjects classified as high risk and observed to have a poor prognosis
NPV (negative predictive value) = percentage of subjects classified as low risk and observed to have a good prognosis
DISCUSSION
This study provides a validated model and classification system to predict the risk of curve progression to surgical indications in untreated AIS patients using the Sanders skeletal maturity system. This model was designed for easy use in all clinical settings where coronal spine views and hand films are obtained at the initial visit. Despite its simplicity, and the 2-3 year time span between baseline and outcome, strong discrimination and calibration were noted in both the BrAIST and validation datasets. The risk classification system produced reasonably accurate predictions in both the low and high risk groups.
This is the third evaluation of the SSMS as a prognostic marker for curve progression. In the first, Sanders et al. used the SMS and Cobb angle to predict the likelihood of surgery (Cobb angle >50 prior to maturity) in a sample of 22 female subjects. Sitoula et al. replicated this study in a larger sample of 161 males and females. These studies are not without their limitations. Neither present the full prediction model, or any performance measures (e.g. discrimination or calibration). Importantly, both samples included a mix of braced and untreated patients without explicitly accounting for the effect of treatment. Although we noted some large differences between the observation and predictions among the three papers, in general all would tend to place each combination of SMS and curve magnitude into the low- and high-risk groups suggested here, indicating a high degree of agreement in terms of discrimination. For example, both Sanders et al. and Sitoula et al. estimate that 100% of SMS 2 patients with Cobb angles of 25-30 degrees would progress to >50 degrees, whereas our estimation and observations suggest a lower prevalence of 75%. This difference in unlikely to result in different treatment plans, as most families and clinicians would agree that all estimates are high enough to initiate bracing or other treatment.
The strengths of this study include the representativeness of the BrAIST sample to the larger population of patients initially presenting for AIS evaluation. The full range of subject characteristics were represented, including both sexes, all curve types, and a wide range of initial Cobb angles and maturity stages. True natural history is reflected in the sample as none were treated with bracing or other modalities. We followed standard procedures for model development and validation, and evidence-based recommendations for the transparent reporting of prognostic modeling. [27]
The sample size available for model development and validation may have biased our findings. Larger samples would permit a model with more variables, and perhaps more predictive power and precision. Ideally, more than 100 subjects with and without the prognosis should be included in external validation samples. [34] Larger datasets from different sources are unlikely, as detailed data from untreated patients is difficult to obtain, and it is unlikely additional data will become available now that multiple strong studies support the effectiveness of bracing. [28, 29, 35, 36] Nonetheless, the development of a simple models, using conservative techniques such as penalized regression, is more likely to result in predictions which generalize to different populations, and are also more likely to be used in clinical practice.
The accuracy of any prognostic model used in practice is also limited by the precision and reliability of the inputs. We encourage clinicians to verify all measurements prior to calculating the probabilities or using the classification system. The Cobb angle is a critical predictor whose reliability has been established in various research contexts, but remains unknown for any random clinician and radiograph. The reliability of the SSMS has been supported but also questioned, [22, 25, 26] especially when distinguishing between stages 2 and 3 (the stage associated with peak height velocity). This distinction is particularly crucial to the outputs of this model. For example, a patient with a single lumbar curve of 30 degrees is predicted to be at high risk (predicted probability = 0.81) if at SMS 1-2, but at low risk (predicted probability = 0.26) if staged at SMS 3. Use of the SSMS system can become more reliable with practice, or by seeking a second opinion.
This model and the resultant probabilities and risk classification can serve two important functions. It can benefit future research by setting benchmarks for comparative effectiveness studies of new brace designs, scoliosis-specific exercises, and non-fusion techniques. The most important function, however, is that of enhanced shared decision making. The primary fear of most families is curve progression leading to surgery. Individualized risk estimates may lead to evidence-based, instead of fear-based, treatment decisions. As tempting as it may be to update bracing indications based on this study, we are purposely not suggesting treatment, or no treatment, based on the estimates or risk classification from this model. As stated by Vickers and Elkins, [37] determining a probability threshold where treatment should occur is only reasonable when the benefits and harms of treatment decisions are well-understood and equally valued by all patients. This is not the case in AIS. Some patients and parents are risk-adverse and request active treatment even when the risk of a poor outcome is low. This was demonstrated by the strong preferences for bracing noted in the BrAIST clinical study. [28, 38] Therefore, we suggest clinicians should provide families with valid prognostic information, and allow them to evaluate, and act on, their own personal interpretations of the estimates and implications.
In summary, we provide evidence for the internal and external validity of a prognostic model for the risk of curve progression to surgical indications using the Sanders skeletal maturity system. This study provides clinicians with additional information to share with families to help them jointly develop and evaluate individualized, risk-based treatment options. We encourage an ongoing process of validation, and study of the potential impact of this model by assessing its ease of use in practice, and most importantly, its influence on treatment decisions.
Acknowledgements
We would like to acknowledge the following site investigators and their research and orthotist colleagues who contributed their time, patient data and expertise to BrAIST: Oheneba Boachie-Adjei, MD, Jacques L. d’Astous, MD, John B. Emans, MD, John M. Flynn, MD, Joseph A. Gerardi, MD, Daniel W. Green, MD, Kenneth J. Guidera, MD, Munish C. Gupta, MD, Kim W. Hammerberg, MD, Henry J. Iwinski, MD, Antony Kallur, MD, Todd Milbrandt, MD, Peter O. Newton, MD, Jean A. Ouellet, MD, Nigel J. Price, MD, Christopher W. Reilly, MD, Elizabeth A. Szalay, MD, Michael L. Schmitz, MD, Kit Song, MD, Peter Sturm, MD, Vishwas Talwalkar, MD, W. Timothy Ward, MD, Klane White, MD, James G. Wright, MD. We would also like to acknowledge the following contributors who provided data for the external validation: Prakash Sitoula, MBBS, Kenneth Rogers, PhD, and Petya Yorgova, MS.
Financially supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health (R21AR049587 and R01AR052113); the Children’s Miracle Network, the Canadian Institutes of Health Research (FRN-81050), the Shriners Hospitals for Children, the University of Rochester, Children’s Mercy Kansas City, the Joan and Phill Berger Charitable Fund, and the Estate of Herb and Nancy Townsend
Appendix
| Section/Topic | Item | Checklist Item | Page | |
|---|---|---|---|---|
| Title and abstract | ||||
| Title | 1 | D;V | Identify the study as developing and/or validating a multivariable prediction model, the target population, and the outcome to be predicted. | X |
| Abstract | 2 | D;V | Provide a summary of objectives, study design, setting, participants, sample size, predictors, outcome, statistical analysis, results, and conclusions. | X |
| Introduction | ||||
| Background and objectives | 3a | D;V | Explain the medical context (including whether diagnostic or prognostic) and rationale for developing or validating the multivariable prediction model, including references to existing models. | 1 |
| 3b | D;V | Specify the objectives, including whether the study describes the development or validation of the model or both. | 1 | |
| Methods | ||||
| Source of data | 4a | D;V | Describe the study design or source of data (e.g., randomized trial, cohort, or registry data), separately for the development and validation data sets, if applicable. | 2-3 |
| 4b | D;V | Specify the key study dates, including start of accrual; end of accrual; and, if applicable, end of follow-up. | A | |
| Participants | 5a | D;V | Specify key elements of the study setting (e.g., primary care, secondary care, general population) including number and location of centres. | 2, A |
| 5b | D;V | Describe eligibility criteria for participants. | 2-3 | |
| 5c | D;V | Give details of treatments received, if relevant. | 2-3 | |
| Outcome | 6a | D;V | Clearly define the outcome that is predicted by the prediction model, including how and when assessed. | 3 |
| 6b | D;V | Report any actions to blind assessment of the outcome to be predicted. | 3 | |
| Predictors | 7a | D;V | Clearly define all predictors used in developing or validating the multivariable prediction model, including how and when they were measured. | 1-3, A |
| 7b | D;V | Report any actions to blind assessment of predictors for the outcome and other predictors. | 3 | |
| Sample size | 8 | D;V | Explain how the study size was arrived at. | A |
| Missing data | 9 | D;V | Describe how missing data were handled (e.g., complete-case analysis, single imputation, multiple imputation) with details of any imputation method. | 3-4 |
| Statistical analysis methods | 10a | D | Describe how predictors were handled in the analyses. | 3, 5,A |
| 10b | D | Specify type of model, all model-building procedures (including any predictor selection), and method for internal validation. | 3-4, A | |
| 10c | V | For validation, describe how the predictions were calculated. | A | |
| 10d | D;V | Specify all measures used to assess model performance and, if relevant, to compare multiple models. | 3, A | |
| 10e | V | Describe any model updating (e.g., recalibration) arising from the validation, if done. | - | |
| Risk groups | 11 | D;V | Provide details on how risk groups were created, if done. | 3 |
| Development vs. validation | 12 | V | For validation, identify any differences from the development data in setting, eligibility criteria, outcome, and predictors. | 2, 4-5 |
| Results | ||||
| Participants | 13a | D;V | Describe the flow of participants through the study, including the number of participants with and without the outcome and, if applicable, a summary of the follow-up time. A diagram may be helpful. | A |
| 13b | D;V | Describe the characteristics of the participants (basic demographics, clinical features, available predictors), including the number of participants with missing data for predictors and outcome. | Table 1 | |
| 13c | V | For validation, show a comparison with the development data of the distribution of important variables (demographics, predictors and outcome). | Table 1 | |
| Model development | 14a | D | Specify the number of participants and outcome events in each analysis. | Table 1 |
| 14b | D | If done, report the unadjusted association between each candidate predictor and outcome. | Table 2 | |
| Model specification | 15a | D | Present the full prediction model to allow predictions for individuals (i.e., all regression coefficients, and model intercept or baseline survival at a given time point). | Table 3 |
| 15b | D | Explain how to the use the prediction model. | Fig 1, 2 | |
| Model performance | 16 | D;V | Report performance measures (with CIs) for the prediction model. | Table 5, Figure 3-4 |
| Model-updating | 17 | V | If done, report the results from any model updating (i.e., model specification, model performance). | - |
| Discussion | ||||
| Limitations | 18 | D;V | Discuss any limitations of the study (such as nonrepresentative sample, few events per predictor, missing data). | 8 |
| Interpretation | 19a | V | For validation, discuss the results with reference to performance in the development data, and any other validation data. | 7 |
| 19b | D;V | Give an overall interpretation of the results, considering objectives, limitations, results from similar studies, and other relevant evidence. | 7 | |
| Implications | 20 | D;V | Discuss the potential clinical use of the model and implications for future research. | 9-10 |
| Other information | ||||
| Supplementary information | 21 | D;V | Provide information about the availability of supplementary resources, such as study protocol, Web calculator, and data sets. | A |
| Funding | 22 | D;V | Give the source of funding and the role of the funders for the present study. | |
Items relevant only to the development of a prediction model are denoted by D, items relating solely to a validation of a prediction model are denoted by V, and items relating to both are denoted D;V. We recommend using the TRIPOD Checklist in conjunction with the TRIPOD Explanation and Elaboration document.
Additional Details Concerning the Samples
BrAIST enrolled patients from 25 pediatric orthopaedic practices in the United States and Canada (ClinicalTrials.gov ). 1 Subjects were enrolled and followed between 2007 and 2013. We queried the BrAIST database for all patients in the observation (untreated) arm. Of the 383 subjects who were enrolled, 243 were braced, and 5 others had been deleted from the database, 190 were braced, and 5 others were not considered (3 subjects were found to have non-idiopathic scoliosis, the consent form could not be located for 1 and data were deleted, 1 subject found to have reached the BrAIST endpoint at time of consent). For the 135 untreated subjects, the prognosis variable for this study was created by the first author without knowledge of the subjects’ BrAIST endpoint or of the value of the risk factors. Nineteen subjects did not reach the endpoints defined for this study. The SMS was not available for one subject. The final sample thus included 115 subjects.
Subjects in the external validation dataset came from three sources. The first source was data from the Nemours/Alfred I. duPont Hospital for Children, which was also used in a paper by Sitoula, Verma, et al. evaluating the Sanders maturity staging system. 2 Subjects were under care between 2005 and 2011. The data were provided to the first author for this study and no attempt was made to verify any of the measurements or classifications. Of 161 subjects, 70 were braced, and 5 subjects had also been enrolled in BrAIST and were therefore not considered for use here. The first author determined the prognosis for the current study, again blinded to the values of the predictors and to the subject’s outcome in the Sitoula study. We were unable to assign a prognosis for 19 subjects, for a total of 67 eligible subjects.
The second source of subjects was electronic medical record data from the University of Iowa. Of the 122 patients with adolescent idiopathic scoliosis treated between 2007 and 2013, 65 were braced and we were not able to determine the prognosis in 7. A baseline hand film for the SMS was not available for 6 patients, resulting in a sample of 44 subjects.
The third source of data was the BrAIST dataset. Results from BrAIST1 and studies at Texas Scottish Rite 3, 4 suggest that a group of patients who average less than 6 hours per day in a brace would have the same prevalence of curve progression to surgical indications as those who were not braced at all. Therefore, to increase the sample size for external validation, we selected the subsample of braced subjects with documented average wear time of less than 6 hours per day. Of 383 enrolled subjects, 243 received a brace. Of these, 41 met the < 6 hours wear time and other inclusion criteria. Thus, from the three sources, 152 subjects were included in the external validation dataset.
Appendix Table 1.
Summary of Final Development and External Validation Datasets
| Development Dataset |
Validation Dataset | ||||
|---|---|---|---|---|---|
| BrAIST | Sitoula et al. | U of IA | BrAIST | ||
| Consented/Reviewed | 383 | 161 | 122 | ||
| Braced | > 6 hours per day | −193 | −70 | −65 | |
| < 6 hours per day | −50 | ||||
| Not Considered | −5 | −5 | |||
| Did not reach current study endpoint | −19 | −19 | −7 | −9 | |
| No hand film for SMS staging available | −1 | −6 | |||
| 67 | 44 | 41 | |||
| Final samples | 115 | 152 | |||
Relationship between Risk Factors in the BrAIST dataset
The maturity indicators age, status of the triradiate cartilage and the SMS were related. Subjects at SMS 1-2 were younger (11.85 years) than those at SMS 3 (12.65 years) or 4+ (13.00 years) (p-values <0.05). Prior to SMS 3, the majority of subjects had an open triradiate cartilage; at SMS 3 and greater, nearly all subjects had closed triradiates (p<0.01). Age and gender were also related: the girls were on average younger than the boys (12.38 vs. 13.20, p<0.02). The largest Cobb angle in curve patterns including a thoracic apex were larger, on average, than those involving the thoracolumbar or lumbar spine only (30.12 vs. 26.67 degrees, p<0.04). Otherwise, no statistically significant relationships were detected between any of the risk factors.
Appendix Table 2.
Unadjusted Relationship between Baseline Characteristics and Risk of Poor Prognosis in the BrAIST Sample (n=115)
| Variable | Unadjusted OR (95% CI*) | p-value | |
|---|---|---|---|
| Age | 0.66 (0.48, 0.91) | 0.01 | |
| Sex | |||
| Female | Ref. | ||
| Male | 2.00 (0.64, 6.27) | 0.23 | |
| Sanders Maturity Stage | 1-2 | Ref.# | |
| 3 | 0.23 (0.08, 0.68) | <0.01 | |
| ≥4 | 0.06 (0.02, 0.17) | <0.01 | |
| Curve Classification | |||
| Thoracic | Ref. | ||
| Thoracolumbar or Lumbar | 0.64 (0.18, 2.24) | 0.48 | |
| Thoracic with Thoracolumbar or Lumbar | 2.00 (0.77, 5.23) | 0.16 | |
| Double Thoracic | 1.02 (0.22, 4.72) | 0.98 | |
| Triple | 2.55 (0.52, 12.55) | 0.25 | |
| Thoracic Apex (1 or more) | Ref. | ||
| No | |||
| Yes | 2.51 (0.87, 7.24) | 0.09 | |
| Triradiate cartilage | Ref. | ||
| Closing | |||
| Open | 4.72 (1.81, 12.32) | <0.01 | |
| Maximum Cobb Angle | 1.17 (1.09, 1.26) | <0.01 | |
Wald confidence intervals
indicates the reference level of the variable for odds ratio calculation
Model Development
Our aim was to develop a clinic-friendly model that could provide risk estimates based on data typically collected at the first clinic visit. We purposely did not consider any risk factors measured from lateral or side-bending films or 3D models from linked PA and lateral films. The potential complexity of the models was also limited by the sample size available in the development dataset. A general rule of thumb is 10-20 events per independent variable, which in this study would be 6. With a small sample, there is an increased risk for underfitting and overfitting. Underfitted models fail to include important risk factors and consequently don’t adequately explain the variation in the outcome. Conversely, including too many variables can lead to overfitting, the situation where the model is too specific to the dataset it was developed in. Overfitted models may not perform well in different samples, as evidenced by smaller indices of prognostic accuracy than those calculated in the model development stage. To guide our choices about which and how many variables to include in the model, we used the Akaike information criteria (AIC) as described below.
The model development process began with evaluation of the relationships between the risk factors and the prognosis. Based on the odds ratios from logistic regression, we selected the variables age (rounded to the nearest year), sex, curve pattern (dichotomized into 2 groups; patterns including at least 1 thoracic apex and single lumbar or thoracolumbar curves), the Cobb angle (the largest one in the case of double or triple curves), status of the triradiate (open or closing) and the SMS (collapsed to 1-2, 3, and 4+).
The AIC is frequently used with model selection procedures. The AIC measures the relative quality of models for a given dataset, thereby providing a means of model selection. Unlike typical forward stepwise regression procedures, variables are not selected or retained based on a pre-specified p-value (typically 0.05-0.20). The forward selection strategy used the criteria p=1.00 to enter and p=1.00 to stay, thereby creating a set of candidate models equal to the number of proposed risk factors. The first model in the set includes the factor explaining the most variance, and successive models are created by adding factors in order of additional variance explained. An AIC is associated with each model. The model with the lowest AIC provides the most information using the fewest number of predictors, thereby balancing the concerns of both under- and over-fitting, and thus maximizes generalizability of the model to new datasets. 5
Appendix Table 3.
Summary of Candidate Models and Akaike Information Criteria
| Step | Candidate Models | AIC Intercept Only |
AIC Intercept And Covariates |
|---|---|---|---|
| 1 | SMS | 161.206 | 131.359 |
| 2 | SMS, Cobb angle | 98.598 | |
| 3 | SMS, Cobb angle, Curve Pattern | 96.638 | |
| 4 | SMS, Cobb angle, Curve Pattern, Sex | 98.195 | |
| 5 | SMS, Cobb angle, Curve Pattern, Sex, Age | 100.146 |
Of this set, the model with the lowest AIC included the 3 variables SMS, Cobb angle, and curve pattern. It should be noted that a set of models including the triradiate was also investigated. A model including the above 3 variables and the triradiate yielded an AIC of 92.710, indicating it was more efficient than the 3-variable model. However, when comparing other indices of model performance (the c-statistic, Brier score, calibration plots and the maximum sensitivity and specificity of the classifications) the model including the triradiate had equivalent discrimination, but was less accurate (higher Brier scores, worse fit between predicted and observed outcomes, and lower estimates of sensitivity and specificity). Also of note is the fact that for many of the BrAIST subjects, the status of the triradiate was not clearly visible on the standing coronal view and was instead evaluated using the side-bending films. Triradiate data were not available in the duPont dataset.
When using small sample sizes for model development, even when the EPV is within the 10-20 guidelines, the resultant coefficients can be biased with large variance (over-optimistic). This can lead to poor performance when the model is applied to new samples. To minimize both the bias and variance, we used Firth’s penalized maximum likelihood estimation when fitting the model 6 using the variables selecting via the AIC.
Validation
Evaluations of the performance of a model can be optimistically biased if estimated from the same data used to develop the model. Therefore, evaluation in different subsamples from the original dataset (internal cross-validation) and/or from different datasets (external validation) are required. Internal validation is a process to evaluate how well a model predicts in the underlying population from which the sample originated, reflecting the reproducibility of the predicted probabilities. External validity (generalizability) is the degree to which the model predicts the outcomes of patients from different settings, populations and measurement conditions. Therefore, it is not required that the development and external validation samples have the same distribution of patient characteristics or the same outcome rates.
Evidence reflecting internal validity was obtained via cross-validation options in the SAS logistic regression procedure (Proc Logistic, SAS® Version 9.4, Cary, NC). Cross-validated predicted probabilities for each observation in the BrAIST dataset were estimated using a one-step approximation to the jackknifing procedure. Jackknife validation usually requires a series of iterative steps, where each observation (subject) is ignored and the model is fitted to the remaining data, and then the refitted model is used to estimate the probability of a poor prognosis for the ignored subject. 7 The jackknifed internal validation dataset then includes the subjects from the development dataset and the cross-validated predicted probabilities from the jackknife procedure. To evaluate external validity, we applied the model to the external validation dataset and calculated the predicted probabilities using the SCORE option in Proc Logistic.
Indices of calibration reflect the accuracy of the predictions for individual subjects by comparing them to the observed outcomes. The Brier score is the mean squared difference between the predicted probabilities and the observed outcomes; the lower the Brier score, the more accurate the predictions. Appendix Table 3 lists the Brier scores for the development, internal and external validation datasets.
Appendix Table 4.
Brier Scores from the BrAIST, Cross- and External Validation Samples
| Brier Score (95% CI) | |
|---|---|
| BrAIST (n=115) | 0.12 (0.08, 0.16) |
| Cross-Validation (n=115) | 0.13 (0.09, 0.17) |
| External Validation (n=152) | 0.12 (0.09, 0.16) |
Calibration plots graphically depict the agreement between the observed prognoses and the predictions. For example, if the model predicts a 40% risk of a poor prognosis, then the observed frequency of that prognosis should be 40 out of 100 (40%) of those with that prediction. To evaluate calibration, the distribution of the predicted probabilities was divided into deciles and the average predicted probability for each decile (x-axis) was plotted against the percentage of subjects in each decile observed to have a poor prognosis (y-axis). Loess smoothing was used to generate the calibration lines for the model. A reference line on the plot represents perfect calibration. Points above the reference line indicate the model is under-predicting the frequency of the outcome; below the line, the model is over-predicting the outcome.
Appendix References
- 1.Weinstein SL, Dolan LA, Wright JG, Dobbs MB. Effects of bracing in adolescents with idiopathic scoliosis. N Engl J Med. 2013. October 17;369(16):1512–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sitoula P, Verma K, Holmes L Jr., Gabos PG, Sanders JO, Yorgova P, et al. Prediction of Curve Progression in Idiopathic Scoliosis: Validation of the Sanders Skeletal Maturity Staging System. Spine. 2015. July 01;40(13):1006–13. [DOI] [PubMed] [Google Scholar]
- 3.Katz DE, Herring JA, Browne RH, Kelly DM, Birch JG. Brace wear control of curve progression in adolescent idiopathic scoliosis. J Bone Joint Surg Am. 2010. June;92(6):1343–52. [DOI] [PubMed] [Google Scholar]
- 4.Karol LA, Virostek D, Felton K, Jo C, Butler L. The Effect of the Risser Stage on Bracing Outcome in Adolescent Idiopathic Scoliosis. J Bone Joint Surg Am. 2016. August 3;98(15):1253–9. [DOI] [PubMed] [Google Scholar]
- 5.Akaike H A new look at the statistical model identification. IEEE Trans on Automatic Control. 1974;AC-19(6). [Google Scholar]
- 6.Moons KG, Donders AR, Steyerberg EW, Harrell FE. Penalized maximum likelihood estimation to directly adjust diagnostic and prognostic prediction models for overoptimism: a clinical example. J Clin Epidemiol. 2004. December;57(12):1262–70. [DOI] [PubMed] [Google Scholar]
- 7.SAS/STAT(R) 9.2 User's Guide, Second Edition. The LOGISTIC Procedure. Predicted Probability of an Event for Classification. . [cited 2018 July 30]; Available from:https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_logistic_sect037.htm#statug.logistic.logisticppec. [Google Scholar]
Footnotes
Human subjects’ research approval for BrAIST was obtained from the local boards of all participating centers; approval for collection and use of additional data was obtained from the University of Iowa and Nemours/Alfred I. duPont Hospital for Children.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Noshchenko A, Hoffecker L, Lindley EM, et al. Predictors of spine deformity progression in adolescent idiopathic scoliosis: A systematic review with meta-analysis. World J Orthop 2015;6:537–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Weinstein SL, Ponseti IV. Curve progression in idiopathic scoliosis. J Bone Joint Surg Am 1983;65:447–55. [PubMed] [Google Scholar]
- [3].Lonstein JE, Carlson JM. The prediction of curve progression in untreated idiopathic scoliosis during growth. J Bone Joint Surg Am 1984;66:1061–71. [PubMed] [Google Scholar]
- [4].Bunnell WP. The natural history of idiopathic scoliosis before skeletal maturity. Spine (Phila Pa 1976) 1986;11:773–6. [DOI] [PubMed] [Google Scholar]
- [5].Peterson LE, Nachemson AL. Prediction of progression of the curve in girls who have adolescent idiopathic scoliosis of moderate severity. Logistic regression analysis based on data from the brace study of the Scoliosis Research Society. J Bone Joint Surg Am 1995;77:823–7. [DOI] [PubMed] [Google Scholar]
- [6].Ward K, Ogilvie JW, Singleton MV, et al. Validation of DNA-based prognostic testing to predict spinal curve progression in adolescent idiopathic scoliosis. Spine 2010;35:E1455–64. [DOI] [PubMed] [Google Scholar]
- [7].Yeung HY, Tang NL, Lee KM, et al. Genetic association study of insulin-like growth factor-i (igf-i) gene with curve severity and osteopenia in adolescent idiopathic scoliosis. Stud Health Technol Inform 2006;123:18–24. [PubMed] [Google Scholar]
- [8].Lam TP, Hung VW, Yeung HY, et al. Quantitative ultrasound for predicting curve progression in adolescent idiopathic scoliosis: A prospective cohort study of 294 cases followed-up beyond skeletal maturity. Ultrasound Med Biol 2013;39:381–7. [DOI] [PubMed] [Google Scholar]
- [9].Yip BH, Yu FW, Wang Z, et al. Prognostic value of bone mineral density on curve progression: A longitudinal cohort study of 513 girls with adolescent idiopathic scoliosis. Sci Rep 2016;6:39220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Cheung J, Veldhuizen AG, Halbertsma JP, et al. The relation between electromyography and growth velocity of the spine in the evaluation of curve progression in idiopathic scoliosis. Spine (Phila Pa 1976) 2004;29:1011–6. [DOI] [PubMed] [Google Scholar]
- [11].LeBlanc R, Labelle H, Forest F, et al. Morphologic discrimination among healthy subjects and patients with progressive and nonprogressive adolescent idiopathic scoliosis. Spine (Phila Pa 1976) 1998;23:1109–15; discussion 15-6. [DOI] [PubMed] [Google Scholar]
- [12].Kindsfater K, Lowe T, Lawellin D, et al. Levels of platelet calmodulin for the prediction of progression and severity of adolescent idiopathic scoliosis. J Bone Joint Surg Am 1994;76:1186–92. [DOI] [PubMed] [Google Scholar]
- [13].Lowe TG, Burwell RG, Dangerfield PH. Platelet calmodulin levels in adolescent idiopathic scoliosis (ais): Can they predict curve progression and severity? Summary of an electronic focus group debate of the ibse. European Spine Journal 2004;13:257–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Ajemba PO, Ramirez L, Durdle NG, et al. A support vectors classifier approach to predicting the risk of progression of adolescent idiopathic scoliosis. IEEE Trans Inf Technol Biomed 2005;9:276–82. [DOI] [PubMed] [Google Scholar]
- [15].Yamauchi Y, Yamaguchi T, Asaka Y. Prediction of curve progression in idiopathic scoliosis based on initial roentgenograms. A proposal of an equation. Spine (Phila Pa 1976) 1988;13:1258–61. [DOI] [PubMed] [Google Scholar]
- [16].Skalli W, Vergari C, Ebermeyer E, et al. Early detection of progressive adolescent idiopathic scoliosis: A severity index. Spine (Phila Pa 1976) 2016. [DOI] [PubMed] [Google Scholar]
- [17].Nault ML, Mac-Thiong JM, Roy-Beaudry M, et al. Three-dimensional spinal morphology can differentiate between progressive and nonprogressive patients with adolescent idiopathic scoliosis at the initial presentation: A prospective study. Spine (Phila Pa 1976) 2014;39:E601–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Kadoury S, Mandel W, Roy-Beaudry M, et al. 3-d morphology prediction of progressive spinal deformities from probabilistic modeling of discriminant manifolds. IEEE Trans Med Imaging 2017;36:1194–204. [DOI] [PubMed] [Google Scholar]
- [19].Hung VW, Qin L, Cheung CS, et al. Osteopenia: A new prognostic factor of curve progression in adolescent idiopathic scoliosis. J Bone Joint Surg Am 2005;87:2709–16. [DOI] [PubMed] [Google Scholar]
- [20].Sanders JO, Khoury JG, Kishan S, et al. Predicting scoliosis progression from skeletal maturity: A simplified classification during adolescence. J Bone Joint Surg Am 2008;90:540–53. [DOI] [PubMed] [Google Scholar]
- [21].Sanders JO, Browne RH, McConnell SJ, et al. Maturity assessment and curve progression in girls with idiopathic scoliosis. J Bone Joint Surg Am 2007;89:64–73. [DOI] [PubMed] [Google Scholar]
- [22].Verma K, Sitoula P, Gabos P, et al. Simplified skeletal maturity scoring system: Learning curve and methods to improve reliability. Spine 2014;39:E1592–8. [DOI] [PubMed] [Google Scholar]
- [23].Sitoula P, Verma K, Holmes L Jr., et al. Prediction of curve progression in idiopathic scoliosis: Validation of the Sanders skeletal maturity staging system. Spine 2015;40:1006–13. [DOI] [PubMed] [Google Scholar]
- [24].Nicholson AD, Sanders JO, Liu RW, et al. The relationship of calcaneal apophyseal ossification and sanders hand scores to the timing of peak height velocity in adolescents. Bone Joint J 2015;97-B:1710–7. [DOI] [PubMed] [Google Scholar]
- [25].Vira S, Husain Q, Jalai C, et al. The interobserver and intraobserver reliability of the Sanders classification versus the risser stage. J Pediatr Orthop 2017;37:e246–e9. [DOI] [PubMed] [Google Scholar]
- [26].Minkara A, Bainton N, Tanaka M, et al. High risk of mismatch between Sanders and Risser staging in adolescent idiopathic scoliosis: Are we guiding treatment using the wrong classification? J Pediatr Orthop 2018. [DOI] [PubMed] [Google Scholar]
- [27].Collins G, Reitsma J, Altman D, et al. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (tripod): The tripod statement. . Br J Surg 2015;102:148–58. [DOI] [PubMed] [Google Scholar]
- [28].Weinstein SL, Dolan LA, Wright JG, et al. Effects of bracing in adolescents with idiopathic scoliosis. N Engl J Med 2013;369:1512–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Katz DE, Herring JA, Browne RH, et al. Brace wear control of curve progression in adolescent idiopathic scoliosis. J Bone Joint Surg Am 2010;92:1343–52. [DOI] [PubMed] [Google Scholar]
- [30].Karol LA, Virostek D, Felton K, et al. The effect of the Risser stage on bracing outcome in adolescent idiopathic scoliosis. J Bone Joint Surg Am 2016;98:1253–9. [DOI] [PubMed] [Google Scholar]
- [31].Akaike H A new look at the statistical model identification. IEEE Trans on Automatic Control 1974;AC-19. [Google Scholar]
- [32].Moons KG, Donders AR, Steyerberg EW, et al. Penalized maximum likelihood estimation to directly adjust diagnostic and prognostic prediction models for overoptimism: A clinical example. J Clin Epidemiol 2004;57:1262–70. [DOI] [PubMed] [Google Scholar]
- [33].Hosmer D, Lemeshow S. Applied logistic regression. 2nd ed New York, NY: John Wiley & Sons; 2000. [Google Scholar]
- [34].Vergouwe Y, Steyerberg EW, Eijkemans MJ, et al. Substantial effective sample sizes were required for external validation studies of predictive logistic regression models. J Clin Epidemiol 2005;58:475–83. [DOI] [PubMed] [Google Scholar]
- [35].Nachemson AL, Peterson LE. Effectiveness of treatment with a brace in girls who have adolescent idiopathic scoliosis. A prospective, controlled study based on data from the brace study of the Scoliosis Research Society. J Bone Joint Surg Am 1995;77:815–22. [DOI] [PubMed] [Google Scholar]
- [36].Danielsson AJ, Hasserius R, Ohlin A, et al. A prospective study of brace treatment versus observation alone in adolescent idiopathic scoliosis: A follow-up mean of 16 years after maturity. Spine (Phila Pa 1976) 2007;32:2198–207. [DOI] [PubMed] [Google Scholar]
- [37].Vickers AJ, Elkin EB. Decision curve analysis: A novel method for evaluating prediction models. Med Decis Making 2006;26:565–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Dolan LA, Sabesan V, Weinstein SL, et al. Preference assessment of recruitment into a randomized trial for adolescent idiopathic scoliosis. J Bone Joint Surg Am 2008;90:2594–605. [DOI] [PMC free article] [PubMed] [Google Scholar]