Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Dec 19;4(27):22356–22362. doi: 10.1021/acsomega.9b02636

A Benchmark for Homomeric Enzyme Active Site Structure Prediction Highlights the Importance of Accurate Modeling of Protein Symmetry

Stephanie C Contreras †, Steve J Bertolani †, Justin B Siegel †,‡,§,*
PMCID: PMC6941179  PMID: 31909318

Abstract

graphic file with name ao9b02636_0006.jpg

Accurate prediction and modeling of an enzyme’s active site are critical for engineering efforts as well as providing insight into an enzyme’s naturally occurring function. Previous efforts demonstrated that the integration of constraints enforcing strict geometric orientations between catalytic residues significantly improved the modeling accuracy for the active sites of monomeric enzymes. In this study, a similar approach was explored to evaluate the effect on the active sites of homomeric enzymes. A benchmark of 17 homomeric enzymes with known structures and a bound ligand relevant to the established chemistry were identified from the protein data bank. The enzymes identified span multiple classes as well as symmetries. Unlike what was observed for the monomeric enzymes, upon the application of catalytic geometric constraints, there was no significant improvement observed in modeling accuracy for either the active site of the protein structure or the accuracy of the subsequently docked ligand. Upon further analysis, it is apparent that the symmetric interface being modeled is inaccurate and prevented the active sites from being modeled at atomic-level accuracy. This is consistent with the challenge others have identified in being able to predict de novo protein symmetry. To further improve the accuracy of active site modeling for homomeric proteins, new methodologies to accurately model the symmetric interfaces of these complexes are needed.

Introduction

Enzymes are proteins that carry out specific chemical reactions that have been utilized in various industries, such as pharmaceuticals, agriculture, and biofuels. Their high specificity, high catalytic efficiency, and nontoxic and ecofriendly characteristics are some reasons that enzymes have gained interest in their use in industrial applications.1,2 Even with these advantages, enzymes are hindered in industrial applications when it comes to stability, catalytic efficiency, and specificity.2 There have been different approaches taken within the field of enzyme engineering to combat these issues, and one of those is computational protein design. This approach is dependent on structure–function relationships and therefore requires a structure of the enzyme of interest.2

Experimentally determined structures of proteins have been obtained with the progress of structure elucidation techniques, such as X-ray crystallography, nuclear magnetic resonance (NMR), and cryogenic electron microscopy, but these techniques have not been able to keep up with the sequencing efforts made over the years. An alternative to these experimental structure elucidation techniques is the computational structure prediction method homology modeling. Homology modeling allows for the determination of a three-dimensional model of a protein sequence (target) using the information of experimentally determined structures of homologous proteins (templates). Previous studies have demonstrated that homology modeling pipelines can result in higher accuracy structures when supplemented with additional information, such as sparse NMR distance constraints, low-resolution cryo-electron microscopy, mass spectrometry-derived cross-linking, and evolutionary relationships derived from sequence homology.3−12

Our lab recently demonstrated that utilizing the knowledge of an enzyme’s reaction mechanism to serve as additional information resulted in significant improvements in the accuracy of the modeling of monomeric enzyme active sites using homology modeling.13 However, many enzymes have multiple, symmetric chains, and therefore it is critical to also evaluate if the integration of knowledge from the enzyme’s reaction mechanisms can improve the active site modeling to atomic-level accuracy for symmetric enzymes. To evaluate symmetric enzymes, a highly curated benchmark of 17 homomeric enzymes was developed in order to examine if both symmetry and catalytic geometric (CG) constraint information would enable an atomically accurate modeling of the enzyme active site.

Results and Discussion

Catalytic Residue Conservation within the Homomeric Enzyme Benchmark

Homomeric enzymes that varied in sequence length, symmetry, and performed different chemical reactions based on enzyme commission (EC) classification were chosen to ensure a diverse set of enzymes were tested with this benchmark (Table 1). The interatomic distances between the catalytic residues serve to define the CG constraints used in modeling each enzyme family. In order to analyze the structural conservation of the catalytic residues used in the modeling of the target sequences for the benchmark, the Cα root-mean-square deviation (rmsd) for the catalytic residues as well as all residues was calculated (Figure 1A).

Table 1. Seventeen Enzymes in the Benchmark.

target bioactive chains length of sequence EC enzyme name PID of nearest template
3mng 2 173 1 human peroxiredoxin 64.6
4bnp 2 416 1 isocitrate dehydrogenase 75.2
1nki 2 135 2 fosfomycin resistance protein A 67.7
1a59 2 378 2 citrate synthase 59.8
2q7o 3 289 2 purine nucleoside phosphorylase (Homo sapiens) 55.8
3bgs 3 289 2 purine nucleoside phosphorylase (H. sapiens) 55.8
3fuc 3 284 2 purine nucleoside phosphorylase (Bos taurus) 55.6
5th5 2 692 2 transketolase 68.5
1ctu 2 294 3 cytidine deaminase 50
2o4p 2 99 3 HIV-1 protease 79.8
4hgo 4 164 3 phosphohydrolase 43.1
1dqx 2 267 4 orotidine 5′-phosphate decarboxylase 52.3
1ovm 4 552 4 indole pyruvate decarboxylase 41.4
1qin 2 183 4 human glyoxalase 42.1
2vbg 2 570 4 branched-chain keto acid decarboxylase 41.4
3fzn 4 534 4 benzoyl formate decarboxylase 44.5
4fua 4 215 4 l-fuculose phosphate aldolase 43.4
Open in a new tab

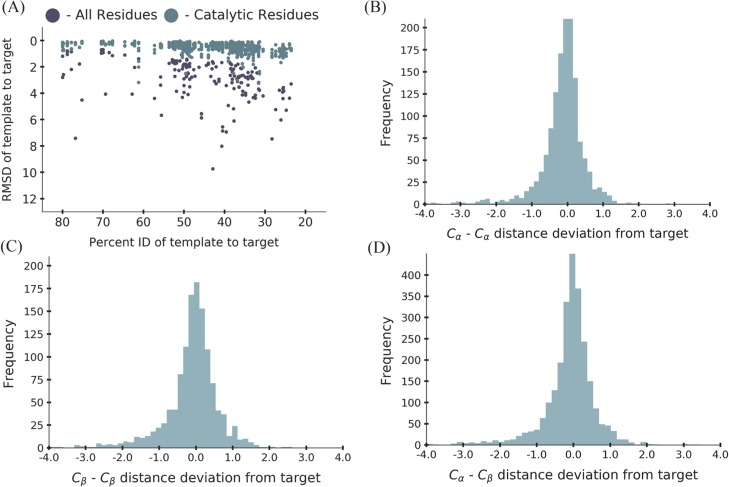
Figure 1.

Figure 1

Open in a new tab

(A) Analysis of the structural conservation between the target crystal structures and their templates used in the benchmark. The points in purple represent the rmsd of all the residues in the enzyme. The points in teal represent the rmsd of the catalytic residues in the enzyme. (B) Analysis of the Cα–Cα distance deviation between the target crystal structure and the templates with a standard deviation of 0.6. (C) Analysis of the Cβ–Cβ distance deviation between the target crystal structure and the templates with a standard deviation of 0.7. (D) Analysis of the Cα–Cβ distance deviation between the target crystal structure and the templates with a standard deviation of 0.7.

As expected, the rmsd of all the residues within the enzyme increased as a function of percent identity between the template and the target (Figure 1A). However, the rmsd of the catalytic residues remained relatively consistent and did not change as a function of the percent identity of the template. The catalytic residues of an enzyme family are well known to be highly conserved across enzyme families in terms of sequence as well as structure.14,15 The Thornton group investigated the relationship between the rmsd values of Cα and Cβ atoms of the catalytic residues of structures within a family versus the percent identity. They also showed that no matter what the percent identity of the structure within an enzyme family, the rmsd was between 1 and 5 Å, with 80% having an rmsd below 1 Å for three and four catalytic residues.15 The trend that is seen with the catalytic residues for this benchmark supports the relationship seen from the work done by the Thornton group and the monomeric benchmark from our group.13

With the analysis showing that the CG constraints for this benchmark were consistent with the previous observations of the structural conservation of catalytic residues, the standard deviations for the atom pairs Cα–Cα, Cβ–Cβ,, and Cα–Cβ were determined to provide bounds to use with CG constraints (Figure 1B–D). The histograms of each of the atom pairs show a Gaussian distribution with standard deviations of 0.6, 0.7, and 0.7 among the Cα–Cα, Cβ–Cβ, and Cα–Cβ pairs of the catalytic residues, respectively. These standard deviations were on par with the standard deviations seen for monomeric enzymes, where the standard deviation was 0.5 for all the three atom pairs.13

Homology Modeling

The target sequences for the 17 enzymes in the benchmark were modeled with the information from symmetry definition files derived from the top template of each target and in the presence and absence of additional CG constraints (Table S3). When applying the CG constraints, weights of 1, 10, 100, and 1000 were evaluated between the Cα–Cα atom pairs (Figure S3). There was only a modest difference in the change in modeling among the four weights; therefore, models generated with a weight of 1 were used for all further analyses as they had the smallest average rmsd and standard deviation.

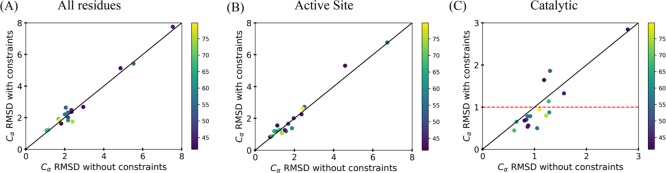
The Cα rmsd values of the two sets of models described above were compared in three categories: all residues, catalytic residues, and active site residues (Figure 2A–C). The graphs pertaining to the rmsd values of all the residues and the active site residues show that on average there is no improvement to the models as a whole with the addition of the CG constraints. This does not hold true though when looking at the rmsd values of the catalytic residues when the CG constraints were implemented. For 12 out of 17 models, there was an improvement resulting in an rmsd of less than 1 Å between the models and crystal structures when the constraints were used. The five where improvement was not seen can be attributed to the use of the low percent identity of the template used to dictate the symmetry when modeling was done.

Figure 2.

Figure 2

Open in a new tab

Analysis of the Cα rmsd of the lowest five models for each enzyme in the benchmark with and without the incorporation of the CG constraints with a weight of 1. The rmsd was determined by comparing the target crystal structure to the models that were generated. Each point represents the average rmsd of the lowest five models, and the color of each point in the graphs represents the percent identity of the top template used for modeling. Any point seen below the line was seen as an improvement in modeling, on the line there was no change, and above the line, it was seen as a lack of improvement. (A) All residue rmsd. (B) Active site rmsd (residues within 8 Å of the ligand). (C) Catalytic residue rmsd.

Even with the improvements seen in the modeling of the catalytic residues with this homomeric benchmark set, as was the case with the monomeric benchmark from our lab, a global analysis of the models highlighted a consistent shift of the symmetric units. Analysis of global protein structures are highlighted in Figure 3, where four representative models are aligned on one chain with the target crystal structure. Qualitatively, it is seen that there is a high level of accuracy for one chain and a systematic error in the atomic details for the placement of symmetric units. This shift could be attributed to the use of symmetry definition files when modeling as it dictates how to generate the initial configuration of the symmetry of all the units within a protein and how the system may be perturbed while maintaining symmetry.5 The exact orientation of the subunits is kept constant throughout the homology modeling simulations, and therefore if this initial placement is not atomically accurate, the subsequent models generated will never be modeled at atomic accuracy.

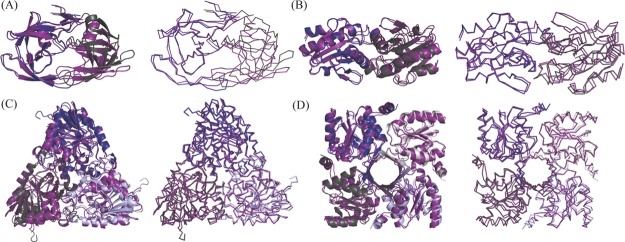
Figure 3.

Figure 3

Open in a new tab

Depictions of four enzymes from the benchmark when modeled using symmetry definition files represented in cartoon and ribbon forms. The crystal structure is depicted in a deep purple color with the models overlaid on top. (A) Model for 2o4p is depicted in blue (chain A) and dark gray (chain B). (B) Model for 3mng is depicted in blue (chain A) and dark gray (chain B). (C) Model for 2q7o is depicted in blue (chain A), dark gray (chain B), and light blue (chain C). (D) Model for 4hgo is depicted in blue (chain A), dark gray (chain B), light blue (chain C), and light gray (chain D).

This occurrence is similar to the results obtained with the oligomeric structure prediction done by Park et al.16 Using symmetry definition files for modeling oligomeric proteins, they found two similar results. The first was an improvement in the structure quality of the monomeric state when modeling the oligomeric state. The second was that the oligomeric state was correctly identified, but the model was not as accurate as other structure prediction methods. The reasons they provided why this occurred were due to poor template selection and incorrect sequence alignment.16 The template selection can be the case here. By choosing the top template’s symmetry definition file to dictate the model’s symmetry, the subtle angstrom difference from the target enzyme symmetry can equate to the shifts seen in modeling. The ribbon images of the models for the four enzymes represented in Figure 3, and the others seen in Figure S7, provide us with a qualitative analysis that supports the results found by Park et al.16

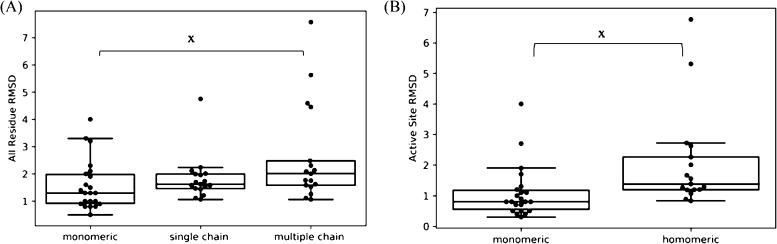
To determine quantitatively if the monomeric modeling with the enzymes in our benchmark also improved when modeling the homomeric state, we examined the rmsd of all the residues and active site residues for the single chain and multiple chains of our models. In addition to the homomeric benchmark, we also examined the rmsd of the monomeric benchmark to determine if the difference came from lower accuracy templates in the homomeric benchmark or if it is specifically from the symmetry information. The all-residue rmsd with the incorporation of CG constraints is seen in Figure 4A and the active site rmsd with the incorporation of CG constraints is seen in Figure 4B. When looking at the active site rmsd for the models from the monomeric benchmark, we can infer that all the machinery is in place with the homology modeling pipeline to improve monomeric models with the use of CG constraints. To provide a critical comparison between the accuracy of the models of the two benchmarks, a two-tailed t test was performed. A p value of significance in Figure 4A was only found between the monomeric versus multiple chain comparison, and there was no significant difference observed between the monomeric versus single chain and single chain versus multiple chain unit comparisons. A significant p value in Figure 4B is seen between the monomeric versus homomeric benchmarks. In addition, the modeling accuracy of the enzyme active sites in monomeric enzymes was found to be significantly higher than what was achieved for homomeric enzymes (Figure S5C). Overall, from this analysis, we can infer that the low accuracy of active site modeling of homomeric enzyme active sites is derived from modeling the symmetric units.

Figure 4.

Figure 4

Open in a new tab

Boxplots comparing the rmsd values between the monomeric and homomeric benchmarks. Each point in (A,B) represents the average rmsd for the lowest five models. The single chain represents the rmsd of only the single chain (chain A) between the crystal structures and models within the homomeric benchmark. The multiple chain represents the rmsd analysis between the symmetric chains (all chains except chain A) of the crystal structures and models within the homomeric benchmark. “x” corresponds to p < 0.05, determined by performing a two-tailed t test. (A) Analysis between the target crystal structure and models with catalytic constraints for all residues. The p value for the monomeric-single chain was 0.37, monomeric-multiple chains was 0.037, and single chain–multiple chain was 0.081. (B) Analysis between the target crystal structure and models with catalytic constraints for active site residues. The p value between the monomeric and homomeric benchmarks was 0.035.

This result identified a direct avenue for future method development, specifically in methods that will further refine the exact positioning of relative subunits within a symmetric protein. Computational methods to sample rigid body orientations within the defined symmetric space could potentially improve the modeling accuracy of homomeric enzymes. Computationally intensive methods to sample rigid body positioning have been highly successful in the design of atomically accurate symmetric proteins and should be explored for how to integrate into the homology modeling pipeline as a potential approach to increase the modeling accuracy of homomeric proteins.17,18

Docking Analysis

Although the active sites of the modeled symmetric enzymes did not achieve atomic accuracy with or without CG constraints, it was still pertinent to evaluate the current docking methods to understand the current performance in these modeled systems. From the homology models generated with and without CG constraints, the respective ligand conformational library was docked into the active site using enzymatic constraints. The enzymatic constraints used in the docking protocol were the distance and angle information that need to be satisfied between the catalytic residues and the ligand in order for the chemical reaction to take place. The rmsd values of the heavy atoms of the ligand were calculated between the two sets of models to evaluate the docking accuracy (Figure 5). The docking simulations carried out for all the enzymes in the benchmark can be seen in Figure S6. The data in Figure 5 show that the rmsd of the ligand showed improvement for about half of the docking runs, whereas the other half did not, with the incorporation of CG constraints during homology modeling. This is not unexpected as there was no significant change observed in the modeling of the active site between these two methods. The five points that have the rmsd greater than 4 Å seen in Figure 5 correspond to the enzymes with PDB codes 1ctu, 1dqx, 1qin, 2o4p, and 4hgo. The zinc metal where catalysis occurs is in close vicinity of the crystal structure ligand even though the ligand rmsd for 1ctu resulted in a higher rmsd when the CG constraints were implemented (Figure S6A). The high rmsd in the ligand for 1dqx can be attributed to the fact that there is one catalytic residue, lysine, interacting with the ligand for the chemical reaction to take place. The limited amount of chemical information added to the docking coupled with the low-accuracy active site modeling of this protein makes this a particularly challenging enzyme to model (Figure S6B). The high rmsd of the ligands for 1qin (Figure S6E), 2o4p (Figure S6F), and 4hgo (Figure S6O) is likely because of the high degrees of freedom present for these ligands. The average number of ligand conformations among the three enzymes was 39 690, whereas the average number of ligand conformations for the other 14 enzymes was 541 (Table S6). This could also highlight the need to apply a filter for ligands that are larger and have many rotatable bonds that are not cofactors, as with thiamine pyrophosphate, to reduce the sample space when docking is performed. This was not used here, and so there was no bias of one conformation over another in the libraries when the docking protocol was carried out.

Figure 5.

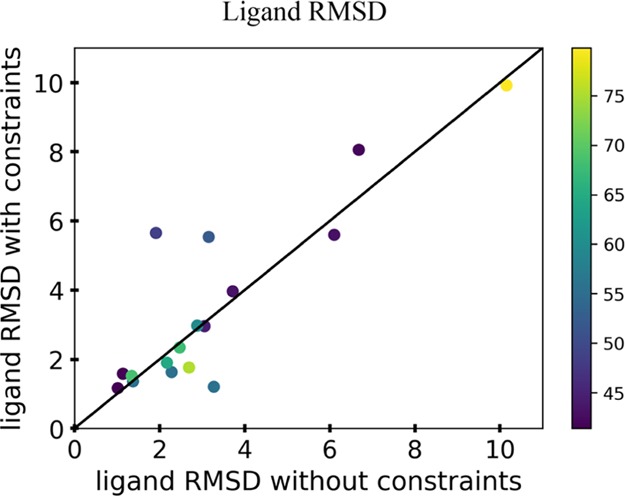
Figure 5

Open in a new tab

Analysis of the ligand rmsd of the 17 enzymes from the benchmark when docking was performed on the lowest five models with and without the incorporation of the enzymatic constraints. The rmsd was determined by the heavy atoms of the ligand and comparing the target crystal structure ligand to the docked ligand of the models. Each point represents the average rmsd of the lowest five models, and the color of each point in the graphs represents the percent identity of the top template used for modeling.

The average rmsd of ligands for models generated without and with CG constraints is 3.26 and 3.47, respectively. For the models without the implementation of CG constraints, roughly 30% had an rmsd less than 2 Å and 70% had an rmsd greater than 2 Å when docking was performed. For the models where CG constraints were implemented, 47% had an rmsd less than 2 Å and 53% had an rmsd greater than 2 Å when docking was performed. Therefore, using current protocols in situations where atomic accuracy is needed, homology modeling has the potential to be useful for enzyme families with a highly conserved placement between symmetric units or monomeric enzymes.

Conclusions

The results obtained from the models generated in this study are in agreement with previous studies which identified the challenges in interfacial modeling between the subunits of symmetric proteins.16 Work pertaining to the improvement of rigid body sampling involved with the symmetry definition files within Rosetta may help to obtain atomic resolution models that could then be used in downstream applications, such as small-molecule docking and design.19,20 An additional factor not taken into consideration in our modeling efforts is the dynamic and flexible nature of protein states. From this arises the question as to what the best route for comparison of our models is, as we could very well be modeling an accurate state of the protein that is not reflected by the crystal structure, which is a known challenge in the field.21−23

The ability to rapidly generate models with atomically accurate active sites of symmetric proteins is of the utmost importance for understanding a protein’s function and our ability to modulate a protein’s functional properties for industrial and medical applications. Although significant strides have been made in recent years at improving the modeling for monomeric proteins, atomically accurate modeling of symmetric proteins remains a significant challenge.19,20,23−25

Methods

Construction of Benchmark Set of Homomeric Enzymes

The benchmark set consists of 17 homomeric enzymes (Table 1). These 17 enzymes were picked on the basis that they ranged from different EC classes, the active sites were at the enzyme interface, and the target crystal structure contained a mechanistically relevant ligand in the active site. The mechanistically relevant molecule served the purpose of ensuring that the residues involved in catalysis for the target crystal structure are geometrically oriented in the correct positions for the chemical reaction associated with that enzyme to occur.

Integration of the Enzyme Reaction Mechanism: CG Constraints

The classification of the catalytic residues that were used for the CG constraints for modeling was the same as those described by the Thornton group: direct chemical role in the mechanism, effect on another residue that is directly involved in the mechanism, stabilization of a transition-state intermediate, and aid in the catalysis by having an effect on the substrate or cofactor.26 The catalytic residues were obtained by performing a literature search for each of the 17 enzymes. These catalytic residues were then checked against the mechanism and catalytic site atlas online database. The ones available on the database matched with what was determined in the literature (Table S1).27

The analysis for the generation of the CG constraints to be utilized during modeling was performed as described previously.13 Briefly, the templates that were used for the modeling of their respective target sequences all belong to the same enzyme family and were all aligned to their respective target crystal structures. The Euclidean coordinates of the Cα and Cβ carbons were extracted to perform the analysis of Cα rmsd and Cα–Cα, Cβ–Cβ, and Cα–Cβ distance deviations. The calculations of the distances derived between the catalytic residues within an enzyme family were performed from the target crystal structure to get all combinations of Cα–Cα, Cβ–Cβ, and Cα–Cβ distances and applied as CG constraints during homology modeling (Figure S2).

Homology Modeling

Three-dimensional models of the 17 targets in the benchmark were generated using the RosettaCM protocol.28 The templates for the generated models were identified using HMMER, and the matches that were chosen were those with the lowest e values, had a percent identity of 80% or below, and had a biological unit available (Table S2).29 The cutoff for the templates was set to 80% to ensure that the target crystal structure, or highly related homologs, was not used as one of the templates. To correlate the sequence position to structure position, PROMALS 3D was used to generate a multiple sequence alignment from the sequences of these templates and the target sequence.30 To fill in the unaligned regions during molecular modeling, structural fragment sets were generated using standard methods31 Evolutionary constraints were used to enhance sampling during multitemplate fragment-based modeling through RosettaCM.10 A weight of 1 was used when modeling was performed with the added CG constraints. One hundred decoys were generated of the target sequence with the lowest five energy models selected to perform docking. The version of Rosetta used for modeling was: 17be250fab3b65d60d806025d7219a5373754924.

Symmetry

The symmetry information of the models was dictated by a symmetry definition file that was generated using a perl script make_symmdef_file.pl found within the Rosetta modeling suite. The script was applied to all the biological units of the templates in the benchmark to generate a symmetry definition file and an input PDB. The input PDB corresponds to a single chain from the template complex and was used in symmetry modeling within the RosettaCM protocol. The symmetry definition file of the top template, defined as the template with the highest sequence homology, for each target sequence was used in modeling (Table S3).

Docking

The ROSETTALIGAND protocol was used for the docking of the ligand into the models of the 17 targets.32,33 The ligand structures for the benchmark were pulled from the crystal structure available from the PDB Web site. The structures were loaded onto GaussView 5.0 to complete the valence of the atoms, and then a conformation library of the ligands was generated using the Spartan’16 suite semiempirical method.34−36 The atoms in the ligands are allowed to sample all conformer spaces, with the exception of those described in Table S4. The conformation library of the ligands generated was used to dock into the models generated. The docking protocol used enzymatic constraints pertaining to the distance and angle information needed to be satisfied between the catalytic residues and the ligand in order for the chemical reaction to take place. The lowest five apo models from the homology modeling protocol described before were used to generate 1000 docking decoys, which gives a total of 5000 docking decoys for each target. A pool of the lowest 10% structures was filtered based on their total score from each of the five apo models. These pooled docked models were then filtered on the basis of their constraint score and interface binding score between the ligand and enzyme. With these criteria, the lowest five docked models were compared to the target crystal structure ligand to calculate the ligand rmsd of the heavy atoms. The version of Rosetta used for docking was: eb376c9763fb0fcbc2d45692a80e423cb7d474f0.

Acknowledgments

We are grateful for the funding and support from UC Davis as well as all the help from RosettaCommons.

Glossary

Abbreviation

CG constraints

catalytic geometric constraints

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b02636.

  • rmsd graphs, templates, catalytic residues,, active sites, and enzyme structures (PDF)

  • Images from the main text and benchmark files used for modeling and docking (github.com/siegel-lab-ucd/homomeric_benchmark) (ZIP)

This work was supported by the University of California Davis, the National Institutes of Health [R01 GM 076324-11], the National Science Foundation [award numbers 1827246, 1805510, 1627539], and the National Institute of Environmental Health Sciences of the National Institutes of Health [award number P42ES004699]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health, National Institute of Environmental Health Sciences, National Science Foundation, or UC Davis.

The authors declare no competing financial interest.

Supplementary Material

ao9b02636_si_001.pdf (8.2MB, pdf)
ao9b02636_si_002.zip (7.4MB, zip)

References

  1. Singh R.; Kumar M.; Mittal A.; Mehta P. K. Microbial enzymes: industrial progress in 21st century. 3 Biotech 2016, 6, 174. 10.1007/s13205-016-0485-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Choi J.-M.; Han S.-S.; Kim H.-S. Industrial applications of enzyme biocatalysis: Current status and future aspects. Biotechnol. Adv. 2015, 33, 1443–1454. 10.1016/j.biotechadv.2015.02.014. [DOI] [PubMed] [Google Scholar]
  3. Huang P.-S.; Boyken S. E.; Baker D. The coming of age of de novo protein design. Nature 2016, 537, 320–327. 10.1038/nature19946. [DOI] [PubMed] [Google Scholar]
  4. Bender B. J.; Cisneros A.; Duran A. M.; Finn J. A.; Fu D.; et al. Protocols for molecular modeling with Rosetta3 and RosettaScripts. Biochemistry 2016, 55, 4748–4763. 10.1021/acs.biochem.6b00444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. DiMaio F.; Leaver-Fay A.; Bradley P.; Baker D.; André I. Modeling symmetric macromolecular structures in Rosetta3. PLoS One 2011, 6, e20450 10.1371/journal.pone.0020450. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Martí-Renom M. A.; Stuart A. C.; Fiser A.; Sánchez R.; Melo F.; Šali A. Comparative Protein Structure Modeling of Genes and Genomes. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 291–325. 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
  7. DiMaio F.; Song Y.; Li X.; Brunner M. J.; et al. Atomic-Accuracy Models from 4.5-Å Cryo-Electron Microscopy Data with Density-Guided Iterative Local Rifinement. Nat. Methods 2015, 12, 361–365. 10.1038/nmeth.3286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ovchinnikov S.; Kamisetty H.; Baker D.; Baker D. Robust and accurate prediction of residue-residue interactions across protein interaces using evolutionary information. eLife 2014, 3, e02030 10.7554/elife.02030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ovchinnikov S.; et al. Large-scale determination of previously unsolved protein structures using evolutionary information. eLife 2015, 4, e09248 10.7554/eLife.09248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Thompson J.; Baker D. Incorporation of evolutionary information into Rosetta comparative modeling. Proteins: Struct., Funct., Bioinf. 2011, 79, 2380–2388. 10.1002/prot.23046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Vortmeier G.; DeLuca S. H.; Els-Heindl S.; Chollet C.; et al. Integrating Solid-State NMR and Computational Modeling to Investigate the Structure and Dynamics of Membrane-Associated Ghrelin. PLoS One 2015, 10, e0122444 10.1371/journal.pone.0122444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kamisetty H.; Ovchinnikov S.; Baker D. Assessing the utility of coevolution-based residue-residue contact predictions in a sequence-and structure-rich era. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 15674–15679. 10.1073/pnas.1314045110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bertolani S. J.; Siegel J. B. A new benchmark illustrates that integration of geometric constraints inferred from enzyme reaction chemistry can increase enzyme active site modeling accuracy. PLoS One 2019, 14, e0214126 10.1371/journal.pone.0214126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wallace A. C.; Laskowski R. A.; Thornton J. M. Derivation 3D coordinate templates for searching structural databases: application to Ser-His-Asp catalytic triads in the serine proteinases and lipases. Protein Sci. 1996, 5, 1001–1013. 10.1002/pro.5560050603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Torrance J. W.; Bartlett G. J.; Porter C. T.; Thornton J. M. Using a library of structural templates to recognize catalytic sites and explore their evolution in homologous families. J. Mol. Biol. 2005, 347, 565–581. 10.1016/j.jmb.2005.01.044. [DOI] [PubMed] [Google Scholar]
  16. Park H.; Kim D. E.; Ovchinnikov S.; Baker D. Automated structure prediction of oligomeric assemblies using Robetta in CASP12. Proteins: Struct., Funct., Bioinf. 2018, 86, 283–291. 10.1002/prot.25387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. King N. P.; Sheffler W.; Sawaya M. R.; Vollmar B. S.; et al. Computational Design of self-assembling protein nanomaterials with atomic level accuracy. Science 2012, 336, 1171–1174. 10.1126/science.1219364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. King N. P.; Bale J. B.; Sheffler W.; McNamara D. E.; et al. Accurate design of coassembling multi-component protein nanomaterials. Nature 2014, 510, 103–108. 10.1038/nature13404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Burman S. S. R.; Nance M. L.; Jeliazkov J. R.. et al. Novel sampling strategies and a coarse-grained score function for docking homomers, flexible heteromers, and oligosaccharides using Rosetta in CAPRI Rounds 37-45. BioRxiv, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Labonte S. S.; Yovanno R. A.; Gray J. J. Flexible backbone assembly and refinement of symmetrical homomeric complexes. Structure 2019, 27, 1041–1051. 10.1016/j.str.2019.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Burkoff N. S.; Várnai C.; Wells S. A.; Wild D. L. Exploring the energy landscapes of protein folding simulations with Bayesian computation. Biophys. J. 2012, 102, 878–886. 10.1016/j.bpj.2011.12.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Wells S. A.; van der Kamp M. W.; McGeagh J. D.; Mulholland A. J. Structure and function in homodimeric enzymes: simulations of cooperative and independent functional motions. PLoS One 2015, 10, e0133372 10.1371/journal.pone.0133372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Moult J.; Fidelis K.; Kryshtafovych A.; Schwede T.; Tramontano A. Critical assessment of methods of protein structure prediction (CASP)-Round XII. Proteins: Struct., Funct., Bioinf. 2018, 86, 7–15. 10.1002/prot.25415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. AlQuraishi M. AlphaFold at CASP13. Bioinformaitcs 2019, 35, 4862. 10.1093/bioinformatics/btz422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bertoni M.; Kiefer F.; Biasini M.; Bordoli L.; Schwede T. Modeling protein quaternary structure of homo- and hetero-oligomers beyond binary interactions by homology. Sci. Rep. 2017, 7, 10480. 10.1038/s41598-017-09654-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Bartlett G. J.; Porter C. T.; Borkakoti N.; Thornton J. M. Analysis of catalytic residues in enzyme active sites. J. Mol. Biol. 2002, 324, 105–121. 10.1016/s0022-2836(02)01036-7. [DOI] [PubMed] [Google Scholar]
  27. Ribeiro A. J. M.; Holliday G. L.; Furnham N.; et al. Mechanism and catalytic site atlas (M-CSA): a database of enzyme reaction mechanisms and active sites. Nucleic Acids Res. 2018, 46, D618–D623. 10.1093/nar/gkx1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Song Y.; DiMaio F.; Wang R. Y.-R.; Kim D.; Miles C.; Brunette T.; Thompson J.; Baker D. High-Resolution Comparative Modeling with RosettaCM. Structure 2013, 21, 1735–1742. 10.1016/j.str.2013.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Finn R. D.; Clements J.; Eddy S. R. HMMER web server: interactive sequence similarity searching. Nucleic Acids Res. 2011, 39, W29–W37. 10.1093/nar/gkr367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pei J.; Grishin N. V.. PROMALS3D: multiple protein sequence alignment enhanced with evolutionary and three-dimensional structural information. Methods in Molecular Biology; Springer, 2014; pp 263–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Gront D.; Kulp D. W.; Vernon R. M.; Strauss C. E. M.; Baker D. Generalized fragment picking in Rosetta: design, protocols and applications. PLoS One 2011, 6, e23294 10.1371/journal.pone.0023294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Meiler J.; Baker D. ROSETTALIGAND: protein-small molecule docking with full side-chain flexibility. Proteins 2006, 65, 538–548. 10.1002/prot.21086. [DOI] [PubMed] [Google Scholar]
  33. Combs S. A.; DeLuca S. L.; DeLuca S. H.; et al. Small-molecule ligand docking into comparative models with Rosetta. Nat. Protoc. 2013, 8, 1277–1298. 10.1038/nprot.2013.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Dennington R.; Keith T. A.; Millam J. M.. GaussView, version 5; Semichem Inc.: Shawnee Mission, KS, 2009.
  35. Spartan ’16; Wavefunction, Inc.: Irvine, CA, 2016.
  36. Shao Y.; Molnar L. F.; Jung Y.; Kussmann J.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. 10.1039/b517914a. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b02636_si_001.pdf (8.2MB, pdf)
ao9b02636_si_002.zip (7.4MB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES