Protein Abundance Biases the Amino Acid Composition of Disordered Regions to Minimize Non-functional Interactions

Abstract

In eukaryotes, disordered regions cover up to 50% of proteomes and mediate fundamental cellular processes. In contrast to globular domains, where about half of the amino acids are buried in the protein interior, disordered regions show higher solvent accessibility, which makes them prone to engage in non-functional interactions. Such interactions are exacerbated by the law of mass action, prompting the question of how they are minimized in abundant proteins. We find that interaction propensity or “stickiness” of disordered regions negatively correlates with their cellular abundance, both in yeast and human. Strikingly, considering yeast proteins where a large fraction of the sequence is disordered, the correlation between stickiness and abundance reaches R = − 0.55. Beyond this global amino-acid composition bias, we identify three rules by which amino-acid composition of disordered regions adjusts with high abundance. First, lysines are preferred over arginines, consistent with the latter amino acid being stickier than the former. Second, compensatory effects exist, whereby a sticky region can be tolerated if it is compensated by a distal non-sticky region. Third, such compensation requires a lower average stickiness at the same abundance when compared to a scenario where stickiness is homogeneous throughout the sequence. We validate these rules experimentally, employing them as different strategies to rescue an otherwise sticky protein fragment from aggregation. Our results highlight that non-functional interactions represent a significant constraint in cellular systems and reveal simple rules by which protein sequences adapt to that constraint. Data from this work are deposited in Figshare, at https://doi.org/10.6084/m9.figshare.8068937.v3.

Highlights

• •Proteins span a wide range of abundance and can engage in non-functional interactions (NFI).
• •Minimizing NFI is a dominant constraint on the composition of disordered regions.
• •This composition bias may cause under-detection of disorder in low abundance proteins.
• •This composition bias does not need to be global across the entire protein sequence.
• •Constraints of NFI can serve to reverse-engineer principles of protein solubility.

Graphical abstract

Introduction

Intrinsically disordered regions (IDRs) are found in proteins across all three domains of life and predominantly among eukaryotes where they cover 35% to 45% of proteomes [1]. IDRs are generally depleted of hydrophobic amino acids, which make them unable to fold autonomously [2], [3]. Consequently, they are characterized by a lack of stable tertiary structure under physiological conditions [4]. The high-conformational variability associated with IDRs grants them unique functional and mechanical properties [4], [5], [6], [7], [8], [9], [10], [11]. For example, nucleoporins are size-filtering devices of the nuclear pore complex containing disordered regions rich in phenylalanine–glycine repeats that influence the nuclear pore complex gating behavior [12]. In addition, disordered regions are notorious for their role in mediating and scaffolding protein-protein interactions [13], [14], [15], [16], [17]. One recognition mechanism involves domain–peptide interactions, where a globular domain such as WW, PDZ, or SH3 recognizes a linear motif in a disordered region [18], [19], [20], [21], [22], [23], [24], [25]. Another class of recognition mechanism has been described as “induced fit” [26], [27], where folding occurs concurrently with binding, promoting highly specific and transient interactions [15], [22], [28], [29], [30] often found in cell signaling and regulation processes [19], [23], [31], [32], [33]. Disordered regions thus play a pivotal role in the evolution [34], [35], [36], [37], [38] and the wiring of protein-protein interactions networks [34], [35], [36], [37], [39], [40], [41], [42].

Importantly, however, properties of disordered regions that promote functional recognition are also expected to promote dysfunctional recognition [43], [44], [45]. Indeed, disordered regions naturally exhibit high solvent exposure, and we know that exposed protein surfaces show a natural tendency to bind one another promiscuously [46], [47], suggesting that a delicate balance exists in cells, between functional (selected) and non-functional (non-selected) binding [44], [48], [49], [50], [51], [52], [53], [54], [55], [56], [57], [58], [59], [60]. Such a delicate balance is reflected in the dosage sensitivity associated with over-expression of proteins that contain disordered regions or that are highly promiscuous [43], [44], [61], [62]. Consistent with this view, proteins containing disordered regions are under tight regulation with shorter half-lives, slower translation, and faster degradation, so as to minimize their presence when they are not needed [48], [57]. In addition, such potential for promiscuous binding is exploited by viruses to hijack cell regulation [63], [64], [65]. Finally, beyond promiscuous and dysfunctional interactions, disordered regions should exhibit specific properties so as not to be recognized as misfolded proteins by cellular chaperones, thereby threatening cellular homeostasis [66], [67], [68], [69], [70], [71].

As for any chemical equilibrium, dysfunctional interactions are expected to be concentration dependent [72], [73]. Therefore, we anticipate that sequence properties protecting against dysfunctional interactions [45], [57], [72], [74], [75], [76], [77] are enriched in IDRs of abundant proteins. To investigate this hypothesis, we considered the proteomes from Saccharomyces cerevisiae and Homo sapiens and compared properties of disordered regions present in low versus high-abundance proteins. As observed before, we saw that disordered regions are twice as rare in the latter [44], [48]. Importantly, however, because abundance spans several orders of magnitude, the small fraction of disordered regions in abundant proteins represents a large mass of disordered residues in the cell, suggesting that these regions must be endowed with properties that render them compatible with high abundance. We show that IDRs’ interaction propensity (stickiness) covaries with abundance more than other physicochemical properties do, including hydrophobicity and beta-amyloid formation propensity. Thus, dysfunctional interactions constrain the overall chemical composition of disordered regions. Analyzing the distribution of stickiness among disordered regions revealed that compensatory effects exist, whereby a non-sticky region in one part of a protein can buffer a sticky region hundreds of amino acids away. We verified this prediction experimentally and showed that an aggregation-prone misfolded protein can be rescued by the addition of charged residues delocalized relative to the sticky, aggregation-prone region.

Results and Discussion

Disorder content and protein abundance are inversely related

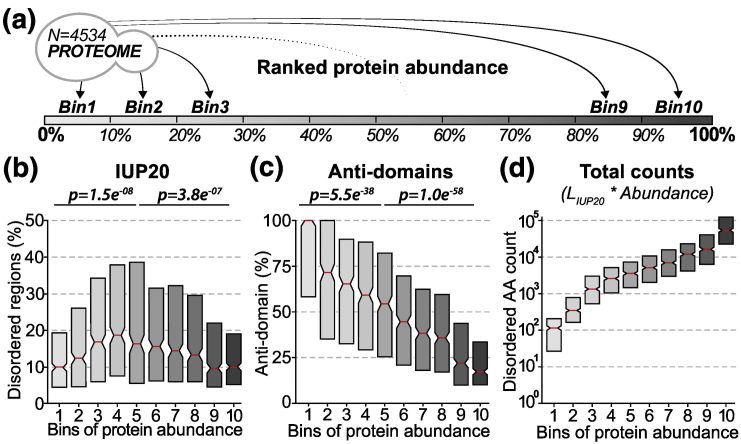
As discussed above, disordered regions are prone to promiscuous binding [43], [78], [79]. The fact that binding is a concentration-dependent process prompts us to compare the distribution of disordered regions among proteins of high versus low abundance. It has been shown before that cellular systems have evolved to regulate the availability of IDRs, whereby proteins enriched in IDRs are less abundant on average [48]. Here, we first confirm this finding. We examined protein disorder content (i.e., the percentage of disordered amino acids per protein) as a function of protein abundance for yeast and human. We defined 10 classes of abundance, henceforth referred to as “bins of abundance” (Figs. 1a and S1a, Table 1). Each bin contains approximately the same number of proteins. Abundance thresholds associated with these bins (in parts per million, or ppm) are kept identical throughout the work, but the number of proteins contained in each bin may differ in subsequent analyses when we concentrate on proteome subsets (e.g., proteins with at least 30 disordered residues). For all non-membrane proteins, we show the distribution of protein disorder content (Figs. 1b and S1b) for each bin of abundance.

Fig. 1.

High-abundance proteins are depleted in disordered regions, yet they dominate the mass fraction of disordered residues in the cell. (a) The full yeast proteome, membrane proteins excluded, is split into 10 bins of protein abundance with equal sizes. Bins 1 and 10 correspond to the 10% proteins with lowest and highest abundance in S. cerevisiae. (b) Boxplot distribution of disorder content across the 10 bins of protein abundance. The disorder content (y-axis) corresponds to the percentage of disordered residues detected per protein using IUPred [84] (see Methods). P values indicate whether the median disorder content significantly differs between bin 5 against bin 1 or 10 (one-sided Wilcoxon signed-rank test). (c) Same as panel b, counting residues not covered by any Pfam [82], [85] or SUPERFAMILY [83], [86] structural domain (“anti-domain”). P values are calculated as in panel b. (d) Boxplot distribution of absolute amino acid counts in disordered regions with increasing levels of protein abundance. The absolute amino-acid counts (y-axis) correspond to the number of disordered amino acids multiplied by the cellular abundance of the protein (in ppm). Each box shows 50% of the density distribution where notches represent the 95% confidence interval around the median (red line).

Table 1.

Equivalence between bins and range of abundance (A) with estimated cellular concentrations (C) for yeast and human

Bins	Deciles (%)	S. cerevisiae (yeast)		H. sapiens (human)
		A (ppm)	C (nM)	A (ppm)	C (nM)
1	0–10	0.003–1.4	0.0–6.5	1e−5–0.1	0.0–0.5
2	10–20	1.4–3.0	6.5–13	0.1–0.3	0.5–1.5
3	20–30	3.0–7.8	13.0–33.9	0.3–0.5	1.5–2.5
4	30–40	7.8–14.1	33.9–65.3	0.5–1.0	2.5–5.0
5	40–50	14.1–23.4	65.3–111.1	1.0–2.1	5.0–10.5
6	50–60	23.4–37.9	111.1–180.9	2.1–4.5	10.5–22.4
7	60–70	37.9–64.9	180.9–311.5	4.5–10.1	22.4–50.8
8	70–80	64.9–119	311.5–583.1	10.1–24.8	50.8–123.6
9	80–90	119–351	583.1–1700	24.8–75	123.6–398.7
10	90–100	351–21,870	1700–109,000	75–30,590	398.7–152,400

Considering the first four bins, we notice that disorder content increases with abundance both in yeast (Fig. 1b) and human (Fig. S1b), although the potential for promiscuous interactions is theoretically increasing. We suggest two possible origins for this trend: (i) Below the abundance range of the fourth bin, disordered regions are not selected against due to very low concentrations equivalent to 5–30 nM (1–7 ppm, Table 1). Such concentrations are indeed below typical affinity constants of domain-peptide interactions (K_d ∼ 0.1–150 μM) [80]. In line with this idea, linear motifs in disordered regions are also depleted in this range of abundance in yeast (Fig. S2). (ii) Disorder prediction methods may under-predict disordered regions [81] among proteins with low abundance due to their enrichment in sticky amino acids that are predominantly hydrophobic, as we will see in the next section. In support of this notion, Pfam [82] and SUPERFAMILY [83] domains become rarer as protein abundance decreases (Fig. 1c), suggesting that disorder should increase rather than decrease.

From the fifth to tenth bins of abundance, however, we observe a continuous decrease of protein disorder content, both in yeast and in human. Protein sequences in the fifth bin contain ∼ 20% disorder on average (∼ 40% in human, Fig. S1), whereas proteins with the highest abundance (tenth bin) contain only ∼ 10% (∼ 25% in human). This difference is highly significant in both species (yeast: p = 3.8 × 10⁻⁰⁷, human: p = 1.8 × 10⁻²¹, Wilcoxon one-sided test). The depletion of disordered regions among high-abundance proteins confirms the findings of Gsponer et al. [48], where IDR-poor proteins exhibit significantly higher abundances than IDR-rich proteins. These ideas also match results from Vavouri et al. [44], who observed that disordered regions and linear motifs were the main determinants of protein toxicity upon over-expression in yeast. Accordingly, we find that disordered regions become depleted of linear motifs in high-abundance proteins (Fig. S2). Overall, these results are consistent with binding promiscuity of disordered regions being a constraint, causing high-abundance proteins to adapt by decreasing their disordered content. Importantly, however, while the depletion is significant, it is not complete. In other words, since protein abundances span several orders of magnitude inside a cell, the ∼ 10% of disordered regions present in high-abundance proteins contribute as much as 60%–75% of all disordered residues in the cell (Fig. 1d). This prompted us to investigate whether these regions bear specific properties that minimize their potential for promiscuous interactions and aggregation.

The stickiness of disordered regions is dependent on protein abundance

We saw in the previous section that disordered regions are expected to exhibit properties minimizing their susceptibility for promiscuous interactions. To evaluate the tendency of disordered regions to engage in promiscuous interactions, we measured their interaction propensity as the average of their amino-acid interaction propensities (Figs. 2a and S3a). Amino-acid interaction propensities were taken from Levy et al. [78] and correspond to the log-ratio of their frequency at protein-protein interfaces relative to protein surfaces (Fig. S4a). Thus, in this “stickiness” scale, the higher the score of an amino acid, the more frequent it is at protein–protein interaction interfaces relative to protein surfaces. The stickiness scale shares similarities with amino-acid solubility, hydrophobicity, and aggregation scales as shown in Fig. S4b. Although the stickiness scale was defined on structured domains, we expect it to reflect the binding propensity of disordered regions as well, because similar frequencies of amino acids are seen at the interface cores of both types of complexes [87].

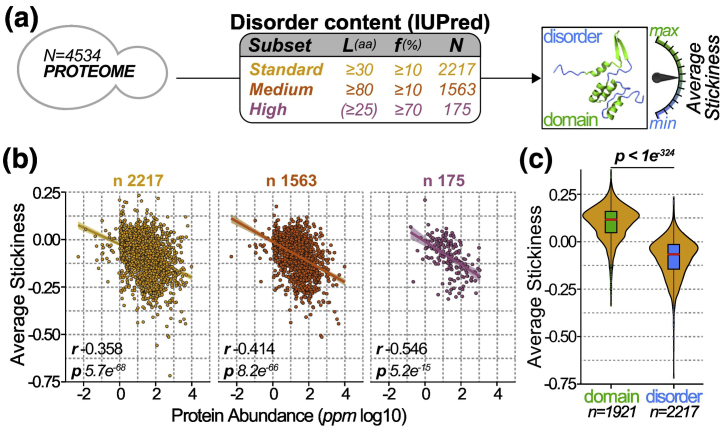
Fig. 2.

The stickiness of disordered regions is anti-correlated with protein abundance. (a) We defined three data sets of proteins with increasing disorder content, referred to as “standard,” “medium,” “high.” Proteins were included or excluded from each data set depending on their disorder content (L) and disorder fraction (f), as indicated in the panel table. The average stickiness of a protein was calculated by the mean score of all its amino acids in disordered regions. (b) Average protein stickiness (y-axis) as a function of protein abundance (x-axis) for disordered regions among the three data sets defined in panel a. The Spearman rank correlation coefficients (r) and the p values (p, Spearman’s rank correlation test) are indicated. The number of proteins (n) within each data set is given above each scatterplot. (c) Distribution of average protein stickiness (y-axis) calculated based on disordered regions (blue), or, for reference, calculated on domains (green) for the same proteins from the standard data set. Boxes correspond to 50% of the probability density around the median (red line). The p value indicates a significant difference between IDR-stickiness and domains stickiness (one-sided Wilcoxon signed-rank test).

Importantly, disordered regions often cover only a small fraction of the protein, and solvent-exposed amino acids outside of these regions may influence the global protein stickiness. For this reason, we used three data sets of proteins with “standard,” “medium,” and “high” disorder content (Figs. 2a and S3a, see Methods) and we anticipate that data sets with higher disorder content should better reflect compositional constraints. We show the distributions of protein length, disorder content, and disorder fraction in these three data sets, for yeast and human (Fig. S5).

We compared the average stickiness (S) of IDRs to their abundance (A) in the cell and observed a negative correlation, consistent with a recent report in yeast [51] and with a similar compositional bias seen among structured domains [78]. The S/A correlation appears stronger in yeast (R = − 0.36, Fig. 2b) than in human (R = − 0.21, Fig. S3b), and is significant in both species (yeast: p = 5.2 × 10⁻⁶⁸ human: p = 1.7 × 10⁻⁷⁵, Spearman’s rank correlation test). The lower correlation seen in human may reflect the ambiguous nature of protein abundance data in multicellular organisms, where it is averaged over tissues. The S/A correlation increased substantially when considering the “median” and “high” disorder-content data sets, to R = − 0.41 and R = − 0.55 in yeast (Fig. 2b), and R = − 0.25 and R = − 0.33 in human (Fig. S3b). Furthermore, if we consider an alternative data set of regions not matched by a known domain (we call this set of regions in protein sequences “anti-domains”), the S/A correlation increases further, reaching − 0.58 for 1453 yeast proteins (Fig. S6). Finally, we saw a similar correlation (R = − 0.37, Fig. S7a) when using disorder predictions from the D²P² database [88], which provides a consensus of several methods (PONDR, PrDOS, PV2, IUPred/ANCHOR, Espritz) [2], [84], [89], [90], [91], [92]. We also saw similar correlations when separating proteins in three groups according to their size (Fig. S7).

For all three disorder-content data sets, the decrease in IDR-stickiness with increasing protein abundance is highlighted with regression lines (Figs. 2b and S3b). The regression shows that IDR stickiness for low-abundance proteins (< 0.1 ppm) is above 0.0, and it decreases down to − 0.2 for proteins with the highest abundance. For reference, we compare this stickiness difference to that seen between structured domains (median, 0.12) and disordered regions (median, − 0.07; Fig. 2c), revealing a similar amplitude and stressing that the compositional bias we report is substantial.

Together, these results indicate that disordered regions present in high-abundance proteins exhibit biased compositions, whereby the fraction of their sticky amino acids is minimized. This observation supports the paradigm of a concentration-dependent optimization of amino acid composition in disordered regions so as to minimize dysfunctional interactions.

Hydrophobicity and β-amyloid propensity exhibit weaker concentration dependence

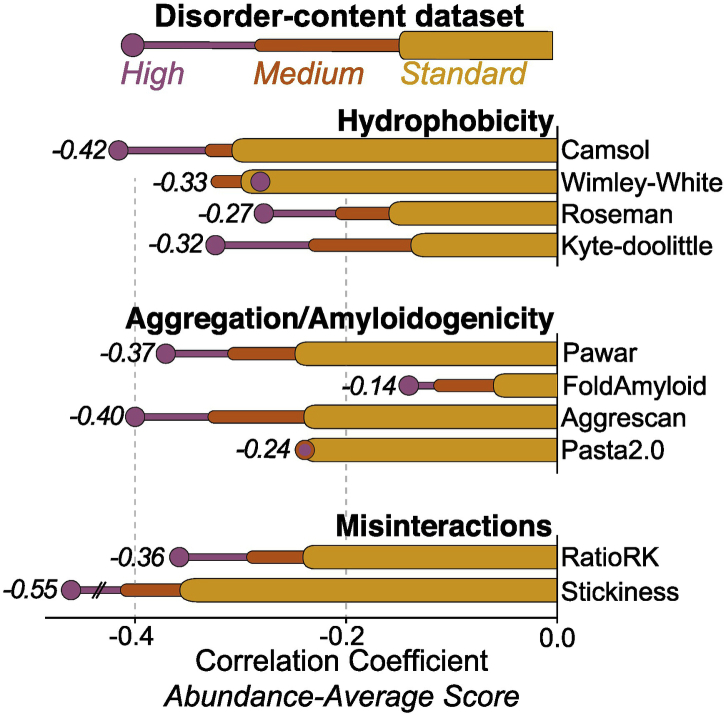
We explored alternative amino-acid interaction rules to explain the concentration-dependent adaptation in amino-acid composition. We tested whether hydrophobicity was at the origin of the correlations observed. Three distinct hydrophobicity scales (Wimley and White [93], Kyte and Doolittle [94], and Roseman [95]) as well as a sequence-based predictor of protein solubility (CamSol [96]) gave significant S/A correlations, albeit of lower magnitude than that observed with the stickiness scale (Figs. 3 and S8). We reached similar conclusions with β-amyloid and aggregation propensity predictors, based on FoldAmyloid [97], Aggrescan [67], Pawar et al. [98], and PASTA 2.0 [99].

Fig. 3.

Impact of abundance on several predicted properties of disordered regions in yeast. We calculated several properties of disordered regions associated with solubility and report their Spearman rank correlation with protein abundance. Colored bars show the correlation coefficients obtained using the same three sets of proteins defined in Fig. 2a: standard (orange), medium (dark orange), and high disorder-content data sets (purple).

A notable feature of the stickiness scale compared to other scales is the fact that it discriminates lysine (K) and arginine (R) as amino acids with a large difference in stickiness (Fig. S9). While lysine is the most under-represented amino acid at protein–protein interfaces (and thus the least sticky), arginine is found with nearly equal frequency at interfaces and surfaces [47], making it a significantly stickier amino acid than lysine. In line with this notion, Warwicker et al. [100] observed that high lysine and low arginine content correlate with protein solubility. This led us to define a minimal stickiness measure based solely on these two amino acids, the RK-ratio (R/(R + K)), which is the number of arginines over the number of both lysines and arginines in disordered regions of a particular protein. The RK-ratio yielded S/A correlation coefficients nearly as high or higher than those obtained using other scales both in yeast (R = − 0.24) and human (R = − 0.12), for the standard data set. For the high disorder-content data set, these values reached R = − 0.36 in yeast (Fig. 3) and R = − 0.2 in human (Fig. S8). The fact that arginine and lysine are considered largely equivalent by other scales (Fig. S9) and that arginine is the most hydrophilic amino acid according to hydrophobicity scales highlights the distinct nature of the stickiness scale and further suggests that promiscuous interactions are selected against among abundant proteins.

Local versus global optimization of stickiness

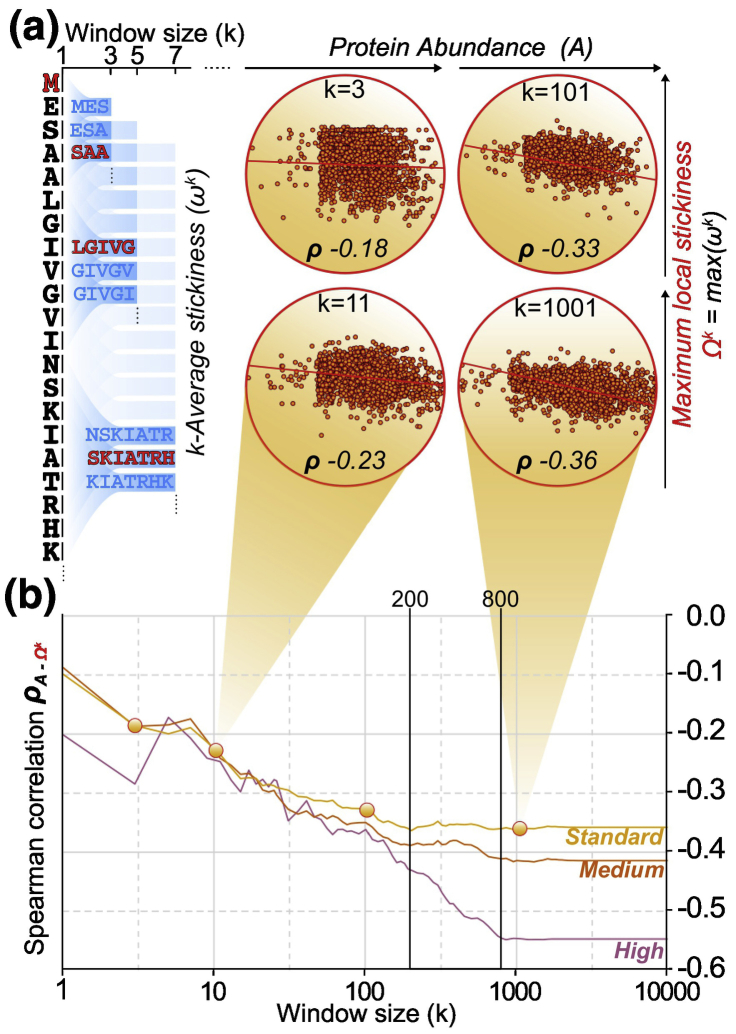
We observed that chemical properties of disordered regions change as a function of their concentration, with interaction-resilient amino acids being enriched in high-abundance proteins. This observation prompted us to ask whether stickiness must be optimized throughout the sequence, or whether compensation mechanisms can occur between different regions, whereby a non-sticky region in one part of the protein may compensate for a sticky one in a distal part and increase protein solubility. To address this question, we defined the local stickiness ω^k as the average stickiness score in a window of k residues sliding through each position i of a protein sequence (Fig. 4a). For each protein, we recorded the maximum local stickiness value as Ω^k = max(ω^k) (see Methods for details). Then, we calculated the Spearman rank correlation between protein abundance and Ω^k (Fig. 4b). We reasoned that the window size maximizing the correlation should reflect the distance in the polypeptide chain over which a highly sticky region can be compensated by a distal non-sticky region. We observed that larger windows improve the abundance-stickiness correlation up to a size of ∼ 200 residues for the standard data set and ∼ 800 residues for the high disorder-content data set, beyond which the correlation stabilizes (Figs. 4b and S10). It is difficult to ascribe a meaning to the actual size of these windows, notably because IDRs that are far in sequence may be close in space, for example, due to the protein’s structure, or due to conformational sampling [101]. However, the fact that the correlation increases with k exceeding several hundred residues does suggest the existence of compensatory effects, whereby a sticky segment in one part of a protein can be tolerated if a non-sticky segment elsewhere in the sequence can compensate for it.

Fig. 4.

Window size over which protein stickiness best correlates with protein abundance. (a) The window-averaged, local stickiness (ω^k) is calculated for windows of increasing size (k), represented here as funnels, sliding over the sequence of each protein. The local stickiness corresponds to the average of amino acid scores within a window of k residues (see Methods for details). For each window size, the maximum local average stickiness Ω^k is correlated against protein abundance. Scatterplots for selected values of k (3, 11, 101, 1001) are shown along with the corresponding Spearman rank correlation coefficient (ρ_k). (b) The Spearman rank correlation coefficient (ρ_k) is reported against increasing window sizes (k) considering residues within disordered regions of yeast proteins among the standard, medium, and high disorder-content data sets.

Heterogeneous distribution of stickiness among disordered segments

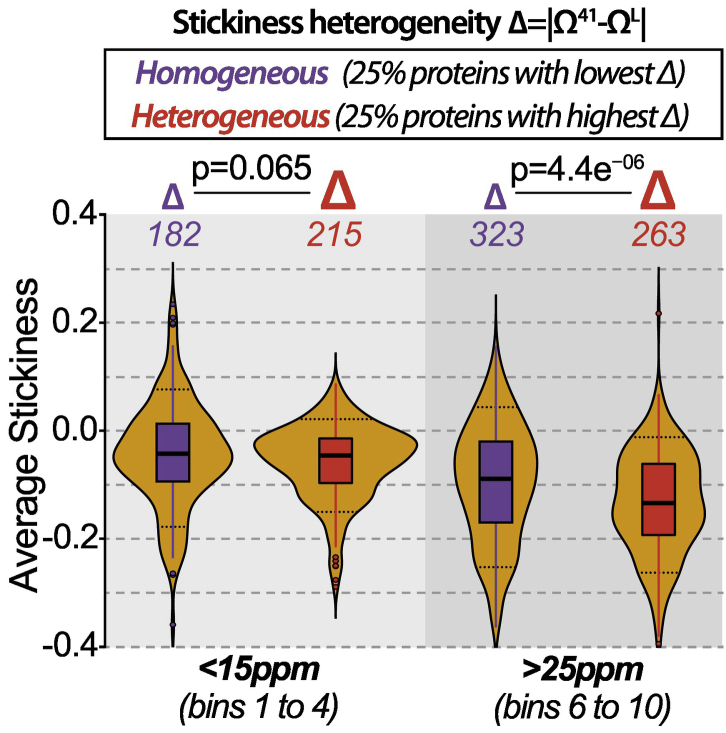
The long-range stickiness effects suggested by the above analysis led us to analyze stickiness homogeneity versus heterogeneity along the sequence. We introduced a measure Δ = Ω^k − Ω^L, the difference between the maximal stickiness in a window of size k and the average stickiness of the protein. A large Δ value indicates a heterogeneous stickiness across the protein, and conversely, a low value would be observed when the distribution of stickiness is homogeneous throughout the sequence. For this analysis, we arbitrarily used in both species a value k equal to 41 for the window size, but the results are robust against different values of k (Fig. S11).

We asked whether proteins with high versus low values of Δ show different average stickiness (Figs. 5 and S12). Among high-abundance proteins (bins 6–10), proteins with heterogeneous stickiness are less sticky on average when compared to proteins with homogeneous stickiness (yeast: p = 4.4 × 10⁻⁰⁶, human: 2.3 × 10⁻²⁹, Wilcoxon one-sided test). This result could be influenced by the window size (k = 41) as well as by protein length, since long proteins are expected to show larger heterogeneity by chance alone, when compared to shorter proteins. Thus, we controlled for these two parameters (Figs. S11 and S13) and observed a consistently lower stickiness in the heterogeneous class when compared to the homogeneous class. For proteins with lower abundance, the average stickiness of the heterogeneous class did not show a consistent difference relative to the homogeneous class.

Fig. 5.

Impact of stickiness heterogeneity on sequence adaptation to high abundance in yeast. Distributions of average stickiness (y-axis) within disordered regions of yeast proteins (standard data set) are displayed as violin shapes. Proteins with low (< 15 ppm, bins 1–4) or high abundance (> 25 ppm, bins 6–10) are further divided based on their stickiness heterogeneity (Δ). Stickiness heterogeneity is defined as the difference between the maximum local stickiness within a 41-residues window and the average IDR-stickiness of the protein. Homogeneous and heterogeneous proteins are those with the 25% lowest and highest Δ, respectively. P values are based on the Wilcoxon test. The number of proteins is given for each class.

These results suggest that delocalized non-sticky regions are not as effective to promote solubility when compared to regions with homogeneous stickiness, among high-abundance proteins. Why different proteins employ different strategies to remain soluble remains to be investigated. We can speculate that functional constraints might require heterogeneous distribution of sticky residues among disordered regions. For example, the highly conserved protein PEX5 contains a long N-terminal IDR harboring several “WxxxF/Y” motifs that mediate recognition and import of proteins from the cytoplasm to the peroxisome [102]. Furthermore, random evolutionary processes are likely to result in heterogeneous stickiness patterns. Indeed, considering a sticky and solvent-exposed region, there would be many more ways of compensating it with non-sticky residues elsewhere in the sequence than by mutating the region itself.

Experimentally assessing how distal non-sticky regions impact protein solubility

The results of the two previous sections led to three main conclusions. First, stickiness is a global sequence property that can involve compensatory effects in protein sequences. Second, the chemically analogous amino acids R and K exhibit markedly different stickiness properties. Third, homogeneous stickiness throughout the sequence is more effective at promoting solubility than heterogeneous stickiness.

To assess these concepts experimentally, we expressed chimeric fluorescent proteins in yeast cells and measured their solubility under the assumption that higher solubility promotes higher abundance in the cytosol. Maximal cytosolic abundance was observed for the wild-type Venus yellow fluorescent protein (YFP) [103], while minimal cytosolic abundance was observed for YFP fused to a sticky polypeptide derived from the mouse dihydrofolate reductase (DHFR) [104], thereafter referred to as YFP-DH (Fig. 6).

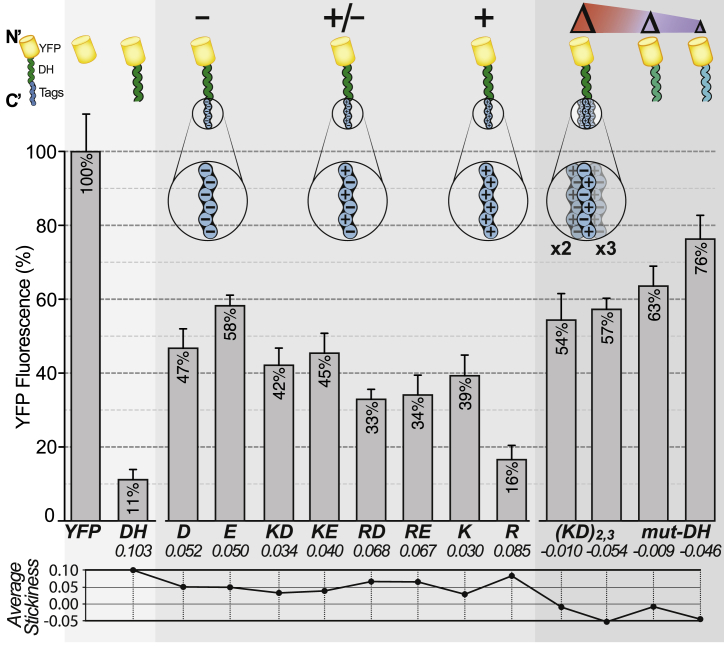
Fig. 6.

Increasing the solubility of a protein using different designs of non-sticky fusion tags. Chimeric proteins were expressed in yeast cells, their abundance was measured by microscopy and is given relative to untagged YFP, which shows highest abundance. Cartoons above the bars depict the composition of the constructs, and the average stickiness calculated from each sequence (YFP excluded) is given underneath the bars (cf. Table S3 for sequences, strains and fluorescence data). The first construct corresponds to untagged YFP used as a reference for normalizing fluorescence levels. The second construct consists of YFP fused to the N-terminal fragment of mouse DHFR [104]) at its C-terminus. Fusion of YFP to this sticky polypeptide decreased fluorescence levels about 10-fold. Non-sticky tags were fused at the C-terminus of YFP-DH and contain charged amino acids. Fluorescence levels achieved with fusion-tags containing six charges are shown in the first set of bars. Longer fusion tags containing 12 or 18 charges were also used, denoted as KD₂ and KD₃. Finally, in the last two constructs (mut-DH), stickiness was decreased by introducing mutations throughout the DH fragment sequence, resulting in a more homogeneous stickiness profile.

Increasing the solubility of a protein using different designs of non-sticky fusion tags. Chimeric proteins were expressed in yeast cells, their abundance was measured by microscopy and is given relative to untagged YFP, which shows highest abundance. Cartoons above the bars depict the composition of the constructs, and the average stickiness calculated from each sequence (YFP excluded) is given underneath the bars (cf. Table S3 for sequences, strains and fluorescence data). The first construct corresponds to untagged YFP used as a reference for normalizing fluorescence levels. The second construct consists of YFP fused to the N-terminal fragment of mouse DHFR [104]) at its C-terminus. Fusion of YFP to this sticky polypeptide decreased fluorescence levels about 10-fold. Non-sticky tags were fused at the C-terminus of YFP-DH and contain charged amino acids. Fluorescence levels achieved with fusion-tags containing six charges are shown in the first set of bars. Longer fusion tags containing 12 or 18 charges were also used, denoted as KD₂ and KD₃. Finally, in the last two constructs (mut-DH), stickiness was decreased by introducing mutations throughout the DH fragment sequence, resulting in a more homogeneous stickiness profile.

We subsequently aimed to increase the solubility of YFP-DH using different non-sticky fusion tags. First, we employed non-sticky tags composed of different combinations of positively and/or negatively charged amino acids fused at the C-terminus of YFP-DH. Overall, all non-sticky tags containing six charged amino acids increased the cytosolic abundance of YFP-DH, confirming that a non-sticky region can, at least partially, rescue from insolubility caused by a distal sticky region. Consistent with previous findings [105], [106], [107], [108], negative charges promoted solubility better than positive charges, with tags based on six aspartate or glutamate yielding cytosolic abundances up to 1.5 times higher than a tag containing six lysines. The increased solubility seen with negatively charged amino acids is at odds with the stickiness scale, where lysine is the least sticky amino acid. This apparent discrepancy may originate in the avoidance of arginine at protein surfaces, leaving lysine as the only non-sticky positively charged amino acid [47]. In line with this idea, the six-arginine tag led to a 2-fold reduction in cytosolic abundance when compared to the six-lysine tag. Tags that were electrostatically neutral gave intermediate cytosolic abundance. Next, we tested the impact of stickiness heterogeneity on solubility. We created two additional non-sticky tags containing 12 and 18 charged residues. These tags decreased the average stickiness and introduced a high heterogeneity. In parallel, we designed two mutant sequences matching the average stickiness obtained with 12 or 18 charged residues, although the mutations were introduced throughout the DH sequence to create a more homogeneous stickiness profile. The addition of 6 charged residues (from 6 to 12) increased the abundance of YFP-DH, but the further addition of charges (from 12 to 18) had little effect, suggesting that delocalized non-sticky regions cannot fully compensate for a distal sticky region. The strategy consisting of mutating sticky regions directly (e.g., mutations introduced in the DH sequence) showed comparatively higher abundance, consistent with homogeneous stickiness leading to higher solubility.

In our interpretation of these experiments, we hypothesize that fusion of the DH sequence to YFP induces its aggregation and degradation. Alternatively, the fusion of the DH sequence may slow down the translation of YFP-DH relative to YFP, reduce its mRNA stability, or decrease the average YFP fluorescence due to interference with the folding of YFP for example. However, it is unlikely that the diverse sequences of the non-sticky tags could consistently rescue from such effects, as their only common property is to be non-sticky. For this reason, the increase of YFP-DH solubility by the non-sticky tags is the most parsimonious explanation explaining their respective increase in fluorescence.

Conclusion

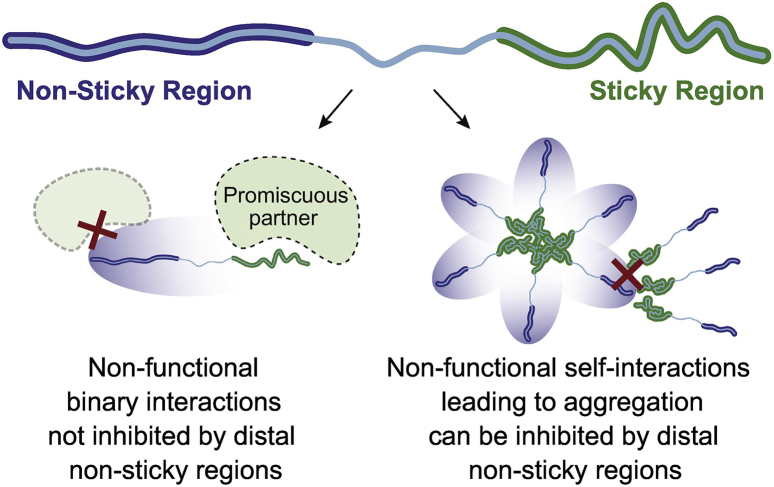
It has been observed previously that proteins containing disordered regions are constrained in terms of their regulation [48], [57]. In addition to regulatory mechanisms, our results show that disordered regions tune their amino-acid composition to their cellular abundance. We observed this trend globally, across the yeast and human proteomes, thus generalizing previous observations made on fewer proteins of known structures [78] and in a recent study [51]. Uniquely, our approach allowed comparing how amino-acid propensities associated with specific properties (hydrophobicity, amyloid formation, aggregation, and protein interactions) covaried with abundance. Interaction propensity or “stickiness” showed the strongest covariation, implying that avoidance of promiscuous interactions is a key property shaping protein sequences. Non-functional interactions can indeed be deleterious due to their potential to sequester proteins into aggregates of misfolded proteins [43], [62], [109], [110], [111] or agglomerates of folded proteins [58], and they may also compete with functional interactions [55], [57], [64], [65], [79], [112]. The local optimization of stickiness in the sequence is expected to minimize deleterious effects associated with binary promiscuous interactions. In contrast, the fact that stickiness can also be optimized globally, across different segments separated by 200 or more amino acids, suggests an adaptation mechanism against promiscuous self-interactions leading to aggregation (Fig. 7). We experimentally validated this concept by rescuing an aggregation-prone protein-fragment after adding non-sticky residues delocalized relative to the sticky region.

Fig. 7.

Hypothetical impact of heterogeneous stickiness on binary interactions versus aggregation. A non-sticky region is not expected to shield a distal sticky region from promiscuous binary interactions (left). However, a non-sticky region may inhibit self-interactions leading to aggregation, if this process involves burying the non-sticky region in a desolvated environment (right).

In addition to the insights into sequence features preventing non-functional interactions, our work has several implications. Practically, our results imply that methods may under- and over-predict disorder in low and high-abundance proteins respectively. For example, IUPred predicts disordered regions as those lacking hydrophobic amino acids to stabilize a folded protein core. Such predictions might be improved further if taking into consideration protein abundance to model the expected hydrophobic and hydrophilic character of globular domains and disordered regions. Our findings may also have important evolutionary implications since protein abundance is known to be the main determinant of sequence conservation across species [113], [114], [115], [116], [117], [118], [119]. It will therefore be important to consider stickiness in comparative sequence analyses, for example, to examine patterns of hydrophobic amino acids [120], and more generally, to understand routes and mechanisms of adaptation to high cellular abundance.

Methods

Filtering proteins

Some proteins have a biased amino-acid composition due to their cellular function. In particular, proteins with transmembrane helices are enriched in hydrophobic residues but these are unlikely to become solvent-exposed. Hence, we discarded all membrane proteins from this study. In order to identify membrane proteins, we used predictions from TMHMM [121] and meta-predictions from TOPCONS [122], [123], [124], [125], [126], [127], [128]. A total of 1913 (29%) yeast and 7297 (36%) human proteins were discarded for which at least one transmembrane segment was predicted according to the consensus prediction from TOPCONS. In the absence of consensus, we relied on the agreement between predictions from TMHMM and three out of five predictors compiled in TOPCONS.

Protein abundance data

Protein abundances were obtained from Pax-Db (v4.0, May 2015) [129], which provides relative abundances for unicellular and multicellular organisms including tissue-specific data. For both organisms, we used overall abundance in the whole organism, inferred from all available data sets (integrated data set). The unit conversion from relative abundance in ppm to cellular concentration in molar was obtained by the following formula: C = (k · A) / N_A where k ≈ 3·10⁶ proteins/fL as an estimate of cellular density of protein molecules per femtoliter (fL) obtained from [130], the Avogadro constant N_A = 6.02 × 10²³ molecules/mol, and A is the abundance (e.g., 1 ppm yields A = 10^-6 and results in C ≈ 5 nM). Table 1 provide the estimated range of cellular concentrations for the 10 bins of abundance.

Intrinsic disorder and domain predictions

We predicted disordered regions in both yeast and human proteomes using IUPred [84], combining short and long disorder predictions. In yeast, we selected the 20% amino acids with the highest disorder probabilities. The human proteome is known to exhibit higher disorder content [88] when compared to yeast, prompting us to use 40% of amino acids with the highest disorder probabilities.

To predict domains, we aligned profiles from Pfam-A (v27.0, May 2013) and Superfamily (v1.75, March 2013) to sequences of both proteomes and kept predictions with an E-value score below 10⁻³.

Defining the three sets of disordered proteins used in the analyses

We defined three data sets containing proteins with increasing disorder content. We refer to these data sets as “standard,” “medium,” and “high.” In yeast, the standard data set consists of 2217 proteins (7619 for human) where IDRs represent at least 10% (20% for human) of the sequence and contain at least 30 residues in total (50 for human). In yeast, the medium data set consists of 1563 proteins (3649 for human) where IDRs represent at least 10% (50% for human) of the sequence and contain at least 80 residues in total (50 in human). Finally, the high disorder data set contains 175 yeast proteins (944 for human), with at least 70% (80% for human) of the sequence being predicted as disordered, and a minimum of 25 disordered residues per sequence (40 residues in human). These criteria are summarized in Fig. 2a (Fig. S3a for human).

Interface propensity (stickiness) scale

Amino-acid interface propensities were obtained from Levy et al. [78]. In this scale, amino-acid interface propensities were calculated by the log-ratio of the frequency at the interface-core versus at the surface, based on a non-redundant set of Escherichia coli proteins of known structure.

$$\text{Interface propensity}\left(\mathrm{AA}\right)=log\left(\frac{{\text{Freq}}_{\mathrm{AA}}^{\text{interface}}}{{\text{Freq}}_{\mathrm{AA}}^{\text{surface}}}\right)$$

This scale (Fig. S4) measures the propensity for an amino acid to interact with other amino acids and thus can be viewed as a “stickiness” score, which serves to estimate the interaction propensity of disordered regions.

Other propensity scales

We employed three distinct amino-acid hydrophobicity scales: (1) Kyte and Doolittle [94] determined vacuum-to-water transfer free energies of amino acid side chain. (2) Roseman [95], [131] estimated the free-energies of completely transferring the amino acids side-chain along with the polypeptide backbone from water to a hydrocarbon phase, correcting for self-solvation effects of polar residues induced by the proximity of flanking non-hydrogen bonded peptide bond. (3) Wimley and White [93] measured the transfer free energy for amino acids from water to the interface of a phosphatidylcholine membrane bilayer.

For CamSol [96], sequence-based predictor of protein solubility, we used opposite values (i.e., scores were multiplied by − 1) to maintain a comparable ranking of amino acids with other scales.

We also considered amino-acid potentials derived from experimental data [132] for three methods that assess β-amyloid formation: Aggrescan [67], FoldAmyloid [97], and pH 7 scale from Pawar et al. [98].

Finally, we applied PASTA 2.0 [99] on protein sequence and kept the highest energy prediction for evaluating the stability of putative cross-beta pairings among disordered regions.

Calculation of global and local average stickiness of disordered regions

The stickiness of a sequence is calculated by the mean of its amino-acid stickiness scores (Fig. S4a). The global stickiness of IDRs in a protein is calculated using residues predicted as disordered, and amino acids outside of IDRs are ignored from the calculation. The local stickiness ω^k corresponds to the mean stickiness score calculated within a window of k residues sliding through each position i of a protein sequence. For each protein, we recorded the maximum local stickiness value as Ω^k = max(ω^k). Disordered regions are scattered along the sequence and can consist of few residues only. Thus, we imposed restrictions to avoid inferring a local stickiness value when the number of disordered residues was too small compared to the size of the window. Specifically, we inferred a local stickiness value only when the number of disordered residues in the window was equal or greater than the lowest value between:

• -half the window size h = (k + 1)/2
• -the size D of the largest disordered segment within the protein

Scanning windows of increasing size, ranging from one residue to the protein length L enabled us to assess distance-dependent fluctuations of the local maximum stickiness. For example, with a window consisting of a single amino acid (k = 1), Ω¹ corresponds to the most sticky amino acid of the protein considered. With a window of size three (k = 3), Ω³ corresponds to the average stickiness of the most sticky stretch of three consecutive amino acids, and so on, and when the window size is the length of a protein L, Ω^L is the average stickiness.

Solubility tags and fusion proteins

Fusion proteins were expressed under the GPD promoter in the p413 plasmid [133]. As an unfolded and insoluble polypeptide chain we used the N-terminal fragment of the mouse DHFR enzyme. This protein fragment contains 108 residues out of 188 in the full-length protein and was fused at the C-terminus of the YFP. Various synthetic sequence tags were also fused at the C-terminus of the DHFR fragment. All cloning was carried out using the PIPE cloning method [134]. The different sequence tags consisted of stretches of charged amino acids separated by glycine and serine residues. All sequences can be found in Table S3. The mutations in DH were determined manually to decrease the stickiness of the fragment while matching the stickiness of the medium and long non-sticky tag variants. Synthetic DNA sequences were ordered from IDT and were cloned by PIPE at the C-terminus of YFP, to yield the “mut-DH” variants.

Imaging and fluorescence quantification

Imaging of cells and processing of the data was carried out as described in Ref. [135]. Briefly, cells were inoculated from their glycerol stock in 384-well glass-bottom optical plates (Matrical) with a pintool (FP1 pins, V&P Scientific) operated by a Tecan robot (Tecan Evo200 with MCA384 head). Cells were grown in YPD for a minimum of 10 h before they reached an optical density of at most 1, and were imaged with a confocal spinning disk microscope using a 60 × plan apo oil-immersion objective. Each image set was composed of two brightfield (BF) images (one in focus and one defocused to facilitate cell segmentation, each with 50-ms exposure) as well as one image quantifying fluorescence with 300-ms exposure. Individual cells were segmented from the brightfield images, and fluorescence intensity was estimated from the 50th quantile of pixel intensity within each segmented cell. For each strain, eight technical replicates were imaged, the median fluorescence across cells (typically over 100 per construct) was calculated, and the mean of the eight replicates and associated standard error are reported.

The following are the supplementary data related to this article.

Supplementary figures

Table S2

Raw amino acid scores for protein solubility prediction: estimated amino acid interaction propensity versus experimentally derived hydrophobicity and aggregation propensities

Table S3

Details of yeast strains, chimeric protein sequences and fluorescence data of YFP-DH constructs

Edited by Monika Fuxreiter