Skip to main content
PMC home page
HHS Author Manuscripts logoLink to HHS Author Manuscripts
. Author manuscript; available in PMC: 2020 Jan 3.
Published in final edited form as: J Acoust Soc Am. 2004 Jan;115(1):66–72. doi: 10.1121/1.1631943

Measurement of dependence of backscatter coefficient from cylinders on frequency and diameter using focused transducers – with applications in trabecular bone

Keith A Wear 1
PMCID: PMC6941413  NIHMSID: NIHMS1064086  PMID: 14758996

Abstract

A theory for the elastic scattering response from a cylinder insonified by a plane wave was previously derived by Faran. In the present paper, the empirical relationship between Faran’s theory and measurements of backscatter coefficient from cylindrical targets using focused transducers is investigated. Experimental measurements of dependence of backscatter coefficient on frequency and diameter for nylon wires are reported. It is found that, under certain conditions (including weak, incoherent scattering), backscatter coefficient measurements from collections of cylindrical scatterers may be meaningfully compared with Faran’s model predictions. At low frequencies, the theory and experimental measurements exhibit similar dependences on frequency and diameter, provided that the scatterers are not too densely packed. At higher frequencies, the fine structure of Faran’s predictions becomes difficult to reproduce experimentally with a focused transducer. Implications regarding applications to characterization of trabecular bone are discussed.

Keywords: backscatter, cylinder, bone

Introduction

Measurements of scattering properties have been demonstrated to be useful for the characterization of many biological tissues (Shung, 1993). Many studies have involved measurement of the backscatter coefficient, which is defined as the differential scattering cross section per unit volume for a scattering angle of 180 degrees (Ishimaru 1978; O’Donnell, 1981; Madsen, 1984).

Numerous algorithms for measurement of backscatter coefficient have been reported. These techniques often assume point-like scatterers producing quasi-spherical scattered waves which may be detected efficiently with spherically-focused transducers. Some techniques have been rigorously validated using Faran’s theory of elastic scattering from spherical scatterers (Faran, 1951; O’Donnell, 1981; Madsen, 1984). Faran’s theory predicts the magnitude of a spherical wave scattered by a sphere, or a cylindrical wave scattered by a cylinder, in response to an incident plane wave. (In the second case, the axis of the cylinder is assumed to be perpendicular to the wave propagation direction). Faran’s equations for spherical scatterers are consistent with the assumptions underlying many backscatter coefficient measurement methods. For example, Faran’s assumption of plane-wave insonification is reasonable for small scatterers insonified by focused transducers provided that the variation of the amplitude and phase of the interrogating beam is negligible across the surface of the scatterer. This is often true when the scatterers are much smaller than the beam cross section. Thus, for small spherical scatterers, comparison of experimental measurements of backscatter coefficient to Faran’s predictions is relatively straightforward.

The case of cylinders is somewhat more difficult than that for spheres. In Faran’s model, cylinders have infinite extent. In practical experiments, the effective scatterer becomes that portion of the cylinder for which the transducer is most sensitive (i.e. the intersection of the beam cross section with the cylinder). But considerable variation of amplitude and phase of the incident beam is likely across the surface of the cylinder, violating Faran’s premise of plane wave insonification. Moreover, the differential scattering cross section (upon which the backscatter coefficient is based) is defined only under conditions in which a scattered field is measured sufficiently distant from the scatterer that it behaves as a spherical wave (Ishimaru, 1978). Since the effective scatterer spans the entire resolution volume, the distance required so that the scattered wave may be thought of as quasi-spherical is much greater for cylinders than for point-like scatterers. Therefore, in the case of interrogating a cylindrical scatterer at the focal region of a focused transducer, the scattered wave may not closely approximate a quasi-spherical form by the time it is received. Thus, the association of Faran’s predictions with measured backscatter coefficients is not as clear as in the case of spherical scatterers.

The objective of this paper is to experimentally investigate the correspondence between Faran’s theory and backscatter coefficient measurements using focused transducers and cylindrical targets. Only the dependences of backscatter coefficient on frequency and diameter are considered here, not the more challenging topic of absolute magnitude. This subject is particularly relevant for the characterization of trabecular bone. Previous measurements of frequency-dependent backscatter from human calcaneus have suggested that scatterers from trabecular bone behave more like cylinders than spheres (Wear, 1999; Wear, 2000). Trabecular bone is known to contain rod-like trabeculae which could help explain this observation. Trabecular bone also contains plate-like structures. The relative preponderance of rod-like structures to plate-like structures increases with age.

Previous experiments have offered much validation for Faran’s theory regarding measurements made with unfocused transducers. Faran himself reported measurements of scattering from metal cylinders at 1 MHz (Faran, 1951). A hydrophone was used to measure the angle dependence of scattering. Excellent agreement between theory and experiment was reported. Ninety-degree scattering from cylindrical (copper and nylon) targets was reported by Lee and co-workers (Lee, 1978), who also found good agreement between their measurements and Faran’s theory.

Faran and Lee et al. used small aperture transducers to insonify cylinders situated in the far field. This resulted in relatively uniform insonification over a substantial length of the cylinder, and, as far as their experiments were concerned, could be taken to approximate plane wave insonification.

Faran’s and Lee et al.’s pioneering work preceded the advent of algorithms for backscatter coefficient measurement using focused transducers in the early 1980’s (O’Donnell, 1981; Lizzi, 1983; Waag, 1983; Madsen, 1984). Unlike the studies of Faran and Lee et al., the present study is based on the measurement of backscatter coefficient using focused (rather than planar) transducers. These days, focused transducers are generally preferred for imaging applications and for measurements on small samples because of their superior lateral resolution. Also, in highly attenuating media, focused transducers are often required in order to overcome attenuation in tissue between the transducer and the region of interest.

Another distinction between the present study and that of Lee et al. is that Lee et al. examined scattering at 90 degrees instead of backscatter. It will be seen that, in the range of frequencies investigated, backscatter from nylon scatterers exhibits a far more complicated form than the quasi-Gaussian response (backscattered intensity vs. frequency) Lee et al. encountered at 90 degrees, hence making the conformity between theory and experiment somewhat more challenging in the present study. (It should be noted however that Lee et al. did observe more complex behavior for copper wires). Finally, agreement between theory and experiment is investigated in the present study over a greater dynamic range of backscatter (two decades) than in Lee’s work (approximately one decade).

Ueda and Akita reported a diffraction correction for backscatter coefficient using echoes scattered by a fine wire (Ueda, 1986). Their method showed excellent agreement with theoretical predictions. Their analysis was restricted to the case for which the diameter of the wire is much smaller than the wavelength of ultrasound. In the present study, the ratio of the cylinder diameter to the wavelength ranges from about 0.05 to 0.8.

There have been several other important contributions regarding scattering from cylinders that neither involve backscatter coefficient measurement nor offer comparisons to Faran’s theory. Li and Ueda have provided a theoretical treatment of scattering of a spherical wave by an elastic circular cylinder (Li, 1990a). The same authors subsequently explored the measurement of scattering from cylinders using cylindrical shell transducers (Li, 1990b). Sheng and Hay investigated backscatter from thin wires situated in the transducer farfield, where the incident wave may be modeled as a spherical wave (Sheng, 1993). Raum and O’Brien developed a technique for determining the spatial and temporal transmit-receive field distributions of a spherically focused high-frequency transducer using a (tungsten) wire target (Raum, 1997).

Methods

Backscatter coefficients are generally associated with media that contain multiple individual scatterers distributed throughout a volume. Measurement methods usually assume incoherent scattering (O’Donnell, 1981; Madsen, 1984). In other words, the phase differences between echoes emanating from scatterer pairs are assumed to be uniformly distributed from 0 to 2π. In this case, the expected received power is simply the sum of the powers scattered by individual scatterers situated within the resolution volume.

A natural approach for investigating this problem experimentally might be to acquire data from phantoms consisting of multiple randomly positioned cylinders per resolution volume. However design and construction of such a phantom would represent a substantial challenge. In the present study, an alternative but essentially equivalent approach was adopted for expediency. Signals were acquired from single cylinders placed at the focus of the transducer. Under the assumptions of weak, incoherent scattering, the dependence of backscatter on cylinder diameter would be expected to be the same for a single scatterer as for a volume containing randomly distributed scatterers. However, the dependence of backscatter on frequency would be expected to be different in the two cases since the size of the resolution volume is frequency-dependent, and therefore the effective number of scatterers contained within the resolution volume is frequency-dependent. In order to account for this effect, measured signal power spectra may be multiplied by a presumed frequency-dependent number of scatterers per resolution cell (see below for details). This approach is consistent with the underlying assumptions for backscatter coefficient measurement and avoids the arduous task of designing and building a phantom containing randomly positioned cylinders. This approach also assumes that the system point spread function is shift-invariant throughout the measurement volume. Backscatter coefficients compensated in this way are referred to below as “expected backscatter coefficients.”

Nylon fishing lines of various diameters (nominally 0.006”, 0.008”, 0.010”, 0.011”, 0.012”, 0.014”, 0.016”, and 0.018”) were interrogated in a water tank in pulse-echo mode. Actual diameters were measured using calipers. Each line had a fishing weight attached to the bottom so that it could be hung vertically. The ultrasound beam propagation direction was perpendicular to the nylon line. In order to compute the predicted backscatter according to Faran’s theory, assumed values for Poisson’s ratio, density (ρ) and longitudinal velocity (cl) for the scattering target were required. Poisson’s ratio for nylon was assumed to be 0.39 and cl was taken to be 2600 m/s (Ondacorp, 2003). Density (ρ) was obtained from measured masses (m) of the spools of fishing line. The measured mass of each spool of fishing line was the sum of the mass of the plastic spool (ms) plus that of the nylon line (ρv) wound around it: m = ms + ρv where the nylon wire volume v was πr2h, r was the nylon line radius, and h was the length. Since r (measured with calipers) and h (specified by manufacturer) were known, ms and ρ could be estimated from a linear regression to measurements of m and v from the eight spools. The density estimated in this way was 1.3 g/cc. The square of the correlation coefficient for the linear fit was 0.98 (95% confidence interval: 0.96 – 1.00), indicating a high uniformity of densities among the eight nylon lines. The theoretical predictions for scattering from a cylindrical nylon target was generated numerically (MATLAB) using Faran’s theory (Faran, 1951) and these material values.

Three different Panametrics (Waltham, MA) ultrasound transducers, with center frequencies ranging from 500 kHz to 2.25 MHz, were used. See Table 1. For low frequency measurements (500 kHz), a Panametrics model 5077 PR pulser/receiver was used. For higher frequencies, a Panametrics model 5800 PR was used. Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis. In order to ensure consistent alignment of nylon lines, the transducer orientation was always adjusted so as to maximize the amplitude of the received time-domain signal.

Table I.

Properties of Panametrics ultrasonic transducers used.

Model Number Center Frequency (MHz) Diameter (inches) Focal Length (inches)
V391 0.5 1.125 2.1
V302 1.0 1.0 2.0
V305 2.25 0.75 1.5
Open in a new tab

Backscatter coefficients were measured using a reference phantom method (Zagzebski et al., 1993) as described previously (Wear, 1999). This method assumes that the location, size, and shape of the region of interest (defined by the gate duration in the axial dimension and the beam width in the lateral dimension) are identical for the specimen for which backscatter coefficient is to be measured and the reference phantom (for which the backscatter coefficient is presumed to be known a priori). In this case, the effects of frequency-dependent diffraction are the same for both measurements and therefore cancel out when the ratio of power spectra is taken. A gate length of 1 cm was used for the reference phantom measurements.

As mentioned above, for the investigation of the expected dependence of backscatter coefficient on frequency, received power spectra from the nylon cylinders were multiplied by a frequency-dependent factor in order to simulate the situation in which numerous cylinders exist within a resolution cell. It is assumed here that all the hypothetical cylinders are oriented parallel to each other and perpendicular to the ultrasound propagation direction. Since the beam width is frequency-dependent, the resolution cell size is frequency-dependent. The effective number of cylinders per resolution cell N is given by

N=nxnz (1)

where nx = effective number of scatterers contained across the lateral dimension of the resolution cell and nz = effective number of scatterers contained across the depth dimension of the resolution cell. The latter quantity is given by

nz=1+Δz/s (2)

where Δz is the length of the rectangular range gate, Δz = cτ/2, c is the speed of sound, τ is the duration of the range gate, and s is the mean scatterer spacing. This factor (nz) does not depend on frequency.

An expression for nx may be obtained as follows. The intensity of the Franhofer diffraction pattern for a circular aperture (the so-called “Airy pattern”) is given by (Goodman, 1968)

I(x)=(kl28z)2[2J1(klx/2z)klx/2z]2 (3)

where J1 is a Bessel function of the first kind, order one, k = 2π / λ, λ is the wavelength, l is the aperture diameter, x is the lateral dimension, and z is the distance from the aperture to the scatterer. This same intensity distribution has been derived for acoustic radiation. (See Kinsler et al., 1982, equation 8.35, and substitute a=l/2, sinθ=x/z). The effect of focusing is to bring the Franhofer pattern from the far field to the focal plane of the transducer. From the principle of reciprocity, the overall system sensitivity, as a function of scatterer position, is the square of the focal plane intensity distribution.

I2(x)=(kl28z)4[2J1(klx/2z)klx/2z]4 (4)

For the purpose of estimating nx, it was assumed that the effective number of scatterers across the lateral direction could be taken to be equal to one (the wire at the focal point) plus the expected number of scatterers to the left plus the expected number of scatterers to the right, given by

nx=1+2Δx/s (5)

where the half width half maximum (HWHM) of I2(x) is denoted by Δx ≈ 0.37zc / (lf) and f is frequency.

Two limitations to this approach should be acknowledged. First, it does not explicitly account for the fact that cylinders near the periphery of the beam are insonified with lower intensities than centrally-positioned cylinders. However it has previously been shown that, for the purpose of measuring backscatter coefficients, the effective number of scatterers may be accurately approximated simply by counting those scatterers included within the 3-dB beam cross section, (O’Donnell and Miller, 1981, equation 15). This approximation is especially valid in the present application as the parameter of interest is only the frequency dependence (rather than the absolute magnitude) of the scatterer number. A second limitation to this approach is that it does not account for the fact that cylinders near the periphery of the beam will have diminished effective heights (i.e. intersections between beam cross section and cylinder) and therefore potentially altered frequency-dependent backscattering properties. Again, it is assumed here that, for the purpose of estimating frequency dependence of scatterer number, the present approach is adequate. An experimental test of this assumption is given in the next section.

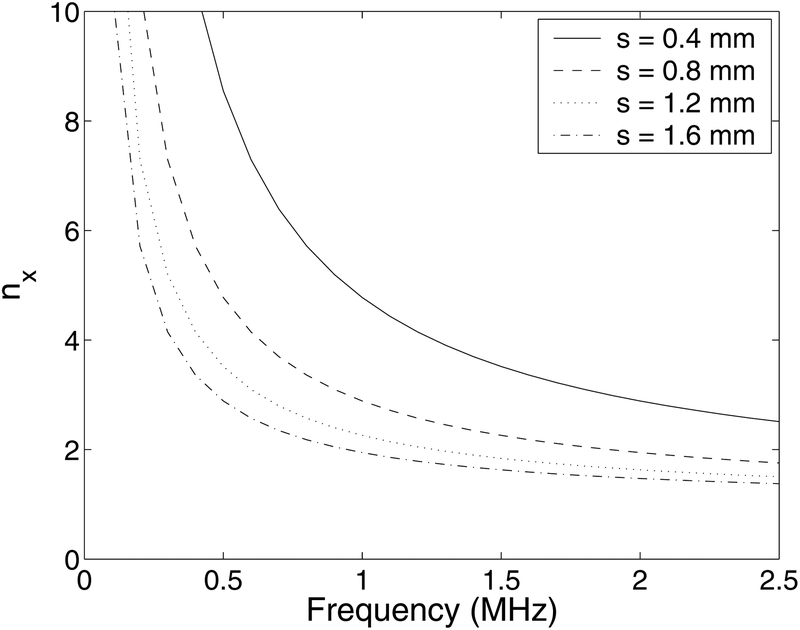
In Figure 1, nx is plotted as a function of frequency for four choices of assumed mean scatterer spacing for an f2 transducer and an assumed sound speed of 1480 m/s (water). It can be seen that for mean scatterer spacings greater than or equal to about 0.8 mm, the approximate mean trabecular spacing for human calcaneus (Ulrich, 1999), and frequencies greater than 1 MHz, the frequency dependence of nx is relatively gradual (especially when compared to Faran’s frequency response from a single cylinder, as will be seen in the next section). Under these conditions, any conclusions regarding the frequency-dependence of backscatter coefficient will not depend critically on the assumed value for mean scatterer spacing.

Figure 1.

Figure 1.

Open in a new tab

The expected number of scatterers (nx) across the lateral dimension as a function of frequency for four different assumed mean scatterer spacings (s).

Results

Figure 2 shows experimental measurements of backscatter coefficient at 500 kHz as a function of diameter of nylon line. The solid line shows the theoretical variation predicted from Faran’s theory (Faran, 1951). The theoretical curve was multiplied by a single diameter-independent scale factor in order to optimally fit the data. Therefore, only the extent of agreement between theory and experiment regarding dependence of backscatter coefficient on scatterer diameter may be assessed from Figure 2. No meaningful conclusions may be drawn regarding the absolute magnitude of backscatter coefficient. Theory and experiment exhibit similar dependences on diameter.

Figure 2.

Figure 2.

Open in a new tab

Backscattered intensity at 500 kHz as a function of diameter of nylon line.

Figure 3 shows expected frequency-dependent backscatter coefficients from the eight nylon wires (diameters shown in upper left of each panel). Also shown are the theoretical backscattered intensities computed using Faran’s theory (solid line). Each theoretical curve was multiplied by a frequency-independent scale factor in order to fit the data. Therefore, only the extent of agreement between theory and experiment regarding dependence of backscatter coefficient on frequency may be assessed from Figure 3. No meaningful conclusions may be drawn regarding the absolute magnitude of backscatter coefficient.

Figure 3.

Figure 3.

Open in a new tab

Backscattered intensity from nylon wires (diameter shown in upper left of each panel). Also shown are the theoretical backscattered intensities computed using Faran’s theory (solid line)

As described in the Methods section, experimental results (but not the theory) shown in Figure 3 were scaled by the effective number of scatterers per resolution cell, assuming a particular value for scatterer spacing, 0.8 mm, which corresponds to the measurement reported by Ulrich et al. (1999) based on their micro computed tomographic analysis of human calcaneus samples. (They reported a mean trabecular separation of 684 microns and a mean trabecular thickness of 127 microns. Mean scatterer spacing is the sum of these two values). Good agreement may be seen in Figure 3 between theory and experiment, especially for the thinner diameters and lower frequencies. The experimental measurements do not always exhibit sufficient resolution to faithfully reproduce Faran’s theory. In particular, for the three thickest diameters, the fine structure of Faran’s predictions at frequencies above about 1.5 MHz becomes noticeably difficult to reproduce experimentally.

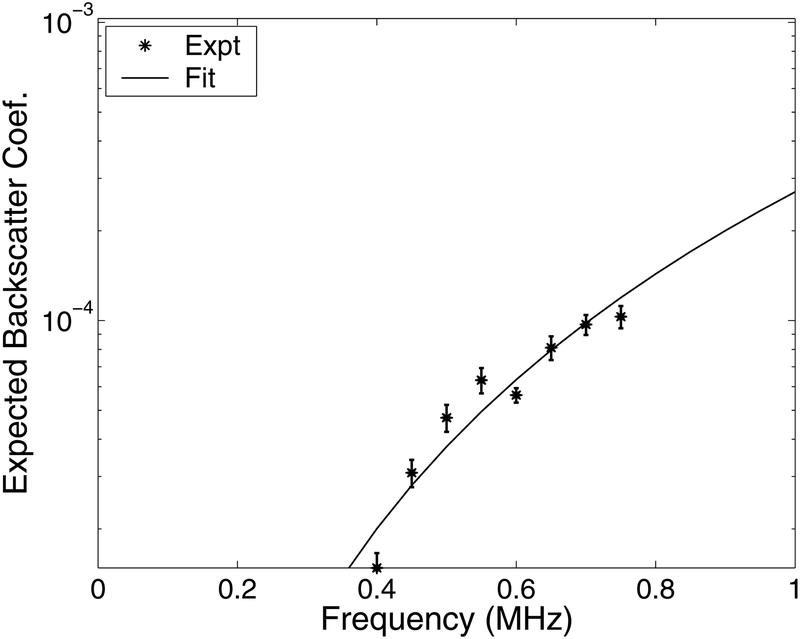
In Figure 4, the dependence of backscatter coefficient for the 150 micron wire as a function of frequency is shown in the low frequency range. This diameter is just slightly larger than the mean value for trabecular thickness in human calcaneus reported by Ulrich et al. (1999) of 127 microns. Again, experimental results were scaled by the effective number of scatterers per resolution cell assuming a scatterer spacing of 0.8 mm (see Figure 1). Also shown is a power law fit to the data, backscatter coefficient = Afm where m = 2.84. This approximate cubic dependence is similar to theoretical predictions by Lizzi et al. (1996) for thin quasi-cylindrical scatterers.

Figure 4.

Figure 4.

Open in a new tab

The dependence of expected backscatter coefficient for the 150 micron (0.006”) wire as a function of frequency. Also shown is a power law fit, backscatter coefficient = Afm where m = 2.84.

Discussion: Applications in Bone

In a previous study (Wear, 1999), backscatter coefficients were measured from human calcaneus in vitro. These frequency dependent backscatter coefficients were compared to Faran’s predictions. This analysis was based on the plausible but unproven assumption that the two frequency-dependent functions should be roughly proportional to each other. The present study offers strong empirical evidence to support this assumption. The present study suggests that backscatter coefficient measurements exhibit similar dependences on frequency and diameter as Faran’s model predicts, provided that the scatterers are not too densely packed. Although the present study neglected attenuation that may arise from a hypothetical ensemble of cylinders throughout the range-gate, its results may be extended to highly attenuating media such as bone because backscatter coefficient measurements from tissues may be accurately compensated for the effects of attenuation (O’Donnell and Miller, 1981, equation 17).

The reference phantom method for measurement of backscatter coefficient used in this study has been experimentally validated using homogeneous phantoms containing spherical or quasi-spherical scatterers (Zagzebski, 1993). The present study adds evidence that it is also appropriate for media containing cylindrical scatterers.

Faran’s model predicts that, at low frequencies, backscattered intensity is approximately proportional to frequency cubed. This effect is seen in the present study in Figure 4, which shows the low frequency backscatter coefficient for the 150 micron diameter nylon wire. In this case, the exponent of the power law fit was found to be 2.84 (approximately cubic). This value is similar to that reported in human calcaneus, 3.26 ± 0.20 (Wear, 1999). Although trabeculae in human calcaneus are oriented in a variety of directions, they are all approximately perpendicular to the ultrasound propagation direction provided that bones are interrogated in the medio-lateral orientation (as is the case in the experiments above and in most commercial bone sonometers).

Empirical power law exponents for human calcaneus in the low frequency range are a little higher than the approximately cubic variation predicted by the cylinder model - 3.26 (Wear, 1999) and 3.38 (Chaffai et al., 2000). The difference of 0.3 – 0.4 may be due in part to multiple scattering, which would have the effect of applying additional high-pass (frequency-cubed) filtering to echoes (via multiple scatters), resulting in measured backscatter coefficients with more rapid than cubic frequency dependence (Wear, 1999). This effect would be expected to be rather small because multiply scattered waves tend to traverse longer path lengths than singly scattered waves and trabecular bone has a very high attenuation coefficient. Another potential contribution to the difference between theory and measurements results from trabecular bone having a more complex geometry than the cylinder model would suggest. Rod-like structures within trabecular bone exhibit a wide range of lengths and in some cases will be shorter than a beam width. Moreover, trabeculae are not perfectly straight (as assumed in the model) but are somewhat curved and jagged. Furthermore, in addition to rod-like structures, trabecular bone also contains plate-like components. Nevertheless, cylinder-like objects (trabeculae) are responsible for an appreciable fraction of the scattering. In addition, only those plate-like structures oriented approximately perpendicular to the ultrasound propagation direction can measurably affect the frequency dependence of scattering. Finally, plates are comparatively rare in bones from older subjects, upon which the data from the studies mentioned above are based.

Trabecular thickness is an important determinant of osteoporotic fracture risk. Noninvasive assessment of trabecular thickness could potentially yield useful diagnostic information. A recent study has shown that the dependence of backscatter coefficient measurements from human calcaneus samples on trabecular thickness is similar to that predicted using Faran’s model (Wear, 2003). The theory predicts that, in the range of morphological and material properties expected for trabecular bone, the backscatter coefficient at 500 kHz should be approximately proportional to trabecular thickness to the power of 2.9. A power law fit to empirical data suggested that backscatter coefficient measurements (from 43 human calcaneus samples) varied as trabecular thickness to the 2.8 power (95% confidence interval: 1.7 – 3.9).

Conclusion

Under certain conditions (including weak, incoherent scattering), backscatter coefficient measurements from collections of cylindrical scatterers may be meaningfully compared with Faran’s model predictions of scattered wave intensities resulting from plane wave insonification. At low frequencies, the two functions exhibit similar dependences on frequency and diameter, provided that the scatterers are not too densely packed. At higher frequencies, the fine structure of Faran’s predictions becomes difficult to reproduce experimentally.

Acknowledgements

The author is grateful for funding provided by the US Food and Drug Administration Office of Women’s Health. The author thanks Timothy Hall, University of Kansas, for providing the reference phantom used in this study.

References

  1. Campbell JA and Waag RC, (1983), “Normalization of ultrasonic scattering measurements to obtain average differential scattering cross sections for tissues,” J. Acoust. Soc. Am, 74, 393–399. [DOI] [PubMed] [Google Scholar]
  2. Chivers RC, (1977), “The scattering of ultrasound by human tissues – some theoretical models,” Ultrasound in Med. & Biol, 3, pp. 1–13, Appendix. [DOI] [PubMed] [Google Scholar]
  3. Chaffai S, Roberjot V, Peyrin F, Berger G, and Laugier P. (2000). Frequency dependence of ultrasonic backscattering in cancellous bone: Autocorrelation model and experimental results. J. Acoust. Soc. Am 108, 2403–2411. [DOI] [PubMed] [Google Scholar]
  4. Faran JJ, Sound scattering by solid cylinders and spheres, (1951). J. Acoust. Soc. Am, 23, 405–418. [Google Scholar]
  5. Goodman JW, (1968). Introduction to Fourier Optics (McGraw-Hill, New York: ). [Google Scholar]
  6. Ishimaru A, (1978). Wave Propagation and Scattering in Random Media. New York, New York, Academic Press, chap. 2. [Google Scholar]
  7. Kinsler LE, Frey AR, Coppens AB, and Sanders JV, (1982). Fundamentals of Acoustics, New York, New York, John Wiley & Sons, chapter 8, p. 179. [Google Scholar]
  8. Lee PPK, Waag RC, and Hunter LP (1978), Swept-frequency diffraction of ultrasound by cylinders and arrays, J. Acoust. Soc. Am, 63, 600–606. [Google Scholar]
  9. Li T, and Ueda M, (1990a), Sound scattering of a spherical wave incident on a cylinder, J. Acoust. Soc. Am, 87, 1871–1879. [Google Scholar]
  10. Li T, and Ueda M, (1990b), Analysis of echoes from a cylinder that includes the directivity of the transmitter and receiver, J. Acoust. Soc. Am, 87, 1880–1884. [Google Scholar]
  11. Lizzi FL, et al. , (1983) “Theoretical framework for spectrum analysis in ultrasonic tissue characterization,” J. Acoust. Soc. Am, 73, 1366–1373. [DOI] [PubMed] [Google Scholar]
  12. Lizzi FL, Astor M, Kalisz A, Liu T, coleman DJ, Silverman R, Ursea R, Ro M, (1996), Ultrasonic spectrum analysis for assays of different scatter morphologies: theory and very-high frequency clinical results, Proc. 1996 IEEE Ultrasonics Symp, vol. 2, 1155–1159. [Google Scholar]
  13. Madsen EL, Insana MF, and Zagzebski JA, (1984), Method of data reduction for accurate determination of acoustic backscatter coefficients, J. Acoust. Soc. Am, 76, 913–923. [DOI] [PubMed] [Google Scholar]
  14. O’Donnell M and Miller JG, (1981), Quantitative broadband ultrasonic backscatter: An approach to nondestructive evaluation in acoustically inhomogeneous materials, J. Appl. Phys 52, 1056–1065. http://ondacorp.com/tables/plastics.htm [Google Scholar]
  15. Raum K and O’Brien WD Jr., (1997), “Pulse-echo field distribution measurement technique for high-frequency ultrasound sources,” IEEE Trans. Ultrason. Ferro. Freq. Cont, 44, 810–815. [Google Scholar]
  16. Sehgal CM and Greenleaf JF, (1984), “Scattering of ultrasound by tissues,” Ultrason. Imaging 6, pp. 60–80, p. 67. [DOI] [PubMed] [Google Scholar]
  17. Sehgal CM, (1993) “Quantitative relationship between tissue composition and scattering of ultrasound,” J. Acoust. Soc. Am, 94, pp. 1944–1952, p. 1945. [DOI] [PubMed] [Google Scholar]
  18. Sheng J and Hay A, (1993), Spherical wave backscatter from straight cylinders: thin-wire standard targets, J. Acoust. Soc. Am, 94, 2756–2765. [Google Scholar]
  19. Shung KK and Thieme GA, ed.s, (1993), Ultrasonic Scattering in Biological Tissues, CRC Press, Boca Raton, FL. [Google Scholar]
  20. Ueda M and Akita M, (1986), Diffraction correction for backscattering coefficient measurement using echoes scattered by a fine wire, Proc. 1986 IEEE Ultrasonics Symp. 0090–5607/86/0000–0913.
  21. Ueda M and Ozawa Y, (1985), “Spectral analysis of echoes for backscattering coefficient measurement,” J. Acoust. Soc. Am, 77, pp. 38–47, p. 39. [Google Scholar]
  22. Ulrich D, van Rietbergen B, Laib A, and Ruegsegger P, (1999), “The ability of three-dimensional structural indices to reflect mechanical aspects of trabecular bone,” Bone, 25, 55–60. [DOI] [PubMed] [Google Scholar]
  23. Wear KA. (1999). Frequency dependence of ultrasonic backscatter from human trabecular bone: theory and experiment. J. Acoust. Soc. Am 106, 3659–3664. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wear KA. (2000). Anisotropy of ultrasonic backscatter and attenuation from human calcaneus: Implications for relative roles of absorption and scattering in determining attenuation. J. Acoust. Soc. Am, 107, 3474–3479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Wear KA and Laib A, (2003) “The Relationship Between Ultrasonic Scattering and Microarchitecture in Human Calcaneus,” accepted for publication in IEEE Trans. Ultrason., Ferro. Freq. Cont, [Google Scholar]
  26. Zagzebski JA, Yao LX, Boote EJ, and Lu ZF, (1993), Quantitative Backscatter Imaging,” in Ultrasonic Scattering in Biological Tissues, edited by Shung KK and Thieme GA, CRC Press, Boca Raton, FL. [Google Scholar]

RESOURCES