Abstract
Genome-wide variation data with millions of genetic markers have become commonplace. However, the potential for interpretation and application of these data for clinical assessment of outcomes of interest, and prediction of disease risk, is currently not fully realized. Many common, complex diseases now have numerous, well-established risk loci, and likely harbor many genetic determinants with effects too small to be detected at genome-wide levels of statistical significance. A simple and intuitive approach for converting genetic data to a predictive measure of disease susceptibility is to aggregate the effects of these loci into a single measure, the genetic risk score. Here, we describe some common methods and software packages for calculating genetic risk scores and polygenic risk scores, with focus on studies of common, complex diseases. We review the basic information needed as well as important considerations for constructing genetic risk scores, including specific requirements for phenotypic and genetic data, and limitations in their application.
Keywords: genetic risk score, polygenic risk score, AUC, disease prediction, complex traits, complex diseases
INTRODUCTION
The purpose of this unit is to give an overview of the application of genetic risk scores (GRS) while also presenting guidelines for using GRS for disease prediction. While genome-wide association studies, which have become routine over the past decade, have yielded major genetic loci—mostly single nucleotide polymorphisms (SNPs)—associated with common, complex diseases (Beck et al., 2014; Buniello et al., 2019), a great deal of the heritability of such diseases remains to be dissected (Manolio et al., 2009). Translating the influence of these static loci, which, unlike clinical measures, do not change, to predict disease risk is not always straightforward. As a rule, many genetic loci contributing to complex, common diseases contribute varying degrees of risk (or protection). Connecting these effects, along with demographic, lifestyle, and environmental risk factors, to disease risk is a daunting task, but through classical and recently-developed methods of analysis, progress is being made toward realizing the potential of this vast body of genetic data. We here review methods for translating genetic information into an assessment of disease risk for complex traits whose genetic component cannot be completely explained by one or several genetic loci of large effect, with emphasis on potential complications and pitfalls.
The purpose of risk scores is twofold: (1) to predict the likelihood of an individual developing disease (or a particular outcome of interest) based on some amount of available information, usually genetic, clinical, demographic, or a combination; and (2) to estimate the level of predictive power that is captured by associated variants. The goal is to be able to predict whether a person is likely to develop disease, a reaction to a drug, etc., based on available genetic information. Predicting a greater proportion of the “risk” for the outcome of interest indicates the level of success of predictors included in the risk score.
The most common approach to evaluate the cumulative effect of many genetic factors with small effect, with or without non-genetic clinical factors, is the genetic risk score (GRS). A GRS can estimate the overall probability, or risk, a person has for developing an outcome of interest based on their genotypes at variants determined to be associated with risk for that outcome. Because an individual’s genetic profile is set at birth, and therefore, because risk for disease could theoretically be determined prior to (most) environmental exposures (Wray et al., 2010),a great deal of hope has been invested into developing these models as an advancement of precision medicine. However, for many complex diseases, it is debatable whether genomic profiling is ready for clinical use (e.g., (Cooke Bailey et al., 2016; Jakobsdottir et al., 2009; Khawaja and Viswanathan, 2018; Schork et al., 2018)). Family history is typically seen as a good proxy for genetic risk as it reflects shared genetic and environmental factors and thus is incorporated into clinical history when possible for genetic diseases (reviewed in (Wray et al., 2010)). Family history is limited, however, by family size, disease prevalence and information available from relatives; and is susceptible to confounding by recollection and referral biases. Furthermore, positive family history reflects a certain level of disease risk, while negative family history does not imply the opposite (Wray et al., 2010). One goal of implementing GRS is to improve upon these factors for a more comprehensive and accurate assessment of disease risk beyond what family history can estimate.
GRS allow for the evaluation of contributions by multiple factors to disease development and outcomes, including, but not limited to, disease susceptibility, progression, and response to treatment. GRS can be based solely on available genetic data or can incorporate environmental, phenotypic, and/or demographic information. Published GRS results tend to vary across studies and are dependent upon the population sample evaluated and the true outcome of interest (i.e., progression from early to late stage disease, disease subtypes, or general disease risk). These are important factors to keep in mind when constructing and evaluating GRS for use in a particular sample.
Prediction accuracy of GRS is most often assessed by measuring the area under the receiver operating characteristic (ROC) curve (AUC), an indicator of model accuracy. The AUC compares the rates of true positives (sensitivity) and false positives (1 – specificity) and indicates the overall performance of predictive models (Janssens et al., 2007). Sensitivity, the probability of correctly classifying an affected individual as affected, indicates the ability of the model to correctly predict individuals with the outcome of interest; specificity, the probability of correctly classifying an unaffected individual as unaffected, indicates the ability of the model to accurately screen out individuals without the outcome of interest. The AUC generally varies between 0.5, indicating a model no better than chance, and 1, indicating a perfect model (Janssens et al., 2007). Models are expected to have an AUC > 0.75 for informative screening of individuals who are at increased disease risk, and very high AUC (as high as 0.99) for a diagnostic test (Janssens et al., 2007). The higher the AUC, the more precise the prediction and thus, the greater the clinical utility of the combination of factors included in the model. However, there are limitations to consider. There are two components to predictive accuracy: the potential accuracy if all genetic factors were known, determined by the trait heritability, and the correlation between the GRS and true genetic risk, determined by the quantity of genetic data and selection of genetic variants for prediction. The AUC is limited by both of these factors but cannot distinguish between them (Wray and Goddard, 2010).
Instead of calculating the AUC, the predictive measure emphasized here, one can also estimate the proportion of trait variability explained by one or more genetic markers. One measure is the population attributable risk (PAR) or population attributable fraction, which in general expresses the fraction of cases attributable to a given exposure (Witte et al., 2014). However, the PAR is not additive over multiple markers. In the case of continuous traits, the multiple R2 (squared correlation) from linear regression measures the trait variance accounted for by the predictors. This may be approximated for binary traits by a pseudo-R2 measure, derived from the likelihood under the models with and without genetic predictors (Menard, 2000; Witte et al., 2014), or by the squared empirical correlation (Tjur, 2009). One popular measure, the Nagelkerke R2, is upwardly biased in samples highly enriched for cases (Choi et al., 2018); the variation by Lee et al. (2002) attempts to correct for this bias.
Where estimates of risk or predicted continuous trait values are available, they may be calibrated to assess agreement of predicted and actual values. One simple calibration technique is to regress the phenotype (as outcome) on the GRS (as predictor); the regression line should have a slope near 1 and y-intercept near 0. A slope considerably greater than 1 suggests overfitting (Goldstein et al., 2015). Several statistical analysis software packages written in R produce calibration plots, especially the caret package (Kuhn, 2008). The Brier Score is a single summary measure of overall prediction performance (i.e., both calibration and discrimination). It is calculated as the mean squared difference between the predicted probability (or risk) and the actual phenotype, with a score of 0 indicating perfect agreement (Steyerberg et al., 2013).
As a practical example of use, GRS have been constructed for many common, complex diseases including age-related macular degeneration (AMD). AMD is one of the few common and complex diseases for which large-effect loci have been identified: the CFH and ARMS2/HTRA1 loci along with ten other loci predict disease risk with an AUC of 0.736 and it has been shown that adding other low-effect SNPs to a GRS for AMD does not significantly strengthen the model (Fritsche et al., 2013). More recent analyses support 52 independently associated AMD variants in 34 loci that contribute varying degrees of risk for advanced AMD and overall explain 27.2% of overall disease risk and more than half of the heritability, but again, the four loci of greatest effect account for most of the explained risk (Fritsche et al., 2016).
An alternative measure of predictive accuracy is based on positive predictive value: the probability that an individual labeled “high-risk” is truly affected. One way to estimate this is to subdivide the sample into a small number of bins, or quantiles, of the GRS, and to estimate predictive value by the proportion of cases and controls in each bin. Fritsche et al. (2016) divided samples into deciles of genetic risk based on the calculated GRS and found that individuals in the highest decile have a 44-fold increased risk for advanced AMD versus individuals in the lowest decile; however, only 22.7% of individuals in the highest decile of genetic risk are predicted to actually have AMD. This highlights a challenge of GRS: while ideally a GRS would easily distinguish between disease-susceptible individuals, the extant understanding of disease pathophysiology and available genetic information must expand concurrently with the increase in genetic disease risk knowledge to inform GRS and in turn enlighten the process of genetic disease prediction.
It is important to note that significance and effect size of optimal genetic variants from a risk-based approach, such as a GWAS by logistic regression, and from a classification-based approach, which focuses on accuracy of distinguishing cases from controls, are not always strongly correlated: strong risk markers might be poor classifiers while good classifiers might not show genome-wide levels of significance (Jakobsdottir et al., 2009; Pepe et al., 2004). For example, Jakobsdottir and colleagues (Jakobsdottir et al., 2009) constructed a three-gene model for AMD risk including variants in CFH and LOC387715 (ARMS2/HTRA1), each of which had achieved genome-wide significance in a logistic regression model (P=9.1×10−13 and 2.3×10−13, respectively), as well as a variant in C2 (P=1.3×10−3). This model yielded an AUC of 0.79, exceptionally high for a complex trait. Despite strong association, however, they calculated that a risk score threshold with a sensitivity of 74% (i.e., that correctly identified 74% of cases) also wrongly classified 31% of controls as cases. Thus, the clinical utility of GRS is likely to be quite limited.
GRS Methods
Many approaches are available to generate GRS. A straightforward method to evaluate the GRS is to choose a number k of independent genetic variants with strong (i.e., genome-wide significance in other studies or datasets) association as risk predictors, and to calculate the GRS as the sum of the effect estimates (log odds ratios), βi, from a logistic regression analysis with additive genetic effect, multiplied by the number of risk alleles, Ni, for each locus:
| Equation 1 |
This formula is directly related to the estimated risk for disease from the logistic model, through the logit (log odds) function, and therefore is statistically intuitive.
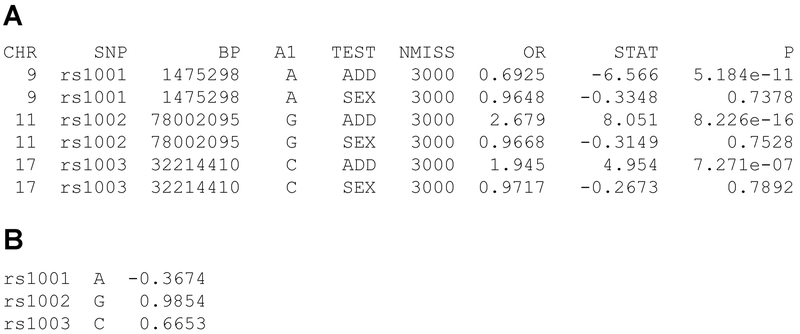
The popular PLINK program for analysis of genome-wide genetic data (Purcell et al., 2007; Chang et al., 2015) implements this approach in a profile scoring method for generating a marker-based GRS. PLINK generates risk scores (“profile scoring”) by means of the --score function, provided binary-format (.bed,.bim,.fam) files from a genetic dataset and a myprofile.raw file with the SNP ID, reference allele and score (or weight) for each allele (Fig. 1), e.g.:
Figure 1.
A, raw output from the --logistic function in PLINK. The column OR contains the odds ratio per copy of allele A1. B, Corresponding PLINK myprofile.raw file, with marker name, reference allele (A1) and ln (OR) from the test of additive effects (lines labeled ADD under TEST).
plink --bfilemydata --score myprofile.raw
This command will generate a file named plink.profile with the following information for each individual: family ID, individual ID, phenotype, number of non-missing SNPs used for scoring, number of named alleles, and total risk score for the individual, the sum of the number of reference alleles (0, 1, or 2) at each SNP multiplied by the (user-defined) ‘score’ for that SNP. A logical choice for the score is the estimated log odds ratio associated with each copy of the minor allele of each tested marker from a logistic regression analysis, as described below.
If a genotype in the score is missing for an individual, the program default is for the value to be imputed based on the sample allele frequency. To change this, the --score-no-mean-imputation flag should be used.
PLINK’s --logistic function for logistic regression covariates reports the odds ratio per copy of the minor allele at each marker (Figure1A, column 6). The natural logarithm of this odds ratio is the value βI in the GRS equation above and is entered as the score for each marker in the myprofile.raw file for PLINK (Figure1B).
A limitation of PLINK’s risk score method is that it calculates the average GRS per non-missing marker, whereas the typical GRS is the sum over all markers. In the case of no missing data, these scores are equivalent; however, a large proportion of missing genotypes may result in atypical values of the average GRS. If this is a concern, it is worth considering removing individuals without complete data at all markers to be evaluated in the GRS.
From this stage, various programs and approaches can be used; several available programs are listed in Table 1. These require varying degrees of analytical and programming experience.
Table 1.
GRS Software
| Program/Package | Functions | Remarks | Website |
|---|---|---|---|
| pROC (R) | ROC, AUC, pAUC, compare AUCs | Requires pre-calculated GRS | https://cran.r-project.org/web/packages/pROC/index.html |
| PLINK | Mean genetic risk per marker | Allows missing data | https://www.cog-genomics.org/plink2 |
| genRoc | Genetic interpretation of AUC | Web-based | http://cnsgenomics.com/shiny/genRoc/ |
| GTX (R) | GRS from meta-analysis results; calculate proportion of variance explained by GRS | grs.summary requires weights for GRS | http://cran.r-project.org/web/packages/gtx |
(R), package or function in the R statistical programming language
Polygenic Risk Scores
To capture additional predictive capacity, the GRS may be extended to loci of small effect, without genome-wide significant associations, in a polygenic risk score (PRS). This approach is particularly valuable for complex traits that lack common risk variants of large effect, including schizophrenia (International Schizophrenia Consortium et al., 2009), height (Boyle et al., 2017), and primary open-angle glaucoma (Gao et al., 2019). In principle, PRS can capture all causal variation measurable from the genotyping panel by single-marker association testing (the “chip heritability”; (Yang et al., 2011)). The predictive power of PRS is limited by the number of SNPs tested and a trait’s heritability and prevalence, but theoretically can be high (e.g., 0.92 for AMD (Wray and Goddard, 2010)). In practice, in some situations a PRS may identify high-risk individuals as if they carried high-impact, Mendelian risk loci, (Khera et al., 2018), and can identify risk classes that could inform a range of treatment options (Torkamani et al., 2018).
Calculating and testing PRS is computationally demanding, but in recent years has become routine (reviewed in (Choi et al., 2018; Maier et al., 2018)). The major obstacle for PRS is correlation among neighboring markers in high-density panels due to linkage disequilibrium (LD). Standard GRS calculations carry the assumption that all the contributing loci are independent, and will be biased in the presence of LD. Current PRS approaches (Table 2) differ mainly in how they account for correlations in effect sizes due to LD and in how they choose the total number of variants to include in the score.
Table 2.
PRS Software
| Software/Program | Approach1 | Traits2 | OS (Language)3 | Website |
|---|---|---|---|---|
| PLINK | P+T (manual threshold) | B, C | L, W, M | https://www.cog-genomics.org/plink2 |
| PRSice-2 | P+T | B, C | L, W, M (R) | http://prsice.info |
| LDpred | Bayesian mixture, P&T | B, C | L, W, M | https://github.com/bvilhjal/ldpred |
| JAMPred | Bayesian mixture | B,C | L, W, M (R+Java) | https://github.com/pjnewcombe/R2BGLiMS |
| PRS-CS | Bayesian mixture | B, C | L (Python 2.x) | https://github.com/getian107/PRScs |
| SBayesR (GCTB) | Bayesian mixture | C | L, M | http://cnsgenomics.com/software/gctb |
| RSS | Bayesian mixture | C | L (MATLAB) | https://stephenslab.github.io/rss/index |
| SBLUP (GCTA) | Linear mixed-effects model | C | L, M | http://cnsgenomics.com/software/gcta/ |
| lassosum | Regularized regression | B, C | L, W, M (R) | https://github.com/tshmak/lassosum |
P+T, pruning and thresholding.
B, binary (case/control); C, continuous.
L, Linux; W, Windows; M, MacOS.Plink binary format is supported by all programs with the exception of RSS, which only requires the summary statistics file. Summary statistics input formatting varies but minimally requires effects estimates and their standard errors, p-values, and Ns. PRSice-2 can additionally take imputed data in Oxford .bgen v1.1/v1.2 format.
Pruning and Thresholding (P+T)
A straightforward approach to address LD is to choose an independent subset of variants from GWAS to use as a standard GRS; the only difference is that here we include variants with modest association not usually highlighted in GWAS. This method, called pruning or (more properly) clumping (Goldstein et al., 2015), begins by selecting the most significant variant and removing from consideration all markers in LD with this index variant greater than a specified r2 cutoff. The most significant remaining marker is selected as a second index variant, and the process repeats until all index variants are found at a given significance level (International Schizophrenia Consortium et al., 2009). Clumping is implemented in PLINK as the --clump command. Required parameters for --clump are clump-p1, the significance threshold for markers in the final independent set; clump-kb, the maximum distance over which to omit markers in LD; and clump-r2, the maximum LD r2 value for “independent” markers (Wray et al., 2014). An additional parameter, clump-p2, is a p value under which clumped SNPs are reported and is not important for selecting the set of PRS variants. For example, a PLINK command to select an independent (r2< 0.1) set of markers with p< 10–4, removing correlated markers up to 500 kilobase pairs from the index variant, is
plink --bfile mydata --clump --clump-p1 0.0001 --clump-p2 1 --clump-r2 0.1 --clump-kb 500
Typically, this procedure is run for several different significance thresholds, and the threshold is chosen with the maximum AUC, pseudo-R2, or other measure of predictive ability (Wray et al., 2014; Choi et al., 2018). Once an optimal set of PRS markers is selected, it is used in the same manner as a GRS.
The R package PRSice-2 (Euesden et al., 2015), built on the PLINK framework, automates the pruning and thresholding (P+T) approach, optimizing the p-value threshold by maximizing significance of association between the PRS and its target trait. It accepts output from PLINK association analyses as summary data and provides fit results across thresholds as p values and as variance explained (R2) by the PRS.
Bayesian and Variable Reduction Models
A second, more advanced class of PRS methods are based on approaches typically used either to perform regression with correlated data and/or to select an optimal subset of predictors in a regression model. Unlike the P+T model, these approaches attempt to model the effects of all markers jointly. Though several of these methods are too new to have been extensively used in the literature, we present them as possibly useful options. The theoretical aspects of these approaches are discussed in greater detail in Choi et al. (2018).
In the Bayesian statistical framework, a prior probability distribution for the parameters of interest is combined with data to produce a refined posterior distribution, from which inference is made. In general, these models apply shrinkage to marker effects (i.e., summary statistics) that incorporates LD information from a reference panel (Choi et al., 2018). Prior distributions are selected that most accurately capture the “genetic architecture”, or contribution of the entire genome to the trait, that consider the LD structure (estimated from genotypes) and overall heritability. The program LDPred (Vilhjálmsson et al., 2015) uses a point-normal prior distribution with a specified causal proportion parameter p. The remaining non-causal variants (proportion 1-p) are assigned an effect of zero. The proportion is specified by the user and generally several values will be considered, with the candidate chosen by cross-validation. A newer method, SBayesR, in the GCTB software package (Lloyd-Jones et al., 2019), expands the point-normal prior with a mixture of normal distributions, allowing for the specification of multiple proportions (adding up to 1). Both methods require specification of the chip heritability, which can be estimated from the data. The RSS package (Zhu and Stephens, 2017) includes additional choices for prior distributions and does not require specification of proportions or heritability. RSS requires MATLAB, and therefore is less accessible to users. PRS-CS (Ge et al., 2019) improves computational efficiency of Bayesian regression by using a continuous shrinkage prior distribution on marker effect sizes. The user must specify a global shrinkage parameter, ϕ, that reflects the proportion of causal variants, but the program can estimate ϕ from GWAS results. All of these models require providing an LD matrix which can be estimated from a reference panel such as 1000 Genomes. SBayesR creates a sparse LD matrix which improves computation and inference, while RSS introduces a shrunken LD matrix. The program GCTB, a Bayesian companion to the popular GCTA package, can create sparse or shrunken LD matrices for use in other software. The JAMPred software applies a similar approach and can account for long-range LD (Newcombe et al., 2019). It should be noted that both RSS and SBayesR currently only analyze continuous phenotypes.
Two PRS methods, SBLUP (Robinson et al., 2017) and lassosum (Mak et al., 2017), use non-Bayesian strategies to consider large numbers of markers jointly. SBLUP, part of the GCTA package (Yang et al., 2011), uses the restricted maximum likelihood (REML) implemented in GCTA to perform a random-effects model to acquire a best linear unbiased predictor (BLUP). It requires the chip heritability as a parameter, but GCTA can estimate this if individual-level data are available. lassosum applies least absolute shrinkage and selection operator (LASSO) regression to downweight, and perhaps omit altogether, effects of correlated markers. Two important parameters for lassosum, which may require optimizing using external data, are λ, which determines the fraction of effects shrunken to 0, and s, the shrinkage parameter (Mak et al., 2017).
Critical Parameters and Complicating Factors
The discriminatory power of the model to determine an individuals’ “risk” is dependent upon the factors included in the model and their contribution to that risk. Several questions regarding the factors included in a GRS must be considered. Are these factors useful predictors in only the population in which they were first detected? Are they consistent across ethnic groups? Does the linkage disequilibrium structure vary between the discovery population and the test population and will this cause differences in model predictability? Are the risk alleles coded consistently across datasets? Are the same DNA strands being evaluated? Critical aspects to consider when constructing a GRS are listed in Table 3.
Table 3.
Considerations for Generating a Genetic Risk Score
| Factor | Considerations |
|---|---|
| Outcome of Interest | Pleiotropy Definition of complex phenotype (component phenotypes) Clinical covariates |
| Loci | P-value threshold (polygenic vs. highly significant loci only) Imputation type/quality Linkage disequilibrium Mode of inheritance Agreement of DNA strand between training and test data Reference (risk) allele coding Build of human genome |
| Sample | Population (ethnic background; admixture) Demographic makeup (age, sex, socioeconomic status, etc.) |
| Weighting | log (OR) from logistic regression Total number of risk variants LD between risk variants (for PRS) |
Choosing an outcome of interest can seem straightforward; however, for common, traits with many genetic determinants, it does require understanding the complexity in the genetic component and in the definition of multifactorial traits, and how these factors interact. As an example, the primary open-angle glaucoma (POAG) phenotype may be defined in many different ways: by the associated traits (endophenotypes) cup-to-disc ratio (CDR), intraocular pressure (IOP), visual field (VF) loss, or by some combination of these (reviewed in (Weinreb et al., 2014)). Fifteen loci have been identified as genetic risk modifiers of disease (Cooke Bailey et al., 2016a; Li et al., 2015; Hysi et al., 2014; Gharahkhani et al., 2014; Wiggs et al., 2012; Thorleifsson et al., 2010; Burdon et al., 2011; Chen et al., 2014) and numerous others identified in POAG endophenotypes have recently shown association with POAG (Khawaja et al., 2018; Gao et al., 2018; MacGregor et al., 2018). The genetic factors identified in studies of POAG and its component phenotypes (such as IOP, CDR, VF changes) overlap but are not identical. Some, but not all, genetic loci are associated with the disease and endophenotypes; GAS7 is associated with intraocular pressure as well as overall POAG (Cooke Bailey et al., 2016b), CDKN2B-AS1 is associated with POAG and normal tension glaucoma, and other optic nerve parameters (reviewed in (Wiggs, 2015)), and POAG-associated loci AFAP1, FOXC1, TXNRD2/GNB1L, and ATXN2/SH2B3 were recently associated with IOP (Khawaja et al., 2018). Choosing variants relevant to constructing a POAG risk score, for example, requires careful consideration and examination of this information. A recent example of a genetic risk score utilizing IOP-associated SNPs to predict POAG had AUC estimates of 0.76 and 0.74 in regression-based glaucoma prediction models in independent datasets (Khawaja et al., 2018). Gao et al. recently reported a PRS associated with IOP and POAG from the UK Biobank (Gao et al., 2019b), wherein the most discriminative model included PRS, age and sex, but, of note, the AUC of the base model (age and sex only) was slightly improved (from 0.713 to 0.766) with the addition of PRS to the model.
Mode of inheritance must also be taken into consideration. The formula described above assumes an additive genetic model (for binary traits, implying multiplicative on the odds scale) for all risk variants. Whereas the true contribution of genetic variants may not follow this model, some prediction accuracy may be lost, despite dominance effects likely not substantially contributing to sporadic, complex diseases (Hill et al., 2008).
When constructing a GRS, DNA strand and risk allele coding are also crucial to keep consistent across studies so as to ensure validity and transferability of GRS. It is also imperative to note that the risk allele is not necessarily always the minor or reference allele and this is a key aspect to keep consistent between studies, since a protective effect of one allele implies risk at the other allele. Further, effect estimates should be estimated in the largest group possible, but not in the group being tested (to prevent model over-fitting). Map positions of older GWAS chips and whole-genome sequencing data may be reported relative to a different build of the human genome than modern GWAS chips (usually GRCh37/hg19).
Special care should be taken when constructing GRS including SNPs with strand-ambiguous alleles A/T or C/G, because the reference allele is not obviously comparable between samples typed on different DNA strands. Ensure that the genotypes from new samples are relative to the same DNA strand (e.g., the Illumina TOP or dbSNP + strand), or, if strand information is absent, compare allele frequencies across samples to identify the common minor allele. In the latter case, A/T and C/G SNPs with minor allele frequency above 0.4 may not be usable, owing to uncertainty in assigning the minor allele.
Most common variants associated with complex disease confer modest effect sizes. Assessing the contribution of these loci, which are identified with increasing frequency in massively large datasets of primarily European ancestry, to smaller or ethnically diverse samples requires careful planning and analysis and thus allelic heterogeneity should also be taken into consideration. In similar populations the true heritability accounts for the possibility of allelic heterogeneity; however, allelic heterogeneity will reduce prediction accuracy if discovery and testing cohorts are not of the same genetic background. In a sample of Amish individuals, Hoffman et al. calculated GRS generated from 19 AMD loci reported in Fritsche et al. (2013) and compared the distribution to that in a non-Amish European American sample (Hoffman et al., 2014). They found that overall the Amish risk scores were significantly lower in the Amish case and control groups, despite similar AMD prevalence, thus providing some insight into the genetic architecture of AMD in the Amish and highlighting important difference in genetic architecture even within European populations.
Cooke et al. (2012) previously evaluated a GRS that included 17 known type 2 diabetes (T2D) risk loci in an African American sample and showed that while the risk allele load was higher in African American cases compared to controls, the high-effect TCF7L2 rs7903146 risk allele accounted for all increased risk in African Americans. Expanding on this work, Keaton and colleagues genotyped additional T2D SNPs to bring the total to 43 SNPs and confirmed that there are ethnic-specific differences in the genetic architecture of T2D when comparing African Americans to European Americans (Keaton et al., 2014). Unfortunately, many of the GRS scores modeled to date have only been evaluated in European Caucasian individuals. This is reflective of the widespread genetic data in this population and the (in comparison) relative shortage of data in individuals of other ancestries (Bustamante et al., 2011). Further studies in individuals of non-European descent are needed to assess predictive models across ethnic groups, as the variants generally do not correspond directly, as mentioned above and as highlighted by studies that evaluated known AMD variants in African Americans and Mexican Americans and only detected association at the ARMS2 A69S variant (Restrepo et al., 2014; Spencer et al., 2012).
PRS offer heightened predictive power over GRS but have special challenges. Immense samples sizes are required to achieve an AUC approaching that theoretically obtainable given heritability and trait prevalence(Dudbridge, 2013). Moreover, PRS as calculated by the approaches discussed here, will miss contributions to overall heritability not normally measured by GWAS, including dominance (if testing with an additive genetic model), epistatic (gene-by-gene), gene-by environment and epigenetic effects, as well as the effects of rare genetic variants and genomic structural variation (Manolio et al., 2009). Thus, the ideal AUC will usually not be achieved even with unlimited data. PRS calculations are computationally burdensome, requiring fast computers and, ideally, should be run under the Linux operating system. They also require tuning parameters whose optimal values may be sample-dependent and difficult to find. Even in P+T methods, the proper p value and r2 thresholds are not a priori clear. Increasing maximum r2 for LD pruning increases prediction power but also increases overfitting (Goldstein et al., 2015). Finally, like GRS, PRS do not generalize well across ethnic groups (Martin et al., 2017, 2019), an important consideration in light of the underrepresentation of non-European samples in genetic research previously mentioned (Bustamante et al., 2011).
In summary, we have reviewed here various methods to construct and evaluate GRS. There are many considerations to keep in mind when implementing a GRS to ensure relevance and reliability, and there are substantial caveats to the use of GRS. All of these elements should be kept in mind when considering using a GRS and when drawing conclusions based on GRS.
Significance Statement.
The past decade has seen phenomenal growth in genetics and genomics knowledge, with exponential increase in available data. Translation of this vast body of information into useful, predictive measures of disease susceptibility, progression or treatment outcome has lagged, however, especially for complex, common diseases with many contributing genetic factors. A popular approach to estimate overall genetic risk, and to summarize the cumulative effects of genetic loci, is the use of genetic risk scores, which aggregate the effects of genetic variants associated with disease. In this Unit, we review common methods for constructing genetic risk scores and polygenic risk scores, with particular attention to their practical application and limitations.
KEY CONCEPTS.
A genetic risk score is an estimate of the cumulative contribution of genetic factors to a specific outcome of interest in an individual. The score may take into account the reported effect sizes for those alleles and may be normalized by adjusting for the total number of risk alleles and effect sizes evaluated.
A polygenic risk score is an extension of the genetic risk score for large numbers of possibly correlated markers. It aims to capture all the heritable variation measurable by the marker panel for prediction.
The area under the curve (AUC) measures the predictive ability of a receiver operating characteristic (ROC) generated based on the genetic risk scores for a sample of individuals. The AUC is a function of the ability of the risk score to correctly identify the presence (sensitivity) or absence (specificity) of the outcome of interest.
Disease prediction is the ability to determine disease state given any number of known factors including, but not limited to, genetic, environmental and lifestyle.
Complex traits and complex diseases have multiple contributing factors, including both genetic variation and environmental factors. They have a clear genetic component but no simple mode of inheritance.
ACKNOWLEDGEMENT
JNCB was supported by the Clinical and Translational Science Collaborative of Cleveland, KL2TR0002547 from the National Center for Advancing Translational Sciences (NCATS) component of the National Institutes of Health and NIH roadmap for Medical Research.
LITERATURE CITED
- Beck T, Hastings RK, Gollapudi S, Free RC, and Brookes AJ 2014. GWAS Central: A comprehensive resource for the comparison and interrogation of genome-wide association studies. European Journal of Human Genetics 22:949–952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyle EA, Li YI, and Pritchard JK 2017. An Expanded View of Complex Traits: From Polygenic to Omnigenic. Cell 169:1177–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buniello A, MacArthur JAL, Cerezo M, Harris LW, Hayhurst J, Malangone C, McMahon A, Morales J, Mountjoy E, Sollis E, et al. 2019. The NHGRI-EBI GWAS Catalog of published genome-wide association studies, targeted arrays and summary statistics 2019. Nucleic acids research 47:D1005–D1012. Available at: http://www.ncbi.nlm.nih.gov/pubmed/30445434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burdon KP, MacGregor S, Hewitt AW, Sharma S, Chidlow G, Mills RA, Danoy P, Casson R, Viswanathan AC, Liu JZ, et al. 2011. Genome-wide association study identifies susceptibility loci for open angle glaucoma at TMCO1 and CDKN2B-AS1. Nature Genetics 43:574–578. Available at: http://www.ncbi.nlm.nih.gov/pubmed/21532571 [DOI] [PubMed] [Google Scholar]
- Bustamante CD, De La Vega FM, and Burchard EG 2011. Genomics for the world. Nature 475:163–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang CC, Chow CC, Tellier LCAM, Vattikuti S, Purcell SM, and Lee JJ 2015. Second-generation PLINK: Rising to the challenge of larger and richer datasets. GigaScience 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Lin Y, Vithana EN, Jia L, Zuo X, Wong TY, Chen LJ, Zhu X, Tam POS, Gong B, et al. 2014. Common variants near ABCA1 and in PMM2 are associated with primary open-angle glaucoma. Nature genetics 46:1115–9. Available at: http://www.nature.com/articles/ng.3078 [DOI] [PubMed] [Google Scholar]
- Choi SW, Mak TSH, and O’Reilly PF 2018. A guide to performing Polygenic Risk Score analyses. bioRxiv:416545. Available at: https://www.biorxiv.org/content/10.1101/416545v1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke Bailey J, Hoffman J, Sardell R, Scott W, Pericak-Vance M, and Haines J 2016a. The Application of Genetic Risk Scores in Age-Related Macular Degeneration: A Review. Journal of Clinical Medicine 5:31 Available at: http://www.mdpi.com/2077-0383/5/3/31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooke Bailey JN, Loomis SJ, Kang JH, Allingham RR, Gharahkhani P, Khor CC, Burdon KP, Aschard H, Chasman DI, Igo RP, et al. 2016b. Genome-wide association analysis identifies TXNRD2, ATXN2 and FOXC1 as susceptibility loci for primary open-angle glaucoma. Nature Genetics 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudbridge F 2013. Power and predictive accuracy of polygenic risk scores. PLoS genetics 9:e1003348 Available at: http://www.ncbi.nlm.nih.gov/pubmed/23555274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Euesden J, Lewis CM, and O’Reilly PF 2015. PRSice: Polygenic Risk Score software. Bioinformatics 31:1466–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritsche LG, Chen W, Schu M, Yaspan BL, Yu Y, Thorleifsson G, Zack DJ, Arakawa S, Cipriani V, Ripke S, et al. 2013. Seven new loci associated with age-related macular degeneration. Nature Genetics 45:433–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritsche LG, Igl W, Bailey JNC, Grassmann F, Sengupta S, Bragg-Gresham JL, Burdon KP, Hebbring SJ, Wen C, Gorski M, et al. 2016. A large genome-wide association study of age-related macular degeneration highlights contributions of rare and common variants. Nature genetics 48:134–43. Available at: http://www.nature.com/articles/ng.3448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao XR, Huang H, and Kim H 2019. Polygenic Risk Score Is Associated With Intraocular Pressure and Improves Glaucoma Prediction in the UK Biobank Cohort. Translational Vision Science & Technology 8:10 Available at: http://www.ncbi.nlm.nih.gov/pubmed/30972231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao XR, Huang H, Nannini DR, Fan F, and Kim H 2018. Genome-wide association analyses identify new loci influencing intraocular pressure. Human Molecular Genetics 27:2205–2213. Available at: http://www.ncbi.nlm.nih.gov/pubmed/29617998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge T, Chen CY, Ni Y, Feng YCA, and Smoller JW 2019. Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nature Communications 10:1776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gharahkhani P, Burdon KP, Fogarty R, Sharma S, Hewitt AW, Martin S, Law MH, Cremin K, Bailey JNC, Loomis SJ, et al. 2014. Common variants near ABCA1, AFAP1 and GMDS confer risk of primary open-angle glaucoma. Nature Genetics 46:1120–1125. Available at: http://www.nature.com/articles/ng.3079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein BA, Yang L, Salfati E, and Assimes TL 2015. Contemporary Considerations for Constructing a Genetic Risk Score: An Empirical Approach. Genetic Epidemiology 39:439–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Goddard ME, and Visscher PM 2008. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genetics 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman JD, Cooke Bailey JN, D’Aoust L, Cade W, Ayala-Haedo J, Fuzzell D, Laux R, Adams LD, Reinhart-Mercer L, Caywood L, et al. 2014. Rare complement factor H variant associated with age-related macular degeneration in the Amish. Investigative Ophthalmology and Visual Science 55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hysi PG, Cheng C-Y, Springelkamp H, Macgregor S, Bailey JNC, Wojciechowski R, Vitart V, Nag A, Hewitt AW, Höhn R, et al. 2014. Genome-wide analysis of multi-ancestry cohorts identifies new loci influencing intraocular pressure and susceptibility to glaucoma. Nature genetics 46:1126–1130. Available at: http://www.nature.com/articles/ng.3087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Schizophrenia Consortium, Purcell SM, Wray NR, Stone JL, Visscher PM, O’Donovan MC, Sullivan PF, and Sklar P 2009. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460:748–52. Available at: http://www.ncbi.nlm.nih.gov/pubmed/19571811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsdottir J, Gorin MB, Conley YP, Ferrell RE, and Weeks DE 2009. Interpretation of genetic association studies: Markers with replicated highly significant odds ratios may be poor classifiers. PLoS Genetics 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssens ACJW, Moonesinghe R, Yang Q, Steyerberg EW, van Duijn CM, and Khoury MJ 2007. The impact of genotype frequencies on the clinical validity of genomic profiling for predicting common chronic diseases. Genetics in medicine : official journal of the American College of Medical Genetics 9:528–35. Available at: http://www.ncbi.nlm.nih.gov/pubmed/17700391 [DOI] [PubMed] [Google Scholar]
- Keaton JM, Cooke Bailey JN, Palmer ND, Freedman BI, Langefeld CD, Ng MCY, and Bowden DW 2014. A comparison of type 2 diabetes risk allele load between African Americans and European Americans. Human Genetics 133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khawaja AP, Cooke Bailey JN, Wareham NJ, Scott RA, Simcoe M, Igo RP, Song YE, Wojciechowski R, Cheng C-Y, Khaw PT, et al. 2018. Genome-wide analyses identify 68 new loci associated with intraocular pressure and improve risk prediction for primary open-angle glaucoma. Nature Genetics 50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khawaja AP, and Viswanathan AC 2018. Are we ready for genetic testing for primary open-angle glaucoma? Eye (London, England) 32:877–883. Available at: http://www.ncbi.nlm.nih.gov/pubmed/29379103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khera AV, Chaffin M, Aragam KG, Haas ME, Roselli C, Choi SH, Natarajan P, Lander ES, Lubitz SA, Ellinor PT, et al. 2018. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nature Genetics 50:1219–1224. Available at: http://www.nature.com/articles/s41588-018-0183-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn M 2008. Building Predictive Models in R Using the caret Package. Journal of Statistical Software 28 Available at: http://www.jstatsoft.org/v28/i05/ [Google Scholar]
- Li Z, Allingham RR, Nakano M, Jia L, Chen Y, Ikeda Y, Mani B, Chen L-J, Kee C, Garway-Heath DF, et al. 2015. A common variant near TGFBR3 is associated with primary open angle glaucoma. Human Molecular Genetics 24:3880–3892. Available at: http://www.ncbi.nlm.nih.gov/pubmed/25861811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd-Jones LR, Zeng J, Sidorenko J, Yengo L, Moser G, Kemper KE, Wang H, Zheng Z, Magi R, Esko T, et al. 2019. Improved polygenic prediction by Bayesian multiple regression on summary statistics. bioRxiv:522961. Available at: https://www.biorxiv.org/content/10.1101/522961v3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacGregor S, Ong J-S, An J, Han X, Zhou T, Siggs OM, Law MH, Souzeau E, Sharma S, Lynn DJ, et al. 2018. Genome-wide association study of intraocular pressure uncovers new pathways to glaucoma. Nature Genetics 50:1067–1071. Available at: http://www.nature.com/articles/s41588-018-0176-y [DOI] [PubMed] [Google Scholar]
- Maier RM, Visscher PM, Robinson MR, and Wray NR 2018. Embracing polygenicity: A review of methods and tools for psychiatric genetics research. Psychological Medicine 48:1055–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak TSH, Porsch RM, Choi SW, Zhou X, and Sham PC 2017. Polygenic scores via penalized regression on summary statistics. Genetic Epidemiology 41:469–480. [DOI] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. 2009. Finding the missing heritability of complex diseases. Nature 461:747–53. Available at: http://www.nature.com/articles/nature08494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AR, Gignoux CR, Walters RK, Wojcik GL, Neale BM, Gravel S, Daly MJ, Bustamante CD, and Kenny EE 2017. Human Demographic History Impacts Genetic Risk Prediction across Diverse Populations. American Journal of Human Genetics 100:635–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin AR, Kanai M, Kamatani Y, Okada Y, Neale BM, and Daly MJ 2019. Clinical use of current polygenic risk scores may exacerbate health disparities. Nature Genetics 51:584–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menard S 2000. Coefficients of Determination for Multiple Logistic Regression Analysis. The American Statistician 54:17 Available at: https://www.jstor.org/stable/2685605?origin=crossref [Google Scholar]
- Newcombe PJ, Nelson CP, Samani NJ, and Dudbridge F 2019. A flexible and parallelizable approach to genome‐wide polygenic risk scores. Genetic Epidemiology 43:730–741. Available at: https://onlinelibrary.wiley.com/doi/abs/10.1002/gepi.22245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe MS, Janes H, Longton G, Leisenring W, and Newcomb P 2004. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. American journal of epidemiology 159:882–90. Available at: http://www.ncbi.nlm.nih.gov/pubmed/15105181 [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, et al. 2007. PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses. The American Journal of Human Genetics 81:559–575. Available at: https://linkinghub.elsevier.com/retrieve/pii/S0002929707613524 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Restrepo NA, Spencer KL, Goodloe R, Garrett TA, Heiss G, Bůžková P, Jorgensen N, Jensen RA, Matise TC, Hindorff LA, et al. 2014. Genetic determinants of age-related macular degeneration in diverse populations from the PAGE study. Investigative ophthalmology & visual science 55:6839–6850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MR, Kleinman A, Graff M, Vinkhuyzen AAE, Couper D, Miller MB, Peyrot WJ, Abdellaoui A, Zietsch BP, Nolte IM, et al. 2017. Genetic evidence of assortative mating in humans. Nature Human Behaviour 1. [Google Scholar]
- Schork AJ, Schork MA, and Schork NJ 2018. Genetic risks and clinical rewards. Nature Genetics 50:1210–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer KL, Glenn K, Brown-Gentry K, Haines JL, and Crawford DC 2012. Population differences in genetic risk for age-related macular degeneration and implications for genetic testing. Archives of ophthalmology (Chicago, Ill. : 1960) 130:116–7. Available at: http://www.ncbi.nlm.nih.gov/pubmed/22232482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, Pencina MJ, and Kattan MW 2013. Prediction models: a framework for some traditional and novel measures. Epidemiology 21:128–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorleifsson G, Walters GB, Hewitt AW, Masson G, Helgason A, DeWan A, Sigurdsson A, Jonasdottir A, Gudjonsson SA, Magnusson KP, et al. 2010. Common variants near CAV1 and CAV2 are associated with primary open-angle glaucoma. Nature Genetics 42:906–909. Available at: http://www.ncbi.nlm.nih.gov/pubmed/20835238 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjur T 2009. Coefficients of determination in logistic regression models - A new proposal: The coefficient of discrimination. American Statistician 63:366–372. [Google Scholar]
- Torkamani A, Wineinger NE, and Topol EJ 2018. The personal and clinical utility of polygenic risk scores. Nature Reviews Genetics 19:581–590. [DOI] [PubMed] [Google Scholar]
- Vilhjálmsson BJ, Yang J, Finucane HK, Gusev A, Lindström S, Ripke S, Genovese G, Loh PR, Bhatia G, Do R, et al. 2015. Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. American Journal of Human Genetics 97:576–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreb RN, Aung T, and Medeiros FA 2014. The pathophysiology and treatment of glaucoma: A review. JAMA - Journal of the American Medical Association 311:1901–1911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggs JL 2015. Glaucoma Genes and Mechanisms. Progress in molecular biology and translational science 134:315–42. Available at: http://www.ncbi.nlm.nih.gov/pubmed/26310163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggs JL, Yaspan BL, Hauser MA, Kang JH, Allingham RR, Olson LM, Abdrabou W, Fan BJ, Wang DY, Brodeur W, et al. 2012. Common variants at 9p21 and 8q22 are associated with increased susceptibility to optic nerve degeneration in glaucoma. PLoS genetics 8:e1002654 Available at: http://dx.plos.org/10.1371/journal.pgen.1002654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witte JS, Visscher PM, and Wray NR 2014. The contribution of genetic variants to disease depends on the ruler. Nature Reviews Genetics 15:765–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wray NR, and Goddard ME 2010. Multi-locus models of genetic risk of disease. Genome medicine 2:10 Available at: http://www.ncbi.nlm.nih.gov/pubmed/20181060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wray NR, Lee SH, Mehta D, Vinkhuyzen AAE, Dudbridge F, and Middeldorp CM 2014. Research review: Polygenic methods and their application to psychiatric traits. Journal of child psychology and psychiatry, and allied disciplines 55:1068–87. Available at: http://www.ncbi.nlm.nih.gov/pubmed/25132410 [DOI] [PubMed] [Google Scholar]
- Wray NR, Yang J, Goddard ME, and Visscher PM 2010. The genetic interpretation of area under the ROC curve in genomic profiling. PLoS genetics 6:e1000864 Available at: http://www.ncbi.nlm.nih.gov/pubmed/20195508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, and Visscher PM 2011. GCTA: A tool for genome-wide complex trait analysis. American Journal of Human Genetics 88:76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, and Stephens M 2017. BAYESIAN LARGE-SCALE MULTIPLE REGRESSION WITH SUMMARY STATISTICS FROM GENOME-WIDE ASSOCIATION STUDIES 1. The Annals of Applied Statistics 11:1561–1592. Available at: https://github.com/stephenslab/rss. [DOI] [PMC free article] [PubMed] [Google Scholar]