Abstract
Brain imaging genomics is an emerging data science field, where integrated analysis of brain imaging and genomics data, often combined with other biomarker, clinical and environmental data, is performed to gain new insights into the phenotypic, genetic and molecular characteristics of the brain as well as their impact on normal and disordered brain function and behavior. It has enormous potential to contribute significantly to biomedical discoveries in brain science. Given the increasingly important role of statistical and machine learning in biomedicine and rapidly growing literature in brain imaging genomics, we provide an up-to-date and comprehensive review of statistical and machine learning methods for brain imaging genomics, as well as a practical discussion on method selection for various biomedical applications.
Keywords: Big data, brain imaging, genomics, machine learning, statistics
I. Introduction
With recent technological advances in acquiring multimodal brain imaging data and high-throughput genomics data, brain imaging genomics is emerging as a rapidly growing research field. It performs integrative studies that analyze genetic variations such as single nucleotide polymorphisms (SNPs), as well as epigenetic and copy number variations (CNVs), molecular features captured by various omics data and brain imaging quantitative traits (QTs), coupled with other biomarker, clinical and environmental data. The goal of imaging genomics is to gain new insights into the phenotypic characteristics and the genetic and molecular mechanisms of the brain, as well as their impact on normal and disordered brain function and behavior. Given the unprecedented scale and complexity of the brain imaging genomics data sets, major computational and statistical challenges have to be met to realize the full potential of these valuable data. Overcoming these challenges has become a major and active research topic in the field of statistical and machine learning, where effective and efficient data analytic methods have been developed to reveal the genetic and molecular underpinnings of neurobiological systems, which can impact the development of diagnostic, therapeutic and preventative approaches for complex brain disorders.
Many advances in brain imaging genomics are attributed to large-scale landmark studies such as the Alzheimers Disease Neuroimaging Initiative (ADNI) [1], the Enhancing Neuro Imaging Genetics through Meta Analysis (ENIGMA) consortium [2], and the UK Biobank [3]. These studies facilitate the availability of big brain imaging genomics data to the worldwide research community, which contributes to the generation of a large body of literature concerning methodological developments and biomedical applications in brain imaging genomics, including a number of review articles summarizing relevant advances from multiple different perspectives.
For example, ADNI is a landmark Alzheimer’s disease (AD) biomarker study. The ADNI cohort constitutes a very rich repository of multi-modal data such as genome-wide genotyping, whole genome sequencing, blood transcriptome, blood epigenome, plasma/serum/cerebrospinal-fluid proteome, plasma/serum metabolome, neuroimaging such as multimodal magnetic resonance imaging (MRI) and positron emission tomography (PET), cognitive, behavioral, and clinical data. Due to its open-science nature, data from ADNI have been widely used by the research community around the world to produce hundreds of publications in brain imaging genomics. These advances were periodically reviewed by the ADNI Genetics Core [4], [5] and the entire ADNI team [1], [6].
ENIGMA is another major initiative that contributes significantly to the field of brain imaging genomics. The ENIGMA consortium is a global team science effort with the shared goal of understanding disease and genetic influences on the brain. The progress of the ENIGMA Consortium has been regularly summarized in several review articles over the years (e.g., [2], [7], [8], [9]). In [2], Thompson et al. provided the most recent update of the ENIGMA consortium, which included over 1,400 scientists from 43 countries studying the human brain using imaging, genomics and other brain metrics.
The UK Biobank [3], a prospective epidemiological cohort of over 500,000 individuals, is another prominent study that offers an enormous amount of brain imaging genomics data. It has a full genetic data release for ~500,000 samples [10], and full brain imaging data release for ~15,000 samples in six modalities [11]. The team completed a large scale genomewide association studies of brain imaging QTs recently, which examined > 11 million SNPs on 3,144 imaging QTs in 8,428 samples for discovery and two additional sets of 930 and 3,456 samples for replication [12]. This study represents the current frontiers in large scale brain imaging genomics, yielding invaluable insights into the genetic architecture of the brain.
In addition to ADNI, ENIGMA and UK Biobank, there are many other research activities in brain imaging genomics, which have yielded various review articles. For example, in [13], Liu et al. reviewed multivariate methods for analyzing and integrating imaging and genetics data. In [14], Yan et al. reviewed regression and correlation methods for brain imaging genomics as well as set-based methods for mining high-level imaging genomics associations. In [15], Mufford et al. reviewed methods and topics of brain imaging genomics in psychiatry. In [16], Liu et al. reviewed multimodal analysis strategies for analyzing and integrating multi-omics data and brain imaging data in the context of schizophrenia studies.
In short, the comprehensive reviews discussed above cover topics in brain imaging genomics from different perspectives. Some focus on reviewing data, methods, analyses and/or results from a specific study such as ADNI [1], [4], [5], [6] or ENIGMA [2], [7], [8], [9]. Some reviews examine the research activities and progress in the context of a specific discipline (i.e., psychiatry in [15]) or disorder (i.e., schizophrenia in [16]). Others provide methodology-oriented reviews on multivariate analyses [13] and machine learning [14]. Given that statistical and machine learning is playing increasingly important roles in biomedical research and new methods are emerging in the literature at a rapid pace [17], we feel that it will be valuable to provide an updated review on the topic of statistical and machine learning in brain imaging genomics. Thus, the goal of this paper is to provide an up-to-date and comprehensive coverage of statistical and machine learning methods for solving problems in brain imaging genomics as well as practical discussion on method selection for various biomedical applications.
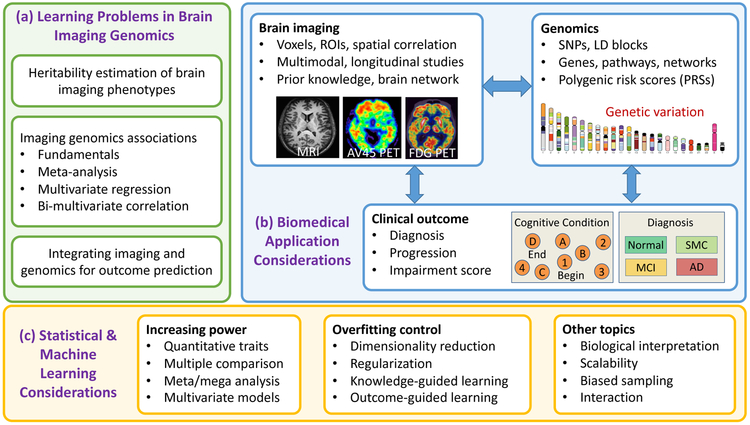
Shown in Figure 1 is the schematic representation of the topics we will cover in this review. The major part of the paper will be devoted to the discussion of methods for solving the following three types of learning problems in brain imaging genomics (see Figure 1(a)).
Fig. 1.
Schematic representation of topics covered in this review. (a) Learning problems in brain imaging genomics: this review is organized by these topics. (b) Biomedical application considerations: these are example topics related to the studied brain imaging, genomics and outcome data. (c) Statistical and machine learning considerations: these are example topics considered by the reviewed statistical and machine learning methods.
First, we will examine the problem of heritability estimation of brain imaging phenotypes in Section II, where the goal is to determine how much phenotypic variation is determined by genetics.
Second, we will explore the problem of learning imaging genomics associations. Since a majority of papers reviewed here belong to this category, we will devote Sections III-VI to this topic. We will review a few fundamental strategies in Section III, including SNP-based methods, polygenic risk scores, multi-SNP methods, multi-trait methods, pathway and network enrichment methods, and interaction methods. We will discuss meta-analysis strategies in Section IV. We will review multivariate regression models in Section V and bimultivariate correlation models in Section VI to identify complex multi-SNP-multi-trait associations.
Third, in Section VII, we will review methods for predicting an outcome of interest by integrating imaging and genomics data, as well as methods for joint association learning and outcome prediction.
Finally, in Section VIII, we will provide 1) a discussion of principles of method selection, based on biomedical application considerations (see Figure 1(b)) and statistical and machine learning considerations (see Figure 1(c)); 2) a discussion on scientific and clinical impact; and 3) a discussion on related work and future directions.
II. Heritability Estimation
Early genetic studies of the brain largely focused on estimating heritability - the proportion of the observed variance in a trait that is explained by additive genetic factors [18]. Well before quantitative genetics was applied to neuroimaging data, classical genetic methods were developed to estimate the proportion of variance in a trait that was due to genetic and environmental factors - as well as random variation, such as measurement errors. The motivation to estimate heritability was that a highly heritable trait might be an attractive target for in-depth genetic analyses, compared to a trait with little or no genetic variance. Below we cover methods to estimate heritability based on genome-wide genotyping data. First, we note that heritability can be estimated based on data collected using twin or family designs, where the degree of genetic influence is estimated from trait correlations in relatives with different degrees of genetic overlap.
A. Twin and pedigree methods
Around 2001, neuroimaging studies of twins began to report correlations in regional brain measures in identical and fraternal twins, whereby identical twins had more similar brain structure than randomly selected pairs of individuals of the same age and sex. According to classical quantitative genetics, if the intra-class correlation is higher in monozygotic (MZ) than dizygotic (DZ) twins, then a trait is heritable. Falconers heritability statistic, h2, is defined as twice the difference between the MZ and DZ intraclass correlations. Thompson et al. [19] reported statistical maps of Falconers h2 statistics, for measures of gray matter density across the cortex, showing significant heritability, in a small MRI study of 80 young adult twins. Later studies built on this approach to fit structural equation models (SEMs) to quantify both genetic and environmental components of variance, for brain measures derived from MRI, diffusion tensor imaging (DTI), electroencephalogram (EEG), and functional MRI (fMRI), also using twin or family designs. A common model used for these studies was the ACE model, which estimates additive genetic (A), common (C) and unique (E) environmental contributions to trait variance (see [20] for a review of early neuroimaging studies using the ACE model).
Brun et al. [21] for example, used a general MRI analysis method called tensor-based morphometry (TBM) to map the heritability of brain morphology in MRI scans from 23 monozygotic and 23 dizygotic twin pairs, using the ACE genetic model. Significance was tested using voxelwise permutation methods. Similar work with other computational anatomy approaches extended the ACE model to scalar maps defined on vertices of 3D surface models of brain structures such as the ventricles [22]. In that study, path coefficients for the ACE model that best fitted the data indicated significant contributions from genetic factors (A=7.3%), common environment (C=38.9%) and unique environment (E=53.8%) to lateral ventricular volume.
Extending the ACE model to diffusion MRI, to assess the genetics of brain white matter microstructure, Shen et al. [23] confirmed the overall heritability of the major white matter tract metrics but also identified differences in heritability. Highly heritable measures were found for tracts connecting particular cortical regions, such as medial frontal cortices, postcentral, paracentral gyri, and the right hippocampus. Later studies reported genetic correlations between measures of cortical gray matter thickness and DTI-derived white matter measures [24]. Comparable methods applied to functional MRI revealed significant heritability for measures of functional synchrony in the brains resting state networks (RSNs). Fu et al. [25] estimated both genetic and environmental effects on eight well-characterized RSNs. To do so, they fitted the classical ACE twin model to the functional connectivity covariance at each voxel in the RSN. Although environmental effects accounted for the majority of variance in widespread areas, specific brain regions showed significant genetic control within individual RSNs.
Methods to estimate heritability advanced as well. Open source tools, such as OpenMx and SOLAR, were adapted to handle brain-derived phenotypes, including entire images. Kochunov et al. [26] examined agreement in the heritability estimates, across a variety of datasets, for four different methods for heritability estimation that have been applied to neuroimaging data. SOLAR-Eclipse (www.solar-eclipse-genetics.org) and OpenMx (openmx.ssri.psu.edu) use iterative maximum likelihood estimation (MLE) methods. Accelerated Permutation inference for ACE (APACE) [27] and fast permutation heritability inference (FPHI) [28] use fast, non-iterative approximation-based methods. Heritability estimates from the two MLE approaches closely agreed on both simulated and imaging data, but the two approximation approaches showed lower heritability estimates when run on data that deviated from normality. The authors advocated a data homogenization approach that improved agreement across packages, using inverse Gaussian transformation to enforce normality on the input trait data.
B. GWAS methods for SNP heritability
As soon as genome-wide genotyping became cheaper and more common, methods were developed to estimate heritability from all genome-wide SNPs. The GCTA method (genomewide complex trait analysis; [29]; https://cnsgenomics.com/software/gcta/), for example, estimates heritability from general population data - and rather than requiring twins or pedigrees, it can be applied to data from individuals who are typically regarded as unrelated. GCTA computes both genetic and phenotypic covariance matrices from trait data and high-density SNP data, after calculating a kinship matrix and a genotypic relatedness matrix (GRM). Based on singular values of the GRM, GCTA estimates the percentage of phenotypic variance explained by all common SNPs (i.e., the SNP heritability of a trait), with a restricted maximum-likelihood linear mixed model (GREML). GCTA has been used to estimate “missing” heritability - the genetic contribution from all SNPs in aggregate - without needing to know exactly which SNPs are contributing to the variance.
Direct application of GCTA to the heritability analysis of high dimensional brain imaging QTs is computationally intractable. To overcome this limitation, in [30], Ge et al. proposed a “Massively expedited genome-wide heritability analysis (MEGHA)” method, which approximates GCTA and is suitable for analyzing a large number of phenotypes efficiently. It was successfully used to create vertex-wise heritability mapping of nearly 300,000 cortical thickness QTs. In [31], Ge et al. proposed a “moment matching method for SNP-based heritability estimation” (MMHE) and further extended the GWAS based heritabilty analysis to handle multidimensional traits (e.g., shape). It was successfully applied to the heritability estimation of the shape of a set of brain structures. In a subsequent study [32], MMHE was used to complete a phenome-wide heritability analysis of the UK Biobank [3].
A related method - linkage disequilibrium score regression (LDSC) [33] - was also developed to estimate heritability due to all SNPs. Remarkably, it does not require individual genotypes at all, but only uses the summary statistics from a genome-wide association study. The approach exploits a feature of the genome called linkage disequilibrium (LD) - the fact that statistical correlations are found in a series of adjacent SNPs. Let N be the sample size, M be the number of all SNPs, and h2 be the heritability of a phenotype due to all SNPs. Given a SNP j, its LD Score lj is defined as , where is the LD between SNPs j and k measured by the squared correlation coefficient. The LD Score lj measures the amount of genetic variation tagged by j. Bulik-Sullivan et al. [33] noted that under a polygenic model, the expected χ2 association statistics for SNP j are
where h2/M is the average heritability explained per SNP, and a measures the contribution of confounding biases, such as cryptic relatedness and population stratification. Based on this, if one regresses the χ2 statistics from GWAS against LD Score (i.e., LD score regression or LDSC), the resulting intercept minus one can serve as an estimator of the mean contribution of confounding bias to the inflated test statistics. Consequently, LDSC can also be used to produce SNP-based heritability estimates for any phenotypes including voxel-based or region-based imaging QTs, partition this heritability into separate categories (based on regions of the genome, such as specific chromosomes, or types of genetic variant), and to calculate genetic correlations between separate phenotypes.
When applied to imaging GWAS (explained below), the LDSC method has revealed patterns of genetic correlations across brain regions, leading to the notion that the brain may be partitioned into genetic modules or sets of regions with overlapping genetic determinants. Classical multivariate twin models had also reported evidence for such genetic clusters [34]. In [34], a multivariate model in 1,038 twins identified a common genetic factor that accounted for almost all the heritability of intracranial volume (0.88) and a substantial proportion of the heritability of all subcortical structures, particularly those of the thalamus (0.71 out of 0.88), pallidum (0.52 out of 0.75) and putamen (0.43 out of 0.89). LDSC has also been used to reveal overlap between genetic loci associated with brain structure and with schizophrenia, based on the summary statistics from various published GWAS [35]. Similar multivariate genetic models show that genetic influences on longitudinal growth or loss rates over time significantly overlap with genetic loci associated with baseline volumes for many structures. This may be an important observation in the quest to identify loci that influence rates of brain development and degeneration [36].
III. Imaging Genomics Associations: Fundamentals
Given an imaging phenotype, heritability analysis estimates how much of its variance is explained by the entire genome or all the SNPs on one or more chromosomes. In order to locate specific genetic variants that contribute to the phenotypic change, genetic association analysis needs to be performed. Thus, a major research theme in brain imaging genomics is how to effectively identify interesting imaging genomics associations, which is the topic to be covered in Sections III-VI. In some cases, heritability analysis can be used as a prescreening step to identify imaging QTs with moderate to high heritability, and subsequent genetic association studies can then be applied only to those heritable QTs (e.g., in [38]).
A major challenge in brain imaging genomics is that both imaging and genomics data are high dimensional. The ability to test over a million SNPs in the genome for associations with hundreds, thousands, or even more imaging traits in the brain induces a huge burden for multiple comparison correction. While failure to properly correct for multiple comparisons leads to a high risk for false discoveries, excessive corrections greatly reduce the power to detect true signals. Thus, multiple comparisons and detection power are two important topics relevant to most association studies reviewed in this paper.
In [39], Lindquist et al. provided an excellent review of a few major statistical approaches to address the problem of multiple comparisons, using neuroimaging studies as an example. The goal is to choose an appropriate threshold to balance between sensitivity (true positive rate) and specificity (true negative rate). Two metrics to quantify the likelihood of obtaining false positives are often used: 1) the family-wise error rate (FWER, the probability of obtaining at least one false positive in a family of tests), and 2) the false discovery rate (FDR, the proportion of false positives among all rejected tests). Bonferroni correction [40], aiming to control the FWER at a user-specified level, is the most common approach for multiple comparison correction. Despite being simple to use, it is very conservative and often reduces detection power. Random field theory (RFT) [41] - a popular approach for controlling the FWER in fMRI studies - takes into consideration the spatial correlation in the images and appears to be less conservative than Bonferroni method. Permutation methods are nonparametric methods that do not make assumptions on the data distribution for controlling the FWER. While they offer substantial improvements in detection power, especially in small sample sizes, they are very computationally expensive; some recent innovations have been used to accelerate permutation testing [42]. The FDR [43] is a newer approach that controls for false positives. It is less stringent than FWER methods and thus has an increased detection power.
While some imaging genomics studies reviewed here employ the above methods for multiple comparison correction, others develop their own strategies for handling the issues of multiple comparisons and detection power. For example, in [44], Hua et al. proposed two strategies to handle multiple comparison and increase the power of detecting imaging genomics associations. On one hand, they treated the imaging QTs of the entire brain as a single multivariate response and used distance covariance to capture the association between all the QTs and each SNP, which greatly reduced the number of statistical tests. On the other hand, they proposed a new FDR-based algorithm that demonstrated an increased detection power compared with two existing FDR methods.
Another critical challenge in brain imaging genomics is the relatively small effect size of SNPs on the brain. Most SNPs account for under 1% of the variance in a brain QT, when considered individually. Thus, the studies reviewed here all needed to address this challenge, and many of these studies have aimed to develop effective strategies with increased detection power to capture interesting imaging genomics associations. For example, one strategy is to reduce the effective number of tests to alleviate the burden of multiple comparison correction; see targeted SNP/QT studies discussed in Section III-A. The second strategy is to measure combined or collective effects of multiple markers together to increase the detection power; see studies discussed in Sections III-B, III-C, III-D, and III-E. The third strategy is to increase the sample size to enable the discovery of individual SNPs with small effect sizes; see studies discussed in Section IV. The fourth strategy is to apply a single multivariate model involving all the studied SNPs and QTs without needing to adjust for multiple testing; see studies discussed in Sections V and VI.
Before covering more advanced statistical and machine learning strategies for mining brain imaging genomic associations in Sections IV-VI, we first review a few fundamental methods in this section. We start from the simplest single-SNP-single-QT approaches, which search for pairwise imaging genomic associations on a SNP-by-SNP and QT-by-QT basis. Next, we discuss strategies using polygenic risk scores, which examine the aggregated effect from a set of disease related SNPs on an imaging QT. Then, we go over basic multi-SNP or multi-trait methods, which aim to learn imaging genomics associations involving either multiple SNPs or multiple traits. After that, we review enrichment analysis methods, which intend to discover high level imaging genomics associations related to biological entities such as biological pathways, functional interaction networks and/or brain circuits. Finally, we briefly discuss interaction methods, which focus on the exploration of epistatic effects instead of main effects.
A. Single-SNP-single-QT methods
Given a set of genetic markers such as SNPs and a set of imaging quantitative traits (QTs), the simplest and most commonly used analytical strategy is to perform pairwise analysis between each SNP and each QT at the individual marker level. A SNP takes a value of 0, 1, or 2 (i.e., the genotype value), indicating the number of minor alleles at the corresponding chromosome location. An imaging QT typically takes a continuous value. A simple linear regression model can be used to examine the additive effect of the SNP on the imaging QT. An alternative strategy is to use Analysis of Variance (ANOVA), which is similar to linear regression but ignores the ordering of the genotype values. It examines the trait mean differences among three genotype groups. Both strategies can be used together with hypothesis testing to obtain a p-value. If multiple pairwise SNP-QT associations are examined, multiple comparison correction needs to be performed to identify significant findings.
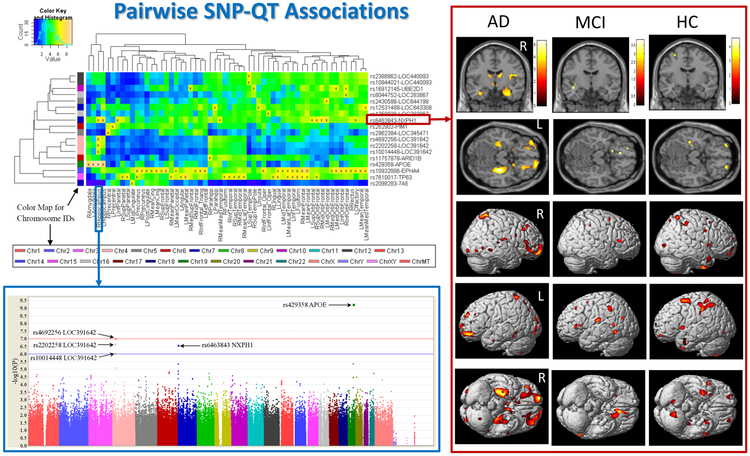
Figure 2 shows three major types of SNP-QT analyses. 1) Targeted QT Analyses: The first type is to perform genetic analysis on one or more targeted imaging QTs. For example, in Figure 2, the bottom left panel (i.e., blue box) shows the Manhattan plot for the GWAS results of gray matter density of the right hippocampus. 2) Targeted SNP Analyses: The second type is to examine the genetic effects of one or more SNPs on all the imaging QTs across the brain. For example, in Figure 2, the right panel (i.e., red box) shows the voxel-based morphometry (VBM) result of mapping the genetic effect of rs6463843 (in the flanking region of the NXPH1 gene) to the brain. 3) Brain-Wide Genome-Wide (BWGW) Analyses: The third type is to perform massive univariate analyses for all the possible SNP-QT pairs across the entire brain and the entire genome. For example, in Figure 2, the top left panel summarizes all the pairwise SNP-QT association findings (only top findings are shown), where blocks labelled with “x” reach the level of p < 10−6. Note that, in [37], p < 10−6 was explored as a somewhat less stringent threshold to identify imaging genomics associations showing a trend towards significance as well as examine clustering patterns of the corresponding SNP and imaging QT findings. Below, we discuss a few example studies in each of these three categories.
Fig. 2.
Example pairwise SNP-QT Associations [37]. (1) The top left panel summarizes all the pairwise SNP-QT association findings, where blocks labelled with “x” reach the level of p < 10−6. (2) The bottom left panel (i.e., blue box) shows the Manhattan plot for the GWAS results of gray matter density of the right hippocampus. (3) The right panel (i.e., red box) shows the voxel-based morphometry result of mapping the genetic effect of rs6463843 (in the flanking region of the NXPH1 gene) to the brain. [Images are reproduced here with permission from Elsevier [37].]
In one targeted QT study [45], Stein et al. performed a genome-wide association study of the bilateral temporal lobe volume as the QT. A linear regression analysis was conducted at each SNP to examine its genetic effect on the QT while covaried for age and sex. In another targeted QT study [46], Scelsi et al. computed a novel disease progression score (DPS) from multimodal neuroimaging data, and performed GWAS on it. The DPS was generated by the GRACE algorithm [47] from longitudinal cortical amyloid burden and bilateral hippocampal volume, providing an estimate of how advanced an individual’s disease progression is in comparison with the cohort average. A linear regression analysis was conducted at each SNP to examine its genetic effect on the DPS while covaried for sex, age at first amyloid scan, education, two principal components of population structure, and number of APOE e4 alleles.
In one targeted SNP study [48], Risacher et al. examined the effect of the APOE e4 SNP rs429358 on several MRI and PET imaging QTs. Specifically, the effects of diagnosis, APOE e4 carrier status, and their interaction on regional amyloid deposition, regional glucose metabolism, hippocampal volume and entorhinal cortex thickness were examined using a two-way analysis of covariance (ANCOVA) and covaried for age and gender. In another targeted SNP study [49], Ho et al. examined the effect of a commonly carried allele of the obesity-related FTO gene on regional brain volume measures captured by MRI. Specifically, the general linear model was used to evaluate the relation of the imaging QT at each voxel to the SNP rs3751812 controlling for age and sex.
In one BWGW study [37], Shen et al. used a brain-wide genome-wide approach to investigate genetic effects on imaging QTs. The studied QTs included 56 volumetric and cortical thickness measures and 86 local gray matter density values for regions of interests (ROIs) across the entire brain. These imaging QTs were pre-adjusted to remove the effects of age, gender, education, handedness and incracranial volume (ICV). A linear regression analysis was conducted at each SNP to examine its genetic effect on each QT. In another BWGW study [45], Stein et al. performed the first voxel-based GWAS analysis. Using tensor-based morphometry to define imaging QTs, they examined genome-wide association at each voxel. A linear regression analysis was conducted at each SNP-by-voxel pair to examine the SNP genetic effect on each voxelwise QT while covaried for age and sex.
Although a voxelwise GWAS enables the examination of imaging genomics associations at the finest resolution, it is facing a major computational challenge given the huge number of univariate SNP-QT associations to test. To overcome this challenge, in [50], Huang et al. proposed a Fast Voxelwise GWAS (FVGWAS) framework to facilitate efficient BWGW study at the voxel level. FVGWAS employs three components to achieve this goal. The first component is a heteroscedastic linear model, which allows a very flexible covariance structure suitable for voxelwise imaging QTs. The second component is a global sure independence screening (GSIS) procedure [51], which can greatly reduce the search space size from NsNv to ~ N0Nv for N0 ⪡ Ns. Here Ns is the number of SNPs, and Nv is the number of voxels. The third component is a detection procedure based on wild bootstrap methods, which is computationally cheap due to no involvement of repeated analyses of simulated datasets. As a result, for standard linear association, the computational complexity of FVGWAS is O((Ns + Nv)n2), outperforming O(nNvNs) for standard voxelwise GWAS [45], where n is the number of subjects. FVGWAS is available at https://www.nitrc.org/projects/fvgwas/.
One issue related to imaging genomics is that most GWAS studies (e.g., ADNI) are based on case-control design, and the data are typically a biased sample of the target population. Directly correlating imaging QTs (as secondary traits) with genotype may lead to biased inference generating misleading results. In [52], Kim et al. compared standard linear regression model and disease status adjusted linear model with two models adjusting for biased case-control sample (i.e., inverse probability weighted regression [53], retrospective likelihood [54]) on the analysis of ADNI data. In [55], Zhu et al. completed a similar systematic evaluation of the biased sampling issue using both simulation and ADNI data. They compared standard linear regression model and disease status adjusted linear model with two models adjusting for biased case-control sample (i.e., retrospective likelihood [54], reparameterization of conditional model in [56]). Although the standard linear analysis was found to be generally valid on the ADNI data in [52], simulation studies in [55] showed that linear regression models without adjusting for biased sampling demonstrated severely inflated Type I error rates in some cases. In general, caution should be taken while analyzing imaging QT data as secondary phenotypes in case-control studies.
Table I summarizes the studies discussed above, where pairwise SNP-QT associations are examined on a SNP-by-SNP and QT-by-QT basis. These single-SNP-single-QT methods are simple and straightforward. The findings discovered by these methods are easy to interpret, since each resulting association involves only one SNP and one QT. Given the high dimensionality of both imaging and genomic data, studies examining a massive number of SNP-QT associations may face major computational and statistical challenges. In addition, multivariate associations involving multiple SNPs or multiple QTs won’t be able to be identified by these methods.
TABLE I.
Example studies using single-SNP-single-QT methods, where pairwise SNP-QT associations are examined on a SNP-by-SNP and QT-by-QT basis.
| Ref | Notes |
|---|---|
| [45] | GWAS, targeted QT, linear regression |
| [46] | GWAS, targeted QT, linear regression |
| [48] | Targeted SNP, targeted QTs, two-way ANCOVA |
| [49] | Targeted SNP, voxelwise QTs across brain, general linear model |
| [37] | GWAS, ROI-based QTs across brain, linear regression |
| [57] | GWAS, voxelwise QTs across brain, linear regression |
| [50] | Fast voxelwise GWAS (FVGWAS): heteroscedastic linear model, global sure independence screening, wild bootstrap |
| [52] | Regression models for analyzing secondary phenotypes |
| [55] | Regression models for analyzing secondary phenotypes |
B. Polygenic risk scores
One approach to identify imaging genomics associations involving multiple SNPs is to use a polygenic risk score (PRS) [58]. A PRS captures the aggregate genetic effect from a set of trait-related SNPs that may not achieve significance at the individual level but collectively may explain a substantial portion of the trait variance. It is often calculated as the sum of their genotype values weighted by their effect sizes on a base phenotype (e.g., case control status). In [59], Dima et al. reviewed the usefulness and applications of PRSs in imaging genetics. In [60], Chasioti et al. reviewed recent progress in PRS in AD and other complex disorders. The cohorts with both brain imaging and genetics data are often much smaller than those designed for large GWAS. A PRS can typically be calculated based on using the SNP-based effect sizes from large GWAS on a base diagnostic phenotype to make full use of the power of the large sample. After that, it can be applied to small samples with imaging data to examine its association with interesting imaging QTs.
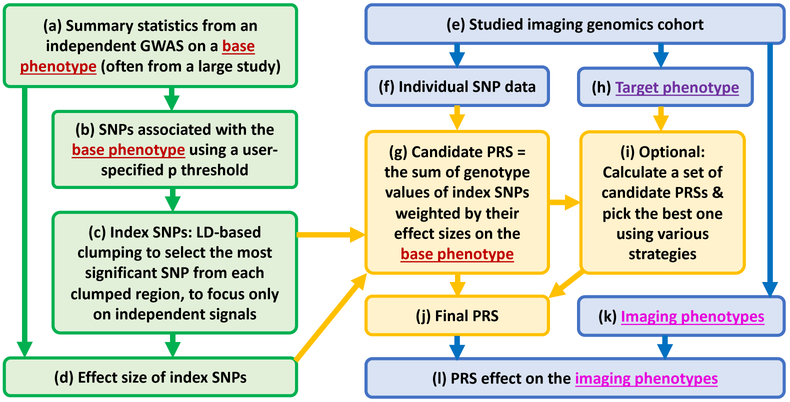
Figure 3 shows an example flowchart to calculate a polygenic risk score (PRS) and apply it to brain imaging genomics studies. First, using the summary statistics from an independent GWAS (often a large-scale landmark study) on a base phenotype (Figure 3(a)), a set of SNPs associated with the base phenotype can be obtained using a user-specified p threshold (Figure 3(b)). Second, linkage disequilibrium (LD) clumping is often performed to select the most significant SNP from each clumped region to form a set of independent loci named as index SNPs (Figure 3(c)). Third, using the effect sizes of index SNPs from the summary statistics data (Figure 3(d)) and individual SNP data (Figure 3(f)) from the studied imaging genomics cohort (Figure 3(e)), one can calculate a PRS, which is the sum of genotype values of index SNPs weighted by their effect sizes on the base phenotype (Figure 3(g)). While this PRS can directly be used, some studies (e.g., [61], [62]) perform an optional step (Figure 3(i)) to calculate a set of candidate PRSs by exploring a few p thresholds and then pick the PRS best predicting the target phenotype (Figure 3(h)) as the final PRS using several strategies described below. Finally, the effect of the resulting PRS on interesting imaging phenotypes can be examined (Figure 3(l)).
Fig. 3.
Example flowchart to calculate a polygenic risk score (PRS) and apply it to brain imaging genomics studies. Step (i) is optional, where various strategies can be used to calculate a set of candidate PRSs (e.g., by exploring a few p thresholds [61], [62]) and pick the PRS best associated with the target phenotype (see (h)) as the final PRS (see (j)). See main text for more details.
In [46], Scelsi et al. performed a PRS study on a novel image-based disease progression score (DPS) discussed in Section III-A, using a workflow similar to that shown in Figure 3. They obtained index SNPs and their effect sizes using the large AD GWAS conducted by the International Genomics of Alzheimer’s Project (IGAP) [63]. Instead of computing one PRS, they calculated 15 PRSs by exploring 15 p thresholds in the range of 0.95 – 10−5. They identified only one PRS with p threshold of 10−4, which is significantly associated with the image-based DPS.
In [61], Mormino et al. performed a PRS study on MRI-derived hippocampal volume, using the workflow shown in Figure 3. They used the IGAP GWAS summary statistics to obtain the index SNPs and their effect sizes. They explored a dozen p thresholds ranging from 5 × 10−8 to 0.05 to generate multiple PRSs. The final PRS was selected as the one best differentiating clinically normal (CN) and AD participants in ADNI-1 sample. This PRS was found to be associated with hippocampal volume for ADNI-1 sample without dementia.
In [62], Sabuncu et al. performed a PRS study on cortical thickness measures. They used the summary statistics from another large-scale GWAS in AD [64] to obtain the index SNPs and their effect sizes. They further screened these SNPs using five different thresholds based on the genetic association results on a subset of ADNI data containing only CN and AD participants to create five different PRSs. The PRS with the highest correlation with Mini-Mental State Examination (MMSE) score and Clinical Dementia Rating Sum of Box (CDR-SB) score and strongest association with AD diagnosis was used in the subsequent imaging genomic analyses on a nonoverlaping ADNI sample containing only CN subjects. This PRS was identified to be associated with AD-specific cortical thickness.
In [65], Tan et al. studied a similar problem on developing a polygenic hazard score (PHS) instead of PRS. They used the IGAP GWAS summary statistics to identify a set of SNPs with p < 10−5. They evaluated these SNPs using the Alzheimer’s Disease Genetics Consortium (ADGC) Phase 1 data. Using a stepwise Cox proportional hazards model, they identified 31 top SNPs and formed a PHS [66]. This PHS was applied to the ADNI data and found to be associated with ADNI imaging phenotypes such as regional amyloid burden using amyloid PET and regional volume loss using MRI.
In [67], Euesden et al. presented PRSice, a software tool for generating PRS. It takes GWAS summary statistics on a base phenotype and genotype data on a target phenotype, and returns a PRS for each individual. It calculates PRS at multiple p thresholds and can select the most predictive one. The software is available at http://prsice.info/.
Table II summarizes the studies described above. A PRS captures the aggregate effect from an ensemble of SNPs related to a base phenotype. In disease-relevant brain imaging genomics studies, examining the effect of a PRS instead of each individual SNP on imaging QTs has great potential to increase statistical power as well as gain meaningful insights into the biological mechanism from genetic determinants to brain endophenotypes, and to disease status. However, there is also some discussion in recent literature regarding potential limitations in PRS-based analyses. For example, bias towards the reference population was observed in [68]. Specifically, the generalizability of a PRS across different populations appeared to be limited. Greater diversity should be prioritized to realize the full potential of PRS. In addition, statistical power differences across diseases and cohorts were also observed in [69]. Several factors could limit the power of a PRS. One factor could be the cohort difference between the base and target GWAS. Another factor could be limited sample sizes of available data for certain diseases, in particular for heterogeneous disorders that can be stratified into different subtypes with even smaller sample size in each group.
TABLE II.
Example studies using polygenic risk scores (PRSs) for brain imaging genomics. A PRS summarizes the aggregate effect from an ensemble of SNPs related to a base phenotype. The effect of the PRS is examined on interesting imaging QTs.
| Ref | Notes |
|---|---|
| [58] | PRS: Power and predictive accuracy |
| [59] | PRS: Usefulness and applications in imaging genetics |
| [46] | Standard PRS workflow, image-based DPS |
| [61] | Standard PRS workflow, hippocampal volume |
| [62] | Standard PRS workflow, cortical thickness |
| [65] | PHS instead of PRS, amyloid and MR imaging QTs |
| [67] | PRSice: PRS software, http://prsice.info/ |
C. Multi-SNP methods
Single-SNP analysis is often limited by the modest SNP effect sizes. Multi-SNP methods examine joint effect from a set of SNPs on a phenotypic trait. It has enormous potential to improve the power of genetic association studies and identify polygenic or multi-locus mechanisms for complex diseases. There are several categories of multi-SNP analysis strategies. The first category focuses on the joint analysis of a set of targeted SNPs based on the prior knowledge. For example, one approach is to analyze a polygenic risk score (PRS) involving top SNPs from an independent GWAS, as previously described in Section III-B. Another approach is to analyze a set of disease-related SNPs from the literature (e.g., [70]). The second category is to perform GWAS at the gene level instead of the SNP level, where the aggregate effect of all the SNPs within each gene on the target phenotype is examined to increase statistical power (e.g., [71], [72], [73]). The third category employs data-driven strategies to automatically identify relevant SNPs from either the entire genome or a set of candidate SNPs [74]. Below, we discuss a few example studies using these strategies. Section VI will cover additional studies using the third category of strategies.
In [70], Apostolova et al. examined the top 20 AD SNPs and their joint effect with brain amyloidosis in an ADNI sample including 322 CN, 496 mild cognitive impairment (MCI), and 159 AD participants. Stepwise multivariate linear regression was used to examine the association between joint exposure of 20 AD risk alleles and mean amyloid burden from florbetapir PET scans while controlling for age, sex and APOE e4 status. Voxelwise 3D stepwise regression was also used to map the genetic effect onto the brain. The study identified an association between several AD SNPs and brain amyloidosis.
In [71], Hibar et al. extended the SNP-based voxelwise GWAS (vGWAS) method [45] to a gene-based voxelwise GWAS (vGeneWAS) method. It was demonstrated on a brain-wide genome-wide study using the same ADNI sample. The joint effect of SNPs within each gene on each voxel was examined using a multiple partial-F test while controlling for age and sex. To address the SNP colinearity issue, a principal component analysis (PCA) was performed on the SNPs within each gene. The “eigenSNPs” capturing the first 95% data variance were then used in the multiple partial-F test. This method can be thought of as a variant of principal component regression (PCReg) [75].
In [72], Ge et al. further extended vGWAS and vGeneWAS to a new SNP-based or gene-based voxelwise GWAS framework with increased power, and demonstrated it on a BWGW study using the same ADNI sample. This method includes three new methodological contributions. The first one is a fast implementation of voxelwise and clusterwise inferences using random field theory to improve statistical power via embracing the spatial correlation in the images. The second one is a multi-locus model based on least square kernel machines (LSKMs) to evaluate the joint effect of multiple SNPs within each gene on each voxelwise QT. The multilocus method employs a semi-parametric regression model [76], where the covariate effects on the QT are modeled linearly and parametrically and the SNP effects on the QT are modelled non-parametrically using the LSKM approach. This method allows for revealing nonlinear effects introduced by the interaction among SNPs. The third contribution is a a fast permutation procedure that uses parametric tail approximation to provide accurate p estimations in an efficient manner.
In [73], Xu et al. proposed a new method called imagingwide association study (IWAS), which was inspired by transcriptome-wide association study (TWAS) [77]. It aims to integrate imaging QTs with GWAS to improve statistical power and biological interpretation. It is a gene-based approach and has two steps involving two sets of GWAS data respectively: 1) the reference GWAS data containing imaging QTs, and 2) the main GWAS data containing target phenotype such as disease status. In the first step, which analyzes the reference GWAS data, for each gene, IWAS estimates a set of SNP weights via regressing an imaging QT on all the SNPs. In other words, it builds a prediction model for the genetic component of the imaging QT. In the second step, which analyzes the main GWAS data, IWAS uses the weights learned in the first step to calculate a weighted genotype score for each gene, and examines its association with the target phenotype. Using strategies described in [78], [79], IWAS can also be applied to the main GWAS data containing only summary statistics. In short, IWAS uses an imaging QT to construct weights for a weighted gene-based GWAS test. The gene-based method reduces the number of tests and boosts statistical power. Also, computing gene scores via extracting genetically controlled components of an imaging QT provides potential opportunities to help interpret GWAS findings.
The above studies developed or employed methods to examine the association between one SNP set and one QT. In [74], Lu et al. proposed a method for examining joint association mapping between a large number (e.g., 105) of SNP sets and a QT. Here the SNP sets can be defined by LD blocks or genes so that multiple SNPs can be combined to increase detection power. A linear mixed-effects model was proposed to simultaneously regress a QT on a large number of SNP sets. This model has the potential to further increase detection power via 1) incorporating the correlation among SNP sets, and 2) greatly reducing the burden of multiple comparison correction. A Bayesian latent variable selection procedure was proposed to select significant latent variables. An efficient Markov Chain Monte Carlo (MCMC) algorithm was proposed to reduce the complexity of major computationally intensive steps in MCMC iterations. The empirical studies was performed on the ADNI sample to identify associations between a few imaging QTs and a number of SNP sets defined by LD blocks and genes, and yielded promising results.
Table III summarizes the studies described above, which are designed to identify multi-SNP-single-QT associations. Compared with single-SNP methods, examining joint effect of a SNP set on an imaging QT can potentially increase statistical power and identify multi-locus or polygenic mechanisms for complex brain phenotype. In addition, the SNP sets are often defined by LD blocks, genes, pathways, known trait-associated variants, or other prior knowledge, which may offer meaningful biological insights for interpreting multi-SNP discoveries.
TABLE III.
Example studies using multi-SNP methods, where multi-SNP-single-QT associations are examined.
| Ref | Notes |
|---|---|
| [70] | Joint effect of target SNPs on imaging QTs, stepwise multivariable linear regression |
| [71] | Multivariate gene-based voxelwise GWAS, PCA and multiple partial F test (a variant of PCReg) |
| [72] | Voxelwise GWAS with increased power, random field theory, semi-parametric regression model with least square kernel machines, fast permutation procedure |
| [73] | Imaging wide association study, weighted gene-based GWAS test, weights capturing genetic component of an imaging QT |
| [74] | Joint association between multiple SNP sets and an imaging QT, linear mixed-effects model, Bayesian latent variable selection |
D. Multi-trait methods
Similar to multi-SNP methods, multi-trait methods provide an alternative means to increase detection power, compared with single-SNP-single-trait analyses. There are several classical strategies to perform multivariate trait analysis, as nicely summarized in [80]. One approach is to first conduct univariate analysis on each trait and then combine their results [81]. For example, a typical strategy is to select the SNP with the minimum p-value with multiple comparison correction. The second approach is to perform dimensionality reduction on the traits and then apply univariate analysis on a small number of extracted trait features. These features could simply be the average trait or first a few components from PCA [82] or canonical correlation analysis (CCA). The third approach is to employ classical multivariate analysis methods such as multivariate analysis of variance (MANOVA) [83] and generalized least squares (GLS) [84], [85]. Below, we discuss a few recently proposed methods for performing multi-trait analyses in brain imaging genomics.
In [80], Zhang et al. proposed a set of new testing methods for identifying single-SNP-multi-QT associations under the framework of generalized estimation equations (GEEs) [86]. They tried to address the challenge that, in multi-QT analyses, there is a lack of a uniformly powerful test. For example, given a QT set, if very few QTs are associated with the target SNP, selecting the QT with minimum p from a set of univariate SNP-QT analyses could be more powerful. On the other hand, if most of the QTs are associated with the SNP, doing a univariate analysis between the average QT and the SNP could be more powerful. With this observation, under the GEE framework, they proposed the SPU(γ) tests (i.e., the sum of powered score (U) tests), for a series of values of γ = 1,2,…, ∞, where a larger γ tends to put higher weights on QTs with stronger associations with the SNP. As a result, SPU(∞) corresponds to the minimum p strategy and SPU(1) corresponds to the average QT strategy. Based on this, they also proposed adaptive SPU (aSPU) test. The aSPU test statistic is defined as the minimum p among all the SPU tests TaSPU = minγ∈ΓPSPU(γ). In other words, aSPU was designed to be an adaptive method that automatically performs data-driven weights adjustment and selects the most powerful weighted test from all these candidates. The empirical study was performed on an ADNI sample to pairwisely associate 20 candidate SNPs to a few imaging QT sets, and the proposed aSPU method outperformed various competing methods.
In [87], Kim et al. further extended the aSPU test to a new test that can identify associations involving multiple SNPs. While aSPU searches for single-SNP-multi-QT associations, the new test is designed to identify multi-SNP-multi-QT associations. Similarly, under the GEE framework, they proposed the SPU(γ1, γ2) tests (i.e., an extension of SPU(γ) to accommodate both multiple QTs and multiple SNPs), for a series of values of γ1 = 1, 2,…, ∞ and γ2 = 1,2,…, ∞. Here a larger γ1 tends to put higher weights on QTs with stronger associations with the SNPs, and γ2 tends to put higher weights on SNPs with stronger associations with the QTs. Based on this, they also proposed the adaptive SPU test for a SNP set (aSPUset). The aSPUset test statistic is defined as the minimum p among all the SPU tests TaSPUset = minγ1∈Γ2,γ2∈Γ2PSPU(γ1, γ2). Clearly, aSPUset is an extension of aSPU to identify multi-SNP-multi-QT associations using the same adaptive method that automatically performs data-driven weights adjustment and selects the most powerful weighted test from all these candidates at both the SNP and trait levels. It has the benefit of measuring the collective effects of multiple SNPs for an increased detection power. The empirical study was performed on an ADNI sample to perform gene-based SNP-set GWAS of 12 imaging QTs within human brain default mode network (DMN). The aSPUset method outperformed competing methods including aSPU, and identified a new gene AMOTL1 not detected by other SNP-based methods.
In [88], Kim et al. proposed a similar adaptive SPU test for single-SNP-multi-QT associations using a proportional odds model (POM). Most methods for mining single-SNP-multi-QT associations associations treated QTs as response and the SNP as predictor. In this approach, they treated the SNP as an ordinal response and multiple QTs as predictors, and developed a similar adaptive SPU (aSPU) test under a POM framework instead of the GEE framework used in [80]. Compared with the GEE-based aSPU, the POM-based aSPU has two advantages: 1) it is easier to handle mixed types of traits (e.g., binary and quantitative), and 2) it can handle high dimensional setting (e.g., QT number > sample size). The empirical studies on ADNI data were performed to identify SNP-based genetic associations with two imaging QT sets, one containing 12 MRI-based QTs related to DMN, and the other containing functional brain connectivity network data among 18 ROIs. Compared with competing methods such as the GEE-based aSPU, the POM-based aSPU performed similarly in both studies that have a low dimensional setting.
In [44], Hua et al. proposed a brain imaging GWAS method on identifying single-SNP-multi-QT associations. The method includes a few components to improve detection power. First, they pooled voxel-level measures into 119 ROI-level QTs for reducing both dimensionality and voxel-level noises. Second, they treated the imaging QTs of the entire brain as a single multivariate response and used distance covariance to capture the association between all the QTs and each SNP. This approach could reduce the number of statistical tests and simultaneously embrace ROI interaction effects. Third, they proposed a new false discovery rate (FDR) based algorithm for multiple testing adjustment, named as local FDR modeling. Empirical study was performed on an ADNI sample to identify SNPs associated with 119 QTs from the entire brain.
In [89], Huang et al. proposed a new functional GWAS (FGWAS) method for efficiently performing whole genome analysis of high dimensional imaging QTs. First, instead of doing a univariate analysis to each SNP and each QT, they treated all the imaging QTs as a single functional response measured in the brain space. They proposed a multivariate varying coefficient model (MVCM, a function-on-scale model) to fit all the imaging QTs (as a functional phenotype) with each SNP via embracing key features of a functional phenotype including spatial smoothness, spatial correlation and low dimensional representation. Second, they introduced a global sure independence screening (GSIS) procedure based on global test statistics [51]. This approach selects NG0 important SNPs, and greatly reduces the genomic search space size from NG to ~ NG0 for NG0 ⪡ NG. Third, they developed an efficient divide-and-conquer algorithm for performing multiple comparison and achieved substantial performance gain on computational time and memory. It can handle functional phenotypes such as 1-D curves, 2-D surfaces and 3-D images. The empirical study on an ADNI sample was performed to identify genetic associations with functional QTs on hippocampal surfaces, and yielded promising results.
Table IV summarizes the studies discussed above, which are designed to identify multi-QT associations with one or more SNPs. Example strategies for performing multi-QT analyses in recent brain imaging genomics studies include adaptive sum of powered score test to identify the most powerful weighted QT score, distance covariance between QT set and each sNP to reduce the number of tests and incorporate interaction effects among QTs, and modeling all the QTs as a single functional response to embrace spatial smoothness and correlation as well as low-rank representation. Compared with single-trait methods, multi-QT genetic association analysis has the potential to not only improve detection power but also reveal complex imaging genomics associations involving multiple contributing QTs.
TABLE IV.
Example studies using multi-trait methods, where single-SNP-multi-QT or multi-SNP-multi-QT associations are examined.
| Ref | Notes |
|---|---|
| [80] | Sum of powered score tests (SPU(γ)), adaptive SPU test for multi-trait-single-SNP associations (aSPU), selection of most powerful weighted test via adjusting weights to the studied data |
| [87] | Sum of powered score tests (SPU(γ1, γ2)), adaptive SPU test for multi-trait-multi-SNP associations (aSPUset), selection of most powerful weighted test via adjusting weights to the studied data |
| [88] | Adaptive SPU test for multi-trait-single-SNP associations (aSPU) under a proportional odds model (POM) instead of the generalized estimation equations (GEE) framework used in [80]. |
| [44] | Brain-wide ROI QTs as a multivariate response, distance covariance between QT set and each SNP, local FDR modeling |
| [89] | Functional GWAS (FGWAS), multivariate varying coefficient model (MVCM), global sure independence screening (GSIS), GWAS of functional QTs including curves, surfaces and volumes |
E. Pathway and network enrichment methods
Pathway and network analyses are routinely used in genomic studies [91]. Analyzing genomic data through sets defined by biological pathways and functional interaction networks offers enormous potential to increase statistical power and translate genomic findings into meaningful biological hypotheses. For example, if we define a SNP set using a pathway of interest, we can employ the multi-SNP methods reviewed in Section III-C to examine the joint effect of this pathway-based SNP-set on any trait. Most of these multi-SNP methods use a single multivariate learning model to relate multiple sNPs to a trait. Here we review another category of popular methods called enrichment analysis, which are widely used in pathway and network analysis of GWAS findings. Different from the multi-SNP methods discussed earlier, an enrichment analysis typically involves two steps: 1) conduct SNP-based or gene-based GWAS on a trait, and 2) perform pathway or network enrichment analysis of the GWAS findings.
One type of the enrichment analysis methods is threshold-based (e.g., hypergeometric test or Fisher’s exact test), and is used to identify pathways or sub-networks that are over-represented by the “significant” GWAS hits. Another type of the enrichment analysis methods is rank-based (e.g., GSEA-SNP [92]), and uses a Kolmogorov-Smirnov-like running sum to quantify the degree to which a pathway- or network-derived gene set is over-represented at the top of the gene list ranked by the GWAS results. These analyses are of high significance. They can identify pathways and networks related to imaging QTs or disease outcomes, which can potentially serve as the foundation for the development of diagnostic, therapeutic and preventative approaches for complex brain disorders. Below we review a few example studies using pathway and network enrichment methods.
In [93], Ramanan et al. performed a genome-wide pathway analysis of memory impairment on an ADNI sample. A composite memory measure was computed from the ADNI neuropsychological test battery and used as the QT in this study. GWAS was performed on this QT but did not yield any significant findings after multiple testing adjustment. A subsequent genome-wide pathway analysis was then conducted through applying GSA-SNP software [94] to the GWAS result, and identified 27 significantly enriched canonical pathways after FDR correction. The resulting pathways include memory-related signaling pathways and pathways related to cell adhesion, neuronal differentiation and outgrowth, or inflammation. These results indicate pathway enrichment analysis could not only offer increased detection power but also yield valuable biological information to help mechanistic understanding.
In [95], Yao et al. expanded the scope of enrichment analysis from GWAS to voxelwise brain imaging studies, and proposed a framework for mining regional imaging genetic associations via voxelwise enrichment analysis. The main idea was to treat an ROI as a set of voxels, similar to a pathway as a set of SNPs or genes in the genomic studies. A post hoc enrichment analysis was performed on the voxelwise statistics to identify ROIs over-represented by the top voxel findings. Fisher’s exact test for independence was used to calculate the enrichment p-value for each ROI. The existing ROI-based methods often collapse the voxel measures into a single value (e.g., the average), and may have limited power when only weak signals exist in part of an ROI. The enrichment-based strategy can properly address this challenge. The empirical study was performed on an ADNI sample to evaluate pairwise associations between 19 AD candidate SNPs and FDG-PET imaging QTs from 116 ROIs across the entire brain. The proposed enrichment method outperformed traditional ROI and voxelwise approaches and identified a number of new significant associations. Some of these new findings were supported by evidences from tissue-specific brain transcriptome data.
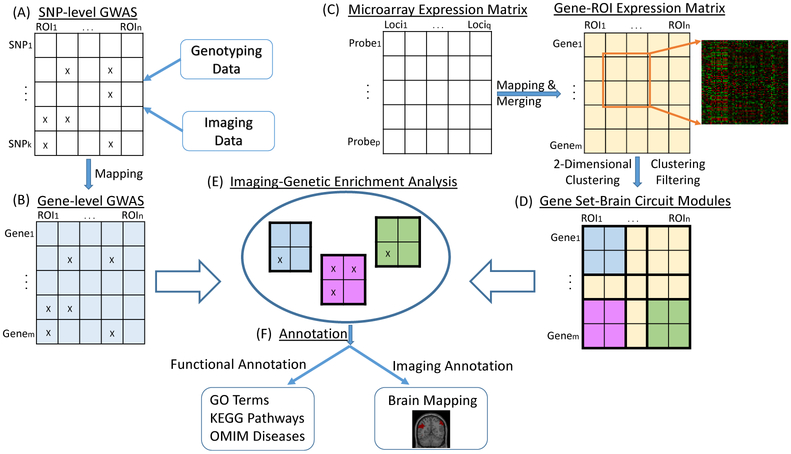
In [90], Yao et al. expanded the scope of enrichment analysis from GWAS to brain imaging genomics studies. They proposed a new two-dimensional enrichment analysis paradigm, called Imaging Genetic Enrichment Analysis (IGEA). IGEA jointly considers meaningful gene sets (GS) and brain circuits (BC), and aims to identify GS-BC pairs over-represented by SNP-QT findings from BWGW imaging genetic association study. To demonstrate the IGEA framework, they used the whole brain transcriptome data from the Allen Human Brain Atlas (AHBA) [96] to construct GS and BC modules so that, within each module, genes share similar expression patterns across ROIs and ROIs share similar expression patterns across genes. Figure 4 shows the IGEA workflow: (A) perform SNP-level GWAS of brain wide imaging QTs; (B) map SNP-level GWAS findings to gene-level summary statistics; (C) construct gene-ROI expression matrix from AHBA data; (D) construct GS-BC modules by performing 2D hierarchical clustering on gene-ROI expression matrix, and then filter out 2D clusters with an average correlation below a user-given threshold; (E) perform IGEA by mapping gene-based GWAS findings to the identified GS-BC modules; and (F) for each enriched GS-BC module, examine the GS using Gene Ontology (GO) terms [97], Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways [98], and Online Mendelian Inheritance in Man (OMIM) disease databases (https://omim.org/), and map the BC to the brain. The empirical study using the brain transcriptome data from AHBA and brain imaging genetics data from ADNI identified 25 significant high-level GS-BC modules, and showed the promise of IGEA on revealing high-level imaging genomic associations.
Fig. 4.
Imaging Genetic Enrichment Analysis (IGEA) framework proposed in [90]. [Images are reproduced here from a Springer open access article [90]].
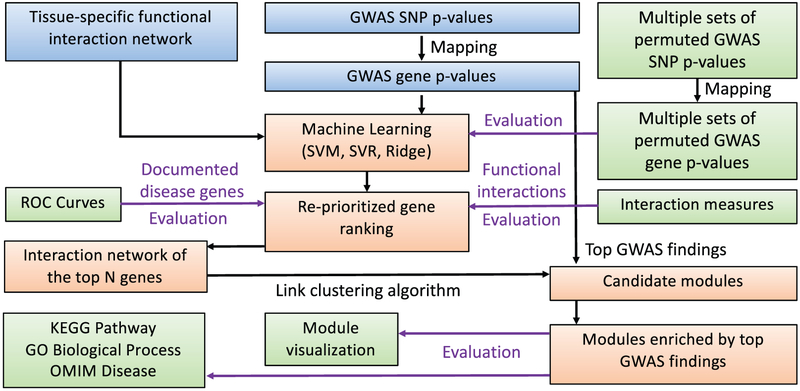
Similar to pathways, biological networks are also valuable prior knowledge that can assist GWAS to identify meaningful high-level genomic associations with a target phenotype. For example, network-based GWAS aims to identify phenotype-associated modules from biological networks [100]. This high-level association evaluates the collective effect of all the SNPs/genes within the network module on the phenotype, and thus provides not only increased detection power but also meaningful biological interpretation. In [99], Yao et al. proposed a module detection method for brain imaging genomics studies using tissue-specific biological networks. Figure 5 shows its workflow. First, GWAS is performed on a target imaging QT. Second, the GWAS results are re-prioritized using the NetWAS approach [101]. NetWAS couples machine learning methods (e.g., support vector machines, ridge regression) with a tissue-specific functional interaction network [102] (specific to the imaging QT in our case) to re-rank the GWAS results. Using network topology information, SNPs connected to more top findings tend to be pushed more towards the top of the re-ranked list. As a result, the top re-prioritized findings tend to be more densely connected than the top findings in original GWAS. Thus, the third step is to identify densely connected modules using only interactions among these top re-prioritized findings. Finally, enrichment analysis is applied to these modules to identify the ones over-represented by the original GWAS findings. The empirical study was performed on an ADNI sample to identify modules related to the mean FDG-PET measure in amygdala, and yielded promising results.
Fig. 5.
The workflow for identifying functional interaction modules from the tissue-specific network using imaging GWAS findings. [Images are reproduced here with permission from Oxford University Press [99]].
Table V summarizes the studies discussed above, which are designed to detect high-level imaging genomic associations related to pathways, networks or brain circuits. The brain imaging genomics studies usually apply the standard enrichment methods widely used in the genomic domain, including both threshold-based and rank-based approaches. In addition to these enrichment calculation methods, various related strategies have been proposed to address specific issues in brain imaging genomics. For example, the enrichment analysis can be transferred from the genomic domain to the imaging domain to perform ROI enrichment analysis based on voxelwise findings [95]. It can also be extended to two dimensional imaging genetic enrichment analysis (IGEA) to mine high level imaging genetic associations based on massive BWGW SNP-QT results [90]. In addition, given the recent availability of tissue-specific networks, the imaging GWAS based module identification can be extended to use the functional interaction network specific to the studied imaging QT (i.e., tissue from the corresponding brain region) [99]. In sum, the enrichment methods examine the collective effect of a SNP/gene set, a QT set, or both, and have the potential to increase detection power. Also, the examined SNP or QT sets correspond to functionally annotated biological entities, and may provide valuable insights into underlying mechanisms.
TABLE V.
Example studies using pathway and network enrichment methods, which aim to detect high-level imaging genomic associations related to pathways, networks or brain circuits.
| Ref | Notes |
|---|---|
| [91] | A review of pathway and network analysis of genomic data |
| [93] | Pathway analysis of memory impairment, GSA-SNP software |
| [95] | ROI enrichment analysis based on voxelwise findings |
| [90] | Two dimensional Imaging Genetic Enrichment Analysis (IGEA) |
| [99] | Tissue-specific network (specific to the imaging QT), network module detection, NetWAS re-prioritization |
A topic relevant to enrichment analysis is prioritization. Enrichment analysis is typically performed at the end of the analysis pipeline (e.g., as a post-hoc analysis of the GWAS findings). Prioritization takes a reverse approach where valuable prior knowledge such as pathway and network information is used to select a small set of genes for subsequent analyses. For example, in [103], Patel et al. used Gene Ontology (GO) [97] to build a biological process network associated with 21 AD seed genes from [63], and then performed imaging genetic analyses targeting at all the genes in the network. In [104], Lorenzi et al. used the GTEx database (https://gtexportal.org/) to screen candidate SNPs generated from imaging genetic analysis of a discovery sample for obtaining potential expression QT loci (eQTL), and then performed another imaging genetic analysis targeting only these prioritized loci in an independent sample. In [105], Grothe et al. used amyloid PET and MRI scans to compute brain-wide spatial patterns of AD-typical amyloid deposition and neurodegeneration, and then used the whole brain gene expression database AHBA [96] to rank and prioritize genes based on their spatial correlation with the above amyloid burden and neurodegeneration patterns. In short, the strength of gene prioritization is twofold: 1) it reduces the burden of multiple testing and has the potential to increase detection power; and 2) the valuable functional annotation knowledge used for prioritization can help with biological interpretation and alleviate the risk for false discoveries. On the other hand, we should also be cautious about its possible limitations such as bias associated with the reference atlas or prior knowledge used for prioritization and difficulty in updating findings according to the evolution of these valuable resources. Finally, in addition to enrichment analysis and prioritization, the pathway and network information can also be incorporated into advanced statistical and machine learning models to guide our search for more complicated imaging genomics associations (e.g., [106], [107], [108]), which will be discussed in Sections V and VI.
F. Interaction methods
Most brain imaging genomics association studies examine main effects of genetic variants on imaging QTs. It is well-known that these main effects can only explain a portion of heritability of the studied QTs. Missing heritability can often be attributed in part to the interaction effects (or epistatic effects) within genetic variants or between genetic and environment factors. These studies are facing major statistical and computational challenges, since an exponentially increasing number of possible tests (to the order of the interaction) significantly reduces the statistical power due to multiple comparison correction. Thus a major topic in epistatic studies is to find an effective search strategy to reduce computational time and increase statistical power. Below we review a few example studies exploring the effects of SNP-SNP interaction or SNP-environment interaction on imaging QTs.
In [109], Zieselman et al. presented a bioinformatics pipeline for the epistatic analysis of an MRI-based QT (i.e., mean grey matter density) using an ADNI sample. The pipeline employed two phases to dramatically reduce the search space. Phase I was focused on identifying a set of genes with significant SNP-SNP interactions, where the Quantiative Multifactor Dimensionality Reduction (QMDR) method [110] was used to examine the SNP-SNP interaction effect on the QT within each gene. 20 genes with 34 SNPs were identified. In Phase II, these genes were uploaded to the Integrative Multispecies Prediction (IMP) Webserver (http://imp.princeton.edu, [111]) to create a gene interaction network that incorporates the prior functional genomics knowledge. Up to 20 additional genes connected to the input genes with a high confidence were allowed to be added to the IMP network. 10 genes (6 original + 4 additional) with 10 SNPs were identified. Finally QMDR was used to examine all pairwise, three-way and fourway SNP-SNP interactions among these 10 SNPs. The most significant finding is a three-way interaction including two SNPs within the olfactory gene cluster and one TRPC4 SNP. The goal of this study was to use the existing knowledge to reduce the possibility of false positives instead of identifying all possible interactions which is a much harder task to accomplish.
In [112], Meda et al. performed a genome-wide interaction analysis (GWIA) of MRI-based atrophy measures in hippocampus and entorhinal cortex using an ADNI sample. Their strategy to reduce the number of tests was to examine 151 million SNP pairs based on the gene-gene interaction patterns in the KEGG pathway database. Linear regression implemented in the INTERSNP software [113] was used to identify epistatic effects while controling for sex, age, education, APOE e4 and clinical status. They identified 109 SNP-SNP interactions for right hippocampal atrophy and 123 for right entorhinal cortex atrophy. These findings were overrepresented in several interesting pathways including the calcium signaling, axon guidance, and ErbB signaling pathways.
In [114], Hibar et al. performed a GWIA of MRI-based temporal lobe volume (TLV) using an ADNI sample. The EPISIS software [115] was employed to screen all possible SNP pairs based on a machine-learning algorithm called sure independence screening (SIS) [51]. SIS is a screen method that evaluates the correlation strength between each SNP pair and the outcome and selects the most associated SNP pairs. In this study, 111 SNP-SNP interaction pairs were obtained after SIS screening. All these interaction terms were then included in a single ridge regression model, where the extended Bayesian Information Criterion (BIC) [116] was used to identify the most relevant SNP pairs. This study identified a significant interaction between rs1345203 and rs1213205.
In [117], Ge et al. presented a kernel machine method (KMM) to evaluate main and interaction effects among multiple genetic and nongenetic variable sets on an imaging QT. Their model includes three separate kernels. The first one is a genetic kernel to measure the epistatic and joint effect of a SNP set on an imaging QT. The SNP sets can be defined by haplotype structure, gene or pathway. The second one is a non-genetic kernel to measure the collective effect of multiple nongenetic factors. The third one is the Hadamard product of the above two kernels to examine their interaction effect. Using an ADNI sample, they applied KMM to explore the interaction effects between each of 21 AD candidate genes and six cardiovascular disease (CVD) risk factors on MRI-based hippocampal volume. Two genes, CR1 and EPHA1, were identified to have such interaction effects with the CVD risk factors.
In [118], Wang et al. proposed a set-based mixed effect model for gene-environment interaction (MixGE) on imaging QT. They reviewed major set-based association tests and grouped them into five categories: 1) burden tests (collapsing variants into a burden score), 2) adaptive burden tests (burden tests using data adaptive weights), 3) variance component tests (examining variance of genetic effects), 4) combined tests and 5) exponential combination tests (both combining burden and variance component tests). Their work is an extension of a combined test named mixed-effects score test (MiST) [119] to examine gene-environment (G×E) effect on imaging QTs. The proposed MixGE method models both fixed and random effects of G×E and examines homogeneous and heterogeneous contributions from a SNP set and their interaction with environment factors on an imaging QT. They employed score statistics instead of direct parameter estimation to accelerate the computation, which enabled the voxelwise analyses. Similar to [117], the empirical study was performed on the same ADNI sample to explore the interaction effects between each of 21 AD candidate genes and the first principal component of six CVD risk factors on hippocampal volume and voxelwise tensor-based morphometry data. The analysis on the hippocampal volume replicated the results of KMM [117]. The analysis on the TBM data suggested an interaction effect of ABCA7 gene and CVD risk on right superior parietal cortex.
Table VI summarizes the studies discussed above, which are designed to examine epistatic effects of genetic variants or their interaction effects with nongenetic factors on brain imaging QTs. Given the major statistical and computational challenges induced by an enormous number of possible tests, studies in the field typically employ various strategies to reduce the search space. For example, one strategy is to examine only a small set of candidate interactions with a potential biological mechanism suggested by functional interaction networks or biological pathways. In this case, we should be aware of the strengths and limitations of the prioritization approach, as discussed in the end of Section III-E. Another strategy is to perform data-driven screening to focus on the analysis of a small number of most promising candidate interactions.
TABLE VI.
Example studies using interaction methods, which aim to examine epistatic effects of genetic variants or their interaction effects with nongenetic factors on imaging QTs.
| Ref | Notes |
|---|---|
| [109] | QMDR, IMP, targeted epistatic analysis guided with statistical filtering and functional genomics knowledge |
| [112] | GWIA, targeted analysis using the KEGG gene-gene interaction patterns, linear regression using the INTERSNP software |
| [114] | GWIA, sure independence screening algorithm (called EPISIS), ridge regression, extended Bayesian Information Criterion (BIC) |
| [117] | Kernel machine method (KMM), joint modeling of epistatic and collective effect from a SNP set, collective effect of non-genetic factors, and interaction between genetic and non-genetic factors |
| [118] | Set-based mixed effect model for gene-environment interaction (MixGE) on imaging QT, score statistics for fast computation |
IV. Imaging Genomics Associations: Meta-Analysis
A key challenge in imaging genomics is the relatively small effect size of genetic variants on the brain - most genetic variants account for under 1% of the variance in a brain measure, when considered individually, meaning that hundreds or even thousands of scans may be needed to detect and independently replicate an effect. An important exception to this rule appears to be the APOE gene; a common form of this gene, APOE4, is carried by around a quarter of the world’s population, and is associated with a roughly 3-fold higher lifetime risk for Alzheimers disease. In elderly people, this genotype is associated with a 1-2 standard deviation lower hippocampal volume [121], relative to carriers of the most common form of the gene, APOE3. Nonetheless, other common genetic variants with large effects on the brain have been extremely difficult to find; as a result, studies have expanded to ten thousand subjects or more, in an effort to find replicable associations [120].
In addition, the ability to test over a million markers in the genome for associations with brain measures means that heavy corrections are often required for multiple statistical testing. A typical genome-wide association study might test over a million independent genetic markers; to avoid reporting false positives, the genetics field established a genome-wide association significance threshold (typically p < 0.05/106, or thereabouts) before an association could be declared significant. The number of traits derived from images in an individual study might also be very large (up to 140 traits in a typical study of cortical thickness and surface area - and well over 106 voxels in an image or 104 edges in a connectivity network). If every trait is tested for genome-wide associations, this leads to even more stringent significance thresholds. Smith and Nichols [123] give a detailed power analysis of association testing in large biobanks, noting the very large samples required. In parallel, several researchers examined the power and data requirements for well-powered studies of image-wide genomewide associations [45], [124] and connectome-wide genomewide association, which performs association tests at each edge in a graph or network model of brain connectivity [38], [20], [125].
Early attempts to reduce the search space in imaging genomics (by focusing on genes more likely to have effects on the brain) largely failed. Ten years ago, several hundred papers had reported associations between variants in specific candidate genes (e.g., COMT, BDNF) and an imaging trait - yet almost none of these was replicated when tested in independent data. Jahanshad et al. [126] pooled regional fractional anisotropy (FA) measures for 6,165 subjects from 11 cohorts worldwide to evaluate effects of 15 candidate SNPs that had been reported in the literature to show associations with white matter microstructure; not a single one of these associations was replicated in independent samples. This “crisis of reproducibility” or “power failure” has also been noted in several branches of science [127] including neuroscience [128], [129].
Modeled on the Psychiatric Genomics Consortium in psychiatric genetics, the ENIGMA Consortium (Enhancing NeuroImaging Genetics through Meta Analysis; http://enigma.ini.usc.edu) was founded in 2009 to address these problems, and perform large scale genome-wide association studies for brain measures derived from MRI [130], DTI [126] and EEG [131]. ENIGMA uses a meta-analytic design to pool evidence from large numbers of cohorts worldwide. ENIGMA has since expanded to include over 50 working groups, focusing on global studies of specific brain diseases, and has published the largest neuroimaging studies to date of 9 brain disorders. Here, we focus on its work in imaging genetics, which can be categorized into studies of common [130] and rare [122] genetic variants and epigenetic variation [132]. These studies may be further subdivided by the data types studied (e.g., MRI and EEG) and methods used (e.g., mass-univariate meta-analysis, tests of genetic overlap between brain traits and other clinical or behavioral traits, and image-wide or connectome-wide testing of genetic associations). We begin with mass-univariate analyses, as they are the simplest.
Stein et al. [120] and Hibar et al. [121] identified over 20 genetic loci associated with the volumes of subcortical brain regions, including the hippocampus, amygdala, thalamus, putamen and other regions of the basal ganglia, and intracranial volume. Manhattan plots of these effects are shown in Figure 6(A-B), for each structure; the evidence of association is shown for each genetic marker (on the x-axis) and each regional volume measure (on the y-axis) using a logarithmic scale, −log10(p). Several aspects are notable from a methodological point of view. First, only hits that are genomewide significant are considered reliable, by convention, due to the large number of statistical tests performed. To attempt to replicate these hits in independent data, ENIGMA partnered with the CHARGE Consortium on a series of papers reporting GWAS in ever increasing sample sizes, of intracranial volume [133], hippocampal volume [121], and all subcortical volumes [134]. Earlier papers performed a simple p-value look-up in the replication data; a later paper performed a meta-analysis of all cohorts.
Fig. 6.
Example ENIGMA results. (A-B) Manhattan plots of GWAS on ICV and subcortical volumes [120], [121]. (C) Catalog of rare variants and their effects on the brain created by partnerships among ENIGMA, deCODE Genetics, and the UK Biobank [122]. [Data adapted, with permission from the authors and publishers].
These analyses were performed using standardized protocols for quality control of the imaging and genomic data, as well as imputation of genetic data to common reference panels, such as the 1000 Genomes reference panel (this step allows the same set of variants to be analyzed across cohorts, even if some sites have used different genotyping chips). A later cortical GWAS [130] led to an annotated atlas of over 200 genetic loci associated with surface area and thickness measures from 70 cortical regions. Parallel work by the UK Biobank reported GWAS for MRI, DTI, and even functional MRI metrics in their first 9,000 subjects scanned [135], [12]. The UK Biobank was subsequently added to the ENIGMA studies as a replication sample, showing generally strong replication [130]. A parallel set of studies also assessed the overlap between these brain-related genetic loci and genetic markers implicated in a range of brain diseases and neuropsychiatric disorders, including Alzheimers disease and Parkinsons disease [130], schizophrenia and bipolar disorder [136], [35], obsessive compulsive disorder [137], Tourette syndrome [138], and even IQ [130], [139].
Holland et al. [140] studied the discoverability of SNPs using GWAS for a range of different traits, including image derived measures. By modeling the effect sizes found empirically for SNPs associated with brain and behavioral traits, they noted that the rate of discovery of SNPs - and the cumulative percentage of variance explained - tends to follow an S-shaped curve. Remarkably, to discover markers that account for over half of the SNP heritability (the proportion of variance due to genotyped SNPs), they estimate that 10,000-10,000,000 participants would be needed, depending on the trait or disease studied (e.g., increasing numbers of subjects were needed to perform a well-powered GWAS of plasma cholesterol levels, regional brain volumes, schizophrenia, and major depression). Differences in SNP discoverability, for each trait, depend on the genetic architecture of each trait - the fraction of the genome that accounts for various proportions of the observed variance, the effect sizes for each SNP in this set, and the minor allele frequency (MAF) of the variants implicated. By estimating these from empirical data, detailed power analyses were reported.
Some Bayesian methods have been proposed to overcome the heavy statistical corrections associated with mass-univariate testing of over a million genetic loci. Smeland et al. [136] categorized markers as belonging to different genetic categories (e.g., lying within and outside known genes, or by functional type, such as enhancers or promoters). As brain-relevant genetic loci have different prevalence in these various genetic categories, Smeland et al. were able to use the conditional FDR (false discovery rate) method to discover some known SNPs more efficiently (i.e., in smaller samples) as well as other genetic markers not yet discovered using existing methods. Similarly, genetic clustering - the quest to identify overlap in genetic influences between traits - has led to genetic connectomes - matrices or graphs of genetic correlations, in which traits with common genetic determination are stored in a matrix, and clustered. Some researchers argue that genetic clustering of voxels in an image, edges in a network, or vertices on surface models of the cortex, may yield more efficient targets for GWAS [141], [142]; such methods are just beginning to be explored.
ENIGMA is also using meta-analysis to assess effects on the brain of other types of genetic variation. ENIGMA’s Epigenetics group identified two sites in the genome where methylation relates to hippocampal volume (N=3, 337; [132]). This type of study is computationally analogous to a GWAS, although methylation occurs at a somewhat lesser number of genetic loci, making the analysis slightly more efficient; nonetheless, thousands of subjects are still needed to detect and replicate individual associations.
As biobanks grow in size, it has become possible to discover and independently replicate effects on the brain of rare genetic loci (with a prevalence of <1:1000 individuals), such as the genetic deletions responsible for 22q deletion syndrome [143], [144]. The ENIGMA CNV Consortium [122] is performing a systematic study of these rare variants; in general, they may have a far greater effect on the brain than common variants, making their effects more efficient to replicate. Partnerships among ENIGMA, deCODE Genetics, and the UK Biobank are creating a catalog of rare variants and their effects on the brain ([122]; see Figure 6(C)). Once the effects on the brain are known for deletions of different sizes, a second round of analyses may be required to determine how specific genetic loci within the deleted region influence the effects.
V. Imaging Genomics Associations: Multivariate Regression
Here we provide a review of machine learning studies that use regression models to identify complex multi-sNP and/or multi-QT associations. Let be the genetic data with p variables on n subjects. Let be the imaging data with q variables on n subjects. We assume that each column of X and Y is normalized with zero mean and unit variance. Most of the regression models discussed below can be described using the following generic regularized loss function framework.
| (1) |
where is the weight matrix for regression of Y on X, and λi is the parameter balancing the loss function and the regularization .
A sparsity-inducing regularization term is often included in these models. The motivation is twofold. First, it is reasonable to hypothesize that only a small number of markers are relevant in the resulting imaging genomics association. The sparsity term can help identify these relevant markers. Second, the sparsity constraint can reduce the model complexity and subsequently reduce the risk of overfitting.
Below we discuss example studies using the four categories of methods: 1) sparse multiple regression (univariate response, W degrades to a vector w), 2) sparse multivariate multiple regression (multivariate response, W is a matrix), 3) sparse reduced rank regression (reducing the rank of W, e.g., W = BAT), and 4) Bayesian regression and neural network models.
A. Sparse multiple regression
We start with a few relatively simple sparse multiple regression models, where the response is a scalar. Some of these (e.g., [106]) will be later extended into its multivariate version.
In [106], Silver et al. proposed the “pathways group lasso with adaptive weights” (P-GLAW) algorithm, which is based on a group lasso model:
| (2) |
where defines the grouping structure of w. The goal is to identify a set of SNPs from X to predict a single imaging QT y. The SNPs are grouped using the pathway knowledge so that the feature selection is done at the pathway level to enhance biological interpretation and generate insightful results. The empirical study was performed on synthetic data simulated based on an ADNI sample and canonical pathways from the Molecular Signals Database (MsigDB, [145]).
In [146], Hao et al. proposed a “tree-guided sparse learning” (TGSL) method, which is also based on a group lasso model but with a tree structure:
| (3) |
where indicates a predefined tree (say T) structure of w, the tree T has l depth level, and the i-th level contains ni nodes organized as . The goal is to identify a set of SNPs from X to predict a single imaging QT y. The SNPs are grouped using a tree structure, which groups SNPs by LD blocks and groups LD blocks by genes. The empirical study was performed on an ADNI sample to predict six target imaging QTs using SNPs from 20 AD genes.
In [147], Wang et al. proposed a “diagnosis-aligned multimodal” (DAMM) method for regressing a target SNP x on multimodal imaging QTs (Ym for m ∈ [1, M]) as follows:
| (4) |
where W = [w1,…,wM]. The first regularization is an l2,1 norm to select features with effects on most of the modalities. The second regularization is a graph laplacian term that encourages the subjects within (between) the same diagnositic group to have similar (different) values in the projected space (i.e., these projected imaging components are aligned with diagnosis). The empirical study was performed on an ADNI sample, where the response is the APOE e4 SNP, and the predictors include two modalities of ROI measures: VBM measure from structural MRI, 2) hyper-graph based clustering coefficient measure from functional MRI.
B. Sparse multivariate multiple regression
Now we focus on sparse multivariate multiple regression models. In [148], Wang et al. proposed a “Group-Sparse Multitask Regression and Feature Selection” (G-SMuRFS) method, which is a structured sparse model (see also Figure 7(a)):
| (5) |
where the group l2,1-norm regularization (∥W∥G2,1,) does feature selection at the group level (e.g., LD-block), and the l2,1-norm regularization (∥W∥2,1) does feature selection at the individual SNP level. The empirical study was performed on an ADNI sample, where 1,224 SNPs from 37 AD genes were used to predict 10 VBM measures and 12 FreeSurfer [150] measures, and SNPs were grouped by LD blocks.
Fig. 7.
Example structured sparse multivariate multiple regression models, where only regression weight matrices W are shown here. Let X be genotype data and Y be imaging QT data. (a) Illustration of the G-SMuRFS model [148] (), where the group l2,1-norm regularization (∥W∥G2,1) does feature selection at the group level (e.g., LD-block), and the l2,1-norm regulesization (∥W∥2,1) does feature selection at the individual SNP level. [Image is reproduced here with permission from Oxford University Press [148]]. (b) Illustration of the TSAL model [149] (), where is a Schatten p-norm regularization term to identify low rank structures (e.g., four green boxes sharing similar patterns), and is an l2,1-norm to select SNPs correlated to most QTs over time (e.g., the red box). [Image is reproduced here with permission from Mary Ann Liebert, Inc. [149]].
In [151], Wang et al. aimed to use longitudinal imaging QT data (Yk for k ∈ [1, t]) to predict SNP data (X), and proposed the following “task-correlated longitudinal sparse regression” (TCLSR) model (each time point treated as a task):
| (6) |
where W = [W1,…,Wt] (the same as that shown in Figure 7(b)), is a trace norm to approximate a low rank representation of W, is an l2,1 norm to select features with effects at most of the time points. The empirical study was performed on an ADNI sample to predict 1,224 SNPs from 37 AD genes using longitudinal imaging QTs.
In [149], Wang et al. studied the same problem as [151] and proposed a new model “temporal structure auto-learning” (TSAL) as follows (see also Figure 7(b)):
| (7) |
where is a Schatten p-norm regularization term to identify low rank structures (e.g., four green boxes sharing similar patterns in Figure 7(b)), and is a l2,1-norm to select SNPs correlated to most QTs over the time (e.g., the red box in Figure 7(b)). Of note, compared with TCLSR (Eq. (6)), Schatten p-norm approximates rank minimization better than the trace norm [152], and l2,0+ norm can achieve a more sparse solution than l2,1 norm. The empirical study was performed on an ADNI sample, where longitudinal imaging QTs were used to predict 3,576 SNPs from 153 AD candidate genes.
In [153], Zhou et al. proposed a “joint projection learning and sparse regression” (JPLSR) model for identifying multi-SNP-multi-QT association. JPLSR model takes the following form (different from the generic form shown in Eq (1)):
| (8) |
The first term is the loss function to find the multi-SNP-multi-QT association. The second term is to project the SNP data and imaging QT data into a joint latent space to aid association discovery. The third term combines two graph laplacian terms (one for SNP data and one for imaging data) to encourage the genetic and imaging components projected to the latent space are aligned with diagnosis. The fourth and fifth terms are two l2,1 norms for selecting relevant imaging and SNP features, respectively. The empirical study was performed on an ADNI sample to relate 93 ROI-based imaging QTs to 3,123 SNPs from top AD candidate genes.
C. Sparse reduced rank regression
Here we focus on reviewing studies using sparse reduced rank regression (SRRR), which is a special type of multivariate multiple regression models for identifying multi-SNP-multi-QT associations from high dimensional imaging genomic data. The major goal is to minimize the rank of the (p × q) regression matrix W. Assuming that W has a reduced rank of r < min(p, q), Vounou et al. [154] proposed to rewrite W as the product of a (p × r) matrix B and (q × r) matrix A: W = BAT. In [154], they studied the following rank-one model (i.e., A and B become two vectors a and b)
| (9) |
where the l1 term is applied to both a and b for sparse feature selection. This model was evaluated using the synthetic imaging genetic data simulated using an ADNI sample.
In [155], Vounou et al. applied a slightly modified version of the above model (Eq (9)) to an ADNI sample, where they use genome-wide SNP data to predict voxelwise longitudinal imaging QTs. They first applied a penalized linear discriminant analysis (LDA) for voxel filtering to identify disease-relevant imaging QTs, and then employed the following SRRR model to predict QT data Y from SNP data X:
| (10) |
where the l1 term is applied for SNP selection. A data re-sampling scheme was used to identify SNPs with high selection probability.
In [107], Silver et al. integrated the P-GLAW idea (Eq (2)) into the SRRR framework (Eq (9)), and proposed the following “pathways SRRR” (P-SRRR) model:
| (11) |
where defines the grouping structure of b. The goal is to identify a set of SNPs from X to predict a set of AD-related imaging QT Y. The SNPs are grouped using the pathway knowledge so that the feature selection is done at the pathway level. The empirical study was performed on an ADNI sample with KEGG canonical pathways from MsigDB [145].
In [156], Zhu et al. proposed a “structured SRRR” (S-SRRR) model for regressing brain-wide imaging QT data Y on genome-wide SNP data X as follows:
| (12) |
where the l2,1 norm regularizes A and B in a row-wise fashion for effective selection of SNP and QT features. The empirical study was performed on an ADNI sample to relate 2,098 SNPs from 153 AD candidate genes to 93 imaging QTs.
In [157], Zhu et al. employed the graph self-representation method [158] to model a sparse matrix capturing the internal partial correlations among the SNP data X as follows:
| (13) |
where the constraint diag(S)=0 was imposed to avoid generating the trivial solution. Integrating the above model (Eq (13)) into the S-SRRR model (Eq (12)), Zhu et al. proposed the following “graph-regularized S-SRRR” (GRS-SRRR) model for regressing Y on X given S as a graph constraint:
| (14) |
The empirical study was performed on the same ADNI sample as in [156].
In [159], Zhu et al. modified the GRS-SRRR model (Eq (14)) into the following “robust graph-regularized S-SRRR” (RGRS-SRRR) model:
| (15) |
Here ∥Y − XBAT∥2,1 and ∥X − XS∥2,1 are the robust versions of and , respecitively, according to [158], [160]. The empirical study was performed on an ADNI sample with 90 imaging QTs and 3,996 SNPs from 153 AD candidate genes.
D. Bayesian regression and neural network models
While many regularized multivariate regression models have been proposed in brain imaging genomics, several Bayesian methods have been studied to achieve similar goals. For example, inspired by G-SMuRFS [148], Greenlaw et al. [161] proposed a Bayesian group sparse multi-task regression (BGSMTR) model for identifying multi-SNP-multi-QT associations while embracing the group structure (e.g., LD blocks, genes) within the SNP data. While G-SMuRFS only provided a point estimate of the regression coefficients, BGSMTR was proposed to allow for full posterior inference such as obtaining interval estimates for the regression parameters. The model was designed as an adapted version of the Bayesian group lasso [162], [163] to accommodate multivariate responses as well as variable selection at both SNP and gene levels. The empirical study was performed on an ADNI sample to predict 56 imaging QTs using 486 SNPs from 33 AD candidate genes.
There are also Bayesian models designed for reduced rank regression. In [164], Zhu et al. proposed a Bayesian generalized low rank regression (GLRR) model for analyzing both high dimensional imaging responses and covariates. Similar to SRRR, GLRR used a low rank representation to approximate the high dimensional weight matrix. It also modeled the high dimensional covariance matrix of imaging responses with a dynamic factor model. Bayesian local hypothesis testing was proposed to identify significant SNP effects on imaging QTs, while controlling for multiple comparisons. An efficient Markov chain Monte Carlo (MCMC) algorithm was developed for posterior computation. The empirical study was performed on an ADNI sample to evaluate the effects of 1,071 SNPs from 40 AD candidate genes on 93 ROI-based volume measures.
In [165], Lu et al. extended the above GLRR model [164] into a Bayesian longitudinal low rank regression (L2R2) model for examining genetic effects on longitudinal imaging responses. L2R2 includes three innovative components. The first one is a low-rank matrix to approximate regression weight matrices and gene-age interaction. The second one is to use penalized splines for characterizing the overall time effect. The third one is a sparse factor analysis model coupled with random effects to embrace spatio-temporal correlations of longitudinal imaging QTs. An efficient MCMC algorithm was used for posterior computation. The empirical study was performed on an ADNI sample to evaluate the effects of 1,071 SNPs from 40 AD candidate genes on longitudinal imaging measures of 93 ROIs.
Neural network models, despite underexplored in brain imaging genomics, have started to attract recent attention. In [166], Wang et al. proposed an “Additive Model via Feedforward Neural networks with random weight” (FNAM). This model was inspired by and adapted from the “feedforward neural networks with random weight” (FNNRW) [167] to enjoy the advantages of 1) modeling the non-linear associations between SNPs and QTs, and 2) computational efficiency over neural nets with back propagation. The improvement of FNAM over FNNRW is that FNAM considers the role of each feature independently in the prediction and thus one can estimate its contribution to help model interpretation. The empirical study was performed on an ADNI sample to examine the genetic effects of 3,123 SNPs from 153 AD candidate genes on 90 VBM measures and 90 FreeSurfer measures.
E. Summary
Table VII summarizes multivariate analysis methods used in the studies discussed above, which aim to reveal complex imaging genomics associations between multivariate SNP data and imaging QT data. At a high level, the methods discussed in Sections V-A, V-B and V-C share a common rationale: they all use regularized regression models to relate SNPs to imaging QTs. While the sparse multiple regression (SMR) models in Section V-A aim to identify multi-SNP-single-QT associations, the sparse multivariate multiple regression (SMMR) models in Section V-B and the SRRR models in Section V-C are designed to identify multi-SNP-multi-QT associations. The SRRR models may be thought of as a special case of the SMMR models, where the regression coefficient matrix W in SMMR is explicitly described as a low rank version W = BAT in SRRR. In general, these models share some common benefits: 1) the regression coefficients directly capture the SNP-QT relations and thus are easy to interpret; and 2) using a single model to analyze the studied SNP and QT data eliminates the need for multiple testing correction and improves the detection power. One pitfall with these models is the high dimensionality of the data, which increases the risk of overfitting. To address this challenge, various regularizations are used in these models to simplify model complexity, incorporate biologically meaningful structure, and thus reduce the overfitting risk. For example, sparsity can be imposed by using l1 or l2,1 norm to simply model complexity (e.g., in G-SMuRFS, SRRR). Meaningful biological structures (e.g., LD block, gene, pathway) can be embraced by using group lasso or group l2,1 norm (e.g., in P-GLAW, TGSL and P-SRRR). Rank minimization can also be modeled as a regularization term (e.g., in TCLSR and TSAL) to address spatial or temporal correlation and reduce model complexity. Besides the above regression models, Bayesian methods have also been studied to achieve similar goals. Neural network methods, although underexplored in this field, have started to appear to address brain imaging genomics problems.
TABLE VII.
Example studies using multivariate regression, which aim to reveal complex imaging genomics associations between multivariate SNP data and imaging QT data.
| Ref | Notes |
|---|---|
| [106] | P-GLAW (pathways group lasso with adaptive weights), multi-SNP-single-QT, group lasso, SNPs grouped by pathway |
| [146] | TGSL (tree-guided sparse learning), multi-SNP-single-QT, group lasso, tree-like group structure (SNPs grouped by LD block, LD blocks grouped by gene) |
| [147] | DAMM (diagnosis-aligned multimodal regression), single-SNP-multi-QT, select ROIs with genetic effects at most modalities, learning diagnosis-related components in the projected space |
| [148] | G-SMuRFS (Group-Sparse Multi-task Regression and Feature Selection), multi-SNP-multi-QT, group l2,1 for feature selection at LD block level, l2,1 for feature selection at SNP level. |
| [151] | TCLSR (task-correlated longitudinal sparse regression), longitudinal imaging QTs to predict SNPs, each time point treated as a task, trace norm for weight matrix rank minimization, l2,1 norm for selecting imaging QTs with effects at most of the time points |
| [149] | TSAL (temporal structure auto-learning), longitudinal imaging QTs to predict SNPs, Schatten p-norm for weight matrix rank minimization, l2,0+ norm for selecting imaging QTs with effects at most of the time points |
| [153] | JPLSR (joint projection learning and sparse regression), multi-SNP-multi-QT, projecting SNP and QT data into a joint latent space, SNP and QT components aligned with diagnosis, l2,1 norm for selection of SNP and QT features |
| [154] | SRRR (sparse reduced rank regression), multi-SNP-multi-QT, reduced rank loss function, l1 norm for selecting SNP and QT features, evaluation on ROI-based simulation data |
| [155] | SRRR (sparse reduced rank regression), multi-SNP-multi-QT, reduced rank loss function, penalized LDA to select diagnosis-related QT, l1 norm and re-sampling for SNP identification, evaluation on voxelwise ADNI data |
| [107] | P-SRRR (pathways SRRR), integration of P-GLAW and SRRR, group lasso on SNP side, SNPs grouped by pathway, identifying QT-related pathways |
| [156] | S-SRRR (structured SRRR), reduced rank loss function, l2,1 norm for selecting SNP and QT features |
| [157] | GRS-SRRR (graph-regularized S-SRRR), incorporation of graph self-representation on the SNP side into S-SRRR |
| [159] | RGRS-SRRR (robust GRS-SRRR), robust version of reduced rank loss function and graph self-representation loss function |
| [161] | BGSMTR (Bayesian group sparse multi-task regression), variable selection at both SNP and gene level, full posterior inference |
| [164] | GLRR (Bayesian generalized low rank regression), low rank approximation of weight matrix, dynamic factor model for imaging covariance, efficient MCMC algorithm for posterior computation |
| [165] | L2R2 (Bayesian longitudinal low rank regression), SNP effects on longitudinal imaging QTs, low rank approximation of weight matrix and gene-age interaction, penalized splines for overall time effect, efficient MCMC algorithm for posterior computation |
| [166] | FNAM (Additive Model via Feedforward Neural networks with random weight), modeling non-linear associations, computational efficiency, flexibility and interpretability of additive models |
VI. Imaging Genomics Associations: Bi-multivariate Correlation
Besides regression models, another category of prominent methods developed for brain imaging genomics studies are bimultivariate correlation models such as sparse canonical correlation analysis (SCCA) and parallel independent component analysis (pICA). Similar to the regression model discussed above, the sparsity is also encouraged in these correlation models to reduce model complexity and the risk of overfitting, as well as identify relevant biomarkers. Here we discuss a few example studies using these strategies to identify complex multi-SNP-multi-QT associations. We will cover 1) fundamental SCCA models, 2) enhanced SCCA models, 3) multimodal and longitudinal SCCA models, and 4) other bimultivariate correlation models.
A. Fundamental SCCA models
Let be the genetic data with p variables on n subjects. Let be the imaging data with q variables on n subjects. We assume that each column of X and Y is normalized with zero mean and unit variance. The most popular bimultivariate correlation models used in brain imaging genomics are SCCA and its variants with various regularization terms. These models can typically be described using the following generic regularized CCA form.
| (16) |
A schematic representation of this reguarlized CCA framework is shown in Figure 8(a) in the context of brain imaging genomics. The goal is to find a genetic component Xu (i.e., a linear combination of the SNPs) and an imaging component Yv (i.e., a linear combination of the imaging QTs) so that their correlation (i.e., uTXTYv s.t. ) is maximized under one or more regularization terms . For example, the conventional SCCA model [168] is formed by introducing two l1 norm terms: and . Various other regularization terms can be defined to achieve different goals such as incorporating group/network structure or other prior knowledge in brain imaging genomics data. Below we discuss a few example studies using regularized SCCA strategies.
Fig. 8.
(a) Schematic representation of a generic reguarlized CCA framework for brain imaging genomics, which aims to find a genetic component Xu and an imaging component Yv so that their correlation (i.e., uTXTYv s.t. ) is maximized under one or more regularizations . For example, the conventional SCCA model [168] is formed by introducing two l1 norm terms: and . (b) Schematic illustration of “Knowledge-guided SCCA” (KG-SCCA) [108]. Two regularizations are introduced into the reguarlized CCA framework shown in (a). On the genomic side, is a group l1 term, where SNPs are grouped by LD blocks. On the imaging side, is a network-guided regularization term (similar to graph laplacian), where ROIs are connected if they share similar co-expression patterns across the genes from the amyloid pathway. [Network inset image is reproduced here with permission from Oxford University Press [108]].
In [169], Du et al. proposed a “structure aware SCCA” (SCCA) model by introducing into Eq (16) two group l1 norms: and . The LD blocks were used to form the SNP grouping structure . The ROIs were used to form the voxelwise imaging QT grouping structure . An empirical study was performed on an ADNI sample to identify multi-SNP-multi-QT associations between voxelwise QTs and and APOE SNPs.
In [108], Yan et al. proposed a “knowledge-guided SCCA” (KG-SCCA) by introduce into Eq (16) the following two regularization terms (Figure 8(b)). On the genomic side, is a group l1 term, where SNPs are grouped by LD blocks. On the imaging side, is a network-guided regularization term (similar to graph laplacian), where ROIs are connected if they share similar co-expression patterns across the genes from the amyloid pathway. Allen Human Brain Atlas (AHBA) [170] was used to get the gene expression data across the brain. An empirical study was performed on an ADNI sample to identify multi-SNP-multi-QT associations between amyloid imaging QTs and and APOE SNPs.
B. Enhanced SCCA models
As shown in Section VI-A, there are three types of regularizations used in SCCA models: 1) l1 norm for flat sparsity, 2) group l1 norm for group sparisity, and 3) graph laplacian type norm to encourage joint selection of features connected in a graph. Below, we discuss a few enhanced SCCA models that are designed to improve some of the above norms.
In [171], Du et al. proposed a SCCA framework using a generic non-convex penalty (GNC-SCCA) to address the challenge that the l1 norm over-penalizes large coeffients and may introduce estimation bias. They tested seven non-convex penalties for replacing the l1 term in an l1-based SCCA. These non-convex penalties were designed to reduce the estimation bias. An empirical study was performed on an ADNI sample to identify multi-SNP-multi-QT associations between voxelwise QTs and 163 SNPs from AD genes.
Although the ideal sparsity inducing term is l0 norm, it is computationally intractable. Thus, l1 norm is typically used to approximate l0 norm. Given that the truncated l1 norm better approximates l0, Du et al. [172] proposed a truncated l1-norm penalized SCCA (TLP-SCCA) via replacing l1-norm with truncated l1-norm, and a truncated group lasso SCCA (TGL-SCCA) via replacing group lasso with truncated group lasso. An empirical study was performed on an ADNI sample to identify multi-SNP-multi-QT associations between voxelwise QTs and 58 SNPs from AD-related genes, where QTs were grouped by ROI and SNPs were grouped by LD block.
GraphNet was proposed in [173] as a regression model with combined graph laplacian and l1-norm regularization terms: ∥u∥GN = uTLu + β∥u∥1, where L is the Laplacian matrix of a given graph. In [174], Du et al. proposed an “absolute value based GraphNet SCCA” (AGN-SCCA) model, which incorporated an extended version of GraphNet regularization into the SCCA framework. The AGN regularizations are modeled as follows:
| (17) |
| (18) |
where L1 and L2 are Laplacian matrices of the correlation matrices of X and Y. Here, they used data-driven correlation as graph constraint to encourage the selection of correlated features together. The newly added absolute value operation allows for the joint selection of both positively and negatively correlated features. An empirical study was performed on an ADNI sample to identify multi-SNP-multi-QT associations between ROI-based imaging QTs and 58 SNPs from AD-related genes.
In [175], Gossmann et al. proposed a “FDR-corrected SCCA” (FDR-SCCA) procedure to introduce false discovery rate (FDR) concept to SCCA and develop a method to control FDR. The existing SCCA methods determine the sparsity parameter using model fit criteria such as cross-validation and permutation. There is a lack of theoretical results to identify an appropriate level of sparsity for true signal discovery. This work proposed a method to define the FDR for canonical weight vectors in SCCA, and used it as a statistical criterion to determine the model sparsity level. An empirical study was performed on an imaging genomics sample from Philadelphia Neurodevelopmental Cohort (PNC) [176] to relate nearly 100,000 SNPs to nearly 5,000 functional connectivity measures extracted from the fMRI data.
C. Multimodal and longitudinal SCCA models
The SCCA models discussed above aim to relate the SNP data to the imaging data of one single modality at one single time point. Attempts have also been made to extend these models to handle multimodal or longitudinal imaging data. We review a few example studies here.
In [177], Du et al. proposed a “multi-task SCCA” (MTSCCA) model to identify bi-multivariate associations between SNP data and multimodal imaging data. Let be the SNP data, (j ∈ [1, M]) be the imaging data of M modalities. MTSCCA is designed as:
| (19) |
where U = [u1 u2 ⋯ uM] and V = [v1 v2 ⋯ vM]. Here the canonical correlation is maximized for each modality separately. The first regularization ∥U∥2,1 is an l2,1 term for SNP feature selection. The second regularization ∥U∥G2,1 is a group l2,1 term for SNP feature selection at the group level (e.g., LD blocks). The third regularization ∥V∥2,1 is an l2,1 term for imaging feature selection across all the modalities. A fast optimization algorithm was implemented and applied to an ADNI sample to identify associations between over 150,000 SNPs from chromosome 19 and ROI-based QTs from three imaging modalities (VBM, FDG-PET, and Amyloid-PET).
In [178], Hao et al. proposed a “temporally constrained group SCCA” (TG-SCCA) model to identify genetic association with longitudinal imaging QTs. Let be the SNP data, (j ∈ [1, t]) be the imaging data at t time points. TG-SCCA is designed as:
| (20) |
where V = [v1 v2 ⋯ vt]. Here the canonical correlation is maximized for each time point separately while maintaining the genetic component the same across all the time points. The first regularization ∥u∥1 is an l1 norm for SNP feature selection. The second regularization ∥V∥2,1 is an l2,1 term for imaging feature selection across all the time points. The third regularization is an fused lasso term to constrain the weight difference between two neighbouring time points. An empirical study was performed on an ADNI sample to identify associations between 85 APOE SNPs and longitudinal VBM QTs from 116 ROIs at four time points.
In [179], Du et al. proposed another longitudinal imaging genetics model based on MTSCCA [177]. It is named as “temporal multi-task SCCA” (T-MTSCCA) and designed as:
| (21) |
where U = [u1 u2 ⋯ ut] and V = [v1 v2 ⋯ vt]. Here the canonical correlation is maximized for each time point separately. The regularization (U on the genomic side contains three components: one l1 norm and one l2,1 norm for feature selection at SNP level, and one group l2,1 norm for feature selection at group level (e.g., LD block). The regularization (V on the imaging side contains three components: 1) a l1 norm for imaging feature selection using flat sparsity, 2) a l2,1 norm for selection imaging features associated at most time points, 3) a fused pairwise l2,1 norm (FP2,1-norm) for joint selection of the same QT at neighbouring time points. Compared with the non-convex fused lasso used in TG-SCCA [178], FP2,1-norm is convex and thus easy to optimize. An empirical study was performed on an ADNI sample to identify associations between 1,085 APOE SNPs and longitudinal VBM QTs from 90 ROIs at four time points.
D. Other bimultivariate correlation models
We now discuss a few other bimultivariate correlation models. In [180], Floch et al. proposed a two step procedure, named as FSPLS (filtering + sparse partial least squares), to identify associations between high dimensional SNP and imaging QT data (e.g., empirical study of real data including 94 subjects with 600,000 SNPs and 34 fMRI QTs). The first step of FSPLS selected top SNPs with minimal p-values via massive univariate association analysis between each SNP-QT pair using linear regression based on an additive genetic model. The second step of FSPLS applied a single sparse partial least squares (SPLS) model to the selected SNP data and full QT data to identify an multi-SNP-multi-QT association. Empirical studies on both simulated and real high dimensional SNP and imaging QT data demonstrated that FSPLS outperformed several competing methods using other regularization and dimensionality reduction strategies coupled with PLS or kernel CCA models. This work also illustrated that the SRRR, SCCA and SPLS models are mathematically equivalent methods, up to specific assumptions on the covariance matrix.
In [181], Fang et al. proposed a “greedy projected distance correlation” (G-PDC) method to examine pairwise gene-ROI associations, where each gene contains a number of SNPs and each ROI contains a number of voxels. Distance correlation measures statistical dependence between two random vectors (e.g., gene vs ROI), and can model nonlinear relationship between them. Projected distance correlation measures conditional dependence based on distance correlation [182]. In this work, given an gene-ROI pair, the goal is to test their independence while controlling for all the other SNPs and voxels. Fang et al. proposed an efficient G-PDC algorithm to enable large-scale imaging genomics analysis. An empirical study was performed on the PNC data [176] to examine the pairwise association between 221 ROIs (containing 27,168 voxels) and 2,035 genes (containing 63,010 SNPs).
In [183], Hu et al. integrated distance correlation model into the CCA framework, and proposed “distance CCA” (DCCA) method. The G-PDC method described above performs pairwise analysis for each possible gene-ROI combination and is still facing large burden for multiple testing correction. The DCCA model was proposed to overcome this limiation by identifying a set of original SNPs and a set of original imaging QTs with the highest distance correlation. The approach was to first construct a distance kernel function and then solve an optimization problem. An empirical study was performed on the PNC data [176] to examine the pairwise association between 264 ROIs (containing 27,384 voxels) and 736 genes (containing 21,487 SNPs).
Parallel independent component analysis (pICA) [184], [185] is another well-established strategy for mining multi-SNP-multi-QT associations. It is a joint estimation procedure to extracte imaging components and genetic components for achieving two goals: 1) maximizing independence among components within each modality using an entropy term, and 2) maximizing components’ correlation between two modalities. In [186], Meda et al. applied pICA to an ADNI sample for identifying multi-SNP-multi-QT associations between genome-wide SNPs and brain-wide ROI-based imaging QTs.
E. Summary
Table VIII summarizes bi-multivariate correlation methods used in the studies discussed above, which aim to identify multi-SNP-multi-QT associations from high dimensional imaging genomic data. Most of these strategies are regularized SCCA models. Similar to the regression models in Section V, these SCCA models also employ l1 or l2,1 norm for feature selection, group l1 or l2,1 norm for feature selection at group level, and graph Laplacian for graph-guided learning. Multimodal and longitudinal SCCA models often include l2,1 norm for feature selection across modalities or time points as well as fussed lasso or fused pairwise l2,1 norm for smoothing neighboring weights along the temporal dimension. Other bimultivariate correlation models include 1) SPLS that is mathematically equivalent to SRRR and SCCA under certain assumptions on the covariance matrix, 2) distance correlation that can model nonlinear associations, and 3) parallel ICA models for joint maximization of within-modality component independence and between-modality component correlation.
TABLE VIII.
Example studies using bi-multivariate correlation methods, which aim to identify multi-SNP-multi-QT associations from high dimensional imaging genomic data.
| Ref | Notes |
|---|---|
| [169] | S2CCA (structure aware SCCA), group 11 norm on both SNP and QT sides, SNPs grouped by LD block, QTs grouped by ROI |
| [108] | KG-SCCA (knowledge-guided SCCA), group l1 norm on genetic side (SNPs grouped by LD block), graph Laplacian type norm on imaging side (ROIs connected by co-expression network) |
| [171] | GNC-SCCA (generic non-convex penalty SCCA), seven non-convex penalties replacing l1 norm to reduce estimation bias |
| [172] | TLP-SCCA (truncated l1-norm penalized SCCA), TGL-SCCA (truncated group lasso SCCA), better approximation of l0 norm, voxels grouped by ROI, SNPs grouped by LD block |
| [174] | AGN-SCCA (absolute value based GraphNet SCCA), incorporation of a GraphNet variant into SCCA, joint selection of both positively and negatively correlated features |
| [175] | FDR-corrected SCCA, incorporation of FDR concept into SCCA |
| [177] | MTSCCA (multi-task SCCA), relating SNP to multimodal imaging QTs, l2,1 norm for SNP selection and QT selection |
| [178] | TG-SCCA (temporally constrained group SCCA), l1 for SNP selection, l2,1 for ROI selection (over time), fussed lasso for smoothing weights between neighbouring time points |
| [179] | T-MTSCCA (temporal multi-task SCCA), l1 and l2,1 for SNP and QT selection, fused pairwise l2,1 norm for smoothing weights between neighbouring time points |
| [180] | FSPLS (filtering + sparse Partial Least Square), two step procedure, univariate filtering, sparse PLS with l1 regularization |
| [181] | G-PDC (Greedy projected distance correlation), examination of pairwise gene-ROI associations, an efficient algorithm |
| [183] | DCCA (Distance CCA), identification of SNP set and QT set with the highest distance correlation |
| [186] | pICA (parallel independent component analysis), joint maximization of within-modality component independence and between-modality component correlation |
VII. Integrating Imaging and Genomics for Outcome Prediction
In addition to identifying imaging genomics associations, another active research topic in brain imaging genomics is how to integrate brain imaging and genomics data for prediction of outcomes of interest such as disease stage, impairment score, and progression status. A relevant interesting topic is to learn the associations among genomics, imaging and the outcome to help understand biological pathway from genetics to brain structure and function, and to cognitive, behavior and diagnostic outcomes. In this section, we first focus on methods for outcome prediction, and then review methods for joint association learning and outcome prediction.
A. Outcome Prediction
We discuss a few example studies using existing conventional prediction models, newly developed machine learning approaches, and state-of-the-art deep learning methods. Of note, all these studies were performed using brain imaging genomics data from the ADNI cohort.
We start with some studies using conventional predictive models. For example, in [187], Dukart et al. examined the role of multimodal imaging (MRI, FDG-PET, Amyloid-PET), neuropsychological, and genetic data as potential biomarkers for identifying MCI patients who will convert to AD in the future. They first built Naive Bayes classifiers to distinguish AD and CN participants using different combinations of the above data modalities. After that, they applied the learned classifier to the MCI cohort for predicting AD conversion status. They achieved 76% accuracy using FDG-PET data, and 87% accuracy using multimodal imaging and genetic data. This shows the promise of the data integration strategy in the context of AD outcome prediction.
In [188], Filipovych et al. proposed a method to create a composite imaging genetic score for predicting MCI conversion to AD. On the imaging side, they used a nonlinear pattern recognition method “COMPARE” [189] to identify AD-relevant volumetric regions. After that, a nonlinear support vector machine (SVM) was applied to imaging measures from these regions to get an imaging score for each individual. On the genomic side, a linear SVM was used to classify AD vs CN, which yielded a polygenic AD-related genetic score for each subject. Finally, a composite imaging genetic score was created as a weighted sum of the imaging score and the genetic score. The empirical study showed that the proposed composite score improved the prediction accuracy.
In [190], Kauppi et al. performed survival analysis using Cox proportional Hazard model to predict time to progression from MCI to AD via integrating a polygenic harzard score (PHS), an imaging based atrophy score and the MMSE score. The PHS was generated using the ADGC data [66], as described in Section III-B. The atrophy score was generated from volumetric measures of a few AD-related ROIs using a linear discriminant analysis (LDA) to distinguish AD vs CN, see [191], [192] for more details. The empirical study showed that combining PHS with atrophy and MMSE significantly improved the prediction performance compared with models without PHS.
Besides conventional prediction methods, new machine learning models have also been proposed for outcome prediction using brain imaging genomics data. For example, in [193], Wang et al. proposed a joint classification and regression framework for multimodal multitask learning (JCRMML). JCRMML was designed to use multimodal imaging (MRI, FDG-PET) and genetic data for joint prediction of diagnositic and cognitive outcomes, and at the same time to identify disease-sensitive and cognition-relevant imaging and genetic biomarkers (Figure 9(a)). It is formulated as a regularized multivariate linear model with feature weight matrix ∥WT∥ shown in Figure 9(b), where a task indicates an outcome response. The loss function includes a logistic regression component for disease classification and a linear regression component for cognitive score regression. JCRMML has two regularization terms. One group l1 term ∥W∥G1 is used for learning group-wise weights for features within a single modality for each task (i.e., a diagnostic or cognitive outcome). One l2,1 term ∥W∥2,1 is used for selecting features associated with most tasks (i.e., outcomes). The empirical study yielded improved performance on prediction both diagnostic and cognitive outcomes, compared with several competing methods.
Fig. 9.
(a) The JCRMML framework [193] performs joint classification and regression via multimodal multitask learning to identify disease-sensitive and cognition-relevant biomarkers from brain imaging genomic data. The identified biomarkers could predict not only disease status, but also cognitive functions to help us better understand the underlying mechanism from gene to brain structure and function, and to cognition and disease. (b) Illustration of the JCRMML feature weight matrix WT. The group l1-norm (G1-norm) learns the group-wise weights for features within a single modality for each task (i.e., outcome) and the l2,1-norm selects features associated with most tasks. [Images are reproduced here with permission from Oxford University Press [193]].
In [194], Zhang et al. examines several machine learning strategies for AD prediction via combining multimodal imaging (MRI and FDG-PET), CSF and SNP data. Specifically, they compared three state-of-the-art feature selection methods. The first is a multiple kernel learning (MKL) method named as SimpleMKL [195]. The second is a high-order graph matching based feature selection (HGM-FS) [196]. The third is sparse multimodel learning (SMML) [197]. The AD prediction model was learned in three steps. 1) A feature selection method was applied to select discriminative features. 2) Each selected feature was multiplied by its learned weight to form a new feature vector. 3) A linear SVM was applied to the new feature vectors to learn a predictor. Empirical studies yielded a few findings: 1) FDG-PET was the modality with the best prediction accuracy, 2) adding SNP data to other modalities could improve prediction accuracy, and 3) HGM-FS worked the best among three feature selection methods.
In [198], Peng et al. proposed a “structured sparse kernel learning” (SSKL) model for AD predication using multimodal imaging (MRI and FDG-PET) and SNP data. They described each feature with a kernel and used the modality information to group kernels to facilitate variable selection at both feature and group levels. An innovative structured sparsity regularization term was further introduced to enable feature sparsity within each modality but encourage non-sparse solution modality-wisely. The intuition is based on the hypothesis that different modalities offer complementary information and including modalities with weaker predictive power may help capture valuable complementary information. Their empirical study yielded promising results.
In [199], Singanamalli proposed a “Cascaded Multi-view Canonical Correlation” (CaMCCo) for classifying CN, MCI and AD using multidimensional imaging, genetics, biomarker and cognitive data. The cascaded framework first classified all subjects as CN vs cognitively impaired (CI), and further classified CI subjects as MCI vs AD. For each binary classification, the class label was used as a separate variable set. Integrating the class label set with all the other modalities, supervised multiview CCA (sMVCCA) [200] was employed to obtain a low dimensional representation of each involved modality, followed by a modality selection step using the diagnostic information. Naive Bayes classification method was then applied to the fused representation of selected modalities to learn a classifier. Empirical study showed that fusion of selected modalities outperformed that using each individual modality and that integrating all the modalities.
Although neural network (NN) models have been highly successful in making prediction for many recent applications in various fields such as computer vision and natural language processing, they have not been widely used in brain imaging genomics. This could be largely attributed to the limited sample size and high dimensionality of the existing imaging genomics data. Some attempts have been made to address this challenge. Below we review a couple of recent studies using NN methods for AD outcome prediction via integrating brain imaging genomics data.
For example, in [201], Zhou et al. presented a three-stage deep feature learning and fusion framework to detect disease status (e.g., CN/MCI/AD) via integrating MRI, FDG-PET and SNP data. In the first stage, they learned feature representation for each modality independently. In the second stage, they used the features learned in Stage 1 to learn joint latent features for each pair of modalities. In the third stage, they learned the diagnostic label using the features learned in Stage 2. This framework can address several challenges. 1) Learning high-level features for each modality in Stage 1 could alleviate data heterogeneity issue. 2) Using the maximum number of all available samples at each stage could help address both the high-dimension-low-sample-size and incomplete modality data issues. Their empirical study showed very promising results that the proposed NN method outperformed a number of non-NN based competing methods.
In [202], Ning et al. proposed another NN framework to detect AD or MCI-to-AD conversion using MRI and SNP data. Their strategy to address high-dimension-low-sample-size is twofold. 1) Instead of examining all the SNPs and imaging QTs, their analysis only targeted at 16 AD-related QTs and 19 AD-related SNPs to reduce the dimensionality. 2) They designed a relatively simple NN with 2 hidden layers, and explored 2, 4, 8, up to 64 nodes in each layer to reduce the model complexity. The proposed NN was fully connected between layers, coupled with shortcut connections linking all the input nodes directly to the output layer. Their empirical study showed promising results that the proposed NN model outperfonned a linear regression model.
Table IX summarizes example studies using machine learning methods for outcome prediction via integrating imaging and genomics data. Some studies directly applied conventional learning methods to the combined data sets and showed improved performances. Some studies developed new learning models to address various challenges such as feature selection at group level, and joint classification and regression. With a couple of successful attempts, NN models have started to attract attentions in the field of brain imaging genomics.
TABLE IX.
Example studies using machine learning methods for outcome prediction via integrating imaging and genomics data.
| Ref | Notes |
|---|---|
| [187] | Naive Bayes classifier, predicting MCI-to-AD conversion |
| [188] | Composite multivariate polygenic and neuroimaging score, predicting MCI-to-AD conversion |
| [190] | Cox proportional hazard model, predicting time to progression from MCI to AD, integrating PHS, atrophy score and MMSE |
| [193] | JCRMML (joint classification and regression framework for multimodal multitask learning), joint logistic regression and linear regression, feature selection at modality level for each outcome, feature selection across all the outcomes |
| [194] | Multiple kernel learning (MKL), high-order graph matching based feature selection (HGM-FS), sparse multimodal learning (SMML), AD prediction using MRI, FDG-PET, CSF and SNP data |
| [198] | SSKL (structured sparse kernel learning), sparsity inside modalities, dense combination between modalities |
| [199] | CaMCCo (Cascaded Multi-view Canonical Correlation), supervised multiview CCA with class label as a new variable set |
| [201] | Stage-wise deep neural network, addressing issues such as data heterogeneity, high-dimension-low-sample-size & incomplete data |
| [202] | Neural network model with two hidden layers, AD outcome prediction using 16 imaging QTs and 19 SNPs |
B. Joint association learning and outcome prediction
Here we review a few example studies exploring the associations among genomics, imaging and outcome. These include four SCCA based studies [203], [204], [205], [206], one study using classic mediation analysis [207], and one study using a newly proposed Bayesian method [208]. While two studies [206], [207] performed the analyses using the PNC data, the other four studies were conducted on the ADNI data.
In [203], Yan et al. proposed a “discriminative SCCA” model in order to identify disease-relevant imaging proteomics associations. Instead of SNP data, Yan et al. analyzed the protein expression data collected from CSF and plasma and studied their relationship to imaging QTs and multi-class diagnostic label (CN, MCI, AD). Figure 10(a) shows a schematic representation of the DSCCA model. It introduced a new graph laplacian regularization to the standard SCCA framework. The graph is defined on the subjects, where subjects within the same diagnositic group are connected. This regularization encourages the identification of canonical components with discriminative power. Figure 10(b) shows a comparision between DSCCA and SCCA, where the imaging component Yv is plotted against the proteomic component Xu. It is clear that the components identified by DSCCA have more discriminative power than those by SCCA. The empirical study using cross-validation showed that DSCCA yielded higher canonical coefficient (CC) on the test data than SCCA.
Fig. 10.
(a) Schematic representation of the DSCCA model [203]. DSCCA incorporates a regularization into SCCA to encourage the identification of canonical components with discriminative power. (b) The imaging component Yv is plotted against the proteomic component Xu. DSCCA components are clearly more discriminative than SCCA components. [Image in (b) is reproduced here from an Open Access chapter by World Scientific Publishing Company [203]].
In [204], Hao et al. proposed an alternative strategy to identify pairwise associations among genomics, imaging, and outcome(s). This was directly implemented by a three way SCCA, which was a joint learning model by combining three pairwise SCCA models to learn a single compoent for each modality (i.e., genomics, imaging, or outcome). Two empirical studies were performed on ADNI imaging genomics data: one using a set of cognitive scores as outcome, and the other using diagnostic status as outcome. In a cross-validation setting, both studies using three way SCCA yielded higher CCs on the test data than that using SCCA.
In [205], Du et al. proposed a joint learning model by combining SCCA and Regression (SCCAR) to identify diagnosisrelevant imaging genomics associations. Let z be the outcome data. The model is defined as:
| (22) |
Here, they would like to jointly learn the imaging component Yv so that it could predict the outcome z (see the first regression term) and is correlated with the genomic component (see the second CCA term). In the empirical study, they used l1 norm for both and . The cross-validation results showed that SCCAR could identify stronger canonical correlations than SCCA in the test data.
In [206], Zille et al. proposed a “Multi-Task Collaborative Regression” (MT-CoReg) method to extract outcome-relevant variables that are co-expressed in both imaging and genomics modalities. Simliar to SCCAR, MT-CoReg was also formulated as a joint learning model by integrating SCCA and linear regression. The major difference is that MT-CoReg allows the imaging component used in the linear regression to predict outcome to be different from that used in the SCCA to correlated with the genetic component. An empirical study was performed on the PNC cohort to analyze the SNP and fMRI data for the study of learning ability as outcome, and yielded promising results.
In [207], Bi et al. performed a genome-wide mediation analysis in order to detect complicated mechanisms of genetic inferences on the outcome implicitly through intermediate imaging QTs. The study was performed on the PNC cohort, analyzing 445,205 SNPs, 204 imaging QTs, and 104 psychiatric and cognitive traits as outcomes. Mediation analysis was performed at the individual marker level using a three-stage procedure. 1) GWAS was performed to identify significant SNP-QT pairs. 2) Each outcome was regressed against each candidate SNP. 3) Each outcome was regressed against each identified SNP and its associated QT. A mediation relationship is established if the SNP is significant in 1) and 2), QT is significant in 3), and the absolute effect size of the SNP is smaller in 3) than 1). Their analysis identified an NMNAT2 SNP assciated with a psychiatric trait through the volume of left superior frontal region.
Performing brain wide genome wide analysis at the single marker level faces a major challenge on multiple comparison correction. To overcome this limitation, A common approach is to learn one single multivariate multiple regression model coupled with some sparsity-inducing regularization. In [208], Batmanghelich proposed such as Bayesian method for probabilistic modeling of imaging, genetics and diagnosis. The goal of this method is to jointly learn the following two predictive relationships in a single Bayesian model: 1) using imaging QTs to predict diagnosis, and 2) using SNPs to predict imaging QTs. The joint model can help identify a set of imaging QTs that not only have a genetic basis, but also are associated with diagnostic status. Their empirical study on the ADNI data yielded promising results.
Table X summarizes example studies for joint learning of imaging genomics associations and outcome prediction model. Four of these studies introduced into the standard SCCA framework one or more components that incorporate outcome information. Empirical studies demonstrated that including outcome information as additional constraints could identify stronger imaging genomics associations, indicating this strategy has a potential to capture true signals and reduce model overfitting.
TABLE X.
Example studies for joint learning of imaging genomics associations and outcome prediction model.
| Ref | Notes |
|---|---|
| [203] | DSCCA (discriminative SCCA), disease-relevant imaging proteomics associations, graph laplacian |
| [204] | Three way SCCA among genomics, imaging and outcomes |
| [205] | SCCAR (joint learning by combining SCCA and regression) |
| [206] | MT-CoReg (Multi-Task Collabora-tive Regression), joint regression and SCCA model |
| [207] | Genome-wide mediation analysis, genetic influence on phenotypica outcome mediated by imaging endophenotype |
| [208] | Bayesian model to identify imaging QTs that have genetic basis and are associated to diagnosis |
VIII. Discussion and Conclusions
A. Summary of learning problems and reviewed methods
We have reviewed three categories of learning problems in brain imaging genomics, as shown in Figure 1(a). In the first catogory, we focused on the learning problem of heritability estimation of brain imaging QTs. The heritability of a trait is defined as the proportion of its observed variance explained by the genetic factors. Given high dimensional brain imaging data, heritability estimation can be used as a screening tool to extract heritable QTs as attractive targets for in-depth genetic analyses. We discussed two types of methods for heritability estimation: one based on data collected using twin or family designs, and the other based on genome-wide genotyping data.
In the second category, we focused on the problem of learning imaging genomics associations, a major theme studied in brain imaging genomics to gain new insights into the genetic and molecular mechanisms of the brain structure and function. Given the high-dimensionality-small-sample-size challenge we are facing in brain imaging genomics, a wide range of methods have been proposed to increase statistical power and enhance biological interpretation via reducing dimensionality, measuring collective effects, and incorporating prior knowledge. We first reviewed a few fundamental strategies, including single-SNP-single-QT methods, polygenic risk scores, multi-SNP methods, multi-trait methods, pathway and network enrichment methods, and interaction methods. We then discussed the important topics of power and sample size and reviewed relevant meta-analysis strategies. After that, we reviewed two major types of multi-sNP-multi-QT methods: multivariate regression models and bi-multivariate correlation models.
In the third category, we focused on the learning problem of integrating imaging and genomics for outcome prediction. This is an important topic studied in brain imaging genomics to gain valuable insights into the outcome-relevant neurobiologocal mechanisms at the genetic, molecular and macroscale brain system levels. Imaging and genomics data capture subject’s characteristics at different scales and from different perspectives, and are naturally considered to contain complementary information for improved outcome prediction. Various machine learning and deep learning methods have been proposed to address relevant data integration challenges such as high dimensionality, small sample size, heterogeneity and incompleteness. We reviewed these learning strategies for outcome prediction using both brain imaging and genomics data, as well as joint learning strategies that could not only identify associations between imaging and genomics data but also use them to accurately predict outcomes.
B. Biomedical application considerations
Figure 1(b) summarizes some biomedical application considerations regarding the studied data sets across multiple disciplines including brain imaging, genomics and clinical outcome research. Careful consideration of the data characteristics and relevant biological structure and knowledge can often provide valuable guidance on the selection of an appropriate method for practical applications. A brain imaging genomics application involves the integrated analysis of brain imaging data, genomics data and optionally clinical outcome data.
First, let us take a look at brain imaging data. Imaging QTs can be extracted from brain scans at multiple scales (e.g., voxels, RoIs, connectivity matrix, etc). Below we discuss a few example strategies for dealing with analytic challenges with these QTs. Although voxelwise analysis (e.g., [57]) can capture the finest details in the brain, it is often under-powered due to its heavy burden of multiple comparison correction and high spatial correlation. There are several strategies to overcome this limitation: 1) use methods like random field theory (e.g., [72]) to reduce the multiple testing burden via embracing spatial correlation, 2) collapse voxel measures into RoI measures to greatly reduce the number of statistical tests (e.g., [37]), 3) measure collective effect of all voxels within an ROI to reduce the test number (e.g., [95]), and 4) perform only targeted SNP analysis (e.g., [49]). Compared with voxelwise analysis, RoI-based analysis has a greatly reduced multiple testing burden, but may not be able to capture detailed spatial patterns. one strategy to leverage this issue is to first identify a small number of interesting SNPs from ROI-based analysis and then map their effects onto the brain in a voxelwise fashion (e.g., [37]). Connectivity matrices are another type of high dimensional imaging QTs. To alleviate the multiple testing burden, besides conducting targeted QT analyses, one can perform heritability analysis to select only highly heritable connectivity QTs for in-depth genetic analysis (e.g., [38]).
Brain imaging data can be collected with multiple modalities. Given the availability of multimodal imaging data, one can employ multimodal learning strategies (e.g., [193]) to make full use of the complementary information offered by multiple imaging modalities. one may also consider methods like [201] to address potential challenges related to multimodal imaging data (e.g., high dimensionality, small sample size, heterogeneity and incompleteness). In addition, brain imaging data can be longitudinal. A longitudinal QT offers a unique power to capture progressive pattern a cross-sectional QT cannot describe and thus is an important biomarker to study. one simple approach could be to examine some summary statistics of a longitudinal QT (e.g., [48]). One can also employ more complicated longitudinal learning models (e.g., [151], [149]) to identify more detailed longitudinal patterns. Finally, there are different types of prior knowledge and structure that can be used to group and connect imaging QTs. For example, voxels can be grouped by ROIs (e.g., [169]), ROIs can be grouped by network components (e.g., DMN [88]), and connected by brain networks (e.g., [108]). Incorporating these prior knowledge into the learning model can help alleviate overfitting and yield biologically interpretable findings.
Second, let us take a look at the genomic data. Traditional GWAs performs univariate analysis at the sNP level, with a huge burden on multiple testing correction. To address this challenge, the following are a few possible strategies: 1) examine a few target sNPs (e.g., [49]) or a polygenic risk score (see section III-B), 2) perform analysis at the sNP-set level (e.g., LD block, gene) (e.g., [71]), 3) perform enrichment analysis using pathways and networks (see Section III-E), and 4) examine a single model involving multiple SNPs (see Sections V-VI). Here, the LD blocks, genes, pathways, and functional interaction networks are biologically meaningful knowledge and structures. They can also be incorporated into the multivariate learning models to reduce overfitting and improve model interpretability.
Third, let us take a look at the clinical outcome data such as disease stage, impairment score and progression status. These are critical data sources for the study of brain disorders. There are several strategies to perform outcome-relevant brain imaging genomics studies. One is to first identify outcome-relevant imaging QTs and then reveal its genetic basis. This can be done as a two step procedure (e.g., [207]) or via a joint learning model (e.g., [208]). The second strategy is to combine imaging and genomics data for an improved outcome prediction (see Section VII-A). The third strategy is to use outcome information to guide the search for imaging genomics associations, which can often reduce overfitting and identify stronger associations (e.g., [203]).
C. Statistical and machine learning considerations
Figure 1(c) summarizes some statistical and machine learning considerations for brain imaging genomics. The first important consideration is the statistical power, since the existing brain imaging data sets typically have high dimensionality and relatively small sample size. The following are a few strategies on how to increase study power. First, compared with case-control analyses, QT studies are shown to have increased statistical power [4], [209]. The second strategy is to employ more powerful multiple testing correction methods by taking into consideration the correlation within imaging and genomics data (e.g., [44]). The third strategy is to increase the sample size via mega- or meta-analysis on combined data set from multiple collaborative sites (see Section IV). The fourth strategy is to reduce the test number by pooling low level measures into high level ones (e.g., averaging voxel measures into ROI measures, aggregating SNP statistics into gene statistics), or simply by applying a single multivariate model involving all the studied SNPs and QTs.
Another important methodological consideration is how to control overfitting and reduce spurious findings for multivariate learning models. To reduce the risk of overfitting, the data fitting flexibility of a learning model should be properly-controlled. One strategy is to reduce the number of variables in the model via dimensionality reduction. For example, one can condense fine level SNP/voxel measures into high level gene/ROI components (e.g., [71], [37]). Another strategy is to include regularization terms in the model to control data fitting flexibility. For example, to increase the feature selection stability, we can group SNPs by LD block (e.g., [169]). To help biological interpretation, we can group SNPs by gene, pathway or network, and/or ROIs by brain network (e.g., [146], [107], [108]). In addition, incorporating outcome information into the learning model can help select outcome-relevant SNP and QT markers and reduce overfitting (e.g., [203]).
There are a few other methodological considerations we briefly discuss below. 1) To help biological interpretation, we can incorporate prior knowledge and structure into the learning methods and try to identify associations between meaningful biological entities such as genes, pathways, ROIs, and genetic and brain networks. One strategy is to perform GWAS enrichment analysis (e.g., [90], [99]) to measure collective effects at the set level. This can reduce the number of tests and increase the detection power. Another strategy is to regularize the learning model using these sources of prior knowledge and structure to guide our search for meaningful associations (e.g., [106], [107], [108], [146]). In both cases, findings are associated with meaningful functional annotation implicating potential biological mechanism and interpretation, which make them less likely to be false discoveries.
2) Scalability is often an important consideration in BWGW studies, particularly if one wants to perform analyses at the voxelwise level. Several efficient algorithms (e.g., [50], [72]) have been proposed to address this consideration. One effective strategy is a global sure independence screening (GSIS) procedure used in [50], which can greatly reduce the search space size from NsNv to ~ N0Nv for N0 ⪡ Ns. Here Ns is the number of SNPs, and Nv is the number of voxels. Another valuable strategy is a fast permutation procedure, proposed in [72], that uses parametric tail approximation to provide accurate p estimations in an efficient manner.
3) Biased sampling is another potential cause for spurious findings. Most GWAS studies (e.g., ADNI) are based on case-control design, and the data are typically a biased sample of the target population. Directly correlating imaging QTs (as secondary traits) with genotype may lead to biased inference generating misleading results. This issue has been considered in several studies (e.g., [52], [55]). Although the standard linear analysis was found to be generally valid on the ADNI data in [52], simulation studies in [55] showed that linear regression models without adjusting for biased sampling demonstrated severely inflated Type I error rates in some cases. In general, caution should be taken while analyzing imaging QT data as secondary phenotypes in case-control studies.
4) Gene-gene interaction has also been studied to identify epistatic genetic effects on imaging QT and to help address miss heritability. Given an exponentially increasing number of possible tests, a major topic in epistatic studies is to find an effective search strategy to reduce computational time and increase statistical power. One strategy is to examine only a subset of candidate interactions with a potential biological mechanism suggested by functional interaction networks or biological pathways (e.g., [109], [112]). Another strategy is to perform data-driven screening to focus on the analysis of a small number of most promising candidate interactions (e.g., [109], [114]).
D. Scientific and clinical impact
Our previous reviews of ADNI brain imaging genomics findings [4], [5] indicated that numerous genes contributing to increased risk for or protection against AD have been identified and replicated using multimodal brain imaging data. These findings implicated immune, mitochondrial, cell cycle/fate, and other biological processes and advanced the mechanistic understanding of AD. Below we briefly discuss a few new example findings with potential scientific and clinical impacts.
According to the most recent ENIGMA review paper [2], the consortium’s GWAS analyses have revealed over 200 genetic loci associated with cortical thickness or surface area, and over 40 common genetic variants associated with subcortical volumes. In addition, the recent UK Biobank GWAS of 3,144 brain imaging QTs identified 148 clusters of SNP-QT associations [12]. These results have provided substantial new insights into the genetic landscape of the brain, and offered great scientific value that could impact and advance research on normal brain development and aging, and neurological and psychiatric disorders.
Given the timelines set in place by the National Alzheimer Project Act (NAPA) (e.g., the goal of effectively treating or preventing AD and related dementias by 2025) and that many clinical trials of therapies for AD have failed in recent years, it becomes an extremely important and timely topic to study brain imaging genomics in AD. In particular, these efforts could accelerate progress in better understanding of the genetic, molecular and neurobiological mechanisms of AD and have subsequent translational impact on disease modeling and drug development. For example, recent ADNI studies have yielded prominent imaging genomics findings such as 1) BCHE and IL1RAP with amyloid QTs [210], [211], 2) PARP1, CARD10, REST, FASTKD2 and ADORA2A with hippocampal morphometry [212], [213], [214], [215], 3) INPP5D with cerebral blood flow [216], and 4) APOE with multimodal imaging QTs [48], [108], [174]. Some of these findings have contributed to genetically based drug targets leading to novel disease model systems (e.g., creation of the IL1RAP knockout mouse [217], nomination of INPP5D as a modeling target (http://agora.ampadportal.org)).
Finally, for many novel statistical and machine learning methods reviewed here, the authors often used the ADNI data to demonstrate the power of the methods to detect interesting and novel imaging genomics signals. Some yielded confirmatory findings matching previous studies, showing the effectiveness of these methods. Some identified novel signals missed by existing methods, showing improved detection power. Of note, the generalizability of findings from many of these new methods needs to be evaluated in additional independent data sets to demonstrate their broader impact in the future.
E. Related work and future directions
In this work, we mostly reviewed the methods developed and employed for analyzing ADNI and ENIGMA data. Similar methods have been investigated in the study of other neurological and psychiatric disorders. For example, the pICA method was first proposed and then widely used in studies of psychiatric disorders [218]. Various SCCA and other multivariate models (e.g., [219], [220], [221], [222], [223]) have been developed and employed in brain imaging genomics applications to study psychiatric disorders. Additional details are available in [224], where Chen et al. provided a recent review on neuroimaging genomics analyses and their translational potential to diagnosis and treatment in mental disorders.
Thanks to the open science nature of the ADNI project and the large-scale global alliance formed by ENIGMA, a large number of researchers around the world have had the chance to analyze the ADNI and ENIGMA data, resulting in a major growth of literature in new statistical and machine learning methods for brain imaging genomics. Of note, the generalization of many of these new methods remains to be evaluated in other independent data sets, which will be an interesting and promising future direction. In particular, given the rapid growth and sheer number of these new developments, we observe no lack of innovation and expect to see the impact of these methods or their enhanced versions to permeate biomedical studies in brain imaging genomics.
Integrating imaging and omics data is also an active research topic in cancer studies, which is often referred to as radiogenomics [225]. In these studies, in addition to SNP data, multi-omics data (e.g., transcriptomics, proteomics, metabolomics, epigenomics) are often collected from the actual tumor tissues. So relating multi-omics data to imaging data becomes a study focus. Note that the omics data are tissue-specific. Thus, the methods reviewed in this paper are mostly focused on relating SNP data to imaging QTs, mainly due to the lack of the available brain tissue in these in-vivo studies. However, with the increasing accumulation of brain samples in some landmark studies (e.g., AMP-AD [226]), more and more omics data will be available for the study of brain disorders. A promising future direction is to adapt many radiogenomics approaches developed for cancer research to the study of brain imaging genomics.
As we aim at understanding mechanisms and pathways, another challenge in brain imaging genomics is how to handle spurious correlations leading to erroneous conclusions. Thus, replication in independent cohorts will be an important step to complete in order to identify true signals. Some sources of spurious correlations such as overfitting and biased sampling have been studied as described earlier. However, systematic investigation of various confounding factors is an underexplored topic and warrants further investigation.
Deep learning models have been highly successful in addressing data-driven problems in biology and medicine [227]. However, they have not been widely used in brain imaging genomics, partly due to the limited sample size and high dimensionality of the existing imaging and genomics data sets. Some recent attempts have been made to develop effective deep learning models for outcome prediction via integrating brain imaging genomics data (e.g., [201]). Given that deep learning has been producing impressive results in both medical image analysis [228], [229] and multi-omics research [230], it is a promising future direction to develop deep learning methods for solving pressing problems in brain imaging genomics.
Given the unprecedented scale, complexity and heterogeneity of the fast growing Big Data in brain imaging genomics, we are facing a variety of other methodological challenges that suggest promising and exciting future research directions. 1) Although multi-cohort integrative data analysis can offer increased statistical power, one major obstacle is that the available data modalities often vary across different studies. Thus, one promising direction is to develop novel machine learning or transfer learning methods that can effectively handle incomplete data modalities and facilitate multi-cohort data integration. 2) Most methods reviewed here analyzed genotyping data and were not designed for examining whole genome/exome sequencing (WGS/WES) data. The rapid growth of WGS/WES data in brain imaging genomics calls for new statistical and machine learning methods that can properly handle their ultrahigh dimensionality and resolution as well as effectively identify both common and rare genetic variants related to imaging QTs. 3) There is also an urgent need for novel scalable computational strategies to support large-scale consortium-based collaborative efforts. For consortia with one single centralized data repository, cloud-based computational and informatics tools are needed to enable the users to directly analyze large-scale data in the cloud. For consortia with multiple local data repositories, distributed computation methods and frameworks could be established to handle the decentralized data sets.
The rapid growth of brain imaging genomics as an emerging data science field is greatly attributed to the public availability of valuable imaging and genomics data sets. For example, thanks to the open-science nature of the ADNI project, hundreds of publications using ADNI imaging genomics data have been produced in the past decade, yielding not only innovative machine learning methods but also novel biomedical discoveries. Similar to ADNI and ENIGMA, more and more landmark studies are producing big data including multidimensional imaging and omics modalities, and make them available to the research community. Shown below are some example landmark studies: 1) Alzheimers Disease Neuroimaging Initiative (ADNI) [1], 2) Enhancing NeuroImaging Genetics through Meta Analysis (ENIGMA) [7], [8], 3) UK Biobank [3], 4) Human Connectome Project (HCP) [231], 5) Accelerating Medicines Partnership - Alzheimer’s Disease (AMP-AD) [226], 6) Mind Clinical Imaging Consortium (MCIC) [232], 7) Pediatric Imaging, Neurocognition, and Genetics study (PING) [233], 8) Parkinsons Progression Markers Initiative (PPMI) [234], 9) The Cancer Genome Atlas (TCGA) [235], and 10) The Cancer Imaging Archive (TCIA) [236]. With this growing availability of brain imaging genomics data, we anticipate to observe many more advances in machine learning and their applications to brain imaging genomics, which will significantly contribute to biomedical discoveries in brain science and the study of brain disorders.
Acknowledgment
We thank Bertrand Thirion and three anonymous reviewers for providing highly valuable comments and feedback on the manuscript. LS was funded in part by NIH R01 EB022574, NIH R01 LM011360, NIH RF1 AG063481 and NSF IIS 1837964. PMT was funded in part by the NIH Big Data to Knowledge (BD2K) program under consortium grant U54 EB020403, by the ENIGMA World Aging Center (NIA R56 AG058854), by the ENIGMA Sex Differences Initiative (R01 MH116147), and a grant to the ENIGMA-PGC PTSD Working Group (R01 MH111671). Additional support was provided by P41 EB015922, RF1 AG041915, U01 AG024904, RF1 AG051710, R21 AG056782, and P01 AG026572.
Contributor Information
Li Shen, Department of Biostatistics, Epidemiology and Informatics, Perelman School of Medicine, University of Pennsylvania, PA 19104, USA.
Paul M. Thompson, Imaging Genetics Center, Mark & Mary Stevens Institute for Neuroimaging & Informatics, Keck School of Medicine, University of Southern California, Los Angeles, CA 90232, USA
References
- [1].Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack J, R. C, Jagust W, Morris JC, Petersen RC, Saykin AJ, Shaw LM, Toga AW, Trojanowski JQ, and I. Alzheimer’s Disease Neuroimaging, “Recent publications from the alzheimer’s disease neuroimaging initiative: Reviewing progress toward improved ad clinical trials,” Alzheimers Dement, vol. 13, no. 4, pp. e1–e85, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28342697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Thompson P, Jahanshad N, Ching CRK, Salminen L, I Thomopoulos S, Bright J, Baune B, Bertoln S, Bralten J, Bruin WB, Blow R, Chen J, Chye Y, Dannlowski U, de Kovel C, Donohoe G, Eyler L, Faraone SV, Favre P et al. , “ENIGMA and global neuroscience: A decade of large-scale studies of the brain in health and disease across more than 40 countries,” PsyArXiv, July 2019. [Online]. Available: https://psyarxiv.com/qnsh7/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, Downey P, Elliott P, Green J, Landray M, Liu B, Matthews P, Ong G, Pell J, Silman A, Young A, Sprosen T, Peakman T, and Collins R, “Uk biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age,” PLoS Med, vol. 12, no. 3, p. e1001779, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25826379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Shen L, Thompson PM, Potkin SG, Bertram L, Farrer LA, Foroud TM, Green RC, Hu X, Huentelman MJ, Kim S, Kauwe JS, Li Q, Liu E, Macciardi F, Moore JH, Munsie L, Nho K, Ramanan VK, Risacher SL, Stone DJ, Swaminathan S, Toga AW, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Genetic analysis of quantitative phenotypes in ad and mci: imaging, cognition and biomarkers,” Brain Imaging Behav, vol. 8, no. 2, pp. 183–207, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/24092460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Saykin AJ, Shen L, Yao X, Kim S, Nho K, Risacher SL, Ramanan VK, Foroud TM, Faber KM, Sarwar N, Munsie LM, Hu X, Soares HD, Potkin SG, Thompson PM, Kauwe JS, Kaddurah-Daouk R, Green RC, Toga AW, Weiner MW, and I. Alzheimer’s Disease Neuroimaging, “Genetic studies of quantitative mci and ad phenotypes in adni: Progress, opportunities, and plans,” Alzheimers Dement, vol. 11, no. 7, pp. 792–814, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26194313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Veitch DP, Weiner MW, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack J, R. C, Jagust W, Morris JC, Petersen RC, Saykin AJ, Shaw LM, Toga AW, Trojanowski JQ, and I. Alzheimer’s Disease Neuroimaging, “Understanding disease progression and improving alzheimer’s disease clinical trials: Recent highlights from the alzheimer’s disease neuroimaging initiative,” Alzheimers Dement, vol. 15, no. 1, pp. 106–152, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30321505 [DOI] [PubMed] [Google Scholar]
- [7].Thompson PM, Stein JL, Medland SE, Hibar DP, Vasquez AA, Renteria ME, Toro R, Jahanshad N, Schumann G, Franke B, Wright MJ, Martin NG, Agartz I, Alda M, Alhusaini S, Almasy L, Almeida J, Alpert K, Andreasen NC, Andreassen OA, Apostolova LG, Appel K, Armstrong NJ, Aribisala B, Bastin ME, Bauer M, Bearden CE, Bergmann O, Binder EB, Blangero J, Bockholt HJ, Boen E, Bois C, Boomsma DI, Booth T, Bowman IJ, Bralten J, Brouwer RM, Brunner HG, Brohawn DG, Buckner RL, Buitelaar J, Bulayeva K, Bustillo JR, Calhoun VD, Cannon DM, Cantor RM, Carless MA, Caseras X, Cavalleri GL, Chakravarty MM, Chang KD, Ching CR, Christoforou A, Cichon S, Clark VP, Conrod P, Coppola G, Crespo-Facorro B, Curran JE, Czisch M, Deary IJ, de Geus EJ, den Braber A, Delvecchio G, Depondt C, de Haan L, de Zubicaray GI, Dima D, Dimitrova R, Djurovic S, Dong H, Donohoe G, Duggirala R, Dyer TD, Ehrlich S, Ekman CJ, Elvsashagen T, Emsell L, Erk S, Espeseth T, Fagerness J, Fears S, Fedko I, Fernandez G, Fisher SE, Foroud T, Fox PT, Francks C, Frangou S, Frey EM, Frodl T, Frouin V, Garavan H, Giddaluru S, Glahn DC, Godlewska B, Goldstein RZ, Gollub RL, Grabe HJ et al. , “The enigma consortium: large-scale collaborative analyses of neuroimaging and genetic data,” Brain Imaging Behav, vol. 8, no. 2, pp. 153–82, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/24399358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Thompson PM, Andreassen OA, Arias-Vasquez A, Bearden CE, Boedhoe PS, Brouwer RM, Buckner RL, Buitelaar JK, Bulayeva KB, Cannon DM, Cohen RA, Conrod PJ, Dale AM, Deary IJ, Dennis EL, de Reus MA, Desrivieres S, Dima D, Donohoe G, Fisher SE, Fouche JP, Francks C, Frangou S, Franke B, Ganjgahi H, Garavan H, Glahn DC, Grabe HJ, Guadalupe T, Gutman BA, Hashimoto R, Hibar DP, Holland D, Hoogman M, Pol HEH, Hosten N, Jahanshad N, Kelly S, Kochunov P, Kremen WS, Lee PH, Mackey S, Martin NG, Mazoyer B, McDonald C, Medland SE, Morey RA, Nichols TE, Paus T, Pausova Z, Schmaal L, Schumann G, Shen L, Sisodiya SM, Smit DJA, Smoller JW, Stein DJ, Stein JL, Toro R, Turner JA, van den Heuvel MP, van den Heuvel OL, van Erp TGM, van Rooij D, Veltman DJ, Walter H, Wang Y, Wardlaw JM, Whelan CD, Wright MJ, Ye J, and E. Consortium, “Enigma and the individual: Predicting factors that affect the brain in 35 countries worldwide,” Neuroimage, vol. 145, no. Pt B, pp. 389–408, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26658930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Bearden CE and Thompson PM, “Emerging global initiatives in neurogenetics: The enhancing neuroimaging genetics through meta-analysis (enigma) consortium,” Neuron, vol. 94, no. 2, pp. 232–236, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28426957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Bycroft C, Freeman C, Petkova D, Band G, Elliott LT, Sharp K, Motyer A, Vukcevic D, Delaneau O, O’Connell J, Cortes A, Welsh S, Young A, Effingham M, McVean G, Leslie S, Allen N, Donnelly P, and Marchini J, “The uk biobank resource with deep phenotyping and genomic data,” Nature, vol. 562, no. 7726, pp. 203–209, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30305743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Alfaro-Almagro F, Jenkinson M, Bangerter NK, Andersson JLR, Griffanti L, Douaud G, Sotiropoulos SN, Jbabdi S, Hernandez-Fernandez M, Vallee E, Vidaurre D, Webster M, McCarthy P, Rorden C, Daducci A, Alexander DC, Zhang H, Dragonu I, Matthews PM, Miller KL, and Smith SM, “Image processing and quality control for the first 10,000 brain imaging datasets from uk biobank,” Neuroimage, vol. 166, pp. 400–424, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29079522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Elliott LT, Sharp K, Alfaro-Almagro F, Shi S, Miller KL, Douaud G, Marchini J, and Smith SM, “Genome-wide association studies of brain imaging phenotypes in uk biobank,” Nature, vol. 562, no. 7726, pp. 210–216, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30305740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Liu J and Calhoun VD, “A review of multivariate analyses in imaging genetics,” Front Neuroinform, vol. 8, p. 29, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24723883 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Yan J, Du L, Yao X, and Shen L, Chapter 14 - Machine learning in brain imaging genomics. Academic Press, 2016, pp. 411–434. [Online]. Available: http://www.sciencedirect.com/science/article/pii/B9780128040768000141 [Google Scholar]
- [15].Mufford MS, Stein DJ, Dalvie S, Groenewold NA, Thompson PM, and Jahanshad N, “Neuroimaging genomics in psychiatry-a translational approach,” Genome Med, vol. 9, no. 1, p. 102, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29179742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Liu J, Chen J, Perrone-Bizzozero N, and Calhoun VD, “A perspective of the cross-tissue interplay of genetics, epigenetics, and transcriptomics, and their relation to brain based phenotypes in schizophrenia,” Front Genet, vol. 9, p. 343, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30190726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Topol EJ, “High-performance medicine: the convergence of human and artificial intelligence,” Nat Med, vol. 25, no. 1, pp. 44–56, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30617339 [DOI] [PubMed] [Google Scholar]
- [18].Visscher PM, Hill WG, and Wray NR, “Heritability in the genomics era–concepts and misconceptions,” Nat Rev Genet, vol. 9, no. 4, pp. 255–66, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/18319743 [DOI] [PubMed] [Google Scholar]
- [19].Thompson PM, Cannon TD, Narr KL, van Erp T, Poutanen VP, Huttunen M, Lonnqvist J, Standertskjold-Nordenstam CG, Kaprio J, Khaledy M, Dail R, Zoumalan CI, and Toga AW, “Genetic influences on brain structure,” Nat Neurosci, vol. 4, no. 12, pp. 1253–8, 2001. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/11694885 [DOI] [PubMed] [Google Scholar]
- [20].Thompson PM, Ge T, Glahn DC, Jahanshad N, and Nichols TE, “Genetics of the connectome,” Neuroimage, vol. 80, pp. 475–88, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23707675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Brun C, Lepore N, Pennec X, Chou YY, Lee AD, Barysheva M, de Zubicaray G, Meredith M, McMahon K, Wright MJ, Toga AW, and Thompson PM, “A tensor-based morphometry study of genetic influences on brain structure using a new fluid registration method,” Med Image Comput Comput Assist Interv, vol. 11, no. Pt 2, pp. 914–21, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/18982692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Chou YY, Lepore N, Chiang MC, Avedissian C, Barysheva M, McMahon KL, de Zubicaray GI, Meredith M, Wright MJ, Toga AW, and Thompson PM, “Mapping genetic influences on ventricular structure in twins,” Neuroimage, vol. 44, no. 4, pp. 1312–23, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19041405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Shen KK, Rose S, Fripp J, McMahon KL, de Zubicaray GI, Martin NG, Thompson PM, Wright MJ, and Salvado O, “Investigating brain connectivity heritability in a twin study using diffusion imaging data,” Neuroimage, vol. 100, pp. 628–41, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24973604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Shen KK, Dore V, Rose S, Fripp J, McMahon KL, de Zubicaray GI, Martin NG, Thompson PM, Wright MJ, and Salvado O, “Heritability and genetic correlation between the cerebral cortex and associated white matter connections,” Hum Brain Mapp, vol. 37, no. 6, pp. 2331–47, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27006297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Fu Y, Ma Z, Hamilton C, Liang Z, Hou X, Ma X, Hu X, He Q, Deng W, Wang Y, Zhao L, Meng H, Li T, and Zhang N, “Genetic influences on resting-state functional networks: A twin study,” Hum Brain Mapp, vol. 36, no. 10, pp. 3959–72, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26147340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Kochunov P, Patel B, Ganjgahi H, Donohue B, Ryan M, Hong EL, Chen X, Adhikari B, Jahanshad N, Thompson PM, Van’t Ent D, den Braber A, de Geus EJC, Brouwer RM, Boomsma DI, Hulshoff Pol HE, de Zubicaray GI, McMahon KL, Martin NG, Wright MJ, and Nichols TE, “Homogenizing estimates of heritability among solar-eclipse, openmx, apace, and fphi software packages in neuroimaging data,” Front Neuroinform, vol. 13, p. 16, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30914942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen X, Formisano E, Blokland GAM, Strike LT, McMahon KL, de Zubicaray GI, Thompson PM, Wright MJ, Winkler AM, Ge T, and Nichols TE, “Accelerated estimation and permutation inference for ace modeling,” Hum Brain Mapp, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/31037793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Ganjgahi H, Winkler AM, Glahn DC, Blangero J, Kochunov P, and Nichols TE, “Fast and powerful heritability inference for family-based neuroimaging studies,” Neuroimage, vol. 115, pp. 256–68, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25812717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Yang J, Lee SH, Goddard ME, and Visscher PM, “Gcta: a tool for genome-wide complex trait analysis,” Am J Hum Genet, vol. 88, no. 1, pp. 76–82, 2011. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/21167468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Ge T, Nichols TE, Lee PH, Holmes AJ, Roffman JL, Buckner RL, Sabuncu MR, and Smoller JW, “Massively expedited genome-wide heritability analysis (megha),” Proc Natl Acad Sci U S A, vol. 112, no. 8, pp. 2479–84, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25675487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ge T, Reuter M, Winkler AM, Holmes AJ, Lee PH, Tirrell LS, Roffman JL, Buckner RL, Smoller JW, and Sabuncu MR, “Multidimensional heritability analysis of neuroanatomical shape,” Nat Commun, vol. 7, p. 13291, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27845344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Ge T, Chen CY, Neale BM, Sabuncu MR, and Smoller JW, “Phenome-wide heritability analysis of the uk biobank,” PLoS Genet, vol. 13, no. 4, p. e1006711, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28388634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Bulik-Sullivan BK, Loh PR, Finucane HK, Ripke S, Yang J, C. Schizophrenia Working Group of the Psychiatric Genomics, Patterson N, Daly MJ, Price AL, and Neale BM, “Ld score regression distinguishes confounding from polygenicity in genome-wide association studies,” Nat Genet, vol. 47, no. 3, pp. 291–5, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25642630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Renteria ME, Hansell NK, Strike LT, McMahon KL, de Zubicaray GI, Hickie IB, Thompson PM, Martin NG, Medland SE, and Wright MJ, “Genetic architecture of subcortical brain regions: common and region-specific genetic contributions,” Genes Brain Behav, vol. 13, no. 8, pp. 821–30, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25199620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Lee PH, Baker JT, Holmes AJ, Jahanshad N, Ge T, Jung JY, Cruz Y, Manoach DS, Hibar DP, Faskowitz J, McMahon KL, de Zubicaray GI, Martin NH, Wright MJ, Ongur D, Buckner R, Roffman J, Thompson PM, and Smoller JW, “Partitioning heritability analysis reveals a shared genetic basis of brain anatomy and schizophrenia,” Mol Psychiatry, vol. 21, no. 12, pp. 1680–1689, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27725656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Brouwer RM, Panizzon MS, Glahn DC, Hibar DP, Hua X, Jahanshad N, Abramovic L, de Zubicaray GI, Franz CE, Hansell NK, Hickie IB, Koenis MMG, Martin NG, Mather KA, McMahon KL, Schnack HG, Strike LT, Swagerman SC, Thalamuthu A, Wen W, Gilmore JH, Gogtay N, Kahn RS, Sachdev PS, Wright MJ, Boomsma DI, Kremen WS, Thompson PM, and Hulshoff Pol HE, “Genetic influences on individual differences in longitudinal changes in global and subcortical brain volumes: Results of the enigma plasticity working group,” Hum Brain Mapp, vol. 38, no. 9, pp. 4444–4458, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28580697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Shen L, Kim S, Risacher SL, Nho K, Swaminathan S, West JD, Foroud T, Pankratz N, Moore JH, Sloan CD, Huentelman MJ, Craig DW, Dechairo BM, Potkin SG, Jack J, R. C, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Whole genome association study of brain-wide imaging phenotypes for identifying quantitative trait loci in mci and ad: A study of the adni cohort,” Neuroimage, vol. 53, no. 3, pp. 1051–63, 2010. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/20100581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Jahanshad N, Rajagopalan P, Hua X, Hibar DP, Nir TM, Toga AW, Jack J, R. C, Saykin AJ, Green RC, Weiner MW, Medland SE, Montgomery GW, Hansell NK, McMahon KL, de Zubicaray GI, Martin NG, Wright MJ, Thompson PM, and I. Alzheimer’s Disease Neuroimaging, “Genome-wide scan of healthy human connectome discovers spon1 gene variant influencing dementia severity,” Proc Natl Acad Sci U S A, vol. 110, no. 12, pp. 4768–73, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23471985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Lindquist MA and Mejia A, “Zen and the art of multiple comparisons,” Psychosom Med, vol. 77, no. 2, pp. 114–25, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25647751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Armstrong RA, “When to use the bonferroni correction,” Ophthalmic Physiol Opt, vol. 34, no. 5, pp. 502–8, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24697967 [DOI] [PubMed] [Google Scholar]
- [41].Worsley KJ, Taylor JE, Tomaiuolo F, and Lerch J, “Unified univariate and multivariate random field theory,” Neuroimage, vol. 23 Suppl 1, pp. S189–95, 2004. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/15501088 [DOI] [PubMed] [Google Scholar]
- [42].Chung MK, Wang Y, Huang S-G, and Lyu I, “Rapid acceleration of the permutation test via slow random walks in the permutation group,” arXiv:1812.06696, 2018. [Google Scholar]
- [43].Benjamini Y and Hochberg Y, “Controlling the false discovery rate: A practical and powerful approach to multiple testing,” Journal of the Royal Statistical Society. Series B (Methodological), vol. 57, no. 1, pp. 289–300, 1995. [Online]. Available: http://www.jstor.org/stable/2346101 [Google Scholar]
- [44].Hua WY, Nichols TE, Ghosh D, and I. Alzheimer’s Disease Neuroimaging, “Multiple comparison procedures for neuroimaging genomewide association studies,” Biostatistics, vol. 16, no. 1, pp. 17–30, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/24963012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Stein JL, Hua X, Morra JH, Lee S, Hibar DP, Ho AJ, Leow AD, Toga AW, Sul JH, Kang HM, Eskin E, Saykin AJ, Shen L, Foroud T, Pankratz N, Huentelman MJ, Craig DW, Gerber JD, Allen AN, Corneveaux JJ, Stephan DA, Webster J, DeChairo BM, Potkin SG, Jack CR Jr, Weiner MW, and Thompson PM, “Genome-wide analysis reveals novel genes influencing temporal lobe structure with relevance to neurodegeneration in alzheimer’s disease,” NeuroImage, vol. 51, no. 2, pp. 542–554, 2010. [Online]. Available: http://www.sciencedirect.com/science/article/B6WNP-4YH56B3-2/2/0a240fe93fd981a1c214d859629daff8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Scelsi MA, Khan RR, Lorenzi M, Christopher L, Greicius MD, Schott JM, Ourselin S, and Altmann A, “Genetic study of multimodal imaging alzheimer’s disease progression score implicates novel loci,” Brain, vol. 141, no. 7, pp. 2167–2180, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29860282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Donohue MC, Jacqmin-Gadda H, Le Goff M, Thomas RG, Raman R, Gamst AC, Beckett LA, Jack J, R. C, Weiner MW, Dartigues JF, Aisen PS, and I. Alzheimer’s Disease Neuroimaging, “Estimating long-term multivariate progression from short-term data,” Alzheimers Dement, vol. 10, no. 5 Suppl, pp. S400–10, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24656849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Risacher SL, Kim S, Nho K, Foroud T, Shen L, Petersen RC, Jack J, R. C, Beckett LA, Aisen PS, Koeppe RA, Jagust WJ, Shaw LM, Trojanowski JQ, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Apoe effect on alzheimer’s disease biomarkers in older adults with significant memory concern,” Alzheimers Dement, vol. 11, no. 12, pp. 1417–1429, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25960448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Ho AJ, Stein JL, Hua X, Lee S, Hibar DP, Leow AD, Dinov ID, Toga AW, Saykin AJ, Shen L, Foroud T, Pankratz N, Huentelman MJ, Craig DW, Gerber JD, Allen AN, Corneveaux JJ, Stephan DA, DeCarli CS, DeChairo BM, Potkin SG, Jack J, R. C, Weiner MW, Raji CA, Lopez OL, Becker JT, Carmichael OT, Thompson PM, and I. Alzheimer’s Disease Neuroimaging, “A commonly carried allele of the obesity-related fto gene is associated with reduced brain volume in the healthy elderly,” Proc Natl Acad Sci U S A, vol. 107, no. 18, pp. 8404–9, 2010. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/20404173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Huang M, Nichols T, Huang C, Yu Y, Lu Z, Knickmeyer RC, Feng Q, Zhu H, and I. Alzheimer’s Disease Neuroimaging, “Fvgwas: Fast voxelwise genome wide association analysis of large-scale imaging genetic data,” Neuroimage, vol. 118, pp. 613–27, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26025292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Fan J and Lv J, “Sure independence screening for ultrahigh dimensional feature space,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), vol. 70, no. 5, pp. 849–911, 2008. [Online]. Available: 10.1111/j.1467-9868.2008.00674.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Kim J, Pan W, and I. Alzheimer’s Disease Neuroimaging, “A cautionary note on using secondary phenotypes in neuroimaging genetic studies,” Neuroimage, vol. 121, pp. 136–45, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26220747 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Schifano ED, Li L, Christiani DC, and Lin X, “Genome-wide association analysis for multiple continuous secondary phenotypes,” Am J Hum Genet, vol. 92, no. 5, pp. 744–59, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23643383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Lin DY and Zeng D, “Proper analysis of secondary phenotype data in case-control association studies,” Genet Epidemiol, vol. 33, no. 3, pp. 256–65, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19051285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Zhu W, Yuan Y, Zhang J, Zhou F, Knickmeyer RC, Zhu H, and I. Alzheimer’s Disease Neuroimaging, “Genome-wide association analysis of secondary imaging phenotypes from the alzheimer’s disease neuroimaging initiative study,” Neuroimage, 2016. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/27717770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Tchetgen Tchetgen EJ, “A general regression framework for a secondary outcome in case-control studies,” Biostatistics, vol. 15, no. 1, pp. 117–28, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24152770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Stein JL, Hua X, Lee S, Ho AJ, Leow AD, Toga AW, Saykin AJ, Shen L, Foroud T, Pankratz N, Huentelman MJ, Craig DW, Gerber JD, Allen AN, Corneveaux JJ, Dechairo BM, Potkin SG, Weiner MW, Thompson P, and I. Alzheimer’s Disease Neuroimaging, “Voxelwise genome-wide association study (vgwas),” Neuroimage, vol. 53, no. 3, pp. 1160–74, 2010. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/20171287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Dudbridge F, “Power and predictive accuracy of polygenic risk scores,” PLoS Genet, vol. 9, no. 3, p. e1003348, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23555274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Dima D and Breen G, “Polygenic risk scores in imaging genetics: Usefulness and applications,” J Psychopharmacol, vol. 29, no. 8, pp. 867–71, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25944849 [DOI] [PubMed] [Google Scholar]
- [60].Chasioti D, Yan J, Nho K, and Saykin AJ, “Progress in polygenic composite scores in alzheimer’s and other complex diseases,” Trends Genet, vol. 35, no. 5, pp. 371–382, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30922659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Mormino EC, Sperling RA, Holmes AJ, Buckner RL, De Jager PL, Smoller JW, Sabuncu MR, and I. Alzheimer’s Disease Neuroimaging, “Polygenic risk of alzheimer disease is associated with early- and late-life processes,” Neurology, vol. 87, no. 5, pp. 481–8, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27385740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Sabuncu MR, Buckner RL, Smoller JW, Lee PH, Fischl B, Sperling RA, and I. Alzheimer’s Disease Neuroimaging, “The association between a polygenic alzheimer score and cortical thickness in clinically normal subjects,” Cereb Cortex, vol. 22, no. 11, pp. 2653–61, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22169231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Lambert JC, Ibrahim-Verbaas CA, Harold D, Naj AC, Sims R, Bellenguez C, DeStafano AL, Bis JC, Beecham GW, Grenier-Boley B, Russo G, Thorton-Wells TA, Jones N, Smith AV, Chouraki V, Thomas C, Ikram MA, Zelenika D, Vardarajan BN, Kamatani Y, Lin CF, Gerrish A, Schmidt H, Kunkle B, Dunstan ML, Ruiz A, Bihoreau MT, Choi SH, Reitz C, Pasquier F, Cruchaga C, Craig D, Amin N, Berr C, Lopez OL, De Jager PL, Deramecourt V, Johnston JA, Evans D, Lovestone S, Letenneur L, Moron FJ, Rubinsztein DC, Eiriksdottir G, Sleegers K, Goate AM, Fievet N, Huentelman MW, Gill M, Brown K, Kamboh MI, Keller L, Barberger-Gateau P, McGuiness B, Larson EB, Green R, Myers AJ, Dufouil C, Todd S, Wallon D, Love S, Rogaeva E, Gallacher J, St George-Hyslop P, Clarimon J, Lleo A, Bayer A, Tsuang DW, Yu L, Tsolaki M, Bossu P, Spalletta G, Proitsi P, Collinge J, Sorbi S, Sanchez-Garcia F, Fox NC, Hardy J, Deniz Naranjo MC, Bosco P, Clarke R, Brayne C, Galimberti D, Mancuso M, Matthews F, I. European Alzheimer’s Disease, Genetic D. Environmental Risk in Alzheimer’s, C. Alzheimer’s Disease Genetic, H. Cohorts for, E. Aging Research in Genomic, Moebus S, Mecocci P, Del Zompo M, Maier W, Hampel H, Pilotto A, Bullido M, Panza F, Caffarra P et al. , “Meta-analysis of 74,046 individuals identifies 11 new susceptibility loci for alzheimer’s disease,” Nat Genet, vol. 45, no. 12, pp. 1452–8, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24162737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Harold D, Abraham R, Hollingworth P, Sims R, Gerrish A, Hamshere ML, Pahwa JS, Moskvina V, Dowzell K, Williams A, Jones N, Thomas C, Stretton A, Morgan AR, Lovestone S, Powell J, Proitsi P, Lupton MK, Brayne C, Rubinsztein DC, Gill M, Lawlor B, Lynch A, Morgan K, Brown KS, Passmore PA, Craig D, McGuinness B, Todd S, Holmes C, Mann D, Smith AD, Love S, Kehoe PG, Hardy J, Mead S, Fox N, Rossor M, Collinge J, Maier W, Jessen F, Schurmann B, Heun R, van den Bussche H, Heuser I, Kornhuber J, Wiltfang J, Dichgans M, Frolich L, Hampel H, Hull M, Rujescu D, Goate AM, Kauwe JS, Cruchaga C, Nowotny P, Morris JC, Mayo K, Sleegers K, Bettens K, Engelborghs S, De Deyn PP, Van Broeckhoven C, Livingston G, Bass NJ, Gurling H, McQuillin A, Gwilliam R, Deloukas P, Al-Chalabi A, Shaw CE, Tsolaki M, Singleton AB, Guerreiro R, Muhleisen TW, Nothen MM, Moebus S, Jockel KH, Klopp N, Wichmann HE, Carrasquillo MM, Pankratz VS, Younkin SG, Holmans PA, O’Donovan M, Owen MJ, and Williams J, “Genome-wide association study identifies variants at clu and picalm associated with alzheimer’s disease,” Nat Genet, vol. 41, no. 10, pp. 1088–93, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19734902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Tan CH, Bonham LW, Fan CC, Mormino EC, Sugrue LP, Broce IJ, Hess CP, Yokoyama JS, Rabinovici GD, Miller BL, Yaffe K, Schellenberg GD, Kauppi K, Holland D, McEvoy LK, Kukull WA, Tosun D, Weiner MW, Sperling RA, Bennett DA, Hyman BT, Andreassen OA, Dale AM, Desikan RS, and I. Alzheimer’s Disease Neuroimaging, “Polygenic hazard score, amyloid deposition and alzheimer’s neurodegeneration,” Brain, vol. 142, no. 2, pp. 460–470, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30689776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Desikan RS, Fan CC, Wang Y, Schork AJ, Cabral HJ, Cupples LA, Thompson WK, Besser L, Kukull WA, Holland D, Chen CH, Brewer JB, Karow DS, Kauppi K, Witoelar A, Karch CM, Bonham LW, Yokoyama JS, Rosen HJ, Miller BL, Dillon WP, Wilson DM, Hess CP, Pericak-Vance M, Haines JL, Farrer LA, Mayeux R, Hardy J, Goate AM, Hyman BT, Schellenberg GD, McEvoy LK, Andreassen OA, and Dale AM, “Genetic assessment of age-associated alzheimer disease risk: Development and validation of a polygenic hazard score,” PLoS Med, vol. 14, no. 3, p. e1002258, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28323831 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Euesden J, Lewis CM, and O’Reilly PF, “Prsice: Polygenic risk score software,” Bioinformatics, vol. 31, no. 9, pp. 1466–8, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25550326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Martin AR, Kanai M, Kamatani Y, Okada Y, Neale BM, and Daly MJ, “Clinical use of current polygenic risk scores may exacerbate health disparities,” Nat Genet, vol. 51, no. 4, pp. 584–591, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30926966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Ibanez L, Farias FHG, Dube U, Mihindukulasuriya KA, and Harari O, “Polygenic risk scores in neurodegenerative diseases: a review,” Current Genetic Medicine Reports, vol. 7, no. 1, pp. 22–29, 2019. [Online]. Available: 10.1007/s40142-019-0158-0 [DOI] [Google Scholar]
- [70].Apostolova LG, Risacher SL, Duran T, Stage EC, Goukasian N, West JD, Do TM, Grotts J, Wilhalme H, Nho K, Phillips M, Elashoff D, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Associations of the top 20 alzheimer disease risk variants with brain amyloidosis,” JAMA Neurol, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29340569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Hibar DP, Stein JL, Kohannim O, Jahanshad N, Saykin AJ, Shen L, Kim S, Pankratz N, Foroud T, Huentelman MJ, Potkin SG, Jack J, R. C, Weiner MW, Toga AW, Thompson PM, and I. Alzheimer’s Disease Neuroimaging, “Voxelwise gene-wide association study (vgenewas): multivariate gene-based association testing in 731 elderly subjects,” Neuroimage, vol. 56, no. 4, pp. 1875–91, 2011. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/21497199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Ge T, Feng J, Hibar DP, Thompson PM, and Nichols TE, “Increasing power for voxel-wise genome-wide association studies: the random field theory, least square kernel machines and fast permutation procedures,” NeuroImage, vol. 63, no. 2, pp. 858–73, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22800732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Xu Z, Wu C, Pan W, and I. Alzheimer’s Disease Neuroimaging, “Imaging-wide association study: Integrating imaging endophenotypes in gwas,” Neuroimage, vol. 159, pp. 159–169, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28736311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Lu ZH, Zhu H, Knickmeyer RC, Sullivan PF, Williams SN, Zou F, and I. Alzheimer’s Disease Neuroimaging, “Multiple snp set analysis for genome-wide association studies through bayesian latent variable selection,” Genet Epidemiol, vol. 39, no. 8, pp. 664–77, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26515609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Wang K and Abbott D, “A principal components regression approach to multilocus genetic association studies,” Genet Epidemiol, vol. 32, no. 2, pp. 108–18, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/17849491 [DOI] [PubMed] [Google Scholar]
- [76].Liu D, Lin X, and Ghosh D, “Semiparametric regression of multidimensional genetic pathway data: least-squares kernel machines and linear mixed models,” Biometrics, vol. 63, no. 4, pp. 1079–88, 2007. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/18078480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Gusev A, Ko A, Shi H, Bhatia G, Chung W, Penninx BW, Jansen R, de Geus EJ, Boomsma DI, Wright FA, Sullivan PF, Nikkola E, Alvarez M, Civelek M, Lusis AJ, Lehtimaki T, Raitoharju E, Kahonen M, Seppala I, Raitakari OT, Kuusisto J, Laakso M, Price AL, Pajukanta P, and Pasaniuc B, “Integrative approaches for large-scale transcriptome-wide association studies,” Nat Genet, vol. 48, no. 3, pp. 245–52, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26854917 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Kwak IY and Pan W, “Adaptive gene- and pathway-trait association testing with gwas summary statistics,” Bioinformatics, vol. 32, no. 8, pp. 1178–84, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26656570 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Svishcheva GR, Belonogova NM, Zorkoltseva IV, Kirichenko AV, and Axenovich TI, “Gene-based association tests using gwas summary statistics,” Bioinformatics, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30860568 [DOI] [PubMed] [Google Scholar]
- [80].Zhang Y, Xu Z, Shen X, Pan W, and I. Alzheimer’s Disease Neuroimaging, “Testing for association with multiple traits in generalized estimation equations, with application to neuroimaging data,” Neuroimage, vol. 96, pp. 309–25, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/24704269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Yang Q, Wu H, Guo CY, and Fox CS, “Analyze multivariate phenotypes in genetic association studies by combining univariate association tests,” Genet Epidemiol, vol. 34, no. 5, pp. 444–54, 2010. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/20583287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Lan H, Stoehr JP, Nadler ST, Schueler KL, Yandell BS, and Attie AD, “Dimension reduction for mapping mrna abundance as quantitative traits,” Genetics, vol. 164, no. 4, pp. 1607–14, 2003. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/12930764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Ferreira MA and Purcell SM, “A multivariate test of association,” Bioinformatics, vol. 25, no. 1, pp. 132–3, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19019849 [DOI] [PubMed] [Google Scholar]
- [84].Li X, Basu S, Miller MB, Iacono WG, and McGue M, “A rapid generalized least squares model for a genome-wide quantitative trait association analysis in families,” Hum Hered, vol. 71, no. 1, pp. 67–82, 2011. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/21474944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Korte A, Vilhjalmsson BJ, Segura V, Platt A, Long Q, and Nordborg M, “A mixed-model approach for genome-wide association studies of correlated traits in structured populations,” Nat Genet, vol. 44, no. 9, pp. 1066–71, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22902788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Liang K-Y and Zeger SL, “Longitudinal data analysis using generalized linear models,” Biometrika, vol. 73, no. 1, pp. 13–22, 1986. [Online]. Available: 10.1093/biomet/73.1.13 [DOI] [Google Scholar]
- [87].Kim J, Zhang Y, Pan W, and I. Alzheimer’s Disease Neuroimaging, “Powerful and adaptive testing for multi-trait and multi-snp associations with gwas and sequencing data,” Genetics, vol. 203, no. 2, pp. 715–31, 2016. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/27075728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Kim J, Pan W, and I. Alzheimer’s Disease Neuroimaging, “Adaptive testing for multiple traits in a proportional odds model with applications to detect snp-brain network associations,” Genet Epidemiol, vol. 41, no. 3, pp. 259–277, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28191669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Huang C, Thompson P, Wang Y, Yu Y, Zhang J, Kong D, Colen RR, Knickmeyer RC, Zhu H, and I. Alzheimer’s Disease Neuroimaging, “Fgwas: Functional genome wide association analysis,” Neuroimage, vol. 159, pp. 107–121, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28735012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Yao X, Yan J, Kim S, Nho K, Risacher SL, Inlow M, Moore JH, Saykin AJ, and Shen L, “Two-dimensional enrichment analysis for mining high-level imaging genetic associations,” Brain Inform, 2016. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/27747820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Ramanan VK, Shen L, Moore JH, and Saykin AJ, “Pathway analysis of genomic data: concepts, methods, and prospects for future development,” Trends Genet, vol. 28, no. 7, pp. 323–32, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22480918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Holden M, Deng S, Wojnowski L, and Kulle B, “Gsea-snp: applying gene set enrichment analysis to snp data from genome-wide association studies,” Bioinformatics, vol. 24, no. 23, pp. 2784–5, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/18854360 [DOI] [PubMed] [Google Scholar]
- [93].Ramanan VK, Kim S, Holohan K, Shen L, Nho K, Risacher SL, Foroud TM, Mukherjee S, Crane PK, Aisen PS, Petersen RC, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Genome-wide pathway analysis of memory impairment in the alzheimer’s disease neuroimaging initiative (adni) cohort implicates gene candidates, canonical pathways, and networks,” Brain Imaging Behav, vol. 6, no. 4, pp. 634–48, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22865056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Nam D, Kim J, Kim SY, and Kim S, “Gsa-snp: a general approach for gene set analysis of polymorphisms,” Nucleic Acids Res, vol. 38, no. Web Server issue, pp. W749–54, 2010. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/20501604 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Yao X, Cong S, Yan J, Risacher SL, Saykin AJ, Moore JH, and Shen L, “Mining regional imaging genetic associations via voxel-wise enrichment analysis,” in BHI19: IEEE International Conference on Biomedical and Health Informatics, 2019, Conference Proceedings. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Allen Institute for Brain Science, “Allen human brain atlas: Technical white paper: Microarray data normalization,” http://www.brain-map.org/, 2013. [Online]. Available: http://help.brain-map.org/download/attachments/2818165/Normalization_WhitePaper.pdf [Google Scholar]
- [97].C. Gene Ontology, “The gene ontology project in 2008,” Nucleic Acids Res, vol. 36, no. Database issue, pp. D440–4, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/17984083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Kanehisa M and Goto S, “Kegg: kyoto encyclopedia of genes and genomes,” Nucleic Acids Res, vol. 28, no. 1, pp. 27–30, 2000. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/10592173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Yao X, Yan J, Liu K, Kim S, Nho K, Risacher SL, Greene CS, Moore JH, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Tissue-specific network-based genome wide study of amygdala imaging phenotypes to identify functional interaction modules,” Bioinformatics, vol. 33, no. 20, pp. 3250–3257, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28575147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Yan J, Risacher SL, Shen L, and Saykin AJ, “Network approaches to systems biology analysis of complex disease: integrative methods for multi-omics data,” Brief Bioinform, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28679163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Song A, Yan J, Kim S, Risacher SL, Wong AK, Saykin AJ, Shen L, Greene CS, and I. Alzheimer’s Disease Neuroimaging, “Network-based analysis of genetic variants associated with hippocampal volume in alzheimer’s disease: a study of adni cohorts,” BioData Min, vol. 9, p. 3, 2016. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26788126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Greene CS, Krishnan A, Wong AK, Ricciotti E, Zelaya RA, Himmelstein DS, Zhang R, Hartmann BM, Zaslavsky E, Sealfon SC, Chasman DI, FitzGerald GA, Dolinski K, Grosser T, and Troyanskaya OG, “Understanding multicellular function and disease with human tissue-specific networks,” Nat Genet, vol. 47, no. 6, pp. 569–76, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25915600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Patel S, Park MT, Alzheimer’s Disease Neuroimaging I, Chakravarty MM, and Knight J, “Gene prioritization for imaging genetics studies using gene ontology and a stratified false discovery rate approach,” Front Neuroinform, vol. 10, p. 14, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27092072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Lorenzi M, Altmann A, Gutman B, Wray S, Arber C, Hibar DP, Jahanshad N, Schott JM, Alexander DC, Thompson PM, Ourselin S, and I. Alzheimer’s Disease Neuroimaging, “Susceptibility of brain atrophy to trib3 in alzheimer’s disease, evidence from functional prioritization in imaging genetics,” Proc Natl Acad Sci U S A, vol. 115, no. 12, pp. 3162–3167, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29511103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Grothe MJ, Sepulcre J, Gonzalez-Escamilla G, Jelistratova I, Scholl M, Hansson O, Teipel SJ, and I. Alzheimer’s Disease Neuroimaging, “Molecular properties underlying regional vulnerability to alzheimer’s disease pathology,” Brain, vol. 141, no. 9, pp. 2755–2771, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30016411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Silver M, Montana G, and I. Alzheimer’s Disease Neuroimaging, “Fast identification of biological pathways associated with a quantitative trait using group lasso with overlaps,” Stat Appl Genet Mol Biol, vol. 11, no. 1, p. Article 7, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22499682 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Silver M, Janousova E, Hua X, Thompson PM, Montana G, and I. Alzheimer’s Disease Neuroimaging, “Identification of gene pathways implicated in alzheimer’s disease using longitudinal imaging phenotypes with sparse regression,” Neuroimage, vol. 63, no. 3, pp. 1681–94, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22982105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Yan J, Du L, Kim S, Risacher SL, Huang H, Moore JH, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Transcriptome-guided amyloid imaging genetic analysis via a novel structured sparse learning algorithm,” Bioinformatics, vol. 30, no. 17, pp. i564–i571, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25161248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [109].Zieselman AL, Fisher JM, Hu T, Andrews PC, Greene CS, Shen L, Saykin AJ, and Moore JH, “Computational genetics analysis of grey matter density in alzheimer’s disease,” BioData Min, vol. 7, p. 17, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25165488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Gui J, Moore JH, Williams SM, Andrews P, Hillege HL, van der Harst P, Navis G, Van Gilst WH, Asselbergs FW, and Gilbert-Diamond D, “A simple and computationally efficient approach to multifactor dimensionality reduction analysis of gene-gene interactions for quantitative traits,” PLoS One, vol. 8, no. 6, p. e66545, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23805232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Wong AK, Park CY, Greene CS, Bongo LA, Guan Y, and Troyanskaya OG, “Imp: a multi-species functional genomics portal for integration, visualization and prediction of protein functions and networks,” Nucleic Acids Res, vol. 40, no. Web Server issue, pp. W484–90, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22684505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Meda SA, Koran ME, Pryweller JR, Vega JN, Thornton-Wells TA, and I. Alzheimer’s Disease Neuroimaging, “Genetic interactions associated with 12-month atrophy in hippocampus and entorhinal cortex in alzheimer’s disease neuroimaging initiative,” Neurobiol Aging, vol. 34, no. 5, pp. 1518 e9–18, 2013. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/23107432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Herold C, Steffens M, Brockschmidt FF, Baur MP, and Becker T, “Intersnp: genome-wide interaction analysis guided by a priori information,” Bioinformatics, vol. 25, no. 24, pp. 3275–81, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19837719 [DOI] [PubMed] [Google Scholar]
- [114].Hibar DP, Stein JL, Jahanshad N, Kohannim O, Hua X, Toga AW, McMahon KL, de Zubicaray GI, Martin NG, Wright MJ, I. Alzheimer’s Disease Neuroimaging, Weiner MW, and Thompson PM, “Genome-wide interaction analysis reveals replicated epistatic effects on brain structure,” Neurobiol Aging, vol. 36 Suppl 1, pp. S151–8, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25264344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Ueki M and Tamiya G, “Ultrahigh-dimensional variable selection method for whole-genome gene-gene interaction analysis,” BMC Bioinformatics, vol. 13, p. 72, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22554139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [116].Chen J and Chen Z, “Extended bayesian information criteria for model selection with large model spaces,” Biometrika, vol. 95, no. 3, pp. 759–771, 2008. [Online]. Available: 10.1093/biomet/asn034 [DOI] [Google Scholar]
- [117].Ge T, Nichols TE, Ghosh D, Mormino EC, Smoller JW, Sabuncu MR, and I. Alzheimer’s Disease Neuroimaging, “A kernel machine method for detecting effects of interaction between multidimensional variable sets: an imaging genetics application,” Neuroimage, vol. 109, pp. 505–14, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25600633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Wang C, Sun J, Guillaume B, Ge T, Hibar DP, Greenwood CMT, Qiu A, and I. Alzheimer’s Disease Neuroimaging, “A set-based mixed effect model for gene-environment interaction and its application to neuroimaging phenotypes,” Front Neurosci, vol. 11, p. 191, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28428742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Sun J, Zheng Y, and Hsu L, “A unified mixed-effects model for rare-variant association in sequencing studies,” Genet Epidemiol, vol. 37, no. 4, pp. 334–44, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23483651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Stein JL, Medland SE, Vasquez AA, Hibar DP, Senstad RE, Winkler AM, Toro R, Appel K, Bartecek R, Bergmann O, Bernard M, Brown AA, Cannon DM, Chakravarty MM, Christoforou A, Domin M, Grimm O, Hollinshead M, Holmes AJ, Homuth G, Hottenga JJ, Langan C, Lopez LM, Hansell NK, Hwang KS, Kim S, Laje G, Lee PH, Liu X, Loth E, Lourdusamy A, Mattingsdal M, Mohnke S, Maniega SM, Nho K, Nugent AC, O’Brien C, Papmeyer M, Putz B, Ramasamy A, Rasmussen J, Rijpkema M, Risacher SL, Roddey JC, Rose EJ, Ryten M, Shen L, Sprooten E, Strengman E, Teumer A, Trabzuni D, Turner J, van Eijk K, van Erp TG, van Tol MJ, Wittfeld K, Wolf C, Woudstra S, Aleman A, Alhusaini S, Almasy L, Binder EB, Brohawn DG, Cantor RM, Carless MA, Corvin A, Czisch M, Curran JE, Davies G, de Almeida MA, Delanty N, Depondt C, Duggirala R, Dyer TD, Erk S, Fagerness J, Fox PT, Freimer NB, Gill M, Goring HH, Hagler DJ, Hoehn D, Holsboer F, Hoogman M, Hosten N, Jahanshad N, Johnson MP, Kasperaviciute D, Kent J, W. J, Kochunov P, Lancaster JL, Lawrie SM, Liewald DC, Mandl R, Matarin M, Mattheisen M, Meisenzahl E, Melle I, Moses EK, Muhleisen TW et al. , “Identification of common variants associated with human hippocampal and intracranial volumes,” Nat Genet, vol. 44, no. 5, pp. 552–61, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22504417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Hibar DP, Stein JL, Renteria ME, Arias-Vasquez A, Desrivieres S, Jahanshad N, Toro R, Wittfeld K, Abramovic L, Andersson M, Aribisala BS, Armstrong NJ, Bernard M, Bohlken MM, Boks MP, Bralten J, Brown AA, Chakravarty MM, Chen Q, Ching CR, Cuellar-Partida G, den Braber A, Giddaluru S, Goldman AL, Grimm O, Guadalupe T, Hass J, Woldehawariat G, Holmes AJ, Hoogman M, Janowitz D, Jia T, Kim S, Klein M, Kraemer B, Lee PH, Olde Loohuis LM, Luciano M, Macare C, Mather KA, Mattheisen M, Milaneschi Y, Nho K, Papmeyer M, Ramasamy A, Risacher SL, Roiz-Santianez R, Rose EJ, Salami A, Samann PG, Schmaal L, Schork AJ, Shin J, Strike LT, Teumer A, van Donkelaar MM, van Eijk KR, Walters RK, Westlye LT, Whelan CD, Winkler AM, Zwiers MP, Alhusaini S, Athanasiu L, Ehrlich S, Hakobjan MM, Hartberg CB, Haukvik UK, Heister AJ, Hoehn D, Kasperaviciute D, Liewald DC, Lopez LM, Makkinje RR, Matarin M, Naber MA, McKay DR, Needham M, Nugent AC, Putz B, Royle NA, Shen L, Sprooten E, Trabzuni D, van der Marel SS, van Hulzen KJ, Walton E, Wolf C, Almasy L, Ames D, Arepalli S, Assareh AA, Bastin ME, Brodaty H, Bulayeva KB, Carless MA, Cichon S, Corvin A, Curran JE, Czisch M et al. , “Common genetic variants influence human subcortical brain structures,” Nature, vol. 520, no. 7546, pp. 224–9, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25607358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [122].Sonderby IE, Gustafsson O, Doan NT, Hibar DP, Martin-Brevet S, Abdellaoui A, Ames D, Amunts K, Andersson M, Armstrong NJ, Bernard M, Blackburn N, Blangero J, Boomsma DI, Bralten J, Brattbak HR, Brodaty H, Brouwer RM, Bulow R, Calhoun V, Caspers S, Cavalleri G, Chen CH, Cichon S, Ciufolini S, Corvin A, Crespo-Facorro B, Curran JE, Dale AM, Dalvie S, Dazzan P, de Geus EJC, de Zubicaray GI, de Zwarte SMC, Delanty N, den Braber A, Desrivieres S, Donohoe G, Draganski B, Ehrlich S, Espeseth T, Fisher SE, Franke B, Frouin V, Fukunaga M, Gareau T, Glahn DC, Grabe H, Groenewold NA, Haavik J, Haberg A, Hashimoto R, Hehir-Kwa JY, Heinz A, Hillegers MHJ, Hoffmann P, Holleran L, Hottenga JJ, Hulshoff HE, Ikeda M, Jahanshad N, Jernigan T, Jockwitz C, Johansson S, Jonsdottir GA, Jonsson EG, Kahn R, Kaufmann T, Kelly S, Kikuchi M, Knowles EEM, Kolskar KK, Kwok JB, Hellard SL, Leu C, Liu J, Lundervold AJ, Lundervold A, Martin NG, Mather K, Mathias SR, McCormack M, McMahon KL, McRae A, Milaneschi Y, Moreau C, Morris D, Mothersill D, Muhleisen TW, Murray R, Nordvik JE, Nyberg L, Olde Loohuis LM, Ophoff R, Paus T, Pausova Z, Penninx B, Peralta JM, Pike B, Prieto C et al. , “Dose response of the 16p11.2 distal copy number variant on intracranial volume and basal ganglia,” Mol Psychiatry, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30283035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].Smith SM and Nichols TE, “Statistical challenges in “big data” human neuroimaging,” Neuron, vol. 97, no. 2, pp. 263–268, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29346749 [DOI] [PubMed] [Google Scholar]
- [124].Medland SE, Jahanshad N, Neale BM, and Thompson PM, “Whole-genome analyses of whole-brain data: working within an expanded search space,” Nat Neurosci, vol. 17, no. 6, pp. 791–800, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24866045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Thompson PM, Hibar DP, Stein JL, Prasad G, and Jahanshad N, Genetics of the Connectome and the ENIGMA Project. Cham (CH): Springer, 2016, pp. 147–164. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28590671 [PubMed] [Google Scholar]
- [126].Jahanshad N, Ganjgahi H, Bralten J, den Braber A, Faskowitz J, Knodt AR, Lemaitre H, Nir TM, Patel B, Richie S, Sprooten E, Hoogman M, van Hulzen K, Zavaliangos-Petropulu A, Zwiers MP, Almasy L, Bastin ME, Bernstein MA, Blangero J, Curran J, Deary IJ, de Zubicary GI, Duggirala R, Fisher SE, Franke B, Fox P, Goldman D, Haberg AK, Hariri A, Hong LE, Huentelman M, Martin NG, Martinot J-L, McIntosh A, McMahon KL, Medland SE, Mitchell BD, Muoz Maniega S, Olvera RL, Oosterlaan J, Peterson C, Royle N, Saykin AJ, Schumann G, Starr J, Stein EA, Sussmann J, Valds Hernndez M. d. C., vant Ent D, Wardlaw JM, Weiner MW, Williamson DE, Winkler AM, Wright MJ, Yang Y, Thompson PM, Glahn DC, Nichols TE, and Kochunov P, “Do candidate genes affect the brains white matter microstructure? large-scale evaluation of 6,165 diffusion mri scans,” bioRxiv, p. 107987, 2017. [Online]. Available: http://biorxiv.org/content/early/2017/02/20/107987.abstract [Google Scholar]
- [127].Ioannidis JP, “Why most published research findings are false,” PLoS Med, vol. 2, no. 8, p. e124, 2005. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/16060722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, and Munafo MR, “Power failure: why small sample size undermines the reliability of neuroscience,” Nat Rev Neurosci, vol. 14, no. 5, pp. 365–76, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23571845 [DOI] [PubMed] [Google Scholar]
- [129].Button KS, “Double-dipping revisited,” Nat Neurosci, vol. 22, no. 5, pp. 688–690, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/31011228 [DOI] [PubMed] [Google Scholar]
- [130].Grasby KL, Jahanshad N, Painter JN, Colodro-Conde L, Bralten J, Hibar DP, Lind PA, Pizzagalli F, Ching CRK, McMahon MAB, Shatokhina N, Zsembik LCP, Agartz I, Alhusaini S, Almeida MAA, Alns D, Amlien IK, Andersson M, Ard T, Armstrong NJ, Ashley-Koch A, Bernard M, Brouwer RM, Buimer EEL, Blow R, Brger C, Cannon DM, Chakravarty M, Chen Q, Cheung JW, Couvy-Duchesne B, Dale AM, Dalvie S, de Araujo TK, de Zubicaray GI, de Zwarte SMC, Braber A. d., Doan NT, Dohm K, Ehrlich S, Engelbrecht H-R, Erk S, Fan CC, Fedko IO, Foley SF, Ford JM, Fukunaga M, Garrett ME, Ge T, Giddaluru S, Goldman AL, Groenewold NA, Grotegerd D, Gurholt TP, Gutman BA, Hansell NK, Harris MA, Harrison MB, Haswell CC, Hauser M, Heslenfeld DJ, Hoehn D, Holleran L, Hoogman M, Hottenga J-J, Ikeda M, Janowitz D, Jansen IE, Jia T, Jockwitz C, Kanai R, Karama S, Kasperaviciute D, Kaufmann T, Kelly S, Kikuchi M, Klein M, Knapp M, Knodt AR, Krmer B, Lancaster TM, Lee PH, Lett TA, Lewis LB, Lopes-Cendes I, Luciano M, Macciardi F, Marquand AF, Mathias SR, Melzer TR, Milaneschi Y, Mirza-Schreiber N, Moreira JCV, Mhleisen TW, Mller-Myhsok B, Najt P, Nakahara S, Nho K, Olde Loohuis LM, Orfanos DP et al. , “The genetic architecture of the human cerebral cortex,” bioRxiv, p. 399402, 2018. [Online]. Available: http://biorxiv.org/content/early/2018/09/03/399402.abstract [Google Scholar]
- [131].Smit DJA, Wright MJ, Meyers JL, Martin NG, Ho YYW, Malone SM, Zhang J, Burwell SJ, Chorlian DB, de Geus EJC, Denys D, Hansell NK, Hottenga JJ, McGue M, van Beijsterveldt CEM, Jahanshad N, Thompson PM, Whelan CD, Medland SE, Porjesz B, Lacono WG, and Boomsma DI, “Genome-wide association analysis links multiple psychiatric liability genes to oscillatory brain activity,” Hum Brain Mapp, vol. 39, no. 11, pp. 4183–4195, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29947131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Jia T, Chu C, Liu Y, Dongen J. v., Armstrong NJ, Bastin ME, Carrillo-Roa T, Braber A. d., Harris M, Jansen R, Liu J, Luciano M, Ori APS, Santiaez RR, Ruggeri B, Sarkisyan D, Shin J, Sungeun K, Gutirrez DT, Ent D. v., Ames D, Artiges E, Bakalkin G, Banaschewski T, Bokde ALW, Brodaty H, Bromberg U, Brouwer R, Bchel C, Quinlan EB, Cahn W, de Zubicaray GI, Ekstrm TJ, Flor H, Frhner JH, Frouin V, Garavan H, Gowland P, Heinz A, Ittermann B, Jahanshad N, Jiang J, Kwok JB, Martin NG, Martinot J-L, Mather KA, McMahon KL, McRae AF, Nees F, Orfanos DP, Paus T, Poustka L, Smann PG, Schofield PR, Smolka MN, Strike LT, Teeuw J, Thalamuthu A, Trollor J, Walter H, Wardlaw JM, Wen W, Whelan R, Apostolova LG, Binder EB, Boomsma DI, Calhoun V, Crespo-Facorro B, Deary IJ, Pol HH, Ophoff RA, Pausova Z, Sachdev PS, Saykin A, Wright MJ, Thompson PM, Schumann G, and Desrivires S, “Epigenome-wide meta-analysis of blood dna methylation and its association with subcortical volumes: findings from the enigma epigenetics working group,” bioRxiv, p. 460444, 2018. [Online]. Available: http://biorxiv.org/content/early/2018/11/05/460444.abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- [133].Adams HH, Hibar DP, Chouraki V, Stein JL, Nyquist PA, Renteria ME, Trompet S, Arias-Vasquez A, Seshadri S, Desrivieres S, Beecham AH, Jahanshad N, Wittfeld K, Van der Lee SJ, Abramovic L, Alhusaini S, Amin N, Andersson M, Arfanakis K, Aribisala BS, Armstrong NJ, Athanasiu L, Axelsson T, Beiser A, Bernard M, Bis JC, Blanken LM, Blanton SH, Bohlken MM, Boks MP, Bralten J, Brickman AM, Carmichael O, Chakravarty MM, Chauhan G, Chen Q, Ching CR, Cuellar-Partida G, Braber AD, Doan NT, Ehrlich S, Filippi I, Ge T, Giddaluru S, Goldman AL, Gottesman RF, Greven CU, Grimm O, Griswold ME, Guadalupe T, Hass J, Haukvik UK, Hilal S, Hofer E, Hoehn D, Holmes AJ, Hoogman M, Janowitz D, Jia T, Kasperaviciute D, Kim S, Klein M, Kraemer B, Lee PH, Liao J, Liewald DC, Lopez LM, Luciano M, Macare C, Marquand A, Matarin M, Mather KA, Mattheisen M, Mazoyer B, McKay DR, McWhirter R, Milaneschi Y, Mirza-Schreiber N, Muetzel RL, Maniega SM, Nho K, Nugent AC, Loohuis LM, Oosterlaan J, Papmeyer M, Pappa I, Pirpamer L, Pudas S, Putz B, Rajan KB, Ramasamy A, Richards JS, Risacher SL, Roiz-Santianez R, Rommelse N, Rose EJ, Royle NA, Rundek T, Samann PG, Satizabal CL et al. , “Novel genetic loci underlying human intracranial volume identified through genome-wide association,” Nat Neurosci, vol. 19, no. 12, pp. 1569–1582, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27694991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [134].Satizabal CL, Adams HHH, Hibar DP, White CC, Stein JL, Scholz M, Sargurupremraj M, Jahanshad N, Smith AV, Bis JC, Jian X, Luciano M, Hofer E, Teumer A, van der Lee SJ, Yang J, Yanek LR, Lee TV, Li S, Hu Y, Koh JY, Eicher JD, Desrivires S, Arias-Vasquez A, Chauhan G, Athanasiu L, Renteria ME, Kim S, Hhn D, Armstrong NJ, Chen Q, Holmes AJ, Braber A. d., Kloszewska I, Andersson M, Espeseth T, Grimm O, Abramovic L, Alhusaini S, Milaneschi Y, Papmeyer M, Axelsson T, Ehrlich S, Roiz-Santiaez R, Kraemer B, Hberg AK, Jones HJ, Pike GB, Stein DJ, Stevens A, Bralten J, Vernooij MW, Harris TB, Filippi I, Witte AV, Guadalupe T, Wittfeld K, Mosley TH, Becker JT, Doan NT, Hagenaars SP, Saba Y, Cuellar-Partida G, Amin N, Hilal S, Nho K, Karbalai N, Arfanakis K, Becker DM, Ames D, Goldman AL, Lee PH, Boomsma DI, Lovestone S, Giddaluru S, Le Hellard S, Mattheisen M, Bohlken MM, Kasperaviciute D, Schmaal L, Lawrie SM, Agartz I, Walton E, Tordesillas-Gutierrez D, Davies GE, Shin J, Ipser JC, Vinke LN, Hoogman M, Knol MJ, Jia T, Burkhardt R, Klein M, Crivello F, Janowitz D, Carmichael O, Haukvik UK, Aribisala BS, Schmidt H, Strike LT et al. , “Genetic architecture of subcortical brain structures in over 40,000 individuals worldwide,” bioRxiv, p. 173831, 2017. [Online]. Available: http://biorxiv.org/content/early/2017/08/28/173831.abstract [Google Scholar]
- [135].Alfaro-Almagro F, Jenkinson M, Bangerter NK, Andersson JLR, Griffanti L, Douaud G, Sotiropoulos SN, Jbabdi S, Hernandez-Fernandez M, Vallee E, Vidaurre D, Webster M, McCarthy P, Rorden C, Daducci A, Alexander DC, Zhang H, Dragonu I, Matthews PM, Miller KL, and Smith SM, “Image processing and quality control for the first 10,000 brain imaging datasets from uk biobank,” Neuroimage, vol. 166, pp. 400–424, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29079522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [136].Smeland OB, Wang Y, Frei O, Li W, Hibar DP, Franke B, Bettella F, Witoelar A, Djurovic S, Chen CH, Thompson PM, Dale AM, and Andreassen OA, “Genetic overlap between schizophrenia and volumes of hippocampus, putamen, and intracranial volume indicates shared molecular genetic mechanisms,” Schizophr Bull, vol. 44, no. 4, pp. 854–864, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29136250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [137].Hibar DP, Cheung JW, Medland SE, Mufford MS, Jahanshad N, Dalvie S, Ramesar R, Stewart E, van den Heuvel OA, Pauls DL, Knowles JA, Stein DJ, Thompson PM, C. Enhancing Neuro Imaging Genetics through Meta Analysis, and C. International Obsessive Compulsive Disorder Foundation Genetics, “Significant concordance of genetic variation that increases both the risk for obsessive-compulsive disorder and the volumes of the nucleus accumbens and putamen,” Br J Psychiatry, vol. 213, no. 1, pp. 430–436, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29947313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [138].Mufford M, Cheung J, Jahanshad N, van der Merwe C, Ding L, Groenewold N, Koen N, Chimusa ER, Dalvie S, Ramesar R, g. Psychiatric Genomics Consortium Tourette Syndrome working, Knowles JA, Lochner C, Hibar DP, Paschou P, van den Heuvel OA, Medland SE, Scharf JM, Mathews CA, Thompson PM, and Stein DJ, “Concordance of genetic variation that increases risk for tourette syndrome and that influences its underlying neurocircuitry,” Transl Psychiatry, vol. 9, no. 1, p. 120, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30902966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139].Jansen PR, Nagel M, Watanabe K, Wei Y, Savage JE, de Leeuw CA, van den Heuvel MP, van der Sluis S, and Posthuma D, “Gwas of brain volume on 54,407 individuals and cross-trait analysis with intelligence identifies shared genomic loci and genes,” bioRxiv, p. 613489, 2019. [Online]. Available: http://biorxiv.org/content/early/2019/04/19/613489.abstract [Google Scholar]
- [140].Holland D, Frei O, Desikan R, Fan C-C, Shadrin AA, Smeland OB, Sundar VS, Thompson P, Andreassen OA, and Dale AM, “Beyond snp heritability: Polygenicity and discoverability of phenotypes estimated with a univariate gaussian mixture model,” bioRxiv, p. 498550, 2018. [Online]. Available: http://biorxiv.org/content/early/2018/12/17/498550.abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- [141].Chiang MC, Barysheva M, McMahon KL, de Zubicaray GI, Johnson K, Montgomery GW, Martin NG, Toga AW, Wright MJ, Shapshak P, and Thompson PM, “Gene network effects on brain microstructure and intellectual performance identified in 472 twins,” J Neurosci, vol. 32, no. 25, pp. 8732–45, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22723713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142].Chen CH, Fiecas M, Gutierrez ED, Panizzon MS, Eyler LT, Vuoksimaa E, Thompson WK, Fennema-Notestine C, Hagler J, J. D, Jernigan TL, Neale MC, Franz CE, Lyons MJ, Fischl B, Tsuang MT, Dale AM, and Kremen WS, “Genetic topography of brain morphology,” Proc Natl Acad Sci U S A, vol. 110, no. 42, pp. 17 089–94, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24082094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [143].Sun D, Ching CRK, Lin A, Forsyth JK, Kushan L, Vajdi A, Jalbrzikowski M, Hansen L, Villalon-Reina JE, Qu X, Jonas RK, van Amelsvoort T, Bakker G, Kates WR, Antshel KM, Fremont W, Campbell LE, McCabe KL, Daly E, Gudbrandsen M, Murphy CM, Murphy D, Craig M, Vorstman J, Fiksinski A, Koops S, Ruparel K, Roalf DR, Gur RE, Schmitt JE, Simon TJ, Goodrich-Hunsaker NJ, Durdle CA, Bassett AS, Chow EWC, Butcher NJ, Vila-Rodriguez F, Doherty J, Cunningham A, van den Bree MBM, Linden DEJ, Moss H, Owen MJ, Murphy KC, McDonald-McGinn DM, Emanuel B, van Erp TGM, Turner JA, Thompson PM, and Bearden CE, “Large-scale mapping of cortical alterations in 22q11.2 deletion syndrome: Convergence with idiopathic psychosis and effects of deletion size,” Mol Psychiatry, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29895892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144].Villaln-Reina JE, Martnez K, Qu X, Ching C, Nir TM, Kothapalli D, Corbin C, Sun D, Lin A, Forsyth JK, Kushan L, Vajdi A, Jalbrzikowski M, Hansen L, Jonas RK, Amelsvoort T. v., Bakker G, Kates WR, Antshel KM, Fremont W, Campbell LE, McCabe KL, Daly E, Gudbrandsen M, Murphy C, Murphy D, Craig M, Emanuel B, McDonald-McGinn D, Vorstman J, Fiksinski A, Koops S, Ruparel K, Roalf D, Gur RE, Schmitt JE, Simon TJ, Goodrich-Hunsaker NJ, Durdle CA, Doherty J, Cunningham AC, Bree M. v. d., Linden DEJ, Owen M, Moss H, Kelly S, Donohoe G, Murphy KC, Arango C, Jahanshad N, Thompson PM, and Bearden CE, “Altered white matter microstructure in 22q11.2 deletion syndrome: A multi-site diffusion tensor imaging study,” Molecular Psychiatry, vol. in press, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [145].Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub TR, Lander ES, and Mesirov JP, “Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles,” Proc Natl Acad Sci U S A, vol. 102, no. 43, pp. 15 545–50, 2005. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/16199517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [146].Hao X, Yao X, Risacher S, Saykin A, Yu J, Wang H, Tan L, Shen L, and Zhang D, “Identifying candidate genetic associations with mri-derived ad-related roi via tree-guided sparse learning,” IEEE/ACM Trans Comput Biol Bioinform, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29993890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [147].Wang M, Hao X, Huang J, Shao W, and Zhang D, “Discovering network phenotype between genetic risk factors and disease status via diagnosis-aligned multi-modality regression method in alzheimer’s disease,” Bioinformatics, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30395195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [148].Wang H, Nie F, Huang H, Kim S, Nho K, Risacher SL, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Identifying quantitative trait loci via group-sparse multitask regression and feature selection: an imaging genetics study of the adni cohort,” Bioinformatics, vol. 28, no. 2, pp. 229–37, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22155867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [149].Wang X, Yan J, Yao X, Kim S, Nho K, Risacher SL, Saykin AJ, Shen L, and Huang H, “Longitudinal genotype-phenotype association study through temporal structure auto-learning predictive model,” J Comput Biol, vol. 25, no. 7, pp. 809–824, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30011249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150].Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, and Dale AM, “Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain,” Neuron, vol. 33, no. 3, pp. 341–55, 2002. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/11832223 [DOI] [PubMed] [Google Scholar]
- [151].Wang H, Nie F, Huang H, Yan J, Kim S, Nho K, Risacher SL, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “From phenotype to genotype: an association study of longitudinal phenotypic markers to alzheimer’s disease relevant snps,” Bioinformatics, vol. 28, no. 18, pp. i619–i625, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22962490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [152].Nie F, Huang H, and Ding C, “Low-rank matrix recovery via efficient schatten p-norm minimization,” Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, pp. 655–661, 2012. [Google Scholar]
- [153].Zhou T, Thung KH, Liu M, and Shen D, “Brain-wide genome-wide association study for alzheimer’s disease via joint projection learning and sparse regression model,” IEEE Trans Biomed Eng, vol. 66, no. 1, pp. 165–175, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29993426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [154].Vounou M, Nichols TE, Montana G, and I. Alzheimer’s Disease Neuroimaging, “Discovering genetic associations with high-dimensional neuroimaging phenotypes: A sparse reduced-rank regression approach,” Neuroimage, vol. 53, no. 3, pp. 1147–59, 2010. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/20624472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [155].Vounou M, Janousova E, Wolz R, Stein JL, Thompson PM, Rueckert D, Montana G, and I. Alzheimer’s Disease Neuroimaging, “Sparse reduced-rank regression detects genetic associations with voxel-wise longitudinal phenotypes in alzheimer’s disease,” Neuroimage, vol. 60, no. 1, pp. 700–16, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22209813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [156].Zhu X, Suk HI, Huang H, and Shen D, “Structured sparse low-rank regression model for brain-wide and genome-wide associations,” Med Image Comput Comput Assist Interv, vol. 9900, pp. 344–352, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28530001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].——, “Low-rank graph-regularized structured sparse regression for identifying genetic biomarkers,” IEEE Trans Big Data, vol. 3, no. 4, pp. 405–414, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29725610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [158].Hu R, Zhu X, Cheng D, He W, Yan Y, Song J, and Zhang S, “Graph self-representation method for unsupervised feature selection,” Neurocomputing, vol. 220, pp. 130–137, 2017. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0925231216305458 [Google Scholar]
- [159].Zhu X, Zhang W, Fan Y, and Alzheimer’s Disease Neuroimaging I, “A robust reduced rank graph regression method for neuroimaging genetic analysis,” Neuroinformatics, vol. 16, no. 3-4, pp. 351–361, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29907892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [160].Zhu X, Li X, Zhang S, Ju C, and Wu X, “Robust joint graph sparse coding for unsupervised spectral feature selection,” IEEE Trans Neural Netw Learn Syst, vol. 28, no. 6, pp. 1263–1275, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26955053 [DOI] [PubMed] [Google Scholar]
- [161].Greenlaw K, Szefer E, Graham J, Lesperance M, Nathoo FS, and I. Alzheimer’s Disease Neuroimaging, “A bayesian group sparse multi-task regression model for imaging genetics,” Bioinformatics, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28419235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162].Park T and Casella G, “The bayesian lasso,” Journal of the American Statistical Association, vol. 103, no. 482, pp. 681–686, 2008. [Online]. Available: 10.1198/016214508000000337 [DOI] [Google Scholar]
- [163].Kyung M, Gill J, Ghosh M, and Casella G, “Penalized regression, standard errors, and bayesian lassos,” Bayesian Anal., vol. 5, no. 2, pp. 369–411, 2010. [Online]. Available: https://projecteuclid.org:443/euclid.ba/1340218343 [Google Scholar]
- [164].Zhu H, Khondker Z, Lu Z, Ibrahim JG, and I. Alzheimer’s Disease Neuroimaging, “Bayesian generalized low rank regression models for neuroimaging phenotypes and genetic markers,” J Am Stat Assoc, vol. 109, no. 507, pp. 997–990, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25349462 [PMC free article] [PubMed] [Google Scholar]
- [165].Lu ZH, Khondker Z, Ibrahim JG, Wang Y, Zhu H, and I. Alzheimer’s Disease Neuroimaging, “Bayesian longitudinal low-rank regression models for imaging genetic data from longitudinal studies,” Neuroimage, vol. 149, pp. 305–322, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28143775 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166].Wang X, Chen H, Yan J, Nho K, Risacher SL, Saykin AJ, Shen L, Huang H, and Adni, “Quantitative trait loci identification for brain endophenotypes via new additive model with random networks,” Bioinformatics, vol. 34, no. 17, pp. i866–i874, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30423101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167].Schmidt WF, Kraaijveld MA, and Duin RPW, “Feedforward neural networks with random weights,” Proceedings., 11th IAPR International Conference on Pattern Recognition. Vol.II. Conference B: Pattern Recognition Methodology and Systems, pp. 1–4, 1992. [Google Scholar]
- [168].Witten DM, Tibshirani R, and Hastie T, “A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis,” Biostatistics, vol. 10, no. 3, pp. 515–34, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19377034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [169].Du L, Yan J, Kim S, Risacher SL, Huang H, Inlow M, Moore JH, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “A novel structure-aware sparse learning algorithm for brain imaging genetics,” Med Image Comput Comput Assist Interv, vol. 17, no. Pt 3, pp. 329–36, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25320816 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170].Zeng H, Shen EH, Hohmann JG, Oh SW, Bernard A, Royall JJ, Glattfelder KJ, Sunkin SM, Morris JA, Guillozet-Bongaarts AL, Smith KA, Ebbert AJ, Swanson B, Kuan L, Page DT, Overly CC, Lein ES, Hawrylycz MJ, Hof PR, Hyde TM, Kleinman JE, and Jones AR, “Large-scale cellular-resolution gene profiling in human neocortex reveals species-specific molecular signatures,” Cell, vol. 149, no. 2, pp. 483–96, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22500809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [171].Du L, Liu K, Yao X, Yan J, Risacher SL, Han J, Guo L, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Pattern discovery in brain imaging genetics via scca modeling with a generic non-convex penalty,” Sci Rep, vol. 7, no. 1, p. 14052, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29070790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172].Du L, Liu K, Zhang T, Yao X, Yan J, Risacher SL, Han J, Guo L, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “A novel scca approach via truncated l1-norm and truncated group lasso for brain imaging genetics,” Bioinformatics, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28968815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [173].Grosenick L, Klingenberg B, Katovich K, Knutson B, and Taylor JE, “Interpretable whole-brain prediction analysis with graphnet,” Neuroimage, vol. 72, pp. 304–21, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23298747 [DOI] [PubMed] [Google Scholar]
- [174].Du L, Huang H, Yan J, Kim S, Risacher SL, Inlow M, Moore JH, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Structured sparse canonical correlation analysis for brain imaging genetics: an improved graphnet method,” Bioinformatics, vol. 32, no. 10, pp. 1544–51, 2016. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26801960 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175].Gossmann A, Zille P, Calhoun V, and Wang YP, “Fdr-corrected sparse canonical correlation analysis with applications to imaging genomics,” IEEE Trans Med Imaging, vol. 37, no. 8, pp. 1761–1774, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29993802 [DOI] [PubMed] [Google Scholar]
- [176].Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, and Gur RE, “Neuroimaging of the philadelphia neurodevelopmental cohort,” Neuroimage, vol. 86, pp. 544–53, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23921101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [177].Du L, Liu K, Yao X, Risacher SL, Han J, Guo L, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Fast multi-task scca learning with feature selection for multi-modal brain imaging genetics,” Proceedings (IEEE Int Conf Bioinformatics Biomed), vol. 2018, pp. 356–361, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30881731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [178].Hao X, Li C, Yan J, Yao X, Risacher SL, Saykin AJ, Shen L, Zhang D, and I. Alzheimer’s Disease Neuroimaging, “Identification of associations between genotypes and longitudinal phenotypes via temporally-constrained group sparse canonical correlation analysis,” Bioinformatics, vol. 33, no. 14, pp. i341–i349, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28881979 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].Du L, Liu K, Zhu L, Yao X, Risacher SL, Guo L, Saykin AJ, Shen L, and for the ADNI, “Identifying progressive imaging genetic patterns via multi-task sparse canonical correlation analysis: a longitudinal study of the adni cohort,” Bioinformatics [ISMB/ECCB 2019 Issue], 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [180].Le Floch E, Guillemot V, Frouin V, Pinel P, Lalanne C, Trinchera L, Tenenhaus A, Moreno A, Zilbovicius M, Bourgeron T, Dehaene S, Thirion B, Poline JB, and Duchesnay E, “Significant correlation between a set of genetic polymorphisms and a functional brain network revealed by feature selection and sparse partial least squares,” Neuroimage, vol. 63, no. 1, pp. 11–24, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22781162 [DOI] [PubMed] [Google Scholar]
- [181].Fang J, Xu C, Zille P, Lin D, Deng HW, Calhoun VD, and Wang YP, “Fast and accurate detection of complex imaging genetics associations based on greedy projected distance correlation,” IEEE Trans Med Imaging, vol. 37, no. 4, pp. 860–870, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29990017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [182].Fan J, Feng Y, and Xia L, “A projection based conditional dependence measure with applications to high-dimensional undirected graphical models,” http://arxiv.org/abs/1501.01617, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [183].Hu W, Zhang A, Cai B, Calhoun V, and Wang YP, “Distance canonical correlation analysis with application to an imaging-genetic study,” J Med Imaging (Bellingham), vol. 6, no. 2, p. 026501, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/31001569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [184].Liu J, Demirci O, and Calhoun VD, “A parallel independent component analysis approach to investigate genomic influence on brain function,” IEEE Signal Process Lett, vol. 15, pp. 413–416, 2008. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19834575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [185].Calhoun VD, Liu J, and Adali T, “A review of group ica for fmri data and ica for joint inference of imaging, genetic, and erp data,” Neuroimage, vol. 45, no. 1 Suppl, pp. S163–72, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19059344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [186].Meda SA, Narayanan B, Liu J, Perrone-Bizzozero NI, Stevens MC, Calhoun VD, Glahn DC, Shen L, Risacher SL, Saykin AJ, and Pearlson GD, “A large scale multivariate parallel ica method reveals novel imaging-genetic relationships for alzheimer’s disease in the adni cohort,” NeuroImage, vol. 60, no. 3, pp. 1608–21, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22245343 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [187].Dukart J, Sambataro F, and Bertolino A, “Accurate prediction of conversion to alzheimer’s disease using imaging, genetic, and neuropsychological biomarkers,” J Alzheimers Dis, vol. 49, no. 4, pp. 1143–59, 2015. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/26599054 [DOI] [PubMed] [Google Scholar]
- [188].Filipovych R, Gaonkar B, and Davatzikos C, “A composite multivariate polygenic and neuroimaging score for prediction of conversion to alzheimer’s disease,” Int Workshop Pattern Recognit Neuroimaging, pp. 105–108, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/24899230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [189].Fan Y, Shen D, Gur RC, Gur RE, and Davatzikos C, “Compare: classification of morphological patterns using adaptive regional elements,” IEEE Trans Med Imaging, vol. 26, no. 1, pp. 93–105, 2007. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/17243588 [DOI] [PubMed] [Google Scholar]
- [190].Kauppi K, Fan CC, McEvoy LK, Holland D, Tan CH, Chen CH, Andreassen OA, Desikan RS, Dale AM, and I. Alzheimer’s Disease Neuroimaging, “Combining polygenic hazard score with volumetric mri and cognitive measures improves prediction of progression from mild cognitive impairment to alzheimer’s disease,” Front Neurosci, vol. 12, p. 260, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29760643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [191].McEvoy LK, Fennema-Notestine C, Roddey JC, Hagler J, J. D, Holland D, Karow DS, Pung CJ, Brewer JB, Dale AM, and I. Alzheimer’s Disease Neuroimaging, “Alzheimer disease: quantitative structural neuroimaging for detection and prediction of clinical and structural changes in mild cognitive impairment,” Radiology, vol. 251, no. 1, pp. 195–205, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19201945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [192].McEvoy LK, Holland D, Hagler J, J. D, Fennema-Notestine C, Brewer JB, Dale AM, and I. Alzheimer’s Disease Neuroimaging, “Mild cognitive impairment: baseline and longitudinal structural mr imaging measures improve predictive prognosis,” Radiology, vol. 259, no. 3, pp. 834–43, 2011. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/21471273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [193].Wang H, Nie F, Huang H, Risacher SL, Saykin AJ, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Identifying disease sensitive and quantitative trait-relevant biomarkers from multidimensional heterogeneous imaging genetics data via sparse multimodal multitask learning,” Bioinformatics, vol. 28, no. 12, pp. i127–36, 2012. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/22689752 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [194].Zhang Z, Huang H, Shen D, and I. Alzheimer’s Disease Neuroimaging, “Integrative analysis of multi-dimensional imaging genomics data for alzheimer’s disease prediction,” Front Aging Neurosci, vol. 6, p. 260, 2014. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/25368574 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [195].Rakotomamonjy A, Bach F, Canu S, and Grandvalet Y, “Simplemkl,” Journal of Machine Learning Research, vol. 9, pp. 2491–2521, 2008. [Google Scholar]
- [196].Liu F, Suk HI, Wee CY, Chen H, and Shen D, “High-order graph matching based feature selection for alzheimer’s disease identification,” Med Image Comput Comput Assist Interv, vol. 16, no. Pt 2, pp. 311–8, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24579155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [197].Wang H, Nie F, Huang H, and Ding C, “Heterogeneous visual features fusion via sparse multimodal machine,” 2013 IEEE Conference on Computer Vision and Pattern Recognition, pp. 3097–3102, 2013. [Google Scholar]
- [198].Peng J, An L, Zhu X, Jin Y, and Shen D, “Structured sparse kernel learning for imaging genetics based alzheimer’s disease diagnosis,” Med Image Comput Comput Assist Interv, vol. 9901, pp. 70–78, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28580458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [199].Singanamalli A, Wang H, Madabhushi A, and I. Alzheimer’s Disease Neuroimaging, “Cascaded multi-view canonical correlation (camcco) for early diagnosis of alzheimer’s disease via fusion of clinical, imaging and omic features,” Sci Rep, vol. 7, no. 1, p. 8137, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28811553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [200].Lee G, Singanamalli A, Wang H, Feldman MD, Master SR, Shih NN, Spangler E, Rebbeck T, Tomaszewski JE, and Madabhushi A, “Supervised multi-view canonical correlation analysis (smvcca): integrating histologic and proteomic features for predicting recurrent prostate cancer,” IEEE Trans Med Imaging, vol. 34, no. 1, pp. 284–97, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25203987 [DOI] [PubMed] [Google Scholar]
- [201].Zhou T, Thung KH, Zhu X, and Shen D, “Effective feature learning and fusion of multimodality data using stage-wise deep neural network for dementia diagnosis,” Hum Brain Mapp, vol. 40, no. 3, pp. 1001–1016, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30381863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [202].Ning K, Chen B, Sun F, Hobel Z, Zhao L, Matloff W, Alzheimer’s Disease Neuroimaging I, and Toga AW, “Classifying alzheimer’s disease with brain imaging and genetic data using a neural network framework,” Neurobiol Aging, vol. 68, pp. 151–158, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29784544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [203].Yan J, Risacher SL, Nho K, Saykin AJ, and Shen L, “Identification of discriminative imaging proteomics associations in alzheimer’s disease via a novel sparse correlation model,” Pac Symp Biocomput, vol. 22, pp. 94–104, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27896965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [204].Hao X, Li C, Du L, Yao X, Yan J, Risacher SL, Saykin AJ, Shen L, Zhang D, and I. Alzheimer’s Disease Neuroimaging, “Mining outcome-relevant brain imaging genetic associations via three-way sparse canonical correlation analysis in alzheimer’s disease,” Sci Rep, vol. 7, p. 44272, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/28291242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [205].Du L, Liu K, Yao X, Risacher S, Guo L, Saykin AJ, and Shen L, “Diagnosis status guided brain imaging genetics via integrated regression and sparse canonical correlation analysis,” in ISBI19: IEEE Int. Sym. on Biomedical Imaging, 2019, Conference Proceedings. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [206].Zille P, Calhoun VD, and Wang YP, “Enforcing co-expression within a brain-imaging genomics regression framework,” IEEE Trans Med Imaging, vol. 37, no. 12, pp. 2561–2571, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28678703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [207].Bi X, Yang L, Li T, Wang B, Zhu H, and Zhang H, “Genome-wide mediation analysis of psychiatric and cognitive traits through imaging phenotypes,” Hum Brain Mapp, vol. 38, no. 8, pp. 4088–4097, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28544218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [208].Batmanghelich NK, Dalca A, Quon G, Sabuncu M, and Golland P, “Probabilistic modeling of imaging, genetics and diagnosis,” IEEE Trans Med Imaging, vol. 35, no. 7, pp. 1765–79, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26886973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [209].Potkin SG, Turner JA, Guffanti G, Lakatos A, Torri F, Keator DB, and Macciardi F, “Genome-wide strategies for discovering genetic influences on cognition and cognitive disorders: methodological considerations,” Cogn Neuropsychiatry, vol. 14, no. 4-5, pp. 391–418, 2009. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/19634037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [210].Ramanan VK, Risacher SL, Nho K, Kim S, Swaminathan S, Shen L, Foroud TM, Hakonarson H, Huentelman MJ, Aisen PS, Petersen RC, Green RC, Jack CR, Koeppe RA, Jagust WJ, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Apoe and bche as modulators of cerebral amyloid deposition: a florbetapir pet genome-wide association study,” Mol Psychiatry, vol. 19, no. 3, pp. 351–7, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23419831 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [211].Ramanan VK, Risacher SL, Nho K, Kim S, Shen L, McDonald BC, Yoder KK, Hutchins GD, West JD, Tallman EF, Gao S, Foroud TM, Farlow MR, De Jager PL, Bennett DA, Aisen PS, Petersen RC, Jack J, R. C, Toga AW, Green RC, Jagust WJ, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Gwas of longitudinal amyloid accumulation on 18f-florbetapir pet in alzheimer’s disease implicates microglial activation gene il1rap,” Brain, vol. 138, no. Pt 10, pp. 3076–88, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26268530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [212].Nho K, Corneveaux JJ, Kim S, Lin H, Risacher SL, Shen L, Swaminathan S, Ramanan VK, Liu Y, Foroud T, Inlow MH, Siniard AL, Reiman RA, Aisen PS, Petersen RC, Green RC, Jack CR, Weiner MW, Baldwin CT, Lunetta K, Farrer LA, S. Multi-Institutional Research on Alzheimer Genetic Epidemiology, Furney SJ, Lovestone S, Simmons A, Mecocci P, Vellas B, Tsolaki M, Kloszewska I, Soininen H, AddNeuroMed C, McDonald BC, Farlow MR, Ghetti B, Indiana M, Aging S, Huentelman MJ, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Whole-exome sequencing and imaging genetics identify functional variants for rate of change in hippocampal volume in mild cognitive impairment,” Mol Psychiatry, vol. 18, no. 7, pp. 781–7, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23608917 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [213].Nho K, Kim S, Risacher SL, Shen L, Corneveaux JJ, Swaminathan S, Lin H, Ramanan VK, Liu Y, Foroud TM, Inlow MH, Siniard AL, Reiman RA, Aisen PS, Petersen RC, Green RC, Jack J, R. C, Weiner MW, Baldwin CT, Lunetta KL, Farrer LA, Study M, Furney SJ, Lovestone S, Simmons A, Mecocci P, Vellas B, Tsolaki M, Kloszewska I, Soininen H, AddNeuroMed C, McDonald BC, Farlow MR, Ghetti B, Indiana M, Aging S, Huentelman MJ, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Protective variant for hippocampal atrophy identified by whole exome sequencing,” Ann Neurol, vol. 77, no. 3, pp. 547–52, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25559091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [214].Ramanan VK, Nho K, Shen L, Risacher SL, Kim S, McDonald BC, Farlow MR, Foroud TM, Gao S, Soininen H, Kloszewska I, Mecocci P, Tsolaki M, Vellas B, Lovestone S, Aisen PS, Petersen RC, Jack J, R. C, Shaw LM, Trojanowski JQ, Weiner MW, Green RC, Toga AW, De Jager PL, Yu L, Bennett DA, and Saykin AJ, “Fastkd2 is associated with memory and hippocampal structure in older adults,” Mol Psychiatry, vol. 20, no. 10, pp. 1197–204, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25385369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [215].Horgusluoglu-Moloch E, Nho K, Risacher SL, Kim S, Foroud T, Shaw LM, Trojanowski JQ, Aisen PS, Petersen RC, Jack J, R. C, Lovestone S, Simmons A, Weiner MW, Saykin AJ, and I. Alzheimer’s Disease Neuroimaging, “Targeted neurogenesis pathway-based gene analysis identifies adora2a associated with hippocampal volume in mild cognitive impairment and alzheimer’s disease,” Neurobiol Aging, vol. 60, pp. 92–103, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28941407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [216].Yao X, Risacher SL, Nho K, Saykin AJ, Wang Z, Shen L, and I. Alzheimer’s Disease Neuroimaging, “Targeted genetic analysis of cerebral blood flow imaging phenotypes implicates the inpp5d gene,” Neurobiol Aging, vol. 81, pp. 213–221, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/31319229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [217].The MODEL-AD Consortium, “Jax stock #003284: Il-1r acp ko mouse strain,” https://www.jax.org/strain/003284, 2019. [Online]. Available: https://www.jax.org/strain/003284 [Google Scholar]
- [218].Pearlson GD, Liu J, and Calhoun VD, “An introductory review of parallel independent component analysis (p-ica) and a guide to applying p-ica to genetic data and imaging phenotypes to identify disease-associated biological pathways and systems in common complex disorders,” Front Genet, vol. 6, p. 276, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26442095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [219].Lin D, Calhoun VD, and Wang YP, “Correspondence between fmri and snp data by group sparse canonical correlation analysis,” Med Image Anal, vol. 18, no. 6, pp. 891–902, 2014. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/24247004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [220].Fang J, Lin D, Schulz SC, Xu Z, Calhoun VD, and Wang YP, “Joint sparse canonical correlation analysis for detecting differential imaging genetics modules,” Bioinformatics, vol. 32, no. 22, pp. 3480–3488, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/27466625 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [221].Hu W, Lin D, Cao S, Liu J, Chen J, Calhoun VD, and Wang YP, “Adaptive sparse multiple canonical correlation analysis with application to imaging (epi)genomics study of schizophrenia,” IEEE Trans Biomed Eng, vol. 65, no. 2, pp. 390–399, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29364120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [222].Alam MA, Lin HY, Deng HW, Calhoun VD, and Wang YP, “A kernel machine method for detecting higher order interactions in multimodal datasets: Application to schizophrenia,” J Neurosci Methods, vol. 309, pp. 161–174, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30184473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [223].Wang M, Huang TZ, Fang J, Calhoun VD, and Wang YP, “Integration of imaging (epi)genomics data for the study of schizophrenia using group sparse joint nonnegative matrix factorization,” IEEE/ACM Trans Comput Biol Bioinform, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30762565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [224].Chen J, Liu J, and Calhoun VD, “Translational potential of neuroimaging genomic analyses to diagnosis and treatment in mental disorders,” Proceedings of the IEEE, vol. 107, no. 5, pp. 912–927, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [225].Antonelli L, Guarracino MR, Maddalena L, and Sangiovanni M, “Integrating imaging and omics data: A review,” Biomedical Signal Processing and Control, vol. 52, pp. 264–280, 2019. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1746809419301326 [Google Scholar]
- [226].Hodes RJ and Buckholtz N, “Accelerating medicines partnership: Alzheimer’s disease (amp-ad) knowledge portal aids alzheimer’s drug discovery through open data sharing,” Expert Opin Ther Targets, vol. 20, no. 4, pp. 389–91, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/26853544 [DOI] [PubMed] [Google Scholar]
- [227].Ching T, Himmelstein DS, Beaulieu-Jones BK, Kalinin AA, Do BT, Way GP, Ferrero E, Agapow PM, Zietz M, Hoffman MM, Xie W, Rosen GL, Lengerich BJ, Israeli J, Lanchantin J, Woloszynek S, Carpenter AE, Shrikumar A, Xu J, Cofer EM, Lavender CA, Turaga SC, Alexandari AM, Lu Z, Harris DJ, DeCaprio D, Qi Y, Kundaje A, Peng Y, Wiley LK, Segler MHS, Boca SM, Swamidass SJ, Huang A, Gitter A, and Greene CS, “Opportunities and obstacles for deep learning in biology and medicine,” J R Soc Interface, vol. 15, no. 141, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/29618526 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [228].Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, van der Laak J, van Ginneken B, and Sanchez CI, “A survey on deep learning in medical image analysis,” Med Image Anal, vol. 42, pp. 60–88, 2017. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/28778026 [DOI] [PubMed] [Google Scholar]
- [229].Lundervold AS and Lundervold A, “An overview of deep learning in medical imaging focusing on mri,” Z Med Phys, vol. 29, no. 2, pp. 102–127, 2019. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30553609 [DOI] [PubMed] [Google Scholar]
- [230].Grapov D, Fahrmann J, Wanichthanarak K, and Khoomrung S, “Rise of deep learning for genomic, proteomic, and metabolomic data integration in precision medicine,” OMICS, vol. 22, no. 10, pp. 630–636, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30124358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [231].Van Essen DC and Glasser MF, “The human connectome project: Progress and prospects,” Cerebrum: the Dana Forum on Brain Science, vol. 2016, pp. cer–10–16, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5198757/ [Google Scholar]
- [232].Gollub RL, Shoemaker JM, King MD, White T, Ehrlich S, Sponheim SR, Clark VP, Turner JA, Mueller BA, Magnotta V, O’Leary D, Ho BC, Brauns S, Manoach DS, Seidman L, Bustillo JR, Lauriello J, Bockholt J, Lim KO, Rosen BR, Schulz SC, Calhoun VD, and Andreasen NC, “The mcic collection: a shared repository of multi-modal, multi-site brain image data from a clinical investigation of schizophrenia,” Neuroinformatics, vol. 11, no. 3, pp. 367–88, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23760817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [233].Jernigan TL, Brown TT, Hagler J, J. D, Akshoomoff N, Bartsch H, Newman E, Thompson WK, Bloss CS, Murray SS, Schork N, Kennedy DN, Kuperman JM, McCabe C, Chung Y, Libiger O, Maddox M, Casey BJ, Chang L, Ernst TM, Frazier JA, Gruen JR, Sowell ER, Kenet T, Kaufmann WE, Mostofsky S, Amaral DG, Dale AM, N. Pediatric Imaging, and S. Genetics, “The pediatric imaging, neurocognition, and genetics (ping) data repository,” Neuroimage, vol. 124, no. Pt B, pp. 1149–1154, 2016. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25937488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [234].Marek K, Chowdhury S, Siderowf A, Lasch S, Coffey CS, Caspell-Garcia C, Simuni T, Jennings D, Tanner CM, Trojanowski JQ, Shaw LM, Seibyl J, Schuff N, Singleton A, Kieburtz K, Toga AW, Mollenhauer B, Galasko D, Chahine LM, Weintraub D, Foroud T, Tosun-Turgut D, Poston K, Arnedo V, Frasier M, Sherer T, and Parkinson’s Progression Markers I, “The parkinson’s progression markers initiative (ppmi) - establishing a pd biomarker cohort,” Ann Clin Transl Neurol, vol. 5, no. 12, pp. 1460–1477, 2018. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/30564614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [235].Tomczak K, Czerwinska P, and Wiznerowicz M, “The cancer genome atlas (tcga): an immeasurable source of knowledge,” Contemp Oncol (Pozn), vol. 19, no. 1A, pp. A68–77, 2015. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/25691825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [236].Clark K, Vendt B, Smith K, Freymann J, Kirby J, Koppel P, Moore S, Phillips S, Maffitt D, Pringle M, Tarbox L, and Prior F, “The cancer imaging archive (tcia): maintaining and operating a public information repository,” J Digit Imaging, vol. 26, no. 6, pp. 1045–57, 2013. [Online]. Available: https://www.ncbi.nlm.nih.gov/pubmed/23884657 [DOI] [PMC free article] [PubMed] [Google Scholar]