Current estimates of T cell kinetics in humans

Derek C Macallan; Robert Busch; Becca Asquith

doi:10.1016/j.coisb.2019.10.002

. 2019 Dec;18:77–86. doi: 10.1016/j.coisb.2019.10.002

Current estimates of T cell kinetics in humans

Derek C Macallan ¹, Robert Busch ², Becca Asquith ^3,^∗

PMCID: PMC6941842 PMID: 31922055

Abstract

Stable isotope labeling is a generally applicable method of quantifying cell dynamics. Its advent has opened up the way for the quantitative study of T cells in humans. However, the literature is confusing as estimates vary by orders of magnitude between studies. In this short review we aim to explain the reasons for the discrepancies in estimates, clarify which estimates have been superseded and why and highlight the current best estimates. We focus on stable isotope labeling of T cell subsets in healthy humans.

Keywords: Lifespan, Half life, Stable isotope labelling, Proliferation rate, Death rate, T cell, Human, In vivo, Best estimates, Naive, Stem cell-like memory, Central memory, Effector memory, Dynamics, Kinetics, Mathematical model

Graphical abstract

Highlights

•
Current best estimates of the proliferation and production of CD4⁺ and CD8⁺ T cell subsets.
•
Explanation of why estimates vary between studies and which estimates have been superseded.
•
Discussion of the implications of model choice.

Introduction

Recent advances in our understanding of human T cell kinetics have resulted from concurrent development of experimental and theoretical approaches. Experimentally, it has been difficult to find a methodology that reliably reports in vivo T cell kinetics. The earliest studies used the rate of loss of therapeutic X ray–induced chromosome changes in patients with ankylosing spondylitis [1] or cancer [2,3]. However, this method is only applicable to patients receiving radiotherapy and assumes that radiation damage does not impact cell lifespan. The next generation of quantitative studies in humans utilised the thymidine analogue bromodeoxyuridine (BrdU) [4] but this too was beset with difficulties, both ethical (BrdU is not without toxicities) and theoretical (BrdU incorporation in DNA may itself perturb cell lifespan [5,6]). The field was revolutionised in the 1990s by the advent of stable isotope labeling [7, 8, 9, 10]. Stable isotopes such as deuterium (²H) are thought to be nontoxic and to have no impact on cell lifespan at the tracer doses used [5,11]. The premise of this approach is that DNA synthesis is a surrogate for cell replication, that the cellular content of DNA is fixed and that nonreplicative DNA synthesis is negligible.

A cursory read of the stable isotope labeling literature can be confusing as the estimated kinetics (proliferation, generation, disappearance rates) of the various T cell subpopulations vary from one study to the next. This is in part due to evolving phenotypic definitions of T cell subsets, in part due to evolving modeling techniques and in part due to differences in nomenclature for the key parameters; even given these explanations some of the discrepancy remains unexplained. Here we review the quantification of T cell subpopulations with the aim of explaining the source of some of these differences between estimates, highlighting the current best estimates. We restrict ourselves to T cells in healthy humans.

Stable isotope labeling: an overview

We start with a very brief overview of the stable isotope labeling method and then consider some of the important points in more detail later. A typical protocol for quantifying cell dynamics in vivo starts with the administration of the stable isotope label into a DNA precursor metabolite, typically either heavy water (²H₂O) or deuterium-labeled glucose (6,6-²H₂-glucose) [5,12]. Blood is sampled at regular time intervals, the cell populations of interest are sorted by fluorescence-activated cell sorting (FACS) and the fraction of labeled deoxyribose in their DNA is quantified by mass spectrometry. Label is gained when cells proliferate and lost when the labeled cell dies, differentiates to another phenotype or exits the blood compartment long-term. The time course of the fraction of labeled DNA thus contains information about cell proliferation and cell disappearance. To extract this information, mathematical models are constructed to describe the process and fitted to the experimental data. This permits the quantification of the rate of proliferation of any cell population that can be sampled and sorted in sufficient quantity in humans in vivo.

Two important considerations in labeling studies are (i) duration of labeling and (ii) data normalisation, both of which are closely related to the choice of label. For glucose, since the body pool is small and dynamic, ²H₂-glucose enrichments peak quickly so labeling periods can be very short (bolus, 10 h, 24 h and 7 day durations have been used [13, 14, 15]). In contrast, because the body water pool is large, ²H₂O labeling takes weeks. The lifespan of the cells of interest determines the optimal labeling period; ideally the target cell population should show considerable but not 100% replacement during the labeling period so that the signal is measurable but not saturated. Consequently, ²H₂-glucose is good for rapidly dividing cells and D₂O is better suited to slowly dividing populations.

In terms of normalisation, isotope labeling requires two normalisation steps: one to adjust for label availability in the individual (determined by dose, timing and dilution by unlabeled glucose/water), and one to scale between label in the plasma and the resulting label in DNA. For both water and glucose protocols, label availability in the plasma/body water is measured at multiple time-points and an empirical curve fitted to describe the enrichment, usually a square pulse with exponential tail for ²H₂-glucose and a logistic growth/exponential decay curve for ²H₂O. The second normalisation step is the scaling parameter (referred to as c, or b_w for ²H₂O labeling and b or b_g for ²H₂-glucose labeling); this is the ratio between label enrichment in newly synthesised DNA and that in plasma. In vitro ²H₂-glucose labeling experiments show that enrichment levels in DNA plateau at about 60–75% of media enrichment [11,12]. This has been attributed to intracellular dilution by unlabeled preformed deoxynucleotide triphosphates and by other pentose precursors [11]. For ²H₂O the scaling factor can be determined within the individual by sampling cells such as monocytes or granulocytes that can be expected to be fully replaced within the labeling period. By estimating their plateau enrichment, the scaling between DNA enrichment and plasma enrichment can be calculated. Deoxyribose contains seven nonexchangeable hydrogen atoms, any of which might potentially be replaced by deuterium in a D₂O labeling study. Consequently, the enrichment seen in deoxyribose exceeds that seen in plasma. The scaling has a binomial dependence on label availability in the plasma (any of the sites can be labeled or not labeled with probability dependent on plasma label enrichment). It can be shown that when n = 7 then, for the plasma enrichments typically attained, the scaling factor would be expected to lie in the range 6.18-6.68 (not 7 as sometimes erroneously stated) [7]. Empirically the scaling factor is observed to lie in the range 3.2–5.2 [14,16]; why there is variation between individuals in what might be expected to be a basic biochemical parameter and why the observed range differs from the theoretically expected range is unclear and indicates that there may be errors in the calculation of this parameter. Label enrichment in DNA is directly proportional both to the scaling factor and to the proliferation rate (Supplementary Information) so an error in the scaling factor will cause the inverse error in the proliferation rate (if b is erroneously estimated to be double the true value, the proliferation rate estimated will be half the true value).

T cell dynamics: what we have learnt

We focus on CD8⁺ T cells in the text and Table 1; analogous numbers for CD4⁺ T cells are provided in Table 2.

Table 1.

Summary of estimates of CD8⁺ T cell generation and proliferation rates in humans.

Population	Phenotype	Generation rate (d⁻¹)	Range (d⁻¹)	Proliferation rate (d⁻¹)	Range (d⁻¹)	Source	Method	Notes
Naïve	CD45RA⁺	0.002 [100% self-renewal, 0% from thymus [19]]	0.0–0.01	0.002	0.0–0.01	Macallan et al. [13] Table 1 ^a	1d ²H₂-glu kh model	Based on best phenotypic definition at time. Will inadvertently have included T_EMRA and T_SCM.
	CD45RO^―CD27⁺	0.0003	0.0003–0.0005	0.0003	0.0003–0.0005	Vrisekoop et al. [16] Table 1 ^a	63d ²H₂O kh model	Based on best phenotypic definition at time. Will inadvertently have included T_SCM.
	CD45RO^―CD27^brightCCR7⁺CD95^―	0.00045	0.0003–0.0006	0.00045	0.0003–0.0006	Costa del Amo et al. [18] Table S2 ^a	49d ²H₂O precursor model
T_SCM	CD45RO^―CD27^brightCCR7⁺CD95⁺	0.01 [64% self-renewal, 35% from naïve pool [18]]	0.006–0.07	0.007	0.002–0.01	Costa del Amo et al. [18] Table 1 and S2 (see notes)	49d ²H₂O precursor model	Paper found evidence for ≥ two subpopulations. Here we report the average rates derived from Table 1 (ratio of subpopulations) and Table S2 (proliferation and disappearance of subpopulations)
Memory	CD45RA^―			0.019	0.006–0.16	Macallan et al. [13] Table 1^¥	1 d ²H₂-glu kh model	Later corrected by Ahmed et al. see below
	CD45RO⁺			0.0028	0.0019–0.006	Vrisekoop et al. [16] Table 1^¥	63d ²H₂O kh model	Later corrected by Westera et al. and Ahmed et al. see below
	CD45RO⁺			0.006	0.004–0.009	Westera et al. [27] in line text (note typo on upper limit of range in original paper, corrected here)^¥	63d ²H₂O multi-exp model	Corrected analysis of Vrisekoop et al. data
	CD45RA^―			0.015	0.006–0.11	Ahmed et al. [28] adjustment taken from Table S1 and applied to Macallan estimates^¥	1d ²H₂-glu kh model	Corrected analysis of Macallan et al. data.
	CD45RO⁺			0.007	0.004–0.009	Ahmed et al. [28] adjustment taken from Figure S7 (ratio of b_w) and applied to Westera estimates ^¥	63d ²H₂O multi-exp model	Further corrected analysis of Vrisekoop et al. data.

Open in a new tab

Estimates (within each subpopulation) provided in chronological order. Estimates shown in bold font are current best estimates, estimates in regular font have been superseded (see final column, notes). All estimates, with the exception of the T_SCM subpopulation parameters, assume there is no input from a precursor population (Box 1). Work from Westera et al. indicates this is a valid assumption for naïve cells. However, for memory cells we cannot necessarily neglect input from the precursor population (in this case naïve cells). Proliferation rate estimates marked ^¥ may therefore need to be revised when additional data are available.

All rates provided as proportion of target cell population and represent the median across study individuals.

Abbreviations: D₂-glu: D₂-glucose, kh model: kinetic heterogeneity model, multi-exp model: multi-exponential model.

Model equations provided in Supplementary Information.

The range is the minimum and maximum value of the point estimate observed across the subjects.

Proliferation rate estimate for naïve cells calculated from production rate based on the finding that 100% of new naïve cells in humans originate from peripheral proliferation [19].

Table 2.

Summary of estimates of CD4⁺ T cell generation and proliferation rates in humans.

Population	Phenotype	Generation rate (d⁻¹)	Range (d⁻¹)	Proliferation rate (d⁻¹)	Range (d⁻¹)	Source	Method	Notes
Naïve	CD45RA⁺	0.004	0.002–0.015	0.004	0.002–0.015	Macallan et al. [13] Table 1 ^a	1d ²H₂-glu kh model	Based on best phenotypic definition at time. Will inadvertently have included T_SCM.
	CD45RO⁻CD27⁺	0.0005	0.0003–0.0009	0.0005	0.0003–0.0009	Vrisekoop et al. [16] Table 1.^a	63d ²H₂O kh model	Based on best phenotypic definition at time. Will inadvertently have included T_SCM.
	CD45RO^―CD27^brightCCR7⁺CD95^―	0.0007	0.0004–0.001	0.0007	0.0004–0.001	Costa del Amo et al. unpub.	49d ²H₂O precursor model
T_SCM	CD45RO^―CD27^brightCCR7⁺CD95⁺	NA	NA	NA	NA			Parameters not estimated for CD4⁺ T_SCM due to lack of additional data (YFV)
Memory	CD45RA^―			0.02	0.01–0.08	Macallan et al. [13] Table 1^¥	1d ²H₂-glu kh model	Later corrected by Ahmed et al. see below
	CD45RO⁺			0.0045	0.002–0.007	Vrisekoop et al. [16] Table 1^¥	63d ²H₂O kh model	Later corrected by Westera et al. and Ahmed et al. see below
	CD45RO⁺			0.0061	0.002–0.01	Westera et al. in line text [27]^¥	63d ²H₂O multi-exp model	Corrected analysis of Vrisekoop et al. data
	CD45RA^―			0.018	0.009–0.05	Ahmed et al. [28] adjustment taken from Table S1 and applied to Macallan estimates^¥	1d ²H₂-glu kh model	Corrected analysis of Macallan et al. data.
	CD45RO⁺			0.0064	0.002–0.01	Ahmed et al. [28] adjustment taken from Figure S7 (ratio of b_w) and applied to Westera estimates ^¥	63d ²H₂O Multi-exp model	Further corrected analysis of Vrisekoop et al. data.
Central memory	CD45RO⁺CCR7⁺			0.010	0.007–0.04	Macallan et al. [43] Table 2^¥	1d ²H₂-glu kh model
Effector memory	CD45RO⁺CCR7^-			0.042	0.02–0.08	Macallan et al. [43] Table 2^¥	1d ²H₂-glu kh model

Open in a new tab

Estimates (within each subpopulation) provided in chronological order. Estimates shown in bold font are current best estimates, estimates in regular font have been superseded (see final column, notes). All estimates assume there is no input from a precursor population (Box 1). Work from Westera et al. indicates this is a valid assumption for naïve cells. However, for memory cells we cannot necessarily neglect input from the precursor population (in this case naïve cells). Proliferation rate estimates marked ^¥ may therefore need to be revised when additional data are available.

The range is the minimum and maximum value of the point estimate observed across the subjects.

All rates provided as proportion of target cell population and represent the median across study individuals.

Abbreviations: D2-glu: D2-glucose, kh model: kinetic heterogeneity model, multi-exp model: multi-exponential model.

Model equations provided in Supplementary Information.

Proliferation rate estimate for naïve cells calculated from production rate based on the finding that 100% of new naïve cells in humans originate from peripheral proliferation [19].

Naïve CD8⁺ T cells. Thymic output and peripheral proliferation both contribute to maintenance of the naïve T cell pool. Since the isotope will label any proliferating cell, no distinction can be made between cells that divided in the periphery and cells that acquired label in the thymus and then entered the periphery [17]. Most models to describe naïve cell dynamics ignore thymic output and attribute all label accrual to naïve cell proliferation; this will tend to lead to an overestimate of proliferation rates and an underestimate of disappearance rates (Box 1). This caveat aside, the first study to investigate naïve T cells using isotope labeling found a median naïve CD8⁺ T cell proliferation rate of p = 0.002 d⁻¹ (corresponding to a doubling time of ln(2)/0.002 = 295 days) [13], Table 1, Table 2. A later study found a considerably slower proliferation rate (p = 0.0003 d⁻¹, doubling time = 2300 days) [16]. Part of this difference can be explained by the problem of evolving phenotypic definitions. Both studies inadvertently included what we would now call non-naïve cells in their sorted “naïve” populations (defined as CD45RA⁺ and CD45RO^―CD27⁺, respectively). This would have included terminally differentiated effectors (T_EMRA) in the first study and stem cell memory T cells (T_SCM) in the second (neither of which had been described at the time). A study using the most recent definition (CD45RO^―CD27^brightCCR7⁺CD95^―) finds that naïve CD8⁺ T cells have a proliferation rate of 0.0005 d⁻¹ (doubling time = 1400 days) [18]. By including an analysis of T cell receptor excision circles (TRECs), a further study split naïve CD4⁺ T cell production into cells arising from the thymus and cells arising from peripheral proliferation. It was shown that in adult humans, in stark contrast to mice, the overwhelming majority of new naïve CD4⁺ cells (approx. 100%) arose from peripheral division [19]. This fascinating result illustrates the importance of studying humans wherever possible. Unfortunately, although T_SCM cells had been described by this point, the analysis used an older definition of naïve T cells (CD45RO^―CD27⁺) which would have included T_SCM cells. True naïve cells have lower proliferation and much higher TREC content than T_SCM cells [18,20,21]; thus a large proportion of peripheral proliferation, which was attributed to naïve cells in this study, may in fact be due to T_SCM cells. Moreover, T_SCM cells are a considerably more frequent population in humans than mice and so the failure to exclude T_SCM cells from the naïve cell gate may partly explain why more replacement by proliferation was seen in humans than mice [20,22]. It would be interesting to redo this important analysis delineating the contribution of true naïve cells and T_SCM cells. It seems likely that the inclusion of T_SCM cells could explain some but not all of the reported difference between mice and humans in the contribution of thymic output.

Box 1. Nomenclature: generation, proliferation, disappearance, turnover and half-lives.Image 6.

For a target population in equilibrium (i.e. at steady state), the generation of new cells (at rate g) either by influx from a precursor (progenitor) population at rate i and/or proliferation (i.e. self-renewal) at rate p, is balanced by cell disappearance (death, differentiation, long-term exit from blood, at rate d) such that g=i+p=d. With a few exceptions [14,18,24,45], the majority of labeling studies ignore the influx from precursor populations (i.e. i is assumed to be zero) and all label accrual is attributed to self-renewal. The impact of this assumption on the rates estimated will depend on both the kinetics and size of the precursor population compared with the target population; the impact of including an upstream compartment has been demonstrated explicitly for neutrophils [14], CD4⁺ memory T cells [24] and CD4⁺ and CD8⁺ T_SCM cells (unpublished work).

The expansion of models to include a nonzero influx term means that two widely used terms in cell kinetics, turnover and half-life, which were previously precisely defined, are now ambiguous. A number of studies report the “turnover rate” of a population which is either the proliferation rate or the disappearance rate. When the influx from the precursor population is assumed to be zero then, for a population at steady state, the proliferation rate equals the disappearance rate and the turnover rate is unambiguously defined. However, when the influx is nonzero, the definition of “turnover” is unclear and we avoid its use in this review. Similarly for the population half-life. With zero influx the half-life (time for the population to halve in size if there was no proliferation) = ln(2)/p = ln(2)/d. However, if nonzero influx is considered, then another parameter can be defined, the “clonal half-life”, ln(2)/(d-p). The clonal half-life is the time for a T cell clone to halve in size whilst the overall population remains at steady state (i.e. without halting proliferation) and likely relates to the longevity of a T cell clone (for zero influx the clonal half-life is infinite). Models describing an upstream/precursor population and a downstream/target cell population were used by Costa del Amo et al. to describe the relationship between naïve and T_SCM cells [18]; the equations are given in Supplementary Information.

This input from a precursor population considered earlier is distinct from the “source” term included in early models of labeling dynamics [46,47]. In these early models the target cell population was assumed to be homogeneous and the source was invoked to explain the observation that the measured disappearance rate typically exceeded the measured proliferation rate despite the fact that the target cell population was of approximately constant size over time. However, the size and nature of the source in these models (typically large and unlabeled) meant it was usually not possible to find a physiological correlate of the source. Instead it was proposed that the discrepancy between the measured proliferation and disappearance rates could be explained by kinetic heterogeneity in the population [17]. That is, if the target population is heterogeneous, then although the measured proliferation rate will be the average proliferation rate of the population the loss of labeled cells will be biased towards the rapidly turning over subpopulation and will therefore overestimate the average disappearance rate of the whole population.

Definitions

Proliferation	p
Disappearance	d
Doubling Time	ln(2)/p
Half-life	ln(2)/d
Clonal half-life	ln(2)/(d-p)
Lifespan	1/d

Open in a new tab

The above-mentioned definitions are correct under the assumption that times to proliferate and disappear are exponentially distributed.

Alt-text: Box 1

Stem cell memory T cells (T_SCM). T_SCM cells are a recently described subpopulation of T cells with stem cell–like properties of self-renewal, clonal longevity and multipotency. It is postulated that they are responsible for maintaining long-lived immune memory [20]. Until 2018, self-renewal and longevity of human T_SCM cells had only been demonstrated in vitro. Using a combination of mathematical modeling, stable isotope labeling, telomere length analysis and data from vaccinees, it was possible to quantify the self-renewal, proliferation and clonal longevity of T_SCM cells in humans in vivo. Unexpectedly, it was found that the average lifespan of a T_SCM clone is short (clonal half-life < 1 year, proliferation rate = 0.007 d⁻¹), far too short to maintain immune memory that can last for decades. However, it was also shown that what we currently define as the T_SCM population (CD45RO^―CD27^brightCCR7⁺CD95⁺ [23]) comprises at least two kinetically distinct subpopulations. One is rapidly replaced (clonal half-life ln(2)/(d-p) = 5 months) which explains the short average lifespan of the bulk T_SCM population, and the other having a clonal half-life of approximately 9 years, consistent with the longevity of immune memory. This long-lived subpopulation had a high degree of self-renewal, with a cell residing without dying or differentiating for 15% of our lifetime. It was postulated that this subpopulation represents the “true” stem cell–like population (the other subpopulation may represent cells transiting to effector status). Interestingly, in apparently healthy asymptomatic individuals, there was ongoing differentiation of naïve cells; the contribution of naïve cells to T_SCM replacement was typically about 50% and never less than 10% (i.e. 10–50% of new T_SCM cells are produced by differentiating naïve cells and 50–90% by division of existing T_SCM cells). Considerable recruitment of naïve cells to the memory pool in the apparent absence of novel antigen has previously been reported for mice [24,25]. To the best of our knowledge this is the first time this surprising observation has been made in humans, and it is important to confirm it using an independent approach.

Memory T cells. Only one stable isotope labeling study of CD8⁺ T cell memory subpopulations (central memory and effector memory) has been carried out [26]. In this study, sampling was restricted to long after the end of labeling, and thus only quantifies the net loss of labeled cells and does not permit the separation of proliferation and disappearance. It is necessary to sample both the uptake and the loss of label to obtain a representative estimate of proliferation [17]. To date this has only been performed for bulk (CD45RO⁺ or CD45RA⁻) CD8⁺ memory T cells (though some CD4⁺ memory subsets have been studied, Table 2). The first such study, which used a 24 h ²H₂-glucose labeling protocol, found that memory CD8⁺ T cells proliferated rapidly (p = 0.019 d⁻¹, doubling time = 36 days). A subsequent study, utilising a 63 d D₂O protocol, found considerably slower proliferation (p = 0.0028 d⁻¹, doubling time = 248 days).

Investigation of this discrepancy by a collaboration between the two groups involved [27,28] has highlighted some critical factors in analysing isotope labeling data. Firstly, in long labeling studies, saturation of subpopulations must be accounted for. Adjusting for saturation in the 63-day ²H₂O study led to revised estimates of p = 0.006 d⁻¹ (doubling time = 116 days). Whether saturation has occurred can be investigated by comparing the fits of models with increasing numbers of subpopulations and checking for a change in the estimated average proliferation rate [27,29]. Secondly, normalisation is critical, particularly for overnight ²H₂-glucose labeling. We postulated that errors may arise from reduced plasma glucose sampling overnight when unlabeled glucose influx (food) is reduced; periods of higher glucose enrichment may thus be missed. A prediction of this postulate (that monocytes would have plateau label of >100%) was borne out. Correcting for these inaccuracies in normalisation decreased proliferation rate estimates made using D₂-glucose (to p=0.015 d^-1) and increased estimates made using D₂O (to p=0.007 d^-1). A more sophisticated approach in which plasma glucose was predicted rather than measured came to very similar conclusions [30]. The estimates from the two studies are now closer together, but there does still appear to be some genuine, unresolved difference. Current best estimates of the proliferation rate of memory CD8⁺ T cells are therefore in the range 0.007-0.015 d⁻¹ (corresponding to a doubling time of between 46 and 99 days).

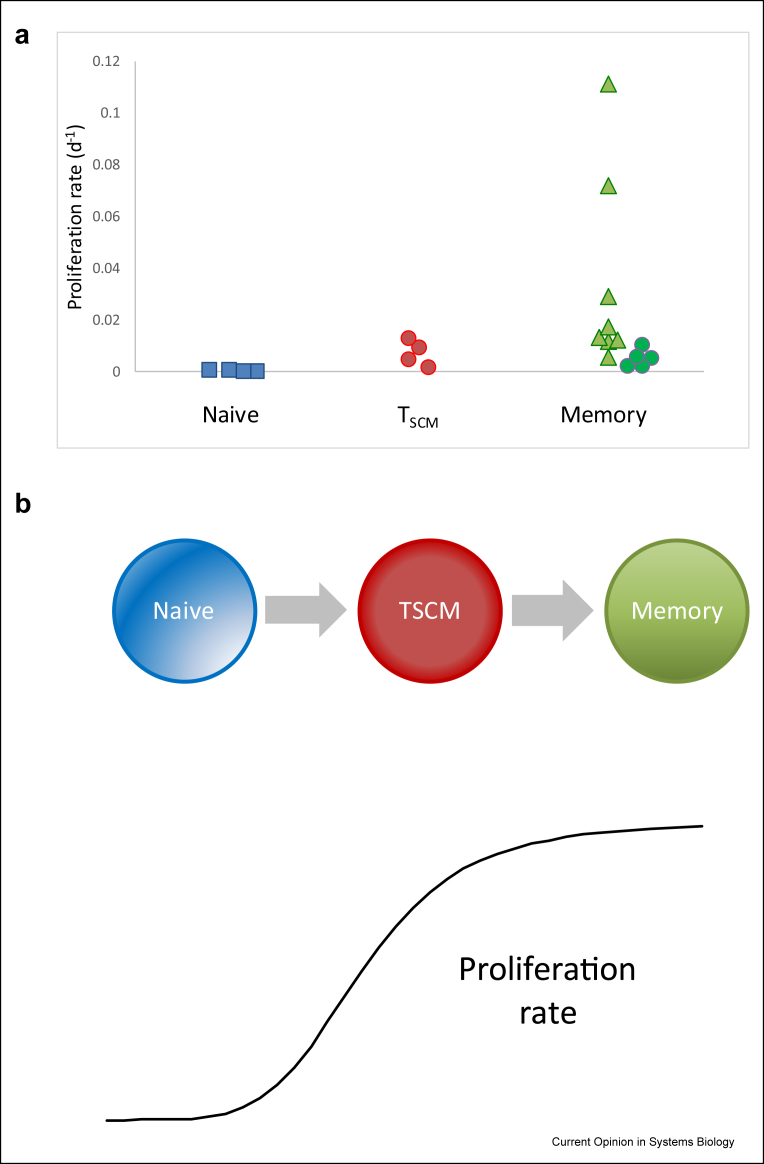
It is interesting that these studies show that more highly differentiated T cells have more rapid proliferation (Fig. 1; see also CD4⁺ subpopulations Table 2) despite the decrease in proliferative potential that is thought to be associated with differentiation [23,31] and the prevalent view that cell senescence is linked with poor proliferation [32, 33, 34].

**Estimates of CD8**⁺**T cell proliferation rates as a function of cell differentiation state**.a. Current best estimates of the proliferation rates for different CD8⁺ T cell subsets in healthy adult humans (Table 1). Naïve T cells. Estimates from Costa del Amo et al. [18]. T_SCM cells. Estimates from Costa del Amo et al. [18]. Memory T cells. Estimates from Macallan et al. adjusted by Ahmed et al. [13,28]. Memory T cells. Estimate from Vrisekoop et al. adjusted by Westera et al., further adjusted by Ahmed et al. [16,28,44].b Cartoon of proliferation rate as a function of differentiation state. All the evidence indicates that naïve T cells proliferate more slowly than T_SCM cells and memory T cells, i.e. estimated T cell proliferation increases with differentiation despite the decrease in proliferative potential that is thought to be associated with differentiation [23,31,32].

Modeling considerations

Mathematical models of T cell kinetics necessarily involve assumptions, firstly because we do not completely understand the biology (e.g. kinetic substructure of T cell populations [17,24], the lineage relationship between T cell subpopulations [35], the rules determining cell fate [36, 37, 38∗∗]) but secondly, more importantly, even if the biology was completely known, it would still be essential to simplify models for parameter inference (if models are overly complex compared with the data, the parameters cannot be estimated). And so mathematical models of T cell dynamics for parameter inference will always contain assumptions. This means that estimates from isotope labeling are necessarily susceptible to model assumptions. This problem was starkly illustrated by a recent debate over the lifespan of neutrophils. In 2012, a paper by Pillay et al. utilising isotope labeling found that, far from being a very short-lived population as previously thought, blood neutrophils had lifespans of about 5 days, at least 10 times longer than previous estimates [39, 40]. If correct, the work by Pillay et al. would have overturned two decades of research. However, a subsequent response proposed that the unexpectedly long lifespans from the labeling study could result from data misinterpretation [41]. This was later confirmed by Lahoz-Beneytez et al. who combined a reanalysis of the data from Pillay et al. as well as generation of new labeling data to show that the 2012 labeling study had included an implicit unphysiological assumption. Lahoz-Beneytez et al. showed that by neglecting the fact that neutrophils are produced by proliferation outside of the observed compartment (i.e. are produced by proliferating precursors in the bone marrow rather than by proliferation of neutrophils in the blood), Pillay et al. had essentially assumed the ratio of blood neutrophils to the bone marrow neutrophil precursor mitotic pool was infinite, leading to a severe underestimate of the neutrophil death rate [14]. Using a more physiological model, Lahoz-Beneytez et al. found the best estimate of neutrophil half-life lay in the range 13–19 h, consistent with the traditional dogma that blood neutrophils are short-lived. More generally, neglecting the upstream compartment will affect kinetic estimates of all cell populations (Box 1). Proliferation rates of memory T cells (currently estimated without allowing for input from the naïve T cell compartment) are also susceptible to such error and may need to be revised once more data are available [18,24].

Future directions

There are a number of areas that are ripe for development. The first area where more research is essential is robustness of parameter estimates to model assumptions. Personally, we routinely examine the impact of assumptions that we are conscious of making (e.g. neglecting recirculation) on our parameter estimates, but this approach is very limited and ad hoc. The problem is compounded because only a few groups work on isotope labeling data and we collaborate closely so there is a lack of independent criticism that comes from having many researchers working independently on the same problem. One way forward may be to use the ideas of parameter estimation from ensemble models that are being developed in the field of climate change modeling; e.g., Ref. [42]. Another area where progress is lacking is the normalisation factor for D₂O labeling, c (b_w): why does this vary between individuals and why does it frequently lie outside the range that would be theoretically expected? An error in normalisation will directly affect proliferation rate estimates and, to a lesser extent disappearance rate estimates. The field has been aware of this problem for more than 10 years yet has failed to progress. And then there are a number of easier problems: “what is the proliferation rate of the various CD8⁺ T cell subpopulations that have yet to be studied e.g. effector memory, central memory, T_EMRA?“, “is the statement that all naïve cell replacement comes from peripheral proliferation in humans true if we exclude T_SCM cells from the naïve cell gate?“, “what happens to our current estimates of memory T cell proliferation if we include input from differentiating naïve T cells?” In short, there has been a decade of considerable progress, but there are still many fundamental questions to be answered and we would urge the community to consider addressing these topics.

Conflict of interest statement

Nothing declared.

Acknowledgments

We are very grateful to all our collaborators and colleagues who have contributed to our thinking on stable isotope labeling and T cell dynamics. This work was funded by the Wellcome Trust (103865), Medical Research Council UK (J007439, G1001052), European Union Seventh Framework Programme (317040) and the European H2020 Programme (764698).

This reviews comes from a themed issue on Systems immunology & host-pathogen interaction

Edited by Thomas Höfer and Grégoire Altan-Bonnet

Footnotes

^{Appendix A}

Supplementary data related to this article can be found at https://doi.org/10.1016/j.coisb.2019.10.002.

Appendix A. Supplementary data

The following is the supplementary data related to this article:

Multimedia component 1

mmc1.docx^{(48.6KB, docx)}

References

1.Buckton K.E., Brown W.M.C., Smith P.G. Lymphocyte survival in men treated with X-rays for ankylosing spondylitis. Nature. 1967;214:470–473. doi: 10.1038/214470a0. [DOI] [PubMed] [Google Scholar]
2.Michie C.A., McLean A., Alcock C., Beverley P.C. Lifespan of human lymphocyte subsets defined by CD45 isoforms. Nature. 1992;360:264–265. doi: 10.1038/360264a0. [DOI] [PubMed] [Google Scholar]
3.McLean A.R., Michie C.A. In vivo estimates of division and death rates of human T lymphocytes. Proc Natl Acad Sci U S A. 1995;92:3707–3711. doi: 10.1073/pnas.92.9.3707. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Kovacs J.A., Lempicki R.A., Sidorov I.A., Adelsberger J.W., Herpin B., Metcalf J.A., Sereti I., Polis M.A., Davey R.T., Tavel J. Identification of dynamically distinct subpopulations of T lymphocytes that are differentially affected by HIV. J Exp Med. 2001;194:1731–1741. doi: 10.1084/jem.194.12.1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Busch R., Neese R.A., Awada M., Hayes G.M., Hellerstein M.K. Measurement of cell proliferation by heavy water labeling. Nat Protoc. 2007;2:3045–3057. doi: 10.1038/nprot.2007.420. [DOI] [PubMed] [Google Scholar]
6.Reome J.B., Johnston D.S., Helmich B.K., Morgan T.M., Dutton-Swain N., Dutton R.W. The effects of prolonged administration of 5-bromodeoxyuridine on cells of the immune system. J Immunol. 2000;165:4226–4230. doi: 10.4049/jimmunol.165.8.4226. [DOI] [PubMed] [Google Scholar]
7.Hellerstein M.K., Neese R.A. Mass isotopomer distribution analysis: a technique for measuring biosynthesis and turnover of polymers. Am J Physiol. 1992;263:E988–E1001. doi: 10.1152/ajpendo.1992.263.5.E988. [DOI] [PubMed] [Google Scholar]
8.Hellerstein M., Hanley M.B., Cesar D., Siler S., Papageorgopoulos C., Wieder E., Schmidt D., Hoh R., Neese R., Macallan D. Directly measured kinetics of circulating T lymphocytes in normal and HIV-1-infected humans. Nat Med. 1999;5:83–89. doi: 10.1038/4772. [DOI] [PubMed] [Google Scholar]
9.Hellerstein M.K. Measurement of T-cell kinetics: recent methodologic advances. Immunol Today. 1999;20:438–441. doi: 10.1016/s0167-5699(99)01529-7. [DOI] [PubMed] [Google Scholar]
10.Hellerstein M.K., Neese R.A. Mass isotopomer distribution analysis at eight years: theoretical, analytic, and experimental considerations. Am J Physiol. 1999;276:E1146–E1170. doi: 10.1152/ajpendo.1999.276.6.E1146. [DOI] [PubMed] [Google Scholar]
11.Macallan D.C., Fullerton C.A., Neese R.A., Haddock K., Park S.S., Hellerstein M.K. Measurement of cell proliferation by labeling of DNA with stable isotope-labeled glucose: studies in vitro, in animals, and in humans. Proc Natl Acad Sci U S A. 1998;95:708–713. doi: 10.1073/pnas.95.2.708. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Macallan D.C., Asquith B., Zhang Y., de Lara C., Ghattas H., Defoiche J., Beverley P.C. Measurement of proliferation and disappearance of rapid turnover cell populations in human studies using deuterium-labeled glucose. Nat Protoc. 2009;4:1313–1327. doi: 10.1038/nprot.2009.117. [DOI] [PubMed] [Google Scholar]
13.Macallan D.C., Asquith B., Irvine A.J., Wallace D.L., Worth A., Ghattas H., Zhang Y., Griffin G.E., Tough D.F., Beverley P.C. Measurement and modeling of human T cell kinetics. Eur J Immunol. 2003;33:2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]
14.Lahoz-Beneytez J., Elemans M., Zhang Y., Ahmed R., Salam A., Block M., Niederalt C., Asquith B., Macallan D. Human neutrophil kinetics: modeling of stable isotope labeling data supports short blood neutrophil half-lives. Blood. 2016;127:3431–3438. doi: 10.1182/blood-2016-03-700336. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Mohri H., Perelson A.S., Tung K., Ribeiro R.M., Ramratnam B., Markowitz M., Kost R., Hurley A., Weinberger L., Cesar D. Increased turnover of T lymphocytes in HIV-1 infection and its reduction by antiretroviral therapy. J Exp Med. 2001;194:1277–1287. doi: 10.1084/jem.194.9.1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Vrisekoop N., den Braber I., de Boer A.B., Ruiter A.F., Ackermans M.T., van der Crabben S.N., Schrijver E.H., Spierenburg G., Sauerwein H.P., Hazenberg M.D. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc Natl Acad Sci U S A. 2008;105:6115–6120. doi: 10.1073/pnas.0709713105. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Asquith B., Debacq C., Macallan D.C., Willems L., Bangham C.R. Lymphocyte kinetics: the interpretation of labelling data. Trends Immunol. 2002;23:596–601. doi: 10.1016/s1471-4906(02)02337-2. [DOI] [PubMed] [Google Scholar]
Costa Del Amo P., Lahoz-Beneytez J., Boelen L., Ahmed R., Miners K.L., Zhang Y., Roger L., Jones R.E., Marraco S.A.F., Speiser D.E. Human TSCM cell dynamics in vivo are compatible with long-lived immunological memory and stemness. PLoS Biol. 2018;16 doi: 10.1371/journal.pbio.2005523. [DOI] [PMC free article] [PubMed] [Google Scholar]; Finds T_SCM cells have the dynamic attributes consistent with “stemness” i.e. self-renewal and clonal longevity. However, this was only true of a subpopulation of what are currently defined as T_SCM cells. Also found high levels of naïve cell differentiation in apparently healthy, asymptomatic individuals.
19.den Braber I., Mugwagwa T., Vrisekoop N., Westera L., Mogling R., de Boer A.B., Willems N., Schrijver E.H., Spierenburg G., Gaiser K. Maintenance of peripheral naive T cells is sustained by thymus output in mice but not humans. Immunity. 2012;36:288–297. doi: 10.1016/j.immuni.2012.02.006. [DOI] [PubMed] [Google Scholar]
20.Gattinoni L., Lugli E., Ji Y., Pos Z., Paulos C.M., Quigley M.F., Almeida J.R., Gostick E., Yu Z., Carpenito C. A human memory T cell subset with stem cell-like properties. Nat Med. 2011;17:1290–1297. doi: 10.1038/nm.2446. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Ahmed R., Roger L., Costa Del Amo P., Miners K.L., Jones R.E., Boelen L., Fali T., Elemans M., Zhang Y., Appay V. Human stem cell-like memory T cells are maintained in a state of dynamic flux. Cell Rep. 2016;17:2811–2818. doi: 10.1016/j.celrep.2016.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Zhang Y., Joe G., Hexner E., Zhu J., Emerson S.G. Host-reactive CD8+ memory stem cells in graft-versus-host disease. Nat Med. 2005;11:1299–1305. doi: 10.1038/nm1326. [DOI] [PubMed] [Google Scholar]
23.Mahnke Y.D., Brodie T.M., Sallusto F., Roederer M., Lugli E. The who's who of T-cell differentiation: human memory T-cell subsets. Eur J Immunol. 2013;43:2797–2809. doi: 10.1002/eji.201343751. [DOI] [PubMed] [Google Scholar]
Gossel G., Hogan T., Cownden D., Seddon B., Yates A.J. Memory CD4 T cell subsets are kinetically heterogeneous and replenished from naive T cells at high levels. Elife. 2017;6 doi: 10.7554/eLife.23013. [DOI] [PMC free article] [PubMed] [Google Scholar]; Detailed study of kinetics of naïve CD4⁺ T cells in mice. Makes a number of interesting findings: (1) high levels of naïve cell differentiation to memory in the absence of deliberate infection (2) in a host/donor model, existing host memory cells were resistant to replacment by newly differentiated donor cells.
25.Vezys V., Masopust D., Kemball C.C., Barber D.L., O'Mara L.A., Larsen C.P., Pearson T.C., Ahmed R., Lukacher A.E. Continuous recruitment of naive T cells contributes to heterogeneity of antiviral CD8 T cells during persistent infection. J Exp Med. 2006;203:2263–2269. doi: 10.1084/jem.20060995. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Ladell K., Hellerstein M.K., Cesar D., Busch R., Boban D., McCune J.M. Central memory CD8+ T cells appear to have a shorter lifespan and reduced abundance as a function of HIV disease progression. J Immunol. 2008;180:7907–7918. doi: 10.4049/jimmunol.180.12.7907. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Westera L., Drylewicz J., den Braber I., Mugwagwa T., van der Maas I., Kwast L., Volman T., van de Weg-Schrijver E.H., Bartha I., Spierenburg G. Closing the gap between T-cell life span estimates from stable isotope-labeling studies in mice and humans. Blood. 2013;122:2205–2212. doi: 10.1182/blood-2013-03-488411. [DOI] [PubMed] [Google Scholar]
28.Ahmed R., Westera L., Drylewicz J., Elemans M., Zhang Y., Kelly E., Reljic R., Tesselaar K., de Boer R.J., Macallan D.C. Reconciling estimates of cell proliferation from stable isotope labeling experiments. PLoS Comput Biol. 2015;11 doi: 10.1371/journal.pcbi.1004355. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Ganusov V.V., Borghans J.A., De Boer R.J. Explicit kinetic heterogeneity: mathematical models for interpretation of deuterium labeling of heterogeneous cell populations. PLoS Comput Biol. 2010;6 doi: 10.1371/journal.pcbi.1000666. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Lahoz-Beneytez J., Schaller S., Macallan D., Eissing T., Niederalt C., Asquith B. Physiologically based simulations of deuterated glucose for quantifying cell turnover in humans. Front Immunol. 2017;8:474. doi: 10.3389/fimmu.2017.00474. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gattinoni L., Speiser D.E., Lichterfeld M., Bonini C. T memory stem cells in health and disease. Nat Med. 2017;23:18. doi: 10.1038/nm.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]; Reviews the authors' seminal discovery of T_SCM cells in humans (original paper not published in last two years so here we highlight linked review instead).
32.Golubovskaya V., Wu L. Different subsets of T cells, memory, effector functions, and CAR-T immunotherapy. Cancers (Basel) 2016 Mar 15;8 doi: 10.3390/cancers8030036. pii: E36. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Brenchley J.M., Karandikar N.J., Betts M.R., Ambrozak D.R., Hill B.J., Crotty L.E., Casazza J.P., Kuruppu J., Migueles S.A., Connors M. Expression of CD57 defines replicative senescence and antigen-induced apoptotic death of CD8+ T cells. Blood. 2003;101:2711–2720. doi: 10.1182/blood-2002-07-2103. [DOI] [PubMed] [Google Scholar]
34.Xu W., Larbi A. Markers of T Cell senescence in humans. Int J Mol Sci. 2017;18 doi: 10.3390/ijms18081742. [DOI] [PMC free article] [PubMed] [Google Scholar]
Akondy R.S., Fitch M., Edupuganti S., Yang S., Kissick H.T., Li K.W., Youngblood B.A., Abdelsamed H.A., McGuire D.J., Cohen K.W. Origin and differentiation of human memory CD8 T cells after vaccination. Nature. 2017 doi: 10.1038/nature24633. [DOI] [PMC free article] [PubMed] [Google Scholar]; Fascinating paper using YFV-vaccination in humans to study the origin of memory (including T_SCM cells). They conclude memory cells are de-differentiated effectors.
36.Wellard C.J., Markham J.F., Hawkins E.D., Hodgkin P.D., editors. The cyton model for lymphocyte proliferation and differentiation. Springer; 2011. [Google Scholar]
37.Marchingo J.M., Kan A., Sutherland R.M., Duffy K.R., Wellard C.J., Belz G.T., Lew A.M., Dowling M.R., Heinzel S. Hodgkin PD: T cell signaling. Antigen affinity, costimulation, and cytokine inputs sum linearly to amplify T cell expansion. Science. 2014;346:1123–1127. doi: 10.1126/science.1260044. [DOI] [PubMed] [Google Scholar]
Heinzel S., Binh Giang T., Kan A., Marchingo J.M., Lye B.K., Corcoran L.M., Hodgkin P.D. A Myc-dependent division timer complements a cell-death timer to regulate T cell and B cell responses. Nat Immunol. 2017;18:96–103. doi: 10.1038/ni.3598. [DOI] [PubMed] [Google Scholar]; Beautiful paper from a series by the Hodgkin group examining the quantitative rules of lymphocyte fate. Here they explore one of the underlying mechanisms.
39.Pillay J., den Braber I., Vrisekoop N., Kwast L.M., de Boer R.J., Borghans J.A., Tesselaar K., Koenderman L. In vivo labeling with 2H2O reveals a human neutrophil lifespan of 5.4 days. Blood. 2010;116:625–627. doi: 10.1182/blood-2010-01-259028. [DOI] [PubMed] [Google Scholar]
40.Tak T., Tesselaar K., Pillay J., Borghans J.A., Koenderman L. What's your age again? Determination of human neutrophil half-lives revisited. J Leukoc Biol. 2013;94:595–601. doi: 10.1189/jlb.1112571. [DOI] [PubMed] [Google Scholar]
41.Li K.W., Turner S.M., Emson C.L., Hellerstein M.K., Dale D.C. Deuterium and neutrophil kinetics. Blood. 2011;117:6052–6053. doi: 10.1182/blood-2010-12-322271. author reply 6053-6054. [DOI] [PubMed] [Google Scholar]
42.Liu Y., Liu Z., Zhang S., Rong X., Jacob R., Wu S., Lu F. Ensemble-based parameter estimation in a coupled GCM using the adaptive spatial average method. J Clim. 2014;27:4002–4014. [Google Scholar]
43.Macallan D.C., Wallace D., Zhang Y., De Lara C., Worth A.T., Ghattas H., Griffin G.E., Beverley P.C., Tough D.F. Rapid turnover of effector-memory CD4(+) T cells in healthy humans. J Exp Med. 2004;200:255–260. doi: 10.1084/jem.20040341. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Westera L., Zhang Y., Tesselaar K., Borghans J.A., Macallan D.C. Quantitating lymphocyte homeostasis in vivo in humans using stable isotope tracers. Methods Mol Biol. 2013;979:107–131. doi: 10.1007/978-1-62703-290-2_10. [DOI] [PubMed] [Google Scholar]
45.Patel A.A., Zhang Y., Fullerton J.N., Boelen L., Rongvaux A., Maini A.A., Bigley V., Flavell R.A., Gilroy D.W., Asquith B. The fate and lifespan of human monocyte subsets in steady state and systemic inflammation. J Exp Med. 2017;214:1913–1923. doi: 10.1084/jem.20170355. [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Bonhoeffer S., Mohri H., Ho D., Perelson A.S. Quantification of cell turnover kinetics using 5-bromo-2'-deoxyuridine. J Immunol. 2000;164:5049–5054. doi: 10.4049/jimmunol.164.10.5049. [DOI] [PubMed] [Google Scholar]
47.Mohri H., Bonhoeffer S., Monard S., Perelson A.S., Ho D.D. Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science. 1998;279:1223–1227. doi: 10.1126/science.279.5354.1223. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Multimedia component 1

mmc1.docx^{(48.6KB, docx)}

[bib1] 1.Buckton K.E., Brown W.M.C., Smith P.G. Lymphocyte survival in men treated with X-rays for ankylosing spondylitis. Nature. 1967;214:470–473. doi: 10.1038/214470a0. [DOI] [PubMed] [Google Scholar]

[bib2] 2.Michie C.A., McLean A., Alcock C., Beverley P.C. Lifespan of human lymphocyte subsets defined by CD45 isoforms. Nature. 1992;360:264–265. doi: 10.1038/360264a0. [DOI] [PubMed] [Google Scholar]

[bib3] 3.McLean A.R., Michie C.A. In vivo estimates of division and death rates of human T lymphocytes. Proc Natl Acad Sci U S A. 1995;92:3707–3711. doi: 10.1073/pnas.92.9.3707. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib4] 4.Kovacs J.A., Lempicki R.A., Sidorov I.A., Adelsberger J.W., Herpin B., Metcalf J.A., Sereti I., Polis M.A., Davey R.T., Tavel J. Identification of dynamically distinct subpopulations of T lymphocytes that are differentially affected by HIV. J Exp Med. 2001;194:1731–1741. doi: 10.1084/jem.194.12.1731. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] 5.Busch R., Neese R.A., Awada M., Hayes G.M., Hellerstein M.K. Measurement of cell proliferation by heavy water labeling. Nat Protoc. 2007;2:3045–3057. doi: 10.1038/nprot.2007.420. [DOI] [PubMed] [Google Scholar]

[bib6] 6.Reome J.B., Johnston D.S., Helmich B.K., Morgan T.M., Dutton-Swain N., Dutton R.W. The effects of prolonged administration of 5-bromodeoxyuridine on cells of the immune system. J Immunol. 2000;165:4226–4230. doi: 10.4049/jimmunol.165.8.4226. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Hellerstein M.K., Neese R.A. Mass isotopomer distribution analysis: a technique for measuring biosynthesis and turnover of polymers. Am J Physiol. 1992;263:E988–E1001. doi: 10.1152/ajpendo.1992.263.5.E988. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Hellerstein M., Hanley M.B., Cesar D., Siler S., Papageorgopoulos C., Wieder E., Schmidt D., Hoh R., Neese R., Macallan D. Directly measured kinetics of circulating T lymphocytes in normal and HIV-1-infected humans. Nat Med. 1999;5:83–89. doi: 10.1038/4772. [DOI] [PubMed] [Google Scholar]

[bib9] 9.Hellerstein M.K. Measurement of T-cell kinetics: recent methodologic advances. Immunol Today. 1999;20:438–441. doi: 10.1016/s0167-5699(99)01529-7. [DOI] [PubMed] [Google Scholar]

[bib10] 10.Hellerstein M.K., Neese R.A. Mass isotopomer distribution analysis at eight years: theoretical, analytic, and experimental considerations. Am J Physiol. 1999;276:E1146–E1170. doi: 10.1152/ajpendo.1999.276.6.E1146. [DOI] [PubMed] [Google Scholar]

[bib11] 11.Macallan D.C., Fullerton C.A., Neese R.A., Haddock K., Park S.S., Hellerstein M.K. Measurement of cell proliferation by labeling of DNA with stable isotope-labeled glucose: studies in vitro, in animals, and in humans. Proc Natl Acad Sci U S A. 1998;95:708–713. doi: 10.1073/pnas.95.2.708. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] 12.Macallan D.C., Asquith B., Zhang Y., de Lara C., Ghattas H., Defoiche J., Beverley P.C. Measurement of proliferation and disappearance of rapid turnover cell populations in human studies using deuterium-labeled glucose. Nat Protoc. 2009;4:1313–1327. doi: 10.1038/nprot.2009.117. [DOI] [PubMed] [Google Scholar]

[bib13] 13.Macallan D.C., Asquith B., Irvine A.J., Wallace D.L., Worth A., Ghattas H., Zhang Y., Griffin G.E., Tough D.F., Beverley P.C. Measurement and modeling of human T cell kinetics. Eur J Immunol. 2003;33:2316–2326. doi: 10.1002/eji.200323763. [DOI] [PubMed] [Google Scholar]

[bib14] 14.Lahoz-Beneytez J., Elemans M., Zhang Y., Ahmed R., Salam A., Block M., Niederalt C., Asquith B., Macallan D. Human neutrophil kinetics: modeling of stable isotope labeling data supports short blood neutrophil half-lives. Blood. 2016;127:3431–3438. doi: 10.1182/blood-2016-03-700336. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] 15.Mohri H., Perelson A.S., Tung K., Ribeiro R.M., Ramratnam B., Markowitz M., Kost R., Hurley A., Weinberger L., Cesar D. Increased turnover of T lymphocytes in HIV-1 infection and its reduction by antiretroviral therapy. J Exp Med. 2001;194:1277–1287. doi: 10.1084/jem.194.9.1277. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] 16.Vrisekoop N., den Braber I., de Boer A.B., Ruiter A.F., Ackermans M.T., van der Crabben S.N., Schrijver E.H., Spierenburg G., Sauerwein H.P., Hazenberg M.D. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc Natl Acad Sci U S A. 2008;105:6115–6120. doi: 10.1073/pnas.0709713105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] 17.Asquith B., Debacq C., Macallan D.C., Willems L., Bangham C.R. Lymphocyte kinetics: the interpretation of labelling data. Trends Immunol. 2002;23:596–601. doi: 10.1016/s1471-4906(02)02337-2. [DOI] [PubMed] [Google Scholar]

[bib18] Costa Del Amo P., Lahoz-Beneytez J., Boelen L., Ahmed R., Miners K.L., Zhang Y., Roger L., Jones R.E., Marraco S.A.F., Speiser D.E. Human TSCM cell dynamics in vivo are compatible with long-lived immunological memory and stemness. PLoS Biol. 2018;16 doi: 10.1371/journal.pbio.2005523. [DOI] [PMC free article] [PubMed] [Google Scholar]; Finds T_SCM cells have the dynamic attributes consistent with “stemness” i.e. self-renewal and clonal longevity. However, this was only true of a subpopulation of what are currently defined as T_SCM cells. Also found high levels of naïve cell differentiation in apparently healthy, asymptomatic individuals.

[bib19] 19.den Braber I., Mugwagwa T., Vrisekoop N., Westera L., Mogling R., de Boer A.B., Willems N., Schrijver E.H., Spierenburg G., Gaiser K. Maintenance of peripheral naive T cells is sustained by thymus output in mice but not humans. Immunity. 2012;36:288–297. doi: 10.1016/j.immuni.2012.02.006. [DOI] [PubMed] [Google Scholar]

[bib20] 20.Gattinoni L., Lugli E., Ji Y., Pos Z., Paulos C.M., Quigley M.F., Almeida J.R., Gostick E., Yu Z., Carpenito C. A human memory T cell subset with stem cell-like properties. Nat Med. 2011;17:1290–1297. doi: 10.1038/nm.2446. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] 21.Ahmed R., Roger L., Costa Del Amo P., Miners K.L., Jones R.E., Boelen L., Fali T., Elemans M., Zhang Y., Appay V. Human stem cell-like memory T cells are maintained in a state of dynamic flux. Cell Rep. 2016;17:2811–2818. doi: 10.1016/j.celrep.2016.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib22] 22.Zhang Y., Joe G., Hexner E., Zhu J., Emerson S.G. Host-reactive CD8+ memory stem cells in graft-versus-host disease. Nat Med. 2005;11:1299–1305. doi: 10.1038/nm1326. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Mahnke Y.D., Brodie T.M., Sallusto F., Roederer M., Lugli E. The who's who of T-cell differentiation: human memory T-cell subsets. Eur J Immunol. 2013;43:2797–2809. doi: 10.1002/eji.201343751. [DOI] [PubMed] [Google Scholar]

[bib24] Gossel G., Hogan T., Cownden D., Seddon B., Yates A.J. Memory CD4 T cell subsets are kinetically heterogeneous and replenished from naive T cells at high levels. Elife. 2017;6 doi: 10.7554/eLife.23013. [DOI] [PMC free article] [PubMed] [Google Scholar]; Detailed study of kinetics of naïve CD4⁺ T cells in mice. Makes a number of interesting findings: (1) high levels of naïve cell differentiation to memory in the absence of deliberate infection (2) in a host/donor model, existing host memory cells were resistant to replacment by newly differentiated donor cells.

[bib25] 25.Vezys V., Masopust D., Kemball C.C., Barber D.L., O'Mara L.A., Larsen C.P., Pearson T.C., Ahmed R., Lukacher A.E. Continuous recruitment of naive T cells contributes to heterogeneity of antiviral CD8 T cells during persistent infection. J Exp Med. 2006;203:2263–2269. doi: 10.1084/jem.20060995. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib26] 26.Ladell K., Hellerstein M.K., Cesar D., Busch R., Boban D., McCune J.M. Central memory CD8+ T cells appear to have a shorter lifespan and reduced abundance as a function of HIV disease progression. J Immunol. 2008;180:7907–7918. doi: 10.4049/jimmunol.180.12.7907. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib27] 27.Westera L., Drylewicz J., den Braber I., Mugwagwa T., van der Maas I., Kwast L., Volman T., van de Weg-Schrijver E.H., Bartha I., Spierenburg G. Closing the gap between T-cell life span estimates from stable isotope-labeling studies in mice and humans. Blood. 2013;122:2205–2212. doi: 10.1182/blood-2013-03-488411. [DOI] [PubMed] [Google Scholar]

[bib28] 28.Ahmed R., Westera L., Drylewicz J., Elemans M., Zhang Y., Kelly E., Reljic R., Tesselaar K., de Boer R.J., Macallan D.C. Reconciling estimates of cell proliferation from stable isotope labeling experiments. PLoS Comput Biol. 2015;11 doi: 10.1371/journal.pcbi.1004355. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib29] 29.Ganusov V.V., Borghans J.A., De Boer R.J. Explicit kinetic heterogeneity: mathematical models for interpretation of deuterium labeling of heterogeneous cell populations. PLoS Comput Biol. 2010;6 doi: 10.1371/journal.pcbi.1000666. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] 30.Lahoz-Beneytez J., Schaller S., Macallan D., Eissing T., Niederalt C., Asquith B. Physiologically based simulations of deuterated glucose for quantifying cell turnover in humans. Front Immunol. 2017;8:474. doi: 10.3389/fimmu.2017.00474. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] Gattinoni L., Speiser D.E., Lichterfeld M., Bonini C. T memory stem cells in health and disease. Nat Med. 2017;23:18. doi: 10.1038/nm.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]; Reviews the authors' seminal discovery of T_SCM cells in humans (original paper not published in last two years so here we highlight linked review instead).

[bib32] 32.Golubovskaya V., Wu L. Different subsets of T cells, memory, effector functions, and CAR-T immunotherapy. Cancers (Basel) 2016 Mar 15;8 doi: 10.3390/cancers8030036. pii: E36. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] 33.Brenchley J.M., Karandikar N.J., Betts M.R., Ambrozak D.R., Hill B.J., Crotty L.E., Casazza J.P., Kuruppu J., Migueles S.A., Connors M. Expression of CD57 defines replicative senescence and antigen-induced apoptotic death of CD8+ T cells. Blood. 2003;101:2711–2720. doi: 10.1182/blood-2002-07-2103. [DOI] [PubMed] [Google Scholar]

[bib34] 34.Xu W., Larbi A. Markers of T Cell senescence in humans. Int J Mol Sci. 2017;18 doi: 10.3390/ijms18081742. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib35] Akondy R.S., Fitch M., Edupuganti S., Yang S., Kissick H.T., Li K.W., Youngblood B.A., Abdelsamed H.A., McGuire D.J., Cohen K.W. Origin and differentiation of human memory CD8 T cells after vaccination. Nature. 2017 doi: 10.1038/nature24633. [DOI] [PMC free article] [PubMed] [Google Scholar]; Fascinating paper using YFV-vaccination in humans to study the origin of memory (including T_SCM cells). They conclude memory cells are de-differentiated effectors.

[bib36] 36.Wellard C.J., Markham J.F., Hawkins E.D., Hodgkin P.D., editors. The cyton model for lymphocyte proliferation and differentiation. Springer; 2011. [Google Scholar]

[bib37] 37.Marchingo J.M., Kan A., Sutherland R.M., Duffy K.R., Wellard C.J., Belz G.T., Lew A.M., Dowling M.R., Heinzel S. Hodgkin PD: T cell signaling. Antigen affinity, costimulation, and cytokine inputs sum linearly to amplify T cell expansion. Science. 2014;346:1123–1127. doi: 10.1126/science.1260044. [DOI] [PubMed] [Google Scholar]

[bib38] Heinzel S., Binh Giang T., Kan A., Marchingo J.M., Lye B.K., Corcoran L.M., Hodgkin P.D. A Myc-dependent division timer complements a cell-death timer to regulate T cell and B cell responses. Nat Immunol. 2017;18:96–103. doi: 10.1038/ni.3598. [DOI] [PubMed] [Google Scholar]; Beautiful paper from a series by the Hodgkin group examining the quantitative rules of lymphocyte fate. Here they explore one of the underlying mechanisms.

[bib39] 39.Pillay J., den Braber I., Vrisekoop N., Kwast L.M., de Boer R.J., Borghans J.A., Tesselaar K., Koenderman L. In vivo labeling with 2H2O reveals a human neutrophil lifespan of 5.4 days. Blood. 2010;116:625–627. doi: 10.1182/blood-2010-01-259028. [DOI] [PubMed] [Google Scholar]

[bib40] 40.Tak T., Tesselaar K., Pillay J., Borghans J.A., Koenderman L. What's your age again? Determination of human neutrophil half-lives revisited. J Leukoc Biol. 2013;94:595–601. doi: 10.1189/jlb.1112571. [DOI] [PubMed] [Google Scholar]

[bib41] 41.Li K.W., Turner S.M., Emson C.L., Hellerstein M.K., Dale D.C. Deuterium and neutrophil kinetics. Blood. 2011;117:6052–6053. doi: 10.1182/blood-2010-12-322271. author reply 6053-6054. [DOI] [PubMed] [Google Scholar]

[bib42] 42.Liu Y., Liu Z., Zhang S., Rong X., Jacob R., Wu S., Lu F. Ensemble-based parameter estimation in a coupled GCM using the adaptive spatial average method. J Clim. 2014;27:4002–4014. [Google Scholar]

[bib43] 43.Macallan D.C., Wallace D., Zhang Y., De Lara C., Worth A.T., Ghattas H., Griffin G.E., Beverley P.C., Tough D.F. Rapid turnover of effector-memory CD4(+) T cells in healthy humans. J Exp Med. 2004;200:255–260. doi: 10.1084/jem.20040341. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] 44.Westera L., Zhang Y., Tesselaar K., Borghans J.A., Macallan D.C. Quantitating lymphocyte homeostasis in vivo in humans using stable isotope tracers. Methods Mol Biol. 2013;979:107–131. doi: 10.1007/978-1-62703-290-2_10. [DOI] [PubMed] [Google Scholar]

[bib45] 45.Patel A.A., Zhang Y., Fullerton J.N., Boelen L., Rongvaux A., Maini A.A., Bigley V., Flavell R.A., Gilroy D.W., Asquith B. The fate and lifespan of human monocyte subsets in steady state and systemic inflammation. J Exp Med. 2017;214:1913–1923. doi: 10.1084/jem.20170355. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] 46.Bonhoeffer S., Mohri H., Ho D., Perelson A.S. Quantification of cell turnover kinetics using 5-bromo-2'-deoxyuridine. J Immunol. 2000;164:5049–5054. doi: 10.4049/jimmunol.164.10.5049. [DOI] [PubMed] [Google Scholar]

[bib47] 47.Mohri H., Bonhoeffer S., Monard S., Perelson A.S., Ho D.D. Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science. 1998;279:1223–1227. doi: 10.1126/science.279.5354.1223. [DOI] [PubMed] [Google Scholar]

PERMALINK

Current estimates of T cell kinetics in humans

Derek C Macallan

Robert Busch

Becca Asquith

Abstract

Graphical abstract

Highlights

Introduction

Stable isotope labeling: an overview