Abstract
Study of the spin-lattice relaxation in the spin-locking state offers important information about atomic and molecular motions, which cannot be obtained by spin lattice relaxation in strong external magnetic fields. The application of this technique for the investigation of the spin-lattice relaxation in biological samples with fibril structures reveals an anisotropy effect for the relaxation time under spin locking, T1ρ. To explain the anisotropy of the spin-lattice relaxation under spin-locking in connective tissue a model which represents a tissue by a set of nanocavities containing water is used. The developed model allows us to estimate the correlation time for water molecular motion in articular cartilage, τc = 30 μs and the averaged nanocavity volume, 〈V〉 ≃ 5400 nm3. Based on the developed model which represents a connective tissue by a set of nanocavities containing water, a good agreement with the experimental data from an articular cartilage and a tendon was demonstrated. The fitting parameters were obtained for each layer in each region of the articular cartilage. These parameters vary with the known anatomic microstructures of the tissue. Through Gaussian distributions to nanocavity directions, we have calculated the anisotropy of the relaxation time under spin locking T1ρ for a human Achilles tendon specimen and an articular cartilage. The value of the fitting parameters obtained at matching of calculation to experimental results can be used in future investigations for characterizing the fine fibril structure of biological samples.
Keywords: cartilage, spin locking, spin lattice relaxation time T1ρ, anisotropy, nanocavity
Graphical Abstract
Locking field strength, molecular motion correlation time dependence, τc, and the spin-lattice relaxation time in a rotating frame, T1ρ, in liquids entrapped in nanocavities are theoretically investigated. We have calculated the anisotropy of T1ρ for a human Achilles tendon specimen and an articular cartilage.
Introduction
Nuclear magnetic resonance (NMR) is widely used in studies of the structure, internal spin interactions, and motion of molecules [1–5]. For example, various rates of molecular motion can be measured by observation at various resonance frequencies [4, 5]. In a magnetic field , nuclear spins precess around the field direction at their Larmor frequency ω0 = γH0, where γ is the nuclear gyromagnetic ratio [1]. An application of the phase shifted two-pulse sequence (called spin-locking) forces the spins to precess around the radiofrequency (RF) field, H1, where [6]. This method brings the magnetization to be parallel to an effective field in the rotating reference frame with a 90° pulse, which is followed by a long RF pulse with 90° phase shift and strength H1 [6]. Since spins are locked by a RF field at a lower frequency, ω1 = γH1, they are sensitive to a lower frequency range of molecular motions [4, 5]. Spin-lock techniques can be employed to study slow molecular motion regimes with the ability to record molecular motion for which the correlation time is larger by several orders than this is detected in strong fields. Therefore, the study of the spin-lattice relaxation in the spin-locking state offers important information about atomic and molecular motions, which cannot be obtained by investigation of the spin lattice relaxation in strong external magnetic [4, 5].
Despite of the extensive use of the spin-locking technique in studies of nuclear spin systems in bulk solids [5, 6], the application of this technique for the investigation of the spin-lattice relaxation in liquids or gases entrapped in nanopores and nanotubes has not been widely adopted [7–11]. Particularly noteworthy is the use of the spin-locking method in magnetic resonance imaging (MRI) to study biological samples with fibril structures [12]. Publications dealing with the application of the spin-locking MRI to characterize tissues showed a sufficiently high efficiency of this method [12–21]. One of the results in these studies was a well-established strong magnetic anisotropy effect for the relaxation time under spin locking, T1ρ. The same phenomenon was revealed many years ago for the second moment of the resonance line [22], local dipolar field and transverse relaxation time, T2 [12, 23, 24].
To explain the anisotropy effects of the local dipolar field and transverse relaxation time in fibril structures, a model of liquid entrapped in nanocavities has been developed [25, 26]. This model is based on averaging of the dipole-dipole interaction (DDI) between spin pairs with taking into account a restricted molecule motion [27, 28]. The averaging gives that DDI between any spin pair is characterized by a single effective constant, which depends on the cavity orientation relative to the magnetic field as well as the cavity form and volume [7–11, 26–29].
In this report we compare the theoretical estimation for the anisotropy of the relaxation time under spin locking T1ρ with published experimental data from an Achilles tendon specimen and articular cartilage specimens [20, 21].
Theory
Averaging of DDI between spins inside nanocavities
The procedure of averaging of DDI between spins inside a nanocavity [25, 26] considers a system consisting of N nuclear spins, I = 1/2, enclosed in a nanocavity in an external field directed along the z -axis. The Hamiltonian of the spin system written in units of frequency can be presented as [1, 2]
| (1) |
where Hz is the Zeeman interaction Hamiltonian,
| (2) |
In a high external magnetic field only secular terms of the Hamiltonian HD describing the dipolar interactions can influence the energy levels to the first order, whereas its off-diagonal terms produce the second-order correction. The secular part Hd of the Hamiltonian HD is given by [1, 2]
| (3) |
where is the Legendre polynomial, rjμ, θjμ, and ϕjμ are the spherical coordinates of the vector connecting two spins, I±j = Ixj ± iIyj, Ixj, Iyj, and Izj are the projections of the spin operator of the j -th nuclear spin on the x −, y −, and z-axes, respectively, (j, μ = 1, 2, …, N), ħ is the Plank constant.
In isotropic bulk liquids, the molecular rotational and transitional motions are rapid and random, so the averaging of dipolar Hamiltonian (3) over all the directions of the vector leads to a zero value [1, 2]. However, the situation with liquids enclosed in nanocavities is sharply different from the isotropic bulk situation. Due to the restricted molecular motion, the averaging of dipolar Hamiltonian (3) can give a nonzero value, and the spin dynamics is governed by the residual dipolar interaction. In this case, the dipolar interactions are not averaged to zero and observable in NMR spectrum if the characteristic time ttran of the transitional diffusion is much less than the characteristic time of the flip-flop process tmag [10, 11]. The diffusion coefficient of water molecules can be estimated by using the Einstein-Stokes equation
| (4) |
where kB is the Boltzmann constant, T is the absolute temperature of the lattice, η is the dynamic viscosity, λ is the effective hydrodynamic radius of a water molecule. Estimations and experiments on water molecules give close values for D ≈ 2.3 × 10−9 m2/s at the room temperature [30].
For protons, the typical NMR time scale, which characterizes the flip–flop transition, is determined by the Hamiltonian (3) [1]:
| (5) |
where r0 = 0.275 nm is the water molecular diameter. The characteristic size lch of a cavity in which the dipolar Hamiltonian (3) does not averaged to zero is estimated from condition: ; i.e. the characteristic size should be less than 710 nm [10, 11].
In a nanocavity, molecules of water undergo restricted diffusion, but nevertheless move randomly throughout the entire cavity during time of the order of ttran and each spin experiences the same averaged dipolar interaction. According ergodic hypothesis [31], the averaging of process parameters over time ttran can be replace by the averaging over the statistical ensemble. Therefore, the time-averaged spatial part of the Hamiltonian can be presented proportional to [27]
| (6) |
where V is the cavity volume. The detailed description of the averaging is given in [27–29].
The spin evolution in such nanocavity can be described by an averaged DDI Hamiltonian
| (7) |
The space-averaged pair coupling constant, Gd, which is the same for any pair of the j -th and μ -th spins, is
| (8) |
where angle θ defines the orientation of a nanocavity with respect to the external magnetic field, , the form-factor F for an elongated ellipsoidal cavity with the principal axes a and b = c is [29]:
| (9) |
and , . In this case, θ is the angle between the external magnetic field and the principal axis a. We note that the angle dependence, 1 – 3cos2 θ, of the coupling constant Gd is the same for any axially symmetric nanocavity.
Repeating the averaging procedure, we obtain the form factor for a cylindrical cavity with diameter d and length l in the following form:
| (10) |
where θ is now the angle between the external magnetic field and the cylindrical cavity axis.
A remarkable result is that anisotropy of the averaged DDI Hamiltonian is determined only by angle θ between the magnetic field and the main axis of the cavity. The residual DDI plays a considerable role in the dynamics of a spin system of liquid confined inside a nanocavity, much like in the spin dynamics in a solid, with an important difference: in the liquid the averaged dipolar coupling constant Gd is the same for all pairs of spins and depends on shape (the form factor F), volume V, and orientation (angle θ) of a cavity. This leads to the angular dependence of Hamiltonian (7) which should manifest itself in anisotropy of NMR characteristics such as the second moment and transverse relaxation time T2 measured on spins in a liquid entrapped in nanocavities. Many fibril biological and human tissues possess a hierarchical structure with characteristic diameters from ~1 nm to several tens of nm and length on the order of 300 nm [12, page 12]. The theoretical predictions for the transverse relaxation time T2 have been confirmed by comparison with experimental data [25, 26]. In these works, tissues were represented as a set of the elongated nanocavities which are formed by the fibril structure and contain water. Here we consider the relaxation time under spin locking T1ρ.
Expression (7) for the DDI Hamiltonian with a single coupling constant makes it possible to obtain analytical expressions for the relaxation rate under spin locking [7],
| (11) |
where n = N / 2V is the molecular concentration and τc is the correlation times for molecular motion.
When ω1τc ≪ 1 the relaxation time T1ρ is independent of the intensity of the RF field
| (12) |
while at ω1τc ≫ 1 the time is proportional to
| (13) |
Note that the angle dependencies of the relaxation rates, T1−1, T2−1, and T1ρ−1 are different [7, 25]: ; ; . Unlike T2−1 and T1ρ−1, the relaxation rate T1−1 is zero at θ = 0, π/2; both relaxation rates T2−1 and T1ρ−1 are zero at the “magic” angles 54.74° and 125.26°.
To estimate the correlation time, we consider the experimental data, presented in [33], for cartilage. In the biological tissue water is contained between fibers and the tissue can be represented as a set of elongated cylindrical nanocavities filled by water. There is a natural distribution of the fibrils and their direction [12] and hence there is distribution of the volume and orientation of the nanocavities. The measured signal from a single cavity is proportional to the number of molecules contained in the cavity. We assume that the signal from a cavity is subject to an exponential law; and hence in a first approximation the relaxation time for the whole sample can be written as:
| (14) |
where 1/T1ρm is the relaxation rate measured in experement, the index “j” notes the number of the cavity and the summation is performed through all the cavities; Nj is the spin number in the j-th cavity, Nz is the total spin number in the sample, . Note, that Nj = Vjn and from Eq. (14) one can result that the measured relaxation time is independent of the volumes of cavities.
Assuming that the correlation time is independent of the RF field frequency from Eq. (14) we obtain
| (15) |
where the indexes “1” and “2” correspond to two experiments with the RF field frequency and , respectively.
Using the experiment results presented in [33, Fig. 8], the maxima T1ρ = 140 ms at ω1 = 2π × 500 1/s and T1ρ = 210 ms at ω1 = 2π × 2000 1/s, we obtain
| (16) |
A close value for τc was obtained using the results in [33, Fig. 9].
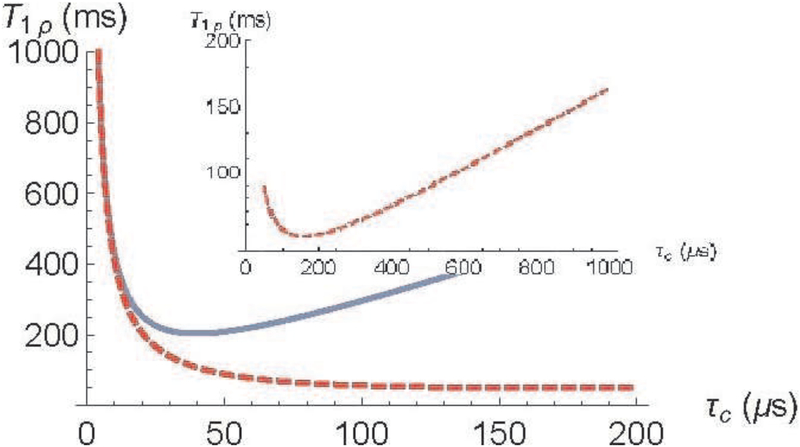
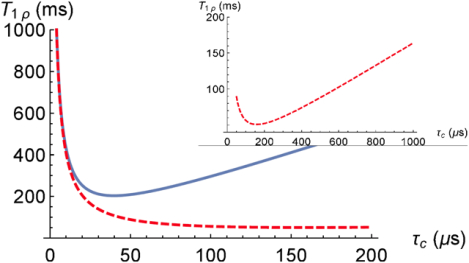
From Eq. (11) the averaged nanocavity volume is estimated as 〈V〉 ≃ 5400nm3 (the molecule concentration in water , the form-factor F = 2π for an elongated cylindrical nanocavity, γ2ħ = 2π × 120 Hz·nm3 for a proton, and the experimental data of the relaxation time T1ρ = 140 ms for ω1 = 2π × 500 1/s). At length 300 nm (see Figure 1.4 in [12])) the averaged diameter of the cavity is about 5 nm, that well agrees with the anatomic structure. Using Eq. (11), the dependences of T1ρ at θ = 0 on the correlation time τc for two values of the locking field strength, ω1 = 2π × 2000 1/s and ω1 = 2π × 500 1/s are presented in Fig. 1. Fig. 1 shows that the minimum of relaxation times T1ρ shifts towards slow molecular motions with decreasing of the locking field strength. One can see from Fig. 1 that at both locking field strengths, ω1 = 2π × 2000 1/s and ω1 = 2π × 500 1/s, at temperature about 300 K the minimum of relaxation times T1ρ is not reached.
Fig. 1.
Relaxation time under spin locking T1ρ as a function of the correlation time, τc: solid blue - , dashed red - . V=5400 nm3, , and F = 2π. The inset shows the minimum of the T1ρ at .
Relaxation rate under spin locking
Eqs. (11) – (13) have been obtained for a single nanocavity and can be used for analysis of the angular dependence of the relaxation time T1ρ for structures containing multiplicity of ideally orientated identical nanocavities. According to Eqs. (11)–(13), at a magic angle, the relaxation rate is strictly zero, which contradicts the experimental data (see, e.g., [12, 20, 21] and references therein). In order to explain this fact, in literature (see Eq. (9.8) on p. 252 in [12], [20]) an anisotropic part of the relaxation rates is frequently associated with the fixed water molecules bound by the fibers. The radius-vector between protons of these motionless (fixed) molecules is directed about parallel to the fibers [22, 33]. To estimate the relaxation time T1ρf for fixed molecules the expression obtained for solid powders is used [34]:
| (17) |
where is the second moment of the dipolar interaction between two protons. The correlation time of the water molecular motion depends on many parameters and can vary in a wide range, e.g., τc = 2 × 10−11 s [1] in bulk water, τc = 30 × 10−6 s for liquid water entrapped between a collagen fiber and τc = 2.6 × 10−6 s for ice [35]. Estimation with correlations times for water entrapped in nanocavity and for absorbed (fixed, ice) water molecule gives T1ρf ≈ 34μs and T1ρf ≈ 260 μs, respectively, at ω1 = 2π × 500 1/s. Thus, equation (17) gives a relaxation time T1ρf which is less by three orders of magnitude, at least, than the measured relaxation times.
The relaxation time due to the spin exchange between protons of the water molecules that are fixed to the surface of the cavity and protons of the molecules in the neighboring water can be estimated according to the model proposed in [36, 37]
| (18) |
where P is the fraction of the bound water molecules, τb is the lifetime of the a water molecule in the bound state to the wall, τb ≈ 20μs [37]. For a cylindrical cavity with diameter d and length l, the fraction of the bound water molecules can be estimated as the ratio of the volume of the cavity to the volume of the wall area with a thickness of one molecule (~0.3 nm) , where is the diameter of the water molecule in nm, d~10 nm. Substituting the values of P, τb, and T1ρf into (18) we obtain T1ρex ≈ 0.3 ms for T1ρf ≈ 34μs and T1ρex ≈ 2.3 ms for T1ρf ≈ 260 μs. Thus, the relaxation time T1ρex due to the exchange is, at least, two order less than the measured relaxation times.
To explain the difference of the measured relaxation rate 1/T1ρm from zero at the magic angle and experimentally observed angular dependence of the rate, we apply completely different approach: we consider a fibrous tissue as a set of inexactly orientated nanocavities containing water. (There is a natural distribution of the fibrils and their direction). This allows us to avoid introduction of an isotropic part.
Really, fibrils of tissue differ in the volume, orientation relative to the magnetic field and, hence, nanocavities containing water have various volumes and orientations and correlation time varies form a cavity to a cavity (Chapter 1 in [12]). To compare with the data obtained in NMR experiments, theoretical expression (11) for the relaxation time should be averaged over many parameters. Here we analyze the angular dependence using the normalized relaxation rate under spin locking
| (19) |
Assuming that the angular distributions of all nanocavity types are the same, one can obtain:
| (20) |
In NMR and MRI experiments, the angle θM between the sample Z0 -axis and the DC magnetic field is determined and a relaxation time as a function of this angle is studied. In the general case, the angle does not coincide with a “preferred direction”, an averaged orientation, of the collagen fibrils. Let us determine the deviation of the main axis of each collagen fibril from the Z0 direction by the polar angle β and azimuthal angle δ. Angular distributions of nanocavities are determined by the anatomical structure of a tested sample. Analysis of data presented in literature showed that the Gaussian distribution well approximates the anatomical structure [25, 26]. In these works, using the distribution approximation the agreement between the theoretical model and experiments for the relaxation rates, T1−1 and T2−1 was achieved. Here we assume also the Gaussian distribution of nanocavities directions over the both angles, the polar β and the azimuthal angle δ with the bivariate normal distribution function. Then
| (21) |
| (22) |
where σβ and σδ are the standard deviations, β0 and δ0 are the means of the distributions,
| (23) |
The angles β0 and δ0 give distinction of the “preferred direction” of the fibrils from the sample axis. More detailed description of the averaging through the nanocavity orientations is presented in [25, 26]. In the general case, NMR experimental results can be approximated by a set of distributions (22) with different parameters standard deviations and distribution means.
Comparison with experimental data
For comparison with experimental data, among a numerous diversity of materials we choose two biological materials containing collagen fibers.
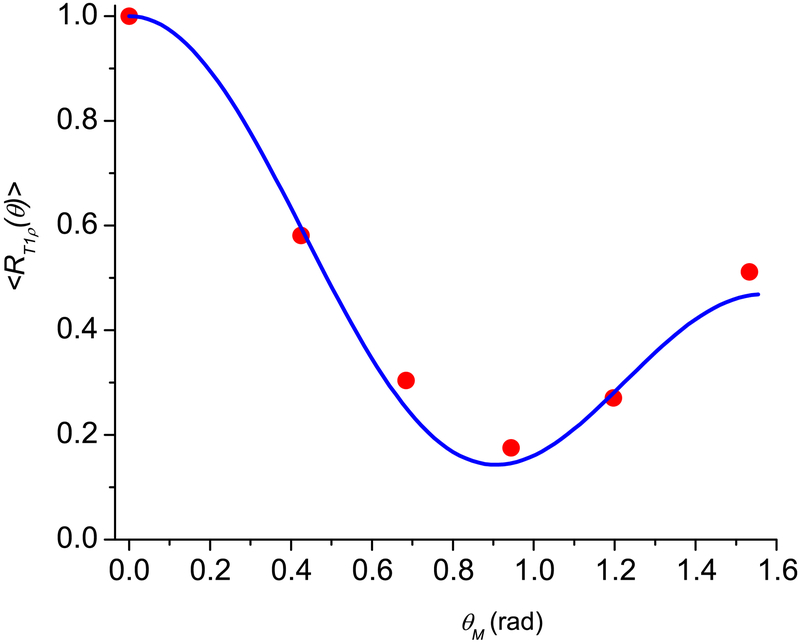
As the first example we consider the experimental data [20] from an Achilles tendon, which has a system of fibrils forming ordered hierarchical long substructures with characteristic diameters from 1 nm to several tens of nm with water between the fibrils. Most of the tissue water resides in long cavities with length of 300 nm [12, 38, 39]. These nanocavities can be approximately considered as very elongated cylinders (l ≫ d) noted above. The angular anisotropy of T1ρ (Fig. 2, spin-lock field of 500 Hz) has been studied in [20]. In this work a 2D ultrashort TE-T1ρ (UTE) pulse sequence was combined with a spin-lock preparation pulse cluster. The relaxation time T1ρ was measured by fitting UTE images acquired with a series of spin-lock times. UTE-T1ρ magic angle imaging was performed on a 3T Signa Twin Speed scanner (GE Healthcare Technologies, Milwaukee, WI) with a 40-mT/m maximum peak gradient amplitude and a 150-mT/m/s maximum slew rate. T1ρ was measured at six angles of 0°, 25°, 40°, 55°, 70°, and 90° relative to the DC magnetic field.
Fig. 2.
Angular dependence of the normalized spin locking relaxation rates 〈R1ρ (θ)〉 for human Achilles tendon specimens. The blue solid line is calculated according to Eq. (24). The red circles are the experimental data from [20]. The fitting parameters are given in Table 1.
As the second example, we consider the experimental data [21] from a study of angular anisotropy effect in human patellar cartilage. After harvesting, a transverse slab of ~5 mm thickness was cut from the specimens. All data acquisitions were performed on a 3T MRI system (Signa HDx, GE Healthcare, Waukesha, WI) with a maximum gradient strength of 40 mT/m and a maximum slew rate of 150 mT/m/ms. A spin-locking field strength of 500 Hz was used for both 2D and 3D T1ρ imaging. The same imaging protocol was applied to each sample at six different angular orientations: 0°, 20°, 40°, 60°, 80° and 100° as well as 0°, 15°, 30°, 45°, 60° and 75° relative to the external magnetic field.
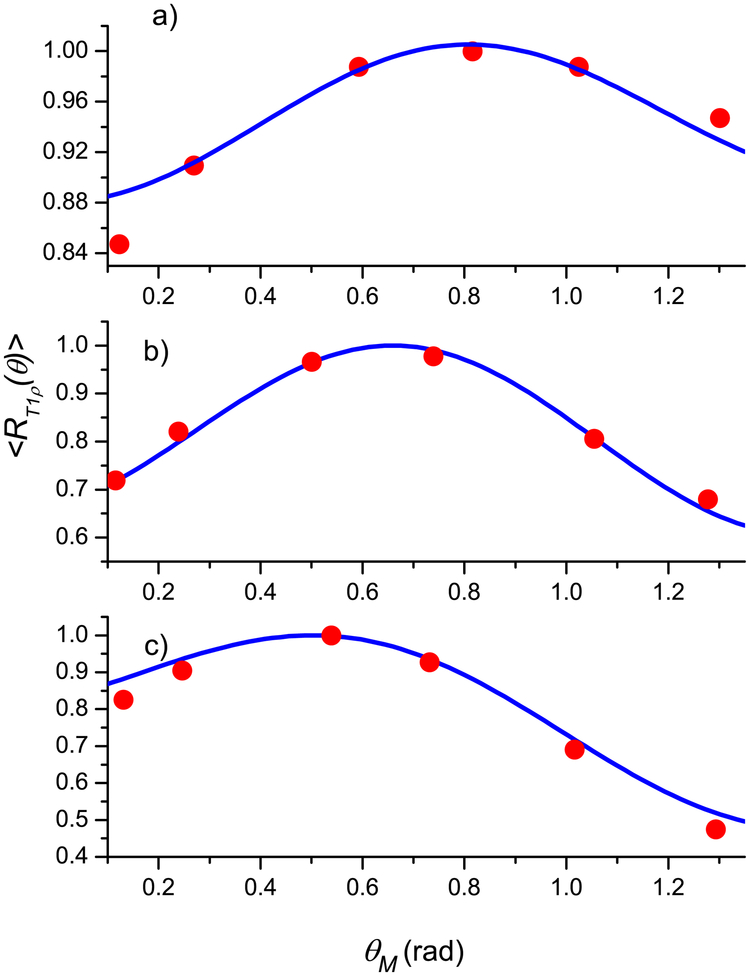
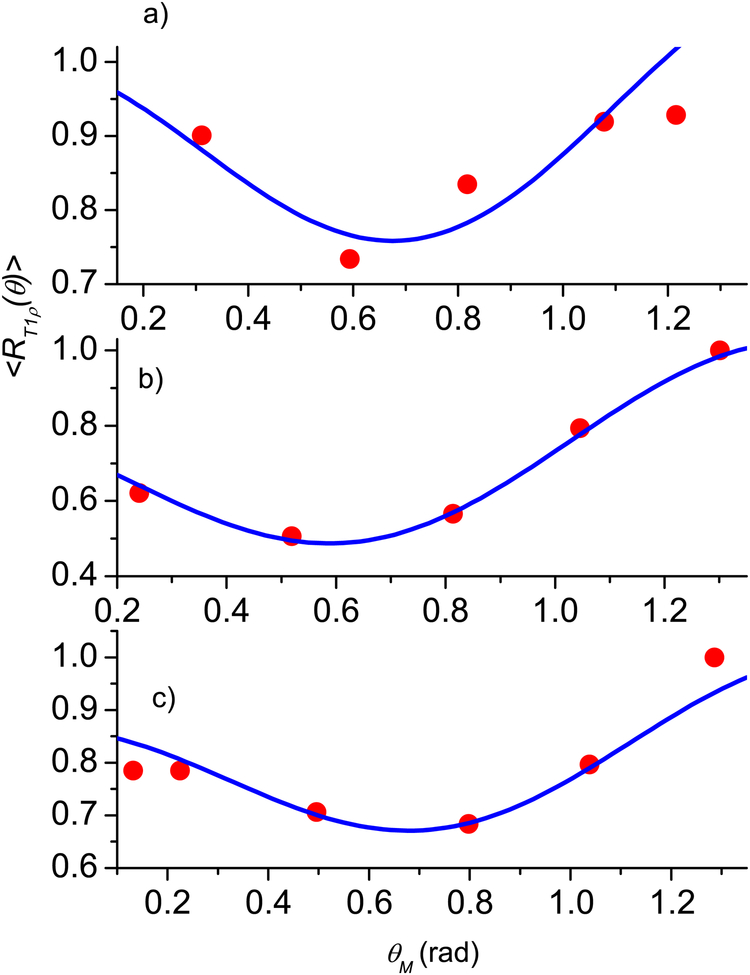
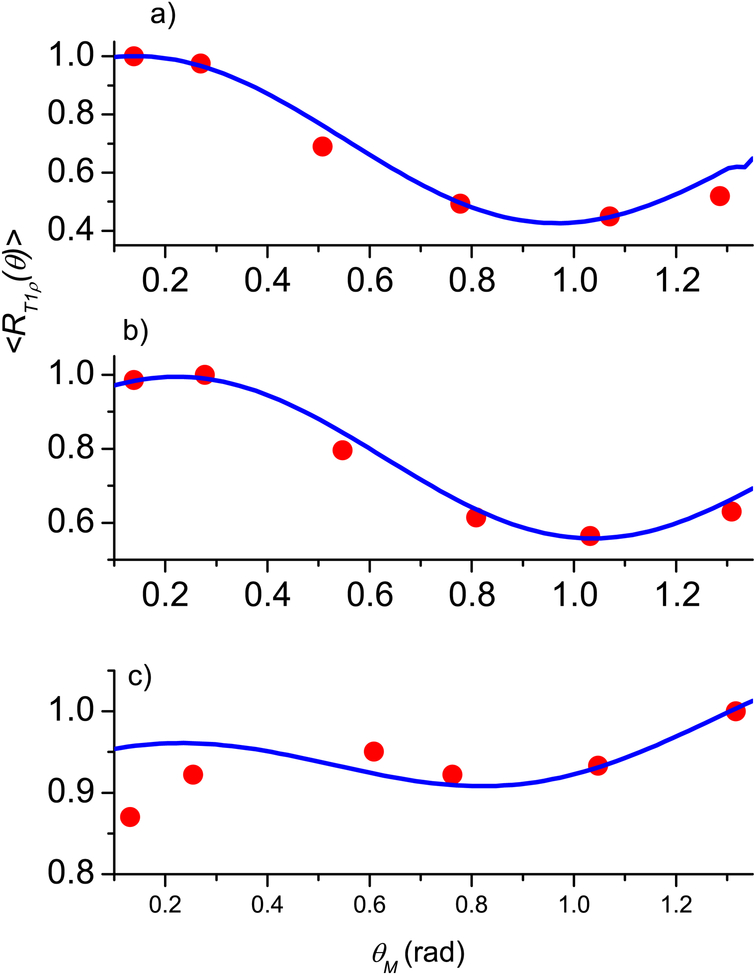
Since articular cartilage is anatomically divided into three topographical regions (medial, apex, and lateral) with three sub-tissue layers (superficial, middle, and deep) in each region, the fibril structure of cartilage (see Fig. 1.2 in [12] and Fig. 9 in [33]) shows that different layers have different preferred directions of the fibrils. However, within each layer, the fibril structure can be represented as a superposition of two types [39, 40] of nanocavity distributions with the preferred orientations perpendicular to each other. A significant anisotropy effect in T1ρ is clearly demonstrated for all three layers in all three regions with maximal angular dependence for the deep and middle layers (see Figs. 3–5 presenting the experimental results from [21, Fig. 3]).
Fig. 3.
Normalized angular dependence of the relaxation rate 〈R1ρ (θ)〉 for the lateral region: the deep (a), middle (b), and superficial (c) layers. Blue solid line - calculations according Eq. (24), red circles - experimental data from [21]. The fitting parameters are given in Table 1.
Fig. 5.
Normalized angular dependence of relaxation rate 〈R1ρ (θ)〉 for the medial region: the deep (a), middle (b), and superficial (c) layers. Blue solid line - calculations according Eq. (24), red circles - experimental data from [21]. The fitting parameters are given in Table 1.
Determination of fitting parameters
The angular dependences of the normalized relaxation rate under spin locking, Eq. (19), is given by Eqs. (21) and (22) in which there are unknown parameters: standard deviations and distribution means. These parameters can be considered as parameters which characterize the fibril structure of a tissue. For obtaining Eq. (11) it is assumed that fibers are straight and nanocavities can be represented by long cylinders. To take into account the real forms of the fibers, their distinction form straight, the fibril structure was represented as a superposition of two types of nanocavity distributions (termed S and R) with different preferred orientations of the fibrils. In both cases the good agreement of the experiment and theoretical results was achieved (Fig. 2–5) when difference between the preferred fibril orientations is about 90°. The normalized inverse relaxation time under spin locking as a function of the angle between the sample axis and the magnetic field can be presented
| (24) |
where ξS and ξR are the weight factors of the distributions with ξS + ξR = 1.
To determine the fitting parameters 〈R1ρ(θM)〉 relative error method with variation of the parameters in wide ranges and then the best parameter set was found from condition that an averaged relative error
| (25) |
is minimal. Here R1ρ(θM)exp is the measured relaxation rate at angle θM and summation through all experimental data for analyzed sample.
Results
Achilles tendon
Fig 2 shows the results for the Achilles tendon, where the maximum of 〈R1ρ(θM)〉 at θM = 0 and the best matching of the calculations according to Eq. (24) was achieved at , β0R = 0, , ξS = 0.05, ξR = 0.95, σβS = σβR = 0.1, and σδS = σδR = 1; ε = 0.023. The standard deviations of these two distributions and the means of the azimuthal angles are equal while the means of the polar angles differ by π / 2 and their weight factors are significantly different, with the R distribution having β0R = 0 and weight factor ξR = 95%.
Let us note that low number (6 points) of the experimental values might lead to inaccurate in determination of the fitting parameters. An increase of the number can cause some variations of them. However, we have applied the same approach for analysis of the T2 angle dependences for an articular cartilage and a sheep Achilles tendon [26, 42]. Our experience in the fitting of the angular dependences of T2 using up to 20 experimental data points [42] allows us to expect that an increase of the data point number does not give significant changes in the fitting parameters.
Articular cartilage
Figs. 3–5 show the results for the articular cartilage, where good agreement between the experiment and theoretical results using Eq. (24) was achieved when the fibril structure was also represented as a superposition of two types of the nanocavity distributions. The fitting parameters of cartilage and the averaged relative error, together with these of the tendon in the first example, are summarized in Table 1. A major complication in the cartilage data, in comparing with tendon, was the position of the maximum relaxation rate, which depends on the region of joint surface (medial, apex, and lateral) and the depth of a sub-tissue layer (superficial, middle, and deep). Several observations can be made by the trends in the fitting parameters.
Table 1.
Fitting parameters for experimental data for a tendon and articular cartilage (angles in degrees).
| Fitting parameters | Tendon | Articular Cartilage | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| lateral | apex | medial | ||||||||
| super | middle | deep | super | middle | deep | super | middle | deep | ||
| ξs =(1−ξR) | 0.05 | 0.50 | 0.50 | 0.30 | 0.50 | 0.46 | 0.50 | 0.30 | 0.30 | 0.50 |
| β0R (°) | 0 | 45.26 | 29.79 | 30.37 | 16.62 | 16.62 | 16.62 | 6.88 | 6.88 | 93.39 |
| β0S (°) | 90 | 135.22 | 119.75 | 120.32 | 106.0 | 106.0 | 106.0 | 100.8 | 96.83 | 48.13 |
| σβ (°) | 5.73 | 17.19 | 5.73 | 2.87 | 26.93 | 9.74 | 3.44 | 21.77 | 17.19 | 22.92 |
| δ0 (°) | 90 | 85.94 | 85.94 | 85.94 | 88.81 | 126.05 | 114.59 | 17.19 | 17.19 | 85.94 |
| σδ (°) | 57.3 | 38.96 | 114.59 | 120.32 | 38.96 | 97.40 | 91.67 | 114.02 | 63.03 | 25.21 |
| relative error, ε | 0.023 | 0.02 | 0.05 | 0.043 | 0.017 | 0.066 | 0.073 | 0.048 | 0.07 | 0.059 |
For tendon, the polar angle β0 is 0° for the R distribution and 90° for the S distribution. Given the weight factor ξS is only 5% for the S distribution, most of the fibers in tendon are oriented along the main sample axis, i.e., the model for a single fibril distribution is nearly sufficient.
For articular cartilage, the values of the angle β0 vary among different regions and different layers. A distinct trend is the nearly consistent 90° difference between the angles β0S and β0R for the two distributions, except in the deep layer in the medial region. Given the nearly equal populations ξS between the two distributions S and R, one may conclude that a more complex fibril structure exists in cartilage than that of an Achilles tendon, and contains two clearly expressed types of the nanocavity distributions for water molecules to sample. Furthermore, the differences in the values of β0R among different topographical regions (lateral, apex, medial) may reflect the shape and curvature of the patellar specimen, as well as the orientation of the specimen in the magnetic field. Finally, the standard deviations σβ are changing for different regions and for different layers, which may be used for characterization of the fibril structure of tissues.
Discussion
The representation of fibril structures by a set of nanocavities containing water allows the model to explain the angular dependence of the relaxation time T1ρ observed in MRI experiments with a human Achilles tendon specimen and an articular cartilage. Considering the nanocavities as long cylinders, we obtained the analytical expression for the averaged dipolar Hamiltonian for spins inside the cavity and, hence, expression (11) for the relaxation time under spin locking. Analysis showed that for axisymmetric cavities the angular dependences of the averaged Hamiltonian and the relaxation time are determined, similarly to a spin pare, by the Legendre polynomial P2 (θM) in which now θM is the angle between the cavity axis and external magnetic field.
Expressions (11)–(13) for the relaxation time give the values close to the experimental data and predict an increase of the time with RF field, ω1. However, Eq. (11) predicts a parabolic increase while the experimental data [16, 20, 38] is well fitted by a linear dependence or even is proportional to . For estimation of the relaxation time, in Eq. (11) the correlation time of the water molecular motion, τc = 30 μs, obtained for water entrapped between a collagen fiber and independent of RF field, ω1, is used. Note, that the correlation time and characteristic time of the transitional diffusion of a water molecule in a nanocavity ttran < tmag ≈ 2.74 × 10−5 s are equal, or even ttran < τc. It is possible to assume that restriction of the molecular motion in nanocavities influences the correlation time.
Using the Gaussian distribution of nanocavity directions which well approximates the anatomical structure tissues [12, 37, 38], the good agreement with the experimental data was obtained by the adjustment of few fitting parameters (the standard deviation, averaged fiber direction, and weight factors). The different parameters were obtained for each layer (superficial, middle, and deep) in each region of articular cartilage.
Thus, the value of the fitting parameters obtained at the matching of calculation to experimental results can be used for characterizing the fine fibril structure of biological samples.
The developed model of fibril tissues well fits most of the experimental data (Figs. 2–5); for the tendon (Fig. 2, the averaged relative error ε = 0.023) is better than the experimental accuracy. However, in some case an error of the fitting can achieve 10%, e.g. Fig. 4c at θM = 00 and Fig. 5a at θM = 750. This can be result of differences of a real distribution of fiber (nanocavity) directions from the Gaussian distribution as well as differences of nanocavity shapes from an axisymmetric one. In the last case the angle dependence of the relaxation rate under spin locking for a single cavity can be differ from P(θM)2. Using other fitting functions and parameters for characterization of the fibril structure requires a more detailed investigation of correlation between the fibril structure and the angular dependence of the NMR signals.
Fig. 4.
Normalized angular dependence of relaxation rate 〈R1ρ (θ)〉 for the apex region: the deep (a), middle (b), and superficial (c) layers. Blue solid line - calculations according Eq. (24), red circles - experimental data from [21]. The fitting parameters are given in Table 1.
The analyzed T1ρ data were obtained on a 3 T whole body MRI, with a max spin lock frequency of 500 Hz. We know from literatures that T1ρ values at 500 Hz can still be influenced significantly by the residual dipolar interaction and hence contain anisotropy similar to the classical T2 in cartilage [12]. A nearly isotropic T1ρ needs a spin lock frequency f of at least 2000 Hz [15, 16, 33]. A nearly isotropic T1ρ was obtained on 4.7 T MRI with a spin lock frequency of 500 Hz in [33]: differences between the relaxation times T1ρ measured in the field parallel to the fibril structure axis and the times in the field directed at the magic angle are less than 15%. Such low anisotropy of T1ρ can be results of the fibril structure. In experiments on a 3 T whole body MRI with f = 500 Hz low anisotropy (~10%) was also obtained (Fig. 4c). On the other hand, in experiments on 4.7 T MRI with f = 500 Hz and f = 2000 Hz the relaxation time varies about 1.5 times with increase of pixel number (depth of a tested range) at both angles (Figs. 8 and 10 in [33]). So, not only angular dependence of the relaxation time but its value can be used for analysis of fine fibril structure of tissues. Further experiments and modeling are planned to differentiate the roles of dipolar interaction in T1ρ dispersion.
Conclusion
Distinctive feature of the relaxation processes in a liquid entrapped in nanocavities is the angular anisotropy of the relaxation times, both the transverse T2 and the spin locking T1ρ. Using the model which is based on representation of a tissue by a set of nanocavities containing water, we explain the anisotropy effect of T1ρ. For comparison of the obtained theoretical results with the experimental data, we choose the data measured by the spin locking technique in the collagen containing connective tissues. Assuming the Gaussian distribution of nanocavity directions, we have calculated the angular anisotropy of the relaxation time under spin locking T1ρ for a human Achilles tendon specimen and an articular cartilage. The good agreement with the experimental data was obtained by adjustment of few fitting parameters - the standard deviation, averaged fiber direction, and weight factors - which characterize the ordering of fibrils. The different parameters were obtained for every sub-tissue layer (superficial, middle, and deep) of each region (medial, apex, and lateral) of the articular cartilage.
Thus, the value of the fitting parameters obtained at matching of calculation to experimental results can be used in future investigations for characterizing the fine fibril structure of biological samples.
*Highlights.
Spin-lattice relaxation in a rotating frame is studied in liquids entrapped in nanocavities. We explain the orientation anisotropy of T1ρ in MRI experiments with biological objects. The correlation time for water molecular motion in articular cartilage was estimated. Using experimental data the averaged nanocavity volume was estimated.
Acknowledgments
This work was supported in part by an NIH R01 grant (AR 069047; PI: Xia).
Grant Support: NIH R01 grant (AR 069047; PI: Xia).
Abbreviations:
- NMR
nuclear magnetic resonance
- MRI
magnetic resonance imaging
- DDI
dipole-dipole interaction
- NIH
National Institutes of Health
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflicts of Interest: The authors report no conflicts of interest.
References
- 1.Abraham A (1961) The principles of nuclear magnetism. Oxford Clarendon Press. [Google Scholar]
- 2.Callaghan PT (1991) Principles of nuclear magnetic resonance microscopy. Oxford Clarendon Press. [Google Scholar]
- 3.Haeberlen U and Waugh JS (1969) Spin-lattice relaxation in periodically perturbed systems. Phys Rev 185:420. [Google Scholar]
- 4.Mehring M (1978) High resolution NMR spectroscopy in solids. Springer-Verlag. [Google Scholar]
- 5.Haeberlen U (1978) High resolution NMR in solids. Academic Press. [Google Scholar]
- 6.Goldman M (1970) Spin temperature and nuclear resonance in solids. Oxford Clarendon Press. [Google Scholar]
- 7.Fel’dman EB, Furman GB, and Goren SD (2012) Spin locking and spin-lattice relaxation in a liquid entrapped in nanosized cavities. Soft Matter 8:9200. [Google Scholar]
- 8.Furman G and Goren S (2011) Dipolar order and spin-lattice relaxation in a liquid entrapped into nanosize cavities. Z Naturforsch 66a:779. [Google Scholar]
- 9.Furman G and Goren S (2012) Spin-lattice relaxation of dipolar energy in fluid confined to nanosized cavities. Materials Science Forum 721:47. [Google Scholar]
- 10.Furman GB, Goren SD, Meerovich VM, and Sokolovsky VL (2015) Multiple-pulse spin locking in nanofluids. RSC Adv 5:44247. [Google Scholar]
- 11.Furman GB, Goren SD, Meerovich VM, and Sokolovsky VL (2015) Nuclear spin-lattice relaxation in nanofluids with paramagnetic impurities. J Magn Reson 261:175–180. [DOI] [PubMed] [Google Scholar]
- 12.Xia Y and Momot K (2016) Biophysics and biochemistry of cartilage by NMR and MRI. the Royal Society of Chemistry, Cambridge UK. [Google Scholar]
- 13.Regatte RR, Akella SVS, Lonner JH, Kneeland JB, and Reddy R, (2006) T1ρ relaxation mapping in human osteoarthritis (OA) cartilage: Comparison of T1ρ with T2. J Magn Reson Imaging 23:547–553. [DOI] [PubMed] [Google Scholar]
- 14.Li X, Cheng J, Lin K, Saadat E, Bolbos RI, Jobke B, Ries MD, Horvai A, Link TM, and Majumdar S (2011) Quantitative MRI using T1ρ and T2 in human osteoarthritic cartilage specimens: correlation with biochemical measurements and histology. Magn Reson Imaging 29:324–334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang N and Xia Y (2011) Dependencies of multi-component T2 and T1ρ relaxation on the anisotropy of collagen fibrils in bovine nasal cartilage. J Magn Reson 212: 124–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang N and Xia Y (2012) Orientational dependent sensitivities of T2 and T1ρ towards trypsin degradation and Gd-DTPA2− presence in bovine nasal cartilage, Magnetic Resonance Materials in Physics. Biology and Medicine (MAGMA) 25: 297–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang N and Xia Y (2013) Experimental issues in the measurement of multi-component relaxation times in articular cartilage by microscopic MRI. J Magn Reson 235:15–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang N and Xia Y (2013) Anisotropic analysis of multi- component T2 and T1ρ relaxations in Achilles tendon by NMR spectroscopy and microscopic MRI. J Magn Reson Imaging. 38:625–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xia Y (2000) Magic-angle effect in magnetic resonance imaging of articular cartilage: a review. Investigative Radiology 35:602. [DOI] [PubMed] [Google Scholar]
- 20.Du J, Statum S, Znamirowski R, Bydder GM and Chung CB (2013) Ultrashort TE T1ρ magic angle imaging. Magn Reson Med 69:682–687. [DOI] [PubMed] [Google Scholar]
- 21.Shao H, Pauli C, Li S, Ma Y, Tadros AS, Kavanaugh A, Chang EY, Tang G, and Du J (2017) Magic angle effect plays a major role in both T1rho and T2 relaxation in articular cartilage. Osteoarthritis and Cartilage 25:2022–2030 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Berendsen HJC (1962) Nuclear magnetic resonance study of collagen hydration. J Chem Phys 36:3297–3305. [Google Scholar]
- 23.Fullerton GD, Cameron IL, and Ord VA (1985) Orientation of tendons in the magnetic field and its effect on T2 relaxation times. Radiology 155:433–435. [DOI] [PubMed] [Google Scholar]
- 24.Henkelman RM, Stanisz GJ, Kim JK, and Bronskill MJ, (1994) Anisotropy of NMR properties of tissues. Magn Reson Med 32:592—601. [DOI] [PubMed] [Google Scholar]
- 25.Furman GB, Goren SD, Meerovich VM, and Sokolovsky VL (2016) Anisotropy of spin-spin and spin-lattice relaxation times in liquids entrapped in nanocavities: Application to MRI study of biological systems. J Magn Reson 263:71–78. [DOI] [PubMed] [Google Scholar]
- 26.Furman GB, Goren SD, Meerovich VM, and Sokolovsky VL (2016) Correlation of transverse relaxation time with structure of biological tissue. J Magn Reson, 270:7. [DOI] [PubMed] [Google Scholar]
- 27.Baugh J, Kleinhammes A, Han D, Wang Q, and Wu Y (2001) Confinement effect on dipole-dipole interactions in nanofluids. Science 294:1505. [DOI] [PubMed] [Google Scholar]
- 28.Rudavets MG and Fel’dman EB (2002) Nonergodic dynamics of a system of nuclear spins 1/2 with identical spin-spin coupling constants. JETP Letters 75:635–637. [Google Scholar]
- 29.Fel’dman EB and Rudavets MG, (2004) Nonergodic nuclear depolarization in nanocavities. JETP 98:207. [Google Scholar]
- 30.Holz M, Heil SR, and Sacco A (2000) Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements. Phys Chem Chem Phys. 2:4740. [Google Scholar]
- 31.Khinchin AI, Mathematical Foundations of Statistical, Mechanics, Dover Publication, Inc, New York, 1949. [Google Scholar]
- 32.Xia Y (2013) MRI of articular cartilage at microscopic resolution. Bone Jt Res 2: 9–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Akella SV, Regatte RR, Wheaton AJ, Borthakur A, and Reddy R (2004) Reduction of residual dipolar interaction in cartilage by spin-lock technique. Magn Reson Med 52:1103–1109. [DOI] [PubMed] [Google Scholar]
- 34.Look DC and Lowe IJ (1966) Nuclear magnetic resonance study of molecular motions in solid hydrogen sulfide. J Chem Phys 44:2995. [Google Scholar]
- 35.Huang Y (2011) A theoretical and experimental study of water proton spin relaxation in liquid, hexagonal-ice and the para-magnetic Gd3+(H2O)8 complex. Thesis (www.diva-portal.org/smash/get/diva2:546063/FULLTEXT01.pdf).
- 36.Foster KR, Resing HA, and Garroway AH, Bounds on “Bound Water”: Transverse Nuclear Magnetic Resonance Relaxation in Barnacle Muscle (1976) Science 194,324. [DOI] [PubMed] [Google Scholar]
- 37.Resing HA, Garroway AH, and Foster KR, Bounds on Bound Water: Transverse and Rotating Frame NMR Relaxation in Muscle Tissue_in “Magnetic Resonance in Colloid and Interface Science” (Resing HA and Wade CG, Eds.), p. 516, A.C.S. Symp. Ser, Vol. 34,American Chemical Society, Washington D.C., 1976. [Google Scholar]
- 38.Erickson SJ, High-resolution imaging of the musculoskeletal system. Radiology, 1997, 205, 593–618. [DOI] [PubMed] [Google Scholar]
- 39.Stolz M, Gottardi R, Raiteri R, Miot S, Martin I, Imer R, Staufer U, Raducanu A, Duggelin M, Baschong W, Daniels AU, Friederich NF,, Aszodi A and Aebi U, Nat. Nanotechnol, 2009, 4, 186–192 [DOI] [PubMed] [Google Scholar]
- 40.Xia Y(1998) Relaxation anisotropy in cartilage by NMR microscopy (μMRI) at 14-μm resolution. Magn Reson Med 39:941. [DOI] [PubMed] [Google Scholar]
- 41.Xia Y, Moody J, and Alhadlaq H (2002) Orientational dependence of T2 relaxation in articular cartilage: A microscopic MRI (μMRI) study. Magn Reson Med 48:460–469. [DOI] [PubMed] [Google Scholar]
- 42.Furman GB, Goren SD, Meerovich VM, Sokolovsky VL, (2018) Dipole-dipole interactions in liquids entrapped in confined space Journal of Molecular Liquids 272 468–473 [Google Scholar]