An Adaptive Trial Design to Optimize Dose-Schedule Regimes with Delayed Outcomes

Summary:

This paper proposes a two-stage phase I-II clinical trial design to optimize dose–schedule regimes of an experimental agent within ordered disease subgroups in terms of toxicity–efficacy tradeoff. The design is motivated by settings where prior biological information indicates it is certain that efficacy will improve with ordinal subgroup level. We formulate a flexible Bayesian hierarchical model to account for associations among subgroups and regimes, and to characterize ordered subgroup effects. Sequentially adaptive decision making is complicated by the problem, arising from the motivating application, that efficacy is scored on day 90 and toxicity is evaluated within 30 days from the start of therapy, while the patient accrual rate is fast relative to these outcome evaluation intervals. To deal with this in a practical way, we take a likelihood-based approach that treats unobserved toxicity and efficacy outcomes as missing values, and use elicited utilities that quantify the efficacy-toxicity trade-off as a decision criterion. Adaptive randomization is used to assign patients to regimes while accounting for subgroups, with randomization probabilities depending on the posterior predictive distributions of utilities. A simulation study is presented to evaluate the design’s performance under a variety of scenarios, and to assess its sensitivity to the amount of missing data, the prior, and model misspecification.

1. Introduction

The primary objective of a phase I clinical trial is to estimate a maximum tolerable dose (MTD) based on a toxicity variable defined in terms of one or more adverse events. Numerous phase I designs have been proposed, such as the algorithm-based 3+3 design (Storer, 1989), many model-based methods including the continual reassessment method (CRM) (O’Quigley, et al., 1990), escalation with overdose control (EWOC) (Babb et al., 1998), Bayesian model averaging CRM (Yin and Yuan, 2009), and model-assisted methods (Liu and Yuan, 2015; Zhou et al., 2018). For a comprehensive review on existing phase I designs, see Zhou et al. (2018). Some Bayesian model-based methods have been extended to deal with late-onset toxicity (Cheung and Chappell, 2000; Yuan and Yin, 2011a).

For molecularly targeted agents and immunotherapies, a toxicity-based MTD is not necessarily the optimal dose. Many phase I-II trial designs have been proposed to use both efficacy and toxicity for decision making. Thall and Cook (2004) proposed a Bayesian phase I-II design based on toxicity-efficacy probability trade-offs. Bekele and Shen (2005) introduced a Bayesian approach to jointly modeling toxicity and biomarker expression. Zhang et al. (2006) utilized a continuation-ratio model to adaptively estimate a biologically optimal dose. Houede et al. (2010) optimized the dose pair of a two-agent combination using ordinal toxicity and efficacy, by maximizing posterior mean utility. This approach was extended by using adaptive randomization (AR) to reduce the chance of getting stuck at a suboptimal dose pair (Thall and Nguyen, 2012). Yuan and Yin (2011b) considered phase I-II drug-combination trials with late-onset efficacy. Guo and Yuan (2016) proposed a Bayesian phase I-II design for precision medicine that incorporates biomarker subgroups. Liu, et al. (2018) developed a Bayesian utility-based phase I-II design for immunotherapy trials. Reviews of phase I-II designs are given by Yuan, Nguyen and Thall (2016).

In many settings, multiple administration schedules are considered, along with different doses. This motivates more complex phase I or I-II designs to optimize dose-schedule treatment regimes (Braun et al., 2005, 2007; Zhang and Braun, 2013; Lee, et al., 2015; Guo et al., 2016). This paper is motivated by a planned phase I-II trial for optimizing dose–schedule of PGF Melphalan as a single agent preparative regimen for autologous stem cell transplantation in patients with multiple myeloma (MM). This disease is heterogeneous, dichotomized in terms of pathogenesis pathways determined by genetic and cytogenetic abnormalities as hyperdiploid or not. Hyperdiploid patients are believed to have a better response rate than non-hyperdiploid (Chng et al., 2006). A review is given by Fonseca, et al. (2009). The trial considers three doses, 200, 225 and 250 mg/m², and three infusion schedules, 30 minutes, 12 hours, and 24 hours, yielding nine treatment regimes. Toxicity is defined as the binary indicator of grade 3 mucositis lasting > 3 days or any grade 4 or 5 non-hematologic or non-infectious toxicity within 30 days from start of infusion. Efficacy is defined as the binary indicator of complete remission evaluated at day 90. Thus, while toxicity is observed soon enough to apply a usual sequentially adaptive toxicity-based decision rule feasibly, the efficacy outcome is evaluated much later. This greatly complicates making outcome-adaptive decisions to optimize dose or dose–schedule based on both toxicity and efficacy.

Our proposed design optimizes the dose–schedule regime in terms of a toxicity–efficacy risk-benefit trade-off quantified by a utility function, allowing the possibility that the optimal regime may differ between disease subgroups. We formulate a Bayesian hierarchical model to characterize associations among dose, schedule, subgroup, and the bivariate toxicity–efficacy outcome. The design includes a two-stage adaptive randomization (AR) scheme that randomizes each newly enrolled patient to a treatment regime using the posterior predictive probability of the regime being the best with respect to the utility.

The rest of the paper is organized as follows. Section 2 presents the probability model, likelihood, and priors. Section 3 gives the trial design, including the utility function, prior elicitation, and rules for trial conduct. In Section 4, we apply the proposed design to the motivating example and conduct simulation studies to examine the design’s performance. We close with a brief discussion in Section 5.

2. Probability Model

2.1. Bayesian hierarchical model

We consider a phase I-II trial with C ordered subgroups and a total of DS treatment regimes obtained from D doses and S treatment schedules. Let n denote the number of patients accrued at an interim point in the trial, and c_i ∈ {1, … , C} be the subgroup of the ith patient, i = 1, … , n. Denote the dose-schedule treatment regime assigned to patient i by r_i = (d_i, s_i), for d_i ∈ {1, … , D}, s_i ∈ {1, … , S}, and the joint toxicity and efficacy outcome ${\mathbf{Y}}_i=(Y_i^T,Y_i^E)$. Since Y_i may depend on both c_i and r_i, the objective of the trial is to find optimal subgroup-specific dose–schedule regimes that can maximize a given utility function.

Similarly to Albert and Chib (1993) and Lee, et al. (2015), to facilitate posterior computation we assume a latent normal vector to characterize the joint distribution of the observed discrete outcome vector. Let ${\xi }_i=({\xi }_i^T,{\xi }_i^E)$ be real-valued bivariate normal latent variables with means that vary with c_i and r_i. We define Y_i by assuming that $Y_i^j=\mathrm{I}({\xi }_i^j>0)$, j = T, E, where I(·) is the indicator function, so the joint distribution of the latent vector [ξ_i|c_i, r_i] induces that of the observed vector [Y_i|c_i, r_i]. Each $Y_i^j$ is assumed to be a binary outcome. Extension to ordinal outcomes is straightforward, but introduces additional complexity in the likelihood and utility. We assume the following Bayesian hierarchical model for [ξ_i | r_i]:

(a) Level 1 prior on ξ_i. Using patient-specific random effects ${ϵ}_i=({ϵ}_i^T,{ϵ}_i^E)$, we assume the following conditional distribution for the latent variables:

$${\xi }_i^j\mid c_i,r_i,{ϵ}_i,{\tilde{\xi }}_{c_i,r_i}^j,{\sigma }_{\xi }^2\sim \mathrm{N}({\tilde{\xi }}_{c_i,r_i}^j+{ϵ}_i^j,{\sigma }_{\xi }^2),j=E,T,i=1,\dots ,n$$ (2.1)

with the variance ${\sigma }_{\xi }^2$ a hyperparameter and ${\tilde{\xi }}_i=({\tilde{\xi }}_{c_i,r_i}^T,{\tilde{\xi }}_{c_i,r_i}^E)$ the mean effects of regime r_i = (d_i, s_i) in subgroup c_i. The following second-level priors on ϵ_i and ${\tilde{\xi }}_{c_i,r_i}$ induce association between ${\xi }_i^T$ and ${\xi }_i^E$, which in turn induces association between $Y_i^T$ and $Y_i^E$.

(b) Level 2 prior on ϵ_i. Assume

$$({ϵ}_i^T,{ϵ}_i^E)\stackrel{i.i.d}{\sim }\mathrm{BN}(0_2,{\Sigma }_{ϵ}),i=1,\dots ,n,$$ (2.2)

where “i.i.d.” represents independent and identically distributed, BN denotes a bivariate normal distribution, 0₂ = (0, 0) and Σ_ϵ is the 2 × 2 matrix with both diagonal elements ζ² and both off-diagonal elements ρζ². The fixed hyperparameters ρ ∈ (−1, 1) and ζ² quantify the association between $Y_i^T$ and $Y_i^E$ via the latent variable model.

(c) Level 2 prior on ${\tilde{\xi }}_{c,r}$. To facilitate information sharing across subgroups, for each regime r = (d, s) we assume that ${\tilde{\xi }}_{c,r}={\stackrel{‒}{\xi }}_r+{\sum }_{c^{\prime }=2}^C{\nu }_{c,r}\mathrm{I}(c^{\prime }=c)$, c = 1, … , C, where ${\overline{\xi }}_r=({\stackrel{‒}{\xi }}_r^T,{\stackrel{‒}{\xi }}_r^E)$ can be treated as the baseline effects for regime r, and the baseline subgroup is c = 1 with ν_{1, r} = 0₂ for all r. The ordering constraint is imposed by choosing the support of ${\nu }_{c,r}=({\nu }_{c,r}^T,{\nu }_{c,r}^E)$ to satisfy the corresponding order constraint. For example, if prior information indicates that Pr(efficacy) in subgroup 1 is greater than Pr(efficacy) in subgroup 2, then we require ${\nu }_{1,r}^E>{\nu }_{2,r}^E$. Thus, this model ensures that the efficacy probabilities are heterogenous across subgroups. When ν_c,r → 0₂ for all (c, r), the model shrinks to the homogeneous case where regime effects in different subgroups are the same.

To define the priors of ${\stackrel{‒}{\xi }}_r$, for schedule s and outcome j = T, E, we denote by ${\stackrel{‒}{\xi }}_{-d,s}^j$ the subvector of ${\stackrel{‒}{\xi }}_s^j=({\stackrel{‒}{\xi }}_{1,s}^j,\dots ,{\stackrel{‒}{\xi }}_{D,s}^j)$ with ${\stackrel{‒}{\xi }}_{d,s}^j$ deleted, for d = 1, … , D. Our model includes the common assumption that the risk of toxicity increases monotonically with dose, which we formalize as

$${\stackrel{‒}{\xi }}_{d,s}^T\mid {\stackrel{‒}{\xi }}_{-d,s}^T\sim \mathrm{N}({\xi }_0^T,{\sigma }_0^{T,2})\mathrm{I}({\stackrel{‒}{\xi }}_{d-1,s}^T<{\stackrel{‒}{\xi }}_{d,s}^T<{\stackrel{‒}{\xi }}_{d+1,s}^T),$$ (2.3)

where $\mathrm{N}({\xi }_0^T,{\sigma }_0^{T,2})$ denotes the hyper-prior normal distribution with mean ${\xi }_0^T$ and variance ${\sigma }_0^{T,2}$, with the truncated support of ${\stackrel{‒}{\xi }}_{d,s}^T$ given by the indicator function. That is, the conditional distribution of the mean ${\stackrel{‒}{\xi }}_{d,s}^T$ is restricted to the subset of the reals determined by the values of the other means, ${\stackrel{‒}{\xi }}_{-d,s}^T$, through the order constraint. These order constraints induce association among different dose levels, ensuring that the latent variable for toxicity increases stochastically in dose d for each schedule s, hence the probability of toxicity increases with d for each s. Such an order constraint can be achieved at each Markov chain Monte Carlo (MCMC) step by generating the proposals of (${\stackrel{‒}{\xi }}_{1,s}^T$, ${\stackrel{‒}{\xi }}_{D,s}^T$) from a multivariate normal distribution, subject to ${\stackrel{‒}{\xi }}_{1,s}^T<\cdots <{\stackrel{‒}{\xi }}_{D,s}^T$. In contrast, we do not impose any monotonicity restriction on efficacy in d, and simply assume that

$${\stackrel{‒}{\xi }}_{d,s}^E\mid {\stackrel{‒}{\xi }}_{-d,s}^E\sim \mathrm{N}({\xi }_0^E,{\sigma }_0^{E,2}),$$ (2.4)

where $\mathrm{N}({\xi }_0^E,{\sigma }_0^{E,2})$ denotes the unconstrained hyper-prior normal distribution. Thus, for each s and c, the dose-efficacy probability relationship can take a wide variety of possible forms.

The priors on ν_{c, r} should be elicited while accounting for prior order. Based on the MM trial with C = 2 ordered subgroups, the toxicity distribution is homogeneous across subgroups, so we assume ${\nu }_{c,r}^T=0$ for each (c, r) combination. Since efficacy in the second subgroup (c = 2) is greater than in the first group (c = 1), we estimate ${\nu }_{2,r}^E$ by borrowing information across dose levels, as follows: ${\nu }_{2,r}^E={\nu }_{2,d,s}^E\stackrel{i.i.d}{\sim }{\mathrm{N}}_{+}({\nu }_{1,r}^E,{\tau }_0^2)$, d = 1, … , D, s = 1, … , S, where ${\mathrm{N}}_{+}({\nu }_{1,r}^E,{\tau }_0^2)$ is a truncated normal distribution with support (${\nu }_{1,r}^E,\infty$), and the variance ${\tau }_0^2$ is prespecified. This ensures that, given r, the efficacy probability in subgroup 2 is strictly greater than that in subgroup 1. For more general trials, if there is an ordering relationship among subgroups in terms of toxicity, say, subgroup 2 has a higher toxicity probability than subgroup 1, the design may account for this by assuming the prior, ${\nu }_{2,r}^T={\nu }_{2,d,s}^T\stackrel{i.i.d}{\sim }{\mathrm{N}}_{+}({\nu }_{1,r}^T,{\tau }_0^2)$, d = 1, … , D, s = 1, … , S, with ${\nu }_{1,r}^T=0$. However, since the MM trial considers a homogeneous toxicity distribution across subgroups, we simply take ${\nu }_{2,r}^T={\nu }_{1,r}^T=0$ in this paper.

To specify the likelihood and posterior, we denote $\tilde{\xi }=\{{\tilde{\xi }}_{c,r},c=1\dots ,C,r=1\dots ,\mathit{DS}\}$. Combining equations (2.1) and (2.2), the joint distribution of (${\xi }_i^T$, ${\xi }_i^E$) can be derived by integrating out ϵ_i, yielding

$$({\xi }_i^T,{\xi }_i^E)\mid c_i,r_i,\tilde{\xi }\stackrel{\mathrm{indep}}{\sim }\mathrm{BN}({\mu }_{c_i,r_i},{\Sigma }_{\xi }),$$ (2.5)

where the mean vector μ_{ci, ri} depends on the ith patient’s subgroup c_i and treatment regime r_i = (d_i, s_i). More precisely, ${\mu }_{c_i,r_i}=({\tilde{\xi }}_{c_i,r_i}^T,{\tilde{\xi }}_{c_i,r_i}^E)$, and Σ_ξ is the covariance matrix with the diagonal elements being ${\sigma }_{\xi }^2+{\zeta }^2$ and the off-diagonal elements being ρζ². As a result, the individual likelihood for the observations of a patient with outcome ($y_i^T$, $y_i^E$) ($y_i^T$, $y_i^E=0,1$) can be parameterized as

$$\begin{gathered} f(y_i^T,y_i^E\mid c_i,r_i,\tilde{\xi })=\mathrm{Pr}({\gamma }_{y_i^T}⩽{\xi }_i^T<{\gamma }_{y_i^T+1},{\gamma }_{y_i^E}⩽{\xi }_i^E<{\gamma }_{y_i^E+1}\mid c_i,r_i,\tilde{\xi }) \\ ={\int }_{{\gamma }_{y_i^T}}^{{\gamma }_{y_i^T+1}}{\int }_{{\gamma }_{y_i^E}}^{{\gamma }_{y_i^E+1}}f({\xi }_i^T,{\xi }_i^E\mid c_i,r_i,\tilde{\xi })\mathrm{d}{\xi }_i^E\mathrm{d}{\xi }_i^T, \end{gathered}$$

where $f({\xi }^T,{\xi }^E\mid c,r,\tilde{\xi })$ is given by (2.5), and the cutoff vector (γ₀, γ₁, γ₂) = (−∞, 0, ∞).

2.2. Delayed outcomes

In the MM study, the toxicity outcome is evaluated within V^T = 30 days, while efficacy is defined as complete remission based on disease evaluation on day V^E = 90. Thus, toxicity can occur at any time during the 30 day assessment window, but efficacy is not known until a patient has reached day 90 of follow up. Consequently, when a regime must be assigned for a newly enrolled patient, the outcomes of some previously treated patients might not have been fully assessed. Formally, at the time of interim decision making, both Y^E and Y^T of previously treated patients are subject to missingness. In the MM study, the amount of missing Y^T data would be much less than the amount of missing Y^E data because the 30-day assessment window for Y^T is much shorter than the 90 days required to evaluate Y^E.

At an interim decision-making time, suppose that patient i has been followed for t_i days. We introduce an indicator vector ${\delta }_i=({\delta }_i^T,{\delta }_i^E)$ to denote the respective missingness of toxicity and efficacy for the ith patient, where ${\delta }_i^j=1$ if $Y_i^j$ has been evaluated and ${\delta }_i^j=0$ if not, for j = T, E. In the MM trial setting, Y^T can be defined as a time-to-event outcome. Suppose X_i denotes the ith patient’s time to toxicity, then $Y_i^T=1$ if X_i ⩽ V^T and $Y_i^T=0$ if X_i > V^T. We have ${\delta }_i^T=\mathrm{I}(t_i⩾\min (X_i,V^T))$ and ${\delta }_i^E=\mathrm{I}(t_i⩾V^E)$. Because V^T < V^E, we have ${\delta }_i^T⩾{\delta }_i^E$, so $({\delta }_i^T,{\delta }_i^E)=(0,1)$ is impossible.

When both $Y_i^T=y_i^T$ and $Y_i^E=y_i^E$ are observed for patient i, i.e., t_i > V^E, the individual likelihood is $f(y_i^T,y_i^E\mid {\delta }_i^T=1,{\delta }_i^E=1,c_i,r_i,\tilde{\xi })=f(y_i^T,y_i^E\mid c_i,r_i,\tilde{\xi })$. Under the mechanism of missing at random, the likelihood of a patient with observed $Y_i^T=y_i^T$ and missing $Y_i^E$, i.e., min(X_i, V^T)) ⩽ t_i < V^E and $({\delta }_i^T,{\delta }_i^E)=(1,0)$, is $f(y_i^T\mid {\delta }_i^T=1,{\delta }_i^E=0,c_i,r_i,\tilde{\xi })=\mathrm{Pr}({\gamma }_{y_i^T}⩽{\xi }_i^T<{\gamma }_{y_i^T+1}\mid c_i,r_i,\tilde{\xi })$, where $\mathrm{Pr}({\gamma }_{y_i^T}⩽{\xi }_i^T<{\gamma }_{y_i^T+1}\mid c_i,r_i,\tilde{\xi })$ is the marginal likelihood of $Y_i^T$ evaluated at $y_i^T$. When both $y_i^T$ and $y_i^E$ are missing, i.e., t_i < min(X_i, V^T) and $({\delta }_i^T,{\delta }_i^E)=(0,0)$, it only is known that the ith patient’s time to toxicity is greater than t_i. In this case, for 0 < t_i < V^T, the likelihood is given by

$$\begin{gathered} \mathrm{Pr}(X_i>t_i\mid {\delta }_i^T=0,{\delta }_i^E=0,c_i,r_i,\tilde{\xi }) \\ =\mathrm{Pr}(Y_i^T=0\mid c_i,r_i,\tilde{\xi })\mathrm{Pr}(X_i>t_i\mid Y_i^T=0,c_i,r_i,\tilde{\xi }) \\ +\mathrm{Pr}(Y_i^T=1\mid c_i,r_i,\tilde{\xi })\mathrm{Pr}(X_i>t_i\mid Y_i^T=1,c_i,r_i,\tilde{\xi }) \end{gathered}$$ (2.6)

$$=1-w_i\mathrm{Pr}(Y_i^T=1\mid c_i,r_i,\tilde{\xi })$$ (2.7)

where we denote $w_i=\mathrm{Pr}(X_i⩽t_i\mid Y_i^T=1,c_i,r_i,\tilde{\xi })$. The first equality above is due to the fact that, given ${\delta }_i^T=0$ and ${\delta }_i^E=0$, all values of ($Y_i^T$, $Y_i^E$) are possible. Suppressing c_i, r_i, $\tilde{\xi }$ for brevity, since 0 < t_i < V^T, $\mathrm{Pr}(X_i>t_i\mid Y_i^T=0)=\mathrm{Pr}(V^T⩾X_i>t_i\mid Y_i^T=0)+\mathrm{Pr}(X_i>V^T\mid Y_i^T=0)=0+1=1$, hence the first summand (2.6) equals $\mathrm{Pr}(Y_i^T=0\mid c_i,r_i,\tilde{\xi })=1-\mathrm{Pr}(Y_i^T=1\mid c_i,r_i,\tilde{\xi })$.

We assume that, conditional on $Y_i^T$, the time-to-toxicity distribution is independent of (c_i, r_i, $\tilde{\xi }$), i.e. X_i does not depend on subgroup or treatment regime given the indicator of toxicity on [0, V^T]. We thus need to estimate w_i in order to obtain a working likelihood for $\mathrm{Pr}(X_i>t_i\mid {\delta }_i^T=0,{\delta }_i^E=0,c_i,r_i,\tilde{\xi })$. Noting that the support of $[X_i\mid Y_i^T=1]$ is (0, V^T), we (model the conditional samples of $[X_i\mid Y_i^T=1]$ based on a scaled Beta distribution, given by

$$\begin{gathered} \text{Sampling model}:X_i\mid Y_i^T=1\sim V^T\times \text{Beta}(\alpha ,\beta ), \\ \text{Priors}:\alpha ,\beta \sim \text{Gamma}({\lambda }_0,{\eta }_0), \end{gathered}$$ (2.8)

where λ₀ and η₀ are the hyperparameters for the Gamma prior distribution. As a result, w_i can be obtained based on the posterior distribution of $[X_i\mid Y_i^T=1]$.

Let ${\mathcal{D}}_n={\{(c_i,r_i,y_i^T,y_i^E,x_i,t_i,{\delta }_i^T,{\delta }_i^E)\}}_{i=1}^n$ be the observed data at the arrival time of the (n + 1)th patient. The joint likelihood for the first n patients can be written as

$$\begin{gathered} L({\mathcal{D}}_n\mid \tilde{\xi },\alpha ,\beta ) \\ =\prod _{i=1}^n\left\{g{(x_i\mid \alpha ,\beta )}^{y_i^T}\times \\ f{(y_i^T,y_i^E\mid {\delta }_i^T=1,{\delta }_i^E=1,c_i,r_i,\tilde{\xi })}^{{\delta }_i^T{\delta }_i^E}\times f{(y_i^T\mid {\delta }_i^T=1,{\delta }_i^E=0,c_i,r_i,\tilde{\xi })}^{{\delta }_i^T(1-{\delta }_i^E)}\times \mathrm{Pr}{(X_i⩾t_i\mid {\delta }_i^T=0,{\delta }_i^E=0,c_i,r_i,\tilde{\xi })}^{(1-{\delta }_i^T)(1-{\delta }_i^E)}\right\} \end{gathered}$$

where g(· | α, β) is the density function of the scaled Beta distribution.

Denote the vector of all hyperparameters by ${\theta }_0=(\rho ,{\zeta }^2,{\sigma }_{\xi }^2,{\lambda }_0,{\eta }_0,{\xi }_0^T,{\xi }_0^E,{\sigma }_0^{T,2},{\sigma }_0^{E,2},{\tau }_0^2)$, and let $\pi (\tilde{\mathit{\xi }},\alpha ,\beta \mid {\theta }_0)$ be the joint prior distribution of ($\tilde{\xi }$, α, β) induced by the hierarchical model (2.1)–(2.4) and the model (2.8) for time to toxicity. The joint posterior distribution of ($\tilde{\xi }$, α, β) is then given by $\pi (\tilde{\xi },\alpha ,\beta \mid {\theta }_0,{\mathcal{D}}_n)\propto \pi (\tilde{\xi },\alpha ,\beta \mid {\theta }_0)L({\mathcal{D}}_n\mid \tilde{\xi },\alpha ,\beta )$, where the posterior samples of $[\tilde{\xi },\alpha ,\beta \mid {\theta }_0,{\mathcal{D}}_n]$, can be obtained via standard Markov chain Monte Carlo sampling methods. The sampling procedure is carried out in two steps. Since the posterior sampling of model (2.8) only depends on the time to toxicity data $\{(X_i,{\delta }_i^T),i=1,\dots ,n\}$, in the first step we simulate the posterior samples of (α, β), as well as those of w_i, because w_i depends solely on the model assumption (2.8). In the second step, we plug the posterior samples of w_i values into equation (2.7) to obtain samples of the remaining parameters. R code for implementing the proposed design is available in Supporting Information.

3. Trial design

We define admissibility criteria to screen out any regimes with excessively high toxicity or unacceptably low efficacy adaptively based on the interim data. Let ${\pi }_{c,r}^j(\tilde{\xi })=\mathrm{Pr}(Y^j=1\mid c,r,\tilde{\xi })$ be the marginal probability of outcome j = T, E. Recall that θ₀ denotes the vector of all fixed hyperparameters. Given a fixed upper limit ${\overline{\pi }}^T$ on ${\pi }_{c,r}^T(\tilde{\xi })$, a fixed lower limit π^E on ${\pi }_{c,r}^E(\tilde{\xi })$, and fixed cutoff probabilities η^T and η^E, for each subgroup c, we define the set ${\mathcal{A}}_c$ of admissible regimes to be all r = (d, s) satisfying the two criteria

$$\mathrm{Pr}\{{\pi }_{c,r}^T(\tilde{\xi })>{\overline{\pi }}^T\mid {\theta }_0,{\mathcal{D}}_n\}<{\eta }^T\text{and}\mathrm{Pr}\{{\pi }_{c,r}^E(\tilde{\xi })<{\underset{¯}{\pi }}^E\mid {\theta }_0,{\mathcal{D}}_n\}<{\eta }^E,$$ (3.1)

similarly to Thall and Cook (2004).

To choose regimes from ${\mathcal{A}}_c$ for each subgroup c, we utilize a utility-based criterion to quantify efficacy-toxicity risk-benefit trade-offs. To do this, a numerical utility U(y^T, y^E) is elicited for each of the four elementary outcome pairs (y^T, y^E) = (0, 0), (1, 0), (0,1), and (1,1). For illustrations of the choice of U in a variety of settings, see Houede et al. (2010), Thall and Nguyen (2012), Yuan, Nguyen and Thall (2016), or Liu, et al. (2018). Since (Y^T, Y^E) are random variables that depend on the patient’s regime r and subgroup c, U(Y^T, Y^E) also is a random variable. Denote y_u = {(y_T, y_E) : U(y_T, y_E) = u}. The posterior predictive distribution (PPD) of U(Y^T, Y^E) for future values (Y^T, Y^E) is derived as follows.

$$\begin{gathered} \mathrm{Pr}\{U(Y^T,Y^E)=u\mid c,r,{\theta }_0,{\mathcal{D}}_n\}=\sum _{{\mathbf{y}}_u}\mathrm{Pr}\{(Y^T,Y^E)={\mathbf{y}}_u\mid c,r,{\theta }_0,{\mathcal{D}}_n\} \\ =\sum _{{\mathbf{y}}_u}{\int }_{\tilde{\xi }}\mathrm{Pr}\{(Y^T,Y^E)={\mathbf{y}}_u\mid c,r,\tilde{\xi }\}\pi (\tilde{\xi }\mid {\theta }_0,{\mathcal{D}}_n)\mathrm{d}\tilde{\xi }, \end{gathered}$$

where $\pi (\tilde{\xi }\mid {\theta }_0,{\mathcal{D}}_n)$ is the marginal posterior of $\tilde{\xi }$ obtained by integrating $\pi (\tilde{\xi },\alpha ,\beta \mid {\theta }_0,{\mathcal{D}}_n)$ over (α, β) under the gamma hyperprior. We denote the random variable [ $U(Y^T,Y^E)\mid c,r,{\theta }_0,{\mathcal{D}}_n$] by U_c,r, = U_c,d,s. Let $u_c^{\max }={\max }_r\{u_{c,r}\}$ be the maximum utility among all considered treatment regimes for subgroup c = 1, … , C, where u_c,r denotes the true mean utility for combination (c, r). The optimal treatment regime for each subgroup c = 1, … , C, is defined as the regime with $u_{c,r}>u_c^{\max }-\underset{¯}{u}$, where u is an indifference margin. In the MM study, we consider u = 5.

The AR procedure of the proposed trial design, which will be given in detail below, depends on the PPD of U_c,r. We define AR with probability of assignment to regime (d, s) within each subgroup c proportional to

$${\omega }_c(d,s)=\mathrm{Pr}\left\{U_{c,d,s}=\underset{d^{\prime }\in \{1,\dots ,D\}}{\max }{U}_{c,d^{\prime },s}\right\}\mathrm{I}\{(d,s)\in {\mathcal{A}}_c\}.$$ (3.2)

In equation (3.2), since U_c,d,s is a random variable, the quantity $\underset{d^{\prime }\in \{1,\dots ,D\}}{\max }$ U_c,d′,s is the maximum among D random variables, and may not equal the maximum utility U(0,1). This equation implies that the AR probability is proportional to the posterior predictive probability of attaining the maximum predicted utility among all admissible dose levels within treatment schedule s, for a future patient. Thus, ω_c(d, s) accounts for both the mean and variation of the utilities from different regimes within the schedule. This PPD-based approach is fundamentally different from the procedures used by Thall and Nguyen (2012), Lee, et al. (2015), and others, where AR probabilities are defined in terms of posterior mean utilities. In the present context, these would be

$$\begin{gathered} u_c(d,s,{\theta }_0,{\mathcal{D}}_n)=E[E\{U(Y^T,Y^E)\mid c,d,s,\tilde{\xi }\}\mid {\theta }_0,{\mathcal{D}}_n] \\ =\sum _{(y^T,y^E)}U(y^T,y^E){\int }_{\tilde{\xi }}f(Y^T=y^T,Y^E=y^E\mid c,d,s,\tilde{\xi })\pi (\tilde{\xi }\mid {\theta }_0,{\mathcal{D}}_n)\mathrm{d}\tilde{\xi }. \end{gathered}$$

AR probabilities ${\omega }_c^{\prime }(d,s)$ among (d, s) pairs for subgroup c then are defined to be proportional to $u_c(d,s,{\theta }_0,{\mathcal{D}}_n)\mathrm{I}\{(d,s)\in {\mathcal{A}}_c\}$.

Compared to the approach of defining AR probabilities ${\omega }_c^{\prime }(d,s)$ based on posterior mean utilities (Thall and Nguyen, 2012; Lee, et al., 2015), the proposed approach of using the PPD of U_c,r to define the AR probabilities ω_c(d, s) leads to a more extensive exploration of the regime space, and thus it addresses the “exploitation versus exploration” problem, which is well known in phase I-II trials (Yuan, Nguyen and Thall (2016), Chapter 2.6) and more generally in sequential analysis (Sutton and Bartow (1998)). This is because the PPD of U_c,r accounts for distributions of future observations. The AR procedure based on the PPD of U_c,r thus tends to have a smaller chance of getting stuck at suboptimal regimes. Since AR treats patients with suboptimal regimes, care must be taken to ensure that its use does not expose patients to unacceptably high risks of high toxicity or low efficacy.

To estimate the optimal subgroup-specific treatment regime that maximizes U(y^T, y^E) across different combinations of (c, r), we divide the trial into two stages. In stage 1, for each subgroup c = 1, … , C, N_1c patients are randomized fairly among the schedules. This is different from standard phase I methods, such as the CRM or EWOC, which use deterministic allocation to treat patients. In the motivating MM study, the toxicity assessment window is 30 days, while efficacy is evaluated much later, at day 90. Thus, toxicity outcomes are observed much sooner than efficacy outcomes, and in stage 1 the data available for making the adaptive decisions are largely toxicity data, with efficacy data collected to facilitate decision making in stage 2. At the end of stage 1, since some previously missing Y^E outcomes may be observed for patients followed to V^E, preliminary estimates of the subgroup-specific optimal regimes can be obtained. For each subgroup c, stage 2 enrolls the remaining N_2c patients with the goal to estimate the globally optimal regime. To achieve this, we propose a procedure that does optimization within schedule, combined with AR across schedules. An optimal dose first is selected within each treatment schedule, and then patients are adaptively randomized among the optimal dose set across schedules. This hybrid approach, of selecting optimal doses and randomizing, balances exploitation versus exploration by allowing sufficient dose exploration (through AR) to reduce the risk of being stuck at suboptimal doses, but also avoids allocating too many patients to suboptimal doses.

Let N^max be the maximum total sample size, and p_c the prevalence of subgroup c = 1, … , C, so ${\sum }_{c=1}^C{p}_c=1$. We bound the maximum sample size $N_c^{\max }$ for subgroup c by p_cN^max. Assume patients are recruited sequentially to each schedule within each subgroup. Let κ be the proportion of patients assigned to each schedule in stage 1, that is, we randomize $\kappa N_c^{\max }$ patients to each schedule in stage 1 for each subgroup. Thus, $N_{1c}=\kappa {\mathit{SN}}_c^{\max }=\kappa {\mathit{Sp}}_c{N}^{\max }$ and $N_{2c}=N_c^{\max }-N_{1c}$. The two-stage trial proceeds as follows.

Stage 1. If the next patient enrolled is in subgroup c,

1.1 Randomly choose a schedule, s, with probability 1/S each.

1.2 If s has never been tested before, then start the subtrial in this schedule at the lowest dose. Otherwise, based on (3.1), determine the admissible set ${\mathcal{A}}_c$ in subgroup c based on the most recent data ${\mathcal{D}}_n$. Subject to the constraint that no untried dose may be skipped when escalating, randomly choose an acceptable dose for the next patient with AR probability proportional to ω_c(d, s), d = 1, … , D. Thus, the AR probability in subgroup c is proportional to the probability that regime (d, s) induces the maximum utility within schedule s, with all (d, s) that are unacceptable in subgroup c given AR probability 0.

1.3 The subtrial for subgroup c is either stopped when the maximum sample size $\kappa N_c^{\max }$ is reached, or terminated early if no dose within this schedule is admissible for subgroup c.

Stage 2. For each newly enrolled patient in subgroup c, first determine the optimal dose $d_c^{\ast }(s)$ that has largest probability of having the maximum utility within each s, i.e., $d_c^{\ast }(s)=\underset{d\in \{1,\dots ,D\}}{\arg \max }\{{\omega }_c(d,s)\}$, s = 1, … , S, where ω_c(d, s) is given by equation (3.2). Then choose the schedule s across schedules with the AR probability proportional to

$${\omega }_c(d_c^{\ast }(s),s)=\mathrm{Pr}\left\{U_{c,d_c^{\ast }(s),s}=\underset{s^{\prime }\in \{1,\dots ,S\}}{\max }{U}_{c,d_c^{\ast }(s^{\prime }),s^{\prime }}\right\}\mathrm{I}\{(d_c^{\ast }(s),s)\in {\mathcal{A}}_c\},s=1,\dots ,S,$$

and assign the new patient dose $d_c^{\ast }(s)$. In other words, in Stage 2, dose first is optimized within each schedule without use of AR, and then AR is applied to randomize patients among doses across all schedules. Repeat this until N_2c patients have been treated in the second stage, and then stop the trial for subgroup c. If no regime is admissible for subgroup c as given by (3.1), then stop the trial in that subgroup.

At the end of the study, based on the complete data ${\mathcal{D}}_{N^{\max }}$, for each subgroup c = 1, … , C, the optimal treatment regime is defined as that with largest probability of having the maximum utility among all regimes, formally $r_c^{\ast }=(d_c^{\ast },s_c^{\ast })=\underset{(d,s)\in {\mathcal{A}}_c}{\arg \max }\mathrm{Pr}\left\{U_{c,d,s}=\underset{(d^{\prime },s^{\prime })}{\max }{U}_{c,d^{\prime },s^{\prime }}\right\}$.

To implement the design in practice, one must prespecify values of the hyperparameters θ₀, the utility function U(y^T, y^E), and the design parameters (N^max, κ, ${\overline{\pi }}^T$, π^E, η^T, η^E). A detailed description of the calibration procedure for the proposed design is provided in Supporting Information.

4. Simulation Study

In this section, we summarize results of a simulation study to investigate the proposed design’s OCs, using the PGF Melphalan trial as a basis for the simulation study design. We consider C = 2 subgroups with equal prevalences p₁ = p₂ = 1/2, assume the toxicity probabilities ${\pi }_{c,r}^T$ are homogeneous across subgroups, but that the efficacy probabilities satisfy ${\pi }_{2,r}^E>{\pi }_{1,r}^E$ for all r = (d, s). We will evaluate sensitivity of the design’s performance to different prevalences. We study D = 3 doses (200, 225, 250 mg/m²) combined with S = 3 infusion schedules, for a total of nine treatment regimes, and 18 different subgroup-specific dose-schedule regime combinations. We assume N^max = 120 patients are accrued, so on average 6.6 patients are allocated to each subgroup-specific dose–schedule regime. This sample size is reasonable, since the maximum sample size using a 3 + 3 design to find an MTD for each of six (c, s) pairs would be similar. Based on preliminary simulations, we take κ = 0.2, leading to N₁₁ + N₁₂ = 72 patients treated in stage 1. When p₁ = p₂ = 1/2, the stage 1 sample size per subgroup is N₁₁ = N₁₂ = 36. Toxicity is monitored during the first V^T = 30 days, and efficacy is evaluated on day V^E = 90. We assume patents are accrued at a rate of 6 per month, arriving according to a Poisson process, so the average inter-arrival time is 5 days. Thus, the expected time to accrue 120 patients is 20 months.

We evaluated the proposed design’s OCs under eight different scenarios, characterized in terms of fixed marginal probabilities of toxicity and efficacy (${\pi }_{c,r}^T$,${\pi }_{c,r}^E$) given in Table 1. The trial data were simulated using (2.1)–(2.2), where we set ${\sigma }_{\xi }^{2,\text{true}}={0.5}^2$, ρ^true = −0.2, ζ^2,true = 0.3². The true values of ${\tilde{\xi }}_{c,r}^{\text{true}}$ were determined by matching ${\pi }_{c,r}^j=1-\Phi (0\mid {\xi }_{c,r}^{j,\text{true}},{\sigma }_{\xi }^{2,\text{true}}+{\zeta }^{2,\text{true}}),j=T,E$. In scenarios 1–6, a regime with an efficacy probability < ${\stackrel{‒}{\pi }}^E=.20$ is considered clinically unimportant, and a toxicity probability > π^T = .15 is considered unsafe. To assess applicability of the design to more general scenarios, regimes with toxicity rate above 30% and an efficacy rate below 30% are considered inadmissible in scenarios 7–8, which are different from the MM trial. The utility function is U(0,1) = 100, U(0, 0) = 60, U(1,1) = 40, U(1, 0) = 0, reflecting the belief that avoiding toxicity is more important than achieving efficacy. The expected utility of each regime under the eight scenarios is displayed in Table 1, and the true optimal treatment regimes are underlined.

Table 1.

True toxicity and efficacy probabilities and utilities (${\pi }_{c,r}^T$, ${\pi }_{c,r}^E$, u_c,r) under eight simulation scenarios, for each dose, schedule, and subgroup. These values for optimal treatment regimes with $u_{c,r}>u_c^{\max }-5$ are underlined, where $u_c^{\max }={\max }_r\{u_{c,r}\}$ is the maximum utility for subgroup c, c = 1, 2. The regimes with a toxicity rate above 15% and, an efficacy rate below 20% are considered inadmissible in scenarios 1–6; The regimes with a toxicity rate above 30% and an efficacy rate below 30% are considered inadmissible in scenarios 7–8.

Scenario		Subgroup 1			Subgroup 2
	s	d=1	d=2	d=3	d=1	d=2	d=3
1	1	(.03,.10,62.2)	(.05,.20,65.0)	(.15,.60,75.0)	(.03,.13,63.4)	(.05,.23,66.2)	(.15,.63,76.2)
	2	(.05,.50,77.0)	(.15,.40,67.0)	(.30,.40,58.0)	(.05,.56,79.4)	(.15,.46,69.4)	(.30,.46,60.4)
	3	(.13,.35,66.2)	(.45,.40,49.0)	(.60,.45,42.0)	(.13,.47,71.0)	(.45,.52,53.8)	(.60,.57,46.8)
2	1	(.10,.30,66.0)	(.27,.40,59.8)	(.55,.50,47.0)	(.10,.40,70.0)	(.27,.50,63.8)	(.55,.60,51.0)
	2	(.25,.25,55.0)	(.30,.30,54.0)	(.40,.40,52.0)	(.25,.35,59.0)	(.30,.40,58.0)	(.40,.50,56.0)
	3	(.08,.15,61.2)	(.12,.35,66.8)	(.25,.35,59.0)	(.08,.25,65.2)	(.12,.45,70.8)	(.25,.45,63.0)
3	1	(.05,.10,61.0)	(.15,.40,67.0)	(.40,.10,40.0)	(.05,.30,69.0)	(.15,.45,69.0)	(.40,.30,48.0)
	2	(.05,.40,73.0)	(.18,.20,57.2)	(.40,.10,40.0)	(.05,.45,75.0)	(.18,.30,61.2)	(.40,.20,44.0)
	3	(.03,.15,64.2)	(.08,.23,64.4)	(.15,.45,69.0)	(.03,.30,70.2)	(.08,.30,67.2)	(.15,.50,71.0)
4	1	(.03,.10,62.2)	(.05,.30,69.0)	(.10,.60,78.0)	(.03,.20,66.2)	(.05,.35,71.0)	(.10,.63,79.2)
	2	(.07,.30,67.8)	(.15,.40,67.0)	(.30,.50,62.0)	(.07,.33,69.0)	(.15,.60,75.0)	(.30,.65,68.0)
	3	(.05,.25,67.0)	(.10,.34,67.6)	(.15,.25,61.0)	(.05,.28,68.2)	(.10,.38,69.2)	(.15,.29,62.6)
5	1	(.05,.10,61.0)	(.12,.25,62.8)	(.20,.33,61.2)	(.05,.15,63.0)	(.12,.30,64.8)	(.20,.38,63.2)
	2	(.07,.05,57.8)	(.13,.45,70.2)	(.25,.30,57.0)	(.07,.20,63.8)	(.13,.50,72.2)	(.25,.40,61.0)
	3	(.02,.23,68.0)	(.05,.15,63.0)	(.08,.10,59.2)	(.02,.28,70.0)	(.05,.45,75.0)	(.08,.28,66.4)
6	1	(.05,.05,59.0)	(.07,.07,58.6)	(.09,.09,58.2)	(.05,.15,63.0)	(.07,.47,74.6)	(.09,.49,74.2)
	2	(.08,.10,59.0)	(.13,.35,66.2)	(.30,.40,58.0)	(.08,.15,61.2)	(.13,.40,68.2)	(.30,.45,60.0)
	3	(.11,.30,65.4)	(.13,.20,60.2)	(.20,.10,52.0)	(.11,.33,66.6)	(.13,.23,61.4)	(.20,.13,53.2)
7	1	(.05,.10,61.0)	(.15,.45,69.0)	(.30,.45,60.0)	(.05,.13,62.2)	(.15,.48,70.2)	(.30,.48,61.2)
	2	(.12,.20,60.8)	(.23,.55,68.2)	(.55,.60,51.0)	(.12,.50,72.8)	(.23,.58,69.4)	(.55,.63,52.2)
	3	(.45,.30,45.0)	(.50,.35,44.0)	(.60,.30,36.0)	(.45,.33,46.2)	(.50,.38,45.2)	(.60,.31,36.4)
8	1	(.05,.10,61.0)	(.10,.20,62.0)	(.15,.50,71.0)	(.05,.15,63.0)	(.10,.25,64.0)	(.15,.53,72.2)
	2	(.10,.15,60.0)	(.25,.15,51.0)	(.40,.15,42.0)	(.10,.20,62.0)	(.25,.20,53.0)	(.40,.20,44.0)
	3	(.07,.25,65.8)	(.08,.25,65.2)	(.18,.25,59.2)	(.07,.25,65.8)	(.08,.30,67.2)	(.18,.60,73.2)

We denote the proposed two-stage design by TD. The design configuration of TD is given in Supporting Information. To show the advantage of borrowing information between subgroups, we compare the TD with a design that conducts a separate trial independently for each subgroup in parallel, with the sample size for subgroup c bounded by p_cN^max, c = 1, … , C. We denote this design by ITD. As a benchmark for comparison, we also implement the complete-data version of the proposed two-stage design, denoted by TD_C, which waits until all toxicity and efficacy outcomes of previously treated patients are completely observed before choosing a regime for the next patient. The TD_C design thus requires repeatedly suspending accrual of new patients prior to each new regime assignment. Therefore, TD_C has a very lengthy trial duration, which is not feasible in practice with late-onset outcomes. To examine the benefit of using the proposed AR probabilities ω_c(d, s), we also include the design using AR probabilities ${\omega }_c^{\prime }(d,s)$ that depends on posterior mean utilities. We denote this design by TD_U. Each design was simulated 1000 times under each scenario.

Table 2 shows the percentages of selecting optimal treatment regimes (OTRs) and the average trial durations of the four designs. In general, the average OTR selection percentages of TD are 71.8 and 74.9 for subgroups 1 and 2, respectively. Since scenarios 7–8 have different definitions of admissible regimes than scenarios 1–6, the desirable performance of TD in scenarios 7–8 also indicates that the proposed TD design is flexible and can be applied to different trial settings. The selection percentage of each regime using TD are given in Table 3. We find that TD is efficient in identifying inadmissible regimes. For example, TD has very small probabilities of selecting the toxic treatment regimes with schedule s = 2 in scenario 2. Similarly, in scenario 8, where the efficacy probabilities of treatment regimes r = (d, 2), d = 1, 2, 3, all are below the lower limit π^E = 0.30, TD is unlikely to select these inefficacious regimes as the OTRs.

Table 2.

Selection percentage for the optimal treatment regime (OTR) within each subgroup, and mean trial durations, for the four designs under the eight scenarios in Table 1. The accrual rate is 6 patients per month.

	Selection percentage of OTR								Trial duration (in months)
	Subgroup 1				Subgroup 2
Scenario	TD	ITD	TDC	TDU	TD	ITD	TDC	TDU	TD	ITD	TDC	TDU
1	88.1	75.4	89.4	88.6	85.0	69.4	89.5	88.8	23.0	26.0	360.0	23.0
2	69.2	58.7	72.4	72.1	67.1	56.2	69.0	70.9	23.1	26.0	360.0	23.0
3	73.7	64.0	74.1	74.7	73.5	62.2	72.6	75.9	23.0	25.9	360.0	23.0
4	60.9	46.1	63.4	47.9	78.4	66.0	79.7	78.0	23.1	26.0	360.0	23.0
5	72.9	70.0	78.9	75.8	85.9	79.0	87.5	86.9	23.0	26.0	360.0	23.0
6	79.8	74.4	78.0	72.9	48.0	59.8	50.8	45.0	23.0	26.0	360.0	23.0
7	82.5	80.9	83.9	72.4	95.6	93.1	96.7	95.3	23.0	26.0	360.0	23.0
8	47.2	35.2	50.9	38.1	65.6	58.6	68.0	54.0	23.0	26.0	360.0	23.0
Average	71.8	63.1	73.9	67.8	74.9	68.0	75.6	74.4	23.0	26.0	360.0	23.0

“TD” is the proposed two-stage trial design; “TD_C” denotes the two-stage trial design based on complete (Y^T, Y^E) data; “TD_U” denotes the two-stage trial design based on AR probabilities ${\omega }_c^{\prime }(d,s)$; “ITD” denotes the independent two-stage design that conducts a separate regime-finding trial for each subgroup.

Table 3.

Regime selection percentage based on the proposed two-stage design under the eight scenarios in Table 1. The accrual rate is 6 patients per month. These values for optimal treatment regimes with $u_{c,r}>u_c^{\max }-5$ are underlined, where $u_c^{\max }={\max }_r\{u_{c,r}\}$ is the maximum utility for subgroup c, c = 1, 2.

Scenario	Schedule/dose	Subgroup 1			Subgroup 2
		1	2	3	1	2	3
1	1	0.0	0.3	38.7	0.1	0.7	33.6
	2	49.4	6.7	0.8	51.4	6.1	0.9
	3	4.0	0.1	0.0	7.1	0.1	0.0
2	1	31.7	11.8	0.3	30.0	13.1	0.2
	2	3.8	0.8	0.6	4.8	1.4	0.2
	3	9.1	37.5	4.4	8.3	37.1	4.9
3	1	1.0	17.3	0.0	3.5	16.6	0.0
	2	56.3	0.7	0.0	49.4	1.4	0.0
	3	3.1	4.2	17.4	5.2	5.0	18.9
4	1	0.1	6.3	60.9	0.9	5.8	56.7
	2	5.8	13.1	3.2	3.9	21.7	3.9
	3	2.7	7.4	0.5	1.8	5.1	0.2
5	1	1.1	8.7	3.1	1.2	5.4	3.2
	2	0.6	57.9	1.6	1.1	50.3	1.8
	3	15.0	11.1	0.9	11.0	24.6	1.4
6	1	0.9	5.2	3.2	0.8	30.6	17.4
	2	2.4	37.1	3.5	1.1	22.6	2.7
	3	42.7	5.0	0.0	22.7	2.1	0.0
7	1	1.1	45.4	4.2	1.0	35.4	2.7
	2	11.2	37.1	0.6	28.9	31.3	0.3
	3	0.4	0.0	0.0	0.4	0.0	0.0
8	1	2.4	7.2	47.2	1.9	5.3	42.3
	2	2.7	0.2	0.0	2.6	0.3	0.0
	3	21.5	11.7	7.1	13.9	10.4	23.3

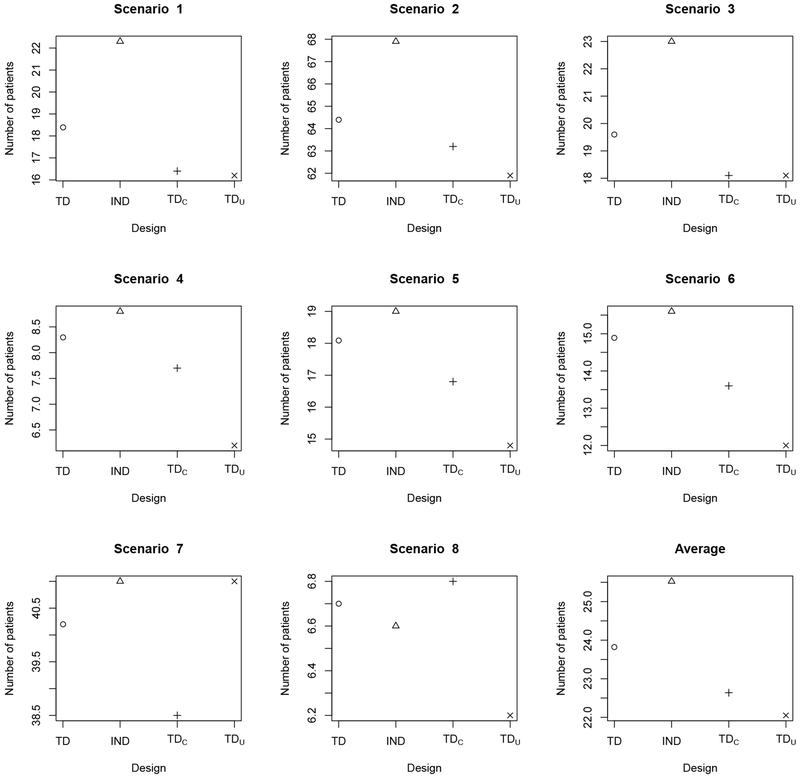
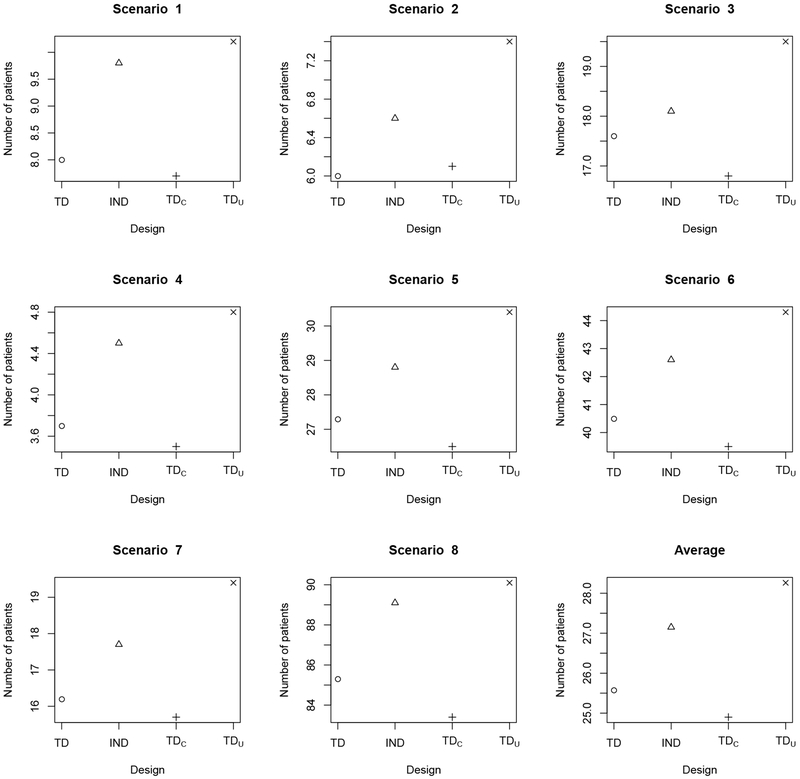
Table 2 shows that the OTR selection percentages of TD are very close to those of TD_C, indicating that TD recovers from efficiency loss due to missing efficacy data early in the trial. Once the missing outcomes are observed, TD efficiently incorporates the new data for subsequent decision making. Since TD_C repeatedly suspends accrual of new patients to wait for full assessments of previously treated patients, on average it would require 360 months to complete a trial with 120 patients. In contrast, TD facilitates real-time decision making with no suspension of accrual, requiring approximately 23 months for the trial, with a negligible drop in OTR selection percentage. Comparing the OTR selection percentages of TD and TD_U in Table 2 shows that, on average, TD performs better than TDu. When there is only one OTR, as in scenarios 4 and 8 for subgroup 1, TD yields approximately 10% higher OTR selection percentages than TD_U, indicating that the use of AR probabilities by TD leads to a more thorough exploration of the treatment regime space. We summarize the total number of patients treated with a toxic regime having true ${\pi }_{c,r}^T>{\stackrel{‒}{\pi }}^T$ in Figure 1, and the total number of patients treated with an inefficacious regime having ${\pi }_{c,r}^E>{\stackrel{‒}{\pi }}^E$ in Figure 2. The results show that, compared to TD_U, TD only exposes 2-3 more patients to overly toxic treatment regimes. For maximum sample size 120 patients, such a risk is generally acceptable. However, because it explores more doses and schedules, TD tends to treat fewer patients at inefficacious regimes than TD_U (See Figure 2).

Figure 1.

Average total number of patients overdosed, i.e. treated with a regime having true ${\pi }_{c,r}^T>{\overline{\pi }}^T=.15$ in scenarios 1–6 and ${\pi }_{c,r}^T>{\overline{\pi }}^T=.30$ in scenarios 7–8, for the TD (circle o), ITD (triangle Δ), TD_C (plus +), and TD_U (cross ×) under the simulation scenarios in Table 1. “TD” is the proposed two-stage trial design; “TD_C” denotes the two-stage trial design based on complete (Y^T, Y^E) data; “TD_U” denotes the two-stage trial design based on AR probabilities ${\omega }_c^{\prime }(d,s)$; “ITD” denotes the independent two-stage design that conducts a separate regime-finding trial for each subgroup.

Figure 2.

Average total number of patients treated with an inefficacious regime having true ${\pi }_{c,r}^E<{\underset{¯}{\pi }}^E=.20$ in scenarios 1–6 and ${\pi }_{c,r}^E>{\underset{¯}{\pi }}^E=.30$ in scenarios 7–8, for the TD (circle ∘), ITD (triangle Δ), TD_C (plus +), and TD_U (cross ×) under the simulation scenarios in Table 1. “TD” is the proposed two-stage trial design; “TD_C” denotes the two-stage trial design based on complete (Y_T, Y^E) data; “TD_U” denotes the two-stage trial design based on AR probabilities ${\omega }_c^{\prime }(d,s)$; “ITD” denotes the independent two-stage design that conducts a separate regime-finding trial for each subgroup.

Table 2 shows the advantage of borrowing information across subgroups, in terms of within-subgroup OTR selection percentage. For nearly all scenarios and subgroups, TD has a larger OTR selection percentage than ITD, with the relative performance between TD and ITD depending on the degree of homogeneity of treatment effects across subgroups. In scenarios 1 and 2, where the locations of the OTRs are the same for the two subgroups, TD greatly outperforms ITD in terms of selection percentages of OTRs, with at least a 10% advantage over ITD for all scenario-subgroup combinations. This is because TD borrows information between subgroups. When the subgroups are relatively homogeneous in terms of treatment effects, TD may be expected to perform better than ITD. In scenarios 3–5, subgroup 2 has one more OTR than subgroup 1, with the remaining OTRs of subgroup 2 the same as those of subgroup 1. In these scenarios, TD again has substantially larger OTR selection percentages than ITD. However, in extremely heterogenous cases, borrowing information may harm TD’s performance. This is shown by scenario 6, where the OTRs are very different for the two subgroups, and the OTR selection percentage in subgroup 2 for TD is less than that of ITD. An advantage of information sharing by the TD method is that, since the toxicity outcomes are assumed to be homogenous, borrowing toxicity information across subgroups helps screen out overly toxic regimes. Since ITD does not borrow information between subgroups, it is more likely to treat patients with overly toxic regimes, illustrated by Figure 1, which gives the total numbers of patients overdosed. Thus, in terms of OTR selection, trial duration, and safety, TD is superior to ITD.

The Supporting Information report extensive sensitivity analyses to examine the OCs of the proposed TD for different maximum sample sizes, N^max. These show that the probability that TD correctly identifies the OTR increases substantially with N^max. For N^max = 300, the average selection percentage of OTR across the eight considered scenarios is as high as 90%. This indicates that the proposed design can recover from situations where it may get stuck early on at suboptimal regimes. We also show that TD is very robust to various subgroup prevalence ratios, patient accrual rates, true underlying models (data generating processes), and prior distributions (with reasonably noninformative priors).

5. Concluding remarks

We have proposed a two-stage phase I-II clinical trial design that does subgroup-specific dose–schedule finding based on a Bayesian hierarchical model, with specific attention to settings where the efficacy outcome is evaluated long after the start of treatment. To accommodate subgroups, the model exploits prior ordering information that the drug should be more effective in one subgroup than the other. The posterior predictive distribution of the utility of each dose-schedule regime is used as a basis for regime selection and adaptive randomization, which is employed to improve reliability. Within-subgroup regime acceptability rules are included for both toxicity and efficacy.

Late-onset outcomes complicate outcome-adaptive trial conduct. We have addressed this problem by using a hybrid two-stage design with adaptive randomization. In stage 1, little efficacy data are available, and mainly toxicity data are utilized for early decision making, primarily to screen out unsafe treatment regimes. When efficacy outcomes of more patients have been assessed in stage 2, efficacy plays a more prominent role in choosing regimes for the remaining patients, and for making final within-subgroup optimal regime selections. Simulations show that the operating characteristics of the proposed design are very similar to those of the benchmark complete-data design, which would require an unrealistically long time to complete the trial. Thus, the proposed design has a minimal loss in efficiency due to accommodating late-onset toxicity/efficacy, while providing a realistic trial duration.