The Cerebral Angiome: High Resolution MicroCT Imaging of the Whole Brain Cerebrovasculature in Female and Male Mice

Abstract

The cerebrovascular system provides crucial functions that maintain metabolic and homeostatic states of the brain. Despite its integral role of supporting cerebral viability, the topologica l organization of these networks remains largely uncharacterized. This void in our knowledge surmises entirely from current technological limitations that prevent the capturing of data through the entire depth of the brain. We report high-resolution reconstruction and analysis of the complete vascular network of the entire brain at the capillary level in adult female and male mice using a vascular corrosion cast procedure. Vascular network analysis of the whole brain revealed sex-related differences of vessel hierarchy. In addition, region-specific network analysis demonstrated different patterns of angioarchitecture between brain subregions and sex. Furthermore, our group is the first to provide a three-dimensional analysis of the complete angioarchitecture and network organization in a single reconstructed data set that encompasses all vessels in the brain of the adult mouse.

Introduction

The cerebral capillary network is the interface between the brain and the periphery and is therefore decisive for adequate delivery of oxygen and nutrients to the brain. Understanding capillary network topology and the angioarchitecture of the conduit vessels that move blood through capillaries is of paramount importance to understand the metabolic activity and function of the nervous system. Despite its unique positioning as the nexus for advancement in a number of fields, a complete description of the topological basis of the cerebral angioarchitecture has not been obtained.

The microvasculature, consisting of the smallest capillaries, has proven hard to image (2, 3). Traditional imaging methods such as ultrasound and magnetic resonance angiography do not have a resolution that is high enough to detect the microvasculature (4–6). Confocal single-photon and two-photon imaging can provide the resolution needed but have depth limitations (7). To resolve the resolution and depth problems, micro-CT imaging, with contrast, can be used. Contrast agents that fill the vessels have made it possible to capture the vasculature in whole organs in 3-D and the same is true for the brain (8–11).

In the present study, we develop three-dimensional data sets of the complete cerebrovascular network of the entire brain from nine mice and evaluate the angioarchitecture at the macro- and microscopic level in female and male mice. The present research describes an angiome of the cerebrovasculature of the entire brain. The overarching goals of the following analyses were to characterize the geometry, topology, and complexity of the cerebrovasculature of the entire brain, then to focus on region specific angioarchitecture in the primary somatosensory cortex, and to compare cerebrovascular topology between sexes. Each of these overarching goals are divided into three phases: the first phase provides global metrics of the angioarchitecture, the second phase characterizes the angioarchitecture by mapping network topology and generating morphometric descriptions of deconstructed network components, and the final phase focuses on network connectivity and the covariance of morphometry and frequency within the population of network components.

Our group is the first to provide an analysis of the complete angioarchitecture and network organization in a single three-dimensional reconstructed data set that encompasses all vessels in the brain of the adult female and male mouse. Our study provides fundamental insight into the cerebral angioarchitecture of female and male mice and describes sexually dimorphic organization that may be of broad interest to the scientific community.

Results

Vascular corrosion casts made by transcardial perfusion of a polyurethane resin (VasQtec, PU4ii) created a structurally precise and highly detailed replica of the complete cerebrovascular network of the entire brain in 3-month female and male mice. The creation of all vascular corrosion casts were performed within procedural parameters that preserved the native size and morphology of blood vessels. Female and male mice that were used in this study were 3.0 – 3.1 months of age, weighed an average of 30 ± 2 grams, and had an average body temperature of 36 ± 0.4 C °. In addition, mice that were used had systolic (164 ± 0.3), diastolic (139 ± 2), and a mean (147 ± 1) arterial pressures that were within the physiological range (12, 13). The duration for producing a single corrosion cast averaged 10-days. The casting procedure occurred in three phases: perfusion, cast processing, and tomographic imaging (Supplemental Figure 1A, C and E). Expectedly, perfusion parameters proved to be most influential to the overall quality of the cast. In our experience, the use of dialysis pumps were most detrimental to the outcome of the cast that seemed to result in “patchy” perfusion of the resin that was observable over the cortex. More so, the use of dialys is pumps usually caused vessel ruptures. We interpret these observations to suggest that the dialys is pump exerts an incompatible perfusion pressure at relatively low flow rate due to the viscosity of the casting resin and its characteristic resistance to flow through the vasculature. To overcome this issue, we found that using a pressurized pump at 160mmHg produced consistent high-quality casts (Supplemental Figure 1B). Noteworthy, we noticed that “good” casts could be predicted and easily observed by the perfusion of several peripheral tissues. First and most simple to observe is the dermis over the premaxilla. A good perfusion resulted in an intense coloration of the dermis to the specific pigment used in the resin composition. A “good” quality cast will often produce a homogenous hue of the skeletal muscles throughout the entire mouse body. However, we found that the perfusion of the liver is most accurately representative of the overall quality of the cerebrovascular cast. This is likely due to the unique physiology of the hepatic vasculature and its sensitivity to systemic perfusion pressure, where it required venous perfusion pressure to drive blood through hepatic circulation then communicate it to the inferior vena cava. Since the hepatic venous system is more extensive than its arterial system, the hepatic tissue will not develop a hue specific to the resin pigment if insufficient systemic perfusion pressure occurs. Additionally, if an excess of perfusion pressure is reached, the liver noticeably swells and at a certain threshold will cause hepatic vessels to rupture that can be seen by non-aided observation. Complete perfusion of the cerebrovasculature by the polyurethane resin was visually apparent in that the casting material entered the venous sinus system by traversing through the arterial network (Supplemental Figure 1C).

Several days are required for the complete hardening of the cast resin. Removal of the casted brain from the skull is a crucial procedure that requires greater care to prevent damage to the casted vasculature or compromise of its native angioarchitecture. Decalcification of the skull with 8% formic acid aids in the opening of the skull followed by 8% potassium hydroxide to de-stabilize the tough extracellular matrix of the skull and meninges (Supplemental Figure 1D). Adequate decalcification and maceration of the skull and meninges is decisive of the recovery of the superior sagittal sinus, transverse sinuses, and inferior cerebral veins. These sinus structures are attached to the meningeal membrane and can easily be broken from the cerebrovasculature when removing the skull. Incidentally, perfusion of the delicate sinus structures are indicative of a complete perfusion of the cerebrovasculature. Specifically, resin that enters the sinus supply must be communicated through the arterial supply indicating transit through the capillary network. If capillary perfusion pressure is not achieved, the casting resin will not transit through the capillary network and will not reach sinus supply. Additionally, evidence of failure to reach capillary perfusion pressure is the observation of casting material in the circle of Willis and the major arteries of the brain while observing an absence of resin at the sinuses and homogenous brain pigmentation. Under 40X magnification, penetrating arterioles and venioles were easily observed confirming complete transit through the vessel hierarchy (Supplemental Figure 1E). Our experience has taught us that it is imperative that the perfusion needle not to perforate into the right ventricle during the perfusion procedure. Perforation of the cardiac septum will allow resin to bypass arterial circulation and compromise perfusion pressure. Virtually, every instance of this resulted in poor quality of the vascular corrosion casts.

Vascular Network Reconstruction

Completed casts were mounted on Plexiglas pedestals with cyanoacrylate adhesive for tomographic imaging (Supplemental Figure 1F). CT imaging routinely produced 4032 Bitmap images with dimensions of 4032 x 2686 pixels that encompassed the complete cerebrovasculature of an entire brain at a voxel size of 2 x 2 x 2 μm encompassing 43.65 gigavoxels (Supplemental Figure 1G). Each data set was coregistered by the alignment of a combination of vascular landmarks and major subregions of the brain. The image quality produced by our reported image acquisition routine was superior; having essentially no signal-noise, imaging artifacts or intens ity variations that are commonly encountered in fluorescence based imaging paradigms. Additiona l ly, neither the loss or resolution nor the dissipation of signal intensity occurred to the internal structures of the brain, indicating that our acquisition routine achieved accurate and complete image collection of the vasculature through the entire thickness of the brain. With these data sets, we were able to reconstruct in three-dimensions the entire cerebrovasculature at one time, allowing for the rotation, inspection and clipping through the entire volume of the brain (Figure 1A). By general inspection of these reconstructed data sets, major subregions of the brain can clearly be identified by the changes in vessel density, hierarchy and organization (Figure 1A, panel 1–4). Reconstructed data sets in three-dimensions resulted in an anticipated organization of the cerebrovasculature. Briefly, the superior sagittal sinus and its neighboring pial vessels covering the surface of the cortex, the cirle of Willis and its emanating major cerebral arteries (Figure 1B), hippocampal vascular networks in the characteristic hippocampal organization (Figure 1A, panel 2), the choroid plexus on the floor of the lateral ventricles (Figure 1A, panel 4), and the caudal rhinal vein (Figure 1C) can be identified.

Figure 1: Three-dimensional reconstruction of the complete cerebrovascular network of the entire adult mouse brain.

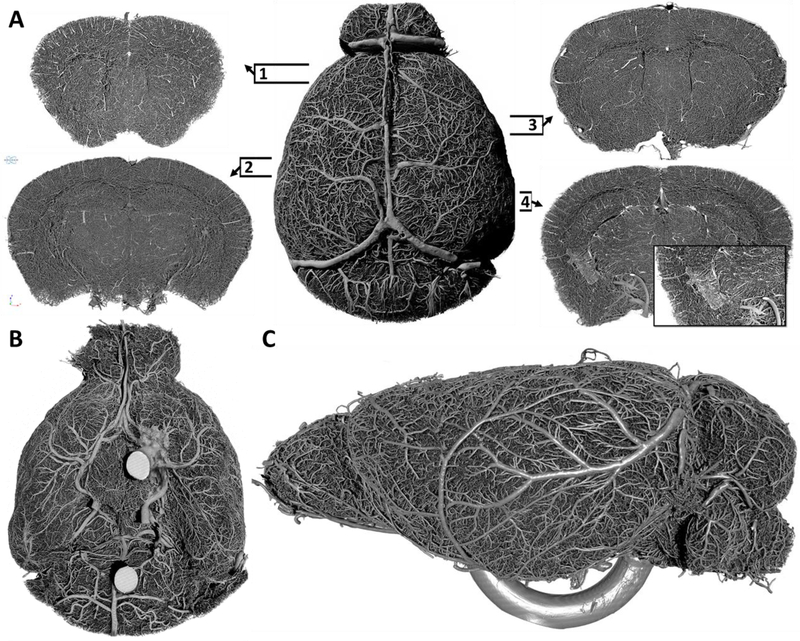
(A) Dorsal perspective of the whole brain vasculature (center) and selected 1 mm thick coronal slices of the volumetric image set to demonstrate the acquisition of imaging data through the entire thickness of the brain and to illustrate the profound density of vessels and the complexity of network connectivity at various brain subregions (1–4). Insert panel in slice four depicts the choroid plexus on the floor of the lateral ventricle. Numbered frames indicate the relative anterior-posterior position of each coronal slice. (B) Ventral perspective of the cerebrovasculature depicting the circle of Willis and the corresponding vascular network. (C) Lateral perspective of the cerebrovasculature depicting surface arterial and venous networks. (Panel B; intense circular structures, panel C; ventral U shaped structure = mount platform for cast).

Structure diameter maps were created for each data set allowing us to color code the hierarchy of vessels based on vessel diameter (Figure 2). Color coded images can be used to aid in navigating through the cerebrovasculature allowing a more intuitive positioning of volume of interest (VOI) boundaries for region specific analyses. Figure 3A depicts a reconstructed data set of the whole brain cerebrovasculature, color-coded to vessel diameter. Figure 3B depicts a digita lly isolated VOI of the prefrontal cortex rotated to an anterior perspective, posterior perspective, and a toggled inward view. Figure 3C depicts a 500 μm thick coronal slice of a brain hemisphere followed by sequential VOI selection and depiction of the primary somatosensory cortex, demonstrating the density of the vasculature and information encompassed by the data set. These data demonstrate the profound interconnectedness of the vasculature and its resulting emergence.

Figure 2: Whole brain vascular network segmentation and color-coding by vessel hierarchy demonstrates the distribution and frequency of vessels.

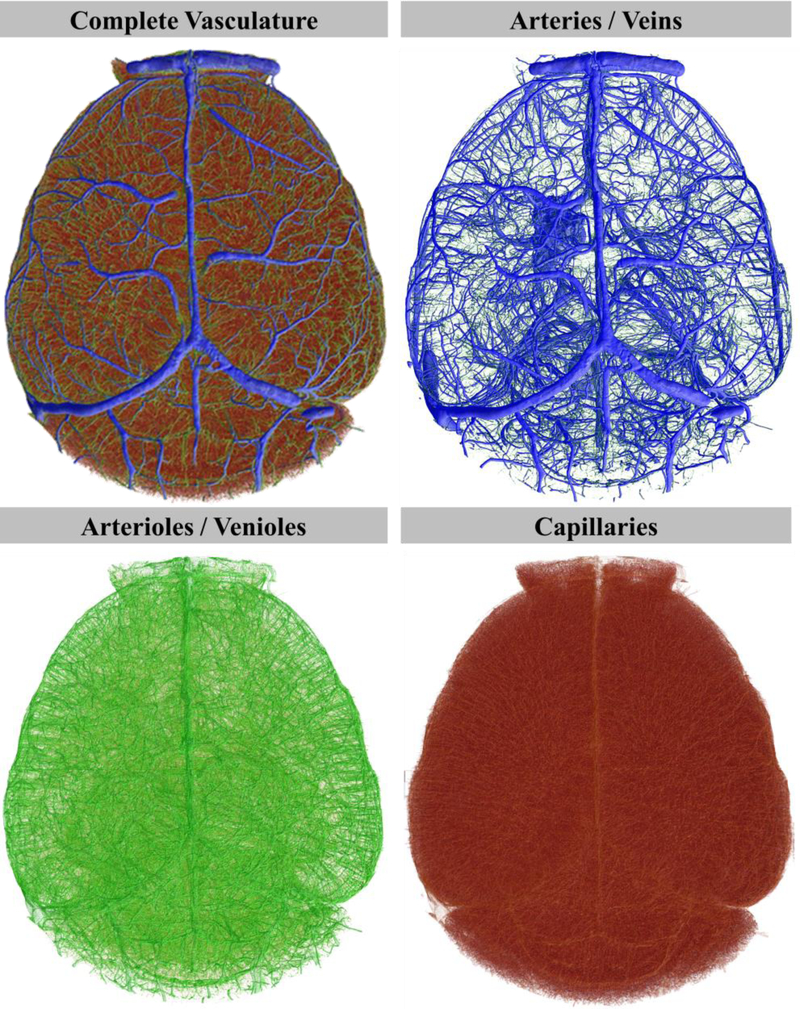
Whole brain volumetric data set produced from a female mouse used to create a vessel thickness map to color-code vessels by hierarchy. Hierarchical classified vessels were migrated to hierarchy-specific volumetric data sets.

Figure 3: Large-scale volumetric data collection of the complete and intact cerebrovascular network at exceptional quality and resolution for microvascular network analysis.

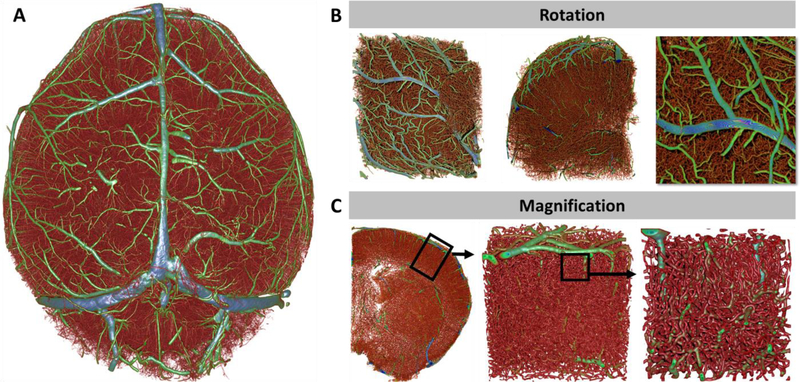
(A) Reconstructed whole-brain data set of the cerebrovasculature color-coded to vessel diameter. (B) Rotated sub-block of the right frontal pole to demonstrate the absence of morphological distortions that can be caused by aberrations of signal intensity. (C) Sequential magnification of the primary somatosensory cortex from a whole brain data set demonstrating the throughput and resolution of the collected data and depict microvascular networks that do not contain gaps or “missing” segment components that are often produced by confocal microscopy. Color-coded vessels from red (small) to blue (large).

Whole Brain Analysis of the Angioarchitecture Demonstrate a Multitude of Vessels that are Morphometrically Similar between the Sexes

For whole brain vascular analysis (Figure 4, table), vessels were automatically identified and segmented by thresholding using the Ridler-Calvard method (14). ROIs were created using a shrink-wrap routine that stretched over holes with a diameter of up to 30 pixels. Two exceptions for a completely automated analysis, before automatic thresholding, the mean gray value of the data sets were manually derived and normalized to a value of 95 by global multiplication of pixel intensity.

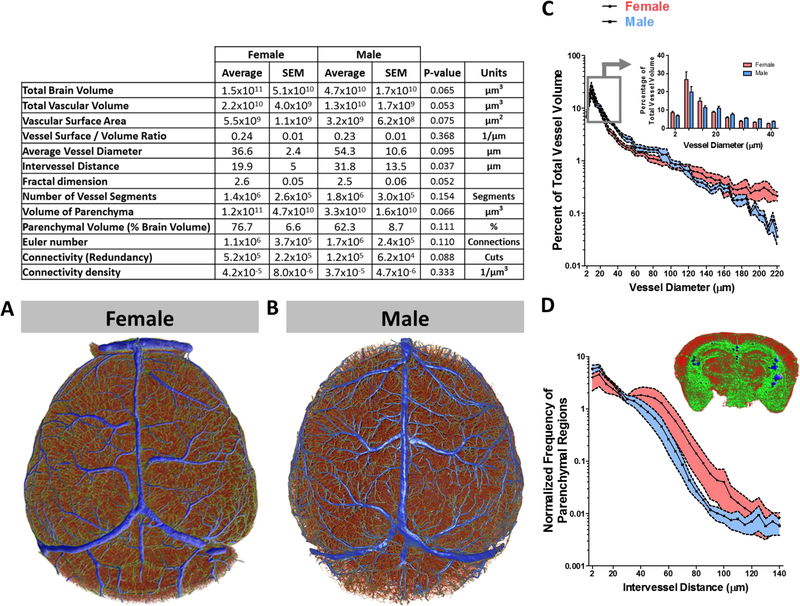
Figure 4: Topological analysis of the cerebrovasculature of the entire brain describes a sex-specific distribution of vessel frequency that is associated with vessel diameter and the frequency of parenchymal regions with intervessel distance.

Complete cerebrovasculature reconstructed, parameterized (table), and color-coded by vessel diameter from (A) female and (B) male mice. (C) Line plot (mean ± SEM) as a function of vessel diameter and the percentage of total vessel volume from female (red, n = 5) and male (blue, n = 4) mice. The grouped bar graph inset depicts expanded data denoted by the box and arrow insert. (D) Line plot (mean ± SEM) as a function of intervessel distance and normalized frequency of parenchymal regions from female (red, n = 5) and male (blue, n = 4) mice. The inset is a three-dimensional reconstructed coronal slab of the parenchyma that is color-coded from small (red) to large (blue) intervessel distance. To compare means, 2-way ANOVA with Bonferroni multiple comparison analysis was used (**, p < 0.01; ***, p < 0.001).

Whole brain vascular analysis demonstrated a broad range of vessel diameters ranging from 2 – 220 μm, with a mean diameter of 36.6 ± 2.4 and 54.3 ± 10.6 μm for female and male mice, respectively. The data revealed that the complete cerebrovascular network is composed of 1.4×10⁶ ± 2.6×10⁵ and 1.8×10⁶ ± 3.0×10⁵ vessel segments for female and male mice, respectively. The average intervessel distance in three-dimensions was 20 ± 5 μm in females and 32 ± 13 μm in males (p = 0.037). Total volume of vessels in the female brain was 2.2×10¹⁰ ± 4.0×10⁹ μm³ and in males was 1.3×10¹⁰ ± 1.7×10⁹ μm³ (p = 0.053). The total volume of the brain parenchyma in microns cubed was 1.5×10¹¹ ± 5.1×10¹⁰ for females and 4.7×10¹⁰ ± 1.7×10¹⁰ for males (p = 0.065).

Although whole brain global-averages of the angioarchitecture in female and male mice appeared somewhat statistically indistinct from one another, specific differences at the level of vessel hierarchy may exist. We used the vessel thickness maps of the entire brain to classify vessels and analyzed vascular volume as a function of vessel diameter to provide a distribution of vessel species relative to the total mass of vessels per brain in female and male mice (Figure 4A and B).

We observed sex-related differences in the distribution of vessels of particular sizes with relatively low intra-group variability. Females appear to have a larger proportion of vessels ranging from 2 – 15 μm (p = 0.08) in diameter, representing roughly 50 ± 6 % of vessels with diameters falling within this range, whereas in males this size accounted for 40 ± 3 %. Males were found to have a greater population of vessels with diameters larger than 15 μm (p = 0.01), having 49 ± 3 % of vessels with diameters falling within 20 – 80 μm in diameter. In females, only 36 ± 3 % of vessels within this range (Figure 4C).

Capillaries form networks varying in density that are acutely tailored to the specific metabolic requirements of the surrounding tissue. The plasticity of capillary formation and regression is crucial for dynamically active cells, such as neurons, where during periods of elevated activity they require capillaries to be closer and more numerous. Capillaries and other small vessels were more numerous in female than in male mice (Figure 4C). Because the density of capillary networks is influenced by localized neuronal activity, and the need to meet metabolic demand, we next asked whether there are sex-related differences in the distance between vessels and by extension the distance between cells of the parenchyma and the nearest vessel. To examine this possibility, we analyzed the distance between vessels in three-dimensions by measuring the radius of the largest sphere that fits between vessels (Figure 4D, insert). The radius of the sphere represents the maximum distance of any given cell in a particular parenchymal space is to the nearest vessel. A map of the distribution of parenchymal spaces as a function of maximum distance to the nearest vessel revealed a larger number of parenchymal spaces with shorter distances in male rather than female mice (Figure 4D).

Capillary networks form the interface for the exchange of molecules to and from the brain parenchyma and peripheral circulation. The total surface area of these capillaries is influential to the extent to which exchange can occur at the blood-brain barrier interface. To gauge the magnitude of this interface, we calculated the parenchymal volume to surface area ratio of capillaries. We found that the capillary surface area to tissue volume ratio of the whole brain to be 17.8 ± 3.2 mm² of capillary surface to every mm³ of brain tissue. Our estimate was in agreement with previous literature reporting the surface area of the blood-brain barrier in mice (15) and in humans (16, 17) to be in range of 9–17 mm² of capillary surface per mm³ of brain tissue.

Whole Brain Analysis of the Vascular Network Topology Reveal an Array of Profoundly Interconnected Vessels

We then examined the network properties of the whole brain vasculature. Consistent with the literature (18, 19), we observed a large prevalence of redundant pathways that formed a highly interconnected network. To measure the geometric connectedness of the network, we used an algorithm to calculate the Euler number and connectivity value of the network in three-dimensions. The Euler number takes into account three classes of events to estimate the total number of connections: islands, bridges, and holes. The connectivity number in a multiply connected network such as capillaries is topologically defined as the maximum number of cuts in the network that could be made without separating the network into two isolated networks (20). Geometric analysis of the complete network revealed an Euler number of 1.1×10⁶ ± 3.7×10⁵ connections in females and 1.7×10⁶ ± 2.4×10⁵ connections in males. The connectivity value revealed 5.2×10⁵ ± 2.2×10⁵ and 1.2×10⁵ ± 6.2×10⁴ number of cuts to the network before splitting into two isolated networks in female and male mice, respectively. Network complexity was measured using Kolmogorov box counting method for fractal dimensions and revealed a fractal dimension of 2.6 ± 0.05 and 2.5 ± 0.06 for female and male mice, respectively.

Region of Interest Acquisition and Preprocessing

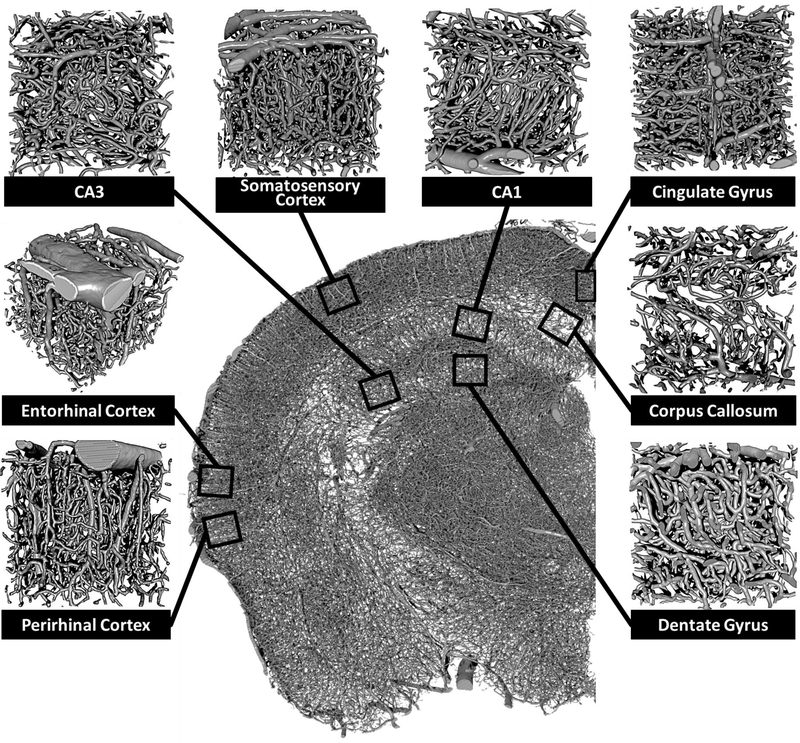
To perform subregion specific vascular analyses, VOIs were digitally dissected from the whole brain data set. Positioning of VOIs was guided by the Allen Mouse Brain Atlas (21) and co-registered to landmarks comprised of arterial branching and positioning. Briefly, the medial orbital prefrontal cortex, cingulate gyrus, somatosensory cortex, corpus callosum, perirhinal cortex, and entorhinal cortex were isolated from the whole brain data sets (Figure 5). To increase the accuracy of the tracing process of the vessel network, the data sets containing the VOIs were optimized by inserting the centerlines of the vessels onto each z-plane of the same data set (Supplemental Figure 2).

Figure 5: Identification and localization of brain subregions for morphometric analysis of the angioarchitecture.

Three-dimensional reconstructed coronal slice of a single hemisphere with overlay box-and-stem insert demarcating the relative location of isolated perirhinal cortex, entorhinal cortex, CA3, somatosensory cortex, CA1, cingulate gyrus, corpus callosum, and dentate gyrus subregion. Subregion-specific vascular data sets were collected in 500 x 500 x 500 um selections.

Region Specific Analysis of the Angioarchitecture Demonstrate a Highly Organized and Emergent Pattern

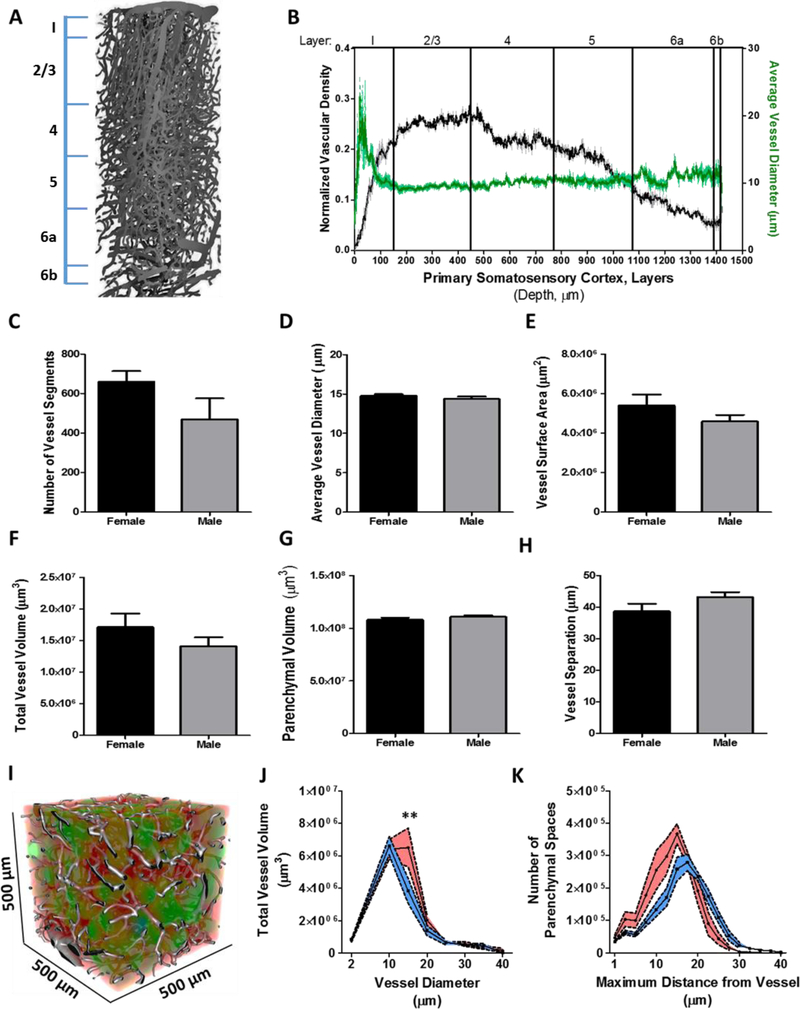
Previous literature has demonstrated that in mice the primary somatosensory cortex receives the greatest vascular density compared to other brain regions (7). In addition, there is a growing interest in understanding the neurovascular coupling involved in nuclear imaging and its relationship with blood-oxygen-dependent (BOLD) signal and neuronal activation (22, 23). Literature focused on the structural relationship of vascular networks in the somatosensory cortex (vS1) barrel field suggests that angioarchitecture of these networks are innately adapted to the topology of tissue (7) and functional modules of the cortical columns in the vS1 barrel field (1). We first assessed the angioarchitecture of the primary somatosensory cortex by global morphometric analysis in female (n = 5) and male mice (n = 5, data set = 500 μm³). Vessel density varied as a function of depth through the layers of the primary somatosensory cortex (Figure 6A). The greatest vascular density was found in cortical layer 2/3 and the lowest density in layer 6b (Figure 6B). The largest average vessel diameter was observed on the cortical surface and then remained constant throughout the depth of the cortex (Figure 6B). Morphometric and geometric analysis of the vascular network revealed modest sex-related differences in 3-month old mice (Figure 6C-K). Vascular analysis was performed on 660 ± 54 and 468 ± 107 vessel segments in female and male mice, respectively (Figure 6C). The calculated average over all vessel segments in the vS1 identified the average vessel diameter to be 14.76 ± 0.22 μm in females and 14.37 ± 0.31 μm in males (Figure 6D). Total vascular surface area was 5.3×10⁶ ± 5.5×10⁵ and 4.5×10⁶ ± 3.3×10⁵ μm² for female and male mice, respectively (Figure 6E). Vessels occupied a total volume of 1.7×10⁷ ± 2.1×10⁶ and 1.4×10⁷ ± 1.4×10⁶ μm³ in female and male mice, respectively (Figure 6F). Whereas, parenchymal volume was observed at 1.0×10⁸ ± 2.1×10⁶ and 1.1×10⁸ ± 1.4×10⁶ μm³ in female and male mice, respectively (Figure 6G). Comparable to the literature (7, 8, 23), we observed an average distance between vessels in the somatosensory cortex to be 38.6 ± 2.4 μm in females and 43.1 ± 1.5 μm in males (p = 0.10) (Figure 6H). Similar to the average intervessel distance of the whole brain, female rather than in male, demonstrated smaller distance between vessels.

Figure 6: The primary somatosensory cortex demonstrates a topological distinct vascular network.

(A) Reconstructed vascular network through the entire depth of the somatosensory cortex (500 x 500 x 1450 um) from a female mouse. Line insert demarcates the boundaries of the cortical layers. (B) Line graph (mean ± SEM) as a function of cortical depth and normalized vascular density (black, n = 3) or average vessel diameter (green, n = 3). Bar graph(s) (mean ± SEM) illustrating the (C) number of vessel segments, (D) average vessel diameter, (E) vessel surface area, (F) total vessel volume, (G) parenchyma l volume, and (H) vessel separation from female (n = 5) and male (n = 4) mice. (I) Reconstructed volumet r ic data set containing the vasculature from the primary somatosensory cortex merged with the parenchyma l image series color-coded to the distance between vessels. Line graph(s) (mean ± SEM) as a function of (J) vessel diameter with total vessel volume and (K) maximum distance from vessel with the number of parenchymal spaces. Statistical comparison was performed by 2-way ANOVA and Bonferroni post hoc test to compare the means (**, p < 0.01).

We next extrapolated on the global calculations of total vascular volume and parenchymal volume by mapping the distribution of vessel and parenchymal space diameter as a function of total volume (Figure 6I). We found that female relative to male mice had a greater volume of vessels with a diameter of 15 μm, occupying a volume of 6.5×10⁶ ± 1.2×10⁶ and 3.8×10⁶ ± 7.7×10⁵ μm³ (p < 0.01) in female and male mice, respectively (Figure 6J). However, when these values were normalized to the percentage of total vascular volume, female mice have greater proportional volume of vessels with diameters that range 5 – 10 μm than male mice (p < 0.001). We then examined parenchymal separation volume to estimate vascularization of the primary somatosensory cortex. To assess somatosensory cortex vascularization, we mapped the distribution of parenchymal separation in three-dimensions as the maximum diameter of an inscribed sphere per parenchymal area as a function of total volume (Figure 6I). Our parenchymal separation analysis revealed a slightly larger total volume of parenchymal spaces with diameters that ranged from 10 – 30 μm in females compared to males (Figure 6K). In contrast, males demonstrated a larger total volume of parenchyma l separation with diameters ranging 40 – 55 μm. Although the distribution of areal parenchyma l diameter as a function of cumulative volume provides an adequate description of the topologica l composition of the parenchyma that touches on the variation of parenchymal compartmentalization, a more direct assessment of the variation of minimum-distances of parenchymal cells to neighboring vessels is needed. We resolved this by examining the average minimum distance within a parenchymal volume and repeated this for all parenchymal zones. Our analysis revealed a heterotypic distribution of shortest distances between female and male mice. Female mice were found to have a greater number of parenchymal zones with smaller average minimum distances than male mice. Specifically, female mice demonstrated 3.2×10⁴ ± 6.5×10³ parenchymal zones with an average minimum distance below 15 μm, whereas male mice contained 2.4×10⁴ ± 2.7×10³ parenchymal zones with distances below 15 μm. Furthermore, parenchymal zones with an average minimum distances of 15 μm showed the largest discrepancy (p = 0.04) between female (3.6×10⁵ ± 3.0×10⁴) and male (2.5×10⁵ ± 3.6×10⁴) mice and accounted for the majority of all parenchyma l zones in both male and female mice (Figure 6K). Our estimates are in agreement with the predictions reported in the literature (7).

Region Specific Analysis of the Vascular Network Topology Reveal a Conserved Network Organization and Connectivity that Covaried with Vessel Hierarchy

The vascular network is highly interconnected and may asymmetrically form connections based on vessel hierarchy and diameter (Figure 7A). We would expect the vascular network to have asymmetric connectivity with a greater number of junction points at the capillary level due to their physiological relevance of distributing the flow of blood. As such, a penetrating arteriole can have a number of branch points along its length whereas capillaries branch at their distal segment (Figure 7B). In contrast, a network with symmetric connectivity should demonstrate a constant value of junctions across varying segment diameters (symmetric distribution). To determine whether the vascular network has asymmetric connectivity, we calculated the number of branch points as a function of parent vessel diameter (26,435 branch points across 7 mice) (Figure 7C). We then compared this to the estimated symmetric distribution of branch points and found that all vessels statistically differed from a symmetric distribution (p < 0.001) except for vessels with diameters of 3 and 7 μm (Figure 7D). We next compared the total number of branch points per average vessel diameter across all other average diameters to determine whether a hierarchy or characteristic vessel diameter forms proportionally greater number of interconnections. We found that vessels with diameters of 4 and 6 μm represented 57 ± 1.5 % of the total population of vessel-vessel connections. Specifically, 21.5 ± 2.2 % (p < 0.0002) and 35.5 ± 1.9 (p < 0.001) % of all vessel junction points were found on vessels with diameters of 4 and 6 μm, respectively. This observation agrees with our prediction that the vascular network of the primary somatosensory cortex has asymmetric connectivity where capillaries are the primary vessel hierarchy that bridge together to form networks. Additionally, our data imply that among capillaries there is an asymmetric distribution of connections that interacts with specific capillary caliber preferential to diameters of 4 and 6 μm (p = 0.000005). We next compared the distribution of branch points by parent vessel diameter across sexes to uncover any sex specific differences in network connectivity. We first compared the total number of branch points over all vessel diameters in the primary somatosensory cortex and found no statistical difference across sex (Figure 7E). Thus, we then hypothesized that between male and female mice there would be no difference in network connectivity in relation to vessel diameter and number of branch points. Our null hypothesis is that there are sex-dependent differences in network connectivity that are related to network component diameter. To assess this we used an equivalence test to determine if the overall distribution of branch points across vessel diameters were similar between the female and male mice and found statistically significant similarity with 95% confidence that the distributions were equivalent (Pearson R = 0.95; p < 0.0001; R² = 0.91). Although we found the overall distribution to be equivalent between female and male mice, we next asked whether the magnitude of network connectivity preferentia l to 4 and 6 μm vessels were similar. This was determined via multiple comparison analysis using a 2-way ANOVA and a Bonferroni post hoc test for level of significance and found that females (1835 ± 490) over males (1082 ± 102) demonstrated a greater number of branch points for vessels with an average diameter of 6 μm (p < 0.01; Figure 7F). These data indicate that in mice regardless of sex, the composition of the vascular network follows a conserved organization of connectivity in respect to capillary diameter. Furthermore, our finding that female mice have a greater number of branch points from vessels with 6 μm diameters suggests that the differences in whole brain angioarchitecture between the sexes were influenced primarily by an elevated number of capillaries with 6 μm diameters.

Figure 7: Vascular network connectivity analysis in the primary somatosensory cortex indicates a preference for interconnections to specific vessel hierarchy.

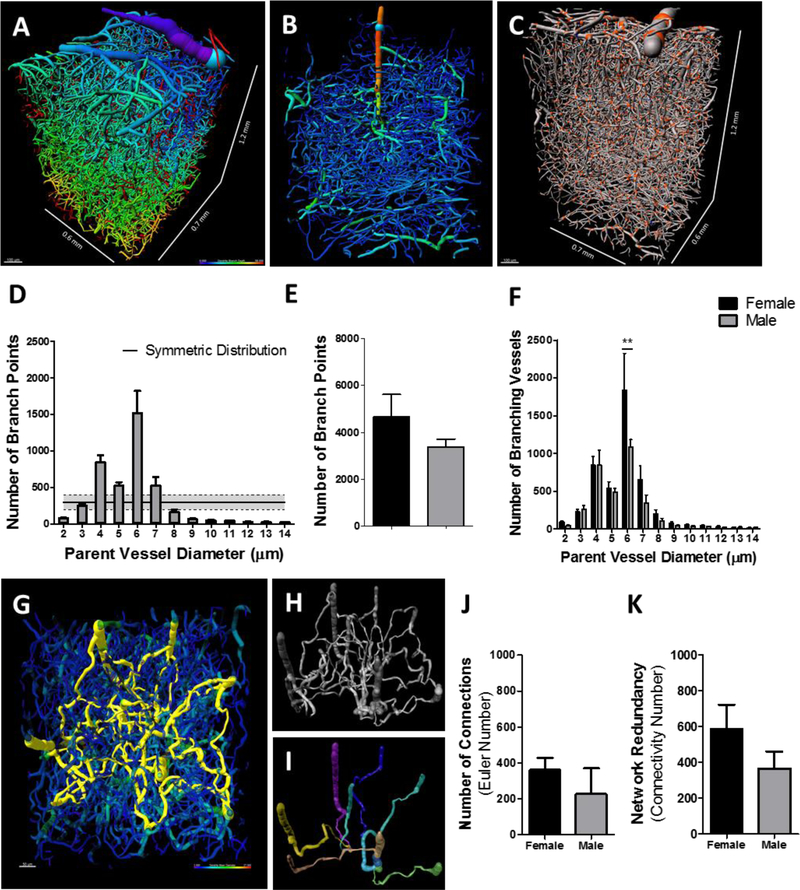
Vascular network through the depth of the somatosensory cortex (A, C) and single penetrating arteriole (B), color-coded to cortical depth (A), vessel diameter (B), and demarcated branch points (C, orange spheres). Bar graph(s) (mean ± SEM) depicting parent vessel diameter as a function to number of branch points (D), total number of branch points (E), and parent vessel diameter as a function to number of branching vessels (F) in female (n = 5) and male (n = 4) mice. Dorsal perspective of a vascular network depicting the shortest pathways of each vessel to all other vessels (yellow) (G). Non-connected vessels segments are colored green and blue. Representative image of the extracted shortest pathways between vessels predicts the network at its most rudimentary form (H). Depiction of the shortest pathways of each arteriole (green, cyan, blue, magenta, yellow, brown) to a veniole (beige), demonstrating the most effective pathway for blood to transit through penetrat ing arterioles and feed into venioles (I). Bar graph(s) (mean ± SEM) demonstrating the number of vessel-to-vessel connections (J) and network redundancy (K) from female and male mice. To compare means, 2-way ANOVA with Bonferroni multiple comparison analysis was used (**, p < 0.01).

Penetrating arterioles deliver blood to subsurface microvascular networks, which drain into the penetrating venioles. There are no pathways to transit blood out of the brain that bypass the capillary network. Arteriovenous anastomoses that form in the brain that are pathological in nature confound the perfusion of blood into capillary beds by rerouting blood flow through a malformed arteriole that feeds blood directly into the corresponding veniole. In a healthy brain, there are a profound number of pathways for blood flow to reach the nearest veniole (Figure 7G). Blood flow can be regulated by modulating the resistance of these pathways individually to redistribute blood by shunting blood flow away or toward specific areas. The capillary angioarchitecture provides redundant pathways for the delivery of blood from any arteriole (Figure 7H). This network redundancy provides multiple direct pathways for blood to transit into and out of a given region (Figure 7I).

To quantify the number of connections within the local vascular network of the primary somatosensory cortex, we used an algorithm to calculate the Euler number and connectivity value of the three-dimensional vascular network and found an average of 310 ± 66 connections in female and male mice together. A comparison of the number of connections in the primary somatosensory cortex in female and male mice revealed 361 ± 67 and 226 ± 142 connections (p = 0.18) in females and males, respectively (Figure 7J). We next measured the redundancy of the vascular network by using an algorithm that randomly cuts the network repeatedly until the network splits into two isolated components. We found that the vascular network of the primary somatosensory cortex could receive 504 ± 95 cuts before breaking apart, regardless of sex. Specifically, our analysis revealed as many as 587 ± 134 and 366 ± 95 cuts to the vascular network of the primary somatosensory cortex before splitting into two isolated networks in female and male mice (p = 0.14), respectively (Figure 7K). These findings demonstrate that the vascular network of the primary somatosensory cortex are profoundly interconnected forming as many as 310 connections able to withstand the removal of 503 segments before network breakdown. Moreover, these observations imply that there is no difference in the interconnectedness of the vasculature between female and male mice.

Sex Differences in Intragroup Interregional Angioarchitecture

Within the brain, there exist subregion-dependent differences in vascular network organization and density. The specific architecture of the vascular network is closely tied to the local metabolic demand. As such, in gray matter regions, the energy requirement is relatively greater than in regions of white matter (22, 24), therefore vascular network density is increased in these zones. Brain structure and organization of neurons differ between subregions. For example, the cortex and hippocampus form layers and these layers demarcate zones in which specific cells can be found. In addition, differences in neuronal activity between brain subregions require specific angioarchitecture. This implies that within the cortex both anatomical organization of cells and local cellular activity within a cortical layer or between cortical layers can influence the local organization and density of the vascular network. This suggests that the topology of the vascular network throughout the brain is highly heterogeneous yet somewhat predictable by its acute responsiveness to local demand of blood perfusion. The goal of this analysis was to describe the magnitude of inter-subregion differences of the cerebrovascular topology. This analysis was achieved by means of geometric assessment of the vasculature then by pairwise comparing these metrics across subregions (Figure 8). We then assessed the magnitude of inter-subregion differences between sexes. The analysis uses intra-group differences in the angioarchitecture then compares the degree of heterogeneity across sex, to provide a metric of the diversity of vascular network parameters in female and male mice.

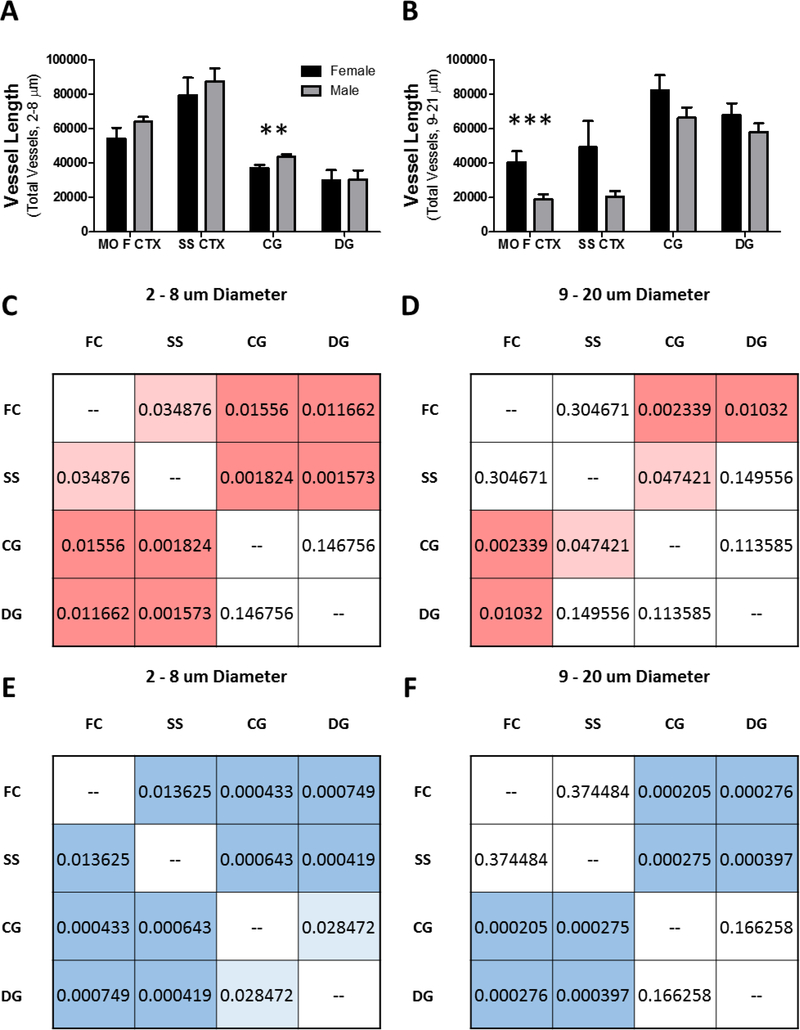
Figure 8: Inter-subregional differences in the vascular architecture vary in magnitude between the sexes.

Grouped bar graph (mean ± SEM) depicting (A) total length of capillaries (2 – 8 μm) and (B) total length of non-capillaries (9 – 21 μm) in micrometers for each of the brain subregions. Inter-subregiona l analyses of the differences in total (C and E) capillary and (D and F) non-capillary length in (C and D) female and (E and F) male mice represented as mean p – values color by hue intensity to the level of significance. Brain subregions (500 x 500 x 500 um): medial orbital prefrontal cortex (MO F CTX), primary somatosensory cortex (SS CTX), cingulate gyrus (CG), dentate gyrus (DG). To compare means, 2 - way ANOVA with Bonferroni multiple comparison analysis was used (**, p < 0.01; ***, p < 0.001).

Subregion-specific vascular network differences can occur through hierarchy specific angiogenesis. Therefore, we categorized vessels by binning into two groups, vessels with diameters of 2–8 and 9–20 μm for capillaries and arterioles/venioles, respectively. For each data set, the total length of vessels that fell into either bin was summated (Figure 8A-B) and compared by 1-way ANOVA across subregions (medial orbital prefrontal cortex, somatosensory cortex, cingulate gyrus, and the dentate gyrus) or students t-test for comparing across the overall average of the subregions. The degree of difference was represented as the p-values per pairwise comparison (Figure 8C-F). We observed the highest density of capillaries in the primary somatosensory cortex versus other brain regions (female, p = 0.0005; male, p = 0.0001). The second highest capillary density was found in the medial orbital prefrontal cortex (female, p = 0.0005; male, p = 0.0001). Whereas, the lowest densities were found in the cingulate gyrus (female, p = 0.003; male, p = 0.002) and dentate gyrus (female, p = 0.003; male, p = 0.02). A comparison of the total capillary length in the cingulate gyrus between female and male mice indicated a greater total length of capillaries in male mice (Figure 8A; p = 0.02). Our finding is consistent with the literature in that the highest capillary density is found in the primary somatosensory cortex in rodents (25).

In contrast we found the highest arteriole/venioles density in the cingulate gyrus (female, p = 0.02; male, p = 0.001) and dentate gyrus (female, p = 0.2; male, p = 0.005) and the lowest in the medial orbital prefrontal cortex (female, p = 0.02; male, p = 0.0004) and primary somatosensory cortex (female, p = 0.2; male, p = 0.001) in both sexes. Comparison of the sum length of arterioles in the medial orbital frontal cortex indicated that females have a greater value than males (Figure 8B; p = 0.01).

Our data indicate clear network differences between the subregions. However, our comparison of subregional differences to the global average is useful to identify a region that contains relatively elevated or reduced densities, but fails to demonstrate differences or similarities in a region-by-region manner. Therefore, we compared the total capillary length of all subregions to all other subregions to assess region similarities and differences (Figure 8C and E). We then performed the same comparison for arteriole/veniole densities across regions (Figure 8D and F). We found that the capillary density in the medial orbital prefrontal cortex and in the somatosensory cortex significantly differed compared to all other regions and most strongly differed from the cingulate gyrus and dentate gyrus in both female (Figure 8C) and male (Figure 8E) mice. In contrast, we found that the capillary density in the cingulate gyrus and in the dentate gyrus contained similar density profiles (p = 0.820) while being significantly different from the medial orbital prefrontal cortex (p = 0.01) and primary somatosensory cortex (p = 0.001).

The comparison of arteriole/venioles profiles between subregions revealed group wise differences between the medial orbital prefrontal cortex and primary somatosensory cortex compared to the cingulate gyrus and dentate gyrus. In female mice the greatest disparity was found between the medial orbital prefrontal cortex and the cingulate gyrus (p = 0.002) or the dentate gyrus (p = 0.01). In males, the medial orbital prefrontal cortex showed a greater dissimilarity compared to the cingulate gyrus (p = 0.0002) and dentate gyrus (p = 0.0002). Similarly in males, there was also strong dissimilarity between the primary somatosensory cortex and the cingulate gyrus (p = 0.0002) or the dentate gyrus (p = 0.0003). Interestingly, both female and male mice demonstrated similar arteriole/venioles profiles between the medial orbital prefrontal cortex and primary somatosensory cortex (female, p = 0.3; male, p = 0.3) and between the cingulate gyrus and the dentate gyrus (female, p = 0.1; male, p = 0.1). We interpret these observations to suggest that brain subregions with similar vascular profiles may demonstrate commensurate activation. Furthermore, similarities and dissimilarities of the vascular profile between subregions were conserved in both female and male mice.

Discussion

We demonstrate a procedure for the acquisition and analysis of the entire cerebrovascular system at a microvessel-relevant resolution and are the first to provide a detailed characteriza t ion of the geometrical and topological properties of the complete system of vessels in the adult female and male mouse brain.

We used a vascular corrosion cast method to replicate the complex structures of the cerebrovasculature (Figure 1). We provide a procedure that yields with high fidelity, a structura lly precise and extensively detailed replica of the complete network of cerebral vessels in adult mice (Supplemental Figure 1). Our imaging paradigm yields a single volumetric data set that encompasses the entire brain at a resolution required to investigate microvasculature (Figure 3). The produced data sets were of high quality, essentially devoid of non-specific signal (background) or imaging aberrations. Volumetric reconstruction of the cerebrovascular system demonstrated the successful capture of the complete geometry of microvascular networks that were absent of segment breakage and disconnected components. We report in detail the analytical models employed to investigate the structural and connective complexity of the brain vasculature from nine mice.

The convoluted nature of the cerebrovascular system requires the use of appropriate mathematical models to represent accurately its geometry, organization, and functional properties. Geometric descriptions of the brain’s vascular system have proven useful (26, 27). Indeed, geometric analysis of the vascular system provides valuable insight to fundamental physiological features such as, branch characteristics and cumulative length (28). However, commensurately important is a description of the vessel network organization using non-integrated parameters. In mathematics, the concept of topology is used when describing an object beyond its geometrical features, rather focusing on its structural connectivity. Topological analysis of the vasculature has only recently emerged in the literature. The reason for this delay is the unavailability of large data sets at the resolution required for robust statistical analyses of the cerebrovasculature (29). In this study, we use both geometrical and topological analysis to describe the morphology and connectivity of the angioarchitecture that represents its structural properties in a physiologically meaningful manner.

There are sex-related differences in cerebral blood flow and metabolism. It is well accepted that females have greater cerebral blood flow than do males (30, 31). However, extensive research also supports the notion that males have a thicker cortex and higher synaptic density than do females (32). Both notions are well accepted in the field yet seem counterintuitive. Having a thicker cortex with a greater number of synapses would intuitively suggest a greater metabolic demand and a corresponding increase of cerebral blood flow. Our data could resolve this conflict by providing insight into the sex differences of the cerebrovascular system; we report our findings that the entire brain vascular network in female mice contain proportionally greater capillary networks than do males (Figure 4C). This discrepancy is likely caused by an elevated number of branching vessels that are 6 μm in diameter in female mice (Figure 7F). However, in contrast to our integrated parameterization of the whole brain, when we consider subregion-specific differences between the sexes we encounter the opposite effect to variable degrees. This is best illustrated in our analysis of the vasculature in the cingulate cortex, in which we observed males to have a greater total length of capillaries than do females (Figure 8A). The increased capillary content in the cingulate cortex of male mice is likely sexually dimorphic and is the result of an underlying difference in subregion activity (33, 34). Importantly, observing no differences in integrated vascular parameters between the sexes does not indicate that the networks are homotopic. For instance, in the primary somatosensory cortex, our analysis revealed a lack of differences in total length of capillaries between the sexes (Figure 8A) indicating commensurate capillary vascularization that intuitively suggests homotopic networks. However, when we analyzed the branching properties of these networks we found a dissimilarity of vessel connectivity that specifically propagated from capillaries with a diameter of 6 μm (Figure 7F) which indicates incongruence of the deconstructed network and heterotopy of the capillary network.

Importantly, we observed cerebrovascular parameters that were similar regardless of sex. These similarities provide us with information of a conserved network at the species level. Analysis of vascular network organization and hierarchical involvement in the formation of network connections demonstrated a precise relationship between parent vessel diameter and number of branching vessels that were similar in both sexes (Figure 7F). This informs us that network formation follows specific rules where its population of vessel components exist and interact differently, and is governed by its hierarchical vessel diameter. Interestingly, we observed two peaks in the distribution of number of branches by parent vessel diameter (Figure 7D). These peaks represented branches emanating from parent vessels with 4 and 6 micron diameters. Although, female mice were found to have a greater number of 6 micron vessel branching, the distribution proportional to other parent vessel diameters was the same between female and male mice. Parent vessels with diameters of 7 microns tended to be greater in females. All other parent vessel diameters were nearly identical between female and male mice. These observations are interpreted to imply that network formation has specific organization where it follows a conserved set of rules that pertain to vessel diameter and connectivity. Specific branching patters that follow a diameter-related organization may be physiologically important for healthy hemodynamic function. It would be interesting to determine if changes in these branching properties of vascular networks occurs during pathology.

The cerebrovascular system is a complex network of highly interconnected pathways that maintain physiological hemodynamic states of blood delivery to support the perpetual activity of neuronal transmission. The consistency and precision of the forces and amount of blood delivery to the various brain regions is critical for normal information processing of neurons (35). Our analysis of whole brain network complexity supports the notion that females more so than males demonstrate complex vascular organization. Fractal dimension is a mathematical concept used to describe the complexity of self-similar structures. The prototypical idea of self-similar repeating functions originated as early as the 1600’s but was only formalized in 1975 by Benoit Mendelbrot who coined the term fractal dimension. Briefly, fractal dimension analysis is used to parameterize structures with undefined functions. For instance, a two-dimensional structure that is too complex to be two-dimensional but does not qualify as a three-dimensional structure. In contrast to topological analysis, measuring fractal dimension provides an index that quantitative ly and qualitatively describe the difference of a structure’s space filling behavior compared to an orthodox geometric structure. In vascular biology, analysis of fractal dimension is used to measure network complexity (36, 37). The quasi-fractal structure of vascular networks is produced by its hierarchical branching patterns (i.e. Figure 7B) that scale many iterations to give rise to progressive ly smaller vessels (36, 38). Our fractal analysis of the whole brain vasculature indicated a fractal dimension of 2.6 and 2.5 in female and male mice, respectively. Our observation is in agreement with the literature, reporting a fractal dimension of 1.82 and 2.17 of the vasculature in subcortical and cortical areas, respectively (37). It is important to note, the relationship between space-filling properties of a structure’s organization with its derived fractal dimension is a measure of the structure’s complexity in terms of its self-similar repetitive nature and the degree of regularity to which its repeated structure propagates through multiple scales. It is incorrect to assume that an object’s fractal dimension and the relationship to space filling properties is a measurement of its density. Qualitatively, the fractal dimension of a vascular structure gauges its branch patterns by assessing the uniformity between its branches of like hierarchical order and the number of branch levels the network produces (i.e. how extensive are the branches in the network and do these branches resemble parent vessel morphology through multiple subsequent branch levels?). Our data suggest that the branching properties in the female brain are more organized and thorough, and are therefore more complex than in male mice.

Vascular network complexity can influence the outcome severity following an ischemic event. Premenopausal women and intact female rodents sustain smaller infarctions than males (39, 40). Some studies argue that sex differences of ischemic stroke sensitivity are caused by gonadal hormones (41). During normal aging in females, sexually dimorphic capillary density and network organization may decline with gonadal hormones resulting in increased sensitivity to ischemic injury. In menopausal women, collateral rarefaction ensues, resulting in increased severity of ischemic injury (42, 43). One study, comparing the number of collateral vessels in female and male mice with the outcome of ischemic injury found no statistical difference in the number of collateral vessels between the sexes while observing smaller infarct volumes in female mice (39). Our data demonstrates a greater total number of capillaries, more extensive capillary-cap illary network, and smaller intervessel distances in female mice than in male mice. In consideration of these findings, we argue that female mice have more complex and robust vascular infrastruc ture that reduces ischemic sensitivity compared to male mice. Moreover, microvascular density rather than number of collateral vessels may cause the sex differences in sensitivity to ischemic injury.

The majority of the literature reporting the cerebral angioarchitecture employs paradigms that utilize fluorescent dyes (1, 44, 45), chromatic dyes (46–48), radio opaque solutions (49), and antibodies targeted against vascular epitopes (50). The unifying limitations of these methods are inadequate imaging depth and the tradeoff between resolution and field of view. Light sheet microscopy (LSM) has become a popular platform for imaging large samples. However, because LSM is an optical imaging method, the quality of the images obtained is dependent on the fluorescence and transparency of the specimen. Mounting of specimens for LSM is also problematic, to prevent shrinkage caused by drying, the specimen must be either embedded or submerged without compromising the transparency of the specimen or increasing signal-noise (51, 52). Similar to other fluorescence based imaging platforms, LSM is prone to image aberrations, blurring, scaling by refractive index, autofluorescence, and signal degradation that progressively get worst with acquisition time and imaging depth (51, 52). To date, the aforementioned techniques have demonstrated difficulty imaging the complete angioarchitecture of the entire brain. Reported in the literature indicate that investigators are encountering complications of achieving perfusion of capillaries (45, 49, 53, 54), observing broken vessel segments (45, 49, 53, 55), and incomplete vascular networks (45, 54, 55).

A growing concern to all fields of research is our current technological limitations. Large data sets are difficult to post-process and even more so to perform three-dimensional quantitat ion and other complex algorithms for vascular network mapping and predictive simulations. We provide a method for imaging the entire brain vasculature, producing a single data set gigabytes in size.

We report a procedure to acquire three-dimensional data sets of the complete cerebrovascular network from the whole brain of adult mice. Our analysis of the whole brain reveled sex-related differences in vascular topology. These differences were observed over the whole brain and varied by brain subregion. Overall, our study describes for the first time, a whole brain analysis of the cerebrovascular network and provides fundamental information for the advancement of vascular research.

Materials and Methods

Animal Usage

Three-month old female (n = 5) and male (n = 4) C57BL/6J mice were used for whole brain vascular analysis. Power analysis for ANOVA designs indicated a sample size of 4 mice per group (power = 0.999) for an effect size of Δ = 1.25. Mice were housed in accordance to IACUC guidelines. Animals were maintained under a light/dark cycle (12 h: 12 h) with food and water available ad libitum.

Vascular Corrosion Cast Preparation

The procedure described below for the preparation of cerebrovascular corrosion casts is shown in Supplemental Figure 1. Before beginning the cerebrovascular casting procedure, mice were transported to the surgical suite approximately 4 hours prior to the procedure to allow an acquisition period to a new environment. The acquisition period reduces the amount of stress the animal experiences and prevents any stress-induced changes to the cerebrovasculature. Mice were deeply anesthetized with 4% isoflurane diffused into a 70% nitrogen and 20% oxygen mixture. After confirming deep anesthetization via tail pinch, mice received an intraperitoneal injection of 25U of heparin in 250μl saline intravenous solution. Mice were then transcardially perfused at 160 mmHg with 0.01M PBS containing 25U/ mL of heparin at physiological pH and warmed to 37° C. Once blood had been completely removed, mice were perfused at 160 mmHg with 4% paraformaldehyde warmed to 37° C. Approximately 5 minutes before complete paraformaldehyde perfusion; the vascular corrosion cast solution was prepared. The PU4ii (VasQtec) corrosion cast solution was prepared by adding 3g (ℓ) of methyl ethyl ketone with 5–10 mg of blue pigment then mixed thoroughly by vortex. Once the pigment was completely dispersed into the solution, 5g (ℓ) of polyurethane resin was added to the solution followed by thorough mixing. Finally, 0.8g (ℓ) of hardener was added to the solution and gently mixed by inverting. After mixing, the final solution was placed into a vacuum chamber for 2 minutes to remove gasses within the solution. The solution was then perfused into the mice at 160mmHg. Once the casting solution began to harden (3 – 5 minutes) and ceased to perfuse the mouse, mice were allowed to remain at room temperature for 4 hours to complete the hardening of the cast. After complete hardening of the cast, mice were decapitated and the skin was removed from the skull with dissecting scissors.

Vascular Corrosion Cast Processing

The isolated skull was decalcified by immersion in 20 mL of 8% formic acid diluted in Milli-Q water then placed in a water bath warmed to 37° C for 5 hours. From our experience, it is important to prevent over decalcification of the skull so that the bone tissue becomes flexible without becoming gelatinous and difficult to remove. Once decalcification was complete, the skull was rinsed with distilled water and then immersed in 20 mL of 8% potassium hydroxide diluted in Milli-Q water then placed in a water bath warmed to 37° C for 4 hours. Following the 4-hour incubation in potassium hydroxide, the skull was rinsed in distilled water and prepared for brain extraction. At this point, the skull was flexible and easy to tare with small forceps. A small incision at the base of the magnum foramen was gently made, and with a pair of small forceps, the incision flap was grasped and pulled upward, breaking the skull up the sagittal suture. With small iris scissors, all major vessels were cut at the floor of the skull by gently lifting the brain. The brain was then removed and the tissue was macerated by immersion into 20 mL of 8% potassium hydroxide solution diluted in Milli-Q water then placed in a water bath at 37 ° C overnight. After the overnight incubation, tissue maceration is usually incomplete and requires the potassium hydroxide to be replaced and incubated at 37° C in a water bath for 24hrs. Once tissue maceration was completed, residual tissue was removed from the vascular cast by washing 3 times for 1 hour with distilled water containing 0.25% Triton X-100 then rinsed 3 times for 5 minutes with Milli-Q water to remove any residual detergent on the cast.

The cleaned casts were placed into a small container and submerged in 20 mL of Milli-Q water to be frozen for lyophilization. Lyophilization of the casts was performed on a benchtop freeze dry system (Labconco) operating at −54 °C and a vacuum pressure of 0.0025 mBar. During the lyophilization process, it is critical that sublimation occurs and that the melting of ice to a liquid state does not occur. The proper sublimation of ice is critical to preserve the physiological architecture of the cerebral blood vessels. In our experience, improper sublimation compromised the structure of the formed vascular casts, often times producing a relatively flattened appearance. Melting of the ice deformed the small capillary structures and was irreversible once the cast completely dried. Successful lyophilization resulted in casts that were rigid and able to maintain moderate pliancy. To allow x-ray detection of the vascular corrosion casts, 6 mL of a 2% solution of osmium tetroxide diluted in Milli-Q water was embedded onto the polyurethane casts by immersion and allowed to incubate overnight at 4° C. Extensive care must be taken when handling solutions or casts containing osmium tetroxide due to its acute toxicity. Proper personal protective equipment should be used and the disposal of waste containing osmium tetroxide should be handled as a p-chemical. Vascular corrosion casts were then removed from the osmium solution with small forceps by gently grasping the cast by the hindbrain. Casts were allowed to air dry for 1 hour, and then mounted with cyanoacrylate adhesive on hexagonal pedestals cut from Plexiglas.

Micro-Computerized Tomographic Imaging

Tomographic images of the whole brain were acquired using a SkyScan 1272 μ-CT (Bruker). The μ-CT system was set to operate at 35 kV and 200μA, no filter, and a 4032-by-2686 frame size. Before initiating the image routine, flat fields were calibrated and the pixel size was set to 2 μm. To optimize the quality of images produced by the scan, the exposure settings were adjusted so that a maximum signal of 35–40% was obtained and a low of 80–90% and an average of 65–75%. Each vascular cast was imaged over a total of 360° at a step size of 0.05° and averaged by 5 images per 0.05°. Each image routine required about 15 hours of scan time and produced a file size of 500GB containing 7,200 images and an additional 400GB and 4,032 images for the final coronal series of the entire cerebrovascular system. After completing the 15 hours scan, the primary data sets were corrected for misalignments, beam hardening, and ring artifacts then converted into a coronal image series. The final data set produced by this imaging routine is a complete coronal series of the entire cerebrovasculature at a pixel resolution of 2 μm separated in the Z direction by 2 μm for a total of 43.65 gigavoxels.

Anatomical Selection of Volume of Interest

The complete set of coronal images were accessed on CTan (Bruker) to isolate a volume of interest (VOI). To prepare image sets for digital isolation of VOIs, the signal intensity of the image series was increased so that capillaries were easily observed. Once the intensity was increased, boundaries of major brain regions were clearly noticeable. Using the Allen Mouse Brain Atlas (21), the VOI was located and selected by tracing. The traced regions were made in square selections of approximately 1.5 – 2.0 mm and dynamically interpolated in the Z direction of 1.5 – 2.0 mm. The result was a cube VOI that was saved as an individual data set. The new data set containing the VOI was filtered in three-dimensions to remove signal noise. The data set was converted into a BMP series of formatted images and saved as a new data series of the isolated and pre-processed VOI.

Image Processing and Optimization for Volume of Interest

The workflow for the optimization of VOI data sets is depicted in Supplemental Figure 2. The binary VOIs were optimized for image analysis and quantification using ImageJ or Imaris software. Each VOI data set was three-dimensionally cropped to 1 x 1 x 1 mm cube. The data sets were then rotated so that a selected landmark was co-registered by rigid transformation similar to the other data sets in the experimental group. Our experience dictates that the major arteries and their specific branching patterns provided the most convenient and consistent landmarks for image co-registration. The intensity of the data series was multiplied by 1.5 so that capillaries were easily seen; however, the signal of the most intense objects should not reach a value of 255. After signal intensity multiplication, a three-dimensional Gaussian blur was applied using a circular mask of 0.65 pixels. Then a background subtraction was used to remove the uniform noise from the data series. Next, the data set was filtered with an unsharp mask to increase the spatial resolution and proximity discrimination of the structures in the data set. This new optimized data set was duplicated and saved as a series of tiff-formatted images. One of the duplicated data sets was used to create vessel centerlines that served to reduce errors during the vessel network-tracing algorithm. Centerlines were created using the 3D/2D skeletonization plugin on ImageJ. With the second duplicated image set, an intensity threshold was set using the Moments algorithm and a binary image series was created. The intensity of the binary image set was subtracted by 150 so that the intens ity of the binary image series was uniformly at 105. Finally, the image series containing the centerlines of the vessels was merged with the processed binary images so that the vessel structures had an intensity of 105 and the centerlines that passed through them contained an intensity of 255. This optimized data series was then filtered with a three-dimensional Gaussian blur and saved as a series of tiff-formatted images.

Volume of Interest Quantification and Analysis of Vascular Networks

The optimized data sets were analyzed with Imaris (Bitplane) software and the vascular networks were quantified. Using the filament trace function in Imaris, the vascular networks were identified. Post filament trace, the vascular networks were visually inspected to ensure that proper vessel connections were made. Vessels that were missed during the filament tracing were manually connected and the vessels that were improperly connected were manually disconnected. Once a proper network was created, a number of statistics were generated and saved as excel sheets. These measurements include vessel diameter, length, volume, area, tortuosity, branch level, and angle in degrees. Vessels were classified by hierarchy that was determined by the mean vessel diameter. Vessels that had a mean diameter of 2 – 8 μm were classified as capillaries, 9 – 34 μm were arterioles and venioles, and > 34 μm were classified as arteries and veins.

Three-Dimensional Vascular Network Analysis

To analyze the vascular network, a network analysis was performed using a custom MATLAB script (available upon request). Before the network analysis was performed, the data sets were rotated so the selected landmarks were co-registered by rigid transformation, to the other data sets in the experimental group. The intensity of the data series was globally multiplied by 1.5 so that capillaries were easily seen; however, the signal of the most intense objects were not allowed to reach a value of 255. After data set wide signal intensity multiplication, a three-dimensional Gaussian blur was applied using a circular mask of 0.65 pixels. Then the background was removed by subtracting the average intensity of a region that was the size of the diameter of the largest vessel and repeated region to region for the entire data set. Next, the data set was filtered by an unsharp mask to increase the spatial resolution and proximity discrimination of the structures in the data set. This new optimized data set was then converted to a binary series by selecting a threshold using the Moments algorithm. The binary data set was duplicated and converted into a local thickness map. The second binary data set was used to extract the centerlines of vessels. Our three-dimensional network analysis processes the centerline data set and derives nodes as vertices with degree 3 or greater and edges as vertices with degree 2 and end-points as vertices with degree 1. Each edge is stored in a matrix containing all of its component pixel identities and the nodes that the edge bridges together. Then the local thickness map is used to characterize the network map for further analysis. The output data for the three-dimensional network analysis was a vascular map containing the parameters of the angioarchitecture for our assessment of network connectivity. The results of this analysis were used to assess the extensivity of the vascular network by measuring the connectedness and branch abundance to the network.

Three-Dimensional Data Rendering

To view the entire vascular network of the whole brain in three-dimensions, the data series was uploaded onto CTvox (Bruker) and the opacity and light intensity was adjusted to provide the best view of the data set. In order to demonstrate a color-coded three-dimensional structure of the vascular network, the data sets containing the VOIs were uploaded onto Imaris (Bitplane), rendered in three-dimensions, and colored based on calculated statistics. Color-coding of the complete vascular network of the entire brain was performed on CTan (Bruker). Additionally, data sets were color-mapped based on vessel separation to allow the visualization of vessel density and intervessel distances.

Group Size and Statistical Analysis

All values are presented as mean ± SEM for 5 female and 4 male brains. The specific statistical analysis used in each experiment was determined based on the intended comparison that was performed. Statistical tests were either student’s t-test or ANOVA, with Bonferroni or Dunnett post-hoc tests. Specifically, Bonferroni’s multiple comparison analysis was used to compare all combinations of the experimental groups, which include sex and brain subregion. Dunnett’s post-hoc test was used for comparison of the experimental groups with a control group. Values of p < 0.05 were considered as significant. Where indicated in the results section, analyses compared between sexes with p-values greater than 0.35 were consolidated into a single representative data. All data are available from the corresponding author upon request.