Non-Negative Matrix Factorization Reveals Resting-State Cortical Alpha Network Abnormalities in the First Episode Schizophrenia-Spectrum

Abstract

Background:

Little is known about neural oscillatory dynamics in first episode psychosis. Pathophysiology of functional connectivity can be measured through network activity of alpha oscillations, reflecting long-range communication between distal brain regions.

Methods:

Resting magnetoencephalographic activity was collected from 31 first episode schizophrenia-spectrum psychosis individuals (FESz) and 22 healthy controls. Activity was projected to the realistic cortical surface, based on structural MRI. The first principal component of activity in 40 Brodmann areas per hemisphere was Hilbert transformed within the alpha range. Non-negative matrix factorization was applied to single trial alpha phase locking values from all subjects to determine alpha networks. Within networks, energy and entropy were compared.

Results:

Four cortical alpha networks were pathological in FESz. The networks involved bilateral anterior and posterior cingulate; left auditory, medial temporal, and cingulate cortex; right inferior frontal gyrus and widespread areas; and right posterior parietal cortex and widespread areas. Energy and entropy were associated with the PANSS Total and Thought Disorder factors for the first 3 networks. Additionally, the left posterior temporal network was associated with Positive and Negative factors and the right inferior frontal network was associated with the Positive Factor.

Conclusions:

Machine learning network analysis of resting alpha-band neural activity identified several aberrant networks in FESz including left temporal, right inferior frontal, right posterior parietal, and bilateral cingulate cortices. Abnormal long-range alpha communication is evident at the first presentation for psychosis and may provide clues about mechanisms of disconnectivity in psychosis and novel targets for non-invasive brain stimulation.

Introduction

Schizophrenia is associated with disabling symptoms including visual and auditory hallucinations, blunted emotion, and deficiencies in attention, decision-making, and working memory. The disorder is often chronic and typically emerges in late adolescence and young adulthood. The exact pathology remains unknown, and its explication is complicated by the progressive course of the disorder (1–3) and the cumulative effects of secondary illness-related factors. These confounds are ameliorated by studying individuals near the emergence of psychosis within the schizophrenia-spectrum. Definitive diagnoses cannot always be made at first episode. Hence, the schizophrenia-spectrum at first episode includes schizophrenia, schizoaffective disorder, schizophreniform disorder, delusional disorder, and psychosis not otherwise specified (NOS).

Schizophrenia involves “disconnection” between neural regions (4–6). Functional connectivity is reduced in schizophrenia (7–11) and this reduction may have an anatomical component (12–14). For example, schizophrenia is associated with reduced structural connectivity in several polymodal hubs and so-called “rich clubs”, centralized hubs at the top of the cortical processing hierarchy (15). This disconnection is also evident in functional activity. Electroencephalography (EEG) and magnetoencephalography (MEG) reflect summed dendritic fields and provide a high-resolution window into real-time neural network activity. MEG allows greater spatial resolution of the cortical sources of neural oscillations because magnetic fields, unlike electric fields, are unaffected by intervening tissue boundaries. In combination with accurate sulcal-gyral models of individual head shape based on structural MRI, MEG activity can be source-resolved to the cortical surface with reasonable spatial resolution of 5–10 mm.

Neural oscillations have a known role in coordinating activity in both local brain networks (16) and networks connecting brain regions over long distances (17). Changes in overall oscillatory activity are observed in schizophrenia (18). Distributed oscillatory networks are characterized through spectral frequency phase relationships between cortical regions. The alpha rhythm, though to reflect, in part, information transfer between distal brain regions (19, 20), is reduced in schizophrenia (11,21).

Alpha power was traditionally associated with vigilance and sustained attention, representing an underlying idle state of the brain. For example, alpha increases when the eyes are closed, and diminishes when the eyes are open (22,23). However, alpha has a role in working memory (24–26) and top-down control (27–30). Alpha phase impacts the synchrony of neuronal activity both locally and between regions of the brain (31). Additionally, alpha activity acts to suppress task-irrelevant processing (31), activate task-relevant processing (29), or both (29,32). Thus, in addition to reflecting the general “idling” of cortical areas, alpha likely plays a role in long-range communication between distal cortical areas.

In that regard, long-distance synchrony in gamma activity between distal cortical areas likely involves alpha oscillations that coordinate between areas (33–36). Importantly, attention effects are not only associated with the alpha-gamma power anti-correlation, but also with cross-frequency coupling. Gamma band bursts entrain to alpha phase, such that sensory gamma bursts become locally organized via PFC-controlled alpha modulations (37). Thus, alpha plays a role in modifying sensory processing via input from executive and other distributed areas. We therefore selectively targeted alpha oscillations for analysis of distributed networks, as it is a biologically viable, empirically demonstrated coordinating frequency between distal cortical areas.

We used alpha phase-locking (38) as an indicator of functional connectivity between regions during the resting state. We assume that there are multiple overlapping networks within the brain that contribute to the observed signal. Thus, we employed a machine-learning clustering technique, non-negative matrix factorization (NMF), to subdivide phase synchrony graphs into functional networks. NMF, traditionally used in applications such as image recognition (39), genetics (40), and natural language detection (41), has previously been used to investigate neural differences between subject groups using fMRI (42). We determined the energy and entropy of these networks to provide network-specific information on alpha irregularity in schizophrenia. Energy measures the overall quantity of information transfer in a system and is akin to the power of the signal that is being communicated. Entropy represents the order/disorder of communication and information transfer within each network and measures the degree of complexity in the neural signal. We specifically aimed to determine networks of interest by relatively light, data-driven computational methods to identify promising network features for future in-depth studies of pathology in early course psychosis, and for potential development of optimal patient-specific precision medicine treatments targeting specific circuits.

Methods and Materials

Participants were 31 first episode schizophrenia subjects (FESz) and 22 healthy controls (HC), group matched for age, gender, and estimated premorbid IQ. FESz and HC differed on SES and MATRICS overall scores, consistent with the deleterious effects of psychosis on functioning and cognition. Parental SES was significantly lower in the FESz (Note: None of the energy or entropy measures reported below correlated with parental SES in either group.). Seven FESz were unmedicated. (See Table 1 for demographic and clinical data). This study was approved by the University of Pittsburgh Institutional Review Board (IRB). All subjects provided informed consent and were paid for participation.

Table 1.

Subject demographic and clinical data.

	FESz	HC	p
n (M/F)	31 (20/11)	22 (13/9)	0.69
Age	21.7 (5.0)	21.7 (3.7)	0.96
SES	26.9 (13.2)	33.4 (12.5)	0.05
PSES	39.6 (14.0)	53.3 (7.6)	<.001
WASI IQ	104.9 (15.2)	106.4 (8.6)	0.69
MATRICS	35.0 (16.6)	49.1 (6.4)	<.001
GAS	38.1 (9.2)
SAPS	6.6 (3.3)
SANS	10.3 (3.1)
PANSS Total	76.5 (15.0)
PANSS Pos	19.4 (5.7)
PANSS Neg	17.3 (4.8)
PANSS TD	11.2 (3.2)
MEDS	205.5 (160.1)
DUP	36

Note: Subject n and sex distributions are number of individuals. Duration of untreated psychosis (DUP) is median value in weeks. All other values are mean (sd). Age is in years. SES = Socioeconomic status. PSES = parental SES. WASI IQ = Wechsler Abbreviated Scale of Intelligence score. MATRICS = Measurement and Treatment Research to Improve Cognition in Schizophrenia Consensus Cognitive Battery composite score. GAS = Global Assessment Scale. SAPS = Scale for the Assessment of Positive Symptoms Global score. SANS = Scale for the Assessment of Negative Symptoms Global score. PANSS Total = Positive and Negative Syndrome Scale Total score. PANSS Pos = Positive and Negative Syndrome Scale Positive Factor score. PANSS Neg = Positive and Negative Syndrome Scale Negative Factor score. PANSS TD = Positive and Negative Syndrome Scale Thought Disorder Factor score. MEDS = Medication in chlorpromazine equivalents (oral dosages from Andreasen et al 2010 [36], depot dosages from Gardner et al 2010 [37]). Significant effects are bolded.

Five minutes of eyes open resting MEG data were collected in a magnetically shielded room. We acquired resting state data with eyes open as we were interested in entropy measures of network-level activity, and spectral entropy is greatest in eyes-open EEG (43). Both EEG and MEG were recorded, but only the resting MEG is reported here. MEG data were recorded using a 306-channel whole-head MEG system (Elekta Neuromag) with a sampling rate of 1000 Hz (online bandpass filter = 0.1–330 Hz). Bipolar leads were placed above and below the left eye (VEOG) and lateral to the outer canthi of both eyes (HEOG). Bipolar ECG leads were placed just below the left and right clavicle. Four head position indicator (HPI) coils were placed between electrodes on the surface of the EEG cap, and locations (relative to the nasion and preauricular points) were recorded using a 3D-digitizer (ISOTRAK; Polhemus, Inc., Colchester, VT). Head position was tracked continuously throughout the experiment. Subjects were instructed to fixate upon a central cross for the duration of the test.

Structural MRI was obtained for use in MEG source modeling. Sagittal T1-weighted anatomical MR images were obtained using a Siemens TIM Trio 3 Tesla MRI system with a multi-echo 3D MPRAGE sequence (TR/TE/TI = 2530/1.74, 3.6, 5.46, 7.32/1260 ms, flip angle = 7°, field of view (FOV) = 220 × 220 mm, 1 mm isotro pic voxel size, 176 slices, GRAPPA acceleration factor = 2).

Head movement correction was completed using Elekta MaxMove and external noise was reduced via the temporal extension of Signal Space Separation (44) implemented in Elekta MaxFilter. Eye-blink and heartbeat artifacts were removed using Adaptive Mixture Independent Component Analysis (45,46) implemented in EEGLab. The MEG sensor locations were registered to structural images using MRILab (Elekta-Neuromag Oy, Helsinki, Finland). The locations of sources were constrained to the gray/white matter boundary segmented from the structural MRI data using Freesurfer (http://www.surfer.nmr.mgh.harvard.edu). This boundary was tessellated into an icosohedron with 5 mm spacing between vertices, resulting in ∼5000 current locations per hemisphere. A forward solution for vertices was modeled as a single sphere. Source activity was then estimated from 204 planar gradiometers using Minimum Norm Estimation (MNE) (47). The noise covariance matrix and forward solution were used to create a linear inverse operator using a loose orientation constraint of 0.4 (48), with depth weighting applied. Sensor covariance was estimated from MEG data collected without a subject in the magnetically shielded room on the same day as resting-state acquisition. Data from individual subjects were then morphed into a standard space (fsaverage) prior to functional connectivity analysis, with 5 mm smoothing.

For data reduction, following MEG cortical surface source projection, the cortical surface was parcellated into 80 Brodmann areas (see Figure 1, processing pipeline). The first principal component across the spatial dimension of the signals from each area was used to represent regional cortical activity. These 80 component signals were bandpass filtered into the alpha band (8–12 Hz), using a 20th-order Butterworth bandpass filter applied bidirectionally to achieve zero-phase filtering. Nominal break frequencies were chosen so that after the zero-phase filtering, the true break frequencies would be at 8 and 12 Hz. Synchrony was estimated between phases of alpha for each pair of Brodmann areas using single-trial phase-locking values (S-PLV) (38). The calculation of S-PLV results in lower temporal resolution when compared to multi-trial PLV but is appropriate for estimating phase-locking between rest-state signals that lack event-initiated epochs. S-PLV is defined as:

$$\text{S}-\text{PLV}(\text{t})=\left|\frac{1}{\text{δ}}{\int }_{\text{t}-\frac{\text{δ}}{2}}^{\text{t}+\frac{\text{δ}}{2}}{e}^{-j({\varphi }_1(\tau )-{\varphi }_2(\tau ))}d\tau \right|,$$

where δ is the width of the window, typically chosen between 6 and 10 times the length of the mid-band period (38). Non-overlapping windows of 600ms were chosen, corresponding to δ = 6 times the mid-alpha band period of 100ms. The instantaneous phase ϕ of component signals was taken to be the phase of the analytic signal obtained using the Hilbert Transform (49). These S-PLV were then used to create a weighted, undirected connectivity graph C for each time window (50). The nodes of C correspond to Brodmann areas and the edges represent the S-PLV, taken to be the functional connectivity, between pairs of Brodmann areas. In total, T connectivity graph matrices C of size (b x b) are generated for each S subjects, where T, S, and b are the number of time windows per subject, subjects, and Brodmann areas, respectively.

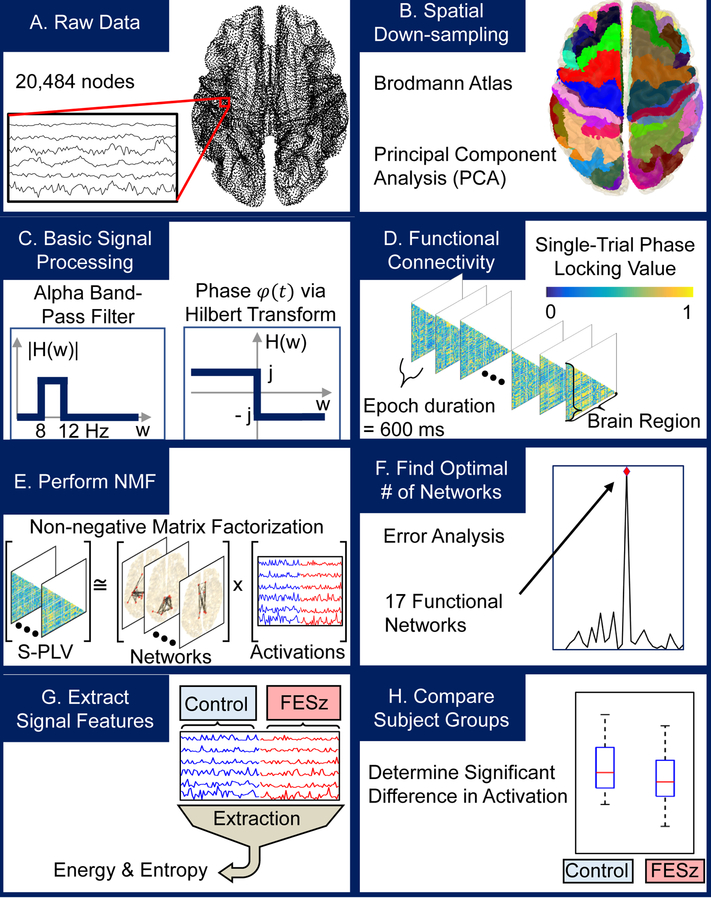
Figure 1.

Processing pipeline. Magnetoencephalography (MEG) data (A) were spatially down-sampled into Brodmann areas using Principal Component Analysis (B), bandpass filtered into the alpha band, and transformed into the analytic signal using the Hilbert transform (C). Analytic signal phases were compared using single-trial phase-locking values (S-PLV) to generate functional connectivity graphs in a windowed manner for each subject (D). Non-negative matrix factorization (NMF) was used iteratively to determine networks (E). The optimal number of networks was determined using error analysis (F). Finally, energy and entropy measurements associated with each network for every subject were determined (G) and compared between control and first episode schizophrenia-spectrum (FESz) subject groups (H).

To extract information from these connectivity graphs, the non-negative matrix factorization (NMF) technique was used. NMF is an unsupervised machine learning algorithm that can be used to decompose an input matrix A into two components: a matrix W of bases, or subgraphs, and a matrix H of their corresponding contributions to the input matrix A (39). Connectivity graphs were combined to serve as the input matrix (A) for NMF which yielded subgraphs (W), taken to be functional resting-state alpha networks, and associated timeseries of contributions (H), taken to be the relative temporal activation of each of these networks. As the synchrony graphs are undirected, all functional relationships were described in a single input matrix A by unwrapping and concatenating the lower triangular of each S-PLV connectivity graph C, resulting in matrix A having dimensions (b*(b-1)/2 x N), where N is the number of time windows over all subjects, S multiplied by T.

Factorization was completed using the sparse, alternating non-negativity constrained least squares approach (51) that is given by the minimization:

$$\underset{\text{W,H}}{\min }\frac{1}{2}\left\{{\Vert A-WH\Vert }_F^2+\eta {\Vert W\Vert }_F^2+\beta \sum _{c=1}^N{\Vert H(:,c)\Vert }_1^2\right\},s.t.W,H\ge 0,$$

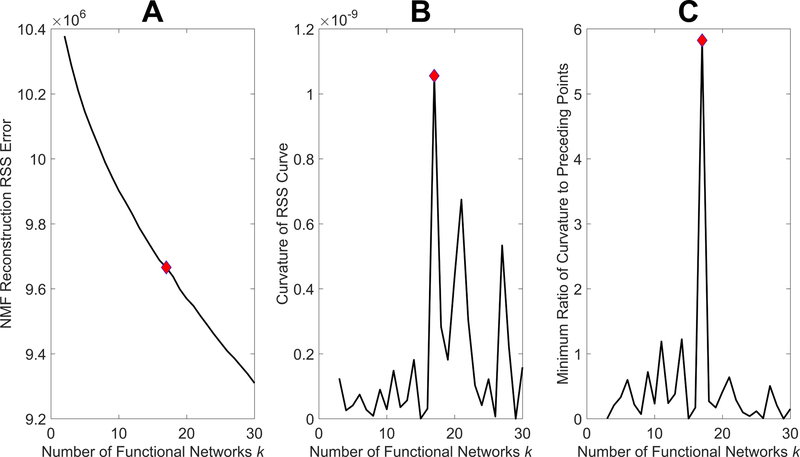
where ${\Vert X\Vert }_F$ is the Frobenius norm given by $\sqrt{{\sum }_{\text{i}=1}^{\text{m}}{\sum }_{\text{j}=1}^{\text{n}}{\left|{\text{X}}_{\text{i,j}}\right|}^2}$, $||\cdot |{|}_1$ is the ${\mathcal{l}}_1$ -norm given by ${\sum }_{\text{i}=1}^{\text{n}}\left|{\text{X}}_{\text{i}}\right|$, and H(:, c) is the c^th column of H. Parameters β and η act to regulate the values in the subgraphs W and activations H, ensuring sparsity of the result while bounding the size of output values. The choice of β as 0.01 and 5 as the square of the maximum value in A was used as these have been shown to be robust values for these parameters (42,52). The sizes of W and H are (b*(b-1)/2 x k) and (k x N) respectively, where k is the number of functional networks, which was chosen by performing NMF iteratively for increasing values of k and selecting the inflection point, or “elbow”, in the reconstruction residual sum of squares (RSS) error curve (51) (Figure 2A). This is the point after which increasing the number of functional networks yields diminishing returns on model fit. Computationally, this was taken to be the point of first large change in curvature (Figure 2B), or more specifically, the point at which the smallest ratio of the curvature to previous curvatures was maximized (Figure 2C). This method was intended to provide a repeatable and conservative way to prevent over-fitting of the model.

Figure 2.

Method for determining number of functional networks. The optimal number of functional networks occurs at the inflection point of the reconstruction residual sum of squares (RSS) error curve generated from iterative runs of non-negative matrix factorization (NMF) with increasing numbers of functional networks (A). This point can be determined as the first point with a large change in curvature (B) or, most apparently, as the point at which the minimum ratio of curvature to the curvature at previous points is greatest (C). These points are represented by red diamonds which correspond to 17 functional networks.

The NMF algorithm was initialized using non-negative double singular value decomposition (NDSVD), which allows for improved factorization speed and provides stable outputs (53). NDSVD is best implemented on sparse inputs, and rather than apply an arbitrary threshold, sparsity of connectivity graphs C was obtained using a threshold from surrogate data analysis. The threshold was taken to be the 95th percentile of the maximum S-PLV generated from 500 pairs of independent white-noise surrogate signals. Previous studies including measures of synchrony have used white-noise surrogates to determine thresholds and have shown this method to be equivalent to other, more computationally heavy methods such as trial-shifted and phase-shuffled surrogates (54,55). Connectivity above what is seen in the surrogate data is likely to “real”, not just the result of noise or random chance. This, this method identifies a reasonable threshold value above which connectivity is unlikely to reflect the result of random error or noise.

The energy (ENG) and entropy (ENT) of the activations associated with each functional network were calculated for individual subjects (42). The energy of a given network, which represents overall activation, was calculated as:

$$\text{ENG}=\sum _{\text{i}=1}^{\text{N}}{\text{W}}_{\text{i}}^2,$$

where N is the length of the activation vector w. The functional network entropy, which quantifies the dynamics of activation, was then calculated using the histogram-based method (56) as:

$$\text{ENT}=\sum _{\text{i}=1}^{\text{N}}-P(x_i)\log P(x_i),$$

where P(x) is the probability function derived from the histogram. Because the measures were not normally distributed (max kurtosis > 30 for each measure), the energy and entropy of functional network activations were compared between FESz and HC using the Wilcoxon rank-sum test. Because this is the first examination of alpha functional networks derived in this fashion, we adopted more liberal initial exploratory analyses, where p <.05 was considered meaningful; however, these data were additionally corrected for multiple comparisons with the Benjamini-Hochberg procedure with a false discovery rate 0.15. To demonstrate the utility of factorization in the analysis, these energy and entropy calculations and comparisons were also performed on the data after filtering into the alpha band (i.e. prior to phase synchrony estimates). A correlation between whole-brain signal power (sum of the magnitude of the Fourier Transform across regions) was also performed. These whole-brain analyses were similarly not normally distributed, so comparisons between subject groups were also made using the Wilcoxon rank-sum test.

Correlations between network activation measures and symptoms were investigated with Spearman’s rank order correlations. Due to the large number of possible correlations between energy and entropy for separate functional networks and individual symptoms, clinical measures were reduced to total, positive, negative, and thought disorder factors of the PANSS. (Significant associations with items are presented in supplemental material, but caution must be used in interpretation.)

Results

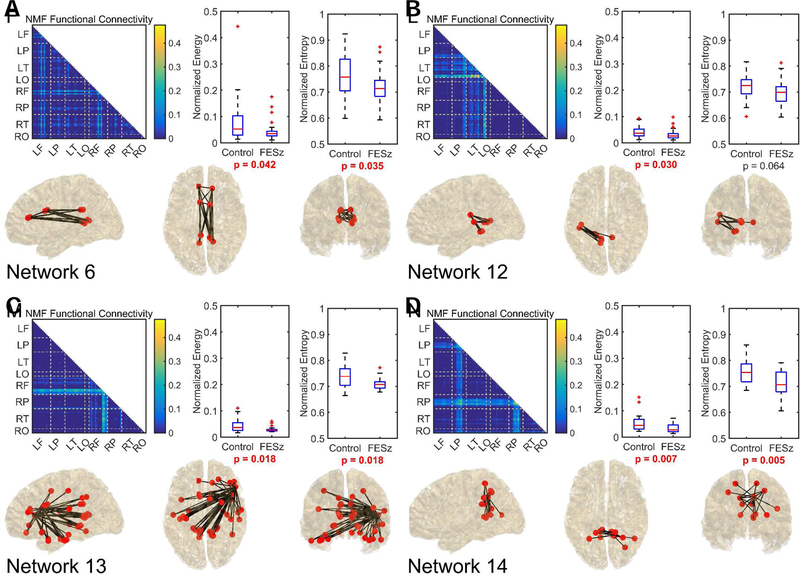
No significant difference between subject groups was observed in whole-brain alpha energy (p = 0.203), entropy (p = 0.401), and power (p = 0.267). Using NMF, 17 functional networks (Figure S1) were determined. Comparisons between groups revealed 4 functional networks that exhibited significantly lower median energy in FESz, one of which survived correction for multiple comparisons (Figure 3). These were Network 6, which consists primarily of distributed alpha coherence in the cingulate cortex; Network 12, which connected left hemisphere auditory cortex with left medial temporal lobe and posterior cingulate; Network 13, which consist of a hub in right inferior frontal cortex Broca’s homologue (BA44 & 45) hub with widespread connectivity (bilateral cingulate, bilateral lateral and medial temporal lobes, right hemisphere prefrontal cortex, and bilateral sensorimotor cortex); and Network 14, a network between posterior cingulate cortex and bilateral superior parietal lobules. Of these four networks, the cingulate network, right inferior frontal network, and the posterior cingulate superior parietal network also showed significant decreases in median activation entropy in FESz. Changes in both entropy and energy of the posterior cingulate superior parietal network survived correction for multiple comparisons.

Figure 3.

The 4 networks that differentiated healthy individuals from first episode schizophrenia spectrum individuals. Networks are represented as a connectivity graph and anatomically on a brain model. Control and first episode schizophrenia-spectrum (FESz) group comparisons of energy and entropy are also provided. In the connectivity graph, each pixel represents a phase-locking relationship between two Brodmann areas. Values closer to the diagonal represent local communication while values in lower left represent cross-hemisphere communication. To further improve an anatomical understanding, dashed lines divide Brodmann areas from different lobes and are identified at the axes by their hemisphere (R-right, L-left) and lobe (F-frontal, P-parietal, T-temporal, O-occipital). The top third of connections by strength are also shown within the brain at sagittal, axial, and coronal views. FieldTrip software (72) was used in generation of these brain visuals. Energy and entropy values have been normalized between highest and lowest observed values across subjects and the p-value associated with the Wilcoxon rank-sum test is given. Comparisons with p < 0.05 are in bolded red text.

Within HC subjects, energy and entropy measures across networks were highly correlated (rho’s 0.48 to 0.99, all p’s <.05). In FESz, energy and entropy were correlated amongst most networks, although Network 6 (bilateral cingulate) and Network 14 (posterior cingulate and bilateral superior parietal cortex) were uncorrelated. In FESz, there were widespread correlations between both energy and entropy measures and clinical symptoms for all networks except Network 14 (posterior cingulate and bilateral superior parietal cortex, See Table 2 and S2). Lower energy and entropy in Network 6 (bilateral cingulate) were associated with more total symptoms and greater thought disorder. Lower energy and entropy in Network 12 (Left posterior temporal) was associated with more total, positive, and negative symptoms and greater thought disorder. Lower energy and entropy in Network 13 (right inferior frontal) were associated with more total and positive symptoms and greater thought disorder.

Table 2.

Spearman’s Correlations of Energy and Entropy with Clinical Measures.

	Bilateral Cingulate (Subnetwork 6)		Left Posterior Temporal (Subnetwork 12)		Right Inferior Frontal (Subnetwork 13)		Posterior Cingulate- Parietal (Subnetwork 14)
	NRG	ENT	NRG	ENT	NRG	ENT	NRG	ENT
Between-Group Differences	2.03	2.10	2.36	2.37	2.35	2.37	2.68	2.82
	0.04	0.04	0.03	0.06	0.02	0.02	0.01*	0.005*
Correlations with Symptoms
PANSS Total	−.40	−.40	−.60	−.61	−.38	−.43	−.10	−.08
	0.04*	0.04*	0.001*	0.001*	0.06	0.03*	0.61	0.69
PANSS Pos	−.35	−.30	−.46	−.45	−.42	−.42	−.18	−.19
	0.08	0.14	0.02*	0.02*	0.03*	0.03*	0.38	0.35
PANSS Neg	−.22	−.23	−.54	−.56	−.15	−.22	−.15	−.13
	0.29	0.25	0.005*	0.003*	0.46	0.29	0.48	0.52
PANSS TD	−.46	−.40	−.54	−.50	−.61	−.66	−.25	−.24
	0.02*	0.04*	0.004*	0.009*	0.001*	<0.001*	0.21	0.23

Note: Values presented for between-group differences are Z scores, and those presented for correlations are Spearman’s rho. NRG = Energy, ENT= Entropy. PANSS Total = Positive and Negative Syndrome Scale Total score. PANSS Pos = Positive and Negative Syndrome Scale Positive Factor score. PANSS Neg = Positive and Negative Syndrome Scale Negative Factor score. PANSS TD = Positive and Negative Syndrome Scale Thought Disorder Factor score. PANSS Item scores follow Factor scores. GAS = Global Assessment Scale. Significant p values (p ≤.05) are bolded. Significant differences with corrections for multiple comparisons (FDR=0.15) are marked with an asterisk.

Discussion

Using a data-driven approach to source-level functional connectivity analysis in alpha-band MEG data, we identified 17 discrete distributed functional networks based upon phase-locking (Figure S1). From the analytical side, the observation that NMF extracts reasonable brain networks from connectivity graphs is an important methodological advance. From the clinical neuroscience side, that several of these data-driven alpha networks were abnormal in FESz is an important new lead in understanding the pathophysiology of the disorder.

Four distributed networks (Figure 3) displayed lower energy in FESz, indicating less coherent alpha activation. The entropy decreases in three of these networks (Networks 6, 13, 14) suggest the networks also are less variable (more stagnant) in their alpha-band activity. Even very early in the disease process, close to the emergence of psychosis in the schizophrenia spectrum, distinct distributed cortical networks are impaired, and can be detected through aberrant alpha band network dynamics. These abnormalities were isolated through S-PLV and NMF and could not be determined using simple whole-brain analyses of alpha power or activity. Thus, NMF holds powerful potential for use on neural data through unbiased identification and isolation of functional networks.

Three of the four abnormal alpha networks were associated with symptoms. From white matter-based connectome analyses, the bilateral cingulate (Network 6) comprises multimodal cortex and cortical hubs (57) and is one of the “rich club” areas of the brain (15). Thus, it is perhaps not surprising that resting pathophysiology in this network was associated with overall symptom severity, but particularly with thought disorder (Table 2). The left posterior medial and lateral temporal cortex network (Network 12) likewise was associated with thought disorder and overall, positive, and negative symptom severity. The associations of left posterior temporal cortex and positive symptoms and thinking disturbance in schizophrenia are well documented (58–60), as is the association of medial temporal pathology with paranoia and other psychosis-like symptoms (61,62). The right inferior gyrus hub (Network 13) comprises the right hemisphere analogue of Broca’s area in ventrolateral PFC and is thought functionally to serve two main roles, stopping motor responses and inhibiting orienting to distracting stimuli (63,64). Adjacent right BA47 may be involved in response-reward processing, including delayed reward versus reward magnitude tradeoffs and risky choices (65,66). Schizophrenia is associated with increased distractibility and perseveration, likely reflecting some involvement of right vlPFC; for example, fMRI studies in schizophrenia show reduced right IFG activity on a stop-signal task (67) and reduced coupling of dorsolateral PFC working-memory areas and right IFG (among other PFC areas) when distractors were presented (68). Finally, the bilateral posterior cingulate and superior parietal network (Network 14) was associated fairly exclusively with emotional withdrawal. Although both the posterior cingulate and parietal cortex serve as cortical hubs (56) and “rich club” areas (15), the right parietal lobe is also associated with social behavior and spatial attention. Thus, these networks defined solely on the basis of source-resolved alpha phase-locking appear to reflect reasonable physiological networks derived via white matter-based connectomics that are known to be compromised functionally and structurally in schizophrenia. It is reasonable to suggest that dysfunction of alpha communication between distal brain areas may play a role in some of the more complex behavioral symptoms in schizophrenia, such as thought disorder. Understanding the network architecture of a biologically validated information carrier frequency (alpha) is an important first step in isolating the systems-level pathophysiology in psychosis.

The analysis in this study is limited by spatially down-sampling into Brodmann areas to reduce dimensionality. This regional simplification of the brain could explain why alpha activity could be substantially represented with 17 functional networks. The development of improved processing techniques, especially those that would decrease the computation load of S-PLV and NMF in higher-dimension datasets would allow for analysis of the brain with less spatial down-sampling. This would remove any biases that may be present due to the Brodmann atlas as well as potentially facilitate in better localization of neural differences between the subject groups. Methods to perform spectral connectivity across all nodes have been developed (69), and do not suffer from potential issues associated with spatial down-sampling. However, accurate functional parcellation of the cortex is needed to translate these purely spatial networks into physiological systems. Currently we are developing methods to parse the brain based on the Human Connectome Project multimodal functional parcellation (70). This would be a significant improvement over anatomic sulcal-gyral schemes (i.e., Desikan, Destreaux methods) and our gross cytoarchitechtonic approach using down-sampled Brodmann areas. A major difference between our study and others is that resting state alpha activity is typically lower in schizophrenia patients, but that was not the case here. It is possible that differences in alpha power arise later in the disease, as these were all individuals at the first episode of psychosis. However, other studies (e.g.73) showed reductions of relative alpha power in EEG at Cz, suggesting the abnormalities is present early in disease course. Eyes open resting activity may identify functional networks that differ from on-task functional networks. Future studies should compare alpha power between eyes-open and eyes-closed conditions as well as active and passive tasks, and compare EEG vs MEG cortical surface resolved measures. Further, such work should investigate changes longitudinally and across the disease course, and compare network segmentation using NMF to other methods such as Graph-ICA (71) on the same MEG dataset. Additionally, while the sample size in this study is similar to others in the literature, it limits the statistical significance of the findings and may allow for over-fitting of outliers in the model. Although this is a relatively large sample of FESz (n=31), it was underpowered for the large number of correlations performed. Thus, caution in interpretation, and replication in an independent sample are needed. However, because this is the first study to use NMF to derive data-driven functional networks in alpha activity showing aberrations in FESz, it is important to examine the full rich set of clinical symptoms in this special sample; 1% of the population at their first transition to psychosis. We leave it to the informed reader’s discretion to interpret the correlations reported for individual items. Medication may affect brain network function, and we are unable to address that possible confound. Still participants were only acutely medicated and had less than 2 months lifetime exposure, so chronic medication effects are unlikely. Future work should assess these possible confounds now that candidate systems have been identified.

Overall, we computationally derived neurophysiological networks that display deficient alpha activity in FESz. These abnormalities were associated most strongly with overall symptom severity and thought disorder, with the left posterior temporal network also associated with positive and negative symptom factors. By isolating these irregular networks hidden within the context of undetectable differences in global alpha activity, NMF proves to be a promising tool to isolate communication networks for detailed analyses of systems-level pathophysiology. Using methods that are relatively light computationally, it is possible to identify networks and regions that show selective dynamic abnormalities close to the emergence of psychosis, which may in turn be central to the etiology of psychopathology. These network locations and dynamic abnormalities also provide features to train future data-driven algorithms and guide investigation of pathology in more complex features. Alpha activity, one of the basic carrier frequencies in the brain that establishes distributed cortical circuits, identifies core areas of pathophysiology in the early schizophrenia spectrum.