Reconstruction of cell-type specific interactomes at single-cell resolution

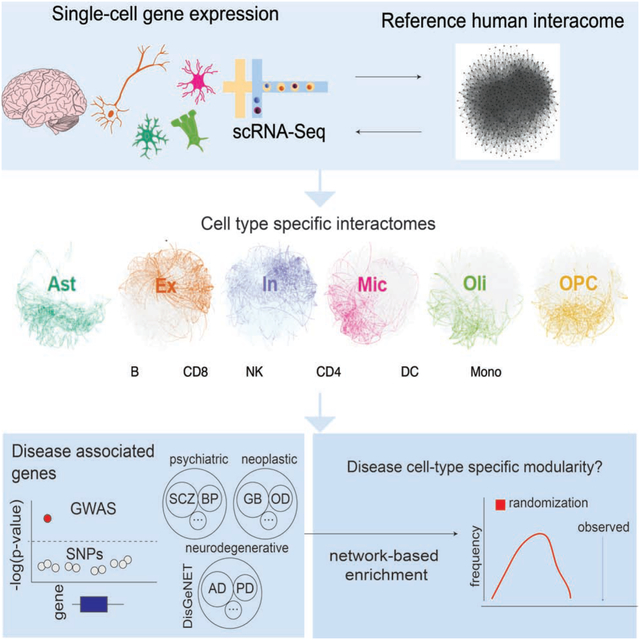
Summary:

The human interactome is instrumental in the systems-level study of the cell and the contextualization of disease-associated gene perturbations. However, reference organismal interactomes do not capture the cell-type-specific context in which proteins and modules preferentially act. Here we introduce SCINET, a computational framework that reconstructs an ensemble of cell-type-specific interactomes by integrating a global, context-independent reference interactome with a single-cell gene expression profile. SCINET addresses technical challenges of single-cell data by robustly imputing, transforming, and normalizing the initially noisy and sparse expression data. Inferred cell-level gene interaction probabilities and group-level interaction strengths define cell-type specific interactomes. We use SCINET to reconstruct and analyze interactomes of the major human brain and immune cell-types, revealing specificity and modularity of perturbations associated with neurodegenerative, neuropsychiatric, and autoimmune disorders. We report cell-type interactomes for brain and immune cell-types, together with the SCINET package.

Graphical Abstract

eTOC

Mohammadi et al. introduce a computational framework to infer the context-specificity of gene interactions based on single-cell transcriptomic data and a reference global interactome.

Introduction

Proteins participate in crosstalking pathways and overlapping functional modules that collectively mediate cell behavior. The complete set of molecular components and interactions form an “interactome,” which, although incompletely characterized, has provided a reference structure for the systems-level study of multiple organisms, and a core framework for network biology (Barabási & Oltvai, 2004). In the past decade, large efforts have reconstructed multiple organismal reference networks (Li et al., 2017; Rolland et al., 2014). The study of the human interactome, in particular, has been instrumental in revealing the structural context, modularity, and potential mechanisms of action of disease associated perturbations (Loscalzo, 2017; Menche et al., 2015), which often tend to disrupt protein-protein interactions (Salmi et al., 2015).

Reference organismal networks, however, do not provide information about the specific spatiotemporal context in which gene interactions might occur (Caldu-Primo et al., 2018), prohibiting the direct study of the context where the effect of their perturbation most likely manifests. One approach to incorporate context into a global interactome network is by considering the transcriptional dynamics of the network’s components, effectively integrating a static snapshot of the space of all potential interactions with context-specific gene expression. This approach has been previously applied to construct tissue-specific networks, taking advantage of bulk gene expression measurements (Mohammadi & Grama, 2016; Magger et al., 2012; Bossi & Lehner, 2009). With the recent development and increasing use of single-cell technologies, it is now possible to profile large-scale cell atlases of heterogeneous tissues and cell populations across multiple organisms (Tabula Muris Consortium et al., 2018; Regev et al., 2017; Rozenblatt-Rosen et al., 2017). The increasing availability of these data provides a unique opportunity to study the context-specificity of molecular interactions at single-cell resolution. A naive approach to infer cell-type-specific networks would be to adopt techniques developed for bulk expression data. In practice, however, single-cell datasets are extremely sparse, with many genes having zero expression values due to both biological and technical reasons (Angerer et al., 2017). Moreover, single-cell profiles enable estimating of interaction strength distributions within cell groups, directly assessing inter-cellular interaction variability. However, the increase in resolution comes at a computational cost due to the increasing size of cell-level data. Therefore, the development of efficient and robust techniques is required to transition to a single-cell network biology.

Here we introduce SCINET (Single-Cell Imputation and NETwork construction), a computational framework that overcomes technical limitations in single-cell data analysis, enabling the reconstruction of single cell and cell-type specific interactomes by integrating a reference interactome with single-cell gene expression data (Figure 1A). SCINET includes multiple features that directly meet challenges associated with single-cell analysis. First, a regression-based imputation step circumvents the high level of noise and sparsity intrinsic to single-cell data by inferring missing values and balancing gene expression levels. Second, a rank-based inverse normal transformation accounts for the large difference in expression distribution among different genes, resulting in comparable expression scales. Third, a statistical framework with analytical closed-form solution enables efficient inference of gene interaction likelihoods. Finally, a subsampling scheme allows the computation of cell-type (group) level interaction strengths, despite cell-level data incompleteness. Altogether, SCINET simply takes as input a reference interactome network, a scRNA-seq count matrix, corresponding cell-type (group) annotations; and it returns a set of cell-type (group) specific weighted networks. Interactions within the resulting cell-type specific interactomes are represented by their estimated mean strength and standard deviation across the cells of each group.

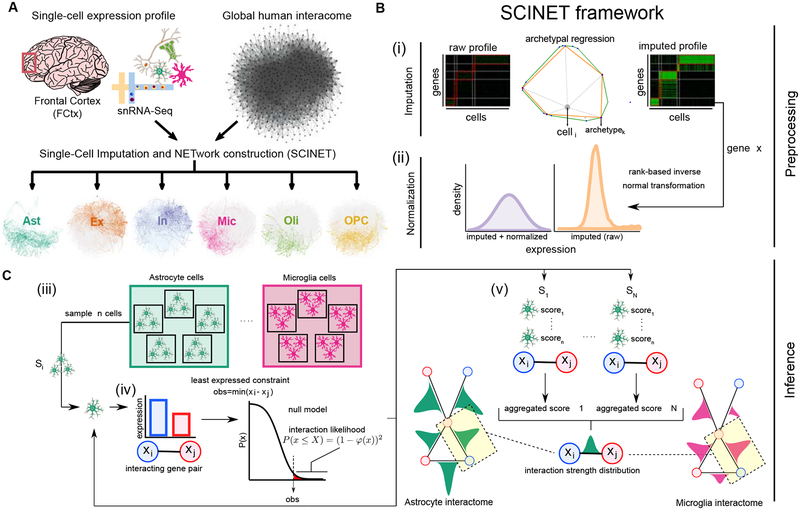
Figure 1. Overview of SCINET.

A, SCINET integrates a reference interactome network with a cell-annotated single-cell transcriptomic dataset to reconstruct cell-group specific interactomes. In this study we applied SCINET to produce cell-type interactomes for the major cell-types of the adult human frontal cortex. B, SCINET preprocesses single-cell expression by first using a matrix decomposition method to interpolate values for missing observations. Subsequently, the distribution of expression values is transformed into a common and comparable distribution using rank-based inverse normal transformation. Preprocessing results in across-gene comparable gene activity scores. C, SCINET infers interaction strength distributions for each interaction and cell-type(group) using an efficient statistical framework introduced here. A sample of n cells of a certain type is randomly chosen from the cell-type population. For each cell, the minimum activity score of each pair of interacting genes is used to quantify the strength of a potential interaction based on the tail of an analytical null model measuring the likelihood of observing such value under independence. The scores computed for the n samples cells are then aggregated into one aggregate score (meta p-value). The sampling procedure is repeated a large number of times. Finally, the mean and variance of the distribution of aggregate scores is recorded for each gene interaction and cell-type (group).

In network analysis, it is intuitively considered that highly connected nodes (i.e., hubs) are major determinants of systems behavior (Kitsak et al., 2010). In fact, hub proteins of reference interactomes in model organisms have been associated with properties suggestive of functional influence and constraint, such as essentiality, conservation, and phenotypic effects upon perturbation (Barabási & Oltvai, 2004). Starting from a reference interactome, where “hubness” is defined based on the invariant number of total interactions for a node, SCINET infers cell-type specific networks; where dynamic interaction strengths capture cell-type specific transcription. The present framework can be used to study the relationship between cell-type specific hubness and the context-specific role of the corresponding genes; as well as the patterns of preferential cell-type modularity of disease associated genes. We explore these general problems in two case studies: human brain and blood cells.

Using single-nucleus RNA-Seq (snRNA-Seq) data from 10,319 cells of the human prefrontal cortex (Lake et al., 2018), scRNA-seq data from 24,944 blood cells (van der Wijst et al., 2018), and an integrative reference interactome combining data from 21 gene interaction resources (Huang et al., 2018), we applied SCINET to infer networks specific to six major cell-types of the human prefrontal cortex and to six major immune cell-types. From brain data, we reconstruct astrocyte, excitatory neuron, inhibitory neuron, microglia, oligodendrocyte, and oligodendrocyte progenitor interactome networks. From blood data, we build CD4 T-cell, CD8 T-cell, natural killer (NK), monocyte, B-cell, and dendritic cell interactome networks. These networks enable the distinction of topologically-specific genes, whose overall interaction strength is highly cell-type-specific, vs. topologically-invariant genes, whose connectivity pattern is not predominantly influenced by the cell-type context. Finally, we use the set of cell-type specific networks to evaluate whether perturbations associated with immune or brain-related disorders show cell-type specific modularity by assessing the strength of the local connectivity of disease genes in each network. Overall, our method and approach provide a general framework to study the context-specificity of global interactome networks using single-cell transcriptional profiles. The SCINET framework is applicable to any organism, cell-type/tissue, and reference network; it is freely available at https://github.com/shmohammadi86/SCINET.

Results

Methodological overview

The core SCINET framework (Figure 1) is based on the following methodological developments: (i) a decomposition method to interpolate values for missing observations in the scRNA-Seq profile, (ii) a parametric approach to project heterogeneous gene expression distributions into a compatible subspace (Figure 1B), (iii) a statistical framework to measure the likelihood of gene interactions within each cell, and (iv) a subsampling approach to aggregate interaction likelihoods of individual cells, reduce noise, and to estimate the underlying distribution and variability of interaction strengths within each cell-type population (Figure 1C).

The first component (i) is built upon our previously developed method ACTION (Mohammadi et al., 2018). Briefly, a single-cell expression matrix is iteratively decomposed into lower dimensional matrices at different levels of granularity defined by a number of low-rank factors (archetypes). This results in a small set of landmark transcriptional states (patterns) that optimally represent the variability in the dataset. We then use the set of discovered patterns to interpolate transcriptional profiles for individual cells (Figure 1B, i) (Methods). The second component (ii) was designed to overcome the fundamental differences in the expression distribution of genes, and their particular skewed distribution across single cells. The original values do not allow a direct comparison of the distributions of different genes. We approached the problem by using a rank-based inverse normal transformation to rescale the gene expression distributions, producing a common, normally distributed subspace. We refer to the resulting interpolated and normalized expression profiles as gene activity scores (Figure 1B, ii). SCINET components (iii) and (iv) introduce a statistical framework that maps gene activity scores to the reference interactome. We assume that the feasibility of occurrence of an interaction within a cell is dictated by the interacting partner with the weakest activity. To formalize this notion, we use the minimum activity score of each pair of interacting genes as a statistic to assess the potential strength of the interaction in a given cell. We quantify such potential for each interaction pair and cell using the tail of an analytical null model measuring the likelihood of observing a certain interaction strength under independence (Methods). We then aggregate strength scores by combining the individual likelihood values within random subsamples of cells into a meta p-value using Fisher’s method (Fisher, 2006). Finally, to account for the variability of the interaction strength scores across cells, component (iv) employs a subsampling scheme to estimate an interaction strength distribution for each interaction and cell-type (Figure 1B, iii–v).

Constructing interactomes for major cell-types of the human cortex

We use single-cell expression data of the human prefrontal cortex reported in (Lake et al., 2018) to infer cell-type specific interactomes. After removing endothelial cells and pericytes (due to the small size and low reliability of cell annotation) and independently combining cells annotated as subtypes of excitatory or inhibitory neurons, we defined a set of cell-type annotations considering the 6 major cell-types of the brain: astrocytes, excitatory neurons, inhibitory neurons, microglia, oligodendrocytes, and oligodendrocyte progenitor cells (Opc). The dataset includes the expression values of 22,002 genes across 10,223 cells. Among these genes, 6,822 were expressed in less than ten cells and were removed from the study, resulting in a total of 15,180 retained genes. We selected as reference human interactome a recently curated gene network, the parsimonious composite network (PCNet) (Huang et al., 2018). PCNet was constructed by integrating 21 network databases, retaining only interactions supported by at least two independent sources; it includes 2,724,724 (2.7M) interactions among 19,781 genes. PCNet is an up-to-date (as of 2018) source of supported gene interactions representative of multiple interaction modalities. Notably, this network has been evaluated with regard to its power to predict network relationships among disease associated genes. After intersecting PCNet and the filtered expression profile, we obtained a reference network of 1,882,141 (1.8M) interactions among 13,581 genes.

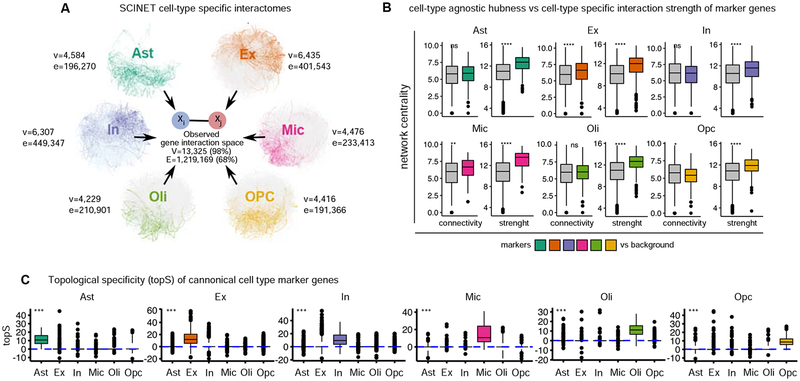
We applied SCINET to the matched scRNA-Seq count matrix and PCNet network to reconstruct 6 cell-type specific networks. These networks have between 4886 and 7331 genes (35.4% and 54.6% of the original PCNet network), with the smallest number of retained genes observed in the oligodendrocyte network and the largest in the excitatory neuron network. For this reconstruction, we considered a bonferroni-adjusted p-value threshold of 0.01 to prune significant edges. After pruning, and retaining only the largest connected component of each network, we obtained a final set of networks including between 4,416 (OPC) and 6,435 (Ex neurons) genes connected by a subset of interactions corresponding to 13.2–30.5% of total interactions in the reference PCNet (Figure 2A). The obtained networks show topological properties similar to those of other complex biological networks, namely skewed degree distributions with a small number of highly connected genes (Figure S1A). The vast majority of gene interactions occur only in one cell-type (private interactions), indicating that SCINET provides high specificity. One exception is interactions shared between Ex and In neurons (neuronal interactions), which account for ~18% of the interactions observed across neurons (Figure S1B). Similarly, Ast and Opc networks share ~15% of the total interactions observed in these two glial cell-types. The two neuronal and two glial progenitor cells (Ast and Opc) respectively share functional properties, which are possibly captured by common interactions recovered by SCINET. Overall, SCINET recovers cell-type specific gene networks whose patterns of shared interactions capture similarities and differences among neuronal and glial populations (Figure S2C).

Figure 2. Patterns of specificity of identified interactions.

A, summary of inferred cell-type specific networks, v, vertices/nodes; e, edges B, patterns of connectivity and interaction strength computed within cell-type specific networks for canonical markers of each cell-type. Statistical test: two-sided Wilcoxon rank sum test. C, distribution of topological-specificity scores computed for each cell-type specific network for canonical transcriptional markers of a particular cell-type. Statistical test: Kruskal–Wallis one-way analysis of variance. Convention for symbols indicating statistical significance: ns: p > 0.05, *: p <= 0.05, **: p <= 0.01, ***: p <= 0.001, ****: p <= 0.0001. See also Figure S1.

Given the high dropout rate of single-cell profiles, gene expression imputation is crucial prior to transformation in order to ensure proper ranking of cells. However, SCINET is robust to the choice of imputation method as it only uses the rank-order statistic to perform the transformation. We verified that pairwise relationships are consistent before and after the proposed transformations by contrasting raw, imputed, and transformed gene activity scores of interacting vs. non-interacting genes (Figure S2A). Furthermore, we corroborated the robustness of the inferred networks by comparing SCINET networks to networks constructed using an alternative imputation technique, MAGIC (van Dijk et al., 2018) -- i.e., substituting SCINET step 1. We observed high overlap among inferred interactions (Figure S2B). The final set of reconstructed brain cell-type interactomes is available as Data S1.

Topological-specificity highlights genes with preferential cell-type influence

We next studied the relationship between cell-type specific hubness and the context-specific role of the corresponding genes. We examined whether known canonical cell-type markers have a distinctive topological role in the networks. We found that total connectivity alone does not discriminate markers from non-marker genes. With the exception of Ex neurons, marker genes do not show a significantly higher number of interactions in their corresponding cell-type, relative to non-marker genes. On the other hand, in all cases, markers do show a significantly higher aggregate interaction strength (sum of SCINET inferred interaction strengths) relative to non-markers in the same cell-type (Figure 2B). This observation suggests that SCINET is able to infer context specific influence as measured by interaction strengths.

To directly quantify the influence of a gene in a given context, while decoupling the effect of its reference connectivity, we introduce a measure of gene topological-specificity (topS). topS decouples the two centrality measures (connectivity and strength) by measuring the deviation of the observed overall strength of the interactions of a gene in a given cell-type, relative to the expected strength under a random model that preserves the reference topology of the interactome but reshuffles cell-type specific interaction strengths (Methods). To verify that topS captures topological information additional to that captured by connectivity and strength, we performed additional simulated perturbation experiments (Albert et al., 2000; Caldu-Primo et al., 2018). In particular, we tested whether rational perturbation strategies (network attacks), where genes are incrementally removed from the network in an order determined by either their total connectivity (node degree), strength (sum of interaction weights), or topS, produce distinct global patterns of network vulnerability. Measuring the effect on network size (number of connected genes) and network connectivity (number of edges) upon each type of network attack, we found that, indeed, topS consistently produces a distinct behavior: unlike degree and strength, network size seems to tolerate topS attacks, while the total network connectivity of the networks is more vulnerable to topS than to either strength or random attacks, yet not as extreme as to degree attacks (Figure S3). Next, we considered whether genes with high topS also display distinctive biological roles. We tested whether curated cell-type marker genes tend to rank high in topS for the corresponding cell-type and not for the others. We found that marker genes, indeed, exhibit a significantly higher topS in the corresponding cell-type (Figure 2C), indicating that the inferred local interaction strengths capture cell-type relevant biological roles that are not explained by reference connectivity alone. Consistent with the cell-type specific increase patterns in topS scores, we found that many of the top ten topS genes for each cell-type correspond to known canonical markers of consistent cell-types (Table S1).

Identification of non-specific genes with cell-type specific interactions

Marker genes by definition are transcriptionally specific -- i.e., are specifically expressed in the cell-type in question. It was previously shown that constitutive proteins may acquire context-specific effects by means of tissue-specific interactions (Bossi & Lehner, 2009). We reasoned that topS will capture such counterintuitive property, even when globally both transcriptional and topological specificity correlate (Figure S4A). We used topS scores to systematically identify genes with a preferentially influential role in a cell-type network that is not explained solely by their expression pattern. By comparing a gene’s measure of transcriptional specificity (tranS) with its topS, we identified groups of genes with high topS and low tranS (Figure S4B). These genes are expressed in multiple cell-types, but, through patterns of cell-type specific interactions, play differential centrality roles across the networks. Among the top 3 genes with the strongest deviation in topS relative to tranS per cell-type, we identify, for example, genes involved in generic functions such as protein folding (HSP90AB1) and energy homeostasis (CKB); as well as genes with more specific functions such as membrane transporters with activity in multiple glial cells (SLC1A2, SLC1A3). Transcriptional and topological specificity scores are available as Table S2.

Cell-type specific network context of disease associated genes

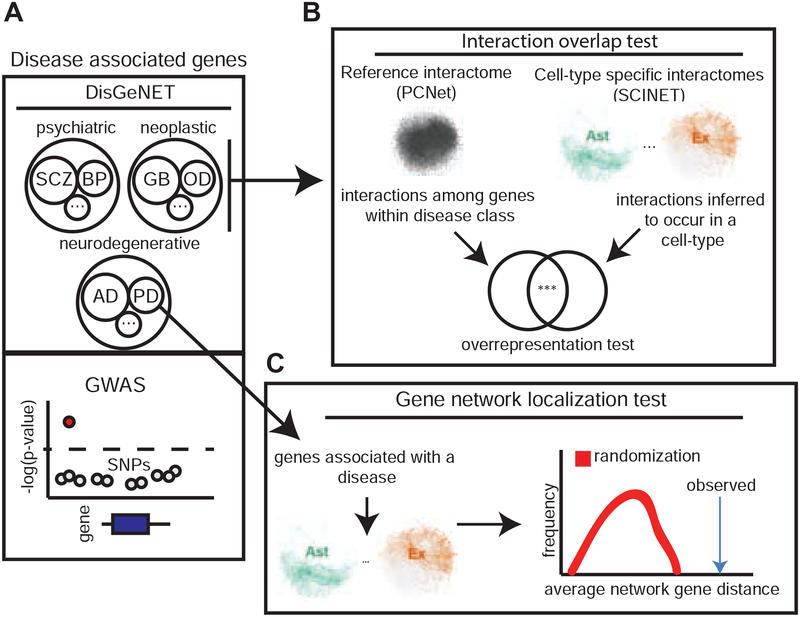
As an example of downstream analysis, we used cell-type interactomes to study the network context of disease associated genes and the patterns of gene interaction variability across cell-types. We employed two statistical tests: one based on the degree of overlap of direct gene interactions among disease genes (interactions overlap test), and the other based on the network localization patterns of disease genes (network localization test) (Figure 3A–C). The overlap of interactions was used to assess whether interactions among genes known to be associated with diseases of the same class tend to unexpectedly occur in a given cell-type (Figure 3B). The network localization of genes was used to test whether genes associated with a specific disease collectively tend to localize close to one another in the interactome of a given cell-type (Figure 3C). This latter analysis is motivated by previous studies showing that disease genes tend to form coherent neighborhoods in the human interactome (Menche et al. 2015). For these analyses, we collected and annotated gene-disease associations for brain-related disorders by matching the DisGeNET database (Piñero et al. 2017) with annotations from the Monarch Disease Ontology (MONDO) (Bello et al., 2018) (Figure 3A). Only genes reported as curated were considered (Figure S5A). We organized diseases in three separate classes: (i) neurodegenerative, (ii) neuropsychiatric, and (iii) neoplastic disorders. In total, we analyzed 5,069 protein coding genes that have been associated with at least one of 29 brain disorders: 5 neurodegenerative, 6 neoplastic, and 18 psychiatric. The genes analyzed are those present in both DisGeNET and PCNet. For additional, independent analyzes, genes genetically associated with disease risk through genome-wide association studies (GWAS) were extracted from either the NHGRI-EBI GWAS catalog or reference studies for Schizophrenia (SCZ) and autoimmune disorders (Methods). All disease associated genes used in the analyses are reported in (Table S3).

Figure 3. Network analysis of disease associated genes,

a, disease associated genes are retrieved from DisGeNET database or independently from particular GWAS studies, and brain-related disorders are classified in 3 disease classes: psychiatric, neoplastic, and neurodegenerative. b, An interaction overlap test is performed to test whether interactions reported in PCNet and connecting genes from the same disease class are overrepresented within the interactions predicted by SCINET to occur in a given cell-type, c, For each individual disease, a network localization test is performed to quantify the degree to which disease genes form compact modules within a given cell-type specific interactome network. See also Figure S5.

Disease-associated genes tend to be connected by cell-type specific interactions

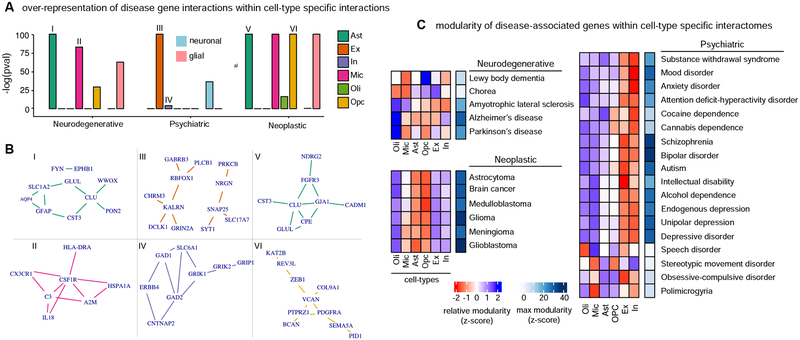
We used the set of “disease genes” associated with brain disorders to perform interactions overlap tests (Figure 3B). We constructed disease subnetworks by extracting from the global interactome only the disease-associated genes and the direct interactions among them. The set of interactions corresponding to all diseases within a disease class was then aggregated to form disease class networks. This analysis resulted in 202,598, 203,324, and 263,950 interactions directly connecting genes associated with neurodegenerative, neuropsychiatric, and neoplastic disorders, respectively. These disease class networks represent context-agnostic interactions among disease-associated genes supported by PCNet. To assess whether gene interactions for different disease classes preferentially occur in specific cell-types, we performed an interaction overlap test for each cell-type: we evaluated the overrepresentation of SCINET cell-type specific interactions within interactions linking genes of a disease group. Overall, our results suggest that disease genes tend to interact with cell-type specific preference, with preferential cell-types being targeted by the different disease classes. The first clear class distinction is that gene interactions associated with neurodegenerative and neoplastic disorders target glial cells, whereas neuropsychiatric disorder genes predominantly interact in neuronal cells (Figure 4A). In terms of specific cell-types, we found that neurodegenerative associated gene interactions are enriched among interactions in microglia and astrocyte specific networks. Neoplastic disorders are depleted among neuronal interactions and overrepresented in astrocyte and OPC interactions. Neuropsychiatric disorders are strongly enriched in excitatory neuron interactions.

Figure 4. Brain-associated disorders converge to cell-type specific modular perturbations,

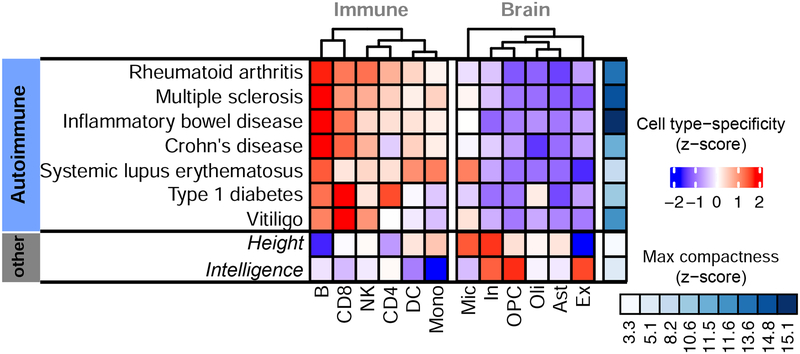
a, over-representation scores for gene interactions between disease-associated genes within cell-type specific interactions are shown for neurodegenerative, psychiatric, and neoplastic disorder groups. Cell-type (Ast, In, Oli, Ex, Mic, OPC) and cell-type group (neuronal, glial) over-representation analysis are considered. Neuronal (blue) or glial (pink) over-representation is highlighted with a rectangle. Roman numbers link cell-type and disease interaction sets with corresponding networks in b. b, top 10 strongest interactions for to associated interaction sets considering in a are shows as networks, c, network modularity scores for genes associated with individual diseases across cell-types are shown. Modularity is estimated by a compactness score that measures the deviation of module size (average measure of inter-gene network distance) relative to random expectation. Relative (z-scaled) modularity across cell-types is shown in blue-red scale. Maximal compactness for a disease is shown in blue scale. See also Figure S5.

For each dominant cell-type by disease class, we extracted the top 10 strongest interactions. In each case we found that such interactions cluster in only one or two connected modules (Figure 4B). These modules do not share genes across cell-types; however, the association of the same cell-type with multiple disease classes is mediated by different genes interacting in the same cell-type. We found Astrocytes as a cell-type strongly associated with both neurodegenerative and neoplastic disorders. Among the top astrocyte gene interactions, two interactions involving the gene CLU (CLU-GLUL and CLU-CST3) are associated with both disorder types. CLU is an example of a highly pleiotropic gene, which is associated with hundreds of diseases (according to DisGeNET associations). In the neurodegenerative context, CLU plays a chaperone role important for the prevention of amyloid aggregation and fibril formation. It also, however, plays a role in cell proliferation of relevance for neoplasia. This multiplicity of function might stem from differential use and perturbation of gene interactions, which could be more extensively studied using SCINET. In this example, we observed that a subset of CLU strong gene interactions occurring in astrocytes distinguishes associations with neoplasia (CPE, GJA1, and FGFR3) from neurodegeneration (PON2, WWOX).

Network analysis reveals cell-type-specific modularity of brain-associated disorders

We next analyzed the modular connectivity of disease genes. We tested whether genes associated with individual brain diseases display non-trivial patterns of interaction across cell-type specific interactomes; this time considering all genes and interactions in each cell-type network. We followed the rationale of network medicine, which seeks to understand the seemingly independent perturbations commonly associated with a disease in terms of their local and global patterns of connectivity in the interactome (Loscalzo, 2017). One way to operationalize such view is through the characterization of disease modules that emerge as dense and tightly compact neighborhoods that topologically localize disease genes within the network (Menche et al., 2015) -- i.e., by performing network localization tests (Figure 3C).

Using the set of curated gene-disease associations, we used network localization tests to assess whether disease-associated genes tend to localize in neighborhoods, forming cohesive modules. To quantify compactness we used an empirical measure of module size (Loscalzo, 2017), defined as the average of the distribution of network distances between pairs of disease genes. To account for the multiplicity of paths between genes, we computed diffusion-based distances (Methods). Finally, to statistically test whether the observed module size deviates from random expectation, we estimated a corresponding null distribution by repeatedly subsampling the same number of genes at random from the network, effectively allowing us to measure the deviation from expectation using a z-score (Figure 3C). Overall, we found that disease genes do localize in the cell-type specific interactomes, and that the degree of modularity of disease perturbations varies across diseases (Figure 4C). Across disease groups, neoplastic disorders show the strongest modularity, with glioblastoma genes being the most compacted. Neurodegenerative disorders showed the least modularity, with the exception of Alzheimer’s disease. Neuropsychiatric disorders, on the other hand, showed strong compactness, with SCZ and BPD having the strongest network localization.

We observed highly variable modularity across cell-type specific networks for each disorder, which again points to a pattern of preferential cell-type specificity for the different diseases (Figure 4C). Diseases within the same group show similar patterns of cell-type specificity that are distinct from those observed in the other groups. All neoplastic diseases tested show modular localization in the astrocyte and Opc networks. Psychiatric disease genes showed preferential modularity in neuronal networks, with the exception of disorders of stereotypic movement and speech, which show the strongest compactness on oligodendrocytes. Unlike the glial/neuronal polarized pattern observed for neoplastic and psychiatric diseases, neurodegenerative disorders showed a more heterogeneous convergence pattern, involving glial and neuronal cell-types in different diseases. For example, we found that genes associated with Parkinson’s disease converge in both Opc and neuron networks.

To exclude the possibility of inadverted gene preselection based on cell-type specificity on the DisGeNET database, we performed the same enrichment analyses using only GWAS genes reported for Schizophrenia. We observed similar neuronal enrichment, with the strongest enrichment in Ex neurons. To test the specificity of the analysis, we included genes associated with height as a negative control and found no enrichment (Figure S5B).

Genes associated with autoimmune-disorders exhibit distinct modularity in immune cell-specific interactomes

Following the same procedure as with brain, we reconstructed 6 blood cell-type specific networks. These networks have between 5,306 and 8,841 genes connected by a subset of interactions corresponding to 2.6–7.7% of total interactions in the reference PCNet, with the smallest network corresponding to Monocytes and the largest to Natural killer cells (Table 1). Consistent with brain cell-type analyses, many of the top ten topS genes for each immune cell-type match known canonical markers (Table S1). We used these networks to analyze the modular connectivity of genes associated with autoimmune disorders across blood cell-types. We considered 7 major disorders: Crohn’s disease, Inflammatory bowel disease, Multiple sclerosis, Rheumatoid arthritis, Systemic lupus erythematosus, Type 1 diabetes, and Vitiligo. For this analysis, we again used disease risk genes identified through unbiased GWAS. To assess the specificity provided by the cell-type dynamic patterns of interaction, we performed network localization tests in both the immune and the brain cell-type networks and included two additional complex traits not directly associated with immunity (i.e., height and intelligence).

Table 1. Immune cell-type interactome statistics.

Genes(n): number of genes; Interactions(n): number of interactions; PCNet(%): percentage of total PCNET global interactions. NK: Natural killer cells; DC: Dendritic cells.

Cell-type	Genes(n)	Interactions(n)	PCNet(%)
B	6,835	675,938	6.201894
CD8	7,766	828,882	7.605192
CD4	5,447	285,011	2.615045
DC	6,301	503,002	4.615165
Monocyte	5,306	351,284	3.223115
NK	8,234	840,776	7.714323

We measured the overall network compactness of the genes associated with each disease, as well as its corresponding cell-type specificity (Figure 5). Specificity is quantified as the relative compactness observed in a given cell-type interactome relative to the compactness in others. We found that neither height nor intelligence are associated with genes forming modules within immune or brain-related networks (low global compactness). On the other hand, we found that all autoimmune disorders are individually associated with genes that do form compact modules within the immune cell-type interactomes, but not within the interactomes of brain cells. One exception was systemic lupus erythematosus (SLE), where associated genes also form a module in the microglia interactome. Microglia are the tissue-resident macrophages of the brain and share pathways with other immune cell-types. This observation is also consistent with the previous finding that lupus antibodies cause cognitive impairment in SLE patients, mediated by activated microglia (Nestor et al., 2018). We observed a strong association between B-cells, which are responsible for auto-antibody production (Hampe, 2012), and the majority of autoimmune disorders. Both type-I diabetes and vitiligo, on the other hand, were found to form gene modularity in T cells, consistent with their reported T-cell mediation (Pugliese, 2017, Byrne et al., 2014). To aid more in-depth analyses of the molecular networks involved in immune disorders, immune cell-type interactomes are available as Data S2.

Figure 5. Modular connectivity of genes associated with autoimmune disorders.

Network modularity scores for genes associated with 7 autoimmune disorders by GWAS. Relative (z-scaled) modularity across cell-types is shown in blue-red scale. Maximal compactness for a disease is shown in blue scale.

Discussion

We introduced SCINET, a computational framework that enables the reconstruction of cell-type specific interactomes by leveraging single-cell transcriptomic data. By inferring and quantifying cell-type specific gene interaction strengths, SCINET provides a cellular context to interpret molecular pathways and functional modules. SCINET can be used to contextualize disease associated genes and their quantifiable influence in different cell-types or conditions, to study potential mediators of functional interactions between cell-types, or to assess the dynamics of interaction usage across developmental or pathological conditions.

In the general context of network biology, we show how SCINET can measure a gene’s network influence score that is context-specific but not explained by either the gene’s reference connectivity or by expression specificity alone. Instead, differential patterns of interactions determine the context specific influence of promiscuously expressed genes. This feature, in turn, could aid the identification of genes with broad expression but condition specific interactions in future studies.

In the context of disease, our results suggest that the contextualization of disease associated genes within the topologies of cell-type specific networks uncovers nontrivial, systems-level interaction patterns that provide information on the phenotypic manifestation of the disease. Genes known to be associated with disease classes tend to present direct mutual interactions that preferentially occur in specific cell-types. For example, neurodegenerative disorders preferentially target interactions in astrocyte and microglia cells, while psychiatric disorders strongly target neuronal specific interactions. Thus, similar to other approaches based on genetic associations and gene expression (Skene et al., 2018), our network-based approach recovers the dominant role of inflammatory glial cells (microglia and astrocytes) in neurodegeneration, and the known role of neuronal cells in psychiatric disorders. On the other hand, the consideration of connectivity patterns involving genes which have not yet been associated with a specific disease enables the identification of cell-type specific modular perturbations.

In the case study of the brain, diseases within the same group show similar patterns of cell-type specificity that are distinct from those observed in the other groups. This observation is consistent with the idea of an association between cell-type convergence patterns of disease perturbations and observed symptomatology, as disorders within the groups more often share patterns and comorbidity than diseases across groups. Moreover, individual diseases show variable modularity across cell-types, a property that we used to define cell-type perturbation profiles for the disorders. The computed profiles are highly similar across phenotypically-related disorders, with strong preferential modularity in cell-types consistent with the biology of the disease. Disorders of stereotypic movement and speech showed the strongest compactness on oligodendrocytes, and observation consistent with the myelinating role of oligodendrocytes, as these disorders involve motor deficiency, which is severely affected in cases of pathophysiology affecting myelin. Indeed, white matter abnormality in the form of delayed or absent myelination has been associated with childhood apraxia of speech (Liégeois & Morgan, 2012). Contrasting neuron types, genes associated with mood and depression disorders seem to perturb more strongly the inhibitory neuron network. Different lines of evidence associate deficits in inhibitory neurotransmission to major depressive disorder, such as the reduction of GABA A receptor-mediated cortical inhibition in both late-life and adult depressed subjects relative to controls (Levinson et al. 2010), (Lissemore et al., 2018).

Our approach also recovers an association of OPC and astrocytes with brain tumors, and suggests an important role of inflammation in neoplasia. These two cell-types have proliferative potential and have been discussed in the context of the cell of origin for malignant gliomas (Zong et al., 2015). However, evidence from the specific origin of the tumors in vivo has been proved challenging, given the overlap in gene signatures of astrocytes and neuron progenitor cells. Although we only considered transcriptional states from the adult human brain, SCINET robustly captures the sternness property of the interactomes of astrocytes and Opc and its association with brain carcinogenesis. Finally, neurodegenerative disorders showed a more heterogeneous convergence pattern, involving glial and neuronal cell-types in different diseases. This observation might point to the relevance of glial-neuronal interactions, and the conditionality of the protective or damaging effect of glial cell states (De Strooper & Karran, 2016). For example, consistent with deficiencies on remyelination having an effect on the proper firing of motor neurons, we found that Parkinson’s disease genes modularly converge in both Opc and neuron networks. The observations of network association among disease genes generalize to the case study of immune cells, where Immune disorders display a strong association with B-cells. These cells are known to play a key role in the pathogenesis of autoimmune disorders via production of autoantibodies and inflammatory cytokines, as well as regulating interactions with T-cells (Hampe, 2012).

SCINET is of general applicability and can be used to analyze any combination of cell conditions and reference (physical and/or functional) interactomes. For cell-type interactome inference, the framework assumes that reliable cell group annotations are available, therefore the resolution in which homogeneous groups of cells representing types can be identified is a potential limiting factor. Overall, our results indicate that the contextualization of contrasting disease/trait associated genes through the topologies of cell-type specific networks from different tissues provides meaningful and interpretable information, thus demonstrating the generality and specificity of SCINET. We envision SCINET as a simple to use computational tool to aid in the design and interpretation of cell-type resolution experiments and to uncover context-specific convergence of heterogeneous and seemingly independent genetic perturbations.

STAR METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for data, associated code, or resources should be directed to and will be fulfilled by the first Lead Author, Shahin Mohammadi (mohammadi@broadinstitute.org). This study did not generate new unique reagents.

METHOD DETAILS

Single-cell data preprocessing

Single nuclei RNA sequencing data from human frontal cortex (9 male, 4 female individuals) reported in (Lake et al. 2018) was downloaded from the Gene Expression Omnibus under SuperSeries accession code GSE97942. After quality control, this dataset contains a total of 10,319 single cells (4,164 and 6,155 cells from BA6 and BA10 regions, respectively). Six major cell-types of the brain were considered: astrocytes, excitatory/inhibitory neurons, microglia, oligodendrocytes, and oligodendrocyte progenitor cells (OPCs). All subtypes of excitatory and inhibitory neurons were independently combined to create cell-type annotation for these two classes. Single-cell RNASeq data of human peripheral blood mononuclear cells (PBMC) reported in (van der Wijst et al. 2018) was downloaded from the European Genome-phenome Archive (EGA) under accession number EGAS00001002560. Raw data contained 28,855 cells from PBMCs of 47 donors. After basic preprocessing, 16,375 protein-coding genes and 24,944 cells representing 6 major blood cell-types (CD4 and CD8 T-cells, NK cells, monocytes, B cells, and dendritic cells) were retained.

Additional reference data sources

The Parsimonious Composite Network (PCNet) (Huang et al., 2018) was used as reference human interactome (NDEx, UUID: f93f402c-86d4-11e7-a10d-0ac135e8bacf). This network was constructed by combining 21 heterogeneous network resources, including STRING, ConsensusPathDB, and GIANT, among others. PCNet retains edges that are supported by at least two independent sources of evidence, which leads to a high-sensitivity and high-specificity network that outperforms any individual network with respect to predicting disease-associated genes (Huang et al., 2018). PCNet was used throughout the study, and we refer to it as the “global human interactome”.

Cell-type marker genes defined in (Lake et al., 2018) were used. Only genes with at least 1-log-fold-ratio difference when cells of a given cell-type are compared against the rest of cells were considered. This resulted in marker genes for astrocytes (79), excitatory neurons (162), inhibitory neurons (304), microglia (45), oligodendrocytes (103), and OPCs (52).

Disease-associated genes were collected from the DisGeNET database (http://www.disgenet.0rg/web/DisGeNET/menu/d0wnl0ads#gdasbefree; RRID:SCR_006178) (Pinero et al., 2017), which aggregates data from GWAS catalogues, animal models, and the scientific literature; preserving the evidence type supporting each disease-gene association. All disorders were mapped to the Monarch Disease Ontology (MonDO) (https://www.ebi.ac.uk/ols/ontologies/mondo) (Bello et al., 2018) and brain-associated disorders corresponding to (i) neurodegenerative, (ii) neuropsychiatric, and (iii) brain cancers were selected. To this end, first diseases that are associated with nervous system (annotated with “nervous system disorder (MONDO_0005071)” term) were selected. Then selected disorders were intersected with disorders annotated with “neurodegenerative disease” (MONDO:0005559), “psychiatric disorder” (MONDO:0002025), and “neoplastic disease or syndrome” (MONDO:0023370) terms. The final dataset contains 5 neurodegenerative disorders, 18 neuropsychiatric disorders, and 6 types of brain cancers. GWAS genes for Schizophrenia were independently obtained from the SZDB2 database (Wu et al., 2017) (http://www.szdb.org), including genes identified by major GWAS consortiums PGC2 and CLOZUK + PGC.

Autoimmune disorders and their associated genes were extracted from the NHGRI-EBI GWAS catalog (https://www.ebi.ac.uk/gwas/) (MacArthur et al., 2017). A total of 7 traits were identified and considered in the study: Crohn’s disease (n=175 genes), Inflammatory bowel disease (n=235), Multiple sclerosis (n=199), Rheumatoid arthritis (n=138), Systemic lupus erythematosus (n=258), Type 1 diabetes (n=87), and Vitiligo (n=70). Two additional traits were extracted to be used as negative control: Height (n=404), Intelligence (n=257).

Compactness and of disease-associated genes

Random-walk methods are effective techniques to establish network-based relationships among disease-associated genes (Köhler et al., 2008). Here, a symmetric version of the random-walk with restart process is used to prioritize disease genes (Vanunu et al. 2010). More specifically, given a cell-type-specific network represented using its adjacency matrix, A, the following stochastic, symmetric transition matrix is defined:

$$P_{sym}=D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$

where $D^{-\frac{1}{2}}$ is a diagonal matrix with the strength of each node (column sums in A) as diagonal elements. Using this transition matrix, the stationary distribution of the random-walk process is defined in closed form as:

$$S=(1-\alpha ){(I-\alpha P)}^{-1}{e}_{gs}$$

where e_gs is a stochastic vector of restart probabilities and α a parameter that adjusts the depth of the random-walk process (^{(1 − α)} is the probability of starting a new random-walk from one of the seed nodes in e_gs). To compute the α parameter, an approach similar to the one proposed in Huang et al. (Huang et al., 2018) was used. Briefly, the optimal choice of α is set using the following linear model against the log10-adjusted number of interactions in the network (nE):

$${\alpha }_{opt}=m\times {\mathit{\text{log}}}_{10}(nE)+b$$

where m = −0.03 andb = 0.75.

Finally, we define the restart probabilities encoded in vector e_gs based on the topological-specificity of the corresponding proteins as follows:

$$e_{gs}(i)=\{\begin{array}{ll}\frac{1}{1+e^{-\left\{z_{\mathit{\text{topo}}}(i)\right\}}},\hfill & v_i\in \mathcal{D}\hfill \\ 0,\hfill & \text{ otherwise }\hfill \end{array}$$

where $\mathcal{D}$ is the disease geneset of interest. The resulting vector was normalized by its sum to construct a stochastic vector to be incorporated in the random-walk.

Topological specificity analysis

A measurement is introduced to decouple the global, context-agnostic connectivity of a gene as provided by its number of interactions in the global interactome, from the cell-type-specific strength of interactions incident to the gene in cell-type-specific network. First, the hubness of each gene in a given cell-type-specific network is computed as the total strength of its local neighbors, represented by w^(celltype)(i) for each protein i. Second, a random model is used to estimate the deviation of this observed hubness relative to random expectation. The random model consists of an ensemble of networks in which the underlying topology of the global interactome is preserved while the cell-type-specific edge weights are reshuffled uniformly at random. For each random network, the strength of interactions is recomputed, resulting in a distribution of gene neighborhood strengths for each gene. Using the mean and standard deviation of each distribution ${\mu }_R^{(\mathit{\text{celltype}})}(i)$ and ${\sigma }_R^{(\mathit{\text{celltype}})}(i)$, respectively; the topological-specificity of each gene in a given network is defined as:

$$z_{\mathit{\text{topo}}}(i)=\frac{\left(w^{(\mathit{\text{celltype}})}(i)-{\mu }_R^{(\mathit{\text{celltype}})}(i)\right)}{{\sigma }_R^{(\mathit{\text{celltype}})}(i)}$$

QUANTIFICATION AND STATISTICAL ANALYSIS

Interpolation and smoothing of expression profiles via ACTION

Archetypal analysis for Cell-Type identificatION (ACTION) (Mohammadi et al., 2018) characterizes the transcriptional landscape of single cells using an optimal set of archetypal states. At the core of this method is an optimization framework to identify characteristic landmarks that can be used to optimally represent the rest of cells. Formally, given an expression matrix $S\in {ℝ}^{\mathit{\text{genes}}\times \mathit{\text{cells}}}$, ACTION identifies a set of archetypal cell states that optimally represent the rest of cells. Each of these archetypal states represents a convex (sparse) combination of cells in the data. In this regard, ACTION reduces the noise from dropouts by local averaging and smoothing of cells, while preserving the subtle state differences by enforcing a sparsity constraint on the number of cells that are being averaged. The original version of the ACTION method was based on a kernel-based formulation. To deal with the rapidly growing scale of the single-cell profiles, we implicitly reduce this kernel (of dimension cell × cell) to another subspace, $S_r\in {ℝ}^{D\times \mathit{\text{cells}}}$, such that the dot-product of columns in the reduced subspace recapitulate the kernel matrix. To this end, we compute the SVD decomposition of the orthogonalized expression profile (based on the ACTION method) as $S_{(\mathit{\text{ortho}})}^T=U_r{\Sigma }_r{V}_r^T$. Then, we compute the reduced expression profile as $S_r={\Sigma }_r{U}_r^T$, in which every row represents a metagene and each column represents a cell. Then the following optimization problem is solved to find a set of landmark cells using convex non-negative matrix factorization (convNMF):

$$\underset{\mathcal{K},H}{\text{min}}{\Vert S_r-\underset{W^{(NMF)}}{\underbrace{S_r(:,\mathcal{K})}}{H}^{(NMF)}\Vert }_F^2$$

$$\text{Subject to}:\sum _j{h}_j^{(NMF)}=1,0\le h_{ij}^{(NMF)}$$

where $h_j^{(NMF)}$ is the j^th column of the H^(NMF) matrix. Using these initial landmark cells encoded in the matrix W^(NMF), we then initialize a round of archetypal analysis (AA) to smooth and denoise them and compute the final archetypal states. Mathematically, we solve the following optimization problem:

$$\underset{\mathcal{K},H_{NMF}}{\text{min}}{\Vert S_r-\underset{W^{(AA)}}{\underbrace{S_{r}C}}{H}^{(AA)}\Vert }_F^2$$

$$\text{Subject to}:\sum _j{h}_j^{(AA)}=1,\sum _j{c}_j=1,0\le h_{ij}^{(AA)},c_{ij}$$

By initializing matrix W^(AA) = W^(NMF), this formulation enables the smoothing of the profile of archetypal cells based on a small number of “close-by” cells, as sparsity is enforced due to norm-1 constraint on the columns of C.

Another modification to the original formulation is that in ACTION the total number of archetypes $(k=\left|\mathcal{K}\right|)$ was fixed. However, different cell-types/states are best captured at different levels of resolutions, and thus different values of k could be optimal for identifying different transcriptional patterns. To address this issue, increasing values of k are allowed by running ACTION at multiple resolutions and then the set of all archetypes across resolutions are combined. The resulting set of archetypes is referred to as the multi-level archetypal set (W^(ML)). Subsequently, the matrix H^(ML) is recomputed by regressing over the W^(ML) matrix. Given the resulting multi-level archetypal profiles, which are of dimension metagene × aggregate archetypes, a reverse projection onto the state space of genes is computed using matrix V_r. Then, for each cell, the matrix H^(ML) is used to interpolate its corresponding expression profile using the archetypes profile. Putting it all together, the described algorithms is implemented in matrix operations as follows:

$$\widehat{S}=V_r{W}^{(ML)}{H}^{(ML)}$$

in which H^(ML) is computed using the multi-level archetypal set, W^(ML). This approach is fundamentally different from common gene imputation methods in that signature genes, which distinguish cell-types, and will have high-values in the interpolated profiles, even when their absolute expression value is small. Furthermore, for larger datasets, given the flexibility of matrix computations, it is possible to interpolate values for only a subset of genes and/or cells of interest -- i.e., by extracting and using in the operation only the corresponding rows/columns.

Transformation of gene expression profiles

The feasibility of an interaction in a given context is assessed by comparing and combining the expression value of each pair of interacting genes. However, different genes have different expression distributions. Moreover, the baseline expression, corresponding to the mean of these distributions, is not comparable, since some genes might be functional at much lower doses than others. To address this issue and to put expression measurements on the same scale, the rank-based inverse Normal transformation technique was used. Given the interpolated expression profile $\widehat{S}$ with m genes and n cells, two independent factors are computed, one for the expression of each gene across cells (row factor) and one for the mean expression of all genes in a given subpopulation of cells (column factor). In the former, given a gene i, its expression profile is sorted across all cells and a rank r_ij is assigned to each interpolated expression profile ${\widehat{s}}_{ij}$, which is then normalized by the total number of cells, $p_{ij}=\frac{r_{ij}}{n+1}$. The row-factor matrix, F^(r), is then computed by projecting the normalized ranks onto the standard Normal distribution: $f_{ij}^{(r)}=-\sqrt{2}\mathbf{\text{erfcinv}}\left(2p_{ij}\right)$, where erfcinv is the inverse of the complementary error function, erfc, defined as:

$$\mathbf{\text{erfc}}(x)=\frac{2}{\sqrt{\pi }}\underset{x}{\overset{\infty }{\int }}{e}^{-t^2}dt$$

Similarly, a column factor for all genes is defined. Given a subset of cells, $\mathcal{C}$, representing the cell-type of interest, columns of interpolated expression profile are averaged within the subspace of $\mathcal{C}:{\mu }_{\mathcal{C}}=\sum _{j\in \mathcal{C}}{\widehat{s}}_{ij}\in {ℝ}^m$. Then, a column factor vector $f_i^{(c)}$ is defined by transforming ${\mu }_{\mathcal{C}}$ in a fashion similar to the row factor. Finally, using the two components, a transformed, interpolated expression profile matrix, T, is defined in which $t_{ij}=\frac{f_{ij}^{(r)}+f_i^{(c)}}{\sqrt{2}}$.

Assessing co-expression dependencies between pairs of interacting proteins

Our working assumption is that an interaction can only happen if both endpoints of the interaction are expressed at a high enough level. Such notion can be formalized by requiring the minimum expression of two interacting proteins to be “large enough”. Given that the expression value of each gene is transformed to follow a standard normal distribution, under the null assumption of independence between the expression value of two genes, the right tail of the min operator can be computed using

$$P(x\le X)={(1-\phi (x))}^2$$

where x = min(t_ij, t_i′j), in which t_ij and t_i′j are the transformed expression values of gene products corresponding to vertices i and i′ incident on an interaction i − i′ in cell j, and φ is the cumulative density function (CDF) of the standard normal distribution.

This definition allows the computation of a p-value for each interaction in a given cell. To account for noise and different sample-size across cell-types a technique similar to ensemble learning was adopted by selecting k cells at random, computing their individual interaction p-values, and combining these p-values into an aggregate meta p-value using the Fisher’s combination method. Specifically, denote by $p_{i{i}^{\prime }}^{(k)}$ the p-value of interaction i − i′ occurring in the k^th sampled cell, then an aggregated p-value statistic is computed by:

$$X_{2k}^2=-2\sum _{k}ln\left(p_{i{i}^{\prime }}^{(k)}\right)$$

When the null hypothesis of each individual test is true and the tests are independent, $X_{2k}^2$ follows a χ² distribution with 2k degrees of freedom, which can be used to compute the meta p-value associated with all tests. This subsampling scheme balances the total number of cells in the given population.

Finally, we note that by repeated application of the resampling method, an empirical distribution over each gene interaction that describes its dynamic characteristics across cells can be estimated. The first moment (mean) of this distribution is used for analyses reported in the paper.

DATA AND CODE AVAILABILITY

The SCINET implementation is freely available from: https://github.com/shmohammadi86/SCINET. Brain cell-type specific interactomes are available in Data S1. Immune cell-type specific interactomes are available in Data S2. Top-ranked topologically-specific proteins are available in Table S1. Transcriptional and topological specificity scores are available in Table S2. Disease-associated gene sets are available in Table S3. All R scripts for generating these is available from https://github.com/shmohammadi86/SCINET/tree/master/demo.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Brain cell-type specific interactomes	This paper	Supplementary Data S1
Immune cell-type specific interactomes	This paper	Supplementary Data S2
Top-ranked topologically-specific proteins	This paper	Supplementary Table S1
Transcriptional and topological specificity scores	This paper	Supplementary Table S2
Disease-associated gene sets	This paper	Supplementary Table S3
snRNAseq of human prefrontal cortex	(Lake et al., 2018)	GSE97942
scRNASeq of human peripheral blood mononuclear cells	(van der Wijst et al., 2018)	EGAS00001002560
Parsimonious Composite Network (PCNet)	(Huang et al., 2018)	NDEx with the UUID: f93f402c-86d4-11e7-a10d-0ac135e8bacf
DisGeNET	(Piñero et al., 2017)	http://www.disgenet.org/web/DisGeNET/menu/downloads#gdasbefree; RRID:SCR_006178
Monarch Disease Ontology (MonDO)	(Bello et al., 2018)	https://www.ebi.ac.uk/ols/ontologies/mondo
SZDB2	(Wu et al., 2017)	http://www.szdb.org
Software and Algorithms
R version 3.5	The R project	https://www.r-project.org/
SCINET	This paper	https://github.com/shmohammadi86/SCINET
R Scripts for generating Interactomes, Scores, Gene Sets, and Protein rankings.	This paper	https://github.com/shmohammadi86/SCINET/tree/master/demo
MAGIC	(van Dijk et al., 2018)	https://github.com/KrishnaswamyLab/MAGIC
Other
GWAS Catalog	(MacArthur, J. et al., 2017)	https://www.ebi.ac.uk/swas/

Highlights.

• SCINET reconstructs cell-type interactomes from scRNA-Seq and network data.

• Single-cell resolution networks allow for analysis of gene interaction dynamics.

• Disease-associated perturbations exhibit cell-type-specific modularity.