Factor Score Regression in the Presence of Correlated Unique Factors

Abstract

Recently, quantitative researchers have shown increased interest in two-step factor score regression (FSR) approaches to structural model estimation. A particularly promising approach proposed by Croon involves first extracting factor scores for each latent factor in a larger model, then correcting the variance−covariance matrix of the factor scores for bias before using this matrix as input data in a subsequent regression analysis or path model. Although not immediately obvious, Croon’s bias correction formulas are predicated upon the standard assumption of conditionally independent uniquenesses (measurement residuals). To our knowledge, the method’s performance has never been evaluated under conditions in which this assumption is violated. In the present research, we rederive Croon’s formulas for the case of correlated uniqueness and present the results of two Monte Carlo simulations comparing the method’s performance with standard methods when the unique factors were correlated in the population model. In our simulations, our proposed Croon FSR approaches outperformed methods that blindly assumed conditionally independent uniquenesses (e.g., uncorrected FSR, traditional Croon FSR, structural equation modeling [SEM] using standard specification), performed comparably to a correctly specified SEM, and outperformed SEMs that correctly specified the unique factor covariances but misspecified the structural model. We discuss the implications of our results for substantive researchers.

Structural equation modeling (SEM) is a powerful, flexible modeling framework that allows for the simultaneous estimation of (a) postulated latent constructs, via a measurement model and (b) postulated causal relations among them, via a structural regression model (cf. Bollen, 1989; Hayduk, 1987; Jöreskog & Sörbom, 1993; Kline, 2016). The ability to estimate measurement and structural parameters simultaneously is as much a weakness as a strength, however, as misspecification in any part of an SEM may result in bias that proliferates throughout the system of equations, rendering all parameter estimates questionable. For example, misspecification in the structural portion of a model, such as omitting a nonzero path or incorrectly assuming conditionally independent disturbances, can cause parameter estimates in the measurement model to shift, obscuring the nature and meaning of the latent constructs being estimated (Devlieger & Rosseel, 2017; Hoshino & Bentler, 2013). Alternatively, misspecification in any part of the model (measurement or structural) risks injecting bias into key structural regression coefficients capturing the relations between latent constructs. This outcome is particularly harmful, because structural relationships are often of greatest interest to empirical researchers (cf. Devlieger, Mayer, & Rosseel, 2016; Devlieger & Rosseel, 2017; Hancock & Mueller, 2011; Hoshino & Bentler, 2013; Lu, Kwan, Thomas, & Cedzynski, 2011). Perhaps more troubling, such misspecifications are not always easily detected using traditional methods (Hancock & Mueller, 2011).

As a potential solution to this problem, a small but growing group of quantitative researchers have begun to recommend switching from simultaneous to multistage estimation procedures such as factor score regression (FSR; Croon, 2002; Devlieger et al., 2016; Hoshino & Bentler, 2013; Lu et al., 2011; Skrondal & Laake, 2001) and factor score path analysis¹ (Devlieger & Rosseel, 2017). In brief, FSR involves two steps: (a) first, estimate the measurement model for each latent factor in a structural regression model separately, extracting factor scores for each; (b) use these factor scores as input data in a subsequent ordinary least squares (OLS) regression or path analysis.

Because factor scores are indeterminate and, therefore, not fully reliable (cf. Grice, 2001; Steiger & Schönemann, 1978), extra care must be taken to avoid bias when treating factor scores as data. Recently, quantitative researchers have suggested two promising approaches to address possible bias when performing FSR. A first approach is to strategically extract factor scores using estimation methods designed to avoid injecting bias in the first place (e.g., using regression factor score estimation for exogenous and Bartlett factor score estimation for endogenous latent variables in the bias-avoiding approach of Skrondal & Laake, 2001). A second approach is to first extract factor scores for all latent constructs using a single estimation method, and then correct the variances and covariances of the factors for bias using analytic formulas (Croon, 2002; cf. Hoshino & Bentler, 2013). Once these variances and covariance have been corrected, they may be used either as sufficient statistics for computing regression coefficients (Croon, 2002; Devlieger et al., 2016; Lu et al., 2011) or as covariance-matrix input for a subsequent path analysis (Devlieger & Rosseel, 2017).

A series of recent simulation studies have shown that Croon’s (2002) bias-correcting FSR approach outperforms the bias-avoiding approach of Skrondal and Laake (2001) under a variety of circumstances (Devlieger et al., 2016; Lu et al., 2011). For example, the bias-avoiding method suffers from attenuated standard errors and its unbiasedness breaks down when coefficients are standardized (Devlieger et al., 2016). Perhaps more crucially, because the bias-avoiding method hinges on using different factor score extraction methods for predictors and outcomes in an analysis, this method cannot easily be extended to the path analytic framework, in which a construct’s role may shift from outcome to predictor in different parts of the model (e.g., a mediating variable that is both predicted by X and predictive of Y; Devlieger & Rosseel, 2017).

For these reasons, in the present article we focus our attention on Croon’s (2002) FSR approach, using his analytic method to derive formulas that accommodate correlated uniquenesses.² In the next section, we briefly review the standard Croon formulas, derived under the assumption of conditionally independent unique factors. Then, we use Croon’s bias-correcting strategy to rederive these formulas under scenarios where unique factors may be correlated. Finally, we briefly compare the rederived Croon formulas with another cutting edge FSR approach proposed by Hoshino and Bentler (2013).

Review of Croon’s FSR Formulas

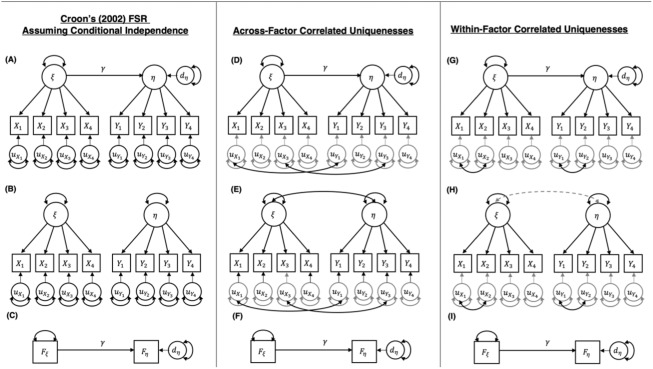
As a basis for introducing Croon’s (2002) bias-correction formulas, assume a researcher is interested in fitting a structural regression model in which an exogenous latent factor, $\mathbf{\xi }$, predicts an endogenous latent factor, $\eta$, with four indicators each. Such a scenario is depicted in Figure 1A. Note that in this panel, all unique factors are conditionally independent after the indicators’ prediction by the latent factor. One strategy for fitting this structural regression model would be to use simultaneous SEM estimation. FSR takes a different approach. At an initial step, each measurement model is fit separately, as depicted in Figure 1B and factor scores are extracted for each. That is, the measurement model for $\mathbf{\xi }$ and the measurement model for $\eta$ are fit in separate runs, and factor scores are extracted for each individual factor model, using either the regression (Thurstone, 1935) or Bartlett estimator (Bartlett, 1937). The final goal is to conduct the structural regression using the factor scores, $F_{\mathbf{\xi }}$ and $F_{\eta }$, as depicted in Figure 1C.

Figure 1.

(A)-(C) visually depict factor score regression (FSR) estimation under conditional independence. (D)-(F) depict FSR under nonzero across-factor correlated uniquenesses. (G)-(I) depict FSR under nonzero within-factor correlated uniquenesses.

As stated above, due to factor indeterminacy, simply conducting an FSR using the raw factor scores would result in a biased structural regression coefficient, $\gamma$ (Croon, 2002; Devlieger et al., 2016; Hoshino & Bentler, 2013; Lu et al., 2011). To mitigate this bias, Croon (2002) derived bias-correction formulas for the factor scores’ variances and covariance (for reviews and derivations, see Croon, 2002; Devlieger et al., 2016; Lu et al., 2011).

Let $p_x$ and $p_y$ denote the number of indicators in the X and Y measurement models, respectively (such that in Figure 1A, $p_x=p_y=4$), and let ${\eta }_X$ and ${\eta }_M$ be unidimensional, as in Figure 1A. By Croon’s formulas, a bias-corrected³ estimate of the latent factor variance is given by

$$\mathrm{var}\left(\mathbf{\xi }\right)=\frac{\mathrm{var}\left(F_{\mathbf{\xi }}\right)-{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Theta }}_{\mathbf{\delta }}{\mathbf{A}\prime }_{\mathbf{\xi }}}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{x}}\prime {\mathbf{A}\prime }_{\mathbf{\xi }}}.$$ (1)

where ${\mathbf{A}}_{\mathbf{\xi }}$ is a $1\times p_x$ factor scoring matrix of regression coefficients used to predict factor scores from the observed indicators, ${\mathbf{\Lambda }}_{\mathbf{x}}$ is a $p_x\times 1$ factor loading matrix obtained from an individual factor model as in the left-hand side of Figure 1B, ${\mathbf{\Theta }}_{\mathbf{\delta }}$ is a $p_x\times p_x$ variance–covariance matrix of the unique factor scores $\mathbf{\delta }$, and $\mathrm{var}\left(F_{\mathbf{\xi }}\right)$ is the observed variance of the extracted factor scores. By assumption in Croon’s original formulas, the unique factors are uncorrelated and ${\mathbf{\Theta }}_{\mathbf{\delta }}$ is a diagonal matrix with unique factor variances on the diagonal and zeros elsewhere. We note that although this formula is written in terms of the exogenous factor, $\mathbf{\xi }$, the same formula applies to the variance of the endogenous factor, $\eta$, if $\mathbf{\xi }$ and $\eta$ are interchanged and if the exogenous matrix ${\mathbf{\Theta }}_{\mathbf{\delta }}$ is replaced by the endogenous matrix ${\mathbf{\Theta }}_{\mathrm{\epsilon }}$, of the endogenous uniqunesses, $\mathbf{\epsilon }$.

Similarly, a bias-corrected estimate of the covariance between $\mathbf{\xi }$ and $\eta$ is obtained by the formula:

$$\mathrm{cov}\left(\mathbf{\xi }\eta \right)=\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\Lambda }{\prime }_{\mathbf{y}}\mathbf{A}{\prime }_{\eta }},$$ (2)

where $\mathbf{A}$, $\mathbf{\Lambda }$, and F are defined as above, with subscripts indicating which factor these quantities refer to. Once these corrected estimates are obtained, they can either be used to construct the structural regression coefficient using standard OLS formulas, as

$$\gamma =\frac{\mathrm{cov}\left(\mathbf{\xi }\eta \right)}{\mathrm{var}\left(\mathbf{\xi }\right)}=\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\Lambda }{\prime }_{\mathbf{y}}{A\prime }_{\eta }}{\left(\frac{\mathrm{var}\left(F_{\mathbf{\xi }}\right)-{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Theta }}_{\mathbf{\delta }}\mathbf{A}{\prime }_{\mathbf{\xi }}}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\Lambda }{\prime }_{\mathbf{x}}\mathbf{A}{\prime }_{\mathbf{\xi }}}\right)}^{-1}.$$ (3)

Or they can be used to construct a variance–covariance matrix that may be used as summary data input in a subsequent path analysis:

$${\Sigma }_{\mathbf{\xi }\eta }=\left[\begin{array}{cc}\mathrm{var}\left(\mathbf{\xi }\right)\hfill & \mathrm{cov}\left(\mathbf{\xi }\eta \right)\hfill \\ \multicolumn{1}{c}{\mathrm{cov}\left(\mathbf{\xi }\eta \right)}& \mathrm{var}\left(\eta \right)\hfill \end{array}\right],$$ (4)

where $\mathrm{var}\left(\mathbf{\xi }\right)$, $\mathrm{var}\left(\eta \right)$, and $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$, are defined using Equations (1) and (2).

The Issue of Correlated Uniquenesses

In simulation studies, Croon’s method outperformed its competitors under a variety of conditions and sample sizes (Devlieger et al., 2016; Devlieger & Rosseel, 2017; Lu et al., 2011). Importantly, FSR appears more robust than simultaneous SEM to structural model misspecifications (Devlieger & Rosseel, 2017). However, the population models in these studies have always assumed conditionally independent unique factors. What if unique factors are not independent? In the following sections, we first address the issue of diagnosing nonzero unique factor covariances before turning to the issue of incorporating unique factor covariances into FSR models.

Diagnosing and Including Correlated Uniquenesses

Before unique factor covariances can be addressed using SEM or FSR, they first have to be known and correctly specified in one’s model. For example, nonzero unique factor covariances might be specified a priori on the basis of theory, or suspected based on research design considerations (as when residuals may be autocorrelated over time in longitudinal studies, cf. Bollen, 1980; Rubio & Gillespie, 1995; Singer & Willett, 2003). Absent an a priori theory dictating the structure of the unique factor covariance matrix, however, analysts must resort to exploratory searches to uncover possible nonzero unique covariances.

If the unique factors were observed variables in one’s data set, it would be a trivial matter to simply compute the complete covariance matrix of the uniquenesses, examining which seem to depart from zero. Because both the common and unique factors are latent rather than observed, however, estimating the full unique factor covariance matrix is impossible in practice. This is because simultaneous SEM estimation requires the specification of at least one across-factor item pair whose covariation is caused entirely by the covariance between the common factors. That is, in a simultaneous SEM model like the one depicted Figure 1D, the structural regression coefficient, $\gamma$, is not algebraically identified unless at least one across-factor correlated uniqueness is fixed to zero. Analogous rules hold for within-factor correlated uniquenesses (Kenny, Kashy, & Bolger, 1998).

For these reasons, nonzero correlated uniquenesses must typically be diagnosed indirectly through the inspection of either standardized covariance residuals or modification indices when standard conditional independence models return substandard model fit (Bollen, 1989; McDonald, 1999; McDonald & Ho, 2002; Saris, Satorra, & Sörbom, 1987; Sörbom, 1989). Because it is well known that sequential specification searches using modification indices generally do not recover the correct population model (MacCallum, 1986; MacCallum, Roznowski, & Necowitz, 1992), we prefer the inspection of standardized (or normalized) covariance residuals.

Although a detailed treatment of this topic is far beyond the scope of the present article, we provide a brief summary here. For item pairs that load on the same factor, larger⁴ positive standardized (or normalized) covariance residuals indicate item pairs whose sample covariances far exceed the covariances implied by the conditional independence model. For item pairs that load on different factors, standardized (or normalized) covariance residuals with larger absolute values that track in the same direction as the covariance between the latent factors indicate item pairs whose sample covariances exceed in absolute value the covariances implied by the conditional independence model. In either case, when the absolute value of the sample covariance between a pair of items far exceeds the absolute value of the model-implied covariance under conditional independence, this suggests that the items in question share additional covariation above and beyond that predicted by the common factor. As such, nonzero unique factor covariances are particularly plausible for these item pairs.

As the preceding discussion implies, unique factors may be correlated either with (a) other unique factors loading on indicators of a different common factor in a larger model (across-factor correlated uniquenesses) or (b) other unique factors loading on indicators of the same common factor (within-factor correlated uniquenesses). The next two sections use Croon’s analytic approach to derive formulas that apply to each of these scenarios, in turn.

Across-Factor Correlated Uniquenesses

Correlated unique factors occur whenever nonzero covariation between two or more indicators remains even after their prediction by a common factor. Such residual covariation may result from a variety of causes, such as the mutual influence of both unique factors by a second common factor in a bifactor model (cf. Gerbing & Anderson, 1984). Perhaps more interestingly, it is possible that the specific factors that influence items tapping different constructs may correlate. Though the decomposition of item variance into common factor variance, specific factor variance, and error variance is as old as factor analysis itself (Crocker & Algina, 2008; Guttman, 1945; McDonald, 1999; Spearman, 1904; Thurstone, 1935, 1947), the implications of specific factors have largely been ignored, and have only recently been the subject of renewed interest in the SEM literature (cf. Bentler, 2017, for a recent discussion of specific factors).

As an example, consider loneliness and depression, which have been well established in the literature as correlated-yet-distinct constructs (Cacioppo, Hawkley, & Berntson, 2003; Hawkley et al., 2008; Russell, Peplau, & Cutrona, 1980). Imagine, further, three items: “I feel alone,” from a loneliness scale, as well as “I feel hopeless,” and “sometimes it is hard to get out of bed in the morning,” both from a depression scale. It seems reasonable to expect that hopelessness and lethargy (amotivation) are both mutually caused by a latent depression factor. But what if there is a stronger correlation between feelings of hopelessness and feelings of loneliness than between feelings of loneliness and feelings of lethargy? If this stronger correlation results from the specific aspects of these items, rather than the strength of the relationship between these items and their respective common factors, a unique factor correlation may be at play.

Figure 1D depicts nonzero covariances between the first indicators and the third indicators on each common factor in our two-factor structural regression model. Assume that the structural regression coefficient, $\gamma$, is the parameter of greatest interest in the model. That is, our hypothetical researcher is not conducting a psychometric analysis of the four-item X and Y scales but, rather, is primarily interested in the unbiased, error-free structural regression between $\mathbf{\xi }$ and $\eta$. Additionally, assume that the unique factor covariances are positive rather than negative, as in the loneliness and depression example above.

What would happen to the estimate of $\gamma$ if the researcher ignored the across-factor correlated uniquenesses and simply fit the conditional independence model of Figure 1A using simultaneous SEM estimation? In the conditional independence model of Figure 1A, the model-implied covariance between two items loading on different common factors is $\mathrm{cov}(X_i,Y_j)={\lambda }_{X_i}\gamma {\lambda }_{Y_j}$. Absent additional information, any of these three parameters—${\lambda }_{X_i}$, $\gamma$, or ${\lambda }_{Y_j}$—could be adjusted in order to fit a larger covariance between items X_i and Y_j.

However, in addition to fitting the covariances between items loading on separate factors, the factor loadings must also minimize misfit in modeling the model-implied covariances between items loading on the same factor. Assuming standardized factors, the model-implied covariance between any two items loading on the same factor is $\mathrm{cov}\left(X_i{X}_j\right)={\lambda }_{X_i}{\lambda }_{X_j}$ for $\mathbf{\xi }$ and $\mathrm{cov}\left(Y_i{Y}_j\right)={\lambda }_{Y_i}{\lambda }_{Y_j}$ for $\eta$, respectively. Thus, the estimated factor loadings have two types of covariances to fit—those between items loading on the same factor and those between items loading on separate factors—whereas the structural regression coefficient needs only fit the covariances between items loading on different factors. For this reason, the estimated factor loadings have more limited latitude to shift if they are to minimize misfit across all observed covariances in which they are expected to play a role.

If Figure 1D is the true model, then, ignoring the nonzero across-factor correlated uniquenesses may result in an inflated structural coefficient, $\gamma$. If the estimated factor loadings, ${\lambda }_{X_i}$ and ${\lambda }_{Y_j}$, are close to their true values, the structural regression coefficient, $\gamma$, will necessarily need to be inflated in order to account for the positive unique factor covariance that is left unmodeled. More precisely, the estimate of $\gamma$ will have to split the difference between item pairs with larger observed covariances, such as $X_1$ and $Y_1$ or $X_3$ and $Y_3$, and item pairs with smaller observed covariances, such as $X_2$ and $Y_2$, in order to minimize the overall model misfit. All else being equal, the larger and more numerous the (positive) unique factor covariances, the more inflated the estimate of $\gamma$ can be expected to become.

Alternatively, what would happen to the estimate of $\gamma$ if a researcher applied Croon’s (2002) original formulas, assuming conditionally independent uniquenesses? At first glance, the Croon method depicted in Figure 1A-C may appear robust to such misspecification. After all, if the within-factor uniquenesses are, in fact, conditionally independent and if each factor model is extracted separately, each factor model’s parameters should be estimated accurately. As such, it stands to reason that FSR may circumvent the usual issues that might result from misspecification of the across-factor uniquenesses.

Unfortunately, this intuition turns out to be incorrect. As formally derived in Appendix A, Croon’s original formulas were predicated upon an assumption of conditionally independent uniquenesses, both within- and across-factors. In a model like Figure 1D, the formula for bias-corrected factor variances in Equation (1) once again remains accurate. In the presence of across-factor correlated uniquenesses, however, Equation (2), for estimating $\mathrm{cov}(\mathbf{\xi },\eta )$, is no longer accurate. As shown in Appendix A, if assuming the standard models for the X and Y indicators, respectively:

$$\begin{array}{c}\mathbf{x}={\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\xi }+\mathbf{\delta }\hfill \\ \mathrm{and}\hfill \\ \mathbf{y}\mathbf{=}{\mathbf{\Lambda }}_{\mathbf{y}}\mathbf{\eta }+\mathbf{\epsilon }\mathbf{,}\hfill \end{array}$$ (5)

where $\mathbf{\delta }$ contains the X model unique factors and $\mathrm{\epsilon }$ contains Y model unique factors, the unbiased estimate of $\mathrm{cov}(\mathbf{\xi },\eta )$ becomes

$$\mathrm{cov}\left(\mathbf{\xi }\eta \right)=\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })-{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)\mathbf{A}{\prime }_{\eta }}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\Lambda }{\prime }_{\mathbf{y}}\mathbf{A}{\prime }_{\eta }},$$ (6)

where $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ is a $p_x\times p_y$ covariance matrix of the X and Y uniquenesses (see Appendix A for further details). Comparing Equation (6) with Equation (2), it is clear that Equation (2) overestimates the true common factor covariance by a quantity equal to $\frac{{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)\mathbf{A}{\prime }_{\eta }}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\Lambda }{\prime }_{\mathbf{y}}\mathbf{A}{\prime }_{\eta }}$ (see Appendix A).

The necessity of accounting for the covariances in $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ suggests that an initial, simultaneous model must be estimated, even if FSR is to be undertaken as a primary method of analysis. With this result in mind, Croon’s formulas can be rederived to appropriately account for nonzero $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ using either of two strategies. A first strategy retains Croon’s original approach of extracting factor scores from each individual factor model, using an estimate of $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ from a simultaneous run in the adjustment term in the formula above. We term this approach Factor Model Croon.

A second strategy applies Croon’s bias-correction method at the level of each connected measurement model, rather than each individual factor model. In the present context, a connected measurement model refers to a measurement model with ≥2 latent factors connected by across-factor correlated uniquenesses. In this approach, factor scores are estimated and extracted for multiple factors at once in a simultaneous model such as the model of Figure 1E. Subsequently, the variance–covariance matrix of the factor scores is corrected for bias resulting from nonzero $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$. We term this approach Measurement Model Croon. The following sections describe each of these approaches, in turn, and detailed derivations of both approaches are reported in Appendices A and B, respectively.

Factor model Croon

Arguably the most direct application of Croon’s (2002) method to structural regression models featuring across-factor correlated residuals would be to retain the factor-model-by-factor-model nature of the original Croon approach, incorporating an estimate of $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ from a simultaneous model in Equation (6). In line with this strategy, we propose the following variant of Croon’s (2002) FSR method for the case of across-factor correlated uniquenesses:

1. First, estimate separate factor models as in Figure 1B. Extract factor scores for each, as well as factor loading matrices ${\mathbf{\Lambda }}_X$ and ${\mathbf{\Lambda }}_Y$, and unique factor variance–covariance matrices for each separate factor, ${\mathbf{\Theta }}_X$ and ${\mathbf{\Theta }}_Y$. In the presence of nonzero within-factor correlated uniquenesses, the specification of Figure 1H may be used instead.

2. Estimate the simultaneous model of Figure 1E, fixing the parameters of each factor model to their estimates from Step 1.⁵ As such, the only estimated parameters should be the covariance(s) between the latent factors, as well as any nonzero unique factor covariances.⁶ Extract the unique factor variance–covariance matrix $\mathrm{\Theta }$. Subset this matrix to obtain the submatrix of covariances between $\mathbf{\delta }$ and $\mathbf{\epsilon }$, $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$.

3. Correct the factor score variances and covariances using the quantities obtained in Steps 1 and 2, via Equations (1) and (6).

4. Run the FSR model, as depicted in Figure 1I.

Based on the analytic derivations in Appendix A, this method should serve to correct Croon’s (2002) original formulas for bias in the presence of across-factor correlated uniquenesses, yielding consistent estimates of the true factor covariances.

Measurement model Croon

A second strategy applies Croon’s bias-correction method at the level of the entire connected measurement model. Let $M_1$ refer to a connected measurement model, such as the model of Figure 1E. Although we focus here on the case of a single measurement model, the subscript 1 implies that there may be more than one connected measurement model in a larger SEM. Let ${\mathbf{\eta }}_{{\mathit{M}}_1}$ be a vector of $m_1$ latent variables in the measurement model and let ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}}$ denote the factor scores extracted from measurement model $M_1$. In the model of Figure 1E, $m_1=2$, ${\mathbf{\eta }}_{{\mathit{M}}_1}$ would consist of latent factors $\mathbf{\xi }$ and $\eta$, and ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}}$ would contain factor score estimates corresponding to these latent variables, extracted simultaneously from the connected measurement model. That is, ${\mathbf{\eta }}_{{\mathit{M}}_1}=\left[\begin{array}{c}\mathbf{\xi }\hfill \\ \multicolumn{1}{c}{\eta }\end{array}\right]$ and ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}}=\left[\begin{array}{c}{F}_{\mathbf{\xi }}\hfill \\ \multicolumn{1}{c}{F_{\eta }}\end{array}\right]$. As derived in Appendix B, the expected variance–covariance matrix of the factor scores, $F_{{\mathbf{\eta }}_{{\mathit{M}}_1}}$, may be written as

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}})={\mathbf{A}}_{{\mathit{M}}_1}{\mathbf{\Lambda }}_{{\mathit{M}}_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1}){\mathbf{\Lambda }}_{{\mathit{M}}_1}\prime {\mathbf{A}}_{{\mathit{M}}_1}\prime +{\mathbf{A}}_{{\mathit{M}}_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{{\mathit{M}}_1}\prime .$$ (7)

Solving algebraically for the variance–covariance matrix of the true latent factors, $\mathrm{cov}({\mathbf{\eta }}_{{\mathit{M}}_1},{\mathbf{\eta }}_{{\mathit{M}}_1})$, yields

$$\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1})={\left({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\right)}^{-1}[\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})-{\mathbf{A}}_{M_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{M_1}\prime ]{({\mathbf{\Lambda }}_{M_1}\prime {\mathbf{A}}_{M_1}\prime )}^{-1}.$$ (8)

Although in principle this formula can be used regardless of which factor score estimator is employed (e.g., regression vs. Bartlett) so long as the matrix product ${\mathbf{A}}_{{\mathit{M}}_1}{\mathbf{\Lambda }}_{{\mathit{M}}_1}$ and its transpose are nonsingular, the Bartlett factor score estimator (Bartlett, 1937) features the desirable property that ${\mathbf{A}}_{{\mathit{M}}_1}{\mathbf{\Lambda }}_{{\mathit{M}}_1}=\mathbf{I}$, circumventing any potential issues with matrix inversion. For this reason, we recommend employing Bartlett estimation when conducting Measurement Model Croon. As noted in Appendix B, when Bartlett estimation is used, Equation (8) reduces to

$$\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1})=\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})-{\mathbf{A}}_{{\mathit{M}}_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{{\mathit{M}}_1}\prime .$$ (9)

In scenarios involving only a single connected measurement model, such as the example of Figure 1D and E and the template models featured in our simulations, this formula is all that is required to obtain a corrected covariance matrix of all latent factors in the model. Although not our main focus, we note that Appendix B contains additional formulas for computing the corrected covariance matrix between two connected measurement models, $M_1$ and $M_2$. In this way, the formulas in Appendix B allow researchers to use Croon’s method for models even more complex than those featured here.

Within-Factor Correlated Uniquenesses

Nonzero covariances may also occur between unique factors that load on items tapping the same construct. Once again, it is possible that such unique factor covariation is due to the unique factors’ mutual causation by a second factor or to the existence of correlated specific factors that influence both items. Whatever the case may be, suppose a researcher is interested in fitting the same structural regression between exogenous $\mathbf{\xi }$ and endogenous $\eta$, but the true unique factor structure is as depicted in Figure 1G. Assume, once again, that the researcher’s primary goal is to accurately estimate the structural regression coefficient, $\gamma$.

What would happen to the estimate of the key structural coefficient, $\gamma$, if a unique factor structure like the one depicted in Figure 1G was ignored? If a researcher used simultaneous SEM estimation to fit the model in Figure 1A, assuming conditionally independent uniquenesses, the factor loadings on $X_1$ and $X_2$ would be inflated to account for the larger covariance between these two items, some of which is actually due to unique factor covariance. The same would be true of the factor loadings on items $Y_1$ and $Y_2$. As a result, the estimate of $\gamma$ that best fits covariances between items with inflated loadings will be smaller than its true value in the population.

For example, let ${\lambda }_{X_1}$ and ${\lambda }_{Y_1}$ represent the factor loadings for the first X and Y indicators, respectively. The model-implied covariance between $X_1$ and $Y_1$ in the model of Figure 1A is $\mathrm{Cov}(X_1,Y_1)={\lambda }_{X_1}\gamma {\lambda }_{Y_1}$. If ${\lambda }_{X_1}$ and ${\lambda }_{Y_1}$ are inflated due to a failure to correctly account for the unique factor covariation in the true population model of Figure 1G, however, the estimate of $\gamma$ will necessarily have to be smaller in order to fit the observed covariance. Similarly, an FSR analysis using Croon’s (2002) formulas from Equations (1) and (2) would result in factor loading matrices, ${\Lambda }_X$ and ${\Lambda }_Y$ with inflated entries, resulting in a similarly deflated estimate of$\gamma$.

Luckily, using Croon’s original formulas in the case of within-factor correlated uniquenesses involves only a simple respecification of the initial factor models from which factor scores are extracted. Instead of fitting each measurement model in a standard manner, assuming conditionally independent uniquenesses, one simply fits each factor model including the correlated unique factors, as depicted in Figure 1H. As a result, the ${\Lambda }_X$ and ${\Lambda }_Y$ matrices from Equations (1) and (2) will be correctly estimated. Furthermore, the unique factor covariance matrices, $\mathrm{\Theta }$, from each factor model will contain some number of nonzero off-diagonal elements (1 each, in the models of Figure 1H). After applying formulas (1) and (2) using these correctly estimated quantities, an FSR analysis may be run, as usual, as depicted in Figure 1I.

Alternatively, though not required to estimate within-factor correlated uniquenesses, the Measurement Model Croon formulas described previously may just as easily be applied. For example, the entire model of Figure 1H may be fit simultaneously (including the factor covariance, represented by a dotted line) and the bias-corrected variance covariance matrix of $\mathbf{\xi }$ and $\eta$ may be computed from the Bartlett-extracted factor scores using Equation (9).

Hoshino and Bentler’s (2013) Alternative FSR Approach

Although Croon’s (2002) FSR method has attracted recent attention, it is important to mention an alternative approach proposed by Hoshino and Bentler (2013). These authors correctly noted that, under standard conditions, the Bartlett factor score estimator (Bartlett, 1937) is a consistent estimator of the true population covariances among the latent factors (cf. Hoshino & Bentler, 2013, section 4.7.2). For example, under conditional independence the true factor covariance is defined by Equation (2) as $\mathrm{cov}\left(\mathbf{\xi }\eta \right)=\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathit{x}}{\mathbf{\Lambda }}_{\mathit{y}}\prime {\mathbf{A}}_{\eta }\prime }$. Because, for Bartlett factor scores extracted from separate unidimensional factor models, ${\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}={\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}\prime }_{\eta }=1$, however, the denominator on the right-hand side of Equation (2) vanishes, leaving $\mathrm{cov}\left(\mathbf{\xi }\eta \right)=\mathrm{cov}{(F_{\mathbf{\xi }},F_{\eta })}_{\mathrm{Bartlett}}$.

Similarly, the denominator varnishes in Equation (1), leaving $\mathrm{var}\left(\mathbf{\xi }\right)=\mathrm{var}\left(F_{\mathbf{\xi }}\right)-{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Theta }}_{\mathbf{\delta }}{\mathbf{A}\prime }_{\mathbf{\xi }}$ or, equivalently, $\mathrm{var}{\left(F_{\mathbf{\xi }}\right)}_{\mathrm{Bartlett}}=\mathrm{var}\left(\mathbf{\xi }\right)+{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Theta }}_{\mathbf{\delta }}{\mathbf{A}\prime }_{\mathbf{\xi }}$. Because the variances of Bartlett factor scores are inconsistent estimates of their true population quantities, Hoshino and Bentler (2013) recommended substituting estimates of the factor variances from the initial measurement model runs in place of the factor score variance in the final covariance matrix of the latent factors.

Like Croon’s method, the Hoshino–Bentler approach can be applied at either the level of the individual factor models or the level of each connected measurement model (Hoshino & Bentler, 2013). We focus here on the connected measurement model implementation, since we employed this version in our simulations below. Recall that, at the level of a single connected measurement model, $M_1$, the variance–covariance matrix of the factor scores is approximated by Equation (7) under Bartlett estimation as ${({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})}_{\mathrm{Bartlett}}=\mathrm{cov}({\mathbf{\eta }}_{{\mathit{M}}_1},{\mathbf{\eta }}_{{\mathit{M}}_1})+{\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}\prime$. In the presence of across-factor correlated uniquenesses, some off-diagonal elements of the matrix ${\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}\prime$ will be nonzero and the corresponding covariances of the Bartlett factor scores will remain biased even if the Hoshino–Bentler correction is applied to the variances on the main diagonal of ${({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})}_{\mathrm{Bartlett}}$. This will be true even when the measurement model from which the factor scores were extracted is correctly specified, including the across-factor correlated uniquenesses.

When there are no across-factor correlated uniquenesses, however—even when there are some nonzero within-factor covariances—all off-diagonal elements of ${\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{{\mathit{M}}_{1_{\mathit{Bartlett}}}}\prime$ will be zero⁷ and the Hoshino–Bentler correction to the main diagonal of ${({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})}_{\mathrm{Bartlett}}$ will result in a consistent estimator of the population covariance matrix. For this reason, the covariance matrix of the latent factors computed using the Hoshino–Bentler (2013) method can be expected to remain a consistent estimator of the true population matrix when there are no nonzero across-factor covariances among the uniquenesses and the model is correctly specified but will exhibit some degree of bias when some covariances among the across-factor uniquenesses are nonzero, even if the measurement model residual structure is correctly specified.

The Present Research

The formulas and rhetorical arguments presented thus far are based entirely on statistical theory and the severity of possible degradations in performance of SEM estimation, standard (uncorrected) Croon FSR, and (in the case of across-factor correlated uniquenesses) the Hoshino–Bentler method under a population model with nonzero correlated uniquenesses remains unknown. Additionally, it is unclear whether the Factor Model and Measurement Model variants of our Croon formulas will perform identically or whether one method will outperform the other under particular circumstances. For example, at smaller sample sizes it is possible that one method might outperform the other. It could be that the smaller, factor-by-factor models will be easier to estimate accurately than a larger connected measurement model, leading to less biased results in smaller samples. Alternatively, it is just as plausible that estimates from larger, connected measurement models will be less biased in small samples, since these estimates are informed by a greater overall number of variables in a richer model.

To provide an initial assessment of the performance of these methods, then, we compare our proposed Factor Model and Measurement Model Croon formulas with (a) simultaneous SEM estimation, (b) uncorrected Croon FSR, (c) FSR using the Hoshino–Bentler (2013) method, and (d) uncorrected FSR using regression and Bartlett factor scores in two Monte Carlo simulations. Below, we refer to Croon’s (2002) original FSR method as either Croon FSR or FSR assuming conditional independence. We refer to our proposed corrections for correlated uniquenesses at the factor model level as either Croon FM or Factor Model Croon and to our proposed corrections for correlated uniquenesses at the measurement model level as either Croon MM or Measurement Model Croon. Finally, we refer to the Hoshino–Bentler method as either the HB method or simply Hoshino–Bentler.

Simulation Studies

To evaluate the efficacy of our proposed FSR methods, and to assess the robustness of simultaneous SEM estimation and standard Croon FSR to misspecification of the measurement model unique factor structure, we conducted two Monte Carlo simulation studies. Simulation 1 examined these methods using a population model with nonzero across-factor correlated uniquenesses. Simulation 2 used a population model with nonzero within-factor correlated uniquenesses. We coded both simulations in R statistical software (R Core Team, 2013) and conducted all SEM analyses using the lavaan package (Rosseel, 2012). Across both simulations, for each unique simulation cell, we generated and analyzed 1,000 simulated data sets.

Simulation 1: Across-Factor Correlated Uniquenesses

Population Model Used in the Simulation

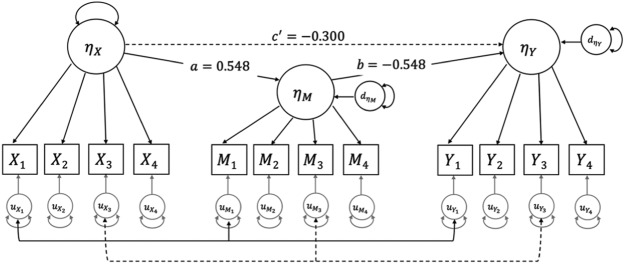
As a population model for Simulation 1, we used the latent variable mediation model displayed in Figure 2. We chose the mediational framework because of its widespread use in the educational and psychological literature, because we wished to assess the potential proliferation of bias in models with at least one indirect pathway, and because, following other authors in this area, we wished to assess the effects of misspecifying the structural model by incorrectly fixing a direct pathway to zero (Devlieger et al., 2016; Devlieger & Rosseel, 2017). The coefficients were taken from the moderate effect size conditions reported in Ledgerwood and Shrout (2011), in which the indirect effect equals ab = .546 * −.546 = .30. All variables in the model were standardized.

Figure 2.

Population model for Simulation 1.

Factors Varied in the Simulation

We varied four primary factors in Simulation 1: the sample size, the reliability of the four indicators used to measure each construct, the strength of the unique factor correlations, and the number of unique factor correlations.

The sample size, N

We simulated four sample sizes: N = {125, 250, 500, 1,000}, representing a range of small and large sample sizes.

Reliability of the indicators

For convenience, we held all population factor loadings equal in all conditions and selected three levels of Cronbach’s alpha (Cronbach, 1951), $\alpha$ = {.7, .8, .9}, corresponding to values of alpha commonly viewed as acceptable by substantive researchers. To keep all indicators on a standardized metric, we used the formulas $\lambda =\sqrt{\frac{\alpha }{4-3\alpha }}$ and ${\sigma }_u^2=\frac{4(1-\alpha )}{4-3\alpha }$ for the factor loadings and unique factor variances, respectively.

Because the unique factor variances are necessarily larger under lower reliability, when less of the total variance of each item is explained by the common factor, we expected the biasing effects of ignoring nonzero correlations among the unique factors to be most severe in the $\alpha =.7$ condition and become progressively less severe as reliability increased.

Strength of the unique factor correlations

We selected unique factor correlations of three different strengths: |r| = {.1, .3, .5}, corresponding to Cohen’s (1988) conventions for small, moderate, and large correlation effect sizes. All else being equal, we expected greater bias to result from misspecifying the measurement model unique factor structure when the strength of the unique factor correlations was higher.

Number of unique factor correlations

Finally, we generated either one or two nonzero across-variable correlated uniquenesses per common factor. This is depicted visually in Figure 2 via the use of solid versus dashed lines in the measurement model unique factor structure. The solid lines represent all unique factor correlations in cells with one correlated uniqueness per common factor. The dashed lines represent additional unique factor correlations in the population model for cells with two correlated uniquenesses per common factor. All else being equal, the more nonzero correlated uniquenesses in a model, the more disruptive an influence these unique variable correlations should have on the resulting parameter estimates.

Figure 3.

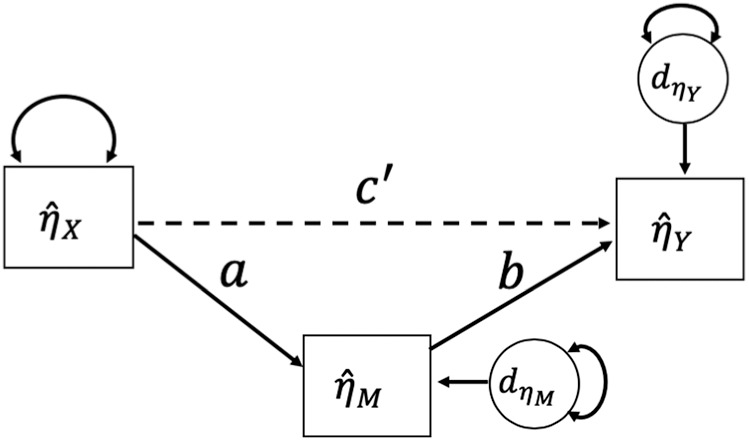
Diagram of factor score regression (FSR) approach to fitting the model of Figure 2.

Analyses Conducted on Each Simulated Data Set

We analyzed each data set using eight different methods: SEM specified under conditional independence, Croon FSR assuming conditional independence, uncorrected FSR using the regression estimator, uncorrected FSR using the Bartlett estimator, Factor Model Croon, Measurement Model Croon, simultaneous SEM with a correctly specified residual structure, and Hoshino–Bentler FSR computed at the connected measurement model level under a correctly specified residual structure.⁸ We note that the first four of these methods assumed conditional independence and ignored possible correlated uniquenesses whereas the latter four of these methods correctly specified the measurement model residual structure, including all nonzero unique factor covariances. For reasons mentioned above, we used Bartlett-estimated factor scores for all variants of Croon’s method.

Additionally, for each estimation method, we conducted two analyses: one with the structural model correctly specified, freely estimating all mediation model pathways, and one with the structural model misspecified, incorrectly fixing the ${\eta }_X\to {\eta }_Y$ pathway to 0 (i.e., imposing the constraint c′ = 0, assuming complete mediation). The rationale for including these analyses was based on prior research that has shown repeatedly that FSR estimation is more robust to structural model misspecification than simultaneous SEM estimation (Devlieger et al., 2016; Devlieger & Rosseel, 2017; Lu et al., 2011). As a result, we expected both simultaneous SEM and correctly specified FSR estimation to perform well when all parts of the model (measurement and structural) were correctly specified, but expected FSR to outperform simultaneous SEM in terms of bias when the structural model (but not the measurement model) was misspecified.

Simulation Outcomes

We assessed the performance of each method using two primary outcome measures: percent bias and mean square error (MSE) of our key structural parameters.

Percent bias

For each population parameter of interest, $\theta$, we computed percent bias as

$$\mathrm{Percent}\mathrm{Bias}=\frac{\overline{\theta }-\theta }{\theta }\times 100$$ (10)

where $\overline{\theta }$ denotes the average parameter estimate from a given estimation method in a given simulation cell. Absolute values of percent bias of 10 or larger are conventionally considered problematic (Enders & Bandalos, 2001; Muthén, Kaplan, & Hollis, 1987).

Mean square error

Additionally, for each parameter of interest we computed MSE in each unique simulation cell using the formula:

$$\mathrm{MSE}=\frac{\sum _{\mathrm{Iter}=1}^{1000}{({\hat{\theta }}_{\mathrm{Iter}}-\theta )}^2}{N_{\mathrm{IterComplete}}},$$ (11)

where ${\hat{\theta }}_{\mathrm{Iter}}$ is the parameter estimate returned by a given estimation method for the current iteration in a given simulation cell, $N_{\mathrm{IterComplete}}$ is the number of iterations with no convergence errors or inadmissible solutions in a given simulation cell,⁹ and $\theta$ is, once again, the true population value. MSE is an overall measure of accuracy that additively combines sampling variance and squared bias. For an unbiased estimator, MSE reduces to an estimate of sampling variability. Lower values of MSE indicate a more efficient and, potentially, less biased estimator.

MSE ratios

In the results below, instead of reporting raw MSE values, we report MSE ratios, computed as

$$\mathrm{MSE}\mathrm{Ratio}=\frac{MS{E}_{ComparisonEstimator}}{MS{E}_{CroonMM}}$$ (12)

That is, for each analysis cell, we formed the ratio of a given estimator to the measurement model version of Croon’s method. MSE ratios equal to 1 indicate estimators that are equivalent in their overall accuracy. Ratios less than 1 indicate scenarios in which a comparison estimator exhibits lower MSE than Croon MM. Ratios greater than 1 indicate scenarios in which the comparison estimator exhibits higher MSE than Croon MM. When both estimators are unbiased, the MSE ratio can be construed as a measure of the relative efficiency of the two estimators.

Simulation 1: Results

The results of Simulation 1 generally fell in line with our predictions. Because the pattern of results was stable across sample sizes, we present results for the N = 125 condition here. Additionally, to preserve space, we present full tables of results from the two correlated uniqueness cells. The one correlated uniqueness conditions followed similar trends, with less pronounced bias (but see the Supplemental Material, available online, for comprehensive results from all other conditions).

Percent bias

Tables 1 and 2 display percent bias of our key structural parameters, a, b, and the ab indirect effect, by (a) estimation method, (b) unique factor structure specification, (c) structural model specification, (d) reliability (alpha level), and (e) strength of the unique variable correlation in the N = 125, two correlated uniqueness cells. Table 1 presents results for the four methods that assume conditional independences, whereas Table 2 presents results for the four methods that correctly specified the measurement model residual structure.

Table 1.

Percent Bias in Models Omitting the Unique Factor Correlations by Parameter and Simulation Condition, Simulation 1: N = 125, 2 Unique Factor Correlations.

	Regression FS			Bartlett FS			Croon			SEM
Path	a	b	ab	a	b	ab	a	b	ab	a	b	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	−28.85	−27.77	−48.53	−28.92	−27.77	−48.66	0.39	−0.81	−0.32	3.80	2.99	7.10
MS	−28.85	−8.37	−34.22	−28.92	−8.38	−34.34	0.39	29.27	30.56	15.99	43.05	66.73
$\alpha (.8)$
CS	−19.11	−18.24	−33.86	−18.92	−18.23	−33.70	0.52	0.80	1.36	2.070	2.44	4.60
MS	−19.11	4.78	−14.72	−18.92	4.79	−14.50	0.52	30.29	31.58	11.04	38.57	54.57
$\alpha (.9)$
CS	−9.26	−9.12	−17.52	−9.30	−9.21	−17.67	0.53	0.32	0.83	1.14	0.86	1.99
MS	−9.26	18.00	7.57	−9.30	17.88	7.40	0.53	30.63	31.79	6.28	34.57	43.53
Unique factor correlation = .3
$\alpha (.7)$
CS	−22.61	−24.30	−41.38	−22.56	−24.11	−41.33	8.93	5.30	14.91	14.34	9.91	25.86
MS	−22.61	−2.34	−23.87	−22.56	−2.11	−23.73	8.93	37.84	50.88	26.15	52.79	93.34
$\alpha (.8)$
CS	−15.91	−16.85	−30.03	−16.06	−16.76	−30.11	4.38	2.36	6.87	6.59	4.60	11.56
MS	−15.91	7.89	−8.73	−16.06	8.00	−8.82	4.38	34.15	40.61	16.12	43.53	67.30
$\alpha (.9)$
CS	−7.86	−7.95	−15.13	−7.87	−7.88	−15.10	2.11	1.99	4.19	2.86	2.73	5.72
MS	−7.86	19.37	10.46	−7.87	19.44	10.50	2.11	32.39	35.64	8.07	36.55	48.08
Unique factor correlation = .5
$\alpha (.7)$
CS	−17.38	−20.77	−34.49	−17.29	−20.85	−34.49	16.20	11.66	30.30	25.87	19.49	51.06
MS	−17.38	3.13	−14.27	−17.29	3.06	−14.21	16.20	45.05	69.24	36.70	62.41	122.36
$\alpha (.8)$
CS	−11.74	−14.56	−24.47	−11.89	−14.40	−24.51	9.39	5.81	16.01	13.33	9.23	24.09
MS	−11.74	11.70	−0.85	−11.89	11.89	−0.87	9.39	38.75	52.39	22.96	49.86	84.80
$\alpha (.9)$
CS	−5.88	−7.14	−12.59	−5.92	−7.14	−12.68	4.34	2.91	7.36	5.40	3.92	9.51
MS	−5.88	21.09	14.41	−5.92	21.07	14.32	4.34	34.24	40.48	10.76	38.85	54.24

Note. Regression FS = Regression FSR method; Bartlett FS = Bartlett FSR method; Croon = Croon’s method using the original formulas uncorrected for unique factor correlations; SEM = structural equation modeling (simultaneous estimation) under the assumption of conditionally independent uniquenesses; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). Boldfaces entries indicate absolute values of percent bias >10.

Table 2.

Percent Bias in Models Correctly Specifying the Unique Factor Structure by Parameter and Simulation Condition, Simulation 1: N = 125, 2 Unique Factor Correlations.

	Hoshino–Bentler			Croon FM			Croon MM			SEM
Path	a	b	ab	a	b	ab	a	b	ab	a	b	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	2.96	2.31	5.50	−3.26	−3.27	−6.42	−0.54	0.30	−0.19	−0.54	0.30	−0.19
MS	2.96	32.87	37.61	−3.26	25.62	22.32	−0.53	29.68	29.81	11.58	38.82	55.82
$\alpha (.8)$
CS	1.71	2.16	3.94	−1.70	−0.71	−2.36	−0.43	0.89	0.47	−0.43	0.89	0.47
MS	1.71	31.95	34.80	−1.70	28.09	26.55	−0.43	29.99	30.03	8.43	36.17	48.38
$\alpha (.9)$
CS	1.01	0.77	1.76	−0.46	−0.35	−0.82	0.04	0.19	0.21	0.04	0.19	0.21
MS	1.01	31.25	33.04	−0.46	29.63	29.52	0.04	30.32	30.86	5.02	33.44	40.67
Unique factor correlation = .3
$\alpha (.7)$
CS	10.23	6.71	17.88	−1.85	−3.31	−5.13	0.38	−0.07	0.42	0.38	−0.07	0.42
MS	10.23	39.55	54.61	−1.85	26.29	24.73	0.38	29.83	31.17	11.33	38.17	54.84
$\alpha (.8)$
CS	4.85	3.22	8.26	−2.21	−2.12	−4.29	−1.27	−0.60	−1.88	−1.27	−0.60	−1.88
MS	4.85	34.99	42.15	−2.21	27.50	25.31	−1.27	29.13	28.13	6.83	34.69	44.66
$\alpha (.9)$
CS	2.35	2.25	4.71	−0.84	−0.10	−0.88	−0.40	0.46	0.11	−0.40	0.46	0.11
MS	2.35	32.72	36.30	−0.84	29.36	28.77	−0.40	30.02	29.99	3.86	32.66	38.34
Unique factor correlation = .5
$\alpha (.7)$
CS	16.42	13.07	32.26	−1.78	−2.88	−4.32	0.07	1.04	1.41	0.05	1.01	1.37
MS	16.42	46.06	70.82	−1.78	26.10	24.71	0.07	29.94	30.86	9.34	36.69	50.45
$\alpha (.8)$
CS	9.48	5.84	16.09	−1.36	−1.96	−3.15	−0.33	−0.62	−0.80	−0.33	−0.62	−0.80
MS	9.48	38.83	52.60	−1.36	27.67	26.60	−0.33	29.17	29.41	6.23	33.64	42.72
$\alpha (.9)$
CS	4.30	3.00	7.43	−0.55	−0.43	−0.99	−0.21	0.13	−0.08	−0.21	0.13	−0.08
MS	4.30	34.28	40.50	−0.55	29.28	29.04	−0.21	29.88	30.09	3.17	31.93	36.66

Note. Hoshino–Bentler indicates Hoshino and Bentler’s (2013) FSR method; Croon FM = Croon’s method corrected for correlated uniquenesses at the factor model level; Croon MM = Croon’s method corrected for correlated uniquenesses at the measurement model level; SEM = structural equation modeling (simultaneous estimation) correctly specifying the correlated residual structure; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). Boldfaced entries indicate absolute values of percent bias >10.

Several trends are worth highlighting. First, examining Table 1, it is clear that standard, uncorrected FSR using the regression or Bartlett estimators exhibited substantial negative bias in all conditions, in line with previous simulation results (Devlieger et al., 2016; Devlieger & Rosseel, 2017; Lu et al., 2011). Second, when the structural model was correctly specified but the unique factor correlations were moderate (.3) or large (.5), both standard simultaneous SEM and standard Croon FSR, which assume conditional independence of all unique factors, showed problematic levels of positive bias.

The bias resulting from ignoring unique factor correlations and assuming conditional independence was worse when reliability was low (α = .7 and .8), and minimal when reliability was high (α = .9). This is intuitive, since high reliability (communality) implies very little leftover unique item variation. Bias was also greatest in the estimates of the indirect effect, a * b. Because the indirect effect is a product of coefficients, the bias in this parameter grew more quickly than that of the direct path coefficients. Since the indirect effect is often the quantity of greatest interest in a mediation analysis, the susceptibility of this coefficient to larger levels of bias is concerning.

Turning to Table 2, we see that the uncorrected Hoshino–Bentler method returned problematically biased parameter estimates when the unique factor correlations were moderate (.3) or high (.5) and when reliability was low (.7) or moderate (.8). In contrast, Croon FM, Croon MM, and simultaneous SEM exhibited little bias when the structural model was correctly specified, even in the lowest sample size condition of N = 125. At this sample size Croon FM did display slightly greater negative bias at lower levels of reliability than Croon MM and correctly specified SEM. This trend quickly dissipated as sample size increased, however.

So far, we have highlighted comparisons among analyses that correctly specified the structural portion of the model, assessing the magnitude of bias resulting only from misspecification of the unique factors in the measurement model. In these cells, Croon FM, Croon MM, and simultaneous SEM all exhibited low levels of bias. When the structural model was misspecified (rows labeled MS in Table 1) by erroneously fixing the direct ${\eta }_X\to {\eta }_Y$ effect, c′, to zero and assuming complete mediation, however, both Croon FM and Croon MM resulted in noticeably lower bias than simultaneous SEM across the majority of simulation cells.

MSE ratios

MSE ratios are presented in Table 3 for the N = 125, two correlated uniquesses per factor conditions for the estimators that correctly specified the unique actor covariance structure. Comparing Croon MM to simultaneous SEM, we see that the methods exhibit equivalent performance when the entire model was correctly specified, but that Croon MM outperforms SEM when the structural model was misspecified. This suggests that Croon MM is no less efficient than simultaneous SEM, all else being equal. Comparing Croon MM with Croon FM, we see that Croon FM exhibited somewhat lower MSEs than Croon MM in a portion of simulation cells. Although the ratios generally did not depart drastically from 1, this suggests that Croon FM may be somewhat more efficient than Croon MM in some cases.

Table 3.

Mean Square Error Ratios in Models Correctly Specifying the Unique Factor Structure by Parameter and Simulation Condition, Simulation 1: N = 125, 2 Unique Factor Correlations.

	Hoshino–Bentler			Croon FM			SEM
Path	a	b	ab	a	B	Ab	a	B	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	0.99	1.06	1.15	0.96	0.89	0.87	1.00	1.00	1.00
MS	0.99	1.16	1.28	0.96	0.80	0.75	1.24	1.51	2.16
$\alpha (.8)$
CS	0.99	1.03	1.07	0.99	0.96	0.95	1.00	1.00	1.00
MS	0.99	1.11	1.19	0.99	0.90	0.87	1.17	1.38	1.91
$\alpha (.9)$
CS	0.99	1.02	1.02	0.99	0.97	0.97	1.00	1.00	1.00
MS	0.99	1.05	1.09	0.99	0.96	0.94	1.09	1.19	1.49
Unique factor correlation = .3
$\alpha (.7)$
CS	1.26	1.30	1.66	0.95	0.97	0.88	1.00	1.00	1.00
MS	1.26	1.58	2.05	0.95	0.83	0.77	1.31	1.48	2.08
$\alpha (.8)$
CS	1.05	1.17	1.31	0.97	0.98	0.96	1.00	1.00	1.00
MS	1.05	1.37	1.68	0.97	0.91	0.88	1.12	1.35	1.85
$\alpha (.9)$
CS	1.02	1.07	1.13	0.99	1.00	0.99	1.00	1.00	1.00
MS	1.02	1.17	1.30	0.99	0.96	0.94	1.06	1.16	1.43
Unique factor correlation = .5
$\alpha (.7)$
CS	1.80	2.01	3.02	1.02	1.08	1.01	1.00	1.00	1.00
MS	1.80	2.11	3.25	1.02	0.83	0.82	1.20	1.40	1.89
$\alpha (.8)$
CS	1.35	1.36	1.79	1.03	1.08	1.03	1.00	1.00	1.00
MS	1.35	1.66	2.28	1.03	0.92	0.90	1.13	1.28	1.66
$\alpha (.9)$
CS	1.07	1.13	1.26	1.00	1.01	1.00	1.00	1.00	1.00
MS	1.07	1.28	1.53	1.00	0.96	0.95	1.05	1.13	1.33

Note. FSR = factor score regression; MSE = mean square error; Hoshino–Bentler indicates Hoshino and Bentler’s (2013) FSR method; Croon FM = Croon’s method corrected for correlated uniquenesses at the factor model level; SEM = structural equation modeling (simultaneous estimation), with correctly specified unique factor structure; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). All MSE ratios are divided by the MSE for Croon’s method corrected for correlated uniquenesses at the measurement model level (Croon MM), that is, MSE_Estimator/MSE_{Croon_MM}.

Simulation 1: Discussion

Simulation 1 provided empirical evidence for several important phenomena. First, ignoring correlated uniquenesses can result in distorted estimates of structural model parameters. These effects are especially pronounced when the number of across-factor correlated uniquenesses is larger, the strength of the unique factor correlations is greater, and the reliability of the indicators is lower. Second, both correctly specified simultaneous SEM and our proposed Croon methods, accounting for correlated uniquenesses, successfully eliminated this bias when the structural model was correctly specified. Third, Croon FSR estimation outperformed simultaneous SEM in terms of bias when the structural model was misspecified. Finally, standard Hoshino–Bentler estimation exhibits bias in the presence of nonzero across-factor correlated uniquenesses, even though the connected measurement model used to compute the HB factor covariance matrix was correctly specified.

Simulation 1 specifically examined across-factor correlated uniquenesses but did not assess within-factor correlated uniquenesses. Simulation 2 used a similar procedure to compare these methods in the presence of nonzero within-factor correlated uniquenesses.

Simulation 2: Within-Factor Correlated Uniquenesses

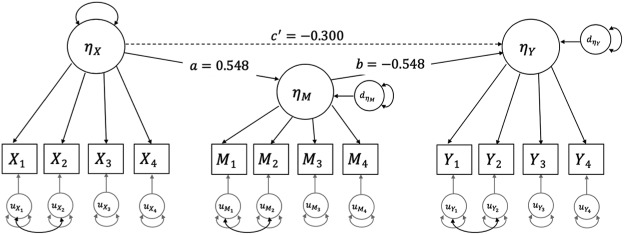
Simulation Design

Figure 4 displays the population model for Simulation 2. This simulation closely mirrored that of Simulation 1 but with two key changes. First, we generated data according to the model in Figure 4, featuring within-factor correlated uniquenesses. Second, because preliminary simulations found noticeable negative bias in key parameters even with only one within-factor correlated uniqueness per common factor, for simplicity we did not include a set of conditions examining two correlated uniquenesses per factor. Otherwise, all design factors were the same.¹⁰

Figure 4.

Population model for Simulation 2.

Simulation 2: Results and Discussion

Mirroring Simulation 1, Tables 4 and 5 display the results for percent bias and Table 6 displays the results for MSE ratios in the N = 125 conditions. As expected, the general trends from Simulation 1 are all apparent here, but the direction of biased has reversed: In the presence of within-factor correlated uniquenesses, biased structural parameters are nearly always attenuated rather than magnified. Once again, simultaneous SEM estimation and standard Croon FSR estimation exhibited bias when the unique factor structure was specified to be conditionally independent. And, once again, this bias was most pronounced under moderate to strong unique factor correlations (.3 and .5) and lower levels of reliability (.7 and .8).

Table 4.

Percent Bias in Models Omitting the Unique Factor Correlations by Parameter and Simulation Condition, Simulation 2: N = 125.

	Regression FS			Bartlett FS			Croon			SEM
Path	a	b	ab	a	b	ab	a	b	ab	a	b	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	−32.91	−30.82	−53.57	−32.73	−30.87	−53.56	−7.55	−7.46	−14.54	−3.31	−3.09	−6.44
MS	−32.91	−13.26	−41.27	−32.73	−13.36	−41.23	−7.55	19.44	11.12	7.89	33.69	45.04
$\alpha (.8)$
CS	−21.68	−21.18	−38.23	−21.40	−21.28	−38.21	−3.58	−4.38	−7.83	−1.53	−2.29	−3.82
MS	−21.68	1.02	−20.30	−21.40	0.85	−20.22	−3.58	24.15	20.38	6.91	32.89	42.85
$\alpha (.9)$
CS	−11.74	−10.59	−21.09	−11.78	−10.56	−21.13	−2.49	−1.55	−4.03	−1.79	−0.77	−2.57
MS	−11.74	15.36	2.29	−11.78	15.39	2.26	−2.49	27.51	24.79	3.03	31.49	35.97
Unique factor correlation = .3
$\alpha (.7)$
CS	−38.91	−36.25	−60.97	−39.09	−35.94	−60.94	−21.00	−19.72	−36.45	−15.10	−13.51	−26.42
MS	−38.91	−21.08	−51.16	−39.09	−20.72	−51.11	−21.00	2.55	−17.97	−5.86	17.95	12.46
$\alpha (.8)$
CS	−25.63	−24.06	−43.46	−25.64	−24.02	−43.45	−11.24	−10.79	−20.76	−8.29	−7.34	−14.97
MS	−25.63	−3.39	−27.54	−25.64	−3.35	−27.53	−11.24	15.38	3.14	−0.89	25.05	24.77
$\alpha (.9)$
CS	−13.51	−12.59	−24.33	−13.53	−12.56	−24.34	−5.46	−4.85	−9.99	−4.49	−3.78	−8.05
MS	−13.51	12.82	−1.87	−13.53	12.84	−1.88	−5.46	23.38	17.21	−0.19	27.49	27.83
Unique factor correlation = .5
$\alpha (.7)$
CS	−47.33	−43.28	−70.13	−47.13	−43.25	−69.96	−37.20	−33.77	−58.45	−33.08	−29.29	−52.63
MS	−47.33	−31.30	−63.27	−47.13	−31.27	−63.09	−37.20	−17.98	−47.75	−27.90	−7.92	−32.26
$\alpha (.8)$
CS	−33.55	−29.27	−52.98	−33.63	−29.27	−53.05	−24.37	−20.63	−39.98	−21.31	−17.29	−34.92
MS	−33.55	−12.11	−41.09	−33.63	−12.11	−41.17	−24.37	0.06	−23.74	−16.33	8.16	−8.66
$\alpha (.9)$
CS	−17.27	−16.25	−30.58	−17.31	−16.26	−30.65	−11.20	−10.63	−20.52	−9.90	−9.10	−17.97
MS	−17.27	7.69	−10.29	−17.31	7.66	−10.37	−11.20	15.57	3.26	−6.57	19.73	12.58

Note. Regression FS = regression FSR method; Bartlett FS = Bartlett FSR method; Croon = Croon’s method using the original formulas uncorrected for unique factor correlations; SEM = structural equation modeling (simultaneous estimation) under the assumption of conditionally independent uniquenesses; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). Boldfaces entries indicate absolute values of percent bias >10.

Table 5.

Percent Bias in Models Correctly Specifying the Unique Factor Structure by Parameter and Simulation Condition, Simulation 2: N = 125.

	Hoshino–Bentler			Croon FM			Croon MM			SEM
Path	a	b	ab	a	b	ab	a	B	ab	a	b	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	−0.24	0.01	−0.34	−7.70	−7.44	−14.52	−0.24	0.01	−0.34	−0.24	0.01	−0.34
MS	−0.24	29.02	29.33	−7.70	19.64	11.34	−0.24	29.02	29.33	12.42	39.08	57.13
$\alpha (.8)$
CS	0.35	−0.31	0.03	−3.49	−3.91	−7.21	0.35	−0.31	0.03	0.35	−0.31	0.03
MS	0.35	29.33	30.44	−3.49	24.60	20.96	0.35	29.33	30.44	9.91	36.42	50.76
$\alpha (.9)$
CS	−0.88	0.29	−0.61	−2.19	−1.06	−3.25	−0.88	0.29	−0.61	−0.88	0.29	−0.61
MS	−0.88	29.72	29.04	−2.19	27.98	25.65	−0.88	29.72	29.04	4.50	33.14	39.64
Unique factor correlation = .3
$\alpha (.7)$
CS	0.07	0.67	1.06	−7.81	−6.83	−13.85	0.07	0.67	1.06	0.07	0.67	1.06
MS	0.07	29.23	30.24	−7.81	19.62	11.39	0.07	29.23	30.24	12.58	39.18	57.63
$\alpha (.8)$
CS	0.03	1.03	1.17	−3.81	−3.01	−6.68	0.03	1.03	1.17	0.03	1.03	1.17
MS	0.03	30.51	31.12	−3.81	25.56	21.38	0.03	30.51	31.12	10.12	37.83	52.45
$\alpha (.9)$
CS	−0.68	−0.27	−0.88	−2.01	−1.53	−3.43	−0.68	−0.27	−0.88	−0.68	−0.27	−0.88
MS	−0.68	29.52	29.16	−2.01	27.79	25.78	−0.68	29.52	29.16	4.99	33.13	40.35
Unique factor correlation = .5
$\alpha (.7)$
CS	0.78	2.08	3.41	−7.47	−6.16	−12.65	0.78	2.08	3.41	0.78	2.08	3.41
MS	0.78	30.65	32.71	−7.47	20.15	12.44	0.78	30.65	32.71	13.76	40.93	61.29
$\alpha (.8)$
CS	−0.66	1.27	0.43	−4.70	−2.74	−7.41	−0.66	1.27	0.43	−0.66	1.27	0.43
MS	−0.66	30.75	30.36	−4.70	25.58	20.27	−0.66	30.75	30.36	9.83	38.22	52.47
$\alpha (.9)$
CS	−0.67	−0.60	−1.11	−2.04	−1.95	−3.80	−0.67	−0.60	−1.11	−0.67	−0.60	−1.11
MS	−0.67	29.30	29.06	−2.04	27.54	25.57	−0.67	29.30	29.06	5.20	33.11	40.72

Note. FSR = factor score regression; Hoshino–Bentler indicates Hoshino and Bentler’s (2013) FSR method; Croon FM = Croon’s method corrected for correlated uniquenesses at the factor model level; Croon MM = Croon’s method corrected for correlated uniquenesses at the measurement model level; SEM = structural equation modeling (simultaneous estimation) correctly specifying the correlated residual structure; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). Boldfaced entries indicate absolute values of percent bias >10.

Table 6.

Mean Square Error Ratios in Models Correctly Specifying the Unique Factor Structure by Parameter and Simulation Condition, Simulation 2: N = 125.

	Hoshino–Bentler			Croon FM			SEM
Path	a	b	ab	a	b	ab	a	b	ab
Unique factor correlation = .1
$\alpha (.7)$
CS	1.00	1.00	1.00	1.09	0.86	0.87	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.09	0.62	0.58	1.27	1.58	2.26
$\alpha (.8)$
CS	1.00	1.00	1.00	1.02	0.94	0.94	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.02	0.76	0.69	1.32	1.44	2.02
$\alpha (.9)$
CS	1.00	1.00	1.00	1.02	0.97	0.98	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.02	0.90	0.86	1.05	1.22	1.55
Unique factor correlation = .3
$\alpha (.7)$
CS	1.00	1.00	1.00	1.15	0.85	0.83	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.15	0.63	0.58	1.28	1.54	2.17
$\alpha (.8)$
CS	1.00	1.00	1.00	1.06	0.94	0.91	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.06	0.76	0.69	1.25	1.44	2.04
$\alpha (.9)$
CS	1.00	1.00	1.00	1.02	0.97	0.99	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.02	0.90	0.86	1.05	1.23	1.57
Unique factor correlation = .5
$\alpha (.7)$
CS	1.00	1.00	1.00	1.07	0.78	0.71	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.07	0.61	0.55	1.26	1.54	2.09
$\alpha (.8)$
CS	1.00	1.00	1.00	1.06	0.94	0.95	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.06	0.75	0.68	1.22	1.45	2.12
$\alpha (.9)$
CS	1.00	1.00	1.00	1.00	0.98	0.97	1.00	1.00	1.00
MS	1.00	1.00	1.00	1.00	0.90	0.86	1.10	1.24	1.59

Note. FSR = factor score regression; MSE = mean square error; Hoshino–Bentler indicates Hoshino and Bentler’s (2013) FSR method; Croon FM = Croon’s method corrected for correlated uniquenesses at the factor model level; SEM = structural equation modeling (simultaneous estimation), with correctly specified unique factor structure; CS = correct structural model specification (c′ path freely estimated); MS = structural misspecification (c′ path constrained to 0). All MSE ratios are divided by the MSE for Croon’s method corrected for correlated uniquenesses at the measurement model level (Croon MM), that is, MSE_Estimator/MSE_{Croon_MM}.

Examining Table 5, all methods performed well when both the measurement and structural models were correctly specified. We note, however, that there was a small but noteworthy effect of sample size in Simulation 2. Specifically, Croon FM was somewhat more biased at lower Ns but this bias became negligible at higher Ns (500 and 1,000). For example, the indirect effects for this method fell above the 10% cutoff when α was low (.7) across the N = 125 conditions. For all other sample sizes, this method produced acceptable levels of bias, however (though the degree of bias was still noteworthy at N = 250; see supplemental results [available online]).

In contrast, both Hoshino–Bentler and Croon MM exhibited minimal bias when the entire model was correctly specified. It is worth noting that because these methods both employed the Bartlett estimator to estimate the latent factor covariances and both employed equivalent corrections to the factor variances, the results for these two methods are identical. Simultaneous SEM performed comparably to these methods when both the measurement model and the structural model were correctly specified, but HB, Croon FM, and Croon MM all outperformed simultaneous SEM when the structural model was misspecified. This was particularly true under low and moderate levels of reliability (.7 and .8) and remained true across all sample size conditions (see supplemental results for details [available online]).

Finally, the vast majority of MSE ratios comparing Croon MM with HB and SEM either approached or exceeded 1, indicating that FSR with correlated uniquenesses performed either equivalently or superiorly in the majority of cases. Once again, Croon MM exhibited lower MSEs in several cases, but this result should be qualified by the higher levels of bias Croon FM displayed in the N = 125 and 250 conditions. Although the lower MSE suggests that Croon FM may be more efficient, the higher levels of bias observed in Table 5 suggest that this reduced sampling variability may be centered on a biased estimate.

Simulation 2: Discussion

Like Simulation 1, Simulation 2 provided a clear pattern of results. This simulation demonstrates that correct estimation of structural parameters suffers when the measurement model unique factor structure is ignored. Furthermore, simple steps can be taken to respecify the model in a manner that preserves the correct unique factor structure, using either simultaneous SEM or FSR. Finally, the Croon FM, Croon MM, and Hoshino–Bentler methods outperformed standard simultaneous SEM methods when the structural model was misspecified (see also Devlieger & Rosseel, 2017).

General Discussion

In the present research, we used Croon’s (2002) bias correction approach to derive formulas for the case of across-factor correlated uniquenesses and explicated how Croon’s original formulas may be employed in the case of within-factor correlated uniquenesses. Additionally, we reported the results of two Monte Carlo simulations comparing these methods’ performance with uncorrected regression and Bartlett FSR, standard Croon FSR assuming conditional independence, and simultaneous SEM estimation. Correctly specified simultaneous SEM estimation, Croon FM, and Croon MM, incorporating correlated uniquenesses, exhibited strong performance in our simulations. In line with previous studies (Devlieger et al., 2016; Devlieger & Rosseel, 2017), Croon FSR outperformed simultaneous SEM estimation when the structural model was misspecified.

Although the estimation of correlated uniquenesses is often discouraged in psychometric studies as a form of fishing for ways to improve fit (cf. Cole, Ciesla, & Steiger, 2007), when the focus is on accurately estimating the structural parameters, rather than the measurement model, our results suggest that the unique factor covariance structure ought not be ignored. Our simulations clearly showed that ignoring the measurement model covariance structure resulted in distorted estimates of key structural parameters across a variety of conditions. This is especially true when the primary goal is the assessment of indirect (mediational) effects, since these parameters quickly grew more biased than any other structural parameter in our simulations.

Our simulations suggest several guidelines for researchers considering applying these methods. If reliability is high (.9) or unique factor correlations low (.1), the measurement model unique factor structure might be ignored with little consequence. If reliability is lower (alpha or omega of .7-.8), the choice of how to model unique factors becomes more urgent. Furthermore, ignoring within-factor correlated uniquenesses risks attenuated structural regression coefficients, whereas ignoring across-factor correlated uniquenesses risks inflated coefficients.

Though both Croon FM and Croon MM performed well in the majority of conditions, our results suggest that when sample sizes are smaller (e.g., N = 125 or 250) Croon MM may be somewhat more accurate. This was especially true when the factor models featured within-factor correlated uniquenesses. For this reason, we recommend Croon MM when attempting to use FSR in small samples with correlated uniquenesses.

The results of our first simulation suggest that across-factor uniquenesses are more harmful to the extent that they are more numerous. Although bias resulted from ignoring even one correlated uniqueness per factor, the bias was more severe when there were two correlated uniquenesses per factor. Our simulations assessed only a simple case in which there were four indicators per factor, but it is possible to (cautiously) extrapolate to other scenarios. All else being equal, it seems reasonable to expect that even one or two correlated uniquenesses might be harmful in factor models with fewer indicators (e.g., two-indicator or three-indicator factors in the context of a larger structural model). Conversely, one or two correlated uniquenesses may not disrupt estimation as severely in factor models with more indicators (e.g., 10 or 20). This suggests that, all else being equal, applied researchers should pay greater heed to the issue of correlated uniquenesses in scenarios with fewer indicators and more numerous unique variable covariances.

Our simulation results mirror our analytic derivations in showing that Hoshino and Bentler’s (2013) method remains unbiased in the presence of within-factor correlated residuals but becomes biased in the presence of across-factor correlated residuals. Of course, correcting the HB method for this bias would be relatively simple. In the spirit of the original method, one manner of accomplishing this would be to use the covariances of the Bartlett factor scores to estimate the covariances between all factors whose measurement models do not feature across-factor correlated uniquenesses but substitute the estimated factor covariances from the initial simultaneous SEM runs in place of the Bartlett covariances between any factors whose measurement models feature across-factor correlated uniquenesses.

Our simulation results also suggest several possible areas for future research. First, if correlated unique factor structures are to be taken seriously by substantive researchers, it will be important to develop reliable and user-friendly methods for correctly identifying nonzero unique factor covariances. Because a model freely estimating all such correlated uniquenesses can never be identified (cf. Kenny, 1979; Kenny et al., 1998), alternative approaches must be used to diagnose the correct covariance structure. If the goal is to extract factor scores and conduct FSR, an intriguing possibility would be to utilize unique factor score estimates from each measurement model of interest¹¹ to diagnose possible nonzero unique factor covariances. Given the potential bias in estimated uniquenesses based on factor scores, however, it will be important to assess the analytic properties of these estimators as well as to empirically test their performance.¹²

Second, future research is needed to extend FSR methods to more complex factor structures, such as hierarchical or bifactor models (Holzinger & Swineford, 1937; McDonald, 1999; Schmid & Leiman, 1957), as well as more complex residual structures (cf. Singer & Willett, 2003, for a review of residual structures in longitudinal models). Finally, as noted by others (Devlieger et al., 2016; Devlieger & Rosseel, 2017), before FSR can be widely implemented, a crucial area of future research will necessarily involve the derivation of accurate standard errors for the path analytic formulation (but see Devlieger et al., 2016, for a viable OLS regression-based standard error for FSR).

In sum, we believe that the present research makes an important contribution to the literature on FSR methods by extending these methods to the case of correlated uniquenesses. Since implementation of matrix-oriented bias correction formulas may prove challenging for many applied researchers, it is our hope that software implementations of these methods (e.g., in lavaan; Rosseel, 2012) incorporate functionality for implementing FSR with correlated unique factor structures in the future.

Appendix A

Deriving Croon’s Formulas With Correlated Across-Factor Uniquenesses at the Individual Factor Model Level

In this appendix, we apply Croon’s (2002) method to derive FSR formulas for the case of across-factor correlated uniquenesses at the level of each individual factor model, following closely the derivation presented in Devlieger, Mayer, and Rosseel (2016). Let $\mathbf{\xi }$ and $\eta$ be exogenous and latent variables in a structural regression model, measured by $p_X$ exogenous indicators x and $p_Y$ endogenous indicators y. In the simulations reported in the main article, $p_X=p_Y=4$. Let $F_{\mathbf{\xi }}$ and $F_{\eta }$ denote the factor scores for $\mathbf{\xi }$ and $\eta$, respectively. Then, $F_{\mathbf{\xi }}$ and $F_{\eta }$ are defined by the following equations:

$$\begin{array}{c}{F}_{\mathbf{\xi }}={\mathbf{A}}_{\mathbf{\xi }}\mathbf{x},\hfill \\ F_{\eta }={\mathbf{A}}_{\eta }\mathbf{y},\hfill \end{array}$$ (A1)

where ${\mathbf{A}}_{\mathbf{\xi }}$ and ${\mathbf{A}}_{\eta }$ are factor scoring matrices—matrices of regression coefficients predicting the latent factor scores from the observed items. The formulas for the corrected variance of each factor score vector remain the same as in Equation (1) in the main article. The task at hand is to solve for the covariance, $\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })$. By Equation (A1), we may define

$$\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })=\mathrm{cov}({\mathbf{A}}_{\mathbf{\xi }}\mathbf{x},{\mathbf{A}}_{\eta }\mathbf{y})={\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}(\mathbf{x},\mathbf{y}){\mathbf{A}}_{\eta }\prime ,$$ (A2)

where the final expression follows from basic covariance algebra applied to matrices and vectors. Define vectors x and y in standard fashion as

$$\begin{array}{c}\mathbf{x}={\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\xi }+\mathbf{\delta }\hfill \\ \mathbf{y}\mathbf{=}{\mathbf{\Lambda }}_{\mathbf{y}}\mathbf{\eta }+\mathbf{\epsilon }\mathbf{,}\hfill \end{array}$$ (A3)

where $\mathbf{\delta }$ and $\mathbf{\epsilon }$ represent unique factors loading onto x and y, respectively. Substituting Equation (A3) into Equation (A2) yields

$${\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}(\mathbf{x},\mathbf{y}){\mathbf{A}}_{\eta }\prime ={\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}({\mathbf{\Lambda }}_{\mathbf{x}}\mathbf{\xi }+\mathbf{\delta }\mathbf{,}{\mathbf{\Lambda }}_{\mathbf{y}}\mathbf{\eta }+\mathbf{\epsilon }){\mathbf{A}}_{\eta }\prime .$$ (A4)

Repeatedly applying the sum rule for model-implied covariances (cf. Kenny, 1979, for a review of covariance algebra rules), this expression becomes

$$={\mathbf{A}}_{\mathbf{\xi }}[{\mathbf{\Lambda }}_{\mathbf{x}}\mathrm{cov}\left(\mathbf{\xi }\eta \right){\mathbf{\Lambda }}_{\mathbf{y}}\prime +\mathrm{cov}\left(\mathbf{\xi }\mathbf{\epsilon }\right)+\mathrm{cov}\left(\mathbf{\eta }\mathbf{\delta }\right)+\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)]{\mathbf{A}}_{\eta }\prime .$$ (A5)

So far, our derivation parallels that reported by Devlieger et al. (2016). At this point, standard model assumptions would set $\mathrm{cov}\left(\mathbf{\xi }\mathbf{\epsilon }\right)=\mathrm{cov}\left(\mathbf{\eta }\mathbf{\delta }\right)=\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)=0$. If some covariances between the x and y uniquenesses are nonzero, however, $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)\ne 0$ and Equation (A5) becomes

$$={\mathbf{A}}_{\mathbf{\xi }}[{\mathbf{\Lambda }}_{\mathbf{x}}\mathrm{cov}\left(\mathbf{\xi }\eta \right){\mathbf{\Lambda }}_{\mathbf{y}}\prime +\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)]{\mathbf{A}}_{\eta }\prime .$$ (A6)

Distributing the ${\mathbf{A}}_{\mathbf{\xi }}$ and ${\mathbf{A}}_{\eta }\prime$ matrices in this expression yields a final expression for the factor score covariance:

$$\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })={\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathrm{cov}\left(\mathbf{\xi }\eta \right){\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime +{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime .$$ (A7)

The uncorrected latent factor covariance, $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$, can be obtained by algebraically rearranging Equation (A7). Subtracting the term ${\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime$ from the right-hand side of Equation (A7) yields

$$\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })-{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime ={\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}\mathrm{cov}\left(\mathbf{\xi }\eta \right){\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime =\mathrm{cov}\left(\mathbf{\xi }\eta \right){\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime ,$$ (A8)

where the final identity follows from the fact that $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$ is a scalar for unidimensional $\mathbf{\xi }$ and $\eta$. Since ${\mathbf{A}}_{\mathbf{\xi }}$, ${\mathbf{\Lambda }}_{\mathbf{x}}$, ${\mathbf{\Lambda }}_{\mathbf{y}}\prime$, and ${\mathbf{A}}_{\eta }\prime$, are matrices with dimensions $1\times p_x$, $p_x\times 1$, $1\times p_y$, and $p_y\times 1$, respectively, the expression ${\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime$ is a $1\times 1$ scalar that can be divided out of both sides of Equation (A8), yielding the corrected latent covariance

$$\mathrm{cov}\left(\mathbf{\xi }\eta \right)=\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })-{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime }{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime }.$$ (A9)

From Equation (A9) it becomes plain that the original Croon (2002) formula, $\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })/({\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime )$, overestimates the true covariance $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$ by a quantity equal to ${\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime /({\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime )$ when $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)\ne 0$. That is,

$$\frac{\mathrm{cov}(F_{\mathbf{\xi }},F_{\eta })}{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime }=\mathrm{cov}\left(\mathbf{\xi }\eta \right)+\frac{{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime }{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime }.$$ (A10)

Thus, when the rightmost term in Equation (A10) goes to zero, Croon’s (2002) original formula will be a consistent estimator of $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$. But as elements of $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ depart from zero, Croon’s original formula will result in an estimate of $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$ that is biased by a quantity equal to $\frac{{\mathbf{A}}_{\mathbf{\xi }}\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right){\mathbf{A}}_{\eta }\prime }{{\mathbf{A}}_{\mathbf{\xi }}{\mathbf{\Lambda }}_{\mathbf{x}}{\mathbf{\Lambda }}_{\mathbf{y}}\prime {\mathbf{A}}_{\eta }\prime }$. Applying the correction formula in Equation (A9) instead, however, will result in a consistent estimator of $\mathrm{cov}\left(\mathbf{\xi }\eta \right)$ (cf. Hoshino & Bentler, 2013, Section 4.7.2).

Finally, it is important to note that $\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)$ represents the $p_x\times p_y$ matrix of covariances between the x and y uniquenesses. For example, with four indicators, as in the simulations reported in the main article, this covariance matrix would be

$$\mathrm{cov}\left(\mathbf{\delta }\mathbf{\epsilon }\right)=\left[\begin{array}{cccc}{\sigma }_{u_{x_1}{u}_{y_1}}\hfill & {\sigma }_{u_{x_1}{u}_{y_2}}\hfill & {\sigma }_{u_{x_1}{u}_{y_3}}\hfill & {\sigma }_{u_{x_1}{u}_{y_4}}\hfill \\ \multicolumn{1}{c}{{\sigma }_{u_{x_2}{u}_{y_1}}}& {\sigma }_{u_{x_2}{u}_{y_2}}\hfill & {\sigma }_{u_{x_2}{u}_{y_3}}\hfill & {\sigma }_{u_{x_2}{u}_{y_4}}\hfill \\ \multicolumn{1}{c}{{\sigma }_{u_{x_3}{u}_{y_1}}}& {\sigma }_{u_{x_3}{u}_{y_2}}\hfill & {\sigma }_{u_{x_3}{u}_{y_3}}\hfill & {\sigma }_{u_{x_3}{u}_{y_4}}\hfill \\ \multicolumn{1}{c}{{\sigma }_{u_{x_4}{u}_{y_1}}}& {\sigma }_{u_{x_4}{u}_{y_2}}\hfill & {\sigma }_{u_{x_4}{u}_{y_3}}\hfill & {\sigma }_{u_{x_4}{u}_{y_4}}\hfill \end{array}\right].$$ (A10)

Appendix B

Deriving Croon’s Formulas With Correlated Across-Factor Uniquenesses at the (Connected) Measurement Model Level

In this appendix, we apply Croon’s (2002) method to derive FSR formulas for the case of across-factor correlated uniquenesses at the level of the connected measurement model. Let ${\mathbf{\eta }}_{M_1}$ be a vector of $m_1$ latent variables in the first connected measurement model under consideration. For example, in the model of Figure 1E${\mathbf{\eta }}_{M_1}=\left[\begin{array}{c}\mathbf{\xi }\hfill \\ \multicolumn{1}{c}{\eta }\end{array}\right]$ and $m_1=2$. Furthermore, let there be $p_{M_1}$ measured indicators in measurement model $M_1$, contained in a $p_{M_1}\times N$ vector ${\mathbf{y}}_{M_1}$. Let ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}$ denote the factor scores extracted from measurement model $M_1$. Then, ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}$ may be defined by the following equation:

$${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}={\mathbf{A}}_{M_1}{\mathbf{y}}_{M_1},$$ (B1)

where ${\mathbf{A}}_{M_1}$ is a $m_1\times p_{M_1}$ factor scoring matrix. The vector ${\mathbf{y}}_{M_1}$ may be written using the usual definition as

$${\mathbf{y}}_{M_1}={\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{{\mathit{M}}_1}+{\mathbf{u}}_{M_1},$$ (B2)

where ${\mathbf{u}}_{M_1}$ is a $p_{M_1}\times N$ vector of unique factor scores with $p_{M_1}\times p_{M_1}$ covariance matrix ${\mathbf{\Theta }}_{M_1}$. In the presence of correlated unique factors, some off-diagonal elements of ${\mathbf{\Theta }}_{M_1}$ will be nonzero. Substituting Equation (B2) for ${\mathbf{y}}_{M_1}$ in Equation (B1) yields

$$\begin{array}{c}\multicolumn{1}{c}{{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}={\mathbf{A}}_{M_1}({\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1}+{\mathbf{u}}_{M_1})}\\ ={\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1}+{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1}.\hfill \end{array}$$ (B3)

Using Croon’s (2002) method, our first task is to derive the expected covariance matrix of the factor scores from the m latent factors in measurement model $M_1$and then correct this expected covariance for bias. The expected covariance of ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}$ with itself may be written:

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})=\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1}+{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1},{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1}+{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1}).$$ (B4)

Once again, repeatedly applying the sum rule for model-implied covariances (cf. Kenny, 1979), this expression becomes

$$\begin{array}{c}\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1},{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{{\mathit{M}}_1})+\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1},{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1})\hfill \\ +\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1},{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{{\mathit{M}}_1})+\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1},{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1}).\hfill \end{array}$$ (B5)

Taking matrices of constants outside their respective covariances yields:

$$\begin{array}{c}{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1}){\mathbf{\Lambda }}_{M_1}\prime {\mathbf{A}}_{M_1}\prime +{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{u}}_{M_1})\hfill \\ +{\mathbf{A}}_{M_1}\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{\eta }}_{M_1}){\mathbf{\Lambda }}_{M_1}\prime {\mathbf{A}}_{M_1}\prime +{\mathbf{A}}_{M_1}\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{u}}_{M_1}){\mathbf{A}}_{M_1}\prime .\hfill \end{array}$$ (B6)

Recognizing that, by definition $\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{u}}_{M_1})=\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{\eta }}_{M_1})=0$ and $\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{u}}_{M_1})={\mathbf{\Theta }}_{M_1}$, we can rewrite the final identity as

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})={\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1}){\mathbf{\Lambda }}_{M_1}\prime {\mathbf{A}}_{M_1}\prime +{\mathbf{A}}_{M_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{M_1}\prime .$$ (B7)

To correct for bias, we simply solve algebraically for $\mathrm{cov}({\mathbf{\eta }}_{{\mathit{M}}_1},{\mathbf{\eta }}_{{\mathit{M}}_1})$:

$$\mathrm{cov}({\mathbf{\eta }}_{{\mathit{M}}_1},{\mathbf{\eta }}_{{\mathit{M}}_1})={\left({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\right)}^{-1}[\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})-{\mathbf{A}}_{M_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{M_1}\prime ]{({\mathbf{\Lambda }}_{M_1}\prime {\mathbf{A}}_{M_1}\prime )}^{-1}.$$ (B8)

Equation (B8) clearly depends on the nonsingularity of the matrix product ${\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}$ and its transpose. Although this matrix product will often be nonsingular using the regression factor score estimator, the Bartlett estimator exhibits the desirable property that ${\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}=\mathbf{I}$. Therefore, to completely avoid any potential issues with singularity of ${\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}$, we recommend using the Bartlett factor score estimator, in which case Equation (B8) simplifies to

$$\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_1})=\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}})-{\mathbf{A}}_{M_1}{\mathbf{\Theta }}_{M_1}{\mathbf{A}}_{M_1}\prime .$$ (B9)

Equations (B8) and (B9) represent the measurement model equations applied in both simulations reported in the article. For the sake of completeness, we derive one additional expectation: the expected covariance between one connected measurement model, $M_1$, and a second connected measurement model, $M_2$. For example, imagine that a researcher expects or diagnoses a connected measurement model, $M_1$, with across-factor correlated uniquenesses, such as the model depicted in Figure 1E and wishes to correlate this measurement model with a second measurement model, $M_2$, that is only connected to $M_1$ via the latent factor covariances. That is, there may be unique factor covariances within each measurement model, $M_1$ and $M_2$, but there are no unique factor covariances across measurement models.

Let ${\mathbf{\eta }}_{M_2}$ be a vector of $m_2$ latent variables in the second measurement model under consideration and let there be $p_{M_2}$ measured indicators in measurement model $M_2$, contained in a $p_{M_2}\times N$ vector ${\mathbf{y}}_{M_2}$. Let ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_2}}$ denote the factor scores extracted from measurement model $M_2$. Then the expected covariance between ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}$ and ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_2}}$ may be defined:

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_2}})=\mathrm{cov}({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}{\mathbf{\eta }}_{M_1}+{\mathbf{A}}_{M_1}{\mathbf{u}}_{M_1},{\mathbf{A}}_{M_2}{\mathbf{\Lambda }}_{M_2}{\mathbf{\eta }}_{M_2}+{\mathbf{A}}_{M_2}{\mathbf{u}}_{M_2}).$$ (B10)

Applying the rules of covariance algebra for matrices, as before, and simplifying yields the expression:

$$\begin{array}{c}{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_2}){\mathbf{\Lambda }}_{M_2}\prime {\mathbf{A}}_{M_2}\prime +{\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{u}}_{M_2}){\mathbf{A}}_{M_2}\prime \hfill \\ +{\mathbf{A}}_{M_1}\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{\eta }}_{M_2}){\mathbf{\Lambda }}_{M_2}\prime {\mathbf{A}}_{M_2}\prime +{\mathbf{A}}_{M_1}\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{u}}_{M_2}){\mathbf{A}}_{M_2}.\hfill \end{array}$$ (B11)

If $M_1$and $M_2$ are truly connected by only the latent factor covariances—that is, if there are no across-measurement-model correlated uniquenesses—then $\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{u}}_{M_2})=0$. Furthermore, by definition $\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{u}}_{M_2})=\mathrm{cov}({\mathbf{u}}_{M_1},{\mathbf{\eta }}_{M_2})=0$. Thus, Equation (B11) simplifies to

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_2}})={\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_2}){\mathbf{\Lambda }}_{M_2}\prime {\mathbf{A}}_{M_2}\prime .$$ (B12)

Solving for $\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_2})$ yields

$$\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_2})={\left({\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}\right)}^{-1}\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathit{M}}_2}}){({\mathbf{\Lambda }}_{M_2}\prime {\mathbf{A}}_{M_2}\prime )}^{-1}.$$ (B13)

As before, however, if Bartlett estimation is used for both ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}}$ and ${\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_2}}$, then ${\mathbf{A}}_{M_1}{\mathbf{\Lambda }}_{M_1}={\mathbf{\Lambda }}_{M_2}\prime {\mathbf{A}}_{M_2}\prime =\mathbf{I}$ and Equation (B13) reduces to

$$\mathrm{cov}({\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_1}},{\mathbf{F}}_{{\mathbf{\eta }}_{{\mathbf{M}}_2}})=\mathrm{cov}({\mathbf{\eta }}_{M_1},{\mathbf{\eta }}_{M_2}).$$ (B14)

Thus, as observed by Hoshino and Bentler (2013), the covariances among factor scores estimated using the Bartlett estimator are consistent estimates of the covariances among the true latent variables.