Abstract
A log-linear model (LLM) is a well-known statistical method to examine the relationship among categorical variables. This study investigated the performance of LLM in detecting differential item functioning (DIF) for polytomously scored items via simulations where various sample sizes, ability mean differences (impact), and DIF types were manipulated. Also, the performance of LLM was compared with that of other observed score–based DIF methods, namely ordinal logistic regression, logistic discriminant function analysis, Mantel, and generalized Mantel-Haenszel, regarding their Type I error (rejection rates) and power (DIF detection rates). For the observed score matching stratification in LLM, 5 and 10 strata were used. Overall, generalized Mantel-Haenszel and LLM with 10 strata showed better performance than other methods, whereas ordinal logistic regression and Mantel showed poor performance in detecting balanced DIF where the DIF direction is opposite in the two pairs of categories and partial DIF where DIF exists only in some of the categories.
Keywords: log-linear model, differential item functioning, DIF in polytomous items
Differential item functioning (DIF), which indicates differential performance on an item across subgroups matching on a criterion such as test score or ability level (Hanson, 1998), provides a piece of evidence for the fairness of a test. For this reason, DIF investigations have been routinely conducted, specifically in large-scale assessments. In large-scale assessments, polytomously scored items are not uncommon, and the use of dichotomously scored items is still popular. This study revisits the DIF investigation for polytomously scored items with a log-linear model (LLM) approach. Our three major motivations to investigate LLM as a DIF method for polytomously scored items are as follows. First, LLM has widespread availability as a popular statistical method to analyze categorical variables. The LLM analysis is typically included in a statistical methods course on categorical data analysis, and learning of LLM as a statistical method provides a sufficient knowledge base to understand and use LLM as a DIF method. Also, most of the statistical packages are usually equipped with the LLM module, which obviates the necessity of a stand-alone program for DIF investigations. Second, LLM is flexible in that it can handle DIF for dichotomously scored or polytomously scored items, better than the two-group comparisons, and uniform as well as nonuniform DIF detection. Third, since Mellenbergh’s (1982) introduction of LLM as a DIF method only for dichotomously scored items, there has been no systematic evaluative study of LLM for polytomously scored item DIF investigations.
A small number of studies have evaluated LLM as a DIF method solely for dichotomous item response data (Kelderman, 1989; Kelderman & Macready, 1990; Welkenhuysen-Gybels, 2004; Welkenhuysen-Gybels & Billiet, 2002; Wiberg, 2009). Among these cited studies, Wiberg (2009) and Kelderman (1989) investigated DIF in real data sets. Wiberg (2009) compared LLM, logistic regression (LR), and Mantel-Haenszel (MH) for both uniform DIF and nonuniform DIF. Based on the findings, he concluded that LLM is more appropriate for mastery tests because this model uses categorical variables. Welkenhuysen-Gybels and Billiet (2002) compared observed conditional score methods (LLM and LR) and unobserved conditional score methods by simulating dichotomous data under the 1-parametric logistic model (1PLM) and the 2-parametric logistic model (2PLM). They considered three factors: item difficulty differences between groups (0.4), item discrimination differences between groups (0.7), and DIF conditions (uniform and nonuniform). They restricted sample size to 1,000 examinees per group and test length to 20 items. The study indicated that LLM and LR performed well across the conditions for uniform DIF and nonuniform DIF under 1PLM and 2PLM. Welkenhuysen-Gybels (2004) expanded the previous study with six factors in the data generation procedure: sample size (1,000/1,000 and 1,000/300), item difficulty differences between groups (0.2 and 0.6), item discrimination differences between groups (0.4 and 0.8), percentage of DIF item (10%, 20%, and 50%), ability distribution (standard normal distribution and data skewed to the left and to the right), and test length (20 and 30 items). They concluded that the item response theory (IRT) method of signed area performed better than the other techniques for uniform DIF whereas observed score methods (LLM and LR) performed better than IRT methods for nonuniform DIF.
In spite of the LLM studies for dichotomous item response data, the performance of LLM has not been investigated for polytomous item response data, and there is a lack of comparative evaluation of LLM with other methods, such as ordinal logistic regression (OLR; French & Miller, 1996), logistic discriminant function analysis (LDFA; Miller & Spray, 1993), Mantel (Mantel, 1963), and generalized Mantel-Haenszel (GMH; Zwick, Donoghue, & Grima, 1993). We find two studies directly related to LLM for polytomous item DIF investigations, which are Dancer, Anderson, and Derlin (1994) and Hanson and Feinstein (1997). Dancer et al. (1994) used LLM for their survey with a polytomously scored real item response data set without considering any performance investigation of LLM with other DIF methods. Hanson and Feinstein (1997) also used LLM with polynomial terms in their equating study for a real data set. They proposed a polynomial log-linear model (PLLM) to detect DIF for polytomous item responses. Since PLLM considers polynomial terms in the LLM structure based on the number of score levels and the number of response categories, it is more complex and harder to implement in general than the LLM. In PLLM, when the number of categories for the variables increases, the degree of the polynomial terms and the number of the nested models increase. PLLM compares all the nested models in an application to DIF investigation until the best model is obtained. As Hanson and Feinstein (1997) suggested, application of PLLM for each item in the test is not realistic because the degree of polynomial terms changes from item to item, and this adds more complexity in using PLLM. LLM, on the contrary, does not require polynomial terms in its modeling and can be extended straightforwardly to the detection of DIF for polytomous items and more than two groups (Agresti, 2013). Because of the common use of polytomously scored items in educational and psychological testing, studying LLM as a DIF method can provide insights into the applicability and performance of LLM for researchers and practitioners who conduct DIF investigations with polytomously scored items.
In general, LLM is used to examine the relationship between categorical variables, so it can be applied to mastery tests or tests that classified normally or ordered the test takers. Additionally, in terms of MH and LR, the modelings of these methods are extended to the polytomous item response data (GMH and OLR). However, LLM can be used for both dichotomous and polytomous item response data without changing the modeling framework. Thus, LLM can be applied to mixed-item format tests (which have both dichotomous and polytomous response items) easily, which can save time for researchers and practitioners. Because of the advantages of LLM we have stated, this study conducted a systematic evaluation of LLM as a DIF method and compared its performance with that of other existing DIF methods for polytomously scored items. For the other compared DIF methods, we limited out attention to the observed score–based DIF methods (LDFA, OLR, GMH, and Mantel), as is LLM.
DIF Detection Methods
LLM and other observed score–based DIF methods are described in this section. LLM is covered in more detail than the other methods because the focus is on LLM in this study. The other methods are briefly introduced because they have been more widely known in the DIF literature, and readers interested in more details should refer to the references cited for the methods. Across all the DIF methods, the matching variable was the observed total test score, and the studied item for DIF was always included in the matching variable.
Log-Linear Model
LLM is a generalized linear model that uses the logarithmic link function. It is used to analyze a multidimensional contingency table when variables are categorical and to investigate the relationship between the variables (Agresti, 2013). In the analysis, all variables are considered as response variables that have Poisson distribution. LLMs follow three steps (Green, 1988):
Models are proposed. LLMs can be built using any combination of factor effects and interaction effects based on the research interest.
Expected cell frequencies, for instance, in a three-dimensional contingency table, and parameter estimates for the models are calculated as follows. For a main effect model,
| (1) |
where is the expected cell frequency for cell ijk in the contingency table, n is the total number of observations, is the probability of falling into the ith category for variable I, is the probability of falling into the jth category for variable J, and is the probability of falling into the kth category for variable K.
LLM is specified by taking the natural logarithm of both sides of Equation 1. Then, for this example, the independence model is obtained as below:
| (2) |
This model is generally represented by the following equation, which is similar to the main effect analysis of variance (ANOVA):
| (3) |
where is the overall effect and , , and are the effects of variables I, J, and K, respectively.
When interaction effects on expected cell frequencies are of interest, interaction terms are added to the independence model.
3. The best-fit model is identified. For each proposed model, the goodness of fit is measured using the Pearson or the likelihood ratio chi-square statistic. Then, the difference between either Pearson or likelihood ratio chi-square statistics for the two nested models is calculated to test the hypothesis that the parsimonious model is as good a fit as the complex model.
Mellenbergh (1982) proposed LLM as a DIF detection method for dichotomously scored items by analyzing a three-dimensional contingency table: Matching criterion score (e.g., strata based on observed test score) × Group (reference or focal group) × Item responses (0 or 1).
The natural logarithm of the expected frequencies in each combination of the three factors (matching strata, group, and item response) is modeled as a function of the three categorical variables. Although internal or external observed/unobserved matching variables can be used, Mellenbergh (1982) suggested the use of an internal observed matching variable. Because LLM analysis requires categorical data, the matching variable should be divided into categories. For contingency table methods, Scheuneman (1979) and Welkenhuysen-Gybels and Billiet (2002) suggested dividing a matching variable into three to five categories in their analysis. However, Clauser, Mazor, and Hambleton (1994) remarked that the number of categories in the matching variable may affect the Type I error rate along with the characteristics of the data set, such as sample size and ability mean difference (impact). For this reason, the number of categories (or strata) in the LLM were varied by two different numbers, 5 (LLM5) and 10 (LLM10), in this study. Generally, the maximum number of levels of the matching variable is desired to differentiate the marginal ability difference or impact from DIF. In this respect, LLM10 was expected to be a better performer than LLM5 whenever impact exists.
With respect to detecting DIF, the saturated model (Equation 4) and the two models nested within the saturated model are taken into consideration (Equations 5 and 6). The saturated model includes all the variables and all possible interactions among the variables:
| (4) |
where is the expected frequency at the ith response level for the kth score level and jth group, is the overall effect, is the effect of the score-level variable, is the effect of the group variable, is the effect of the item response variable, is the interaction effect of score level and group level, is the interaction effect of score level and response level, is the interaction effect of group and response levels, and is the interaction effect of score, group, and response levels.
Nonsaturated models are obtained by removing the three-way interaction and/or two-way interactions from the saturated model. For the purpose of DIF detection, two nonsaturated models nested in the saturated model are considered:
| (5) |
and
| (6) |
The DIF analysis starts with comparing Models 1 and 3 using the likelihood ratio chi-square difference test under the hypothesis that Model 3 fits as well as Model 1. When the difference test is not significant, it indicates that the studied item has no DIF. If the test is significant, the studied item shows DIF. To find out what kind of DIF it is, first, Model 2 and Model 1 are compared using the likelihood ratio chi-square difference test, under the hypothesis that the Model 2 fits as well as Model 1. The rejection of the hypothesis indicates that the studied item has nonuniform DIF. If the test is not significant, the item does not show nonuniform DIF. Then, Model 2 and Model 3 are compared using the likelihood ratio chi-square difference test, under the hypothesis that the Model 3 fits as well as Model 2. When the test is significant, the studied item includes uniform DIF. In this study, DIF investigation for an item was conducted by the general DIF test and the uniform DIF test. No DIF was recorded if the general DIF test was not significant, whereas DIF was recorded when the two tests were significant.
Generalized Mantel–Haenszel and Mantel Methods
The GMH method is an extension of the MH method for nominal variables with more than two categories (Mantel & Haenszel, 1959). When there are j response categories, the GMH test statistic follows the chi-squared distribution with (j− 1) degrees of freedom. It considers the distribution of all the item categories to assess how differently the item functions among the groups. The matching variable is divided into k strata. For each stratum, a contingency table is created for the two groups of examinees. Then, GMH tests the null hypothesis that there is no conditional association between the item response categories and group membership. Rejection of the null hypothesis indicates DIF.
On the other hand, Mantel (1963) presented an extension of the MH method to test the null hypothesis of no association between an ordinal variable and a factor of interest across all strata. In the application of the Mantel method to DIF investigations, the item scores are considered as ordinal, whereas the other variables are treated as nominal.
As in GMH, a contingency table is arranged for item responses and a group variable at each score level. The null hypothesis of no DIF is tested by the chi-square statistic with 1 degree of freedom.
Ordinal Logistic Regression
French and Miller (1996) argued that using cumulative logit in the LR model is applicable for polytomously scored items with I number of categories. Because LR requires a binary dependent variable, the polytomous responses for an item are recoded as a series of dichotomously scored subitems, and then LR is applied for each of the dichotomously scored subitems. For an item having I categories (), the OLR DIF modeling for the item response category i is presented as
| (7) |
| (8) |
and
| (9) |
where k is the item score, is the matching criterion score for person s, is the group variable for person s, is the interaction between the matching criterion and the group variable for person s, is the intercept of the model, and , , and are the slopes of the model related to the matching criterion, the group variable, and the interaction between the matching criterion and the group variable, respectively. The significant difference in the likelihood ratio test for Model 1 and Model 3 indicates general DIF (Zumbo, 1999). After general DIF is investigated, the difference in the likelihood ratio test for Model 3 and Model 2 is used to test for nonuniform DIF. If the difference is significant, the item is flagged as a nonuniform DIF item. If the difference is not significant, Models 1 and 2 are compared by using the likelihood ratio test to investigate uniform DIF. When the difference in the likelihood ratio test for Models 1 and 2 is significant, the item is flagged as a uniform DIF item (French & Miller, 1996). In this study, as in the French and Miller study, the general DIF test and the uniform DIF test were used. No DIF was recorded if the general DIF test was not significant, whereas DIF was recorded when the two tests were significant.
Logistic Discriminant Function Analysis
Miller and Spray (1993) proposed LDFA as a DIF detection method for polytomous cases. In terms of the DIF identification process, LDFA calculates the probability of an examinee being in group g when the examinee has a total score of X and an item score of U.
The LDFA models used in the DIF analysis for an item are written as follows:
| (10) |
| (11) |
and
| (12) |
where is the item response (or score) for person s, is the matching criterion for person s, is the group variable for person s, is the interaction between the matching criterion and the item response variable for person s, is the intercept of the model, and , , and are the slopes of the model related to the matching criterion, the item response variable, and the interaction between the matching criterion and the item response variable, respectively. First, the difference in the likelihood ratio tests for Model 1 and Model 2 is used to detect nonuniform DIF. If the difference test is significant, the item is flagged as nonuniform DIF. Otherwise, the difference in the likelihood ratio tests for Models 2 and 3 is used to detect uniform DIF. When the difference between the likelihood ratio tests for Model 2 and Model 3 is significant, the item is flagged as uniform DIF (Miller & Spray, 1993). For detecting DIF for a studied item in this study, the general DIF test and the uniform DIF test were used. No DIF was recorded if the general DIF test was not significant, whereas DIF was recorded when the two tests were significant.
Methods
Polytomous graded item responses (0, 1, 2, 3, and 4) for 10-item tests were generated using Samejima’s (1969) graded response model (GRM). The number of options in each item was five. The item discrimination parameter () and threshold parameters () for each item were borrowed from Wang and Su’s study (2004). Because almost all the items in Wang and Su’s study were difficult, they were adjusted by subtracting the constant value of 0.5 from all the threshold parameters to make the items have approximately medium difficulty. The average of the item discrimination values for data generation was 1.63, with minimum (min) = 1.46 and maximum (max) = 1.85. The averages of were −0.84 (min = −1.11 and max = −0.59), −0.10 (min = −0.81 and max = 0.4), 0.61 (min = 0.3 and max = 0.87), and 1.76 (min = 1.44 and max = 1.96), respectively.
The data sets were simulated under a combination of three factors:
Sample size: Studies in the past have examined DIF in polytomous cases with a variety of sample sizes that have ranged from 750 to 4,000 (French & Miller, 1996; Gomez-Benito, Hidalgo, & Zumbo, 2013; Kristjansson, Aylesworth, McDowell, & Zumbo, 2005; Wang & Su, 2004; Woods, 2011). In this study, LLM was compared with Mantel, GMH, OLR, and LDFA by taking into account small, medium, and large sample size conditions, considering both equal and unequal sample sizes for the focal and reference groups. Six levels were considered (200F/200R, 200F/400R, 300F/500R, 500F/500R, 300F/1,000R, and 1,000F/1,000R), where F and R represent the focal and the reference group, respectively.
Mean ability difference (impact): Earlier studies found that when the ability mean difference increased, the Type I error rates increased for GMH, Mantel, and LDFA (Kristjansson, 2001; Wang & Su, 2004). Kristjansson (2001) indicated that when the ability mean difference increased, OLR was less affected by the difference compared with Mantel, GMH, and LDFA. In the present study, three levels of mean ability difference were considered: θR = θF ~ N(0, 1); θF ~ N(−0.25, 1) and θR ~ N(0.25, 1); and θF ~ N(−0.5, 1) and θR ~ N(0.5, 1).
Types of DIF: There are many different ways to create DIF items. Our design was based on Wang and Su’s (2004) framework for generating DIF items. As in Wang and Su’s study, the parameter difference between the two groups was set as 0.25 to represent moderate DIF, which was based on Raju’s (1988) averaged sign area formula for GRM. Seven types of DIF were considered: no DIF, constant DIF, balanced DIF, partial_1, partial_2, partial_3, and partial_4 (Table 1). In this study, one item in a simulated test was designated as a studied item, which has DIF as described or no DIF. The threshold parameters for the studied item when there is no DIF are , , , and .
Table 1.
Types of DIF for DIF Simulation.
| DIF Conditions | ||||
|---|---|---|---|---|
| NoDIF | ||||
| Constant | ||||
| Balanced | ||||
| Partial_1 | ||||
| Partial_2 | ||||
| Partial_3 | ||||
| Partial_4 |
Note. b Fi and bRi represent item threshold parameters for the focal and reference groups, respectively. DIF = differential item functioning.
Previous studies have used test lengths from 10 to 40 items (Gomez-Benito et al., 2013; Kristjansson et al., 2005; Wang & Su, 2004; Woods, 2011) for Mantel, GMH, OLR, and LDFA. Wang and Su (2004) reported that the Type I error rate and power for the Mantel and GMH methods were slightly increased under the GRM when the number of items was higher than 10. They concluded that 10 items with five categories /provided reliable results because the total test score ranged from 0 to 40. In this study, the test length was fixed at 10 items with five categories. The statistical language R (R Core Team, 2013) was used to construct 6 × 3 × 7 = 126 (six levels of sample size, three levels of ability mean difference, and seven levels of DIF types) data simulation conditions. A total of 1,000 replications were created for each condition. For each data set, LLM and all the other DIF methods described previously were applied for testing DIF. The R language and the SAS program (SAS Institute, Cary, NC) were used to conduct LLM, Mantel, GMH, OLR, and LDFA.
We calculated the Type I error rate (rejection rate) and the power (DIF detection rate) for each of the methods and the 126 data-simulating conditions (each of which had 1,000 replications). Type I error rate is the proportion of significant results in the DIF investigation of the studied item that has no DIF. On the other hand, power is the proportion of significant results in testing DIF for the studied item that has DIF. Precisely speaking, because an inflated Type I error affects power, the Type I error rates of the methods should be comparable when comparing the powers of different methods (Jodoin & Gierl, 2001). Thus, readers should be careful in interpreting the detection rates as powers among the different methods when their Type I error rate differences are not small. Readers should understand that our use of the term power is very approximate rather than rigorous.
A repeated-measures ANOVA, where the DIF method was the within-subjects factor and the other data simulation factors (sample size, mean ability difference, and type of DIF) were between-subjects factors, was conducted to investigate statistically and practically the significant effects on the Type I error rate and power. In addition to statistical significance (under , practical significance was evaluated using an effect size . When > .01, in other words explaining the variation in the data at least 1%, the effect was considered practically significant. In this study, an effect was selected as an important effect for discussion when it is both statistically and practically significant.
Results
Although all the simulation factors were used in ANOVA, note that the foci of the analysis were the DIF method factor and its interactions with the other factors. The interpretations of the effects centered on those effects that were both statistically and practically important. Mauchly’s test for all the ANOVAs showed that the sphericity assumption was not tenable, thus the results from the Greenhouse-Geisser approach were reported for the ANOVA results. Power comparison is properly made when the Type I error rate is controlled, that is, when the compared methods are showing the same or very similar levels of Type I error rates. Our results below for Type I error rates show that the DIF methods exhibited different Type I error rates, and the expression of power when DIF exists, though long, was preferred to power for this reason.
Type I Error Rate (Rejection Rate)
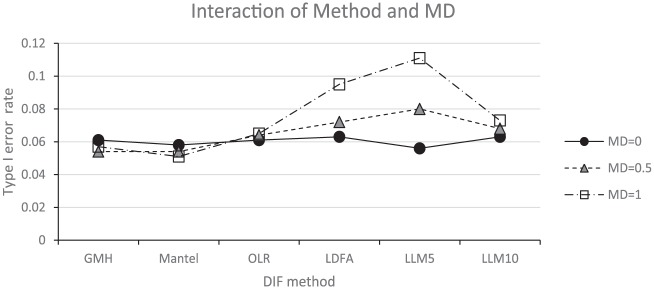
Table 2 shows the ANOVA results for the Type I error rates. The DIF method (Method) factor was both statistically and practically significant. Its interaction with the mean difference (MD) was also statistically and practically significant. This interaction means that the sizes of the Type I error rate differences among the DIF methods depended on the level of MD. The Method × MD interaction plot is shown in Figure 1. The six DIF methods’ marginal (or overall) Type I error rates across all the simulation conditions were 0.057, 0.054, 0.063, 0.076, 0.082, and 0.068 for GMH, Mantel, OLR, LDFA, LLM5, and LLM10, respectively. However, the Type I error rate differences among these methods depended on MD. When MD = 0, all the methods performed very similarly. As MD became larger, for example, MD = 1, the differences in the Type I error rates increased. Particularly LDFA and LLM5 exhibited noticeable inflation in the Type I error rates compared with other methods when there were group mean differences. Both methods showed error rates about twice as large as the nominal Type I error rate (0.095 and 0.111 for LDFA and LLM5, respectively) when MD = 1.
Table 2.
Analysis of Variance for Type I Error Rates.
| Source | Sum of squares | df | Mean square | F | p | η 2 |
|---|---|---|---|---|---|---|
| Between subjects | 18345.49 | 17 | ||||
| MD | 4074.57 | 2 | 2037.29 | 8.628 | .007 | 0.090 |
| N | 11909.71 | 5 | 2381.94 | 10.088 | .001 | 0.264 |
| Sample size within groups | 2361.20 | 10 | 236.12 | |||
| Within subjects | 26738.16 | 35 | ||||
| Method | 10461.38 | 1.95 | 5379.50 | 26.18 | <.001 | 0.232 |
| Method×MD | 8854.87 | 3.89 | 2276.70 | 11.08 | <.001 | 0.196 |
| Method ×N× MD | 3425.23 | 9.72 | 352.27 | 1.71 | .149 | 0.076 |
| Method × Sample size within groups | 3996.69 | 19.45 | 205.52 | |||
| Total | 45083.65 |
Note. N and MD indicate sample size and ability mean difference between reference group and focal group, respectively. df = degrees of freedom; DIF = differential item functioning. The effects that are statistically and practically significant are highlighted in boldface.
Figure 1.
Interaction of differential item functioning method (Method) and mean difference (MD) for Type I error rates.
One between-subjects effect, sample size, was both statistically and practically significant. When the sample sizes were equal, the Type I error rates were 0.059 (500F/500R) and 0.061 (1,000F/1,000R) for LDFA and LLM5, respectively. With unequal sample sizes, the Type I error rates ranged from 0.053 to 0.081, showing that a large sample size tended to yield slightly higher Type I error rates.
Power (DIF Detection Rates When DIF Exists)
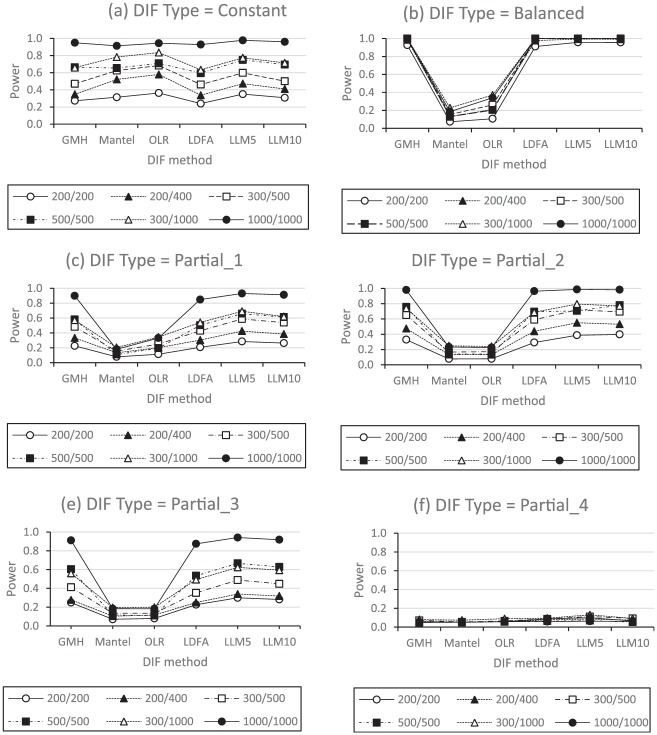
Table 3 shows the ANOVA results for power when DIF exists. For the between-subjects effects, DIF type (DT), N, and their interaction (DT ×N) were both statistically and practically significant. Among the within-subjects effects, the DIF method as a main effect and its interactions with DT, N, and DT ×N were also both statistically and practically significant. Because the three-way interaction of Method × DT ×N was statistically and practically significant, which subsumes the other statistically and practically significant effects, we focus on this three-way interaction. This three-way interaction means that the sizes of the differential power among the six DIF methods were dependent on not only DT but also N. Figure 2 shows the three-way interaction through the mean interaction plots for Method ×N conditional on DT. In general, all the methods tended to show better power as the total sample size (which combines the reference and focal groups’ sample sizes) increased. However, the power differences among the DIF methods were not similar when the total sample size changed. In addition, the pattern of the Method ×N interaction depended on DT. When DT was constant, the power differences among the methods as N changes were not large. When DT = balanced, the differences in power among the DIF methods were the smallest. When DT = Partial_1 through Partial_3, the power differences among the DIF methods became larger as the total sample size became larger. For DT = Partial_4, all the DIF methods’ power values were very low, ranging from 0.049 to 0.131 only. In the DT = Partial_4 condition, DIF was simulated for the highest-category boundary threshold parameter, , when there was no DIF. Thus, this very high threshold parameter appears to be responsible for this lower performance in detecting DIF for DT = Partial_4.
Table 3.
Analysis of Variance for Power (DIF Detection Rate When DIF Exists).
| Source | Sum of squares | df | Mean square | F | P | η2 |
|---|---|---|---|---|---|---|
| Between subjects | 39717648.66 | 108 | ||||
| DT | 27259917.94 | 5 | 5451983.59 | 6954.97 | <.001 | 0.388 |
| MD | 18357.15 | 2 | 9178.58 | 11.71 | <.001 | 0.000 |
| N | 8718996.16 | 5 | 1743799.23 | 2224.53 | <.001 | 0.124 |
| DT × MD | 65371.68 | 10 | 6537.17 | 8.34 | <.001 | 0.001 |
| DT×N | 3610413.01 | 25 | 144416.52 | 184.23 | <.001 | 0.051 |
| MD ×N | 5397.85 | 10 | 539.79 | 0.69 | .730 | 0.000 |
| Sample size within groups | 39194.87 | 50 | 783.90 | |||
| Within subjects | 30554242.67 | 349.11 | ||||
| Method | 15673151.27 | 3.24 | 4844487.39 | 18231.84 | <.001 | 0.223 |
| Method×DT | 12307740.23 | 16.18 | 760851.36 | 2863.40 | <.001 | 0.175 |
| Method × MD | 79454.52 | 6.47 | 12279.49 | 46.21 | <.001 | 0.001 |
| Method×N | 1171518.90 | 16.18 | 72422.05 | 272.56 | <.001 | 0.017 |
| Method × DT × MD | 70889.54 | 32.35 | 2191.16 | 8.25 | <.001 | 0.001 |
| Method×DT×N | 1191181.16 | 80.88 | 14727.51 | 55.43 | <.001 | 0.017 |
| Method × MD ×N | 17324.15 | 32.35 | 535.48 | 2.02 | .002 | 0.000 |
| Method × Sample size within groups | 42982.90 | 161.76 | 265.72 | |||
| Total | 70271891.33 | 457.11 |
Note. N, MD, and DT indicate sample size, ability mean difference between reference group and focal group, and type of DIF, respectively. df = degrees of freedom; DIF = differential item functioning. The effects that are statistically and practically significant are highlighted in boldface.
Figure 2.
Interaction of method by sample size (N) by differential item functioning type (DT).
Another noticeable observation from the three-way interaction was that the power values of Mantel and OLR were clearly inferior to the power of other methods except when DT was constant. LDFA and LLM5 showed approximately comparable performance with GMH and LLM10, but the Type I error rates (shown in Figure 1) of LDFA and LLM5 were higher than for other methods when MD exists.
Conclusion and Discussion
Investigating DIF for polytomously scored items in educational and psychological testing is very important to ensure fair and valid testing. This study examined the performance of six observed score–based DIF methods applicable to polytomously scored item tests through simulation. For the DIF methods’ performance, both Type I error rate and power (or, more suitably, DIF detection rates) when DIF exists were investigated. For practitioners, which method should be used is a major concern. The best DIF method should have a well-controlled Type I error rate and as high a power as possible when DIF exists.
For Type I error rates, the six DIF methods showed differential rates depending on the existence of group mean ability differences. LDFA and LLM5 showed an increase in Type I error rates as the mean ability increased, reaching nearly twice as large as the nominal significance level. The comparison of power showed that Mantel and OLR were not as sensitive as the other DIF methods in detecting DIF. Although when DIF type was constant, these methods showed comparable performance with the other DIF methods, it is not advisable to recommend the use of these two methods. The reason is that the type of DIF is not known in real data analysis, and there is no guarantee of a constant DIF type when DIF exists. Both Mantel and OLR suffer from poor power for other types of DIF presence. LDFA and LLM5 showed comparable power with GMH and LLM10, but because of their inflated Type I error rates in the presence of group ability mean differences, LDFA and LLM5 cannot be recommended either. The use of five strata in LLM seems to be too rough to define the number of ability levels when the size group ability mean difference increases.
Considering the above observations, we are left with GMH or LLM10 for recommendation. The overall Type I error rates for GMH and LLM10 were 0.057 and 0.068, respectively. The overall power values were 0.546 and 0.574, respectively. The power of LLM10 was slightly higher than that of GMH in general. Higher Type I error rate is typically associated with higher power, and the overall slightly higher power of LLM10 reflects this. LLM10 showed better-controlled Type I error rate.
Assuming that the practitioner chooses a DIF method, a typical next question is about the sample sizes. Table 4 summarizes the power values of GMH and LLM10 in addition to the Type I error rates according to the sample sizes used in this study. To ensure at least a 50% chance of detecting DIF to decrease Type II errors, our results indicate sample sizes of at least 300 for the smaller group and 500 for the larger of the two comparing groups. For practitioners, LLM as a DIF method could be considered as an alternative for DIF investigations for polytomously scored items. Especially when sample sizes are as small as 200 per group, then LLM with 10 strata (LLM10 in this study) could provide comparable or better performance. Comparing with GMH, both the slightly increased Type I error rate and the slightly better power should be properly weighed in considering LLM10. Theoretically, the LLM approach has an advantage over the other methods. LLM can be straightforwardly extended to accommodate testing explicitly the nonuniform DIF null hypothesis, multiple groups (more than two), and simultaneous DIF investigation of more than a single studied item (Wiberg, 2007).
Table 4.
Performance of GMH and LLM10 for Different Sample Sizes.
| Sample size (N)a |
||||||
|---|---|---|---|---|---|---|
| Method | 200_200 | 200_400 | 300_500 | 500_500 | 300_1,000 | 1,000_1,000 |
| Power | ||||||
| GMH | 0.34 | 0.41 | 0.51 | 0.61 | 0.60 | 0.80 |
| LLM10 | 0.38 | 0.45 | 0.55 | 0.63 | 0.63 | 0.81 |
| Type I error rate | ||||||
| GMH | 0.05 | 0.06 | 0.07 | 0.05 | 0.07 | 0.05 |
| LLM10 | 0.05 | 0.07 | 0.09 | 0.06 | 0.08 | 0.05 |
Note. GMH = generalized Mantel-Haenszel; LLM = log-linear model.
The first number in the sample size is for the focal group, and the second number is for the reference group.
Though this study incorporates important aspects of DIF investigation in its simulation, several limitations must be noted. First, the way DIF was generated is limited to a constant shift in a category threshold parameter. DIF produced by different item discrimination parameters in the GRM across the groups, for example, was not included. Second, the scope of the DIF methods included in the study was restricted to observed score–based DIF methods for polytomously scored items. Other parametric and nonparametric IRT DIF methods (e.g., SIBTEST in Shealy & Stout, 1993; parametric IRT likelihood ratio test in Thissen, Steinberg, & Wainer, 1993) could be included for further comparisons. Third, the difference between the ability distributions of the two groups was operationalized using the ability mean difference. Standard deviations, however, for example, may vary from one group to another in real data. Fourth, this study investigated the performance of LLM as a DIF detection method by having a single studied item that may have DIF and the rest of the items have no DIF. The simulation scenario mimicked a situation where an operational test exists and each item in a new set of field test items is investigated for DIF with the existing operational test. The effect of the existence of DIF items in nonstudied items in a test on DIF detection has not yet been investigated for LLM. Jodoin and Gierl (2001) as well as Narayanan and Swaminathan (1996) reported that the increase of DIF items in nonstudied items in a test was associated with increased Type I error rate and decreased power for the LR DIF method. We conjecture similar results for LLM, but empirical evidence for this claim and the detailed behavior of LLM as a DIF method under this DIF contamination scenario can be investigated in the future.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Gonca Yesiltas  https://orcid.org/0000-0002-7291-7083
https://orcid.org/0000-0002-7291-7083
References
- Agresti A. (2013). Categorical data analysis (3rd ed.). Hoboken, NJ: Wiley. [Google Scholar]
- Clauser B., Mazor K. M., Hambleton R. K. (1994). The effects of score group width on the Mantel-Haenszel procedure. Journal of Educational Measurement, 31, 67-78. [Google Scholar]
- Dancer L. S., Anderson A. J., Derlin R. L. (1994). Use of log-linear models for assessing differential item functioning in a measure of psychological functioning. Journal of Consulting and Clinical Psychology, 62, 710-717. [DOI] [PubMed] [Google Scholar]
- French A. W., Miller T. R. (1996). Logistic regression and its use in detecting differential item functioning in polytomous items. Journal of Educational Measurement, 33, 315-332. [Google Scholar]
- Gomez-Benito J., Hidalgo M. D., Zumbo B. D. (2013). Effectiveness of combining statistical tests and effect sizes when using logistic discriminant function regression to detect differential item functioning for polytomous items. Educational and Psychological Measurement, 75, 875-897. [Google Scholar]
- Green J. A., (1988). Loglinear analysis of cross-classified ordinal data: Applications in developmental research. Child Development, 59, 1-25. [PubMed] [Google Scholar]
- Hanson B. A. (1998). Uniform DIF and DIF defined by differences in item response functions. Journal of Educational and Behavioral Statistics, 3, 244-253. [Google Scholar]
- Hanson B. A., Feinstein Z. S. (1997). Application of a polynomial loglinear model to assessing differential item functioning for common items in the common-item equating design (ACT Research Report Series 97-1). Retrieved from http://www.act.org/content/dam/act/unsecured/documents/ACT_RR97-01.pdf
- Jodoin G. M., Gierl M. J. (2001). Evaluating Type I error and power rates using an effect size measure with the logistic regression procedure for DIF detection. Applied Measurement in Education, 14, 329-349. [Google Scholar]
- Kelderman H. (1989). Item bias detection using loglinear IRT. Psychometrika, 54, 681-697. [Google Scholar]
- Kelderman H., Macready G. B. (1990). The use of loglinear models for assessing differential item functioning across manifest and latent examinee groups. Journal of Educational Measurement, 27, 307-327. [Google Scholar]
- Kristjansson E. (2001). Detecting DIF in polytomous items: An empirical comparison of the ordinal logistic regression, logistic discriminant function analysis, Mantel, and generalized Mantel-Haenszel procedures (Doctoral dissertation). University of Ottawa, Ottawa, Ontario, Canada. [Google Scholar]
- Kristjansson E., Aylesworth R., McDowell I., Zumbo B. D. (2005). A comparison of four methods for detecting differential item functioning in ordered response items. Educational and Psychological Measurement, 65, 935-953. [Google Scholar]
- Mantel N. (1963). Chi-square tests with one degree of freedom: Extensions of the Mantel-Haenszel procedure. Journal of the American Statistical Association, 58, 690-700. [Google Scholar]
- Mantel N., Haenszel W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22, 719-748. [PubMed] [Google Scholar]
- Mellenbergh G. J. (1982). Contingency table models for assessing item bias. Journal of Educational Statistics, 7, 105-118. [Google Scholar]
- Miller T. R., Spray J. A. (1993). Logistic discriminant function analysis for DIF identification of polytomously scored items. Journal of Educational Measurement, 30, 107-122. [Google Scholar]
- Narayanan P., Swaminathan H. (1996). Identification of items that show non-uniform DIF. Applied Psychological Measurement, 20, 257-274. [Google Scholar]
- R Core Team. (2013). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Raju N. S. (1988). The area between two item characteristic curves. Psychometrika, 53, 495-502. [Google Scholar]
- Samejima F. (1969). Estimation of latent ability using a response pattern of graded scores (Psychometric Monograph No. 17). Richmond, VA: Psychometric Society; Retrieved from https://www.psychometricsociety.org/sites/default/files/pdf/MN17.pdf [Google Scholar]
- Scheuneman J. D. (1979) A method of assessing bias in test items. Journal of Educational Measurement, 16, 143-152. [Google Scholar]
- Shealy R., Stout W. (1993). A model-based standardization approach that separates true bias/DIF from group ability differences and detects test/DTF as well as item bias/DIF. Psychometrika, 58, 159-194. [Google Scholar]
- Thissen D., Steinberg L., Wainer H. (1993). Detection of differential item functioning using the parameters of item response models. In Holland P. W., Wainer H. (Eds.), Differential item functioning (pp. 67-113). Hillsdale, NJ: Lawrence Erlbaum. [Google Scholar]
- Wang W. C., Su Y. H. (2004). Factors influencing the Mantel and generalized Mantel-Haenszel methods for the assessment of differential item functioning in polytomous items. Applied Psychological Measurement, 28, 450-480. [Google Scholar]
- Welkenhuysen-Gybels J. (2004). The performance of some observed and unobserved conditional invariance techniques for the detection of differential item functioning. Quality & Quantity, 38, 681-702. [Google Scholar]
- Welkenhuysen-Gybels J., Billiet J. (2002). A comparison of techniques for detecting cross-cultural inequivalence at the item level. Quality & Quantity, 36, 197-218. [Google Scholar]
- Wiberg M. (2007). Measuring and detecting differential item functioning in criterion-referenced licensing test: A theoretic comparison of methods (Educational Measurement No. 60). Umeå, Sweden: Umeå University. [Google Scholar]
- Wiberg M. (2009). Differential item functioning in mastery tests: A comparison of three methods using real data. International Journal of Testing, 9, 41-59. [Google Scholar]
- Woods C. M. (2011). DIF testing for ordinal items with Poly-SIBTEST, the Mantel and GMH tests, and IRT-LR-DIF when the latent distribution is non-normal for both groups. Applied Psychological Measurement, 35, 145-164. [Google Scholar]
- Zumbo B. D. (1999). A handbook on the theory and methods of differential item functioning (DIF): Logistic regression modeling as a unitary framework for binary and Likert-type (ordinal) item scores. Ottawa, Ontario, Canada: Directorate of Human Resources Research and Evaluation, Department of National Defense. [Google Scholar]
- Zwick R., Donoghue J. R., Grima A. (1993). Assessment of differential item functioning for performance task. Journal of Educational Measurement, 30, 233-251. [Google Scholar]