Abstract
Hyporheic exchange between a river channel and its floodplain region assists in mediating processes such as nutrient removal and temperature regulation. Floodplain restoration in the form of levee setbacks are often carried out to improve the hyporheic exchange. In this study Light Detection and Ranging (LiDAR) data were used along with the head data from observation wells and stage data from rivers to setup and calibrate a groundwater model for 458 km2 of area within Gap to Gap reach of the Yakima River, WA. This area has witnessed several efforts of floodplain restoration in the form of levee setbacks. The groundwater model was used to quantify hyporheic flow emerging from the Yakima River in steady and transient states during pre-restoration (using LiDAR data of 2008) and post-restoration period (after levee setback using LiDAR data of 2013). The comparison of results from the model runs during pre and post-restoration periods showed that the length of the pathlines increased after levee setback for both steady and transient state model simulations. The largest increase of about 62 m was noticed in the month of September 2014 (pre: 398 m and post: 460 m). The study also showed that the direction of the flow changed following levee setback, expanding the area for hyporheic flux exchange between surface and groundwater. The model run during transient state also suggested that pathlines were longer during drier months compared to wet months. Overall, the study showed that levee setbacks improved the hyporheic connection between surface and groundwater in the Yakima floodplain which demonstrates that levee setback can provide a valuable hydrologic tool to restore ecosystem processes in previously leveed rivers.
Keywords: Hyporheic flow, MODFLOW, Floodplain, Levee setback
1. Introduction
The movement of water between river channel and floodplain plays a crucial role in influencing the river ecosystem (Poff et al., 1997) and over the years, its study had gathered considerable interest (Stanford and Ward, 1993, Ward et al., 1999, Forshay and Stanley, 2005, Helton et al., 2014, Stoffels et al., 2016). Some of this research has focused specifically on the hydrology of the hyporheic zone, defined as the region where groundwater and surface water interaction takes place (Dahm et al., 1998, Faulkner et al., 2012). Realizing the importance of connectivity between river and floodplain and their role in designing the habitats in flood plain areas (Snyder et al., 2002, Stanford et al., 2002), tens of thousands of river restoration projects have taken place across the world and will continue as infrastructure ages (Doyle et al., 2008). In the United states alone there were 37,099 river restoration projects as listed in National River Restoration Science Synthesis (NRRSS) database as of July 2004 (Bernhardt et al., 2005), many of which intend to enhance connectivity between river and floodplain.
In view of this, it is also essential to evaluate the effects of implementing restoration projects to benefit ecosystems (González et al., 2015, Pess et al., 2005). Several studies have investigated the effect of river and stream restoration and connectivity on the hydrology and water quality (Tockner et al., 1998, Gergel et al., 2002, Singer and Dunne, 2004, Singer and Dunne, 2006, Bukaveckas, 2007, Kroes et al., 2015, Ahilan et al., 2016). Other ecohydrologic benefits of hyporheic flow in floodplains have also been studied (Rains et al., 2004, Singer et al., 2014, Sargeant and Singer, 2016). Different methods have been applied to assess the effects of restoration projects on the hydrology and ecosystem. For instance, Tague et al., 2008 used statistical modelling to study the effects of channel restoration on the hydrology of the streamflow and groundwater at El Dorado County, California. The results from their statistical analysis indicated that the streamflow during snowmelt recession increased significantly after restoration. This was attributed to lower channel gradient from the infilling of the channel and greater storage in the riparian channel. Heine and Pinter (2012) studied the before and after effects of levees on the floodplain by using regression residual analysis to compare the step-trends in the stage discharge curves before and after levees. It was found that flood conveyance capacity reduces after the levee constructions due to the shortening of floodplain width. Apart from the use of empirical models, a finite difference groundwater model, MODFLOW (McDonald and Harbaugh, 1984) has been used effectively to study the effect restoration projects on groundwater flow (Kasahara and Hill, 2006, Rogiers et al., 2011, Traum et al., 2014).
Although MODFLOW has been applied to restoration hydrology research, there is limited evaluation of hyporheic flow pre and post restoration in large river floodplain systems. Kasahara and Hill (2006) studied the effect of stream restoration on flow in the hyporheic zone in some lowland streams in Toronto, Canada. Surface and groundwater interactions in degraded lowland streams were improved by constructing riffles and steps. Rogiers et al. (2011) developed a transient MODFLOW model to study the effect of river restoration on the local groundwater and ecological system. It was noticed in the study that the high-resolution transient modeling considerably improved the assessment of groundwater fluctuations. While MODFLOW can be used to assess the impact of restoration on the groundwater and surface water interaction, it is often difficult to compare the hydrology of the system pre and post-restoration due to data limitations. This evaluation of hyporheic flow in floodplains that undergo levee setback that also coincides with necessary hydrologic data are critical opportunities to advance understanding of restoration in large river floodplain systems. Thus, there is a critical need to develop example groundwater model systems that can demonstrate the before and after effects of restoration projects on the hyporheic flow, particularly with respect to levee setback and large river reconnection. Further, to better understand the seasonality of river discharge effects, the application of transient models can elucidate the temporal variations in the hyporheic flow and inform future river floodplain management decisions.
The Gap to Gap reach of the Yakima River, Washington (Fig. 1) has experienced nearly 50 floods since 1894 with the largest flood in 1933 (Yakima County, WA, 2006–2016), which led to the construction of a federal levee system (Anchor and LLC, 2014). Levees were constructed for controlling erosion and flood protection. While levees are intended to prevent overbank flows (Heine and Pinter, 2012), they can adversely affect the river floodplain ecosystems through loss of connection between river and floodplain (e.g. Poff et al., 1997, Gergel et al., 2002). Considering the importance of hydrologic connectivity between river channel and floodplains (Snyder et al., 2002, Stanford et al., 2002), the floodplain restoration in Gap to Gap region of Yakima Watershed was undertaken to improve flood control and to preserve the habitat of salmonids (Snyder and Stanford, 2001). The restoration is being done through levee setback which is a commonly used hydro-geomorphic strategy that focuses on alteration of water to initiate modifications in the ecosystem (González et al., 2015). In other words, during levee setback levees are moved further away from the river to improve the river floodplain ecosystem. While it is assumed that the levee setback improves the connectivity between surface and groundwater in flood plain areas, to the best of our knowledge the effect of levee setback on the direction and length of pathlines of hyporheic flow has not been studied. So the hypothesis of the study was that levee setbacks improve the surface water and groundwater connection in the floodplain regions.
Fig. 1.
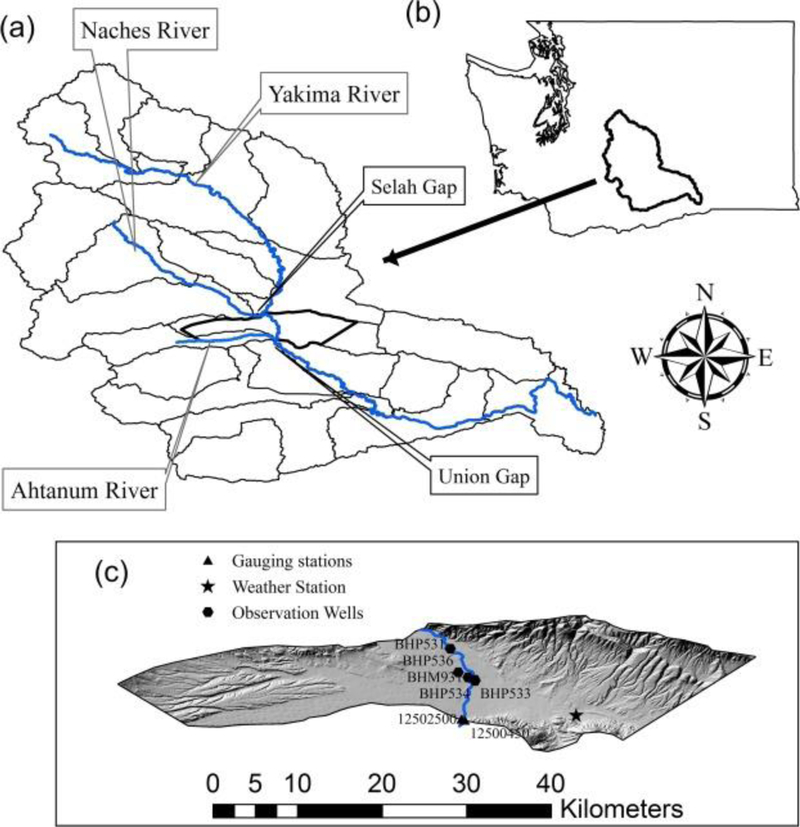
(a) Yakima basin with Rivers: Yakima, Naches and Ahtanum Creek; (b) map of Washington State with the location of Yakima Basin; (c) LiDAR imagery (1m horizontal resolution) of the Gap to Gap study area along with Yakima River (blue line) and the locations of observation wells (black hexagons) and weather station (black star).
In an earlier attempt to study the groundwater hydrology and chemistry in the Yakima Watershed, a MODFLOW model used by USGS for the entire Yakima River Basin (Ely et al., 2011). The Yakima Basin covers 16,058 km2 and it was represented in the MODFLOW grid using 600 rows and 600 columns with a uniform length of approximately 305 m. In our study, we focus on the Gap to Gap region which is a part of Yakima Basin (Fig. 1), using a groundwater MODFLOW model with much finer resolution for grid size. In the model developed by USGS the aquifer was considered as confined, while in this study the model is developed with an unconfined aquifer. This will help describe the hydrology of Gap to Gap region in greater depth and aid in the analysis of hyporheic flow in unconfined zone. In addition to the MODFLOW model we will use a particle tracking system, MODPATH (Pollock, 1994) to track the flow pathlines for particles emerging from the Yakima River. Length of the pathlines and their residence time will be used to evaluate the changes in the areal extent of hyporheic exchange due to levee setbacks. For instance, longer pathlines should correspond to larger area for hyporheic exchange.
Hyporheic exchange between river and floodplains not only improves the hydrologic connectivity between surface and groundwater, it may help regulate stream temperature (Fernald et al. 2006), improve biological connectivity (Stanford and Ward, 1993) and nutrient removal (Hill et al., 2000, Forshay and Stanley, 2005). The overall goal of this study is to determine the effect of floodplain restoration activities (specifically levee setback) on the hydrology of the study area. The specific objectives were to: (i) parameterize a groundwater model for the Gap to Gap region of Yakima Watershed using MODFLOW; (ii) simulate groundwater flow for pre and post-restoration using the LiDAR data from 2008 and 2013, respectively; and (iii) compare hyporheic flow pathlines emerging from Yakima River for pre and post-restoration.
2. Methodology
2.1. Study area
The Gap-to Gap region is a part of the Yakima basin (Fig. 1a) bounded by Selah Gap in the North and Union Gap from south. It is located in Yakima County, Washington (Fig. 1b) and is drained mostly by the Yakima River. The Yakima River originates from Cascade Mountains, converges with Naches River (north-west of the study area; Fig. 1a) and confluence with Ahtanum Creek (south west of the study area; Fig. 1a) and finally joins Columbia River. It travels a distance of approximately 14 km from Selah Gap to Union Gap (Gap to Gap). The climate of study area (Fig. 1c) is mostly semi-arid and it receives approximately 0.2 m of precipitation with the majority occurring between October and March. It encompasses an area of approximately 458 km2.
The study area geology is a part of the Columbia River Basalt Group (CRBG, formed by sequences of lava flows of basalt during Miocene Epoch. Since then it has experienced subsidence and other compressions resulting in folds and faults (Tolan et al., 2009). These folds and faults act as barriers with low permeability to groundwater flow (Burns et al., 2015). In addition to the basalt faults and folding, the study area comprises of the lowlands where CRBG is overlain by consolidated and unconsolidated sedimentary deposits (from the Quaternary age). For additional details about the geology of Yakima River Basin, refer to Fuhrer et al., 1994, Jones et al., 2006.
According to the National Land Cover Database of 2011, obtained from Multi-Resolution Land Characteristics Consortium (Homer et al., 2015), approximately 23 percent of the study area is developed open spaces, and residential areas. The rest of the study area is dominated by shrubs (36.9%), followed by agricultural (27.7%) and pasture (8.2%) land.
2.2. Digital elevation data
The topographic input data, such as elevation and slope for the watershed and its elements (rivers, drains, observation wells), were obtained from the Light Detection and Ranging (LiDAR) data collected during flights in 2008 and 2013. The data were obtained from Yakima County and were collected using aircraft by Quantum Spatial (Sheboygan, Wisconsin) for Rogers Surveying, Inc. (Richland, Washington). LiDAR data were verified using surveyed data collected at various check points along Yakima and Naches River. Maximum and minimum error on comparing LiDAR data with the checkpoints was 0.2 m and −0.08 m with an average of 0.03 m. The LiDAR data obtained in 2008 is representative of the topographic conditions before the restoration (levee setback) and the 2013 LiDAR data represent conditions post-restoration in the form of levee setback. Fig. 2 presents a comparison of the channel cross-sections obtained from the two datasets for transects at two different places along the Yakima River. While, at the first transection A (Fig. 2), the levee was setback by about 200 m towards the southeastern side, at the second transect, B, levee was setback by about 330 m towards west. Similar levee setbacks were achieved at other places along the Yakima River.
Fig. 2.
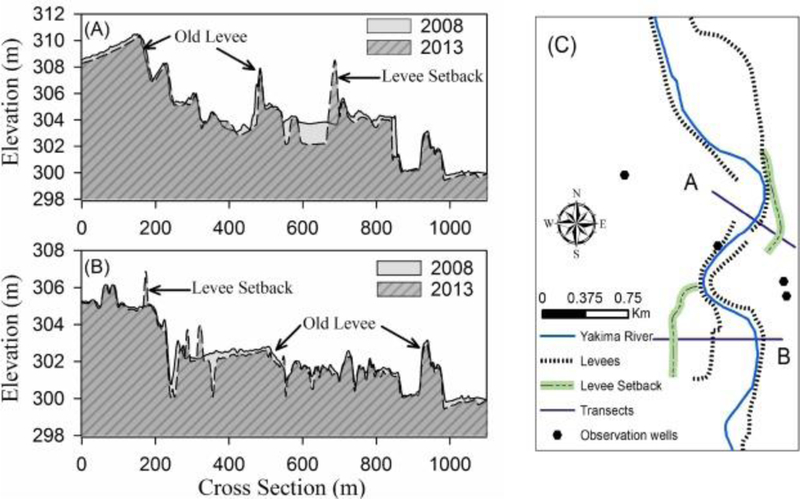
Cross-section (A and B) and plan (C) views of river channel across the transects (A and B) where levees were setback. Cross-sections were developed using LiDAR data from 2008 and 2013.
2.3. Hydrologic data
Observation wells were installed by the US EPA Office of Research and Development in the study area. Groundwater table elevation data were collected between 2013 and 2015 for 5 different wells (BHP 531, BHP 533, BHP 534, BHP 536, and BHM 931) located on either side of the Yakima River (Table 1; Fig. 1). The data were collected using leveloggers from Solinst (Solinst Canada Ltd., Ontario, Canada). Water table elevation data from wells were compensated using the Barologger data. Barologger data were downloaded from weather station network, AgWeatherNet managed by Washington State University (http://weather.wsu.edu/?p=88650). The weather station is located approximately 10 km east of the Yakima River at Moxee, WA (Fig. 1).
Table 1.
Location of the observation wells (latitude and longitude) along with their ground surface elevation and installation date.
| Well | Installation date | Latitude | Longitude | Elevation (m) |
|---|---|---|---|---|
| BHP531 | 1/26/2013 | 46.61049 | −120.48377 | 318.6 |
| BHP533 | 1/29/2013 | 46.57737 | −120.45779 | 301.9 |
| BHP534 | 1/29/2013 | 46.57630 | −120.45751 | 301.6 |
| BHP536 | 1/31/2013 | 46.58553 | −120.47556 | 311.5 |
| BHM931 | 1/24/2013 | 46.58014 | −120.46517 | 305.4 |
River stage data were obtained for Yakima River (USGS station 12500450 at Union Gap) and Ahtanum Creek (USGS station 12502500 at Union Gap) from USGS website. Fig. 3 presents river stage data (m) for Yakima River and Ahtanum Creek along with the precipitation data (mm) from weather station located at Moxee, WA (Fig. 1), obtained from AgWeatherNet (http://weather.wsu.edu/?p=92850). The stage at Ahtanum Creek was slightly higher than Yakima River. The flow in Yakima River is regulated by dams and irrigation canals.
Fig. 3.
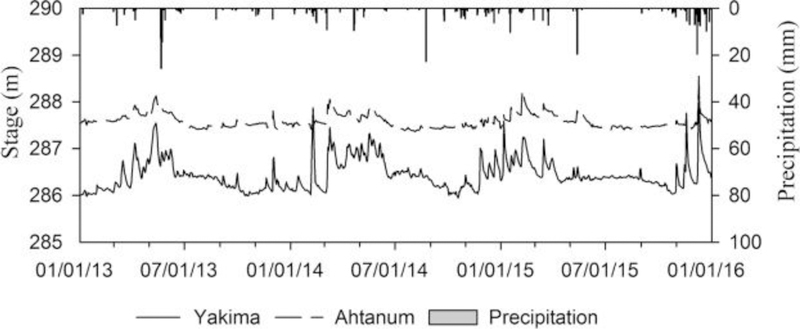
Comparison of stage at Yakima River and Ahtanum Creek for a period from January 1, 2013 to December 31, 2015. Precipitation data obtained from weather station at Moxee, WA is also presented for the same period.
2.4. Hydrogeological units
Borehole data were collected by the US EPA Office of Research and Development from various locations (n = 668) in the study area with the deepest cross-section at approximately 490 m below ground surface. Although the exact locations of the boreholes were unavailabel from the data logs, the sections in a township where the boreholes were located were known. For the purpose of constructing hydrogeology of the study area to setup the groundwater model, the locations of the boreholes were determined by generating random points within different sections of various townships. The randomization of borehole locations was achieved by using “Create Random Points” tools from ArcToolbox (ArcGIS version 10.3). The data from borehole logs were narrowed down to five types of soil materials, the first two material types consisted of larger particles (sand and gravel), third material type included particles smaller than sand (such as silt and clay), basalt was recognized as the fourth material category and strongly cemented material of sand, clay and gravel was also found during the borehole data collection which was categorized as the fifth material type, cemented. The median and range (maximum, minimum and interquartile range (IQR)) of hydraulic conductivity (m/day) obtained using slug test for all the categories are presented in Table 2. The borehole data were used to simulate the hydrogeology of the study area. Details about the model setup are presented in next section.
Table 2.
Hydraulic conductivities (m/day) of the materials obtained from slug tests in Gap to Gap region of the Yakima Watershed.
| Material | Number of samples | Minimum | Maximum | IQR* | Median |
|---|---|---|---|---|---|
| Gravel | 9 | 11.66 | 711.44 | 17.50 | 44.31 |
| Sand | 23 | 0.66 | 286.08 | 19.77 | 6.45 |
| Clay | 4 | 0.94 | 6.00 | 3.03 | 3.94 |
| Basalt | 3 | 1.05 | 1.05 | 31.25 | 1.05 |
| Cemented | 2 | 0.66 | 0.71 | 0.03 | 0.69 |
Inter Quartile Range.
2.5. MODFLOW and MODPATH
A groundwater flow model was setup for the Gap to Gap region of Yakima, Watershed using MODFLOW model developed by USGS (MODFLOW-2005, Harbaugh, 2005). The principal equation solved in the model for simulating ground-water flow is (McDonald and Harbaugh, 1984)
| 1 |
where h is potentiometric head (m); Kxx, Kyy refers to the values of horizontal hydraulic conductivities (m day−1) in the direction of x and y coordinate axes and Kzz to the vertical hydraulic conductivity (m day−1) along the z axis; Ss is the specific storage (m−1) of the porous media, W is a volumetric flux per unit volume into or out of the groundwater system, representing sources of water such as precipitation and sinks such as evapotranspiration. Various options exist to solve the finite difference approximation to the above equation; in this study Preconditioned Conjugate-Gradient 2 (PCG2: Hill, 1990) package was used to solve the groundwater flow equations.
The study area is comprised of CRBG units and the permeability of CRBG units declines by several orders of magnitude at depths below 600 m from the ground surface (Ely et al., 2014). The groundwater model for Gap to Gap region was developed as a single layer unconfined aquifer with a depth of 600 m. The bottom of the layer was considered as a no-flow condition. The elevations for top surface of each cell were obtained by mapping the model to LiDAR data. The model was discretized into 220 rows and 660 columns. Vertical discretization was obtained using Hydrogeologic Unit-Flow (HUF) package (Anderman and Hill, 2000) as implemented by a user interface known as Groundwater Modeling System (GMS version 8.3; AQUAVEO, Provo, Utah). The HUF package was used to divide the thickness of model into several hydrological layers based on the borehole data. This package also provides a convertible option which allows the simulation of fluctuating saturation condition within an unconfined aquifer by the substitution of specific yield for specific storage in the above equation. The specific yields for the materials were obtained from a U.S. Geological Survey report prepared by Heath (1983) as gravel: 0.19, sand: 0.22, clay:0.02, basalt: 0.08. For cemented material the specific yield was assumed to be 0.19, since most of the cemented material were composed of gravels.
Transitional Probability Geostatistical Software (T-PROGS; Carle, 1999) was used for simulating geology of the study area using boreholes data. GMS does not allow layers with single sequence to be used in construction of the hydrogeology for the MODFLOW model, so the borehole data from the borehole logs that only had one sequence were eliminated. Finally, 1,688 data points (from 266 individual boreholes) were used for creating MODFLOW layers.
Several individual packages are provided in MODFLOW to represent the boundary conditions for any specific site and to simulate the hydrologic system. The packages that were used for model setup of Gap to Gap region in Yakima watershed included River, Barrier, Drain, Recharge and Evapotranspiration package. The details about these packages can be found at Harbaugh, 2005.
The study area is bounded on all the sides by intense folds of the Columbia River Basalt Group. The hydrologic barriers present due to low hydraulic conductivities of the CRBG units were used as the boundary conditions of north, east, west and south east side of the model (Fig. 4). The barriers were classified into three categories based on their hydraulic characteristic (hydraulic conductivity/width of the horizontal flow barrier) values which were obtained from the MODFLOW model developed by USGS for the Yakima Basin (Ely et al., 2011): Low (0.000005 day−1; northern boundary), Medium (0.000039 day−1; eastern boundary) and High (0.00042 day−1; western boundary). Ahtanum River was used to represent the southwest boundary of the groundwater model (Fig. 4). The River package was used to represent the surface and groundwater interactions of Yakima and Ahtanum rivers (McDonald and Harbaugh, 1984) as,
| 2 |
where, Q is the flow between surface and groundwater, C is river conductance, h2 is the elevation of the river bottom and can be estimated from the LiDAR data and h1 is the head in the river. The value of riverbed conductance can be obtained by calibration. Details about calibration process are presented in the next section. Drain discharge is also estimated using similar equation by replacing riverbed conductance with the drain conductance. The locations of drains were obtained from the National Hydrography Dataset obtained from USGS.
Fig. 4.
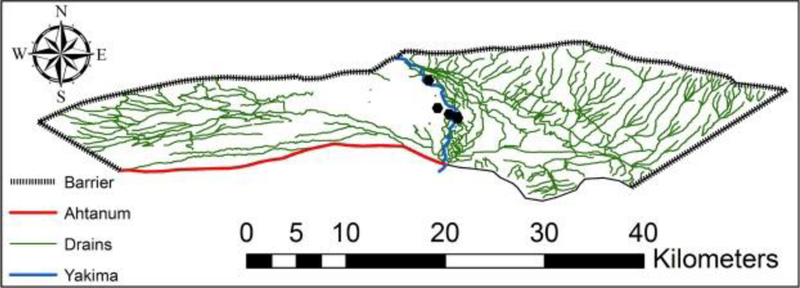
Conceptual model showing boundary conditions (Barriers and Ahtanum River), along with Yakima River, Drains and locations of observation wells.
Recharge and evapotranspiration were specified for the top face of the model.
A particle tracking system, MODPATH (Pollock, 1994), was used to generate pathlines of hyporheic flow in the form of groundwater emerging from Yakima River. The pathlines were generated from points generated adjacent to the Yakima River. The hyporheic flows were compared for MODFLOW models developed using LiDAR data from the years 2008 and 2013. The analysis of these pathlines could also be used to reveal temporal changes in the movement of groundwater in the hyporheic flow between the river and its floodplain during different times of year.
2.6. Model calibration and validation
The model was calibrated using Parameter Estimation (PEST version 12.2) in two phases. The model independent PEST, calibrates the model by minimizing the least square error between the model simulated and observed value using an algorithm developed by Doherty (2016). In the initial phase model was run in steady state for the data corresponding to February 1, 2013 and was calibrated to obtain the optimum values for hydraulic conductivity, river and drain conductance by minimizing the simulated and observed head at the observation wells. It is important to note that no precipitation was observed on February 1, 2013. The heads achieved using the calibrated model for steady state were used to provide starting head for the transient state model. In the second phase, the model was run from February 1, 2013 to September 5, 2013 and was calibrated again to obtain optimal values for river, drain conductance, and specific yield to accurately represent the transient behavior of the five wells in the study area.
In the validation phase, parameters obtained after the calibration were used to run the MODFLOW model from September 8, 2013 to June 24, 2015. It should be noted that for the validation phase, data were not availabel for observation wells BHP531 and BHP536 between September 8, 2013 to November 10, 2013, so for these two wells observed and simulated head values were compared between November 11, 2013 to June 24, 2015.
2.7. Hyporheic flow before and after levee setback in steady state
The pathlines for hyporheic flow were developed using MODPATH by generating particles at the cells adjacent to the Yakima River. In order to compare the pathlines during pre and post-restoration (levee setback) conditions, the MODFLOW and MODPATH models were run using LiDAR data from 2008 and 2013 in steady state. The length, time and velocity attributes of the pathlines emerging near the transects A and B (Fig. 2), before and after levee setback (using 2008 and 2013 LiDAR data) were compared visually (using figures) and compared statistically. All the statistical analyses were conducted using R software (R 3.2.5). The attributes of the pathlines were checked for normality using Shapiro-Wilk test (Shapiro and Wilk, 1965) and the differences in their medians were compared using Mann-Whitney test (Mann and Whitney, 1947).
2.8. Hyporheic pathlines during transient period
The transient MODFLOW model was run on monthly basis for entire calibration and validation period. Subsequently, MODPATH was used to generate hyporheic lines emerging from the Yakima River. It should be noted that although the calibration and validation were conducted on daily basis, due to the computational limitations, pathlines were generated using MODFLOW and MODPATH runs on monthly basis. The length of pathlines and their residence time were compared visually using boxplots and statistically using Mann-Whitney test (Mann and Whitney, 1947). A statistical test, Tbats (De Livera et al., 2011) was conducted to detect any seasonal trends.
3. Results and discussion
This section presents the results from MODFLOW model simulations during steady and transient state, along with the hyporheic flow pathlines results from MODPATH simulations.
3.1. Model calibration
In the initial phase, the model was setup for steady state using the observed data for various elements such as heads at the observation wells, river stages for the Yakima River and Ahtanum Creek and precipitation and evapotranspiration on February 1, 2013. The model was calibrated for heads at all the observation wells. Model parameters used for calibration include hydraulic conductivity, river and drain conductance. The river conductance multiplier values were 71.70 m2 /day and 5.22 m2/day for Yakima River and Ahtanum Creek, respectively. Drain conductance was estimated as 607.49 m2 /day using parameter estimation. The hydraulic conductivity values for gravel, sand, clay, basalt and cemented material were 378, 66.83, 6.00, 1.05, and 0.66 m/day respectively. Results of the observed and computed heads for the observation wells are presented in Table 3. While the mean absolute error was 0.34 m, the maximum absolute residual head was 0.43 m for southernmost well BHP 533 and minimum residual was for the northernmost well BHP 536 (Table 3). According to one of the criteria for evaluating model calibration results, the residual head should be less than 10% of the variability in the field data across the model domain (Khadri and Pande, 2016). The low residual values for observation wells (compared to 10% variability in field data, 1.70 m) suggest that model was calibrated appropriately for heads at all the grids. It is important to note that no precipitation was observed on February 1, 2013.
Table 3.
Comparison of observed and simulated heads at the observation wells after calibration of the model during steady state.
| Well | Observed | Simulated | Residual |
|---|---|---|---|
| BHP 531 (m) | 316.82 | 316.41 | 0.41 |
| BHP 533 (m) | 300.44 | 300.86 | −0.43 |
| BHP 534 (m) | 300.06 | 300.41 | −0.35 |
| BHP 536 (m) | 305.84 | 305.67 | 0.17 |
| BHM 931 (m) | 302.68 | 303.07 | −0.36 |
3.2. Transient calibration
In the second stage, the model was calibrated during transient state (transient calibration) with the first day (February 1, 2013) as the steady state. The model was further calibrated to improve the groundwater simulations during the transient state from February 1, 2013 to September 5, 2013. The drain conductance value obtained after calibration during transient run was 975.18 m2/day. While the optimum value for the conductance of Yakima River estimated after the calibration during transient period was 87.79 m2/day, the conductance for Ahtanum River (5.22 m2/day) remained unchanged after transient calibration. This could be due the fact that the observation wells are in close proximity to Yakima River (Fig. 1), rendering the value of conductance of Yakima River critical for better estimation of heads at the observation wells. In contrast, Ahtanum Creek is farther away from the observation wells (Fig. 1) and changes in the conductance of Ahtanum River did not improve the simulated heads at the observation wells. Further alterations to the values of other parameters did not improve the model performance. The results from the transient calibration are presented in the form of plots for the five observation wells (Fig. 5). It can be noticed that although the model was able to predict mean behavior of the transient heads at the observation wells, it was not able to capture the peaks and the magnitude of several other fluctuations. The model performance can be improved by using more accurate boundary conditions (Chinnasamy and Hubbart, 2014). For instance, the boundary on southwest side was represented by using River package for Ahtanum creek, and observed stage data were only availabel for the downstream end and the upstream data were interpolated. The model performance could improve if the observed data were availabel for the upstream end as well. Similarly, this could also be attributed to the rainfall data which were obtained from the gauge located at Moxee, WA. Rainfall data for the period of our study were not availabel at any other rain gauge closer to the study area. The model simulations can also be further improved with gauge adjusted higher resolution Next Generation Radar (NEXRAD) rainfall data (Skinner et al., 2009).
Fig. 5.
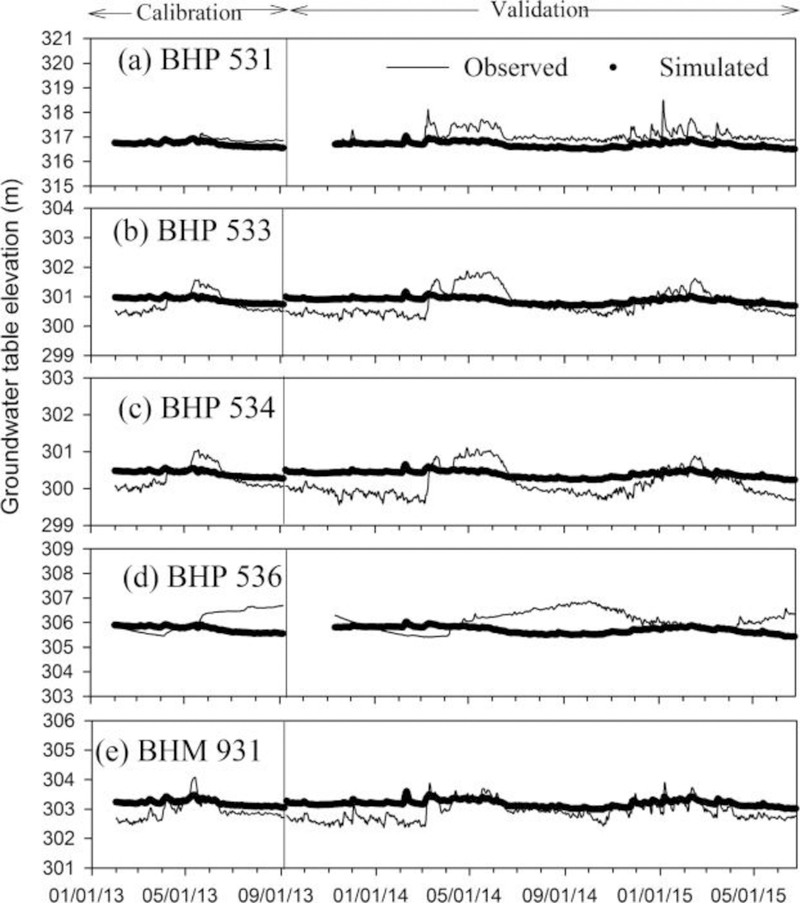
Spline curves presenting observed and model simulated heads for five wells near Yakima River during calibration and validation periods of the transient state model simulations.
Model performance during the calibration period was also measured using different statistical parameters (Table 4). Mean error (Me) between observed and simulated heads at different observation wells was between −0.36 m and 0.27 m. Maximum error was highest for observation well BHP 536 (1.15). Compared to other wells, the observed head at BHP 536 was behaving differently during the calibration period. While the observed head at BHP 536 was decreasing until 4 April 2013, after that the head kept on increasing and was highest at the end of the calibration period (306.7 m), resulting in maximum error (Table 4). In contrast to the observed heads at other wells it is possible that some malfunction occurred with the levelogger at observation well BHP 536, during the data collection. Other small differences between the observed and simulated heads at the observations can be attributed partially to the variation in river width and the grid cells of the model (Brunner et al., 2010).
Table 4.
Comparison of observed and simulated heads at the observation wells during calibration and validation periods for the transient state model simulations.
| Calibration | Validation | |||||||
|---|---|---|---|---|---|---|---|---|
| n | Me (m) | Ma (m) | Mx (m) | n | Me (m) | Ma (m) | Mx (m) | |
| BHP 531 | 217 | −0.15 | 0.16 | 0.31 | 592 | −0.36 | 0.36 | 1.64 |
| BHP 533 | 217 | 0.13 | 0.28 | 0.65 | 655 | 0.09 | 0.34 | 0.92 |
| BHP 534 | 217 | 0.11 | 0.26 | 0.61 | 655 | −0.30 | 0.34 | 1.16 |
| BHP 536 | 217 | −0.36 | 0.53 | 1.15 | 592 | −0.39 | 0.51 | 1.35 |
| BHM 931 | 217 | 0.27 | 0.32 | 0.74 | 655 | 0.27 | 0.31 | 1.12 |
Me = Mean error, Ma = Mean absolute error, Mx = Maximum error.
3.3. Transient validation
The validation was conducted by running the model from September 8, 2013 to June 24, 2015. The results from the validation are presented in the graphs (Fig. 5). Data were not availabel for BHP 531 and BHP 536 for the period between September 8, 2013 to November 10, 2013. Similar to the observation in calibration phase, it was noticed that while the simulated data for BHP 536 followed the same trend as other wells, the observed heads for BHP 536 had different trend compared to observed heads at other wells. The model performance was also evaluated using statistical measures (Table 4). Maximum residual was for BHP 531 well (1.64 m) on January 6, 2015 during validation period. This could be attributed to the rainfall data. For instance, while the peak groundwater level was observed on January 6, 2015, rainfall was not detected by the gauge. Overall, the lower range of mean errors (−0.39 to 0.27) and mean absolute errors (0.16 – 0.53) suggest that model was able to simulate fluctuations in the ground water levels during the transient period in the Gap to Gap.
3.4. Pre and Post-restoration hyporheic flow
3.4.1. Hyporheic flow during steady state
Hyporheic flow pathlines were obtained by generating particles at the grids adjacent to the grids representing Yakima River and were tracked using MODPATH. The pathlines were obtained by using head solutions obtained from calibrated model at steady state condition on February 1, 2013. In an attempt to compare the pathlines from pre and post-restoration (levee setback) periods, the model parameterized using LiDAR data from 2013 was also run in steady state using the LiDAR data of 2008. The pathlines created for the particles generated adjacent to the Yakima River were compared for the models with LiDAR from 2008 and 2013 (Fig. 5). It was observed (visually from Fig. 6) that pathlines for the hyporheic flow were longer after levee setback (using 2013 LiDAR data). The longer pathlines corresponds to the greater spatial extent of hyporheic zone resulting in larger area for ecosystem processes such as improved microbial activities and greater nutrient retention (Kasahara and Wondzell, 2003, Lautz and Siegel, 2006). Konrad et al. (2008) documented that levee setback resulted in an improved river-floodplain connectivity and increase in aquatic habitat area in glacial-melt water rivers. While, it was observed that near Transect A, the direction of flowlines shifted anti-clockwise moving from south and southeast towards east, the direction of flowlines near the Transect B, changed clockwise from southeast to south and southwest. The shift in flow directions of the hyporheic flow pathlines due to levee setback resulted in more area for connectivity between the river and the floodplain.
Fig. 6.
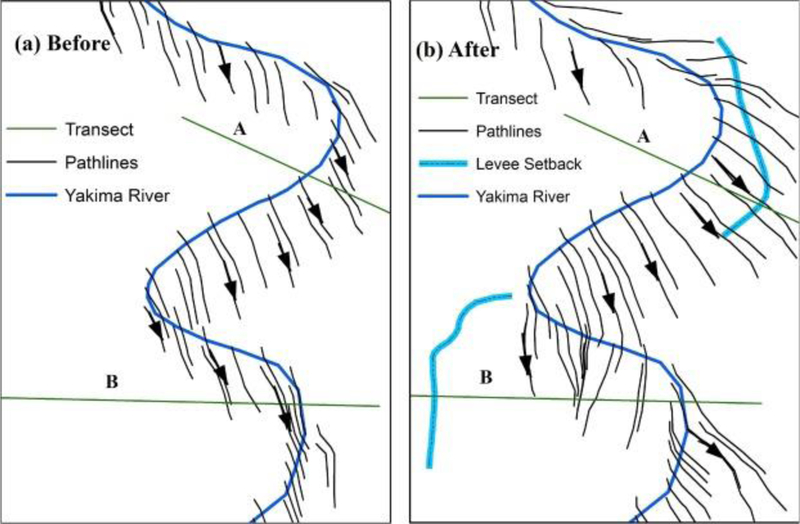
Pathlines of hyporheic flow emerging from particles located adjacent to the Yakima River generated using MODPATH model with LiDAR data (a) before levee setback from 2008 and (b) after levee setback from 2013.
The Shapiro-Wilk normality test was conducted on the attributes of hyporheic pathlines (length, time and velocity) near transects A and B (Fig. 6) before and after levee setback. The sample data for all the attributes passed the normality test (with p-value higher than 0.05), except for time taken for pathlines at Transects A during post-restoration which was almost normal with a p-value of 0.05. The medians of the attributes of pathlines are presented in Table 5. The results from the Mann-Whitney test established that the median length of hyporheic pathlines increased significantly after restoration, suggesting that levee setback helped in the increase of surface and groundwater interaction. It was noticed that the residence time for the pathlines near the transects reduced significantly after levee setback resulting in increased velocity at which the water travels.
Table 5.
Comparison of medians of length, time and velocity of pathlines at transects A and B before and after levee setback for MODFLOW models in steady state. The medians of length, time and velocity for all the pathlines are also presented.
| Length | Time | Velocity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Before | After | p-value | Before | After | p-value | Before | After | p-value | ||
| Transect A | 258.42 | 398.04 | <0.001 | 344.12 | 342.33 | <0.001 | 0.75 | 1.16 | <0.001 | |
| Transect B | 258.04 | 364.45 | 0.001 | 343.20 | 341.95 | <0.001 | 0.75 | 1.07 | 0.001 | |
| Overall | 252.65 | 324.00 | <0.001 | 344.63 | 343.02 | <0.001 | 0.74 | 0.95 | <0.001 | |
The normality test conducted on the attributes for all the pathlines emerging from Yakima River within Gap to Gap region during pre and post-restoration suggested that data were not normally distributed for most of the attributes. Hence, the non-parametric Mann-Whitney test was conducted to test the statistical difference between the medians of the attributes of pathlines from pre and post-restoration periods. The results from the Mann-Whitney test (Table 5) also revealed that while the travel time of pathlines reduced significantly after restoration, the length of all the pathlines were significantly greater after restoration. This shows that overall, for the shorter residence time the area of hyporheic zone increased significantly after the restoration. In other words, surface and groundwater interaction area increased after levee setback.
3.4.2. Transient period-hyporheic lines
Hyporheic flow pathlines were generated during calibration period (February 2013 – September 2013) and validation period (September 2013 – June 2015) for pre (before levee setback using LiDAR data from 2008) and post-restoration (after levee setback using LiDAR data from 2013). The results from the model simulations in the form of length of pathlines and their residence time for different months are presented for pre-restoration (Fig. 7) and post-restoration (Fig. 8) periods. The residence times of the hyporheic pathlines during pre and post-restoration periods varied between 30 days – 225 days and 30 days – 274 days, respectively. Longest pathlines during both pre and post-restoration periods (Fig. 9) occurred during September 2014 (pre: 398.19 m and post:460.57 m) which was relatively drier month with an average rainfall of 0.27 mm. In contrast May 2013 during which the Gap to Gap region experienced highest amount of average rainfall (1.88 mm) had much shorter pathlines of 137.2 m and 160.9 m for pre and post-restoration periods, respectively. Faulkner et al., 2012 also encountered similar results with longer pathlines during wet seasons compared to drier seasons in their study of hyporheic flow patterns in river floodplain. During drier periods, hyporheic flow follows deeper potentiometric surfaces compared to wet periods (Faulkner et al., 2012), resulting in early re-emergence of hyporheic flow to the surface. Overall, the longer pathlines occurred during the months of August to October (Fig. 9). Shorter pathlines were observed near the barriers on upstream and near the boundary at downstream. The shorter pathlines near the boundaries could be attributed to the low hydraulic conductivities of folds and faults from basalt layer since hydraulic conductivity has been identified as one of the dominating factors in controlling the extent of the hyporheic flow (Lautz and Siegel, 2006). For the entire time period of transient model simulation, most of the hyporheic flow was directed away from the river in southeast direction. A trend was also noticed in the boxplots (Fig. 7, Fig. 8) with longer pathlines during September to February. Although trends were noticed in the time series boxplots representing the length of the pathlines, results from the Tbats test suggested that they were not statistically significant.
Fig. 7.
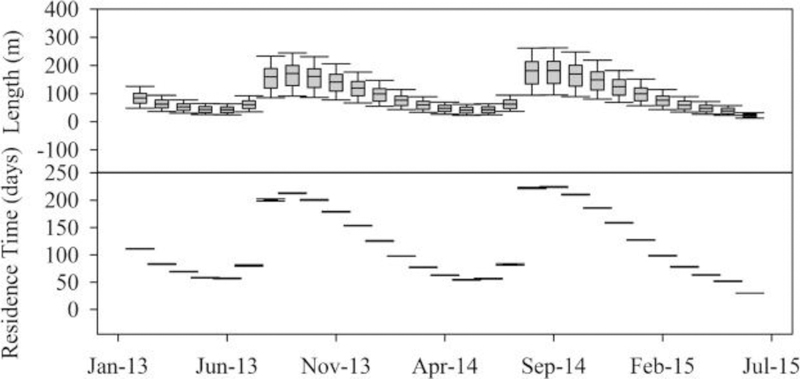
Boxplots of the length and residence time of the hyporheic flow pathlines emerging from Yakima River during pre-restoration (using LiDAR data from 2008) for January 2013 – July 2015.
Fig. 8.
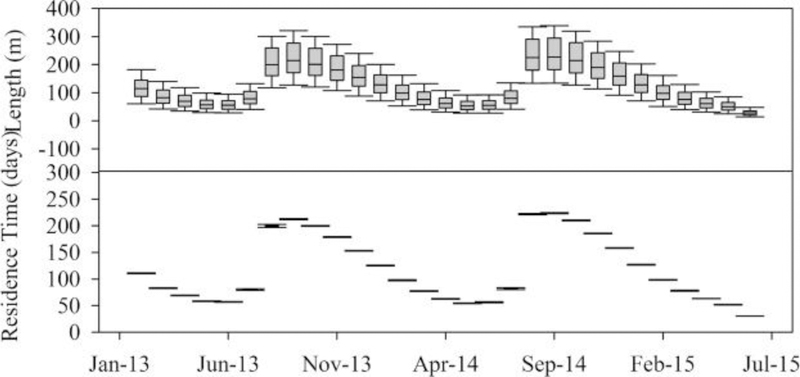
Boxplots of the length and residence time of the hyporheic flow pathlines emerging from Yakima River during post-restoration (using LiDAR data from 2013) for January 2013 – July 2015.
Fig. 9.
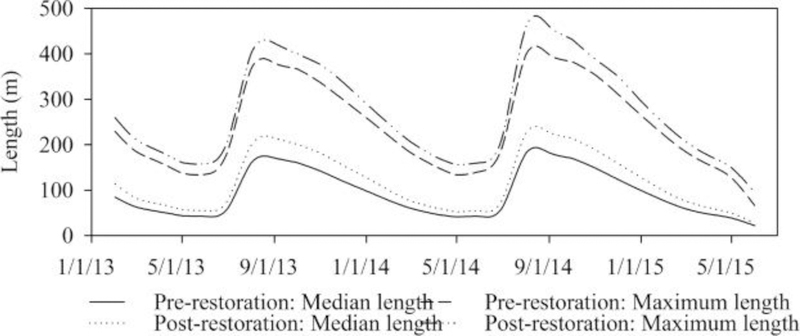
Monthly median and maximum lengths of the hyporheic flow pathlines emerging from Yakima River during pre and post-restoration periods (using LiDAR data from 2008 and 2013) for January 2013 – July 2015.
The length of pathlines obtained during different months for pre and post-restoration periods did not pass the normality test conducted using Shapiro-Wilk test. A non-parametric test, Mann-Whitney test was used to compare the medians of length of hyporheic pathlines during different months for the entire period (February 2013 – June 2015). The test showed that significant difference (P ≤ 0.001) exist between the length of pathlines obtained for each month during pre and post-restoration. The monthly average increase in the median length of pathlines after restoration was 28% during the transient period. The standard error of increase was estimated to be 1.30 m. The biggest difference between the medians (44.9 m) was observed in the month of September 2014. Overall, the comparisons of the pathlines during pre and post-restoration periods showed that after levee setback, a larger area of river connected flood plain corresponded with greater hyporheic flow.
This work shows that levee setback and a larger area of river connected floodplain with greater groundwater and surface water interaction provides the hydrologic structure and opportunity for more hyporheic ecosystem processes. Although the effects of river connection (Kondolf et al., 2006) and the drivers of hyporheic flow (Poole et al., 2006) are complex. An expanded hyporheic zone with more hydrologically connected floodplain area may enhance biogeochemical cycling (Fischer et al., 2005) with more opportunity for biogeochemical reactions in the surface (Forshay and Stanley, 2005), subsurface (Hill et al., 2000), and carbon-rich wet fringe (Forshay and Dodson, 2011) of the floodplain that include processes such as nitrification, denitrification, metal redox and immobilization. These processes can result in the retention of excess nutrients, pathogens and metals (Herzog, 2016). This restored hydrology may also support greater diversity of habitat in the surface and subsurface (Sedell et al., 1990, Stanford and Ward, 1988). Thus, the restoration of floodplains that include levee setback could be useful in improving the ecosystem of the river and its adjacent floodplains. This study provides a base for evaluating hydrological changes that occur due to levee setback, future studies should further investigate the ecological changes that occur when hyporheic flow and floodplain reconnection occurs to ensure that the desired ecosystem processes and associated restoration goals are achieved. In addition to this hydrologic study further evaluation of the ecosystem outcomes will be a valuable future contribution to improve restoration efforts where large scale hydrologic re-connection and enhanced groundwater and surface water interaction has been achieved through levee setback.
4. Conclusions
The parameterized groundwater model was used to study the effects of floodplain restoration on hyporheic flow in Gap to Gap region of Yakima Basin during steady and transient states. The attributes of hyporheic flow pathlines generated from the particles adjacent to Yakima River were compared for pre and post-restoration periods. It was noticed that at two transects along the Yakima River where levee setback occurred, there was change in the directions of hyporheic pathlines. The change in the directions of the pathlines resulted in wider area of coverage and likely surface water and groundwater interactions. Statistical tests conducted to compare the lengths of the hyporheic pathlines for pre and post-restoration conditions, showed that restoration in the form of levee setback resulted in increase in the length of pathlines after floodplain restoration. Model simulations during transient state showed that the longest pathlines during both pre and post-restoration (pre: 398.19 m and post:460.57 m) occurred in relatively drier periods. Overall this study supported the hypothesis that flood plain restoration efforts in the form of levee setback should improve the hyporheic flow in the floodplain regions. The improved hyporheic flow and river reconnection to greater floodplain area should improve the ecosystems conditions that support more opportunities for enhanced biogeochemical processing, improved water quality, and restoration of habitat to occur.
Highlights.
Floodplain restoration in the form of levee setback can improve hyporheic flow between rivers and their floodplain region.
Hyporheic pathlines emerging from the rivers tend to be relatively longer during drier periods.
MODFLOW can be used to assess the impact of floodplain restoration activities on river and floodplain ecosystem.
Acknowledegement
The authors gratefully acknowledge the work of Peter Price and Laura Hockenbury for their development of the well log database used in the model. We also acknowledge Sandy Halstead, Roseanne Lorenzana, Sheila Flemming, Jennifer MacDonald, and Bruce Duncan for their initiation and support of this work. We also thank Ryan Anderson, Russell Neil, Justin Groves, Marja Copeland, Kanchan Shrestha, and Avery Richardson, The City of Yakima, Scott Schafer, Marc Cawley, Washington State Department of Transportation, Larry Mattson, William Sauriol, Yvette Lujan.
References
- Ahilan et al., 2016 Ahilan S, Guan M, Sleigh A., Wright N., Chang H.The influence of floodplain restoration on flow and sediment dynamics in an urban river J. Flood Risk Manage. (2016), 10.1111/jfr3.12251 [DOI] [Google Scholar]
- Anchor QEA, LLC, 2014 Q.E.A. Anchor, LLC Technical Memorandum Gap to Gap Floodplain Restoration and Enhancement Plan Yakima County, Kennewick, Washington (2014) [Google Scholar]
- Anderman and Hill, 2000 Anderman ER, Hill MC MODFLOW-2000, The U.S. Geological Survey Modular Ground-Water Model – Documentation of the Hydrogeologic-Unit Flow (HUF) Package U.S. Geological Survey, Denver, CO: (2000) [Google Scholar]
- Bernhardt et al., 2005 Bernhardt ES, Palmer MA, Allan JD, Alexander G., K, B., Brook S.,. ‥ O’Donnell TK (2005). Synthesizing U.S. River Restoration Efforts. AAAS. Retrieved August 29, 2016, from http://science.sciencemag.org/content/sci/308/5722/636.full.pdf [DOI] [PubMed] [Google Scholar]
- Brunner et al., 2010 Brunner P., Simmons CT, Cook PG, Therrien R.Modeling surface water-groundwater interaction with MODFLOW: some considerations Groundwater, 48 (2) (2010), pp. 174–180 [DOI] [PubMed] [Google Scholar]
- Bukaveckas, 2007 Bukaveckas PA Effects of channel restoration on water velocity, transient storage, nutrient uptake in a channelized stream Environ. Sci. Technol., 41 (5) (2007), pp. 1570–1576 [DOI] [PubMed] [Google Scholar]
- Burns et al., 2015 Burns ER, Williams CF, Ingebritsen SE, Voss CI, Spane FA Deangelo J.Understanding heat and groundwater flow through continental flood basalt province: insight gained from alternative models of permeability/depth relationships for the columbia plateau, USA Geofluids, 15 (2015), pp. 120–138, 10.1111/gfl.12095 [DOI] [Google Scholar]
- Carle, 1999 Carle SF Transition Probability Geostatistical Software, Version 2.1, User Manual University of California, Davis: (1999) [Google Scholar]
- Chinnasamy and Hubbart, 2014 Chinnasamy P., Hubbart JA Potential of MODFLOW to model hydrological interactions in a semikarst floodplain of the ozark border forest in the central United States Earth Interact, 18 (2014), pp. 1–24 [Google Scholar]
- Dahm et al., 1998 Dahm CN, Grimm NB, Marmonier P., Valett HM Nutrient dynamics at the interface between surface waters and groundwaters Freshwater Biol, 40 (1998), pp. 427–451 [Google Scholar]
- De Livera et al., 2011 De Livera AM, Hyndman RJ, Snyder RD The generic accessor functions fitted.values and residuals extract useful features of the value returned by bats and associated functions J. Am. Stat. Assoc, 106 (496) (2011), pp. 1513–1527 [Google Scholar]
- Doherty, 2016 Doherty J.PEST Model Independent Parameter Estimation, User Manual (sixth ed.), Watermark Numerical Computing, Bethesda, MD: (2016) [Google Scholar]
- Doyle et al., 2008 Doyle MW, Stanley EH, Havlick DG, Kaiser MJ, Steinbach G., Graf WL, Riggsbee JA Aging infrastructure and ecosystem restoration Science, 319 (2008), p. 286. [DOI] [PubMed] [Google Scholar]
- Ely et al., 2011 Ely DM, Bachmann MP, Vaccaro JJ Numerical Simulation of Groundwater Flow for the Yakima River Basin Aquifer System, Washington U.S. Geological Survey Scientific Investigations Report, Reston, Virginia: (2011), pp. 2011–5155 [Google Scholar]
- Ely et al., 2014 Ely DM, Burns ER, Morgan DS, Vaccaro JJ Numerical Simulation of Groundwater Flow in the Columbia Plateau Regional Aquifer System, Idaho, Oregon, and Washington (ver. 1.1, January 2015) U.S. Geological Survey Scientific Investigations Report, Reston, Virginia: (2014) 2014–5127 [Google Scholar]
- Faulkner et al., 2012 Faulkner BR, Brooks JR, Forshay KJ, Cline SP Hyporheic flow patterns in relation to large river floodplain attributes J. Hydrol, 448–449 (2012), pp. 161–173 [Google Scholar]
- Fernald et al., 2006 Fernald AG, Landers DH, Wigington PJ Water quality changes in hyporheic flow paths between a large gravel bed river and off-channel alcoves in Oregon, USA River Res. Appl, 22 (2006), pp. 1111–1124 [Google Scholar]
- Fischer et al., 2005 Fischer H., Kloep F., Wilzcek S., Pusch MT A river’s liver – microbial processes within the hyporheic zone of a large lowland river Biogeochemistry, 76 (2) (2005), pp. 349–371 [Google Scholar]
- Forshay and Dodson, 2011 Forshay KJ, Dodson SI Macrophyte presence is an indicator of enhanced denitrification and nitrification in sediments of a temperate restored agricultural stream Hydrobiologia, 668 (2011), pp. 21–34 [Google Scholar]
- Forshay and Stanley, 2005 Forshay KJ, Stanley EH Rapid nitrate loss and denitrification in a temperate river floodplain Biogeochemistry, 75 (2005), pp. 43–64 [Google Scholar]
- Fuhrer et al., 1994 Fuhrer GJ, McKenZie SW, Rinella JF, Sanzolone RF, Skach KA Surface-Water-Quality Assessment of the Yakima River Basin in Washington: Analysis of Major and Minor Elements in Fine-Grained Streambed Sediment, 1987, with a section on Geology, by Gannett Marshall W. U.S. Geological Survey, Denver, CO: (1994) [Google Scholar]
- Gergel et al., 2002 Gergel SA, Dixon MD, Turner MG Consequences of human-altered floods: levees, floods, and floodplain forests along the wisconsin river Ecol. Appl, 12 (6) (2002), pp. 1755–1770 [Google Scholar]
- González et al., 2015 González E., Sher AA, Tabacchi E., Masip A., Poulin M. Restoration of riparian vegetation: a global review of implementation and evaluation approaches in the international, peer-reviewed literature J. Environ. Manage, 158 (2015), pp. 85–94 [DOI] [PubMed] [Google Scholar]
- Harbaugh, 2005 Harbaugh AW MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model—the Ground-Water Flow Process. U.S. Department of the Interior U.S. Geological Survey, Reston, VA: (2005) [Google Scholar]
- Heath, 1983 Heath RC (1983). Basic Ground-Water Hydrology. Reston, Virginia: U.S. Geological Survey Water Supply Paper; 2220. [Google Scholar]
- Heine and Pinter, 2012 Heine RA, Pinter N. Levee effects upon flood levels: an empirical assessment Hydrol. Processes, 26 (21) (2012), pp. 3225–3240, 10.1002/hyp.8261 [DOI] [Google Scholar]
- Helton et al., 2014 Helton AM, Poole GC, Payn RA, Izurieta C., Stanford JA Relative influence of the river channel, floodplain surface, and alluvial aquifer on simulated hydrologic residence time in a montane river floodplain Geomorphology, 205 (2014), pp. 17–26 [Google Scholar]
- Herzog, 2016 Herzog SP, Higgins CP, McCray JE Engineered streambeds for induced hyporheic flow: enhanced removal of nutrients, pathogens, and metals from urban streams J. Environ. Eng, 142 (1) (2016), 10.1061/(ASCE)EE.1943-7870.0001012 [DOI] [Google Scholar]
- Hill, 1990 Hill MC Preconditioned Conjugate-Gradient 2 (PCG2), A Computer Program for Solving Ground-Water Flow Equations U.S. Geological Survey, Denver, Colorado: (1990) [Google Scholar]
- Hill et al., 2000 Hill AR, Devito KJ, Campagnolo S., Sanmugadas K. Subsurface denitrification in a forest riparianzone: Interactions between hydrology and supplies ofnitrate and organic carbon Biogeochemistry, 51 (2000), pp. 193–223 [Google Scholar]
- Homer et al., 2015 Homer CG, Dewitz JA, Yang L., Jin S., Danielson P., Xian G., Megown K. Completion of the 2011 national land cover database for the conterminous united states-representing a decade of land cover change information Photogramm. Eng. Remote Sens, 81 (5) (2015), pp. 345–354 [Google Scholar]
- Jones et al., 2006 Jones MA, Vaccaro JJ, Watkins AM Hydrogeologic Framework of Sedimentary Deposits in Six Structural Basins, Yakima River Basin, Washington U. S. Geological Survey, Denver, CO: (2006) [Google Scholar]
- Kasahara and Hill, 2006 Kasahara T., Hill AR Modeling the effects of lowland stream restoration projects on stream-subsurface water exchange Ecol. Eng, 32 (2006), pp. 310–319 [Google Scholar]
- Kasahara and Wondzell, 2003 Kasahara T., Wondzell SM Geomorphic controls on hyporheic exchange flow in mountain streams Water Resour. Res, 39 (1) (2003), p. 1005, 10.1029/2002WR001386 [DOI] [Google Scholar]
- Khadri and Pande, 2016 Khadri SF, Pande C. Ground water flow modeling for calibrating steady state using MODFLOW software: a case study of Mahesh River basin, India Model. Earth Syst. Environ. (2016), 10.1007/s40808-015-0049-7 [DOI] [Google Scholar]
- Kondolf et al., 2006 Kondolf GM, Boulton AJ, Daniel S., Poole GC, Rahel FJ, Stanley EH, Nakamura K. Process-based ecological river restoration:visualizing three-dimensional connectivity and dynamic vectors to recover lost linkages Ecol. Soc, 11 (2006) [Google Scholar]
- Konrad et al., 2008 Konrad CP, Black RW, Voss F., Neale CMU Integrating remotely acquired and field data to assess effects of setback levees on riparian and aquatic habitats in glacial-melt water rivers River Res. Applic, 24 (2008), pp. 355–372, 10.1002/rra.1070 [DOI] [Google Scholar]
- Kroes et al., 2015 Kroes DE, Schenk ER, Noe GB, Benthem AJ Sediment and nutrient trapping as a result of a temporary Mississippi river floodplain restoration: the Morganza spillway during the 2011 Mississippi river flood Ecol. Eng, 82 (2015), pp. 91–102 [Google Scholar]
- Lautz and Siegel, 2006 Lautz LK, Siegel DI Modeling surface and ground water mixing in the hyporheic zone using MODFLOW and MT3D Adv. Water Resour, 29 (11) (2006), pp. 1618–1633, 10.1016/j.advwatres.2005.12.003 [DOI] [Google Scholar]
- Mann and Whitney, 1947 Mann H., Whitney D. On a test of whether one of two random variables is stochastically larger than the other Ann. Math. Stat, 18 (1) (1947), pp. 50–60 [Google Scholar]
- McDonald and Harbaugh, 1984 McDonald MG, Harbaugh AW A modular three-dimensional finite difference groundwater flow model U.S. Geological Survey Open-File Report; 83–875 (1984) [Google Scholar]
- Pess et al., 2005 Pess GR, Morley SA, Hall JL, Timm RK Monitoring stream and watershed Roni P. (Ed.), Monitoring Stream and Watershed Restoration, American Fisheries Society, Maryland: (2005), pp. 127–166 [Google Scholar]
- Poff et al., 1997 Poff NL, Allan JD, Bain MB, Karr JR, Prestegaard KL, Richter BD, Stormberg JC The natural flow regime Bioscience, 47 (11) (1997), pp. 769–784 [Google Scholar]
- Pollock, 1994 Pollock DW User’s Guide for MODPATH/MODPATH-PLOT, Version 3: A Particle Tracking Post-processing Package for MODFLOW, the U.S. Geological Survey Finite-difference Ground-water Flow Model U.S. Geological Survey Open-File Report; 94–464, Reston, Virginia: (1994) [Google Scholar]
- Poole et al., 2006 Poole GC, Stanford JA, Running SW, Frissell CA Multiscale geomorphic drivers of groundwater flow paths: subsurface hydrologic dynamics and hyporheic habitat diversity J. North Am. Benthological Soc, 25 (2006), pp. 288–303 [Google Scholar]
- Rains et al., 2004 Rains MC, Mount JE, Larsen EW Simulated changes in shallow groundwater and vegetation distributions under different reservoir operations scenarios Ecol. Appl, 14 (1) (2004), pp. 192–207 [Google Scholar]
- Rogiers et al., 2011 Rogiers B., Lermytte J., De Bie E., Batelaan O. Evaluating the impact of river restoration on the local groundwater and ecological system: a case study in ne flanders Geologica Belgica, 14 (3–4) (2011), pp. 265–276 [Google Scholar]
- Sargeant and Singer, 2016 Sargeant CI, Singer MB Sub-annual variability in historical water source use by Mediterranean riparian trees Ecohydrology, 9 (7) (2016), pp. 1328–1345 [Google Scholar]
- Sedell et al., 1990 Sedell JR, Reeves GH, Hauer FR, Stanford JA, Hawkins CP Role of refugia in recovery from disturbances: modern fragmented and disconnected river systems Environ. Manage, 14 (1990), pp. 711–724 [Google Scholar]
- Shapiro and Wilk, 1965 Shapiro SS, Wilk MB An analysis of variance test for normality Biometrika, 52 (3–4) (1965), pp. 591–611 [Google Scholar]
- Singer and Dunne, 2004 Singer MB, Dunne T. An empirical-stochastic, event-based model for simulating inflow from a tributary network: theoretical framework and application to the Sacramento River basin, Water Resour Res, California (2004), 10.1029/2003WR002725 [DOI] [Google Scholar]
- Singer and Dunne, 2006 Singer MB, Dunne T. Modeling the influence of river rehabilitation scenarios on bed material sediment flux in a large river over decadal timescales Water Resour. Res, 42 (12) (2006), 10.1029/2006WR004894 [DOI] [Google Scholar]
- Singer et al., 2014 Singer MB, Sargeant CI, Piégay H., Riquier J., Wilson RJ, Evans CM Floodplain ecohydrology: climatic, anthropogenic, and local physical controls on partitioning of water sources to riparian trees Water Resour. Res, 50 (5) (2014), pp. 4490–4513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skinner et al., 2009 Skinner C., Bloetscher F., Pathak C. Comparison of NEXRAD and rain gauge precipitation measurements in south florida J. Hydrol. Eng, 14 (3) (2009) [Google Scholar]
- Snyder and Stanford, 2001 Snyder EB, Stanford JA Review and Synthesis of River Ecological Studies in the Yakima River, Washington, with Emphasis on Flow and Salmon Habitat Interactions U.S. Bureau of Reclamation, Polson, Montana: (2001) [Google Scholar]
- Snyder et al., 2002 Snyder EB, Arango CP, Eitemiller DJ, Stanford JA, Uebelacker ML Floodplain hydrologic connectivity and fisheries restoration in the Yakima River, USA Internationale Vereinigung für theoretische und angewandte Limnologie: Verhandlungen, 28 (2002), pp. 1653–1657 [Google Scholar]
- Stanford et al., 2002 Stanford JA, Lorang MS, Matson PL The Reaches Project: Ecological and Geomorphic Dtudies Supporting Normative Flows in the Yakima River Basin, Washington, Final Report 2002 US Department of the Interior, Bureau of Reclamation; Yakima, WA: (2002) [Google Scholar]
- Stanford and Ward, 1988 Stanford J., Ward J. The hyporheic habitat of river ecosystems Nature, 335 (1988), pp. 64–66 [Google Scholar]
- Stanford and Ward, 1993 Stanford JA, Ward JV An ecosystem perspective of alluvial rivers: connectivity and the hyporheic corridor J. N. Am. Benthol. Soc, 12 (1) (1993), pp. 48–60 [Google Scholar]
- Stoffels et al., 2016 Stoffels RJ, Rehwinkel RA, Price AE, Fagan WF Dynamics of fish dispersal during river-floodplain connectivity and its implications for community assembly Aquat. Sci, 78 (2) (2016), pp. 355–365 [Google Scholar]
- Tague et al., 2008 Tague C., Valentine S., Kotchen M. Effect of geomorphic channel restoration on streamflow and groundwater in a snowmelt-dominated watershed Water Resour. Res, 44 (2008), p. W10415, 10.1029/2007WR006418 [DOI] [Google Scholar]
- Tockner et al., 1998 Tockner K., Schiemer F., Ward JV Coservation by restoration: the management concept for a river-floodplain system on the danube river in Austria Aquat. Conserv. Mar. Freshwater Ecosyst, 8 (1998), pp. 71–86 [Google Scholar]
- Tolan et al., 2009 Tolan T., Lindsey K., Porcello J. A Summary of Columbia River Basalt Group Physical Geology and its Influence on the Hydrogeology of the Columbia River Basalt Aquifer System: Columbia Basin Ground Water Management Area of Adams, Franklin, Grant, and Lincoln Counties June 2009 The Columbia Basin Ground Water Management Area of Adams, Franklin, Grant, and Lincoln Counties, Othello, Washington: (2009) [Google Scholar]
- Traum et al., 2014 Traum JA, Phillips SP, Bennett GL, Zamora C., Metzger LF Documentation of a Groundwater Flow Model (SJRRPGW) for the San Joaquin River Restoration Program Study Area, California Us Geological Survey, Reston, Virginia: (2014) [Google Scholar]
- Ward et al., 1999 Ward JV, Tockner K., Schiemer F. Biodiversity of floodplain river ecosystems: ecotones and connectivity Regulated Rivers: Res. Manage, 15 (1999), pp. 125–139 [Google Scholar]
- Yakima County, WA, 2006–2016 Yakim County WA (2006-2016). Yakima River Basin Flood History. Retrieved 9 16, 2016, from www.yakimacounty.us: [Google Scholar]


