Analysis of the CYP1A1 mRNA Dose-Response in Human Keratinocytes Indicates that Relative Potencies of Dioxins, Furans, and PCBs Are Species and Congener Specific

Abstract

Reports indicate that toxic equivalency factors (TEFs) based primarily on rodent data do not accurately predict in vitro human responsiveness to certain dioxin-like chemicals (DLCs). To investigate this in cells responsive to dioxins and relevant to chloracne, normal human epidermal keratinocytes were treated with 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD) and several DLCs, each with a TEF value of 0.1, representing three classes of congeners. We estimated half maximal effective concentration (EC50)–based donor-specific relative potency (REP) values for cytochrome P450 1A1 (CYP1A1) messenger RNA (mRNA) induction for TCDD, 1,2,3,6,7,8-hexachlorodibenzo-p-dioxin (HxCDD), 2,3,7,8-tetrachlorodibenzofuran (TCDF), 1,2,3,6,7,8-hexachlorodibenzofuran (HxCDF), and 3,3′,4,4′,5-pentachlorobiphenyl (PCB 126). We also determined EC50-based population-level REP values (n = 4) for CYP1A1 mRNA induction for TCDD, HxCDF, and PCB 126. Furthermore, an alternative factor, the relative threshold factor (RTF) based on the low end (threshold) of the dose-response curve, was calculated. Our results demonstrated that HxCDF had a population-based REP value of 0.98, 9.8-fold higher than its assigned TEF value of 0.1. Conversely, PCB 126 had an REP value of 0.0027 and an RTF of 0.0022, 37-fold and 45-fold less than its assigned TEF of 0.1, respectively. The REP values for HxCDD and TCDF were 0.24 and 0.10, respectively, similar to their assigned value of 0.1. Therefore, although the DLCs tested in the current study all possessed the same assigned TEF value of 0.1, congener-specific differences in REPs and RTFs were observed for human keratinocytes. These congener-specific discrepancies are likely because of differences in interspecies factors that have yet to be defined.

The estimation of risk to human health from exposure to environmental contaminants such as polychlorinated dibenzo-p-dioxins, polychlorinated dibenzofurans (PCDFs), and polychlorinated biphenyls (PCBs) is currently based on the potency of these chemicals in nonhuman animal models of toxicity. For risk assessment purposes, these dioxin-like chemicals (DLCs) are assigned toxic equivalency factor (TEF) values relative to 2,3,7,8-tetrachlorodibenzo-p-dioxin (TCDD) by the World Health Organization (WHO) (Van den Berg et al., 2006). These values have been generated predominantly from results of in vitro and in vivo rodent experiments measuring events downstream of activation of the aryl hydrocarbon receptor (AHR) (Haws et al., 2006). However, a number of studies indicate that, compared with rat cells, human cells in culture are less sensitive to certain AHR agonists and more sensitive to others (Lipp et al., 1992; Nagayama et al., 1985; Silkworth et al., 2005; Zeiger et al., 2001). In particular, a study of freshly isolated human hepatocytes resulted in an ethoxyresorufin-O-deethylase (EROD)–based relative potency (REP) value of 0.003 for 3,3',4,4',5-pentachlorobiphenyl (PCB 126), which is 33-fold lower than the current TEF value of 0.1 (Silkworth et al., 2005). This work was recently expanded employing a subset of the same fresh human hepatocytes used by Silkworth et al. (2005) to demonstrate that half maximal effective concentration (EC50)–based REP values of PCB 126 for 47 AHR-responsive genes have a geometric mean of 0.002 (Carlson et al., 2009). In contrast, several PCDFs were more potent in human lymphoblastoid cells, as measured by aryl hydrocarbon hydroxylase activity, than would be predicted from their TEF values (Nagayama et al., 1985).

Recent reports (EPA, 2009; NRC, 2007a,b) have endorsed the development of in vitro approaches for modern toxicity testing. Such approaches include the improvement of models used to extrapolate across species, the development of a better mechanistic understanding of dose-response, and the development of a more complete understanding of human toxicity pathways. Because it is thought that activation of the AHR is the initial step required (Fernandez-Salguero et al., 1996) for all subsequent toxicity of DLCs and that cytochrome P450 1A1 (CYP1A1) messenger RNA (mRNA) induction correlates well with the potency of DLCs (Poland and Knutson, 1982), AHR-mediated induction of CYP1A1 gene expression, although not responsible for all DLC toxicities (Uno et al., 2004), is a very sensitive, quantitative, and useful indicator of AHR activation.

In order to address these goals and to expand previous observations regarding the potency of DLCs in human cells to an additional cell type, we have studied the induction of CYP1A1 mRNA in normal human epidermal keratinocytes (NHEKs) exposed to TCDD and several DLCs. NHEKs are responsive to AHR agonists in culture and are highly relevant to the most frequently observed TCDD-mediated toxicity in humans, chloracne (Sutter et al., 2009). To test whether differences previously observed in vitro between rat and human cell responses extend to this tissue and also apply to additional DLCs, we studied five congeners representing dioxins, furans, and biphenyls. We chose a representative and potent congener from each group: TCDD, 2,3,7,8-tetrachlorodibenzofuran (TCDF), and PCB 126. In addition, 1,2,3,6,7,8-hexachlorodibenzo-p-dioxin (HxCDD) was tested because of its prevalence in the environment (Hedgeman et al., 2009). To match the chlorination pattern of HxCDD, 1,2,3,6,7,8-hexachlorodibenzofuran (HxCDF) was chosen as a second furan. Each of these chemicals has been assigned a TEF value of 0.1 (Van den Berg et al., 2006). Our goal in performing this research was to test whether the assigned TEFs accurately predicted the REPs of these DLCs in a relevant human cell type, thereby providing information that could be used to more closely estimate the risk that exposure to these chemicals may pose to the human population.

MATERIALS AND METHODS

Chemicals.

PCB 126 was obtained from Accustandard (New Haven, CT). HxCDD and HxCDF were obtained from Cambridge Isotope Laboratory (Andover, MA). TCDD and TCDF were gifts from W. F. Greenlee (The Hamner Institutes for Health Sciences) and Dow Chemical, respectively. Dimethyl sulfoxide (DMSO) was obtained from Sigma (St Louis, MO).

HRGC/HRMS analysis.

Vista Analytical Laboratory performed high resolution gas chromatography/high resolution mass spectroscopy (HRGC/HRMS) analysis of test chemicals using Modified Environmental Protection Agency Methods 8290/1668 to quantify contaminants. The concentration of each of the chemical stock solutions was verified, and contaminants were identified. The purity of each congener was as follows: TCDD, 99.57%; HxCDD, 99.52%; TCDF, 100.0%; HxCDF, 99.62%; and PCB 126, 99.75%. The contaminants altered the toxic equivalence of the chemical being tested by less than 1%. For the TCDD, the only contaminant was 0.43% 1,2,3,7,8-pentachlorodibenzo-p-dioxin (PeCDD). For the HxCDD, the two contaminants were 0.38% 1,2,3,4,6,7,8-heptachlorodibenzo-p-dioxin and 0.10% 1,2,3,7,8-PeCDD. For HxCDF, the three contaminants were 0.16% 2,3,4,7,8-pentachlorodibenzofuran (PeCDF), 0.15% 1,2,3,7,8-PeCDF, and 0.07% 1,2,3,4,7,8,9,-HpCDF. For PCB 126, the five contaminants were 0.16% PCB 81, 0.04% PCB 77, 0.02% PCB 169, 0.02% PCB 157, and 0.01% PCB 118.

Cell culture.

Neonatal foreskin NHEKs, purchased from Lonza (Walkersville, MD), were grown in Keratinocyte-serum-free medium (Invitrogen, Carlsbad, CA). Confluent fifth passage NHEKs were incubated in complete media (50 μg/ml bovine pituitary extract and 5 ng/ml epidermal growth factor [EGF]) for 48 h, changed to basal media (no supplements or serum) for 24 h, and then treated with chemicals in basal media for the time indicated or for 48 h in the dose-response studies (Sutter et al., 2009). Rat hepatoblastoma–derived H4IIE American Type Culture Collection cells were grown in Dulbecco's modified Eagle's medium supplemented with 10% fetal bovine serum, 2% L-glutamine, and penicillin/streptomycin. Confluent cells were incubated in basal media (no supplements or serum) for 24 h and then treated with vehicle control (0.7% DMSO) or chemical in basal media for 48 h in triplicate. Serum-free exposure media were used because serum components (e.g., bovine serum albumin) can significantly reduce the cellular uptake of TCDD and DLCs (Hestermann et al., 2000). The chemical concentrations tested were the following: TCDD (0.001, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, and 100nM), PCB 126 (0.01, 0.1, 0.3, 1, 3, 10, 30, 100, 300, 1000, 3000, and 10,000nM), or TCDF, HxCDF, and HxCDF (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100, and 300nM).

Although Rat H4IIE cells are not from the same tissue origin as NHEKs and are thus unable to serve as a direct cell type–specific, interspecies comparison, this sensitive rodent cell line has been previously determined to give replicable DLC REPs consistent with the TEFs. Therefore, we utilized H4IIE cells primarily to validate the bioactivity of low concentrations of our chemical congeners and to check for consistency of rodent-derived REPs under our experimental conditions.

Cell viability assay.

Cell viability was measured by a 3-4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide (MTT) assay (Sigma). Cells were treated with vehicle and chemicals for 48 h, after which 75 μl of MTT solution and 750 μl of Hank's balanced salt solution were added to the cells, and plates were incubated for 2 h 30 min at 37°C. The solubilization solution (750 μl) was added to the plates to dissolve the formazan crystals, and the plates were incubated again for another 30 min. Optical density was measured at 570 nm using a spectrophotometer.

Biochemical analyses.

Total RNA was isolated using RNA Stat-60 (Tel-Test). Real-time PCR was carried out using the Roche LightCycler 480, LC480 SYBR Green I Master, and the following primers (5′-3′): for human CYP1A1, CATCCCCCACAGCACAACAAGAGA and GCAGCAGGATAGCCAGGAAGAGAA and for rat Cyp1a1, CTTCACACTTATCGCTAATGG and TGGGGTCTGAGGCTATGG. Beta actin (ACTB) was used as the reference for sample normalization using the following primers: for human ACTB, TGGTGGGCATGGGTCAGAAG and GTCCCGGCCAGCCAGGTCCAG and for rat Actb, TCCACCCGCGAGTACAACCTTCTT and GGCCCGGGGAGCATCGTC. The mRNA levels were measured in at least three separate samples for each chemical concentration except in the following cases. Out of the complete data set, there were three samples (donor 1: 3nM TCDF treatment and donor 2: 3nM TCDD and 0.01nM HxCDF treatments) from which RNA values were not obtained and seven samples that were excluded because the values of their ACTB mRNA were greater than or equal to the mean ACTB level of their respective donor ± 3 SDs (z-ratio ≥ 3). These were from donor 1: 3nM TCDD and 0.01nM HxCDF treatments; donor 2: 30nM TCDD treatment (one of the six samples); donor 3: DMSO treatment (one of nine samples) and 1000nM PCB 126 treatment; and donor 4: 10,000nM PCB 126 treatment.

PCR efficiencies (E) were calculated from the slopes of the standard curves using the equation, E = 10^(−1/slope). Standard curves using serial dilutions (NHEK cDNA input of 40–0.0004 ng [n = 3]) resulted in a high degree of linearity of CYP1A1 and ACTB mRNA values. The R² value for both human CYP1A1 and human ACTB was 0.996. The calculated efficiency, E, for PCR amplification was 1.88 and 1.95 for CYP1A1 and ACTB, respectively. Standard curves using serial dilutions (H4IIE cDNA input of 20–0.00002 ng [n = 5]) also resulted in a high degree of linearity of rat Cyp1a1 and Actb mRNA values. The R² value for rat Cyp1a1 was 1.000 and rat Actb was 0.999. The calculated PCR efficiency, E, was 1.94 and 1.98 for rat Cyp1a1 and rat Actb, respectively. Relative quantification of the mRNA was determined using the calculated efficiencies and the previously described method (Pfaffl, 2001). For each NHEK replicate culture, CYP1A1 expression was normalized relative to the housekeeping gene ACTB and also within each donor, relative to the mean CYP1A1 gene expression level (average of the three replicate cultures) at the TCDD concentration that achieved the highest induction. The resulting normalized data were termed “relative CYP1A1 expression index.” All the experimental values for CYP1A1 and ACTB were in the linear range of each of the standard curves and well within our limits of detection, determined to be at least twofold lower than the lowest experimental value. When PCR was carried out on samples that did not include reverse transcriptase, the values of CYP1A1 amplification were 75-fold lower than the lowest experimental value, demonstrating that all our experimental values are far above background levels of CYP1A1 amplified from contaminating genomic DNA.

Dose-response models for individual donors.

A modified version of the Hill equation (Hill, 1910, 1913) was employed for dose-response modeling defined as follows:

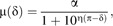(1)

where μ(δ) was the estimated mean response (i.e., relative CYP1A1 expression index) at concentration δ (log₁₀ nanomolar), α the maximal agonist effect (i.e., the change in height of the right asymptote), π the potency (log₁₀ nanomolar) at α/2 (i.e., the 50% effective concentration; EC50), and η the Hill coefficient. The baseline expression level at δ = −∞ was set to be constant at zero, allowing for a more simplified Hill model without constraints. This was a reasonable assumption because the vehicle control expression values did not exceed the 0.01 relative response level (i.e., 1% of the mean maximal CYP1A1 level for TCDD exposure) for any one cell culture and more complex models not making this assumption did not result in significantly better fits (data not shown). It is important to note that vehicle control data were omitted from the dose-response modeling procedure to avoid log₁₀ transformation of 0nM.

Because the goal of the current study was to accurately estimate DLC REP values, nonlinear dose-response curves were fit simultaneously for TCDD and DLCs using similar procedures to those described previously (Carlson et al., 2009; Toyoshiba et al., 2004). Initially, REP dose-response models were generated separately for each donor-specific data set. To achieve this, the following indicator Equation 2 was employed:

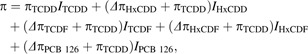(2)

where π_TCDD was the estimated log₁₀ EC50 for TCDD (i.e., the base chemical) and Δπ was the relative change in log₁₀ EC50 (from TCDD) for the indicated DLC. The indicator functions (I) are equal to 1 when calculating the response of the subscripted chemical; otherwise they are equal to 0. Therefore, if the log₁₀ EC50s for both TCDD and PCB 126 were identical, then the estimated Δπ_{PCB 126} would be equal to 0. Thus, the DLC REP can be easily derived from Δπ using Equation 3.

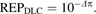(3)

Because dose-response data for HxCDD and TCDF were only determined for donor 1 NHEKs, Equation 2 for the remaining donors did not include parameters for these congeners.

Although it was expected that each 0.1 TEF DLC congener would act as a full AHR agonist in human keratinocytes to generate parallel dose-response curves of equal maximal agonist effect, preliminary analyses indicated that for some donors the maximal agonist effect (i.e., α) varied significantly among TCDD and DLCs. Therefore, a more complex model was also generated with separate α parameter estimates for each congener (designated by appropriate subscripts). Conversely, an assumption of parallel dose-response curves among congeners appeared legitimate, allowing for the Hill coefficient η to be set not to vary among chemical congeners. Thus, 2 nested models (see below) were attempted for each donor-specific data set.

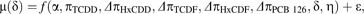(Model 1)

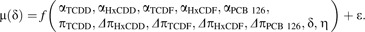(Model 2)

A generalized nonlinear least squares procedure (Pinheiro and Bates, 2004) was used to fit each model where parameters in Equation 1 were explained by f(), and ϵ represents the residual error of μ(δ) and assumed to be independently distributed as N (0,σ²). Again, congener-specific parameters for HxCDD and TCDF were only used for donor 1 NHEK models and omitted for the other donors. The more complex Model 2 was selected over Model 1 only if it was deemed a better fit by likelihood ratio test (LRT, p ≤ 0.05) and comparison of Akaike information criteria (Akaike, 1974). Because residual analyses indicated significant heteroscedastic residual variance with predicted response for each best-fit dose-response model, a residual variance modeling procedure was employed as previously described (Carlson et al., 2009). In order to generate EC50 maximum likelihood (ML) estimates and approximate 95% confidence intervals (CIs) for each DLC, best-fit models were reparameterized to produce a separate π parameter for each DLC rather than Δπ parameters. In addition, dose-response data for the rat cell line H4IIE were modeled in a manner identical to that described above.

Population-level dose-response model.

Following the donor-specific dose-response modeling procedure, data from all donors for the chemical congeners TCDD, HxCDF, and PCB 126 were combined to formulate a “population-level” REP model that would provide model parameter estimates for the average individual in the sampled population. Examination of the donor-specific model outputs revealed that a separate parameter for the maximal agonist effect (α) would likely be required for each chemical congener as done in the donor-specific Model 2. In addition, variability among donors in α_HxCDF, α_{PCB 126}, and π_TCDD would necessitate implementation of a nonlinear mixed-effects model (Lindstrom and Bates, 1990; Pinheiro and Bates, 2004) with random effects allowing these parameters to vary among donors. Furthermore, to permit for subsequent reparameterization of the model to estimate DLC EC50s and approximate 95% CIs, random effects allowing Δπ_HxCDF and Δπ_{PCB 126} to vary among donors were also included in the model. The Hill coefficient η was set to remain constant among chemical congeners (i.e., parallel dose-response curves), as in both Models 1 and 2. Analysis of the donor-specific model output also indicated that the η parameter did not vary much among donors. The full population REP model was defined as follows:

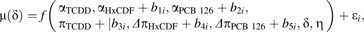(Model 3)

where each parameter in Equation 1 was explained by f() whose arguments included five random effects (i.e., b_1i–b_5i) representing the variability in the fixed terms α_HxCDF, α_{PCB 126}, π_TCDD, Δπ_HxCDF, and Δπ_{PCB 126}, respectively, among the donors i. The value of index i ranged from 1 to 4 (i.e., the four human donors). All random effects in Model 3 were assumed to be normally distributed with mean 0 and variance-covariance matrix ψ (i.e., a general positive-definite matrix) independently for each donor i. The residual error ϵ_i was assumed to be independently distributed as N (0,σ²) and independent of any random effects.

Threshold model.

A population-level “hockey stick” model was generated to estimate TCDD, HxCDF, and PCB 126 potencies at dose-response thresholds in the low-dose region using piecewise regression procedure similar to those described elsewhere (Bacon and Watts, 1971; Lutz and Lutz, 2009; Seber and Wild, 2003; Yanagimoto and Yamamoto, 1979). Arguably, the best scale in which to define a threshold response would be in log-log space, where both the response and concentration are log₁₀ transformed (Bailey et al., 2009a,b; Slob, 2007; Williams et al., 2009), thereby accentuating very small changes in gene expression at low exposure levels. Thus, both concentration and response were log₁₀ transformed prior to dose-response modeling for this procedure. Data at the high concentration end (i.e., right asymptote) of sigmoid curves of each chemical were subsequently removed in a nonbiased manner to generate hockey stick dose-response shapes as they did not inform the dose-response at lower response points (see Supplementary Data section). The piecewise equation was defined as follows:

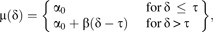(4)

where μ(δ) was the log₁₀-transformed mean response at concentration δ (log₁₀ nanomolar), α₀ the baseline expression level at δ = −∞, τ the break point (i.e., threshold) concentration, and β the slope of the dose-response above τ. It is important to note that this equation is continuous at δ = τ, where a flat line with slope zero and y-intercept α₀ intersects a second line with slope β.

A nonlinear modeling procedure was employed to allow for direct estimation of threshold locations (Seber and Wild, 2003). All three chemical congeners were modeled simultaneously, as was done with Models 1–3, but instead of estimating REP values for HxCDF and PCB 126 at the EC50 level, the REP values were determined at the threshold concentration τ level. Therefore, we defined this new “low-dose” REP as the relative threshold factor (RTF). An indicator equation similar to Equation 2 was generated, where τ_TCDD was the estimated threshold concentration for TCDD and Δτ_HxCDF and Δτ_{PCB 126} were the relative changes in the threshold concentration for HxCDF and PCB 126, respectively. By replacing Δπ with Δτ in Equation 3, the RTF for each DLC can be derived. The final nonlinear mixed-effects model was defined as follows:

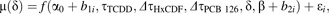(Model 4)

where each parameter in Equation 4 was explained by f() whose arguments included 2 random effects (i.e., b_1i and b_2i) representing the variability in the fixed terms α₀ and β, respectively, among the donors i. The value of index i ranged from 1 to 4 (i.e., the four human donors). Random effects in Model 4 were assumed to be normally distributed with mean 0 and variance-covariance matrix Ψ (i.e., a general positive-definite matrix) independently for each donor i. The residual error ϵ_i was assumed to be independently distributed as N (0,σ²) and independent of any random effects.

Statistical functions.

The “gnls” function in the R package nlme version 3.1-96 (Pinheiro and Bates, 2004) was used to fit Models 1 and 2 and the function “nlme” from the same package was used for Models 3 and 4. The “method” argument for Models 3 and 4 was set to “ML” or maximized log likelihood. All functions were implemented in R version 2.10.1 (R Development Core Team, 2006). The starting value selection procedure employed for each model is described in detail in the Supplementary Data section. A semiparametric (residual based) bootstrap method (10,000 resamplings) was employed to approximate 95% CIs for chemical-specific threshold models in a manner identical to that previously described by Toms and Lesperance (2003).

RESULTS

Characterization of Test Chemical Treatments

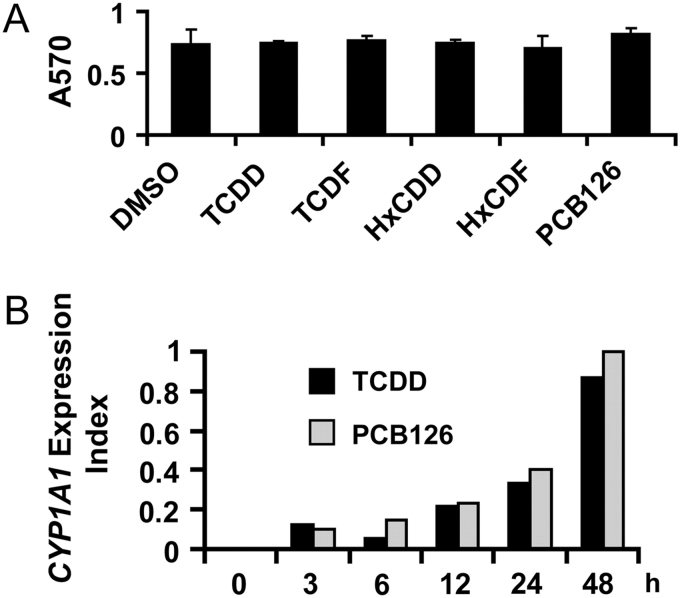
TCDD-mediated increases in CYP1A1 mRNA in donor 1 NHEKs have been previously demonstrated to be greatest in confluent cultures in which EGF was omitted (Sutter et al., 2009). Cell culture conditions in the studies presented here are similar to those previously described to ensure maximal responsiveness of CYP1A1 mRNA. MTT cell–based viability assay in NHEKs indicated that at the maximum concentration used in these studies, none of the chemicals caused cell toxicity (Fig. 1A), consistent with previous results using TCDD in numerous cultures of cells (Knutson and Poland, 1980). A time-course study measuring CYP1A1 mRNA in NHEKs (Fig. 1B) indicated that TCDD (10nM) had a response that was parallel and similar in magnitude to PCB 126 (10,000nM). These concentrations were selected based on the study of Silkworth et al. (2005). Because these responses continued to increase up to 48 h and for consistency with the exposure duration of previous dose-response studies conducted in our laboratory using fresh human and rat hepatocytes (Carlson et al., 2009; Silkworth et al., 2005), this time of exposure was chosen for the dose-response studies and longer exposure durations were not analyzed.

FIG. 1.

(A) NHEKs were treated with control vehicle (DMSO, 0.7%), TCDD (100nM), TCDF (300nM), HxCDD (300nM), HxCDF (300nM), or PCB 126 (10,000nM) for 48 h. Cell viability was determined using the MTT assay as described in Materials and Methods section, which measures absorbance at 570nM. The results are presented as mean ± SD (n = 3). (B) NHEKs were treated with TCDD (10nM) or PCB 126 (10,000nM) for 0, 3, 6, 12, 24, and 48 h. Real-time PCR was used to determine the level of CYP1A1 mRNA. Levels of mRNA are expressed in units relative to the maximum, given a value of 1.

Dose-Response for Individual Donors

NHEKs from four donors were used to study the CYP1A1 mRNA concentration-response. Initially, dose-response was determined for TCDD and four DLCs with assigned TEFs of 0.1 (i.e., HxCDD, TCDF, HxCDF, and PCB 126) in only donor 1 NHEKs. Because both HxCDD and TCDF appeared to produce the expected REP of 0.1 for donor 1 NHEKs, only TCDD, HxCDF, and PCB 126 were tested in NHEKs from donors 2–4.

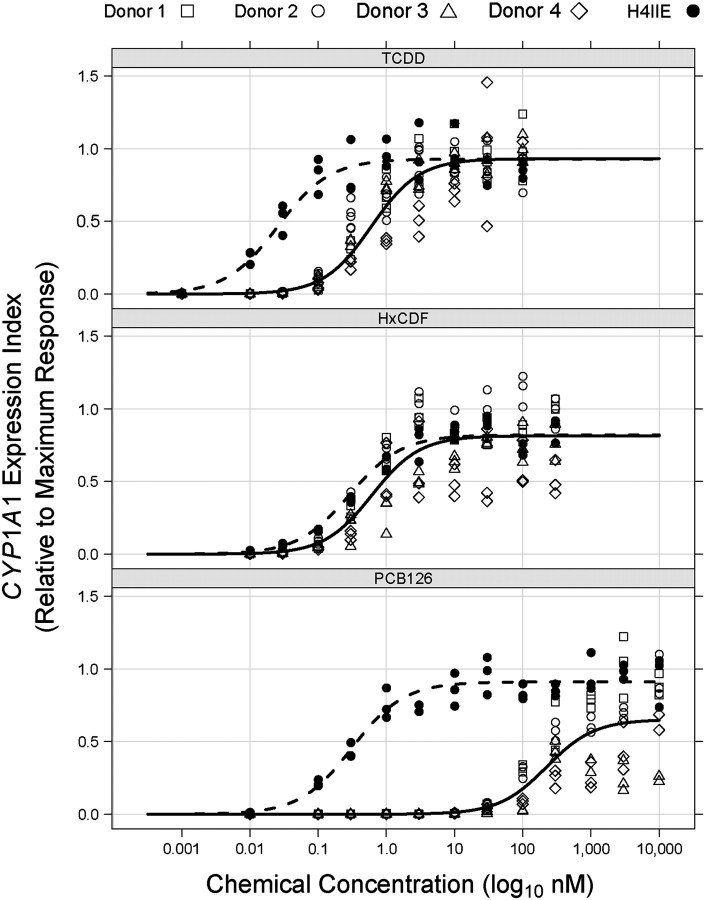
Donor-specific REP models were initially generated separately for NHEKs from each of the four donors, and model output data are given in Table 1 and presented graphically in Figure 2. The more complex Model 2, with separate maximal agonist effect parameters (i.e., α) for each chemical, was selected for donors 1, 3, and 4 by a log LRT (p ≤ 0.05), whereas the more parsimonious Model 1 (i.e., same α for all congeners) was selected for donor 2 NHEKs (p = 0.4974). Model residual variance was seen to increase with increasing fitted values (i.e., heteroscedastic residual variance) for all donor-specific REP models, necessitating residual variance modeling procedures which greatly improved residual variance homogeneity.

TABLE 1.

Donor-Specific REP Model Outputs

Chemical	Culture	Maximal agonist effecta	Hill coefficient	EC50 (nM)	REP	WHO TEFb
TCDD	Donor 1	0.98 (0.90–1.06)c	1.4 (1.3–1.6)	0.56 (0.43–0.72)	1	1
	Donor 2	0.92 (0.88–0.95)	1.3 (1.2–1.5)	0.32 (0.26–0.39)	1	1
	Donor 3	0.94 (0.85–1.03)	1.4 (1.1–1.6)	0.45 (0.33–0.62)	1	1
	Donor 4	0.91 (0.76–1.06)	1.1 (0.9–1.3)	1.41 (0.82–2.43)	1	1
HxCDD	Donor 1	1.19 (1.11–1.28)	1.4 (1.3–1.6)	2.32 (1.85–2.91)	0.24 (0.17–0.33)	0.1
TCDF	Donor 1	0.89 (0.81–0.98)	1.4 (1.3–1.6)	5.44 (4.02–7.35)	0.10 (0.07–0.15)	0.1
HxCDF	Donor 1	0.91 (0.85–0.98)	1.4 (1.3–1.6)	0.53 (0.41–0.68)	1.06 (0.75–1.49)	0.1
	Donor 2	0.92 (0.88–0.95)	1.3 (1.2–1.5)	0.39 (0.30–0.51)	0.82 (0.61–1.10)	0.1
	Donor 3	0.72 (0.65–0.79)	1.4 (1.1–1.6)	0.99 (0.69–1.42)	0.45 (0.29–0.70)	0.1
	Donor 4	0.59 (0.50–0.68)	1.1 (0.9–1.3)	0.65 (0.37–1.16)	2.16 (1.09–4.30)	0.1
PCB 126	Donor 1	0.92 (0.83–1.01)	1.4 (1.3–1.6)	188.58 (143.81–247.28)	0.0030 (0.0021–0.0042)	0.1
	Donor 2	0.92 (0.88–0.95)	1.3 (1.2–1.5)	204.12 (157.08–265.25)	0.0016 (0.0012–0.0021)	0.1
	Donor 3	0.32 (0.25–0.38)	1.4 (1.1–1.6)	156.08 (87.51–278.38)	0.0029 (0.0015–0.0054)	0.1
	Donor 4	0.51 (0.36–0.65)	1.1 (0.9–1.3)	377.39 (176.08–808.86)	0.0037 (0.0017–0.0084)	0.1

^aResponse units are relative CYP1A1 expression index as described in the Materials and Methods section.

^b Van den Berg et al. (2006).

^cAll data are expressed as ML estimate and 95% CI (in parentheses).

FIG. 2.

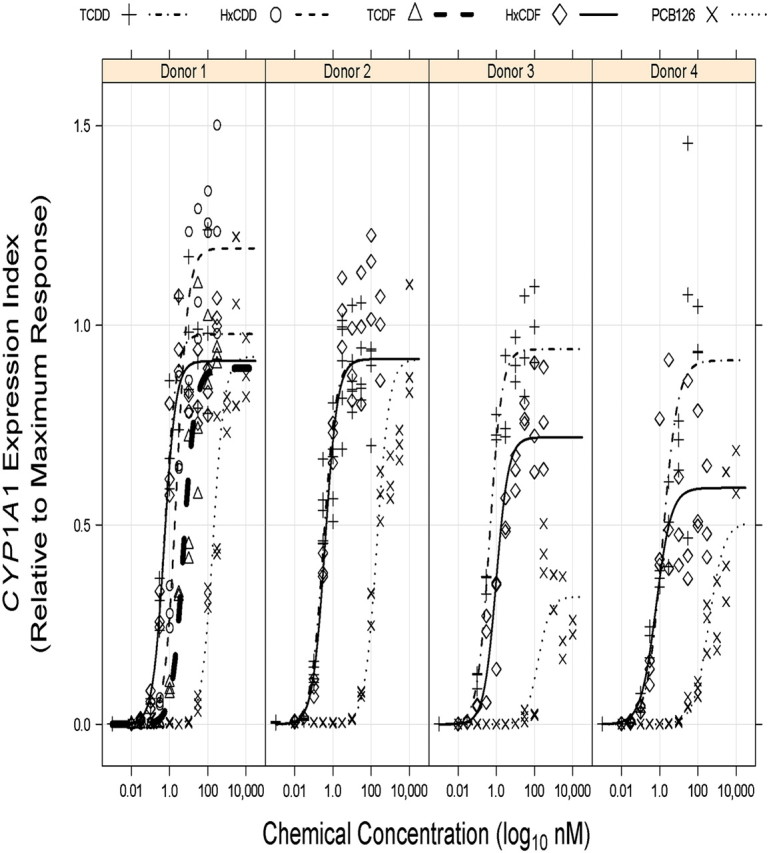
CYP1A1 mRNA increases in NHEKs from four donors treated with DLCs modeled as individual donors. NHEKs from donor 1 were treated with DMSO (0.7%) or increasing concentrations of TCDD, TCDF, HxCDD, HxCDF, or PCB 126 for 48 h (see Materials and Methods section for concentrations). NHEKs from donors 2–4 were treated with DMSO (0.7%) or increasing concentrations of TCDD, HxCDF, or PCB 126 for 48 h. The individual culture data points were graphed relative to the average maximum TCDD response reached by each individual donor. Curves represent predicted responses generated by the models described in the Materials and Methods section.

As indicated earlier, the estimated REP values for HxCDD (0.24) and TCDF (0.10) for donor 1 NHEKs were within the half order of magnitude uncertainty prescribed to their assigned TEFs of 0.1 (Van den Berg et al., 2006), whereas considerable deviations for estimated REP values of HxCDF (1.1) and PCB 126 (0.003) from their TEFs of 0.1 were determined (Table 1). Consistent with the donor 1 model, dose-responses for donors 2–4 revealed relatively higher HxCDF and lower PCB 126 REP estimates than the assigned TEF of 0.1. Model estimates for the Hill coefficient were similar across the donors, whereas the TCDD EC50 for donor 4 NHEKs was relatively higher than estimates for the other three donors. The maximal agonist effects elicited by PCB 126 and HxCDF in NHEKs from donors 3 and 4, but not donors 1 and 2, were clearly lower than that observed for TCDD (Fig. 2), indicating that these congeners may not always act as full agonists of the AHR in NHEKs.

Population Dose-Response

Observations made from the donor-specific modeling procedure were used to formulate a population-level REP model that simultaneously fit dose-response data for TCDD, HxCDF, and PCB 126 from all donor NHEK cultures. Because we were interested in parameter estimates representing the average individual of our “population” and the approximate 95% CIs surrounding each parameter, a mixed-effects modeling procedure was implemented. Donor-specific data given in Table 1 suggested that random effects accounting for donor-to-donor variability in EC50s (and REP values) and the maximal agonist effect for both HxCDF and PCB 126 might be necessary. These assumptions were justified by log-likelihood ratio testing among various population REP models when donor-specific data were combined (data not shown). Residual variance of the final population REP model was heteroscedastic with increasing fitted values, but implementation of several residual variance modeling procedures failed to generate any convergent models. The final population REP model output data are given in Table 2, and the population-level predicted values are plotted in Figure 3. For comparative purposes and to validate previous observations using our current experimental protocols, dose-response data from the rat hepatoma cell line H4IIE, modeled in a manner identical to that used for NHEK donor–specific modeling, are also depicted in Table 2 and Figure 3. Consistent with the donor-specific models, the NHEK population REP model estimated relatively higher HxCDF and lower PCB 126 REPs than the assigned TEF of 0.1 (Table 2). In addition, the estimated population-level maximal agonist effect for PCB 126 (i.e., α_PCB126) was relatively lower than those of TCDD and HxCDF, indicating that PCB 126 may not always act as a full AHR agonist in NHEKs. In stark contrast to these observations, the rat H4IIE cell line model estimated REP values for HxCDF (0.088) and PCB 126 (0.082) that are close to their assigned TEF of 0.1. The estimated TCDD EC50 for H4IIE cells was similar to the ∼0.01nM TCDD EC50 value previously reported for H4IIE cells by Peters et al. (2004). Figure 3 clearly demonstrates approximately 725-fold lower sensitivity of NHEKs to PCB 126 than the rat H4IIE cell line. This species difference in responsiveness to PCB 126 is well beyond the approximate 23-fold difference seen between TCDD EC50s from the two species and similar to that previously observed for EROD induction in fresh human and rat hepatocytes (Carlson et al., 2009; Silkworth et al., 2005). Interestingly, cells from both species appeared to be nearly equally responsive (i.e., approximately twofold difference) to HxCDF (Table 2).

TABLE 2.

“Population-Level” REP Model Outputs

Model parameter	NHEK cell population model	Rat H4IIE cell line modela
Maximal agonist effectb
TCDD	0.93 (0.90–0.96)c	0.93 (0.88–0.98)
HxCDF	0.81 (0.65–0.98)	0.82 (0.77–0.88)
PCB 126	0.65 (0.41–0.89)	0.91 (0.86–0.96)
Hill coefficient	1.2 (1.1–1.4)	1.1 (1.1–1.2)
EC50 (nM)
TCDD	0.60 (0.31–1.19)	0.026 (0.020–0.032)
HxCDF	0.62 (0.38–1.01)	0.29 (0.23–0.36)
PCB 126	224.73 (115.08–439.86)	0.31 (0.25–0.39)
REP
HxCDFd	0.98 (0.38–2.52)	0.088 (0.067–0.115)
PCB 126d	0.0027 (0.0018–0.0039)	0.082 (0.062–0.108)

^aAlthough not derived from the same cell type as NHEKs, model output data for rat line H4IIE cell line are given to reiterate previously determined responses of a sensitive rodent cell type under current experimental conditions.

^bResponse units are as described for relative CYP1A1 expression index in the Materials and Methods section.

^cAll data are expressed as ML estimate and 95% CI (in parentheses).

^dCurrent WHO TEF is 0.1 (Van den Berg et al., 2006).

FIG. 3.

CYP1A1 mRNA increases in NHEKs from four donors treated with TCDD, HxCDF, and PCB 126 modeled together as a population and compared with the rat liver cell line H4IIE. Relative CYP1A1 levels from NHEKs from each donor and from H4IIE cells after 48 h treatment with TCDD (upper panel), HxCDF (middle panel), and PCB 126 (lower panel) are plotted as indicated. Each point in the graphs represents an individual sample. Data were modeled as described in the Materials and Methods section, resulting in a population-level prediction curve for NHEKs (solid line) and the predicted response of rat H4IIE cells (dashed line).

Calculation of a Population Threshold

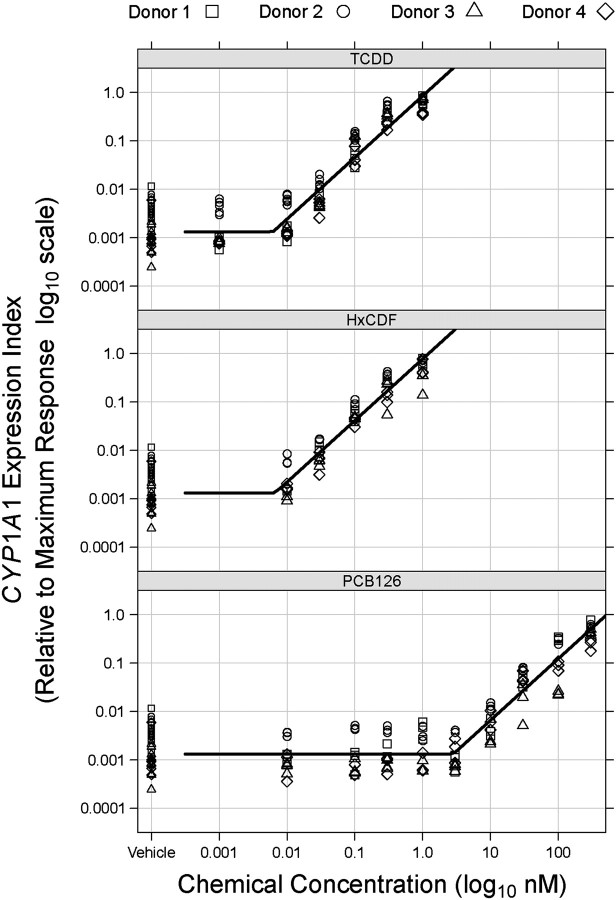
Although the nonlinear mixed-effects procedure employed to generate a population REP model appeared to accurately account for the large variability seen among donors in maximal agonist effect, the resulting model was very complex and its residual variance increased with increasing predicted response level. Since accurate estimation of both EC50s and EC50-derived REP values depend upon precise determination of the right asymptote of the sigmoid dose-response curve (i.e., maximal agonist effect), we sought to take advantage of the strikingly similar response among donors apparent at lower chemical concentrations (as observed in Fig. 3) to develop an alternative method to assess potency and REP using our data. To achieve this, a population threshold model, resembling a hockey stick in shape, was developed where the initial dose-response relationship is flat across chemical concentrations (zero slope) followed by a concentration-dependent, linearly increasing response beyond an unknown threshold. This model directly estimated the TCDD threshold concentration (i.e., τ_TCDD) and RTFs for HxCDF and PCB 126. Residual variance of the final threshold model was homogeneous across all response levels (i.e., the assumption that residuals were independent and identically distributed was justified).

The population threshold model output data are given in Table 3, and Figure 4 depicts the predicted population-level response obtained for each chemical. For entirely informational purposes, relative CYP1A1 expression indices of the vehicle control samples used in this study are also included in Figure 4, although vehicle control data were not used in the actual threshold modeling. A more complex model allowing the slope of the initial line segment below the threshold to deviate from zero (i.e., a concentration-effect below threshold) did not prove a better fit by log LRT (p = 0.7018). Overall, the RTFs generated in the population threshold modeling procedure (Table 3) were entirely consistent with REP values derived from full dose-responses shown in Table 2, demonstrating that the clear divergence of HxCDF and PCB 126 NHEK-derived REP values from their assigned TEFs also occurs in the low concentration-effect region.

TABLE 3.

Threshold Model Outputs

Model parameter	Estimate
Baseline response levela	1 × 10−3 (7 × 10−4 to 3 × 10−3)b
Threshold concentration (nM)
TCDD	0.0062 (0.0052–0.0073)
HxCDF	0.0067 (0.0056–0.0079)
PCB 126	2.8 (2.4–3.3)
RTFc
HxCDFd	0.93 (0.81–1.07)
PCB 126d	0.0022 (0.0019–0.0025)
Slope below thresholde	0
Slope above threshold	1.27 (1.17–1.37)

^aResponse units are relative CYP1A1 expression index.

^bAll data are expressed as ML estimate and 95% CI (in parentheses).

^cREP derived with threshold concentrations instead of EC50s.

^dCurrent WHO TEF is 0.1 (Van den Berg et al., 2006).

^eThis model parameter is forced to equal zero.

FIG. 4.

Models of apparent population thresholds for NHEKs treated with TCDD, HxCDF, and PCB 126. Relative CYP1A1 mRNA increases from each of the four donors treated with TCDD (upper panel), HxCDF (middle panel), and PCB 126 (lower panel) were plotted and analyzed as described in Materials and Methods section. Each point in the graphs represents an individual sample, and curves are the population-level response predicted by the threshold model. Note that both axes are log₁₀ transformed.

Our analyses to validate our methods for relative quantitative real-time PCR (see Materials and Methods section) demonstrated that we were able to accurately detect low levels of CYP1A1 mRNA transcripts in the control samples and the samples below the apparent threshold concentrations. In addition, increases in Cyp1a1 mRNA in H4IIE cells were detected by exposure to low concentrations of chemicals, although they did not elicit a response in NHEKs, demonstrating that the chemicals are biologically available at these lower concentrations (Fig. 3).

Several mathematical caveats are always associated with threshold modeling, including convergence problems because of log-likelihood surfaces with multiple local maxima/flat ridges and the possibility of discontinuous first derivatives (Bacon and Watts, 1971; Seber and Wild, 2003). For a nonlinear piecewise model such as the one employed in the current study, careful attention needs to be paid to the choice of starting values for threshold parameters (Brenden and Bence, 2008). We conducted a grid search (Lerman, 1980) of “residual sum of squares” profiles using simple linear models to generate optimal starting values for threshold concentrations and RTFs. In addition, the stability of parameter estimates of the final threshold model was verified by varying threshold starting values in 0.2nM increments throughout the concentration ranges. Finally, examination of the log-likelihood surfaces for various parameter combinations in the population threshold model did not reveal the possibility of local maxima (data not shown).

Another problem commonly encountered in piecewise regression is that the assumption of asymptotic normality for the threshold parameter distribution might not be always justified (Feder, 1975a,b; Hinkley, 1969, 1971), making the ML approximation method for derivation of asymptotic CIs in the nlme function (Lindstrom and Bates, 1990) potentially unreliable. Generally, investigators will attempt various alternative methods to estimate threshold uncertainty such as inversion of the F statistic and/or bootstrapping (Toms and Lesperance, 2003); however, such analyses using our threshold model are somewhat impeded because of inherent difficulty in how to fix some parameters and not others and a lack of resampling methods for multilevel mixed-effects models.

Nonetheless, we did attempt to address these issues. Less complex threshold models were generated separately for each chemical congener, without random effects, and 95% CIs were approximated using a semiparametric (residual based) bootstrapping method (first row in Table 4). Using this strategy, we were unable to obtain a convergent model for HxCDF, primarily because of a lack of information regarding the location of the baseline expression level α₀. Next, chemical-specific mixed-effects models were generated with random effects for baseline expression α₀ and slope after threshold β parameters among donor cultures (second row of Table 4). Although we still could not model HxCDF, relatively narrower approximated 95% CIs were estimated for both TCDD and PCB 126 models. It is important to note that the 95% CIs for these chemical-specific mixed-effects models were derived using the nlme ML approximation method, which assumed asymptotic normality. Finally, all three congeners were modeled simultaneously, as was done in Model 4, but the assumption of parallel slopes (i.e., β parameter) among the congeners was not made (third row of Table 4). By borrowing information regarding the baseline expression level across chemicals, the HxCDF dose-response could now be modeled. It is also evident that our previous assumption regarding the existence of parallel dose-responses among chemicals after the threshold (model in the fourth row of Table 4) clearly did not affect the estimation of threshold concentrations to any extent. Thus, the final implementation of a nonlinear mixed-effects threshold model allowed for robust estimation of threshold locations of all three congeners by accounting for donor-to-donor variability in model parameters and “borrowing” information across chemicals, resulting in threshold and RTF estimates with relatively narrow approximated 95% CIs.

TABLE 4.

Effects of Various Approaches/Assumptions on Threshold Dose-Response Modeling

Model	Threshold concentration (nM)
	TCDD	HxCDF	PCB 126
Chemical specifica	0.0067 (0.0046–0.0094)b	DNCc	2.7 (1.9–4.2)
Chemical specific with random effectsd	0.0067 (0.0052–0.0086)	DNC	2.7 (2.2–3.4)
Multi-chem with random effectse	0.0068 (0.0057–0.0083)	0.0060 (0.0048–0.0075)	2.7 (2.2–3.3)
Multi-chem with random effects and parallel slopef	0.0062 (0.0052–0.0073)	0.0067 (0.0056–0.0079)	2.8 (2.4–3.3)

^aSingle chemical nonlinear least squares models without random effects; 95% CIs were estimated using semiparametric (residual) bootstrapping (see Materials and Methods section).

^bAll data are expressed as ML estimate and 95% CI (in parentheses).

^cDid not result in a convergent model.

^dSingle chemical nonlinear mixed-effects models with random effects allowing the baseline expression level and slope after the threshold to vary among donors. The asymptotic 95% CIs for this model were derived using the nlme function.

^eNonlinear mixed-effects model using data from all three chemical congeners with random effects allowing for baseline expression level and slope after threshold to vary among donors. The slope after threshold was not assumed to be parallel among the chemicals. The asymptotic 95% CIs for this model were derived using the nlme function.

^fSame “population-level” threshold model described in Table 3 and Figure 4. This model assumed parallel slopes across chemicals, an important assumption of the current TEF approach (Van den Berg et al., 2006).

DISCUSSION

The concept of TEFs, where DLCs are ranked relative to the potency of TCDD, was developed as a means to quantify exposure to DLCs through dietary intake (Van den Berg et al., 2006). Because TEFs are designed to reflect both pharmacokinetic and pharmacodynamic aspects of DLC toxicity, the TEF committee has given REPs derived from in vivo rodent feeding studies more weight than those determined using in vitro cell culture techniques. Nonetheless, this expert panel did realize the potential utility of in vitro REPs, particularly in characterizing the potency of DLCs lacking any reliable in vivo data (Van den Berg et al., 2006). In fact, in vitro REPs exist for most DLCs possessing TEFs in the Haws et al. (2006) database, with some congeners entirely lacking in vivo–derived REPs (e.g., HxCDD). Further examination of the Haws et al. (2006) database has revealed a relatively high concordance among in vitro and in vivo REPs for at least some DLCs. For example, the 50th percentile in vitro and in vivo REPs for HxCDF (also used in the current study) are 0.063 and 0.081, respectively (Haws et al., 2006). Interestingly, the 50th percentile of PCB 126 REPs derived from in vitro studies (i.e., 0.05) was a half order of magnitude lower than that for in vivo studies (i.e., 0.1), primarily because of the inclusion of eight relatively lower REP estimates derived from four studies using human cell lines whose geometric mean REP was 0.007 compared with a geometric mean of 0.1 for 21 nonhuman cell–derived REPs (Haws et al., 2006). Overall, such in vitro to in vivo comparisons using rodent data could potentially be combined with in vitro REP estimates generated using human cells to begin to address the cross-species extrapolation of TEF values from rodents to humans using a “parallelogram” approach similar to that previously described by Sobels (1980). However, caution should be given regarding in vitro to in vivo extrapolations for DLCs whose pharmacokinetics might vary significantly from that of TCDD (e.g., 2,3,4,7,8-PeCDF; Budinsky et al., 2006).

It is generally accepted that the AHR mediates most, if not all, of the toxic responses associated with dioxin exposure. Although not responsible for all toxicities related to AHR activation, CYP1A1 induction represents an endpoint that remains a sensitive indicator of the potency of a DLC to elicit a toxicological response. As activation of the AHR is clearly accepted as an early key event in the mode of action of DLCs, human in vitro studies, which measure this activation, provide information more relevant to humans, as well as decrease the use of laboratory animals. Relevancy to humans as well as reducing animal use are recognized by the National Research Council as important goals of future toxicological testing for determination of human health risk (NRC, 2007b). The application of the in vitro–derived human potency factors for DLCs is a prime example that embraces this vision.

A number of in vitro studies indicate that potency of DLCs, as measured by CYP1A1 induction, differ between rodent and human cells (Carlson et al., 2009; Nagayama et al., 1985; Silkworth et al., 2005; Westerink et al., 2008; Zeiger et al., 2001). To expand on these previous observations, we compared the concentration-dependent induction of CYP1A1 mRNA in NHEKs treated with TCDD to the concentration-dependent induction of CYP1A1 mRNA by treatment with four other DLCs. The chosen compounds, HxCDD, TCDF, HxCDF, and PCB 126, representing three different classes of congeners, dioxins, furans, and biphenyls, each had a TEF of 0.1. The initial study (NHEKs from donor 1) indicated that the REP values for HxCDD and TCDF were similar to their TEF values of 0.1 and these congeners were not further analyzed; yet, the REP values for HxCDF and PCB 126 differed from their assigned TEF. A population analysis of NHEKs from four donors indicated that the REP value for PCB 126 was 37.0 times lower and for HxCDF was 9.8 times higher than their TEF values. This indicates that NHEKs are less sensitive to PCB 126 but more sensitive to HxCDF than would be predicted by their assigned TEF values and that the TEF values of HxCDD and TCDF accurately predict the in vitro human response compared with TCDD. Because some, but not all, REP values of dioxins and furans deviated from their assigned TEF of 0.1, the results do not support a generalization for all congeners with a similar chlorination patterns. In addition, our results indicate that the differences between in vitro human and rodent responses may be congener specific and reiterate that the current TEF values do not always accurately predict the response of human cells to DLCs.

In the current study, we also present a threshold dose-response model used to determine RTFs for HxCDF and PCB 126 in the low concentration region. We fully appreciate the controversy surrounding the existence/absence of dose-response thresholds within the realm of toxicology and have no intention to add fuel to a topic that will be argued ad infinitum. Our threshold dose-response model was generated with a clear purpose in mind, to better estimate the REPs of DLCs from an in vitro assay system. Residuals of the population-level REP model, using the full dose-response for each chemical, were heteroscedastic largely because of huge variability in response at higher chemical concentrations both between NHEK donors and within replicate cultures. Furthermore, PCB 126 and, to a lesser extent, HxCDF appeared to act as partial AHR agonists in some NHEK donors. Similar problems were also apparent in a previous study using fresh human hepatocytes (Carlson et al., 2009) and will likely be encountered with greater frequency with increased use of untransformed human cell cultures. These aforementioned observations put into question REP values derived by comparing EC50s as suggested by Van den Berg et al. (2006) because EC50s rely mainly upon accurate estimation of the maximal agonist effect (right asymptote), and REP values additionally assume that DLCs act as full AHR agonists to generate maximal responses equal to that of TCDD.

Therefore, we took advantage of the strikingly consistent dose-response observed at lower concentrations, which demonstrated a clear break point in CYP1A1 expression from a relatively flat baseline level to a somewhat monotonically increasing induction. The resulting threshold model estimated RTF values very close to the EC50-based REP values. This concordance indicates that RTFs could function not only in support of EC50-based REP values but also possibly substitute for REP values when a maximum response cannot be accurately determined. However, as noted by others (Howard et al., 2010; Sutter et al., 2006), REP values (and likewise RTFs) would not accurately predict responses of partial agonists at high doses, although the relevancy of potency differences at very high doses to endpoints of interest may be dubious. Furthermore, if the most potent dioxin-like PCB congener (i.e., PCB 126) does not always act as a full AHR agonist in human cells, then application of the TEF scheme to mixtures containing other less potent dioxin-like PCBs, previously demonstrated to act as very weak agonists or display no activity at all in human cells (Vamvakas et al., 1996; Westerink et al., 2008; Zeiger et al., 2001), will certainly overpredict toxicity.

The apparent threshold for CYP1A1 induction observed in the current study is entirely consistent with previous observations of a switch-like mechanism of CYP1A1 induction, where within a single cell CYP1A1 is either at a low constitutive expression level or fully induced upon chemical exposure and induction magnitude varies from cell to cell even for the H4IIE cell line (reviewed by Wilson, 2004). This switch-like CYP1a1 response has been demonstrated in rodent hepatocytes in vitro and in the rat liver in vivo in response to TCDD and PCB 126 (Bars and Elcombe, 1991; Broccardo et al., 2004, 2005; French et al., 2004; Tritscher et al., 1992). Such switch-like gene regulatory systems have been described elsewhere and are prevalent in biological systems (Ertel and Tozeren, 2008; Lipshtat et al., 2010). We believe that the threshold concentrations determined in the current study, particularly for PCB 126, are not technical artifacts. The subthreshold concentrations of PCB 126 had biological activity in rat H4IIE cells. Also, CYP1A1 expression levels in the vehicle control and subthreshold concentration exposure groups were well above the background noise of the assay (see Materials and Methods section). Linear mixed-effects regression of PCB 126 data (untransformed) from 0 to 3nM (i.e., within the threshold concentration 95% CI) did not have a positive slope and was not significantly different from a flat zero slope line (data not shown). Because of the extremely high sensitivity of the real-time PCR assay employed, it is conceivable that below the threshold concentration, no or very few NHEKs were switched “on,” although we did not look at expression on a cell-by-cell basis.

This study in NHEKs investigated the response of a single gene, CYP1A1, to exposure to DLCs, which arguably resulted in a gene-specific REP or RTF. Such “functional selectivity” has been observed for certain receptor ligands where variation exists among REPs across different cellular responses (Kenakin, 2007; Michel and Alewijnse, 2007; Urban et al., 2007). However, a previous toxicogenomic study using fresh human and rat hepatocytes exposed to TCDD or PCB 126 in vitro demonstrated a relative consistency of EC50-derived PCB 126 REP estimates across different genes and functional gene categories, indicating that TEFs might be endpoint invariant, at least within this specific cell type (Carlson et al., 2009). It would be of interest to conduct a similar toxicogenomic examination of additional AHR-regulated genes in human keratinocytes in the future, specifically using the novel RTF approach employed in the current study.

The reasons for the large discrepancies between rodent and human in vitro concentration-responses to DLCs, as observed previously and in the current study, are not readily apparent. When receptor affinity is considered, it is clear that the AHR in the sensitive mouse strain, AhR b-1, has a 10-fold higher affinity for TCDD (Ema et al., 1994; Harper et al., 1988) than the human AHR because of an amino acid substitution at amino acid 381 in human receptor (Ramadoss and Perdew, 2004) and that the rat AHR has an approximately twofold higher affinity for TCDD than human AHR (Fan et al., 2009). Interestingly, the relative (to TCDD) rat and human AHR affinities for a number of DLCs, including PCB 126, were found to be similar (Fan et al., 2009), indicating that receptor affinity accounts for a nonspecific decrease in sensitivity for most if not all DLCs in human cells compared with rodent cells but cannot explain why human cells are much less sensitive to a DLC such as PCB 126 or more sensitive to one such as HxCDF than the rodent-based TEF would predict. In addition to the general 10-fold decrease in human sensitivity, the NHEK-derived REP for CYP1A1 induction calculated here for PCB 126 is 26–55 times lower than its TEF of 0.1 and for HxCDF approximately 4–10 times greater, indicating that there are other factors besides the affinity for the AHR that determine sensitivity. It has been suggested that ligand-specific coactivator or corepressor recruitment, that is also dependent upon the species, is likely to determine the sensitivity of a species to DLCs (Flaveny et al., 2008; Zhang et al., 2008). One study using a two-hybrid assay suggests that utilization of certain coactivators by the AHR is dependent on the binding of specific AHR ligands as well as cell context (Zhang et al., 2008); another demonstrates that human and mouse AHRs differ in their ability to interact with coactivators containing LXXLL motifs, suggesting differential recruitment of coactivators between mouse and human AHRs, resulting in differential transcriptional regulation of target genes (Flaveny et al., 2008). As the factors comprising the AHR transcriptional complex become better understood, the study of ligand-dependent differential cofactor recruitment will likely provide mechanistic data to begin to understand human sensitivity or insensitivity to certain DLCs.

Although these mechanisms for differences in ligand-specific sensitivity between rat H4IIE cells and human keratinocytes are not clear, we do have the ability to measure human in vitro responses and rank the potency of DLCs in human cells, which we and others have shown are different from rodent responses in vitro and in vivo. Although this study did not exhaustively analyze all DLCs, we have been able to demonstrate that the differences in sensitivities between rodent and human cells are congener specific, indicating underlying complex molecular differences. Inclusion of human in vitro data in the evaluation of DLCs should allow scientists to more accurately determine the risk to human health from exposure to DLCs. This is especially important because TEFs are already being used in the exposure and human health assessment of TCDD and related compounds to determine risk of exposures to environmental mixtures of DLCs.

FUNDING

General Electric Company and the W. Harry Feinstone Center for Genomic Research.