Abstract
The rate of meiotic recombination is one of the central factors determining genome-wide levels of linkage disequilibrium which has important consequences for the efficiency of natural selection and for the dissection of quantitative traits. Here we present a new, high-resolution linkage map for Populus tremula that we use to anchor approximately two thirds of the P. tremula draft genome assembly on to the expected 19 chromosomes, providing us with the first chromosome-scale assembly for P. tremula (Table 2). We then use this resource to estimate variation in recombination rates across the P. tremula genome and compare these results to recombination rates based on linkage disequilibrium in a large number of unrelated individuals. We also assess how variation in recombination rates is associated with a number of genomic features, such as gene density, repeat density and methylation levels. We find that recombination rates obtained from the two methods largely agree, although the LD-based method identifies a number of genomic regions with very high recombination rates that the map-based method fails to detect. Linkage map and LD-based estimates of recombination rates are positively correlated and show similar correlations with other genomic features, showing that both methods can accurately infer recombination rate variation across the genome. Recombination rates are positively correlated with gene density and negatively correlated with repeat density and methylation levels, suggesting that recombination is largely directed toward gene regions in P. tremula.
Keywords: linkage disequilibrium, linkage map, linked selection, methylation, nucleotide diversity, recombination
Meiotic recombination (hereafter recombination) is an important evolutionary force that directly alters levels of linkage disequilibrium (e.g., Wright 1931). Recombination therefore has important consequences for how effective natural selection is at removing deleterious mutations (Felsenstein 1974), increasing the frequency of beneficial mutations (Barton 1995) and for determining the resolution of association mapping for the dissection of quantitative traits (Nordborg and Weigel 2008). Recombination rates are known to vary between species, among individuals within species and even among different regions in a genome (Nachman 2002).
Local recombination rates have been shown to be positively correlated with neutral genetic diversity across a wide range of organisms (reviewed in Nachman 2002). One possible explanation for such an association is that cross-over events and/or associated processes, such as gene conversion and double-strand break repair, have direct mutagenic effects and thus act to increase nucleotide polymorphism (e.g., Kulathinal et al. 2008). An alternate explanation is that natural selection has indirect effects on sites linked to a site under selection and therefore also acts to reduce diversity on these sites (Begun and Aquadro 1992). Since recombination breaks down linkage disequilibrium, areas of high recombination are characterized by a rapid decay of linkage disequilibrium and linked selection will hence impact fewer sites in the vicinity of a selected site in these regions (Begun and Aquadro 1992). Conversely, in areas of low recombination rates, linkage disequilibrium will be extensive and indirect selection will impact a larger genomic region. Variation in recombination rates across the genome will generate an association between recombination and sequence diversity. Local variation in recombination rates is therefore an important factor for understanding how natural or artificial selection shapes sequence diversity across the genome of an organism. Recombination rates are also known to be associated with a number of different genomic features, such as gene density, repeat density, and cytosine methylation, although the magnitude and direction of these associations are still under debate. Recombination rates have been shown to be both positively and negatively correlated with gene density (positively: e.g., Wang et al. 2016, negatively: e.g., Giraut et al. 2011), GC-content (positively: Kim et al. 2007, negatively: Giraut et al. 2011), repeat density and methylation levels (positively: e.g., Rodgers-Melnick et al. 2015, negatively: Giraut et al. 2011). Characterizing associations between recombination rates and various genomic features at the genus or species level is thus important to avoid making incorrect assumptions about the strength and/or direction of these associations.
Traditionally, recombination rates have been estimated from the relationship of marker positions in linkage maps (Stapley et al. 2017) and more recently recombination rates have also been linked to physical regions of a genome through whole genome sequencing (Nachman 2002). However, producing linkage maps is time consuming and may even be infeasible in some species as it in many cases requires controlled crossing of known parents and the establishment of a large segregating progeny population (Stapley et al. 2017). Therefore, methods have been developed that infer recombination rates from linkage disequilibrium (LD) between segregating polymorphisms in individuals sampled from natural populations (e.g., McVean et al. 2004, Chan et al. 2012). Due to the relative ease of obtaining sequence information with modern sequencing methods even from wild populations, these LD-based methods for estimating recombination rates have been widely employed (e.g., McVean et al. 2004, Kulathinal et al. 2008 Silva-Junior and Grattapaglia 2015, Wang et al. 2016, Booker et al. 2017). Detailed knowledge of local variation in recombination rates can be used to infer the action of linked selection by establishing a correlation between the levels of nucleotide diversity and recombination rates across the genome of an organism (McVean et al. 2004, Chan et al. 2012). Using polymorphism data to infer recombination rates and then using these inferred recombination rates to explain variation in genetic diversity could be problematic, but simulations and studies performed using well-established animal model species such as Mus musculus (Booker et al. 2017) and in a number of Drosophila species (Kulathinal et al. 2008, Chan et al. 2012) suggest that indirect methods for estimating recombination rates are not strongly affected by natural selection. However, comparisons of LD-based and genetic linkage map-based methods for estimating recombination rates are not readily available in plant species. Genome structure, and in particular local rates of recombination, show large scale differences between plants and animals (Haenel et al. 2018), and it would therefore also be valuable to assess how well indirect methods for inferring recombination rates perform in plants.
The genus Populus has emerged as an important model system for forest genetics due to its rapid growth rate, ability to generate natural clones and a manageable genome size of ca. 480 Mbp distributed across a haploid set of 19 (2n = 38) chromosomes (Taylor 2002, Lin et al. 2018). Furthermore, both large and small scale synteny is highly conserved across species in the genus, enabling the transfer of genetic resources between species within the genus (Jansson and Douglas 2007). Further interest in Populus has been spurred by their economical (e.g., Taylor 2002) and ecological importance (e.g., Kouki et al. 2004) and over the past two decades a growing number of the ca. 40 species in the genus have been fully sequenced, including Populus trichocarpa (Black cottonwood) (Tuskan et al. 2006), P. euphratica (Ma et al. 2013) and P. tremula (European aspen) (Lin et al. 2018). Linkage maps have also been produced for many of the species in the genus (e.g., Paolucci et al. 2010, Tong et al. 2016), including Populus tremula (Zhigunov et al. 2017) but these maps have generally been relatively coarse, utilizing a few hundred up to a few thousand markers and typically employing mapping populations consisting of fewer than 300 progenies. Consequently, many of these maps have failed to resolve the expected 19 linkage groups typical for the genus and there is thus a need for developing a high-resolution, fine-scale linkage maps for the whole genus. P. tremula is a species of special interest within the genus as it has the largest distribution of any tree species in Eurasia, spanning from Spain and Scotland in the west to pacific China and Russia in the east, Iceland and northern Scandinavia in the north to northern Africa and southern China in the south (Luquez et al. 2008). Such extensive geographic distribution means P. tremula has adapted to a great variety of different environments, making it a promising species for studying the effects of spatially varying selection and adaptation (e.g., Farmer 1996, Luquez et al. 2008, Wang et al. 2018). Here we present a newly developed, fine-scale genetic map for Populus tremula and use this map to anchor scaffolds from the current draft genome assembly of P. tremula (Potra v1.1, Lin et al. 2018) to chromosomes. We then use this new resource to estimate local variation in recombination rates and use this to assess the correlation with recombination rates inferred from data on linkage disequilibrium in sample of unrelated individuals. We assess how different genomic features, such as gene density, repeat content and methylation levels are associated with estimates of local recombination rates. These results provide a valuable resource for enhancing our understanding of genome evolution and the recombination landscape in Populus and will also further facilitate the identification of loci controlling quantitative traits of ecological and economic value.
Material and methods
Plant material
In 2013, a controlled F1 cross was performed between two unrelated P. tremula individuals (UmAsp349.2 x UmAsp229.1) from the Umeå Aspen (UmAsp) collection that consists of c. 300 individuals collected in the vicinity of Umeå in northern Sweden (Fracheboud et al. 2009). This cross yielded 764 full sib progenies that were planted and monitored in a common garden at the Forestry Research Institute of Sweden’s research station in Sävar, 20 km north-east of Umeå (63.9N 20.5E). In addition, we utilized SNP data for 94 individuals of P. tremula belonging to the SwAsp collection that consists of 116 individuals sampled from 12 sites across Sweden (6-10 individuals per site, Luquez et al. 2008) displaying no population structure (Wang et al. 2018). The SNP data has previously been described in Wang et al. (2018) and consists of 4,425,109 SNPs with a minor allele frequency exceeding 5%.
DNA extraction and sequence capture
In 2015 leaf samples were collected from all progenies of the F1 cross. DNA was extracted using the Qiagen Plant Mini kit according to manufacturer guidelines and sent to Rapid Genomics (http://www.rapid-genomics.com) for genotyping using sequence capture probes. The probe set contain 45,923 probes of 120 bases each that were designed to target unique genic regions in the v1.1 P. tremula genome assembly (Lin et al. 2018), as well as an additional 70 probes that were designed to specifically target the putative sex determination region on chromosome 19 of the P. trichocarpa genome assembly v3.0 (https://phytozome.jgi.doe.gov/pz/portal.html). Parents and all offspring were subjected to sequence capture and subsequently sequenced on an Illumina HighSeq 2000 platform using paired-end (2x100bp) sequencing to an average depth of 15x per sample. All sequence capture data were delivered from Rapid Genomics in the spring of 2016. In addition, the two parents of the F1 cross were whole-genome re-sequenced to an average depth of 15x on an Illumina HiSeq 2500 platform with paired-end sequencing (2x150 bp) at the National Genomics Infrastructure at the Science for Life Laboratory in Stockholm, Sweden.
All raw sequencing reads were mapped against the complete P. tremula v.1.1 reference genome using BWA-MEM v.0.7.12 (Li and Durbin 2009) using default parameters. Following read mapping, PCR duplicates were marked using Picard (http://broadinstitute.github.io/picard/) and local realignment around indels was performed using GATK RealignerTargetCreator and IndelRealigner (McKenna et al. 2010; DePristo et al. 2011). Genotyping was performed using GATK HaplotypeCaller (version 3.4-46, (DePristo et al. 2011; Van der Auwera et al. 2013) with a diploid ploidy setting and gVCF output format. CombineGVCFs was then run on batches of ∼200 gVCFs to hierarchically merge samples into a single gVCF and a final SNP call was performed using GenotypeGVCFs jointly on the combined gVCF file, using default read mapping filters.
Construction of a high-density linkage map
Linkage maps were built separately for the two parents using a pseudo-testcross strategy (Grattapaglia & Sederoff 1994) by employing bi-allelic SNPs that were segregating according to Mendelian expectations. Pairwise estimates of recombination frequency were calculated between all markers and marker pairs showing no evidence for recombination were collected into bins and one representative marker was used for map construction. Markers were grouped into linkage groups (LGs) using a LOD threshold of 12 and ordered using the Kosambi mapping function as implemented in the BatchMap software (Schiffthaler et al. 2017). AllMaps (Tang et al. 2015) was used to create physical chromosomes from the P. tremula genome assembly v.1.1 (Lin et al. 2018) and the male and female genetic maps, with equal weight given to the two maps. For more details about the construction of the genetic and physical maps, please refer to Supplementary Methods.
Genetic map and linkage disequilibrium-based recombination rates
The genetic and physical maps for all 19 P. tremula chromosomes were read into MareyMap (Rezvoy et al. 2007, https://cran.r-project.org/web/packages/MareyMap) and the ‘sliding window’ method in MareyMap was used to estimate recombination rate in windows of 1 Mbp with a step size of 250 kbp. We only used windows with at least 8 SNPs in order to avoid regions with large gaps being assigned recombination values.
To generate a LD-based recombination map we used LDhelmet v.1.10 (Chan et al. 2012) with a random subset of 25 diploid individuals (i.e., 50 haplotypes) from the SwAsp data set (Wang et al. 2018). We used the default values from the LDhelmet manual as Populus tremula has similar levels of nucleotide polymorphism and extent of linkage disequilibrium as Drosophila melanogaster, on which the default settings in LDhelmet are based upon (Wang et al. 2016). As LDhelmet outputs estimates of recombination in units of ρ/bp whereas the genetic map is in units of cM, we converted the LDhelmet results to cM distances following the method outlined in Booker et al. (2017). We did this to be able to make comparisons between the recombination rates estimated using the two methods. The conversion assumes that the physical size of a chromosome is constant for the two methods so that the cumulative genetic distance in either cM or ρ should be the same but on different scales. The cumulative ρ was calculated by multiplying the ρ/bp estimates with the distance in bp between the adjacent SNP’s and then summed across chromosomes. Knowing the cumulative ρ and corresponding cM-values, it is possible to derive a ‘scaling factor’ to calculate cM values from the corresponding ρ values. The resulting cM values were read into MareyMap and recombination rates were estimated as described earlier for the genetic map-based recombination map. More details on the estimation of recombination rates from the genetic maps can be found in Supplementary Methods.
Correlation of recombination rate estimates, genetic correlates of recombination rate and model of recombination rate
We compared recombination rates inferred from the consensus genetic map or from the sequence data by calculating Spearman’s rank correlations (hereafter correlations) across 1 Mbp windows. We also assessed correlations between the two recombination rates and a number of genomic features, including gene density, repeat density, GC-content, substitution density, neutral diversity (π) and methylation.
Gene and repeat density were estimated using bedtools (Quinlan 2014) based on the annotation for the v1.1 P. tremula genome (Lin et al. 2018, ftp://plantgenie.org/Data/PopGenIE/Populus_tremula/v1.1/gff3/). GC-content was calculated from the genome FASTA using an in-house developed awk script (modified from: https://www.biostars.org/p/70167/#70172). The original script was modified to have window functionality across a FASTA sequence and to take into consideration sequence gaps. Windows with more than 80% gaps (N) were discarded to avoid biased results.
Substitutions relative to P. trichocarpa were estimated from a vcf-file with SNP-calls for a single Populus trichocarpa individual mapped against the P. tremula reference genome v1.1. Comparisons of putative substitutions were then made against a list of SNP positions from the 94 SwAsp P. tremula data set. Substitutions relative to P. tremuloides were inferred in a similar way based on SNP calls from five P. tremuloides individuals mapped against the P. tremula reference genome v1.2 (Lin et al. 2018). Files containing old, new and the total number of substitutions were used to calculate substitution densities in windows across the genome. Neutral genetic diversity (π) was estimated using vcftools and only fourfold degenerate sites or intergenic sites located at least 2 kbp from an annotated gene. For nucleotide diversity calculations, data for all 94 SwAsp samples were used.
Methylation levels were estimated using bisulfite sequencing data from six SwAsp individuals that were bisulfite sequenced using two biological replicates per individual. Samples were sequenced using paired-end (2x150) sequencing on an Illumina HiSeq X at the National Genomics Infrastructure facility at Science for Life Laboratory in Uppsala, Sweden. Methylation levels were estimated using the Bismark tools (Krueger and Andrews 2011, https://www.bioinformatics.babraham.ac.uk/projects/bismark/). Following trimming and quality control, sequence reads were mapped against polymorphism-substituted versions of the P. tremula v1.1 assembly (Lin et al. 2018) for each individual sample. Following read mapping BAM files were deduplicated to remove optical duplicates. Methylation levels were then extracted separately for the different methylation contexts (GpG, CHG and CHH) and average values were calculated across 1 Mbp window using a step size of 250 kbp across the P. tremula genome. Further details on the handling of the methylation sequencing data can be found in Supplementary Methods. Correlations between the two recombination maps and between the recombination maps and the various genomic features were calculated in R (R Core Team 2018). We also assessed the independent effects of different genomic features on the two recombination rate estimates using multiple regression.
Data availability
The raw sequencing reads used for the construction of the genetic map and raw bisulfate sequencing reads are available from ENA under study number PRJEB34662 (https://www.ebi.ac.uk/ena/data/view/PRJEB34662). BatchMap input files for the female and male genetic maps, the two component maps and the consensus map files as well as all processed files of the bisulfate sequencing data are available from zenodo.org under DOI number 10.5281/zenodo.3257544 (https://doi.org/10.5281/zenodo.3257544). Additional scripts and files used for the analyses are available at https://github.com/parkingvarsson/recombination_rate_variation. All SNP data used for population genomic analyses is already publicly available through ENA under accession number PRJNA297202 (https://www.ebi.ac.uk/ena/data/view/PRJNA297202). A filtered VCF files with final SNP data are available to download from zenodo.org under DOI number 10.5281/zenodo.3546316 (https://doi.org/10.5281/zenodo.3546316). Supplemental material available at figshare: https://doi.org/10.25387/g3.8481641.
Results
P. tremula linkage maps
14,598 unique markers in the female map and 13,997 unique markers in the male map were distributed across 3,861 and 3,710 scaffolds, respectively. Markers in both parental framework maps grouped into 19 linkage groups (LGs), corresponding to the haploid number of chromosomes in Populus (Table 1). Among the mapped scaffolds, 19 scaffolds contained markers that mapped to different positions within the same LG, but that were more than 20 cM apart (Supplemental Material, Figure S3) and 340 scaffolds contained markers that mapped to two or more LGs (Figures S2 and S4). These scaffolds were split according to criteria described in Supplementary methods. Additionally, there were 49 scaffolds split within gene models (Figure S5). Two ambiguous markers in scaffold Potra001073 were removed. After splitting 14,596 (12,900 binned) and 13,996 (12,382 binned) markers from 4,184 and 4,011 scaffolds remained. These markers spanned 4072.72 cM and 4053.68 cM for the female and male framework maps, respectively. The parental maps were used to produce a consensus genetic map consisting of 19,519 markers derived from 4,761 scaffolds spanning 4059.00 cM (Table 1). Linkage groups (LG) were assigned to the corresponding P. trichocarpa homologs through synteny assessment (Table 1, Figure S1).
Table 1. Summary of female male and consensus linkage maps for each chromosome.
| Chr | LG | Female | Male | Consensus | |||||
|---|---|---|---|---|---|---|---|---|---|
| Probe markers | Bin markers | Size (cM) | Probe markers | Bin markers | Size (cM) | Probe markers | Size (cM) | ||
| 1 | 6 | 1,784 | 1,573 | 498.0 | 1,737 | 1,542 | 499.3 | 2,417 | 498.8 |
| 2 | 3 | 1,054 | 924 | 266.3 | 1,028 | 904 | 268.3 | 1,407 | 266.3 |
| 3 | 8 | 826 | 736 | 229.9 | 790 | 695 | 235.3 | 1,117 | 235.2 |
| 4 | 1 | 813 | 728 | 217.2 | 835 | 736 | 263.0 | 1,128 | 220.5 |
| 5 | 7 | 965 | 842 | 284.5 | 947 | 836 | 270.6 | 1,293 | 271.9 |
| 6 | 14 | 1,241 | 1,108 | 311.1 | 1,116 | 993 | 294.3 | 1,602 | 296.4 |
| 7 | 18 | 572 | 497 | 161.9 | 501 | 450 | 155.1 | 765 | 155.5 |
| 8 | 12 | 895 | 781 | 227.4 | 824 | 726 | 211.0 | 117 | 215.5 |
| 9 | 2 | 697 | 617 | 171.5 | 640 | 578 | 171.6 | 879 | 172.2 |
| 10 | 4 | 1,026 | 901 | 279.0 | 1,015 | 879 | 270.8 | 1,388 | 273.7 |
| 11 | 16 | 515 | 460 | 181.4 | 541 | 480 | 180.7 | 724 | 182.0 |
| 12 | 17 | 515 | 452 | 142.4 | 486 | 429 | 140.7 | 678 | 143.3 |
| 13 | 11 | 586 | 530 | 173.7 | 608 | 531 | 176.4 | 822 | 178.7 |
| 14 | 5 | 733 | 655 | 194.3 | 702 | 609 | 182.0 | 983 | 194.3 |
| 15 | 10 | 553 | 505 | 145.8 | 593 | 532 | 157.9 | 777 | 159.2 |
| 16 | 19 | 383 | 334 | 145.8 | 220 | 195 | 125.8 | 430 | 145.4 |
| 17 | 15 | 488 | 433 | 155.5 | 447 | 394 | 148.9 | 647 | 149.4 |
| 18 | 13 | 591 | 502 | 156.3 | 592 | 531 | 166.2 | 792 | 165.5 |
| 19 | 9 | 361 | 322 | 130.6 | 375 | 342 | 135.8 | 500 | 135.8 |
| Total | 14,598 | 12,900 | 4072.7 | 13,997 | 12,382 | 4053.7 | 19,519 | 4059.0 | |
Physical assembly Potra v1.2
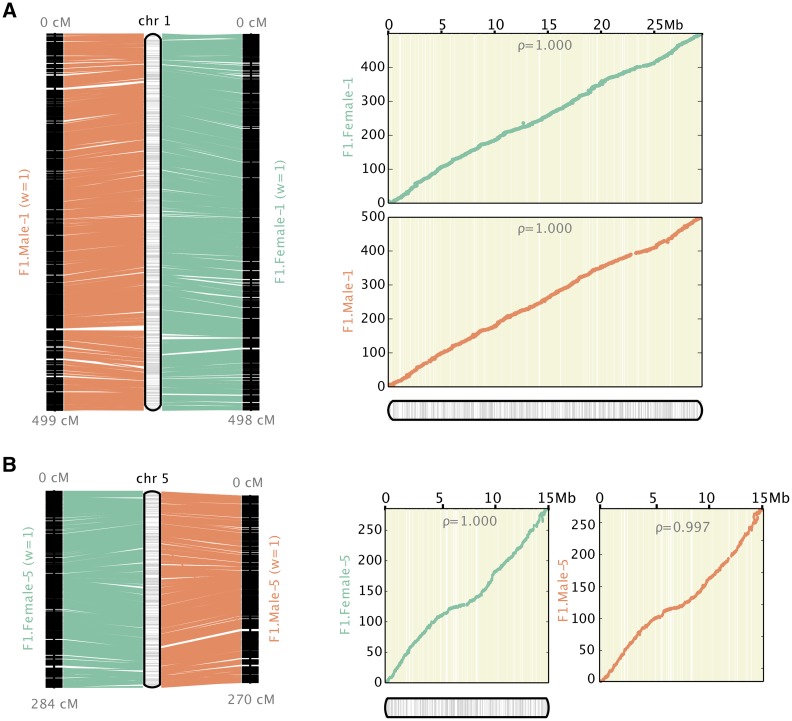
The parental framework maps were used to produce a physical map, Potra v1.2, of the P. tremula chromosomes that we used to estimate recombination maps (Figure 1, Figure S6). The scaffolds anchored from the parental framework maps spanned 210.7 Mbp and 205.1 Mbp for the female and male respectively. This corresponds to 54.6% and 53.1% of the 385.8 Mbp covered by the v1.1 assembly (Table S1). Of the 4,761 scaffolds with markers, 96.6% could be anchored in the assembly providing a total physical assembly consisting of 223.4 Mbp. This corresponds to 57.9% of the v1.1 P. tremula assembly (Lin et al. 2018) (Table 2). 75.7% of the physical map was both anchored and oriented, while the remaining 24.3% was only anchored. 199,967 of the v1.1 assembly scaffolds were not covered by the framework maps and thus could not be anchored to the physical map. There was a clear distinction between the scaffolds we could and could not anchor to the Potra v1.2 assembly. The median length for the 4214 scaffolds anchored in the map was 37 kbp and these scaffolds contain 26,808 predicted gene models. Conversely, the median length on unanchored scaffolds was only 0.3 kbp and they collectively contain only 8,501 predicted gene models (Table 2). After the initial assembly, gap estimation added 43 Mbp of gap sequences across the genome, increasing the estimated total size of the v1.2 assembly to 265 Mbp. This is approximately 55% of the 479 Mbp genome size estimated for P. tremula (Lin et al. 2018).
Figure 1.
Genetic maps and resulting physical map created by Allmaps for Chr1 and Chr5. The left panel shows the marker distribution (in cM) for the genetic maps and the anchored genomic region (in Mbp) for the physical map, while the right panel is showing the Marey maps, i.e., the correspondence between the physical (x-axis) and recombination-based (y-axis) position of markers. The female map is depicted in green and the male map is depicted in orange.
Table 2. Summary of physical assembly Potra v1.2.
| Anchored | Oriented | Unplaced | |
|---|---|---|---|
| Markers (unique) | 19,302 | 15,597 | 215 |
| Markers per Mbp | 86.4 | 92.2 | 1.3 |
| Gene elements | 26,808 (75.9%) | NA | 8501 (24.1%) |
| N50 Scaffolds (bp) | 2,071 | 1,589 | 238 |
| Scaffolds | 4,599 | 2,759 | 200,129 |
| Scaffolds with 1 marker | 1,151 | 0 | 133 |
| Scaffolds with 2 markers | 999 | 787 | 17 |
| Scaffolds with 3 markers | 620 | 384 | 7 |
| Scaffolds with >=4 markers | 1,829 | 1,588 | 5 |
| Total bases | 223,381,844 (57,9%) | 169,187,619 (43,9%) | 162,436,408 (42,1%) |
Recombination estimates
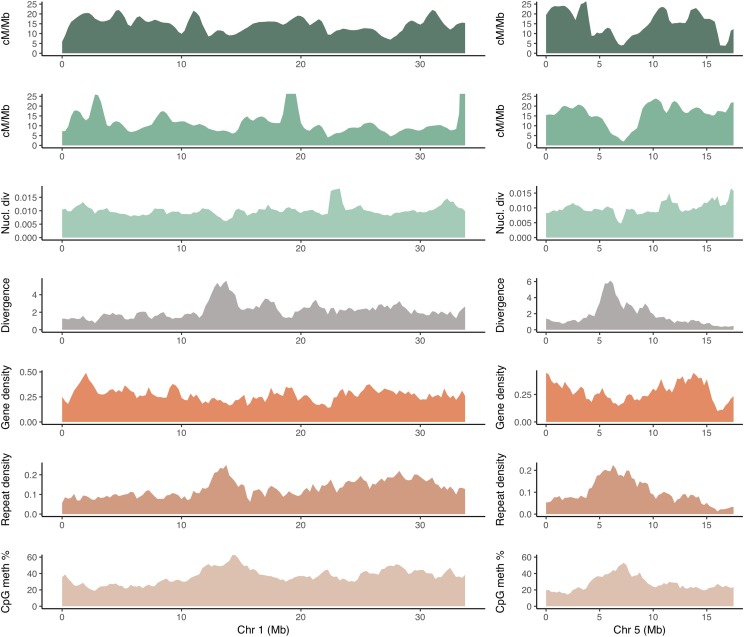
Recombination estimates were produced based on the consensus linkage map (LMB) and from LD data (LDB) derived from 25 randomly selected individuals from the SwAsp collection. The LMB recombination rate estimates varied between 1.605 cM/Mbp on chromosome 4 to 26.911 cM/Mbp on chromosome 11, while the LDB estimates varied between 1.969 cM/Mbp on chromosome 5 to 231.801 cM/Mbp on chromosome 1. The median estimated recombination rate in the LMB map was 16.0 cM/Mbp with a mean of 15.6 cM/Mbp, whereas the median recombination rate for the LDB map was 14.0 cM/Mbp with a mean of 16.1 cM/Mbp (Table S2, Figure S7). The majority of all recombination rate estimates (97%) for both maps fell in the range of 2 - 27 cM/Mb (Figure 2, Figure S8). There were 20 windows where the LDB estimates are 1.5-15-fold higher compared to the corresponding rates from the LMB estimates and 2-14-fold higher than the mean recombination rate estimate from the LDB map. 13 of these windows had recombination rates exceeding 27 cM/Mbp, while seven were within 2-27 cM/Mbp. Conversely, there were also 23 windows where the LDB estimates were 2-4 times lower than the corresponding LMB estimates (Figure 2, Figures S8 and S9).
Figure 2.
Recombination rates and genomic features calculated in 1 Mbp windows across chromosome 1 and 5 with a step size of 250kbp. A) Recombination rate estimated from the linkage map (cM/Mbp) B) Recombination rate estimated from sequence LD data (cM/Mbp) C) Nucleotide diversity (1/bp) D) Divergence (sites/Mbp) E) Gene density (percentage coding/Mbp) F) Repeat density (percentage repeats/Mbp) G) CpG methylation (percentage/Mbp).
Correlation of recombination rate estimates and genomic features
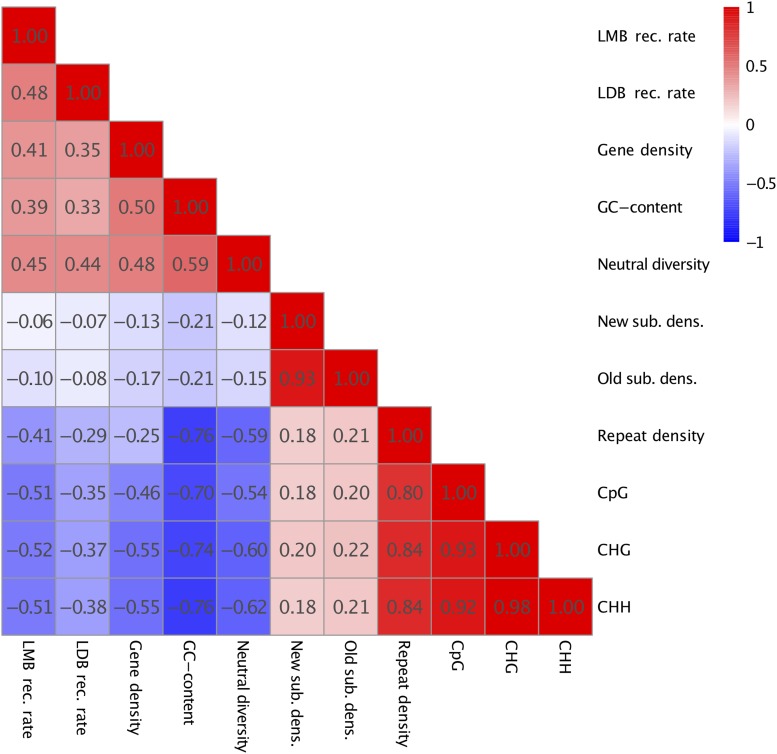
The Spearman’s rank correlation between recombination rate estimates for the LMB and LDB maps was 0.478 (Figure 3). This was the strongest positive correlation of all of the correlations calculated for both maps and strongest correlation overall for the LDB map. Correlations between the LMB and LDB recombination maps and neutral diversity were the second strongest positive correlations for both maps, 0.447 and 0.442 respectively. This correlation was the second strongest overall for LDB map. Correlation with neutral diversity was also the only variable where there was no notable decrease in the correlation coefficient from the LMB to the LDB recombination maps (Figure 3).
Figure 3.
Correlations between recombination rates and genomic features. All correlations are significant (P < 0.01) with the exception of those marked with * (P > 0.01).
For the LMB map we observed strong negative correlations with CHG methylation (-0.515), CHH methylation (-0.511) and CpG methylation (-0.505). For the LDB map the corresponding correlations were -0.379 (CHH), -0.371 (CHG) and -0.353 (CpG). Methylation levels were also strongly correlated with each other (0.918-0.984) and with repeat density (0.800-0.840). Repeat density was also moderately negatively correlated with recombination rate estimates from both the LMB (-0.408) and LDB maps (-0.291). Both recombination maps showed only weak correlations (-0.1<ρ<0.1) with either old or new neutral substitution densities (-0.06 - -0.1). Neutral substitution densities and neutral diversity showed only weak negative correlations (Figure 3). Overall, the LMB estimates displayed consistently stronger correlations with the different genomic features compared to the LDB estimates. This is in line with 5% of the total variation being explained by a multiple regression model for the LDB recombination estimates compared to 35% variation explained for the LMB estimates (Table 3).
Table 3. Multiple regression of recombination rate and various genomic features.
| Factor | Estimate | Std. Error | t | p | |
|---|---|---|---|---|---|
| Linkage map-based recombination rates | |||||
| Gene density | 0.225 | 0.037 | 6.12 | 1.3e-9 | |
| Repeat density | −0.111 | 0.069 | −1.60 | 0.111 | |
| GC content | −0.182 | 0.042 | −4.37 | 1.36e-5 | |
| GpG methylation | −0.360 | 0.050 | −7.18 | 1.25e-12 | |
| Nucleotide diversity | 0.140 | 0.034 | 4.07 | 5.0e-5 | |
| Substitution density | −0.038 | 0.056 | −0.685 | 0.493 | |
| R2 = 0.345 | |||||
| LD-based recombination rates | |||||
| Gene density | −0.009 | 0.031 | −0.11 | 0.836 | |
| Repeat density | 0.218 | 0.083 | 2.63 | 8.6e-3 | |
| GC content | 0.111 | 0.050 | 2.22 | 0.027 | |
| GpG methylation | −0.021 | 0.060 | −0.36 | 0.717 | |
| Nucleotide diversity | 0.176 | 0.041 | 4.26 | 2.2e-5 | |
| Substitution density | −0.163 | 0.067 | −2.47 | 0.015 | |
| R2 = 0.054 |
Discussion
P. tremula fine-scale genetic maps and physical assembly Potra v1.2
The genetic maps presented here are the most marker-dense maps produced for P. tremula to date. Our female map is only 20 cM larger than the male map, despite having 518 more informative markers (Table 1) and most chromosomes have size differences of less than 10 cM between sexes (Table 1, Figure S6). However, in cases where we observed differences between the maps for the two sexes exceeding 10 cM, the male map is shorter in all but one case. These results, together with the overall shorter linkage map for the male, could suggest overall lower recombination rates in males, in line with what has been observed in many other highly outcrossing plant species (Lenormand and Dutheil 2005). The high marker density in our framework genetic maps allowed us to anchor 57.9% of the P. tremula v1.1 genome assembly on to the expected 19 chromosomes, providing us with the first chromosome-scale assembly for P. tremula (Table 2).
The map length in the section Populus, to which P. tremula belongs (Wang et al. 2014), has previously been estimated to be 1,600-3,500 cM (e.g., Zhang et al. 2004, Paolucci et al. 2010, Zhigunov et al. 2017). The most relevant comparison for our purposes is the recently produced linkage maps in P. tremula by Zhigunov et al. (2017). Their map contains 2000 informative markers with an average marker distance of 1.5 cM that were observed in 122 progenies, resulting in a total map length of 3000-3100 cM. Our framework maps are much denser with ca. 12000-13000 informative markers (Table 1) and with an average distance of ∼0.3 cM between markers. In addition, our map is based on a mapping population consisting of 764 progenies and we are hence able to achieve a far greater resolution in our maps. However, larger data sets, both with respect to the number of markers and the number of progenies used, increase the risk of genotyping errors. Genotyping errors will ultimately lead to an inflation of map sizes as errors can be interpreted as recombination events during map creation and this could help explain why our maps are roughly 1000 cM longer than those reported by Zhigunov et al. (2017), given that we use 5-7 -fold more markers and a mapping population that is six times larger.
On the other hand, our framework genetic maps are similar in size to the ca. 4200 cM and 3800 cM maps presented by Tong et al. (2016) for the more distantly related species Populus deltoides and Populus simonii, respectively. The large size of these maps led Tong et al. (2016) to suggest that their maps were suffering from inflation due to the difficulty of properly ordering a large number of markers within a linkage group. While we likely also suffer from such size inflation, these issues appear to be less severe in our P. tremula parental maps, which contain between 8-14 times the number of markers used in the P. deltoides (1601) and P. simonii (940) maps and yet yield linkage maps of similar size. One explanation for this is our considerably larger mapping population compared to the P. deltoides and P. simonii maps (299 progenies). A greater number of segregating progenies helps mitigate the problems of ordering a larger number of markers by increasing resolution of recombination detection.
Recombination rate estimates
Recombination rates estimated from both the consensus linkage map and from polymorphism data showed substantial variation across all chromosomes on Mbp scales (Figure 2). For the consensus genetic map-based estimates and LD-based estimates, the majority of our observations fell in the range 0-27 cM/Mbp (Figure 2, Figure S8) which is similar to what has been observed in other plants such as Arabidopsis thaliana (Giraut et al. 2011), Populus trichocarpa (Slavov et al. 2012) and Eucalyptus grandis (Silva-Junior and Grattapaglia 2015), where recombination rates across chromosomes mostly fall within 0-25 cM/Mbp.
We observed a small number of genomic windows where the LDB recombination rates were either 1.5-15-fold higher or lower than the corresponding estimates based on the consensus genetic map (Figure 2, Figure S8). While we do not know for certain what causes these large differences in recombination rates, a possible explanation could be that such windows harbor recombination hotspots or coldspots that the comparatively coarse linkage map fails to detect. Recombination hotspots, with local recombination rates 10 to 100-fold higher than the genome-wide average, have been observed in a number of species, including Drosophila melanogaster (Chan et al. 2012), Arabidopsis thaliana (Kim et al. 2007), Zea mays (He and Dooner 2009), Oryza sativa (Si et al. 2015) and Eucalyptus grandis (Silva-Junior and Grattapaglia 2015). Similarly, coldspots have been identified in Zea mays (He and Dooner 2009) and Oryza sativa (Si et al. 2015) among others. Hotspots or coldspots for recombination are, however, often quite restricted in size (Choi and Henderson 2015), spanning only a few kbp, and the relatively coarse recombination maps produced here are consequently not suitable for accurate detection of such regions. It is also worth noting that in species with lower levels of diversity, the resolution of LD based estimates would be lower and the power to detect hot- and coldspots for LDB and LMB estimates may not differ much for these species.
The average recombination rate in P. tremula is 2-27 times higher than those found in a number of, mostly domesticated, plant and animal species (reviewed in Henderson (2012) and Tiley and Burleigh (2015)), suggesting that P. tremula exhibits recombination rates that are among the highest recorded in the animal and plant kingdoms. Of the species covered in these reviews, P. trichocarpa (Slavov et al. 2012) makes for the most interesting comparison since it is one of the few undomesticated species listed, is closely related to P. tremula and has previously been compared with P. tremula (Wang et al. 2016). Despite the close relationship, the average recombination rate in P. trichocarpa (Slavov et al. 2012) is less than a third of what we estimated for P. tremula. Similar observations were previously made by Wang et al. (2016) who found that population-based recombination rates in P. trichocarpa were on average only a quarter of the corresponding values in P. tremula. Wang et al. (2016) argued that the differences they observed in recombination rates between P. tremula and P. trichocarpa could at least partly stem from differences in the effective population size (Ne) of the two species (Wang et al. 2016). In light of this, it would be interesting to perform further comparisons of recombination rates between P. tremula and other Populus species that have wide distribution ranges and large Ne, such as P. deltoides (Tong et al. 2016) or P. tremuloides (Wang et al. 2016).
Correlations between recombination rate and genomic features
Recombination rate estimates from the consensus linkage map and from polymorphism data showed a moderately strong positive correlation (>0.4) (Figure 3). A similar correlation between linkage map and LD-based estimates of recombination was also observed in Mus musculus by Booker et al. (2017), suggesting that LDB recombination rate estimates are reliable substitutes for genetic map-based recombination rate estimates. A recent study in Gasterosteus aculeatus (Shanfelter et al. 2019), however, found even stronger correlations between the two estimates (∼0.8).
We observed a strong positive correlation between recombination rate and gene density (0.45 and 0.41 respectively) (Figure 3). This is in line with earlier observations in plants (Tiley and Burleigh 2015, Stapley et al. 2017) and implies that recombination may be linked to gene-dense regions through a higher recruitment of the recombination machinery to euchromatic genome regions. Preferential recruitment of recombination to euchromatic genome regions has also been put forward as an explanation for why recombination rates across plants generally show stronger correlations with gene density compared to genome size (Henderson 2012, Tiley and Burleigh 2015). Studies in plants like Arabidopsis thaliana and Oryza sativa have shown that while crossover events are enriched in genic regions, they mostly occur in promoters a few hundred bps upstream of the transcription start site or downstream of the transcription termination site (Choi et al. 2013, Marand et al. 2019).
We observed negative correlations between local recombination rates and both repeat density and methylation (Figure 3), in line with earlier results that highlighted the role of chromatin features in establishing crossover locations in plants (Choi et al. 2013, Marand et al. 2019). For instance, Choi et al. (2013) showed that methylation is lower at observed sites of crossovers and Rodgers-Melnick et al. (2015) showed that cross-over density in Zea mays is negatively correlated with repeats and CpG methylation. All methylation contexts were highly correlated in our data and also strongly correlated with repeat density (≥0.8, Figure 3), in line with the observation that most repetitive elements in plant genomes are strongly methylated (Saze and Kakutani 2011).
Compared to earlier results from P. tremula, we observed a weaker correlation between recombination rates and gene density (Wang et al. 2016). One possible reason for this is likely to be the reference genome used. Wang et al. (2016) based their analyses on the P. trichocarpa reference genome whereas our analyses were based on a de novo assembly for P. tremula. The P. trichocarpa assembly, while more contiguous than our current P. tremula assembly, is less ideal for these types of analyses since divergence between the two species leads to substantially reduced rates of read mapping primarily in intergenic regions (Lin et al. 2018). Our current assembly, while only representing 55% of the expected genome size of P. tremula, likely offers a more unbiased set of genomic regions where we are able to call genetic variants. In contrast, the data derived from using the P. trichocarpa reference genome likely suffers from under-representations of repeat-rich regions and other intergenic regions (Wang et al. 2016).
GC-content was positively correlated with both our recombination rate estimates, similar to what has been observed in humans (Homo sapiens) (e.g., Fullerton et al. 2001) and Arabidopsis thaliana (Kim et al. 2007) among others. However, when GC-content was included in a multiple regression model with other genomic features, the direct effect of GC content was actually negative for the LMB recombination rate (Table 3). GC-content is strongly correlated with gene density (0.50) in P. tremula, and gene density is in turn also strongly positively correlated with recombination (Figure 3). The strand separation needed in the strand invasion of meiotic recombination is harder to achieve in areas with high GC-content due to higher annealing energy and can explain why GC-content has a direct negative effect on recombination rates when effects of gene density are accounted for (Table 3, e.g., Mandel and Marmur 1968).
Effects of linked selection on patterns of nucleotide diversity in P. tremula
Both of our recombination rate estimates were strongly correlated with nucleotide diversity at putatively neutral sites (Figure 3). A positive correlation between local recombination rate and nucleotide polymorphism is usually interpreted as a signature of ubiquitous natural selection acting either through positive (hitchhiking) or negative (background) selection (Begun and Aquadro 1992). Alternatively, such a correlation could also arise if recombination itself is mutagenic (Begun and Aquadro 1992). However, if recombination is mutagenic one also expects to see a correlation between recombination and sequence divergence at neutral sites (Begun and Aquadro 1992). Our data show little evidence supporting the idea that recombination has a direct mutagenic effect as we observed only a weak and negative correlation between local recombination rates and substitutions at putatively neutral sites (Figure 3). In light of this, and in line with earlier results, we observed that linked selection has pervasive effects on neutral diversity across the P. tremula genome (Ingvarsson 2010, Wang et al. 2016).
Conclusions
Our high-density Populus tremula genetic maps and the new chromosome-scale genome assembly we present here provide a valuable resource not only for P. tremula, but also for comparative genomics studies within the entire genus Populus. Estimates of recombination rates derived from two different approaches were in broad agreement and showed similar correlations various genomic features. However, our results suggest that LD-based estimates of recombination might be especially useful for identifying fine scale recombination variation and for identifying features such as recombination hot- or cold-spots as it is based on information derived from population-scale variation. We have also verified and extended the observation that linked selection is an important force shaping genome-wide variation in P. tremula by showing that the positive correlation between local recombination rates and nucleotide diversity and neutral sites is robust even when factoring in the effects of other genomic features. Although a positive correlation between recombination and diversity is a hallmark signature of linked selection, the pattern can be established by either positive or negative selection. We have earlier documented evidence for both a reduction in levels of standing variation due to recurrent hitchhiking (Ingvarsson 2010) and a reduction in the efficacy of purifying selection at eliminating weakly deleterious variants in regions of low recombination (Wang et al. 2016). More work is thus needed to assess the relative importance of positive and negative selection in shaping genome-wide variation in P. tremula and having access to the resources developed here will facilitate these studies.
Acknowledgments
NRS, PKI and SJ planned and designed the research. RPA, CB, BS, KR, NRS and PKI performed experiments, conducted fieldwork and analyzed data. RPA, CB and PKI wrote the manuscript.
The research has been funded through research grants from the Swedish Research Council (PI), the Knut and Alice Wallenberg Foundation (PI, BS) and ‘Trees and Crops for the Future’ (NRS, PKI and SJ). The authors acknowledge support from the National Genomics Infrastructure in Stockholm funded by Science for Life Laboratory, the Knut and Alice Wallenberg Foundation and the Swedish Research Council, and SNIC/Uppsala Multidisciplinary Center for Advanced Computational Science for assistance with massively parallel sequencing and access to the UPPMAX computational infrastructure through projects b2011141 and SNIC 2017/1-499.
Footnotes
Supplemental material available at figshare: https://doi.org/10.25387/g3.8481641.
Communicating editor: M. Hufford
Literature Cited
- Van der Auwera, G. A., M. O. Carneiro, C. Hartl, R. Poplin, G. Del Angel et al., 2013 From FastQ data to high confidence variant calls: the Genome Analysis Toolkit best practices pipeline. Curr. Prot. Bioinf. 43: 11.10.1–33. 10.1002/0471250953.bi1110s43 [DOI] [PMC free article] [PubMed]
- Barton N. H., 1995. Linkage and the limits to natural selection. Genetics 140: 821–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begun D. J., and Aquadro C. F., 1992. Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature 356: 519–520. 10.1038/356519a0 [DOI] [PubMed] [Google Scholar]
- Booker T. R., Ness R. W., and Keightley P. D., 2017. The recombination landscape in wild house mice inferred using population genomic data. Genetics 207: 297–309. 10.1534/genetics.117.300063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan A. H., Jenkins P. A., and Song Y. S., 2012. Genome-wide fine-scale recombination rate variation in Drosophila melanogaster. PLoS Genet. 8: e1003090 10.1371/journal.pgen.1003090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi K., and Henderson I. R., 2015. Meiotic recombination hotspots - a comparative view. Plant J. 83: 52–61. 10.1111/tpj.12870 [DOI] [PubMed] [Google Scholar]
- Choi K., Zhao X., Kelly K. A., Venn O., Higgins J. D. et al. , 2013. Arabidopsis meiotic crossover hot spots overlap with H2A.Z nucleosomes at gene promoters. Nat. Genet. 45: 1327–1336. 10.1038/ng.2766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo M. A. E., Banks R., Poplin K. V., Garimella J. R., Maguire J. R. et al. , 2011. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet. 43: 491–498. 10.1038/ng.806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farmer R. E., Jr, 1996. The genecology of Populus. pp. 33–55 in: Biology of Populus and its implications for management and conservation, edited by Stettler R., Bradshaw T., Heilman P., Hinckley T., NRC Research Press, Ottawa, Canada. [Google Scholar]
- Felsenstein J., 1974. The evolutionary advantage of recombination. Genetics 78: 737–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fracheboud Y., Luquez V., Björkén L., Sjödin A., Tuominen H. et al. , 2009. The control of autumn senescence in European aspen. Plant Physiol. 149: 1982–1991. 10.1104/pp.108.133249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fullerton S. M., Carvalho A. B., and Clark A. G., 2001. Local rates of recombination are positively correlated with GC content in the human genome. Mol. Biol. Evol. 18: 1139–1142. 10.1093/oxfordjournals.molbev.a003886 [DOI] [PubMed] [Google Scholar]
- Giraut L., Falque M., Drouaud J., Pereira L., Martin O. C. et al. , 2011. Genome-wide crossover distribution in Arabidopsis thaliana meiosis reveals sex-specific patterns along chromosomes. PLoS Genet. 7: e1002354 10.1371/journal.pgen.1002354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grattapaglia D., and Sederoff R., 1994. Genetic linkage maps of Eucalyptus grandis and Eucalyptus urophylla using a pseudo-testcross: mapping strategy and RAPD markers. Genetics 137: 1121–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He L., and Dooner H. K., 2009. Haplotype structure strongly affects recombination in a maize genetic interval polymorphic for Helitron and retrotransposon insertions. Proc. Natl. Acad. Sci. USA 106: 8410–8416. 10.1073/pnas.0902972106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haenel Q., Laurentino T. G., Roesti M., Berner D., 2018. Meta-analysis of chromosome-scale crossover rate variation in eukaryotes and its significance to evolutionary genomics. Mol. Ecol. 27: 2477–2497. [DOI] [PubMed] [Google Scholar]
- Henderson I. R., 2012. Control of meiotic recombination frequency in plant genomes. Curr. Opin. Plant Biol. 15: 556–561. 10.1016/j.pbi.2012.09.002 [DOI] [PubMed] [Google Scholar]
- Ingvarsson P. K., 2010. Natural selection on synonymous and nonsynonymous mutations shapes patterns of polymorphism in Populus tremula. Mol. Biol. Evol. 27: 650–660. 10.1093/molbev/msp255 [DOI] [PubMed] [Google Scholar]
- Jansson S., and Douglas C. J., 2007. Populus: a model system for plant biology. Annu. Rev. Plant Biol. 58: 435–458. 10.1146/annurev.arplant.58.032806.103956 [DOI] [PubMed] [Google Scholar]
- Kim S., Plagnol V., Hu T. T., Toomajian C., Clark R. M. et al. , 2007. Recombination and linkage disequilibrium in Arabidopsis thaliana. Nat. Genet. 39: 1151–1155. 10.1038/ng2115 [DOI] [PubMed] [Google Scholar]
- Kouki J., Arnold K., and Martikainen P., 2004. Long-term persistence of aspen – a key host for many threatened species – is endangered in old-growth conservation areas in Finland. J. Nat. Conserv. 12: 41–52. 10.1016/j.jnc.2003.08.002 [DOI] [Google Scholar]
- Krueger F., and Andrews S. R., 2011. Bismark: a flexible aligner and methylation caller for Bisulfite-Seq applications. Bioinformatics 27: 1571–1572. 10.1093/bioinformatics/btr167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulathinal R. J., Bennett S. M., Fitzpatrick C. L., and Noor M. A. F., 2008. Fine-scale mapping of recombination rate in Drosophila refines its correlation to diversity and divergence. Proc. Natl. Acad. Sci. USA 105: 10051–10056. 10.1073/pnas.0801848105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenormand T., and Dutheil J., 2005. Recombination difference between sexes: a role for haploid selection. PLoS Biol. 3: e63 10.1371/journal.pbio.0030063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., and Durbin R., 2009. Fast and accurate short read alignment with burrows-wheeler transform. Bioinformatics 25: 1754–1760. 10.1093/bioinformatics/btp324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y.-C., Wang J., Delhomme N., Schiffthaler B., Sundström G. et al. , 2018. Functional and evolutionary genomic inferences in Populus through genome and population sequencing of American and European aspen. Proc. Natl. Acad. Sci. USA 115: E10970–E10978. 10.1073/pnas.1801437115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luquez V., Hall D., Albrectsen B. R., Karlsson J., Ingvarsson P. K. et al. , 2008. Natural phenological variation in aspen (Populus tremula): the SwAsp collection. Tree Genet. Genomes 4: 279–292. 10.1007/s11295-007-0108-y [DOI] [Google Scholar]
- Mandel M., Marmur J., 1968. [109] Use of ultraviolet absorbance-temperature profile for determining the quanine plus cytosine content of DNA. Methods Enzymol. 12: 195–206. 10.1016/0076-6879(67)12133-2 [DOI] [Google Scholar]
- Ma T., Wang J., Zhou G., Yue Z., Hu Q. et al. , 2013. Genomic insights into salt adaptation in a desert poplar. Nat. Commun. 4: 2797 10.1038/ncomms3797 [DOI] [PubMed] [Google Scholar]
- Marand A. P., Zhao H., Zhang W., Zeng Z., Fang C. et al. , 2019. Historical meiotic crossover hotspots fueled patterns of evolutionary divergence in rice. Plant Cell 31: 645–662. 10.1105/tpc.18.00750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKenna A., Hanna M., Banks E., Sivachenko A., Cibulskis K. et al. , 2010. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 20: 1297–1303. 10.1101/gr.107524.110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. A. T., Myers S. R., Hunt S., Deloukas P., Bentley D. R., et al. 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]
- Nachman M. W., 2002. Variation in recombination rate across the genome: evidence and implications. Curr. Opin. Genet. Dev. 12: 657–663. 10.1016/S0959-437X(02)00358-1 [DOI] [PubMed] [Google Scholar]
- Nordborg M., and Weigel D., 2008. Next-generation genetics in plants. Nature 456: 720–723. 10.1038/nature07629 [DOI] [PubMed] [Google Scholar]
- Paolucci I., Gaudet M., Jorge V., Beritognolo I., Terzoli S. et al. , 2010. Genetic linkage maps of Populus alba L. and comparative mapping analysis of sex determination across Populus species. Tree Genet. Genomes 6: 863–875. 10.1007/s11295-010-0297-7 [DOI] [Google Scholar]
- Quinlan, A. R. 2014 BEDTools: The Swiss‐army tool for genome feature analysis. Curr. Prot. Bioinf. 47: 11.12.1–11.12.34. [DOI] [PMC free article] [PubMed]
- R Core Team, 2018 R: A language and environment for statistical computing. R Foundation for statistical Computing, Vienna, Austria. https://www.R-project.org/. [Google Scholar]
- Rezvoy C., Charif D., Guéquen L., and Marais G. A. B., 2007. MareyMap: an R-based tool with graphical inter-face for estimation recombination rates. Bioinformatics 23: 2188–2189. 10.1093/bioinformatics/btm315 [DOI] [PubMed] [Google Scholar]
- Rodgers-Melnick E., Bradbury P. J., Elshire R. J., Glaubitz J. C., Acharya C. B. et al. , 2015. Recombination in diverse maize is stable, predictable, and associated with genetic load. Proc. Natl. Acad. Sci. USA 112: 3823–3828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saze H., and Kakutani T., 2011. Differentiation of epigenetic modifications between transposons and genes. Curr. Opin. Plant Biol. 14: 81–87. 10.1016/j.pbi.2010.08.017 [DOI] [PubMed] [Google Scholar]
- Schiffthaler B., Bernhardsson C., Ingvarsson P. K., and Street N. R., 2017. BatchMap: A parallel implementation of the OneMap R package for fast computation of F1 linkage maps in outcrossing species. PLoS One 12: e0189256 10.1371/journal.pone.0189256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanfelter A. F., Archambeault S. L., and White M. A., 2019. Divergent Fine-Scale Recombination Landscapes between a Freshwater and Marine Population of Threespine Stickleback Fish. Genom Evol. Biol. 11: 1573–1585. 10.1093/gbe/evz090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva-Junior O. B., and Grattapaglia D., 2015. Genome-wide patterns of recombination, linkage disequilibrium and nucleotide diversity from pooled resequencing and single nucleotide polymorphism genotyping unlock the evolutionary history of Eucalyptus grandis. New Phytol. 208: 830–845. 10.1111/nph.13505 [DOI] [PubMed] [Google Scholar]
- Si W., Yuan Y., Huang J., Zhang X., Zhang Y. et al. , 2015. Widely distributed hot and cold spots in meiotic recombination as shown by the sequencing of rice F2 plants. New Phytol. 206: 1491–1502. 10.1111/nph.13319 [DOI] [PubMed] [Google Scholar]
- Slavov G. T., Difazio S. P., Schackwitz M. J., Muchero W., Rodgers-Melnick E. et al. , 2012. Genome resequencing reveals multiscale geographic structure and extensive linkage disequilibrium in the forest tree Populus trichocarpa. New Phytol. 196: 713–725. 10.1111/j.1469-8137.2012.04258.x [DOI] [PubMed] [Google Scholar]
- Stapley J., Feulner P. G. D., Johnston S. E., Santure A. W., and Smadja C. M., 2017. Variation in recombination frequency and distribution across eukaryotes: patterns and processes. Philos. Trans. R. Soc. Lond., B 372 10.1098/rstb.2016.0455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H., Zhang X., Miao C., Zhang J., Ming R. et al. , 2015. ALLMAPS: robust scaffold ordering based on multiple maps. Genome Biol. 16: 3 10.1186/s13059-014-0573-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor G., 2002. Populus: Arabidopsis for forestry. Do we need a model tree? Ann. Bot. 90: 681–689. 10.1093/aob/mcf255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiley G. P., and Burleigh J. G., 2015. The relationship of recombination rate, genome structure, and patterns of molecular evolution across angiosperms. BMC Evol. Biol. 15: 194 10.1186/s12862-015-0473-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong C., Li H., Wang Y., Li X., Ou J. et al. , 2016. Construction of high-density linkage maps of Populus deltoides × P. simonii using restriction-site associated DNA sequencing. PLoS One 11: e0150692 10.1371/journal.pone.0150692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuskan G. A., DiFazio S., Jansson S., Bohlmann J., Grigoriev I. et al. , 2006. The genome of black cottonwood, Populus trichocarpa (Torr. & Gray). Science 313: 1596–1604. 10.1126/science.1128691 [DOI] [PubMed] [Google Scholar]
- Wang J., Ding J., Tan B., Robinson K. M., Michelson I. H. et al. , 2018. A major locus controls local adaptation and adaptive life history variation in a perennial plant. Genome Biol. 19: 72 10.1186/s13059-018-1444-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Du S., Dayanandan S., Wang D., Zeng Y., and Zhang J., 2014. Phylogeny reconstruction and hybrid analysis of Populus (Salicaceae) based on nucleotide sequences of multiple single-copy nuclear genes and plastid fragments. PLoS One 9: e103645 10.1371/journal.pone.0103645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Street N. R., Scofield D. G., and Ingvarsson P. K., 2016. Natural selection and recombination rate variation shape nucleotide polymorphism across the genomes of three related Populus species. Genetics 202: 1185–1200. 10.1534/genetics.115.183152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S., 1931. Evolution in mendelian populations. Genetics 16: 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D., Zhang Z., Yang K., and Li B., 2004. Genetic mapping in (Populus tomentosa x Populus bolleana) and P. tomentosa Carr. using AFLP markers. Theor. Appl. Genet. 108: 657–662. 10.1007/s00122-003-1478-7 [DOI] [PubMed] [Google Scholar]
- Zhigunov A. V., Ulianich P. S., Lebedeva M. V., Chang P. I., Nuzhdin S. V. et al. , 2017. Development of F1 hybrid population and the high-density linkage map for European aspen (Populus tremula L.) using RADseq technology. BMC Plant Biol. 17: 180 10.1186/s12870-017-1127-y [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The raw sequencing reads used for the construction of the genetic map and raw bisulfate sequencing reads are available from ENA under study number PRJEB34662 (https://www.ebi.ac.uk/ena/data/view/PRJEB34662). BatchMap input files for the female and male genetic maps, the two component maps and the consensus map files as well as all processed files of the bisulfate sequencing data are available from zenodo.org under DOI number 10.5281/zenodo.3257544 (https://doi.org/10.5281/zenodo.3257544). Additional scripts and files used for the analyses are available at https://github.com/parkingvarsson/recombination_rate_variation. All SNP data used for population genomic analyses is already publicly available through ENA under accession number PRJNA297202 (https://www.ebi.ac.uk/ena/data/view/PRJNA297202). A filtered VCF files with final SNP data are available to download from zenodo.org under DOI number 10.5281/zenodo.3546316 (https://doi.org/10.5281/zenodo.3546316). Supplemental material available at figshare: https://doi.org/10.25387/g3.8481641.