Cardiorespiratory motion-tracking via self-refocused rosette navigators

Abstract

Purpose:

To develop a flexible method for tracking respiratory and cardiac motions throughout MR and PET-MR body examinations that requires no additional hardware and minimal sequence modification.

Methods:

The incorporation of a contrast-neutral rosette navigator module following the RF excitation allows for robust cardiorespiratory motion tracking with minimal impact on the host sequence. Spatial encoding gradients are applied to the FID signal and the desired motion signals are extracted with a blind source separation technique. This approach is validated with an anthropomorphic, PET-MR-compatible motion phantom as well as in 13 human subjects.

Results:

Both respiratory and cardiac motions were reliably extracted from the proposed rosette navigator in phantom and patient studies. In the phantom study, the MR-derived motion signals were additionally validated against the ground truth measurement of diaphragm displacement and left ventricle model triggering pulse.

Conclusion:

The proposed method yields accurate respiratory and cardiac motion-state tracking, requiring only a short (1.76 ms) additional navigator module, which is self-refocusing and imposes minimal constraints on sequence design.

1 |. INTRODUCTION

Many strategies have been proposed for tracking respiratory and cardiac (aka cardiorespiratory) motions during MRI; however a robust and general solution that is clinically feasible is still elusive. Cardiorespiratory motion tracking is important in a variety of clinical contexts. For example, free-breathing abdominal imaging has emerged as an attractive alternative to breath-hold procedures, due to the higher scan efficiency and improved patient comfort.^6,12 When imaging the heart, both respiratory and cardiac motions need to be managed. Therefore, many free-breathing imaging protocols require tracking either respiratory and cardiac motion¹² or employ some combination of cardiac triggering/gating and breath-holds.¹⁰ Another emerging application of cardiorespiratory motion tracking is for motion correction of positron emission tomography (PET) data during a simultaneous PET-MR exam. Following the recent introduction of integrated PET-MR,⁸ several works have demonstrated that motion information obtained from MR data can be used to compensate for patient motion during the PET image reconstruction.^4,11,16

One approach to motion tracking is to use external sensors, such as the respiratory bellows and electrocardiogram (ECG). However, this increases the patient setup time and does not always yield reliable results.²⁵ In particular, the bellows require careful positioning, and optimal placement depends on whether the patient is a chest breather or abdominal breather.²³ The signal amplitude may not provide an accurate surrogate for diaphragm position, particularly when the diaphragm position drifts throughout the scan. Similarly, ECG-based cardiac motion tracking also faces several practical challenges. The voltage signal that is measured by ECG may not correlate well with actual heart motion, especially for patients with arrhythmia. Additionally, at high fields, magnetohydrodynamic (MHD) effects distort the ECG signal, which further complicates tracking.¹⁵

A potential alternative to external tracking devices is the use of MR navigators, which derive motion information directly from the MR signal.¹⁷ Besides eliminating the need to setup additional devices, navigators also provide a more direct measurement of internal organ motion and hence may yield more reliable motion tracking signals. Pencil beam navigators have been used for tracking diaphragm motion²⁰ but the additional selective RF pulse can decrease scan efficiency and alter the imaging signal. It has been shown that a variety of pulse sequences are “self-navigating,” such as radial sequences which repeatedly sample a central point (or line) in k-space. In this case, motion information is obtained directly from the same data collected for image formation, so the aforementioned limitations of navigator echoes are avoided.

For example, in⁵ the prewinder gradients for the phase encodes are slightly modified to obtain a so-called “butterfly navigator” every repetition. This is an interesting way to obtain motion-tracking information with minimal overhead for cartesian sequences; however, since the butterfly navigator is directly linked to the imaging trajectory, it requires non-trivial, trajectory-dependent modifications to the original sequence. Further, it is not clear how to extend this technique to non-cartesian trajectories or echo-planar acquisitions. Henningsson et al.¹⁴ show that for a balanced SSFP sequence, one can add phase-encoding to the startup profiles to obtain image-based navigators (iNAV), but similarly to,⁵ this technique does not generalize easily to different sequences. It also appears that the timing resolution of these iNAVs is insufficient for cardiac motion tracking since they rely on ECG-gating. In¹² and¹⁷ both respiratory and cardiac motion tracking information is obtained from self-gating sequences. In both cases, some central portion of k-space is repeatedly sampled at a regular interval as a byproduct of the trajectory design. The temporal fluctuations in this k-space data are then used to infer respiratory and cardiac motions. The primary limitation with all of the above mentioned techniques is that the navigation information is tightly linked to the imaging sequence, so they do not allow for continuous motion-tracking across arbitrary MRI sequences.

Brau et al. propose a solution³ which essentially converts an arbitrary imaging sequence into a self-navigated one by inserting a short (20 μs) readout immediately after slice selection and gradient refocusing. Respiratory information is obtained directly from this free induction decay (FID) signal, and only trivial sequence modifications are required; image contrast and scan efficiency are virtually unchanged. Similar FID navigators, utilizing information from multiple coil channels, have also been used to track head motion.⁹ In this work, we expand on this concept by adding a small amount of spatial encoding during the readout of the FID and introduce an unsupervised learning method for automatically extracting the respiratory and cardiac motion surrogate signals from the raw navigator data. In particular, we utilize a self-refocused rosette trajectory, which effectively encodes cardiorespiratory motion without impacting image contrast. This approach mostly retains the versatility of a pure FID navigator while improving the robustness of cardiac motion extraction. Therefore, it has the potential to be a robust, general solution for simultaneously tracking respiratory and cardiac motion during arbitrary pulse sequences without the need for external tracking devices. This could be particularly useful for motion correction during simultaneous PET-MR exams. In particular, this manuscript is a significant expansion upon our previous work in Rigie et al.²⁴

In the first part of this manuscript, we validate the proposed navigation method and automatic motion parameter extraction with a dynamic thorax phantom² that provides realistic and controllable cardiorespiratory motion. Subsequently, the technique is applied to several human patient scans in order to demonstrate robustness and clinical feasibility.

2 |. METHODS

All scans were performed on a 3T Siemens Biograph mMR (Siemens Healthcare, Erlangen, Germany) using a T1-weighted, golden angle radial stack-of-stars in-house prototype sequence (TR/TE = 12.7/5.3ms, BW = 488Hz/Pixel, 256 × 256 × 80 reconstructed 3D volume, 1.36 × 1.36mm in-plane resolution, 4.5 mm slice thickness, Figure 1), modified to incorporate a rosette¹⁹ navigator readout. Respiratory and cardiac motion surrogates were extracted from the multi-coil navigator data via the second-order blind identification (SOBI) algorithm,¹ which was subsequently used to sort k-space data into motion states

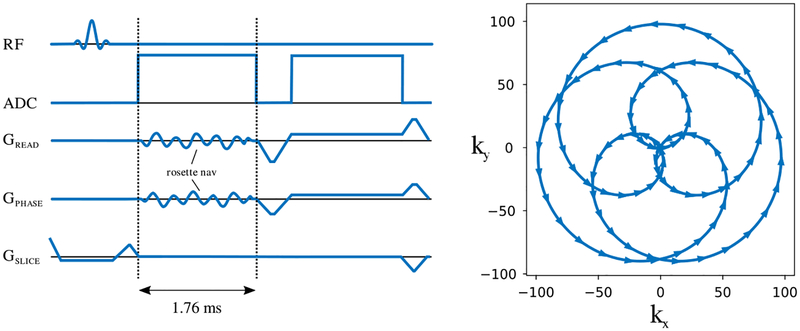
FIGURE 1.

Rosette navigator. The rosette navigator is placed directly after the RF excitation and prior to the imaging readout. Its short duration (1.76 ms) and self-refocusing trajectory ensure minimal impact on image contrast

2.1 |. Self-refocused rosette navigator

The proposed navigator is placed directly after the RF pulse, prior to the frequency encoding gradient and has a readout length of 1.76 milliseconds. Because of its short duration and self-refocusing trajectory, it can be incorporated into a variety of clinical sequences without impacting image contrast and while imposing minimal constraints on the sequence design. The primary constraint is that the host sequence should have an echo time TE >1.76 ms to accommodate this additional readout. The trajectory of the rosette navigator is shown in Figure 1 along with a diagram of the rosette-navigated radial stack-of-stars sequence used in the this work. In this implementation, frequency encoding gradients associated with the navigator module are placed directly after the slab-selective pulse which is already part of our stack-of-stars base sequence; however, the navigator works equally well with a nonselective RF pulse, which we demonstrate in Section 2. 2.5.

The aforementioned rosette trajectory can be expressed by the following formulae:

$$k_x\propto \text{cos}\alpha \pi t\text{sin}\beta \pi t$$ (1)

$$k_y\propto \text{sin}\alpha \pi t\text{sin}\beta \pi t$$ (2)

where t ∈ [0,1], α = 7, and β = 3. This trajectory has the beneficial property of being self-refocusing and imposes minimal constraints on the gradient hardware. Additionally, the parameters α and β can be tuned to achieve a variety of related navigator trajectories. The specific trajectory used in this work has not been specifically optimized for the proposed motion extraction task but works robustly across our datasets. Other self-refocusing trajectories would also likely provide sufficient information for motion extraction.

2.2 |. Respiratory and cardiac motion extraction

Because of the short duration of the navigator readout compared to the respiratory and cardiac motions of interest,⁷ we neglect any motion occurring during this time and consider each navigator readout to be a static snapshot of the present motion state. Thus, at intervals of Δt = TR, we get a complex data vector $\overrightarrow{x}$ with length M = N_coils·N_samp, where N_coils and N_samp refer to the number of coil elements and the number of ADC samples along the readout, respectively. We refer to this vector hereafter as a “coil fingerprint”. The total number of coil fingerprints is given by N = τ/TR, where τ is the total scan time. Typically, each coil fingerprint may be on the order of 10³−10⁵ elements depending on the number of coil channels. In this work, the number of channels varied between 5 and 7, due to automatic coil selection. Prior to motion extraction, the coil fingerprints need to be arranged into a 2D real matrix. This is accomplished by first concatenating each M-element navigator readout as separate columns into an M × N complex matrix X. This complex matrix is then expanded into to the real-valued, (2M) × N “coil-fingerprint matrix” (CFM) X′, where

$$X^{\prime }=\left[\begin{array}{c}\text{Re}(X)\\ \text{Im}(X)\end{array}\right]$$ (3)

The extraction of motion surrogates from the CFM involves three primary steps: (1) dimension reduction, (2) blind source separation, and (3) motion component identification

2.2.1 |. Dimension reduction

Dimension reduction is achieved via principal component analysis (PCA). The matrix X′ is reduced to only a handful of components which characterize most of the variation in the coil fingerprints. The reduced representation is given by

$$T_L=W_L{X}^{\prime }$$ (4)

where the rows of W_L are the L largest eigenvectors of XX^T, and L is chosen so that λ_min/Tr(XX^T) ≥ 0.005. Hence, the discarded eigenvectors account for no more than 0.5% of the total variance. In some cases, the respiratory and cardiac surrogates can already be clearly identified within the components of T_L. However, often these signals are fused to one another or contaminated by artifacts.

2.2.2 |. Blind source separation

The previous PCA step already yields components (the rows of T_L) which are uncorrelated because PCA diagonalizes the covariance matrix. However, this condition by itself is insufficient for identifying independent signals. To see why that is, consider T_L with zero mean and unit variance. The rows being uncorrelated implies $T_L{T}_L^H=I$; however we can form another signal matrix T′_L = T_LQ, where Q is an arbitrary orthogonal matrix, and by construction T′_L also has uncorrelated rows because $T_L^{\prime }{\left(T_L^{\prime }\right)}^H=T_{L}Q{Q}^H{T}_L=T_L{T}_L^H=1$. Therefore, the principal components may actually represent mixtures of various motion signals and sequence dependent artifacts unrelated to motion.

SOBI breaks this indeterminacy by considering a set of autocovariance matrices at different time lags τ₁, τ₂, …τ_p. The τ-time-lagged covariance matrix C(τ) for a given signal matrix X is given by

$$C_{ij}(\tau )=x_i(t-\tau )x_j^H(t).$$ (5)

Thus, SOBI seeks to jointly diagonalize C(τ₁), C(τ₂), …C(τ_p). Since it is generally not possible to diagonalize more than two matrices simultaneously, SOBI instead finds an approximate solution my minimizing the following joint diagonalization (JD) criterion:

$$V*={\text{argmin}}_V\sum _{k=1}^p\text{off}\left(V^{H}C\left({\tau }_k\right)V\right).$$ (6)

The “off” of an n × n matrix M is defined as

$$\text{off}(M)\equiv \sum _{i\ne j}{\left|M_{ij}\right|}^2$$ (7)

If a single time lag τ = 0 were used, the approach would be equivalent to principal component analysis; however, by considering multiple time lags, the robustness of the source identification is greatly enhanced.¹ We found that the results of SOBI are not very sensitive to the number of time lags and fixed p = 200 for all cases. In general, larger p should improve robustness at the cost of longer computation time. There is an efficient procedure for minimizing Equation 6, which is described fully in.¹ In our case, SOBI is applied after PCA. Therefore, the signal vectors x_i and x_j in Equation 5 are the i^th and j^th rows of T_L, respectively.

Once the unitary matrix V* is obtained as the joint diagonalizer of C(τ₁), C(τ₂), …, C(τ_p), the estimated source signals S can be related to the original coil-fingerprint matrix X′ by

$$S=V^H{W}_L{X}^{\prime },$$ (8)

where each row of S represents one estimated independent signal vector.

2.2.3 |. Motion component identification

Finally, the respiratory and cardiac signals are automatically identified by selecting the SOBI component s(t) (i.e. one row of S) that maximizes the ratio

$$r=\frac{{\int }_{f_{\text{min}}}^{f\text{max}}|\widehat{s}(f){|}^{2}df}{{\int }_{-\infty }^{\infty }|\widehat{s}(f){|}^{2}df},$$ (9)

where ŝ(f) is the Fourier Transform of s(t), and the frequency window [f_min,f_max] is selected to encompass a reasonable range for either respiration or heart rate. For all subjects, we have used [0.1 Hz,0.6 Hz] and [0.8 Hz,1.7 Hz] for respiratory and cardiac, respectively. This criterion favors signals with a fundamental frequency inside of the expected physiological range and also disfavors signals with spurious peaks outside of this range. We find that this helps to reject periodic artifacts even if their fundamental frequency is similar to the physiological signals because they have prominent harmonics at higher frequencies, whereas the quasi-periodic physiological motions do not.

These steps of dimension reduction, blind source separation, and motion component selection are all linear operations, so they can be concatenated into a single linear operation. As a result, two weight vectors w_r and w_c are learned, which relate the respiratory and cardiac motion surrogates ϕ_r and ϕ_c back to the coil fingerprints:

$${\varphi }_r=w_r^H{X}^{\prime }$$ (10)

$${\varphi }_c=w_c^H{X}^{\prime }.$$ (11)

More precisely, the row vectors $w_r^H$ and $w_c^H$ are simply the two rows of the matrix V^HW_L that correspond to the signals selected according to the frequency criterion in Equation 9.

Thus, once this motion model training is performed, subsequent navigators could be converted to motion gating signals on-the-fly. We found 1 min of training data to be adequate. After this training phase, subsequent navigators could be used for real-time triggering. Similar to other motion-sorted reconstruction methods, e.g.,^12,17,22 this relies on the assumption of cyclic motion: implicitly, it is assumed that all motion states are observed during the training phase and reoccur in a cyclic manner throughout the remainder of the study. Note, this is less restrictive than an assumption of periodic motion, which would also require the redundant motion states to repeat according to a precise and constant period

2.3 |. Data organization and image reconstruction

Once motion surrogates are extracted from the rosette fingerprints, they can be used to reconstruct dynamic image frames. First, the 1D respiratory and cardiac surrogate signals are obtained. Subsequently, they are used to partition the MR data into a discrete number of motion states based on the amplitude of the respiratory and cardiac surrogates, I_R(t) and I_C(t). For simplicity we set the thresholds for each partition so that all motion states have approximately the same amount of MR data. In this work, we used 5 respiratory and 5 cardiac states, resulting in 25 total motion states. Any number of motion states could be used; however, there exists a tradeoff between image quality and motion blurring. Practically, the number of motion states used in the reconstruction is a design choice impacted by the desired reconstruction speed, available memory on the reconstruction server, and image acquisition time. Our primary interest is in PET-MR motion correction, where typically between 5 and 10 motion states are used for both respiratory and cardiac binning. See, for example.¹⁶

Our MRI reconstruction model is very similar to that of¹² and minimizes the objective function

$${\text{argmin}}_d\frac{1}{2}\Vert FCd-m{\Vert }_2^2+{\lambda }_r{\Vert {\nabla }_{r}d\Vert }_1+{\lambda }_c{\Vert {\nabla }_{c}d\Vert }_1+{\lambda }_{xyz}{\Vert {\nabla }_{xyz}d\Vert }_1,$$ (12)

where F is the nonuniform fast Fourier transform (NUFFT) and ∇_c and ∇_r are finite differencing operators along the cardiac and respiratory dimensions, respectively. C and m can be expanded as

$$C=\left[\begin{array}{l}{C}_1\hfill \\ C_2\hfill \\ ⋮\hfill \\ C_{{\text{N}}_{\text{coils}}}\hfill \end{array}\right],m=\left[\begin{array}{l}{m}_1\hfill \\ m_2\hfill \\ ⋮\hfill \\ m_{{\text{N}}_{\text{coils}}}\hfill \end{array}\right],$$ (13)

where C_i and m_i are the coil sensitivity map and k-space data from the i^th coil element, respectively. The optimizer d is a 5D image volume with three spatial dimensions and two extra motion dimensions indexing the respiratory and cardiac states. Additional details on the data sorting can also be found in.¹² To solve Equation 12, we performed 30 iterations of the nonlinear conjugate gradient algorithm with corner rounding to handle the non-differentiable total variation penalties and set λ_c = λ_r = λ_xyz = 0.01.

2.4 |. Phantom study

Evaluation of respiratory and cardiac motion extraction was performed with an MR-compatible, anthropomorphic motion phantom.² The phantom (see Figure 2) is a life-sized human torso model with a plastic thorax, inflatable silicone lungs, a deformable left ventricle model (LVM), and a liver compartment. Respiration is simulated by driving the diaphragm with a pneumatic piston, while cardiac motion is achieved by inflating the inner cavity of the LVM with water. Contraction occurs passively due to the elasticity of the LVM. The position of the diaphragm and cardiac triggering are recorded to a log file, which provides a ground truth against which we validated our navigator-based motion extraction. Specifically, we compared the respiratory motion surrogate to the analog measurement of the diaphragm displacement and the cardiac motion surrogate to the LVM triggering pulses.

FIGURE 2.

Anthropomorphic motion phantom. Photograph of the motion phantom (left) and a diagram (right) showing its compartments. Respiratory motion is achieved by driving the diaphragm structure with a pneumatic piston. Cardiac motion is achieved by inflating the inner cavity of the left ventricle model with water

The MR imaging was performed on the Siemens Biograph mMR according to the specifications mentioned earlier with 1280 radial views, resulting in a scan time of 10 min and an average acceleration factor of ≈9.8. This scan was repeated 5 times under different motion conditions:

• Static End Inspiration—The LVM and diaphragm are fixed with the diaphragm in its most inferior position.

• Static End Expiration—The LVM and diaphragm are fixed with the diaphragm in its most superior position.

• Respiration Only (Periodic)—The LVM is fixed and respiration occurs with a constant period.

• Respiration Only (Aperiodic)—The LVM is fixed and respiration occurs with quasi-random variations in breathing rate and depth.

• Respiration and Cardiac Motion (Aperiodic)—Both cardiac and respiratory motions are simulated. The respiration model matches the previous condition.

Respiratory and cardiac motion surrogates were automatically extracted and used to reconstruct dynamic MR image frames according to the procedure outlined previously.

Simultaneously, a 10 min Fluorodeoxyglucose (FDG) PET body scan was performed. The PET listmode data were motion-sorted in the same manner as the MR data, and the image frames were reconstructed using an ordinary Poisson ordered subsets expectation maximization procedure with 3 iterations and 21 subsets. The image matrix was set to 172 × 172 with a pixel size of 4.173 × 4.173 mm and a slice thickness of 2.031 mm.

2.5 |. Human studies

In addition to the phantom study, we also tested the proposed motion extraction procedure on 13 human subjects. MRI scanning parameters are identical to the phantom study except only 800 radial views were acquired, resulting in a scan time of approximately 6 min and an average acceleration factor of ≈15.6. Motion extraction, MR data sorting, and reconstruction were performed in an identical manner to the phantom study. In this case, the motion surrogates were visually confirmed by ensuring that the reconstructed image frames contain respiratory and cardiac motions when traversing the corresponding motion dimension. Additionally, all but one of the human subjects were also scanned with an alternate version of the sequence wherein the gradients were not applied during the navigator readout. In this case, the navigator is a pure FID navigator. This serves as a control to demonstrate the importance of the frequency encoding information obtained due to the rosette trajectory.

2.6 |. Extension to 2D sequences

Several additional human studies were performed as a proof-of-concept to illustrate how the proposed techniques can be incorporated into 2D multi-slice imaging sequences. This is more challenging than the 3D case since the excited volume changes throughout imaging. The rosette navigator module was embedded in a 2D, T2-weighted turbo spin echo (TSE) sequence (TR = 1s,BW = 521Hz/pixel,32 × 4 mm slices, 1.09 mm in-plane resolution). An extra nonselective RF pulse was also added directly before the navigator readout. This was not necessary in the 3D case because, during imaging, the entire volume is excited, so the imaging signal can be used both for imaging and navigation. A small flip-angle of six degrees is used, so that the navigation has minimal impact on the imaging signal.

Separating the motion signals from sequence related artifacts is also slightly more challenging in the 2D case because the spurious signals from other slices contaminate the navigator data. The temporal behavior of these sequence-related artifacts is constant for all scans, so they can be estimated and subtracted by performing a reference scan of a static phantom using the same imaging parameters as the scan to be corrected. Subsequent data processing is identical to the 3D acquisition. This navigated TSE sequence was repeated on six human volunteers.

3 |. RESULTS

3.1 |. Phantom study

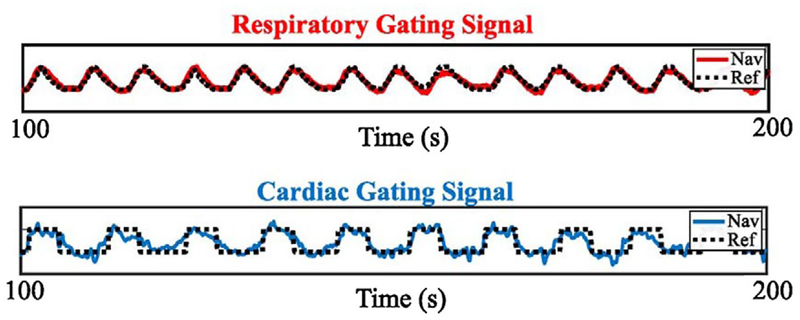
Figure 3 shows the 13 components obtained after performing dimension reduction (PCA) and blind source separation (SOBI) on the rosette coil fingerprint data from the phantom study with both respiratory and cardiac motions enabled. Prior to dimension reduction, this navigator data had a dimensionality of 45056. The respiratory and cardiac components, which were automatically identified according to Equation 9, are color-coded in red and blue, respectively. The extracted respiratory and cardiac signals are overlayed on top of the reference measurements (black) provided by the phantom in Figure 4. Both of the signals extracted from the navigator data match up very well with the reference signals. For the respiration signal, we found that 50% of the sampled points had a displacement error of less than 1.05 mm with respect to the reference signal, while 75% of sampled points had a displacement error of less than 1.74 mm, and 95% of sampled points had an error of less than 2.76 mm.

FIGURE 3.

Navigator extracted SOBI components. Shown above are the 13 components extracted by the SOBI algorithm. The respiratory (red) and cardiac components (blue) are automatically selected according to their spectral density

FIGURE 4.

Extracted motion signals vs. ground truth. The respiratory (red) and cardiac (blue) signals obtained from the navigator are compared to ground truth measurements from the phantom. For respiration the reference signal is an analog measurement of diaphragm position, and for cardiac motion, the reference signal is the triggering pulse

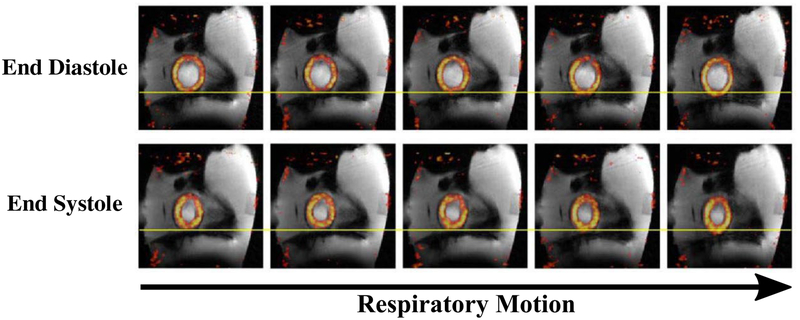
Figure 5 shows a sagittal slice of the fused PET and MR reconstructions of the motion phantom. In total, 25 motion state images were reconstructed comprised of 5 respiratory and 5 cardiac motion states. For compactness, the five respiratory states are only shown at end diastole (top) and end systole (bottom). The contraction of the heart structure is visually apparent when comparing the top and bottom rows. The respiratory motion is more difficult to discern in this static representation but some superior/inferior diaphragm and heart displacements can be observed, moving from left to right along a row of the motion-state matrix.

FIGURE 5.

Phantom study: reconstructed motion-sorted images. The respiratory and cardiac signals are used to sort the MR and PET listmode data. In this case, the respiratory and cardiac cycles were each divided into five unique states, resulting in 25 total motion states. A subset of the associated MR and PET reconstructions is shown in the fused images above (sagittal plane)

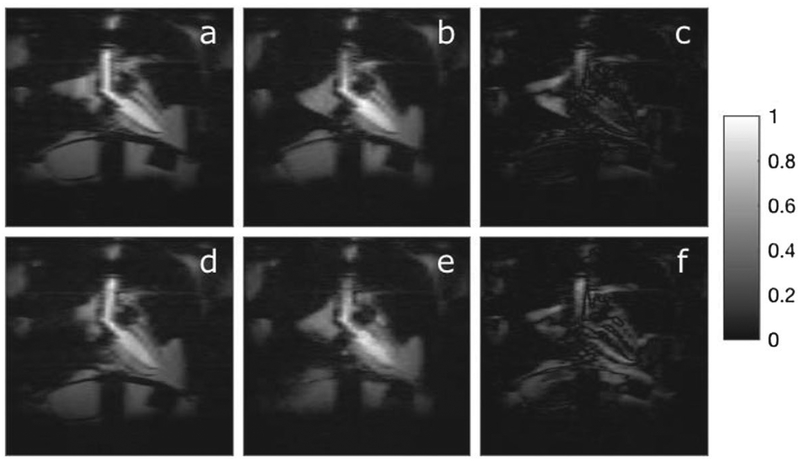
The two static scans, taken at end inspiration and end expiration, were used to validate the motion states reconstructed from the dynamic data, which is depicted in Figure 6. Panels (a) and (d) were reconstructed from the static end expiration and end inspiration scans, respectively. Panels (b) and (e) are the corresponding motion state images reconstructed from the dynamic data based on the respiratory and cardiac gating signals in Figure 4. Panels (c) and (f) are the difference images for end expiration and end inspiration respectively. In general, agreement is good but some structures are slightly blurred in the dynamic reconstructions, such as the diaphragm. We note that some blurring is expected in the motion-binned images (c) and (f), simply due to the fact that they utilize only 4% the amount of data as images (a) and (d), which were reconstructed from the static phantom scans. These acceleration factors are achieved via a compressed sensing type reconstruction with total variation regularization along the motion dimensions. Furthermore, the motion-sorting process is subject to some error due to misclassification of motion states, noncyclic motions, and intrastate motion.

FIGURE 6.

Phantom study: motion sorted images vs. ground truth. Above, we compare ground truth images acquired of the static phantom fixed in either end expiration (a) or end inspiration (d) to the corresponding motion states reconstructed from the gated motion-enabled: (b) is end expiration and (e) is end inspiration. In the static scans, the heart is fixed at end systole. Images (c) and (f) are the difference images for end expiration and end inspiration respectively

3.2 |. Human studies

Several of the human subjects were also scanned with an identical version of the sequence without the rosette navigator to verify that contrast is not impacted. Static reconstructions from the data acquired with and without the navigator are shown in Supporting Information Figure S1 in the supporting materials. Note that these images are not absolutely identical because they were acquired at different time points.

Figure 7 shows the respiratory and cardiac motion surrogates that were extracted from the navigator data for the four human subjects. Each of these signals appears to be a plausible descriptor of respiratory/cardiac motion in terms of shape and frequency. The gating signals were verified qualitatively by reconstructing dynamic MR image sequences and observing the resulting videos. The cardiac gating signal for Patient 3 appears to exhibit a “dicrotic notch,” which is discussed further in the Discussion section.

FIGURE 7.

Human study: representative gating signals. The low-pass-filtered respiratory and cardiac signals obtained from the navigator are shown above for four human subjects. These signals are extracted according the steps described above in a fully automated manner. The cardiac gating signal for Patient 3 appears to exhibit a dicrotic notch, which is discussed further in the Discussion section

As in Figure 5 of the 25 reconstructed motion state images (sagittal plane) from one patient are shown in Figure 8.

FIGURE 8.

Human study: motion sorted images. The respiratory and cardiac signals are used to sort the MR data into 25 distinct motion states. In this case, the respiratory and cardiac cycles were each divided into five states. A subset of the associated MR reconstructions is shown in the images above (sagittal plane)

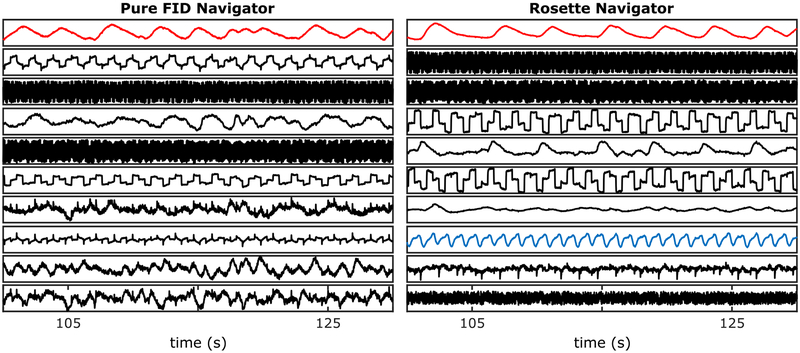
As a control, we also acquired several datasets with the navigator gradients switched off. We still have a 1.76μs readout following the RF pulse; since there is no spatial encoding, it is just a pure FID signal. It is well known that respiratory motion can be derived from repetitive data acquired at the k-space center. However, we were unable to reliably extract cardiac motion from only the FID navigator data. Figure 9 illustrates the SOBI components obtained from our motion extraction procedure for the pure FID navigator (left) and the rosette navigator (right). The rosette spatial encoding improves the accuracy of the respiratory motion estimate (red) and makes it possible to extract cardiac motion (blue).

FIGURE 9.

Rosette navigator vs. FID navigator. Shown above is a comparison between the rosette navigator (right) and the control (left), in which no spatial encoding gradients are played out resulting in a pure FID navigator. The spatial encoding improves the accuracy of the respiratory motion estimate (red) and also makes it possible to extract cardiac motion (blue)

We also extracted respiratory and cardiac gating signals from a modified TSE sequence, described earlier. This was repeated in six volunteers. A representative example is shown in Figure 10

FIGURE 10.

Navigating a 2D TSE sequence. Shown here are the respiratory (red) and cardiac (blue) gating signals obtained from the rosette navigator data embedded in a 2D, T2-weighted turbo spin echo sequence. In this case, a non-selective pulse is required prior to the navigator readout because the imaging is done slice-by-slice

4 |. DISCUSSION

The proposed cardiorespiratory motion tracking technique, using self-refocusing rosette navigators, has been experimentally validated with an MR-compatible motion phantom. The respiratory and cardiac motion surrogates derived from the navigator data matched up well with the ground truth diaphragm displacement and cardiac triggering signals. The gating signals were further validated by performing gated 5D reconstructions with the cardiac and respiratory motion states representing two additional motion dimensions. Additionally, the method has been successfully applied to 13 human volunteer datasets, demonstrating its robustness in a realistic clinical setting.

Our findings indicate that a pure FID navigator is insufficient for extracting cardiac motion and that the additional spatial encoding provided, e.g. by the proposed rosette navigator is necessary for dual gating. Some other works have reported success in extracting cardiac motion signals from a k-space-center navigator,^12,18 but these utilized balanced steady-state free precession (SSFP) sequences, which have excellent contrast between the blood pool and the myocardium.²⁷ Imaging with SSFP sequences is much more challenging at 3T due to shorter $T_2^{*}$ values and larger B₀ inhomogeneities,²⁶ which cause off-resonance artifacts. For this reason, cardiac imaging at 3T more commonly utilizes fast gradient echo sequences, which have very poor contrast in the heart, making it more challenging to extract a cardiac gating signal. We also note that, so far, all commercially available PET-MR scanners have 3T magnets. Therefore, our proposed navigation technique may be of particular interesting for cardiac motion-correction in PET-MR.

One interesting observation is that there exists a prominent notch in cardiac gating signal extracted from Patient 3, which is not seen in the other examples. A similar feature is sometimes observed in pulse oximetry and referred to as a “dicrotic notch.” The dicrotic notch coincides with a small dip in aortic pressure caused by the closing of the aortic valve during ventricular systole. While this is a possible explanation for the shape of this cardiac gating signal, comparison with a pulse oximeter reading would be needed for confirmation.

In these studies, the full process of extracting motion surrogates from the navigator data was completely automated using the same settings for all datasets. They key algorithmic design choices were determining the number of principal components to retain during the dimensionality reduction step and the frequency windows to use for identifying the respiratory and cardiac motion components. For the dimensionality reduction step, we found it effective to choose the cutoff based on the size of the eigenvalues λ₁, λ₂, … λ_N relative to λ_max. The specific cutoff used in this study of 0.5% was chosen empirically. This choice is mostly important for recovering the cardiac motion surrogate, since the respiratory motion tends to be mostly concentrated in the first principal component, while the cardiac motion signal is relatively weaker. The respiratory and cardiac frequency windows of [0.1 Hz, 0.6 Hz] and [0.8 Hz,1.7 Hz] were selected to cover wide range of typical respiration and heart rates. In practice, these windows could be more narrowly customized by measuring the patient’s heart and respiration rate prior to the examination.

While the proposed method offers a number of advantages to other approaches, such as not needing external tracking devices and being compatible with a variety of pulse sequences, it does have several practical limitations. Firstly, it requires modifying all MRI pulse sequences for which motion tracking is desired, whereas external tracking devices operate independent of the imaging sequence. While the navigator readout is relatively short (1.76 ms) it may still impose some design limitations on rapid T1-weighted imaging sequences with very short repetition times or ultrashort echo time (UTE) type sequences. For sequences with a very short TE, one option is to place the navigator after the imaging readout. Furthermore, we believe that it is likely possible to further shorten the readout length of 1.76 ms by altering the trajectory, but a detailed analysis of the navigator trajectory is left for future investigations.

We also want to emphasize that the particular stack-of-stars sequence and image reconstruction methods used here, which are very similar to those in,¹² are merely one example to demonstrate the proposed cardiorespiratory motion tracking technique. The primary contribution of this work was to demonstrate a flexible technique for tracking respiratory and cardiac patient motions in arbitrary MRI sequences without depending on external devices. This is achieved by combining the proposed self-refocused rosette navigator and automated motion-signal extraction algorithm. This scheme is quite general and can be combined with a huge variety of other sequences and image reconstruction methods

5 |. CONCLUSIONS

We have demonstrated a robust, flexible method for tracking respiratory and cardiac motion automatically using rosette navigators. The proposed navigation method can be incorporated into a variety of sequences without impacting image contrast. The approach has been validated on an anthropomorphic motion phantom, which provides ground truth motion measurements, as well as 13 human datasets. The extracted motion information has been used to perform motion-gated reconstructions from scans acquired during free breathing.

Supplementary Material

Figure S1

FIGURE S1 The image on the left was acquired using the aforementioned stack-of-stars sequence with the rosette navigator, while the one on the right was acquired using the same host sequence, excluding the navigator. We note that the contrast is not visibly affected by the presence of the extra navigation module