Comparison of measurements of phase velocity in human calcaneus to Biot theory

Abstract

Biot’s theory for elastic propagation in porous media has previously been shown to be useful for modeling the dependence of phase velocity on porosity in bovine cancellous bone in vitro. In the present study, Biot’s theory is applied to measurements of porosity-dependent phase velocity in 53 human calcanea in vitro. Porosity was measured using micro computed tomography for some samples (n=23) and estimated based on bone mineral densitometry for the remaining samples (n=30). Phase velocity at 500 kHz was measured in a water tank using a through-transmission technique. Biot’s theory performed well for the prediction of the dependence of sound speed on porosity. The trend was quasi-linear, but both the theory and experiment show similar slight curvature. Root mean square error (RMSE) of predicted versus measured sound speed was 15.8 m/s.

I. INTRODUCTION

Motivated by geophysical applications, M. A. Biot developed a theory for elastic propagation in porous media (Biot 1956a, 1956b, 1956c, 1962, 1963). As reviewed by Haire and Langton (1999), Biot’s theory has been applied by several investigators to model propagation in bovine cancellous bone, with more success in prediction of velocity than attenuation.

The mathematics of Biot theory is thoroughly reviewed in the references given above. Briefly, Biot considered a porous solid frame filled with a fluid. An ultrasound wave propagating through the composite loses energy due to friction between the frame and the fluid. Biot obtained a quadratic equation for longitudinal phase velocity, based on the material properties of the two media and the mechanical properties of the frame structure. The two solutions correspond to so-called “fast” and “slow” waves. These two waves correspond to the solid and fluid moving in phase and out of phase respectively.

Previous efforts have compared Biot’s predictions to measurements in bovine cancellous bone. Williams (1992) measured the dependence of longitudinal velocity on porosity in tibia in vitro and found good agreement with Biot’s predictions. Williams measured fast wave velocity in the direction parallel to the predominant trabecular orientation. Hosokawa and Otani (1997, 1998) measured velocity in femoral distal epiphysis in vitro in both parallel and perpendicular orientations. In the parallel orientation, they observed distinct fast and slow longitudinal waves, both with porosity-dependent velocities commensurate with Biot’s predictions. In the perpendicular orientation, in which fast and slow waves converge into a single wave, their measurements also matched theory. Mohamed et al. (2003) also reported good agreement between Biot theory and measurements of fast and slow waves in tibia in vitro. Hughes et al. (2003) argued that while both types of waves are observable in vitro, conditions required for slow wave propagation are not as easily attained in vivo, in which water is replaced by marrow, at typical diagnostic frequencies. (In addition, it is difficult to achieve propagation parallel to the trabeculae in vivo, which also complicates separation of the two types of waves.) Lee et al. (2003) successfully applied the modified Biot-Attenborough model to predict measurements of velocity and attenuation in tibia.

This report describes a comparison of porosity-dependent phase velocity in human calcaneus with Biot’s theory.

II. METHODS

A. Bone Specimens

Data from two sets of human calcaneus samples were used. Direct estimates of porosity, obtained using micro computed tomography (micro CT), were performed for one set (n = 23). For the other set (n = 30), micro CT measurements were not available. For these samples, porosity was estimated from dual energy x-ray absorptiometry (DEXA) measurements (see below).

The calcaneus samples (both genders, ages unknown) were defatted using a trichloro-ethylene solution as described previously (Wear, 2000a). The lateral cortical layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The thicknesses of the samples varied from 12 to 21 mm. In order to remove air bubbles, the samples were vacuum degassed underwater in a desiccator. After vacuum, samples were allowed to thermally equilibrate to room temperature prior to ultrasonic interrogation. Ultrasonic measurements were performed in distilled water at room temperature. The temperature was measured for each experiment and ranged between 19.1°C and 21.2°C. The relative orientation between the ultrasound beam and the calcanea was the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction.

B. Micro Computed Tomography

3D reconstructions for one set (n=23) of cancellous bone samples were generated using micro CT (Ruegsegger et al., 1996). A desktop fan-beam microCT scanner (Scanco μCT 40) situated at Scanco Medical AG in Bassersdorf, Switzerland was used. It utilized a microfocus X-ray source with 7 μm spot size, 70 kVp, 8 W (114 μA). The detector was a CCD array containing 2048 X 64 elements with 24 μm pitch. The resolution was 8 μm (10% Modulation Transfer Function). Quantitative microstructural properties were extracted from the 3D data sets using methods of Hildebrand and co-workers (Hildebrand and Ruegsegger, 1995). Measurements of ratio of bone volume to total volume (BV.TV) were performed on each of the 23 calcaneal specimens. The voxel size (nominal resolution) was 5 microns. 300 transverse slices (9 mm) were acquired from each specimen. From these 300 slices, a complete (square) cross region was taken, resulting in a volume of interest of about 12 × 12 × 9 mm for each bone sample.

C. Bone Densitometry

Micro CT data were not available for all samples. For some samples (n=30) bone mineral density (BMD) was measured using a Hologic QDR 2000 dual energy x-ray absorptiometry (DEXA) system operating in single beam mode. Areal density was determined for central regions of interest (ROIs) so that cortical bone was excluded. (Although, as mentioned above, lateral cortical plates were removed, some cortical bone remained around the peripheries of the samples. See Wear, 2000b, figure 1.) The cross sections of the regions of interest were rectangular. The regions of interest were drawn to approximate ultrasound interrogation regions in the central parts of the specimens. Duplicate measurements were performed on each specimen. The average coefficient of variation for the duplicate areal density determinations was 1.6%. The average areal density (g/cm²) was divided by the thickness of each sample to give the so-called “apparent density” of the skeletal frame (g/cm³).

1.

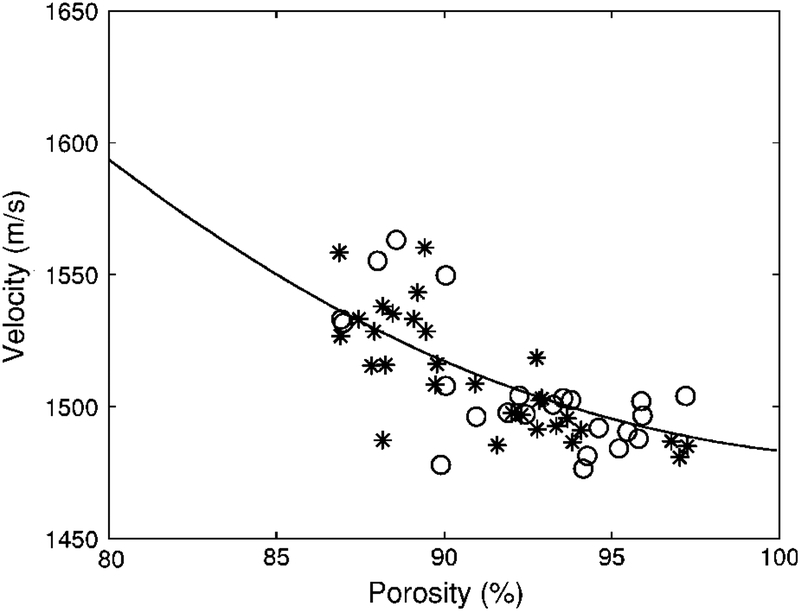
Phase velocity vs. porosity for the human calcaneus samples. The solid curve is the prediction from Biot theory. The samples for which porosity was directly measured (using micro CT) are denoted by circles (n=23). The samples for which porosity was indirectly measured (using DEXA) are denoted by asterisks (n=30). The Young’s modulus (E_s) for the solid bone material was assumed to be 8.3 GPa. (See Methods / Model Parameters section.)

The porosities of the samples were estimated as follows. The apparent density d_b of the skeletal frame is equal to (1 – β) d_s, where β is the porosity and d_s is the density of the trabecular bone material. Porosities were computed from the DEXA measurements of apparent density d_b and an assumed value for d_s−−1.8 g/cm³ for human trabecular bone (see Table 1).

Table 1.

Model parameters.

Parameter	Source	Value	Reference
Density of trabecular bone material	Various human	1.8 g/cm3	Keaveny, 1993
Density of fluid (water)		1 g/cm3
Young’s modulus of trabecular bone material	Human tibia	8.3 GPa	Rho, 1993
Bulk modulus of fluid (water)		2.2 GPa	Williams, 1992
Poisson’s ratio for trabecular bone material	Many bones and bone-like materials	0.3	Grenoble, 1972
Poisson’s ratio for skeletal frame	Bovine tibia	0.23	Williams, 1989 Hosokawa, 1998
s, where tortuosity = 1–s(1–1/β) and β = porosity		0.25	Williams, 1992
Exponent m, where Eb=EsVfm, Es=Young’s modulus of trabecular bone material, Eb=Young’s modulus of skeletal frame, and Vf=volume fraction of bone.		Obtained by curve fitting

The assumption of constant density of the trabecular material was not a serious shortcoming because, as with other investigations (McKelvie and Palmer, 1991; Williams, 1992; Hosokawa and Otani, 1997; Hosokawa and Otani, 1998; Mohamed, 2003), a constant value of trabecular material density was assumed for computations of Biot’s theoretical model anyway.

Some investigators have used Archimedes’ principle to estimate porosity of trabecular bone samples (Hosokawa and Otani, 1997; Hosokawa and Otani, 1998; Mohamed, 2003). For applications in calcaneus, there are two main limitations to this approach. One limitation is that it is difficult to control the degree of water saturation of the bone. Archimedes’ principle works well for substances that do not soak up water (e.g. rocks) but is not as reliable for substances that do (e.g. sponges). Trabecular bone lies somewhere in between these two extremes. The second limitation is an imprecise registration of tissue volumes corresponding to ultrasound and density measurements. Ultrasonic measurements are typically made in the central regions of bone samples. The bone sample is typically larger than the beam cross section in order to ensure that all received ultrasound passes through, rather than around, the bone. Archimedes’ method measures trabecular volume of the entire bone sample and therefore produces a weighted average of density within the region of interest (the central part) and density of regions not interrogated with ultrasound (the periphery). This is problematic for bones like the calcaneus that are quite heterogeneous. The advantage of DEXA is that a desired region of the bone, which corresponds closely to the ultrasonic interrogation region, may be isolated for density measurement.

D. Ultrasonic Methods

Biot theory predicts phase velocity. The phase velocity of propagating wave, c_p, is a function of angular frequency, ω, and is given by (Morse and Ingard, 1986, and Duck, 1990)

$$c_p(\omega )=\frac{\omega }{k(\omega )}$$ (1)

where ω=2πf, f is frequency, k = 2π/λ, and λ is wavelength. The relationship between phase velocity and group velocity of a broadband pulse, c_g, is given by (Morse and Ingard, 1986, and Duck, 1990)

$$c_g=\frac{c_{pc}}{1-\frac{{\omega }_c}{c_{pc}}{\left(\frac{\partial c_p}{\partial \omega }\right)}_{\omega ={\omega }_c}}$$ (2)

where c_pc is the phase velocity at the center frequency, ω_c.

Phase velocity may be computed using Equation (2) and measurements of group velocity if the dispersion of the medium, ∂c_p/∂f = (2π)⁻¹ ∂c_p/∂ω, is known. Dispersion, ∂c_p/∂f was assumed to be −26.25 m/s per MHz, which is the average value of measurements in human calcaneus reported by four groups (Nicholson et al., 1996; Strelitzki and Evans, 1996; Droin et al, 1998; Wear, 2000a).

To measure group velocity, bone samples were interrogated in a water tank using a pair of coaxially-aligned Panametrics (Waltham, MA) 1” diameter, focused (focal length = 1.5”), broadband transducers with center frequencies of 500 kHz. Using Fourier-based (Wear, 2004) and non-Fourier-based (Wear, 2000b) models for diffraction, as reported previously, it was possible to establish that the beam cross-section was smaller than the cross-sectional areas of the bone samples. A Panametrics 5800 pulser/receiver was used. Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

Arrival times of received broadband pulses were measured with and without the sample in the water path. Group velocity, c_g, was computed from

$$c_g=\frac{c_w}{1+\frac{c_w\Delta t}{d}}$$ (3)

where d is the thickness of the bone sample, Δt is the difference in arrival times (bone sample present versus bone sample absent), and c_w is the temperature-dependent speed of sound in distilled water given by (Kaye and Laby, 1973)

$$c_w=1402.9+4.835T-0.047016T^2+0.00012725T^{3}m/s$$ (4)

where T is the temperature in degrees Celsius (measured with a digital thermometer). Each arrival time was computed as follows. First, the digitized received pulse was bandpass filtered (400 – 800 kHz). Then the signal envelope was computed using the Hilbert transform. The point in time corresponding to the maximum signal envelope was taken to be the arrival time. Because of frequency-dependent attenuation, other commonly-used markers that are not at the center of the pulse (such as zero crossings or the leading edge of the pulse) can produce substantial errors in estimates of group velocity (Wear, 2000c; Waters et al., 2005).

These substitution techniques can potentially exhibit appreciable error if the speed of sound differs substantially between the sample and the reference (Kaufman et al., 1995). Apparently, the sound speed in calcaneus, ranging approximately from 1475 m/s to 1650 m/s (Droin et al., 1998), is sufficiently close to that of distilled water at room temperature, 1487 m/s (Kaye and Laby, 1973), that diffraction-related errors may be ignored for an experimental geometry such as the one used here (Droin et al., 1998).

E. Model Parameters

Biot’s theory requires several input parameters to describe the material and structural properties of the solid and fluid media. Table 1 shows values used in the present study. Values for human cancellous bone were used when available.

The value for (wet) tissue density (d_s) for human trabecular bone material has been reported by several researchers to lie within the range of 1.6 to 2.0 g/cm³ (Keaveny and Hayes, 1993). A value of 1.8 g/cm³ was chosen for the present study.

Rho et al. (1993) pointed out that the range of measurements of Young’s modulus for human trabecular bone material measured by bending tests is 3.2 – 7.8 GPa while that measured by buckling and ultrasound is 8.7 – 12.7 GPa. They argued that the former method tends to underestimate while the latter method tends to overestimate Young’s modulus. They concluded that the actual value is likely to lie near the upper end of the former range or the lower end of the latter range. Following this reasoning, a compromise value of 8.3 GPa was chosen for the present study. Admittedly, there is considerable uncertainty associated with this parameter.

Poisson’s ratio is near 0.3 for a wide variety of bones and bone-like materials (Grenoble, 1972). Poisson’s ratio for the skeletal frame (as opposed to the trabecular bone material) was taken from the measurements of Williams and Johnson (1989) on bovine tibia. Following Williams (1992) and Hosokawa and Otani (1998), the value of s, where tortuosity = 1–s(1–1/β) and β = porosity, was taken to be 0.25. Williams chose this value to be consistent with Biot’s predictions for hydrodynamic flow in tubes of circular cross sections and random orientations. This value seems to work consistently well for cancellous bone (Williams, 1992; Hosokawa and Otani, 1997; Hosokawa and Otani, 1998).

Following Williams (1992) and Hosokawa and Otani (1998), the value for the exponent m, where E_b=E_sV_f^m, E_s=Young’s modulus of trabecular bone material, E_b=Young’s modulus of skeletal frame, and V_f=volume fraction of bone, was a free parameter to be optimized by curve fitting.

III. RESULTS

Figure 1 shows velocity vs. porosity for the 53 human calcaneus samples. The solid curve shows the prediction of Biot’s theory. The samples for which porosity was directly measured (using micro CT) are denoted by circles (n=23). The samples for which porosity was indirectly measured (using DEXA) are denoted by asterisks (n=30). Values for the exponent m (see Methods / Model Parameters section above) obtained by curve fitting were 1.73 (n=23, micro CT subset), 1.76 (n=30, DEXA subset), and 1.75 (all 53 samples taken together). The root mean square errors of the curve fits were 16.91 m/s (n=23, micro CT subset), 14.8 m/s (n=30, DEXA subset), and 15.81 m/s (all 53 samples taken together).

IV. DISCUSSION

Biot’s theory performs moderately well for the prediction of the dependence of longitudinal phase velocity on porosity in human calcaneus in vitro. The trend is quasi-linear but both the theory and experiment show similar slight curvature.

Two factors make the comparison of Biot’s theory with measurements more difficult in the present study on human calcaneus than in previous studies in bovine femur or tibia. First, the range of porosities found in the present study in human calcaneus (86 – 98%) is considerably narrower than that found in bovine cancellous bone: about 65 – 92% (Williams, 1992), about 70 – 90% (Hosokawa and Otani, 1997 and 1998), and 21 – 67% (Mohamed et al., 2003). Second, the previous studies in bovine cancellous bones were performed on specimens with relatively consistent trabecular orientation (see, for example, Hosokawa and Otani, 1998, Figure 1). Due to heterogeneity and complex loading patterns on the human calcaneus, trabecular structure was less regular in the present study. This led to a greater range of velocities observed at a given porosity, manifested as scatter in Figure 1. Such a degree of scatter (a band of velocity measurements up to 50 m/s wide) is commonly encountered in human trabecular bone in vitro. (See, for example, Laugier et al., 1997, Figure 4, and Alves et al., 1996, Figure 5.)

The experimental dependence of phase velocity on porosity was similar for the two sets of calcanea. (Compare circles with asterisks in Figure 1.) In addition, curve-fitting of Biot theory (with exponent m as the free parameter, see Methods / Model Parameters section and Table 1) yielded essentially identical values for both data sets: 1.73 (n=23) and 1.76 (n=30). This similarity provides further justification for the indirect method of porosity estimation (described above in Methods / Bone Densitometry) based on the assumption of constant material density.

The value for exponent m obtained (by curve fitting) using all 53 calcaneus specimens of 1.75 is somewhat less than that obtained by Hosokawa and Otani (1998) of 2.14 for bovine femoral distal epiphysis for propagation perpendicular to the predominant trabecular orientation. For propagation in the parallel direction, Williams (1992) obtained m = 1.23 while Hosokawa and Otani (1998) obtained m = 1.46. For reasons given above, the organization of trabeculae may not be as consistent in human calcaneus as bovine femur or tibia. This could explain why the value of m measured in the present study is between the perpendicular and parallel extremes reported for bovine cancellous bone.

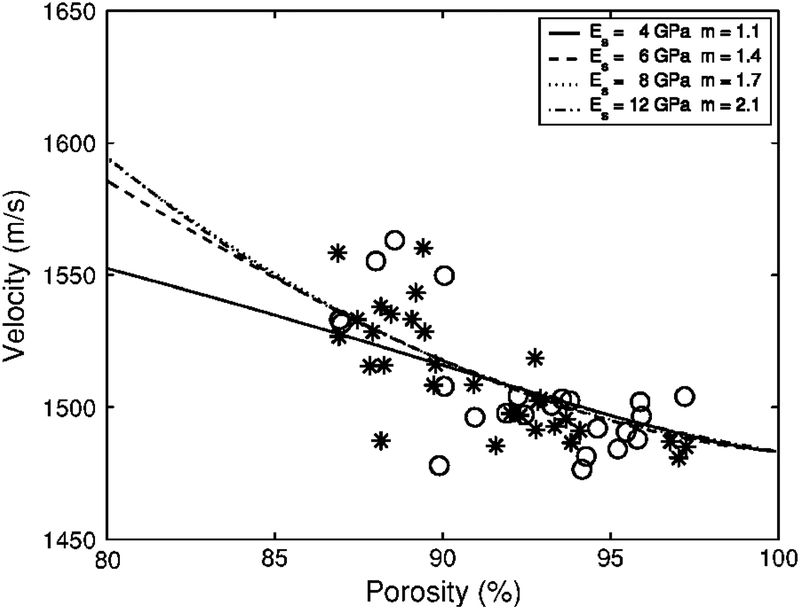
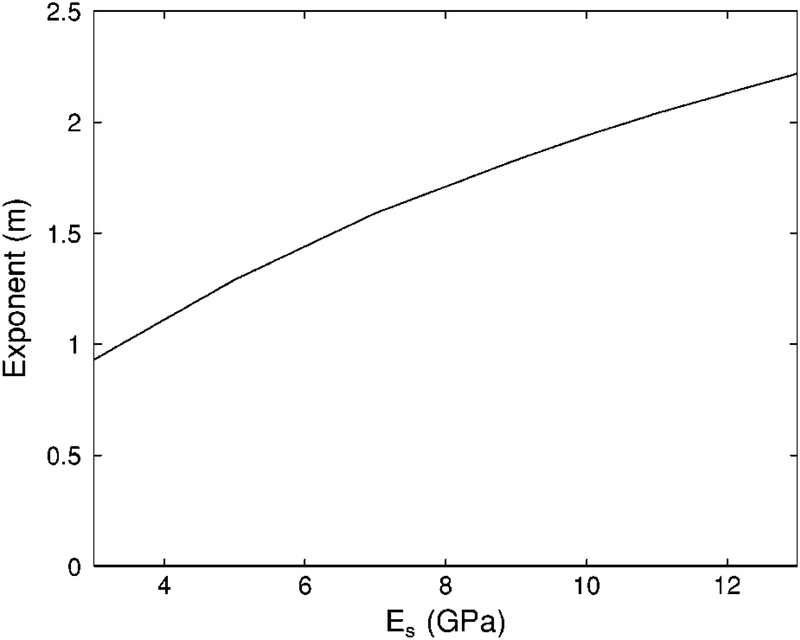
As mentioned above in the Methods / Model Parameters section, there is considerable uncertainty regarding the value of the Young’s modulus for the trabecular bone material (E_s). Therefore, it is appropriate to investigate the sensitivity of the theoretical fit to the assumed value for E_s. Figure 2 shows minimum RMSE fits of Biot theory (with exponent m as the free parameter) to the data for four different assumed values for E_s spanning the range of measurements reported in the literature. The four fits conform to the data comparably well over the range of porosities investigated. Figure 3 shows the approximately linear dependence of the optimum value for m on the assumed value for E_s. The optimum value (in a minimum RMSE sense) for m increases by approximately 0.13 for every 1 GPa increase in E_s.

2.

Biot theory for phase velocity vs. porosity for 4 different values for Young’s modulus (E_s) for the solid bone material.

3.

The exponent m for the minimum RMSE Biot theory fit to experimental data as a function of Young’s modulus (E_s) for the solid bone material. (See Discussion section.)

As pointed out by Hughes et al. (1999), two limitations of Biot’s model are that 1) it depends on a great number of parameters that are not known with high certainty, and 2) it does not allow for anisotropy. This second factor contradicts Hans et al.’s (1999) measurements of anisotropy of sound velocity in human trabecular lumbar spine (c = 1715, 1662, and 1676 m/s in axial, sagittal, and coronal orientations respectively). To overcome these limitations of the Biot model, Hughes et al. introduced the application of the so-called stratified model (Schoenberg, 1984) to the characterization of cancellous bone, in which bone is represented as a periodic array of bone-marrow layers. Hughes et al. found good agreement between theoretical predictions and experimental measurements of the angular dependence of phase velocities in bovine tibial and femoral epiphyses. Padilla and Laugier (2000) used the stratified model to predict conditions under which the slow wave is observable. Their results were consistent with measurements reported by Hughes et al. Wear (2001) showed that the stratified model successfully predicts negative dispersion in layered polystyrene-water phantoms and in human calcanea. Wear also found, however, that predictions of absolute phase velocity derived from the stratified model were too dependent upon assumed values for material and structural properties to be of much practical value. Lin et al. (2001) successfully used the stratified model to predict the dependences of velocity and attenuation on porosity in sheep femoral trabecular bone. Kaczmarek et al. (2002) applied the stratified model to the study of bovine femoral cancellous bone in the high frequency limit. Although the stratified model predicts many empirical observations, its alternating layer structure is a crude approximation, at best, to cancellous bone. While the Biot model is isotropic and less parsimonious than the stratified model, it more closely accommodates the physical porous structure of cancellous bone. Each model has its relative merits.

Lee et al. (2003) reported success in applying the modified Biot-Attenborough (MBA) model to not only velocity but also dispersion and attenuation in bovine cancellous tibia. It is conceivable that this refinement to the Biot theory could more accurately model phase velocity in human calcaneus. However, it is improbable that this could be proven with the present data set. Because of the scatter in the data (particularly at lower porosities), it is unlikely that any plausible (i.e. relatively smooth) model function could produce a dramatic decrease in RMSE compared with the Biot model (see Figure 2). In addition, the MBA model requires two fitting parameters (referred to as s₂ and s₃) that are unknown for human calcaneus. Therefore the more parsimonious Biot model was used in the present study rather than the MBA model.

Due to a more complex trabecular structure and a narrower range of porosities, it is more difficult to assess the compatibility of Biot’s theory with human calcaneus than bovine femur or tibia. Nevertheless, Biot’s theory performs reasonably well in predicting the dependence of phase velocity on porosity in human calcaneus.