Extraction of Process-Structure Evolution Linkages from X-ray Scattering Measurements Using Dimensionality Reduction and Time Series Analysis

Abstract

The rapid development of robust, reliable, and reduced-order process-structure evolution linkages that take into account hierarchical structure are essential to expedite the development and manufacturing of new materials. Towards this end, this paper lays a theoretical framework that injects the established time series analysis into the recently developed materials knowledge systems (MKS) framework. This new framework is first presented and then demonstrated on an ensemble dataset obtained using small-angle X-ray scattering on semi-crystalline linear low density polyethylene films from a synchrotron X-ray scattering experiment.

Introduction

The discovery and curation of process-structure-property (PSP) linkages in materials, their efficient communication to manufacturing experts, and their exploitation in the design of improved materials are the main rate-limiting bottlenecks in the advancement of many technologies. While it has been recognized that an accelerated design cycle for advanced materials can have a significant economic impact [1–8], in practice, the design cycle often takes decades. Some of the challenges encountered in the discovery and curation stage include material property dependence on extreme values of microstructure distributions, metastability of microstructures during processing and/or use, variations in data collection protocols, and uncertainty in data, models, and model parameters [9, 10]. Additionally, the multiscale (or hierarchical) nature of material structure necessitates a high-dimensional representation and poses a central challenge in establishing high-value PSP linkages [10–13]. The large descriptor space needed to capture the salient details of the material structure creates a major challenge that, in turn, demands a significant amount of data analysis in extracting reliable and useful PSP linkages.

Differences in processing routes for metals and alloys even with a fixed chemical composition can significantly influence the material internal structure (i.e., microstructure) and its associated macroscopic properties. In the case of polymeric materials, minute differences in chemistry and chemical composition can produce dramatic differences in properties across members of the same polymer family. Consider, for example, the case of the commodity polymer polyethylene (PE) represented chemically by the formula (CH ₂-CH ₂) _n, which spans an application range from grocery bags [14] to bulletproof vests [15]. In reality, the same chemical formula represents a family of PEs that can be subclassified into a variety of grades on the basis of factors such as density, crystallinity, average molecular chain length, extent of chain branching, and polymer architecture [16]. The type of PE and the choice of processing conditions under which it is converted to finished product influences the hierarchical structural assembly of the PE chains from nanoscale to microscale and, ultimately, has a profound impact on the macroscopic properties.

Constructing a PSP linkage, even for a well-understood polymer such as PE, is non-trivial. First, a descriptor space where the chemical architecture attributes of different grades of PE can be quantified, either directly or through a surrogate, is required. Second, microstructures (i.e., the hierarchical internal structures) resulting from various processing conditions and resultant PEs need to be quantified either through experiments or simulations. Third, the properties of PEs emerging from the combination of chemistry, processing, and microstructure must be evaluated.

The recently developed materials knowledge systems (MKS) combines concepts from sophisticated physics-based composite theories [17, 18], signal processing [19], and machine learning [20–22] to establish a new framework for pursuing PSP linkages. These linkages can be established at separable time and length scales relevant to the material hierarchical structure in order to communicate the salient information for both the top-down (referred to as localization) and the bottom-up (referred to as homogenization) scale-bridging. The Python package PyMKS [23] provides a code base to efficiently establish these linkages.

The MKS framework has thus far been applied largely to capturing structure-property linkages from data generated by multiscale models [13, 24–28]. These structure-property linkages are, in general, less complex than the process-structure linkages as they do not require a rigorous treatment of the structure evolution over time. The extension of the MKS framework to process-structure linkages necessitates the introduction of time series analysis.

The extension to process-structure relationships is a critical component of the MKS framework. Only with this extension is it actually possible to formulate a complete and comprehensive set of PSP linkages needed in a material innovation effort. With the complete formulation of PSP linkages (typically in the form of metamodels or surrogate models), it is possible to address inverse problems in materials and/or process design, where the goal is to identify a process recipe capable of producing a material with an improved combination of properties or performance metrics. Furthermore, such surrogate models lend themselves to an integrated community effort for curating and sharing material knowledge (in the form of PSP linkages) at different length and time scales which can also be effectively communicated and digested by manufacturing experts.

This paper lays the theoretical foundation to merge time series analysis with sophisticated physics-based composite material theories to create robust structure-processing linkages. The combination of these two domains provides a rigorous framework that can be used to accelerate the development of materials. The viability of the proposed framework is demonstrated using X-ray scattering measurements on linear low-density polyethylene subjected to different strain levels. In this example, the imposed plastic strain on the sample is treated as a process variable, and therefore, our goal is to relate this process variable to suitable structure descriptors in PE using the data acquired in X-ray scattering measurements.

Theoretical Framework

The MKS framework provides templatable protocols that can be used to create PSP linkages. These protocols start by introducing the concepts of local state space and microstructure function. Most simply, the local state could be the collection of thermodynamic state variables (or order parameters) needed to uniquely define a material system, such as orientation, chemical concentration, crystal structure, phase, and so on. The local state space defines the space of all possible local states used to define a material system for a given problem. The microstructure function introduces a probabilistic interpretation of the microstructure by converting the structure into a probability distribution over local states. In prior work, this function has been mostly used to describe static microstructures. In this work, our interest is in capturing details of microstructure evolution in manufacturing processes. Consequently, we first extend the existing framework [29, 30] to include time as an independent variable in addition to the spatial variables used in describing any given microstructure.

Employing discretized (i.e., binned) representations of space indexed by s, time indexed by n, and local state indexed by h, m _j[h,s,n] provides a discretized description of the evolving microstructure indexed by j. More specifically, m _j[h,s,n] denotes the probability of finding h in voxel s during the time step n in the evolving microstructure labeled j. It is very important to recognize that j in the formalism presented in this paper indexes a microstructure evolution pathline, i.e., the time history followed by a microstructure in any selected processing operation represented as a pathline in the microstructure space. In many ways, this represents a significant extension to the MKS framework presented in prior work [24, 26, 28–32], where the microstructures were simply indexed to denote distinct (static) microstructures. However, in the formalism presented in this paper, the index j represents a complete set of microstructures capturing the details of time evolution of a microstructure in a selected processing step. This extension is essential to the application of time series analysis to process-structure evolution linkages in materials science.

Formally, the expected value of the microstructure function is the measured material structure expressed as

$$E_j\left[h\right|s,n]=\sum _{h\in H}h{m}_j[s,n,h]$$ 1

Additionally, the binning of the local state space introduces a consolidated discretized variable space where both tensoral and scalar quantities needed to define material structure may be conveniently mapped to a simple index h.

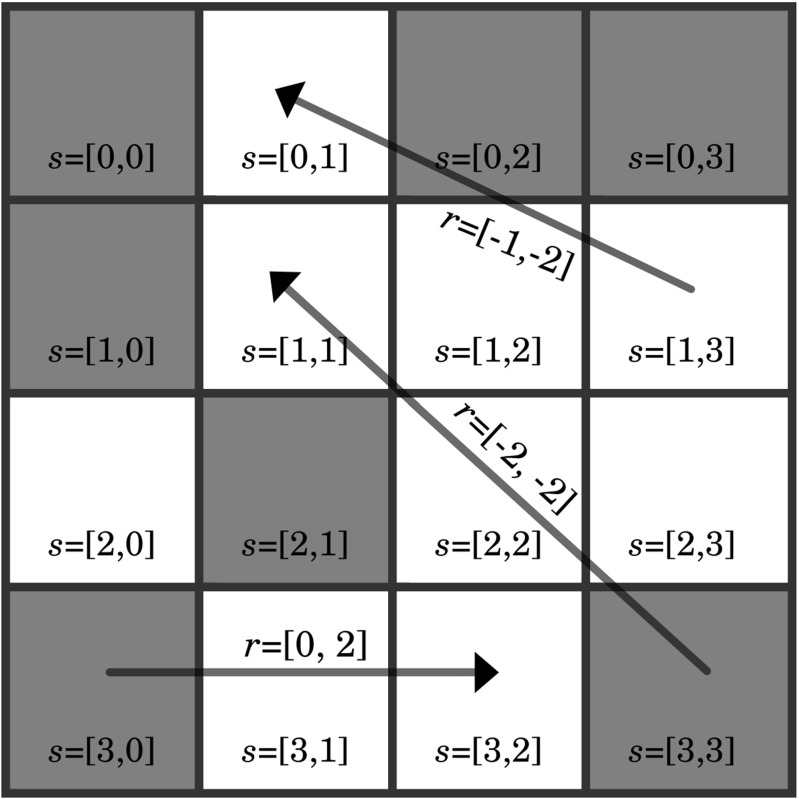
The homogenization (bottom-up scale-bridging) protocol starts by converting the raw structure information into the microstructure function (also referred to as digitizing the microstructure) based on the local states (e.g., phase identifier, chemical composition, lattice orientation). An idealized example of discretized microstructure with two discrete local states can be found in Fig. 1. In this example, the image is segmented such that each voxel is assigned to one of two possible local states colored white and gray.

Fig. 1.

Idealized digitized microstructure with two local states shown by the white and gray voxels. The relative spatial locations for two voxels are described by a discretized vector r

Using the microstructure function, we can compute spatial correlations between local states as [13, 29, 33, 34].

$$f_j[h,h^{\prime },r,n]=\frac{1}{{\mathrm{\Omega }}_j[r,n]}{\sum }_{s\in S}{m}_j[h,s,n]m_j[h^{\prime },s+r,n]$$ 2

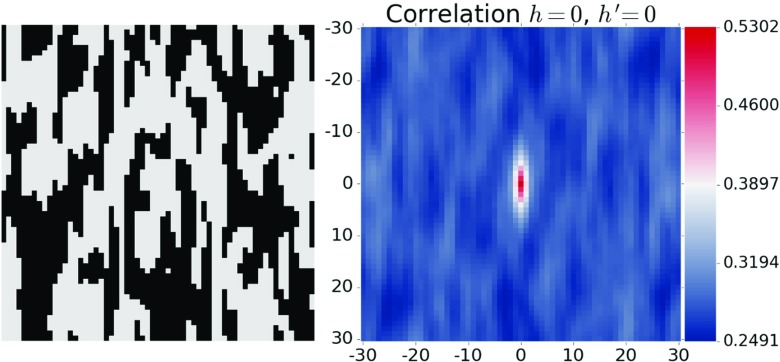
In Eq. 2, Ω_j[r,n] is a normalization factor that provides a count of the total number of times it is actually feasible to evaluate both m _j[h,s,n] and m _j[h ^′,s + r,n]. This normalization factor can therefore depend on the discretized vector r and the time step n (allowing for changes in the microstructure volume with time). A full set of two-point statistics is defined by all possible vectors that can be defined within an image [13, 29, 33, 34]. Two-point statistics f _j[h,h ^′,r,n] are most efficiently computed via discrete Fourier transforms [29]. The transformation of material structure information into two-point statistics provides the benefit of creating a natural origin or a point of reference (usually taken as r=0) that can be used to objectively compare spatial arrangements of the local states across a given microstructure as shown in Fig. 2.

Fig. 2.

Discretized microstructure (left) and its two-point statistics (right). Each pixel in the two-point statistics image depicts the probability of finding the selected local states at the ends of a vector whose tail is at the origin and the head is at the pixel itself (Color figure online)

Creating structure-property linkages or classification models with the raw two-point statistics is difficult due to the large feature space and collinear features. Low-dimensional microstructure descriptors can be created using dimension reduction techniques such as principal component analysis (PCA) or one of its variants [35, 36]. PCA is a global unsupervised distance-preserving linear transformation, which then finds its way naturally into the known physics-based theories [37]. Additionally, accurate approximations to PCA are computationally faster than other dimensionality reduction techniques [38]. In the MKS framework, PCA is used to create low-dimensional microstructure descriptors using linear combinations of the two-point statistics. Mathematically, this transformation can be expressed as

$$f_j[l,n]\approx \sum _{k=1}^K{\mu }_j[k,n]\varphi [k,l]+\overline{f\left[l\right]}$$ 3

In Eq. 3, f _j[l,n] is a feature vector that includes all two-point statistics deemed important for the problem (l indexes all unique combinations of h, h ^′, and r included in the analysis; see [39] for guidance on how to make such selections) at time step n. As defined earlier, j identifies a particular microstructure evolution pathline. ϕ[k,l] and $\overline{f\left[l\right]}$ are the estimated time-independent PCs and the time-independent mean values of the selected features, respectively. K is the total number of PCs. μ _j[k,n] are the time-dependent PC scores and are taken as the low-dimensional descriptors for microstructure evolution pathline j. Often, most of the variation in a dataset can be captured by only a few PC scores. Let k=1,2,...,K ^∗ denote this low-dimensional representation of the microstructure, where K ^∗ is many orders of magnitude smaller than the large number of microstructure statistics included in the analysis. Previous studies have successfully used these protocols to create structure-property linkages with effective properties or microstructure classification models that could be used to objectively quantify the variation in microstructures due to changes in manufacturing processes [13, 29, 30, 34]. A related protocol for localization (i.e., top-down scale-bridging) has also been applied successfully to a variety of multiscale material phenomena [12, 24–27, 32].

While previous MKS studies have successfully captured structure-property linkages, the application of the same framework to establishing process-structure evolution linkages requires the extensions developed and presented in this paper. As noted earlier, this extension is specifically designed to facilitate the application of time series analysis techniques. Time series modeling approaches can be separated into methods that work in the frequency domain such as spectral analysis [40–42] and wavelets [43–45], and methods that work in the time domain. The time domain methods can be further separated into three main categories: autoregresive integrated moving average (ARIMA) models [46], state space models [47–53], and non-parametric regression machine learning models [54–56], notably neural networks.

ARIMA models were developed by Box and Jenkins [46] and predict the evolution of time series data based on previous values and previous errors. The advantages of ARIMA models are that (i) the model has a relatively small number of parameters, (ii) the parameters can be estimated via ordinary least squares, and (iii) the model itself and its parameters are relatively intuitive. The model requires that non-linear trends be removed from the data, and if the residuals are normally distributed, simple estimates for the variance-covariance matrix of the parameters are available [46].

State space models estimate a joint probability over latent state variables and observed measurements. A Kalman Filter [47] can be used when the latent state variable is assumed to be continuous, while hidden Markov models can be used with discrete latent variables [48–50]. State space models can be viewed as recursive Bayesian estimation [57] and are well suited for streaming noisy data. The models create a linear function using a Markov assumption (only the previous state is needed to predict the current state), although extensions of the models have been made to account for non-linearities [51–53]. The drawbacks from this method are that (i) the parameter estimation is non-convex and (ii) the dynamics of the system must be well understood a priori to create transition models to update the latent state variables.

Neural networks have been successfully applied to time series analysis as well as other sequential learning problems. The most notable model is long short-term memory neural network (LSTM) [54]. LSTM introduces the concept of a memory block which contains gates that control the flow of information into and exiting the memory block as well as information carried into the next time step [55]. This model has been shown to outperform the previous two methods with non-stationary data [56], but optimization of neural network parameters is non-convex and typically requires a significant amount of data [55].

In this study, an extension to the MKS homogenization framework is presented based on a non-parametric extension to ARIMA models for time series data gathered from synchrotron based in situ X-ray scattering measurements. In experiments of this type, the material system under investigation is constantly exposed to an X-ray beam which allows the internal structure to be probed continuously. Simultaneously, the thermodynamic state variables for the system, i.e., processing conditions, are perturbed and the resulting changes in the properties of the material under investigation are observed and recorded. These state variables can include temperature, pressure, and electric fields or their combinations. Using this tri-component approach of simultaneously monitoring structural changes continuously while manipulating the process variables and recording the corresponding properties permits the construction of a time series-based process-structure linkage. Although our work towards establishing PSP linkages is demostrated on X-ray scattering data, the approach can be extended to data from in situ experiments utilizing a variety of microscopy, tomography, neutron scattering, and spectroscopic techniques.

Time Series Analysis for Process-Structure Evolution Linkages

State space models enjoy certain advantages in handling noisy data and can be adapted to in-line learning from streaming data. But in order to avoid divergence and minimize error, these models require a priori knowledge of the dynamics of the system to create state transition matrices. Although some work has been done to empirically calibrate these transition matrices [58, 59], the dynamics of low-dimensional microstructure descriptors is generally not well understood. While LSTMs have shown significant predictive power when optimized with a large dataset, in many practical applications, material datasets are not large enough [60]. For these reasons, LSTM and state space models were not used in this study.

ARIMA models require information from previous prediction errors (at prior time steps). This makes multistep predictions challenging with a moving average component while autoregressive models only require information from predictions at prior time steps. As a result, autoregressive models lend themselves better to multistep predictions. A non-parametric regression method call multivariate adaptive regression splines (MARS) was developed by Friedmen [61] and later applied to time series analysis by Lewis and others [62, 63]. In time series applications, the method is referred to as time series multivariate adaptive regression splines (TSMARS). TSMARS has been shown to work well in a moderate dimensional setting (in our case, the number of PCs is expected to be 20 or less) and moderate-sized data (between 50 and 1000 datapoints) [61].

In the present application, TSMARS will be used to estimate a function, $\mathcal{F}$, connecting the current microstructure descriptors μ[k,n] with their prior values as well as potentially with processing parameters η[n]. Mathematically, this function can be expressed as

$${\widehat{\mu }}_j[k,n]=\mathcal{F}\left({\mu }_j\right[k,n-1],{\mu }_j[k,n-2],\mathrm{...}\eta [n],\eta [n-1],\mathrm{...})+\epsilon$$ 4

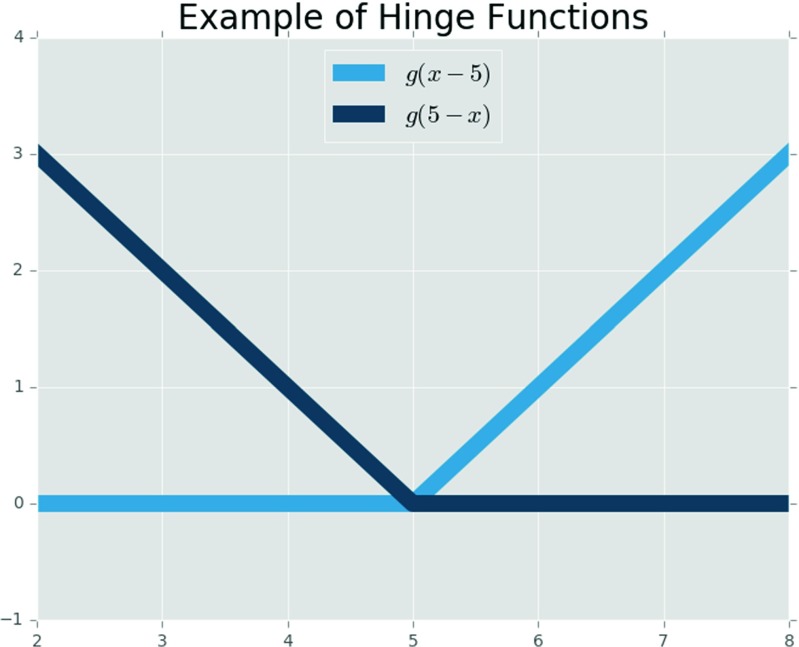
In Eq. 4, μ _j[k,n−i] and η[n−i] are the microstructure descriptor (i.e., k ^th PC score) and the processing parameter, respectively, at the discrete time step (n−i). The function $\mathcal{F}$ is expressed as a linear combination of basis functions, each of which is (i) a constant, (ii) a hinge function with knot point at an observed input location, or (iii) a product of the hinge functions. The coefficients in the series are commonly estimated via least squares regression. A hinge function can be defined as in Eq. 5, and an example of two hinge functions meeting at a knot equal to 5 is shown in Fig. 3.

$$g\left(x\right)=\left\{\begin{array}{cc}x,& \text{if}x>0.\\ 0,& \text{otherwise}.\end{array}\right.$$ 5

Fig. 3.

An example of two hinge functions meeting at a knot with value of five (κ=5) (Color figure online)

In the example used in this study, strain values correlate with time steps (i.e., the same strain history is imposed on all samples); therefore, strain does not provide additional information. Therefore, the function $\mathcal{F}$ will only be written in terms of the previous values of the microstructure descriptors μ _j[k,n−i] for the remainder of the paper.

The TSMARS estimation consists of three major steps.

1. A forward pass greedily adds basis functions in mirror image pairs to minimize mean squared error (MSE) until a stopping criteria is reached.

2. A pruning or backward pass removes the least important basis functions greedily to avoid over-fitting according to generalized cross validation (GCV).

3. Coefficients for the basis functions are estimated using least squares.

Detailed explanations of MARS and TSMAR can be found in published literature [61–63].

In this study, the iterations of the forward pass were stopped if (i) the R-squared value was greater than 0.999 or (ii) the change in the R-squared was less than 0.001. The number of PCs, K, and the autoregressive order, P, are the two hyper-parameters in the model development; these were optimized for the process-structure linkage extracted in this work using a leave one sample out cross-validation approach. When selecting the range over which to search, three practical issues need to be considered. (i) P determines the number of initial images that need to be provided to the model at the time of prediction. As a result, a sufficiently accurate model with a low value of P is desired. (ii) As K increases, the amount of variation retained in the low-dimensional microstructure descriptors μ _j[k,n] also increases (i.e., we obtain a more complete description of the microstructure). (iii) While the time complexity for prediction is O(N P K), where N is the number of time steps, the time complexity for estimation is O(N ²(P K)³). The last two issues require an optimized value of PCs where a sufficient amount of the variation is captured without the run time becoming too large.

During the cross-validation process, each of the samples was systematically left out during the estimation of the model parameters. After each of the estimations, the first P images from the sample not used during the estimation were provided as initial conditions for the model. The prediction process recursively used predictions from the previous time steps in the model (i.e., if P=1, then ${\widehat{\mu }}_j[k,n+i]$ is used to predict ${\widehat{\mu }}_j[k,n+i+1]$). The MSE values, as defined in Eq. 6, were computed over the predicted time steps.

$$\frac{1}{\mathrm{NK}}\sum _{k=1}^K\sum _{n=1}^N{\left({\widehat{\mu }}_j\right[k,n]-{\mu }_j[k,n\left]\right)}^2$$ 6

Application

In a conventional synchrotron X-ray scattering experiment, the specimen under investigation is irradiated by a collimated beam of monochromatic X-rays. The incident X-rays interact non-destructively with the electrons in the specimen. This interaction results in a fraction of the X-rays deviating from their original collimated path, i.e., results in scattering. The spatial distribution of electrons in a material, the electron density distribution, is a characteristic of the material. In turn, the scattering of incident X-rays due to the electron density distribution is characteristic of that microstructure. The scattered X-rays, which are captured on a 2D detector plate, create a 2D scattering pattern which contains the relevant microstructural information. Depending on the type of X-ray scattering technique used for investigation, the microstructure of a material can be characterized across length scales spanning from 0.1 nm to 1 μm [64].

Small-Angle X-ray Scattering of Partially Crystalline Polymers

Small-angle X-ray scattering (SAXS) is a subset of X-ray scattering techniques wherein inhomogeneities or two-phase microstructural features at the mesoscale between 1 nm and 100 s of nm can be probed in a specimen. In this work, we use SAXS to investigate the mesoscopic structure of semi-crystalline polymer films of linear low-density polyethylene (LLDPE), a grade of PE. Semi-crystalline polymers comprise of a microstructure wherein the polymer chains can organize into crystalline and non-crystalline domains. The crystalline domains consist of tightly packed polymer chains that have become regularly ordered to form lamellae while amorphous domains are formed from loose disordered arrangements of the polymer chains. In an ideal case, the crystalline and non-crystalline domains are separated by a sharp interface, and therefore, the two domains can be considered to be separate local states. Most importantly, the electron density in crystalline domains, ρ _c, is greater than the electron density in the amorphous domains, ρ _a.

A single SAXS pattern provides an average description of all the spatial arrangements of crystalline and amorphous domains within the scattering volume at that instant of time. The time series data used in this application of the MKS homogenization approach are image sequences of such SAXS patterns obtained while simultaneously recording the stress and strain data of the individual specimens during uniaxial tensile stretching. The dataset therefore provides insight into the evolution of the semi-crystalline microstructure at the mesoscale for different LLDPEs under uniaxially applied stress and strain.

For this case study, X-ray scattering data serve as a surrogate for two-point statistics. Mathematically, X-ray scatterings from a two-phase microstructure have been shown to correspond to the Fourier transform of the autocorrelation of the difference in electron density [65].

Materials and Methods

Melt blown films of two LLDPE polymers, henceforth referred to as LLDPE1 and LLDPE2, were supplied by ExxonMobil Chemical Company (EMCC). Both the LLDPEs were statistical copolymers of ethylene and hexene, where the hexene comonomer was incorporated along the backbone chain in the form of butyl short-chain branching (SCB). The densities for LLDPE1 and LLDPE2 were 0.912 and 0.923 g/cm ³. The density variation between the two polymers arose from the differing levels of SCB incorporation. The melt flow index for each of the polymers was 1.0 (ASTM-D1238) and the molecular weight distributions for these LLDPEs were also similar. Both polymers were converted into films by the method of film blowing into two series of blown films. The first series of films had a blow up ratio (BUR) of 2.5 while the second series had a BUR of 3. The BUR is a standard processing parameter which describes the manufacture of blown films. Within each series, three films were fabricated with average thicknesses of 20,30, and 75 μm, thereby totaling 12 films. The labeling scheme followed in the current work to describe tensile specimens for in situ testing is described in Table 1.

Table 1.

Labeling of tensile specimens made from blown films of the two LLDPE polymers

Polymer	Film label	BUR	Thickness (μm)	Images
LLDPE1	LLDPE1.1a	2.5	20	182
	LLDPE1.1b	2.5	30	191
	LLDPE1.1c	2.5	75	195
	LLDPE1.2a	3	20	191
	LLDPE1.2b	3	30	195
	LLDPE1.2c	3	75	191
LLDPE2	LLDPE2.1a	2.5	20	191
	LLDPE2.1b	2.5	30	195
	LLDPE2.1c	2.5	75	61
	LLDPE2.2a	3	20	227
	LLDPE2.2b	3	30	199
	LLDPE2.2c	3	75	206

SAXS experiments were performed at beamline 12-IDC of the Advanced Photon Source (APS) at the Argonne National Laboratory (ANL). In these experiments, the X-ray beam had an energy of 12 keV (i.e., a wavelength of 1.0332 Å) and the beam dimensions were 200 μm × 200 μm. X-rays scattered by the LLDPE film specimens were detected by a MAR CCD detector situated at a distance of 2426 mm from the LLDPE specimen. The detector pixel size was 175 μm. A fixed exposure time of 0.1 s was utilized while taking SAXS snapshots. SAXS patterns were collected every 3 s. This time interval was determined based on the minimum detector readout time per pattern. A portable tensile stage, made by Linkam Scientific Instruments, was utilized for the tensile measurements. The Linkam stage was operated at a tensile deformation rate of 25.4 mm/min. The collection of SAXS data and deformation data was synchronized such that the first SAXS pattern in any of the image sequences was always obtained from an unstrained pristine specimen at t ₀.

In this study, a process-structure evolution linkage is sought between the applied strain (process parameter) and the evolution of the anisotropic crystalline and amorphous structure in LLDPE polymers. Traditional approaches to create similar process-structure evolution linkages reduce the 2D SAXS intensity plots to 1D by either (i) assuming that the material is isotropic and integrating out the angular information from the raw data [66–68] or (ii) studying 1D intensity plots along selected angles [69, 70]. More advanced techniques use the 1D intensity plots to create 2D collection functions to look at changes over time [71, 72]. Indeed, all of these techniques are aimed at reducing the dimensionality of the structure information obtained from the scattering measurements. In the present study, we take an objective (data-driven) approach to dimensional reduction using the MKS framework described earlier. One of the main advantages of the MKS approach is that we can retain a significantly larger amount of the information in the reduced dimensional representation of the microstructure with a remarkable ability to recover almost the full representation when needed. This is mainly because of the use of the PCA and storing the information on the PCs and the mean values of the feature distributions, as will be illustrated later in this case study.

Data Processing

Prior to analysis, the contrast X-ray scattering images were transformed by taking the log of the intensity. In order to normalize the difference in intensity due to film thickness, each of the images was normalized by their mean intensity value.

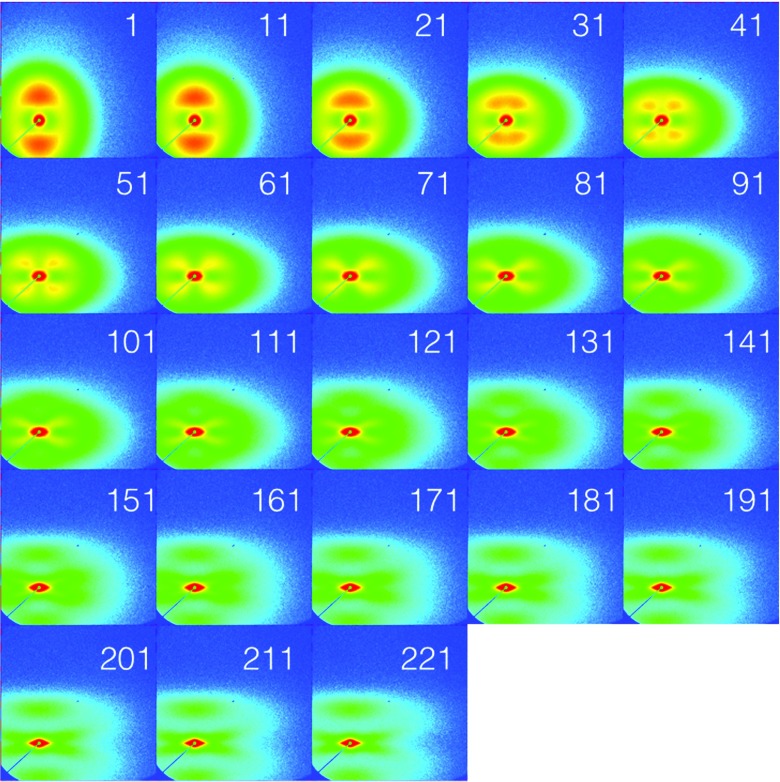
PCA was done on the complete set (ensemble) of 2224 images from the 12 samples (see Table 1). Each scattering image (such as those shown in Fig. 4) was represented as a vector of 422,500 intensities. In other words, the dimensionality of the measured structure information is 422,500, which is clearly unwieldy to extract high value process-structure evolution linkages. Figure 5b shows the explained variance in the complete ensemble of the measured structures as a function of the number of PCs. This essentially means that fewer than 20 PCs would be enough to recover most of the original microstructure information. This is indeed a remarkable reduction in dimensions, from 422,500 to less than 20, while capturing 88% of the differences between the individual structures in the ensemble. The full ensemble of structures is shown in the first three PCs in Fig. 5a. In this visualization, the structure evolution in each of the 12 samples is tracked by assigning distinct colors and symbols to each sample. Consequently, we can visualize the structure evolution in each sample as a single pathline.

Fig. 4.

An example of the typical evolution in 2D SAXS patterns with increasing strain for a tensile specimen of LLDPE2.2a. Strain is applied in the vertical direction with a tensile deformation rate of 25.4 mm/min. The numbers indicate the SAXS pattern number; an interval of 3 s between consecutive patterns is strictly maintained. Every tenth image is displayed for clarity. The intensity is log scaled to highlight the characteristic features in the SAXS evolution with strain (Color figure online)

Fig. 5.

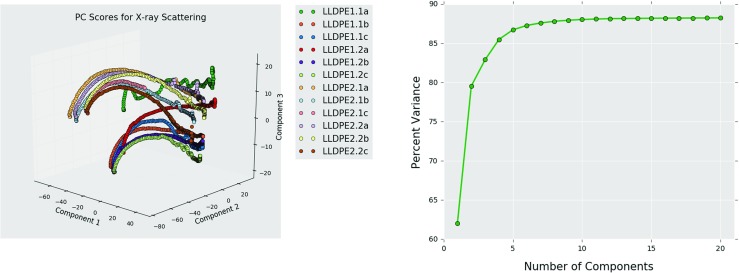
a Principal component scores for X-ray scattering images from the 12 different samples and b the percent variance captured as a function of the number principal components (Color figure online)

The mean and the first five PCs are reshaped from vectors into the original images and are presented in Fig. 6. As explained in Eq. 3, the image titled mean is the time-independent mean of the entire ensemble. Images titled PC1 through PC5 identify the most distinguishing features in the X-ray scattering images in an orthogonal frame. PC1 appears to increase the contribution from short vectors, at the expense of long vectors. PC2 appears to impart a large bias in the horizontal direction compared to the vertical direction. The higher order PCs are capturing increasing complex features. The large dimension of each PC makes it very difficult to understand all of the information embedded in each component. Physical interpretation of the PCs in the MKS framework is a current area of major research interest.

Fig. 6.

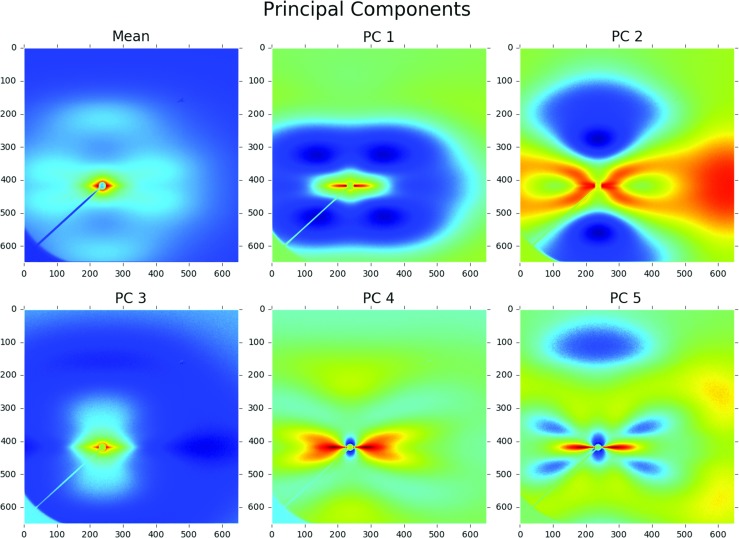
The mean and first five principal components computed doing principal component analysis on 2224 images. 86.7% of the variance in the dataset is captured by the first five principal components (Color figure online)

Model Selection, Estimation, and Validation

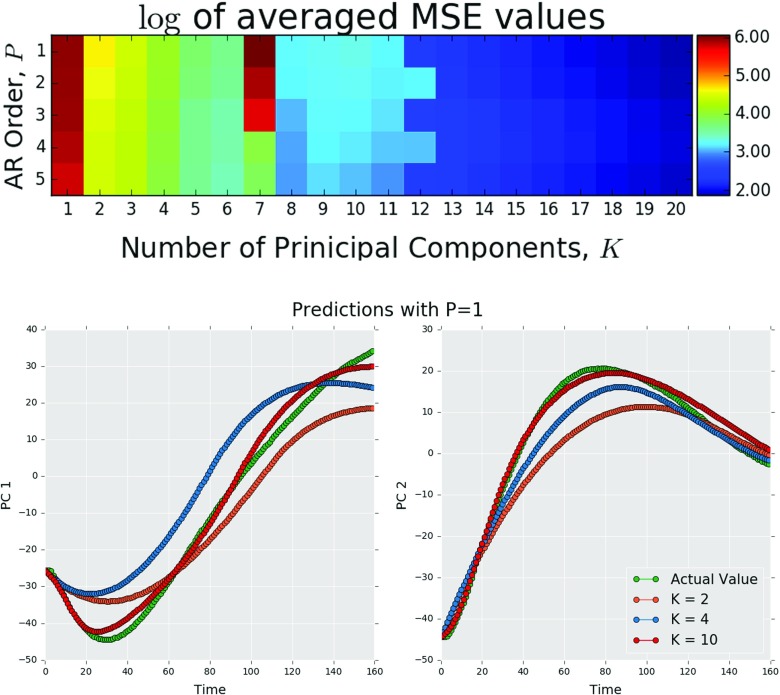
The results from the leave one sample out cross-validation process can be found on the top image in Fig. 7. It was found that as the number of PCs increased, the mean MSE value decreased. When K is small, the mean MSE value decreases as P increases, but this trend reverses as the K gets large. In general, the value of P had less effect on the MSE value as the number of PCs increased. This essentially means that we are likely to extract a better model by capturing in more detail the structure information in the immediately preceding one to two timesteps as opposed to retaining less structure information over a larger number of the preceding timesteps. Indeed, the model with the lowest mean MSE value was found to have P=1 and K=20 and had an average value of 6.8 overall all calibrations. The general trend indicates that the model accuracy would continue to increase as the number of PCs increases but with diminishing returns and higher computational costs. The bottom images in Fig. 7 qualitatively show that the predictions for PCs 1 and 2 improve as the total number of PCs, K, increases.

Fig. 7.

Log of the mean MSE values created using leave one sample out cross-validation as a function of the autoregressive order P and total number of principal components K (above). Mean MSE values for PCs 1 and 2 decrease as the number of the total number of principal components K increases (below) (Color figure online)

In order to demonstrate the utility of this method, the results from models with the maximum and minimum MSE values found during the cross-validation process for P=1 and K=20 are shown in Figs. 8 and 9. Using the predicted low-dimensional microstructure descriptors, a low rank approximation of the X-ray scattering images was created as shown in Eq. 3. The model used to predict sample LLDPE1.2b had the lowest MSE value of 2.11. Figure 9 shows the actual final image and the final predicted image using the reduced-order image as well as the entire microstructure evolution pathline (in the PC space). The model used to predict sample LLDPE2.2b had a MSE value of 19.9. The measured and predicted images are shown in Fig. 9 along with the predictions of the entire microstructure evolution pathline. Interestingly, in spite of the large differences in the error measures, both predictions in Figs. 8 and 9 have retained the relevant scattering information.

Fig. 8.

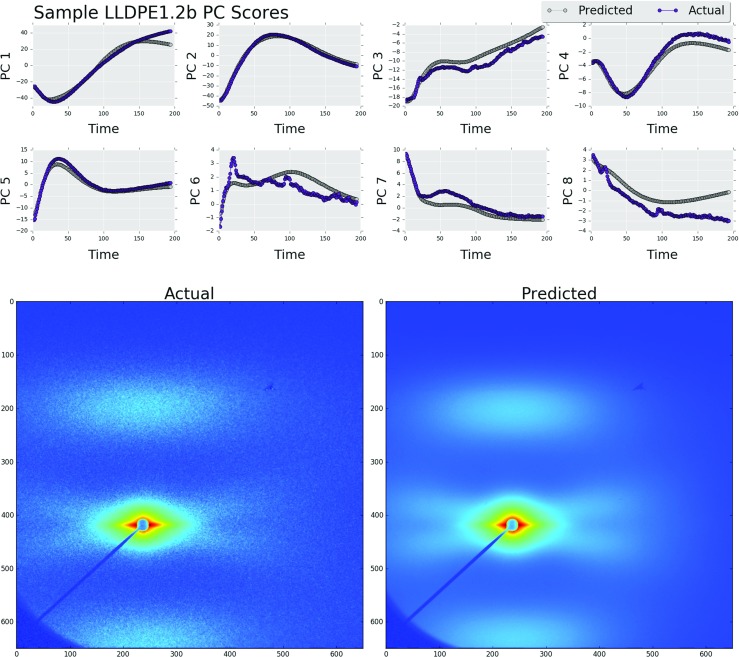
Predicted and actual principal component scores for sample LLDPE1.2b (above). The original image (bottom left) and the predicted image (bottom right). The mean squared error value over the predicted principal component scores had a value 2.11 (Color figure online)

Fig. 9.

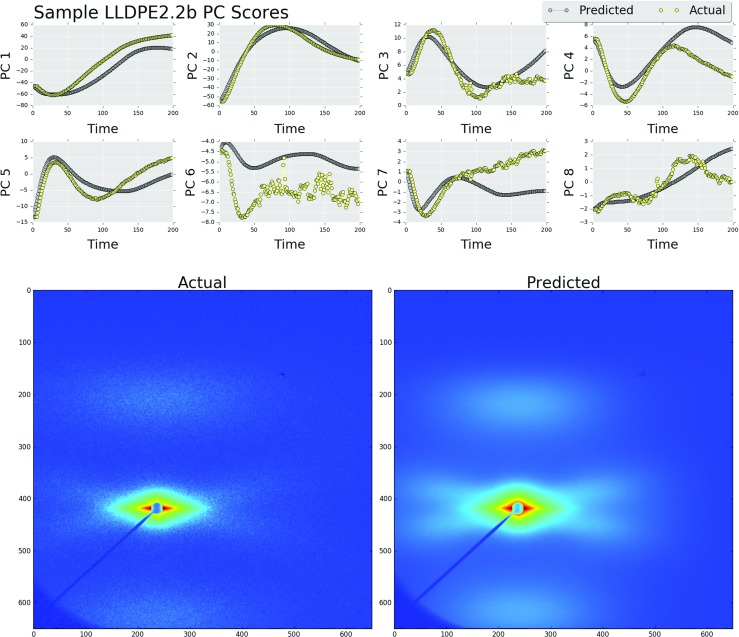
Predicted and actual principal component scores for sample LLDPE2.2b (above). The original image (bottom left) and the predicted image (bottom right). The mean squared error value over the predicted principal component scores had a value 19.9 (Color figure online)

Leave one sample out cross-validation was used in this study for two reasons: (i) consideration of the least and most accurate models allows for an unbiased assessment of the method’s utility and robustness, and (ii) leave one sample out cross-validation is equivalent to a traditional train-test split where 11 samples are used to calibration and one sample is used for validation, repeated 12 times in the present case study. Most practical material development efforts have limited data, and this approach provides an excellent strategy for building useful models with limited data.

Conclusion

In this paper, an extension of the MKS homogenization framework is presented to allow extraction of process-structure evolution linkages from multiscale material datasets. This extension was accomplished by extending the definition of the discretized microstructure function to include details of its temporal variation. Most importantly, this extension was accomplished in a way that allowed the continued application of PCA for low-dimensional representation of the material structure and its time evolution in a selected processing step as a structure evolution pathline. This is particularly significant as this is the only known dimensionality reduction algorithm that employs a distance-preserving linear transformation, which allows a natural insertion into established composite theories (for establishing the complementary structure-property linkages) and is computationally low cost. Therefore, the framework presented here potentially offers the broadest interoperability with complementary PSP linkages needed to objectively guide the material innovation efforts. Furthermore, the framework presented here was amenable to the application of time series multivariate adaptive regression splines (TSMARS). The viability and potential of this extended framework was demonstrated through an application on an ensemble of small-angle X-ray scattering images obtained from in situ plastic deformation of low-density PE samples. It was seen that the proposed framework exhibited remarkable accuracy in capturing the highly non-linear and complex characteristics of structure evolution in these experiments.

The theoretical framework outlined in this paper provides a strong foundation to connect time series analysis and sophisticated composite theories to create robust process-structure evolution linkages. Together with process-structure linkages, this method can be used to create comprehensive process-structure-property linkages in a format that can be readily accessed and utilized by the material development community and shared with manufacturing experts.