Obesity and Bone Health Revisited: A Mendelian Randomization Study for Koreans

ABSTRACT

Epidemiologic studies have replicated positive associations between obesity and bone health, but their mechanisms are still debatable. We aimed to scrutinize an association between bone health and obesity using genetic instrumental variables (IVs) with the distinction of general versus abdominal obesity. We selected independent IVs of body mass index (BMI) and BMI‐adjusted waist circumference (aWC, a proxy of a central fat distribution) by combining novel genomewide searches from the Korean Genome Epidemiology Study (KoGES) consortium and existing reports. We evaluated the associations of obesity indices with bone health measures for weight‐bearing and non–weight‐bearing bones, applying standard Mendelian randomization analyses. The IVs for BMI and aWC selected from KoGES cohort studies (n = 14,389) explained its own trait only, negating the mutual correlation at the phenotypic level. Two‐stage least squares analyses using an independent cohort study (n = 2507, mean age = 44.4 years, men = 44.3%) showed that BMI but not aWC was positively associated with bone mineral density (BMD for weight‐bearing bones: 0.063 ± 0.016 g/cm² per one standard deviation increase in BMI), implying the fat distribution might be neutral. The association was weaker for non–weight‐bearing bones (BMI on BMD: 0.034 ± 0.011 g/cm²), and for postmenopausal women the association was absent. Obesity increased both bone area and bone mineral content (BMC) to a lesser degree, but the increase in BMC was not evident for menopausal women. When we stratified the weight into lean body mass and fat mass, the increase in BMD was more evident for lean body mass, and fat mass showed a beneficial role only for men and premenopausal women. Our findings suggest that bone health might gain little from obesity, if any, through its added weight, and other means to prevent bone loss would be essential for postmenopausal women. © 2019 American Society for Bone and Mineral Research.

Introduction

Bone health is a priority public health issue associated with osteoporosis, fractures, and increased mortality following fracture in old age.1 Worldwide, 6.6% to 22.1% of people over age 50 years were estimated to have osteoporosis.2, 3 Although obesity is a well‐established health risk, it has shown beneficial effects on bone health such that increased body mass index (BMI) is associated with higher bone mineral density (BMD).4, 5 Despite somewhat consistent findings in human studies, the ostensibly positive associations between obesity and bone health has been scrutinized because: fat accumulation impairs bone health in animal studies6, 7; certain types of bone fracture rates increase for obese individuals8; and subgroup analysis according to obesity indices, bone sites, sex, and menopausal status frequently showed inconsistent findings.4, 5, 9, 10

Evidence suggests that the excess fat accumulation may have an agathokakological effect on bone: beneficial roles through increased mechanical loading and secretion of osteotropic hormones, and harmful influences through releasing osteoclastic factors such as inflammatory cytokines.6, 11 Multiple epidemiologic studies attempted to dissect the association between BMI and bone into weight‐bearing and hormonal effects by subgroup analysis according to weight‐bearing sites. Supposedly, a stronger association between obesity and BMD in weight‐bearing (WB) bones than that with BMD in non–weight‐bearing (non‐WB) bones would support the importance of weight‐bearing effects, whereas no difference by the sites of bones would refute it. Some studies showed stronger associations for WB bones,4, 5 which were, however, not consistent with some studies.10

Because central obesity is a surrogate of visceral fat with more endocrinological activities than subcutaneous fat, using different obesity indices would add information to differentiate the role of fat accumulation on bone health.12 In epidemiologic studies, waist‐hip ratio, waist circumference (WC), and BMI‐adjusted WC (aWC) are used as surrogate indices of central adiposity.13, 14 Associations between central obesity indices and bone are inconsistent, with both positive15, 16, 17 or non‐association,15 or a negative association when aWCs were used to adjust the weight effects of fat accumulation.18, 19 The discrepancy between studies might have stemmed, at least partially, from the high correlation between general and central obesity.

Considering the bone fracture risk, the nature of the association between obesity and bone becomes more complicated. Bone density is an established determinant of fracture risk,20 but previous studies have reported that obesity either increased or decreased fracture risk depending on sites, age groups, and sex.21, 22, 23 Obesity‐related risk factors of fracture, such as sedentariness and frequent falls, only partly explain the increased risk of bone fracture for the obese.21, 22, 23 To disentangle this complexity, we used different aspects of bone measures including BMD, bone area (BA), bone mineral content (BMC), and area‐adjusted BMC (aBMC), which was suggested to assess the volumetric density better than BMD.24

The Mendelian randomization (MR) approach utilizes genetic variants associated with risk factors as instrumental variables (IVs) to test an association. With appropriate IVs representing the risk factors of interest, but independent of potential confounders by design, MR may allow a test for the presence of causal associations.25 Using an MR approach, we attempted to assess the associations between different obesity and bone health indices. Moreover, we expected that IVs associated with only one of either general or central obesity would allow a test for each component of obesity to discriminate the intercorrelated effects at the phenotypic level.

Our study aims to scrutinize the observed association between obesity and bone using an MR approach. To this end, we estimated and compared the findings from conventional and MR approaches, for each index of obesity and bone health metrics.

Subjects and Methods

Study participants

The Korean Genome Epidemiology Study (KoGES) is a population genome cohort studies in Korea consisting of six prospective cohorts, which has been collecting epidemiologic, clinical, and genomic information since 2003.26 We selected participants with both obesity indices and genomewide dense genetic marker information. The Healthy Twin Study, one of the KoGES consortia, is a twin‐family cohort study that recruited same‐sex twins over the age of 30 years and their related family members. Detailed study protocols and information have been described.27 From the Healthy Twin Study, we included participants who had undergone anthropometric measurements, genotyping of whole‐genome markers, and a whole‐body dual‐energy X‐ray absorptiometry (DXA) scan for bone indices. We excluded participants if they were under hormone replacement therapy, recently treated for cancer or hyperthyroidism/hypothyroidism, or currently taking medication for osteoporosis. Postmenopausal women were defined as having no menstruation at least for 12 consecutive months, and either 55 years of age or older, or natural menopause not by surgery or other medication. All participants provided written informed consent and this study was approved by the Institutional Review Board of Samsung Medical Center and Seoul National University (2005‐08‐113). This study was conducted in accordance with the World Medical Association Declaration of Helsinki.

Measurements: anthropometry, bone measures, and related traits

For anthropometry, body weight and height were measured to the nearest tenth kilogram and centimeter using Tanita weighing scales (Tanita UK Ltd, Uxbridge, UK) and Harpenden stadiometers (Holtain Ltd, Crymych, UK). BMI was calculated as a ratio of body mass (kg) to height squared (m²), and waist circumference was measured in the standing position at the point between the lower rib margin and the iliac crest. aWC was obtained by taking residuals from the linear regression of WC on BMI. We expected that aWC would represent central fat distribution independent of general fat accumulation because WC was associated with abdominal visceral fat with a given BMI by Janssen and colleagues.13 Lean body mass (LBM) and fat mass (FM) were measured using DXA.

Bone measures comprised subregional BMD and BA of whole‐body scans. Spinal bone was calibrated separately for the thoracic (T‐) and lumbar (L‐) vertebrae (Supporting Fig.  1). BMD was measured by DXA scanning, and BMC was calculated multiplying BMD by projected BA; area‐adjusted BMC (aBMC) was estimated as residuals from the linear regression model of log‐transformed BMC adjusted for log‐transformed BA. Bones of lower limbs and L‐spine were grouped as WB; and those from upper limbs and T‐spine as non‐WB. Skull bones were analyzed as a different category due to possible differences in physiologic environments. Scans showing any abnormal spinal curvature were excluded from final analysis. Bone measures were taken using one DXA device (Delphi A; Hologic, Bedford, MA, USA) in one clinical center.

Age, smoking, drinking, and physical exercise information were collected through questionnaires about lifestyle. Drinkers were classified as heavy drinkers if they consumed more than drinks on a single occasion more than twice a month; otherwise, as moderate drinkers. Regular physical exercise was defined as moderate to vigorous according to intensity of physical activity done more than three times per week.

Construction of mutually independent IVs of BMI and aWC

Genotyping, quality control, and imputation methods for different cohorts of Korea are described in the Supporting Methods. To calculate the genetic risk scores (GRS) for BMI, we considered single‐nucleotide polymorphisms (SNPs) that reached genomewide significance (p < 5 × 10^–8) in a large genomewide association study (GWAS) of East Asian populations.28 For the GRS of aWC, because reliable reports were lacking, a de novo GWAS analysis was performed using two population‐based cohorts from KoGES consortium—Korean Association Resource (KARE) and Health Examinee (HEXA) study26—plus a cohort that recruited health examinees from the Seoul National University Hospital and the Gangnam Center for Health Promotion (SNUH‐HP).29 Detailed methods for the GWAS and these cohorts are described in the Supporting Methods. We calculated GRS for BMI and aWC from significant genetic markers by weighting their previously reported (BMI, with replicated findings) beta values or simply summing up the newly‐estimated counts of risk alleles (aWC, without replicated findings). GRS formulas for BMI and aWC are presented as follows:

$$\mathrm{B}\mathrm{M}\mathrm{I}\mathrm{G}\mathrm{R}\mathrm{S}=\sum ({\mathrm{\beta }}_{\mathrm{i}}\times \mathrm{\#}\mathrm{o}\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{k}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{S}\mathrm{N}{\mathrm{P}}_i),i=i\mathrm{t}\mathrm{h}\mathrm{S}\mathrm{N}\mathrm{P}$$

$$\mathrm{a}\mathrm{W}\mathrm{C}\mathrm{G}\mathrm{R}\mathrm{S}=\sum \left(\mathrm{\#}\mathrm{o}\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{k}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{S}\mathrm{N}{\mathrm{P}}_i\right)$$

Statistical analyses

We evaluated the associations between obesity and BMD using BMI, aWC, FM, LBM, and percent body fat as exposure variables and WB BMD and non‐WB BMD as outcome variables. We stratified the analysis by sex and menopausal status for women.

We assessed the intercorrelations between obesity (BMI, WC, aWC, body fat percentage, FM, and LBM) and BMD measures (WB bones, non‐WB bones, and skull) at both phenotypic and genotypic levels, involving the Healthy Twin Study data. We estimated phenotypic correlations after adjusting the familial relationship as random effects. For genetic correlations, we applied genetic variance component analysis to break down the phenotypic correlation into genetic versus nongenetic correlation based on kinship matrix, using SOLAR Eclipse v7.6.4 (see Supporting Fig.  5, for more details).30 For all correlation measures, we adjusted for age and sex, and for fat mass and lean mass; we also adjusted for the square of height. We also applied the linkage disequilibrium (LD) score regression method31 to replicate genetic correlations between obesity indices (BMI and aWC from the GIANT Consortium data32, 33) and BMD at heel bones (UK Biobank34).

The directed acyclic graph (DAG) underpinning our MR study is shown in Supporting Fig.  2. To assess the strengths of IV for BMI and aWC, we used the F statistics and R ² value of the GRS over the phenotypic measures for Equation (1) (G→X of Supporting Fig.  2). We considered F statistic larger than 10 as having potential strength to explain the phenotypes.25 We used two‐stage least squares (2SLS) regression to fit the IV models35 of Equation (1) to obtain estimates of the causal association between adiposity and bone measures of Equation (2). In the second stage (Equation (2)), the predicted exposure values ($\hat{X}$) based on the genotype (G) were plugged in another least‐squares regression of each bone index (outcome, Y) to estimate the magnitude of causal association that is theoretically uninfluenced by confounding (C).

$$\mathrm{X}=a_1+b_{1}G+c_{1}C+u_1$$ (1)

$$\mathrm{Y}=a_2+b_2\hat{X}+u_2$$ (2)

Standard errors (SEs) from each regression were taken into account in a concerted way to prevent inflated type I error by ignoring the variance of the first stage (Equation (1)). The ivreg2 command in STATA (version 10; StataCorp., College Station, TX, USA) was used.35 To provide a standardized comparison between measures of different scale, estimates from both conventional ordinary least squares (OLS) and IV regressions (2SLS) were reported per one standard deviation (SD) increase in BMI and aWC. Age and sex were included to generate adjusted OLS and IV estimates. To test endogeneity, we additionally performed a Durbin‐Wu‐Hausman test for each regression. The null hypothesis of this test is that the exposure X is exogenous so that the estimate obtained by OLS is consistent. Rejection of the null hypothesis indicates the IV estimate is a consistent and useful estimator compared to the OLS estimate in the presence of endogeneity.36 The ivendog command in STATA (version 10) was used followed by ivreg.

We estimated the statistical power to detect a causal association allowing the alpha error of 0.05, for given sample sizes, effect sizes of OLS and MR models, R ² of IV, and variances of exposure and outcome variables. We used the “mRnd”37 program for the power calculations. Also, we conducted sensitivity analyses including and excluding the participants diagnosed with osteoporosis.

To test the pleiotropy of genetic markers constituting the IVs, we used MR‐Egger regression.38 In this procedure, we fitted obesity measures on obesity‐related genetic instruments (x axis) versus bone health measures regressed on the IVs (y axis), as regression coefficients and SEs. We assessed the presence of horizontal pleiotropy by evaluating whether the y‐intercept term significantly deviates from zero, which implies the effect of IVs on bone when the IVs have no effects on obesity (influences not through obesity). All analyses were undertaken using the data analysis software STATA, version 10.

Results

Among 3500 individuals from the Healthy Twin Study, subjects with anthropometric, bone measures and genetic data were included. Participants who were under treatment for cancer or hyperthyroidism/hypothyroidism, under hormone replacement therapy, taking medications for osteoporosis, or who did not have specific bone measures for T‐, and L‐spine were excluded, leaving 2507 individuals for the MR analysis (flowchart is shown in Supporting Fig.  3). Baseline characteristics of these participants are shown in Table 1. BMD levels at all bone regions were higher for men than women, and higher for premenopausal than postmenopausal women.

Table 1.

Characteristics of the Study Participants

		Women
Variables	Men (n = 1433)	All (n = 2067)	Premenopausal (n = 1437)	Postmenopausal (n = 594)	Total (n = 3500)
Age (years)	44.68 ± 14.37	44.14 ± 13.23	37.12 ± 7.71	60.52 ± 8.22	44.36 ± 13.7
Anthropometric
Height (cm)	169.9 ± 6.41	157.03 ± 5.69	158.16 ± 5.43	154.37 ± 5.39	162.30 ± 8.72
Weight (kg)	70.73 ± 10.64	57.07 ± 8.59	56.42 ± 8.58	58.50 ± 8.50	62.66 ± 11.62
BMI (kg/m2)	24.45 ± 3.06	23.14 ± 3.33	22.54 ± 3.19	24.52 ± 3.29	23.68 ± 3.29
Waist circumference (cm)	85.06 ± 8.09	77.86 ± 9.04	75.70 ± 8.31	82.95 ± 8.79	80.81 ± 9.36
Fat mass (kg)	15.67 ± 5.45	18.34 ± 5.51	17.64 ± 5.39	20.21 ± 5.39	17.16 ± 5.64
Lean body mass (kg)	51.06 ± 6.73	35.60 ± 4.64	35.64 ± 4.54	35.48 ± 4.88	42.44 ± 9.54
% Body fat	22.26 ± 5.49	32.37 ± 6.17	31.42 ± 5.88	34.87 ± 6.23	27.89 ± 7.73
BMD a
Upper limbs	0.835 ± 0.082	0.679 ± 0.059	0.692 ± 0.052	0.645 ± 0.064	0.748 ± 0.105
Lower limbs	1.257 ± 0.117	1.070 ± 0.110	1.088 ± 0.089	1.023 ± 0.142	1.153 ± 0.146
Thoracic spine	0.884 ± 0.156	0.798 ± 0.19	0.831 ± 0.202	0.712 ± 0.115	0.836 ± 0.181
Lumbar spine	1.070 ± 0.172	1.062 ± 0.223	1.098 ± 0.152	0.968 ± 0.329	1.066 ± 0.202
Skull	2.017 ± 0.318	2.11 ± 0.338	2.175 ± 0.311	1.93 ± 0.345	2.068 ± 0.333

Values are mean ± SD.

BMD = bone mineral density.

^aAnalyses using bone measures included 2507 samples (1110 men, 1015 premenopausal women, and 382 postmenopausal women).

For the IVs of BMI and aWC, we used 13 and 12 SNP markers showing genomewide‐level associations with respective phenotypes. The characteristics of participants for GWAS of aWC are shown in Supporting Table  1. The results of replication or independent GWAS analyses regarding the selection process is further described in the Supporting Methods and Supporting Table  2.

Supporting Table  3 presents first‐stage regression results for each BMI and aWC GRS with each corresponding risk phenotypes, as well as with each other risk phenotype for comparison. Each GRS showed F value >10 and explained variance above 1%; and, F value <10 and explained variance <1% with the other obesity phenotype, suggesting that these GRS adequately proxy each adiposity but independent of one another (IV assumption I). Also, there were no overlaps between BMI SNPs and aWC SNPs. The plot of obesity measures by both GRSs also showed that each GRS only reflects its corresponding variable (Supporting Fig.  4). To assess whether the IVs had randomization effects on other confounders (IV assumption II), we divided both BMI and aWC GRSs into tertiles in ascending order, then compared the value of known covariates: age, sex, smoking status, alcohol consumption, and physical exercise (Supporting Table  4). All of the covariate values did not differ between each GRS (G) tertile, whereas they did differ between the tertiles of the obesity phenotypes per se (X).

In the phenotypic level analysis, BMI was positively associated with BMD measured in both WB and non‐WB sites, while BMI only showed a positive association with aBMC of WB sites (Table 2, Supporting Table  5). On the other hand, aWC showed no association with BMD and was negatively associated with aBMC of both WB and non‐WB sites for men and women before menopause. Findings from MR analyses are largely compatible with previous studies, suggesting that BMI was causally associated with BMD in WB sites (mean ± SE for overall: 0.063 ± 0.016 g/cm²; men: 0.062 ± 0.020 g/cm²; premenopausal women: 0.075 ± 0.023 g/cm², all estimates per one SD change in BMI; Table 2). Subgroup analysis suggested that BMI was not associated with BMD of WB bones for postmenopausal women. For non‐WB bones, BMI still showed a causal association for men, but with the smaller magnitude and less consistent between subgroups (mean ± SE for overall: 0.034 ± 0.011 g/cm² per one SD change in BMI). For women, BMI showed no causal association with BMD for non‐WB sites (Table 2). Along with the increase in BMI (per one SD), BA increased very similarly for both WB and non‐WB sites (43.0 cm² and 40.8 cm²), but the increase in the BMC in WB sites (95.8 g) was greater than that for non‐WB bones (51.4 g) (Table 3, Supporting Table  5). For all models using IVs, aWC did not show any meaningful associations with BMD (Table 2, Table 3). For skull bones, BMI increased the BMD; and, aWC decreased the BMD from the conventional analysis, but IV analyses negated the associations at the phenotypic level (Table 2).

Table 2.

Comparison Between Observational and Instrumental Variable Analyses of the Effect of Obesity on BMD

						Women
			Men (n = 1110)			All (n = 1397)			Premenopausal (n = 1015)			Postmenopausal (n = 382)			Total (n = 2507)
Variables	Sites of bones	Method	β ± SE	p	DWH	β ± SE	p	DWH	β ± SE	p	DWH	β ± SE	p	DWH	β ± SE	p	DWH
BMI	WB	OLS	0.044 ± 0.003	<0.0005		0.041 ± 0.003	<0.0005		0.042 ± 0.003	<0.0005		0.036 ± 0.007	<0.0005		0.046 ± 0.002	<0.0005
		MR	0.062 ± 0.020	0.002	0.341	0.056 ± 0.024	0.021	0.528	0.075 ± 0.023	0.001	0.127	0.007 ± 0.072	0.922	0.683	0.063 ± 0.016	<0.0005	0.267
	non‐WB	OLS	0.031 ± 0.003	<0.0005		0.024 ± 0.002	<0.0005		0.024 ± 0.002	<0.0005		0.022 ± 0.003	<0.0005		0.027 ± 0.001	<0.0005
		MR	0.048 ± 0.015	0.002	0.229	0.014 ± 0.016	0.381	0.534	0.026 ± 0.018	0.145	0.920	−0.016 ± 0.037	0.661	0.231	0.034 ± 0.011	0.002	0.553
	Skull	OLS	0.047 ± 0.024	0.049		0.071 ± 0.016	<0.0005		0.059 ± 0.019	0.002		0.09 ± 0.031	0.004		0.036 ± 0.013	0.007
		MR	0.058 ± 0.142	0.683	0.945	0.225 ± 0.138	0.103	0.254	0.269 ± 0.161	0.095	0.175	0.113 ± 0.272	0.677	0.937	0.120 ± 0.097	0.214	0.397
aWC	WB	OLS	−0.006 ± 0.004	0.152		−0.003 ± 0.003	0.362		−0.004 ± 0.003	0.275		0.007 ± 0.008	0.353		0.002 ± 0.003	0.416
		MR	0.054 ± 0.032	0.091	0.039	0.045 ± 0.043	0.291	0.222	0.051 ± 0.070	0.467	0.377	0.063 ± 0.062	0.311	0.332	0.043 ± 0.027	0.107	0.106
	non‐WB	OLS	0 ± 0.003	0.883		−0.006 ± 0.002	0.004		−0.005 ± 0.003	0.045		0 ± 0.004	0.947		−0.001 ± 0.002	0.639
		MR	0.045 ± 0.024	0.057	0.036	0.029 ± 0.028	0.311	0.178	0.061 ± 0.063	0.333	0.181	0.017 ± 0.028	0.532	0.505	0.036 ± 0.019	0.055	0.033
	Skull	OLS	−0.014 ± 0.028	0.603		−0.05 ± 0.018	0.005		−0.04 ± 0.021	0.065		−0.028 ± 0.032	0.391		−0.049 ± 0.015	0.001
		MR	0.019 ± 0.192	0.923	0.865	0.458 ± 0.256	0.073	0.013	1.067 ± 0.742	0.150	0.004	0.017 ± 0.226	0.942	0.827	0.242 ± 0.153	0.113	0.041

Bold values of p are significant.

BMD = bone mineral density; SE = standard error; P‐value from Durbin‐Wu‐Hausman test for equality of MR (Mendelian randomization) and OLS (ordinary least squares) method; BMI = body mass index; WB = weight‐bearing bones; non‐WB = non–weight‐bearing bones except for skull; aWC = waist circumference adjusted for BMI.

Table 3.

Instrumental Variable Analysis of the Effect of Obesity on Bone Variables

				Women
		Men (n = 1110)		All (n = 1397)		Premenopausal (n = 1015)		Postmenopausal (n = 382)		Total (n = 2507)
Variables	Sites of bones	β ± SE	p	β ± SE	p	β ± SE	p	β ± SE	p	β ± SE	p
BMI
BMC	WB	95.93 ± 27.42	<0.0005	79.60 ± 26.76	0.003	111.33 ± 31.24	<0.0005	−6.65 ± 67.79	0.922	95.52 ± 19.56	<0.0005
	non‐WB	67.59 ± 13.86	<0.0005	26.74 ± 12.04	0.026	42.99 ± 13.51	0.001	−16.5 ± 32.2	0.608	51.4 ± 9.26	<0.0005
	Skull	1.40 ± 63.45	0.982	58.68 ± 53.43	0.272	84.39 ± 60.59	0.164	6.53 ± 113.34	0.954	28.2 ± 40.15	0.482
BA	WB	38.16 ± 13.7	0.0050	40.75 ± 15.61	0.009	57.11 ± 19.08	0.003	−4.29 ± 35.98	0.905	43.03 ± 10.37	<0.0005
	non‐WB	47.22 ± 9.92	<0.0005	27.90 ± 10.67	0.009	41.52 ± 12.42	0.001	−9.15 ± 26.95	0.734	40.79 ± 7.36	<0.0005
	Skull	−0.78 ± 10.4	0.940	4.07 ± 11.2	0.716	10.03 ± 12.03	0.404	−9.15 ± 26.41	0.729	2.39 ± 7.37	0.746
BMD	WB	0.062 ± 0.020	0.0020	0.056 ± 0.024	0.021	0.075 ± 0.023	0.001	0.007 ± 0.072	0.922	0.063 ± 0.016	<0.0005
	non‐WB	0.048 ± 0.015	0.0020	0.014 ± 0.016	0.381	0.026 ± 0.018	0.145	−0.016 ± 0.037	0.661	0.034 ± 0.011	0.002
	Skull	0.058 ± 0.142	0.683	0.225 ± 0.138	0.103	0.269 ± 0.161	0.095	0.113 ± 0.272	0.677	0.120 ± 0.097	0.214
aBMC	WB	0.018 ± 0.016	0.251	0.015 ± 0.023	0.509	0.017 ± 0.021	0.421	0.01 ± 0.065	0.879	0.016 ± 0.013	0.211
	non‐WB	0.004 ± 0.018	0.834	−0.015 ± 0.024	0.529	−0.018 ± 0.026	0.488	−0.003 ± 0.052	0.952	−0.006 ± 0.014	0.642
	Skull	0.054 ± 0.042	0.199	0.103 ± 0.055	0.059	0.094 ± 0.057	0.097	0.136 ± 0.142	0.341	0.065 ± 0.033	0.050
aWC
BMC	WB	156.53 ± 49.65	0.002	3.08 ± 43.13	0.943	−13.78 ± 78.64	0.8610	35.37 ± 54.17	0.514	73.45 ± 34.01	0.031
	non‐WB	57.41 ± 22.99	0.013	24.4 ± 22.3	0.274	50.96 ± 48.3	0.2910	14.87 ± 22.92	0.517	37.05 ± 16.88	0.028
	Skull	−46.58 ± 85.66	0.587	166.65 ± 94.7	0.078	378.26 ± 263.65	0.151	30.2 ± 94.61	0.750	57.17 ± 60.94	0.348
BA	WB	94.36 ± 24.96	<0.0005	−22.94 ± 25.93	0.376	−37.93 ± 53.21	0.4760	−6.35 ± 28.44	0.823	35.54 ± 16.82	0.035
	non‐WB	38.14 ± 15.77	0.0160	16.00 ± 18.53	0.388	29.29 ± 36.46	0.4220	13.02 ± 20.19	0.519	22.72 ± 12.74	0.075
	Skull	−25.34 ± 14.87	0.088	29.6 ± 18.61	0.112	65.42 ± 46.26	0.157	6.16 ± 21.60	0.775	−0.74 ± 10.95	0.946
BMD	WB	0.054 ± 0.032	0.091	0.045 ± 0.043	0.291	0.051 ± 0.0700	0.4670	0.063 ± 0.062	0.311	0.043 ± 0.027	0.107
	non‐WB	0.045 ± 0.024	0.057	0.029 ± 0.028	0.311	0.061 ± 0.063	0.3330	0.017 ± 0.028	0.532	0.036 ± 0.019	0.055
	Skull	0.019 ± 0.192	0.923	0.458 ± 0.256	0.073	1.067 ± 0.742	0.150	0.017 ± 0.226	0.942	0.242 ± 0.153	0.113
aBMC	WB	−0.034 ± 0.021	0.116	0.054 ± 0.037	0.14	0.083 ± 0.076	0.28	0.041 ± 0.042	0.323	0.006 ± 0.019	0.746
	non‐WB	0.011 ± 0.025	0.654	0.017 ± 0.032	0.606	0.041 ± 0.069	0.558	0.005 ± 0.031	0.879	0.018 ± 0.021	0.382
	Skull	0.103 ± 0.062	0.098	0.138 ± 0.084	0.102	0.271 ± 0.209	0.196	0.053 ± 0.083	0.521	0.132 ± 0.054	0.015

Bold values of p are significant.

SE = standard error; BMI = body mass index; BMC = bone mineral content; WB = weight‐bearing bones; non‐WB = non–weight‐bearing bones except for skull; BA = bone area; BMD = bone mineral density; aBMC = area‐adjusted bone mineral content; aWC = waist circumference adjusted for BMI.

When we examined the obesity‐bone association with each component of bone measure, BMD and aBMC showed differences in the causal models: BMD generally showed positive associations with BMI (Table 3), whereas aBMC did not show such an association even for WB sites (Supporting Table  5). BMI did show a positive association with aBMC for WB sites in a conventional analysis (0.013 g increase per one SD of BMI, Supporting Table  5). In the WB sites, both conventional and MR analysis indicated that BA and BMC increase as BMI increases; the relative increase of BMC to BA is larger for the MR analysis than that for the conventional models (Supporting Table  5).

We observed positive correlations between different obesity measures and BMD for both WB and non‐WB sites except for aWC (Supporting Fig.  5). Genetic correlations followed similar patterns as those at the phenotypic level, suggesting that the genetic correlations contribute a significant part of the phenotypic correlations. When we replicated genetic correlation for European Ancestry (GIANT consortium data for BMI and aWC; and UK Biobank data for BMD at heel bones), the LD score regression analysis showed compatible findings that only BMI, but not aWC showed positive and significant correlations with BMD of heel bones (Supporting Table  6).

When we explored the patterns of relationship between BMD and aBMC with the increase in BMI (at phenotype level), the increase in the BMD were linear for both WB and non‐WB sites, whereas the aBMC of WB sites did not show linear increase for BMI above 23; aBMC of non‐WB sites did not show any meaningful trends with BMI (Fig. 1).

Figure 1.

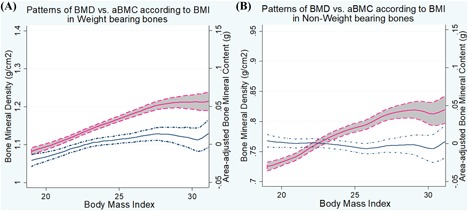
BMD versus aBMC against BMI in weight‐bearing (A) and non–weight‐bearing bones (B). Patterns of BMD (red line) and aBMC (blue line) against BMI are shown using STATA version 10. Gray shades between two dotted lines represent 95% confidence interval. (A) For weight‐bearing bones, both BMD and aBMC increase as BMI increases, but the magnitude of increase was greater for BMD compared to aBMC. Also, aBMC showed no increasing trend for BMI above 23. (B) For non–weight‐bearing bones, BMD increased with the increase of BMI, whereas aBMC remained constant by the change of BMI.

To further scrutinize the association between obesity and BMD, we inspected the general trends in BMD of WB (unadjusted) across the changes in LBM and FM of the whole body according to sex and menopausal status (Fig. 2). BMD increased linearly along the increase in LBM for all three groups; BMD also increased as the increase in FM for men and premenopausal at a lesser degree, but the increase was not evident for postmenopausal with the increase at more than 10 kg of FM. On the other hand, the increase in the BMD along the increase in the LBM did not differ between premenopausal and postmenopausal.

Figure 2.

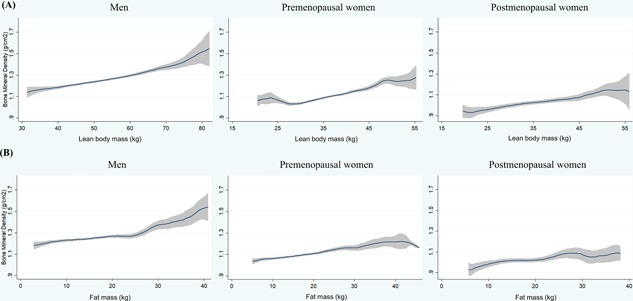
Graphical comparison of BMD in weight‐bearing bones against LBM (A) and FM (B) by subgroups. General trends in BMD of weight‐bearing bones are presented against (A) LBM and (B) FM by three subgroups: men, and premenopausal and postmenopausal women. For all three groups, BMD increased linearly as the increase of LBM. BMD also increased as the increase of FM for men and premenopausal women, whereas the beneficial role of FM was not evident for postmenopausal women.

Statistical power for analyses of all measures is shown in Supporting Table  7. For BMI, this study generally conferred an adequate level of statistical power (the association with BMD of WB bones: 0.81; non‐WB bones: 0.53). However, the power for the analyses of aWC was modest (0.3 to 0.39 for BMD of WB, non‐WB, and skulls), probably due to the smaller proportion of variance explained by IV and smaller effect size estimates, compared with those for BMI. When the participants diagnosed with osteoporosis were excluded for sensitivity analysis, the results were similar with the initial analysis (Supporting Table  8).

We also performed an MR‐Egger regression analysis to examine whether the association between obesity and BMD is robust to horizontal pleiotropy that could violate the assumptions of MR (the exclusion restriction criterion). Figure 3 illustrates the associations between the 13 BMI related variants and BMI with WB and non‐WB BMD in the form of scatter plots. The slope of the line is the MR‐Egger regression estimate of the causal effect using all variants as IVs. MR‐Egger regressions showed no meaningful intercept when the IVs do not have any effects on BMI, supporting that the BMI‐bone association observed in the MR analysis might not stem from unexplained pleiotropic effects (WB: intercept = 8.9 × 10^–4 [p = 0.547], β_IV = 0.015 [p = 0.013]; non‐WB: intercept = –4.0 × 10^–4 [p = 0.667], β_IV = 0.010 [p = 0.008]). MR‐Egger regressions for aWC, presented in Supporting Fig.  6, also showed little pleiotropic effect of aWC on both WB and non‐WB BMD (WB: intercept = 0.004 [p = 0.114], β_IV = –0.043 [p = 0.144]; non‐WB: intercept = 0.004 [p = 0.191], β_IV = –0.017 [p = 0.417]).

Figure 3.

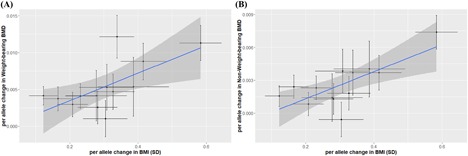
MR‐Egger regression plots for BMI and BMD in weight‐bearing (A) and non–weight‐bearing bones (B). Results from MR‐Egger regression analysis to assess horizontal pleiotropy are presented. Blue line represents the MR‐Egger regression estimate for the association between BMI and BMD in weight‐bearing (A) and non–weight‐bearing bones (B). For both sites, the y‐intercept estimates were not significantly different from zero (weight‐bearing bones: = 0.001, p = 0.55; non–weight‐bearing bones: = –0.004, p = 0.67), suggesting that there is no horizontal pleiotropy.

Discussion

Our study shows that BMI is positively associated with BMD of WB and non‐WB sites, whereas aWC is neutral to BMD. The presence of BMI association in non‐WB sites might be interpreted either by supportive WB effects of these sites or other hormonal effects of fat accumulation. In the sex‐stratified analyses, men showed positive associations between BMI and BMD in all sites, whereas women showed the positive association in WB bones only. When IV of aWC independent of BMI was introduced, MR analysis negated the negative association between aWC and BMD at the phenotypic level. Because aWC represents a relative fat distribution, the association of aWC with BMD would logically predict more non‐WB effects of fat accumulation. Overall, our findings suggest that the osteotropic effects of fat accumulation might be mainly through WB effects with little, if any, hormonal effects.

From the MR approach studying causal associations between general and central obesity and bone health, the positive association between BMI and BMD is mainly through WB effect and relative central fat distribution is neutral to bone health. Our MR findings of central obesity and bone contrast with our own findings at the phenotypic level and also previous studies reporting the negative association between bone health and visceral fat measured using CT scans.18, 39 Our findings suggest that epidemiologic findings between central obesity measures and BMD might have reflected residual correlations between general and central obesity. An MR analysis, by using genetic markers as IV, not only provides a causal insight but also might enable independent measures of highly interdependent traits.

BMD, in general, is an established predictor of bone strength and fracture risk.20 Our findings, however, might raise a question whether the increase in BMD for the obese has the same nature as BMD in normal or osteoporotic subjects. The increase in BMI shows a distinct increase in both BA and BMD. In the initial stage of osteoporosis, BMD decreases with small changes in BA. Lacking true volumetric BMD measures in our study, the introduction of another bone measure, aBMC, might add insight to this issue of bone strength. aBMC, presumably a better proxy of volumetric bone density,24 does not show a meaningful increase along BMI. As shown in Fig. 1, aBMC does not show a linear increase against the increase in BMI in both WB bones (Fig. 1 A) and non‐WB bones (Fig. 1 B). If aBMC better reflects the strength of cortical bone,24, 40, 41 being obese would not be protective against bone fracture risk with more concomitant risk factors such as more frequent falls.8, 21, 22 The association of obesity with bone fracture is more complicated and debatable than that with BMD, but the study by Chan and colleagues42 suggested that BMI does not have a meaningful association with reduced risk of fracture even considering the increase in BMD.

When we further stratified body weight into LBM and FM, the increase in BMD was more evident along the increase in LBM (Fig. 2 A) compared to that in FM (Fig. 2 B). The difference was remarkable for menopausal women: the increase in LBM led to a similar increase in BMD for both premenopausal and postmenopausal women whereas FM only had a beneficial role for the premenopausal. This finding suggests postmenopausal women who are most vulnerable to osteotropic changes might not benefit from the gain of FM.

In subsequent MR‐Egger regression analyses, observed influences of IVs of BMI were exerted mainly through BMI, because no significant intercept effects (when BMI = 0) were found (WB: ${\hat{\beta }}_0$ = 0.001, p‐value = 0.55, Fig. 3 A; non‐WB: ${\hat{\beta }}_0$ = −0.004, p‐value = 0.67, Fig. 3 B). Both WB and non‐WB bones showed the same profiles, suggesting that pleiotropic effects might not be the alternative explanations for the BMI‐BMD association.

This study confers advantages over previous studies in several aspects. First, the MR method provided a causal insight to the observed association between obesity and bone health, which was not possible with conventional analysis. Second, we dissected obesity into BMI and fat distribution. BMI and WC are almost inseparable traits in reality, but using genetic instruments could grasp the independent characteristics of them, resulting in a more precise interpretation of the association. Third, stratification by sites of bones could further divide the weight loading effect and hormonal effect of the association. Fourth, we included over 2500 participants from a single cohort. Thus, obesity and bone indices were measured using a uniform protocol and there is no difference in a population structure. Fifth, this compared the findings of BMD and aBMC from a homogenous population study of adult Asians where all the protocols were uniformly applied. It is not likely thus, that our findings are derived from population stratification or heterogeneity between studies. Finally, our study examined and fulfilled the basic premises of MR analysis, and also attempted to introduce more robust genetic IVs compared to previous MR studies about obesity and bone health.43, 44, 45

Our study also has several limitations and would require cautions for interpretation. First, subgroup analyses according to each stratum by sex and menopausal status resulted in a modest sample size. The lack of significant associations for the MR analyses on the aWC might require caution, because the statistical power for the association between aWC and BMD was moderate. Given the formal power calculation, the negative findings from subgroup MR analysis might imply both lack of association and insufficient statistical power. However, it is not likely that the lack of association between aWC and BMD mainly reflects the insufficient power, considering that additional analyses of genetic correlations or MR‐Egger are largely consistent with the MR findings, and the smaller estimate (Beta_MR) for aWC‐BMD contributed significantly for the reduced power. Second, the aWC was used as a proxy of central fat distribution, but ours cannot replace a study that measures accurate visceral fat amount such as one using abdominal CT scans. However, aWC with more sample sizes might estimate influences from visceral fat particularly when waist circumference is adjusted for BMI.46, 47 Third, we compared the findings from BMD with those from aBMC, but aBMC is a proxy measure and more accurate volumetric bone density measure was not taken in our study. Additionally, measurements on upper lumbar spinal columns and femoral neck were not available, which are popularly used to assess osteoporotic fracture risk. We tried to examine whether our findings of obesity and bones can be replicated for femur neck using publically available data: BMI showed protective statistically significant protective influence on the femoral neck in the independent MR analysis, but aWC did not demonstrate this causal association with femur neck (Supporting Table  9). Finally, the findings from our study were primarily derived from the Korean population and some cautions might be needed in generalizing the results to other populations. However, the same analysis from the European descent (Supporting Table  9) showed similar results, and it is not likely that our results are ethnicity‐specific.

In conclusion, our findings suggest that BMI is beneficial to bone health mainly through weight‐bearing effect, but non‐WB bones also benefit from the BMI with a lesser degree. The positive association between BMI and BMD was stronger for men than women, probably due to larger lean body mass. Our findings suggest that an increase in BMD due to BMI might be a causal association, but this positive association is not found for postmenopausal women who are the primary concerns for bone health. Central obesity, and probably the visceral fat that aWC represents, would at the most have a neutral role in bone health, so that the same preventive measures to manage abdominal obesity would be valid in considering bone health, too. Our findings cannot be directly extrapolated to the BMI association with fracture risk, but considering that obesity does not increase the BMD level for postmenopausal women, any attempts to increase BMI to prevent osteoporotic fractures for postmenopausal women might need to be discouraged.

Disclosures

All authors state that they have no conflicts of interest.

Supporting information

Supporting Data S1.