Optimizing Cancer Treatment Using Game Theory

Abstract

IMPORTANCE

While systemic therapy for disseminated cancer is often initially successful, malignant cells, using diverse adaptive strategies encoded in the human genome, almost invariably evolve resistance, leading to treatment failure. Thus, the Darwinian dynamics of resistance are formidable barriers to all forms of systemic cancer treatment but rarely integrated into clinical trial design or included within precision oncology initiatives.

OBSERVATIONS

We investigate cancer treatment as a game theoretic contest between the physician’s therapy and the cancer cells’ resistance strategies. This game has 2 critical asymmetries: (1) Only the physician can play rationally. Cancer cells, like all evolving organisms, can only adapt to current conditions; they can neither anticipate nor evolve adaptations for treatments that the physician has not yet applied. (2) It has a distinctive leader-follower (or “Stackelberg”) dynamics; the “leader” oncologist plays first and the “follower” cancer cells then respond and adapt to therapy. Current treatment protocols for metastatic cancer typically exploit neither asymmetry. By repeatedly administering the same drug(s) until disease progression, the physician “plays” a fixed strategy even as the opposing cancer cells continuously evolve successful adaptive responses. Furthermore, by changing treatment only when the tumor progresses, the physician cedes leadership to the cancer cells and treatment failure becomes nearly inevitable. Without fundamental changes in strategy, standard-of-care cancer therapy typically results in “Nash solutions” in which no unilateral change in treatment can favorably alter the outcome.

CONCLUSIONS AND RELEVANCE

Physicians can exploit the advantages inherent in the asymmetries of the cancer treatment game, and likely improve outcomes, by adopting more dynamic treatment protocols that integrate eco-evolutionary dynamics and modulate therapy accordingly. Implementing this approach will require new metrics of tumor response that incorporate both ecological (ie, size) and evolutionary (ie, molecular mechanisms of resistance and relative size of resistant population) changes.

Herein, we frame cancer treatment as a contest in which the physician enters a predator-prey–like game with the patient’s cancer cells. Therapy options represent the physician’s strategies. Cure occurs if therapy drives the cancer populations extinct. But, for most metastatic cancers, extinction is not achievable because the cancer cells are active “players” in the game. They respond to treatment by evolving effective strategies of therapy resistance. The physician-predator can also “evolve” in the sense that he or she can vary treatments over time.

Contests such as between the physician and cancer cells can be framed mathematically using game theory. Developed by Von Neumann and Morgenstern,¹Nash,² and others,³ game theory describes the strategies (choices), payoffs (consequences), and dynamical interactions involving both individuals and populations. Although initially focused on conflict⁴ and cooperation in economics,⁵ Maynard-Smith and Price⁶ pioneered its application to evolutionary dynamics. In evolutionary games,⁷ the players inherit rather than choose their strategies, and their payoffs are survival and proliferation. Game theoretic approaches have been applied to management of antibiotic resistance⁸ and control of agricultural pests,⁹ as well as cancer progression¹⁰ and treatment.¹¹

The cancer therapy predator-prey game differs from those in nature in ways that limit the physician: he or she does not gain a fitness advantage from killing cancer cells and his or her strategies are constrained by costs, ethics, and treatment toxic effects. However, cancer therapy also contains elements of social/economic games¹² that result in asymmetries that confer critical advantages on the physician, as follows.¹³

First, only the physician is rational and can anticipate future events. In contrast, cancer cells, typical of evolving organisms in nature, can only respond to what is happening or has happened. In particular, cancer cells can never anticipate or adapt to future conditions that differ from current or prior circumstances.

Second, there is a consistent sequence in the game because the physician always makes the first move by applying therapy and only then can cancer cells “play” by responding through the evolution of resistance strategies. Even if the molecular machinery of resistance is present prior to treatment, it is not under selection as a resistance strategy until treatment. Because of this, cancer therapy is a leader-follower game.¹⁴ First investigated by von Stackelberg,¹⁵ analyses of leader-follower dynamics (or “Stackelberg games”) identify critical advantages to the leader. The physician’s “first move,” along with the ability to anticipate subsequent cancer cell responses, provides a critical opportunity to obtain more favorable outcomes by steering and/or limiting the cancer cell’s resistance strategies.^16,17 Furthermore, when therapy is administered episodically or in cycles, the first-move advantage can be used to probe the tumor for available resistance strategies. This “pursuit and evasion” game has been extensively investigated through optimization methods in differential game theory (games with time-varying strategies),^16,17 such as the principle of optimality by Bellman.¹⁸ Thus, the physician can use information obtained in initial treatment cycles to progressively inform and optimize subsequent cycles.

Methods

Cancer Therapy as a Game

We frame cancer therapy as a game theoretic contest in which the physician assumes a predator-like role by attacking and killing cells within the cancer population. While some cancers may contain a single homogeneous cell population, we assume that most malignant tumors contain multiple subpopulations with varying sensitivities to available therapies. The physician begins the game by applying some treatment. Even as many (perhaps most) cancer cells die, survivors adapt and evolve counter (resistance) strategies. As the game progresses, the physician can then play the game by applying additional treatments, which can be identical to or different from prior treatments. With each new treatment, the tumor cells continue responding and adapting.

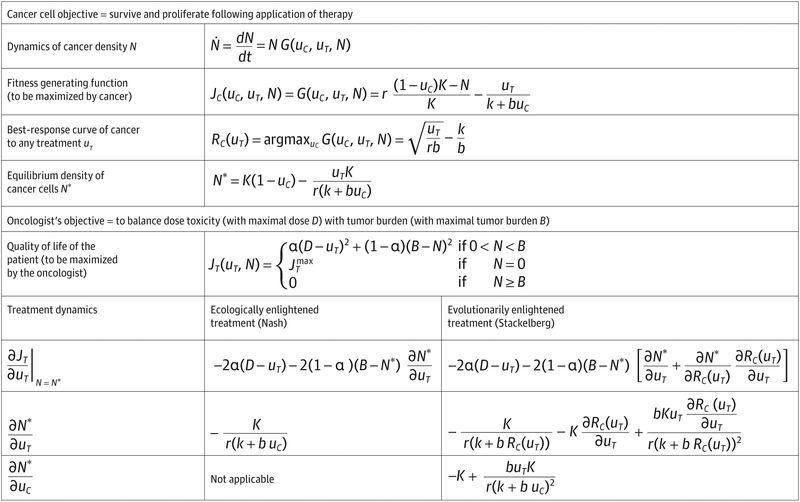
Our game theoretic model builds on a well-established mathematical formalism developed over several decades. Figure 1 and Figure 2 provide a brief outline of the quantitative methods and dynamics of the cancer therapy game. However, within the text we frame the discussion entirely in qualitative terms, reserving the formal mathematical analysis for a future publication.

Figure 1. Mathematical Formulas for Cancer Therapy Game.

An example of a cancer therapy game in which the cancer cells evolve strategies to maximize their net proliferation rates, and the physician aims to balance drug toxicity with overall tumor burden. Two approaches by the physician are considered: (1) Therapy that aims to maximize patient outcome given the current resistance strategy of the cancer cells. This treatment strategy results in a Nash equilibrium; (2) Therapy that aims to maximize patient outcome by anticipating the evolutionary and ecological response of the cancer cells. This therapy results in a Stackelberg equilibrium and a better outcome than the Nash equilibrium (see Figure 2).

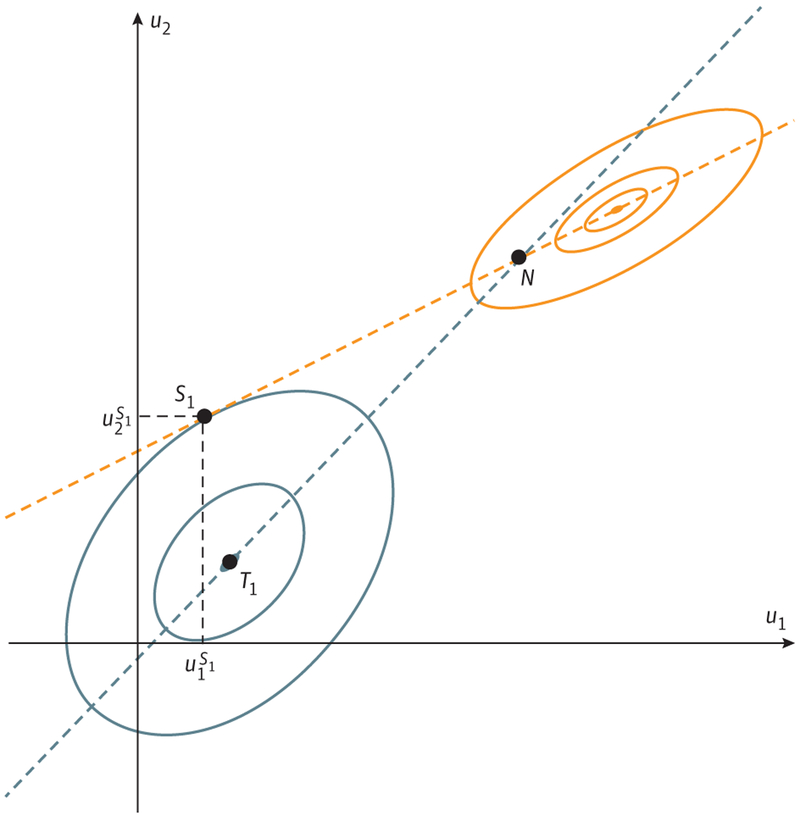
Figure 2. Nash and Stackelberg Equilibria.

We assume a 2-player game in which player 1 and player 2 choose actions u₁ and u₂ to maximize their payoffs J₁(u₁, u₂) and J₂(u₁, u₂), respectively. The graph shows level curves of payoffs J₁(u₁, u₂) (solid blue curves) and J₂(u₁, u₂) (solid orange curves) in the (u₁, u₂)-space. Player 1 would like to achieve point T₁ (his or her absolute maximum, known also as team optimum in game theory), and we investigate whether he or she can get close to this outcome when playing simultaneously with player 2 and when playing first. The blue dashed line denotes the best response of player 1 to any action of player 2 and the orange dashed line denotes the best response of player 2 to any action of player 1 (both obtained by maximizing a corresponding player’s payoff for any choice of the other player). If the players play simultaneously, the outcome lies at the intersection of the 2 best-response curves, the Nash equilibrium (N). However, if the physician (player 1) applies treatment with foreknowledge of the best-response curve of tumor cells, he or she can, as the leader, play the strategy u₁ with superscript S₁ based on that information. In contrast, the nonrational, follower cancer cells can only respond with the strategy on their best-response curve. The physician can anticipate this outcome; the cancer cells cannot. By exploiting his or her leadership role, the physician can both anticipate and steer the cancer cells’ resistance evolution toward a much better patient outcome corresponding to the point S₁, the Stackelberg equilibrium.

Current treatment protocols for metastatic cancer typically apply a drug or drug combination at maximum tolerated dose (MTD), either continuously or in repeated identical cycles. Response metrics are changes in tumor volume based on imaging Response Evaluation Criteria in Solid Tumors (RECIST) and/or serum biomarkers. The same treatment regimen continues until there are unacceptable toxic effects or unambiguous evidence of tumor progression.

Implicit in conventional treatment strategies (whether using MTD or metronomic drug scheduling) is that maximum benefit to the patient requires maximum tumor cell killing. In metastatic, incurable clinical settings, this strategy is intuitively appealing. Yet, it may be evolutionarily unwise. As shown in Figures 2, 3, and 4, maximum cell killing is an optimal strategy only if no cancer cells are capable of evolving a successful resistance to the applied therapy. However, if 1 or more cancer subpopulations are resistant a priori or capable of evolving adaptations quickly (ie, before the treatment kills them), this strategy will fail.

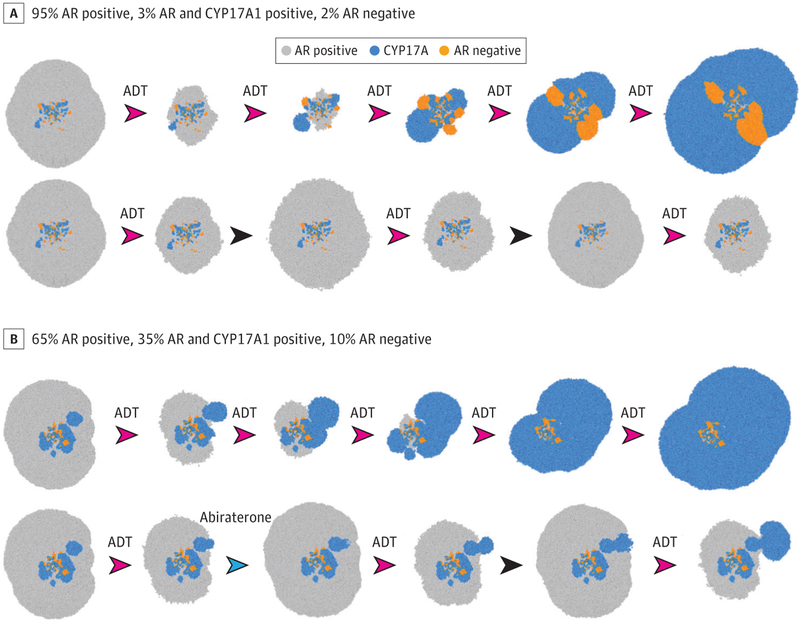
Figure 3. Adaptive Strategies for Metastatic Castration-Sensitive Prostate Cancer.

Computer simulations of treatment outcomes using methods outlined in Gallaher et al¹⁹ and similar to the models used to design ongoing clinical trials.¹¹ The subpopulations are color coded, and the area of each simulation represents total tumor burden. The model assumes a newly presented prostate cancer metastasis with different initial distributions of resistant and sensitive subpopulations. A, A pretreatment biopsy finds that 95% of the cancer cells express androgen receptor (AR) but not CYP17A, 3% are both AR and CYP17A1 positive, and 2% are AR negative. The frequency of the cell populations suggests that the fitness of the AR-positive phenotype is much higher than AR-negative or CYP17A phenotypes. In the top row, continuous androgen deprivation therapy (ADT) rapidly selects for resistant populations with the dominant clones overexpressing CYP17A, leading to tumor progression. An alternative approach replaces continuous ADT with the protocol used in Zhang et al.¹¹ Androgen deprivation therapy is administered until the tumor burden is reduced by half (based on prostate-specific antigen measurements) and then withdrawn. In the absence of therapy, the fitness advantage of the AR-positive cells allows them to grow at the expense of the resistant populations, thus prolonging tumor control with ADT. B, The initial biopsy shows the AR-positive phenotype to be 65% of the cells, with 35% CYP17A1 and 10% AR negative. Because the relative fitness advantage of the AR-positive cells is not as great as in A (based on the higher relative fractions of AR-negative and CYP17A1 phenotypes), the adaptive strategy in A will not be as successful (simulation not shown). An alternative evolutionary strategy in the lower row alternates treatments directed against AR-positive (ADT) and CYP17A1 (abiraterone) cells, as well as treatment holidays to control the AR-positive and CYP17A1 populations while maximally reducing the growth of the AR-negative cells. Many other strategies (eg, addition of docetaxel) are available, and similar simulations can allow the treating physician to devise a patient-specific protocol that optimizes outcomes. Each arrowhead represents a treatment period. The drug used is above the arrowhead (red arrowheads indicate ADT; blue arrowheads, abiraterone). No specified drug indicates a treatment holiday (black arrowheads).

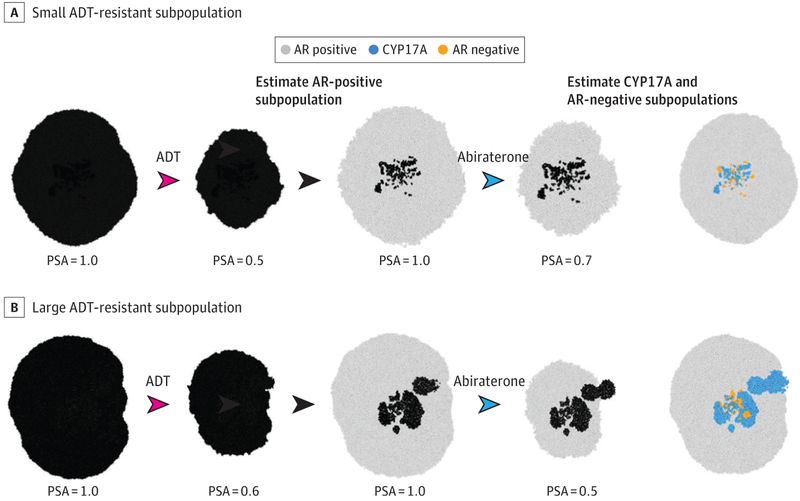
Figure 4. Using the Bellman Theorem to Guide Brief Applications of Treatment to Estimate the Size of Resistant Populations and Their Strategies.

As a simplified example of this “unmasking process,” we use the simulations in Figure 3 but assume that the metastatic prostate cancer is presenting with unknown cellular composition. Because nearly all precastration metastatic prostate cancer initially responds to androgen deprivation therapy (ADT), we assume that the androgen receptor (AR)-positive population is dominant. Here we wish to determine the size of the resistant populations by giving brief pulses of ADT and abiraterone. A, Here the ADT-resistant subpopulations are small. Initial treatment with a pulse of ADT causes a marked decrease in tumor size (measured with prostate-specific antigen [PSA]). This allows the treating physician to estimate the fraction of the AR-positive population. The physician can then briefly apply abiraterone. The smaller decrease in tumor size is used to estimate the size of the CYP17A1 phenotypes population. All other cancer cells can then be assumed to be AR negative, allowing an evolution-based treatment similar to that shown in Figure 3A. B, Here the initial combinations of ADT and abiraterone show that the population expressing CYP17A is much larger and indicate the need for combined therapy as shown in Figure 3B. Each arrowhead represents a treatment period (red arrowheads indicate ADT; blue arrowheads, abiraterone). The drug used is above the arrowhead. No specified drug indicates a treatment holiday (black arrowheads).

In fact, under these game theoretic conditions, maintenance of a constant drug regimen at MTD cedes evolutionary control to the cancer cells. As followers, the cancer cells can begin to adapt only when the treatment is applied. They are at a disadvantage because therapy begins as a Stackelberg game in which the physician is the leader. However, by administering the same drugs and doses within each treatment cycle, the physician subjects cancer cells to a constant and predictable selection force. By adapting to the physician’s current therapeutic regime, the cancer cells are simultaneously adapting to the physician’s future (identical) treatments. Consider cancer treatment as a rock-paper-scissors game in which almost all cells within the cancer play, for example, “paper.” It is clearly advantageous for the treating physician to play “scissors.” Yet, if the physician only plays “scissors,” the cancer cells can evolve to the unbeatable resistance strategy of “rock.”

Thus, continuous application of a single, high dose-density drug regimen provides a shorter-term ecological success (tumor response or remission), but failure to anticipate the longer-term evolutionary arc permits the tumor to evolve resistance unopposed. Consider an eager dog that chases a squirrel by running directly at it. Coyotes, in contrast, have learned that squirrels respond to pursuit by running toward the nearest tree and, therefore, do the same. In the former contest, the squirrel becomes the leader as the dog follows it in a wide arc toward and up the tree. In the latter, the coyote leads and prevents the squirrel from executing its evasive strategy.

Thus, by changing therapy only when the tumor evolves resistance and progresses, the physician has become the follower. He or she simply reacts to evolution of resistance by the leader tumor cells. In this setting, as shown in Figure 2 and Figure 3, the strategy of continuous treatment at MTD until progression is rarely the best available strategy. In fact, it is frequently the poorest strategic approach to the cancer therapy game.

In the context of game theory (the Table provides a glossary of game theory terms), when the physician does not fully use his or her advantages as a rational leader, he or she loses the opportunity to both anticipate and steer. Figure 2 represents a graphical depiction of the cancer therapy game. In the absence of a leader and follower, each player in a time-dependent game such as cancer therapy responds to the actions of the other players. The cancer evolves a best response to the current and ongoing therapy. When the physician observes the shift in cancer strategy—for example, radio-graphic progression—he or she can adjust treatment based on available literature that has demonstrated the best response (ie, second-line treatment) to the current strategies of the cancer cells. Each move and countermove sees both the cancer cells’ strategies and physician’s therapy strategies moving along their respective best-response curves. This can lead to either a perpetual evolutionary arms race (if the cancer cells’ and physician’s best response curves do not intersect) or a Nash solution in which the 2 curves intersect. At the Nash equilibrium, neither player (cancer or physician) gains an advantage by unilaterally altering their strategy. Such outcomes are the norm for evolutionary games in nature (Figure 2).

Table.

Glossary of Game Theory Terms

Term	Definition
Game	Any situation in which a player’s payoff depends on the player’s own strategy and the strategies of the other players
Players	Participants in the game
Strategies (or actions)	Choices that players make
Payoffs	Benefits that accrue to the player that depend on his or her strategy and the strategies of the other players
Best reply Ri(uj) of player i to action uj of player j	The payoff-maximizing strategy for player i given that player j uses strategy uj
Nash equilibrium or solution	An equilibrium state in which no player can increase his or her payoff by unilaterally deviating from his or her current strategy; in a Nash equilibrium the strategy of each player is a best reply to strategies of other players
Stackelberg equilibrium (or solution) with player i as the leader and the other players as followers	An equilibrium state in which player i obtains the highest possible payoff for himself or herself when the other players use their best reply strategy to the strategy of the leader (player i); the leader’s payoff is always at least as good as and mostly much better than his or her payoff at the Nash equilibrium

Game theory models have clear implications for current cancer therapy.^20–23 If cancer cells can find an adaptive strategy either through existing molecular mechanisms already encoded in the human genome or acquisition of a resistant mutation, survival and progression of a cancer population is an assured outcome. Furthermore, using any conventional cancer treatment approach (whether MTD or metronomic therapy) designed to kill the maximum number of cancer cells while ignoring the underlying evolutionary dynamics, the physician has no available strategy to improve current outcomes.

Exploiting Game Theoretic Advantages in Cancer Therapy

Exploiting the asymmetries in the cancer treatment game will likely require abandoning the current static treatment protocols in favor of dynamic therapy designs that explicitly integrate the evolutionary dynamics of resistance. As demonstrated in Figure 3, a physician can exploit the lead position in the Stackelberg game by anticipating the resistance strategies of the cancer cells. By understanding both the available molecular mechanism(s) of resistance and the Darwinian dynamics that govern the proliferation of resistant phenotypes, treatments can be modified, using mathematical models when necessary, to prolong the time to progression, and perhaps even cure. The key is to have some foreknowledge or estimate of the cancer cell’s best response curve. If I do X, how will the cancer cells respond and adapt over time? Just as the coyote can anticipate the squirrel’s escape options, as leader, the physician can choose to steer the cancer. A Stackelberg solution requires the leader to choose his or her best outcome along the other player’s best response curve. This solution will be at least as good, and generally much better, than the Nash solution.

Are such strategies achievable in clinical settings? A few recent trials have demonstrated successful integration of evolutionary principles into treatment protocols. For example, bipolar androgen therapy^24–26 anticipates androgen receptor overexpression as an adaptive resistance mechanism in metastatic castration-resistant prostate cancer. To exploit this adaptive strategy, bipolar androgen therapy administers androgen to induce a tumor response and to restore normal androgen expression, rendering them once again vulnerable to androgen deprivation therapy (ADT). A study by Antonia et al²⁷ demonstrated that when small cell lung cancers evolved resistance to immunotherapy, their response to subsequent cytotoxicity greatly increased. A study¹¹ treating patients with metastatic castration-resistant prostate cancer with abiraterone explicitly applied a game theoretic mathematical to delay onset of resistance.

Treatment With Imperfect Knowledge of Tumor Cells’ Strategies–Applications of Differential Game Theory

In a perfect-information Stackelberg game, the physician would be continuously aware of the evolutionary and ecological states of the tumor. However, in reality physicians must often treat cancers with drugs for which the molecular mechanisms and eco-evolutionary dynamics governing resistance are poorly understood or entirely unknown. Furthermore, while the game dynamics occur continuously, tumor responses are measured through tests obtained at intervals of weeks or months. During the time between tests, treatments typically remain fixed except in cases of toxic effects. In the terminology of differential games, clinical cancer treatment is an unusual contest that can be “open loop” and “closed loop” at different time points. That is, during each cycle of therapy, the game, from the physician’s view, is an open-loop game because he or she cannot directly observe the strategies of the cancer cells and, therefore, cannot adjust his or her treatment strategy. However, at some time points, the game could²⁸ become closed loop if the associated tests reveal the strategies of the cancer cells during the prior cycle.

The recursive dynamics during cycles of therapy, particularly in tumors in which several effective treatment strategies are available, provide a potential opportunity to probe the tumor to determine and measure key resistant and sensitive populations (Figure 4). The therapy probes would then give way to a more definitive therapy based on knowledge of (1) the strategies available to the cancer populations, (2) an estimate of their current relative sizes, (3) observed past and estimated future changes in cancer populations, and (4) past and present evolutionary dynamics.

From the late 1950s, dynamic programming and calculus of variations were developed to control systems (initially rockets) in which actions can and should vary with time (eg, the Bellman¹⁸ principle of optimality, the Pontryagin maximum principle²⁹). By the 1970s, dynamic programming expanded into differential game theory. Here, 2 players have time-dependent strategies. Each tries to maximize accrued payoffs or some payoff defined over a fixed time (eg, pursuit evasion games found in nature, dogs and squirrels, or in modern weapons systems). These complex, seemingly intractable problems are solved by breaking them into a sequence of small, nested subproblems. Optimal strategies are uncovered by recursively combining the solutions to each subproblem.^11,17,30,31

Figure 4 represents a highly simplified example of how an oncologist “leader” can use the Bellman principle of optimality to probe the tumor with short bursts of different therapies to uncover the availablecancercells’strategiesandtherelativesubpopulationsizes. This “revealed information” can optimize outcomes in subsequent rounds of the game. An interesting alternative approach is physical perturbation of the tumor (eg, by focused ultrasound), which causes cancer cells to release macromolecular biomarkers. A preclinical study showed how these serum markers accurately reflect the intratumoral population distribution.³²

Discussion

The therapeutic contest between physicians and cancer cells contains 2 important asymmetries. First, only the physician can plan ahead and anticipate the cancer’s responses. In contrast, the cancer cells simply die or survive on the basis of current conditions and their heritable sensitivity or resistance to the therapy. Second, cancer therapy is a Stackelberg game in which the physician can both influence overall tumor burden and potentially steer the evolutionary trajectory of the cancer cells toward outcomes more favorable to the patient. In terms of the evolution of resistance, the physician can anticipate while the cancer cells can only react.

These asymmetries give the physician substantial advantages. However, current treatment regimens for metastatic cancers such as continuous MTD or identical cycles of intermittent therapy do not exploit these advantages. By playing the same strategy repeatedly, current cancer treatments greatly increase the likelihood of cancer cells evolving effective countermeasures. Thus, because therapy is changed only when the tumor progresses, the leader physician becomes the follower. Although standard practice for decades, administering drugs at maximum tolerated dose until progression represents a poor strategy.

We suggest that cancer treatment protocols can benefit from explicit consideration of these asymmetries and the physicians’ advantages as the leader in the cancer therapy Stackelberg game. In general, the physician can exploit his or her advantages by developing more strategic approaches³³ to cancer therapy that carefully define and exploit the critical dynamics that govern success and failure in each treatment and by linking treatments in a well-constructed sequence that takes advantage of their potential synergies. These include the following.

Define the Goal of Treatment

When applied with curative intent and with reasonable expectation of that outcome, therapy should use evolutionary dynamics to maximize the probability of cancer cell extinction. Importantly, curative intent does not necessarily require application of initial therapy at MTD. In fact, extinction of a population may best be achieved through a strategic sequence of treatments in which, for example, the initial therapy is designed to generate a small, homogeneous resistant population that is then eradicated by a second treatment that specifically targets the adaptive strategy. This approach, termed “double-bind therapy”^20,34,35 or, more colorfully, a “sucker’s gambit,”³⁵ has been extensively analyzed and can be observed clinically.^27,36 Thus, for many cancers, the maximum probability for cure may actually occur during second-line therapy.

Alternatively, when cure is not achievable, the goal should explicitly focus on maximizing the time to progression. Here, evolutionary dynamics are harnessed to suppress the growth of resistant phenotypes. Because the physician cannot, by definition, control resistant cells, the therapeutic strategy must focus on adaptive approaches that retain treatment-sensitive cells to suppress the growth of resistant cells.

Include a Resistance Management Plan

Increasing numbers of cancer therapies are available, and many produce an initially highly favorable response. Yet, most metastatic cancers remain fatal because malignant cells have a remarkable capacity to evolve resistance leading to tumor progression and treatment failure. Fortunately, this topic has been investigated. In fact, resistance management plans³⁷ (RMPs) have been used (and often mandated) for decades in the application of pesticides in agricultural systems.³⁸ Resistance management plans identify and/or anticipate the mechanisms of resistance by the pests; monitor for the emergence, distribution, and abundance of resistant pest populations; and integrate evolutionary principles to create pesticide application protocols that reduce the emergence and proliferation of resistant phenotypes. In almost all cases, the RMP recommends reduced and more judicious applications of pesticides.¹²

Cancer treatment RMPs will require important changes in both drug development and application. Pharmaceutical companies, like pesticide manufacturers,³⁷ will need to define the molecular mechanisms through which cancer cells become resistant to the drug. For oncologists, RMPs can exploit a number of evolution-based strategies to delay or suppress proliferation of resistant phenotypes. We note, however, that these eco-evolutionary dynamics can be highly patient specific.¹¹ Thus, the role of precision medicine³⁹ in oncology should be expanded. That is, in addition to identifying molecular signatures that predict response to certain therapies in pretreatment screens, precision medicine should also seek to identify molecular properties that will confer resistance. Then, as feasible, metrics of tumor responses (ecological dynamics) and cancer cell type frequencies (evolutionary dynamics) should be used to adjust therapy in terms of both dose scheduling and drugs used. The metrics of eco-evolutionary dynamics become the means for anticipating the cancer’s responses, for avoiding an arms race or Nash equilibrium, and for bringing about a Stackelberg solution.

Perform “After Action Reports”

Outcomes of military and emergency activities are often analyzed through after action reports.⁴⁰ They encourage self-evaluation⁴¹—what did I do right and what did I do wrong? Current clinical research in oncology focuses on evaluation of cohorts within some well-defined treatment protocol. In contrast, after action reports focus on evaluating the outcomes of every patient, even those not enrolled in a formal protocol, by asking, Was the stated goal of treatment (ie, cure or control) achieved? If not, what are plausible explanations for failure and could outcomes have been improved by altering the treatment goal or the RMP?

Conclusions

Cancer therapy is a Stackelberg game. Game theoretic analyses of cancer therapy suggest that “precision medicine”³⁹ in oncology can be broadened from its current focus on molecular targets that maximize the probability of immediate response. Additionally, precision medicine should incorporate the cancer therapy game to anticipate and steer patient-specific and treatment-specific evolutionary dynamics that govern the emergence and success of resistant populations. Even with initially well-targeted therapies, resistance leads to failure, progression, and patient death. Taking control of the Stackelberg game will require (1) the application of dynamic and sophisticated therapies and (2) the investigation of response metrics that move beyond the current focus on changes in tumor size (ie, the tumor ecology) and include measurements of the sensitive and resistant subpopulations (evolutionary state and dynamics). Emerging technologies that investigate circulating DNA and tumor cells^42–44 will probably become key. New image analytic tools (eg, radiomics⁴⁵ and habitat imaging⁴⁶) may generate biomarkers for treatment-sensitive and treatment-resistant intratumoral population through clinical computed tomography and magnetic resonance imaging studies. Finally, even with imperfect understanding of the resistance mechanisms and the size of resistant subpopulations, judicious applications of initial therapy can reveal the eco-evolutionary dynamics. As the cancer cells’ strategies and future responses become unmasked, the physician can adjust subsequent treatment cycles accordingly.