Abstract
The performance of a metallic microwave resonator that contains a dielectric depends on the separation between metallic and dielectric surfaces, which affects radio frequency currents, evanescent waves, and polarization charges. The problem has previously been discussed for an X-band TE011 cylindrical cavity resonator that contains an axial dielectric tube [J. S. Hyde and R. R. Mett, Appl. Magn. Reson. 48, 1185–1204 (2017)]. Here, a short rutile dielectric tube inserted into a loop-gap resonator (LGR) at X-band, which is called a dielectric LGR (dLGR), is considered. The theory is developed and experimental results are presented. It was found that a central sample loop surrounded by four “flux-return” loops (i.e., 5-loop–4-gap) is preferable to a 3-loop–2-gap configuration. For sufficiently small samples (less than 1 μL), a rutile dLGR is preferred relative to an LGR both at constant Λ () and at constant incident power. Introduction of LGR technology to X-band EPR was a significant advance for site-directed spin labeling because of small sample size and high Λ. The rutile dLGR introduced in this work offers further extension to samples that can be as small as 50 nLwhen using typical EPR acquisition times.
Keywords: dielectric resonator, loop-gap resonator, inductively coupled, electron paramagnetic resonance, single crystal and polycrystalline rutile
Graphical Abstract
1. INTRODUCTION
In this paper we consider the introduction of a dielectric resonator (DR) into the sample region of a loop-gap resonator (LGR). The dimensions of the DR and LGR are commensurate and the sample region of the LGR is freely accessible. A theoretical analysis is provided followed by a description of a practical resonator. Initial experimental results are reported using an aqueous spin label sample. The DR was machined from a single crystal of TiO2 (rutile). The structure is robust and easy to use. It offers a way to extend X-band EPR spectroscopy to remarkably small samples.
The electron paramagnetic resonance (EPR) LGR [1] is an assemblage of loops with net inductance L and gaps with net capacitance C that satisfy the resonance condition
| (1) |
Here, ω is the microwave radian frequency. The sample is inserted into one of the loops which is called the sample loop. However, this equation is not a sufficient description of the lumped circuit parameters L and C. Faraday’s law
| (2) |
where μ0 is the magnetic permeability of free space, must also be satisfied. Most of the energy associated with the electric field resides in the capacitive gaps, but a portion of that energy is used to create ∇ × E, which in turn leads to H1 in the sample loop. This paper is a study of the effect of a dielectric tube placed in the sample loop of an LGR on the value of H1 at the sample.
There is a long history of enhancement of an EPR signal when using a quartz dewar insert in a cavity resonator. It is noted that the sample as well as insert lie in the region of maximum curl ∇ × E. Stoodley called this H1 enhancement at the sample the “sucking in” effect [2]. The benefit from the perspective of EPR lies largely in the reduced sample volume at constant “concentration sensitivity.” Here, it is assumed that the incident power is reduced to a value that yields an H1 in the sample that is the same as occurs without a quartz dewar. Thus, the degree of saturation is the same. It is observed that the sample volume is decreased while the signal-to-noise ratio shows little change. The goal of this paper is similar: to arrive at a geometry that will maintain the concentration sensitivity for small samples by using dielectric tubes of exceptionally high dielectric constant. We seek improved sensitivity for extremely small samples. We mostly consider rutile (TiO2) single crystal tubes with a dielectric constant of about 100. No prior citations have been found for this configuration.
The dielectric tube will resonate in free space at some microwave frequency, as will the LGR. When they are assembled, however, the resonance properties are that of a network with two modes. It is an error to consider this structure as a two-stage assembly of resonators in series. This perspective was introduced by Terman [3], who studied coupled resonators at low radio frequencies, and extended to the geometry of a DR inside a cavity resonator by the authors [4].
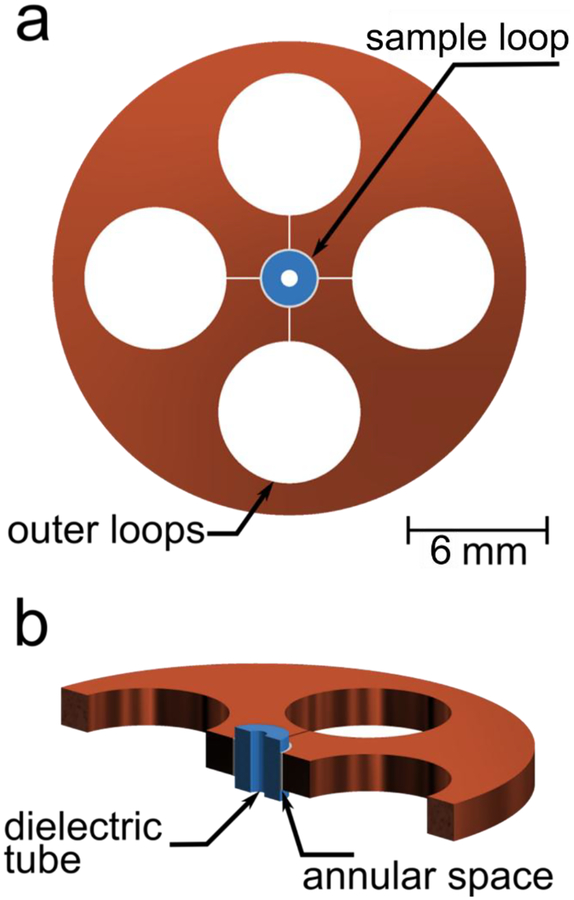
Our LGR geometry has a sample loop that contains the dielectric element, which has a hole to accommodate the sample tube. We had more success early in the project using a 5-loop–4-gap LGR with four return flux loops, see Fig. 1, and have not returned to other configurations with lower numbers of return flux loops.
Figure 1:
The core of the dLGR consists of a 5-loop–4-gap LGR (orange) with a rutile dielectric (blue) in the sample loop: (a) top view; (b) perspective cutaway view.
We have identified a basic issue. The mode of a DR is typically TE01δ where the electric field is circumferential, including the evanescent field. Placement in a conducting metal cylinder where the electric field must be perpendicular to the plane of the conductor gives rise to a conflict. We have concluded that there must be an annular region of free space between the dielectric and the inner diameter (ID) of the sample loop. The conflict is resolved, as we will report, by polarization charges on the surface of the dielectric. Inspection of Fig. 2 reveals that there are both radial and circumferential components of the electric field at the dielectric surface that arise around the loop. The circumferential discontinuities of the inner loop LGR wall (i.e., the four gaps) are responsible for the radial component; the circumferential symmetry of the DR and LGR loop gives rise to the circumferential electric field component.
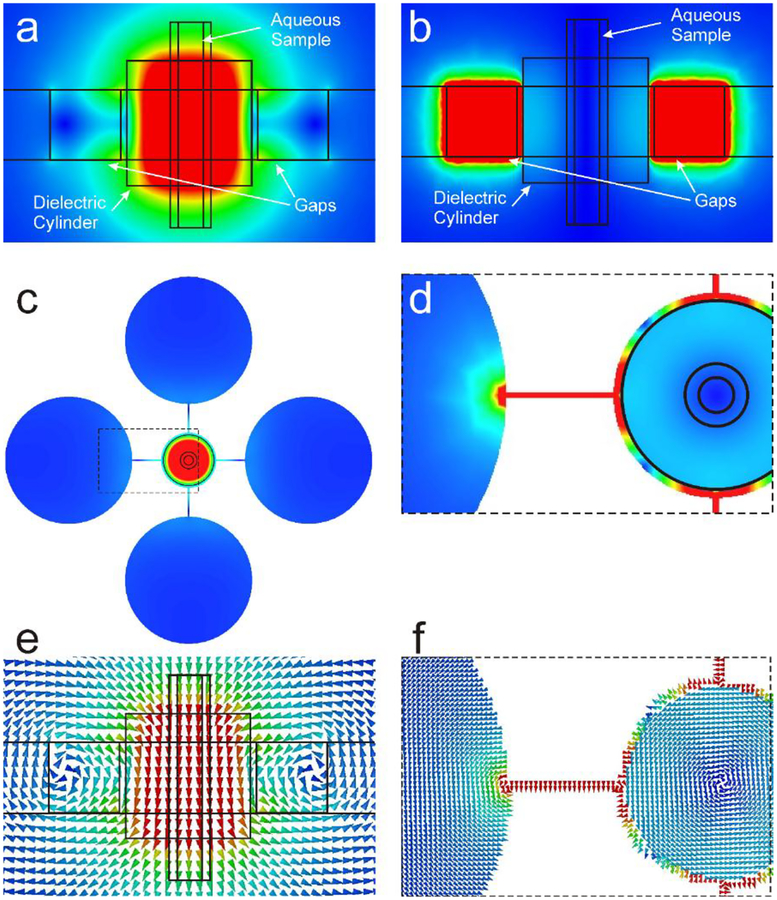
Figure 2:
Finite element simulations for the PC rutile dLGR at X-band with dimensions shown in Tables 1 and 2 and an AWG26lw PTFE sample tube (see Appendix B) with aqueous sample. (a, c) Magnetic field magnitude, red to blue indicates 0.3 mA/m to zero. (b, d) Electric field magnitude red to blue indicates 0.1 V/m to zero. (e) Magnetic field vectors. (f) Electric field vectors.
A dielectric cylinder with high dielectric constant offers an opportunity to obtain a high EPR signal with low sample volume. Consider a DR oscillating in the TE01δ mode with equal diameter and length and a hole at the center for an EPR sample. This mode is much like a cylindrical TE011 cavity mode often used for EPR, only much smaller [5]. Within this mode, a cylindrical surface exists, where the axial radio frequency (RF) magnetic field is zero, which defines an “inner core.” This core is placed in the sample loop of an LGR. The LGR provides the means for support of the return magnetic flux. The dielectric core would oscillate in the TE01δ mode if it were removed from the LGR, but at a higher microwave frequency. The dLGR is an undersized DR placed inside the inner loop of an LGR. For an isolated DR, the axial RF magnetic field is zero at a radius 6%–10% smaller than the dielectric surface radius [4].
Dielectric cavity inserts have been used to increase the EPR signal. A study [4] of the resonator efficiency Λ of a DR placed inside a cavity compared with a DR alone and the cavity alone showed that the maximum Λ is nearly that of an isolated DR. No Λ enhancement beyond that of the isolated DR was seen. Analysis indicates two reasons for this: 1) the cavity Λ is much smaller than the DR Λ, and 2) the Q of the cavity is much larger than the Q of the DR. The second reason is consistent with Terman’s analysis of coupled circuits [3]: maximum secondary response is achieved when the Qs of the primary and secondary coils are equal in addition to the condition of critical coupling.
Because a dielectric shortens the electromagnetic wavelength by the square root of the real part of the dielectric constant relative to free space, a dielectric can be used to localize the RF magnetic field and increase the resonator efficiency [1, 4],
| (3) |
where B1 is the maximum available RF magnetic field magnitude at the sample and Pl represents the total power loss in the resonator. If the spins are saturated, the signal is directly proportional to Λ, and if the spins are not saturated, the signal is proportional to Λ2 [6].
In this work, two types of rutile were investigated: polycrystalline (PC) and single crystal (SC). The PC rutile used in this work is a low-loss sintered homogeneous TiO2 ceramic called K-100 from TCI Ceramics, Inc. (Bethlehem, PA), an affiliate of National Magnetics Group, Inc. The measured specification received from the company was a homogeneous dielectric constant of 100.3 and loss tangent 2.5 × 10−4 at 9.4 GHz. The SC rutile was obtained from MTI Corporation (Materials Tech. Intl.) (Richmond, CA). SC rutile is birefringent. According to Tobar et al., [7] for frequencies between 2.5 and 5.5 GHz, the relative dielectric constant is 165 parallel to the c-axis (the (001) direction) and 86 perpendicular. The loss tangent is 10−4 parallel to the c-axis and 8.5 × 10−5 perpendicular. Since the Q of a DR [4, 8–10] is equal to the inverse of the loss tangent, a Q of 4,000 for the PC rutile and between 10,000 and 12,000 for the SC rutile can be expected, depending on the polarization of the electric field. It is possible to have the c-axis of the crystal lie parallel or perpendicular to the axis of the LGR. In the present work, analysis and simulations of both orientations are discussed, but experimental results are reported only for the perpendicular orientation. The perpendicular orientation produces the largest resonator efficiency because one of the two electric field components in the dielectric lie in the direction of the largest dielectric constant, and the electromagnetic fields are azimuthally asymmetric, unlike the parallel orientation. These effects are described in further detail below. To fabricate the perpendicular orientation, the SC rutile was ground into a cylindrical shape with the cylinder axis perpendicular to the c-axis and placed parallel to the inner loop LGR axis.
Defects in PC rutile have been extensively studied using EPR spectroscopy [11]. Similar results were found by us. Possibly the EPR signals could be subtracted out when using PC rutile tubes. However, as shown in Sec. 5, background EPR signals of the SC rutile were much lower and that material was preferred in this work.
2. ANALYTIC THEORY
In [4], an analytic expression for the peak resonator efficiency of a DR placed inside a cylindrical TE011 X-band cavity was developed in order to answer the scientific question as to whether it was possible for the resonator efficiency of the coupled system to be larger than that of a DR alone. It was found that the answer was no: the maximum resonator efficiency could be only about 99% of that of the DR alone under specific conditions that involve DR size and resonance frequency relative to the cavity. The analytic theory included a capacitively-coupled circuit model in which lumped-circuit values of inductance, capacitance, and resistance were derived from analytic expressions for the RF field solutions of the cavity and the DR. The lumped circuit component values were expressed in terms of the physical dimensions and Q of the cavity and DR. Results of the analytic theory closely matched finite element simulations.
In the present work, we develop an analytic theory for the dLGR using similar methods to determine whether the peak resonator efficiency of the dLGR can be larger than the DR alone. The results indicate that the peak resonator efficiency of the dLGR with sample placed in the dielectric can at best only match that of the DR alone at fixed frequency. Perhaps surprisingly, this is true even under conditions where the LGR has zero ohmic losses. Results of the analytic theory closely match finite element simulations.
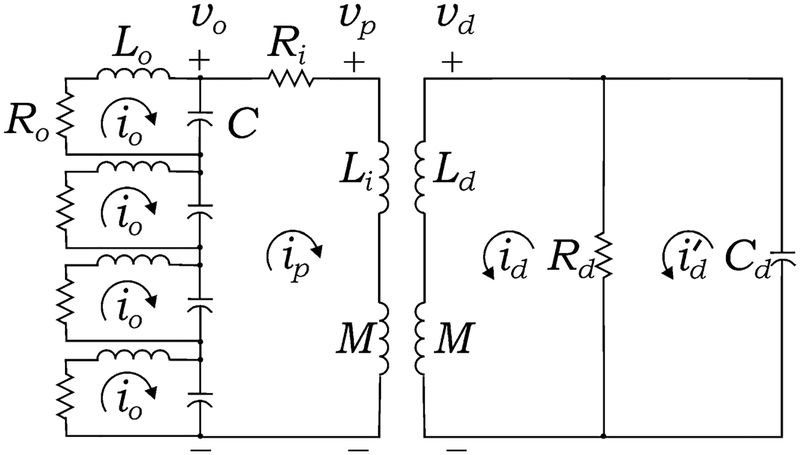
First, we show the analytic model of the DR. The model is similar to that of [4] except, in order for the results to be fully consistent with the finite element simulations, a parallel RLC resonance was required instead of a series RLC. The physical reason for this is described in the next section. Next, we show the analytic model of the 5-loop–4-gap LGR. The model is the same as that developed previously for describing the nonuniformity of the axial RF field in LGRs at Q-band [12] and the influence of long and short coupling irises on the LGR at Q-band [13]. The analytic model includes effects of RF current flow in the capacitive gaps, fringing electric fields in the loops close to the gaps, and fringing electric and magnetic fields in the end regions of the LGR. Finally, the two resonant systems, DR and LGR, are coupled using a standard mutual inductance model [14]. Theory for the dLGR is developed and results are discussed.
A. TE01δ dielectric mode and DR model
In Sec. IIB of [4], a magnetic boundary condition was used to obtain a coupled system of equations for the resonance frequency of the TE01δ mode in the dielectric. Analytic electromagnetic field solutions were used to find expressions for the stored energy and power dissipated in the DR, which were used to determine the Q and the resonator efficiency. From these results, equivalent circuit values of the DR were expressed in terms of the DR physical dimensions. Then, the resonator efficiency was expressed in terms of the equivalent circuit values.
In [4], a series RLC resonant circuit was used for the DR. However, in the present work, it was found that a parallel RLC model was needed for results of the analytic theory of the coupled system to be consistent with the finite element simulations. This is because the loss in the dielectric depends on the electric field (emf). In a parallel RLC circuit, the emf across the inductor, capacitor, and resistor are the same, so loss arising from the loss tangent in the dielectric is accurately modeled by a high resistance across the capacitor. In the case of a series RLC circuit, ohmic dissipation from conduction currents is more closely modeled by the series resistance. When inductive coupling is added to the parallel RLC circuit, an emf contributed by the coupled circuit (LGR) can directly produce a loss in addition to the emf of the TE01δ mode. This is not true for the series RLC circuit.
The two changes needed to convert the DR circuit from a series to a parallel RLC resonant circuit consist of the parallel resistance Rd = QdωdLd replacing Eq. (22) of [4] and the isolated DR resonator efficiency
| (4) |
replacing Eq. (25) of [4]. It can be shown that Eq. (4) results from the substitution Rd → Rd/Qd2 and vd = jωLdid in Eq. (25) of [4]. The same symbol definitions as [4] are used.
Results of the analytic model for an isolated DR are shown in Table 1 for PC rutile and SC rutile in the parallel and perpendicular orientations (Sec. 1). For the perpendicular orientation of the SC rutile, the effect of an anisotropic crystal with the parallel axis along one of the electric field polarization directions was included by using a geometric average of the parallel and perpendicular corresponding relative dielectric constants and loss tangents. Table 1 shows that PC rutile has the lowest Λ, which is caused by the high loss tangent. At 9.5 GHz, the diameter of the PC rutile DR is between those of the parallel and perpendicular SC rutile. This is because of the random orientation of the high ϵr = 165 and two low ϵr = 86 dielectric constants of the polycrystals in each of the three spatial dimensions, which causes an average ϵr = 100.3. The perpendicular SC orientation exhibits the highest Λ even with a slightly higher loss tangent than the parallel orientation because the largest dielectric constant lies in one of the two electric field polarization directions. Also shown in the Table 1 are the properties of the PC and SC perpendicular DRs for the smaller sizes used for the dLGR.
Table 1:
Isolated rutile D/L = 1 DR properties
| description | diameter (mm) | f (GHz) | Q | Λ (G/W1/2) |
|---|---|---|---|---|
| PC | 2.66 | 9.50 | 4,000 | 35.8 |
| 2.40 | 10.55 | 39.8 | ||
| SC parallel orientation | 2.88 | 9.50 | 11,800 | 54.7 |
| SC perpendicular orientation | 2.45 | 9.50 | 10,800 | 67.1 |
| 2.30 | 10.10 | 71.4 |
B. LGR fields and model
In [12], an analytic model of an LGR with m equal outer loops and gaps and one inner loop was developed. The model includes the inductance and resistance of each loop and each gap. Each gap is modeled as two capacitors in parallel joined at the location of the RF conduction current null in each gap as determined by flux conservation. Inductance and resistance arise in each capacitor from the RF current and magnetic flux. Current flows around each loop largely in the first RF skin depth starting and ending at each current null around each gap. Additional capacitance from fringing electric fields near the edges of each gap in each loop is also included. The basic lumped-circuit topology of the 5-loop–4-gap is shown on the left-hand side of Fig. 3 with M = 0. The sizes of the outer loops are physically much larger than the inner loop and are not drawn to scale in the diagram. Circuit component values of the LGR were expressed in terms of the LGR physical dimensions as described in Sec. 2 of [12] and Appendix B of [13]. In the present work, we use the same model and component values with the same symbol definitions as those in Appendix B of [13]. These component values lead to frequency and Q of the LGR at cutoff that were in reasonable agreement with finite element simulations.
Figure 3:
dLGR coupled circuit diagram. The LGR is on the left and the DR is on the right.
In [12], a waveguide model was developed and used to account for the effect of the impedance of each end of the LGR on the axial uniformity of the RF fields inside the inner loop and the resonant frequency and Q. When the LGR is short compared with a free space wavelength, the effect of the LGR end fringing fields can be included by placing the fringing capacitance given by Eq. (15) of [12] in parallel with the gap capacitance,
| (5) |
and the fringing inductance given by Eq. (16) of [12] in parallel with the inner loop inductance,
| (6) |
Because the ohmic resistance arises from the same current that causes the inductance, the inner loop resistance was then scaled accordingly,
| (7) |
Using Eq. (3) and arguments presented in Sec. IIA of [4], the isolated LGR resonator efficiency can be expressed as
| (8) |
where the inner loop effective area includes part of each gap, and the current ratio between the inner and outer loops is given by ip/io = −4 Lo/Li′. Shown in Table 2 are predictions of the analytic model for the isolated LGR for the dimensions used for the dLGR. The slightly larger ID was used with the PC rutile and the smaller with the SC perpendicular rutile dimensions shown in Table 1.
Table 2:
5-loop–4-gap isolated LGR dimensions (mm) and properties
| description | larger ID | smaller ID |
|---|---|---|
| gap thickness | 0.076 | |
| outer loop diameter | 6.0 | |
| inner loop diameter | 2.60 | 2.50 |
| length | 1.35 | 1.4 |
| gap width | 1.35 | 1.4 |
| f (GHz) | 11.15 | 11.35 |
| Q | 1,600 | 1,540 |
| Λ (G/W1/2) | 7.19 | 7.31 |
C. Coupled DR and LGR (dLGR) model and solution method
A primary aim of the analysis is to predict the mode frequencies, Q and resonator efficiencies for the modes of the dLGR for a range of physical dimensions, coupling strengths, and aqueous sample sizes. Because there is substantial magnetic flux shared between the inner loop of the LGR and the DR TE01δ mode, the mutual inductive coupling circuit of Fig. 3 was developed. The DR and LGR models are the same as presented in Secs. 2A and 2B and are mutually inductively coupled. The mutual inductance model is the same as that used for two coupled coils described in [14]. In order to simplify the analysis, the circuit is considered to be excited with a voltage vo, Fig. 3, [14]. The circuit equations are shown in Appendix A. The input impedance Zin ≡ vo/iin can be written as
| (9) |
where the fourth-order denominator
| (10) |
In these equations, , Qd = Rd/ωd/Ld, , Qi = ωiLi′/Ri′, , Qo = ωoLo/Ro, and the coupling coefficient . Equations (9) and (10) are similar to Eqs. (3) and (4) of [14]. Complex eigenfrequencies can be found from the solutions of . These eigenfrequencies can be expressed algebraically in closed form in terms of the seven parameters defined after Eq. (10). The expressions are lengthy.
The real resonance frequencies of the circuit can be found by solving . We find, neglecting terms of ,
| (11) |
When k = 0, the system decouples into the LGR resonance and the dielectric resonance. The LGR resonance frequency is given by
| (12) |
Equation (12) is equivalent to Eqs. (2), (3), and (6) of [13] and Eq. (7) of [12]. For k > 0, Eq. (11) can be solved for the resonance frequencies of the coupled system,
| (13) |
There is a high frequency mode ω0+ in which the magnetic fields of the LGR and dielectric are antiparallel and a low frequency mode ω0− where they are parallel [4, 14].
In order to determine the resonator efficiency of the coupled LGR and DR (dLGR) in terms of the circuit parameters and physical dimensions, Faraday’s law can be used to relate the total emf in the dielectric (see Fig. 3) to the total magnetic flux in the dielectric, vd = jωB1Ad, where Ad is the cross sectional area of the dielectric loop as given by Eq. (24) of [4]. Using Eq. (3),
| (14) |
where the ratios ip/vd and ip/io can be determined from the circuit equations in Appendix A,
| (15) |
| (16) |
These equations are exact. In the subsequent analysis, it was found necessary to use exact ratios to obtain the behavior of the resonator efficiency for low coupling coefficients, but higher order terms in the eigenmode frequencies Eq. (13) were not needed.
In comparing Eq. (4) and Eq. (14), it is seen that despite the superposition of magnetic flux from the LGR and the dielectric, there is no enhancement of the resonator efficiency at fixed frequency. The reason is that the increased magnetic flux coming into the DR from the LGR is necessarily accompanied by an increase in emf (electric field) in the dielectric due to Faraday’s law. But since the dielectric losses are proportional to the square of the electric field, the flux from the LGR increases the dielectric losses and will not increase the resonator efficiency. Consequently, the resonator efficiency can never exceed the resonator efficiency of a DR alone at fixed frequency. The parallel RLC circuit model of the DR captures this physics, but a series RLC model does not in the presence of the mutual inductive coupling. This prediction of the circuit model was shown to be consistent with the finite element simulations, even when the LGR losses were set to zero.
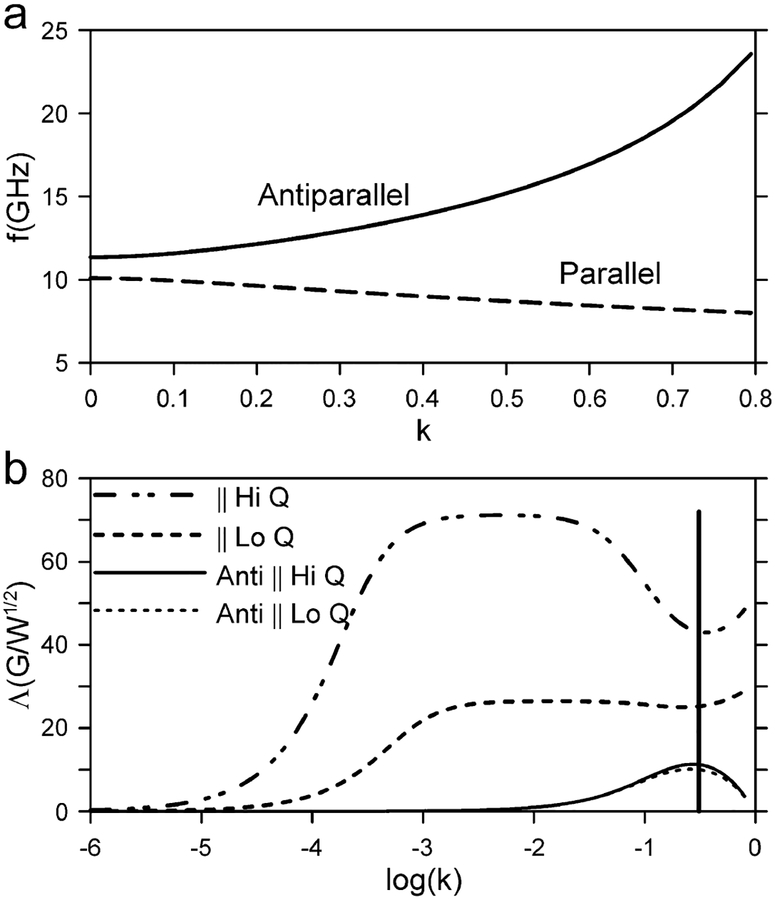
Results of the analytic theory are shown in Fig. 4a, b in which the coupling coefficient is scanned. Dimensions used for the dLGR are for the SC rutile DR and smaller ID LGR shown in Tables 1 and 2 along with resulting parameters. Two cases are shown in Fig. 4: 1) a high-Q case where the sample size is approximately 50 nL or smaller, and 2) a low-Q case where the Q of the DR Qd is 1,500. The low-Q case simulates the presence of an AWG26 polytetrafluoroethylene (PTFE) sample tube (see Appendix B) filled with about 400 nL of water. Figure 4a illustrates that at low k, the frequencies of the parallel and antiparallel modes start at the respective resonance frequencies of the isolated LGR and DR, respectively. As k increases, the frequencies diverge. The corresponding resonator efficiencies are zero at k = 0 because the DR is not energized. For the no sample case, as k increases, the resonator efficiency, Fig. 4b, plateaus near the resonator efficiency of the DR alone, 71.2 G/W1/2. The plateau occurs near k = 0.004. This value is more than an order of magnitude larger than the k for maximum power transfer, which is [3]. As k increases further, the resonator efficiency drops because it is increasingly coupled to the lower Q-value LGR. Then, as k increases beyond 0.3, the resonator efficiency rises slightly. This is caused by the decrease in frequency of the parallel mode with increased coupling and is consistent with Eq. (14). With sample, there is similar overall behavior but the middle plateau in the resonator efficiency is lower, about 26.5 G/W1/2. For the dLGR shown, the k-value can be calculated as 0.308. For this value, the analytic theory predicts a parallel mode frequency of 9.28 GHz and corresponding resonator efficiency from Eq. (14) of 43.1 G/W1/2 with no sample. With sample, the coupled frequency is the same and the resonator efficiency becomes 25.2 G/W1/2. If the DR has a lower Qd of 1,000, the peak plateau of the resonator efficiency is lower, 21.5 G/W1/2.
Figure 4:
(a) Frequencies and (b) resonator efficiencies of the two modes predicted by the analytic model for SC rutile in the perpendicular orientation. For (b), a high-Q case corresponding to no sample and a low-Q case corresponding to an aqueous sample are shown. The vertical line indicates the k-value of the fabricated dLGR, 0.308.
3. FINITE ELEMENT SIMULATIONS
Finite element simulations were done using ANSYS High Frequency Structure Simulator (HFSS) (Canonsburg, PA) version 17.1 running on a Dell Precision Tower 7910 with dual 12 core Intel Xeon E2–2670 v.3 2.3 GHz processors with hyper-threading and 512 GB of RAM. The birefringence of the SC rutile was simulated in ANSYS HFSS by setting the appropriate values of the dielectric tensor (relative dielectric constant and loss tangent) for each of the three spatial dimensions of the crystal. From the HFSS fields calculator, various parameters were calculated from each of the simulations. The peak resonator efficiency [1, 4, 6] was calculated using a form of Eq. (3) where the total power loss in the resonator is adjusted until the amplitude of the peak rotating RF magnetic field component in the sample is equal to 1 G,
| (17) |
where max indicates the maximum value in the sample volume and the power losses include the metallic walls, dielectric, sample, and sample holder. The same symbols as [6] are used. The saturable EPR signal was calculated using [6, 15, 16]
| (18) |
where the integral is over the sample volume. In order to evaluate the uniformity of the RF magnetic field over the sample volume, we introduce the rms resonator efficiency,
| (19) |
which can be compared to Eq. (17). Using Eqs. (17) and (18), Eq. (19) can be written as
| (20) |
The dLGR was designed using ANSYS HFSS by first inserting a PC rutile DR (ϵr = 100 tan δ =10−3 [17]) resonant at 9.5 GHz into the inner loop of a 5-loop–4-gap LGR of similar height to the DR. An overall goal was to make minimal modifications to both the dielectric and the LGR to achieve a nominal resonance frequency of 9.5 GHz for the parallel mode of the dLGR. The size of the dielectric was reduced about 10% and the size of the LGR gaps was changed to minimize RF currents on the LGR walls and maximize the Q of the dLGR. Reducing the height of the LGR and making the gaps square reduced the magnetic field in the gaps and produced an RF magnetic field null near the center of the LGR gaps, substantially increasing the Q compared with a wide range of other considered configurations. The capacitance of the LGR gaps was reduced to accommodate the enhanced magnetic flux in the inner loop caused by the “sucking in” effect [2] in the dielectric. The return flux of the dielectric flows primarily through the outer loops of the LGR. A 0.1 mm annular air gap between the dielectric and the inner LGR loop wall was needed to permit the RF fields in the DR to resemble the TE01δ mode. The RF fields for the final design are shown in Fig. 2a–f with dimensions of the PC rutile and larger ID LGR given in Tables 1 and 2.
The dielectric of the dLGR has a hole to accommodate an AWG26 light wall (lw) PTFE sample tube (see Appendix B) filled with water. The dielectric constant of 20⁰C water was set at 61.61 and loss tangent 0.518 [18] and, for PTFE, 2.08 and 3.7 × 10−4, respectively [17]. According to the simulations, f = 9.510 GHz, Q = 948, Λ = 14.8 G/W1/2, Vs = 393 nL, and Ss = 1.84 V. In the dLGR of Fig. 2, 73% of the power is dissipated in the dielectric, 9% in the sample, and 18% in the metal. Also, 50% of the magnetic energy and 55% of the electric energy are in the dielectric. This compares with 72% and 99%, respectively, for an isolated DR. The Q of the combined structure is 26% higher than an isolated DR with the same sample and sample tube.
Progressively reducing the air gap below 0.1 mm was found to cause a monotonically decreasing resonance frequency, an increase in the strength of the RF magnetic field in the dielectric halfway between the LGR gaps, and a corresponding decrease near the LGR gaps. The resonance frequency lowering is caused by an increase of the capacitance of the LGR gaps from the proximity of the dielectric. For a 0.01 mm air gap and no other dimensional changes for PC rutile, the frequency drops 8%, the Q increases 9%, and the resonator efficiency goes up 1.8%. The magnitude of the RF currents in the gaps is smaller than for the 0.1 mm gap, and the magnetic field null near the gaps extends into the dielectric. For zero gap, the resonance frequency drops 41%, the Q drops 34%, and the resonator efficiency drops 26%. The return flux is strong inside the gaps.
As described in Sec. 1, SC rutile is birefringent and has a lower loss tangent than PC rutile. When the c-axis of the crystal is oriented parallel to the dLGR axis, the TE01δ mode is governed by the lower, perpendicular dielectric constant only, and the theoretical Λ of the DR with no sample is 54.7 G/W1/2 as shown in Table 1. When the c-axis of the crystal is oriented perpendicular to the dLGR axis, 23% higher Λ is obtained from the higher ϵr of the parallel orientation. However, the fields are no longer azimuthally symmetric. The effect of birefringence on the fields in the perpendicular orientation is shown in Fig. 5a, b. It is seen that the magnetic fields are only slightly asymmetric, but the electric field is significantly more intense in the regions of smaller ϵr. Only this orientation was used in the SC rutile simulations and experiments because of the higher Λ.
Figure 5:
Finite element simulations of SC rutile, top views. (a) Magnetic field magnitude. (b) Electric field magnitude. The azimuthal asymmetry of the electric field arising from the birefringence of the SC rutile is more prominent than for the magnetic field.
A detailed study of the effect of the sample size on the resonator efficiency, Q, EPR signal, and uniformity of the SC rutile dLGR is shown in Table 3. For comparison, each calculation was also done for an isolated DR and an isolated 5-loop–4-gap LGR of similar dimensions to the LGR of the dLGR. Dimensions of the DR and LGR were adjusted as described below to obtain resonance near 9.5 GHz. In all cases, the dielectric outer diameter (OD) and length and the LGR dimensions were fixed for all sample tube sizes. For the DR simulations, a perfectly conducting boundary was used to model the effects of the dielectric and sample losses only. In addition, the diameter and length of the DR were larger, 2.67 mm, to make the resonance frequency nominally 9.5 GHz. For the LGR simulations, the LGR height was made to match the dielectric height (2.3 mm) in the dLGR. In addition, the gaps were square, the gap thickness reduced to 0.025 mm, and the ID 1.35 mm to make the nominal resonance frequency 9.5 GHz. It is seen that the lower loss tangent of the SC rutile makes Λ quite large, but only for very small samples. As the sample size increases, Λ rapidly decreases. The decrease is more rapid for the DR than the dLGR. For the LGR, the decrease in Λ is much smaller but starts from a much smaller value. For the dLGR, the peak Λ is smaller than the DR but gives the same Λ for sample diameters between AWG26 and AWG24. In practice, the AWG26 sample tube (0.46 mm ID, 0.76 mm OD) is considered small but reasonable to an EPR spectroscopist. For the LGR, the Λ is much smaller for all sample sizes. It is also seen that the uniformity is best for the LGR. The dLGR is about 3% more uniform than the DR. This is caused by the parallel mode LGR fields adding to the DR fields. It can also be seen that the dLGR dielectric is 16% shorter than for the DR. This puts the dLGR results at a comparative disadvantage by lowering the resonator efficiency, uniformity, and EPR signal compared with the DR.
Table 3:
Comparison of SC DR, dLGR, and 5-loop–4-gap LGR properties with different sample sizesa
| sample tube | f (GHz) | Q | Λ (G/W1/2) | Vs (nL) | Ss (V) | % Λnon | Λrms (G/W1/2) | |
|---|---|---|---|---|---|---|---|---|
| DR | none | 9.460 | 11,200 | 61.3 | - | - | - | - |
| AWG32sw | 9.477 | 6,490 | 43.9 | 135 | 1.89 | 18.0 | 36.0 | |
| AWG30lw | 9.495 | 4,600 | 35.9 | 194 | 2.23 | 17.9 | 29.5 | |
| AWG28lw | 9.514 | 2,560 | 26.3 | 304 | 2.54 | 18.3 | 21.5 | |
| AWG26lw | 9.539 | 1,440 | 19.5 | 437 | 2.68 | 18.8 | 15.8 | |
| AWG24lw | 9.582 | 723 | 13.4 | 653 | 2.76 | 18.9 | 10.9 | |
| AWG22lw | 9.672 | 305 | 8.36 | 1,060 | 2.77 | 19.6 | 6.72 | |
| AWG20lw | 9.798 | 150 | 5.64 | 1,560 | 2.72 | 20.6 | 4.48 | |
| dLGR | none | 9.393 | 5,390 | 41.5 | - | - | - | - |
| AWG32lw | 9.406 | 4,240 | 34.2 | 116 | 1.34 | 15.3 | 29.0 | |
| AWG30lw | 9.419 | 3,500 | 30.1 | 167 | 1.69 | 15.5 | 25.4 | |
| AWG28lw | 9.434 | 2,380 | 24.1 | 262 | 2.12 | 15.6 | 20.3 | |
| AWG26lw | 9.452 | 1,530 | 18.8 | 377 | 2.37 | 15.9 | 15.8 | |
| AWG24lw | 9.484 | 847 | 13.5 | 563 | 2.54 | 16.1 | 11.3 | |
| AWG22lw | 9.552 | 381 | 8.69 | 911 | 2.62 | 16.8 | 7.23 | |
| AWG20lw | 9.646 | 194 | 5.95 | 1,340 | 2.60 | 17.8 | 4.89 | |
| LGR | none | 9.523 | 435 | 9.73 | - | - | - | - |
| AWG32sw | 9.523 | 426 | 9.57 | 116 | 0.475 | 5.20 | 9.07 | |
| AWG30lw | 9.523 | 416 | 9.48 | 167 | 0.676 | 5.30 | 8.98 | |
| AWG28lw | 9.521 | 389 | 9.24 | 262 | 1.02 | 5.92 | 8.69 | |
| AWG26lw | 9.518 | 349 | 8.83 | 377 | 1.40 | 5.99 | 8.30 | |
| AWG24lw | 9.511 | 279 | 7.98 | 563 | 1.86 | 6.70 | 7.45 | |
| AWG22lw | 9.491 | 174 | 6.42 | 911 | 2.36 | 7.79 | 5.92 | |
| AWG20lw | 9.450 | 100 | 4.99 | 1,340 | 2.63 | 8.76 | 4.55 | |
| AWG18lw | 9.550 | 53.6 | 3.52 | 2,050 | 2.71 | 11.3 | 3.12 |
See Appendix B.
The results of Table 3 are consistent with predictions of the analytic theory. The maximum Λ is achieved with the smallest sample. For all resonators, as the sample gets larger, the resonator efficiencies and Qs drop. Both are significantly lower for the LGR than for the DR or dLGR. For very small sample, the peak Λ and Q are higher for the DR than the dLGR, and as the sample size increases, they drop more quickly for the DR than the dLGR. Between the DR and dLGR, there is a crossover in Q from AWG28 to AWG26 and peak Λ from AWG26 to AWG24. However, the DR is axially larger than the dLGR at fixed frequency and so the sample volume is larger for the DR for the same diameter sample tube. This makes the ΛV product always larger in the DR than the dLGR, consistent with the analytic theory, Eqs. (4) and (14). This is seen directly in the values of the saturable signal Ss, shown in Table 3, which are proportional to the integrated ΛV; see Eqs. (17) and (18). The Ss values are maximum for AWG22 for both the DR and the dLGR. For the LGR, the Ss values monotonically increase with sample size and exceed those of the DR and dLGR for sample tubes with a larger diameter than AWG18.
The analytic theory shown in Fig. 4b indicates that if the coupling coefficient is decreased from the value for the current dLGR (shown as the vertical line), the resonator efficiency should increase for sufficiently small sample. This prediction was tested using ANSYS HFSS. For the no-sample case, simulations were done in which the inner LGR loop diameter was increased in order to reduce the coupling coefficient. It was found that the resonator efficiency did increase as the inner LGR loop was increased. The dielectric diameter and length were also increased to maintain 9.5 GHz. With a dielectric diameter of 2.65 mm, an inner LGR loop diameter of 10.7 mm, and an outer LGR loop diameter of 1.2 mm, the resonator efficiency and Q increased to 59.3 G/W1/2 and 10,200, respectively, approaching the DR Qs shown in Tables 1 and 3. In this limit, the LGR acts simply as a coupler to the DR.
4. FABRICATION
100 kHz modulation penetration through the shield of the resonator was achieved using copper gilding foil with a thickness of 2.9 μm as determined by weight and density for the conducting shield surrounding the dLGR. (Gilding foil of different types including copper is available from Wehrung & Billmeier Gold Leaf, LLC, Sheboygan, WI.) The skin depth of copper at 100 kHz is 210 μm and at 9.5 GHz is 0.68 μm. Consequently, the foil is substantially transparent to the modulation but not the RF. The copper foil surrounds the LGR body but is spaced apart from it with a 1.1 mm G-10 fiberglass layer. The foil overlaps each end of the LGR body by 6 mm and is electrically floating.
A housing and matching mechanism from a JAGMAR (Krakow, Poland) LGR was used to build the dLGR. Photographs of the dLGR assembly are shown in Figs. 6–8. The housing has a fitting that feeds purge gas around the coupling loop and into the region of the dLGR, Fig. 6. The left Rexolite piece, Fig. 8, is inserted through the LGR body, which has a set of spring-loaded pins that center and hold the Rexolite. O-rings provide a gas seal on the Rexolite and serve as a safety valve from overpressure. Gas flows through the left Rexolite plate, around the rutile dielectric element, and out through a long extension to the left Rexolite plate that also guides the sample tube. The coupling loop passes through a cutout in the Rexolite, Fig. 7, and aligns with an outer loop of the copper LGR, Fig. 8. This LGR component of the dLGR was fabricated by electric discharge machining by Integrity Wire EDM (Sussex, WI, USA). The rutile dielectric element is shown centered in the inner LGR loop. The left and right Rexolite pieces hold the rutile concentrically in the inner LGR loop with an air gap of 0.1 mm around the circumference the dielectric element, Fig. 8. The sample tube is shown threaded through the rutile. An aluminum spacer (not shown) beneath the shield on the right side provides a symmetrical shield to the brass LGR body shown in Fig. 8. The outer sleeve has a copper gilding foil shield under the red heat-shrink tubing. When assembled, the rutile is held firmly leaving a slight gap vertically with the LGR. Nylon set screws in the lower Rexolite piece press vertically to secure the LGR. Matching was accomplished by varying the distance between the coupling loop and an outer LGR loop using the JAGMAR mechanism.
Figure 6:
Assembled dLGR made from a JAGMAR (Krakow, Poland) LGR housing.
Figure 8:
Central section of fabricated dLGR assembly shown partly disassembled. The copper 5-loop–4-gap LGR is between two pieces of Rexolite that hold the SC rutile dielectric concentrically in the inner loop of the LGR. A PTFE sample tube goes through the SC rutile dielectric.
Figure 7:
Left half of dLGR assembly with a view of the inductive coupling loop.
A fiberglass tube was press fit to the LGR body, and the diameter of the copper LGR piece was trimmed to fit the fiberglass tube. The press fit centers and holds the LGR piece while providing a 0.13 mm air gap between the Rexolite and the LGR metal on each side of the LGR gaps. The Rexolite pieces are also press fit into the fiberglass tube. The rutile is slightly longer than the LGR, which allows a fitted hole and controlled depth in the Rexolite discs to center the dielectric element in two directions. The presence of the Rexolite was verified to have a negligible effect on the electromagnetic performance of the dLGR using finite element simulations. The sample tube enters through holes in the Rexolite. During modeling, it was determined that axial symmetry was important to suppress unwanted modes. Consequently, the Rexolite discs on each side were made to be the same thickness. An aluminum end spacer was added along with four nylon-tipped set screws to press against the LGR in an RF field null point after assembly. With the LGR in place and the rutile mounted on a sample tube, the fiberglass tube was slid into place, aligning the coupling loop on one of the outer loops. Then the set screws were adjusted to push the LGR against the top Rexolite piece.
The sample hole in the K-100 PC rutile dielectric piece was bored using a 0.51 mm diameter diamond wheel followed by a 0.64 mm diameter diamond wheel on a lathe turning about 1,000 rpm. The final size of 0.76 mm diameter was obtained by using a copper wire and diamond paste rotating slowly. The OD was ground using a diamond wheel on a jig grinder to size. Since the pieces were already 2.54 mm OD, little material needed to be removed to reach 2.4 mm. The length was cut with a cutoff wheel and trimmed to a 3.17 mm length on a surface grinder. No annealing was done.
As provided by the manufacturer, MTI Corporation, the SC rutile was a flat cylindrical disc of 16 mm diameter and 3.04 mm thickness. According to MTI Corporation, the crystal orientation of the SC rutile cylindrical disc axis is parallel to the c-axis (Sec. 1), meaning that the high dielectric constant is parallel to the cylindrical disc axis. The SC rutile piece in the perpendicular orientation was fabricated by cutting the disc in a direction perpendicular to the axis on a surface grinder using a diamond cutoff wheel to form three pieces—a rectangular center piece and two wing pieces. The rectangular piece was mounted in a suitable collet with the long dimension of the piece parallel to the collet axis. Then the sample hole was bored using a 0.51 mm diamond wheel followed by a 0.64 mm diamond wheel and finally a 0.76 mm diamond wheel. These were drilled at about 7,000 rpm. The final size of the hole was obtained by using a copper wire and diamond paste rotating slowly. The OD was then ground on a jig grinder using a 300-grit diamond wheel made with a special nonmetallic binder (500 BINM Resin Bond, Diagrind, Inc., Orland Park, IL) to minimize residue that could produce EPR signals. The grinding wheel, rotating at 30,000 rpm, traveled around the piece. The radius of the wheel travel was adjustable in increments of 2.5 μm. Finally, the length was cut with a cutoff wheel and trimmed to length on a surface grinder. The crystal is quite brittle and machining operations must be done with care. The final size is 2.37 mm in diameter and 3.16 mm in length with a 0.76 mm diameter hole for the sample tube.
5. EPR CHARACTERIZATION
Frequency and Q measurements were made using an Agilent Technologies (Santa Clara, CA) E8363C PNA Network Analyzer calibrated using Electronic Calibration Module N4691–60001. Q measurements were made by observing the frequencies of the S11 −6 dB points on either side of resonance. EPR measurements were made using a Varian (Palo Alto, CA) E-line series X-band EPR spectrometer with an E102 microwave bridge and V7200 9” magnet. Results from the PC and SC rutile dLGRs with an AWG26lw sample tube with a 520 nL sample volume were compared to a 2-loop–1-gap LGR (Molecular Specialties, Milwaukee, WI) with a TPX (methyl-pentene polymer) sample tube with a 2.1 μL sample volume. This LGR is a version of resonator No. 2 in Table 1 of [19]. Resonator efficiency measurements were obtained with 600 μM PADS (peroxylamine disulfonate dianion) (Fremy’s salt) in a 50 mM aqueous solution of K2CO3 under nitrogen using the method given in Refs. [20, 21].
EPR spectra were obtained using the stable, biologically relevant nitroxide standard 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO). Figure 9 compares 100 μM TEMPO saturable EPR signals between the PC rutile dLGR and the 2-loop–1-gap LGR. The signal level of the PC rutile is about 90% of the LGR signal for a sample about four times smaller. A comparison of experimental and finite element simulation results for these resonators can be found in Table 4. In these simulations, the fabricated dimensions of the rutile reported in Sec. 4 (which are different than those listed in Table 3) were used. The simulated saturable EPR signal ratio between the dLGR and 2-loop–1-gap LGR is 45%. The prominent background signal in the spectrum recorded for the PC rutile dLGR was unchanged with signal averaging. The features are repeatable from scan to scan and theoretically could be subtracted out. However, when the dielectric is repositioned in the static magnetic field, the EPR background signal was found to change. This background signal makes K-100 (Sec. 1) inconvenient for use in EPR. See [11].
Figure 9:
Comparison of EPR signals for 100 μM TEMPO (room temperature, room air) between a PC rutile dLGR with an AWG26lw PTFE sample tube and a 2-loop–1-gap LGR with a TPX capillary at the same value of B1. The background features in the dLGR spectrum are reapeatable; see text. The dLGR signal was taken at a power level of 1 mW and the LGR at 4 mW. The width of each spectrum is 100 G.
Table 4:
Comparison of dLGR and 2-loop–1-gap LGR properties
| type | f (GHz) | Q | Λ (G/W1/2) | Vs (nL) | Ss (V) | Ssratio | Λrms (G/W1/2) | |
|---|---|---|---|---|---|---|---|---|
| LGR | experimental | 9.460 | 204 | 5.3 | 2150 | - | 1 | - |
| simulated | 9.373 | 354 | 5.22 | 2150 | 4.72 | 1 | 4.95 | |
| PC dLGR | experimental | 9.393 | 1,560 | - | 519 | - | 0.90 | - |
| simulated | 9.254 | 1,540 | 13.8 | 519 | 2.12 | 0.45 | 11.0 | |
| SC dLGR | experimental | 8.997 | 1116 | 11.7 | 517 | - | 0.95 | - |
| simulated | 8.903 | 1,610 | 20.1 | 517 | 3.02 | 0.64 | 16.2 |
Figure 10 compares the EPR signals between an SC rutile dLGR and the 2-loop–1-gap LGR. It is seen that the saturable signal level of the dLGR is about 95% of the LGR despite a sample volume for the dLGR that is four times smaller. The saturable EPR signal levels calculated from the finite element simulations differ by 30%, 3.0 V for the dLGR and 4.7 V for the 2-loop–1-gap LGR as shown in Table 4. Unlike for the PC rutile, background signals with the SC rutile are very small, making the SC rutile favorable for use in EPR. Fremy’s salt experiments were done to obtain the resonator efficiencies for the SC rutile dLGR and the 2-loop-1-gap LGR, which were 11.7 G/W1/2 with maximum line height at 0.072 mW and 5.3 G/W1/2 with maximum line height at 0.35 mW, respectively. These results are in fair agreement with the peak Λs from the finite element simulations, 20.1 G/W1/2 for the dLGR and 5.2 G/W1/2 for the LGR as shown in Table 4. Because of axial spatial B1 nonuniformities, it may be more accurate to compare the experimental resonator efficiency parameters to the rms Λs shown in Table 4, 16.2 G/W1/2 and 4.9 G/W1/2, respectively. Experimental validation of the modulation model, which did not include the coupling loop, was not done, making a direct comparison of the experimental results with the finite element simulations difficult.
Figure 10:
Comparison of EPR signals for 100 μM TEMPO (room temparature under nitrogen) between an SC rutile dLGR with an AWG26lw PTFE sample tube and a 2-loop–1-gap LGR with a TPX capillary at the same value of B1. The EPR signals are of similar amplitude with four-times smaller sample volume. The signal-to-noise ratios differ by 1%. The dLGR signal was taken at a power level of 0.2 mW and the LGR at 0.8 mW. The width of each spectrum is 100 G.
6. DISCUSSION
Electromagnetic synergy between the DR and the LGR occurs in the dLGR in three ways. First, the dielectric concentrates the magnetic field in the inside of the inner loop, which reduces the field on the LGR inner loop wall, resulting in reduced ohmic dissipation in the LGR. Second, the concentration of magnetic field permits the gaps to be designed with a magnetic field null in the middle of the gaps, which also reduces ohmic dissipation. Third, the dielectric generates polarization charge on the dielectric surface, which shields the sample from the strong dipole electric fields of the gaps and decreases dissipation in the sample. The result is that the resonator efficiency of the dLGR approaches but does not exceed that of the DR alone at fixed frequency and sample size, as shown by the analytic model Eqs. (4) and (14) and verified by finite element simulations.
Results of this work indicate that the dLGR can have higher concentration sensitivity than an LGR for sample sizes smaller than 2 μL at X-band. For the present experiment, the dLGR was designed to accommodate an AWG26 sample tube with a sample size of 400 nL. The concentration sensitivity of this structure nearly matches that of a DR. For samples smaller than 400 nL, the ID of the sample loop of the LGR body of the dLGR can be increased (lowering k) such that the concentration sensitivity can match that of a DR. The advantage of the dLGR is the convenience of the overall design. The LGR acts as a coupling structure to the DR.
For aqueous sample sizes smaller than 50 nL, analytic theory and finite element simulations indicate that a factor of six higher peak resonator efficiency (60 G/W1/2) can be obtained using SC rutile in the perpendicular orientation compared with an LGR alone. However, a significant reduction in resonator efficiency occurs with increasing sample size because of RF losses in the sample. For a 130 nL sample size, a peak resonator efficiency of 44 G/W1/2 using an AWG32 standard wall (sw) sample tube (see Appendix B) with a saturable EPR signal level of 80% of the current dLGR design could be achieved. This requires an appropriately designed LGR body with a lower coupling coefficient than the existing design. The fabricated dLGR accommodates an AWG26lw sample tube, which gives a sample size of 400 nL and a peak resonator efficiency of 19 G/W1/2. This value is similar to that of a DR of the same frequency and sample size. For sample sizes larger than 2,000 nL, an LGR can have a larger saturable EPR signal than a rutile dLGR or DR for the same sample size. Experimental results using TEMPO and Fremy’s salt are in fair agreement with the finite element simulations.
The present report is thought to be the first to describe a cylindrical resonator for EPR that was machined from a single crystal of rutile. Background signals were minimal, and no fundamental challenges were identified that arose from the birefringence of the crystal. It was expected, when the study began, that the combination of the LGR with a rutile insert in the sample loop would be synergistic. In fact, the LGR was mostly advantageous as a means to support the dielectric, the sample, and the microwave coupling structure.
The LGR was introduced by Froncisz and Hyde for use at S-band [19]. The primary benefit was that it allowed EPR studies on smaller samples than a cavity resonator because of the high Λ, Eq. (3). A further benefit was discovered when the structure was extended to 35 GHz and then to 94 GHz. The high Λ coupled with low Q led to an increase in bandwidth compared with cavity resonators, which was advantageous in certain experiments. Over the intervening years, it was established that the Λ at X-band in conventional LGR geometries could not exceed a value of 10 G/W1/2, with a value of 8 G/W1/2 being more representative. Cavity resonators typically exhibit values of about 1 G/W1/2. Studies reported in the present paper indicate that the value of Λ using rutile can be about six times higher than an LGR. To achieve this result with aqueous samples, volumes are typically of the order of 50 nL at X-band. These results have a number of implications for future investigations using continuous wave (CW) EPR.
Extensions to low frequency, for example, 1 GHz, and to high frequency, 94 GHz, seem within reach. Separation of hyperfine and Zeeman interactions in spin label studies on very small samples using multifrequency resonators that are based on rutile is feasible.
In our hands, studies on small samples are usually carried out at W-band; studies at the more commonly used X-band frequency are now possible.
Continuous flow studies using a dLGR fed by the output of a mixing chamber require less sample.
Because of the small sample diameter, studies at high pressure without sample tube breakage become feasible.
The time scale for gas exchange, for example, change in the oxygen-nitrogen mixture flowing over the sample, can be much shorter because of the small sample tube diameter.
A relatively unexplored range of conditions for EPR spectroscopy of free radicals in liquids is defined by the high value of H1 at the sample and an intermediate degree of motional narrowing. Hyde and Thomas found that the spin label second harmonic absorption spectrum out-of-phase with response to magnetic field modulation is a useful display for characterization of very slow rotational diffusion [22]. Extension to higher Λ, higher or lower modulation frequency, shorter rotational correlation times and alternative displays is possible using the dLGR. These displays can be presumed to contain information about spin-label dynamics.
One of the benefits of high Λ is that experiments that require a predetermined value of H1 at the sample are carried out at much lower incident power. A consequence is that phase noise when tuned to the dispersion is greatly reduced. In CW EPR under conditions of low microwave power saturation, the dispersion and absorption are related by a Hilbert transformation, and high Λ combined with simultaneous detection effectively increases the signal-to-noise ratio (SNR) by 21/2. Under conditions of high microwave power saturation, the dispersion signal can be much more intense than the absorption, and high Λ significantly increases the SNR. Adiabatic rapid passage experiments belong to this class.
The LGR was found to be valuable in pulse EPR because of the high values of H1 that can be obtained with relatively low incident power. Specifically, the LGR is always used for saturation recovery (SR) experiments. There are two broad categories of SR methods: 1) short pulse to study transverse relaxation processes such as rotational diffusion in a sample that has an anisotropic spin Hamiltonian, and 2) long pulse to examine spin lattice relaxation after transverse relaxation processes have reached equilibrium. High pulse power can contribute to the experimental dead time, which places limitations on the short pulse method. Achieving the same value of microwave field at the sample with a pulse of much lower power incident on a dLGR can help to reduce dead time. In addition, the pulse can be shorter for the same tip angle.
The dielectric tube resonator (DTR) was previously introduced from this laboratory in a theoretical study [16]. Rutile was extensively analyzed, and use of cavity resonators containing rutile tubes of various diameters was found to be an attractive strategy for further development of the DTR, particularly in a configuration that resulted in uniform field along the sample tube axis. This paper on the dLGR presents a methodology to fabricate from a single crystal of rutile a cylinder that can be suitable for use in the DTR.
The DTR paper [16] also considered sapphire, and it now seems possible to design a dLGR that uses sapphire. Such a structure would be expected to have a lower Λ but a higher sample volume than the rutile dLGR. The trade-off can be expected to be of practical value.
In summary, the main benefits of the rutile dLGR are the high Λ and development of EPR technology for smaller samples. Both CW and pulse EPR benefit. Extension from X-band to both higher and lower microwave frequencies is anticipated, and other dielectrics may be found to be useful.
ACKNOWLEDGEMENTS
Research reported in this publication was supported in part by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number P41EB001980. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors thank Dr. Oleg Grinberg for discussion of EPR properties of SC rutile and how to obtain it.
APPENDIX A
A complete set of circuit equations derived from the defined mesh currents and component voltage drops of Fig. 3 and are given by
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
Since there are seven voltage and current quantities and six equations, the ratio between any two of these quantities can be found by solving the system of equations for one quantity in terms of the other (e.g., by Mathematica).
APPENDIX B
The following table shows the dimensions of the various standard wall (sw) and light wall (lw) polytetrafluoroethylene (PTFE) sample tubes used in the present work. They are manufactured by Zeus Industrial Products, Inc., Orangeburg, SC, and are based on the American Wire Gauge (AWG).
Table B1:
PTFE sample tube sizes
| sample tube | ID (mm) | OD (mm) |
|---|---|---|
| AWG32sw | 0.25 | 0.51 |
| AWG30lw | 0.30 | 0.61 |
| AWG28lw | 0.38 | 0.69 |
| AWG26lw | 0.46 | 0.76 |
| AWG24lw | 0.56 | 0.86 |
| AWG22lw | 0.71 | 1.02 |
| AWG20lw | 0.86 | 1.17 |
| AWG18lw | 1.07 | 1.37 |
REFERENCES
- [1].Hyde JS and Froncisz W, Loop gap resonators, in: Hoff AJ (Ed.), Advanced EPR: Applications in Biology and Biochemistry, Elsevier, New York, 1989, pp. 277–306. [Google Scholar]
- [2].Stoodley LG, The sensitivity of microwave electron spin resonance spectrometers for use with aqueous solutions, J. Electron. Control 14 (1963) 531–546. [Google Scholar]
- [3].Terman FE, Radio Engineers’ Handbook, McGraw-Hill handbooks, McGraw-Hill, New York, 1943, pp. 148–172. [Google Scholar]
- [4].Mett RR, Sidabras JW, Golovina IS and Hyde JS, Dielectric microwave resonators in TE011 cavities for electron paramagnetic spectroscopy, Rev. Sci. Instrum 79 (2008) 094702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Dykstra RW and Markham GW, A dielectric sample resonator for enhanced sensitivity of EPR signals, J. Magn. Reson 69 (1986) 350–355. [Google Scholar]
- [6].Hyde JS, Sidabras JW, and Mett RR, Resonators for Multifrequency EPR of Spin Labels, chapter 5.2, in: Misra SK (Ed.), Multifrequency Electron Paramagnetic Resonance: Theory and Applications, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011, pp. 244–270. [Google Scholar]
- [7].Tobar ME, Krupka J, Ivanov EN and Woode RA, Anisotropic complex permittivity measurements of mono-crystalline rutile between 10 and 300 K, J. Appl. Phys 83 (1998) 1604–9. [Google Scholar]
- [8].Yee HY, Natural resonant frequencies of microwave dielectric resonators (correspondence), IEEE Trans. Microwave Theory Tech. 13 (1965) 256–256. [Google Scholar]
- [9].Pozar DM, Microwave Engineering, 4th edn., Addison-Wesley, New York, 1990, secs. 7.5, 7.8. [Google Scholar]
- [10].Pospieszalski MW, Cylindrical dielectric resonators and their applications in TEM line microwave circuits, IEEE Trans. Microwave Theory Tech 27 (1979) 233–238. [Google Scholar]
- [11].Misra SK, Andronenko SI, Tipikin D, Freed JH, Somani V, and Prakash O, Study of paramagnetic defect centers in as-grown and annealed TiO2 anatase and rutile nanoparticles by a variable-temperature X-band and high-frequency (236 GHz) EPR, J. Magn. Magn. Mater 401 (2016) 495–505, 10.1016/j.jmmm.2015.10.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Mett RR, Sidabras JW, and Hyde JS, Uniform RF fields in loop-gap resonators for EPR spectroscopy, Appl. Magn. Reson 31 (2007) 573–589. [Google Scholar]
- [13].Mett RR, Sidabras JW, and Hyde JS, Coupling of waveguide and resonator by inductive and capacitive irises for EPR spectroscopy, Appl. Magn. Reson 35 (2008) 285–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Mett RR, Sidabras JW and Hyde JS, MRI surface-coil pair with strong inductive coupling, Rev. Sci. Instrum 87 (2016) 124704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Sidabras JW, Mett RR and Hyde JS, Aqueous flat cells perpendicular to the electric field for use in electron paramagnetic resonance spectroscopy II. Design, J. Magn. Reson 172 (2005) 333–341. [DOI] [PubMed] [Google Scholar]
- [16].Hyde JS and Mett RR, EPR Uniform Field Signal Enhancement by Dielectric Tubes in Cavities, Appl. Magn. Reson 48 (2017) 1185–1204, 10.1007/s00723-017-0935-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Von Hippel AR, Dielectric Materials and Applications, Artech House, Boston, 1954. [Google Scholar]
- [18].Ellison WJ, Permittivity of pure water, at standard atmospheric pressure, over the frequency range 0–25 THz and the temperature range 0–100 °C, J. Phys. Chem. Ref. Data 36 (1) (2007) 1–18. [Google Scholar]
- [19].Froncisz W and Hyde JS, The loop-gap resonator: a new microwave lumped circuit ESR sample structure, J. Magn. Reson 47 (1982) 515–521. [Google Scholar]
- [20].Nesmelov YE, Gopinath A and Thomas DD, Aqueous sample in an EPR cavity: sensitivity considerations, J. Magn. Reson 167 (2004) 138–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Kooser RG, Volland WV and Freed JH, ESR relaxation studies on orbitally degenerate free radicals. I. Benzene anion and tropenyl, J. Chem. Phys 50, (12) (1969) 5243–5257. [Google Scholar]
- [22].Hyde JS and Thomas DD, New EPR methods for the study of very slow motion, Application to spin-labeled hemoglobin, Ann. N. Y. Acad. Sci 222 (1973) 680–692. [DOI] [PubMed] [Google Scholar]