Abstract
To decipher cell state transitions from single-cell transcriptomes it is crucial to quantify weak expression of lineage determining factors, requiring computational methods sensitive to variability of lowly expressed genes. We here introduce VarID, a computational method that identifies locally homogenous neighborhoods in cell state space, permitting the quantification of local gene expression variability. VarID delineates neighborhoods with differential gene expression variability and reveals pseudo-temporal dynamics of variability during differentiation.
With the advent of a growing number of single-cell sequencing technologies our ability to decipher the cell type composition of complex tissues is rapidly improving. Single-cell transcriptomes can reveal manifolds in cell state space representing trajectories of cell state transitions1. It is of core interest to understand the molecular control of these transitions, but the investigation of transcription factor and signaling networks underpinning cell state transitions is frequently hindered by the low and highly variable expression of these classes of genes. Since differences of lowly expressed genes are difficult to detect due to technical and biological noise2, we here introduce a method for the inference of local variability; increased local variability could indicate the onset of expression in local neighborhoods, or the response to fluctuating signaling inputs from the microenvironment. Available methods for the inference of noise parameters2–4 were not designed for complex mixtures of cell types and do not permit the local estimation of variability.
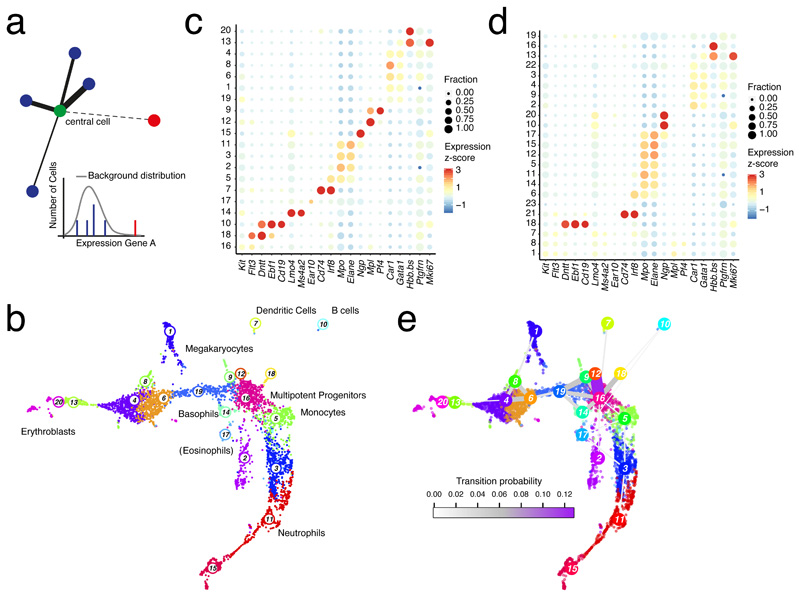
A fundamental challenge is the definition of local neighborhoods in cell state space, since admixtures of distinct cell types or states could inflate the variability estimates. Since k-nearest neighbor (knn) networks have successfully been used for the inference of cell types5,6 and differentiation trajectories7 we reasoned that the k-nearest neighborhood would be a useful starting point. We devised a statistical test to determine if the expression levels of all genes for each neighbor are in accordance with the expected distribution of the “central” cell. We have previously demonstrated that unique molecular identifier (UMI)-derived transcript counts are well described by a negative binomial distrubtion2, which is uniquely determined by mean and variance. We thus learn a local mean by averaging expression across the central cell and its knns with weights determined by their similarity to the central cell (Methods). An additional parameter α can be varied to adjust the degree of locality. We next determine the variance associated with the local mean estimate from a global background distribution. As we showed previously8,9, the mean-variance relation in logarithmic space is well described by a second order polynomial, robustly averaging across genes of similar mean expression (Supplementary Fig. 1a). Hence, a local mean allows us to define local background distributions for all genes, and links to any of the knns with expression levels not explained by this distribution are discarded (Fig. 1a). The resulting pruned knn-network thus only connects locally homogenous neighborhoods.
Figure 1. Locally homogenous neighborhoods enable sensitive cell type identification.
a, Strategy for inferring locally homogenous neighborhoods by pruning knn-networks. Links are removed if the transcript levels in a neighboring cell are not explained by a local background model. Thickness of links represents the likelihood of belonging to the same cell state. b, Uniform Manifold Approximation and Projection for Dimension Reduction (UMAP) representation21 of mouse hematopoietic progenitor single-cell RNA-seq data10 highlighting clusters inferred by Louvain clustering on the pruned knn-network (k=10 and α=10). Cell type labels are based on marker gene expression. c, Dot plot showing the expression z-score of lineage-specific marker genes across all clusters from (b). The dot size indicates the fraction of cells expressing a gene. d, Dot plot showing expression of lineage-specific marker genes across all clusters inferred by Seurat5,6. See (c) for details. e, UMAP representation with links connecting cluster medoids. The thickness and color of a link indicates the transition probability between the connected clusters. (b-d) Data from n=2 biologically independent experiments.
To identify distinct cell states and types we applied Louvain density clustering to the pruned network. To demonstrate increased sensitivity of cell type detection when using the pruned network, we analyzed murine hematopoietic progenitor single-cell transcriptomes10 (Fig. 1b,c). We recovered all lineages described in the original study, and resolved additional sub-populations such as Mplhigh versus Pf4high megakaryocyte states, Ebf1high pro-B cells and Dntthigh progenitors, and eosinophils (Fig. 1b,c). These sub-populations remain unresolved when clustering is performed on the full network (Supplementary Fig. 1b-c) or when Seurat5,6 analysis is performed (Fig. 1d and Supplementary Fig. 1d-f). As the clustering depends on the choice of the parameters α and knn, we evaluated the resolution of rare populations within this dataset, i.e. lymphoid progenitors, B cells, basophils, eosinophils, dendritic cells, and megakaryocytes, based on the resolution of the expression domains of corresponding marker genes (Supplementary Fig. 1g). This analysis supports α=10 and knn=10 as an optimal parameter choice. We observed similar clustering performance when determining knns with a supplied Pearson’s correlation-based distance matrix and when using the default method, i.e. based on Euclidean distances in principle component analysis (PCA) space (Supplementary Fig. 1h, Methods).
We next predicted transition probabilities between the inferred clusters on the pruned knn-network. Assuming a random starting cell within a given cluster, one can readily compute the probability to transition into another cluster within a single step on the network (Methods). These probabilities were in very good agreement with known differentiation pathways (Fig. 1e): multipotent progenitors (cluster 16) were directly linked to megakaryocytes, dendritic cells, basophils, monocytes, and the major branches of erythrocytes and neutrophils, respectively.
In order to explore differences in lowly expressed genes between cell states, we derived estimates of gene expression variability in local neighborhoods on the pruned knn-graph. To account for the convex variance-mean dependence in logarithmic space as a consequence of biological and technical noise2–4,11 (Fig. 2a), we fitted a second order polynomial to the baseline level of the combined technical and biological variability (Methods). This allowed us to regress out the systematic baseline mean-dependence and directly compare corrected variability estimates between neighborhoods (Fig. 2b). As an alternative approach, we followed a recently published method based on a negative binomial generalized linear model with the total transcript count of each cell as independent variable12. After averaging regression parameters across genes of similar mean expression (Methods, Supplementary Fig. 2), the variance of the Pearson residuals should in theory be independent of the mean expression. In order to test the sensitivity and specificity of VarID for the detection of genes with enhanced variability, we performed a simulation experiment, which revealed that significantly variable fold changes >1.25 can be detected at a false positive rate ~5% and a true positive rate >50% depending on the average expression (Supplementary Fig. 3).
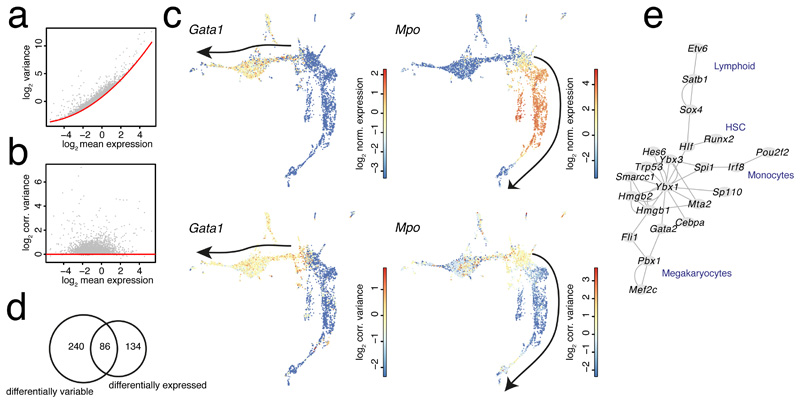
Figure 2. Inferring local variability in hematopoietic progenitor cell state space.
a, Scatterplot showing variance and mean of the transcript count of all genes across all cells in the mouse hematopoietic dataset in logarithmic space. The red line indicates a second order polynomial fit to the baseline level of the variance comprising technical and biological variability. b, Scatterplot showing corrected variance of transcript counts as a function of the mean in logarithmic space after eliminating the mean-dependence by subtracting the baseline fit. The red line indicates the baseline level of the corrected variability. c, UMAP representation highlighting normalized gene expression (upper panel) and corrected variability (lower panel) for Gata1 (left) and Mpo (right). The black arrow indicates the erythrocyte (left) or neutrophil (right) differentiation trajectory. d, Venn diagram showing the overlap of genes with enhanced local variability (one-sided Wilcoxon rank sum-test P<0.001, Benjamini Hochberg corrected, foldchange >1.25) and differentially expressed genes (P<0.001, Benjamini Hochberg corrected, see Methods, foldchange >1.25 between the populations) in cluster 16 versus the remaining cells. e, Heatmap of normalized expression (left) and corrected variance (right) for the top 50 genes with enhanced variability from (d) ordered by decreasing log2-foldchange of variability between cluster 16 and the remaining cells. Clusters were manually grouped by lineage. Hierarchical clustering of rows was performed based on gene expression. f, Gene regulatory network predicted by GENIE3 run on all transcriptional regulators among the genes with enhanced variability, using the full dataset as input. (a-e) Data from n=2 biologically independent experiments.
To explore differences in gene expression variability across cell states, we inferred local estimates of the corrected variability for the murine hematopoietic progenitors using the first approach, i.e. corrected variance (Fig. 2a,b), since a residual mean-variance dependence remained for the second approach (Supplementary Fig. 2a,b). We noticed that increased local variability is frequently associated with the onset of lineage markers in multipotent progenitors (cluster 16), e.g., the early erythrocyte lineage transcription factor Gata1 or the neutrophil marker Mpo (Fig. 2c). However, while the corrected variability remains high in case of Gata1 throughout erythrocyte differentiation, it becomes strongly suppressed for Mpo with increasing expression during neutrophil differentiation (Fig. 2c), indicating gene-specific dynamics of expression variability.
We next extracted all genes with increased local variability within the multipotent progenitor population (cluster 16) in comparison to the remaining populations (one-sided Wilcoxon rank sum-test P<0.001, Benjamini Hochberg corrected, foldchange >1.25). Differentially variable genes exhibited only limited overlap with differentially expressed genes (P<0.001, Benjamini Hochberg corrected, see Methods, foldchange >1.25 between the populations, Fig. 2d). Comparing corrected variability of the top 50 variable genes with their expression across cell clusters revealed groups of genes with stochastic expression in cluster 16 and markedly increasing expression, e.g., on the neutrophil branch, such as Mpo, Prtn3, or Elane, and classes of genes which are also most highly expressed in cluster 16, such as Flt3, Cd27, Cd34, and Il12a. To investigate stochasticity of transcriptional regulators relevant for lineage decisions, we selected all transcriptional regulators13 from the list of significantly variable genes in cluster 16 and predicted a regulatory network by running GENIE314 (Methods, Fig. 2f and Supplementary Fig. 2c). This network recovered modules associated with hematopoietic stem cells (HSCs) comprising Runx215 and Hlf16, the megakaryocyte lineage (Pbx1, Fli1, Mef2c)17, the lymphoid lineage (Satb118, Etv619), and monocyte differentiation (Spi1, Irf8)17, indicating variable activity of lineage-associated transcription factors in multipotent progenitors.
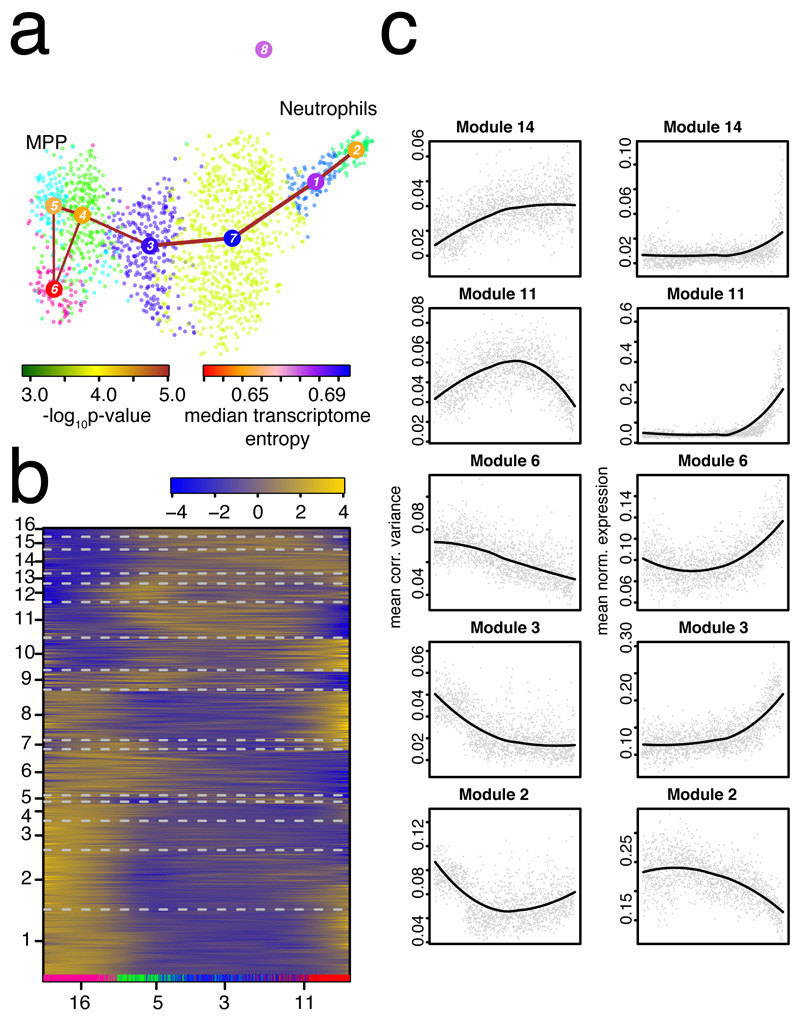
To investigate dynamics of variability during differentiation, we focused on the neutrophil branch and inferred a pseudo-temporal ordering of single-cell transcriptomes with StemID28 (Fig. 3a). We then ordered the pseudo-temporal profiles of gene expression (Supplementary Fig. 4a) and of the corrected variability (Fig. 3b) into co-expressed and co-variable modules, respectively, using self-organizing maps as implemented in FateID8. We observed modules with distinct variability profiles, such as genes with increased variability at naïve and mature states (e.g. module 1 and 8), or during intermediate stages (e.g. module 11). Modules with similar dynamics of variability did not necessarily exhibit comparable gene expression dynamics (Fig. 3c and Supplementary Fig. 4a). Of note, particular modules were enriched in specific functions (Methods, Supplementary Fig. 4b,c).
Figure 3. Exploring dynamics of gene expression variability during neutrophil differentiation.
a, Separate RaceID3/StemID28 analysis all cells from the original clusters 16, 5, 3, and 11. The link color indicates the link p-value and the vertex color represents transcriptome entropy. The link p-value and transcriptome entropies were derived by StemID28. b, Self-organizing map (SOM) of pseudo-temporal corrected variability profiles inferred by FateID8 using the variability matrix as input. The color indicates the z-score of loess-smoothed profiles. Cells were ordered along the trajectory connecting clusters 5, 4, 3, 7, 1, and 2 in (a) by StemID2. Original clusters (cf. Fig. 1b) are highlighted at the bottom. Modules were obtained by grouping SOM nodes based on correlation of averaged profiles (Pearson correlation > 0.85). Only modules with >10 genes are shown in the map. Genes with >2 transcripts in at least one cell were included. c, Pseudo-temporal variability (left) and corresponding gene expression (right) profiles averaged across all genes in a module. Pseudo-temporal profiles were normalized to the same scale by dividing transcript counts and corrected variabilities by the sum across all cells on the trajectory. (a-c) Data from n=2 biologically independent experiments.
To investigate the impact of a perturbation on gene expression variability, we co-analyzed hematopoietic cells sequenced from bone marrow after 48h of EPO stimulation10 together with the cells sequenced from the normal bone marrow. EPO stimulation leads to an expansion of the erythroid lineage at the expense of the other lineages10. Our analysis confirmed that transcriptome changes upon EPO-stimulation only affect the erythroid lineage (Supplementary Fig. 5a-c), and revealed an enrichment of innate immunity pathways among genes with increased variability in EPO-stimulated versus normal erythrocyte progenitors (Supplementary Fig. 5d) (ReactomePA P<0.002, Methods). This finding suggests that progenitors of other lineages could indeed be diverted towards the erythrocyte fate upon EPO-stimulation. Importantly, there is only marginal overlap with differentially expressed genes, and those do not exhibit a significant functional enrichment other than for rRNA processing (Supplementary Fig. 5e).
Finally, application of VarID to murine intestinal epithelial cells20 revealed stochastic activity of secretory lineage transcription factors in Lgr5+ intestinal stem cells, suggesting the existence of secretory fate-biased stem cells (Supplementary Results and Supplementary Fig. 6-8).
In conclusion, by quantifying dynamics of gene expression variability, VarID reveals stochastic activity of lineage regulators involved in cell state transition and facilitates the investigation of the molecular control of fate decision by single-cell RNA-sequencing.
Online Methods
The VarID Method
Inference of a pruned k-nearest neighbor network
The first step of VarID is the inference of a k-nearest neighbor (knn) network. This network can be constructed based on different metrics. As one alternative, a user-defined distance matrix can be provided, or directly computed by VarID, e.g., by using the Euclidean metric, Spearman’s or Pearson’s correlation. Since for datasets with tens of thousands of cells, computation and storage of a distance matrix is prohibitive due to massive memory requirements, VarID provides an alternative approach. After an initial principal component analysis to achieve dimensionality reduction, a fast knn search is performed based on the Euclidean metric in PCA space. The number of principal components used can be specified and is set to 100 by default to ensure that the major variability is captured. We recommend keeping this default setting. Since the memory requirement for distance matrices of n cells scales with O(n*n) and the fast knn search (using the FNN R-package v1.1.3) scales with O(n), the difference in memory requirement will be substantial for large datasets.
To eliminate the effect of cell-to-cell variability in total transcript counts, or sequencing depth, on the dimensional reduction and the downstream analysis, an optional regression with a negative binomial error model by a generalized linear model is computed, with the total transcript count of a cell as independent variable, following a recently proposed method12. If xij is the transcript count of gene i (i=1, …, G) in cell j (j=1, …, N), we compute a negative binomial generalized linear model
| (1) |
with a log link function. The negative binomial distribution is over-dispersed and has been shown to be suitable for modeling technical and biological noise in single-cell RNA-seq data2. The dispersion parameter θij is estimated during the regression in addition to the intercept βij0 and the coefficient βij1. θij determines the deviation of mean and variance :
| (2) |
Following a similar procedure as Hafemeister and Satija12, information is shared between genes by a locally weighted scatter plot smoothing (loess),
| (3) |
resulting in the dependence of the parameters solely on the expression level m.
The resulting knn network is subject to pruning in the next step. For this purpose, a background model of the combined technical and biological variability is defined, using raw transcript counts as input. The variance vi and the mean mi across the entire dataset are computed for each gene i, and the variance-mean dependence across all genes is fitted by a second order polynomial after log-transformation, in order to obtain a function va capturing the average dependence of the expression variability on the mean expression m,
| (4) |
following a similar approach as previously implemented in RaceID9, to share information across genes with similar expression levels. The variance derived from this function fit for a fixed mean uniquely defines a negative binomial distribution, which serves as a background model.
| (5) |
For every cell j a background model is inferred based on the local mean μij for each gene i. To account for the impact of sampling noise and to avoid skewing of the mean estimate by neighbors sampled from a distinct distribution representing a different cell state, a local expression mean for cell j is computed as a weighted mean across the cell j and its k-nearest neighbors. The cell j receives a user defined weight α and the weights wl of its k-nearest neighbors are determined by their relative similarities. This is achieved by representing the size-normalized transcript count vector zj of a cell j as a weighted sum of the size-normalized transcript count vectors zl of its k-nearest neighbors (l = j1,…,jk).
| (6) |
| (7) |
Here, xj denotes the vector of transcript counts xij for all genes i in cell j. The inference of the weights wl is an optimization problem, which is solved by quadratic programming. α determines the weight of the central cell j in comparison to its neighbor and thus controls the degree of locality for the mean expression estimate.
The local mean μj denotes the vector of mean expression values μij for all genes i in cell j and uniquely defines a local transcript count distribution based on the inferred variance-mean relation (eq. (5)). For each of the knns, the probability of the observed transcript count is computed for every gene from this local distribution. More precisely, for every gene the hypothesis is tested that the observed expression is explained by the respective distribution, and the p-value for rejecting this hypothesis is computed as the probability of residing in one of the two tails of the distribution, i.e. a two-sided test is performed. The total number of null hypotheses thus corresponds to the number of tested genes. In order to control for the family-wise error rate at a given p-value threshold, a Bonferroni correction is performed, resulting in link probabilities pijl for gene i between cell j and its k-nearest neighbors (l = j1,…,jk). The minimum of these link probabilities, pjl =mini(pijl) is compared to a probability threshold (Ptr = 0.01 by default) and all neighbors with pjl < Ptr are pruned. This minimum is also assigned as link probability for further analysis.
The resulting pruned knn network connects only cells sampled from overlapping transcript count distributions across all genes. To accelerate the computation, the pruning procedure can be performed on a subset of selected genes, e.g. based on expression or enhanced variability. The latter is implemented in VarID using the RaceID3 criterion for the selection of highly variable genes, i.e. genes with expression variance exceeding the background level (eq. (5)).
Inferring cell type clusters and transition probabilities
The pruned knn network can be used to derive cell types by Louvain clustering. These clusters enable an improved separation of cell types and states compared to Louvain clustering on the unpruned network. Transition probabilities reflecting the inter-cluster connectivity can be derived based on the probability pjl of links connecting cells in different clusters. The underlying idea is to model the probability of transitioning into a different cluster within one step on the knn network.
First, a cell j is selected randomly, i.e. with probability pc=1/nc if nc is the number of cells in cluster c. Next, the link probabilities pjl are multiplied by the probability pl=1/nl of randomly selecting a link, if nl is the number of remaining links after pruning, giving the probability of transitioning across a particular link in a cluster:
| (8) |
The transition probability between two clusters c1 and c2 is now be computed by summing up the probabilities of all links connecting these clusters:
| (9) |
Estimating local variability
The main goal of VarID is the quantification of local properties relying on the availability of local neighborhoods with homogenous cell state composition. We focus on the quantification of local gene expression variability. In the following sections, we describe two alternative approaches for the elimination of the variance-mean dependence implemented in VarID.
Option 1: Direct regression of the variance-mean dependence
A major problem is the dependence of the transcript count variance on the average transcript count. We observed that the baseline level of the variance as a function of the mean exhibits a convex behavior after log-transformation. This is mainly due to the presence of two sources of technical noise, i.e. sampling noise and global cell-to-cell variability in sequencing efficiency on top of biological variability2. To capture the baseline level of the noise, we split the gene variances into 100 equally populated bins after ordering by increasing mean expression. For each bin, we retain only the data points with variances below the 5%-quantile of the variance distribution within this bin. We then performed a least square regression of a second order polynomial to the remaining data points across all bins (cf. eq. (4)) to obtain a function vb capturing the baseline variability as a function of mean expression m.
| (10) |
The local variability vlij of gene i in the neighborhood of cell j, given by cell j and its nearest neighbors (l = j1,…,jp) that remained after pruning, is now estimated as the variance of the transcript counts xil across the neighborhood of cell j, divided by vb(mij), where mij is the mean of the transcript counts xil of gene i across the pruned neighborhood of cell j:
| (11) |
Option 2: Eliminating the variance-mean dependence regressing out total transcript counts from the expression data
As an alternative approach, the local variability vlpij of gene i in the neighbourhood of cell j is computed as the variance of the Pearson residuals computed from a negative binomial generalized linear model with log link function (eq. (1)):
| (12) |
| (13) |
with
| (14) |
Pathway Enrichment Analysis
Symbol gene IDs were first converted to Entrez gene IDs. Pathway enrichment analysis was implemented using the ReactomePA22 package (v1.22.0). Pathway enrichment analysis was done on genes taken from the different modules in the SOMs. All expressed genes remaining after expression filtering were taken as universe.
VarID parameters
For the analysis of the murine hematopoietic progenitors10, we downloaded the dataset GSE89754 from GEO and extracted the raw unique molecular identifier (UMI) counts for the basal bone marrow data and for the EPO-treated condition. VarID is integrated in the RaceID analysis pipeline and part of RaceID v0.1.4 available on CRAN. We removed the following genes and correlating gene groups in the filtering step (CGenes parameter): mitochondrial genes (mt*), ribosomal genes (Rpl*, Rps*), and predicted genes with Gm-identifiers (Gm*). Only cells with at least 1,000 transcripts were retained. We ran VarID with no_cores=5 and default parameters otherwise. For the analysis of murine intestinal epithelial cells20, we downloaded dataset GSE92332 from GEO and extract the atlas UMI counts. We noticed that libraries from male and female mice were combined in this dataset. Libraries B1 and B2 upregulated Xist expression and clustered separately from the remaining libraries in an initial analysis. To avoid a strong gender-related batch effect, we discarded these libraries. We removed the following genes and correlating gene groups in the filtering step (CGenes parameter): the proliferation marker Mki67, ribosomal genes (Rpl*, Rps*), and predicted genes with Gm-identifiers (Gm*). Only cells with at least 1,000 transcripts were retained. We ran VarID with regNB=FALSE for the pruning step, no_cores=5, and default parameters otherwise.
Seurat analysis
Seurat (v3.0.0) was run on the raw counts but retaining only genes and cells that remained after the VarID filtering step in order to ensure comparability. We chose default parameters and resolution=1. We tested increasing the resolution parameter, but this led to more unstable clusters and did not improve the detection of rare populations.
Prediction of Gene Regulatory Network
To infer gene regulatory networks GENIE314 was run using the R Bioconductor package GENIE323 (v1.0.0) with default parameters on the full dataset. For the hematopoietic progenitor dataset, links with importance >0.095 where retained. For the intestinal dataset, links with importance >0.08 were retained.
Differential gene expression analysis
Differential gene expression analysis was performed using the diffexpnb function of the RaceID3 (v0.1.4) algorithm. Differentially expressed genes between two subgroups of cells were identified similar to a previously published method24. First, negative binomial distributions reflecting the gene expression variability within each subgroup were inferred based on the background model for the expected transcript count variability computed by RaceID3. Based on these distributions, a p-value for the observed difference in transcript counts between the two subgroups was calculated and multiple testing corrected by the Benjamini-Hochberg method.
Supplementary Material
Acknowledgments
This study was supported by the Max Planck Society, the German Research Foundation (DFG) (SPP1937 GR4980/1-1, GR4980/3-1, and GRK2344 MeInBio), by the DFG under Germany’s Excellence Strategy (CIBSS – EXC-2189 – Project ID 390939984), by the ERC (818846 — ImmuNiche — ERC-2018-COG), and by the Behrens-Weise-Foundation.
Footnotes
Author Contributions
D. G. conceived the method and performed the analysis
Competing interests
The author declares no competing interests.
Data availability
Primary data used in this manuscript was downloaded from GEO with accession code GSE89754 for the hematopoietic data10, and GSE92332 for the intestinal data20.
Code availability
VarID is integrated in the RaceID v0.1.4 package available from CRAN or github (https://github.com/dgrun/RaceID3_StemID2_package). Source code for reproducing the results of this manuscript is available on github (https://github.com/dgrun/VarID_analysis).
References
- 1.Grün D. Revealing routes of cellular differentiation by single-cell RNA-seq. Curr Opin Syst Biol. 2018;11:9–17. [Google Scholar]
- 2.Grün D, Kester L, van Oudenaarden A. Validation of noise models for single-cell transcriptomics. Nat Methods. 2014;11:637–40. doi: 10.1038/nmeth.2930. [DOI] [PubMed] [Google Scholar]
- 3.Vallejos CA, Marioni JC, Richardson S. BASiCS: Bayesian Analysis of Single-Cell Sequencing Data. PLoS Comput Biol. 2015;11:e1004333. doi: 10.1371/journal.pcbi.1004333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Eling N, Richard AC, Richardson S, Marioni JC, Vallejos CA. Correcting the Mean-Variance Dependency for Differential Variability Testing Using Single-Cell RNA Sequencing Data. Cell Syst. 2018;7:284–294.e12. doi: 10.1016/j.cels.2018.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Macosko EZ, et al. Highly Parallel Genome-wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell. 2015;161:1202–1214. doi: 10.1016/j.cell.2015.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Satija R, Farrell JA, Gennert D, Schier AF, Regev A. Spatial reconstruction of single-cell gene expression data. Nat Biotechnol. 2015;33:495–502. doi: 10.1038/nbt.3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Setty M, et al. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat Biotechnol. 2016;34:637–645. doi: 10.1038/nbt.3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Herman JS, Sagar, Grün D. FateID infers cell fate bias in multipotent progenitors from single-cell RNA-seq data. Nat Methods. 2018;15:379–386. doi: 10.1038/nmeth.4662. [DOI] [PubMed] [Google Scholar]
- 9.Grün D, et al. Single-cell messenger RNA sequencing reveals rare intestinal cell types. Nature. 2015;525:251–5. doi: 10.1038/nature14966. [DOI] [PubMed] [Google Scholar]
- 10.Tusi BK, et al. Population snapshots predict early haematopoietic and erythroid hierarchies. Nature. 2018;555:54–60. doi: 10.1038/nature25741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brennecke P, et al. Accounting for technical noise in single-cell RNA-seq experiments. Nat Methods. 2013;10:1093–5. doi: 10.1038/nmeth.2645. [DOI] [PubMed] [Google Scholar]
- 12.Hafemeister C, Satija R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. bioRxiv. 2019 doi: 10.1101/576827. 576827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hu H, et al. AnimalTFDB 3.0: a comprehensive resource for annotation and prediction of animal transcription factors. Nucleic Acids Res. 2019;47:D33–D38. doi: 10.1093/nar/gky822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huynh-Thu VA, Irrthum A, Wehenkel L, Geurts P. Inferring Regulatory Networks from Expression Data Using Tree-Based Methods. PLoS One. 2010;5:e12776. doi: 10.1371/journal.pone.0012776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liting X, Gerstein R, Socolovsky M, Castilla LH. Deletion Of Core Binding Factors Runx1 and Runx2 Leads To Perturbed Hematopoiesis In Multiple Lineages. Blood. 2013;122 [Google Scholar]
- 16.Komorowska K, et al. Hepatic Leukemia Factor Maintains Quiescence of Hematopoietic Stem Cells and Protects the Stem Cell Pool during Regeneration. Cell Rep. 2017;21:3514–3523. doi: 10.1016/j.celrep.2017.11.084. [DOI] [PubMed] [Google Scholar]
- 17.Paul F, et al. Transcriptional Heterogeneity and Lineage Commitment in Myeloid Progenitors. Cell. 2015;163:1663–1677. doi: 10.1016/j.cell.2015.11.013. [DOI] [PubMed] [Google Scholar]
- 18.Doi Y, et al. SATB1 Expression Marks Lymphoid-Lineage-Biased Hematopoietic Stem Cells in Mouse Bone Marrow. Blood. 2015;126 [Google Scholar]
- 19.Jones CL, et al. ETV6 Regulates Pax5 Expression in Early B Cell Development. Blood. 2016;128 [Google Scholar]
- 20.Haber AL, et al. A single-cell survey of the small intestinal epithelium. Nature. 2017;551:333–339. doi: 10.1038/nature24489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.McInnes L, Healy J, Melville J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. 2018. Preprint at arXiv https://arxiv.org/abs/1802.03426v2. [Google Scholar]
- 22.Yu G, He Q-Y. ReactomePA: an R/Bioconductor package for reactome pathway analysis and visualization. Mol Biosyst. 2016;12:477–9. doi: 10.1039/c5mb00663e. [DOI] [PubMed] [Google Scholar]
- 23.Aibar S, et al. SCENIC: single-cell regulatory network inference and clustering. Nat Methods. 2017;14:1083–1086. doi: 10.1038/nmeth.4463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Anders S, Huber W. Differential expression analysis for sequence count data. Genome Biol. 2010;11:R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.