Accelerated Mono and Biexponential 3D-T1ρ Relaxation Mapping of Knee Cartilage Using Golden Angle Radial Acquisitions and Compressed Sensing

Abstract

Purpose:

To use golden-angle (GA) radial sampling and compressed sensing (CS) for accelerating mono and biexponential three dimensional (3D) spin-lattice relaxation time in the rotating frame (T_1ρ) mapping of knee cartilage.

Methods:

GA radial stack-of-stars and Cartesian 3D-T_1ρ-weighted knee cartilage datasets (n=12) were retrospectively undersampled by acceleration factors (AFs) 2–10. CS-based reconstruction using eight different sparsifying transforms were compared for mono and biexponential T_1ρ-mapping of knee cartilage, including spatio-temporal finite differences (STFD), wavelets, dictionary from Principal Component Analysis (PCA), and exponential decay models (EXP), and also low rank (LR) and low rank plus sparse models (L+S). Complex-valued fitting was used and Marchenko–Pastur principal component analysis (MP-PCA) filtering also tested.

Results:

Most CS methods performed well for an AF of 2, with relative median normalized absolute deviation (MNAD) below 10% for monoexponential and biexponential mapping. For monoexponential mapping, radial sampling obtained a MNAD below 10% up to AF of 10, while Cartesian obtained this level of error only up to AF of 4. Radial sampling was also better with biexponential T_1ρ mapping, with MNAD below 10% up to AF of 6.

Conclusion:

GA radial acquisitions combined with CS outperformed Cartesian acquisitions for 3D-T_1ρ mapping of knee cartilage, being it a good alternative to Cartesian sampling for reducing scan time and/or improving image and mapping quality. The methods EXP, STFD, and LR obtained the best results for radial sampling patterns.

INTRODUCTION

The spin-lattice relaxation time in the rotating frame (T_1ρ) has shown to be sensitive to the proteoglycan content of the cartilage (1,2) and the T_1ρ relaxation mapping useful for early detection of osteoarthritis (OA) (3). In order to produce T_1ρ maps, many T_1ρ-weighted images must be acquired, taking a long acquisition time, especially if biexponential relaxation models are desired (4). While monoexponential models are still predominant in OA, a recent study (5) suggested that biexponential mapping of cartilage can provide better diagnostic performance. In (6,7), it is shown that change of multiexponential relaxation components can be clearly observed with cartilage degradation.

Recently, compressed sensing (CS) has been used to reduce the acquisition time of T_1ρ mapping. For monoexponential T_1ρ mapping of cartilage, CS has been studied in (8–10), while for biexponential T_1ρ mapping, it has been studied in (11). These studies demonstrated that CS can reduce acquisition time by 10 times, with an error of 6.5% for monoexponential models (10) and 15% for biexponential models (11).

Those previous studies show that keeping good image quality as acceleration factor (AF) increases is extremely important for rapidly obtaining good relaxation maps. According to (12), successful CS acceleration is obtained when the incoherently measured data is accurate. In MRI this essentially translates into low noise and incoherent k-space sampling (13). Artifacts from incoherent sampling are easily reduced or removed by sparse reconstruction (14–16), but the measured data need to be as reliable as possible, in other words, strong signal and low noise.

Noise can be reduced by improving k-space signal-to-noise ratio (SNR), i.e. the SNR of the acquired k-space data (17). Considering the same scanner, k-space SNR can be improved by using different pulse sequences (18), by capturing more k-space lines, or even using multiple receiving coils (19). Incoherent k-space sampling for CS reconstruction can be obtained by choosing an optimal sampling pattern (13,15,20,21). After that, one only needs to combine it with adequate sparse reconstruction.

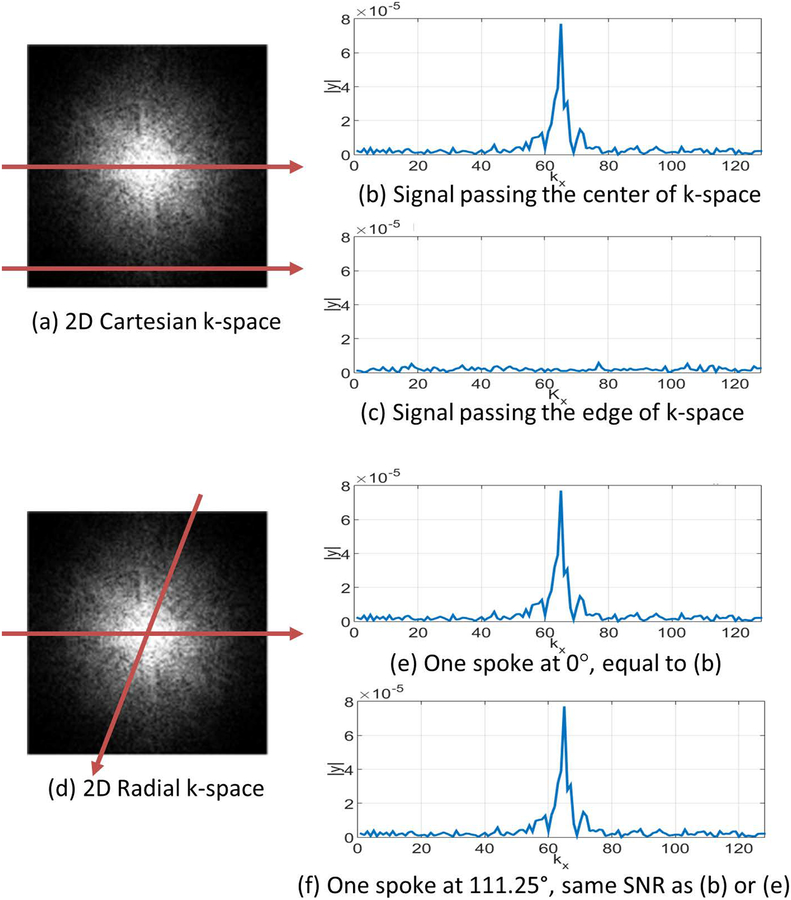
In this sense, one way to improve image quality in accelerated T_1ρ acquisitions, with relatively good k-space SNR and high incoherence is to modify the k-space sampling trajectory and use multiple receiving coils. In this study, we investigate the use of radial sampling, specifically golden angle (GA) radial acquisitions (22), which was shown to be among the most incoherent radial patterns with proven success in CS-MRI (23,24). Radial patterns sample the low frequencies of k-space at every readout, capturing k-space parts where the signal is stronger than noise more often than Cartesian does, see Figure 1. If the level of the acquisition noise (its variance) is similar in both acquisition schemes then the radial k-space data should have higher k-space SNR than Cartesian. Even though radial images reconstructed with methods such as regridding (25) may have lower image SNR than Cartesian, as noted in (26), this depends on the reconstruction method and it does not behave the same way when regularized reconstructions, such as CS, are used (27). We observe this in practice with our T_1ρ acquisition protocol, as shown later in this study (refer to Table 1, supporting information figures S1 and S2). Finding an optimal incoherent Cartesian sampling pattern is also possible (28,29), but when measurements are noisy, some redundancy is desired in order to average the measurements in favor of signal, reducing random noise. In this sense, GA radial sampling provided a better tradeoff between redundancy and incoherence for CS-T_1ρ mapping of knee cartilage than the previously used Cartesian sampling with Poisson disk (10,11), see Supporting Information Figure S1 for comparison.

Figure 1:

Illustration of the differences in radial and Cartesian sampling. In (a), the Cartesian pattern captures parallel readout lines. The line is shown in (b) cross the central frequency and has a stronger signal, while the line shown in (c) captures the edge of the k-space and has a weaker signal. In (d), radial sampling always captures lines crossing the center of the k-space, so all k-space lines have stronger signals, as shown in (e)-(f).

Table 1:

Estimated normalized noise standard deviation, shown in percentage and SNR for Cartesian and radial acquisitions using MP-PCA, considering noise in the k-space (for radial k-space, SNR values are different after gridding), and in the reconstructed images with SENSE and L+S using fully sampled data.

	Cartesian-Sampling		GA Radial-Sampling
	Normalized noise standard deviation	SNR	Normalized noise standard deviation	SNR
k-space data (raw)	30.1%	2.87	1.3%	74.51
Regridded k-space data	30.1%	2.87	7.5%	13.03
SENSE Reconstruction (Fully-sampled)	11.5%	8.54	3.2%	30.17
L+S Regularized Reconstruction (Fully-sampled)	7.8%	12.4	0.3%	365.90

Good balance between SNR and incoherence is not the only advantage of radial acquisition. Radial sampling is also more robust to motion (22,27) and resolution can be easily increased within the same scan time. In radial sampling, the readout direction spans a 2D plane (in 3D radial stack-of-stars). By adjusting pulse sequence parameters, radial sampling can easily increase k-space coverage for higher frequencies, leading to higher image resolution. In Cartesian sampling, readout direction is always the same, so only one direction can exploit this advantage. Supporting Information Figure S2 shows some T_1ρ-weighted images from Cartesian and radial acquisition for comparison. Note that in all images the acquisition time and the number of k-space samples are the same.

These advantages may render radial acquisition a better option than Cartesian for accelerated T_1ρ mapping. Potentially reducing acquisition time even further than Cartesian, or obtaining more accurate relaxation maps when the same acceleration is used. In this paper, we use k-space radial sampling, following golden angle increments (approx. 111.25°), in order to improve the quality of the compressed sensing-accelerated 3D-T_1ρ mapping of human articular cartilage.

METHODS

Radial and Cartesian-MRI Data Acquisition

Five in vivo human knee 3D-T_1ρ-weighted datasets were acquired with 10 different TSLs using a modified 3D golden angle radial stack-of-stars sequence (24), which follows the details of radial acquisition described in (22). The radial lines comprehend the k_x-k_y plane, and they are stacked in the k_z Cartesian direction. The details of the radial T_1ρ pulse sequence are shown in Supporting Information Figure S4. Fourier Transform is applied in k_z direction to separate 3D radial data into multiple slices. Seven in vivo human knee 3D-T_1ρ-weighted datasets were acquired with 10 different TSLs using a modified 3D Cartesian turbo-Flash sequence (4). The physical readout direction is the k_x direction in Cartesian acquisitions, where Fourier Transform is applied to separate 3D Cartesian data into multiple slices on the k_y-k_z plane. However, in order to keep our notation simplified, we will denote the slices as in the k_x-k_y plane as in radial acquisitions.

The MRI scans were performed using a 3T clinical MRI scanner (Prisma, Siemens Healthcare, Erlangen, Germany) with a 15-channel Tx/Rx knee coil (QED, Cleveland OH). The general 3D-T_1ρ acquisition parameters were the same for both: TR/TE=7.60ms/3.86ms, flip angle=12°, matrix size 256×128×64, longitudinal magnetization restoration delay=1000ms, 64 k-space lines captured per preparation pulse, spin-lock frequency=500Hz, slice thickness=2mm, the field of view (FOV)=160mm×160mm, and receiver bandwidth=510 Hz/pixel.

The T_1ρ-weighted scans of the knee were acquired in the sagittal plane from twelve healthy volunteers (age=29.6±7.5 years), with 10 TSLs including 2/4/6/8/10/15/25/35/45/55ms, and total acquisition time of a knee is 32 minutes. This study was approved by the institutional review board (IRB) and all the volunteers consented before scanning.

Estimating Noise Levels and Signal to Noise Ratio:

In order to estimate the standard deviation of the noise and the respective SNR, we use the Marchenko–Pastur Principal Component Analysis (MP-PCA) method from (30). This method is able to separate a matrix into two matrices, one containing the structured signal and other containing uncorrelated Gaussian noise, such as $\mathit{y}=\stackrel{-}{\mathit{y}}+\stackrel{-}{\mathit{\eta }}$. The normalized noise level can be computed by:

$${\stackrel{-}{\mathit{\sigma }}}_{\stackrel{-}{\mathit{\eta }}}={\mathit{\sigma }}_{\stackrel{-}{\mathit{\eta }}}/{\mathit{\sigma }}_{\mathit{y}},$$ [1]

where σ_y is the estimated standard deviation of the data (k-space data or reconstructed image), and ${\mathit{\sigma }}_{\stackrel{-}{\mathit{\eta }}}$ is the estimated standard deviation of the noise. The estimated ${\mathit{\sigma }}_{\stackrel{-}{\mathit{\eta }}}$ of k-space data matched the scanner noise calibrations obtained previously to the T_1ρ scans. The SNR, which is the ratio of the noise-free data $\stackrel{-}{\mathit{y}}$ by the pure noise $\stackrel{-}{\mathit{\eta }}$, is given by:

$${\mathit{S}\mathit{N}\mathit{R}}_{\mathit{y}}={\mathit{\sigma }}_{\stackrel{-}{\mathit{y}}}/{\mathit{\sigma }}_{\stackrel{-}{\mathit{\eta }}},$$ [2]

This algorithm is applied to Cartesian and radial k-space data (for radial data, MP-PCA is applied to the original domain and to the regridded Cartesian domain) and reconstructed images (complex-valued images), in order to estimate the noise levels and SNR presented in Table 1 and Supporting Information Figure S2.

Synthetic Phantoms and Ground Truth

In order to have experiments with ground truth, we generate several synthetic knee images with known mono or biexponential maps. The relaxation maps were created from real Cartesian knee T_1ρ-weighted images. Fully sampled Cartesian data were reconstructed with SENSE (31), their exponential decays were estimated, the values were inspected to make sure they were in knee cartilage ranges, and synthetic images were artificially generated (see figures 2, 3 and 5). Cartesian and radial k-space data were computed, using FFT and NUFFT, and Gaussian noise was added in k-space, according to the measured noise levels of the acquisitions, from Table 1.

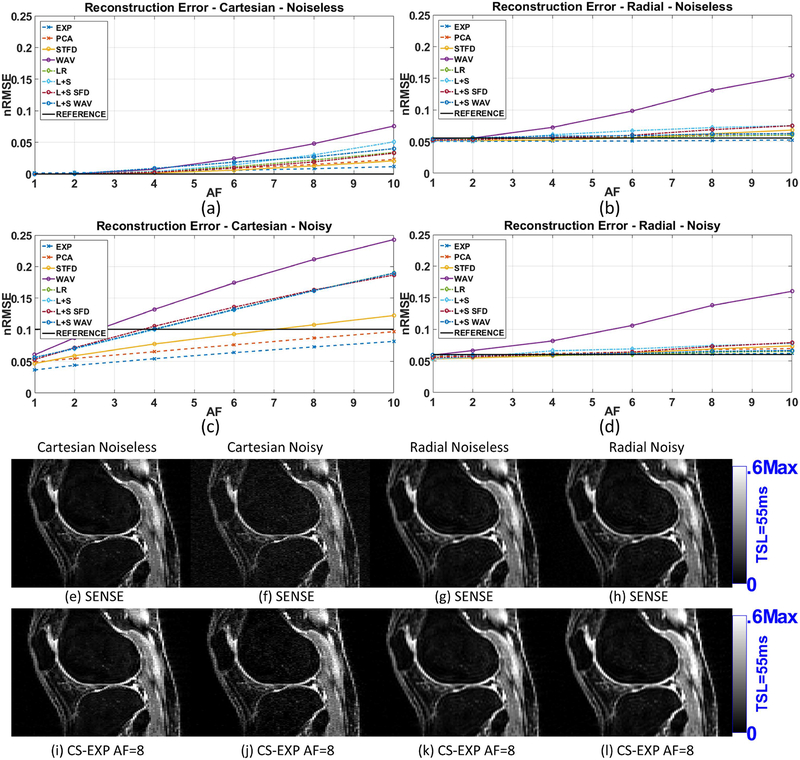
Figure 2:

Results for reconstruction error (nRMSE) of the synthetic phantom, including (a) Cartesian with no noise in the acquisition, (b) radial with no noise, (c) Cartesian noisy (SNR=2.87), and (d) radial noisy (SNR=74.51). All nRMSE values are computed comparing reconstructions with ground truth. Representative images are shown in (e)-(l).

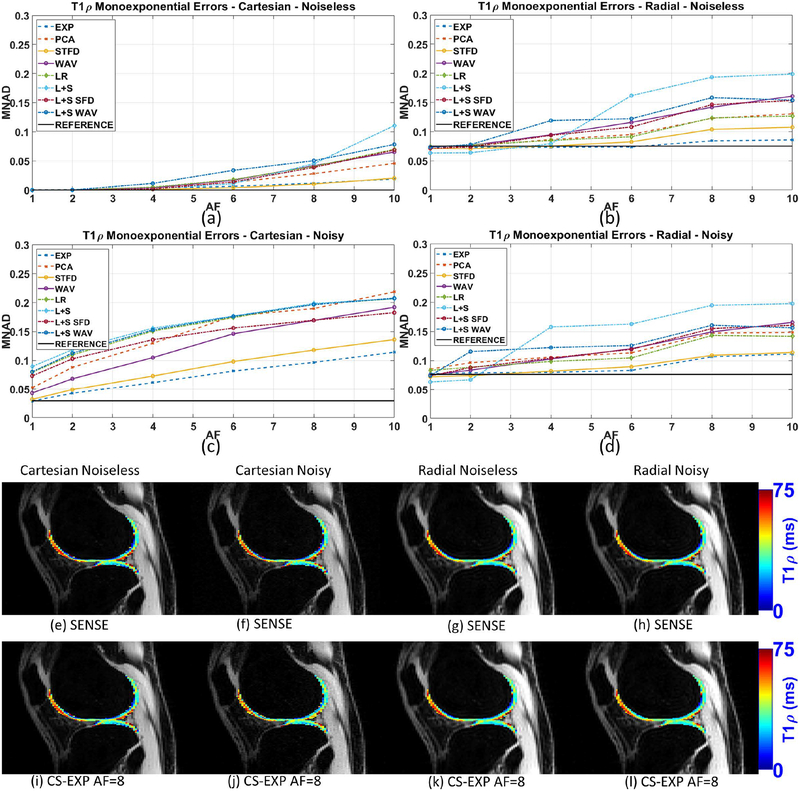
Figure 3:

Results for monoexponential T_1ρ mapping error (MNAD) of the synthetic phantom, including (a) Cartesian with no noise in the acquisition, (b) radial with no noise, (c) Cartesian noisy (SNR=2.87), and (d) radial noisy (SNR=74.51). All MNAD values are computed comparing T_1ρ maps with ground truth. Representative T_1ρ maps are shown in (e)-(l).

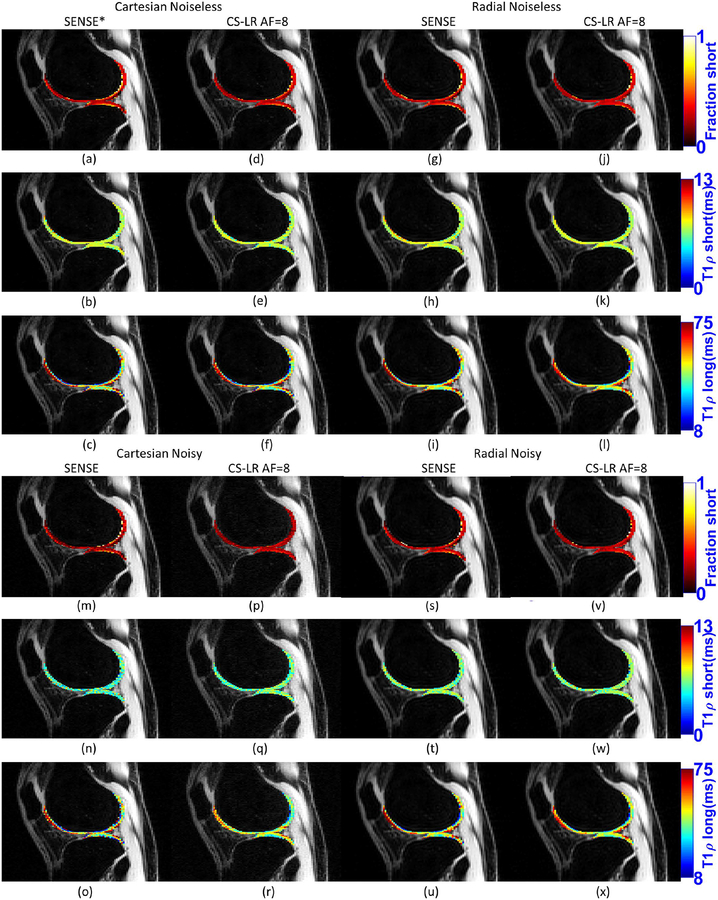
Figure 5:

Selected visual results for biexponential T_1ρ mapping, showing the fraction of the short component, time of the short component and time of the long component, for SENSE reconstruction and CS with AF=8 and LR regularization, Cartesian and radial, noisy and noiseless. The images of Cartesian noiseless SENSE (a)-(c) are exactly like the ground truth.

Retrospective Undersampling

The 3D-golden angle radial stack-of-stars k-space data were retrospectively undersampled by reducing the number of radial k-space lines, or projections (24). The “full-sampled” GA radial dataset has 128 k-space lines, to match the same number of k-space points as the Cartesian acquisition. This is less than π/2 × 128 as recommended for standard radial acquisitions, but more than enough for radial MRI with multiple coils (27). The undersampling process removes the number of projections required by a specific acceleration factor (AF). To simulate prospective sampling as close as possible, the projections are removed in sequential block for each TSLs, but starting at a different point in each TSL, so the sequence of angles is not the same for two consecutive TSLs. For example, for AF=2, the data of the first TSL uses only the projections from 1 to 64 (from all 128 captured golden angle projections starting at 0°), the second TSL uses projections from 65 to 128. The AF is defined as the ratio of the number of k-space lines used for reconstruction by the total number of measured k-space lines. The sampling pattern for Cartesian acquisitions followed the Poisson disk, as used in (10), with different sampling pattern for each TSL.

Reconstruction Algorithms

In previous studies (10,11) the reference method for reconstruction was SENSE (31), with fully-sampled data, which solves:

$$\widehat{\mathit{x}}={\text{argmin}}_{\mathit{x}}{‖\mathit{y}-\mathit{F}\mathit{C}\mathit{x}‖}_2^2,$$ [3]

where x is a vector that represents one of the N_Z reconstructed image sequences, originally of size N_x × N_y × N_t, with N_x being the image size in the x-axis and N_y the size in the y-axis, N_t is the number of TSLs. The vector y represents the captured k-space. For Cartesian acquisitions the original size of y is N_x × N_y × N_t × N_c, where N_c is the number of coils. The matrix C contains the coil sensitivities and phase compensation (15,32), F the Fourier transforms of all sensitivity-weighted images. For radial acquisitions, the original size of y is N_s × N_r × N_t × N_c, where N_s is the number of samples on each radial k-space line and N_r is the number of radial lines. The squared l₂-norm or Euclidean norm, ${‖\mathit{e}‖}_2^2$, is the sum of the squared magnitudes.

SENSE is a good method for reconstruction of fully-sampled Cartesian data, as shown in (10). For radial acquisitions, however, iterative conjugate gradient SENSE (CG-SENSE) reconstruction (33) are required, basically because Equation 3 represents an ill-posed problem. In ill-posed problems as these (34,35), noise may be amplified and some residual undersampling artifact may exist. The use of regularization is mandatory in order to produce useful images, in the case of CG-SENSE, the regularization is done by running just a few iterations (35), but this may not be enough to properly regularize the inverse. The most suitable approach to solve for radial acquisition would be using a side penalty such as the ones used in CS, even for “fully-sampled” data. The coil sensitivity maps, required by the multichannel coil reconstructions were estimated using ESPIRiT (36) from the synthesized Cartesian k-space area produced with a low-resolution regridding using NUFFT (25). We also used low-order phase information, following (15,32), for phase compensation. Phase compensation assures the reconstructed images have nearly zero-phase for later complex-valued fitting in the T_1ρ mapping step.

Following (10,11), eight different regularization functions are compared for CS. Our focus here is to compare radial and Cartesian acquisitions, but the type of regularization used can affect the reconstructions differently for Cartesian and radial trajectories.

The regularization penalties, described in Table 2, use l₁-norm with different sparsifying transforms, nuclear-norm (37,38) of the Casorati matrix representation of the image, i.e. low rank (LR) model, and the low rank plus sparse (L+S) model, where the nuclear-norm and the l₁-norm are combined (39). In the Casorati matrix, each row contains the magnetization signal of one particular voxel over TSL.

Table 2:

Different compressed sensing methods, their corresponding equations, and minimization algorithm, a brief description, median computational time to converge (Intel Skylake 6148 core@2.4GHz, 32GB DDR4–2666DIMM) adjusted per slice.

CS Method	Equation	Minimization algorithm	Transform/Dictionary	median comp. time Cartesian	median comp. time Radial
STFD	[4]	MFISTA-VA-FGP	Spatial and temporal finite difference, spatial order 1 and temporal order 2	134 sec	1319 sec
WAV	[5]	MFISTA-VA	3D Wavelet transform (2D+time) Daubechies 4, with 4 levels of decomposition.	152 sec	445 sec
PCA	[5]	MFISTA-VA	Unitary transform from temporal PCA of fully-sampled data	44 sec	264 sec
EXP	[5]	MFISTA-VA	Overcomplete temporal dictionary of exponentials with 50 relaxation times between 0.75 and 300 ms	201 sec	776 sec
LR	[6]	MFISTA-VA	Applied to a NyNz × Nt matrix formed with the reshaped NyNzNt × 1 vector.	57 sec	244 sec
L+S	[7]	MFISTA-VA	Same as LR, plus identity for l1-norm	50 sec	408 sec
L+S SFD	[7]	MFISTA-VA-FGP	Same as LR, plus spatial finite difference for l1-norm	87 sec	1091 sec
L+S WAV	[7]	MFISTA-VA	Same as LR, plus 2D spatial wavelet for l1-norm, also Daubechies 4, with 4 levels.	152 sec	597 sec

The l₁-norm (15) regularized CS problems are posed as:

$$\widehat{\mathit{x}}={\text{argmin}}_{\mathit{x}}{‖\mathit{y}-\mathit{S}\mathit{F}\mathit{C}\mathit{x}‖}_2^2+\mathit{\lambda }{‖\mathit{T}\mathit{x}‖}_1,$$ [4]

or

$$\widehat{\mathit{x}}=\mathit{D}{\text{argmin}}_{\mathit{u}}{‖\mathit{y}-\mathit{S}\mathit{F}\mathit{C}\mathit{D}\mathit{u}‖}_2^2+\mathit{\lambda }{‖\mathit{u}‖}_1,$$ [5]

Where the vector x, matrices C and F are described after Equation 3. For Cartesian acquisitions, the undersampling matrix S is a diagonal matrix, where the non-sampled k-space points have zeros in their diagonal positions; the respective elements in y are replaced by zeros as well. For radial acquisitions, the SF is a (N_x × N_y × N_t × N_c)×(N_s × N_r × N_t × N_c) mapping, performed by the undersampled Non-Uniform Fast Fourier Transform (NUFFT) (40).

The l₁-norm, ‖u‖₁, is the sum of the magnitudes, and λ is the regularization parameter. The transform T and dictionary D are chosen as described in Table 2. In this table, transform T contains the spatiotemporal FD (STFD) (41–43) set to order 1 spatially and order 2 temporally. Fixed dictionary models for D are utilized for 3D wavelet transform (44), WAV in Table 2, or for overcomplete multiexponential dictionary D, EXP in Table 2 (6,45), with much more columns than rows. Learned dictionary models for D can be created using temporal principal component analysis (PCA) (46), using singular value decomposition (SVD) on the Casorati representation (47).

The LR reconstruction is defined as:

$$\widehat{\mathit{x}}={\text{argmin}}_{\mathit{x}}{‖\mathit{y}-\mathit{S}\mathit{F}\mathit{C}\mathit{x}‖}_2^2+\mathit{\lambda }{‖\mathit{x}‖}_{*}.$$ [6]

In [3], ‖x‖_* represents the matrix nuclear-norm (37) where x is reshaped as a N_yN_x × N_t Casorati matrix, and the SVD is utilized at each iteration using the currently available reconstruction (48).

The L+S reconstruction (39) is given by:

$$\widehat{\mathit{l}},\widehat{\mathit{s}}={\text{argmin}}_{\mathit{x}}{‖\mathit{y}-\mathit{S}\mathit{F}\mathit{C}(\mathit{l}+\mathit{s})‖}_2^2+{{\mathit{\lambda }}_{\mathit{l}}‖\mathit{l}‖}_{*}+{\mathit{\lambda }}_{\mathit{s}}{‖\mathit{T}\mathit{s}‖}_1,$$ [7]

where x is decomposed into a sparse part s and a low rank part l, recombined by x = l + s. The low rank part uses of the nuclear-norm ‖l‖_*, while the sparse part uses of the l₁-norm with a specific sparsifying transform T, as listed in Table 2 for L+S reconstructions. This is also an overcomplete description of the images to be reconstructed (49). The highly correlated temporal part is represented by the LR component, while the temporally varying part, usually sparse in some spatially transformed domain, is represented by the sparse part. In (50), a similar combination of low rank and wavelet sparsity was studied for T₂ mapping.

Also following (10), and its supplemental material, the regularization parameters, λ or λ_l and λ_s, were adjusted in order to minimize ${‖{\widehat{\mathit{x}}}_{\mathit{\lambda }}-{\mathit{x}}_{\text{ref}}‖}_2$ where ${\widehat{\mathit{x}}}_{\mathit{\lambda }}$ is the CS reconstruction and x_ref is the fully-sampled SENSE reconstruction or the ground truth (synthetic experiments). The CS reconstruction was performed using the monotone fast iterative shrinkage-thresholding algorithms with variable acceleration (MFISTA-VA) (51). All methods stopped when ‖x_i+1 − x_i‖₂/‖x_i+1‖₂ < 10⁻⁵, or when i > 600, being i the iteration index.

Exponential Models and Fitting Algorithms

The T_1ρ relaxation is usually considered an exponentially decaying process. Magnitude models, such as the ones used in (10,11), require compensation for bias since noise follows a Rician distribution when only the magnitude of the signal is utilized (52). Since noise levels differ considerably among different acquisitions and kinds of reconstruction, we used complex-valued models (53). The complex-valued monoexponential model is described as:

$$x(t,\mathit{n})=a\left(\mathit{n}\right)exp\left(-\frac{t}{\tau \left(\mathit{n}\right)}\right),$$ [8]

with complex-valued a(n). Note the relaxation time τ(n) is real-valued.

The complex-valued biexponential model can be written as:

$$x\left(t,\mathit{n}\right)=a\left(\mathit{n}\right)\left(f_s\left(\mathit{n}\right)exp\left(-\frac{t}{{\tau }_s\left(\mathit{n}\right)}\right)+f_l\left(\mathit{n}\right)exp\left(-\frac{t}{{\tau }_l\left(\mathit{n}\right)}\right)\right),$$ [9]

where a(n) is complex-valued. However, the fractions of short and long components at position n, given by 0 ≤ f_s(n) ≤ 1 and f_l(n) = 1 − f_s(n), and the T_1ρ relaxation times of the short and long components, given by τ_s(n) and τ_l(n), are all real-valued.

The biexponential T_1ρ parameters estimation, or simply fitting process, was done using non-linear least squares, using models of Equation 8 and 9, where the minimization was done using conjugate gradient Steihaug’s trust-region (CGSTR) algorithm (54). The CGSTR algorithm stopped at a maximum of 1500 iterations for monoexponential, or 3500 iterations for biexponential, or else when normalized parameter update is lower than 10⁻⁵. Biexponential estimation started with monoexponential fitting results, classifying them as short (0.5–10ms) or long (10–300ms), depending on its estimated monoexponential T_1ρ relaxation time. Similar to (55), F-test was utilized for detecting mono/biexponential voxels. We follow the F-test method from (56), voxels were assumed to have biexponential behavior if F-ratio>5.14 (p-value=0.05) related to monoexponential. This means the sum of the squares (SS) of the biexponential fitting process is reduced significantly compared to monoexponential fitting. Also, both fractions (f_s(n) and f_l(n)) need to be higher than 5% in order to be a valid biexponential in these experiments.

Spatial filtering, used as denoising over the regions of interest (ROIs), prior to the parameter estimation is sometimes helpful (57) to improve the quality of the estimated parameters. In this paper, we compare the non-filtered results with MP-PCA denoising (58).

Analysis of the CS Reconstruction and Fitting

The performance of the CS methods was evaluated according to the quality of the reconstructed images and the quality of the estimated T_1ρ parameters. Image reconstruction quality was assessed using normalized root mean squared error (nRMSE) against SENSE reconstruction of the fully-sampled data or the ground truth (for the synthetic phantom). The nRMSE is defined as:

$$\mathit{n}\mathit{R}\mathit{M}\mathit{S}\mathit{E}(\widehat{\mathit{x}},{\mathit{x}}_{\text{ref}})={‖\widehat{\mathit{x}}-{\mathit{x}}_{\text{ref}}‖}_2/{‖{\mathit{x}}_{\text{ref}}‖}_2.$$ [10]

The fitting process was applied only on each specific ROI, as shown in Supporting Information Figure S3. For in vivo knee cartilage, 5 ROIs were employed, following (4): medial femoral cartilage (MFC), medial tibial cartilage (MTC), lateral femoral cartilage (LFC), lateral tibial cartilage (LTC), and patellar cartilage (PC). In those regions, the T_1ρ parameters, including T_1ρ times and fractions for short and long components, from CS reconstructions were compared against the parameters obtained from the reference reconstruction (and ground truth, when available).

The quality was assessed using normalized absolute deviation (NAD) of the parameters obtained in each voxel position n, given by:

$$\mathit{N}\mathit{A}\mathit{D}\left(\mathit{n}\right)=\frac{\left|p\left(\mathit{n}\right)-p_{ref}\left(\mathit{n}\right)\right|}{(p\left(\mathit{n}\right)+p_{ref}\left(\mathit{n}\right))/2},$$ [11]

where p(n) is the T_1ρ time for the monoexponential model in Equation 8 or one of the four biexponential parameters (f_s(n), f_l(n), τ_s(n), τ_l(n)) for Equation 9. Voxels in which any of the fractions were lower than 5% were excluded from the biexponential evaluation. As observed here and in (4), small fractions had inaccurate estimated T_1ρ parameters, even for fully-sampled images, leading to unrealistic NADs.

The errors in T_1ρ mapping were quantized by the median of NADs (MNAD):

$$\mathit{M}\mathit{N}\mathit{A}\mathit{D}\left(\mathit{R}\mathit{O}\mathit{I}\right)={\text{median}}_{\mathit{n}\in \mathit{R}\mathit{O}\mathit{I}}\left(\frac{\left|p\left(\mathit{n}\right)-p_{ref}\left(\mathit{n}\right)\right|}{(p\left(\mathit{n}\right)+p_{ref}\left(\mathit{n}\right))/2}\right),$$ [12]

The ROI in Equation 12 can comprehend a specific ROI as shown in Supporting Information Figure S3, or all ROIs. An MNAD of 0.1 corresponds to a median deviation of 10% on the parameters compared to the reference method.

In order to compare parameters among different in-vivo subjects and acquisition, where voxel-based metrics is not possible, we used median parameters of an ROI, given by:

$$\stackrel{-}{p}\left(\mathit{R}\mathit{O}\mathit{I}\right)=\underset{\mathit{n}\in \mathit{R}\mathit{O}\mathit{I}}{\text{median}}p\left(\mathit{n}\right).$$ [13]

The median, in Equation 13, is used as a robust measurement of central tendency of the parameters of the relaxation model (times and fractions) in the ROI. If the cartilage is not well segmented, wrongly segmented voxels not belonging to the cartilage, which can be considered as outliers, may corrupt mean values. This is strongly diminished by using the median. The variability of relaxation parameters are measured by the median of the absolute deviation (MAD), given by:

$$\mathit{M}\mathit{A}\mathit{D}\left(\mathit{R}\mathit{O}\mathit{I}\right)=\underset{\mathit{n}\in \mathit{R}\mathit{O}\mathit{I}}{\text{median}}\left|p\left(\mathit{n}\right)-\stackrel{-}{p}\left(\mathit{R}\mathit{O}\mathit{I}\right)\right|.$$ [14]

The MAD is also more robust than standard deviation as a measure of variability.

The percentage error of the median values (PEMV) of a ROI is also presented for comparison of median values of parameters obtained by a particular method in comparison with the values obtained by the method of reference. The PEMV is given by:

$$\mathit{P}\mathit{E}\mathit{M}\mathit{V}\left(\mathit{R}\mathit{O}\mathit{I}\right)=100\times \frac{\stackrel{-}{p}\left(\mathit{R}\mathit{O}\mathit{I}\right)-{\stackrel{-}{p}}_{ref}\left(\mathit{R}\mathit{O}\mathit{I}\right)}{(\stackrel{-}{p}\left(\mathit{R}\mathit{O}\mathit{I}\right)+{\stackrel{-}{p}}_{ref}\left(\mathit{R}\mathit{O}\mathit{I}\right))/2}.$$ [15]

RESULTS

Evaluating Normalized Noise and SNR

In this study, we apply the MP-PCA to separate the noise from the signal of interest. The MP-PCA (30,58) works by observing the singular values of a random matrix, related to noise, follows a Marchenko-Pastur distribution. The components of the signal of interest, reshaped as a matrix, usually compose a low rank matrix, while pure noise (reshaped as a matrix) usually keep full rank. By separating the components of the singular value decomposition using truncation, two matrices can be recovered: one with the filtered signal and another with the noise. We apply the MP-PCA in k-space, in order to have an estimation of the noise level of the acquired data. The k-space data was reshaped in a matrix of size (N_yN_x) ×(N_tN_c) for Cartesian and of size (N_sN_r) ×(N_tN_c) for radial before applying MP-PCA. As an exercise of curiosity, we measured SNR of radial k-space data gridded into a Cartesian grid, to account for density compensation and interpolation effects. However, note that compressed sensing reconstruction of radial data do not need explicit gridding of k-space data, since this is done implicitly during iterative reconstruction using NUFFT. We also applied the MP-PCA to the images reconstructed with SENSE and with L+S regularization (as a reference for regularized methods). The 3D images were reshaped in a matrix of size (N_yN_x) ×(N_tN_z), and the normalized results are shown in Table 1.

In Table 1 we clearly see lower normalized noise and better k-space SNR in the radial acquisitions (normalized noise of 1.3%, SNR of 74.51 in the original radial k-space, and normalized noise of 7.5%, SNR of 13.03 after regridding it to Cartesian) than in Cartesian acquisitions (normalized noise of 30.1%, SNR of 2.87). This happens because of the stronger signal in radial acquisitions since the central area of the k-space is measured in each projection. Using SENSE reconstruction, the difference between radial (normalized noise of 3.2%, SNR of 30.17) and Cartesian (normalized noise of 11.5%, SNR of 8.54) is reduced, basically due to artifacts and amplification of the noise in radial reconstruction (since it is an ill-posed problem). This increase in noise that happens with radial acquisition can also be seen in the regridded k-space measurements.

Regularization is extremely important in the case of radial reconstructions, but it also works as a denoising procedure in Cartesian reconstructions. Using L+S reconstruction the SNR is largely improved for radial images (normalized noise of 0.3%, SNR of 365.90), but only marginally increased for Cartesian (normalized noise of 7.8%, SNR of 12.40).

Experiments with Synthetic Phantoms

In order to have a comparison with ground truth, we used synthetic phantoms of the knee joint. This evaluation shows how good CS acceleration is with Cartesian and GA radial acquisitions. Note that the levels of noise in Cartesian and radial experiments are different, in order to match measured values observed in Table 1.

Figures 2(a)–(b) show the reconstruction errors (nRMSE) for noiseless Cartesian and radial acquisitions using different CS reconstructions when comparing with the ground truth. Figures 2(c)–(d) show the nRMSE for noisy Cartesian (k-space SNR=2.87) and radial (k-space SNR=74.51). Some of the reconstructed images are shown in figures 2(e)–(l).

Note that in the noiseless case, figures 2(a)–(b), Cartesian acquisition perform much better. Radial acquisitions do not sample the k-space entirely, only a central circle (27), leaving out important high-frequency components. The advantage of radial acquisition is seen in the noisy case of figures 2(c)–(d). In the noisy case, due to a better SNR, radial reconstructions outperform Cartesian. Note that without acceleration (AF=1, no undersampling), some CS methods perform a denoising effect in Cartesian data, generating results better than those from SENSE (the reference method). For noisy radial acquisition, CS reconstructions performed very close to SENSE even for high AFs.

Figures 3(a)–(b) show the monoexponential mapping errors (MNAD) for noiseless Cartesian and radial acquisitions using different CS reconstructions when comparing with the ground truth. Figures 3(c)–(d) show the MNAD for noisy Cartesian and radial. Same monoexponential T_1ρ maps are shown in figures 3(e)–(l).

Results for the noiseless case in figures 3(a)–(b) show the advantage of Cartesian when the noise is low or inexistent. Cartesian performed better than radial in this case. In the noisy case, in figures 3(c)–(d), we should see an advantage on radial acquisitions. However, Cartesian performed better for some methods at small AF (up to 4-fold), while radial was better for higher AF, such as 6-fold and up. We also noted the increase in MNAD with AF was much slower for radial acquisitions.

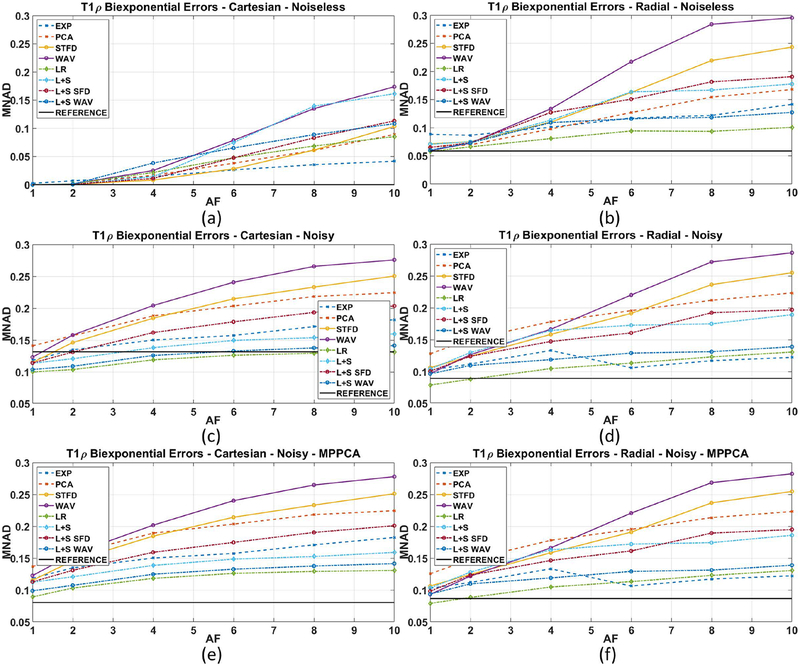
Figures 4(a)–(b) show the biexponential mapping errors (MNAD) for noiseless Cartesian and radial acquisitions using different CS reconstructions when comparing with the ground truth. Figures 4(c)–(d) show the MNAD for noisy Cartesian and radial. Figures 4(e)–(f) show the biexponential errors (MNAD) for noisy Cartesian and radial acquisitions when MP-PCA filtering prior to the biexponential fitting process is used.

Figure 4:

Results for biexponential T_1ρ mapping error (MNAD) of the synthetic phantom, including (a) Cartesian with no noise in the acquisition, (b) radial with no noise, (c) Cartesian noisy (SNR=2.87), and (d) radial noisy (SNR=74.51), and also (e) MP-PCA filtered Cartesian noisy, and (f) MP-PCA filtered radial noisy. All MNAD values are computed comparing all parameters of the biexponential maps with ground truth.

Results from figures 4(a)–(b) confirm the advantage of Cartesian acquisition when noise is inexistent. SENSE and most CS methods performed better with Cartesian. Results from figures 4(c)–(d), with the noisy data, show that radial acquisition is better, with most CS methods performing better in radial for all AF. However, the reconstruction method is also very important. Note that CS with WAV produced poor results in both acquisitions. Results from figures 4(e)–(f), with the noisy data and MP-PCA denoising filtering used before fitting, show substantial improvement of SENSE and some CS methods with noisy Cartesian. However, there was very little change in results with radial data. This is expected because MP-PCA filters basically noise, which is much stronger in Cartesian SENSE. Essentially, these results indicate the problem with Cartesian acquisitions is the noise. If SNR is good, or noise is reduced by filtering, Cartesian is a good alternative. Also, radial acquisitions show errors from not sampling k-space entirely, this can be seen even in a noiseless acquisition. However, the level of noise is small, which means that the captured samples are very reliable and high AF can be used with very little increase in errors. Some examples of biexponential maps are shown in Figure 5.

Experiments with In-vivo Knee Cartilage Data

Our goal is to find suitable CS scheme, combining acquisition and reconstruction that perform well with in-vivo knee cartilage. So far, we should expect results with noisy data, in which measured noise levels are shown in Table 1. However, we do not have ground truth. The reference method, SENSE, is shown to generate images no better than CS for AF=1. At this point, the results in this section only show how good CS can replace SENSE. Supporting Information Figure S5 shows the synthetic results when compared to SENSE instead of the ground truth, which can connect the synthetic results with what will be observed here.

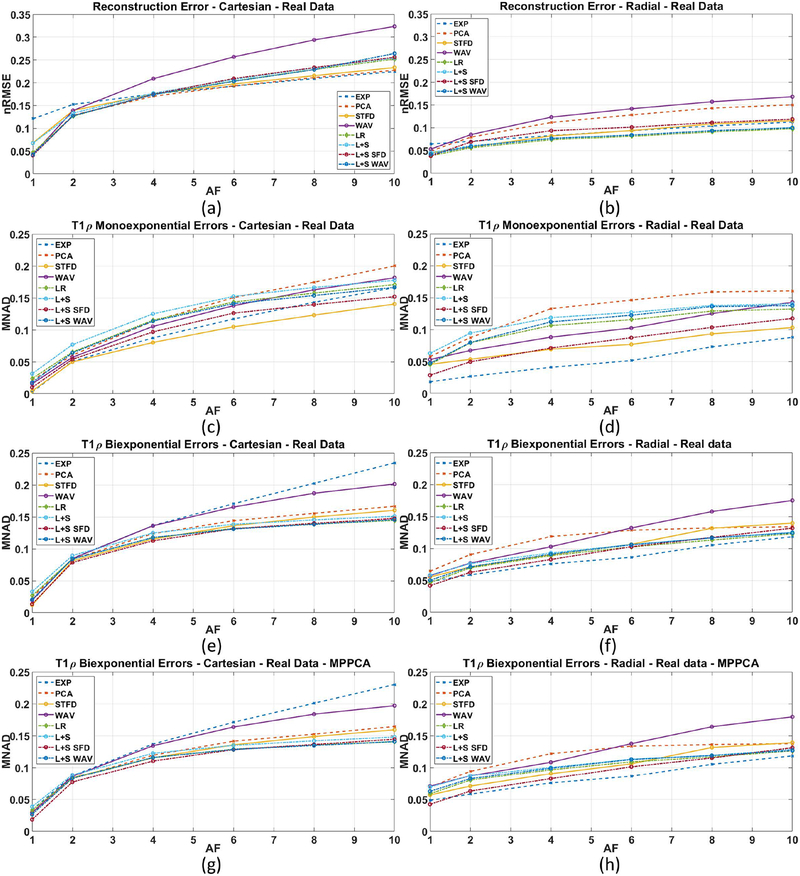
Figure 6(a)–(b) shows the resulting reconstruction error (nRMSE) for Cartesian and GA radial data. At AF=1 (no acceleration), most Cartesian and radial CS methods have an error or 5% (nRMSE=0.05). As AF increases, however, the error of most CS Cartesian methods increases quickly, while most CS radial methods performed better, having a lower error when compared to fully-sampled SENSE.

Figure 6:

Results for human knee cartilage, including: reconstruction error (nRMSE) for (a) Cartesian and (b) radial sampling; monoexponential T_1ρ mapping error (MNAD) for (c) Cartesian and (d) radial sampling; biexponential T_1ρ mapping error (MNAD) for (e) Cartesian and (f) radial sampling; and biexponential T_1ρ mapping error (MNAD) for (g) Cartesian and (h) radial sampling when MP-PCA pre-filtering is used. All errors are compared to the reference method, SENSE.

Figure 6(c)–(d) shows the MNAD for monoexponential T_1ρ mapping for Cartesian and radial. In these plots, radial acquisition performed better with most CS methods, especially at high AF. Figure 6(e)–(f) shows the MNAD for biexponential T_1ρ mapping for Cartesian and radial. Also in this case we observe advantage of radial acquisitions, except for AF=1. Note that the MP-PCA filtering changed very little the results, as shown in Figure 6(g)–(h).

It is also important to evaluate the obtained in-vivo parameters of the cartilage to make sure bias are in acceptable levels. We evaluated the central tendency of the mono and biexponential T_1ρ parameters using median, and the variability, or dispersion, using MAD. The in-vivo values of all healthy volunteers were measured at each ROI and shown in supporting information tables S1–S5 for SENSE reconstruction and some selected CS methods at AF=4, for Cartesian and radial acquisitions. The results in this tables show very similar median parameters between Cartesian and radial methods, with smaller variability and smaller PEMV observed in radial acquisition.

As observed in supporting information tables S1–S5, the measured median monoexponential T_1ρ time was 36.8ms for Cartesian SENSE, and ranged between 35.2~36.5ms in CS Cartesian methods at AF=4, while it was 37.5ms for radial SENSE and ranged from 36.2~37.9ms in CS radial methods. The median biexponential parameters was: a) time short 5.7~6.1ms, time long 40.7~43.0ms, short fraction 15.0~16.8%, and long fraction 83.2~85.0% for Cartesian, and b) time short 5.7~6.2ms, time long 41.9~43.5ms, short fraction 14.5~16.6%, and long fraction 83.4~85.5% for radial.

Overall Classification

In order to have an overall quantification of the results, we compute MNAD for all the results with synthetic noisy and in-vivo knee cartilage datasets together, all compared to the reference. The first score, in Tables 3A–B, is simply the MNAD of all monoexponential errors (NADs), from a total of 4 noisy synthetic datasets and 12 in-vivo knee cartilage datasets, when no-filter is utilized, including Cartesian and Radial acquisitions. The second score in Table 3C–D is the MNAD of all biexponential errors (NADs).

Table 3:

Median of the normalized absolute difference (MNAD) of the T_1ρ maps for A) monoexponential models using Cartesian sampling, B) monoexponential models using radial sampling, C) biexponential models using Cartesian sampling and D) biexponential models using radial sampling. Bold-marked results represent CS methods and corresponding AF that obtained MNAD below 10% on monoexponential and biexponential models.

A. MNAD of Monoexponential Errors with Cartesian Data
AF 2		AF4		AF 6		AF8		AF 10
EXP	0.045	STFD	0.076	STFD	0.101	STFD	0.120	STFD	0.137
STFD	0.047	EXP	0.078	EXP	0.106	EXP	0.130	EXP	0.151
WAV	0.057	L+S SFD	0.101	L+S SFD	0.129	L+S SFD	0.143	L+S SFD	0.155
L+S SFD	0.059	WAV	0.103	WAV	0.137	L+S WAV	0.160	L+S WAV	0.172
PCA	0.064	PCA	0.114	L+S WAV	0.146	WAV	0.162	LR	0.176
L+S WAV	0.069	L+S WAV	0.119	LR	0.147	LR	0.163	L+S	0.181
LR	0.070	LR	0.120	PCA	0.152	L+S	0.171	WAV	0.182
L+S	0.081	L+S	0.129	L+S	0.155	PCA	0.176	PCA	0.201
B. MNAD of Monoexponential Errors with Radial Data
AF 2		AF 4		AF 6		AF 8		AF 10
EXP	0.027	EXP	0.039	EXP	0.048	EXP	0.068	EXP	0.078
L+S SFD	0.048	STFD	0.063	STFD	0.071	STFD	0.087	STFD	0.095
STFD	0.048	L+S SFD	0.069	L+S SFD	0.085	L+S SFD	0.103	L+S SFD	0.116
WAV	0.058	WAV	0.081	LR	0.094	LR	0.119	LR	0.121
LR	0.060	LR	0.083	WAV	0.097	WAV	0.120	L+S WAV	0.130
L+S WAV	0.074	L+S WAV	0.098	L+S WAV	0.108	L+S WAV	0.128	WAV	0.138
L+S	0.077	L+S	0.116	L+S	0.124	L+S	0.140	L+S	0.144
PCA	0.082	PCA	0.118	PCA	0.130	PCA	0.145	PCA	0.147
C. MNAD of Biexponential Errors with Cartesian Data
AF 2		AF 4		AF 6		AF 8		AF 10
STFD	0.081	STFD	0.115	L+S WAV	0.134	L+S WAV	0.142	LR	0.148
L+S SFD	0.085	L+S SFD	0.117	LR	0.135	LR	0.142	L+S WAV	0.149
WAV	0.087	LR	0.121	L+S SFD	0.135	L+S SFD	0.144	L+S SFD	0.152
PCA	0.087	L+S WAV	0.121	STFD	0.136	STFD	0.150	L+S	0.157
EXP	0.088	PCA	0.125	L+S	0.143	L+S	0.151	STFD	0.162
LR	0.089	L+S	0.129	PCA	0.146	PCA	0.158	PCA	0.170
L+S WAV	0.089	EXP	0.136	WAV	0.167	WAV	0.190	WAV	0.205
L+S	0.095	WAV	0.136	EXP	0.168	EXP	0.199	EXP	0.228
D. MNAD of Biexponential Errors with Radial Data
AF 2		AF 4		AF 6		AF 8		AF 10
EXP	0.063	EXP	0.078	EXP	0.086	EXP	0.103	EXP	0.115
LR	0.065	LR	0.082	LR	0.094	LR	0.107	LR	0.115
L+S SFD	0.066	L+S SFD	0.086	L+S WAV	0.104	L+S WAV	0.116	L+S WAV	0.122
STFD	0.070	STFD	0.091	L+S SFD	0.105	L+S SFD	0.122	L+S	0.133
WAV	0.075	L+S WAV	0.091	STFD	0.109	L+S	0.125	PCA	0.134
L+S WAV	0.076	L+S	0.102	L+S	0.114	PCA	0.132	L+S SFD	0.135
L+S	0.077	WAV	0.103	PCA	0.126	STFD	0.136	STFD	0.145
PCA	0.090	PCA	0.115	WAV	0.137	WAV	0.167	WAV	0.184

From Table 3A–B, one can notice that a median error below 10% (bold marked) is expected for monoexponential mapping when using Cartesian with AFs up to 4 with the methods STFD and EXP, and radial with AFs up to 10 for the same methods. According to Table 3C–D, one can expect an MNAD for biexponential models below 10% up to AF of 2 for Cartesian CS methods, while one can push acceleration up to AF of 6 with the radial CS methods EXP and LR.

DISCUSSION

Recommended CS Methods for T_1ρ mapping

For AF=2, almost all CS methods produced good results, for Cartesian and radial acquisitions, mono and biexponential mappings. However, the use of higher AF should be done carefully. Cartesian acquisitions can safely go up to AF of 4 on monoexponential mapping using STFD and EXP. Radial acquisitions can be pushed to AF of 10-fold with methods such as EXP and STFD for mono, and to AF of 6-fold with EXP and LR for biexponential mapping.

Cartesian vs Radial Acquisitions

Considering our T_1ρ sequences available, this study shows that GA radial acquisitions enable higher acceleration than Cartesian. This happened because of the better k-space SNR of GA radial together with good incoherence. The better k-space SNR makes sense, since radial samples the central area of k-space, where the signal is stronger, more often than Cartesian (as reported in Table 1). We did not observe streaking artifacts affecting the cartilage region in our experiments using radial MRI. However, it is important not to ignore this possibility, especially for high AF and in cartilage areas far from the image center.

According to results in supporting information tables S1 to S5, the median values of mono and biexponential relaxation parameters are more similar to the reference in the radial acquisitions. This can also be observed by the PEMV values. Also the variability of the parameters between voxels in a ROI, measured by MAD, are smaller with radial acquisition, which is likely due to better SNR.

Computational Issues

Radial reconstructions are slower than that of Cartesian ones. This happens because even fast operators, such as NUFFT, are far slower than the Cartesian FFT. As observed in Table 2, on average CS radial reconstructions took 6.5× more time to converge than Cartesian reconstructions.

Comparison with Previous Studies

This is the first study that compares CS acceleration for Cartesian and radial T_1ρ mapping, considering mono and biexponential models. CS radial acquisition has been studied for sodium imaging before (59). Inspired by the results in (59), we decided to test it with T_1ρ mapping.

Cartesian CS has been successfully utilized for monoexponential T_1ρ mapping before. In (8) a combination of CS and autocalibration reconstruction (ARC) was utilized for knee cartilage T_1ρ monoexponential mapping errors close to 5%, or lower, for AFs around 2. In (60), three specific CS-like methods: integrating PCA and dictionary learning (PANDA), focal underdetermined system solver with PCA (k-t FOCUSS-PCA) and model-based dictionary learning (MBDL) were compared to accelerate brain and spine T_1ρ mapping up to AF of 4. T_1ρ relaxation errors between 8.9% and 12% were reported. In (9), a combined reconstruction with locally adaptive iterative support detection (k-t LAISD) and joint image reconstruction and sensitivity estimation in SENSE (JSENSE) method was proposed for knee cartilage T_1ρ mapping, with acceleration up to 3 and 3.5. In (61) blind compressed sensing (BCS) was applied to monoexponential T₂ and T_1ρ mapping of the brain.

In (11) it was observed that Cartesian biexponential T_1ρ mapping using magnitude-only models is more unstable than with monoexponential models, since it is more sensitive to noise and the bias caused by noise (52). One of the reasons is the demanded SNR and stability of biexponential fitting (7). However, here we observed that using complex-valued fitting, with the model proposed in Equation 9, biexponential T_1ρ mapping became much more stable. By using this new complex-valued fitting, the error levels of biexponential mapping dropped to similar levels obtained with monoexponential mapping, much lower than the errors observed in (11) with magnitude-only fitting. The complex-valued fitting was robust enough to produce similar median T_1ρ parameters among different acquisitions and reconstructions. One of the advantages of the complex-valued fitting is that it does not require any compensation due to noise (52). This study also differ from our previous Cartesian studies (10,11) on two other aspects. Now the MP-PCA filter is used, instead of 3×3 averaging filter, and MFISTA-VA (51) is used for CS reconstruction.

Limitations of This Study and Future Directions

In this study, we did not evaluate prospective undersampling. However, an example of radial acquisition with AF=2 is displayed in Supplemental Figure S2 (d)–(e) as example. We hope to address this in the future, together with an automatic choice of the regularization parameter, when a fully-sampled reference is not available. In this study, the best CS methods previously studied (10,11) were included. However, the list of far from exhaustive.

The MP-PCA is a relatively new tool for noise estimation and denoising. Unfortunately, there are no studies validating it for knee cartilage mapping yet. However, in our preliminary tests, the MP-PCA provided an exact estimation of the noise levels on the synthetic data. The MP-PCA (30,58) works well when the k-space data or image sequence can be reshaped into a low-rank matrix, while noise is complex-valued and Gaussian, as is the case in this paper.

This study used golden-angle radial sampling, which allowed higher AFs for T_1ρ mapping. However, the “fully-sampled” reference, as well as AF=1, used the same angles each TSL. It is important to investigate using different angles for different TSLs. It may be an interesting alternative to use fewer k-space lines per TSL but more TSLs for better temporal resolution. Spatiotemporal regularization (via STFD and LR) can help correlate different spatial information in each TSL improving the quality of T_1ρ mapping.

Improving reconstruction speed with radial sampling shown to be very important, in order to produce radial T_1ρ maps in processing time similar to the ones with Cartesian sampling. Methods such as MFISTA-VA (51) provide a significant improvement over FISTA (62), but this is still not enough for radial sampling.

CONCLUSION

This study showed that GA radial sampling combined with CS produced 3D-T_1ρ mapping of knee cartilage with lower median error than Cartesian, for mono and biexponential models. The best results were obtained by CS methods such as EXP, STFD, and LR, However, other methods can also be considered depending on other factors of interest.

GA radial sampling and regularized reconstruction were able to accelerate T_1ρ scans up to AF of 10, with MNAD below 10% for monoexponential, compared to AF of 4 with Cartesian sampling. For biexponential models, CS with radial sampling was able to accelerate T_1ρ scans up to AF of 6, with MNAD below 10%, compared to AF of 4 with Cartesian. These results considered evaluation on noisy synthetic phantoms as well as in vivo knee cartilage without any pre-filtering.

Supplementary Material

Supp info

Supporting Information Figure S1: The error in SENSE reconstructions in the fully-sampled noiseless case is zero in the Cartesian sampling, shown in (a), but non-zero in the radial sampling, shown in (b), due to not sampling the k-space entirely. This is an advantage of Cartesian sampling. However, in the fully-sampled noisy case, shown in (e)-(f), radial may have a lower error, but the error is still mostly due to undersampling than due to the noise, the noise-only part is shown (i)-(j). As we apply acceleration factor (AF) of 4, as shown in (c)-(d) for the noiseless case, both methods are affected by undersampling (sampling pattern is Poisson disk in the Cartesian case). The error is larger when noise is included, as shown in (g)-(h), but the error caused only by noise, as shown in (k)-(l) (when error only due to undersampling is subtracted), is much smaller in the radial sampling.

Supporting Information Figure S2: Visual comparison of resolution and SNR of Cartesian and Radial acquisitions. In these examples, the acquisition time and number of k-space samples are the same (Cartesian is k_z × k_y = 256 × 128, Radial is k_s × k_r = 256 × 128, refer to section “Reconstruction Algorithm” for details), However, in radial acquisitions at (e)-(f) a stronger gradient was used to cover higher frequencies than (b)-(c). This allow us to increase the final number of pixels with more details, keeping the same acquisition time and k-space data size. The images (e)-(f) corresponds to a prospective CS acceleration factor of 2. The measured SNR on k-space/image-space, using MP-PCA, are: (a) 6.2/16.4, (b) 54.4/25.2, (c) 54.4/107.9, (d) 7.2/17.8, (e) 26.5/5.8, (f) 26.5/13.2. Note that k-space SNR is larger in radial sampling, but different reconstruction methods (SENSE or CS-STFD) lead to different image SNR.

Supporting Information Figure S3: The regions of interest (ROIs) consider: (a) medial femoral cartilage (MFC), in red, and medial tibial cartilage (MTC), in cyan; (b) lateral femoral cartilage (LFC), in yellow, and lateral tibial cartilage (LTC), in green; and (c) patellar cartilage (PC), in blue. In this figure only one slice is shown, each ROI extends across five consecutive slices where the specified cartilage is well defined.

Supporting Information Figure S4: Description of the (a) T_1ρ pulse sequence used for golden angle radial acquisition, including fat surpression, T_1ρ preparation, and a sequence of multiple k-space imaging readouts of the same radial trajectory in the kx-ky plane, but with phase encoding position in Cartesian kz direction (acquisition starts with the first projection crossing the central k-space in kz axis, and alternates to the high-frequency components) and (b) 3D k-space pattern.

Supporting Information Figure S5: Results of the synthetic phantom, including (a)-(b) reconstruction error (nRMSE), (c)-(d) monoexponential and (e)-(f) biexponential T_1ρ mapping error (MNAD) of the Cartesian and radial noisy data, and (g)-(h) biexponential T_1ρ mapping with pre-filtering using MP-PCA. This figure uses the same synthetic data as in figures 2, 3 and 4, but instead of using a comparison with ground truth, it compares all parameters with the ones obtained from fully-sampled SENSE reconstruction, as done in the in-vivo experiments.

Supporting Information Table S1: Central tendency (median, Eq. 13), variability (median of the absolute deviation, Eq. 14), and percentage error (PEMV, Eq. 15) of Monoexponential T_1ρ values (in ms) in different ROI of the cartilage (according to regions observed in Supporting Figure S3) for the reference method (SENSE) and selected CS methods with AF=4, considering Cartesian and radial acquisition.

Supporting Information Table S2: Central tendency (median, Eq. 13), variability (median of the absolute deviation, Eq. 14), and percentage error (PEMV, Eq. 15) of Biexponential T_1ρ time of the short component (in ms) in different ROI of the cartilage (according to regions observed in Supporting Figure S3) for the reference method (SENSE) and selected CS methods with AF=4, considering Cartesian and radial acquisition.

Supporting Information Table S3: Central tendency (median, Eq. 13), variability (median of the absolute deviation, Eq. 14), and percentage error (PEMV, Eq. 15) of Biexponential T_1ρ time of the long component (in ms) in different ROI of the cartilage (according to regions observed in Supporting Figure S3) for the reference method (SENSE) and selected CS methods with AF=4, considering Cartesian and radial acquisition.

Supporting Information Table S4: Central tendency (median, Eq. 13), variability (median of the absolute deviation, Eq. 14), and percentage error (PEMV, Eq. 15) of Biexponential T_1ρ fraction of the short component (in %) in different ROI of the cartilage (according to regions observed in Supporting Figure S3) for the reference method (SENSE) and selected CS methods with AF=4, considering Cartesian and radial acquisition.

Supporting Information Table S5: Central tendency (median, Eq. 13), variability (median of the absolute deviation, Eq. 14), and percentage error (PEMV, Eq. 15) of Biexponential T_1ρ fraction of the long component (in %) in different ROI of the cartilage (according to regions observed in Supporting Figure S3) for the reference method (SENSE) and selected CS methods with AF=4, considering Cartesian and radial acquisition.

Supporting Information Table S6: Median of the normalized absolute difference (MNAD) of the T_1ρ maps for A) monoexponential models using Cartesian sampling, B) monoexponential models using radial sampling, C) biexponential models using Cartesian sampling and D) biexponential models using radial sampling. Bold-marked results represent CS methods and corresponding AF that obtained MNAD below 10% on monoexponential and biexponential models. All results using MP-PCA pre filtering.

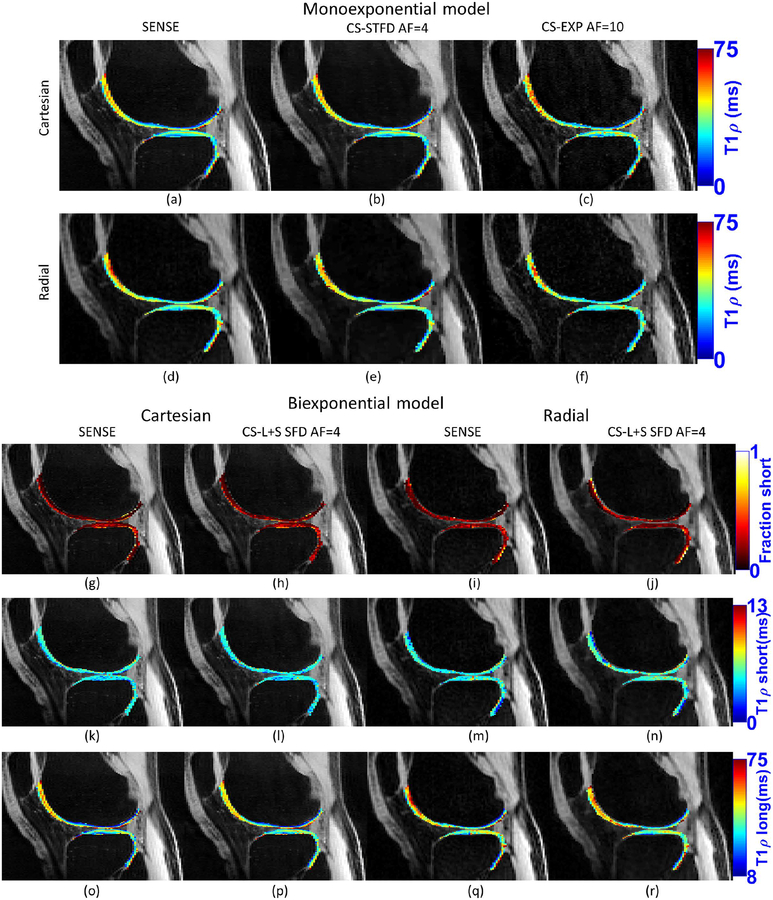
Figure 7:

Example of monoexponential and biexponential maps for real acquired data of the same volunteer. Maps produced with fully-sampled SENSE and accelerated CS with Cartesian and radial sampling.