A General Workflow for Characterization of Nernstian Dyes and Their Effects on Bacterial Physiology

Abstract

The electrical membrane potential (V_m) is one of the components of the electrochemical potential of protons across the biological membrane (proton motive force), which powers many vital cellular processes. Because V_m also plays a role in signal transduction, measuring it is of great interest. Over the years, a variety of techniques have been developed for the purpose. In bacteria, given their small size, Nernstian membrane voltage probes are arguably the favorite strategy, and their cytoplasmic accumulation depends on V_m according to the Nernst equation. However, a careful calibration of Nernstian probes that takes into account the tradeoffs between the ease with which the signal from the dye is observed and the dyes’ interactions with cellular physiology is rarely performed. Here, we use a mathematical model to understand such tradeoffs and apply the results to assess the applicability of the Thioflavin T dye as a V_m sensor in Escherichia coli. We identify the conditions in which the dye turns from a V_m probe into an actuator and, based on the model and experimental results, propose a general workflow for the characterization of Nernstian dye candidates.

Significance

The phospholipid bilayer of a biological membrane is virtually impermeable to charged molecules. Much like in a rechargeable battery, cells harness this property to store an electrical potential that fuels life reactions but also transduces signals. For the case of bacteria, which are small in size and possess a stiff cell wall, arguably the most popular approach to measuring membrane voltage are Nernstian probes, which accumulate across the bacterial membrane according to the Nernst equation. This study characterizes the undesired effects Nernstian probes can have on cell physiology, which can be crucial for the accurate interpretation of experimental results. Using mathematical modeling and experiments, the study provides a general, simple workflow to characterize and minimize these effects.

Introduction

Living cells maintain an electric potential difference (V_m) across the plasma membrane that acts like a capacitor. This is achieved by active transport of ions:

$$V_m=F\times \frac{Q_{in}}{C},$$ (1)

where Q_in is the intracellular charge (in moles), C the membrane capacitance, and F the Faraday constant. Membrane potential stands at the basis of fundamental biological processes such as signal transduction and energy production (1,2). For the latter, V_m adds up to the chemical potential of protons arising from their concentration difference across the membrane to result in the proton electrochemical gradient, the so-called proton motive force (PMF). The PMF drives numerous cellular processes, most notably the production of ATP (2), import of nutrients or osmolites (3, 4, 5, 6), and rotation of the bacterial flagellar motor (BFM) (7), and it is necessary for cell division (8).

The notion that V_m lies at the very basis of life motivated decades long efforts to measure it (9). The first direct technique dates to 1939 and relies on the mechanical insertion of microelectrodes into squid giant axons (10). The method led to the development of the patch-clamp technique, which advanced the understanding of neuron signal transduction (11, 12, 13). However, the applicability of microelectrodes for the measurement of bacterial V_m is limited, owing to the small size of the organisms and the presence of the cell wall (14,15). Some of the subsequently developed methods overcome such limits with the use of molecular sensors (16), grouped into two categories: conformational-change-based sensors and Nernstian sensors. The former are static molecules or proteins that sit inside the membrane or in its close proximity and change conformation or electron distribution in response to changes in V_m, which, in turn, affect the optical properties of the chromophores (17, 18, 19). Here, we focus on the latter, the Nernstian sensors, and on the parameter range in which they serve as V_m indicators, using E. coli as the model organism.

Nernstian sensors are charged molecules that can diffuse across the biological membranes and distribute according to the Nernst equation:

$$V_m=\frac{RT}{zF}\text{ln}\left(\frac{c_{out}}{c_{in}}\right),$$ (2)

where R, T, z, F, c_out, and c_in denote, respectively, gas constant, temperature, valence of the charged molecule, Faraday’s constant, and external and internal concentrations of the charged molecule. For a measurement to be attained, these molecules need to emit a signal that is a proxy for their number. Therefore, Nernstian V_m dyes are usually radiolabeled or fluorescent molecules (16,20), and V_m is calculated from Eq. 2 by measuring the cytoplasmic (c_in) and the external dye concentrations (c_out) (21).

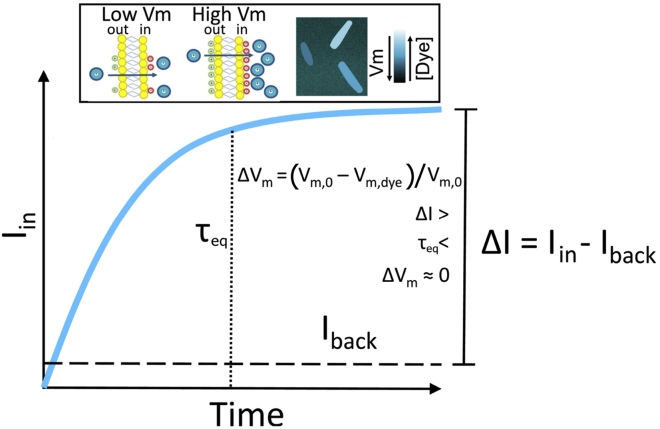
However, Nernstian dyes are used in complex biological systems, and a number of factors can be responsible for an incomplete adherence to a fully Nernstian behavior. In Fig. 1, we give a cartoon representation of the tradeoffs imposed on a Nernstian dye by plotting the dye intensity inside E. coli’s cytoplasm against the time. The chosen dye concentration should be such that the signal is sufficiently above the background (ΔI is sufficiently large). Yet, with increasing dye concentration, a cell’s V_m is more likely to be affected by the dye. This caveat is inherent to positively charged dyes because these directly lower V_m and more so at higher concentrations (22). The first requirement for a Nernstian dye is thus the existence of a range of concentrations that give sufficient signal without extensively affecting the V_m. Likewise, cellular processes should not interfere with the Nernstian behavior of the dye, for example, by actively importing or exporting it. Instead, the dye should be able to diffuse across the membrane, and its diffusion constant will determine the time it takes for the dye to equilibrate across the membrane in agreement with Eq. 2 (τ_eq in Fig. 1). All phenomena that occur quicker than τ_eq are beyond the dye’s temporal resolution, and all the measurements taken before τ_eq do not faithfully report V_m. Lastly, different dyes bind to the membrane or form aggregates to a different extent (21,23)). However, as long as the dyes do not self-quench at any point (24) or undergo signal enhancements, a constant and well-defined correlation function between the free dye concentration and the signal can be obtained, thus enabling quantitative V_m measurements (most commonly, this is done by separating the signal from the free and bound dye with careful calibration (21,23)).

Figure 1.

A schematic plot of a Nernstian dye equilibration curve. Equilibration time, τ_eq, is defined as the time at which the dye internalized by the cell, dye I_in, reaches 90% of its final value. V_m,0 and V_m,dye indicate the membrane potential before and after the addition of the dye, respectively. I_back is the fluorescence intensity of the background. Inset: cartoon showing the mechanism of accumulation of cationic dyes, which accumulate more in cells with a more negative V_m. To see this figure in color, go online.

To summarize, to be used as an ideal Nernstian sensor, a cationic dye should 1) give a sufficiently high signal without affecting cell’s V_m; 2) diffuse through the membrane with τ_eq on the order of minutes; 3) stay inert, despite being charged, and not form bonds or in any way interact with the cell; and 4) have constant signal per molecule. Yet, when using such dyes, these requirements are rarely assessed in a systematic manner before measurements commence. In this work, we identify a workflow that should be adopted, for a given choice of the dye, organism, and external environment, to identify the parameter range in which Nernstian dyes act as sensors rather than actuators, i.e., molecules that actively decrease or increase the V_m. We start with a mathematical model that helps us understand relationships and define tradeoffs between dye working concentration and signal intensity, equilibration time, and V_m perturbation. We then show how the identified workflow can be used to benchmark new Nernstian dyes by characterizing the recently reported dye Thioflavin T (ThT) used in Bacillus subtilis (25) for use in E. coli. We describe the physiological range in which ThT enables V_m sensing in E. coli, and, in the range in which we find it turns into an actuator, we investigate the mechanistic reasons. Our workflow can be applied to the characterization of other Nernstian dyes and provide novel insights for the established ones.

Methods

Bacterial strains

All experiments in which no mutation is explicitly indicated were carried out in the MG1655 strain. For the BFM speed assay, we used MG1655 carrying the FliC-sticky mutation from (26). ΔtolC mutants were obtained from the Keio collection (27). Kanamycin resistance of the Keio deletion strain was removed via one-step inactivation with the plasmid pCP20 (28). Kanamycin resistance inactivation and elimination of the pCP20 plasmid were confirmed via kanamycin (50 μg/mL), chloramphenicol (31 μg/mL), and ampicillin (100 μg/mL) sensitivity tests. Both the strain carrying the ΔtolC mutation and MG1655 wild type (WT) were transformed with plasmid pTP20-mKate2 (Fig. S1) for cytoplasmic volume measurements. pTP20-mKate2 contains the red fluorescent protein mKate2 and the ribosomal binding site of mCherry. The plasmid was constructed as follows: the backbone from pWR20 (29) and the sequence containing the ribosomal binding site of mCherry and mKate2 were PCR-amplified. The products were purified, cleaved with the restriction enzymes AvrII and NotI (New England Biolabs, Hitchin, UK), and ligated using T4 DNA ligase (Promega, Chilworth, UK). Chemically competent cells were transformed with the ligation mixes, and transformants were confirmed by colony PCR and subsequently sequenced. A map of the plasmid and the primers are given in Fig. S1 and Table S1. All the strains used in the study are summarized in Table S2.

Bacterial growth conditions

Cells for fluorescence microscopy were grown from an overnight culture by diluting it 1:80 times in Luria-Bertani broth (0.5% yeast extract, 1% Bacto Tryptone, 1% NaCl). The culture was shaken at 220 rpm at 37°C and harvested at OD₆₀₀ = 0.3–0.5. Cells were then washed into fresh LB or MM9 + glucose medium (50 mM Na₂HPO₄, 25 mM NaH₂PO₄, 8.5 mM NaCl, 18.7 mM NH4Cl, 0.1 mM CaCl₂, 1 mM KCl, 2 mM MgSO₄, 1× modified Eagle’s medium essential amino acids (Gibco, Paisley, UK), and 0.3% glucose). For the simultaneous BFM speed and ThT fluorescence measurements, cells were grown from an overnight culture by diluting it 1:80 times in TB (1% Bacto Tryptone, 0.5% NaCl) at 200 rpm and 30°C. Cells were harvested at OD₆₀₀ = 0.8 as before (30) and washed into fresh MM9 via centrifugation. Growth curves in the presence of ThT were obtained in a Spectrostar Omega microplate reader (BMG, Ortenberg, Germany) using a flat-bottom 96-well plate that was covered with a lid during the experiments (Costar, Glasgow, UK). Each well contained 200 μL of growth media, either MM9 + glucose or MM9 + glycerol (50 mM Na₂HPO₄, 25 mM NaH₂PO₄, 8.5 mM NaCl, 18.7 mM NH4Cl, 0.1 mM CaCl₂, 1 mM KCl, 2 mM MgSO₄, 1× modified Eagle’s medium essential amino acids (Gibco), and 0.3% glycerol), and was inoculated with 2 μL (1:100 dilution) of an overnight culture and a given concentration of ThT. Plates were grown at 37°C with 300 rpm shaking (double orbital mode). ThT (Acros Organics, Loughborough, UK) solutions were prepared from a 10 mM stock of ThT in water made at least monthly and stored at 4°C in the dark.

Fluorescence microscopy

Imaging was carried out in a custom-built microscope with a 100× oil immersion objective lens (Nikon, Tokyo, Japan) and a neutral white LED as a source of illumination (Cairn Research, Faversham, UK), and images were taken with an iXon Ultra 897 EMCCD camera (Andor, Belfast, UK) (31,32). ThT fluorescence was measured with ZET436/20× and ET525/40 m, and mKate2 and propidium iodide (PI) fluorescence with ET577/25× and ET632/60 m (Chroma Technology, Bellows Falls, VT) excitation and emission filters, respectively. Images were taken at 1 min intervals, exposure time was 50 ms and Andor camera gain 25. We note that ThT undergoes a spectral shift and intensity increase when highly concentrated or when spatially constricted, either by binding to amyloid fibrils or by viscosity (33, 34, 35). Our choice of filters aims at minimizing these effects and the damage that shorter wavelengths cause to E. coli (36). Cells were imaged in a custom-built flow cell (Fig. S2; (26)) and attached to the coverslip surface as before (26,30). Briefly, 1% poly-L-lysine (Sigma-Aldrich, Gilingham, UK) is flushed through the flow cell and washed with 3–5 mL of growth media after 10 s. Polystyrene particles (beads) with a diameter of 1 μm (Bangs Laboratories, Fishers, IN), were delivered into the flow cell and allowed to attach to the coverslip surface. After 10 min, unattached beads were flushed away with 1–2 mL of growth media. Next, 200 μL of cells were delivered to the flow cell and allowed to attach for 10–30 min, after which the unattached cells were removed with 1 mL of growth medium. 10 μM ThT in growth media was delivered with a peristaltic pump (Fusion 400; Chemyx, Stafford, TX) using 50 μL/min flow rate while imaging. We deliver 5 μM of PI stain (MP Biomedicals, Loughborough, UK) in the same way. 5 mM PI stock solution (in water) was stored at 4°C in the dark. Images were stabilized in x, y, and z positions using a bead attached to the coverslip and back-focal-plane interferometry (29,37). Cells grow attached to the poly-L-lysine surface with expected growth rates (given the medium), as previously reported (38) and seen in Videos S1 and S2.

Video S1. E. coli Growing in LB Medium in Our Flow Cell before Addition of the ThT Dye

Image shown in gray-scale. In yellow we colour the frames that correspond to addition of the dye but without epifluorescence imaging. While the dye is present in the medium, it does not enter the cytoplasm, and thus the cells continue to grow. We colour in cyan the frames where both the ThT and epifluorescence imaging is happening at the same time. ThT now enters the cytoplasm and cells stop growing. The brightfield images correspond to one of the experiments presented in Fig. 5 E.

Video S2. Growth of E. coli in Our Flow Cell, in MM9 + Glucose Medium, in the Presence of Epifluorescence Illumination

The brightfield images are from one of the experiments in Fig. S10. Cells grow in our flow cell when epifluorescence imaging is turned on.

Motor speed measurements

Single motor speeds were measured as before (26,30). Briefly, we sheared flagellar filaments by passing them through two syringes with narrow-gauge needles (26 gauge) connected by plastic tubing. The cell attachment protocol was as above, except 0.5 μm beads (Polysciences, Warrington, PA) were delivered after cell attachment allowing them to attach to filament stubs. Motor speed was measured during continuous flow that delivered MM9 + glucose medium supplemented with 10 μM ThT. Back-focal-plane interferometry setup and recording conditions are as before (30).

Data analysis

Motor speed traces

Raw traces of the position of the bead attached to the filament stub were analyzed by a moving-window discrete Fourier transform as in (30). From the obtained motor speed traces, DC frequency (50 Hz) was removed, speeds lower than 5 Hz were ignored, and subsequently a median filter (window size 11) was applied (26). We note that we use a WT strain for which the BFM can change rotational direction, which appears as a negative speed after application of the moving-window Fourier transform. However, for the purpose of the PMF measurements, these short intervals can be disregarded, and we only show the speed values above 0 Hz.

Fluorescence images

The image analysis was carried out with custom-written software. From fluorescence images, rectangles containing “flat” cells, i.e., cells that are uniformly attached to the coverslip surface, as well as background rectangles within each cell-containing rectangle, were manually selected (29,37). The edge of the cell was identified within the cell-containing rectangle by applying a global threshold via the Otsu’s method (39). Total cells’ intensity values were obtained by summing up and averaging pixel belonging to the cells. Values obtained from the background rectangles at the time points when ThT was loaded in the channel but cells had not taken it up yet were subtracted from the cell intensity values. The beads used for image stabilization stain easily with ThT and were used as a point of reference for dye entry (which, in our case, occurred 7–10 min from the start of imaging). We show fluorescence intensity traces that start at the point of ThT entry but note that cells were exposed to fluorescence illumination in the 7–10 min interval before. For the low fluorescence values characteristic of the early stages of dye equilibration, our script fails to identify cells, in which case we linearly interpolate values between two closest events of successful cell identification. Cell area was measured from intensity profiles, by normalizing them and counting the pixels above 30% of maximum intensity as described previously (29,37).

Plate reader data

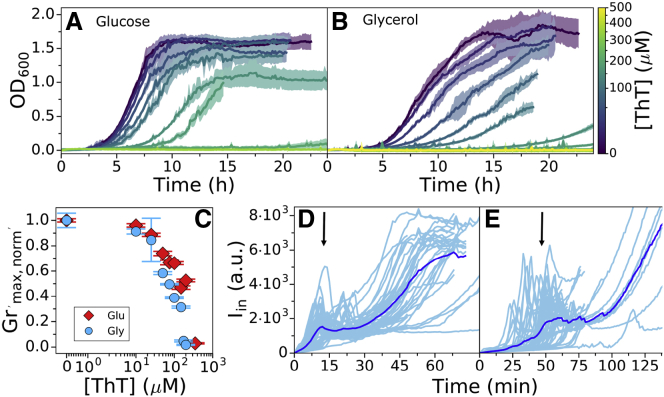
Individual growth curves were analyzed with the software deODorizer from (40). To extract the maximum growth rate, three or more repeats in the same condition were aligned by the chosen OD value (usually OD ∼ 0.4) using the growth curve that reached it first (in the given condition). The maximum growth rates given in Fig. 3 C were normalized by the maximum growth rate in [Dye]_out = 0 condition.

Figure 3.

E. coli growth in the presence of ThT. E. coli growing in MM9 media supplemented with (A) glucose or (B) glycerol at increasing ThT concentration (color map) is shown. ThT concentrations in (A) are 10, 25, 50, 75, 100, 200, and 350 μM and in (B) are 10, 25, 50, 75, 100, 150, 175, and 200 μM. The error bars are standard deviations. (C) Maximum growth rates from (A) and (B) for each ThT concentration are given in red and blue, respectively. Each condition was done at least in triplicate, and error bars are the standard deviation. (D) I_in against time in LB and in (E) MM9 + glucose media is shown. Individual cells are shown in cyan (45 in D and 52 in E from at least nine independent experiments), and the average trace is shown in blue. The imaging conditions and I_ex = 10 μM are the same for (E) and (D). The black arrows indicate the intensity peaks. To see this figure in color, go online.

Results

Mathematical model of Nernstian dye’s behavior defines its working parameter range

To predict and understand the mutual effects of dye concentration and cell physiology, we turn to a mathematical model. We assume that the cytoplasmic and extracellular liquids are electrical conductors separated by a membrane, which we treat as a parallel-plate capacitor (Eq. 1; (41,42)). We model the membrane as a single lipid barrier and do not distinguish between the inner and outer membrane of E. coli. In the Supporting Materials and Methods, we discuss a more detailed model that includes both membranes and allows for the existence of a small V_p across the outer membrane in addition to the V_m across the inner membrane. We account for four types of charge carriers and assume that all are monovalent to simplify the model without altering the results with respect to V_m dye behavior: 1) negatively charged molecules to which the membrane is close to nonpermeable, denoted Y (this includes surface charges on the inside of the membrane); 2) cationic species actively pumped outward, denoted C⁺; 3) anionic species, which equilibrate across the membrane A⁻; and 4) cationic species that equilibrate across the membrane (playing the part of a cationic dye). Thus, Q_in is

$$Q_{in}=V_{cell}\times \underset{\text{General Form}}{\underbrace{\sum _x{z}_x{\left[x\right]}_i}}=V_{Cell}\times \underset{\text{This manuscript}}{\underbrace{\left({\left[Dye\right]}_{in}+{\left[C^{+}\right]}_{in}-{\left[A^{-}\right]}_{in}-{\left[Y\right]}_{in}\right)}},$$ (3)

where V_cell is the intracellular volume, z_x the valency of species x, and [x]_i its intracellular concentration (we only consider z_x = ±1). The extracellular concentrations and [Y]_in are constants set by the initial conditions (we assume that the cell does not affect the ionic composition of its environment, and we treat [Y]_in as unable to cross the membrane). We also assume that the cell uses only one type of pumps for cations, and note that [Dye]_in and [Dye]_out are experimentally determined from fluorescence intensity signal (see Fig. 6 later in the text).

Figure 6.

Proposed workflow for characterizing the Nernstian behavior of a candidate cationic membrane voltage dye. The working concentration is estimated in steps 1–4; we define it as the maximum dye concentration that does not affect membrane voltage and that yields sufficient amount of signal. 1) The MNC is estimated. 2) The MNC is tested for sufficient signal intensity and the shape of the equilibration profile is inspected. 3) The effect of the dye on V_m is determined by measuring τ_eq at different below-MNC concentrations. 4) Different τ_eq for different dye concentrations indicate that the probe is altering V_m and the working concentration should be reduced and the protocol resumed from step 2. Equal τ_eq indicates that the probe is not altering V_m. 5) Common procedures to test the expected Nernstian dye responses can then be applied, such as the introduction of a ionophore that neutralizes V_m or changes in external pH that induce changes in V_m (21). 6) I_in from the free dye should be separated from the I_in from the bound dye, and [Dye]_in should be calculated from I_in by taking into account the microscope’s points spread function. 7) Because the effects depend on the physiological state of the cell, the procedure should be repeated for every experimental condition. To see this figure in color, go online.

The charge separation, and thus V_m, is achieved in the close proximity of the bilayer so that the rest of the cell’s cytoplasm stays electroneutral (42,43) and in two ways: first, by pumping $C_{in}^{+}$ outwards and thus creating a negatively charged intracellular environment, and second, by maintaining [Y]_in. Pumping C⁺ outwards against its electrochemical gradient requires free energy, which we consider a constant and label ΔG_E (where ΔG_E < 0). For example, in the case of a proton/ion antiporter with 1:1 exchange stoichiometry, the free energy is the PMF itself; for a similar antiporter with 2:1 proton/ion stoichiometry, it is 2× PMF; and for ATP hydrolysis, ΔG_E is the amount of work given by hydrolyzing one ATP.

The rate at which C⁺ is pumped out of the whole cell, given in mol/m³/s, is

$$j_P=k_P\times \left(1-e^{\Delta G_P/\left(RT\right)}\right),$$ (4)

where k_P is a function that describes the specifics of the transport mechanism by a given pump; here, we keep it a constant. ΔG_P depends on the electrochemical potential of the pumped cation $\left(\Delta G_{C^{+}}\right)$ and ΔG_E. Therefore, the rate of pumping (positive flux means C⁺ is extruded) depends on the intracellular ionic composition via V_m and [C⁺]_in:

$$\Delta G_P=\Delta G_E-\Delta G_{C^{+}},$$ (5)

$$\Delta G_{C^{+}}=F\times V_m+RT\times \text{ln}\left(\frac{{\left[C^{+}\right]}_{in}}{{\left[C^{+}\right]}_{out}}\right).$$ (6)

Note that for the pump to move C⁺ outward, j_P > 0, and consequently ΔG_E < $\Delta G_{C^{+}}$, i.e., the free-energy-providing reaction has to be able to overcome the electrochemical gradient of the C⁺. The chosen functional dependency of j_P gives the simplest pump kinetics, sufficient for our purpose, that can be expanded to include more complex pumping scenarios (44).

Finally, the dye, the anion, and the cation leak through the membrane (positive flux means x is moved inward) at the rate

$$j_{L,x}=k_{L,x}\times \left(1-e^{\Delta G_x/\left(RT\right)}\right),x\in \left\{Dye,C^{+},A^{-}\right\},$$ (7)

$$\Delta G_x=F\times V_m+RT\times \text{ln}\left(\frac{{\left[x\right]}_{in}}{{\left[x\right]}_{out}}\right).$$ (8)

Similarly to k_P, k_L,x is a function whose shape depends on the mechanisms by which an ion leaks across the E. coli membrane, which, in turn, depends on the electrostatic potential at a position z within the membrane, V(z). To the best of our knowledge, V(z), and consequently dV(z)/dz, is not known for E. coli. Therefore, we chose Eyring’s model, which has been verified for cationic leakage across the mitochondrial membrane (45) and that assumes V(z) abruptly changes in the middle of the lipid bilayer such that dV(z)/dz = 0 everywhere but at the geometrical middle of the membrane, where dV(z)/dz = V_m (46). We then have

$$k_{L,x}=\frac{S_{cell}}{V_{cell}}\times P_x\times {\left[x\right]}_{out}\times e^{-\frac{F\times V_m}{2\times RT}},\text{with}x\in \left\{Dye,C^{+},A^{-}\right\},$$ (9)

where S_cell denotes the cell’s surface area and P_x the permeability of the membrane for x ∈ {Dye, C⁺, A⁻} (obtained by assuming the solubility-diffusion model (47)).

At steady state, Dye and A⁻ equilibrate across the membrane according to the Nernst equation (d[Dye]_in/dt = j_L,Dye = 0 $\iff$ ΔG_Dye = 0, leading to Eq. 2), whereas for the monovalent cation, d[C⁺]_i/dt = 0 $\iff j_{L,C^{+}}=j_P$. Next, we introduce a new variable (“pump-leak ratio”), defined as

$$\rho =k_P/k_{L,C^{+}}=k_P\times \frac{V_{cell}}{S_{cell}\times P_{C^{+}}\times {\left[C^{+}\right]}_{out}}\times e^{\frac{F\times V_m}{2\times RT}},$$ (10)

and rewrite the steady-state condition for C⁺ as

$$\left(1-e^{\Delta G_{C^{+}}/\left(RT\right)}\right)=\rho \times \left(1-e^{\left(\Delta G_E-\Delta G_{C^{+}}\right)/\left(RT\right)}\right).$$ (11)

Given a certain extracellular composition ([Dye]_out, [C⁺]_out, and [A⁻]_out) and taking into account that [Dye]_in and [A⁻]_in are defined by the Nernst equation at steady state, Eq. 11 gives us a unique solution for steady-state V_m for a set of {[Y]_in, ρ, ΔG_E} values while reducing the number of computational steps needed to reach it (see also the later paragraph describing computational steps of the model further).

We note from Eq. 11 that changing the functional dependency of $k_{L,C^{+}}$ or k_P does not affect how the steady-state V_m,0 depends on ρ. However, the dynamics of dye equilibration and the steady-state potential after addition of the dye, relative to the steady-state potential in absence of the dye (ΔV_m = (V_m,0 − V_m,Dye)/V_m,0), do. For example, had we assumed that the mechanism by which the ions leak across the E. coli membrane is better described by the Goldman-Hodgkin-Katz flux equation for k_L,x (48), we would have obtained a slightly different dye equilibration profile (Fig. S3). However, the conclusions we reach based on our model predictions will not change because we are interested in the changes of the intracellular dye concentration dynamics at different extracellular dye concentrations, V_m,0 or P_Dye. These partial derivatives of the intracellular dye concentration are invariant to the choice of k_L,x and k_P.

Having constructed the model, we obtain the computational data in Fig. 2 in two steps. In the first step, we allow the oridinary differential equation (ODE) system described by Eqs. S20 and S21 to reach the steady state (V_m,0) for a three-dimensional grid of {[Y]_in, ρ, ΔG_E}. We note that in this step, we do not need to specify cation permeability nor the rate function for leakage $k_{L,C^{+}}$ because we define the values of ρ, which is the ratio of the two (ρ = 0 for the anion and the dye). We then use the obtained V_m,0 as the initial condition for the second step of the numerical experiment, which requires us to specify 1) the rate function for leakage (Eq. 9), 2) the permeability of the membrane to the dye P_Dye, and 3) the concentration of the dye in the extracellular space [Dye]_out, which does not affect the cation pumping rate in our model.

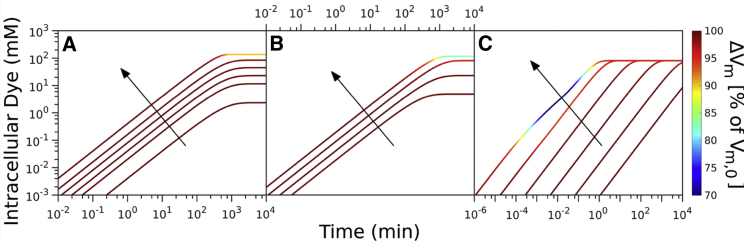
Figure 2.

Computational data describing the parameter landscape associated with cationic dye usage as Nernstian sensors. (A) V_m,0 = −140 mV, Y_i = 150 mM, I_Na = 210 mV. Intracellular dye concentration as a function of time is shown for extracellular dye concentrations 10, 50, 100, 200, 400, and 1000 μM. The arrow indicates increasing [Dye]_out. (B) Extracellular dye concentration of 100 μM is shown; Y_i = 150 mM, ΔG_E = −210 mV. Intracellular dye concentration as a function of time is shown for different V_m,0: −220, −180, −140, and −100 mV. The arrow indicates increasing absolute value of the V_m,0. (C) Extracellular dye at 100 μM is shown; V_m,0 = −180 mV, Y_i = 150 mM, ΔG_E = −210 mV. Intracellular dye concentration as a function of time is shown for different apparent permeabilities of the membrane to the dye: 10⁻¹², 10^−10.8, 10^−9.6, 10^−8.4, 10^−7.2, 10⁻⁶ m/s. The arrow indicates increasing permeability. To see this figure in color, go online.

To explore the tradeoffs imposed on a Nernstian dye (Fig. 1), we first look at the choice of the working concentration. Increasing the [Dye] gives better signal/noise ratio but can affect V_m,0, as depicted in Fig. 2 A. For a fixed V_m,0, [Y]_i, and ΔG_E, changing the external dye concentrations ([Dye]_out) improves the signal/noise ratio and shortens τ_eq but, at the same time, increasingly depolarizes the membrane. The extent by which ΔV_m drops does not solely depend on the [Dye]_out but also on the initial V_m,0. Fig. 2 B shows dye equilibration profile for a fixed [Dye]_out but for different V_m,0, indicating that highly polarized cells are more susceptible to V_m loss. Apart from the value of V_m,0, ΔV_m will also depend on the charged permeable and nonpermeable species that are generating it, as shown in Fig. S4. If a given V_m,0 value is generated in the presence of a higher concentration of charged, impermeable intracellular species or at a higher energetic cost, ΔV_m will increase for the same [Dye]_out. Thus, the extent to which a given [Dye] becomes an actuator and affects the ΔV_m is context-dependent, and the dye working concentration should be determined for each specific physiological condition. Additionally, Fig. 2 A shows that increasing [Dye]_out shortens τ_eq, but only when V_m,0 is affected, as seen in Fig. S5.

Lastly, we look at the dye equilibration profile for different permeabilities of the membrane to the dye (P_Dye) in Fig. 2 C and show that for higher P_Dye, the same concentration of the dye lowers V_m,0 more. Fig. S4 shows τ_eq as a function of P_Dye for different V_m,0.

The working concentration of Nernstian dye ThT for E. coli is in μM range

Guided by the model predictions, we devise an experimental workflow for assessing the parametric range in which a candidate cationic dye behaves like an ideal Nernstian sensor. We choose ThT for the purpose; it has recently been used as a V_m dye in B. subtilis (25), but it has not been characterized for use in E. coli. We start by identifying the working concentration that gives sufficiently large signal yet minimizes the membrane voltage perturbation, ΔV_m. Because we do not have access to ΔV_m directly, we grow the cells in the presence of ThT and use the growth rate as a proxy for affected ΔV_m. We also know from our model predictions that ΔV_m is context-dependent, so we perform the experiment in two different media. Fig. 3, A and B show E. coli growth curves in MM9 media supplemented with glucose or glycerol, respectively (see Materials and Methods for detailed media composition), and in the presence of a range of ThT concentrations. To assess the effect of different ThT concentrations in these two media, we plot growth rates, obtained from growth curves in Fig. 3, A and B, against the ThT concentration. Fig. 3 C demonstrates that 10 μM ThT or less does not significantly affect the growth rate in either media, and we call this concentration the maximum noninhibitory concentration (MNC). The growth rate reduction we observe for higher ThT concentrations is media-dependent (Fig. 3 C). The result is consistent with the finding of our model that the effect of the dye on a cell’s physiology is environment-dependent. It could be caused by a different V_m,0, difference in charged permeable and nonpermeable species that achieve the V_m,0, difference in the initial membrane permeability, or any combination of these factors.

We next check that the highest ThT concentration that does not affect the growth rate (MNC), 10 μM, gives sufficiently high signal/noise ratio by observing the dye equilibration in different media. For this purpose, we no longer grow the cells in the presence of ThT (see also Materials and Methods). We note that if sufficient ΔI is achieved with 10 μM ThT, we would further check that ΔV_m < 1% by measuring the τ_eq with both 10 μM and a lower dye concentration. If ΔV_m < 1%, we expect τ_eq not to change based on the results of our model (Fig. 2 A). Fig. 3 D shows I_in in time in LB, and Fig. 3 E shows the same in MM9 media supplemented with glucose. In both cases, fresh medium with ThT is continuously supplied using a customized flow cell (see Materials and Methods), and in both cases, ΔI is sufficiently high. However, observed profiles are different from expected (Fig. 1) and show a characteristic initial peak and a subsequent large increase that plateaus (Video S3). We reasoned that the peak could either be a real fluctuation in V_m or it could indicate an unknown dye export mechanism.

Video S3. Equilibration of ThT in LB

Dynamics of ThT equilibration in a flow slide in LB medium from the experiments in Fig. 3 D. Images are taken every minute.

Deletion of the multidrug efflux pumps component TolC influences ThT dynamics in E. coli

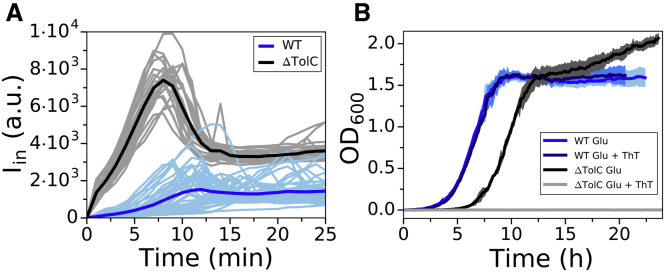
To determine whether the observed peak in I_in is due to active export of the dye, we first check that in E. coli, ThT is not a multidrug efflux pump substrate. We are motivated by previous reports that show dyes such as ethidium bromide and Nile red are substrates of pumps belonging to the five bacterial structural families: ATP-binding cassette, resistance/nodulation/division, multidrug and toxic compound extrusion, major facilitator superfamily, and small multidrug resistance (49, 50, 51, 52, 53). Fig. 4 A shows dye equilibration curves in a WT strain compared to the strain bearing a deletion of TolC, which is a gene encoding for an outer membrane protein that is a ubiquitous component of multidrug efflux pumps (54). The I_in peak in the deletion mutant did not disappear; instead, the intensity level of the peak was even higher, suggesting that the qualitative difference between the expected (Fig. 1) and the observed equilibration curve (Fig. 4 A) is not due to ThT export by TolC. Interestingly, in the mutant, the peak also occurred earlier in time during the loading and with less cell-to-cell variability. We next tested the effect of the ThT dye on the ΔTolC mutant growth rates, and for this purpose, we again grew the two strains in the presence of ThT (Fig. 4 B). We found that at the MNC for the WT, the mutants’ growth was inhibited over the course of our experiment. Two different mechanisms could explain the results in Fig. 4: 1) ThT is a substrate of the multidrug efflux pumps or 2) membrane permeability of the TolC mutant is higher (55). In the first scenario, the strain lacking TolC accumulates more ThT than the WT (Fig. 4 A) and is therefore more affected by it (Fig. 4 B). In the second scenario, based on our model, we expect the intensity peak to appear earlier and at a higher [Dye]_in (Fig. S12, C and D), which is what we observe in Fig. 4 A. We currently cannot distinguish between the two hypotheses, which could be contributing to the observed equilibration profiles at the same time.

Figure 4.

Comparison of WT and ΔTolC mutant response to ThT. (A) I_in versus time for the WT (cyan) and ΔTolC (gray) loaded in LB is shown. WT traces are reproduced from Fig. 3D, and ΔTolC traces were obtained from five independent experiments to give 23 single-cell traces. Averaged traces for the WT and ΔTolC are given in blue and black, respectively. (B) Growth curves of WT and ΔTolC in MM9 + glucose media are given in blue (reproduced from Fig. 3A) and black, respectively. Growth curves in the same media, but in the presence of 10 μM ThT, are given in cyan (WT) and gray (ΔTolC). The shaded areas show standard deviation and cyan and blue growth curves for the WT overlap. To see this figure in color, go online.

Changing the membrane permeability during ThT loading can lead to loss of V_m

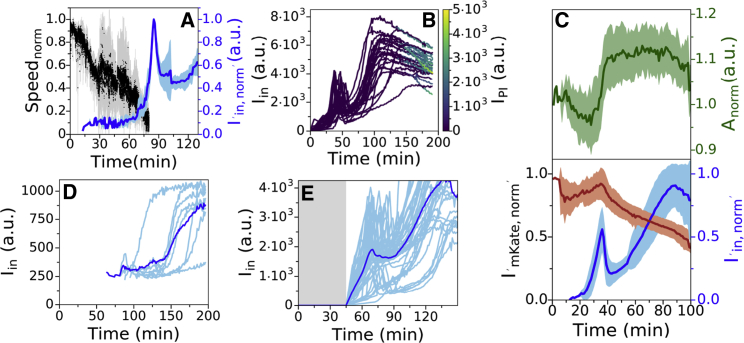
We next tested our second hypothesis, that the I_in peak is due to a decrease in V_m. To this end, we performed measurements of BFM speed (26) during ThT loading. The BFM is a rotary molecular motor roughly 50 nm in size that enables bacterial swimming (7) via PMF-driven rotation (56, 57, 58, 59). The motor speed (ω) varies linearly with PMF (59,60), which enables its use as a PMF indicator and, when pH_in = pH_out, as a V_m indicator as well (26). In our conditions, pH_out is 7 and pH_in is 7.86 (Fig. S7), making the contribution to the PMF from ΔpH ∼50 mV. Thus, even if during our experiment, ΔpH goes to 0, we can learn about the V_m behavior from the PMF measurements via the motor speed. We measure ω as before, using back-focal-plane interferometry (61) and a polystyrene bead attached to a short filament stub (see Materials and Methods) (26,30,62,63).

Figs. 5 A and S8 show simultaneous measurements of ThT intensity and normalized motor speed during dye equilibration in MM9 + glucose. The motor speed decreases during ThT equilibration, and the BFM stops at the point of the I_in peak. Furthermore, the BFM does not resume spinning even as I_in further increases, suggesting that the second ThT intensity increase that culminates in a plateau is not driven by V_m. To confirm the result, during ThT equilibration, we supplemented the medium with PI. PI permeates bacterial membrane that lost its integrity and significantly enhances its quantum yield upon binding to DNA, which is commonly interpreted as an indication of cell death (64,65). We found that the cells stained with PI, although ThT intracellular concentration remained high (Figs. 5 B and S9). In addition, at the time point of I_in decrease, cellular volume suddenly increases, and the cytoplasmically expressed fluorescent protein mCherry-mKate2 hybrid (referred to as mKate2 for brevity) (66) starts leaking out of the cell (Fig. 5 C and Video S4).

Figure 5.

(A) Average traces of ThT fluorescence (in blue) and motor speed (in black) simultaneously measured in five individual cells (individual cell traces are given in Fig. S6). The shaded areas show the standard deviation, and the motor speed has been normalized to the initial value as described in Materials and Methods. (B) ThT (y axes) and PI (color map) equilibration profile in LB are shown. 25 individual traces are given. (C) Average of ThT (in blue), mKate2 (in red) fluorescence, and cell area (in green) simultaneously measured in 12 individual cells from three independent experiments is shown. The shaded areas show the standard deviation. (D) Equilibration profile of 1 μM ThT in LB is shown. Eight single-cell traces and average trace are given in cyan and blue, respectively. (E) Equilibration profile of 10 μM ThT in LB in the absence (gray shaded area) and presence of epifluorescent illumination (light area) is shown. The dye was flowed in the flow cell for the whole length of the experiment, and imaging conditions in the light area were the same as in Figs. 3 and 5D. 44 cells from eight independent experiments are given. To see this figure in color, go online.

Video S4. Characteristic Single-Cell Volume Change and Cytoplasmic Marker Loss during ThT Equilibration

Dynamics of cytoplasmic mKate2 fluorescent signal (right) during ThT equilibration (left) from the experiment in Fig. 5 C. Images are taken every minute.

These results are in contradiction with our estimate of dye working concentration, and we wondered, based on Fig. 2 C, whether the changes in P_Dye could be the explanation. The cell culture in Fig. 3 was briefly exposed to light at 600 nm every 7.5 min, whereas cells in our flow cell were exposed to light of 435 nm every minute for the purpose of imaging the ThT dye. We have previously reported loss of V_m and PMF due to light-induced decrease of E. coli membrane’s resistance at effective powers higher than ∼17 mW/cm² and for a combination of 395 and 475 nm wavelengths (26). Light damage is wavelength-dependent (36), and we therefore characterized the light damage caused by our imaging conditions, i.e., 435 nm wavelength and effective power of P_eff ∼ 11 mW/cm². Fig. S10 shows a decrease in BFMs’ speed and thus the cell’s PMF. However, the PMF is not fully lost, indicating that the loss of PMF observed in Fig. 5 A is likely caused by the combination of light-induced increase in P_Dye and exposure to 10 μM ThT.

To prove it, we exposed the bacteria to 10 μM ThT in LB as before, but this time, we observed the cells under brightfield illumination for 45 min, at which point we turned on the 435 nm light used for epifluorescence imaging of ThT. Fig. 5 E shows that after 45 min, cells not exposed to 435 nm light did not take up ThT. This is in contrast to Fig. 3 D, in which cells exposed to 435 nm light from the start took up ThT in the first 30 min.

Actively changing membrane permeability has been used to facilitate loading of Nernstian sensors (21), and Fig. 5 E shows that this can change the dye into an actuator because it can influence V_m. Our mathematical model predicts that if a given concentration of the dye is lowering V_m, an even lower concentration of the dye will result in a change of τ_eq (Fig. S5). Because the dye equilibration profiles in Fig. 3 D do not follow the theoretically expected curve (Fig. 1), we cannot calculate τ_eq. However, from Fig. 5 A, we know that initial rise in the dye intensity is still driven by V_m; therefore, we can qualitatively compare the timing of the initial rise at different [Dye]_out. Fig. 5 D shows that for 1 μM concentration of ThT, the rise in I_in happens later in time than at [Dye]_out = 10 μM (Fig. 3 D). Thus, 10 μM ThT in LB under 435 nm light affects V_m. Assessing the suitability of the dye working concentration by confirming that a lower dye concentration does not alter τ_eq is a suitable additional control we propose, especially if P_Dye is being altered as part of the experiments.

We note that in our plate reader experiments (Fig. 2), we observed the effect of the dye (above 10 μM) on cell growth, whereas in our microscopy experiments, in the absence of light damage, ThT does not permeate WT cells. We thus wanted to confirm that at higher concentrations, ThT permeates the cells on a longer timescale, and for this purpose, we imaged the cells from the wells at representative ThT concentrations in MM9 + glucose (10, 50, and 100 μM) and MM9 + glycerol (10 μM). As expected, we found that on a longer timescale in MM9 glucose, cell brightness increases with the extracellular dye concentration, and that in MM9 + glycerol, at 10 μM, ThT signal from the cells is overall greater than in glucose (Fig. S11).

Having identified the mechanisms behind the shape of the ThT loading curve we observed in Fig. 3, we should now be able to reproduce it with our mathematical model. We focus only on the part of the equilibration curve that is V_m-driven, i.e., up to the point V_m drops to zero (as indicated in Fig. 5 A). Beyond, the increase in I_in is not driven by a Nernstian equation and thus not accounted for in our model. Based on Fig. 5 A, we assume that V_m decays exponentially immediately after addition of the dye (26): $V_m\left(t\right)=V_{m,0}\times 2^{t/t_{1/2}}$, where t_1/2 is the time at which voltage is half that of V_m,0. The dynamics of dye entry are then modeled by Eyring’s rate law, Eq. 9, taking into account V_m,0, t_1/2, and P_Dye (see Supporting Materials and Methods for further details on the model). Fig. S12 shows that the model reproduces the peak in [Dye]_in observed in Fig. 3. Immediately upon addition, the positively charged dye moves inwards because its extracellular concentration is higher than the intracellular and the cell is negatively polarized. Thus, [Dye]_in increases and becomes greater than [Dye]_out until the electrochemical potential reaches ΔG_Dye = 0 (at the peak). As the V_m decays and because [Dye]_in > [Dye]_out, the dye now starts moving outwards, and its intracellular concentration decreases. In Video S1. E. coli Growing in LB Medium in Our Flow Cell before Addition of the ThT Dye, Video S3. Equilibration of ThT in LB, [Dye]_in decreases to zero, whereas experimental I_in starts increasing after the peak and never reaches zero. The difference is explained by the fact that cells with high I_in after the peak are no longer viable (Fig. 5, A and B), and thus, the behavior of the dye is no longer governed with the Nernstian equation. In Fig. S12, E and F, we indicate the part of the experimental equilibration curve to which our model is applicable.

The time at which the peak occurs, as well as its intensity, depends on P_Dye as follows: 1) the time of the peak decreases with increasing P_Dye and increases with increasing t_1/2, and 2) the intensity of the peak increases with increasing P_Dye and t_1/2 (Fig. S9, C and D). The dye still equilibrates according to Eq. 2; however, this is achieved transiently at the time of the peak, which is the time point at which V_m can be calculated from Eq. 2. Because V_m varies during the course of the experiment, the V_m measured at the peak is not equal to V_m,0. Nonetheless, if we measure V_m(t)/V_m,0 as well as calculate the V_m at the time of the peak using Eq. 2, in principle, we can estimate V_m,0 as well. Therefore, charged dyes can be used to estimate initial V_m even in conditions in which they act as actuators and collapse V_m, if the dynamical shape of the V_m loss is known.

Discussion

Nernstian probes are a popular choice for estimating bacterial V_m because the concentration of the free dye directly depends on V_m according to the Nernst equation. Despite the wide usage, the probes are often not sufficiently calibrated before use in different conditions. Here, we present a mathematical model that shows tradeoffs between requirements imposed on the dye: sufficient signal/noise ratio, sufficiently short dye equilibration time, and minimal effect on the cells’ physiology. Based on the model results, we characterize in E. coli the fluorescent dye ThT, recently used in B. subtilis (25). Finally, we propose a general workflow for the characterization of Nernstian dye candidates (Fig. 6).

Results of our model show that the dye working concentration that does not affect V_m is context-dependent, e.g., it can be different for different external media. The model also predicts that if ΔV_m = 0 at a chosen dye working concentration, lower dye concentrations should leave τ_eq unchanged. The finding offers a simple test to confirm the suitability of the chosen dye working concentration.

For the case of E. coli and ThT as the candidate Nernstian dye, we experimentally find that the dye equilibration profile does not follow the theoretical expectation (Fig. 1). We test two possible explanations for the shape of the equilibration profile we observe in Fig. 2: 1) involvement of active efflux pumps and 2) significant V_m decrease during ThT equilibration. Although we find that the strain lacking one of the efflux pumps shows a different equilibration profile when compared to the WT, it still does not behave as theoretically expected. Instead, we find that the permeability of E. coli’s membrane to ThT is low. Permeabilizing the membrane by light of relatively short wavelengths to facilitate sufficient ThT entrance into the cell causes significant V_m reduction, which subsequently results in cell death. The finding is consistent with previous results that show that E. coli’s membrane needs to be permeabilized with EDTA to achieve experimentally reasonable loading times of tetramethyl rhodamine methyl ester (TMRM) dye (21). EDTA is thought to increase the permeability of E. coli by chelating the metal ions that cross-link the lipopolysaccharide (LPS) (67). Some evidence also suggests that it might interact directly with lipids destabilizing the membrane (68). The equilibration profiles we observe for the efflux pump mutant strain can be explained either by the change in membrane permeability between the two strains or by active efflux.

We summarize the results from our model and experiments, as well as previous work on Nernstian V_m dye usage, in a workflow (Fig. 6). We believe it is sufficiently simple and general to provide a common standard for benchmarking the cationic dye behavior and thus improve the robustness of V_m measurements. It starts with a protocol to identify the dye working concentration (Fig. 6, steps 1–4). This is first carried out by assaying the effect of the dye on bacterial growth, as we did in Fig. 3, A–C, because it is a physiological variable that is easy to measure and it will likely be affected by changes in V_m (step 1). In step 1, we identify the MNC as the maximum dye concentration that does not affect growth. We use it to measure the dye equilibration profile in step 2. This allows us not only to make sure that with the MNC, we are obtaining the expected shape of the equilibration profile, but also that the MNC gives sufficiently high intracellular signal. Next, we further test, as we did by comparing Figs. 3 D and 5 D, whether the MNC is affecting V_m by checking that τ_eq for the MNC and a chosen concentration below it stay the same (step 3). If the below-MNC concentration and the MNC do not show the same τ_eq, steps 1–3 need to be repeated for progressively lower dye concentrations until either the signal from the intracellular dye becomes too low or τ_eq does not differ between the two tested concentrations. In the second case, the higher concentration can be considered suitable. The next step in the workflow is more commonly performed when assaying V_m dyes (16,21), where cells’ V_m is changed in a known way, e.g., by exposing the cells to ionophores and observing V_m collapse (step 5). Finally, quantifying V_m requires estimation of [Dye]_in from I_in measurements, which can be done by distinguishing the free from the bound dye and by taking into account that the obtained I_in is a convolution of [Dye]_in and the microscope point spread function (21,23) (step 6). Because the dye’s behavior is context-dependent, steps 1–6 should be repeated for each new experimental condition. Furthermore, if the dye fails any of the steps in the proposed workflow, it is not suitable for use as a Nernstian sensor. For example, ThT for the case of E. coli failed in steps 2 and 3, which is why we did not need to perform subsequent steps of the workflow.

Author Contributions

L.M., G.T., C.-J.L., F.B., and T.P. conceived the experiments and the computational work. L.M., T.T., Y.P., and Y.L. performed experiments. G.T. performed computational work. L.M. analyzed experimental data. L.M., G.T., C.-J.L., F.B., and T.P. interpreted the results and wrote the manuscript.

Editor: Amy Palmer.