Irregular Chromatin: Packing Density, Fiber Width, and Occurrence of Heterogeneous Clusters

Abstract

How chromatin is folded on the length scale of a gene is an open question. Recent experiments have suggested that, in vivo, chromatin is folded in an irregular manner and not as an ordered fiber with a width of 30 nm that is expected from theories of higher order packaging. Using computational methods, we examine how the interplay between DNA-bending nonhistone proteins, histone tails, intrachromatin electrostatic, and other interactions decide the nature of the packaging of chromatin. We show that although the DNA-bending nonhistone proteins make the chromatin irregular, they may not alter the packing density and size of the fiber. We find that the length of the interacting region and intrachromatin electrostatic interactions influence the packing density, clustering of nucleosomes, and the width of the chromatin fiber. Our results suggest that the heterogeneity in the interaction pattern will play an important role in deciding the nature of the packaging of chromatin.

Significance

The genetic code in our cells is stored in a long electrically charged polymer called DNA. In an organism, cells of all types (skin cells, brain cells, etc.) have exactly the same genetic code but function very differently. This functional difference is achieved by packaging parts of DNA differently in different cells. Exactly how DNA is packaged inside living cells so as to achieve this functional diversity is an interesting open question. In this article, we simulate the packaging of DNA into chromatin, accounting for certain facts known from recent experiments. Our work provides a plausible explanation for why chromatin is seen to be organized in an irregular manner as small clusters of different sizes.

Introduction

DNA is a very long polymer that contains the genetic code. Inside biological cells, DNA is not in its bare form; rather, it is folded and packaged with the help of a large number of proteins and chemical groups into a functional structure known as chromatin (1). The purpose of folding DNA into chromatin is not just for the packaging and storage of the polymer but also for regulating the accessibility and reading of the genetic code. How this one-dimensional sequence information is folded and packaged into a three-dimensional (3D) chromatin organization is poorly understood. Research in the last few decades has shown that stretches of DNA are wrapped around a multimer complex of histone proteins, leading to the formation of an array of nucleosomes (2,3). However, exactly how this nucleosomal array is further folded and packaged is an open question (4).

In the packaging of chromatin, the nature of interaction and structural details of nucleosomes are thought to play an important role (5,6). DNA is a negatively charged polymer, whereas histone proteins are predominantly positively charged. In a nucleosome, histone protein subunits (H2A-H2B, H3-H4) have tail-like regions, giving rise to a nucleosome complex that has multiple tails protruding out of the core region (7). Given that these tails are electrostatically charged and that various chemical modifications (e.g., acetylation) can alter the charge density, the histone tails and electrostatic interactions are thought to play crucial roles in higher order packaging of chromatin (8, 9, 10). Apart from the core histones, the linker histone (H1) is also thought to play an important role in chromatin organization. The H1 protein is known to bind between DNA segments that are entering and exiting a nucleosome and thought to stabilize the nucleosome (11, 12, 13, 14, 15).

How a string of nucleosomes, known as 10-nm wide chromatin, gets folded further to form a higher order structure is a question that has not been settled, even after nearly four decades of research (4,16). In vitro reconstitution of chromatin, based on the array of nucleosomes, suggested that the nucleosomes will form a regular zig zag–like structure, with a width of 30 nm (7,17,18). Based on other in vitro experiments, there is also an alternate hypothesis that the chromatin should be solenoid, with a 30-nm width (19,20). Simple polymer physics theories, accounting for certain physical aspects of DNA stiffness and the structure of the nucleosomes, predicted regular 30-nm chromatin organization (21, 22, 23, 24). The extent of the folding of this string of nucleosomes into chromatin is measured by computing the packing density, which is roughly defined as the number of nucleosomes packed in every 11-nm effective length of the chromatin fiber. Analysis of in vitro experimental data and simulation results showed that the packing density of 30-nm chromatin fiber can vary from 6 nucleosomes/11 nm to 12 nucleosomes/11 nm, depending on different conditions (13,14,18, 19, 20,25, 26, 27, 28, 29, 30, 31, 32, 33).

However, most of the recent experiments suggest that, in vivo, chromatin does not have any regular structure (34, 35, 36, 37). Cryo-electron microscopy study on mitotic and interphase cells suggest that the 30-nm fiber is not the basic structure of chromatin in vivo (34, 35, 36). Recent studies with advanced electron microscopy techniques to visualize chromosomes in interphase and mitotic cells suggest that chromatin is folded into an irregular chain having ∼5–24-nm wide structures (38). Super-resolution microscopy studies have shown that nucleosomes form domains with a wide range of diameter, presumably regulated by internucleosomal interactions (39,40). Chromatin conformation capture (Hi-C) experiments suggest that in interphase chromatin is not a homogeneous or a regular structure (41). It is organized into topologically associated domains (TADs (42,43)) and lamina-associated domains (44) that have open (euchromatin) and compact (heterochromatin) domains distributed across the nucleus and have a fractal nature (41,45).

There have been many recent theoretical/computational studies trying to understand the irregular nature of chromatin (10,46, 47, 48). It has been hypothesized that molecular crowding in the cell may lead to the formation of irregular chromatin (35). It has been shown that the variability in linker length and other factors give rise to a polymorphic structure of chromatin (48,49). Our own earlier work suggested that DNA-bending nonhistone protein (NHP) can make chromatin irregular (47).

Even though there is a vast literature on chromatin organization, many important questions remain unanswered. Given that chromatin is irregular on the length scale of genes, the first question is about its compactness. How compact is the irregular chromatin when compared to the regular structures? How does the irregular nature influence the packing density? Given that recent experiments have observed chromatin fibers having a wide range of widths, can we have a theoretical explanation for this heterogeneity in widths? Given that chromatin is heterogeneous in terms of interaction potentials (e.g., spatial variation of histone modifications), how will this affect chromatin configurations? Does the spatial extent/variation in the modification pattern affect the packing density and width?

In this article, we address these questions by performing coarse-grained molecular simulations and studying chromatin organization in 3D. We simulate a polymer model of chromatin having nucleosomes with explicit histone tails, electrostatic interactions, and other intrachromatin interactions. We also account for the spatial variations of the interaction potentials to mimic interaction heterogeneity due to histone modification patterns. We show how DNA-bending NHPs and heterogeneous interactions among nucleosome particles affect the packaging of irregular chromatin. Our work suggests how chromatin could achieve <30-nm width, even when it is in a packaged heterochromatin state.

Materials and Methods

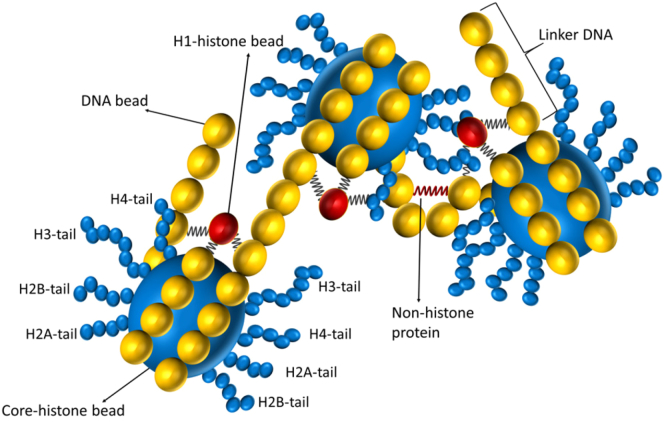
We present a coarse-grained model in which chromatin is modeled as a set of bead-spring chains that have five major parts, namely 1) the DNA polymer chain, 2) the core histone, 3) explicit histone tails, 4) the linker histone, and 5) the DNA-bending NHP (see Fig. 1).

Figure 1.

Schematic diagram describing the model. DNA is modeled as a polymer made of type 1 beads (yellow) with a diameter of 3.4 nm. 14 DNA beads are wrapped around the core histone bead (type 2, big blue bead, 5.25 nm in diameter). Histone tails are modeled as flexible bead-spring polymer chains in which each histone-tail bead (type 3, small blue bead) is 1.56 nm in diameter and have the following lengths: tail 1 (H2A) = 4 beads, tail 2 (H2B) = 5 beads, tail 3 (H3) = 8 beads, and tail 4 (H4) = 5 beads. H1 histone (red bead, type 4) is connected to three DNA beads—the entry bead, exit bead, and the central bead of the DNA wrapped around the core histone bead. DNA-bending NHP is modeled as a spring (red) connecting two beads in the linker region.

The DNA polymer is modeled as a bead-spring chain that has N_d beads connected by N_d − 1 springs (Fig. 1). A nucleosome is modeled as one big bead representing the core histone octamer on which 14 DNA beads are wrapped around in 1.75 turns. To explicitly model histone tails, we introduce eight small flexible polymers emanating from the core histone as shown in Fig. 1. The DNA polymer bead has a diameter of 3.4 nm, whereas the octamer core histone bead has a diameter of 5.25 nm. The details of each histone-tail polymer length is as follows: H2A tail = 6.2 nm (four beads), H2B tail = 7.8 nm (five beads), H3 tail = 12.6 nm (eight beads), and H4 tail = 7.8 nm (five beads) (23). We fix the first bead of each histone tail on the core histone bead such that the first bead and the core histone bead behave like a rigid body. We introduce the linker histone H1 as a separate bead (diameter = 2.9 nm (50)), which interacts via a harmonic spring with the two DNA beads entering and exiting the nucleosome as well as with the nucleosome. The H1 bead constrains the DNA tangent vectors entering and exiting the nucleosomes, ensuring known structural features of nucleosomes.

Now, we describe the energetics of the chromatin system that we consider. Throughout this article, we will use notation with subscript (α,β) ∈ {d,h,t,l}, where d,h,t,l stand for the DNA bead, histone bead, tail bead, and linker bead, respectively. For example, the diameter of a DNA bead will be represented by σ_d, whereas that of the tail bead will be σ_t, and so on. All beads in the system are connected with their respective neighbors using a harmonic potential given by the general formula as follows:

$$U^{spring}=\sum _{\alpha ,\beta }\sum _{i,j}\frac{k_{\left(\alpha ,\beta \right)}^{spring}}{2}{\left[\left|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}\right|-\left(\frac{{\sigma }_{\alpha }+{\sigma }_{\beta }}{2}\right)\right]}^2,$$ (1)

where ${\mathbf{r}}_{\alpha }^{\left(i\right)}$ and ${\mathbf{r}}_{\beta }^{\left(j\right)}$ are position vectors of i^th and j^th beads of types α and β; $k_{\left(\alpha ,\beta \right)}^{spring}$ is the corresponding spring constant. 1) For DNA-DNA bead interaction, α = d, β = d, j = i + 1 and i, ranges from 1 to N_d − 1. 2) For histone core-DNA interaction, α = d, β = h, i ranges from 1 to N_h (where N_h is the total number of nucleosomes), and j takes 14 values, for each i, representing the identity of the corresponding histone-bound DNA beads. 3) For tail-tail bead interaction, α = t, β = t, j = i + 1, and i = N_t − 1, where N_t is number of the tail bead. 4) For DNA and linker histone interaction, α = l, β = d, i ranges from 1 to N_l (where N_l is total number of linker histones), and j stands for three DNA bead positions at the entry site, exit site, and the center (where the DNA bead is wrapped around the histone) along the dyad axis. The interaction energy of the NHPs is also calculated using Eq. 1. A NHP binds at any linker region between two linker DNA beads α and β. The energy cost here represents the constraint that the local DNA is bent because of the presence of NHPs. If there are ν NHPs, each having a size spanning three beads, i is the count of the NHPs varying from 1 to ν, j = i + 3, and ν/N_h is called protein density. The total spring energy (U^spring) is obtained by summing over with appropriate nearest neighbor bead pairs α,β. Apart from the nearest neighbor spring interaction described above, any two beads interact via the standard Lennard-Jones (LJ) potential (U^LJ) such that $U^{LJ}=\sum _{\alpha ,\beta }\sum _{i,j}4{\mathrm{\epsilon }}_{\left(\alpha ,\beta \right)}\left[\left({\left({\sigma }_{\alpha }+{\sigma }_{\beta }/2\right)}^{12}/{\left(|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|\right)}^{12}\right)-\left({\left({\sigma }_{\alpha }+{\sigma }_{\beta }/2\right)}^6/{\left(|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|\right)}^6\right)\right],$ when $|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|<2.5\left(\left({\sigma }_{\alpha }+{\sigma }_{\beta }\right)/2\right)$, and U^LJ = 0 otherwise. That is, the energy is zero when $|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|\ge 2.5\left(\left({\sigma }_{\alpha }+{\sigma }_{\beta }\right)/2\right)$. Here, ε_(α,β) is the corresponding potential well depth. All beads interact with each other using screened electrostatic potential. We use the standard Debye-Huckel potential and compute this energy of chromatin (23) as follows: $U^{electro}=\frac{C}{{\mathrm{\epsilon }}^w}\sum _{\alpha ,\beta }\sum _{i,j}\left[\left(q_{\alpha }{q}_{\beta }/\left(|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|\right)\right){\text{e}}^{-\kappa \left(|{\mathbf{r}}_{\alpha }^{\left(i\right)}-{\mathbf{r}}_{\beta }^{\left(j\right)}|\right)}\right],$ where q_α and q_β are effective charges of beads, κ is the inverse of the Debye length (κ = 1 nm⁻¹), ε^w is the dielectric constant (set to 80, assuming a water-like medium), and C is a constant as per the screened Coulomb electrostatic potential energy formula (51). Total charges on wrapped DNA are estimated as −296e (52). 14 DNA beads wrap around the core histone, so charge value for one DNA bead q_d = −296/14 = −21.14e. The core histone bead (without tails) has a charge of q_h = 52e (52). We take charge on each histone-tail bead q_t = 2e such that the total charge on one nucleosome (wrap DNA + core histone + histone tails) is maintained as −156e (52). Charges for histone H1 are taken as q_l = 13.88e (23).

The semiflexible nature of the DNA chain is introduced through a bending potential (U^bend) for DNA beads as follows: $U^{bend}=\frac{k^{bend}}{{\sigma }_d}{\sum }_{i=1}^{N_d-1}\left(1-\text{cos}{\theta }^{\left(i\right)}\right)$, where k^bend is the bending stiffness of DNA, and θ⁽ⁱ⁾ is the angle between two nearby bonds in the bead-spring model.

The total energy of the chromatin in this model is given by U^tot = U^spring + U^electro + U^LJ + U^bend. This system was simulated using molecular dynamics simulation package LAMMPS in which the simulator solves Newton’s equations with viscous force and a Langevin thermostat ensuring an NVT ensemble with temperature T = 300 K (53). We obtained chromatin configurations (3D positions of all beads) as a function of time. Most of the parameters used in simulations are taken from known experimental data or earlier computational studies (23,50,52,54). Apart from the bead sizes and charges mentioned earlier, the spring constants are assumed to have a large value ($k_{\left(\alpha ,\beta \right)}^{spring}=k^{spring}=$ 0.17 kcal/mol/Å) such that the bonds are stable and do not fluctuate a lot. We used an integration time step of Δt = 359.5 fs and the damping time for the thermostat of 0.035 ns. We run the simulations for a time (0.04 ms) that is much longer than the time it takes for the system to reach a steady state that has constant mean energy and radius of gyration. The details about the parameters are given in the Table S1.

Results and Discussion

We present below the results from our study, using computer simulations, in which we examined how the chromatin organization alters as we vary different interaction potential energies (electrostatic, LJ), DNA-bending due to NHPs, and the length of the interacting domain. We will discuss how heterogeneity in interaction potential energies will lead to heterogeneous chromatin configurations.

Role of different interactions in chromatin packaging

To mimic effects due to changes in various plausible interactions, we simulated the system, varying the parameters associated with two potential energies—electrostatic interaction energy and LJ interaction energy.

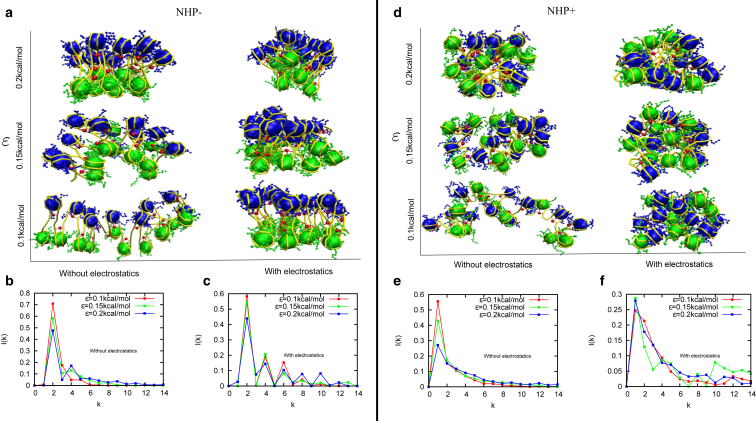
First, we present results from a simulation of a chromatin made of 20 nucleosomes, accounting for histone tails, and H1 linker histones, but not considering the DNA-bending NHPs. 3D configurations of such a chromatin for different values of interaction potential strengths are shown in Fig. 2 a. In the left panel within Fig. 2 a, we have chromatin for different LJ interaction strengths but with no electrostatic interactions. In the right panel, chromatin configurations for exactly the same condition but with electrostatic interactions are shown. When electrostatic interaction is present, the chromatin is more compact. The positive charges of the histone tails attract with negatively charged parts of the chromatin. This leads to a compact structure.

Figure 2.

Snapshots of chromatin configurations and the corresponding contact probabilities between k^th neighbor nucleosomes (I(k)) in the absence (NHP−) and presence (NHP+) of DNA-bending nonhistone proteins (NHPs) that bind along linker DNA regions. The results are presented for four cases, as follows: case 1: simulations with no NHPs and no electrostatic interactions (left column of (a), and (b)); case 2: no NHPs but with electrostatic interactions (right column of (a), and (c)); case 3: with NHPs and no electrostatic interactions (left column of (d), and (e)); case 4: with NHPs and with electrostatic interactions (right column of (d), and (f)). All the results are presented for three different strengths of LJ (ɛ) interaction potentials (see text for details).

Based on nucleosome structure data, we know that each tail bead in our coarse-grained model has one or more sites that can be acetylated. Acetylation will reduce electrostatic interaction in the tails. Our “without electrostatics” results are comparable to configurations of a chromatin with highly acetylated nucleosomes; we get open structures when there is no electrostatic interactions and relatively more compact structures with electrostatic interactions analogous to chromatin with acetylated and deacetylated nucleosomes. This is consistent with earlier findings (5,48).

If we go along the column from bottom to top (Fig. 2 a), we find chromatin organization for different values of ε (LJ interaction strength). For small values of ε, chromatin is more open, whereas for larger values of LJ interaction strengths, the chromatin is compact. Here, we introduced the attractive part of the U^LJ to mimic different types of interactions mediated by various proteins (like HP1) or other interactions that may bring together nucleosomes (55, 56, 57). The repulsive part of LJ mimics steric hindrance.

We then computed I(k)—the probability that a nucleosome is in contact with its k^th neighbor—from the above-discussed 3D chromatin configurations (see Supporting Materials and Methods and Fig. 2, b and c). We find that, irrespective of electrostatic interactions and the strength of the LJ interactions, the most prominent peak is at k = 2. Note that when we change the strength of the LJ, in the absence of electrostatics, the height of the prominent peak varies. This is indeed related to the compact packaging of the zig zag structure. In the open form (low LJ), the zig zag is more loose; hence, only next-neighbor nucleosomes (k = 2) mainly interact. Far away nucleosomes (k > 2) are not contributing to I(k). However, for large LJ, the chromatin is compact, and far away nucleosomes have a higher chance of being close; hence, I(k) values for k > 2 are larger. Because total probability is 1$\left(\sum _{k}I\left(k\right)=1\right)$, this reduces the peak value of I(2) for large LJ values. Similarly, when electrostatic interactions are present, the compactness of the chromatin is reflected in higher k > 2 peaks.

Even compact chromatin structures are irregular in the presence of DNA-bending NHPs

Here, we investigate the interplay between DNA-bending due to NHPs and electrostatic/LJ interactions in deciding the 3D folding of chromatin. We did simulations similar to the ones described earlier but introduced NHPs that bind in the linker region and bend DNA, assuming an NHP density of 0.5 per linker region. Typical snapshots of chromatin 3D configurations are shown in Fig. 2 d with (right panel) and without (left panel) electrostatic interactions; also see the LJ variation along the vertical axis. Without electrostatics, for small LJ, the chromatin is in open configuration. As we increase the LJ interaction (high ɛ), the chromatin becomes more compact. When electrostatic interactions were switched on (right panel), we got relatively compact structures for all values of ɛ.

The important point to note is that in this figure (Fig. 2 d), as opposed to the earlier case in Fig. 2 a, different color beads (odd and even numbered beads with blue and green colors, respectively) are well mixed, suggesting an irregular organization of chromatin. The presence of NHPs have created an irregular chromatin even with electrostatic interactions and high LJ interactions.

Quantification of the 3D structure using contact probability I(k) shows that, in the presence of NHPs, irrespective of electrostatic interactions and the strength of the LJ interactions, the most prominent peak is at k = 1 (Fig. 2 e). It is interesting to see that even for the high compact form of chromatin, structures are irregular in the presence of NHPs. Note that when we change the strength of the LJ, with no electrostatic interaction, the height of the prominent peak (peak at k = 1) varies. This is indeed related to the compact packaging of the irregular structure. In the open form (low LJ), the irregular structure is more loose; hence, only the neighbor nucleosomes (k = 1) mainly interact. Far away nucleosomes (k > 2) are contributing relatively less to I(k). However, for large LJ, the chromatin is compact, and far away nucleosomes have a higher chance of being close; hence, I(k) values for k > 1 are higher. Because total probability is 1 $\left(\sum _{k}I\left(k\right)=1\right)$, this reduces the peak value of I(1) for large LJ values. In Fig. 2 f, with electrostatic interactions, the structure is highly compact and irregular; hence, the I(k) peaks are roughly the same for all values of LJ interaction strengths.

Regular versus irregular chromatin: packing density, fiber width, and mean cluster size

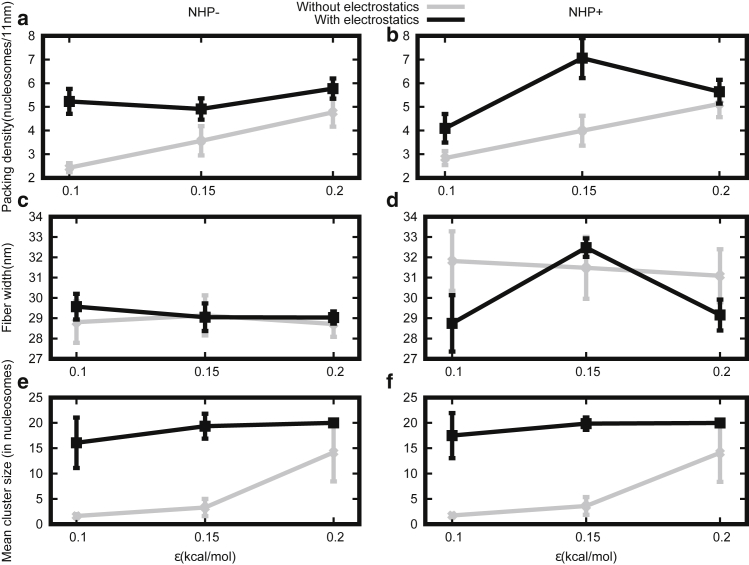
We computed the packing density to know the compaction of different chromatin structures for the discussed earlier cases. Packing density measures roughly the number of nucleosomes packed in every 11 nm of effective chromatin length (30) (see Fig. S1). First, we consider chromatin organization with no NHPs; these are regular ordered chromatin structures as seen in the earlier results (Fig. 2 a). In the absence of NHPs and in the presence of electrostatic interactions, the packing density is ∼6 nucleosomes/11 nm (see Fig. 3 a, black curve) as expected for zig zag or regular chromatin (13,18, 19, 20,25, 26, 27, 28). The results show that the chromatin is highly packed, even for a very small LJ interaction strength (ε = 0.1 kcal/mol), and remains nearly the same for larger LJ interaction strengths (ε = 0.2 kcal/mol). In the absence of electrostatic interactions (Fig. 3 a, gray curve), the packing density is much smaller (∼2–3 nucleosomes/11 nm) than the case with electrostatic interactions, suggesting that the electrostatics plays an important role in packaging. On increasing the strength of the LJ interactions from ε = 0.1 to ε = 0.2 kcal/mol, we found that the packing density increased slightly but remained smaller than that of the chromatin with electrostatic interactions.

Figure 3.

Packing density, fiber width, and mean cluster size are plotted for different LJ strengths (ε), in the absence of NHPs (NHP−, left side) and the presence of NHPs (NHP+, right side). (a and b) Without electrostatic interaction, the packing density increases with ɛ (gray curves). With electrostatic interaction, packing density is ∼6 nucleosomes/11 nm (black curve). (c and d) Chromatin fiber diameter (width) for different parameters is shown. With (black curve) and without (gray curve) electrostatic interaction, the fiber diameter is ∼30 nm (constant) for all cases. (e and f) Without electrostatic interaction, mean cluster size increases on increasing the LJ (ε) parameter (gray curve), but with electrostatic interaction, it remains constant (black curve). In all the subfigures, the vertical bars represent SD.

With DNA-bending NHPs, we got a packing density of 4–7 nucleosomes/11 nm in the presence of electrostatic interactions (Fig. 3 b). This implies that even though our models with NHPs do not give rise to regular/ordered structure, the packing/compaction remains similar to that of what is observed in in vitro experiments. Our theory predicts that DNA-bending NHPs will make chromatin irregular but will have similar compaction as observed in the case without NHPs (13,18, 19, 20,25, 26, 27, 28). The findings for the case with no electrostatic interactions are also similar to the case without NHPs—a lower packing density that increases as a function of LJ interaction strengths. We also computed a packing density in a different way to obtain DNA length in a volume having a unit of bp/nm³. As described in the Supporting Materials and Methods, we divided the total DNA length with the volume of chromatin—the resulting density may be called DNA density. The results for this density are shown in Fig. S2. The range of the widths we obtain are ∼0.04–0.16 bp/nm³, which is comparable with the numbers reported in experiments (58,59) (see Fig. S2, a and b).

In Fig. 3, c and d, we present our results for fiber width in the absence and presence of NHPs, with (black curve) and without (gray curve) electrostatics. Interestingly, for all the cases, the width is ∼30 nm. This width is computed according to a simple definition based on polymer physics ideas (see Supporting Materials and Methods for details). We know (from Fig. 2 b) that in the presence of NHPs, chromatin is irregular; we also know that in the absence of electrostatic interactions, the chromatin is relatively more open. However, in all these cases, the width is ∼30 nm. This shows that the width as a quantity, as defined here, cannot easily distinguish between regular and irregular and open and compact chromatin. However, note that the packing density in Fig. 3, a and b could distinguish between open and compact chromatins (gray and black curves). We also did simulations restricting the LJ interactions only between nucleosomes and computed packing density and width. The results are shown in Fig. S3.

Because both compact and open structures are seen to have similar width, to improve the quantification, we computed how nucleosomes are clustered near one another. Any two nucleosomes that are closer than 2.5 times its diameter (2.5σ_h) are considered to be in the same cluster (see Supporting Materials and Methods). We find that the open chromatin is not just one cluster but many small clusters with a few nucleosomes in each—see Fig. 3, e and f (gray curve) in which the mean cluster size is small (∼2–5), and hence, the mean cluster number is large (4–10). On the other hand, the compact chromatin is nearly one cluster—∼20 nucleosomes are part of the same cluster (see Fig. 3, e and f, black curve). This suggests that open chromatin, even though it appears like a loose zig zag visually, may not appear as a single entity (punctate) in experiments (like electron microscopy) in which the density and cluster size can affect the measurement.

Role of chromatin length in packing density and fiber width

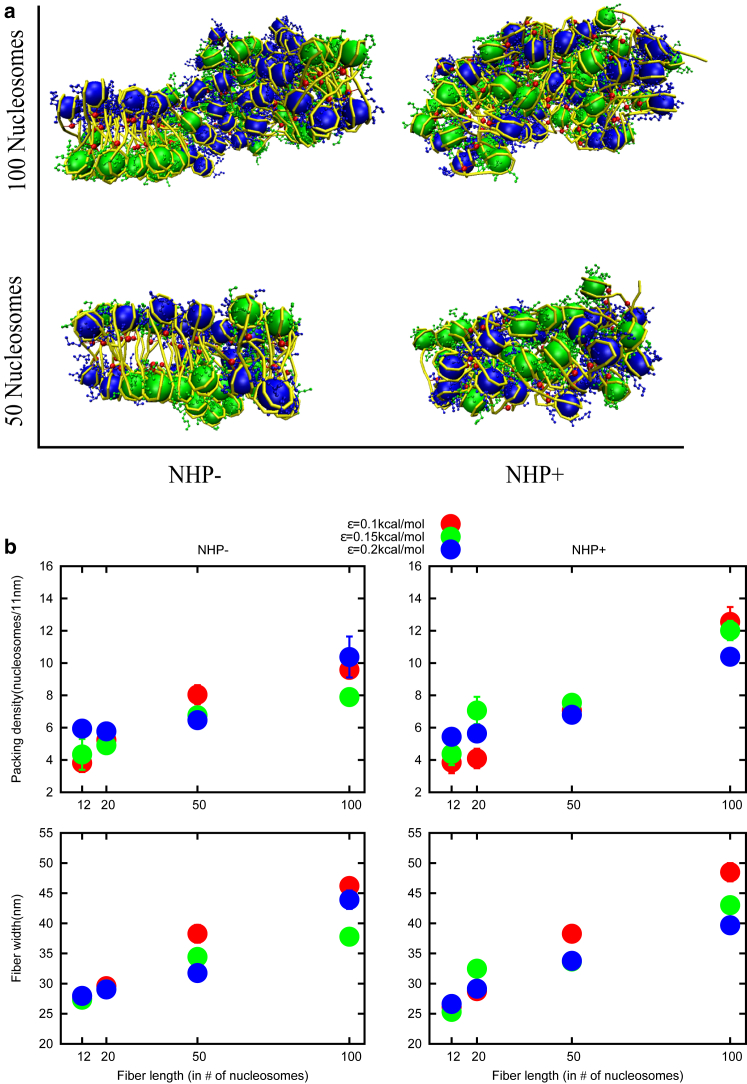
So far, we studied packing density, fiber width, and cluster size for a chromatin with 20 nucleosomes. We found that even though the NHPs make the chromatin irregular, a compact chromatin fiber has a packing density of ∼6 nucleosomes/11 nm and a width of ∼30 nm. How do packing density, width of the fiber, and other parameters vary as we change the length of the polymer? In this section, we simulated chromatin fibers of many different lengths, starting with chromatin with 12 nucleosomes going up to 100 nucleosomes. In Fig. 4 a, snapshots of the chromatin structure for polymers with 50 nucleosomes and 100 nucleosomes are shown in the absence and presence of NHPs. Packing densities and fiber widths for different lengths (12, 20, 50, and 100 nucleosomes) are shown in Fig. 4 b. In the absence (left panel) and presence (right panel) of NHPs, packing densities and fiber widths increase when increasing the polymer length from 12 nucleosomes to 100 nucleosomes. The longer the polymer, the more the width and higher the packing density. For polymers with 20 or more nucleosomes, the width is 30 nm or above; the packing density is above 6 nucleosomes per 11 nm. This result suggests that if we pack chromatin, even in an irregular manner, with high compaction, one will get structures having a width of 30 nm or more. We have also computed cluster size as a function of length, leading to similar conclusions (see Fig. S4).

Figure 4.

(a) Snapshots of simulation results of 50 nucleosomes and 100 nucleosomes in the absence and presence of NHPs (left to right) for ε = 0.15. Neighboring nucleosomes (odd, even) are shown in different colors so that the regular/irregular organization is more visible to the eye. (b) Shown is the packing density and fiber width on varying chromatin fiber length in the absence and presence of NHPs for different LJ interaction strengths (ε). Packing densities and fiber widths increase as we increase the chromatin length. Colors red, green, and blue represent different LJ interaction strengths ε = 0.1, 0.15, and 0.2 kcal/mol, respectively.

We also examined how interactions would affect the organization of the 100-nucleosomes chromatin. To test this, we varied the electrostatic parameter (κ), representing change in electrostatic interactions, and LJ attraction parameter ɛ. Interestingly, for certain values of these parameters, we obtained globular conformations showing interdigitated chromatin as suggested in recent articles (60) (see Fig. S5, a and b).

Long chromatin: emergence of multiscale nature in chromatin packaging

Chromatin is complex because of its multiscale nature. The interactions and organization at the nucleosome level will decide its higher order folding properties at the scale of a gene or a few genes. Whereas some set of experiments probe nucleosome-scale properties, some other set of experiments (Hi-C, fluorescence in situ hybridization, microscopy, etc.) probe the behavior of chromatin in the length scale of a few genes or the whole chromatin (40,61, 62, 63). It requires a good model and theoretical investigation to reconcile and understand experimentally seen properties at the nucleosome length scale to the experimental features observed in the length scale of genes (64). Here, we have a simulation of 100 nucleosomes, with many of the important interactions (electrostatic, internucleosome interactions), right physics at the nucleosome level (DNA entry-exit angles), and presence of important factors such as DNA-bending proteins. Having put together all these, we investigate the properties that are emerging when quantities relevant to Hi-C experiments are measured.

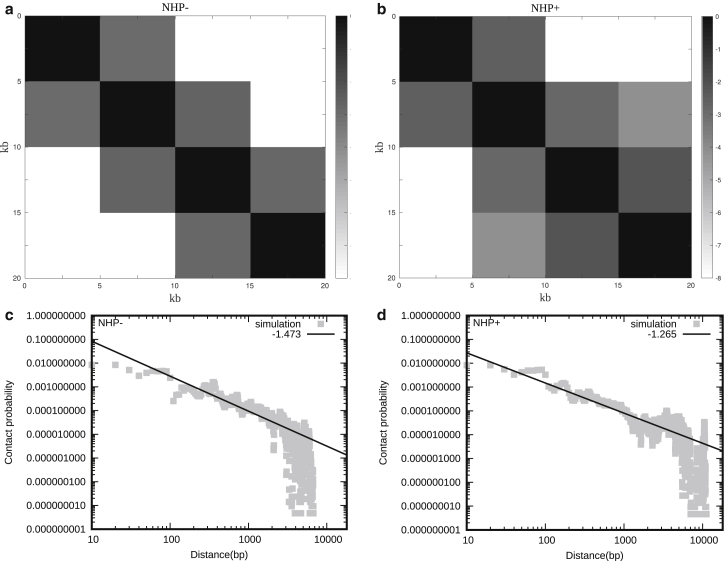
To compare our model (100 nucleosomes in Fig. 4 a) with Hi-C experiments (62,63), we computed the contact map with the probability of contact (P_ij) between any two DNA segments i and j in 5-kb bins (see Fig. 5, a and b). Interestingly, we find TAD-like structures (contact domains) emerging; in the absence of NHP, the TAD-like interaction squares are too regular and homogeneous (squares having a size of 2 × 2) (see Fig. 5 a indicating a regular chromatin assembly). Each domain interact with its neighbor domain only. This is the Hi-C map representing a population of configurations, as shown in Fig. 4 a (top left) (NHP−). The configuration there is like a stiff fiber and does not bend/fold further in the length scale of ∼20 kb (100 nucleosomes). However, in the presence of DNA-bending NHPs, bigger TAD-like domains emerge; first, there is a 3 × 3 square formed, and, for example, the second segment (5–10-kb segment) is interacting with the fourth segment (15–20 kb segment). This could be a consequence DNA-bending due to NHPs. We also have heterogeneous domains—domains of sizes 2 × 2 and 3 × 3 in this example. This could be a result of the local irregular nature. This NHP + results are closer to Hi-C contact maps (62,63) in the sense that here too we have the emergence of domains of different sizes. To understand the nature of packaging further, we computed contact probability (P(s)) as a function of contour distance s (distance along the DNA backbone). This shows a power-law decay (Fig. 5, c and d) with exponents similar to what is reported in the literature (41,65). In the absence of NHP (NHP−), contact probability is fitted with P(s)∼s^−1.473, and in the presence of NHP (NHP+), contact probability is fitted with P(s)∼s^−1.265. As is well known in the literature, such power laws indicate the fractal nature and the nature of the self-organization of chromatin (41). Recent studies have known that the power law in chromatin organization does not have a unique exponent; rather, it is varying around −1 to −1.5 (66,67). We also computed the contact probability for different electrostatic screening parameters (κ) and got similar results (see Fig. S5, c and d).

Figure 5.

(a and b) Contact maps (P_ij) from our simulations, between different 5-kb segments (bins), in the absence (NHP−) and presence of NHP (NHP+). The color scheme varies from black to white, representing high to low contact counts (log(P_ij)). (c and d) Shown is contact probability as a function of contour distance (distance along the DNA backbone) in the absence and presence of NHP, calculated from the simulations (gray curve). The black line is a guide to the eye indicating power-law behavior, suggesting the fractal nature of the self-organization.

Our results also suggest that simple self-organization can lead to TAD-like structures (contact domains). This may be very useful in the context of many new results emerging from different laboratories, indicating that perturbation of various looping factors may not majorly affect gene expression (68,69). Our results point to a plausible scenario in which self-assembly could bring enhancer and promoters in the vicinity, making certain looping factors redundant. The natural extension of our above-mentioned results, in which we have emergence of TAD-like behavior from basic internucleosomal interactions, is to investigate how domain boundaries emerge in such a model of self-organization. The establishment of heterogeneous interaction potentials could be one way to make boundaries between different domains. Below, we discuss this possibility.

Spatial variation in histone modifications and interaction potentials

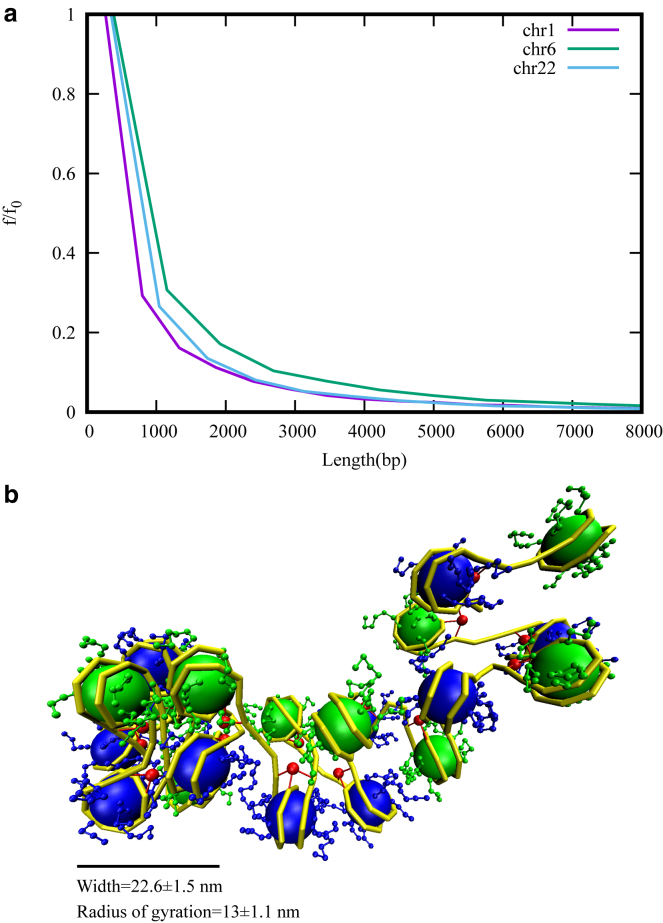
In the sections above, we found that chromatin has a width of 30 nm or above even if the chromatin is as small as 20 nucleosomes. However, in the context of in vivo chromatin, recent experiments report large regions of chromatin having a width of <30 nm (38). Given the interactions we described above, it is a puzzle how one could get regions having a width of <30 nm. It is also interesting to investigate how one can introduce separation between different domains in such a model for self-organization that we discussed above. To address these puzzles, we turn our attention to histone modifications. We know that histone modifications vary spatially (along the contour of a chromatin) and can influence the nature of effective interactions between the different parts of the chromatin (70). The presence of certain methylations (like H3K9me3) could lead to the recruitment of certain proteins (like HP1) and induce high attractive interactions between chromatin segments (55, 56, 57). The absence/presence of acetylations could also affect the local electrostatic potentials, leading to heterogeneous interactions. All these will affect the packaging and clustering of nucleosomes. To understand this heterogeneity in interactions, as an example, we examined the extent of H3K9me3 modifications along the chromatin fiber length. Using chromatin immunoprecipitation sequencing data available in public databases, we asked the following question. What is the length of the typical contiguous patch of chromatin having H3K9me3 modification? We defined any two modification peaks as a part of the same contiguous patch if the separation between the peaks is less than 1000 bp. Using this definition, we computed length distribution of contiguous patches of chromatin having H3K9me3 modifications for 22 human chromosomes for human T cells in (71) (see Figs. 6 a and S6). The distributions peak at small values of length, suggesting that very long contiguous patches are rare. The mean length of H3K9me3 modification patches across all chromosomes is ∼1600 bp, and the gap length between two contiguous patches is ∼2200 bp. If we convert in terms of nucleosomes, this is equivalent to chromatin having ∼8 nucleosomes with modifications and ∼12 nucleosomes without.

Figure 6.

(a) Frequency (f) distribution of lengths of contiguous patches having H3K9me3 modifications, for three different chromosomes, scaled with maximal frequency (f₀). See Fig. S6 for a similar plot for all chromosomes. Most of the patches are smaller in length; very long patches are rare. (b) A snapshot of the chromatin structure with NHPs and heterogeneous interactions is shown; the system was simulated with electrostatic interactions in the first eight nucleosomes and with no electrostatic interaction in the remaining 12 nucleosomes. Note that the radius of gyration or “width” of the dense cluster indicate a length scale less than 30 nm. To see this figure in color, go online.

To mimic the essence of spatial variation in modifications, we simulated 20 nucleosomes in which we introduced electrostatic interactions into one fraction (eight nucleosomes), and the other fraction (12 nucleosomes) was left with no electrostatic interactions. In choosing such a pattern of interaction, we assumed that the absence of repressive methylation marks anticorrelates active acetylation marks. However, we stress that we do not intend to account for any direct one-to-one relation between the modifications and interactions. Our aim is only to mimic heterogeneous interactions at the length scales relevant in biology. The U^LJ was kept uniform (ε = 0.1 kcal/mol), and the linker regions were bent with NHPs with a density of 0.5. The resulting chromatin structure is shown in Fig. 6 b. The eight nucleosomes with electrostatic interactions form one cluster, whereas the other 12 nucleosomes divided into many small clusters. Note that, here, the chromatin is irregular because of the presence of NHPs. We calculated the width of the single cluster of eight nucleosomes, which is 22.6 ± 1.5 nm, and the corresponding radius of gyration is 13 ± 1.1 nm. The other small clusters have widths varying from a single-nucleosome width (∼5−10 nm) to two or three nucleosome widths (10–20 nm). These results are comparable to recent experimental results in which they found predominantly fiber width to be in the range of 5–24 nm (38). The distribution of the contiguous patch lengths of histone modifications suggest that chromatin configurations must be computed with nonuniform interaction potentials, and it will result in a chromatin in which most of the regions have widths of <30 nm; regions of higher widths are possible depending on the length of the interaction pattern. In other words, heterogeneity in interactions resulting from actively maintained spatial variation of histone modifications may determine the width of chromatin fibers in vivo. The two domains we saw—one domain having a big cluster, and the other domain having many small clusters—may also suggest that these spatial variations in interaction potentials can introduce separation between different TAD-like contact domains in a model for self-organization of chromatin.

Another factor that might affect chromatin organization is the irregular spacing between nucleosomes (72,73). In some regions, because of nucleosome loss, there can be long linker lengths. This may also be linked to the spatial variation of histone modifications in which certain modifications would lead to nucleosome loss/disassembly. In Fig. S7 a, we present results of our simulation having irregular nucleosome spacing (linker DNA) randomly chosen between 21 and 147 bp (two beads to 14 beads of coarse-grained linker DNA). The chromatin configurations are irregular, and I(k) is high for many values of k, confirming the irregular nature (see Fig. S7 b). We also computed how such an irregular chromatin, due to long irregular linker regions, form clusters (Fig. S7 c). The result shows that chromatin with nucleosome loss lead to many clusters, each having one to three nucleosomes on average.

Conclusions

In this work, we examined the width, packing density, and clustering properties of chromatin that is irregular because of the binding of DNA-bending NHPs. We find that the DNA-bending NHPs will make chromatin irregular; however, the resulting structure can have a similar packing density and width as that of the chromatin without NHP (regular). We examined how different factors, such as the length of the chromatin and the nature/strength of interactions, determine the width, packing density, and clustering properties of chromatin. In our simulations, we explicitly accounted for histone tails and electrostatic interaction and varied the length of chromatin across several nucleosomes (length of a typical gene to many genes). We showed that electrostatic interactions make the chromatin more compact, whereas a chromatin simulated without electrostatic interactions is more open. This is consistent with the fact that reduction in net positive charges (hence, reduction in electrostatic interactions) due to acetylation of histone tails leads to more open chromatin. We examined how the nucleosomes are clustered in a highly packed chromatin and in an open chromatin. We calculated the mean cluster size of simulated structures and showed that open chromatin is essentially many small clusters of nucleosomes; they may not appear as a single thick fiber in many experiments. We varied fiber length and calculated packing densities and fiber widths and showed that both quantities increase with fiber length. Then, we addressed the resulting puzzle as to why one does not observe highly packed chromatin fibers of a width of 30 nm or above in vivo. We argued that one of the missing components here could be the heterogeneity in interactions resulting from histone modifications. We simulated chromatin configurations, considering this heterogeneity in interactions, and showed that heterochromatin structure could have a typical width less than 30 nm if the typical length of interaction patterns are very small. We also computed coarse-grained contact maps, similar to what is obtained in Hi-C experiments, predicting the probability of contact between two large segments. The map showed TAD-like contact domains, suggesting that our model has the right ingredients for investigating multiscale nature of chromatin. Our model can start to connect experiments probing two different length scales—connecting chromatin features in the length scale of nucleosomes to the chromatin features in the length scale of genes.

We have done molecular dynamics simulations solving Langevin equations for chromatin polymer; the results presented are chromatin configurations at thermal equilibrium. Although our work could be a very good representation of chromatin reconstituted in vitro, we must explicitly state the assumptions involved in using our model to interpret in vivo results. Living cells are not in thermal equilibrium, and the ATP-dependent activity will affect chromatin organization. Hence, while using this work to understand chromatin in vivo, we assume that our work models regions of chromatin that are not active, in which ATP-dependent nucleosome dynamics and transcription are negligible. It is also assumed that the role of activity in the regions of our interest is only to maintain the nucleosome positioning and internucleosomal interaction potentials—ATP-dependent enzymes maintain certain histone modification states, maintain the length of interaction patches, and maintain certain concentrations of DNA-bending proteins. It must be stressed that we are only simulating chromatin of lengths ≤100 nucleosomes. However, the real chromatin is much longer; here, we assume that the interactions of far away regions do not affect the region of our interest. This is a reasonable assumption for regions that are known to be a part of topological domains in which local interactions dominate. It is believed that such heterochromatic regions will have 30-nm wide chromatin structures. However, our work suggests that even there, depending on the nature of histone modifications, one may get chromatin widths even smaller than 30 nm. We have assumed that electrostatic interactions obey a Debye-Huckel potential; however, fluctuations of counterions and other charged constituents are not accounted for in this description of the interactions. These are some of the limitations of our model. Even though some of the earlier chromatin studies have accounted for DNA twist, we have not included the twist of the DNA explicitly here (74, 75, 76). Because we coarse grained 10.5-bp DNA (size of one helical repeat) into one bead, the twist length scale is below our coarse-graining size. Hence, we neglected the twist. Moreover, because our aim is to study the role of DNA-bending NHPs, we assumed that once those proteins are bound, the DNA will be bent in random orientations, decreasing the effect of twisting/orientations. However, neglecting twist is an approximation, and there is a scope of examining whether our assumptions are valid or not by doing a work with a twist in the future.

Suggestion for new experiments to test our prediction

Experimentally, our findings can be tested in a few different ways. One can possibly perform in vitro chromatin reconstitution experiments with NHPs and measure the width, packing density, and cluster sizes. Our prediction is that the chromatin will be irregular but with a width of ∼30 nm, if the length is appropriately chosen as we have shown in our results; however, depending on the nature of the modifications, one may not find the chromatin as one cluster but many small clusters of nucleosomes. This may be repeated for many different lengths and quantities measured as a function of length. Our work also suggests that one should experiment with heterogeneity in interactions; this may be introduced by appropriately mutating charged/neutral amino acids in the tail region in a fraction of the histones. This will bring heterogeneity in electrostatic interactions, and according to our predictions, this can lead to alterations in the width and packing density of chromatin. We also predict how the width (size) of chromatin vary as a function of fiber lengths (number of nucleosomes) or the length of the interaction patch.

To conclude, in this work, we simulated chromatin on the length scale of a few genes, accounting for various factors. Our results show the importance of heterogeneity in interactions and the role of NHPs. This work should be considered a step in the direction toward a more complete model to study the chromatin states and the dynamics of chromatin, accounting for realistic details like protein-binding and interactions due to histone modifications. We hope that this work will lead to further experimentation and computation.

Author Contributions

Both authors (G.B. and R.P.) designed the research. G.B. performed simulations and plotted figures. Both authors analyzed the data and wrote the article.

Editor: Anatoly Kolomeisky.