Abstract
Objectives. To describe and compare 3 garbage code (GC) redistribution models: naïve Bayes classifier (NB), coarsened exact matching (CEM), and multinomial logistic regression (MLR).
Methods. We analyzed Taiwan Vital Registration data (2008–2016) using a 2-step approach. First, we used non-GC death records to evaluate 3 different prediction models (NB, CEM, and MLR), incorporating individual-level information on multiple causes of death (MCDs) and demographic characteristics. Second, we applied the best-performing model to GC death records to predict the underlying causes of death. We conducted additional simulation analyses for evaluating the predictive performance of models.
Results. When we did not account for MCDs, all 3 models presented high average misclassification rates in GC assignment (NB, 81%; CEM, 86%; MLR, 81%). In the presence of MCD information, NB and MLR exhibited significant improvement in assignment accuracy (19% and 17% misclassification rate, respectively). Furthermore, CEM without a variable selection procedure resulted in a substantially higher misclassification rate (40%).
Conclusions. Comparing potential GC redistribution approaches provides guidance for obtaining better estimates of cause-of-death distribution and highlights the significance of MCD information for vital registration system reform.
Information on causes of death at the national level provides critical inputs for the development of national health policies and evaluation of population health. However, problematic assignment of the underlying cause of death (UCD) frequently occurs because of the complicated assignment process of the cause-of-death classification system and inconsistent practice procedure in completing death certificates.1 According to the World Health Organization (WHO), the definition of UCD is as follows: “the disease or injury which initiated the chain of morbid events leading directly to death, or the circumstances of the accident or violence which produced the fatal injury.”2(p34) Because of uncertainty regarding the UCD or lack of knowledge and practice of the correct procedures for completing a death certificate, the certifying physicians sometimes mistakenly assign intermediate cause of death (e.g., cardiac arrest, heart failure), ill-defined conditions or symptoms (e.g., dyspnea), or unspecified codes within larger groups of causes (e.g., ill-defined sites of cancer) as the UCD. These so-called garbage codes (GCs) provide useless information for public health analysis; therefore, they should not be designated as the UCD.3
Algorithm-based approaches have been used to reassign GCs to informative UCDs with the aim of improving the quality and utility of mortality statistics.4,5 These methods have frequently been applied to secondary mortality data (at the aggregated level), but they suffer from the drawback of not considering the heterogeneity of GCs across countries and health care systems. For the purpose of redistribution, alternative approaches, including multinomial logistic regression6 (MLR) and coarsened exact matching7 (CEM), have used individual-level information embedded within mortality data. The shortcoming of MLR is that it requires assumptions about how variables are related to the outcome, whereas CEM assumes the underlying probability structure that enforces complete interdependencies of predictors. However, the empirical performance and scalability of the 2 data-driven approaches have not been well assessed.8
In addition to the MLR and CEM approaches, we explored a new nonparametric method—the naïve Bayes classifier (NB), which has the advantage of fast implementation and low risk of overfitting. We evaluated and compared the classification performance and scalability of 3 data-driven approaches (NB, CEM, and MLR) using empirical data sets in Taiwan and simulated data sets under diverse scenarios.
METHODS
All deaths in Taiwan are required by law to be registered, and death registry data sets provide timely and complete information regarding the cause of death. Nonetheless, GCs accounted for more than 15% of registered deaths in 2016, higher than any other single cause of death.9 We obtained vital registration data at the individual level, including age, sex, residence, and marital status as well as date, manner, and place of death. We obtained data for multiple causes of death (MCDs) from the Multiple Causes of Death data set. These data have been collected by the Department of Statistics, Ministry of Health and Welfare since 2008, with cause of death coded according to the International Statistical Classification of Diseases and Related Health Problems (ICD)-10.10
Garbage Code and Underlying Cause of Death
We categorized the GCs for cause of death into 9 groups; septicemia, volume depletion, ill-defined cancer site, heart failure, ill-defined cardiovascular diseases, renal failure, ill-defined injury, ill-defined conditions, and other ill-defined codes (GC01–GC09; Table A, available as a supplement to the online version of this article at http://www.ajph.org).11 Because of the practical difficulty of assigning each GC to a specific UCD, we constructed a condensed classification system of mutually exclusive and collectively exhaustive groups of crucial cause of death (Table A), consistent with the guidelines of WHO and those reported in previous studies.12–14 Nonetheless, our model can be generalized to any grouping system. Users can choose an appropriate grouping system based on the required level of detail in mortality information and sample size considerations (limiting the model complexity without overfitting). We further matched the groups of mapping lists to corresponding GCs according to physiological mechanisms and domain knowledge (Table B, available as a supplement to the online version of this article at http://www.ajph.org).2,13
Redistribution Models
To probabilistically redistribute the GCs to target UCDs, we defined the analysis as solving a classification problem, given individual characteristics and MCDs. We implemented 2-step analyses for model construction and application. First, we used non-GC death records to construct 3 types of prediction model (NB, CEM, and MLR), incorporating individual-level information such as demographics and MCDs as the predictors. For each type of prediction model, we carried out variable selection using fivefold cross-validation. We selected and retrained the best-performing models using the complete non-GC records. Second, we applied the best-performing model constructed in the previous step to GC records, which were redistributed probabilistically to their potential UCDs. We conducted model construction and GC redistribution separately for each year.
Sex, age (5-year groups), marital status, urbanization level of residence,15 month of death, manner of death, and the level of health care facility that issued the death certificate constituted the full set of predictor variables. In addition to using each full model that included all available predictor variables, we applied a selection procedure to exclude redundant covariates (excess variables that did harm to the predictive ability). The 3 types of prediction model are briefly described in the following paragraphs, and detailed descriptions are provided in the supplemental material.
NB classifier, a generative approach that estimates the conditional probability of target UCDs using Bayes’ theorem, is written as:
 |
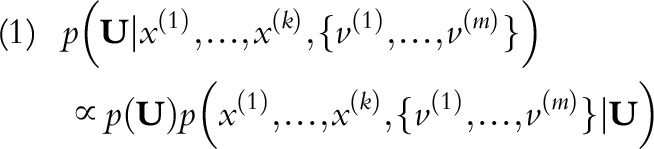where U is an r-length vector corresponding to r target UCD categories. Together, k predictors (x) and m contributing MCDs (v) are used to infer the probabilities of potential UCDs. Notably, m varies among individuals, so we consider MCDs as a set for each individual. NB further invokes conditional independence assumptions among predictors; therefore:
 |
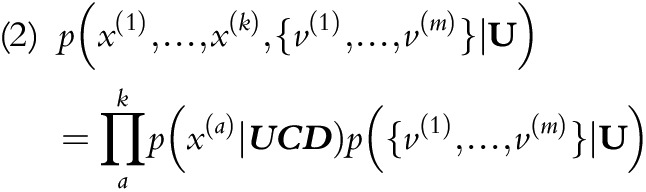We calculated the maximum likelihood estimates of the constituent probabilities on the right-hand side directly from the data. To assess the effect of interdependencies among predictor variables, we added tree- and forest-augmented naïve Bayes classifiers (TANB and FANB), as well as joining operations in the variable selection procedure for NB, as the sensitivity analysis (sections 1–3 of the Appendix, available as a supplement to the online version of this article at http://www.ajph.org).
CEM comprises the following procedures: (1) matching the individuals according to predictor variables and (2) proportionally redistributing the individual according to the target UCD distribution in the matched group. Although CEM is often depicted algorithmically, it can be formulated as a special case of the NB classifier that joins all predictor variables used (Appendix, section 4).
MLR is a discriminative approach that has parameterization of target probabilities that are distinct from NB and CEM. It is formulated as r - 1 independent binary logistic regression models:
 |
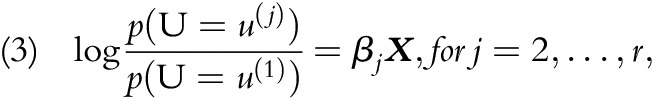where a total of r target UCD categories (
) are present, and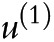 
is set as the reference category. 
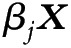is the linear predictor, including predictor variables and indicator variables of contributing MCDs (Appendix, section 5).
Variable Selection and Model Evaluation
We used backward sequential elimination (BSE) and backward sequential elimination joining (BSEJ) algorithms to search for the most parsimonious model and to improve predictive ability.16 The procedure comprised the following steps: (1) evaluating submodels generated by the elimination or joining operation, (2) testing the reduction in prediction error, and (3) proceeding to the next iteration, or reporting the current model (Appendix, section 6).
We evaluated each model on the basis of its out-of-sample average classification error, obtained from fivefold cross-validation. We randomly partitioned non-GC death records into 5 groups; we selected one at a time as the validation set, and the rest formed the training set. Because we used 0/1 loss function as the error measure (erri), we interpreted the average classification error as the misclassification rate:
 |
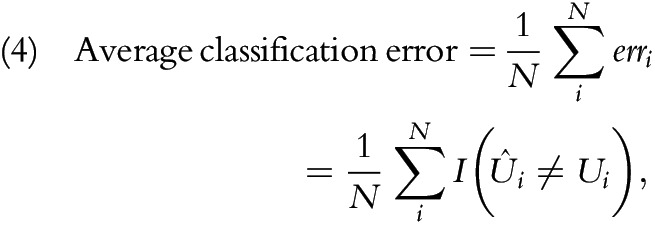where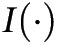 
is an indicator function that returns 1 when the condition is true and 0 when it is false (Appendix, section 7). In addition, we performed a simulation analysis to evaluate the potential effects of missing data, sample size, and number of redundant covariates on the predictive performance of 3 models (Appendix, section 8). In summary, we compared 6 models, which were 3 full models (NB, CEM, MLR) and 3 models with variable selection procedures (NB_BSEJ, CEM_BSE, and MLR_BSE).
Garbage Code Redistribution
The type of GC can also inform meaningful target UCD groups. For example, ill-defined cancers should be redistributed exclusively to cancer-related UCD groups, and heart failure should be reassigned to noncommunicable diseases apart from cancers and mental and neurological conditions. This GC–UCD mapping list comes with the cause-of-death classification system and is based on physiological mechanisms and domain knowledge (Table B).2,13 We applied this mapping list in the final prediction step for all models to prevent the prediction of implausible UCD categories. For each GC record, we ignored the predicted probabilities of implausible UCD categories and renormalized the remaining distribution (Appendix, section 9). We conducted data management using SAS 9.3 (SAS Institute, Cary, NC) and performed all statistical analyses and predictions using R 3.6.1 (http://www.r-project.org).
RESULTS
Table 1 presents the frequency of GCs by key covariates in Taiwan from 2008 to 2016. The proportion of GC deaths accounted for 13.1% of total deaths and was higher among women (14.7%) than men (12.7%). Of the 9 groups of GC deaths, ill-defined condition (33.5%), ill-defined cardiovascular disease (CVD; 25.8%), septicemia (17.4%), and heart failure (16.6%) were the major groups, accounting for 93.6% of all GCs. The distribution of GC pattern varied by covariates; for example, the GC deaths among people aged 15 to 65 years were more likely to be designated as ill-defined CVD than those in other age groups, and GC deaths that occurred in hospitals exhibited a higher proportion of septicemia than did other places of death.
TABLE 1—
Frequency Distribution of Garbage Codes by Key Covariates: Taiwan, 2008–2016
| GC Type Validation, No. (%) |
|||||||||
| Covariate | GC,% | Septicemia | Volume Depletion | Ill-Defined Cancer | Heart Failure | Ill-Defined CVD | Undetermined Intent | Ill-Defined Condition | Ill-Defined Infectious |
| Sex | |||||||||
| Male | 12.7 | 18 712 (17.4) | 1 345 (1.3) | 2 954 (2.8) | 15 425 (14.4) | 28 591 (26.7) | 3 170 (3.0) | 36 922 (34.4) | 135 (0.1) |
| Female | 14.7 | 13 882 (17.3) | 1 288 (1.6) | 2 061 (2.6) | 15 617 (19.5) | 19 724 (24.6) | 1 574 (2.0) | 25 966 (32.4) | 95 (0.1) |
| Age, y | |||||||||
| Birth–14 | 10.1 | 161 (11.8) | 30 (2.2) | 12 (0.9) | 40 (2.9) | 154 (11.3) | 119 (8.7) | 838 (61.3) | 14 (1.0) |
| 15–64 | 10.5 | 5 570 (12.7) | 538 (1.2) | 1 949 (4.4) | 3 643 (8.3) | 13 392 (30.6) | 3 504 (8.0) | 15 141 (34.6) | 64 (0.1) |
| ≥ 65 | 14.8 | 26 863 (18.9) | 2 065 (1.5) | 3 054 (2.1) | 27 359 (19.2) | 34 769 (24.4) | 1 121 (0.8) | 46 909 (33.0) | 152 (0.1) |
| Urbanizationa | |||||||||
| 1 | 14.1 | 7 732 (18.9) | 535 (1.3) | 1 236 (3.0) | 6 391 (15.6) | 11 254 (27.5) | 1 031 (2.5) | 12 649 (30.9) | 63 (0.2) |
| 2 | 13.5 | 5 566 (17.9) | 441 (1.4) | 941 (3.0) | 4 860 (15.7) | 7 864 (25.3) | 849 (2.7) | 10 485 (33.8) | 38 (0.1) |
| 3 | 13.5 | 8 018 (15.9) | 731 (1.4) | 1 329 (2.6) | 7 903 (15.6) | 13 597 (26.9) | 1 422 (2.8) | 17 507 (34.6) | 65 (0.1) |
| 4 | 13.1 | 5 566 (17.0) | 462 (1.4) | 779 (2.4) | 5 894 (18.0) | 7 538 (23.1) | 820 (2.5) | 11 581 (35.4) | 29 (0.1) |
| 5 | 13.8 | 2 448 (16.4) | 207 (1.4) | 335 (2.2) | 2 653 (17.8) | 3 637 (24.4) | 288 (1.9) | 5 346 (35.8) | 15 (0.1) |
| 6 | 12.7 | 2 822 (18.5) | 231 (1.5) | 356 (2.3) | 2 993 (19.6) | 3 837 (25.1) | 267 (1.7) | 4 757 (31.1) | 17 (0.1) |
| 7 | 11.9 | 442 (21.3) | 26 (1.3) | 39 (1.9) | 348 (16.8) | 588 (28.3) | 67 (3.2) | 563 (27.1) | 3 (0.1) |
| Month of death | |||||||||
| 1–4 | 14.3 | 11 426 (16.6) | 964 (1.4) | 1 601 (2.3) | 11 665 (16.9) | 18 173 (26.4) | 1 553 (2.3) | 23 442 (34.0) | 90 (0.1) |
| 5–8 | 13.1 | 10 616 (18.2) | 814 (1.4) | 1 695 (2.9) | 9 689 (16.6) | 14 684 (25.1) | 1 666 (2.8) | 19 237 (32.9) | 66 (0.1) |
| 9–12 | 13.4 | 10 552 (17.6) | 855 (1.4) | 1 719 (2.9) | 9 688 (16.1) | 15 458 (25.7) | 1 525 (2.5) | 20 209 (33.6) | 74 (0.1) |
| Married | |||||||||
| Yes | 16.0 | 17 129 (15.9) | 1 558 (1.4) | 2 092 (1.9) | 17 912 (16.6) | 26 954 (25.0) | 2 990 (2.8) | 38 842 (36.1) | 143 (0.1) |
| No | 11.2 | 15 465 (19.4) | 1 075 (1.3) | 2 923 (3.7) | 13 130 (16.4) | 21 361 (26.8) | 1 754 (2.2) | 24 046 (30.1) | 87 (0.1) |
| Place of death | |||||||||
| Hospital | 10.5 | 20 938 (31.5) | 1 732 (2.6) | 3 066 (4.6) | 16 772 (25.2) | 11 000 (16.5) | 1 087 (1.6) | 11 750 (17.7) | 126 (0.2) |
| Clinic | 10.6 | 10 (5.4) | 1 (0.5) | 2 (1.1) | 32 (17.2) | 51 (27.4) | 4 (2.2) | 85 (45.7) | 1 (0.5) |
| Care facility | 13.9 | 60 (4.2) | 1 (0.1) | 11 (0.8) | 214 (15.1) | 546 (38.5) | 11 (0.8) | 572 (40.3) | 3 (0.2) |
| Residence | 14.4 | 11 044 (12.6) | 768 (0.9) | 1 770 (2.0) | 12 568 (14.3) | 25 488 (29.1) | 557 (0.6) | 35 456 (40.4) | 60 (0.1) |
| Other | 23.4 | 542 (1.7) | 131 (0.4) | 166 (0.5) | 1 456 (4.6) | 11 230 (35.5) | 3 085 (9.7) | 15 025 (47.4) | 40 (0.1) |
| Manner of death | |||||||||
| Natural | 13.7 | 32 588 (18.6) | 2 632 (1.5) | 5 015 (2.9) | 31 036 (17.7) | 48 305 (27.6) | 1 (0) | 55 367 (31.6) | 230 (0.1) |
| Accident | 0.0 | 6 (20.7) | 1 (3.4) | 0 | 6 (20.7) | 9 (31.0) | 2 (6.9) | 5 (17.2) | 0 |
| Unknown | 99.5 | 0 | 0 | 0 | 0 | 1 (0.0) | 4 741 (38.7) | 7 516 (61.3) | 0 |
| Total | 13.5 | 32 594 (17.4) | 2 633 (1.4) | 5 015 (2.7) | 31 042 (16.6) | 48 315 (25.8) | 4 744 (2.5) | 62 888 (33.5) | 230 (0.1) |
Note. CVD = cardiovascular diseases; GC = garbage code.
Level of urbanicity is as follows: 1 = high, 2 = medium, 3 = new township, 4 = normal township, 5 = aging township, 6 = agriculture township, and 7 = remote township.
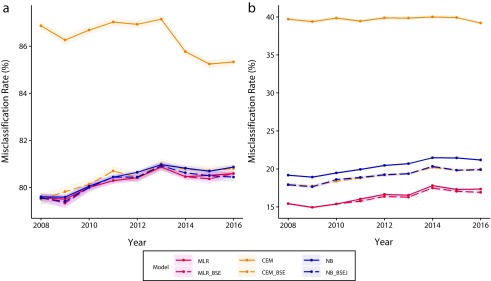
The misclassification rate for each model is shown in Figure 1 (see Tables C and D, available as a supplement to the online version of this article at http://www.ajph.org, for model contents). Redistribution models without MCD information had misclassification rates of approximately 80%, and all methods performed similarly throughout the years (Figure 1, left panel). Variable selection made a distinction only between CEM and CEM_BSE, suggesting the vulnerability of CEM regarding redundant covariates. Frequently dropped redundant variables included urbanization level and month of death (Table C). By contrast, NB and MLR were less sensitive to redundant covariates as they tended to retain all variables after the selection procedure. Depending on the year, NB_BSEJ had selected joined variables, such as sex–age and place–manner of death, implying an interactive effect of these variables. However, the performance levels of NB, NB_BSEJ, TANB, and FANB were indistinguishable (Figure A, available as a supplement to the online version of this article at http://www.ajph.org).
FIGURE 1—
Model Performance for Multinomial Logistic Regression (MLR), Coarsened Exact Matching (CEM), and Naïve Bayes Classifier (NB), (a) Without and (b) With Multiple Causes of Death Data: Taiwan, 2008–2016
Note. The color bands represent 95% confidence intervals. BSE = backward sequential elimination; BSEJ = backward sequential elimination and joining.
Incorporating MCD information substantially reduced the misclassification rate and improved the relative performance of all assessed models (Figure 1, right panel). MLR (15%–17% misclassification) consistently exhibited higher performance than all other models over the years, whereas MLR_BSE showed nonsignificant additional improvement. The models with the next-highest performance were NB_BSEJ, CEM _BSE, and NB (18%–21% misclassification); the full CEM model had the worst performance, with almost 40% misclassification. Again, CEM was considerably more sensitive to the variable selection procedure than was NB, whereas MLR was almost unaffected. Notably, CEM_BSE and NB_BSE dropped many of the variables from the complete set (Table D), suggesting that MCD information dominates in the inference of potential UCDs. Accordingly, we selected the best performance model that we found in the first stage of the analyses (MLR_BSE with MCD information) to redistribute GC records. Because the variable selection procedure resulted in different variable sets in each year, and cross-year predictions increased the classification error (Table E, available as a supplement to the online version of this article at http://www.ajph.org), we retrained the model and predicted GC deaths separately by year.
Throughout the study period, the proportion of GCs in the general population remained comparable (Figure B, available as a supplement to the online version of this article at http://www.ajph.org). Approximately 28% of GC-registered deaths were redistributed to other cardiovascular causes, followed by other noncommunicable diseases (10.4%), chronic respiratory diseases (10.3%), and mental and neurological diseases (8.6%). Overall, we observed no significant changes in the relative frequency of UCDs. However, when we considered specific subgroups, the impact of GC redistribution may have been enough to alter the ranking of the top causes of death. For example, the rankings of respiratory infections, other cancer, other noncommunicable diseases, other cardiovascular diseases, and mental or neurological conditions increased in the male population (Table 2). Other causes of death declined after GC reassignment, resulting in substantial reshuffling of the rankings. A higher number of attainable GCs resulted in an increased potential for change in the rankings or proportion of target UCDs. For instance, the proportion of other cardiovascular diseases was increased by the large number of heart failure and ill-defined cardiovascular disease registrations, which accounted for 45.7% of all the GCs. Conversely, the proportion and ranking of all cancers declined because of the infrequent occurrence of ill-defined cancer GCs (2.6%).
TABLE 2—
Changes in Ranking and Proportion of Top Causes of Death Among Males Before and After Redistribution of Garbage Codes: Taiwan, 2016
| Rank |
||||
| Underlying Cause of Death | Before | After | Change | Change in Proportion,a % |
| Digestive cancer | 1 | 3 | ▼ 2 | −0.92 |
| Respiratory infections | 2 | 1 | ▲ 1 | −0.20 |
| Other cancer | 3 | 2 | ▲ 1 | −0.54 |
| Stroke | 4 | 6 | ▼ 2 | −0.27 |
| Chronic respiratory diseases | 5 | 5 | … | +0.18 |
| Ischemic heart disease | 6 | 8 | ▼ 2 | −0.30 |
| Lung cancer | 7 | 9 | ▼ 2 | −0.84 |
| Other noncommunicable diseases | 8 | 7 | ▲ 1 | +0.26 |
| Liver cancer | 9 | 10 | ▼ 1 | −0.76 |
| Diabetes mellitus | 10 | 11 | ▼ 1 | +0.13 |
| Cirrhosis | 11 | 13 | ▼ 2 | −0.36 |
| Other cardiovascular | 12 | 4 | ▲ 8 | +3.55 |
| Mental and neurological conditions | 13 | 12 | ▲ 1 | +0.76 |
Proportion of underlying cause of death (UCD) after redistribution minus the proportion of UCD before redistribution.
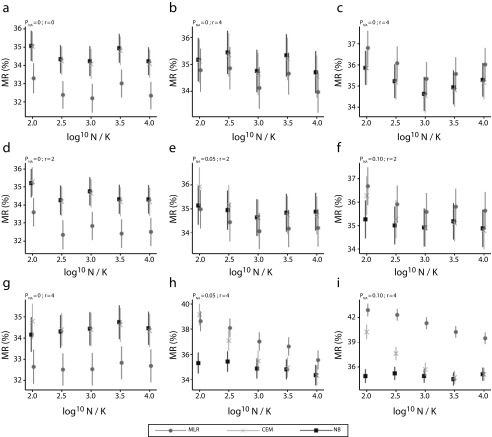
We performed simulation analyses for 9 different scenarios that varied with the quality of data (as percentage of missing values, PNA) and modeling procedure (as number of redundant covariates, r). In the optimistic scenario of no missing data (Figure 2), MLR had the best performance among all 3 methods regardless of redundant variables or sample size. The performance of MLR, nonetheless, was sensitive to the quality of data and number of redundant covariates included. In more challenging scenarios, the performance of MLR was tied with or even surpassed by both CEM and NB with the growing amount of missing information and redundant covariates. In the worst case, where there are more redundant covariates than effective ones, the misclassification rate for NB was significantly better than those for CEM and MLR (by ∼6%). Furthermore, CEM and MLR were found sensitive to relative sample size in challenging scenarios, whereas NB was able to perform comparably well even with a small data set.
FIGURE 2—
Misclassification Rate (MR) of Multinomial Logistic Regression (MLR), Coarsened Exact Matching (CEM), and Naïve Bayes Classifier (NB) by Relative Sample Size (log10N/K) Under Different Scenarios: Taiwan, 2008–2016
Note. The 9 scenarios are generated from the combination of proportion of missing data (PNA, valued 0%, 5%, or 10%) and number of redundant covariates (r, valued 0, 2, or 4). Each scenario contains 1000 iterations, where there are K = 20 target underlying-cause-of-death groups, 2 effective covariates, and a set of multiple causes of death.
DISCUSSION
The redistribution of GCs to appropriate underlying causes had a significant effect on cause of death at the population level—particularly throughout the past decade, when the proportion of GCs in the Taiwan vital registry system remained high. In this study, we compared 2 redistribution models (CEM and MLR) with a newly proposed NB model. If MCDs were not considered, all 3 models performed poorly, but in the presence of MCD information, the MLR model outperformed the other models. Therefore, the MLR model, combined with variable selection and MCD information, is suggested for GC redistribution in Taiwan. We also found that the CEM model had a high risk of overfitting and high sensitivity to redundant covariates, contradictory to the general preferences of nonparametric methods. Apart from the established mapping list for appropriate pairs of GCs and UCDs, these procedures were made verifiable, data driven,12–14 and adaptive to MCD information. Our results showed that most GC deaths were redistributed to other cardiovascular diseases (28%), other noncommunicable disease (10.4%), and chronic respiratory diseases (10.3%). Adjustment for GCs can alter the rankings of UCDs, particularly in some subgroups; therefore, it is necessary that the government urgently prioritize policies relevant to these diseases and that public awareness of these diseases be increased.
Correcting or adjusting the systematic bias in health data is critical for epidemiological studies or burden-of-disease estimates at the national and subnational levels. For example, compared with cancer, a systematically higher percentage of GCs for cardiovascular diseases were reassigned by the redistribution procedure, leading to a reshuffling of the most crucial causes of death in Taiwan. We reassigned each GC death to 1 of several fractions of UCDs, which may compensate for the shortage of current cause-of-death designating rules. Current ICD rules use a categorical or classified system for designating UCDs and assign only 1 cause for each death.2 However, in some cases—for example, heart failure deaths or ill-defined causes of death—several diseases lead to a given death, and the death may have been prevented or postponed by removing any 1 of the contributing disease factors. For public health purposes, understanding the entire chain of diseases that contribute to a given death, particularly for those registered as a GC, is critical for developing a death prevention program. Therefore, assigning each GC multiple UCDs not only conserves the uncertainty about the true underlying cause but also benefits future health policymaking.
The classification performance is highly affected by MCD information. In the absence of MCDs, the most effective model was only approximately 20% accurate, implying that these predictors are limited to the use of inferring potential UCDs. Nonetheless, there was a 16% increase in accuracy, compared with randomly guessing (4% accuracy). Incorporating MCD information boosted the performance of all models by large margins, with MLR having the highest accuracy (83%–85%), followed by NB with a variable selection procedure (81%–82% accuracy) and CEM with a variable selection procedure (81%–82% accuracy). Such findings suggest that collecting contributing MCDs should be a necessary step to improving the quality of mortality statistics, regardless of any redistribution model. Notably, by contrast with the absence of MCDs, the model selection process of NB and CEM dropped most predictor variables (Table D). In other words, the MCD information contributed most to the learned models and made most variables redundant or even harmful. We analyzed the information gained by predictors in the NB model and found that MCDs accounted for 33.8% of information gained in the redistribution model (Table F, available as a supplement to the online version of this article at http://www.ajph.org).
One previous study claimed a stronger preference for the nonparametric method (CEM) over the parametric method (MLR) for fast implementation and weaker assumption.7 However, in the present study, we found that MLR was optimal and less affected by redundant covariates (high robustness). We also found that CEM without a model selection process performed worse than other models by a large margin, suggesting a reappraisal of these redistributing methods. Previously, the major opposition to MLR was that it enforces strong assumptions about how variables are related to the outcome (as a linear predictor). However, CEM also invokes its own assumptions about the underlying probability structure, which is the complete interdependencies among predictors. Such assumptions increase the model complexity of CEM, hence the risk of overfitting (Table G, available as a supplement to the online version of this article at http://www.ajph.org), especially when the data do not feature such ubiquitous correlative structures.
A naïve Bayes model, retaining the advantage of fast implementation yet opposing the assumption of CEM, is therefore proposed. The optimal nonparametric model likely lies within the spectrum of NB (accounting for no interdependencies) and CEM (accounting for all interdependencies). To be sure, we investigated the interdependencies among predictors by calculating their conditional mutual information, of which no strong correlation was found (Table H, available as a supplement to the online version of this article at http://www.ajph.org). We also implemented a “joining” operation in the variable selection procedure, as well as augmented NB models. We found that augmented NB models (TANB, FANB) performed slightly worse than NB, implying that the benefits of accounting for interdependency structures did not outweigh the additional complexity created by augmented models. Likewise, joined variables were rarely included in the variable selection of NB_BSEJ; therefore, we believe that the interdependencies among the predictors in our data are inconsequential.
Although we selected MLR as the optimal model to redistribute GC-coded records, such a decision could change from data set to data set, with varying natures like the level of interdependencies among predictors, percentage of missing information, and size. In particular, our data set is untainted by missing values, but it offers only a few predictors with minor interdependencies. Notably, NB and CEM can conveniently handle missing values by treating them as a distinct category, whereas MLR would, by default, omit the whole observation unless an imputation algorithm was applied. In fact, our supplemental simulation experiment revealed that the performance of MLR deteriorated as the missing information grew, hence leaving NB as the optimal model. Alternatively, if the predictors were correlated, models accounting for variable interdependencies (e.g., CEM and augmented NB models) would be expected to perform better. Also, the size of the data set could affect the optimal performance of these models. Generative methods (e.g., NB and CEM) converge faster to their asymptotic error, which is, however, usually higher than the asymptotic error of the discriminative approach (MLR).17 In brief, there is hardly a universally optimal method for redistributing GCs in every situation. We suggest that users be aware of the nature of the data set and pilot different methods before full-scale implementation.
Several limitations need to be considered. First, we have no reference (gold standard) for the true UCD among individuals registered with a GC. Therefore, the validation analysis used only those with a non-GC UCD as the validation reference. Additional chart review or linking of National Health Insurance data are required for model validation. Also, we used an a priori conceptual target list that satisfied pathophysiological plausibility for GC reassignment. However, there is no available evidence that physicians exclusively miscode GC deaths from pathophysiologically related underlying causes.
Vital statistics constitute the basic reference for health policy development. In particular, the mortality rankings provide a general picture for the development of health policies and priority setting. However, without adjustment for GC, the vital statistics are inapplicable for public health purposes, leading to biased vital statistics. Our analysis provides quantitative guidance for a future GC reassignment procedure. This study highlights the potential use of multiple cause of death data to improve the quality of vital data. Our finding deserves attention for vital registration system reform. The attempt to apply a machine learning approach to public health practices also provides insights into the interdisciplinary application of innovative computer science.
ACKNOWLEDGMENTS
This work was supported by the Higher Education Sprout Project, Ministry of Education in Taiwan (project grant NTU-CC-108L891601) and the Sustainability Science Research Program, Academia Sinica in Taiwan (project grant AS‐SS‐107‐01).
We thank Chuhsing Kate Hsiao for insightful comments on the revised version of the article.
CONFLICTS OF INTEREST
The authors declare no conflicts of interests or financial conflicts.
HUMAN PARTICIPANT PROTECTION
This study was approved by the Research Ethics Committee, National Taiwan University Hospital (institutional review board permit number: 201805047W).
REFERENCES
- 1.Mathers CD, Fat DM, Inoue M, Rao C, Lopez AD. Counting the dead and what they died from: an assessment of the global status of cause of death data. Bull World Health Organ. 2005;83(3):171–177. [PMC free article] [PubMed] [Google Scholar]
- 2. World Health Organization. International Statistical Classification of Diseases and Related Health Problems. Vol 1. Geneva, Switzerland: World Health Organization; 2004.
- 3.Murray CJ, Lopez AD. The Global Burden of Disease: A Comprehensive Assessment of Mortality and Disability From Diseases, Injuries, and Risk Factors in 1990 and Projected to 2020: Summary. Geneva, Switzerland: World Health Organization; 1996. [Google Scholar]
- 4.Ahern RM, Lozano R, Naghavi M, Foreman K, Gakidou E, Murray CJ. Improving the public health utility of global cardiovascular mortality data: the rise of ischemic heart disease. Popul Health Metr. 2011;9(1):8. doi: 10.1186/1478-7954-9-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dwyer-Lindgren L, Bertozzi-Villa A, Stubbs RW et al. US county-level trends in mortality rates for major causes of death, 1980–2014. JAMA. 2016;316(22):2385–2401. doi: 10.1001/jama.2016.13645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Murray CJ, Dias RH, Kulkarni SC, Lozano R, Stevens GA, Ezzati M. Improving the comparability of diabetes mortality statistics in the US and Mexico. Diabetes Care. 2008;31(3):451–458. doi: 10.2337/dc07-1370. [DOI] [PubMed] [Google Scholar]
- 7.Stevens GA, King G, Shibuya K. Deaths from heart failure: using coarsened exact matching to correct cause-of-death statistics. Popul Health Metr. 2010;8(1):6. doi: 10.1186/1478-7954-8-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hoffman RA, Venugopalan J, Qu L, Wu H, Wang MD. Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics. New York, NY: Association for Computing Machinery; 2018. Improving validity of cause of death on death certificates; pp. 178–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lo W-C, Ku C-C, Chiou S-T et al. Adult mortality of diseases and injuries attributable to selected metabolic, lifestyle, environmental, and infectious risk factors in Taiwan: a comparative risk assessment. Popul Health Metr. 2017;15(1):17. doi: 10.1186/s12963-017-0134-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lin Y-P, Lu T-H. Trends in death rate from diabetes according to multiple-cause-of-death differed from that according to underlying-cause-of-death in Taiwan but not in the United States, 1987–2007. J Clin Epidemiol. 2012;65(5):572–576. doi: 10.1016/j.jclinepi.2011.09.010. [DOI] [PubMed] [Google Scholar]
- 11.Naghavi M, Makela S, Foreman K, O’Brien J, Pourmalek F, Lozano R. Algorithms for enhancing public health utility of national causes-of-death data. Popul Health Metr. 2010;8(1):9. doi: 10.1186/1478-7954-8-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. GBD 2017 Disease and Injury Incidence and Prevalence Collaborators; Spencer L James, Degu Abate, Kalkidan Hassen Abate, et al. Global, regional, and national incidence, prevalence, and years lived with disability for 354 diseases and injuries for 195 countries and territories, 1990–2017: a systematic analysis for the Global Burden of Disease Study 2017. Lancet. 2018;392(10159):1789–1858. [DOI] [PMC free article] [PubMed]
- 13.Foreman KJ, Naghavi M, Ezzati M. Improving the usefulness of US mortality data: new methods for reclassification of underlying cause of death. Popul Health Metr. 2016;14(1):14. doi: 10.1186/s12963-016-0082-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.WHO Methods and Data Sources for Global Burden of Disease Estimates: 2000–2011. Geneva, Switzerland: Dept of Health Statistics Information Systems, World Health Organization; 2013. [Google Scholar]
- 15.Liu C-Y, Hung Y-T, Chuang Y-L et al. Incorporating development stratification of Taiwan townships into sampling design of large scale health interview survey [in Chinese] J Health Manag. 2006;4(1):1–22. [Google Scholar]
- 16.Pazzani MJ. Searching for dependencies in Bayesian classifiers. In: Fisher D, Lenz H-J, editors. Learning From Data: Artificial Intelligence and Statistics V. New York, NY: Springer New York; 1996. pp. 239–248. [Google Scholar]
- 17.Ng AY, Jordan MI. On discriminative vs generative classifiers: a comparison of logistic regression and naive Bayes. Paper presented at: Advances in Neural Information Processing Systems Meeting; December 9–14, 2002; Vancouver, British Columbia.