Abstract
Modeling and simulation provides quantitative information on target coverage for dose selection. Optimal model selection often relies on fit criteria and is not necessarily mechanistically driven. One such case is discussed where healthy volunteer data of an anti‐myostatin monoclonal antibody domagrozumab were used to develop different target‐mediated drug disposition models; a quasi‐steady state (QSS) rapid binding approximation model, a Michaelis−Menten (MM)‐binding kinetics (MM‐BK) model, and an MM‐indirect response (MM‐IDR) model. Whereas the MM‐BK model was identified as optimal in fitting the data, with all parameters estimated with high precision, the QSS model also converged but was not able to capture the nonlinear decline. Although the least mechanistic model, MM‐IDR, had the lowest objective function value, the MM‐BK model was further developed as it provided a reasonable fit and allowed simulations regarding growth differentiation factor‐8 target coverage for phase II dose selection with sufficient certainty to allow for testing of the underlying mechanistic assumptions.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Target‐mediated drug disposition model equivalence has been tested post hoc or using simulated data. Testing model equivalence in terms of impact on target coverage and as a driver for model selection has not been discussed.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ This analysis evaluated which different pharmacokinetic/pharmacodynamic models could be tested for biologics targeting a soluble target and what should be the potential factors driving model selection.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ Model selection should not be guided by statistical attributes alone, but rather resemble a balance of mechanistic features, statistical attributes, and, very importantly, intent of application.
HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?
☑ Future trial simulations seeking target coverage should consider the limitations of the models in predicting uncertainty. This could lead to severely overpredicting or underpredicting target coverage with the risk of taking nondevelopable molecules forward or stopping potential molecules prematurely.
Modeling and simulation (M&S) has been guiding decision making in drug discovery and development for > 2 decades. Applications of M&S include aiding target prioritization and selection, steering optimization of drug properties, providing insight into drug mechanism of action, supporting identification of mechanistic biomarkers, and enabling selection of dosing regimens and patient populations to balance efficacy and safety. In the clinical development space, application of M&S spans selection of first‐in‐human (FIH) dose, bridging across different disease populations or between adults and children, identifying relevant prognostic efficacy and safety end points, and identifying sources of variability in exposure and/or response.1, 2 Furthermore, M&S is essential for accelerated development programs where decisions often need to be made based on limited data. In these scenarios, it is imperative that the applied M&S approaches strike the right balance between complicated mechanistic models and parsimonious models that adequately characterize available data.
A model is a mathematical equation or set of equations to capture a given profile under a set of assumptions. Therefore, these models could range from empirical, semimechanistic to mechanistic. The basic principle of all models is to characterize the data first. Then follows the debate on which is a better model balancing assumptions, has better model fit characteristics, and decides the model being empirical, semimechanistic or mechanistic. Here, we discuss such a case for domagrozumab (PF‐06252616), a humanized IgG1 monoclonal antibody (mAb) that selectively neutralizes a soluble target, myostatin (also known as growth differentiation factor 8). M&S approaches were instrumental in supporting accelerated timelines by bridging information from healthy adults to pediatric patients (age 6–10 years) with Duchenne muscular dystrophy (DMD).3 Specifically, population M&S approaches were utilized to characterize the domagrozumab pharmacokinetics/pharmacodynamics (PK/PD) in healthy adults, and this in conjunction with different scaling approaches was considered to support phase II dosing of domagrozumab in pediatric patients with DMD.4
For domagrozumab, the exposure obtained from an FIH study in healthy adults exhibited typical mAb‐like PK with some nonlinearity at lower doses and dose‐dependent accumulation of total myostatin.3 A target‐mediated drug disposition (TMDD) mechanism can often be used to describe the nonlinear component of the mAb PK, with a first mathematical model developed by Mager and Jusko.5 Since then, several approximations of the model have been proposed and applied to describe PK/PD of numerous mAbs.6 In the absence of a better mechanistic understanding, the PD effects of drugs are often characterized using more general approaches. In particular, indirect response (IDR) models are then used to describe mechanisms like inhibition or stimulation of the production or degradation of factors controlling the measured effect.7, 8
For domagrozumab, M&S was used to select doses for pediatric patients with DMD using initially a PK/PD modeling approach on healthy adult data, then subsequently using the derived model to simulate free domagrozumab PK exposure and PD (total myostatin concentration and myostatin target coverage), assuming similar variability in the adult and pediatric population. Different simulation scenarios, including varying dose, frequency, and route of administration, were evaluated to arrive at the final dosage for patients with DMD. However, a first step involved selecting the best model that characterized FIH data. To arrive at the best model, we used various TMDD model approximations and IDR models to systematically analyze the FIH data for domagrozumab, with the intent to understand the advantages and limitations of various proposed model structures, while preferably identifying the best model based not solely on statistical inference. To this end, parameter estimates across models were compared and relationships on mathematical equivalence of models utilized to isolate key structural features that control model performance.
Methods
Clinical study, PK, and myostatin data
A phase I, dose escalating, double‐blind, randomized, placebo‐controlled study was conducted to evaluate the safety, tolerability, PK, and PD of domagrozumab in adult healthy subjects. This study included escalating single i.v. doses of 1, 3, 10, 20, and 40 mg/kg (infused over 2 hours) and a single s.c. dose of 3 mg/kg. The study also included a repeat dose cohort that received an i.v. dose of 10 mg/kg (infused over 2 hours) every 2 weeks for a total of 3 doses. Study details, including demographics, PK, and myostatin assay details, were reported earlier.3
Mathematical models
A step‐wise modeling approach was taken where a series of models were tested to understand how they describe the data, follow biological understanding, and make parameter interpretation meaningful. To characterize the serum profiles of free domagrozumab and total myostatin, three types of structural models were considered, in the order of the mechanistic understanding viz. quasi‐steady state (QSS) model (Figure 1 a), Michaelis−Menten (MM) binding kinetics (MM‐BK) model9, 10 (Figure 1 b), and two indirect response (MM‐IDR2 and MM‐IDR3) models7, 8 (Figure 1 c). The set of differential equations that describe each model are as follows:
Figure 1.
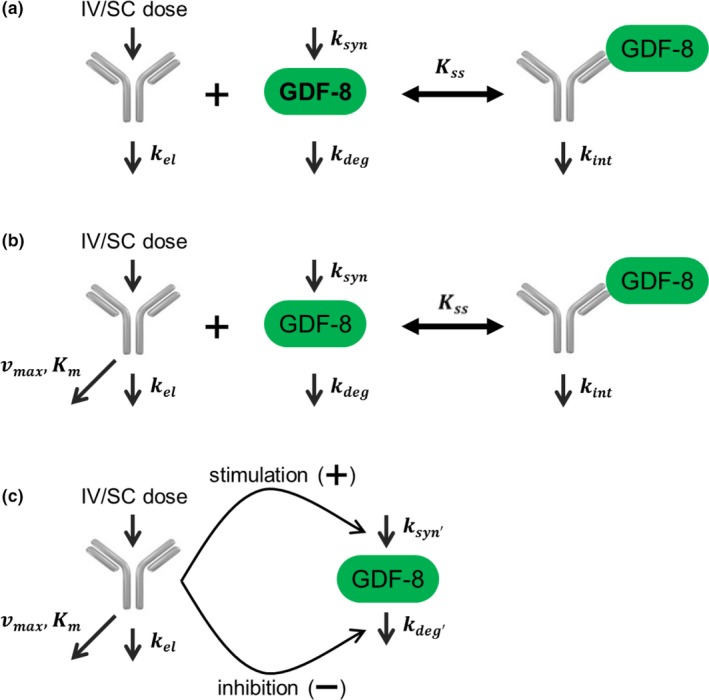
Schematic representations of quasi‐steady state (QSS) model (a), Michaelis−Menten‐binding kinetic(MM‐BK) model (b) and indirect response (IDR) models (c). kdeg, first order degradation; kel, first order elimination; kint, first order internalization; km, kinetic metabolite; kss, steady state constant; ksyn, zero‐order synthesis; Vmax, maximal rate of metabolism.
QSS model
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where D tot,C and D C represent total and free domagrozumab concentrations in the central compartment; A D and A P represent free domagrozumab amounts in the depot and peripheral compartments; M tot represents total myostatin concentration in the central compartment; V C and V P represent the volumes of the central and peripheral compartments. Inf represents the amount of domagrozumab infused over 2 hours for i.v. administration, k int the first order internalization rate of domagrozumab‐myostatin complex, k deg the degradation constant of myostatin, and K SS the steady‐state constant (when k int is not negligible compared with the complex dissociation rate).
The i.v. administration of domagrozumab was modeled as an infusion into the central compartment (V C), whereas s.c. administration was modeled using a depot compartment that releases the bioavailable amount at an absorption rate (k a) into the central compartment. Free domagrozumab in the V C distributes into peripheral tissues (k 12, k 21) and is eliminated systemically with a first order elimination. Myostatin is assumed to have a zero‐order synthesis and follows first order degradation (k deg) in the central compartment. At baseline under homeostasis, in the absence of domagrozumab, when the myostatin synthesis and degradation are equal, the myostatin synthesis rate is calculated as the product of degradation rate and baseline myostatin concentration (k syn = k deg M tot (0) = k deg M 0). During model fitting k 12, k 21, and k el (elimination rate) were expressed in terms of two compartmental PK parameters as follows:
where CL is the domagrozumab clearance from the central compartment, and Q the intercompartmental distribution clearance.
The differential equations governing domagrozumab dynamics in peripheral and depot compartments are the same across all models and are, therefore, not repeated for MM‐BK and IDR models.
MM‐BK model
The QSS model reduces to the quasi‐equilibrium model when the internalization rate of the drug‐target complex is much smaller than its dissociation rate.9 Thus, the QSS model is a more general approximation of the full TMDD model. To characterize the nonlinear PK observed for domagrozumab and the total myostatin accumulation that constituted PD, another model was evaluated that involved a variant of the MM model.
In this model, domagrozumab is eliminated by both linear and nonlinear mechanisms, where the latter is described by an MM approximation. Graphical evaluation of the PK data and preliminary PK modeling supported the need for the linear and nonlinear components. For the MM‐BK model, it was assumed domagrozumab modulates myostatin through binding, but this interaction does not impact domagrozumab free concentrations. The model is described by a set of differential equations as follows:
| (6) |
| (7) |
where vmax is the maximum nonlinear elimination rate; and K M is the free domagrozumab concentration at half‐maximal nonlinear elimination rate. All other parameters have been previously defined. It should be noted that Eq. (6) is same as Eq. (4).
The MM‐BK model implemented here is different from the MM models described previously.9, 10 First, the nonlinear terms for PK and PD are characterized by different threshold parameters, K M for PK and K SS for PD. Second, as PD does not impact PK in this model, vmax is assumed to be constant and does not depend on total myostatin concentrations. Decoupling of the PK and PD allows the domagrozumab PK to decline nonlinearly through K M while preserving the accumulation of total myostatin that is driven by the binding constant K SS. The Gibiansky and Frey11 model describing the impact of IL‐6R on tocilizumab is an example where similar model assumptions were used, plausibly to achieve a balance between mechanistic and model fit.
MM‐IDR2 and MM‐IDR3 models
In the IDR models, the differential equations governing free domagrozumab dynamics are the same as in the MM‐BK model. Differences are mainly stemming from the PD interactions in the model. In the MM‐IDR2 model, domagrozumab inhibits total myostatin degradation, whereas in the MM‐IDR3 model domagrozumab promotes total myostatin synthesis. Both these hypothetical mechanisms are physiologically unlikely, but for the purposes of following the basic principles of modeling, were included into the model building to present an alternative mathematical characterization to the postdose accumulation of total myostatin.
MM‐IDR2
| (8) |
MM‐IDR3
| (9) |
where Imax and Smax represent the maximum domagrozumab‐dependent fold changes in myostatin degradation and synthesis rates, respectively, IC50 and SC50 the domagrozumab concentrations at half‐maximal myostatin degradation and synthesis rates, respectively, and γ the Hill coefficient that controls the sharpness in response. All other parameters have been defined above.
Population PK/PD analysis
Population PK/PD analysis involved the use of nonlinear mixed effects modeling as implemented in NONMEM version 7.2 (ICON Development Solutions, Ellicott City, MD). The first order conditional estimate with interaction method in NONMEM was used for model fitting, whereas the R statistical package version 2.15.2 (Vienna, Austria) was used for data visualization and model evaluation. Serum concentrations of free domagrozumab and total myostatin were modeled in log and linear domains, respectively. Each of the four models was fitted simultaneously to domagrozumab PK and total myostatin data.
Model simulations
Final MM‐BK and MM‐IDR2 models were used to simulate free domagrozumab exposure and total myostatin levels for 500 individuals using NONMEM version 7.2. MM‐BK and MM‐IDR2 were specifically selected for simulations as MM‐BK provided the balance between mechanistic and model fit, whereas MM‐IDR2 provided the best model fit. The following domagrozumab dosing regimen in patients with DMD were simulated: 5 mg/kg every 4 weeks for 16 weeks followed by 20 mg/kg every 4 weeks for 16 weeks followed by 40 mg/kg every 4 weeks for 16 weeks. Target coverage defined as the percentage of myostatin bound by domagrozumab was calculated for the MM‐BK and MM‐IDR2 models as described previously.4
MM‐BK model
| (10) |
MM‐IDR2 model
| (11) |
Results
Characterizing nonlinear PK via TMDD model approximations
Although overall, the QSS model captured the PK data reasonably well (Figure 2 a), it underperformed in capturing the nonlinear decline in the domagrozumab concentrations, especially at low (1 mg/kg) and high (40 mg/kg) doses. By contrast, the MM‐BK model captured the nonlinear decline in the domagrozumab concentrations much better (Figure 2 b) without compromising the quality of the fits for the total myostatin concentrations (compare Figure 3 a and Figure S1 A). From an optimization perspective, the better performance of the MM‐BK model is reflected in its substantially lower objective function value (OFV; see Table 1 ∆OFV = −723). Notably, the estimates for all common parameters across the two models are within twofold of each other, with V C and V P being the least and most different parameters (Table 1). The MM‐BK model consists of two additional parameters, vmax (0.002 nmol/hour/kg) and K M (10.1 nM). The latter's differentiation from the steady‐state binding constant K SS (4.39 nM) is responsible for the better performance of the MM‐BK model over the QSS model. In the typical formulation of the MM model, K SS equals K M,10 however, we allowed the two parameters to take different values, which essentially decouples domagrozumab PK from total myostatin PD.
Figure 2.

Predictions of free domagrozumab serum concentration for quasi‐steady state model (a) and Michaelis−Menten‐binding kinetic model (b) following single and repeat dose administrations of domagrozumab. Blue circles are observations, solid red curve is population prediction, and dashed gray line is lower limit of quantification (LLOQ) of pharmacokinetic assay (0.2 nM). Orange crosses represent samples dropped from analysis. For plotting purposes, domagrozumab serum concentration below the LLOQ was imputed as 0.1 nM (gray circles). BLQ, below the limit of quantification; DV, observed concentrations; PRED, population prediction.
Figure 3.
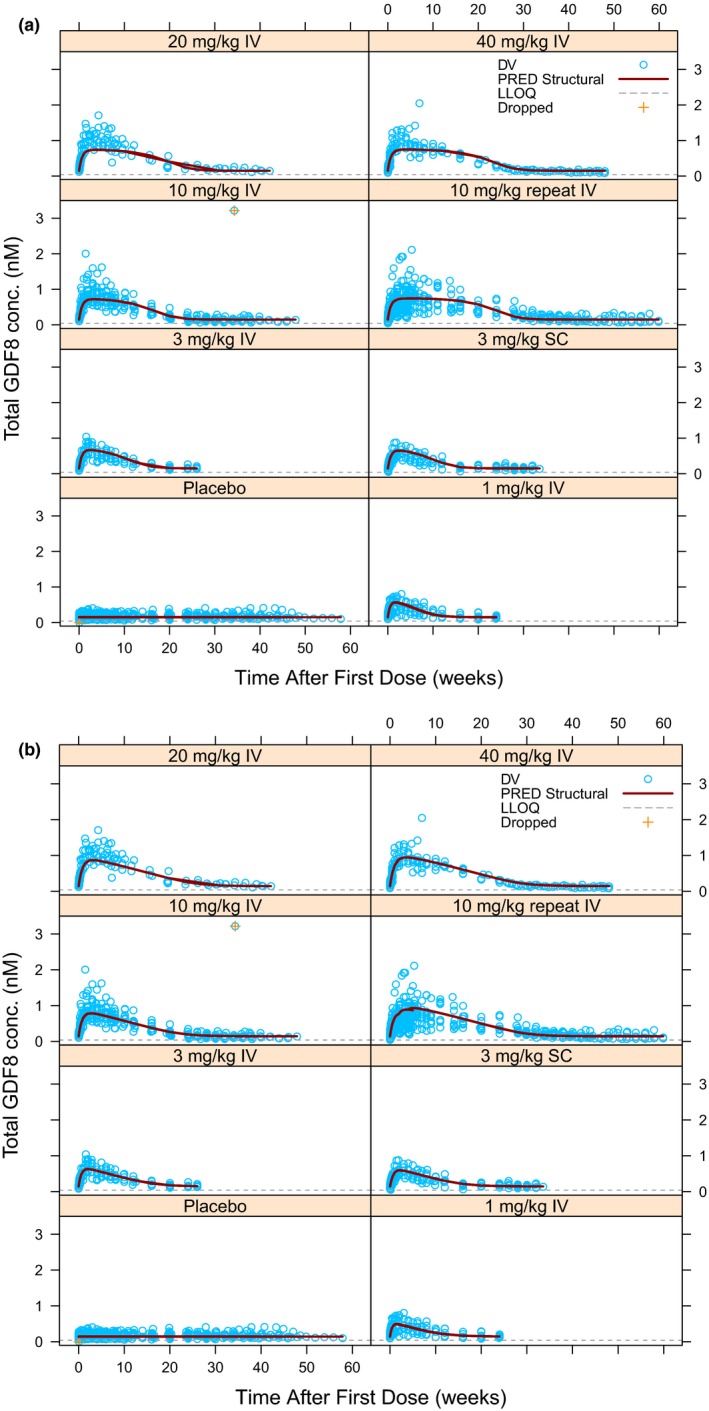
Predictions of total myostatin serum concentration for Michaelis−Menten‐binding kinetic model (a) and Michaelis−Menten‐indirect response 2 model (b) following single and repeat dose administrations of domagrozumab. Symbols have the same meaning as Figure 2. The lower limit of quantification (LLOQ) of total myostatin assay was 0.04 nM. The concentration of 3.216 nM from 10 mg/kg i.v. single dose cohort was dropped as an outlier. For plotting purposes, myostatin serum concentration for one subject in the 10 mg/kg i.v. single dose cohort was imputed as missing. BLQ, below the limit of quantification; DV, observed concentrations; PRED, population prediction.
Table 1.
Parameter estimates (% RSE) for QSS, MM‐BK, MM‐IDR2, and MM‐IDR3 models
| QSS | MM‐BK | MM‐IDR2 | MM‐IDR3 | |
|---|---|---|---|---|
| OFV | −11,851.649 | −12,574.706 | −12,863.052 | −12,857.027 |
| Condition # | 172 | 234 | 320 | 378 |
| PK parameters | ||||
| CL (mL/hour/kg) | 0.108 (4.56) | 0.102 (5.49) | 0.100 (6.61) | 0.100 (6.47) |
| V C (mL/kg) | 48 (8.79) | 46 (11.6) | 46 (12.2) | 46 (13.7) |
| Q (mL/hour/kg) | 0.398 (44.7) | 0.326 (11.8) | 0.317 (12.7) | 0.318 (13.1) |
| V P (mL/kg) | 18 (13.5) | 33 (5.8) | 34 (6.0) | 34 (6.9) |
| k a (1/hour) | 0.010 (11.7) | 0.009 (13.3) | 0.009 (13.8) | 0.009 (14.4) |
| F bio | 0.62 (8.0) | 0.73 (10.0) | 0.73 (11.5) | 0.72 (10.4) |
| PD parameters | ||||
| K SS (nM) | 1.99 (2.72) | 4.39 (3.99) | – | – |
| IC50/SC50 (nM) | – | – | 3.81 (25.1) | 124 (33.7) |
| k int (1/hour) | 0.013 (8.25) | 0.009 (7.14) | – | – |
| γ | – | – | 0.530 (3.81) | 0.646 (3.58) |
| k deg (1/hour) | 0.063 (2.98) | 0.046 (2.57) | 0.044 (2.77) | 0.007 (3.31) |
| M 0 (nM) | 0.141 (4.36) | 0.149 (4.34) | 0.144 (4.72) | 0.145 (4.94) |
| Vmax (nmol/hour/kg) | – | 0.002 (26) | 0.002 (25.2) | 0.002 (26.7) |
| K M (nM) | – | 10.1 (10.7) | 11.3 (10.4) | 10.8 (10.4) |
| Imax/Smax | – | – | 0.89 (1.58) | 6.67 (7.5) |
| Random and residual variability parameters | ||||
| RUV PK (%) | 25.5 (1.12) | 18.4 (1.58) | 18.3 (1.76) | 18.3 (1.67) |
| RUV PD (%) | 22.0 (1.06) | 22.0 (2.22) | 20.4 (2.08) | 20.5 (2.18) |
| IIV, CL (%) | 19.6 (30.5) | 21.3 (52.5) | 21.9 (61.5) | 21.6 (60.9) |
| IIV, V C (%) | 29.8 (36.4) | 28.9 (34.2) | 28.7 (35.4) | 28.8 (35.1) |
| IIV, M 0 (%) | 31.1 (27.7) | 29.1 (20.7) | 30.9 (22.7) | 31.4 (22.5) |
| IIV, k int (%) | 31.2 (18.8) | 27.3 (29.5) | – | – |
| IIV, vmax (%) | – | 62.1 (48.2) | 60.2 (45.7) | 61.8 (49.0) |
| IIV, IC50/SC50/(%) | – | – | 80.7 (28.9) | 77.8 (31.4) |
| IIV, Imax/Smax (%) | – | – | 4.4 (47.9) | 22.7 (42.6) |
CL, clearance; Fbio, bioavailable amount; IC50, half‐maximal inhibitory concentration; IIV, interindividual variability; Imax, maximum unbound systemic concentration; ka, absorption rate; kdeg, degradation constant; kint, first order internalization; km, kinetic metabolite; KSS, steady‐state constant; MM‐BK, Michaelis−Menten‐binding kinetic; MM‐IDR, Michaelis−Menten‐indirect response; OFV, objective function value; PD, pharmacodynamic; PK, pharmacokinetic; Q, intercompartmental distribution clearance; QSS, quasi‐steady state; RSE, relative standard error; RUV, residual unexplained variability; SC50, half‐maximal synthesis rate; Smax, maximum synthesis rate; Vc, volume of the central compartment; Vmax, maximal rate of metabolism; VP, volume of the peripheral compartment.
The PK parameters obtained from these two models indicated domagrozumab possesses attributes of a typical mAb (i.e., slow clearance (CL ~ 0.1 mL/hour/kg), small central volume (V C ~ 46 mL/kg), and limited distribution into tissues (V P ~ 18–33 mL/kg)). The models also showed domagrozumab is slowly absorbed (k a ~ 0.01 1/hour) after s.c. injection with a relative bioavailability of > 62%. The PD parameters obtained from these two models pointed to a myostatin half‐life of 11–15 hours (0.693/k deg), which increases approximately fivefold to 55–77 hours (0.693/k int) when it is bound to domagrozumab in a complex. The in vivo binding parameter calculated as the steady‐state binding constant was found to be 1.99–4.39 nM, whereas the estimated baseline myostatin (0.141–0.149 nM) was close to the observed baseline (0.06–0.296 nM). All the above parameters were estimated with high precision (% relative standard error (RSE) < 30%) except Q in the QSS model, which was estimated with a precision of 45%.
The interindividual variability (IIV) for the four common parameters between the QSS and MM‐BK models (CL, V C, M 0, and k int) were well‐estimated below 32%. In case of the MM‐BK model, the IIV was also estimated for vmax and was found to be about 60%. The residual errors in the domagrozumab PK were determined at 26% and 18% for the QSS and MM‐BK models, respectively. For both the QSS and MM‐BK models, residual error in myostatin was about 22%.
Characterizing total myostatin accumulation via IDR models
To better characterize total myostatin dynamics, two IDR models were also evaluated, which modified the PD framework while retaining the PK module from the MM‐BK model. Both IDR models were capable of capturing the postdose accumulation of total myostatin. Examining total myostatin predictions for these two IDR models showed the alternative mathematical structure was indeed better at capturing the PD profiles as it overcame the plateauing effect observed with the QSS and MM‐BK models (compare Figure 3 a and Figure S1 A with Figure 3 b and Figure S1 B). The superior performance of these IDR models was also evident from their substantially lower OFVs in comparison to the MM‐BK model (see Table 1, MM‐IDR2 model OFV = −12,863 and MM‐IDR3 model OFV = −12,857). As expected from the similarity of the PK module (Figure S2 ), the estimates of various PK parameters (CL, V C, Q, V P, vmax, K M, k a, and bioavailable amount F bio) for the two IDR models were almost identical to those of the MM‐BK model. PD parameter M 0 was comparable across all the models, which may be ascribed to the fact that the underlying PD module (i.e., M tot differential equation) is identical in case of the absence of domagrozumab (note setting D C = 0 in all four models). As expected, k deg was similar between QSS and MM‐BK models. Although k deg was also numerically similar for MM‐IDR2, it was approximately sixfold lower for MM‐IDR3. It should be noted here that the k deg does not have the same mathematical meaning when comparing between the more mechanistic (QSS and MM‐BK) vs. the semimechanistic (MM‐IDR2 and MM‐IDR3) models.
All parameters for the two IDR models were well‐estimated (%RSE < 30%). The IIVs for three common parameters between MM‐IDR2 and MM‐IDR3 models (CL, V C, and M 0) were about 30% or less, whereas the IIV for the fourth common parameter vmax was about 60%, which is in line with the estimate for the MM‐BK model. The IIV estimates for IC50 and SC50 were substantially higher at about 80%, whereas for Imax and Smax they were below 25%. The residual errors for domagrozumab and myostatin were estimated at about 18% and 20%, respectively, for both IDR models.
Evaluating model performance through visual predictive checks and target coverage predictions
The previous section showed that the MM‐IDR2 model performs best in terms of characterizing both the domagrozumab nonlinear PK and the total myostatin accumulation. However, a reasonable description of the available data is only one aspect of the model evaluation and an equally important feature is its predictive performance, which can be assessed through visual predictive checks (VPCs) intending to ultimately determine its usefulness. Note, we did not expect VPCs for the QSS model to perform well, as its characterization of the PK/PD data is poorest among all four models, neither for the MM‐IDR3 model, as its overall performance is quite comparable to that of the MM‐IDR2 model. Comparing the VPCs for total myostatin for the MM‐BK and MM‐IDR2 models (Figure 4) shows the latter performs better with regard to the prediction at higher doses (≥ 10 mg/kg) as it accommodates high concentrations better. Because these two models were built on the same PK module, the VPCs for domagrozumab serum concentrations are expected to perform identical and, hence, are not shown.
Figure 4.
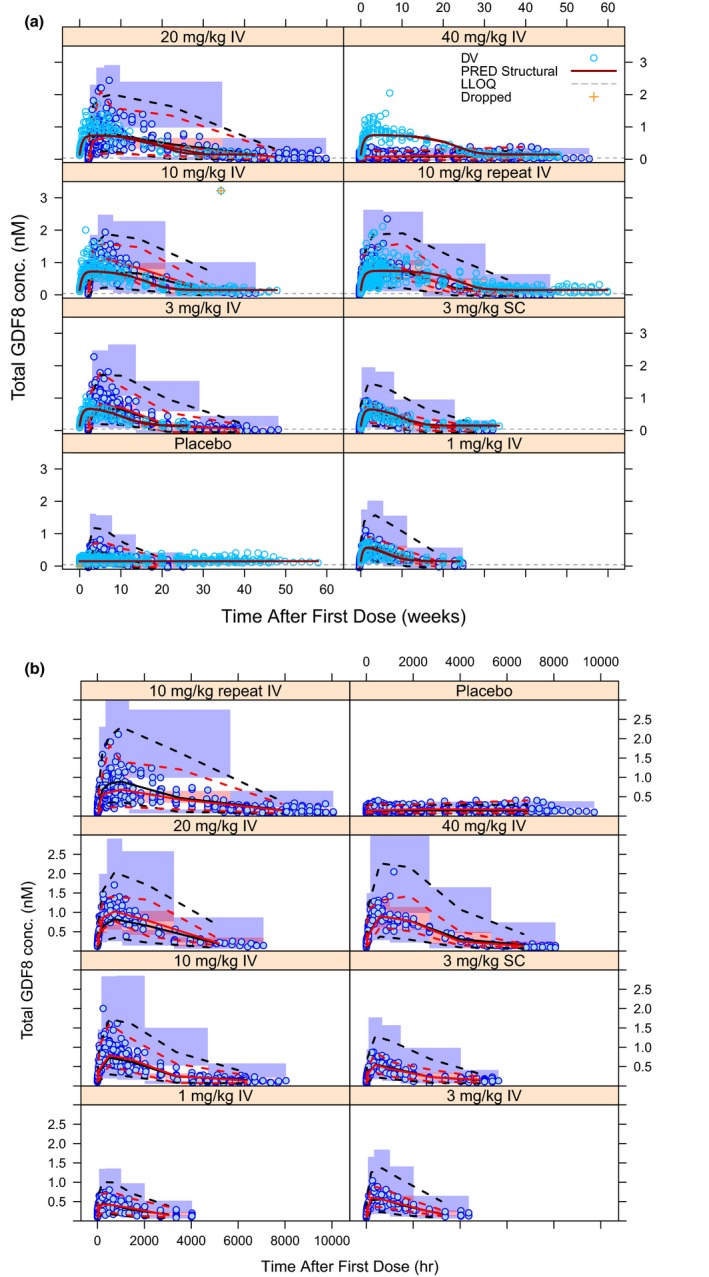
Visual predictive check for total myostatin concentrations for Michaelis−Menten‐binding kinetic model (a) and Michaelis−Menten‐indirect response 2 model (b). Blue circles are observations. Solid red and black curves represent median of observed data and model predictions. Dashed red and black curves represent 2.5th and 97.5th percentiles of observed data and model predictions. Shaded regions represent the simulation based 95% confidence interval for the corresponding percentiles. GDF8, growth and differentiation factor‐8. PRED, population prediction.
A quantitative understanding of PK/PD and its relationship to target coverage is fundamental to drug development; hence, predictions of target coverage for the MM‐BK and the MM‐IDR2 model are essential to be compared. Although, as expected, simulations (see Model simulations; domagrozumab 5 mg/kg every 4 weeks for 16 weeks followed by 20 mg/kg every 4 weeks for 16 weeks followed by 40 mg/kg every 4 weeks for 16 weeks) for the domagrozumab PK reveal no difference across the two models (Figure 5 a,b), the dynamics of target coverage are quite different (Figure 5 c,d). Although, for the MM‐BK model, the serum target coverage ranges from 90% after 4 weeks to nearly 100% after 48 weeks, the MM‐IDR2 model predicts the serum target coverage to range only from 40% after 4 weeks to about 80% after 48 weeks. This difference in target coverage is a direct consequence of the difference in the total myostatin accumulation (Figure 5 e,f, also observed earlier in Figure 3). Because the domagrozumab PK is identical for both models, the model with larger accumulation of total myostatin (i.e., the MM‐IDR2 model) translates into lower target coverage, despite having similar baseline myostatin levels.
Figure 5.
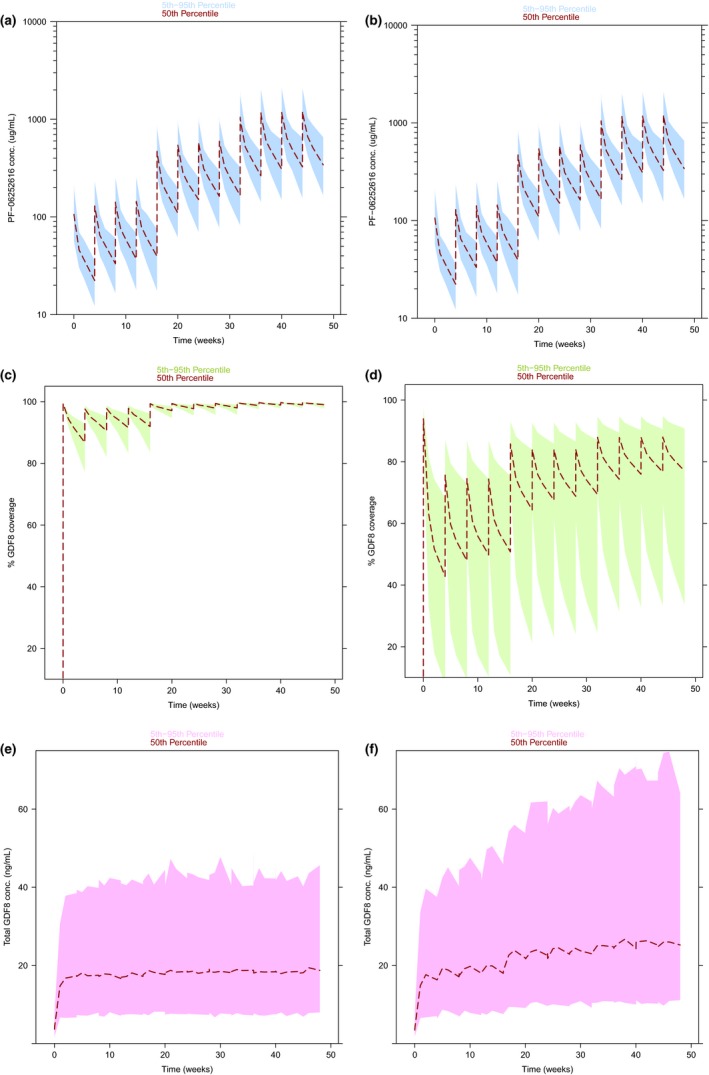
Domagrozumab pharmacokinetic, target coverage, and total myostatin predictions for Michaelis−Menten‐binding kinetic model (a,c,e) and Michaelis−Menten‐indirect response 2 model (b,d,f). Dashed curves represent median profiles and shaded regions represent 95% prediction intervals. The dosing regimen selected for these simulations is the one being currently tested in patients with Duchenne muscular dystrophy; 5 mg/kg every 4 weeks for 16 weeks followed by 20 mg/kg every 4 weeks for 16 weeks followed by 40 mg/kg every 4 weeks for 16 weeks.
Discussion
To overcome model overparameterization and convergence issues with the full TMDD model, different approximations have been proposed, namely the quasi‐equilibrium, QSS and MM models.9, 10 Another model that has broad applicability due to simple model structure and flexibility is an indirect response model. Interestingly, Gibiansky and Gibiansky12 compared the relationship between TMDD and indirect response models and demonstrated that indirect response models could be used to estimate TMDD model parameters and unobservable free target concentrations important for PD modeling. The objective of this current analysis was to select suitable model candidates from four such probable FIH population PK/PD models of domagrozumab namely, a QSS, a MM‐BK, an MM‐IDR2, and an MM‐IDR3 model (Figure 1). To arrive at the final model, an iterative process was considered. The PK part of the model was first attempted (except for the QSS model) followed by a simultaneous PK/PD modeling approach. The selected model was to be used for dosage selection of domagrozumab in patients with DMD aged 6–10 years old. To translate the model parameters from healthy volunteers to patients with DMD and to simulate coverage and select dosage in patients with DMD, first, literature was reviewed to identify if data exist that could justify model translation. Then the following assumptions about similarity were made to simulate coverage in patients with DMD; on the variability, the domagrozumab exposure‐PD effect relationship and the impact of covariates between healthy volunteers and patients with DMD.
The comparative analysis showed that among the two approximations of a full TMDD model—QSS and MM‐BK—only the latter is capable of capturing the nonlinear decline in the domagrozumab PK (Figure 2). As mentioned in the Methods section, a linear two compartment model was also explored as an alternative, to characterize domagrozumab's PK. However, as observed in Figure 2 a,b the PK profile has an inflexion point near 10 μM concentration. A linear model was not able to capture the shape of the profile (Figure S4 ), in contrast to a model with both a linear and a nonlinear component.
There are a number of plausible reasons why the MM‐BK model better captured the nonlinear decline. The QSS model, which preserves more of the mechanistic details of the general TMDD model, fails to capture the nonlinear PK as the parameter controlling it, K SS, is a binding constant primarily governed by domagrozumab binding to myostatin and the latter's consequential accumulation. The MM‐BK model, however, breaks the connection between PK and PD, permitting more flexibility through independent control of nonlinear terms in PK and PD. Specifically, the MM‐BK model enables an independent control by allowing the binding parameters K SS and K M to take on different values. Essentially the assumption K SS ≠ K M implies the nonlinear clearance of mAb is not solely due to target binding and might include binding to other forms of target or nonspecific binding. As such, the MM‐BK approximation of the full TMDD model is especially useful in characterizing a nonlinear PK when either known biology does not support a direct link between PK and observed PD or an incomplete understanding of the underlying biology prevents incorporating potentially relevant mechanistic features. Interestingly, Yan et al.13 suggested that even though the PK of a drug follows TMDD properties, this might not always be discernable from concentration‐time profiles based on goodness of fit and precision metrics, unless the limit of detection allows for the measurement of low concentrations and/or a sufficient dose‐ranging study is conducted. Under such limiting conditions, precise parameter estimates may not be achievable with a TMDD model, and the MM model would be preferred.
Further comparisons between the MM‐BK and IDR models revealed that the IDR models are better at characterizing myostatin dynamics (Figure 3) because they allow for sublinearity (γ < 1) in the mathematical framework describing the PD. The better performance of the IDR models may be explained by the parameters controlling the nonlinear PD response in the IDR and the MM‐BK models. A previous theoretical work showed that the PD modules of a QSS model and an MM‐IDR2 model with hill coefficient γ = 1 are mathematically equivalent.12 This result was obtained by a simple rearrangement of the various terms in the M tot differential equation and consequent reparameterization, such that Imax = (1 − (k int/k deg)) and IC50 = K SS describe the relationships for mathematical equivalence of the two models. Although this analysis was performed with a QSS model, these relationships are also applicable to the MM‐BK model as the two models utilize the same PD framework. Substituting k int and k deg with the MM‐BK model parameter estimates provides Imax = 0.8 and IC50 = 4.39 nM, which are comparable with the parameter values estimated by fitting our version of the MM‐IDR2 model that includes a Hill coefficient, γ ≠ 1.
As such, the MM‐IDR2 model is equivalent to the MM‐BK model in most aspects except for the Hill coefficient (γ = 0.530), which makes the PD response sublinear and more graded, and this, in turn, is reflected in the absence of a plateauing effect. The better performance of the MM‐IDR3 model might also be due to a sublinear (γ = 0.646) PD response, although it is difficult to rule out the effect of Smax and SC50 as they are not related to the MM‐BK model parameters due to a lack of mathematical equivalence.
On the contrary, the MM‐BK model was preferable due to the consequence of the fit of the data that provided reasonable prediction intervals of target coverage (Eq. (9), Figure 5). It should be noted here that the true coverage could only be corroborated from the model. However, with a more sensitive free myostatin assay, where actual myostatin free concentrations were measured over time, an observed coverage calculation would be feasible.
Overall, the MM‐BK model was most desirable as it provided a balance among mechanistic explanation, capturing exposure, and target modulation with precision and predicting target coverage. Further, with majority of RSEs below 15% and shrinkage not > 25%, the MM‐BK model was selected for further model development.
It is important to note that the various models analyzed here are simplistic representations of the known physiological processes. For example, these models ignore myostatin synthesis and distribution in peripheral and target tissues, and also disregard the competition between domagrozumab and myostatin receptor for myostatin binding sites. Although these simplifications enable robust PK/PD analysis by reducing model dimensionality, they compromise mechanistic understanding of observed data. For instance, the absence of mechanistic components may undermine the understanding of various processes that could lead to identifying the nonlinearity in the domagrozumab PK appropriately. In addition, it may not readily explain why domagrozumab binding to soluble target myostatin leads to rapid clearance of the drug target complex.
Preliminary target coverage can be estimated using empirical approaches (e.g., using a simple drug‐receptor binding equation). However, modeling and simulation is important to understand coverage over time and uncertainty around it. Time and uncertainty in coverage, in turn, will drive the dose and regimen selection to ensure a certain percentage of patients can achieve and maintain a certain coverage over time.
A quantitative understanding of target coverage, therefore, is essential for drug development to select dose regimens that might provide an adequate coverage for a required duration. This becomes even more important in accelerated programs where data, for instance dose ranges, may be limited. Of the four models studied here only the QSS and MM‐BK models include an appropriate level of a mechanistic component of target binding to directly predict target coverage. In the past, IDR models have been shown to be mathematically equivalent to the QSS model, thereby arguing that IDR models are, in fact, mechanistic models capable of predicting target coverage.12 Elsewhere, mathematical equivalence was utilized to build a relationship between tocilizumab and target coverage (unbound sIL‐6R concentrations), relating target coverage to changes in neutrophil and platelet counts.11 Similarly, our MM‐IDR2 model developed here was used to predict target coverage. Comparing target coverage predictions for our MM‐BK and MM‐IDR2 models showed that the latter resulted in significantly larger prediction intervals. Despite better characterization of PK/PD data by the MM‐IDR2 model (only based on a change in the OFV) it is not preferable because of the larger uncertainty in the predictions, partly driven by the large IIV in IC50 and the model structure. Thus, choosing the “right” model based on statistical attributes does not always enable application to clinical trial design. In this exercise, we chose the MM‐BK model as the most appropriate model as it: (i) provided reasonable (although not the best) fit; (ii) allowed target coverage simulations with less uncertainty for phase II dose selection; and (iii) allowed for mechanistic explanation of the PD modulation.
Yan et al.13 provided guidelines using QSS and MM models for TMDD model selection. Recommendations included fitting array of models to data, assessing and comparing model precision parameters, and goodness of fit criteria. This current work builds on those recommendations and highlights the importance of using M&S approaches appropriately after thorough consideration of the objectives behind the analyses as the molecule transitions between different phases of drug development. In summary, this model comparison highlights that goodness of a model fit can only be one aspect of a model evaluation, model structure, and its impact on prediction uncertainty influences model usability and should be considered in model selection as well.
Funding
The analyses presented here were sponsored by Pfizer.
Conflict of Interest/Disclosure
A.T. was an employee of Pfizer and held significant number of Pfizer stocks. I.B. was an employee of Pfizer and holds significant number of Pfizer stocks. P.L.S.C. and L.H. are employees of Pfizer and hold significant number of Pfizer stocks/options.
Author Contributions
A.T., I.B., P.L.S.C., and L.H. wrote the manuscript. I.B. and L.H. designed the research. A.T., I.B., P.L.S.C., and L.H. performed the research. A.T., I.B., and P.L.S.C. analyzed the data.
Supporting information
Figure S1. Predictions of total myostatin serum concentration for QSS and MM‐IDR3 models.
Figure S2. Predictions of free Domagrozumab serum concentration for MM‐IDR2 and MM‐IDR3 models.
Figure S3. Diagnostic plots for the final models.
Figure S4. Predictions of free Domagrozumab serum concentration for Linear 2 compartment PK model following single and repeat dose administrations of Domagrozumab.
Acknowledgment
Abhinav Tiwari, a young and budding clinical pharmacologist and Pfizer colleague, passed away in 2018. Dr. Tiwari had an acute, severe condition that remained undiagnosed. During his remission, he was concerned about the status of this manuscript, which reflects on his perseverance and dedication. The authors wanted to acknowledge Dr.Tiwari by completing this work.
References
- 1. Chien, J.Y. , Friedrich, S. , Heathman, M.A. , de Alwis, D.P. & Sinha, V. Pharmacokinetics/pharmacodynamics and the stages of drug development: role of modeling and simulation. AAPS J. 7, 544–559 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Huang, S.M. , Abernethy, D.R. , Wang, Y. , Zhao, P. & Zineh, I. The utility of modeling and simulation in drug development and regulatory review. J. Pharm. Sci. 102, 2912–2923 (2013). [DOI] [PubMed] [Google Scholar]
- 3. Bhattacharya, I. et al Safety, tolerability, pharmacokinetics, and pharmacodynamics of domagrozumab (PF‐06252616), an antimyostatin monoclonal antibody in healthy subjects. Clin. Pharmacol. Drug Dev. 7, 484–497 (2017). [DOI] [PubMed] [Google Scholar]
- 4. Bhattacharya, I. , Manukyan, Z. , Chan, P. , Heatherington, A. & Harnisch, L. Application of quantitative pharmacology approaches in bridging pharmacokinetics and pharmacodynamics of domagrozumab from healthy subjects to pediatric patients with Duchenne muscular disease. J. Clin. Pharmacol. 58, 314–326 (2018). [DOI] [PubMed] [Google Scholar]
- 5. Mager, D.E. & Jusko, W.J. General pharmacokinetic model for drugs exhibiting target‐mediated drug disposition. J. Pharmacokinet. Pharmacodyn. 28, 507–532 (2001). [DOI] [PubMed] [Google Scholar]
- 6. Dua, P. , Hawkins, E. & van der Graaf, P.H. A tutorial on target‐mediated drug disposition (TMDD) models. CPT Pharmacometrics Syst. Pharmacol. 4, 324–337 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Sharma, A. & Jusko, W.J. Characteristics of indirect pharmacodynamic models and applications to clinical drug responses. Br. J. Clin. Pharmacol. 45, 229–239 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Dayneka, N.L. , Garg, V. & Jusko, W.J. Comparison of four basic models of indirect pharmacodynamic responses. J. Pharmacokinet. Biopharm. 21, 457–478 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Gibiansky, L. , Gibiansky, E. , Kakkar, T. & Ma, P. Approximations of the target‐mediated drug disposition model and identifiability of model parameters. J. Pharmacokinet. Pharmacodyn. 35, 573–591 (2008). [DOI] [PubMed] [Google Scholar]
- 10. Gibiansky, L. & Gibiansky, E. Target‐mediated drug disposition model: approximations, identifiability of model parameters and applications to the population pharmacokinetic‐pharmacodynamic modeling of biologics. Expert Opin. Drug Metab. Toxicol. 5, 803–812 (2009). [DOI] [PubMed] [Google Scholar]
- 11. Gibiansky, L. & Frey, N. Linking interleukin‐6 receptor blockade with tocilizumab and its hematological effects using a modeling approach. J. Pharmacokinet. Pharmacodyn. 39, 5–16 (2012). [DOI] [PubMed] [Google Scholar]
- 12. Gibiansky, L. & Gibiansky, E. Target‐mediated drug disposition model: relationships with indirect response models and application to population PK‐PD analysis. J. Pharmacokinet. Pharmacodyn. 36, 341–351 (2009). [DOI] [PubMed] [Google Scholar]
- 13. Yan, X. , Mager, D.E. & Krzyzanski, W. Selection between Michaelis‐Menten and target‐mediated drug disposition pharmacokinetic model. J. Pharmacokinet. Pharmacodyn. 37, 25–47 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Predictions of total myostatin serum concentration for QSS and MM‐IDR3 models.
Figure S2. Predictions of free Domagrozumab serum concentration for MM‐IDR2 and MM‐IDR3 models.
Figure S3. Diagnostic plots for the final models.
Figure S4. Predictions of free Domagrozumab serum concentration for Linear 2 compartment PK model following single and repeat dose administrations of Domagrozumab.


