Predictive modeling in urgent care: a comparative study of machine learning approaches

Abstract

Objective

The growing availability of rich clinical data such as patients’ electronic health records provide great opportunities to address a broad range of real-world questions in medicine. At the same time, artificial intelligence and machine learning (ML)-based approaches have shown great premise on extracting insights from those data and helping with various clinical problems. The goal of this study is to conduct a systematic comparative study of different ML algorithms for several predictive modeling problems in urgent care.

Design

We assess the performance of 4 benchmark prediction tasks (eg mortality and prediction, differential diagnostics, and disease marker discovery) using medical histories, physiological time-series, and demographics data from the Medical Information Mart for Intensive Care (MIMIC-III) database.

Measurements

For each given task, performance was estimated using standard measures including the area under the receiver operating characteristic (AUC) curve, F-1 score, sensitivity, and specificity. Microaveraged AUC was used for multiclass classification models.

Results and Discussion

Our results suggest that recurrent neural networks show the most promise in mortality prediction where temporal patterns in physiologic features alone can capture in-hospital mortality risk (AUC > 0.90). Temporal models did not provide additional benefit compared to deep models in differential diagnostics. When comparing the training–testing behaviors of readmission and mortality models, we illustrate that readmission risk may be independent of patient stability at discharge. We also introduce a multiclass prediction scheme for length of stay which preserves sensitivity and AUC with outliers of increasing duration despite decrease in sample size.

INTRODUCTION AND BACKGROUND

The increasing adoption of electronic health records (EHR) systems has brought in unprecedented opportunities for the field of medical informatics. There are lots of research works on utilization of such data on different tasks such as predictive modeling,¹ disease subtyping,² and comparative effectiveness research.³ Machine learning (ML) approaches are common tools for implementing these tasks.

Because of the popularity of artificial intelligence (AI) in recent years, ML, as a way of realizing AI, has been developing rapidly. Tons of ML approaches have been proposed. However, from an application perspective, the users would have difficult times on choosing the right ML algorithm for the right problem. This is the reason why we usually see different papers adopted different approaches but without explicit explanations on the motivation and rationale.

In this article, we aim to fill in such gap by conducting a systematic comparative study on the applications of different ML approaches in predictive modeling in health care. The scenario we care about specifically is in Emergency Room/Urgent Care, where fast pace decisions need to be made to determine acuity of each visit and allocate appropriate amount of resources. A growing community in medical informatics focusing on quality improvement has elucidated the relevance of these factors to medical errors and overall quality of care.⁴ Accurate predictive modeling can help recognize the status of the patients and environment in time and allow the decision makers to work out better plans. Many research on predictive modeling in emergency room has been conducted in recent years, such as identification of high-risk patients for in-hospital mortality,⁵ length of intensive care unit (ICU) stay outliers,⁶ 30-day all-cause readmissions, and predicting differential diagnoses for admissions,^7,8 which have been proven to be useful in different aspects including decreasing unnecessary lab tests⁹ and increasing the accuracy of inpatient triage for admission decisions.^10,11

In terms of ML algorithms, many of them have been applied in those tasks.^12–15 In particular, since 2012, deep learning models have achieved great success in many applications involving images,^16,17 speech,¹⁸ and natural language processing.¹⁹ Researchers in medical informatics have also been exploring the potentials of those powerful models.²⁰ Lipton et al showed that recurrent neural networks (RNN) using only physiologic markers from EHR can achieve expert-level differential diagnoses over a wide range of diseases.²¹ Choi et al showed that by using word embedding techniques for contextual embedding of medical data, diagnostic, and procedural codes alone can predict future diagnoses with sensitivity as high as 0.79.²² More recently, benchmark performances for decomposition and length of stay (LOS) predictions have also been investigated.²³ The key technical differences in these studies come from 2 major components: (1) patient representation which represents each patient into a structured data point for modeling, and (2) learning algorithm which infers patterns from the patient representations and delivers a predictive model. In this article, we will compare several state-of-art patient representation and ML algorithms across 4 benchmark tasks and discuss clinical insights derived from the results.

METHODS

Data set description

The Medical Information Mart for Intensive Care (MIMIC-III) database obtained from Physionet.org was used in our study.²⁴ This data set was made available by Beth Israel Hospital and includes deidentified inpatient data from their critical care unit from 2005 to 2011. MIMIC-III captures hospital admission data, laboratory measurements, procedure event recordings, pharmacologic prescriptions, transfer and discharge data, diagnostic data, and microbiological data from 46 520 unique patients. In total, there were 58 976 unique admissions and 14 567 unique International Statistical Classification of Diseases and Related Health Problems (ICD)-9 diagnostic codes.²⁴ When considering only nonpediatric patients (age 18) and discounting admissions without multiple transfers or length of ICU stay <24 h, there were a total of 30 414 unique patients and 37 787 unique admissions. A summary of demographic distribution of patients can be found in Supplementary Table S1.

Predictive tasks in assessment

Four learning tasks are adopted in our study as the benchmarks of those ML algorithms.

In-hospital mortality

In-hospital mortality task was modeled as a binary classification problem. In total, there were 4155 adult patients (13%) who experienced in-hospital mortality, of which 3138 (75.5%) were in the ICU setting. Traditionally, SAPS and SOFA scores are used to evaluate mortality risk.²⁵ Depending on the disease, SAPS-II predicts within a wide range (0.65–0.89) of area under receiver operating characteristic curve (AUC) scores, depending on the critical conditions being studied.²⁶ Our study evaluates performance of predictive models using AUC. Sensitivity, specificity, and f1-scores were included to aid the interpretation of AUC scores due to the presence of class-imbalance.

Length of stays

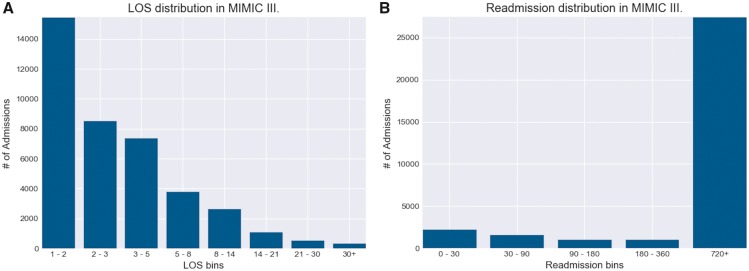
Prediction of length of ICU stays remain an important task for identifying high-cost hospital admissions in terms of staffing cost and resource management.⁶ Accurate predictions of outliers in ICU stays (eg 1–2 weeks) may greatly improve inpatient clinical decisions. We formulated LOS as a multiclass classification problem using bins of lengths (1, 2), (3, 5), (5, 8), (8, 14), (14, 21), (21, 30), (30+, ) to reflect the range of possible LOS values in terms of days. As shown in Figure 1, this binning scheme smoothly captured the exponential decay of LOS with increasing number of days.

Figure 1.

Distribution of length of stays (LOS) and readmission in MIMIC-III. A, The Distribution of patient volume for each ICU length of stay range. This binning scheme allowed for patient volumes to follow smooth exponential decay with increasing LOS time. Bins 5–8 and 8–14 are of particular interest, as these are frequently used as lower thresholds for defining “LOS outliers” for identifying high-cost admissions. B, The distribution of patient volume for each time-to-readmission range, measured in days. Due to the fact that few patients in MIMIC-III had multiple admissions, the amount of patients that fall under the 720+ days category greatly outnumbers the rest. MIMIC-III, Medical Information Mart for Intensive Care.

To evaluate the performance on LOS task, AUC, f1-score, sensitivity, and specificity were calculated for each bin, and a microaveraged AUC and f1 scores were calculated for the overall performance of the model across all bins. AUC and f1-scores were chosen to facilitate the interpretation of LOS performance in comparison with other tasks.

Differential diagnoses

We examined the top 25 most commonly appearing conditions (ICD-9 codes) in MIMC-III using a multilabel classification framework (see Supplementary Material Section S8.3). Supplementary Table S2 shows these diagnoses with their associated absolute and relative prevalence (%) among the MIMIC-III population. To evaluate the performance of predictions, AUC, f1-score, sensitivity, and specificity scores were calculated for each disease label, and a microaveraged AUROC and f1-score were calculated for each admission.

Readmission prediction

We investigate 2 types of readmissions: all-cause 30-day readmission, where number of positive cases amount to 1884 (5.1%) of total admissions; and variable length readmissions. For the latter, we use bins to generate 6 classes (bins) associated with each admission that correspond to observed time-to-readmission: (1, 30), (30, 90), (90, 180), (180, 360), (360, 720), (720+, ), measured in days, and the prediction problem is formulated as a multiclass prediction problem. Both approaches are evaluated with AUC, F1, sensitivity, and specificity scores.

Patient features

Diagnosis codes

There are 14 567 unique ICD-9 diagnostic codes in MIMIC-III data, which would lead to high-dimensional very sparse representations for patients if we treat each distinct code as 1D.²⁷ Therefore, we use the ICD-9-CM instead. The ICD-9-CM codes are designed to capture the group-level disease specificity by only using the first 3 letters of their full length codes. In this way, we reduce the feature dimension to 942 ICD-9 group codes. Supplementary Figure S1 shows distribution of diagnostic codes and diagnostic categories in MIMIC-III.

Temporal variables

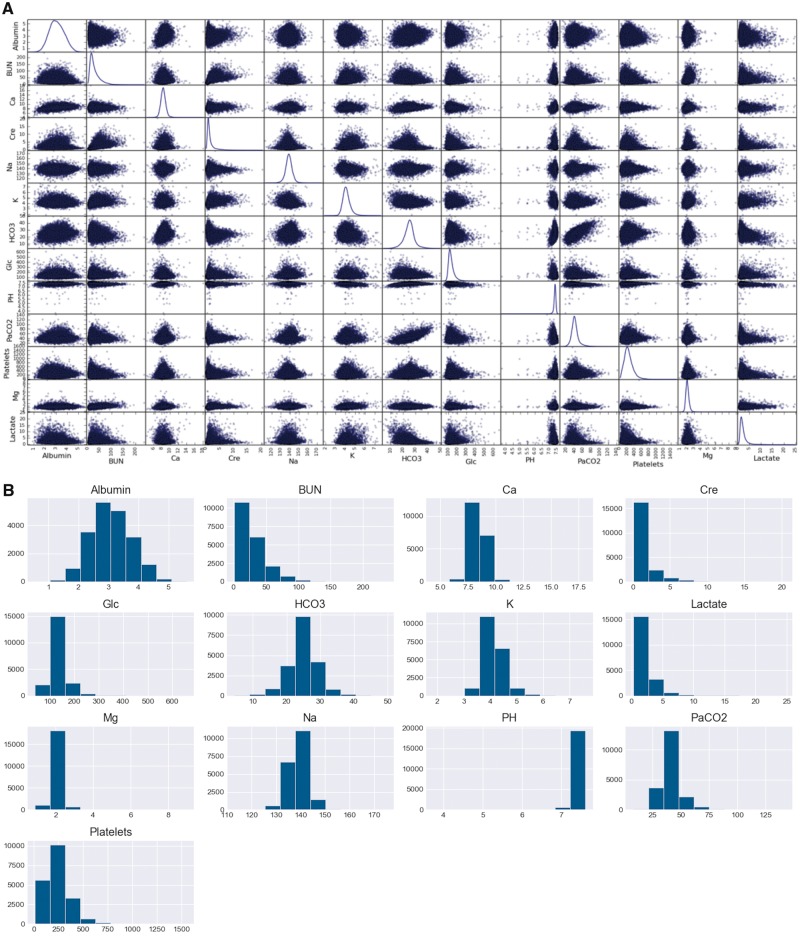
To capture the temporal patterns of complex diseases, we also consider temporal variables of the 6 most frequently sampled vital signs and top 13 most frequently sampled laboratory values for downstream prediction tasks. Since sampling frequency differs greatly per inpatient admission, we took hourly averages of time-series variables up to the first 48 hours of each admission across all prediction tasks. This approach resembles hourly sampling methods from previous studies.^21,23 Each temporal variable was standardized by taking the difference with its mean and dividing by its standard deviation. Figure 2 further summarizes the distributions of these variables. Missing data were imputed with the carry-forward strategy at each time-stamp.

Figure 2.

Distribution of physiologic time-series variables in MIMC-III. A, The kernel density distribution of lab values used in the comparative study. Each variable follows a Gaussian distribution with magnesium and PH having the lowest variance. B, The histogram view of laboratory variable distributions. BUN, creatinine, platelets, and serum lactate measurements demonstrate right-skew behavior while PH is left-skewed.

Demographics

In addition, we also consider patients’ demographic variables such as age, marital status, ethnicity and insurance information for each patient. Age was quantized into 5 bins (18, 25), (25, 45), (45, 65), (65, 89), (89+, ).

Feature representations

Based on the aforementioned types of features, performances were compared across 4 types of feature representation strategies: (i) Physiologic features only which is denoted x19 (19 physiologic time-series variables) for sequential and x48 (48 h average) for classic models. (ii) Diagnostic histories only, denoted as w2v for word2vec embeddings²⁸ and onehot²⁹ for one-hot vector representations. (iii) Combined visit-level and demographic information-level representation as denoted by w48 for classic models and x19_h2v or x19_demo for sequential models. (iv) Embedded sentence-level representation,¹⁵ denoted as sentences for all kinds of models. Specifics of these representations can be found in the Supplementary Material of this article.

Visit-level representation (physiologic features only)

For collapse models [Support Vector Machines (SVM), Logistic Regression (LR), Ensemble Classifiers, and Feed-Forward MLPs), raw hourly averages for each time-series variable was converted into 5 summary features per variable: minimum value, maximum value, mean, standard deviation, and number of observations for the duration of the admission. We denote this representation as X48. For sequential models, we simply use the standardized hourly average data per admission to establish this baseline, denoted as X19.

History-level representation (diagnostic history only)

In more recent papers, it has been proposed that sequential data may be more effectively represented in embedded representations, where each event is mapped onto a vector space of related events.^22,28 Embedding techniques such as word2vec allow for sparse representations of medical history to be transformed into dense word vectors whose mappings also capture contextual information based on co-occurrence.

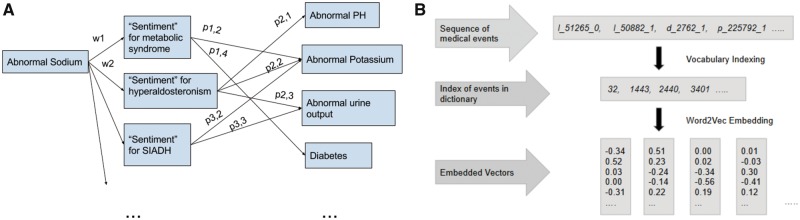
As shown in Figure 3, each admission was treated like a sentence, with medical events occurring as neighboring words. In a sliding window fashion, word2vec takes the middle word of each sliding window and learns the most likely neighboring words. This representation strategy was denoted as w2v. As an additional baseline, sum of one-hot vectors was also used to represent diagnostic history for collapse models, denoted as onehot.

Figure 3.

word2vec embedding of medical events. A, The general architecture of skip-gram embedding used to map sparse one-hot representation of medical codes into dense word vector embeddings. Given a series of discrete medical events, center, and neighboring events are generated in a sliding window fashion, where the neural network learns the relationships nearby words for contextual representation. The weights which map input events onto the hidden layers are used as a filtering layer for future inputs for prediction tasks. B, An overview of the word2vec pipeline for transforming input features from the EHR into word vector representations. Sentence-level representation is being shown here, but word2vec can be used exclusively for diagnostic codes in visit-level representations as well.

Combined representation

Mixed time-series and static representations were used for both sequential and collapse models. For collapse models, Word2Vec embeddings of diagnostic history was concatenated with summary features from time-series data as features for prediction. This was denoted as W48 (w2v + x48). For sequential models, we utilized 2 separate layers of input: the x19 input was fed into recurrent layer, and its output was merged with the w2v input layer. The hierarchical sequential models were labeled as x19_h2v when both diagnostic and demographic histories were used for the w2v input, and x19_demo when only demographic word2vec inputs were used. The latter case applied only to the prediction of differential diagnoses, where diagnostic history of admissions were used as labels rather than as features.

Embedded representation

In this representation scheme, both diagnostic history and time-series variables were treated as word vectors for representation. For each admission, time-series data (l_) and diagnostic history (d_) in the sequence they were encountered during the admission. To differentiate the type of event, each feature is labeled with prefix “l_” for labs or vital signs and “d_” for diagnosis. Time-series variables were discretized and included in the feature vector depending on whether or not the observed event was within 1 standard deviation of its mean value. For example, if an observed lab value (eg l_51265, sodium) was 2 standard deviations above its normal value, the sentence vector for the admission would include the ITEMID of the lab (eg [ .., l_52165, d_341, … ]). In this setting, we were able to map abnormal time-series values with frequently co-occurring diagnostic codes in the same word-vector space.

Types of predictive models

Collapse models

Collapse models are standard ML models which do not consider temporal information. In this study, we examined SVM, Random Forest (RF), Gradient Boost Classifier (GBC), LR, and Feed-forward Multi-Layer Perceptron (MLP).

Sequential models

Two RNN models were examined in this study: the bidirectional Long Short-term Memory (LSTM) model^30,31 and the Convolutional Neural Network w/ LSTM model (CNN-LSTM).³² Regularization was implemented with Dropout and L2 regularization at each LSTM layer. For binary and multilabel classification tasks, sigmoid activation function was used at the fully connected output layer, and binary cross-entropy was used as loss function. For the multiclass case (eg LOS and readmission bins), softmax activation was used at the output layer with categorical cross-entropy as loss function. Adam optimizer with initial learning rate of 0.005 was used in both cases.

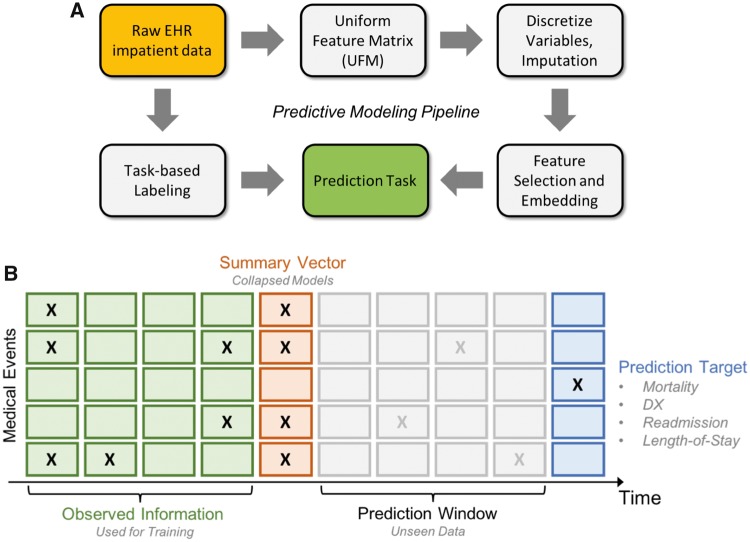
Refer to Supplementary Material Section S8.2 for details about the mechanics of these models as well as the hyperparameter tuning procedures. Our code is available at https://github.com/illidanlab/urgent-care-comparative for the features and models presented in this article. Figure 4 provides an overview of the workflow of our experiment from preprocessing to prediction.

Figure 4.

Overview of workflow. A, The overview of our experimental pipeline from preprocessing to prediction. Raw EHR data is first processed into Uniform Feature Matrix (UFM), where key features such as hourly averaged vital signs, ICD-9 group codes and lab values are extracted per patient and aligned. Labels for each task is then extracted for each relevant patient. Additional preprocessing is performed for different features (eg embedding, described below). Once features are normalized and aligned, prediction is performed for each task. B Uniform Feature Matrix (UFM) used for prediction. The “prediction window” refers to the elapsed time between data used for feature construction and the event of prediction (eg 30 days postdischarge in readmission).

RESULTS

In-hospital mortality prediction

Table 1 summarizes the top performances of models on the mortality prediction task. Sequential models significantly out-performed the collapse models in AUC (P-value <.05 for all sequential vs collapse comparisons, see Supplementary Table S6.) and achieved the highest AUC score of 0.949 (0.003 std). In general, diagnostic codes alone yielded the poor performance for both classic and sequential models. Time-series data alone achieved the closest performance to combined visit- and history-level representations for both sequential and classical models. In fact, the highest sensitivity score (0.911) was achieved by vanilla LR with only physiologic data (x48). Sentence-level representation yielded consistent scores in the 0.70–0.76 range across most models, but it did not capture the same level of sensitivity and specificity as did exclusively time-series and mixed feature representations.

Table 1.

Summary of top performing mortality models w/ representation schemes

Rank	Model	AUC	F1	Sn	Sp	P-value
Classic models
1	MLP w/ W48	0.855 (0.0058)	0.546 (0.011)	0.877 (0.0071)	0.834 (0.007)	.0019
2	RF w/ W48	0.843 (0.0073)	0.523 (0.005)	0.864 (0.019)	0.821 (0.0052)	.0018
3	GBC w/ W48	0.773 (0.0098)	0.437 (0.013)	0.759 (0.024)	0.786 (0.017)	.014
Sequential models
1	LSTM w/ x19 + h2v	0.949 (0.003)	0.623 (0.012)	0.883 (0.016)	0.887 (0.0073)	.0001
2	CNN-LSTM w/ x19+h2v	0.940 (0.0071)	0.633 (0.031)	0.852 (0.04)	0.895 (0.023)	.0022
3	CNN-LSTM w/ x19	0.933 (0.006)	0.587 (0.025)	0.854 (0.016)	0.868 (0.018)	.0025

Note: Each performance metric is evaluated across 5 stratified shuffle splits. The mean performance is reported with the standard deviation in parenthesis. The P-value is calculated by comparing the AUC of a given model with the baseline performance with LR and physiologic markers. More extensive pairwise statistical t-tests are shown in Supplementary Table S6.

Abbreviations: AUC: area under receiver operating characteristic curve; F1: f1-score; Sn: sensitivity; Sp: specificity; MLP: Multi-Layer Perceptron; RF: Random Forest; LSTM: Long Short-term Memory; CNN: Convolutional Neural Network; GBC: Gradient Boost Classifier.

Bold values indicate best performance.

When comparing mortality prediction performance between various embedding techniques, the most notable performance boost occurred when RNN models achieved significantly greater AUC (0.907 for LSTM and 0.933 for CNN) and f1-scores (0.526 for LSTM and 0.587 for CNN) while using visit-level features when compared to the next best model (feed-forward MLP architecture w/ 0.816 AUC, 0.519 f1-score). Similarly, when using mixed visit- and history-level features, LSTM and CNN preserved around 10% AUC increase and 15% f1-score increase in comparison to MLP and ensemble models. The key advantage of sequential models over MLP is that they capture temporal relationships between time-steps with sequentially presented data. While previous studies have cited ability of inflammatory markers and vital signs for in-hospital mortality prediction,^13,33 notable performance difference between our collapse and sequential models suggests that 48 h temporal trends may greatly augment the predictive ability of physiologic markers.

LOS prediction

Table 2 summarizes performance for various models across 8 LOS ranges. In admissions resulting in 1–5 ICU days, MLP w/ x48 achieved the highest AUC and f1-scores. LR w/ w48 achieved the highest AUC and f1-scores for durations greater than 5 days. In fact, the highest performance achieved by LR w/48 was in predicting outlier cases >30 days with AUC of 0.934 and f1-score of 0.173. In predicting LOS outliers between 8 and 14 days, LR w/48 achieved AUC of 0.840 and f1-score of 0.372. Performance patterns were similar between sequential and LR, where the lowest performance occurred for predictions between 2 and 5 days (AUC ranging from 0.62 to 0.74) and highest performance occurred for predictions between 8 and 30+ outlier days (AUC ranging from 0.83 to 0.89).

Table 2.

Summary of top performing LOS predictors w/ representation schemes

Bins	Model	AUC	F1	P-value
Classic models
1–3 d	MLP w/ x48	0.791 (0.0043)	0.746 (0.0072)	.0034
3–5 d	MLP w/ w48	0.653 (0.018)	0.444 (0.029)	.081
5–8 d	LR w/ w48	0.705 (0.006)	0.298 (0.007)	.121
8–14 d	LR w/ w48	0.840 (0.0079)	0.372 (0.014)	.029
14–21 d	LR w/ x48	0.887 (0.019)	0.264 (0.015)	.033
21–30 d	LR w/ x48	0.917 (0.011)	0.182 (0.01)	.0016
30+	LR w/ w48	0.934 (0.011)	0.173 (0.0041)	.0028
Micro	LR w/ w48	0.747 (0.0025)	0.419 (0.0018)	.051
Sequential models
1–3 d	CNN-LSTM w/ x19	0.758 (0.0055)	0.615 (0.015)	.013
3–5 d	CNN-LSTM w/ x19	0.645 (0.0047)	0.139 (0.031)	.092
5–8 d	CNN-LSTM w/ x19	0.736 (0.0029)	0.103 (0.012)	.088
8–14 d	CNN-LSTM w/ x19	0.838 (0.0055)	0.181 (0.037)	.055
14–21 d	CNN-LSTM w/ x19	0.877 (0.009)	0.112 (0.025)	.0046
21–30 d	LSTM w/ x19+h2v	0.879 (0.025)	0.135 (0.032)	.011
30+	LSTM w/ x19+h2v	0.889 (0.027)	0.165 (0.07)	.005
Micro	CNN-LSTM w/ x19	0.846 (0.001)	0.368 (0.010)	.00014

Note: Each performance metric is evaluated across 5 stratified shuffle splits. The mean performance is reported with the standard deviation in parenthesis. The P-value is calculated by comparing the AUC of a given model with the baseline performance with random forest classifier and diagnostic histories. More extensive pairwise statistical t-tests are shown in Supplementary Table S8.

Abbreviations: LOS: length of stay; AUC: area under receiver operating characteristic curve; F1: f1-score; CNN: Convolutional Neural Network; MLP: Multi-Layer Perceptron; LR: Logistic Regression; LSTM: Long Short-term Memory.

Bold values indicate best performance.

One notable trend was that while the AUC scores consistently increased as the outlier days increased, the f1-scores decreased, as did the sample size of the bins. For example, LR with mixed physiologic and diagnostic features produced average AUC scores of 0.748, 0.579, 0.705, 0.84, 0.887, and 0.917 for LOS ranges (1, 2), (2, 3), (3, 5), (5, 8), (8, 14), (14, 21), and (21, 30). The progression of f1-scores were: 0.704, 0.372, 0.34, 0.298, 0.372, 0.264, and 0.173. Interestingly, the sensitivity values also progressively increased for increasing LOS bins: 0.804, 0.695, 0.659, 0.748, 0.878, 0.916, 0.953, and 0.955. Such pattern suggests that the trade-off occurred for positive predictive values (PPV), which dramatically decreased for longer LOS days. This can be attributed to the fact that the absolute number of outlier patients decreased dramatically with increasing LOS days. Since PPV is sensitive to the proportion of positive samples while sensitivity is not, the change in f1-score can be explained by the distribution of labels rather than a decrease in true-positive prediction by the models. In fact, the AUC, sensitivity, and specificity increased with LOS bins for most models, suggesting that our binning technique was especially helpful in discriminating LOS outliers with increasing duration of stay.

Differential diagnoses prediction

Table 3 summarizes the performances of models across various key differential diagnoses in MIMIC-III. Overall, sequential models did not significantly improve performance when compared to MLP (see Supplementary Table S7). CNN-LSTM using hierarchal inputs from visit- and history-level information performed best among sequential models, but differences were not significant (P-value >.05).

Table 3.

Summary of top performing DDX predictors w/ representation schemes

DDX	Model	AUC	F1	P-value
Classic models
CHF	MLP w/ x48	0.784 (0.00238)	0.488 (0.00689)	.000273
CAD	MLP w/ x48	0.798 (0.00612)	0.52 (0.011)	.000498
Afib	MLP w/ x48	0.745 (0.00218)	0.401 (0.0121)	.00260
Sepsis	MLP w/ x48	0.883 (0.00422)	0.312 (0.0101)	9.99E−5
AKF	MLP w/ x48	0.886 (0.00387)	0.505 (0.0106)	3.82E−5
CKD	MLP w/ x48	0.870 (0.00612)	0.276 (0.0173)	.000121
T2DM	MLP w/ x48	0.742 (0.00584)	0.199 (0.0175)	.00435
Hyperlipidemia	MLP w/ sentences	0.751 (0.00519)	0.17 (0.00178)	.00269
Pneumonia	MLP w/ x48	0.723 (0.00492)	0.001 (0.00112)	.00658
Micro	MLP w/ x48	0.806 (0.0021)	0.328 (0.003)	.000123
Sequential models
CHF	LSTM w/ x19 + demo	0.785 (0.00346)	0.455 (0.0211)	.000469
CAD	CNN w/ x19 + demo	0.793 (0.00486)	0.480 (0.0382)	.000629
Afib	LSTM w/ x19 + demo	0.768 (0.00534)	0.341 (0.0494)	.00161
Sepsis	LSTM w/ x19	0.862 (0.00892)	0.254 (0.0268)	.000332
AKF	CNN w/ x19	0.863 (0.00729)	0.488 (0.0285)	.000208
CKD	CNN w/ x19 + demo	0.872 (0.00611)	0.172 (0.0154)	.000115
T2DM	LSTM w/ x19 + demo	0.746 (0.00881)	0.144 (0.0213)	.00736
Hyperlipidemia	CNN w/ x19 + demo	0.749 (0.0122)	0.175 (0.048)	.0115
Pneumonia	CNN w/ x19 + demo	0.723 (0.0115)	0.006 (0.00106)	.0216
Micro	CNN w/ 19 + demo	0.803 (0.00308)	0.306 (0.0105)	.000224

Note: Each performance metric is evaluated across 5 stratified shuffle splits. The mean performance is reported with the standard deviation in parenthesis. The P-value is calculated by comparing the AUC of a given model with the baseline performance using LR using physiologic markers. More extensive pairwise statistical t-tests are shown in Supplementary Table S7.

Abbreviations: DDX: differential diagnoses; AUC: area under receiver operating characteristic curve; F1: f1-score; Sn: sensitivity; Sp: specificity; CHF: congestive heart failure; CAD: coronary arteriolar disease; Afib: atrial fibrillation; AKF: acute kidney failure; CKD: chronic kidney disease; T2DM: type II diabetes mellitus; MLP: Multi-Layer Perceptron; CNN: Convolutional Neural Network; LSTM: Long Short-term Memory.

Bold values indicate best performance.

Our models were able to predict renal diseases with the highest performance (0.887–0.895 AUC between MLP and CNN-LSTM models) presumably due to the inclusion of blood urea nitrogen levels (BUN) and creatinine as features. BUN-to-creatinine ratio is commonly used as a clinical metric for evaluating glomerular performance and intactness of renal nephrons. Similarly, essential hypertension yielded high AUC scores across most models due to our inclusion of systolic bood pressure and diastolic blood pressure data across time. However, interesting patterns emerge when we were able to identify disease phenotypes without using the gold standard clinical markers typically associated with those conditions.

For example, cardiovascular conditions such as atrial fibrillation (Afib) and congestive heart failure (CHF) are often confirmed by ECG (usually via 24 h Holtz monitor) and echocardiography (stress-induced or otherwise), respectively. Our study shows that RNNs, using only vital signs, demographic information, and a subset of metabolic panel lab values, were able to capture their prevalence with as high as 0.785 AUC and 0.395 sensitivity scores for CHF and 0.768 AUC and 0.328 sensitivity scores for Afib. In comparison, the gold standard measurement with 24 h Holtz monitor detects Afib with sensitivity of 0.319 at annual screenings and tops out at 0.71 if done monthly.³⁴ Because Afibs occur spontaneously in many cases, they can be easily missed during physical exams unless Holtz monitors or expensive implantable devices are used for longitudinal monitoring. The predictive ability of physiologic-markers alone for CHF and arrhythmic events suggest the possibility that arrhythmic cardiac pathologies yield temporal changes in physiologic regulation that is screenable in the acute setting.

There were several diseases for which sensitivity and f1-scores were very low across all model predictions. For example, all classic models with the exception of MLP failed to predict (AUC of 0.50) depressive disorder (psychiatric), esophageal reflux (GI), hypothyroidism (endocrine), tobacco use disorder (behavioral), pneumonia and food/vomit pneumonitis (infectious), chronic air obstruction (respiratory, may be seasonal or trigger-dependent), and nonspecific anemia (hematologic). The most surprising condition of the above-mentioned cases was hypothyroidism, which is known to cause long-term physiologic changes in metabolism and vital signs. While it is possible that the physiologic markers did not capture the progression of these diseases, the cause of underperformance was likely due to the duration of our observation window (48 h), which may have failed to capture the longitudinal or trigger-based temporal patterns of more chronic diseases.

Prediction for all-cause readmission within a 30-day window

Table 4A summarizes the top performing models for binary and multiclass classification of readmission events. Ensemble classifiers (RF and GBC) produced comparable performances to RNN models in both tasks. In both the multiclass and the binary classification case, the best performing sequential model was hierarchal LSTM using mixed visit- and history-level features. However, this architecture was only able to achieve a mean AUC score of 0.580 (0.009 std) and f1-score of 0.112 (0.004 std) on test sets across 5-fold cross-validation. The best performing collapsed model was RF classifier using mixed physiologic and history features (RF w/ w48), which achieved an AUC of 0.582 (0.007 std) and f1-score of 0.122 (0.003 std).

Table 4.

Summary of top performing readmission models w/ representation schemes

Rank	Model	AUC	F1	Sn	Sp	P-value
Classic models
1	RF w/ w48	0.582 (0.0067)	0.122 (0.0025)	0.601 (0.02)	0.563 (0.0086)	.0387
2	LR w/ w2v	0.577 (0.0067)	0.123 (0.0023)	0.574 (0.031)	0.592 (0.0211)	.0469
3	RF w/ 48h	0.577 (0.009)	0.121 (0.003)	0.571 (0.021)	0.583 (0.004)	.0657
Sequential models
1	LSTM w/ x19 + h2v	0.580 (0.00914)	0.112 (0.0043)	0.548 (0.0192)	0.565 (0.0206)	.0606
2	LSTM w/ x19	0.554 (0.00648)	0.108 (0.0028)	0.538 (0.0168)	0.554 (0.0214)	.107
3	LSTM w/ w2v	0.552 (0.0154)	0.107 (0.0038)	0.567 (0.0404)	0.524 (0.0272)	.199

Note: Each performance metric is evaluated across 5 stratified shuffle splits. The mean performance is reported with the standard deviation in parenthesis. The P-value is calculated by comparing the AUC of a given model with the random classifier with AUC of 0.50 and variance of 0.0015.

Abbreviations: AUC: area under receiver operating characteristic curve; F1: f1-score; Sn: sensitivity; Sp: specificity; RF: Random Forest; LR: Logistic Regression; LSTM: Long Short-term Memory.

DISCUSSION

Key features and models for each task

Our results show that sequential models are most suitable for in-hospital mortality prediction, where temporal patterns of simple physiologic features are adequate in capturing mortality risk. Deep models in general significantly out-perform nondeep models for the differential diagnostic task (Supplementary Table S5), but temporal information from sequential models did not provide additional benefit when compared to MLP. For LOS prediction, collapse models and deep models provided similar performance across various time-ranges. More important difference was in feature selection, where physiologic markers significantly out-performed diagnostic histories in predicting LOS range for both deep and nondeep models (Supplementary Table S8). Our results for all-cause readmission suggests the need for additional features for this particular task. Physiologic and diagnostic histories alone do not capture the defining elements of this particular clinical problem. A summary table is provided in Supplementary Table S9 which briefly summarizes the best model and features for each task.

Readmission as a separate problem from patient stability

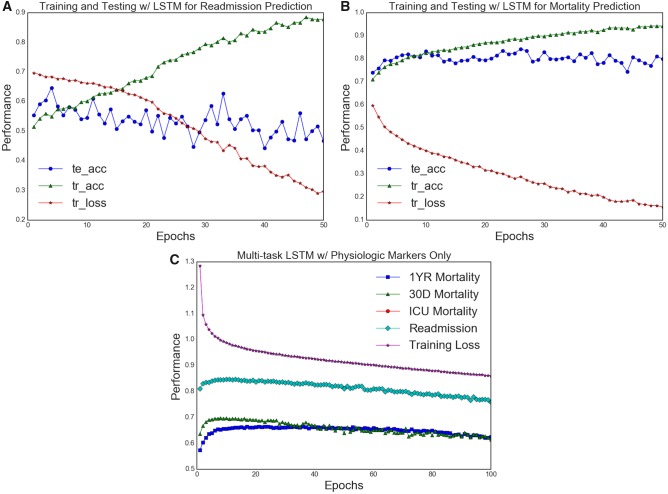
Figure 5A and B shows the differences in generalizability of RNN models for the mortality and readmission tasks. In both cases, bidirectional LSTMs were trained with 5-fold cross-validation to illustrate learning behavior and test-set generalization for readmission and mortality tasks. For both cases, it was clear that the training AUC was increasing with each training iteration (epoch), while the loss function was decreasing consistently. However, only in the mortality case did we observe an increase in testing AUC, which should ideally follow the training AUC behavior. In the readmission case, the training AUC approached 0.90+ over 30 epochs, but the testing AUC increased from 0.50 toward 0.57–0.61 range and fluctuated for the following epochs (>5). Such behavior exemplified most, if not all, of our model training behaviors for this task. This discrepancy points to the idea that perhaps our feature representation was inadequate in capturing risk factors for readmission. In particular, examining patterns in diagnostic history, health care coverage (as represented by insurance policy, marital status, and ethnicity in our case), and physiological markers may be insufficient in capturing the key contributing factors of hospital readmission.

Figure 5.

Comparison of training performance for readmission and mortality tasks. A comparison between the training data of readmission and mortality tasks. A, 5-fold validation training data of vanilla bidirectional LSTM trained on physiologic time-series data only. Training AUC is demarcated tr_auc while testing AUC is demarcated te_auc. B, 5-fold validation training data of the same model architecture and feature selection on the readmission task. In both cases, the training AUC scores increased with decreasing loss the training set, but only in the mortality task are the train-test results generalized. This suggests a wide disparity between in the readmission task samples which the models could not capture. C, A model training data captured in multitask learning of readmission, in-hospital mortality, 30-day, and 1-year mortality. All AUC scores shown in C are testing data only. With increasing epochs, only mortality models improved. More importantly the training patterns show that knowledge transfer from mortality tasks did not improve readmission predictions.

We further examined the dependence of readmission on the “stability” of patients. The all-cause 30-day readmission has classically been formulated as a problem of accurately depicting patient stability upon discharge from inpatient facilities. If this were the case, then there should exist parallel patterns in postdischarge mortality and readmission. Figure 5C demonstrates a supplementary experiment done with multitask learning of in-hospital mortality, 30-day readmission, 30-day and 1-year mortality. Here, vanilla bidirectional LSTM was used for training across 100 epochs over 5-fold validation, with the average values across different k-folds visualized in the summary plot. We see that while there was knowledge transfer across in-hospital mortality, 30-day mortality and 1-year mortality, the 30-day readmission task did not stand to gain any additional performance boost from the added knowledge captured by the mortality prediction tasks. In fact, testing AUC patterns of 30-day mortality differed greatly from that of testing AUC for 30-day readmission. The LSTM model, using only temporal physiologic data, was able to capture generalizable performance across all mortality tasks but not the readmission task.

CONCLUSION

In this study, we leveraged performance differences between patient feature representations and predictive model architectures to capture insight from clinical tasks. One notable limitation of this study is the exclusion of procedural and medication data from our analysis of clinical outcomes. The fact that inclusion of demographic features such as insurance policy, marital status, gender and race of the patients did not benefit our readmission prediction models points to the possibility that accurate risk models for more complex tasks such as readmission may require feature selection to include environmental factors such as medication progression, procedural follow-up and access to transportation. For example, previous studies have cited that system-level factors such as medicine reconciliation, access to transportation and coordination with primary providers may play pivotal roles in unplanned readmission and postdischarge mortality.^35–39 Future studies may include medication administration, drug history and adverse effect data to build a more comprehensive picture of postdischarge risk factors. Lastly, we note that the scope of this study includes identifying the optimal model and feature representation techniques for various clinical tasks; future investigations may address the interpretability of deep models and differences in feature importance for the various tasks.

FUNDING

This research project was supported in part by National Science Foundation under grants IIS-1615597 (JZ), IIS-1565596 (JZ), IIS-1749940 (JZ), IIS-1650723 (FW), IIS-1716432 (FW), IIS-1750326 (FW) and Office of Naval Research under grants N00014-17-1-2265 (JZ).

Conflict of interest statement. None declared.

CONTRIBUTORS

All authors provided significant contributions to:

• the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work.

• drafting the work or revising it critically for important intellectual content.

• final approval of the version to be published.

• agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

FT was responsible for majority of data acquisition, implementation of experiments, and result interpretation. CX and FW provided major editing of writing and guided the design of experiments. JZ provided original conception of the project and guided the majority of experimental formulations.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.