Modulation of Kinesin’s Load-Bearing Capacity by Force Geometry and the Microtubule Track

Abstract

Kinesin motors and their associated microtubule tracks are essential for long-distance transport of cellular cargos. Intracellular activity and proper recruitment of kinesins is regulated by biochemical signaling, cargo adaptors, microtubule-associated proteins, and mechanical forces. In this study, we found that the effect of opposing forces on the kinesin-microtubule attachment duration depends strongly on experimental assay geometry. Using optical tweezers and the conventional single-bead assay, we show that detachment of kinesin from the microtubule is likely accelerated by forces vertical to the long axis of the microtubule due to contact of the single bead with the underlying microtubule. We used the three-bead assay to minimize the vertical force component and found that when the opposing forces are mainly parallel to the microtubule, the median value of attachment durations between kinesin and microtubules can be up to 10-fold longer than observed using the single-bead assay. Using the three-bead assay, we also found that not all microtubule protofilaments are equivalent interacting substrates for kinesin and that the median value of attachment durations of kinesin varies by more than 10-fold, depending on the relative angular position of the forces along the circumference of the microtubule. Thus, depending on the geometry of forces across the microtubule, kinesin can switch from a fast detaching motor (median attachment duration <0.2 s) to a persistent motor that sustains attachment (median attachment duration >3 s) at high forces (5 pN). Our data show that the load-bearing capacity of the kinesin motor is highly variable and can be dramatically affected by off-axis forces and forces across the microtubule lattice, which has implications for a range of cellular activities, including cell division and organelle transport.

Significance

Kinesins are cytoskeletal motors that transport cargos along microtubules. Single-bead, optical-trapping assays have been used to show that the speed and run length of kinesin are affected by mechanical load. We found that this widely used assay introduces a vertical force on the motor not accounted for in previous experiments, and this force decreases kinesin’s attachment duration. Using an assay geometry that minimizes vertical forces, we found that a 180° change in the azimuthal position between a pair of net opposing forces applied between kinesin and microtubules can lead up to a 10-fold increase in the kinesin attachment duration. These results reveal a previously unknown versatility of kinesin’s load-bearing capacity, which has implications for the physiological roles of kinesin.

Introduction

Microtubules are cytoskeletal filaments essential for long-distance transport of intracellular cargos toward their plus and minus ends via kinesin and dynein motors, respectively (1). The stepping behavior of kinesin has been studied in detail at the single molecule level, both in the presence and in the absence of external loads on the motor (2, 3, 4, 5, 6, 7, 8). The effects of external forces parallel to the microtubule on kinesin have largely been studied using the single-bead optical tweezers assay (2). Forces lateral to its traveling path have also been shown to affect kinesin’s processivity (9). Recent theoretical work suggests that an additional vertical force component due to contact of the single bead with the underlying microtubule has not been accounted for, and this force component must be considered when interpreting kinesin behavior acquired using this assay (10).

In contrast to the single-bead assay, vertical forces on kinesin are expected to be negligible (see quantification below) when using a dual optical tweezers configuration in the three-bead assay (11), but this assay has not been commonly used to study kinesin processivity. Additionally, in the three-bead assay, when the trapped beads are attached to different protofilaments, shear forces can be applied along the microtubule long axis with varied geometries, which might affect kinesin activity (12). Indeed, recent experimental studies have shown longitudinal expansion of microtubules by 1.3–1.6% in the absence of external forces upon the binding of saturating kinesin concentrations (13,14).

To experimentally explore any effect of the direction of forces applied to the kinesin-microtubule complex, we used single-bead (Fig. 1, A and B) and three-bead assays (Fig. 1, C and D) to explore the role of vertical forces and forces across the microtubule lattice on kinesin activity. We found that vertical forces in the three-bead assay accelerate kinesin detachment from microtubules. Additionally, we found that the median attachment duration of kinesin varies by more than 10-fold, depending on the relative angular position of the forces along the circumference of the microtubule.

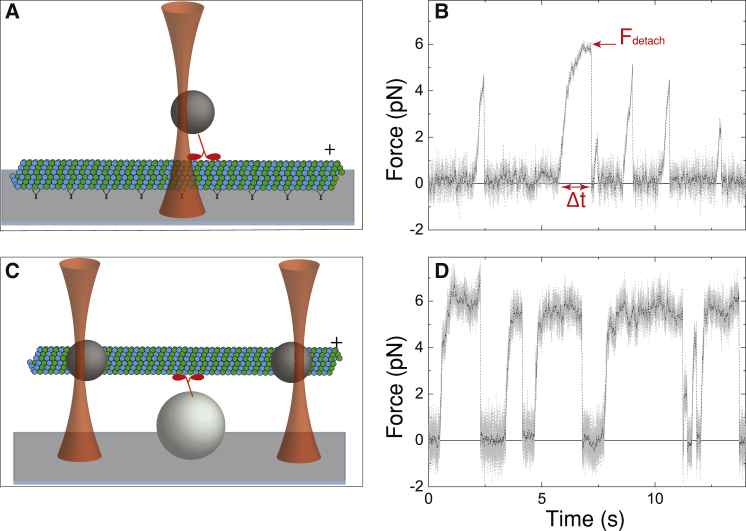
Figure 1.

Single- and three-bead assays for kinesin-microtubule interaction. Shown are cartoon representations (not drawn to scale) of (A) the single-bead assay and (C) the three-bead assay. (A) A microtubule (green and blue) is immobilized on a glass coverslip (gray surface) via antibody or streptavidin (black). A kinesin molecule (red) attached on a bead (gray sphere) is brought into contact via optical tweezers (brown). (C) A microtubule is attached to two laser-trapped beads via streptavidin-biotin linkage. The microtubule assembly (microtubule dumbbell) is brought in contact with a single kinesin molecule, attached on a surface-immobilized spherical pedestal. Shown are representative raw (gray) and smoothed (black) force traces of a single kinesin molecule interacting with (B) a surface-immobilized microtubule in the single-bead assay (dia. = 0.82 μm) and (D) a microtubule dumbbell in the three-bead assay. The force (F_detach) at which the kinesin detaches (red arrow in (B)) from the microtubule and the duration Δt of the corresponding force ramp (double red arrow in (B)) can be calculated directly from the data for every force ramp. To see this figure in color, go online.

Materials and Methods

Reagents

GTP and paclitaxel (Taxol) were purchased from Cytoskeleton (Denver, CO). Guanosine-5′-[(α,β)-methyleno]triphosphate, sodium salt (GMPCPP), the nonhydrolyzable analog of GTP, was purchased from Jena Bioscience (Jena, Germany). Piperazine-N, N′-bis (2-ethanesulfonic acid) (PIPES), ATP, and glucose were purchased from Sigma (St. Louis, MO). HEPES and dithiothreitol (DTT) were purchased from GoldBio (St Louis, MO). EGTA, MgCl₂, and KCl were purchased from Thermo Fisher Scientific (Waltham, MA). Sterile collodion (nitrocellulose) 2% in amyl acetate and amyl acetate were purchased from Electron Microscopy Sciences (Hatfield, PA). d-Biotin was purchased from Avidity (Aurora, CO). Chloroform solutions of 1,2-dioleoyl-sn-glycero-3-phosphocholine and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl), mini extruder, Nuclepore track-etch membrane (50 nm) from Whatman, and filter support disks 10 mm from Whatman were purchased from Avanti Polar Lipids (Alabaster, AL). High vacuum grease, silicone elastomer base (184 Sylgard), and the corresponding elastomer curing agent were manufactured by Dow Corning (Midland, MI). 2% Dimethyldichlorosilane in octamethylcyclooctasilane (PlusOne Repel-Silane ES) was purchased by GE Healthcare (Chicago, IL). Optical adhesive Norland 65 was purchased from Norland Products (Cranbury, NJ).

Microbeads

Dry silica beads (dia. = 5.0 μm), streptavidin polystyrene beads (dia. = 0.51 μm, 1.0% w/v; dia. = 0.82 μm, 1.0% w/v; dia. = 1.05 μm, 0.5% w/v), and rabbit anti-6XHis polystyrene beads (2r = 0.61 μm, 0.1% w/v) were purchased from Spherotech (Lake Forest, IL).

Proteins

Unlabeled and labeled (biotin and tetramethylrhodamine (TRITC)) lyophilized tubulin from porcine brain were purchased from Cytoskeleton. Neutravidin was purchased from Life Sciences (St. Louis, MO). Casein powder, glucose oxidase from Aspergillus niger, and bovine liver catalase were purchased from Sigma (St. Louis, MO). Mouse monoclonal anti-6xHis antibody was purchased from Abcam (Cambridge, MA). Biotinylated mouse anti-5xHis antibody was purchase from QIAGEN (Hilden, Germany). Mouse anti-tubulin β3 antibody from Bio-Rad Laboratories (Hercules, CA). We used a 6xHis-GFP-labeled truncated human kinesin-1 heavy chain construct (aa 1–560 (15)) with an AviTag sequence susceptible to biotinylation added at the C-terminus (16). The protein was expressed in Escherichia coli, purified using cobalt resin from Clontech Laboratories (now Takara Bio USA, Mountain View, CA) (15). Biotin ligase BirA (Avidity) was used to biotinylate AviTag-kinesin (17).

Casein solution

Casein solution 20 mg/mL in 20 mM HEPES and 200 mM NaCl (pH 8.8) was placed under gentle stirring, either for 2–4 h at room temperature or overnight at 4°C. Solution was centrifuged at 110,000 g at 4°C for 20 min, and supernatant was filtered through 150-mL rapid-flow filters, 50 mm in diameter and 0.2 μm pore size (Thermo Fisher Scientific). Concentrations were determined using the Bradford method, and solutions (8–13 mg/mL) were stored in 1-mL aliquots at −80°C. When using GMPCPP microtubules, casein solution was prepared in KCl instead of NaCl because GMPCPP hydrolyzes faster in the presence of Na traces (18).

Rectangular ridges

Nine parts of silicone elastomer base were added to one part of the corresponding elastomer curing agent in a 50-mL screw-top cup conical tube (Corning, Tewksbury, MA) and were mixed gently by reversing the tube multiple times. The mixture was left undisturbed for 15 min. A chrome mask with the desired pattern of rectangular ridges (4 mm long, 2 μm wide, 1 μm tall, and 10 μm apart) was placed face-up in a Pyrex borosilicate glass petri plate (Corning). The glass plate and the mask were placed next to a glass beaker containing 30 mL of 2% dimethyldichlorosilane solution in a vacuum chamber under a fume hood. A drop of 5 μL of 2% dimethyldichlorosilane (GE Healthcare) was added on the mask, and a hard vacuum was applied for 30 min. After releasing the vacuum, the elastomer solution was gently poured on top of the chrome mask in the glass plate, and the hard vacuum was reapplied for another 30 min to remove trapped air. To speed elastomer curing, the glass plate was placed at 105°C for 1 h. Using a razor blade, the cured elastomer on top of the chrome mask was removed and was used as a stamp to fabricate rectangular ridges on glass coverslips. Elastomer stamps were exposed to ultraviolet (UV) plasma for no more than 4 s and were then placed in a petri dish face up. Dimethyldichlorosilane (5 μL of 2%) was placed on each stamp and left under the hard vacuum for 30 min in the presence of a glass beaker containing 30 mL of 2% dimethyldichlorosilane solution. Stamps were then placed gently face down against ∼4 μL of optical adhesive (Norland 65) on glass coverslips and left for 5 min. To cure the optical adhesive, coverslips were exposed to UV light for 10 min. After gently removing the stamps, the cured optical adhesive on each coverslip was washed with 0.5 mL of methanol and dried in a fume hood. Coverslips with cured optical adhesive were used within 24 h of preparation. A differential interference contrast microcopy image of the ridges and a fluorescent microscopy image of microtubules (5% TRITC tubulin) attached on the ridges are shown in Fig. 3 B (inset) and Video S1.

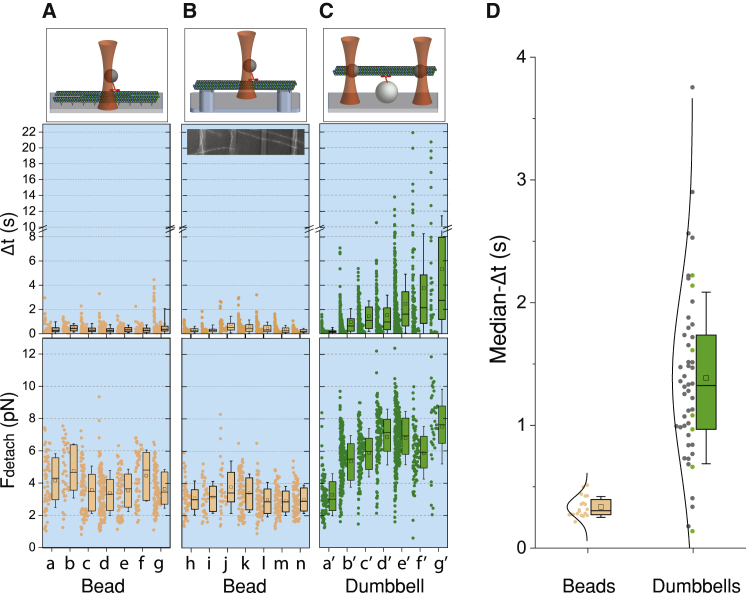
Figure 3.

Kinesin’s attachment durations and detachment forces for single and three-bead assays. Cartoon representations for each assay are shown on the top panel of plots (A–C). Shown are representative distributions of Δt and F_detach and their corresponding box statistics in the middle and bottom panels, respectively, for (A) different pairs of beads (“a” to “g”) and surface-immobilized microtubules (Table S1), (B) different pairs of beads (“h” to “n”) and microtubules suspended between rectangular ridges, and (C) different microtubule dumbbells (“a’” to “g’”). The inset in the middle panel (B) is an image of fluorescent microtubules suspended over rectangular parallel ridges (light gray stripes) (Materials and Methods; Video S1). For each box statistics representation, the length corresponds to the interquartile range (IQR), the error bars to SD, the midline to the median value, and the square inside each box to the average value. (D) Shown are the distribution and box statistics of the median-Δt for single kinesin molecules interacting with microtubule dumbbells (n = 50) and surface-immobilized microtubules (n = 20) under resisting load. The green points correspond to the examples shown in plot (C). The black lines, which mainly serve as a guide to the eye, represent a normal distribution with the same mean and SD as the corresponding data. To see this figure in color, go online.

Supported lipid bilayers

Biotinylated supported lipid bilayers (SLBs) were prepared as in (19). In a round bottom flask, 77 μL of 12.7 mM 1,2-dioleoyl-sn-glycero-3-phosphocholine was mixed with 10 μL of 0.9 μM 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl). The flask was attached to a rotatory evaporator, and the solution was thermally equilibrated in a water bath at 36°C for 5 min. A hard vacuum was applied (30 min) to remove chloroform, resulting in a lipid film. The lipid film was dissolved in 2 mL (0.5 mM total lipid concentration) of buffer HNa100 (HEPES (pH 7.0) and 100 mM NaCl) by rigorously vortexing the flask for 2 min at room temperature. The lipid suspension was subjected to at least four freeze-thaw cycles, followed by extrusion (11 passes) through 50-nm pores using a mini extruder (Avanti Polar Lipids) to form small unilamellar vesicles. Chambers were assembled by pairs of detergent-washed and UV plasma-cleaned glass coverslips. Small unilamellar vesicles were introduced in the chambers and incubated for 30 min. Chambers were placed in a humid box to prevent chambers from drying out. Chambers were washed by 3 × 100 μL with HNa100. Chambers were kept in a humid box until used within the same day.

Kinesin attachment to polystyrene beads

Streptavidin-coated beads (10 μL) 0.82 μm in diameter were mixed with 89.5 μL of 2 mg/mL casein in BRB80 (pH 7.5) and bath sonicated for 1 min. Biotinylated anti-5xHis antibody (0.5 μL) was added, and bead solution was constantly rotated at 4°C for at least 1 h. d-Biotin was added to a final concentration of 2.6 μM and incubated for 1 h at 4°C under constant rotation. Bead solution was washed three times with 100 μL of 2 mg/mL casein by centrifugation at 6000 g at 4°C for 5 min. Beads were stored at 4°C under constant rotation and were used within a month. Beads conjugated with anti-5xHis antibody (9 μL) were incubated with biotinylated kinesin-1 (1 μL) under constant rotation at 4°C for at least 4 h. To ensure single molecule interactions, the kinesin-1 concentration was chosen so that no more than 1 out of 4 beads would interact with surface-immobilized nonbiotinylated microtubules when assayed in the optical tweezers (20). Beads (2 μL) decorated with kinesin-1 were diluted to a final volume of 50 μL with the appropriate reagents (see final solution in chamber preparation) and injected into the chamber. For surface-immobilized biotinylated microtubules, 8 μL of rabbit anti-6xHis polystyrene beads (0.61 μm in diameter) were mixed with 2 μL of casein 10 mg/mL and 2 μL of the appropriate concentration of kinesin-1. Beads were diluted 1:12 to a final volume of 50 μL and injected into the chamber. For experiments comparing the effect of the bead’s size, all three different sizes of beads were treated in parallel with the same stock of proteins and reagents, and single molecule experiments were done the same day.

Microtubule preparation

All tubulin solutions were 5 mg/mL in BRB80 (pH 6.9) supplemented with 1 mM GTP. Unlabeled tubulin solution (20 μL) was mixed with 20 μL of biotinylated tubulin and 2 μL of TRITC tubulin. Tubulin solutions were centrifuged at 300,000 g at 4°C for 10 min using a TLA-100 rotor (Beckman Coulter). Tubulin in the supernatant was polymerized by incubating in the dark at 37°C for 20 min. Taxol (1.75 μL of 2 mM) was then added, followed by 10-min incubation at 37°C. Additional taxol (1 μL of 2 mM) was added and incubated for another 10 min at 37°C. Polymerized tubulin solution was centrifuged at 40,000 g at 25°C for 20 min. Supernatant was discarded, and the microtubule-containing pellet was resuspended by rigorous pipetting in 50 μL of BRB80 (pH 6.9) supplemented with 40 μM taxol. Microtubules were kept at room temperature away from light and used within 5 days of preparation. For GMPCPP-stabilized microtubules, GTP and taxol were both excluded from the above protocol. Rather, 5 μL of 10 mM GMPPCP was added just before incubation of tubulin solution in a water bath at 37°C, and tubulin was polymerized for 30 min.

Experimental chamber preparation

All solutions introduced in the experimental chambers and the necessary dilutions of stock solutions were prepared in buffer BRB80 (pH 7.5). All glass coverslips were rectangular 22 × 40 mm and 1.5-mm thick (Thermo Fisher Scientific).

Single-bead assay on a solid surface

Nitrocellulose-coated coverslips were assembled into flow chambers as described (21) and used within 24 h of preparation. In experiments with rectangular ridges, one of the coverslips contains the imprinted optical adhesive. The volume of the experimental chambers was ≤20 μL. Solutions were introduced in the chamber in the following sequence: 20 μL of 0.05 mg/mL anti-tubulin antibody (Bio-Rad Laboratories) for 5 min, 50 μL of 2 mg/mL casein for 4 min, 4 × 25 μL of 125 nM microtubules supplemented with 2 mg/mL casein and 20 μM taxol for 4 × 1 min, washed with 100 μL of 2 mg/mL casein, and 50 μL of final solution with kinesin beads, 2 mM ATP, 2 mM MgCl₂, 50 μM DTT, 20 μM taxol, 5 mg/mL glucose, 1500 units/mL of glucose oxidase, and 0.2 units/mL of catalase. The open ends of the chamber were sealed with vacuum grease to prevent evaporation during the experiment.

Single-bead assay on SLBs

Solutions were introduced in chambers with SLB in the following sequence and for the following incubation times: 50 μL of 0.24 mg/mL neutravidin for 2 min, 4 × 25 μL of 1 μM 48% biotinylated microtubules supplemented with 20 μM taxol 4 × 1 min, 100 μL of 5 μM d-biotin supplemented with 20 μM taxol, and 50 μL of final solution with kinesin-decorated beads (rabbit anti-6xHis polystyrene beads, dia. = 0.61 μm), 2 mM ATP, 2 mM MgCl₂, 50 μM DTT, 20 μM taxol, 5 mg/mL glucose, 1500 units/mL of glucose oxidase, and 0.2 units/mL of catalase. The open ends of the chamber were sealed with vacuum grease.

Three-bead optical tweezers assay

Nitrocellulose-coated flow chambers containing silica spherical pedestals (dia. = 5.0 μm) were prepared as described (21). Solutions were introduced in the chamber in the following sequence: 20 μL of 0.2 mg/mL anti-6xHis antibody (Abcam) for 5 min, 50 μL of 2 mg/mL casein for 4 min, 50 μL of kinesin-1 construct ≤1 nM supplemented with 2 mg/mL casein for 5 min, washed with 100 μL of 2 mg/mL casein, and 50 μL of final solution containing 5 nM 48% biotinylated microtubules, 2 mM ATP, 2 mM MgCl₂, 50 μM DTT, 20 μM taxol (excluded when GMPCPP microtubules were used), 5 mg/mL glucose, 1500 units/mL of glucose oxidase, and 0.2 units/mL of catalase. Before sealing the chamber with vacuum grease, 3–4 μL of streptavidin beads (dia. = 0.82 μm) diluted 1:30 in final solution without microtubules were introduced from one side of the chamber. The concentrations of kinesin used were such that no more than one out of four kinesin-decorated spherical immobilized pedestals interacted with microtubule dumbbells. The fraction of interacting spherical pedestals as a function of kinesin concentration is much better described by a Poisson distribution that one or more (reduced χ² = 0.012, ν = 3) rather than two or more (reduced χ² = 7.2, ν = 3) kinesin dimers are interacting with a microtubule dumbbell (Fig. S1). The titration results compare well with single molecule titration for the single-bead assay (20). In many studies that use the single-bead assay, the fraction of interacting beads for single molecule measurements ranges from 0.5 to 0.25 (4,22, 23, 24). The concentrations of kinesin used in the current study were such that no more than one out of four kinesin-decorated spherical immobilized pedestals interacted with microtubule dumbbells, which corresponds to the fraction of interacting spherical pedestals ≤0.25.

Optical tweezers experiments

Single molecule interactions between microtubules and kinesin were recorded at 20°C in a dual-beam optical trap system using a 63× water objective with a numerical aperture of 1.2 (25,26). For each trapped bead, the trap stiffness (pN/nm) and the system-calibration factor (pN/V) were determined by fitting a Lorentzian function to the corresponding power spectrum of their Brownian motion before microtubule attachment. Microtubule dumbbells were subjected to pretensile forces of 2–9 pN by moving the two laser beams apart. The trap stiffness of the individual laser beams for single-bead assays was 0.029–0.058 pN/nm and for three-bead assays were 0.045–0.090 pN/nm. Higher stiffness than the single-bead assay was required in the three-bead assay to accommodate pretensile and kinesin-generated forces. A piezoelectric stage controller was used for position manipulation of single beads over surface-immobilized microtubules or microtubule dumbbells on top of spherical pedestals to scan for interactions. Data were filtered at 1 kHz, digitized with a sampling rate of 2 kHz, and recorded using in-house software written in LabVIEW. Forces traces in Fig.1 were smoothed using the Savitzky-Golay filter of second polynomial order and a 50-point half window (Origin 2018b). To measure interactions between kinesin and microtubule dumbbells under zero pretensile force between the two beads (Fig. 2, D, H, and L), the laser that was trapping the minus-end streptavidin bead was shut off while kinesin was interacting with a dumbbell under pretensile forces. Only new processive kinesin runs, after the trap had been switched off, were quantified (Δt, F_detach) for this assay. After turning off the minus-end trap, thermal fluctuations of the microtubule when kinesin was not attached would often drive the microtubule away from the anchored kinesin. Therefore, the same procedure of detecting interactions under pretensile forces and then switching off the minus-end laser trap was repeated hundreds of times to collect a sufficient number (>30) of interactions between kinesin and dumbbells in the absence of pretensile forces (minus-end trap off).

Figure 2.

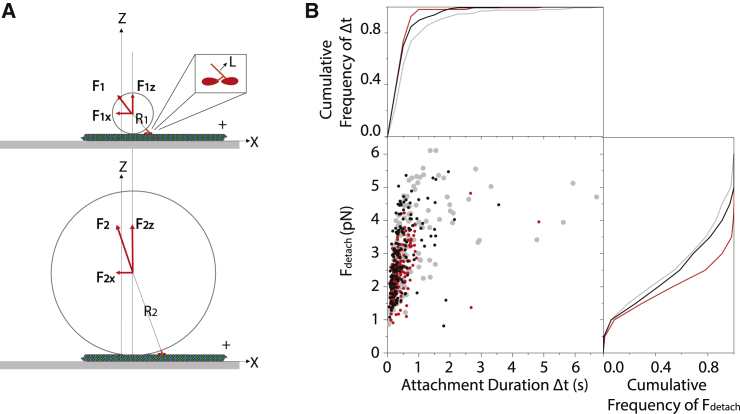
Kinesin detaches faster and at lower forces for larger size beads. (A) Shown is a cartoon representation of the single-bead assay with two different sizes of beads R₂ = 4·R₁ and the same displacement along the microtubule relative to the center of the laser trap. The length L of the attached kinesin construct, shown as an inset, is drawn almost to scale relative to R₁ and R₂. The components (F_x, F_z) and the vectors of the total force F that opposes kinesin’s movement are indicated by the red arrows. Mechanical equilibrium dictates that F should be opposite to the force produced by kinesin and lay along the radius of the bead. For the same stiffness of the trap F_1x = F_2x and F_1z < F_2z, see Eq. 1 and Table 1. (B) Shown is a scatter plot of detachment forces F_detach and attachment durations Δt for beads with three different diameters of 0.51 μm (gray), 0.82 μm (black), and 2.1 μm (red). The cumulative distributions of F_detach and Δt are plotted as solid lines of corresponding colors along the right and top axis of the graph, respectively. To see this figure in color, go online.

Stall forces

Stall forces were calculated by averaging within each data set all force plateaus that lasted at least 0.1 s before the detachment of kinesin (22). To qualify as plateau, the SD of the force should not exceed 5% of the average force value within the 0.1-s time window before detachment. In the case of the three-bead assay, however, a 10% threshold was used because of increased thermal fluctuations of the microtubule dumbbells.

Results

Kinesin attachment durations are longer for the three-bead assay over the single-bead assay

A two-headed kinesin construct (Materials and Methods (27)) was site-specifically bound to single beads (dia. = 0.82 μm; Materials and Methods), which were held in a stationary optical trap as the motor stepped along coverslip-attached taxol-stabilized GDP microtubules. Processing kinesin pulled the bead out of the center of the trap, increasing the resisting force on the kinesin until the motor detached from the microtubule (Fig. 1 A and B), resulting in the bead moving rapidly back to the center of the trap before the motor reengaged to start another run. The corresponding force traces were similar to those published previously with the same kinesin construct, ATP concentration, and bead diameter (22). For each processive run, the force component F_x at detachment (F_detach) and the duration of attachment (Δt) were measured (Fig. 1 B).

Measurements were also performed using a dual laser trap and the three-bead assay (Fig. 1 C). The three-bead assay has been used mostly for single molecule studies of the nonprocessive actomyosin complex (11,25) and less frequently for microtubule interacting motors (27, 28, 29). Two streptavidin-coated polystyrene beads (dia. = 0.82 μm), trapped by two laser beams ∼10 μm apart, were brought in contact with a taxol-stabilized biotinylated GDP microtubule in solution until a stable “dumbbell” assembly was formed (Fig. 1 C). Initial shear pretensile forces (F_pretensile = 2–9 pN) were applied to the dumbbells by moving the two laser beams further apart. Kinesin molecules were anchored on surface-immobilized spherical pedestals (dia. = 5.0 μm) against which microtubule dumbbells were brought in contact. Single molecule kinesin motility resulted in the displacement of the dumbbells relative to the surface-immobilized kinesin. Single kinesin molecules (Materials and Methods; Fig. S1) interacting with microtubule dumbbells in the presence of 2 mM MgATP reached forces ≥5 pN more frequently and remained attached at these high forces remarkably longer than observed in the single-bead assay (Fig. 1, B and D), resulting in higher average detachment forces (see quantification below).

Kinesin attachment durations in the single-bead assay depend on bead diameter

Recent theoretical work has suggested that in the single-bead assay, an additional vertical force component due to contact of the bead with the underlying microtubule may accelerate the detachment of kinesin from the microtubule (10). To explore if this vertical force component contributes to the strikingly different results between the single and three-bead assays (Fig. 1), we performed single-bead experiments for three different bead diameters (2.1, 0.82, and 0.51 μm; Materials and Methods). The vertical force component (F_z) experienced by the bead (10) is expected to scale with the radius (R) as follows:

$$F_z=F_x/{\left[{\left(1+\frac{L}{R}\right)}^2-1\right]}^{1/2},$$ (1)

where F_x is the force measured by the laser trap, and L (∼35 nm) is the length of the kinesin construct (Fig. 2 A). The resulting measurements of F_detach and Δt for the three different sizes of the bead at 2 mM MgATP are plotted in Fig. 2 B, and statistical values are shown in Table 1. The corresponding distributions of both Δt and F_detach for the largest (2.1 μm; n = 164, four beads) and smallest (0.51 μm; n = 166, four beads) bead diameter are statistically significantly different (p < 0.001, Mann-Whitney, nonparametric comparison). As can be seen from the cumulative frequency distributions of Δt and F_detach (Fig. 2 B), kinesin detaches faster from the microtubule and reaches lower detachment forces when it is bound to the 2.1-μm beads rather than to the smaller 0.51-μm beads (Table 1). The percentage of events that ended in stalls decreased from 30% to 5% and 0% with increasing bead diameter (Table 1). The corresponding stall force values of 4.4 ± 0.81 and 4.9 ± 0.43 pN (SD) are in good agreement with 5.3 ± 1.2 pN, which was measured for the same kinesin construct previously (22) and is within the lower range of previous measurements of 4.8–7.4 pN for longer kinesin 1 constructs at saturating ATP (2,3,5,22,23). The average detachment force <F_detach> of 2.9 ± 1.1 pN (SD) is also comparable with a previously measured value of 4.4 ± 1.4 pN (22) for the same kinesin construct and bead diameter (0.82 μm).

Table 1.

Single-Bead Assay Measurements of Forces and Attachment Durations

Bead Diameter (μm)	<Fdetach> (pN)	Median-Δt (s)	Fstall (pN)	% Stall Events	Fz/Fxa
0.51	3.1 ± 1.2	0.44	4.4 ± 0.81	30	1.8
0.82	2.9 ± 1.0	0.33	4.9 ± 0.43	5	2.4
2.1	2.5 ± 0.74	0.31	NA	0	3.8

NA, not applicable.

^aCalculation of the F_z/F_x, according to Eq. 1, assuming F_x = 5 pN and L = 35 nm.

We checked different substrates and microtubule surface-attachment strategies and found no effect on the mechanical activity of kinesin stepping along microtubules attached 1) to a solid surface via tubulin antibody or via streptavidin or 2) to a biotinylated SLB via streptavidin (Materials and Methods). Representative measurements for different surfaces and attachments are shown in Fig. 3 A (Table S1).

To test if the lack of surface attachments along the microtubule segment that interacts with kinesin may lead to the different behaviors observed in Fig. 1, we fabricated parallel rectangular pedestals (4 mm long, 2 μm wide, 1 μm tall, and 10 μm apart; Materials and Methods and Video S1) over which we were able to suspend and immobilize microtubules (Fig. 3 B; Video S1). We performed the single-bead assay along the suspended part of the microtubule and observed force and attachment durations (dia. 0.82 μm, <F_detach > = 3.1 ± 1.9 pN (SD, n = 432 runs); weighted mean (Supporting Materials and Methods) <median-Δt >_w = 0.30 ± 0.11 s (SD_w, weighted SD; n = 7)), similar to surface-immobilized microtubules (Fig. 3 B).

Kinesin exhibits a broad range of microtubule attachment durations in the three-bead assay

Representative examples of the distribution and statistics of Δt and F_detach between kinesin and different microtubule dumbbells are shown in Fig. 3 C. The median duration, median-Δt, of the runs produced by kinesin and each dumbbell varied by more than an order of magnitude between different dumbbells (0.14 and 3.8 s) and followed a unimodal symmetric distribution (Fig. 3 D) with <median-Δt >_w = 1.3 ± 0.59 s (SD_w, n = 50). Single beads interacting with surface-immobilized microtubules did not demonstrate such a variability, and the corresponding value was <median-Δt >_w = 0.34 ± 0.083 s (SD_w, n = 20) (Fig. 3 D). Comparisons of the distributions of the median-Δt values (Fig. 3 D) as well as the variances (Fig. S3), which are usually associated with higher uncertainties, between the two assays showed that they were statistically different at the 0.001 confidence level (p = 1.5 E−11 and p = 6.2 E−7 respectively; Mann-Whitney test, see Materials and Methods).

More frequent high force events in the dumbbell assay were the result of kinesin remaining attached and stepping for larger distances against the stationary trap rather than resulting from changes in kinesin’s velocity. Ensemble averages of force ramps of individual interactions indicate that kinesin’s average velocity values in the single-bead (300 ± 65 nm/s) and dumbbell (280 ± 83 nm/s) assays were within 10% of each other at forces below 3 pN (Fig. S2). Therefore, the large variability of attachment durations in the three-bead assay resulted in a large range of <F_detach> values (2.8 and 8.0 pN).

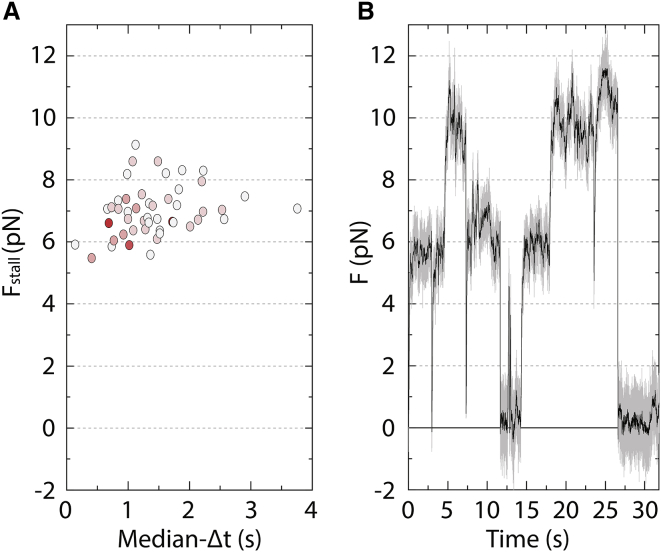
We ruled out the possibility that the large variability in attachment durations in the three-bead assay was due to multiple kinesin molecules interacting with the microtubule by examining the stall forces (see Materials and Methods), which are expected to be additive for multiple molecules (10). The average stall force, 6.8 ± 0.74 pN (SD, n = 48 dumbbells), was within the range previously measured for single kinesin using the single-bead assay (4.8–7.4 pN at saturating ATP (2,3,5,22,23)). As expected for single molecule measurements, the stall forces for each dumbbell were also found to be similar and independent of median-Δt (Fig. 4 A), and the force plateaus during prolonged attachments were similar for all the kinesin runs within each data set (Fig. 1 D; (10,23,30)). Finally, increasing the density of surface-attached kinesin resulted in plateaus of double the force (Fig. 4 B; (10)).

Figure 4.

Stall forces for microtubule dumbbells do not scale with attachment durations. (A) Shown is a scatter plot of the stall force F_stall for each dumbbell as a function of the corresponding median-Δt. In all cases, the fraction of interacting spherical pedestals was ≤0.25. Each scatter point corresponds to a different dumbbell and is the average of force plateaus that lasted for at least 0.1 ms before kinesin detachment. The shading of points scales with the corresponding number of force plateaus for each point, with darker shading indicating a higher number. The value of F_stall doesn’t scale and correlates poorly with the corresponding median-Δt (r = 0.25 and p = 0.08 > 0.05). (B) Shown is an example of a raw force trace (gray) and its smoothed version (black) when the fraction of interacting pedestals was 0.50. Unlike in Fig. 1D, not all the force plateaus are similar, and the higher force plateaus ∼10 pN are approximately twice as high as the lower ones ∼5 pN because of the engagement of more than one kinesin molecule with the microtubule dumbbell. To see this figure in color, go online.

To determine if the observed variability in attachment durations and detachment forces for microtubule dumbbells depended on the microtubule nucleotide state or protofilament number, GMPCPP was used to produce stable microtubules (31,32). GMPCPP filaments exhibited a similar broad range of median-Δt values as the taxol-stabilized preparation (compare Fig. 3 B; Fig. S3).

The large range of kinesin-microtubule attachment durations is not due to variations in pretensile forces within the microtubule or tilting of the dumbbell

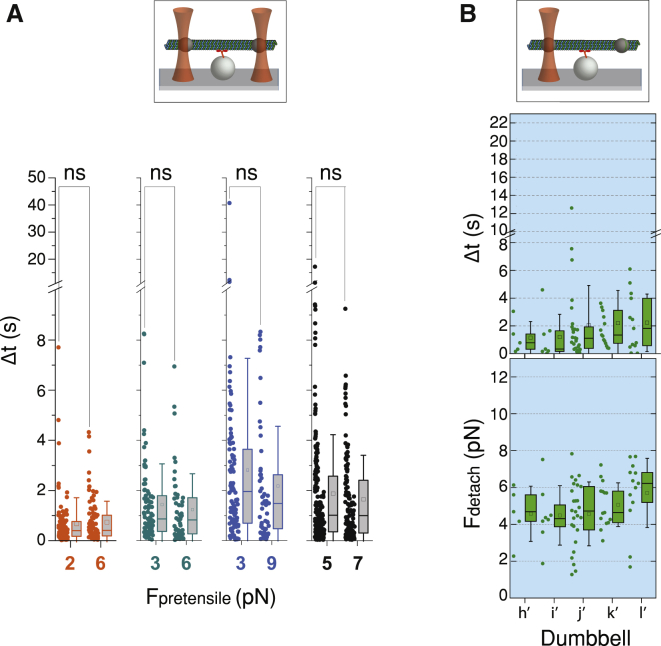
The Δt distribution did not depend on the magnitude of the pretensile forces on the dumbbell microtubule in the range of 2–9 pN (Fig. 5 A). Additionally, when no pretensile forces were applied and only the plus-end bead of the microtubule was trapped, kinesin achieved statistically significantly (p < 0.001, Mann-Whitney test) larger dwell times and detachment forces than the single-bead assay (Figs. 3, A and B and 5 B). Note that for most of the dumbbells, <F_detach> (∼6 pN) was greater than F_pretensile (∼4 pN), indicating that the load on kinesin is provided mainly by the bead attached to the plus-end (Supporting Materials and Methods).

Figure 5.

Attachment durations between kinesin and dumbbells under different pretensile forces as well as only when one bead was trapped. (A). Shown are the distribution and box statistics of attachment durations Δt between kinesin and four different microtubule dumbbells (different colors), each subjected to two different values of pretensile forces in the range between 2 and 9 pN. Statistical comparison showed that the magnitude of the pretensile forces for any given dumbbell doesn’t seem to have an effect on the distribution of Δt (Mann-Whitney test; p > 0.05). (B) Shown are microtubule dumbbells (“h’” to “l’”) laser trapped only by the bead at the plus end while interacting with single kinesin. Top panel: cartoon representation of the assay is shown. Middle panel: distributions and the corresponding box statistics for microtubule attachment duration Δt are shown. Bottom panel: distributions and the corresponding box statistics for detachment forces F_detach are shown. Error bars correspond to SD. To see this figure in color, go online.

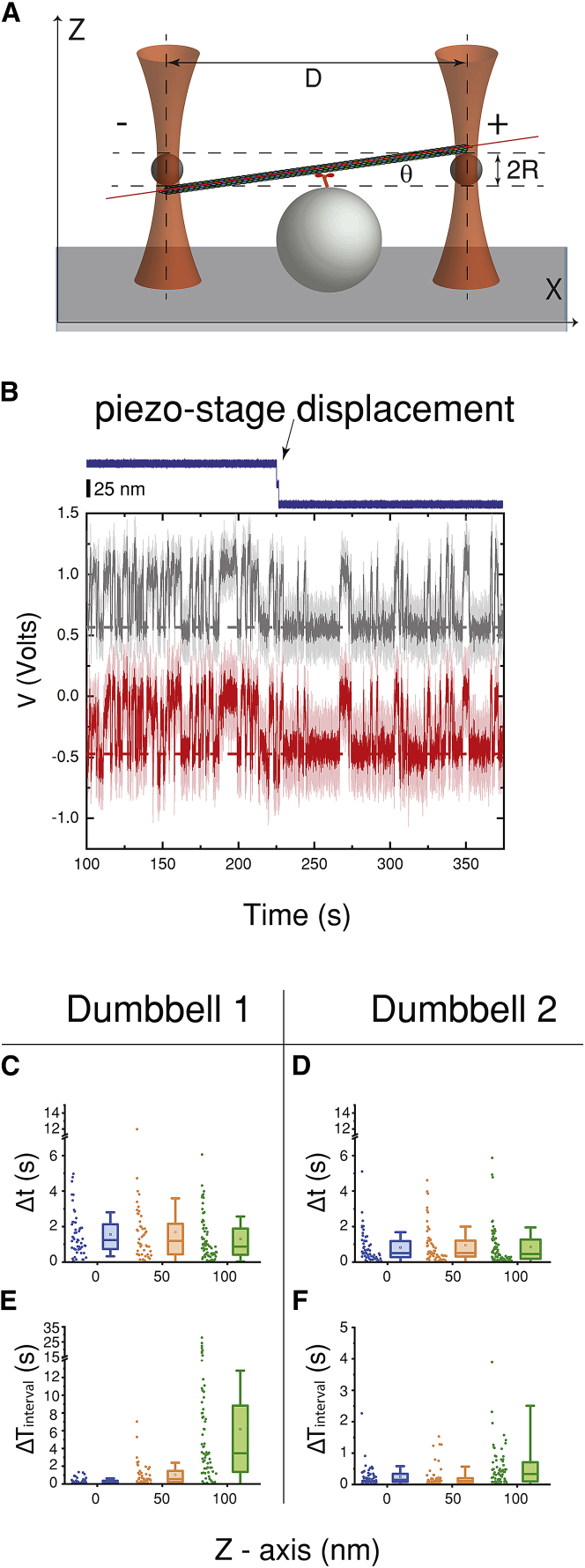
To test if the broad distribution of median-Δt (Fig. 3 D) in the dumbbell assay is due to variable angles of the microtubule’s long axis relative to the coverslip (Fig. 6 A), we tested the sensitivity of the Δt distribution for a given dumbbell to changes in z displacement. This nonparallel geometry of the dumbbell could come about by trapped beads being attached to diametrically opposite protofilaments, whereas the microtubule is on the zx plane (Fig. 6). Under such a condition, the change in displacement in z direction is expected to be ∼8 nm for a 100 nm processive run in x direction. Because the stiffness of the laser trap in the z direction is in general smaller than in the x direction (k_x ≅ 0.05 pN/nm) (33,34), the z component of the force is not expected to exceed ∼0.4 pN. (Analogous arguments show that forces along the y direction are expected to be close to 0.4 pN because k_x ≅ k_y > k_z). We found that increasing the position of the z axis substantially more than expected during a processive run (50 and 100 nm) did not have any significant effect on the Δt distribution (Fig. 6, B–F) but rather only changed the probability of kinesin attachment. However, the z force developed in the single-bead assay is expected to be larger than ∼12 pN (dia. = 0.82 μm, L = 35 nm, and F_x = 5 pN; Eq. 1). This larger force has been proposed to accelerate the detachment kinetics of kinesin (10) and lead to a narrow distribution of median-Δt as we see in our single-bead experiments (Fig. 3 D).

Figure 6.

Variability in the z position of microtubule dumbbells does not affect their attachment duration with kinesin. (A) Shown is a cartoon representation (not drawn to scale) of the configuration for which the angle θ between the microtubule axis and the x axis becomes maximal θ_max = arctan (2R/D) = 4.7°, (2R = 0.82 μm, D ∼10 μm). Assuming that the microtubule is infinitely stiff, as the kinesin moves upwards along the microtubule, a force of 5 pN in the x direction (k_x ≅ 0.05 pN/nm) would correspond to a two-dimensional displacement of Δx ≅ 100 nm and Δz = Δx·tanθ ≅ 8 nm. Because the stiffness of the laser trap in the z direction is in general smaller than in the x direction (33,34), the z component of the force is not expected to exceed 0.4 pN. (B) Shown is a sample of raw data traces (voltage versus time) for the x position of the two trapped beads (gray and red colors) during multiple interactions between a microtubule dumbbell and a kinesin molecule. The dark color traces are smoothed versions of the light color ones, and the horizontal dashed lines indicate the positions of the two beads when the dumbbell is not attached to kinesin. The z position of the piezo stage is shown by the blue trace (top), and a total 50-nm displacement (Scale bars, 25 nm) of the dumbbell further away from the kinesin is indicated by the arrow. Note the decrease in the frequency of interactions after the z displacement. (C) and (D) show plots of the distribution of Δt for two different dumbbells at three different z positions (three different colors) relative to the surface-attached kinesin. The distributions of Δt for each dumbbell are not significantly different from each other at the 0.05 significance level (Kruskal Wallis test). (E) and (F) show the corresponding distribution of the time intervals ΔT_interval between successive kinesin-microtubule interactions in each case. The distributions of ΔT_interval for each dumbbell are significantly different from each other at the 0.05 significance level (Kruskal Wallis test), in contrast to the corresponding Δt distributions. Increasing the separation between the microtubule dumbbell and the surface-attached kinesin affects only the frequency of their interaction and not the distribution of Δt. Error bars correspond to SD. To see this figure in color, go online.

Kinesin-microtubule attachment durations depend on the relative azimuthal separation of net opposing forces

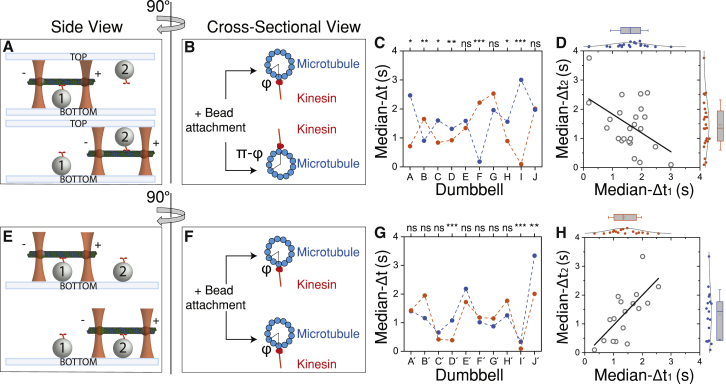
The relative angular position around the cylindrical surface of the microtubule 1) between the two dumbbell bead attachment points, and 2) between the attachment of the dumbbell beads and surface-immobilized kinesin vary among dumbbell assemblies (Fig. S4; Video S2). We will be referring to the angular separation between protofilaments around the axis of the microtubule as the relative azimuthal position, φ, using cylindrical coordinate terminology (Fig. S4; Video S2). Because of the variability in the azimuthal position of the beads around the microtubule, the relative position of the pair of net opposing forces between the interacting kinesin and the microtubule is variable. If this azimuthal variability is responsible for the broad distribution of attachment durations (Fig. 3 D), then we predict that the attachment durations of kinesins interacting at diametrically opposite protofilaments of the same microtubule dumbbell should be different.

To test this proposal, we collected two data sets for each dumbbell (n = 24 dumbbells). First, the dumbbell was brought into contact with a pedestal on the bottom of the experimental chamber to determine median-Δt₁ and then to a pedestal on top of the same chamber to determine median-Δt₂ (Fig. 7 A). By testing this pair of interactions, we are probing diametrically opposite sides of the microtubule, which is equivalent to rotating the microtubule around its axis and thus changing the relative azimuthal position between the beads and the kinesin (Fig. 7 B). For the purpose of simplicity, in Fig. 7 B, we show only the relative azimuthal position φ between the plus-end bead and the interacting kinesin. We found the median-Δt₁ and median-Δt₂ to be anticorrelated with a Pearson coefficient of −0.5 (p = 0.02). Note that the short and long interactions did not always occur on the same side of the chamber but were rather random, arguing against a systematic artifact causing the anticorrelation (Fig. 7 C). Indeed, the distributions of median-Δt₁ and median-Δt₂ are similar to each other (Fig. 7 D) and to the distribution in Fig. 3 D.

Figure 7.

The interaction between kinesin and microtubule dumbbells depends on the relative azimuthal position φ of opposing forces. Shown is a cartoon representation of experiments in which the same dumbbell is brought against two different interacting pedestals “1” and “2” (A and B) in opposing surfaces (top and bottom) or (E and F) along the same surface. In (B and F), φ or π-φ indicate the relative azimuthal position between the protofilament that the plus (+) end bead is attached and the one that interacts with kinesin (see also Fig. S5; Video S2). Plots of median-Δt for 10 different microtubule dumbbells, each against two different pedestals (Δt₁, Δt₂; blue and red scatter points): (C) on the top and bottom surface and (G) along the same surface of the experimental chamber. Dumbbells “I” and “J” in plot (C) are the same dumbbells with “I′” and “J′,” respectively, in plot (G). For each dumbbell, the statistical significance of the comparison between the corresponding distributions of attachment durations for median-Δt₁ and median-Δt₂ is shown on top of plots (C) and (G) (Mann-Whitney test; ns = not significant, ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001). (D) and (H) are scatter plots of median-Δt₁ and median-Δt₂, and solid lines represent linear fits. The distribution and statistics of median-Δt₁ and median-Δt₂ are plotted on the top and the right, respectively, of the plots (D) and (H). To see this figure in color, go online.

To establish that the anticorrelation between median-Δt₁ and median-Δt₂ was due to a significant change of the relative azimuthal position, φ, we tested the same dumbbell (n = 17) against two different pedestals on the same side of the experimental chamber (Fig. 7, E and F). These experiments would reflect any variability due to differences in surface-attachment orientations of kinesin and in its relative position with the interacting microtubule dumbbell. In contrast to the previous experiment, the Pearson correlation coefficient for median-Δt₁ and median-Δt₂ is positive 0.7 (p = 0.001) (Fig. 7 G and H). It is likely that the actual values of both correlation and anticorrelation coefficients are underestimated because we do not have a fine positional control at the protofilament level. The azimuthal position φ will not always be exactly the same for spherical pedestals across the same surface (Fig. 7 F) and not always exactly π-φ for spherical pedestals in opposing surfaces (Fig. 7 B).

Discussion

Kinesin motility is highly sensitive to assay geometry

Our results show that the attachment duration and the magnitude of opposing forces that can be sustained by the microtubule-kinesin complex, or else kinesin’s load-bearing capacity, is highly variable and can be dramatically affected by the relative orientation between the force vector and the microtubule track. The presence of a larger force component vertical to the microtubule in the single-bead assay (F_z/F_x = 2.4 pN, when Fx = 5 pN; Table 1) relative to three-bead assay (F_z/F_x ≤ 0.08, when Fx = 5 pN; Table 1) is the likely reason for the observed differences in <median-Δt > of the microtubule-kinesin complex between the two assays, supporting a recent theoretical study (10). Notably, recurring long attachments at similar high force plateaus ≥5 pN between single molecule kinesin and microtubules at saturating ATP concentrations were observed previously with a microneedle assay, which is not predicted to have a large vertical force component (3).

Therefore, a key finding of this work is that one needs to consider assay geometry, bead size, and tether length when designing and interpreting single-bead experiments for kinesin-1 and possibly other cytoskeletal motors. Although vertical forces likely exist on kinesins as they function in the cell, they must be experimentally controlled to define force-dependent parameters. Vertical forces can be experimentally minimized by the use of the three-bead assay or long tethers for motor attachments in the single-bead assay.

Kinesin motility is affected by forces across the microtubule lattice

When opposing forces are oriented mainly along the microtubule axis (three-bead assay), kinesin’s load-bearing capacity is highly variable between dumbbells and appears to depend on the relative azimuthal position of the pair of opposing forces around the circumference of the microtubule. Depending on its location on the microtubule, kinesin can switch from a fast detaching motor to a persistent motor that can sustain its microtubule attachment at high forces (>5 pN) for extended lengths of time, with almost an order of magnitude difference.

The load-bearing capacity of kinesin has been shown previously to depend on the rightward or leftward direction of sideway forces larger than 1 pN (9), resulting in changes of ∼15% in kinesin’s velocity, ∼50% in its run length, and ∼1.7-fold in attachment durations. Although these effects are significant, they are not as large as the variability observed in microtubule attachments durations in the three-bead assay. Sideways loads in the three-bead assay can be produced either by y or z forces, and these forces may differ from dumbbell to dumbbell. However, the y and z force components in the three-bead assay are not expected to exceed 0.4 pN (<1 pN), and our data indicate that changes of this magnitude do not have a significant effect on kinesin’s microtubule attachment durations (Fig. 6). Therefore, although sideways forces may affect kinesin’s attachments durations, they do not explain the large variability observed in the three-bead assay.

We propose the mechanism for the observed variability of kinesin’s load-bearing capacity in the three-bead assay to be related to the structural plasticity of the microtubule (35). Interestingly, recent structural studies have shown biochemically induced expansion and cross-sectional deformation of microtubules upon the binding of molecular motors in the absence of external mechanical forces (13,14,36). It is also possible that cooperative clustering of different post-translationally modified tubulin isoforms during microtubule polymerization may play a role, such that not all the protofilaments of a microtubule are equivalent interacting substrates for kinesin under opposing forces. Nevertheless, our findings point to a more general mechanism by which the duration of the interaction between microtubules and binding partners can be a more complex function of the geometry of forces than previously appreciated.

In summary, this work shows that assay geometry and the relative geometry of forces across the microtubule lattice affect kinesin processivity. Thus, care must be taken when interpreting and modeling force-dependent, single molecule motility data as the full force vector must be accounted for. This work also impacts our understanding of kinesin cell biology as the microtubule structure and mechanics likely play an underappreciated role in the regulation of the motor’s activity.

Author Contributions

S.P., H.S., and E.M.O. designed the experiments. S.P. performed the experiments and analyzed the data. S.P., H.S., and E.M.O. wrote the manuscript.

Editor: David Sept.