A Level Set Method for Image Segmentation in the Presence of Intensity Inhomogeneities With Application to MRI

Abstract

Intensity inhomogeneity often occurs in real-world images, which presents a considerable challenge in image segmentation. The most widely used image segmentation algorithms are region-based and typically rely on the homogeneity of the image intensities in the regions of interest, which often fail to provide accurate segmentation results due to the intensity inhomogeneity. This paper proposes a novel region-based method for image segmentation, which is able to deal with intensity inhomogeneities in the segmentation. First, based on the model of images with intensity inhomogeneities, we derive a local intensity clustering property of the image intensities, and define a local clustering criterion function for the image intensities in a neighborhood of each point. This local clustering criterion function is then integrated with respect to the neighborhood center to give a global criterion of image segmentation. In a level set formulation, this criterion defines an energy in terms of the level set functions that represent a partition of the image domain and a bias field that accounts for the intensity inhomogeneity of the image. Therefore, by minimizing this energy, our method is able to simultaneously segment the image and estimate the bias field, and the estimated bias field can be used for intensity inhomogeneity correction (or bias correction). Our method has been validated on synthetic images and real images of various modalities, with desirable performance in the presence of intensity inhomogeneities. Experiments show that our method is more robust to initialization, faster and more accurate than the well-known piecewise smooth model. As an application, our method has been used for segmentation and bias correction of magnetic resonance (MR) images with promising results.

I. Introduction

INTENSITY inhomogeneity often occurs in real-world images due to various factors, such as spatial variations in illumination and imperfections of imaging devices, which complicates many problems in image processing and computer vision. In particular, image segmentation may be considerably difficult for images with intensity inhomogeneities due to the overlaps between the ranges of the intensities in the regions to segmented. This makes it impossible to identify these regions based on the pixel intensity. Those widely used image segmentation algorithms [4], [17], [18], [23] usually rely on intensity homogeneity, and therefore are not applicable to images with intensity inhomogeneities. In general, intensity inhomogeneity has been a challenging difficulty in image segmentation.

The level set method, originally used as numerical technique for tracking interfaces and shapes [14], has been increasingly applied to image segmentation in the past decade [2], [4], [5], [8]-[12], [15]. In the level set method, contours or surfaces are represented as the zero level set of a higher dimensional function, usually called a level set function. With the level set representation, the image segmentation problem can be formulated and solved in a principled way based on well-established mathematical theories, including calculus of variations and partial differential equations (PDE). An advantage of the level set method is that numerical computations involving curves and surfaces can be performed on a fixed Cartesian grid without having to parameterize these objects. Moreover, the level set method is able to represent contours/surfaces with complex topology and change their topology in a natural way.

Existing level set methods for image segmentation can be categorized into two major classes: region-based models [4], [10], [17], [18], [20], [22] and edge-based models [3], [7], [8], [12], [21]. Region-based models aim to identify each region of interest by using a certain region descriptor to guide the motion of the active contour. However, it is very difficult to define a region descriptor for images with intensity inhomogeneities. Most of region-based models [4], [16]-[18] are based on the assumption of intensity homogeneity. A typical example is piecewise constant (PC) models proposed in [4], [16]—[18]. In [20], [22], level set methods are proposed based on a general piecewise smooth (PS) formulation originally proposed by Mumford and Shah [13]. These methods do not assume homogeneity of image intensities, and therefore are able to segment images with intensity inhomogeneities. However, these methods are computationally too expensive and are quite sensitive to the initialization of the contour [10], which greatly limits their utilities. Edge-based models use edge information for image segmentation. These models do not assume homogeneity of image intensities, and thus can be applied to images with intensity inhomogeneities. However, this type of methods are in general quite sensitive to the initial conditions and often suffer from serious boundary leakage problems in images with weak object boundaries.

In this paper, we propose a novel region-based method for image segmentation. From a generally accepted model of images with intensity inhomogeneities, we derive a local intensity clustering property, and therefore define a local clustering criterion function for the intensities in a neighborhood of each point. This local clustering criterion is integrated over the neighborhood center to define an energy functional, which is converted to a level set formulation. Minimization of this energy is achieved by an interleaved process of level set evolution and estimation of the bias field. As an important application, our method can be used for segmentation and bias correction of magnetic resonance (MR) images. Note that this paper is an extended version of our preliminary work presented in our conference paper [9].

This paper is organized as follows. We first review two well-known region-based models for image segmentation in Section II. In Section III, we propose an energy minimization framework for image segmentation and estimation of bias field, which is then converted to a level set formulation in Section IV for energy minimization. Experimental results are given in Section V, followed by a discussion of the relationship between our model and the piecewise smooth Mumford–Shah and piecewise constant Chan-Vese models in Section VI. This paper is summarized in Section VII.

II. Background

Let Ω be the image domain, and $I:\mathrm{\Omega }\to \Re$ be a gray level image. In [13], a segmentation of the image I is achieved by finding a contour C, which separates the image domain Ω into disjoint regions Ω₁,⋯,Ω_N, and a piecewise smooth function u that approximates the image I and is smooth inside each region Ω_i. This can be formulated as a problem of minimizing the following Mumford-Shah functional

$${\mathcal{F}}^{MS}(u,C)=\underset{\mathrm{\Omega }}{\int }{(I-u)}^{2}d\mathbf{x}+\mu \underset{\mathrm{\Omega }\backslash C}{\int }|\nabla u{|}^{2}d\mathbf{x}+\nu |C|$$ (1)

where |C| is the length of the contour C. In the right hand side of (1), the first term is the data term, which forces u to be close to the image I, and the second term is the smoothing term, which forces u to be smooth within each of the regions separated by the contour C. The third term is introduced to regularize the contour C.

Let Ω₁,⋯,Ω_N be the regions in Ω separated by the contour C, i.e. $\mathrm{\Omega }\backslash C={\cup }_{i=1}^N{\mathrm{\Omega }}_i$. Then, the contour C can be expressed as the union of the boundaries of the regions, denoted by C₁,⋯,C_N, i.e. $C={\cup }_{i=1}^N{C}_i$. Therefore, the above energy ${\mathcal{F}}^{MS}(u,C)$ can be equivalently written as

$$\begin{gathered} {\mathcal{F}}^{MS}\left(u_1,\cdots ,u_N,{\mathrm{\Omega }}_1,\cdots ,{\mathrm{\Omega }}_N\right) \\ =\sum _{i=1}^N\left(\underset{{\mathrm{\Omega }}_i}{\int }{\left(I-u_i\right)}^{2}d\mathbf{x}+\mu \underset{{\mathrm{\Omega }}_i}{\int }{\left|\nabla u_i\right|}^{2}d\mathbf{x}+\nu \left|C_i\right|\right) \end{gathered}$$

where u_i is a smooth function defined on the region Ω_i. The methods aiming to minimize this energy are called piecewise smooth (PS) models. In [20], [22], level set methods were proposed as PS models for image segmentation.

The variables of the energy ${\mathcal{F}}^{MS}$ include N different functions u₁,⋯,u_N. The smoothness of each function u_i in Ω_i has to be ensured by imposing a smoothing term $\mu {\int }_{{\mathrm{\Omega }}_i}{\left|\nabla u_i\right|}^{2}d\mathbf{x}$ in the functional ${\mathcal{F}}^{MS}$. To minimize this energy, N PDEs for solving the functions u_1,⋯,u_N associated with the corresponding smoothing terms are introduced and have to be solved at each time step in the evolution of the contour C or the regions Ω₁,⋯,Ω_N. This procedure is computationally expensive. Moreover, the PS model is sensitive to the initialization of the contour C or the regions Ω₁,⋯,Ω_N. These difficulties can be seen from some experimental results in Section V-A.

In a variational level set formulation [4], Chan and Vese simplified the Mumford-Shah functional as the following energy:

$$\begin{gathered} {\mathcal{F}}^{CV}\left(\varphi ,c_1,c_2\right)=\underset{\mathrm{\Omega }}{\int }{\left|I(\mathbf{x})-c_1\right|}^{2}H(\varphi (\mathbf{x}))d\mathbf{x} \\ +\underset{\mathrm{\Omega }}{\int }{\left|I(\mathbf{x})-c_2\right|}^2(1-H(\varphi (\mathbf{x})))d\mathbf{x} \\ +\nu \underset{\mathrm{\Omega }}{\int }|\nabla H(\varphi (\mathbf{x}))|d\mathbf{x} \end{gathered}$$ (2)

where H is the Heaviside function, and ϕ is a level set function, whose zero level contour C = {x : ϕ(x) = 0} partitions the image domain Ω into two disjoint regions Ω₁ = {x : ϕ(x) > 0} and Ω₂ = {x : ϕ(x) < 0}. The first two terms in (2) are the data fitting terms, while the third term, with a weight v > 0, regularizes the zero level contour. Image segmentation is therefore achieved by find the level set function ϕ and the constants c₁ and c₂ that minimize the energy ${\mathcal{F}}^{CV}$. This model is a piecewise constant (PC) model, as it assumes that the image I can be approximated by constants c₁ and c₂ in the regions Ω₁ and Ω₂, respectively.

III. Variational Framework for Joint Segmentation and Bias Field Estimation

A. Image Model and Problem Formulation

In order to deal with intensity inhomogeneities in image segmentation, we formulate our method based on an image model that describes the composition of real-world images, in which intensity inhomogeneity is attributed to a component of an image. In this paper, we consider the following multiplicative model of intensity inhomogeneity. From the physics of imaging in a variety of modalities (e.g. camera and MRI), an observed image I can be modeled as

$$I=bJ+n$$ (3)

where J is the true image, b is the component that accounts for the intensity inhomogeneity, and n is additive noise. The component b is referred to as a bias field (or shading image). The true image J measures an intrinsic physical property of the objects being imaged, which is therefore assumed to be piecewise (approximately) constant. The bias field b is assumed to be slowly varying. The additive noise n can be assumed to be zero-mean Gaussian noise.

In this paper, we consider the image I as a function $I:\mathrm{\Omega }\to \Re$ defined on a continuous domain Ω. The assumptions about the true image J and the bias field b can be stated more specifically as follows:

• (A1) The bias field b is slowly varying, which implies that b can be well approximated by a constant in a neighborhood of each point in the image domain.

• (A2) The true image J approximately takes N distinct constant values c₁,⋯,c_N in disjoint regions Ω₁,⋯,Ω_N, respectively, where ${\left\{{\mathrm{\Omega }}_i\right\}}_{i=1}^N$ forms a partition of the image domain, i.e. $\mathrm{\Omega }={\cup }_{i=1}^N{\mathrm{\Omega }}_i$ and Ω_i ∩ Ω_j = ∅ for i ≠ j

based on the model in (3) and the assumptions A1 and A2, we propose a method to estimate the regions ${\left\{{\mathrm{\Omega }}_i\right\}}_{i=1}^N$, the constants ${\left\{c_i\right\}}_{i=1}^N$, and the bias field b. The obtained estimates of them are denoted by ${\{{\widehat{\mathrm{\Omega }}}_i\}}_{i=1}^N$, the constants ${\left\{{\widehat{c}}_i\right\}}_{i=1}^N$, and the bias field $\widehat{b}$, respectively. The obtained bias field $\widehat{b}$ should be slowly varying and the regions ${\widehat{\mathrm{\Omega }}}_1,\cdots ,{\widehat{\mathrm{\Omega }}}_N$ should satisfy certain regularity property to avoid spurious segmentation results caused by image noise. We will define a criterion for seeking such estimates based on the above image model and assumptions A1 and A2. This criterion will be defined in terms of the regions Ω_i, constants c_i, and function b, as an energy in a variational framework, which is minimized for finding the optimal regions ${\{{\widehat{\mathrm{\Omega }}}_i\}}_{i=1}^N$, constants ${\left\{{\widehat{c}}_i\right\}}_{i=1}^N$, and bias field $\widehat{b}$. As a result, image segmentation and bias field estimation are simultaneously accomplished.

B. Local Intensity Clustering Property

Region-based image segmentation methods typically relies on a specific region descriptor (e.g. intensity mean or a Gaussian distribution) of the intensities in each region to be segmented. However, it is difficult to give such a region descriptor for images with intensity inhomogeneities. Moreover, intensity inhomogeneities often lead to overlap between the distributions of the intensities in the regions Ω₁,⋯,Ω_N. Therefore, it is impossible to segment these regions directly based on the pixel intensities. Nevertheless, the property of local intensities is simple, which can be effectively exploited in the formulation of our method for image segmentation with simultaneous estimation of the bias field.

based on the image model in (3) and the assumptions A1 and A2, we are able to derive a useful property of local intensities, which is referred to as a local intensity clustering property as described and justified below. To be specific, we consider a circular neighborhood with a radius ⍴ centered at each point y ∈ Ω, defined by ${\mathcal{O}}_{\mathbf{y}}\triangleq \{\mathbf{x}:|\mathbf{x}-\mathbf{y}|\le \rho \}$. The partition ${\left\{{\mathrm{\Omega }}_i\right\}}_{i=1}^N$ of the entire domain Ω induces a partition of the neighborhood ${\mathcal{O}}_{\mathbf{y}}$, i.e., ${\left\{{\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i\right\}}_{i=1}^N$ forms a partition of ${\mathcal{O}}_{\mathbf{y}}$. For a slowly varying bias field b, the values b(x) for all x in the circular neighborhood ${\mathcal{O}}_{\mathbf{y}}$ are close to b(y), i.e.

$$b(\mathbf{x})\approx b(\mathbf{y})\text{for}\mathbf{x}\in {\mathcal{O}}_{\mathbf{y}}.$$ (4)

Thus, the intensities b(x)J(x) in each subregion ${\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i$ are close to the constant b(y)c_i, i.e.

$$b(\mathbf{x})J(\mathbf{x})\approx b(\mathbf{y})c_i\text{for}\mathbf{x}\in {\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i.$$ (5)

Then, in view of the image model in (3), we have

$$I(\mathbf{x})\approx b(\mathbf{y})c_i+n(\mathbf{x})\text{for}\mathbf{x}\in {\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i$$

where n(x) is additive zero-mean Gaussian noise. Therefore, the intensities in the set

$${\mathbf{I}}_{\mathbf{y}}^i=\left\{I(\mathbf{x}):\mathbf{x}\in {\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i\right\}$$

form a cluster with cluster center m_i ≈ b(y)c_i, which can be considered as samples drawn from a Gaussian distribution with mean m_i. Obviously, the N clusters ${\mathbf{I}}_{\mathbf{y}}^1,\cdots ,{\mathbf{I}}_{\mathbf{y}}^N$, are well-separated, with distinct cluster centers m_i ≈ b(y)c_i, i = 1,⋯,N (because the constants c₁,⋯,c_N are distinct and the variance of the Gaussian noise n is assumed to be relatively small). This local intensity clustering property is used to formulate the proposed method for image segmentation and bias field estimation as follows.

C. Energy Formulation

The above described local intensity clustering property indicates that the intensities in the neighborhood ${\mathcal{O}}_{\mathbf{y}}$ can be classified into N clusters, with centers m_i ≈ b(y)c_i, i = 1,⋯,N. This allows us to apply the standard K-means clustering to classify these local intensities. Specifically, for the intensities I(x) in the neighborhood ${\mathcal{O}}_{\mathbf{y}}$, the K-means algorithm is an iterative process to minimize the clustering criterion [19], which can be written in a continuous form as

$$F_{\mathbf{y}}=\sum _{i=1}^N\underset{{\mathcal{O}}_{\mathbf{y}}}{\int }{\left|I(\mathbf{x})-m_i\right|}^2{u}_i(\mathbf{x})d\mathbf{x}$$ (6)

where m_i is the cluster center of the i-th cluster, u_i is the membership function of the region Ω_i to be determined, i.e. u_i(x) = 1 for x ∈ Ω_i and u_i(x) = 0 for x ∉ Ω_i. Since u_i is the membership function of the region Ω_i, we can rewrite F_y as

$$F_{\mathbf{y}}=\sum _{i=1}^N\underset{{\mathrm{\Omega }}_i\cap {\mathcal{O}}_{\mathbf{y}}}{\int }{\left|I(\mathbf{x})-m_i\right|}^{2}d\mathbf{x}.$$ (7)

In view of the clustering criterion in (7) and the approximation of the cluster center by m_i ≈ (y)c_i, we define a clustering criterion for classifying the intensities in ${\mathcal{O}}_{\mathbf{y}}$ as

$${\mathcal{E}}_{\mathbf{y}}=\sum _{i=1}^N\underset{{\mathrm{\Omega }}_i\cap {\mathcal{O}}_{\mathbf{y}}}{\int }K(\mathbf{y}-\mathbf{x})|I(\mathbf{x})-b(\mathbf{y})c_i{|}^{2}d\mathbf{x}$$ (8)

where K(y − x) is introduced as a nonnegative window function, also called kernel function, such that K(y − x) = 0 for $\mathbf{x}\notin {\mathcal{O}}_{\mathbf{y}}$. With the window function, the clustering criterion function ${\mathcal{E}}_{\mathbf{y}}$ can be rewritten as

$${\mathcal{E}}_{\mathbf{y}}=\sum _{i=1}^N\underset{{\mathrm{\Omega }}_i}{\int }K(\mathbf{y}-\mathbf{x})|I(\mathbf{x})-{b(\mathbf{y})c_i|}^{2}d\mathbf{x}.$$ (9)

This local clustering criterion function is a basic element in the formulation of our method.

The local clustering criterion function ${\mathcal{E}}_{\mathbf{y}}$ evaluates the classification of the intensities in the neighborhood ${\mathcal{O}}_{\mathbf{y}}$ given by the partition ${\left\{{\mathcal{O}}_{\mathbf{y}}\cap {\mathrm{\Omega }}_i\right\}}_{i=1}^N$ of ${\mathcal{O}}_{\mathbf{y}}$. The smaller the value of ${\mathcal{E}}_{\mathbf{y}}$, the better the classification. Naturally, we define the optimal partition ${\left\{{\mathrm{\Omega }}_i\right\}}_{i=1}^N$ of the entire domain Ω as the one such that the local clustering criterion function ${\mathcal{E}}_{\mathbf{y}}$ is minimized for all y in Ω. Therefore, we need to jointly minimize ${\mathcal{E}}_{\mathbf{y}}$ for all y in Ω. This can be achieved by minimizing the integral of ${\mathcal{E}}_{\mathbf{y}}$ with respect to y over the image domain Ω. Therefore, we define an energy $\mathcal{E}\triangleq \int {\mathcal{E}}_{\mathbf{y}}d\mathbf{y}$, i.e.,

$$\mathcal{E}\triangleq \int \left(\sum _{i=1}^N\underset{{\mathrm{\Omega }}_i}{\int }K(\mathbf{y}-\mathbf{x}){\left|I(\mathbf{x})-b(\mathbf{y})c_i\right|}^{2}d\mathbf{x}\right)d\mathbf{y}.$$ (10)

In this paper, we omit the domain Ω in the subscript of the integral symbol (as in the first integral above) if the integration is over the entire domain Ω. Image segmentation and bias field estimation can be performed by minimizing this energy with respect to the regions Ω₁,⋯,Ω_N, constants c₁,⋯,c_N, and bias field b.

The choice of the kernel function K is flexible. For example, it can be a truncated uniform function, defined as K(u) = a for |u| ≤ ρ and K(u) = 0 for |u| > ρ, with a being a positive constant such that $\int K(\mathbf{u})=1$. In this paper, the kernel function K is chosen as a truncated Gaussian function defined by

$$K(\mathbf{u})=\{\begin{array}{ll}\frac{1}{a}{e}^{-|\mathbf{u}{|}^2/2{\sigma }^2},\hfill & \text{for}\left|\mathbf{u}\right|\le \rho \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (11)

where a is a normalization constant such that $\int K(\mathbf{u})=1$, σ is the standard deviation (or the scale parameter) of the Gaussian function, and ρ is the radius of the neighborhood ${\mathcal{O}}_{\mathbf{y}}$.

Note that the radius ρ of the neighborhood ${\mathcal{O}}_{\mathbf{y}}$ should be selected appropriately according to the degree of the intensity inhomogeneity. For more localized intensity inhomogeneity, the bias field b varies faster, and therefore the approximation in (4) is valid only in a smaller neighborhood. In this case, a smaller ρ should be used as the radius of the neighborhood ${\mathcal{O}}_{\mathbf{y}}$, and for the truncated Gaussian function in (11), the scale parameter σ should also be smaller.

IV. Level Set Formulation and Energy Minimization

Our proposed energy $\mathcal{E}$ in (10) is expressed in terms of the regions Ω₁,⋯,Ω_N. It is difficult to derive a solution to the energy minimization problem from this expression of $\mathcal{E}$. In this section, the energy $\mathcal{E}$ is converted to a level set formulation by representing the disjoint regions Ω₁,⋯,Ω_N with a number of level set functions, with a regularization term on these level set functions. in the level set formulation, the energy minimization can be solved by using well-established variational methods [6].

In level set methods, a level set function is a function that take positive and negative signs, which can be used to represent a partition of the domain Ω into two disjoint regions Ω₁ and Ω₂. Let $\varphi :\mathrm{\Omega }\to \Re$ be a level set function, then its signs define two disjoint regions

$${\mathrm{\Omega }}_1=\{\mathbf{x}:\varphi (\mathbf{x})>0\},\text{and}{\mathrm{\Omega }}_2=\{\mathbf{x}:\varphi (\mathbf{x})<0\}$$ (12)

which form a partition of the domain Ω. For the case of N > 2, two or more level set functions can be used to represent N regions Ω₁,⋯,Ω_N. The level set formulation of the energy $\mathcal{E}$ for the cases of N = 2 and N > 2, called two-phase and multiphase formulations, respectively, will be given in the next two subsections.

A. Two-Phase Level Set Formulation

We first consider the two-phase case: the image domain Ω is segmented into two disjoint regions Ω₁ and Ω₂. In this case, a level set function ϕ is used to represent the two regions Ω₁ and Ω₂ given by (12). The regions Ω₁ and Ω₂ can be represented with their membership functions defined by M₁(ϕ) = H(ϕ) and M₂(ϕ) = 1 − H(ϕ), respectively, where H is the Heaviside function. Thus, for the case of N = 2, the energy in (10) can be expressed as the following level set formulation:

$$\mathcal{E}=\int \left(\sum _{i=1}^N\int K(\mathbf{y}-\mathbf{x}){\left|I(\mathbf{x})-b(\mathbf{y})c_i\right|}^2{M}_i(\varphi (\mathbf{x}))d\mathbf{x}\right)d\mathbf{y}.$$ (13)

By exchanging the order of integrations, we have

$$\mathcal{E}=\int \sum _{i=1}^N\left(\int K(\mathbf{y}-\mathbf{x}){\left|I(\mathbf{x})-b(\mathbf{y})c_i\right|}^{2}d\mathbf{y}\right)M_i(\varphi (\mathbf{x}))d\mathbf{x}.$$ (14)

For convenience, we represent the constants c₁,⋯,c_N with a vector c = (c₁,⋯,c_N). Thus, the level set function ϕ, the vector c, and the bias field b are the variables of the energy $\mathcal{E}$, which can therefore be written as $\mathcal{E}(\varphi ,\mathbf{c},b)$. From (14), we can rewrite the energy $\mathcal{E}(\varphi ,\mathbf{c},b)$ in the following form:

$$\mathcal{E}(\varphi ,\mathbf{c},b)=\int \sum _{i=1}^N{e}_i(\mathbf{x})M_i(\varphi (\mathbf{x}))d\mathbf{x}$$ (15)

where e_i is the function defined by

$$e_i(\mathbf{x})=\int K(\mathbf{y}-\mathbf{x}){\left|I(\mathbf{x})-b(\mathbf{y})c_i\right|}^{2}d\mathbf{y}.$$ (16)

The functions e_i can be computed using the following equivalent expression:

$$e_i(\mathbf{x})=I^2{\mathbf{1}}_K-2c_{i}I(b\ast K)+c_i^2\left(b^2\ast K\right)$$ (17)

where * is the convolution operation, and 1_k is the function defined by 1_k(x) = ∫ K(y − x)dy, which is equal to constant 1 everywhere except near the boundary of the image domain Ω.

The above defined energy $\mathcal{E}(\varphi ,\mathbf{c},b)$ is used as the data term in the energy of the proposed variational level set formulation, which is defined by

$$\mathcal{F}(\varphi ,\mathbf{c},b)=\mathcal{E}(\varphi ,\mathbf{c},b)+\nu \mathcal{L}(\varphi )+\mu {\mathcal{R}}_p(\varphi )$$ (18)

with $\mathcal{L}(\varphi )$ and ${\mathcal{R}}_p(\varphi )$ being the regularization terms as defined below. The energy term $\mathcal{L}(\varphi )$ is defined by

$$\mathcal{L}(\varphi )=\int |\nabla H(\varphi )|d\mathbf{x}$$ (19)

which computes the arc length of the zero level contour of ϕ and therefore serves to smooth the contour by penalizing its arc length [4], [10]. The energy term ${\mathcal{R}}_p(\varphi )$ is defined by

$${\mathcal{R}}_p(\varphi )=\int p(|\nabla \varphi |)d\mathbf{x}$$ (20)

with a potential (energy density) function $p:[0,\infty )\to \Re$ such that p(s) ≥ p(1) for all s, i.e. s = 1 is a minimum point of p. In this paper, we use the potential function p defined by p(s) = (l/2)(s−l)². Obviously, with such a potential p, the energy ${\mathcal{R}}_p(\varphi )$ is minimized when |∇ϕ| = 1, which is the characteristic of a signed distance function, called the signed distance property. Therefore, the regularization term ${\mathcal{R}}_p(\varphi )$ is called a distance regularization term, which was introduced by Li et al. [11] in a more general variational level set formulation called distance regularized level set evolution (DRLSE) formulation. The readers are referred to [11] for the necessity and the mechanism of maintaining the signed distance property of the level set function in DRLSE.

By minimizing this energy, we obtain the result of image segmentation given by the level set function ϕ and the estimation of the bias field b. The energy minimization is achieved by an iterative process: in each iteration, we minimize the energy $\mathcal{F}(\varphi ,\mathbf{c},b)$ with respect to each of its variables ϕ, c, and b, given the other two updated in previous iteration. We give the solution to the energy minimization with respect to each variable as follows.

1). Energy Minimization With Respect to ϕ

For fixed c and b, the minimization of $\mathcal{F}(\varphi ,\mathbf{c},b)$ with respect to ϕ can be achieved by using standard gradient descent method, namely, solving the gradient flow equation

$$\frac{\partial \varphi }{\partial t}=-\frac{\partial \mathcal{F}}{\partial \varphi }$$ (21)

where $\partial \mathcal{F}/\partial \varphi$ is the Gâteaux derivative [1] of the energy $\mathcal{F}$.

By calculus of variations [1], we can compute the Gâteaux derivative $\partial \mathcal{F}/\partial \varphi$ and express the corresponding gradient flow equation as

$$\begin{gathered} \frac{\partial \varphi }{\partial t}=-\delta (\varphi )\left(e_1-e_2\right)+\nu \delta (\varphi )\mathrm{div}\left(\frac{\nabla \varphi }{|\nabla \varphi |}\right) \\ +\mu \mathrm{div}\left(d_p(|\nabla \varphi |)\nabla \varphi \right) \end{gathered}$$ (22)

where ∇ is the gradient operator, div(·) is the divergence operator, and the function d_p is defined as

$$d_p(s)\triangleq \frac{p^{\prime }(s)}{s}.$$

The same finite difference scheme to implement the DRLSE, as described in [11], can be used for the level set evolution (22). During the evolution of the level set function according to (22), the constants c₁ and c₂ in c and the bias field b are updated by minimizing the energy $\mathcal{E}(\varphi ,\mathbf{c},b)$ with respect to c and b, respectively, which are described below.

2). Energy Minimization With Respect to c

For fixed ϕ and b, the optimal c that minimizes the energy $\mathcal{E}(\varphi ,\mathbf{c},b)$, denoted by $\widehat{\mathbf{c}}=\left({\widehat{c}}_i,\cdots ,{\widehat{c}}_N\right)$, is given by

$${\widehat{c}}_i=\frac{\int (b\ast K)I{u}_{i}d\mathbf{y}}{\int \left(b^2\ast K\right)u_{i}d\mathbf{y}},i=1,\cdots ,N$$ (23)

with u_i(y) = M_i(ϕ(y)).

3). Energy Minimization With Respect to b

For fixed ϕ and c, the optimal b that minimizes the energy $\mathcal{E}(\varphi ,\mathbf{c},b)$, denoted by $\widehat{b}$, is given by

$$\widehat{b}=\frac{\left(I{J}^{(1)}\right)\ast K}{J^{(2)}\ast K}$$ (24)

where $J^{(1)}={\sum }_{i=1}^N{c}_i{u}_i$ and $J^{(2)}={\sum }_{i=1}^N{c}_i^2{u}_i$. Note that the convolutions with a kernel function K in (24) confirms the slowly varying property of the derived optimal estimator $\widehat{b}$ of the bias field.

B. Multiphase Level Set Formulation

For the case of N ≥ 3, we can use two or more level set functions ϕ₁,⋯,ϕ_k to define N membership functions M_i of the regions Ω_i, i = 1,⋯,N, such that

$$M_i\left({\varphi }_1(\mathbf{y}),\cdots ,{\varphi }_k(\mathbf{y})\right)=\{\begin{array}{ll}1,\hfill & \mathbf{y}\in {\mathrm{\Omega }}_i\hfill \\ 0,\hfill & \text{else}.\hfill \end{array}$$

For example, in the case of N = 3, we use two level set functions ϕ₁ and ϕ₂ to define M₁(ϕ₁, ϕ₂) = H(ϕ₁)H(ϕ₂), M₂(ϕ₁, ϕ₂) = H(ϕ₁)(1 – H(ϕ₂)), and M₃(ϕ₁, ϕ₂) = 1 – H(ϕ₁) to give a three-phase level set formulation of our method. For the four-phase case N = 4, the definition of M_i can be defined as M₁(ϕ₁, ϕ₂) = H(ϕ₁)H(ϕ₂), M₂(ϕ₁, ϕ₂) = H(ϕ₁)(1 − H(ϕ₂)), M₃(ϕ₁, ϕ₂) = (1 − H(ϕ₁))H(ϕ₂), and M₄(ϕ₁, ϕ₂) = (1 − H(ϕ₁))(1 − H(ϕ₂)).

For notational simplicity, we denote these level set functions ϕ₁,⋯,ϕ_k by a vector valued function Φ = (ϕ₁,⋯,ϕ_k). Thus, the membership functions M_i(ϕ₁(y),⋯,ϕ_k(ϕ)) can be written as M_i(Φ). The energy $\mathcal{E}$ in (10) can be converted to a multiphase level set formulation

$$\mathcal{E}(\mathrm{\Phi },\mathbf{c},b)=\int \sum _{i=1}^N{e}_i(\mathbf{x})M_i(\mathrm{\Phi }(\mathbf{x}))d\mathbf{x}$$

with e_i given by (16).

For the function Φ = (ϕ₁,⋯,ϕ_k), we define the regularization terms $\mathcal{L}(\mathrm{\Phi })={\sum }_{j=1}^k\mathcal{L}\left({\varphi }_j\right)$ and ${\mathcal{R}}_p(\mathrm{\Phi })={\sum }_{j=1}^k{\mathcal{R}}_p\left({\varphi }_j\right)$, where $\mathcal{L}\left({\varphi }_j\right)$ and ${\mathcal{R}}_p\left({\varphi }_j\right)$ are defined by (19) and (20) for each level set function ϕ_j, respectively. The energy functional $\mathcal{F}$ in our multiphase level set formulation is defined by

$$\mathcal{F}(\mathrm{\Phi },b,\mathbf{c})\triangleq \mathcal{E}(\mathrm{\Phi },b,\mathbf{c})+{\mathcal{R}}_p(\mathrm{\Phi }).$$ (25)

The minimization of the energy $\mathcal{F}(\mathrm{\Phi },\mathbf{c},b)$ in (25) with respect to the variable Φ = (ϕ₁,⋯,ϕ_k) can be performed by solving the following gradient flow equations:

$$\begin{gathered} \frac{\partial {\varphi }_1}{\partial t}=-\sum _{i=1}^N\frac{\partial M_i(\varphi )}{\partial {\varphi }_1}{e}_i+\nu \delta \left({\varphi }_1\right)\mathrm{div}\left(\frac{\nabla {\varphi }_1}{\left|\nabla {\varphi }_1\right|}\right) \\ +\mu \text{div}(\left(d_p\left(\left|\nabla {\varphi }_1\right|\right)\nabla {\varphi }_1\right) \\ ⋮ \\ \frac{\partial {\varphi }_k}{\partial t}=-\sum _{i=1}^N\frac{\partial M_i(\varphi )}{\partial {\varphi }_k}{e}_i+\nu \delta \left({\varphi }_k\right)\mathrm{div}\left(\frac{\nabla {\varphi }_k}{\left|\nabla {\varphi }_k\right|}\right) \\ +\mu \mathrm{div}\left(d_p\left(\left|\nabla {\varphi }_k\right|\right)\nabla {\varphi }_k\right). \end{gathered}$$ (26)

The minimization of the energy $\mathcal{E}(\mathrm{\Phi },\mathbf{c},b)$ can be achieved by the same procedure as in the two-phase case. And it is easy to show that optimal c and b that minimize the energy $\mathcal{E}(\mathrm{\Phi },\mathbf{c},b)$ are given by (23) and (24), with u_i = M_i(Φ) for i = 1,⋯,N.

C. Numerical Implementation

The implementation of our method is straightforward. The level set evolution in (22) and (26) can be implemented by using the same finite difference scheme as for the DRLSE provided in [11]. While we use an easy full domain implementation to implement the proposed level set method in this paper, it is worth pointing out that the narrow band implementation of the DRLSE, provided in [11], can be also used to implement the proposed method, which would greatly reduce the computational cost and make the algorithm significantly faster than the full domain implementation.

In numerical implementation, the Heaviside function H is replaced by a smooth function that approximates H, called the smoothed Heaviside function H_ϵ, which is defined by

$$H_{ϵ}(x)=\frac{1}{2}\left[1+\frac{2}{\pi }\arctan \left(\frac{x}{ϵ}\right)\right]$$ (27)

with ϵ = 1 as in [4], [10]. Accordingly, the dirac delta function δ, which is the derivative of the Heaviside function H, is replaced by the derivative of H_ϵ, which is computed by

$${\delta }_{ϵ}(x)=H_{ϵ}^{\prime }(x)=\frac{1}{\pi }\frac{ϵ}{{ϵ}^2+x^2}.$$ (28)

At each time step, the constant c = (c₁,⋯,c_N) and the bias field b are updated according to (23) and (24), with u_i = M_i(ϕ) defined in Section IV. Notice that the two convolutions b * K and b² * K in (17) for the computation of e_i also appear in the computation of ${\widehat{c}}_i$ in (23) for all i = 1,⋯,N. Another two convolutions (IJ⁽¹⁾) * K and J⁽²⁾ * K are computed in (24) for the bias field $\widehat{b}$. Thus, there are a total of four convolutions to be computed at each time step during the evolution of ϕ. The convolution kernel K is constructed as a w × w mask, with w being the smallest odd number such that w ≥ 4 * σ + 1, when K is defined as the Gaussian kernel in (11). For example, given a scale parameter σ = 4, the mask size is 17 × 17.

The choice of the parameters in our model is easy. Some of them, such as the parameters μ and the time step Δt, can be fixed as μ = 1.0 and Δt = 0.1. Our model is not sensitive to the choice of the parameters. The parameter v is usually set to 0.001 × 255² as a default value for most of digital images with intensity range in [0, 255], The parameter σ and the size of the neighborhood ${\mathcal{O}}_{\mathbf{y}}$ (specified by its radius ⍴) should be relatively smaller for images with more localized intensity inhomogeneities as we have mentioned in Section III-C.

V. Experimental Results

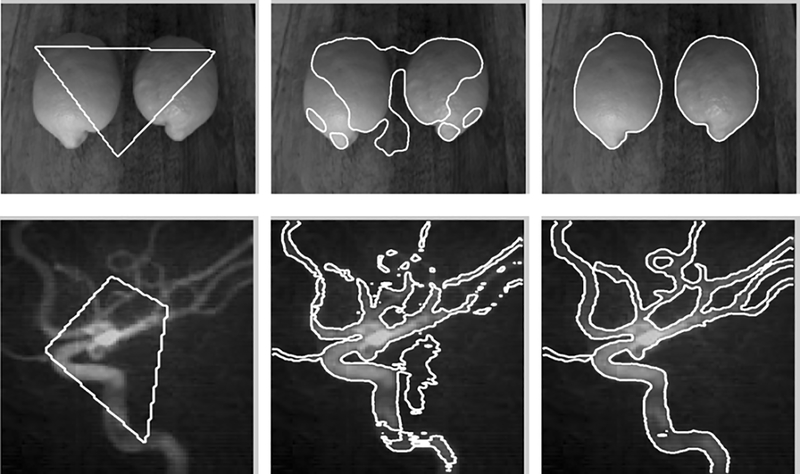
We first demonstrate our method in the two-phase case (i.e. N = 2). Unless otherwise specified, the parameter σ is set to 4 for the experiments in this section. All the other parameters are set to the default values mentioned in section IV-C. Fig. 1 shows the results for a camera image of limon and a computed tomography angiography (CTA) image of blood vessel. The curve evolution processes are depicted by showing the initial contours (in the left column), intermediate contours (in the middle column), and the final contours (in the right column) on the images. Intensity inhomogeneities can be clearly seen in these two images. Our method is able to provide a desirable segmentation result for such images.

Fig. 1.

Segmentation for an image of limon (upper row) and a CT image of vessel (lower row). The left, middle, and right columns show the initial contours (a triangle for the limon image and a quadrangle for the vessel image), the intermediate contours, and the final contours, respectively.

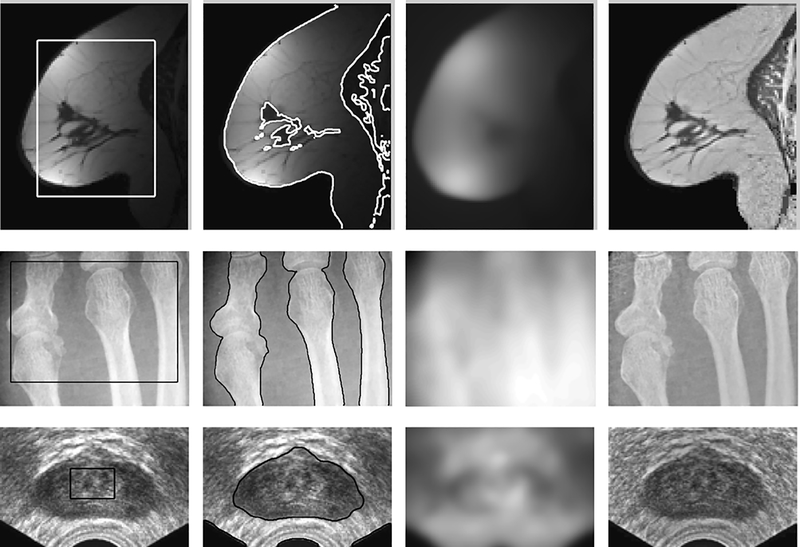
The estimated bias field $\widehat{b}$ by our method can be used for intensity inhomogeneity correction (or bias correction). Given the estimated bias field $\widehat{b}$, the bias corrected image is computed as the quotient $I/\widehat{b}$. To demonstrate the effectiveness of our method in simultaneous segmentation and bias field estimation, we applied it to three medical images with intensity inhomogeneities: an MR image of breast, an X-ray image of bones, and an ultrasound image of prostate. These images exhibit obvious intensity inhomogeneities. The ultrasound image is also corrupted with serious speckle noise. We applied a convolution with a Gaussian kernel to smooth the ultrasound image as a preprocessing step. The scale parameter of the Gaussian kernel is chosen as 2.0 for smoothing this ultrasound image. The initial contours are plotted on the original images in Column 1 of Fig. 2. The corresponding results of segmentation, bias field estimation, and bias correction are shown in Columns 2, 3, and 4, respectively. These results demonstrate desirable performance of our method in segmentation and bias correction.

Fig. 2.

Applications of our method to an MR image of breast, an X-ray image of bones, and an ultrasound image of prostate. Column 1: Initial contour on the original image; Column 2: Final contours; Column 3: Estimated bias field; Column 4: Bias corrected image.

A. Performance Evaluation and Method Comparison

As a level set method, our method provides a contour as the segmentation result. Therefore, we use the following contour-based metric for precise evaluation of the segmentation result. Let C be a contour as a segmentation result, and S be the true object boundary, which is also given as a contour. For each point P_i, i = 1,⋯,N, on the contour C, we can compute the distance from the point P_i to the ground truth contour S, denoted by dist(P_i, S). Then, we define the deviation from the contour C to the ground truth S by

$$e_{\text{mean}}(C)=\frac{1}{N}\sum _{n=1}^N\mathrm{dist}\left(P_i,S\right)$$

which is referred to as the mean error of the contour C. This contour-based metric can be used to evaluate a subpixel accuracy of a segmentation result given by a contour.

1). Robustness to Contour Initialization

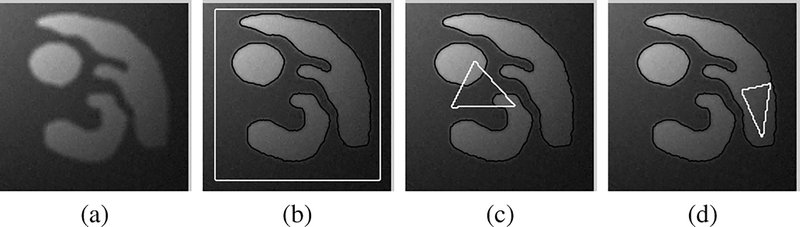
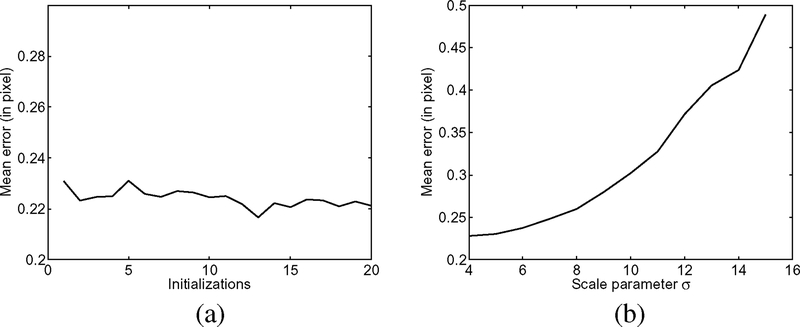
With the above metrics, we are able to quantitatively evaluate the performance of our method with different initializations and different settings of parameters. We applied our method to a synthetic image in Fig. 3 with 20 different initializations of the contour and the constants c = (c₁, c₂). For examples, we show three of the 20 initial contours (white contours) and the corresponding results (black contours) in Fig. 3. In these three different initializations, the initial contour encloses the objects of interest [in Fig. 3(b)], crosses the objects [in Fig. 3(c)], and totally inside of one object [in Fig. 3(d)]. Despite the great difference of these initial contours, the corresponding results are almost the same, all accurately capturing the object boundaries. The segmentation accuracy is quantitatively verified by evaluating these results in terms of mean errors. The mean errors of these results are all between 0.21 and 0.24 pixel, as shown in Fig. 4(a). These experiments demonstrate the robustness of our model to contour initialization and a desirable accuracy at subpixel level.

Fig. 3.

Robustness of our method to contour initializations is demonstrated by its results for an synthetic image in (a) with different initial contours. The initial contours (white contours) and corresponding segmentation results (black contours) are shown in (b–d).

Fig. 4.

Segmentation accuracy of our method for different initializations and different scale parameters σ. (a) Mean errors of the results for 20 different initializations; (b) Mean errors of the results for 12 different scale parameters σ, with σ = 4, 5, … , 15.

2). Stable Performance for Different Scale Parameters

We also tested the performance of our method with different scale parameters σ, which is the most important parameter in our model. For this image, we applied our method with 12 different values of σ from 4 to 15. The corresponding mean errors of these 12 results are plotted in Fig. 4(b). While the mean error increases as σ increases, it is below 0.5 pixel for all the 12 different values of σ used in this experiment.

B. Comparison With Piecewise Smooth Model

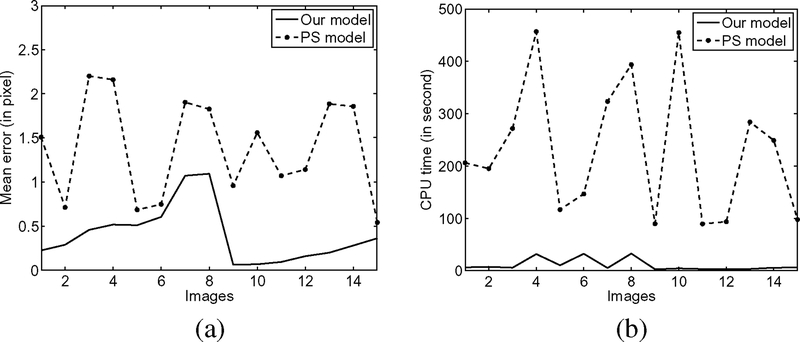
We can also quantitatively compare our method with the PS model on synthetic images. We generated 15 different images with the same objects, whose boundaries are known and used as the ground truth. These 15 images are generated by smoothing an ideal binary image, adding intensity inhomogeneities of different profiles and different levels of noise. Fig. 5 show three of these images as examples, with the corresponding results of our model and the PS model in the middle and bottom rows, respectively. We use the same initial contour (the circles in the top row) for the two models and all the 15 images. It is obvious that our model produces more accurate segmentation results than the PS model. To quantitatively evaluate the accuracy, we compute the mean errors of both models for all the 15 images, which are plotted in Fig. 6(a), where the x-axes represent 15 different images. As shown in Fig. 6(a), the errors of our model are significantly lower than those of the PS model.

Fig. 5.

Performances of our method and the PS model in different image conditions (e.g. different noise, intensity inhomogeneities, and weak object boundaries). Top row: Initial contours plotted on the original image; Middle row: Results of our method; Bottom row: Results of the PS model.

Fig. 6.

Comparison of our model and the PS model in terms of accuracy and CPU time. (a) Mean errors. (b) CPU times.

On the other hand, our model is much more efficient than the PS model. This can be seen from the CPU times consumed by the two models for the 15 images [see Fig. 6(b)]. In this experiment, our model is remarkably faster than the PS model, with an average speed-up factor 36.43 in our implementation. The CPU times in this experiment were recorded in running our Matlab programs on a Lenovo ThinkPad notebook with Intel (R) Core (TM)2 Duo CPU, 2.40 GHz, 2 GB RAM, with Matlab 7.4 on Windows Vista.

C. Application to MR Image Segmentation and Bias Correction

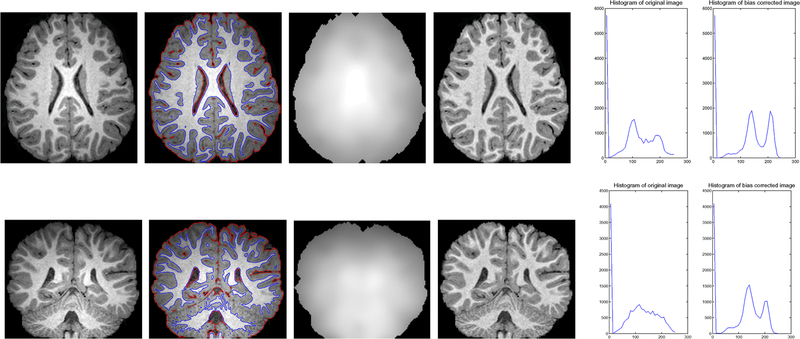
In this subsection, we focus on the application of the proposed method to segmentation and bias correction of brain MR images. We first show the results for 3T MR images in the first column of Fig. 7. These images exhibit obvious intensity inhomogeneities. The segmentation results, computed bias fields, bias corrected images, are shown in the second, third, and fourth column respectively. It can be seen that the intensities within each tissue become quite homogeneous in the bias corrected images. The improvement of the image quality in terms of intensity homogeneity can be also demonstrated by comparing the histograms of the original images and the bias corrected images. The histograms of the original images (left) and the bias corrected images (right) are plotted in the fifth column. There are three well-defined and well-separated peaks in the histograms of the bias corrected image, each corresponding to a tissue or the background in the image. In contrast, the histograms of the original images do not have such well-separated peaks due to the mixture of the intensity distribution caused by the bias.

Fig. 7.

Applications of our method to 3T MR images. Column 1: Original image; Column 2: Final zero level contours of ϕ₁ (red) and ϕ₂ (blue), i.e. the segmentation result; Column 3: Estimated bias fields; Column 4: Bias corrected images; Column 5: Histograms of the original images (left) and bias corrected images (right).

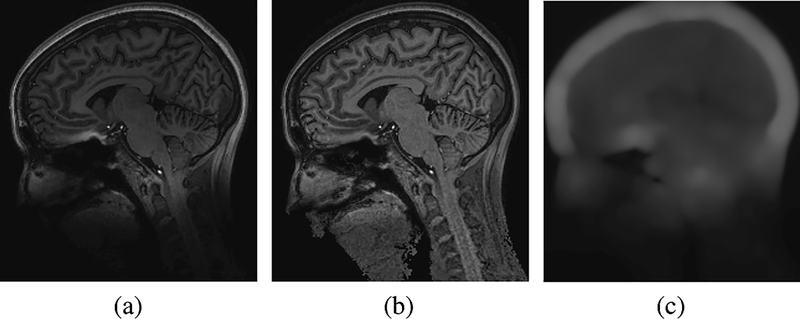
Our method has also been tested on 7T MR images with promising results. At 7T, significant gains in image resolution can be obtained due to the increase in signal-to-noise ratio. However, susceptibility-induced gradients scale with the main field, while the imaging gradients are currently limited to essentially the same strengths as used at lower field strengths (i.e., 3T). Such effects are most pronounced at air/tissue interfaces, as can be seen at the base of the frontal lobe in Fig. 8(a). This appears as a highly localized and strong bias, which is challenging to traditional methods for bias correction. The result for this image shows the ability of our method to correct such bias, as shown in Fig. 8(b) and (c).

Fig. 8.

Application to a 7T MR image. (a) Original image; (b) Bias corrected image; (c) Computed bias field.

VI. Relation With Piecewise Constant and Piecewise Smooth Models

It is worth pointing out that our model in the two-phase level set formulation in (14) is a generalization of the well-known Chan-Vese model [4], which is a representative piecewise constant model. Our proposed enemy $\mathcal{E}$ in (14) reduces to the data fitting term in Chan-Vese model when the bias field b is a constant b = 1. To show this, we need the fact that $\int K(\mathbf{y}-\mathbf{x})d\mathbf{x}=1$ and recall that M₁(ϕ) = H(ϕ) and M₂ (ϕ) = 1−H(ϕ). Thus, for the case of b = 1, by changing the order of summation and integration in (14), the energy $\mathcal{E}$ can be rewritten as

$$\begin{gathered} \mathcal{E}=\sum _{i=1}^2\int \left(\int K(\mathbf{y}-\mathbf{x}){\left|I(\mathbf{x})-c_i\right|}^2{M}_i(\varphi (\mathbf{x}))d\mathbf{y}\right)d\mathbf{x} \\ =\sum _{i=1}^2\int \left({\left|I(\mathbf{x})-c_i\right|}^2{M}_i(\varphi (\mathbf{x}))\int K(\mathbf{y}-\mathbf{x})d\mathbf{y}\right)d\mathbf{x} \\ =\sum _{i=1}^2\int {\left|I(\mathbf{x})-c_i\right|}^2{M}_i(\varphi (\mathbf{x}))d\mathbf{x} \\ =\int {\left|I(\mathbf{x})-c_1\right|}^{2}H(\varphi (\mathbf{x}))d\mathbf{x} \\ +\int {\left|I(\mathbf{x})-c_2\right|}^2(1-H(\varphi (\mathbf{x})))d\mathbf{x} \end{gathered}$$

which is exactly the data fitting term in the Chan-Vese model (2). The Chan-Vese model is a piecewise constant model, which aims to find constants c₁ and c₂ that approximate the image I in the regions Ω₁ = {ϕ > 0} and Ω₂ = {ϕ < 0}, respectively.

Our model is also closely related to the piecewise smooth Mumford-Shah model. The Mumford-Shah model performs image segmentation by seeking N smooth functions u₁,⋯,u_N defined on disjoint regions Ω₁,⋯,Ω_N ⊂ Ω, respectively, through a computationally expensive procedure as briefly described in Section II.

Different from the Mumford-Shah model, our model aims to find the multiplicative components of the image I: a smooth function b and a piecewise constant function J. The obtained b and J yield a piecewise smooth function bJ as an approximation of the image I. From the energy minimization processes in our method and the Mumford-Shah model as described before, it is clear that the former obtains the piecewise smooth approximation, thereby yielding the image segmentation result, in a much more efficient way than the latter.

VII. Conclusion

We have presented a variational level set framework for segmentation and bias correction of images with intensity inhomogeneities. Based on a generally accepted model of images with intensity inhomogeneities and a derived local intensity clustering property, we define an energy of the level set functions that represent a partition of the image domain and a bias field that accounts for the intensity inhomogeneity. Segmentation and bias field estimation are therefore jointly performed by minimizing the proposed energy functional. The slowly varying property of the bias field derived from the proposed energy is naturally ensured by the data term in our variational framework, without the need to impose an explicit smoothing term on the bias field. Our method is much more robust to initialization than the piecewise smooth model. Experimental results have demonstrated superior performance of our method in terms of accuracy, efficiency, and robustness. As an application, our method has been applied to MR image segmentation and bias correction with promising results.

Biography

Chunming Li received the B.S. degree in mathematics from Fujian Normal University, Fujian, China, the M.S. degree in mathematics from Fudan University, Shanghai, China, and the Ph.D. degree in electrical engineering from University of Connecticut, Storrs, CT, in 2005.

He is currently a researcher in medical image analysis at the University of Pennsylvania, Philadelphia. He was a Research Fellow at the Vanderbilt University Institute of Imaging Science, Nashville, TN, from 2005 to 2009. His research interests include image processing, computer vision, and medical imaging, with expertise in image segmentation, MRI bias correction, active contour models, variational and PDE methods, and level set methods. He has served as referee and committee member for a number of international conferences and journals in image processing, computer vision, medical imaging, and applied mathematics.

Rui Huang received the B.S. degree in computer science from Peking University, Beijing, China, in 1999, the M.E. degree in intelligent systems from Chinese Academy of Sciences, Beijing, China, in 2002, and the Ph.D. degree in computer science from Rutgers University, Piscataway, NJ, in 2008.

He has been a Postdoctoral Research Associate at Rutgers since 2008. His research interests are deformable models, graphical models, image and object segmentation, shape analysis, and face recognition.

Zhaohua Ding received the B.E. degree in biomedical engineering from the University of Electronic Science and Technology of China, Sichuan, in 1990, the M.S. degree in computer science and the Ph.D. degree in biomedical engineering, both from The Ohio State University, Columbus, in 1997 and 1999, respectively.

He was a Research Fellow at the Department of Diagnostic Radiology, Yale University, New Haven, CT, from 1999 to 2002. From July 2004, he was an Assistant Professor at the Vanderbilt University Institute of Imaging Science and Department of Radiology and Radiological Sciences. His research focuses on processing and analysis of magnetic resonance images and clinical applications.

J. Chris Gatenby received the B.Sc. degree in Physics from University of Bristol, U.K., and the Ph.D. degree in medical engineering and physics from the University of London, U.K.

He is currently a MR Physicist at Diagnostic Imaging Sciences Center (DISC) and Integrated Brain Imaging Center (IBIC) in the Department of Radiology, University of Washington. He was a Visiting Scientist at the Department of Diagnostic Radiology, Yale University, New Haven, CT, from 1990 to 1994. From 1994 to 1996, he was a Post-Doctoral Fellow at the Department of Radiology, University of California, San Francisco. He was an Associate Research Scientist at the Department of Diagnostic Radiology, Yale University, from 1996 to 2002. He was an Assistant Professor at Vanderbilt University Institute of Imaging Science, from 2002 to 2010.

Dimitris N. Metaxas (M’93) received the Diploma degree in electrical engineering from the National Technical University of Athens, Greece, in 1986, the M.Sc. degree in computer science from the University of Maryland, College Park, in 1988, and the Ph.D. degree in computer science from the University of Toronto, Toronto, ON, Canada, in 1992.

He has been a Professor in the Division of Computer and Information Sciences and a Professor in the Department of Biomedical Engineering, Rutgers University, New Brunswick, NJ, since September 2001. He is directing the Center for Computational Biomedicine, Imaging and Modeling (CBIM). He has been conducting research on deformable model theory with applications to computer vision, graphics, and medical image analysis. He has published more than 200 research articles in these areas and has graduated 22 Ph.D. students.

Dr. Metaxas is on the editorial board of Medical Image Analysis, associate editor of GMOD, and editor in CAD, and he has several best paper awards. He was awarded a Fulbright Fellowship in 1986, is a recipient of a U.S. National Science Foundation Research Initiation and Career award, a U.S. Office of Naval Research YIP, and is a fellow of the American Institute of Medical and Biological Engineers. He is also the program chair of ICCV 2007 and the general chair of MICCAI 2008.

John C. Gore received the Ph.D. degree in physics from the University of London, London, U.K., in 1976.

He is the Director of the Institute of Imaging Science and Chancellors University Professor of Radiology and Radiological Sciences, Biomedical Engineering, Physics, and Molecular Physiology and Biophysics at Vanderbilt University, Nashville, TN. His research interests include the development and application of imaging methods for understanding tissue physiology and structure, molecular imaging, and functional brain imaging.

Dr. Gore is a Member of National Academy of Engineering and an elected Fellow of the American Institute of Medical and Biological Engineering, the International Society for Magnetic Resonance in Medicine (ISMRM), and the Institute of Physics (U.K.). In 2004, he was awarded the Gold Medal from the ISMRM for his contributions to the field of magnetic resonance imaging. He is Editor-in-Chief of the journal Magnetic Resonance Imaging.