Nested case-control data analysis using weighted conditional logistic regression in The Environmental Determinants of Diabetes in the Young (TEDDY) study: A novel approach

Abstract

Background:

A nested case-control (NCC) design within a prospective cohort study can realize substantial benefits for biomarker studies. In this context, it is natural to consider the sample availability in the selection of controls to minimize data loss when implementing the design. However, this violates the randomness required for the selection, and it leads to biased analyses. An inverse probability weighting may improve the analysis, but the current approach using weighted Cox regression fails to maintain the benefits of NCC design.

Methods:

This paper introduces weighted conditional logistic regression. We illustrate our proposed analysis using data recently investigated in TEDDY. Considering the potential data loss, the TEDDY NCC design was moderately selective in its selection of controls. A data-driven simulation study was performed to present the bias correction when a non-random control selection was ignored in the analysis.

Results:

The TEDDY data analysis showed the standard analysis using conditional logistic regression estimated the parameter: −0.015 (−0.023, −0.007). The biased estimate using Cox regression was −0.011 (95% confidence interval: −0.019, −0.003). Weighted Cox regression estimated −0.013 (−0.026, 0.0004). The proposed weighted conditional logistic regression estimated −0.020 (−0.033, −0.007), showing a stronger negative effect size than the one using conditional logistic regression. The simulation study also showed that the standard estimate of β ignoring the non-random control selection tends to be greater than the true β (i.e., positive relative biases).

Conclusion:

Weighted conditional logistic regression can enhance the analysis by offering flexibility in the selection of controls, while maintaining the matching.

1. INTRODUCTION

Prospective cohort studies are utilized to assess how incident events are influenced by the characteristics of interest in participants followed over time. However, the collection of prospective data can require substantial resources, especially when the incidence of events is low. When resources are limited, it may not be feasible to gather the data from the full cohort over the entire follow-up. A nested case-control (NCC) design is the primary choice in a prospective cohort study to avoid such situations without compromising many of the benefits from the full cohort analysis (1,2). In modern epidemiological studies, as it becomes relatively easier to manage multi-center or international prospective cohort studies, the use of an NCC design has increased, especially when expensive biomarker analyses such as high throughput genomics are pursued (3–5).

An NCC design includes all event cases up to a specific follow-up time, but selects only a pre-determined number of controls for each case from the event free subjects at the time when a case developed the event (6). Assuming the selection of controls for each case was at random, conditional logistic regression is the standard statistical analysis. However, when the design is used for biomarker analyses, the selection of controls often depends on the availability of biospecimen samples since no data can be expected without the corresponding sample. This helps improve efficiency by reducing missing data, but it can introduce bias that may not be accounted for in the analysis using standard analytic tools.

In this paper, we propose an alternative selection bias corrected analysis in an NCC design. By adopting the approach by (7) for a matched case-control data analysis, our approach maintains the matching and suggests how to obtain the control selection probability from the full cohort. This approach is illustrated in the application of the plasma 25-hydroxyvitamin D [25(OH)D] concentration analysis presented recently in an NCC study from The Environmental Determinants of Diabetes in the Young (TEDDY) (8). A TEDDY data driven simulation study was conducted to assess the effect of bias correction. The performance of the simulation was described in relation to the effect size and the selection parameter of the factor of interest.

2. BACKGROUND

2.1. Nested case-control design

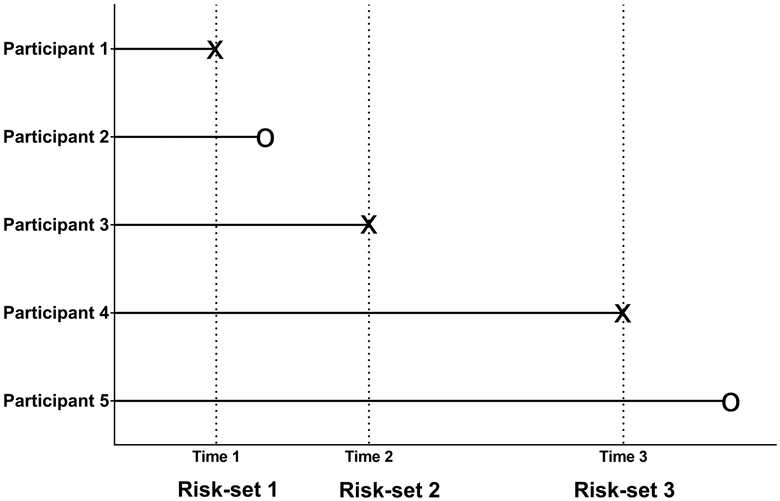
In a prospective cohort study, we observe time of event or censoring for each participant in follow-up, whichever comes first. When time of event is observed, a “risk-set” is constructed, which includes all participants in follow-up at the event time. Figure 1 illustrates a hypothetical prospective cohort study with 5 participants followed; of those, participants 1, 3 and 4 developed the event at time 1, 2 and 3. Hence, three risk-sets are constructed corresponding to each event: risk-set 1 by participant 1 including all 5 participants, risk-set 2 by participant 3 including participants 3, 4 and 5, and risk-set 3 by participant 4 including participants 4 and 5.

Figure 1.

Hypothetical example to show a prospective cohort study with 5 participants followed

An NCC design includes all cases in follow-up but selects controls for a case from those event free participants in the case’s risk-set in a prospective cohort study. In Figure 1, participants 1, 3 and 4 are included as cases, and controls for each case are selected from the case’s risk-set. For example, participants 2 to 5 are potential controls for participant 1 (case 1) in risk-set 1, but participant 5 is the only potential control for participant 4 (case 3) in risk-set 3. In this design, controls are expected to be randomly selected without replacement in a risk-set (i.e., for better efficiency) but with replacement across risk-sets as long as the next risk-sets include them (i.e., for the independence between risk-sets). Hence, a participant can appear more than once in different case-control sets since the participant can appear in different risk-sets by his/her observed time. However, case-control sets are independent of each other, assuming that risk-sets are independent of each other in the full cohort analysis. This implies that the information given for one case-control set is independent of the information given for another case-control set.

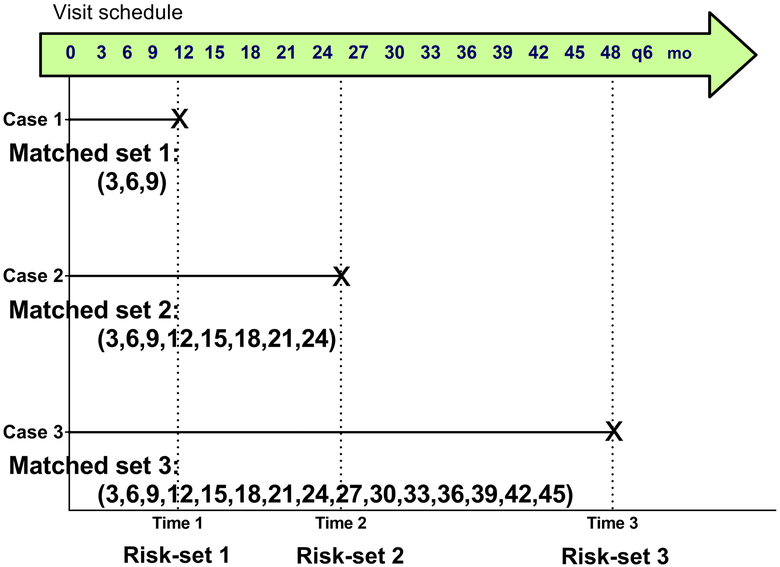
Since controls are selected from the same risk-set as the case, an NCC design is considered a matched case-control design with the risk-set as a matching factor. Therefore, this design can also match on potential confounders at a subject-level. Also, with or without intention, this risk-set matching leads to matching on longitudinal data collected between a case and its matched controls (i.e., a sample-level matching). As shown in Figure 2, through the risk-set matching, the longitudinal data in each matched case-control set is determined, depending on the case’s event time. In the first set, only 3 observations per participant can be compared between the case and its matched controls, while 15 observations can be compared in the third set. If the matching is broken, this sample-level matching will introduce unforeseen bias in the analysis, in addition to that from the subject-level matching.

Figure 2.

Hypothetical example to show possible variability in the number of longitudinal data between matched sets in a nested case-control design

2.2. Nested case-control data analysis

2.2.1. Conditional logistic regression

In a matched case-control data analysis, conditional logistic regression is primarily used to examine the association between the event and characteristics measured by the time of event. The conditional odds can be written as below:

$$\frac{P(Y=1|X,Z,S=1)}{P(Y=0|X,Z,S=1)}= \frac{P(S=1|Y=1,X,Z)}{P(S=1|Y=0,X,Z)} \frac{P(Y=1|X,Z)}{P(Y=0|X,Z)}$$ [1]

Where Y is the indicator of being the case, X is the vector of characteristics of interest, Z is the vector of matching factors and S is the indicator of being included in the matched case-control design. The assumption that the selection is at random implies that the selection does not depend on X, which is the characteristics of interest {i.e., P(S = 1|Y,X,Z) = P(S = 1|Y,Z)}. Therefore, equation [1] can be written as

$$logitP\left(Y=1\text{|}S=1,X,Z\right)=logitP\left(Y=1\text{|}X,Z\right)+f\left(Z\right)$$ [2]

where $f\left(Z\right)=\text{log}\{\frac{P\left(S=1\text{|}Y=1,X,Z\right)}{P\left(S=1\text{|}Y=0,X,Z\right)}\}=\text{log}\{\frac{P\left(Y=1\text{|}S=1,Z\right)}{P\left(Y=0\text{|}S=1,Z\right)}\frac{P\left(Y=0\text{|}Z\right)}{P\left(Y=1\text{|}Z\right)}\}=\text{log}\{\frac{P\left(Y=0\text{|}Z\right)}{P\left(Y=1\text{|}Z\right)}\}-\text{log}\left(m\right)$, for 1 to m (the number of controls) matched case-control design. Then, the function f(Z) is canceled out, and the conditional likelihood for standard conditional logistic regression becomes

$$L\left(\beta \right)={\prod }_{i=1}^n\frac{\text{exp}\left\{X_{i0}\left(t\right)\beta \right\}}{{\sum }_{j\in R{s}_i}\text{exp}\left\{X_{ij}\left(t\right)\beta \right\}}$$ [3]

where n is the number of cases, and the set Rs_i includes the case 0 and m controls matched to the case in the i^th matched case-control set, j = 0, 1,2,..m. For an NCC design, X_ij(t) can be defined as the j^th subject’s characteristics of interest by the event time t of the case in the i^th set, since the design is matched by the case’s risk-set. Although the likelihood [3] is the same as the partial likelihood for full cohort analysis, the risk in Rs_i is fixed by the design, as opposed to the one constructed by chance in the full cohort analysis. The regression parameter β corresponds to the log of the odds ratio for a unit change of X_ij(t), as the likelihood is formed by modeling the odds.

2.2.2. Weighted Cox regression

If the matching is broken in an NCC design, the participants included in the design may be considered as a sub-cohort selected from the full cohort. Then, weighted Cox regression can be a choice for selective cohort analysis with the weight being the inverse selection probability for each participant (9–11). The weighted partial likelihood can be written as

$$L\left(\beta \right)={\prod }_{i=1}^n\frac{\text{exp}\left\{X_{i0}\left(t\right)\beta +Z_{i0}\Upsilon \right\}}{{\sum }_{j\in M_i}{W}_j\text{exp}\{X_{ij}\left(t\right)\beta +Z_{ij}\Upsilon \}}$$ [4]

Where W_i is the inverse of the selection probability (p_i) for the i^th subject in the sub-cohort (i.e., $W_i=\frac{1}{p_i}$), M_i is the risk-set including the subjects in an NCC design who were being followed at the case i ‘s event time. Note that this approach assumes the risk in M_i is constructed at random among the subjects included in an NCC design. Here, the regression parameter β may correspond to the log of the hazard ratio for a unit change of X_ij(t), after adjusting for the matching factors.

This approach has been used to analyze secondary events observed other than the primary for cases in the design (12,13). This approach can be viewed as a selection bias corrected analysis but breaks the matched design. When the study design implements the matching at a sample level, breaking the matching introduces the variability that cannot be properly controlled in the analysis. Also, it may reduce the efficiency. For example, in Figures 1 and 2, if participant 5 was a control for participant 1, the pair could have processed three samples at 3, 6 and 9 months in the same batch by the sample level matching. In this weighted Cox regression analysis, participant 5 can be also in risk-set 2 and 3, but this participant’s information is incomplete for those risk-set analyses since those three samples would have been only analyzed by the NCC design.

3. WEIGHTED CONDITIONAL LOGISTIC REGRESSION FOR NESTED CASE-CONTROL ANALYSIS

In equation [1], the assumption that the selection in the design is random leads to the standard conditional likelihood for inference in equation [3]. In an NCC design, all cases are included, so the assumption remains true for cases {i.e., P(S = 1|Y = 1,X,Z) = 1}. However, the assumption for the selection of controls {i.e., P(S = 1|Y = 0,X,Z) = P(S = 1|Y = 0,Z)} may not be true. When, P(S = 1|Y = 0,X,Z) ≠ P(S = 1|Y = 0,Z) instead of equation [2], the log odds for an NCC design becomes as follows:

$$logitP\left(Y=1\text{|}S=1,X,Z\right)=logitP\left(Y=1\text{|}X,Z\right)-\text{log}\{P(S=1|Y=0,X,Z)\}$$ [5]

Then, by denoting W_ij as the inverse of the selection probability {i.e., $\frac{1}{P(S=1|Y=0,X,Z)}$} for the j^th subject in the i^th set, the standard conditional likelihood [3] becomes

$$L\left(\beta \right)={\prod }_{i=1}^n\frac{\text{exp}\left\{X_{i0}\left(t\right)\beta \right\}}{{\sum }_{j\in R{s}_i}{W}_{ij}\text{exp}\left\{X_{ij}\left(t\right)\beta \right\}}$$ [6]

which is the conditional likelihood for weighted conditional logistic regression. Note that the set Rs_i stays the same as [3] by keeping the matching in the design.

Since the full cohort from which the NCC design participants are selected is available, the full cohort data can be used to estimate the selection probability P(S = 1|Y = 0,X,Z) for those selected controls. We fit a logistic regression model on the factor of interest X and the matching factors Z for the estimation of the selection probability. If we have complete data on X and Z, the probability estimator is expected to be unbiased. However, X is most likely unavailable in the full cohort since an NCC design is utilized to avoid having to collect that in the full cohort. Also, as a part of Z, the risk-set matching for an NCC design needs to be translated to an individual level in the full cohort. Instead of X and the risk-set matching, we use proxy variables that can explain the selection in an NCC design. Our motivation to consider P(S = 1|Y = 0,X,Z) ≠ P(S = 1|Y = 0,Z) is when controls’ sample availability is incorporated in the selection of controls for biomarker studies. Moreover, the size of risk-set, which can directly affect the probability of control selection, is mostly determined by the duration of follow-up. Thus, we propose to use those factors related to the study compliance or duration of follow-up as the proxy variables.

This inverse selection probability weighting approach is also useful when the characteristics for event free subjects using the data from an NCC design are of interest. When matching factors other than risk-set were used in an NCC design, the characteristics in selected controls become similar to their cases, rather than those in event free participants in the cohort. Hence, the controls included in an NCC design cannot be directly used to make inference on event free population about the characteristics collected in an NCC design. In this context, this selection bias corrected approach can also help make the inference.

4. APPLICATION: TEDDY nested case-control design

TEDDY is a prospective cohort study across six participating clinical centers: the Pacific Northwest Diabetes Research Institute, Seattle, Washington; the Barbara Davis Center, Denver, Colorado; a combined Georgia/Florida site at the Medical College of Georgia, Augusta, Georgia and the University of Florida, Gainesville, Florida; University of Turku, (Turku, Oulu and Tampere, Finland); Lund University, Malmö, Sweden; and the Diabetes Research Institute, Munich, Germany (14,15). TEDDY enrolled 8,676 children before 4.5 months of age through newborn screening for high risk HLA-DR-DQ genotypes and will follow them up until 15 years of age to identify genetic and environmental triggers of type 1 diabetes (T1D). The protocol was approved by Institutional Review Boards at participating centers, and all participants provided written informed consent before participation in the study.

In order to perform analyses across various biomarkers, TEDDY set up two NCC designs: one for islet autoimmunity (IA, the pre-diabetic endpoint) and the other for T1D. At close of the cohort for the NCC design (i.e., sampling time), the median follow-up age was 40 months (first quartile=25 and the third quartile=60). Additional matching factors were having a first-degree relative with T1D (T1D family history), sex, and clinical center located in the region where the participant was enrolled. TEDDY selected controls based on their sample availability in the six potential controls randomly selected from each risk-set (16). This was not completely a selective selection, but the bias could still affect the analysis. For example, if three controls were randomly selected, through 100 bootstrap samples, the odds ratio for a factor can be expected to be 1.89 with 95% confidence interval (1.87, 1.91). But if the factor was analyzed in the 1 to 3 TEDDY NCC design (8), the odds ratio estimate is 1.96.

TEDDY recently investigated whether plasma 25(OH)D concentration (nmol/L) throughout childhood is associated with development of IA in the 1 to 3 TEDDY NCC design (8). The childhood 25(OH)D concentration was defined as the average of 25(OH)D measured up to each case’s event time. The authors analyzed 376 matched sets including 1,041 controls with at least one measure of 25(OH)D prior to each case’s event time, using standard conditional logistic regression. There was a total of 1,375 participants: 376 participants developed IA and 999 participants who were IA-free at sampling time. We used this data to illustrate our proposed selection bias corrected analysis.

4.1. Selection probability estimation

Since cases are also potential controls until they develop the event of interest, the population for event free subjects (i.e., Y=0) includes cases by their event time, as well as event free subjects by their censored time at the time of design. A logistic regression model was used to estimate the selection probability for being included as a control in the NCC design for IA. We considered the factors related to retention in TEDDY as proxy variables. Previously, TEDDY identified such factors as country where the participant was enrolled, sex, illness experienced during the first year, maternal age, father’s study participation, maternal lifestyle behaviors, and accuracy of the mother’s risk perception (17,18). Therefore, the logistic regression model considered the matching factors (T1D family history, child’s sex, and clinical center), the observed age (age of IA for IA cases and age of censoring at sampling for IA-free children), and those pre-identified factors related to dropouts in TEDDY. The final model included the factors with P < 0.1 (shown in Table 1). As expected, the matching factors were significantly associated with the control selection, along with the observed age showing older children being more often included. Participants with characteristics associated with higher compliance were more likely to be included as controls (positive father’s study participation, older maternal age, and more reported illnesses within the first year). The selection probability was estimated from the final logistic regression model fit.

Table 1.

Estimates of selection model by logistic regression from the TEDDY full cohort

		Odds ratio	95% confidence interval
			Lower	Upper
Observed age (Months)		1.027	1.024	1.030
Clinical center	Colorado	0.780	0.637	0.954
	Georgia	0.597	0.462	0.771
	Washington	0.576	0.457	0.725
	Finland	1.139	0.966	1.344
	Germany	0.928	0.714	1.207
	Sweden	1
Sex	Girls	0.758	0.668	0.861
	Boys	1
T1D family history	Yes	3.320	2.793	3.946
	No	1
Father’s participation	Yes	1.855	1.166	2.952
	No	1
Maternal age (Years)		1.018	1.005	1.031
Number of illness in the first year		1.016	0.999	1.033

4.2. Computation

For the selection bias corrected analyses, the inverse of the selection probability estimate was applied as a weight for the regression parameter estimation. Taking into account the variability of the selection probability estimation, the jackknife variance was calculated and an approximation of the 95% confidence interval was obtained. Without weighting, the standard likelihood analysis was applied to obtain the regression parameter estimate and 95% confidence interval.

As an illustrative purpose, Cox regression was applied after adjusting for those additional matching factors, in order to examine the association between childhood 25(OH)D concentration and IA. The average of 25(OH)D was analyzed as a time varying covariate by calculating it in each risk-set. Without a weighting, ignoring the NCC design, this produces a biased analysis since those subjects in the NCC design are handled as if they were the full TEDDY cohort. As shown in Table 2, the biased regression parameter estimate was −0.011 (95% confidence interval: −0.019, −0.003). The standard analysis using conditional logistic regression estimated the parameter −0.015 (−0.023, −0.007). Although this is supposed to be the best, it may be also biased due to the moderate selective control selection based on the sample availability in TEDDY. In applying weighted Cox regression adjusted for the matching factors, the parameter estimate became −0.013 (−0.026, 0.0004), with a slightly larger variation. When we applied the proposed weighted conditional likelihood, the estimate was −0.020 (−0.033, −0.007), showing a stronger negative effect size than the one using conditional logistic regression.

Table 2.

Association between childhood 25(OH)D concentration (average by event time, nmol/L) and Islet Autoimmunity (IA) in the TEDDY 25(OH)D analysis

Approach	Selection bias correction	Likelihood	Regression parameter estimate	95% confidence interval
				Lower	Upper
Keeping the matching1	Without	Conditional3	−0.015	−0.023	−0.007
	With	Weighted conditional4	−0.020	−0.033	−0.007
Breaking the matching2	Without	Partial3	−0.011	−0.019	−0.003
	With	Weighted partial4	−0.013	−0.026	0.0004

¹Conditional logistic regression was used. Childhood 25(OH)D concentration was calculated with the measures by the case’s age of IA for each matched set.

²Cox regression adjusted for clinical center, sex and T1D family history was used. Childhood 25(OH)D concentration was calculated at each risk-set to be analyzed as a time dependent covariate.

³Likelihood variance estimation

⁴Jackknife variance estimation

We also summarized the childhood 25(OH)D concentration by the case-control status (Table 3). By the nature of the design, the data for controls are available only up to the time of event of the cases to whom they were matched. If a case was also included as a control for another case, breaking the matching implies that the data as a control from the case are excluded from the analysis. On the other hand, our approach that keeps the matching includes the data as a control from the case, by the assumption that the matched sets are independent of each other by the design. The mean childhood 25(OH)D concentration was 51.33 nmol/L (standard deviation of 16.82) in the cases and 54.63 nmol/L (16.77) in the controls, respectively. When the proposed weighting was applied, the weighted mean in the controls was 55.04 nmol/L (17.21).

Table 3.

The mean 25(OH)D concentration (nmol/L) at the status of IA free in the TEDDY 25(OH)D analysis

		Characteristics of	N	Mean (Standard deviation)
			376	51.33 (16.82)
Cases	Selection bias correction
Controls (Keeping the matching)	Without	Controls	1041	54.63 (16.77)
	With	Event free subjects in the cohort	1041	55.04 (17.21)
Event free subjects (Breaking the matching)	Without	Selective event free subjects at the time of the design	999	54.83 (16.74)
	With	Event free subjects at the time of the design, by the cases’ event time	999	55.11 (17.24)

5. SIMULATIONS

Based on the TEDDY data, a simulation study was conducted to assess the bias when a non-random control selection was ignored in an NCC design. The controls selected were determined by the 1 to 3 TEDDY NCC design. The prevalence model for IA given a covariate X was determined from the logistic regression model fit as logitP(Y = 1|Z^a) = −3.1533 + g(Z^a)

in the TEDDY cohort. When Z^a denotes the matching factors other than the risk-set, g(Z^a) = −0.0365 * Colorado – 0.3430 * Georgia – 0.4431 * Washington + 0.4103 * Finland + 0.0610 * Germany + 1.0339 * FDR – 0.2423 * Girl in the TEDDY design. All variables are indicators; for example, FDR=1 if the child has a T1D family history as defined in TEDDY. We assumed the prevalence model for IA given a covariate X as

$$logitP\left(Y=1\text{|}X,Z^a\right)=\beta 0+g\left(Z^a\right)+\beta *X$$ [7]

Based on the invariance property of the odds ratio, we assumed the covariate model for X as logitP(X = 1|Y,Z^a) = g(Z^a) + β * Y, resulting in:

$$P\left(X=1\text{|}Y,Z^a\right)=1/\left\{1+\text{exp}\left(-g\left(Z^a\right)-\beta *Y\right)\right\}$$ [8]

Assuming the control selection from event free subjects in the cohort also depended on X and Z^a, the selection model can be written as logitP(S = 1|Y = 0,Z^a,X) = r(Z^a) + α * X, where r(Z^a) is a linear function of Z^a and α is the selection parameter for the dependency between S and X. Then, we can assume logitP(X = 1|Y = 0,Z^a,S) = s(Z^a) + α * S, resulting in:

$$logitP\left(X=1\text{|}Y=0,Z^a,S=1\right)-logitP\left(X=1\text{|}Y=0,Z^a,S=0\right)=\alpha$$ [9]

Using [8], we first generated X for the cases (Y = 1), given β (effect size). For event free subjects (Y = 0), using [8] and [9], X was generated for those selected as controls (S = 1) and those not selected in the cohort (S = 0), respectively, given β and α.

Based on the randomly generated X and the given factors Z, we estimated P(S = 1|Y = 0,Z,X) by fitting a logistic regression model and obtained the estimate of β using the standard conditional logistic regression ignoring the non-random selection, as well as the proposed conditional logistic regression weighted by the inverse selection probability. Then, the relative bias was obtained as the difference from the estimate of β by fitting the likelihood [6] in the simulated cohort. Two selection probabilities were considered for Z: (1) the matching factors other than risk-set (i.e., Z^a); and (2) in addition to (1), the proxy variables for the risk-set matching, which are the observed age, father’s study participation, maternal age and illness within the first year. This process was repeated 100 times, and the mean and standard deviation of the relative bias are reported in Table 4.

Table 4.

Simulation results from 100 replications: Relative bias (Empirical standard deviation)

True effect size β	Selection parameter α	Conditional logistic regression
		Without selection bias correction	With selection bias correction
			Selection probability estimation on the matching factors other than risk-set	Selection probability estimation on the matching factors other than risk-set + TEDDY compliance factors including the observed age
−2.0	−1.25	0.972 (0.065)	−0.200 (0.054)	−0.174 (0.065)
	−0.75	0.592 (0.069)	−0.360 (0.071)	−0.351 (0.079)
−1.5	−1.25	0.984 (0.061)	−0.075 (0.048)	−0.038 (0.063)
	−0.75	0.596 (0.059)	−0.224 (0.058)	−0.213 (0.067)
−1.0	−1.25	0.995 (0.061)	0.083 (0.055)	0.135 (0.071)
	−0.75	0.602 (0.056)	−0.080 (0.050)	−0.059 (0.062)
−0.02	−1.25	1.012 (0.070)	0.663 (0.150)	0.726 (0.148)
	−0.75	0.608 (0.061)	0.295 (0.074)	0.342 (0.084)

Without the correction, the estimate of β tends to be greater than the true β (i.e., positive relative biases). A stronger selection parameter showed greater bias when the non-random selection was ignored. With the correction, bias was reduced but still remained. We suspect that this is because the simulated biases were generated without reflecting the risk-set matching when the controls selected were based on that. The bias reduction varied depending on the combination of effect size and selective parameter, but it was generally improved when the proxy variables for the risk-set matching were considered in the selection probability estimation.

6. DISCUSSION

NCC studies are particularly advantageous for longitudinal biomarker studies as they can reduce the high cost and labor associated with collecting complete data in prospective cohort studies. The choice of this design for biomarker studies is growing, not only because it requires a small selection of non-cases, but also because the design can be used with greater flexibility to match on longitudinal variables such as the sample availability/compliance. As the NCC studies become more popular and more flexibly designed, the importance of how well the choice of statistical tool fully respects the way the study is constructed will be vital to produce valid findings from the study.

A key aspect of an NCC design is the selection of a control to pair with a case at a specific time based on the case’s event. The control is selected among the event free subjects at the specific time unique to each case (i.e., the risk-set matching). The chance of the selection must be independent of when the subjects drop out of the study or later become a case themselves in the full cohort (i.e., between risk-set independence). In practice, often a desire is to avoid selecting any controls that become eventually cases in the closed cohort at the time of the design. However, this modifies the risk-sets and violates the between risk-set independence. Then, the design becomes neither an NCC design nor a case-control design, and no standard statistical methods for either design will produce valid analyses. If the implementation of an NCC design maintained the between risk-set independence, the choice of analytical tool should be one of those methods conditioning on the matching. When the matching is ignored (i.e., broken), no statistical modeling will be sufficient to remove the bias given the complexity of longitudinal matching nested within the subject level of matching. For this reason, breaking the matching should be the last choice in the NCC data analysis.

In this paper, we considered when controls were selectively chosen within a risk-set, in order to avoid selecting controls without necessary data for the implementation of an NCC design. We proposed an inverse probability weighting within the matching strata and analyzed the NCC data with weighted conditional logistic regression. Although weighted Cox regression has been available for non-random NCC design, this technique requires the matching to be broken and considers those included in the design as a sub-cohort. This application fails to support the choice of an NCC design to begin with. In order to estimate the selection probability of controls, we used a logistic regression model with the factors related to dropout and compliance.

We illustrated our approach using the TEDDY data analysis. However, the TEDDY NCC design was not completely selective since six potential controls were randomly selected first, from which three were selected based on availability of samples. Therefore, the difference we presented between with and without weighting in the conditional logistic regression analysis may not be greater than that if the design was completely selective. In our simulation study, we kept the status of TEDDY case-control and considered two types of selection probability estimation with and without proxy variables for the risk-set matching. We showed the bias in the analysis without weighting and the bias reduction in weighted conditional logistic regression with both types of weighting. The weighting that considered those factors for the risk-set matching performed better in general but still failed to remove the bias completely. It is likely because the simulated biases did not reflect the risk-set matching when the TEDDY control status was used. Nevertheless, performance may be improved with better estimates of the selection in a future study.