Routing of hippocampal ripples to subcortical structures via the lateral septum

Summary

The mnemonic functions of hippocampal sharp wave ripples (SPW-Rs) have been studied extensively. Because hippocampal outputs affect not only cortical but also subcortical targets, we examined the impact of SPW-Rs on the firing patterns of lateral septal (LS) neurons in behaving rats. A large fraction of SPW-Rs were temporally locked to high frequency oscillations (HFOs; 120–180 Hz) in LS, with strongest coupling during NREM sleep, followed by waking immobility. However, coherence and spike-LFP coupling between the two structures were low, suggesting that HFOs are generated locally within the LS GABAergic population. This hypothesis was supported by optogenetic induction of HFOs in LS. Spiking of LS neurons was largely independent from the sequential order of spiking in SPW-Rs but, instead, correlated with the magnitude of excitatory synchrony of the hippocampal output. Thus, LS is strongly activated by SPW-Rs and may convey hippocampal population events to its hypothalamic and brainstem targets.

eTOC blurb

Tingley and Buzsaki 2019 describe that hippocampal sharp wave ripple-related bursts are routed to subcortical structures through the lateral septum.

Introduction

Current theories on the function of hippocampal sharp-wave ripples (SPW-Rs) relate mainly to the consolidation of recent experiences and planning of future actions (Buzsáki, 2015; Foster, 2017; Jadhav et al., 2009; Papale et al., 2016; Pfeiffer, 2018). Specifically, sequential firing patterns within SPW-Rs are thought to ‘replay’ recently experienced episodes and planning of routes (Diba and Buzsáki, 2007; Gupta et al., 2010; Karlsson and Frank, 2009; Pfeiffer and Foster, 2015; Skaggs and McNaughton, 1996). Both of these ideas tacitly assume that the main function of the SPW-R is to convey content-specific hippocampal messages to the neocortex (Ji and Wilson, 2016; Ólafsdóttir et al., 2016; Peyrache et al., 2009; Rothschild et al., 2017; Sirota et al., 2003a; Wang and Ikemoto, 2016) or subcortical structures (Dragoi et al., 1999; Girardeau et al., 2017; Gomperts et al., 2015; Lansink et al., 2009; Pennartz et al., 2004; Sjulson et al., 2018), although many of these patterns may reflect pre-existing dynamics of balanced networks (Buzsáki, 2019; Dragoi and Tonegawa, 2011; Grosmark and Buzsáki, 2016; Stella et al., 2019). While it is clear that hippocampal SPW-Rs co-occur with brain-wide fluctuations in activity (Logothetis et al., 2012), most of these regions do not have strong monosynaptic connections with the hippocampal formation. We reasoned that such coupling relationships likely emerge through multi-synaptic brain circuits and sought to examine which brain regions may serve as a conduit, receiving direct hippocampal inputs, thus allowing for SPW-R propagation out of the hippocampus.

A major target of the hippocampal system is the lateral septum (LS), where the density of hippocampal afferents is ~20-fold higher when compared to entorhinal regions or ~180-fold higher when compared to prefrontal targets (Tingley and Buzsáki, 2018). This makes the LS the recipient of massive convergent excitation from the hippocampal-subicular-entorhinal population. This major anatomical connection may convey hippocampal activity to its hypothalamic, mesencephalic and brainstem projections (Leroy et al., 2018; Swanson and Cowan, 1979). In light of these anatomical connections, we set out to examine the hippocampal-LS circuit by simultaneously recording activity patterns of the hippocampus and LS in the behaving rat.

Results

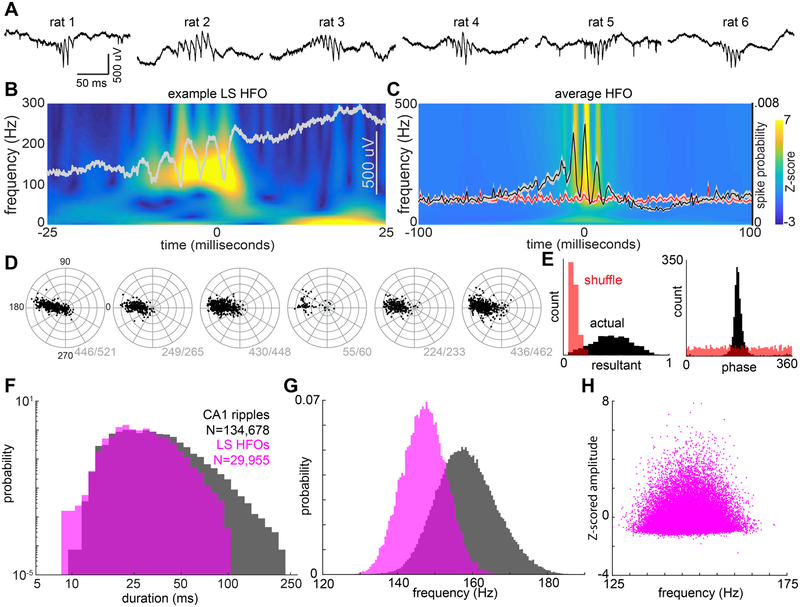
Using silicon probes, we simultaneously recorded neurons in the hippocampus (CA1 and CA3) and LS while animals slept and performed behavioral tasks. Behavioral paradigms consisted of traversing one of three different linear track mazes. Further details of the surgical procedures and behavioral experiments have been published (Tingley and Buzsáki, 2018). During initial recordings in LS (N = 6 rats), we observed transient high frequency oscillations (HFOs) in the 120–180 Hz frequency range in each animal (Figure 1A, B) and an associated robust increase in the firing probability of LS neurons (Figure 1C). On average, 16% of LS neurons participated in any given event, firing an average of 0.23 spikes per event (Figure S1A, B). Across entire recordings, the vast majority of LS neurons (1840 of 1989; 92%) were significantly phase-locked to the 120–200 Hz frequency band, with a strong unimodal phase preference for the trough of each cycle (Figure 1D, E). These events were significantly shorter in duration (27±9 vs 31±14 milliseconds) and slower in frequency (147±5.7 vs 159±8 Hz) than CA1 ripples recorded from the same animals (Figure 1F, G; rank-sum test; P < 0.01). However, they showed no significant correlation between event amplitude and peak frequency (Figure 1H).

Figure 1. HFO events in LS are synchronized population bursts.

(A) Example LS high frequency oscillations (HFOs). Each raw trace is an example event from one animal (20 kHz). (B) Example power spectrum (wavelet transform) for a single LS HFO event (grey overlay is the raw trace). (C) Average power spectrum across all events (N = 6 animals, 29,955 events). Overlay: LS HFO event triggered LS spike probability, normalized by number of events (black trace; N = 1,989 neurons). Red line is the average spiking probability for an equivalent number of randomly selected segments for each recording. Bounds are +/− 3 SEM. (D) For each animal (N = 6), each black dot indicates the resultant magnitude and phase angle preference for a single neuron. 1840 of 1989 neurons were significantly (P < 0.05; Rayleigh test) phase-locked to 120–180 Hz oscillations. Radial axis is 0 to 1 (resultant length). Grey values are the number of significantly phase-locked neurons for each animal. (E) Left: Histogram of all resultant magnitudes (black) and shuffled control (red). Right: Histogram of mean phase angles (black) and shuffled control (red) for significantly phase locked neurons (P < 0.05). (F) Histograms of CA1 ripple durations (black) and LS HFO durations (magenta). (G) Histograms of CA1 ripple peak frequencies (black) and LS HFO peak frequencies (magenta) (H) Scatter plot of LS HFO peak frequency (X-axis) and amplitude (Y-axis).

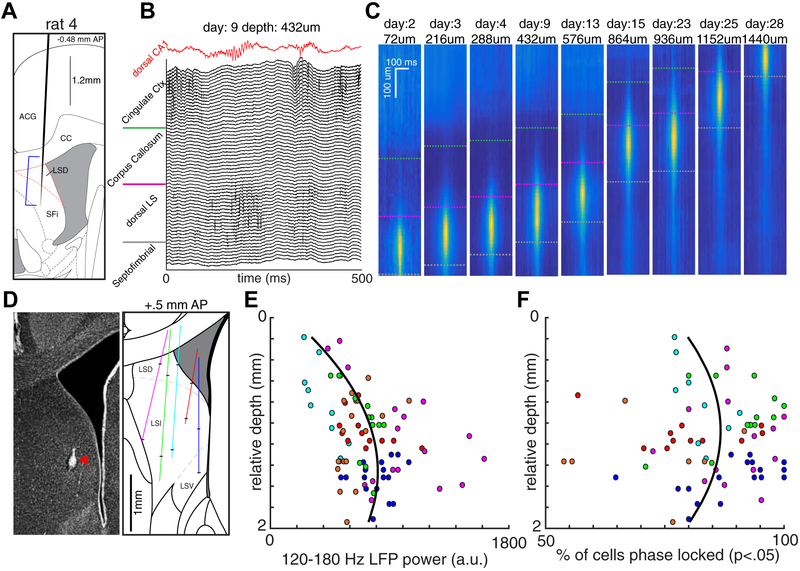
We only observed HFO events at recording sites that were confined to the LS (Figure 2A–C). Across recordings in each animal, we adjusted the electrode sites to record from progressively deeper regions within LS (Figure 2D). Both the power of HFOs and the proportion of phase-locked neurons were highest in the intermediate LS and tapered off as recordings approached either the dorsal or ventral border of LS (Figure 2E, F; Figure S1C, D). We also observed consistent temporal lags in LS HFOs between recording sites, suggesting a stereotyped direction of propagation common to all such events (Figure 3A, B). Across four animals where recording sites spanned the anterior-posterior axis, we observed temporal offsets with the posterior recording sites leading more anterior recording sites (Figure 3C). Temporal offsets could also be observed on electrode pairs aligned to the medial-lateral axis and the dorsal-ventral axis (Figure 3C). With these temporal offsets and the known distances between each pair of recording sites, we estimated that the travel speed was 1.01 meters per second in the posterior-to-anterior direction (N = 4 animals), 0.53 meters per second in the medial-to-lateral direction (N = 1 animal), and 2.19 meters per second in the dorsal-to-ventral direction (N = 4 animals). Together, these data suggest that the LS HFO is a travelling wave that propagates along a vector that largely aligns with the hippocampal afferent projections into the LS and efferent projections towards hypothalamic regions (Risold and Swanson, 1997; Swanson and Cowan, 1979; Tingley and Buzsáki, 2018).

Figure 2. Localization of HFOs to lateral septum.

(A) Single-shank silicon probe placement for one animal. Blue bracket indicates the span of 64 recording sites, spaced over 1260 μm for a single day. (B) Raw LFP traces for all 64 channels during a LS HFO event spanning multiple brain regions. Red trace is simultaneously recorded LFP from CA1 pyramidal layer. (C) Heat maps of 120–180 Hz power during LS HFOs across days and recording depths. Green line, border between cingulate cortex and corpus callosum; pink and grey interrupted lines, span of recording sites in LS. (D) Left: Representative histological localization of recording site from animal (red trace in summary). Taken from (Tingley and Buzsáki, 2018). Right: Diagram of recording tracks from 5 animals. Black tick marks denote the approximate first and last recording for each animal. (E) Average 120–180 Hz power of LS HFO events for each animal and recording depth. (F) The proportion of neurons significantly phase-locked (P < 0.05; Rayleigh test) to 120–180 Hz oscillations for each animal and recording depth. Colors for each dot match the respective tracts in panel D. Black lines are the best polynomial fit (order = 2).

Figure 3. LS HFOs are travelling waves.

(A) Top: Sagittal view of lateral septum, and silicon probe layout spanning AP and DV axes. Bottom: Coronal view of the lateral septum, and silicon probe layout spanning ML and DV axes. (B) Example average LS HFO across 5 shanks oriented along the AP axis (N=337 events, 200 μm spacing). Red line follows the trough across temporal delays. (C) For each pair of recording electrodes aligned to one axis (AP, ML, or DV; 20–800 μm apart), the temporal lag between troughs was calculated (Y-axis) and compared with the physical distance between electrodes (X-axis). Left: LS HFOs are travelling waves in the posterior-to-anterior direction. Middle: LS HFOs are travelling waves in the medial-to-lateral direction. Right: LS HFOs are travelling waves in the dorsal-to-ventral direction.

Next, we examined whether pairs of simultaneously recorded LS neurons (across different shanks) exhibited a pre-existing temporal structure during HFOs, and whether these temporal correlations were modified by waking experience on familiar mazes. Three cross-correlograms for each pair of LS neurons (N= 7,172; 53 sessions) were calculated from spikes occurring during HFOs in the home cage prior to maze traversal (PRE), during maze traversal (BEHAV), and during HFOs after maze traversal (POST; Figure 4A). These cross-correlograms were first examined for changes in co-activation strength using an ‘excess’ correlation method (See STAR Methods (Cheng and Frank, 2008)). We extended the original analysis to examine whether neuron pairs showed fast timescale coactivation that exceeded what would be expected by chance. By randomly jittering each spike by ±200 milliseconds, we found that the excess correlations for HFOs during the PRE and POST epochs were much greater than expected by chance, while excess correlations during the BEHAV epoch were also slightly greater than chance levels (Figure S3A; rank-sum test; P < 0.01). This analysis also revealed that during LS HFOs there is a higher degree of co-activation than observed during behavior or expected given LS firing rates (rank-sum test; P < 0.001 for PRE vs BEHAV and BEHAV vs POST), possibly reflecting joint hippocampal excitation. It also suggested that the degree of co-activation observed is not modulated by waking experience in a familiar environment (Figure 4B; rank-sum test; P = 0.36; PRE vs POST). At the level of single sessions, we did not observe any consistent change in co-activation from the PRE to the POST epochs. Only 7 out of 53 sessions had significantly different excess-correlation values for PRE and POST epochs (rank-sum test; P < 0.01), three where PRE was less than POST and four where PRE was greater than POST.

Figure 4. Temporal structure of HFO spiking is not modulated by highly familiar experiences.

(A) Upper: Example theta phase-position plots for two neurons that were simultaneously recorded. Lower: Cross-correlograms for the two example neurons for HFOs prior to behavior (left; green), during traversal of a linear track (middle; black), and during HFOs after the behavioral session (right; blue). Solid lines are smoothed with a 5-ms Gaussian kernel. Dashed lines are the same CCG smoothed with a 200-ms Gaussian kernel. (B) For all LS cell pairs (Y-axis) the excess correlation is shown for HFOs prior to maze traversal (green), maze traversal (black), and after maze traversal (blue). (C) For all LS recordings, the correlations of temporal biases are shown. X-axis is the correlation between PRE and BEHAV epochs, Y-axis is the correlation between BEHAV and POST epochs. (D) Temporal compression of LS cell pair CCGs during PRE (green) or POST (blue) epochs, relative to BEHAV epoch show correlations that exceed chance but decrease in magnitude with larger compression. Red traces show the average correlations expected when one cross-correlogram is circularly permuted.

We also assessed the temporal ordering of spike pairs during HFOs in relation to the temporal ordering observed during maze traversal (Skaggs and McNaughton, 1996). Across recordings, the spiking structure during HFOs prior to and after maze performance showed correlations with the spike ordering during maze traversal that were similar (Figure 4C; N = 53 recordings; Two-way T-test; P = 0.85). Finally, we examined temporal compression of spiking activity, defined as the correlation between the cross-correlogram from the behavior epoch (±120 milliseconds; Figure 4A; lower middle) and a temporally warped cross-correlogram from HFOs (PRE or POST). These warped cross-correlograms ranged from ±120 milliseconds (compression factor = 1) to ±2.4 milliseconds (compression factor = 50; Figure S3B). We found correlations significantly higher than chance (up to ~20-fold compression; P < 0.01) of cross-correlograms calculated between maze traversal and HFOs that occurred in the PRE and POST sessions (Figure 4D). However, the strength of this compression was similar for HFOs recorded prior to, and after, maze traversal (P > 0.01 for all compression factors). These analyses favor the interpretation that co-activation and temporal structure of LS spike pairs observed during LS HFOs reflect a pre-existing dynamic and not prior experience in highly familiar environments.

Additionally, we observed a systematic increase in firing rates during post-behavior NREM sleep in CA1, as well as CA3 and LS populations (Figure S2A, B; Pavlides and Winson, 1989)). When controlling for this change in overall rate — both by down-sampling to rate match (Giri et al., 2019) or increasing bin size — we did not observe fast timescale reactivation of LS-LS cell pairs that exceeded what would be expected by chance, given the observed changes in firing rate (Figure S2C). We found similar results for HPC and HPC-LS pairs, consistent with prior reports that the magnitude of reactivation decreases as environments become familiar (Giri et al., 2019). Only HPC cell pairs had a significant difference between PRE and POST epochs, when examining the correlation of temporally compressed cross-correlograms (Figure S3D).

While these results may differ from the impact experience has on HPC firing patterns, the alignment of these travelling waves with the innervation pattern of hippocampal fibers, and the fact that the hippocampus provides the main excitatory drive to LS (Risold and Swanson, 1997; Tingley and Buzsáki, 2018), led us to hypothesize that these events may be coupled in some way with hippocampal activity. Across recordings with sleep and behavioral sessions, we primarily observed HFO events during NREM sleep (Figure 5A). While this is similar to the state-dependent occurrence of hippocampal SPW-Rs (Buzsáki et al., 1983), the overall rates of LS HFOs were significantly lower than hippocampal SPW-Rs (Figure 5B). We also examined the finer timescale relationship between hippocampal SPW-Rs and LS HFOs (Figure 5C). While some events were observed to occur independently (Figure 5C; left two examples), many LS HFOs occurred in close temporal proximity to dorsal hippocampal SPW-Rs (Figure 5C; right two examples). Across recordings, we observed a reliable coupling of events across structures (Figure 5D) with a median peak-to-peak temporal lag of 6.4 ± 4.2 milliseconds (CA1 leading LS). Additionally, the strength of coupling between hippocampal SPW-Rs and LS HFOs was dependent upon the brain state of the animals. HPC-LS coupling was significantly stronger during NREM sleep than during the waking immobile state (two-way T-test with Bonferroni correction; P < 0.001; Figure 5D, E). This state-dependent coupling could also be observed when examining the percentage of LS HFO events that occurred within ±25 milliseconds of a CA1 ripple (NREM = 0.3; WAKE = 0.15; P < 6.6e-6 two-way T-test; Figure 5E inset) and in the SPW-R triggered LS firing rates (two-way T-test with Bonferroni correction; P < 0.001; Figure 5F).

Figure 5. State dependence and hippocampal coupling of LS HFOs.

(A) LS HFO occur more often during NREM sleep. Top: Raster of LS HFO occurrences (magenta lines). Middle: CA1 Power spectrum across ~7.5 hour recording and the associated state scoring. Bottom: Scored state for the duration of the recording. (B) LS HFOs occur primarily during slow-wave sleep. For each recording, the rate of LS HFOs (magenta; N = 89 recordings) during wake (dashed) and NREM (solid) are shown. Same for CA1 ripples in black (N = 53 recordings). (C) Four example events from simultaneous CA1 and LS recordings. Top: Raw traces for LS (magenta) and CA1 (black). Bottom: 120–180 Hz Z-scored power for LS and CA1 channels. (D) Cross-correlogram of CA1 ripples with LS HFO events during wake (top panel) and NREM sleep (bottom panel) for all recordings. (E) Average cross-correlogram between CA1 ripples and LS HFOs (N = 42 recordings). Blue dots indicate bins with significantly different coupling during NREM sleep (two-way T-test; p < 0.001) Inset: Coupling of CA1 ripples and LS HFOs (within ±25 ms) is significantly higher during NREM sleep. (F) Average cross-correlogram between CA1 ripples and LS neuron firing rates (N = 1,313 neurons). Black trace is for CA1 ripples during NREM sleep, red trace is for CA1 ripples during wake. Inset: Magenta is CA1-LS average 120–180 Hz phase coherence relative to CA1 ripples. Black trace is an equivalent number of randomly jittered time windows. Bounds are ±3 standard deviations.

There are at least two potential underlying mechanisms to explain the presence of HFOs in the lateral septum given the current data. First, LS HFOs may be ‘inherited’ from the hippocampus, such that the ripple oscillation itself is transferred to the LS wave-by-wave. Alternatively, the spiking output from the hippocampus, during SPW-Rs, provides the necessary level of excitatory drive for the induction of a locally generated oscillation in LS. Three observations argue in favor of local origin of LS HFOs. First, LS HFOs were significantly shorter than hippocampal SPW-Rs (Figure 1F) and were accompanied by a suppression of firing immediately following the population burst (Figures 1C, 5F). A direct inheritance of the hippocampal SPW-R would predict similar duration and firing patterns. Second, LS spiking activity was not phase-locked to individual waves of hippocampal SPW-Rs and phase coherence between HFOs and SPW-Rs was not significantly different from a shuffled distribution (Figure 5F inset). Third, optogenetic activation of the LS GABAergic population induced HFOs, reminiscent of the spontaneous events (Figure 6). Using a GABAergic specific promoter, we expressed ChR2 in a majority of the LS population (Figure 6A, B; (Dimidschstein et al., 2016)). Using a Gaussian waveform of blue light (450 nm), mimicking the envelope of SPW-R-induced hippocampal excitation, local oscillations of ~140 Hz could be reliably induced (Figure 6C–E; S2).

Figure 6. Optogenetic production of LS HFOs.

(A) Experimental paradigm for optogenetic experiments (B) Histological verification of recording site (left) and virus expression (right). (C) Black trace is one example LS response to a 100 millisecond Gaussian light pulse (blue trace). (D) Heat map is the average wavelet transform across identical stimulations (rows are Z-scored). Color axis is −1 to 4. (E) Top: Average power spectral densities during stimulation show significant increases in ~140 Hz power for both animals. Red trace is a no-stimulation control, where an equal number of time windows were selected one second after each stimulation. Bounds are ±1 standard deviation. Bottom: Black traces are P-values for two-way T-tests conducted at each frequency band between the stimulation and no-stimulation power spectra. Red trace is P < 0.01

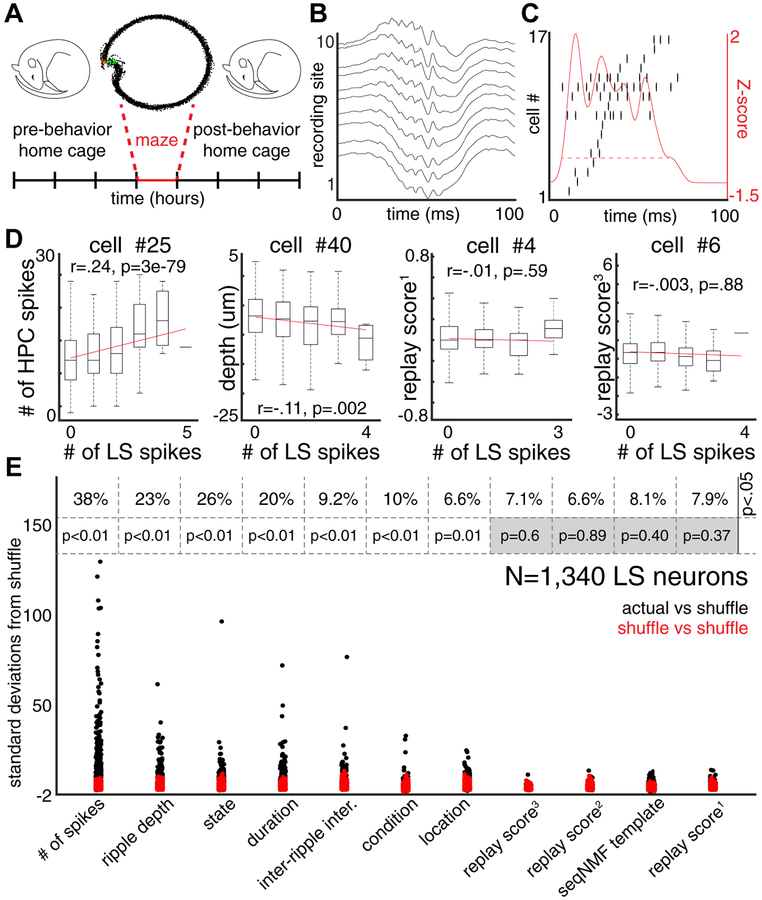
These findings suggest that LS populations can integrate hippocampal SPW-R activity and transmit shorter duration but highly synchronized population bursts to its hypothalamic and brainstem targets. Therefore, we examined which features of the hippocampal SPW-R best predicted responses of LS neurons. The experimental paradigm and data collected (Figure 7A–C) allowed for the extraction of several candidate features for every hippocampal SPW-R (Figure 7D). The first feature we examined was the number of action potentials elicited by the hippocampal population during SPW-Rs. For many LS neurons (38%), this measure significantly predicted the number of action potentials elicited in the postsynaptic LS neuron (Figure 7D, E). The next feature we examined was the average anatomical depth of neurons participating in a SPW-R, within the CA1 cell body layer (i.e. deep to superficial). For a set of LS neurons (23%), the recording depth of the active CA1 population correlated significantly with the number of action potentials elicited (Figure 7D, E). The brain state of the animal (Wake/NREM) within which the SPW-R occurred was yet another factor. As expected from the data presented in Figure 5, the rate of spiking for some LS neurons (26%) was significantly predicted by brain state (Figure 7E). The duration of hippocampal events could also be used to significantly predict firing rates for ~20% of the LS neurons (Figure 7E).

Figure 7. LS neuron firing is predicted by the magnitude and anatomical location of HPC SPW-Rs, but not ripple ‘content’.

(A) Example diagram of experimental paradigm for all recordings. (B) LFP traces of a single HPC SPW-R. (C) Spiking activity from 17 CA1 neurons during the ripple shown in C and their summed (Z-scored) firing. (D) Four example LS neurons showing the relationship between LS firing (X-axis) and number of CA1 spikes, recording depth, and replay scores, respectively (Y-axes). Examples were selected from neurons within ± 5% of the mean for each distribution. (E) Ripple features examined to predict LS neuron firing (X-axis). Y-axis is the number of standard deviations that the mean squared error (MSE) was from a distribution of MSE values calculated from shuffled data for the same neuron. For every feature, each neuron is shown twice, as a black dot (actual data vs shuffled distribution) and as a red dot (one shuffled iteration vs shuffled distribution). The percentage of neurons surpassing P < 0.05 (two-way T-test) are shown above for each ripple feature.

Neuronal sequences that occur during active experience are thought to be ‘replayed’ during hippocampal SPW-Rs (Skaggs and McNaughton, 1996). We, therefore, asked whether LS neurons can specifically ‘read out’ this precise temporally organized spiking. As different analytical approaches emphasize different aspects of neural data (Tingley and Peyrache, 2019), we used three common replay quantification methods that have been previously developed: 1) the rank-order correlation between spiking order during each ripple with the firing rate maps from maze traversal ((Diba and Buzsáki, 2007; Foster and Wilson, 2006); replay score 1). 2) the maximized integral under the line of best fit (i.e. the discrete approximation of the Radon transform; (Toft, 1996)), of the posterior probability matrix calculated with a Bayesian approach ((Davidson et al., 2009); replay score 2), and 3) the normalized linear weighted correlation of the posterior probability matrix calculated with a Bayesian approach ((Grosmark and Buzsáki, 2016); replay score 3). The firing rates of only a minority of LS neurons—7.9, 6.6, and 7.1% respectively—could be significantly predicted by the sequential structure of hippocampal events captured by these methods (Figure 7D, E).

As the proportion of hippocampal SPW-Rs that can be decoded as ‘replay’ events is small in the hippocampus (5–20%; (Davidson et al., 2009; Dragoi and Tonegawa, 2011; Foster and Wilson, 2006; Grosmark and Buzsáki, 2016; Karlsson and Frank, 2009; Michon et al., 2019; Wu and Foster, 2014), we reasoned that perhaps some navigation-independent sequential structure in other hippocampal SPW-Rs, not detectable from overt behavioral correlates, may drive LS neuron firing. To examine this possibility, we took an unsupervised variance decomposition approach (Mackevicius et al., 2019). This method allowed us to extract sequential activity patterns from hippocampal SPW-Rs without relying on a pre-existing template. Across recordings, we were able to capture >95% of the variance in hippocampal SPW-R spiking activity with 40 ‘template sequences’ (Figure S5). We could then ask whether any of these identified templates correlated with firing of LS neurons. As with the ‘replay’ scores, we found that the percentage of LS neurons whose action potential firing could be significantly predicted with these templates was small (Figure 7E; 8.1%; P < 0.05).

Given these analyses, we had two distributions for each ripple feature (i.e., duration, number of spikes, replay scores, etc.; Figure 7E), the comparisons of actual data with a shuffled distribution (black points) and the comparison of a shuffled iteration with a shuffled distribution (red points). We then asked, for each ripple feature, whether these two distributions were significantly different (rank-sum test). The P-values for each of these statistical tests demonstrated that all spike content-independent ripple features were significantly different from chance (left seven columns), while all spike content-based ripple features were not significantly different from chance (Figure 7E; right four columns; bottom row).

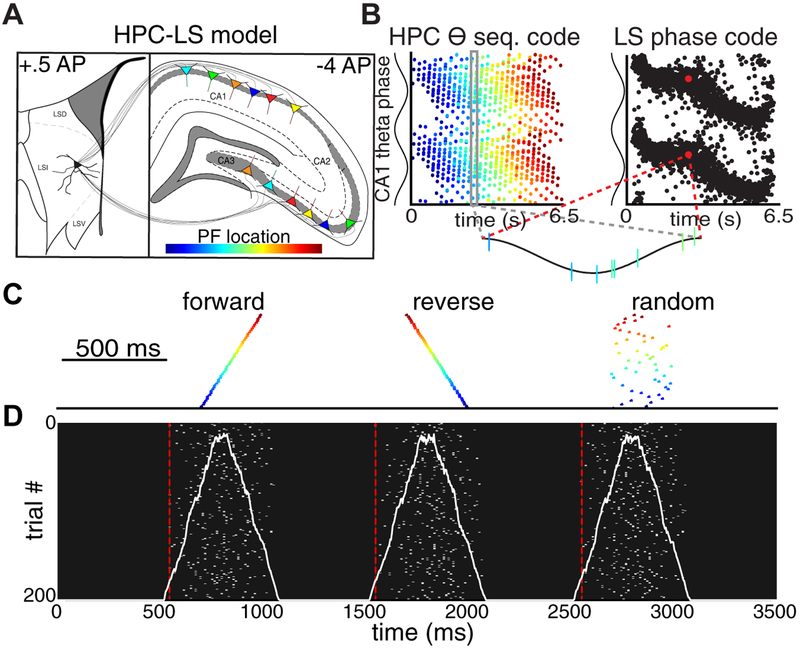
Thus, responses of LS neurons to hippocampal drive is related most strongly to the magnitude of synchronized excitation (i.e., the number of spikes within a SPW-R), rather than the precise temporal organization within particular SPW-R events. This analysis yielded qualitatively similar results for all ripple features when only ‘coupled’ events—SPW-Rs and HFOs co-occurring within ±50ms of each other—were examined. To further examine this phenomenon, we utilized a model of the hippocampus-LS circuit that replicates previously described in vivo rate-independent phase encoding of spatial position ((Tingley and Buzsáki, 2018); Figure 8A). During simulated ‘maze traversals’ this model reads out hippocampal theta sequences and converts them into a pure spike-phase, rather than spike-rate, code for position (Figure 8B). By providing the model with temporally compressed forward, reverse, or scrambled replay events (Figure 8C), we observed that the response of the postsynaptic model LS neuron was nearly identical for all three event types (Figure 8D). Thus, during periods of high excitatory drive, information about the sequential ordering of hippocampal neurons is lost and the LS neurons’ firing rate best corresponds to the magnitude of the depolarization brought about by the simulated hippocampal population output.

Figure 8. Temporal compression disrupts sequence reading in model HPC-LS circuit.

(A) Biophysical model of CA1/CA3 place field populations that provide convergent input to a LS neuron. Colors indicate the location of place fields along a simulated track. (B) The HPC-LS circuit transforms a population theta sequence code into a rate-independent phase code. Model and figure are adapted from (Tingley and Buzsáki, 2018). (C) Forward, reverse, and scrambled ‘replay’ sequences were created in the presynaptic CA1/CA3 populations and the output LS neuron was examined. (D) Across trials with different jittered noise (Y-axis), the firing dynamics of the postsynaptic LS neuron (X-axis) were indistinguishable for different compressed spiking sequences

Discussion

We demonstrated the presence of a locally generated high frequency oscillation in the LS. Many, but not all, LS HFOs co-occurred with dorsal hippocampal SPW-Rs with the highest probability of coupling occurring during NREM sleep. This appears to be an inverse relationship of what is observed between hippocampus and prefrontal cortex (Tang et al., 2017), suggesting there may be a state-dependent routing of SPW-Rs to cortical or subcortical structures, affecting prefrontal circuits more effectively during waking, whereas exerting a stronger impact on LS neurons during NREM sleep. It remains to be explored whether the ‘uncoupled’ events were in fact coupled with unmeasured intermediate or ventral hippocampal or subicular SPW-Rs, or some other unidentified brain region. The HFOs were localized exclusively to LS recording sites. Recordings more dorsal, in deep layers of anterior cingulate cortex, showed down state-coupled activity approximately 50 milliseconds after the CA1 SPW-R as has been previously observed (Sirota et al., 2003b). Recordings in medial septum, did not have such HFOs and showed primarily a suppression in firing rates (Dragoi et al., 1999). We also found that LS HFOs are traveling waves whose directionality closely matches the anatomical inputs coming from the hippocampus and its own outputs to hypothalamic and brainstem nuclei.

High frequency oscillations in LS

Previous work has found that a population of LS neurons encode spatial trajectories of the animal in their theta cycle spike timing, but not their spike rates (Tingley and Buzsáki, 2018). In the current analyses, spiking of LS neurons during HFO events reflected a pre-existing co-activation and temporal organization across cell pairs that was not significantly altered by exposure to a familiar environment. Yet, it remains to be seen whether experience in novel environments is capable of altering this rate-independent phase code or the degree of synchrony and ordering of LS populations during HFOs. It is possible that the position-dependent synaptic weight matrix—necessary for our HPC-LS circuit model which replicates these phenomena— is learned. The localization of HFOs within the LS, and the increased rate of events during NREM sleep suggest LS HFOs have a different physiological mechanism than fast oscillatory activity which has been observed in other subcortical structures during REM and waking (Haufler and Pare, 2014) and LS gamma-band activity during food motivated locomotion (Carus-Cadavieco et al., 2017).

LS HFOs did appear to have a different mechanism of generation than hippocampal or neocortical ripple oscillations. Our optogenetic experiments and the lack of phase coherence between structures suggest that a depolarizing envelope is all that is required for the local production of HFOs, while the ripple component of the SPW-R does not appear to be necessary for HFO production. Thus, the high degree of convergence in this circuit, and the high level of synchronous spiking output during SPW-Rs may provide the necessary level of excitation to locally induce these HFOs, without transferring the hippocampal ripple oscillation in a wave-by-wave manner. In response to this depolarizing drive, locally connected GABAergic LS neurons are forced to synchronize, a mechanism that has been modelled extensively (Brunel and Hakim, 1999; Brunel and Wang, 2003; Geisler et al., 2005). This high degree of synchronization across neurons also suggests that the main source of each HFO cycle observed in the LFP is the highly overlapping action potentials of neurons that surround the recording electrode (Schomburg et al., 2012).

Hippocampal assembly sequences are not transmitted to LS

Sequential activity during hippocampal SPW-Rs is hypothesized to be critical for consolidating past experiences and for planning or imagining future actions (Buzsáki, 2015; Carr et al., 2011; Diba and Buzsáki, 2007; Foster, 2017; Papale et al., 2016; Pfeiffer, 2018). Within this framework, the neuronal sequences in the hippocampus call up and order neocortical cell assemblies. A requisite prediction of such a model is that postsynaptic neurons receiving unique hippocampal activity patterns must be able to differentiate events based on the temporal organization within these spike sequences. Operating in parallel to this hypothetical corticopetal mechanism, excitatory hippocampal output also massively converges on the neurons of the LS (Swanson and Cowan, 1975; Swanson et al., 1981).

The spiking activity of LS neurons depended mainly on the magnitude of synchrony of hippocampal pyramidal neurons during SPW-Rs, irrespective of their precise temporal organization. This can be contrasted with the theta state, where LS neurons are capable of reading out hippocampal sequences (Tingley and Buzsáki, 2018). These findings and our modeling work here suggest that this difference can be explained by the greatly increased level of excitation that occurs during temporally compressed hippocampal ‘replay’. Thus, whether the same LS circuit can (during theta) or cannot (during SPW-Rs) read out neuronal sequences from its inputs may depend largely on the degree of convergence and the magnitude of neuronal synchrony. In fact, we were unable to find any regime of realistic parameters for the model CA1/CA3-LS circuit where phase precession was preserved during the ‘theta state’, and the LS reader was also capable of differentiating temporally compressed sequences. However, these simulations are limited and did not fully explore the potential impact of short-term facilitation or depression, neuromodulatory state, post-synaptic circuit computation, or other phenomena capable of modifying network function. Our data does not imply the absence of temporally organized neuronal activity in LS, only that the neuronal patterns we examined during hippocampal SPW-Rs do not correspond to learning related hippocampal sequences during maze behavior.

Routing of hippocampal output to subcortical targets

A long series of past works have examined the various potential roles of LS in effecting behavior. Following LS lesion, Brady and Nauta (1953) originally described changes in ‘general emotional reactivity’ ((Brady and Nauta, 1953) see also (Spiegel et al., 1940)). Subsequently different authors have attributed specific roles of the LS in anxiety (Chee and Menard, 2013; Parfitt et al., 2017), arousal (Li et al., 2015), aggression (Wong et al., 2016), contextual memory (Besnard et al., 2019; Jarrard, 1993; Leutgeb and Mizumori, 2002; Vouimba et al., 1998), food intake (Azevedo et al., 2019; Scopinho et al., 2008; Sweeney and Yang, 2015, 2016; Terrill et al., 2016), spatial memory (Jaffard et al., 1996; Simon et al., 1986), sexual behavior (Tsukahara et al., 2014), sexually dimorphic social play (Veenema et al., 2013), social preference (Shin et al., 2018), social memory (Leroy et al., 2018; Lukas et al., 2013), reward and addiction (Cornish et al., 2012; Heath, 1963; Luo et al., 2011; McGlinchey and Aston-Jones, 2018; Le Merrer et al., 2007; Olds and Milner, 1954; Sartor and Aston-Jones, 2012; Zahm et al., 2010), gastric motility (Gong et al., 2013), and endocrine responses to stress (Anthony et al., 2014; Usher et al., 1974; Yadin and Thomas, 1996). It remains to be seen whether multiple descending circuits operate in parallel, each with a unique behavioral function, or whether the behavioral phenotypes observed with LS manipulation are aspects of a single corticofugal computation. We speculate that several of the above phenotypes point towards a single deficit, of contextually appropriate action-selection. For example, context-dependent goal directed behaviors, whether food exploration, aggression, or drug-seeking activities, may link the context-defining neuronal patterns in the dorsal hippocampus to subcortical structures via LS (Luo et al., 2011).

While our findings cannot unify this heterogeneity of behavioral effects, they do demonstrate that this anatomical route—from HPC, through LS to other subcortical targets, such as the hypothalamus, mesencephalon and ventral tegmental area—is highly active during SPW-Rs and appears to filter which aspects of its inputs are transmitted. In turn, this subcortical funneling of hippocampal output, active primarily during consummatory behaviors and NREM sleep, can drive activity in regions that are known to modulate the metabolic and motivational state of animals through the endocrine (Del Rey et al., 2008) and peripheral nervous systems (Shimazu, 1987). A potential implication of our observations is that depending on the physiological mechanism of a particular behavior (e.g., anxiety or drug-seeking activity), drugs administered during theta (mostly waking) or SPW-R states (mostly nonREM sleep) might induce opposite or differential effects. The significance of SPW-R-induced physiological effects and their behavioral consequences remain to be explored.

STAR METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and datasets should be directed to and will be fulfilled by György Buzsáki (gyorgy.buzsaki@nyumc.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

The experiments were performed on the same Long-Evans rats 3 males and 2 females) which were described in Tingley and Buzsaki (2018). A detailed description of behavioral training, surgical procedures and histological results are available there. Each recording consisted of three periods of time recorded continuously; 1) pre-behavior home cage, 2) maze traversal, and 3) post-behavior home cage. One additional animal included here, was implanted with a tetrode microdrive (rat 1) and included in the phase locking analysis. The dataset used for Figure 6 consists of 62 recordings with both CA1 and LS simultaneously recorded (N = 37) or CA3 and LS simultaneously recorded (N = 25). For CA3 recordings, a reference electrode placed in CA1 was used to detect SPW-Rs. No significant differences were observed when using CA1 or CA3 populations and these recordings were therefore merged. Ripple depth was not analyzed for CA3 populations. Two additional rats were used for the optogenetic experiments (see optogenetic experiments section for details).

METHOD DETAILS

Recording/Data processing

Recordings were conducted using the Intan RHD2000 interface board, sampled at 20 kHz. Amplification and digitization were done on the head stage. Waveform extraction and initial clustering was conducted using SpikeDetekt and Klustakwik. Example parameters for these algorithms can be found in the GitHub repository (https://github.com/DavidTingley/papers). Briefly, the 20 kHz raw signal was bandpass filtered (600 Hz - 9.5 kHz) with a 3^rd order Butterworth filter. Threshold crossings greater than 5 standard deviations above the mean, of this signal, were extracted for waveform classification (1.6 millisecond windows around the crossing). Principle components analysis (PCA) was then used to compress the data, and the first 5 principle components were used for semi-automated clustering. A mixture of Gaussians clustering method was used initially, then manual waveform discrimination was conducted using the Klustaviewa software suite. Waveform amplitude was utilized during this stage to assess unit stability. Any waveforms that changed significantly throughout the duration of the recording were discarded. Waveform isolation quality was quantified using the isolation distance metric (https://github.com/buzsakilab/buzcode) and the waveform amplitude.

For one animal, position within the environment was tracked with two head mounted LED’s (1 blue, 1 red) and an overhead camera (Basler, 30 Hz). For the other four animals, position was tracked with the OptiTrack camera system. IR reflective markers were mounted in unique positions on each animals’ head stage and imaged simultaneously by six cameras (Flex 3) placed above the behavioral apparatus. Calibration across cameras allowed for the three-dimensional reconstruction of the animals’ head position, and head orientation, to within 1 mm (avg. displacement error = .70 mm ± 1.5 mm) at 120 Hz.

Position data was analyzed and segmented using a custom Matlab software suite. Only ballistic trials, without stopping or deviation from the trained trajectory, were extracted for further analysis. These trials made up ~90–95% of all trials attempted for any given recording.

Optogenetic experiments

Two rats were injected with AAV-DLX-ChR2-mCherry, one in the right lateral septum and the other bilaterally. Two injections at 4.2mm and 4.6mm DV of 250uL each were conducted. After four weeks, 200-μm optic fibers and 50-μm tungsten recording wires were implanted in each injected region. Square pulses and Gaussian waveforms were generated with a PulsePal device (Sanworks; v2) and transmitted to a laser diode driver (Thorlabs; LDC205C). Coupling efficiency was estimated using a photometer (Thorlabs; PM100D) and all power measurements provided are the mW/mm² at the fiber tip prior to implantation.

Significance testing for power spectral density changes induced by optogenetic stimulation were conducted as the following. One second windows of the raw LFP (1.25kHz) were taken around every stimulation, and an equal number of one second windows were taken one second after each stimulation (i.e. when stimulation was not occurring, but the animal was in a similar brain state). For each window the log-scaled power spectral density was calculated for frequencies ranging from 1 to 200 Hz. For each frequency band (1–200 Hz), statistical testing (two-way t-test) was conducted on the distribution of power values where stimulation actually occurred, compared with the distribution of power values taken from windows without stimulation.

Histology

Animals were anesthetized and electrolytic marker lesions were made (4 μA for 4 seconds). While still under anesthesia, they were injected with a lethal dose of Euthasol (Virbac AH, Inc.) and were perfused with 200mL of 4% paraformaldehyde 15 minutes after injection. Brains were removed and post-fixed in 10% paraformaldehyde overnight. Brains were then sliced in 80 μm slices using a vibratome (Leica VT1000S). A DAPI stain was used to localize probe and fiber tracks (Flouroshield with DAPI; Sigma).

QUANTIFICATION AND STATISTICAL ANALYSIS

Ripple detection

A modified version of a previously reported detection algorithm was used for both hippocampus and LS HFO detection (Csicsvari et al., 1999). Input parameters for the algorithm are stored in each of the MATLAB data structures storing ripple events. The code is available at https://github.com/buzsakilab/buzcode (bz_FindRipples.m). Ripples were detected by filtering (120–200Hz; Butterworth; order = 3) the raw LFP (1.25 kHz) and calculating the normalized squared signal (NSS). The NSS was then used to identify peaks above a threshold merging neighboring events and discarding events with excessive duration. Thresholds are computed as multiples of the standard deviation of the NSS. The peak power threshold was set to five standard deviations and the beginning/end cutoff was set to two standard deviations above the mean NSS. The duration limits were set to 15 and 250 milliseconds. An additional ‘noise’ channel was provided to the algorithm that was not anatomically near CA1 (and did not have ripples in the LFP signal). This channel was used to exclude EMG related artifact that had power in the 120–200 Hz range. High power 120–200 Hz events occurring on this ‘noise’ channel were used to identify and exclude simultaneously occurring 120–200 Hz high power events on the ‘ripple’ channel. The same 5 standard deviation threshold was applied to the NSS of this channel for detecting events. If such noise events occurred within the start/stop times for an event detected on the ripple channel, it was excluded as noise. For recordings without a ‘non-ripple’ channel, the estimated EMG was used for this exclusion criteria (Schomburg et al., 2014). The same detection algorithm was used for both LS and HPC.

Start and stop times for each ripple were considered the first timestamp where the 120–200 Hz power dropped below 2 standard deviations prior to, and following, the ripple peak (max power value > 5 standard deviations). Ripple duration was calculated as the difference between stop and start times. The instantaneous frequency for each ripple was calculated by 1) applying the Hilbert transform to the bandpass filtered (120–200 Hz) LFP, 2) unwrapping these phase angles and median filtering (± 6 bins), and 3) taking the difference between samples nearest the peak power bin of the ripple and dividing by two pi. The ripple amplitude was taken as the maximum NSS value between start/stop times for each ripple.

For visualizing the power spectrum of LS HFOs, CA1 ripples, and LS optogenetically induced responses (Figures 1B, 6D and S4B), the Morlet wavelet transform was used for the frequency range from 1 to 300 Hz using linearly spaced 1 Hz bins. To capture fast timescale power fluctuations, the number of cycles was set to 5 for CA1 ripples, and 3 for LS HFOs (Cohen, 2019).

Phase locking analysis

Epochs of time where the 120–200 Hz power (4^th order Butterworth bandpass filter; 7 millisecond RMS smoothing) was continuously above two standard deviations from the mean were identified. The phase angles for each timestamp where an action potential occurred within these epochs was calculated using the real component of the Hilbert transform. For each neuron, a histogram of phase angles was calculated for all action potentials that occurred within these LFP power thresholded epochs. While no threshold was set on the brain state (NREM vs Wake), the vast majority of identified epochs occurred during NREM sleep (Figure 3B). The circular mean and resultant vector were then calculated using these histograms for each neuron (Berens, 2009). For a null distribution, LFP phase angles were circularly shifted by a random offset and the phase angle histograms were then recalculated (10 iterations). As low spike counts can introduce inconsistent phase locking estimates (Vinck et al., 2010), only neurons recorded in LS with greater than 50 spikes occurring during high power epochs were included in this analysis.

The percentage of phase-locked cells was calculated for every recording session (N = 8–74 neurons; mean = 29.6 ± 15.5). Each dot in Figure 2F represents a single recording session, where the Y-axis is the estimated relative depth of recordings sites, and the X-axis is the percentage of neurons that were significantly phase locked within that recording.

State scoring

A previously described semi-automated sleep scoring algorithm was used (Watson et al., 2016). It calculates a spectrogram from the raw LFP (1.25kHz) using a 10-second window FFT, sliding at 1-second intervals, at logarithmically spaced frequencies from 1 to 100 Hz. Briefly, this algorithm then uses a set of heuristics when examining the EMG, theta band ratio (4–9 Hz divided by 2–16 Hz), and broadband LFP. The estimated EMG is the summed pairwise zero-lag correlation between non-neighboring electrodes (separate shanks; >200um distance) using the bandpass filtered (300–600 Hz; 3^rd order Butterworth) local field potential (Schomburg et al., 2014). The theta band ratio is the 4–9 Hz power from the spectrogram, dividing by the 2–16 Hz power. The broadband LFP spectrogram was then compressed using principal components analysis (PC1 always corresponding to <20Hz power).

The algorithm then uses these data in a sequence of separations, finding troughs that maximally split peaks in each distribution. In all recordings, manual inspection of scoring was conducted. In some cases, manual curation of algorithm parameters or specific segments of recordings was conducted in order to best identify brain state. Development of an improved state scoring algorithm provides similar results, often with less manual curation (Levenstein et al., 2019).

Relative anatomical depth within CA1

The spatial localization of the CA1 pyramidal cell layer was estimated by aligning two metrics. The first was the estimated center of the CA1 pyramidal cell layer, using the ripple-band power measured across different recording sites of a silicon probe that spanned the entire layer (Mizuseki et al., 2011). This estimation uses the 120–200 Hz power profile, during CA1 SPW-Rs, across all electrodes on a given silicon shank that fully spans the CA1 pyramidal cell layer. As the ripple-band power decreases at more superficial or deeper electrode positions, a peak in 120–200 Hz power can be found that corresponds the center of the layer (Ylinen et al., 1995).

The second metric used the action potential waveform for each neuron across the three recording electrodes with the largest action potential waveform amplitude. These amplitudes were interpolated across (actual spacing 20 μm; interpolated to 5 μm spacing using cubic spline) and used to estimate the approximate somatic position of the neuron, relative to the recording sites (this assumes the action potential amplitude is largest at the soma). The relative depth for each neuron was then taken as the spatial offset between the estimated somatic position of the neuron and the estimated center of the CA1 pyramidal cell layer.

Relative anatomical depth within LS

The spatial localization of LS neurons was estimated using several parameters. First, the implantation depth of each silicon probe was recorded during surgery. Second, every time the silicon probe was moved (ventral movements of 0 to 288 μm per day) the turn depth was recorded. Third, histological verification of the silicon probe location at the end of each experiment (using marker lesions; Figure 2D) was examined. These data were then combined to estimate the complete electrode path and relative position on each day. In several instances, anatomical boundaries further improved position estimation (i.e., passing through the lateral ventricle, passing through the corpus callosum, reaching medial septal theta burst neurons). The estimated anatomical depth for each recording was assigned prior to any analysis of LFP power or phase locking.

Spatiotemporal patterns of population activity

The methods for quantifying activity patterns across hippocampal neural populations were taken from a variety of previous works. The ‘ripple-depth’ was quantified as the average anatomical depth (i.e., deep or superficial) for all neurons firing at least one action potential in a given event (See Relative anatomical depth in CA1 section for details).

The inter-ripple interval for each event was defined as the mean of the durations immediately preceding, and following, a given ripple. The ripple ‘condition’ was defined as the experimental epoch (pre-behavior, behavior, or post-behavior) within which the event occurred. The replay scores consisted of 1) the rank-order correlation between spike times during spatial traversal and spike times of a given event (Foster and Wilson, 2006); 2) the ‘replay score’, which is the integral under the line of best fit, using the radon transform of the posterior probability matrix (Davidson et al., 2009); and 3) the ‘sequence score’, a normalized linear weighted correlation of the posterior probability matrix (Grosmark and Buzsáki, 2016).

A recently developed unsupervised method of spatiotemporal quantification of neural populations was also used (Mackevicius et al., 2019). This method allows for the examination of consistently occurring neural sequences without relying on a behavioral ‘template’ to relate too. Thus, if commonly ‘replayed’ spike sequences in HPC populations reliably predicted the firing dynamics of LS neurons, but were not tied to the experimental paradigm we imposed, this method allowed for the identification and analysis of such events.

Reactivation analysis

The reactivation analysis was conducted as in (Kudrimoti et al., 1999; Pennartz et al., 2004). Explained variance (EV) was calculated by comparing pre-behavior NREM ripple epochs with behavioral epochs, while reverse explained variance was calculated by comparing post-behavior NREM ripple epochs with behavioral epochs. Briefly, the EV metric is computed from the cell-pair coherence, r_1,2 for a given set of epochs 1 and 2.

$$r_{1,2}=\frac{1}{N}{\rho }_1^T{\rho }_2$$

Where ρ₁ and ρ₂ are the z-scored vectors of correlation coefficients from all cell pairs during epochs 1 and 2, and N is the total number of cell pairs. Then EV is defined as:

$$EV={\left(\frac{r_{\mathit{\text{BEHA}}V,\mathit{\text{POST}}}-r_{\mathit{\text{BEHA}}V,PRE}{r}_{PRE,\mathit{\text{POST}}}}{\sqrt{\left(1-r^2\mathit{\text{BEHA}}V,PRE\right)\left(1-r^{2}PRE,\mathit{\text{POST}}\right)}}\right)}^2$$

The REV control metric, developed by Pennartz et al., 2004, is calculated by switching the position of PRE and POST in the equation above.

However, as pair-to-pair correlations have been shown to fluctuate with firing rate ((De La Rocha et al., 2007)), this method is susceptible to fluctuations in basal firing rates between conditions ((Pavlides and Winson, 1989); Figure S2 A, B). Thus, we reasoned that altering the bin size for this analysis would allow us to capture only the slow time scale firing rate fluctuations (large bin size), and both the fast timescale reactivation and slow firing rate fluctuations (small bin size). We used bin sizes of 25 milliseconds for fast timescale reactivation, and 1 second to capture slower timescale fluctuations in firing rates. In each set of cell pairs (HPC, HPC-LS, and LS) we still observed an increase in EV, compared to REV, when using 1-second bins. As this is likely due to firing rate differences, we adopted a rate-matching method (Giri et al., 2019) to further examine this. Briefly, the method estimates the firing rates for a neuron in the PRE and POST session, then removes single action potentials randomly until the firing rates are as close as can be achieved. Then, both the EV and REV analyses are conducted on the remaining PRE and POST data.

Excess correlation analysis

As in (Cheng and Frank, 2008), cross-correlograms (CCG) were calculated for neuron pairs (1 millisecond bins; ±200 milliseconds) for each epoch of the recording sessions (PRE, BEHAV, and POST). Only spike pairs where both neurons fired more than 5 spikes within 200 milliseconds of each other were included. Varying this limit up to a threshold of 20 spikes per cell did not qualitatively change any results. Each CCG was convolved separately with two different Gaussian windows (5 milliseconds and 200 milliseconds). This leads to two versions of the CCG, one that captures fast timescale fluctuations and one that captures slower timescale fluctuations. By subtracting the 0-bin between these CCGs, the difference between these vectors indicates whether there is more or less coactivation between cell pairs at faster or slower timescales. This approach was then applied to different epochs of the recording (PRE, BEHAV, POST) to assess whether changes in coactivation are observed. That is, if the degree of fast timescale co-fluctuations in spiking activity increases in a particular epoch, the excess correlation should be higher for that epoch relative to overs. It is important to note that because this method only examines the 0-bin of the CCG, it is susceptible to changes in the shape (i.e. temporal bias or structure) of the CCG.

An additional spike jittering comparison was added to the original analysis to verify that these excess correlations exceed what might be expected by chance (i.e. given the variability in jittered CCGs). Every spike was randomly jittered by ±200 milliseconds (random uniform distribution) and the same analysis described above was applied (Figure 3A).

Temporal bias analysis

This analysis attempted to exactly replicate the analysis of (Skaggs and McNaughton, 1996). Briefly, three CCGs were taken for every cell pair, separating spikes from PRE, BEHAV, and POST epochs. The temporal bias for a given epoch was then calculated as:

$$B_{ij}={\int }_0^{200}{x}_{ij}(t)dt-{\int }_{-200}^0{x}_{ij}(t)dt$$

Then, the temporal bias for each epoch (B_pre, B_behav, and B_post), calculated as the sum of spikes within the 200 milliseconds prior to, after following, the 0-bin, could then be compared. Thus, for every cell pair there are three temporal bias scores that are used to make two comparisons (PRE vs BEHAV and BEHAV vs POST). Only cell pairs recorded across different shanks were analyzed. All included cell pairs from a given recording were then concatenated into temporal bias vectors. If many cell pairs are modulated by an experience, such that the temporal bias during the BEHAV epoch is preserved during the POST epoch, then the B_behav and B_post vectors should be more strongly correlated than B_pre and B_behav These correlations of temporal bias vectors have been interpreted as a summarizing statistic of whether environmental exposure is capable of inducing temporal reorganization of spiking activity during the POST epoch (Skaggs and McNaughton, 1996).

Temporal compression analysis

Pairs of neurons from the same brain region (LS, CA1, or CA3) were taken. Spikes from each neuron, occurring during a particular epoch (PRE, BEHAV, or POST) were cross-correlated (1-millisecond bins). For pairs of these cross-correlograms (PRE vs BEHAV or BEHAV vs POST), a window of ±120 milliseconds around zero-lag was taken and correlated (compression factor = 1; Figure S3B top). This correlation could then be used to measure the degree of similarity between the structure of spiking between two epochs. Incrementally, a smaller time window of the cross-correlogram from HFOs (PRE or POST) was taken (±120 to ±2.4 milliseconds) and interpolated to 241 data points to match the 1 millisecond bins from the BEHAV cross-correlogram. These temporally warped cross-correlations were then correlated with the ±120 millisecond BEHAV cross-correlogram. As with all temporal warping comparisons, we were faced with the issue of either 1) excluding portions of the PRE/POST CCGs or 2) including irrelevant portions of the BEHAV CCG as we examined higher levels of temporal compression. We chose to keep the BEHAV CCG constant (±120 milliseconds) and use progressively smaller portions of the PRE/POST CCGs. As these neurons have been shown to carry a rate-independent phase code, our reasoning behind this selection was that inclusion of larger portions of the BEHAV CCG (beyond a single theta cycle) would not capture additional features of the data.

Spiking model of HPC-LS circuit

The spiking simulations conducted here were derived from code originally developed in (Tingley and Buzsáki, 2018). The model utilizes the python programming language with the pyNN and NEURON simulator packages (Davison et al., 2009; Hines and Carnevale, 1997). The model includes 50 CA1 and 50 CA3 ‘place cells’ (Hodgkin-Huxley equations) that are driven by ramping current injection to fire at particular time points in the simulation (i.e. tiling a simulated space as an animal moves) for a duration of 1000 milliseconds (~30 centimeters at typical running speed). These neurons also receive a second subthreshold continuous input that is an 8 Hz sinusoid to mimic the theta oscillation. The combination of these two inputs causes each simulated neuron to phase precess through its tuning field (Jaramillo et al., 2014). CA3 simulated neurons received a 180-degree phase shifted theta oscillation to match experimental findings (Dragoi et al., 2006). Default parameters for the Hodgkin-Huxley neurons were as follows:

$$\text{cellparams }=\left\{\text{'}\text{gbar\_Na}\text{'}:20.0,\text{'}\text{gbar\_K}\text{'}:6.0,\text{'}\text{g\_leak}\text{'}:0.01,\text{'}\text{cm}\text{'}:0.2,\text{'}\text{v\_offset}\text{'}: -63.0,\text{'}\text{e\_rev\_Na}\text{'}:50.0,\text{'}\text{e\_rev\_K}\text{'}:-90.0,\text{'}\text{e\_rev\_leak}\text{'}: -65.0,\text{'}\text{e\_rev\_E}\text{'}: -6.0,\text{'}\text{e\_rev\_I}\text{'}: -71.0,\text{'}\text{tau\_syn\_E}\text{'}:1.0,\text{'}\text{tau\_syn\_I}\text{'}:2.0,\text{'}\text{i\_offset}\text{'}:0.0\right\}$$

All 100 of these simulated neurons were made to have a single synaptic connection with one LS neuron (Hodgkin-Huxley equations; same parameters as above). Four synaptic weight matrices were examined in detail (Tingley and Buzsáki, 2018). For the current work, the ramping synaptic weight matrix, derived from experimental data, was used.

Only two parameters were changed for the current simulations (Figure 8). The rate-of-change of the simulation was greatly accelerated, and no theta input was provided. Thus, the ramping current injection elicited a single action potential in each CA1 or CA3 neuron. Rather than a ~100 millisecond gap (~3 centimeter at typical running speeds) between the peaks of neighboring ‘place fields’, there was a ~6-millisecond gap between single action potentials for neighboring place cells (i.e. roughly a 16-fold temporal compression). For the first simulation, the order of injected ramps into the CA1 and CA3 populations matches exactly that ‘experienced’ on the simulated maze (i.e. the order of spiking that induce rate-independent phase precession when no temporal compression is applied). For the second simulation, the order of injected ramps into the CA1 and CA3 populations is inverted to occur in exactly the opposite order (i.e. a reverse replay event). For the third simulation, the order of injected ramps into the CA1 and CA3 populations is randomly permuted such that the order is no longer related to the CA1/CA3 place field locations. The entire simulation was run 200 times with small jitter added to each current ramp (±3 milliseconds) to assess reliability. See the Key Resources Table for accessing the code and Binder server on which it can be run.

KEY RESOURCES TABLE

Resource	Source	Identifier/Location	Description
REAGENTS
AAV-DLX-ChR2-mCherry	Addgene	https://www.addaene.ora/browse/article/22659/
DAPI antibody	Sigma-Aldrich	Cat#: D8417 SIGMA
SUBJECTS
Rat: Long-Evans	Charles River	Cat#: Crl:LE 006	2 female, 6 male adults
DATA AND SOFTWARE
Analysis tools	Buzsaki Lab	https://github.com/buzsakilab/buzcode	Analysis tools used throughout the paper
Data visualization scripts	David Tingley	https://github.com/DavidTingley/papers	Example MATLAB scripts that recreate each main figure
Python simulation of HPC-LS circuit	David Tingley	https://mybinder.ors/v2/sh/DavidTinsley/papers/master
HPC/LS recording data	David Tingley	CRCNS (will be uploaded upon publication)
Projection density data	Allen Brain Institute	http://connectivity.brain-map.org/
Klustaviewa	Rossant et al., 2016	https://github.com/klusta-team/klustaviewa
Spikedetekt2	Cortical Processing Laboratory (UCL)	https://github.com/klusta-team/spikedetekt2
Klustakwik2	Kadir et al., 2014	https://github.com/klusta-team/klustakwik/
Position decoder	Meyers E., 2013	http://www.readout.info/
MATLAB	MathWorks	https://www.mathworks.com/
pyNN	Davison et al., 2008	http://neuralensemble.org/PyNN/
Statistical tools	T-test with Bonferroni correction	https://www.mathworks.com/matlabcentral/fileexchange/4114-t-test-with-bonferronicorrection
OTHER
Silicon probe (5×12, 6×10, 8×8, and 4×8)	Neuronexus	https://neuronexus.com/
Silicon probe (1×64)	Cambridge Neurotech	https://www.cambridgeneurotech.com/
Intan RHD2000	Intan technologies	http://intantech.com/RHD2000_evaluation_system.html
Motive tracking system	Optitrack	http://optitrack.com/	6 Flex3 camera system

DATA AND CODE AVAILABILITY

General analysis code is available here (https://github.com/buzsakilab/buzcode), while code specific to figures/analyses in this manuscript are available here (https://github.com/DavidTingley/papers). The dataset will be uploaded to CRCNS (https://crcns.org/).

Highlights.

• Lateral septal neurons can synchronize to produce local high-frequency oscillations

• Lateral septal high-frequency oscillations are coupled to hippocampal ripples

• The magnitude, but not content, of hippocampal ripples are read out by lateral septum